Influence of Die Geometry on Electromagnetic Riveting of Ti-6Al-4V: An Explicit Finite Element Analysis

Abstract

Electromagnetic riveting (EMR) is a high-speed solid-state joining technique with growing relevance in aerospace manufacturing, particularly for titanium alloys such as Ti-6Al-4V. Although the mechanical behavior of EMR joints has been previously studied, the specific influence of die geometry on rivet deformation and joint integrity remains insufficiently understood. In this work, an explicit finite element analysis was conducted using ANSYS Explicit Dynamics to assess the effect of three die geometries (90°, 70°, and 45°) on the mechanical and thermal response of Ti-6Al-4V rivets and plates. The Johnson–Cook constitutive model was employed to capture high strain-rate deformation behavior. Key process metrics, including radial expansion, Von Mises stress, plastic work, and adiabatic temperature rise, were analyzed for each configuration. The results show that sharper die angles (90°) promote greater rivet expansion but also induce higher stress concentrations in the plates, while shallower dies (45°) produce smoother stress distributions with reduced deformation. All configurations demonstrated significant adiabatic temperature rise (approximately 250 °C) in the high-deformation zones. This indicates that thermal softening contributes to the material flow, although the process remains below the phase transformation temperature of Ti-6Al-4V. Overall, the findings highlight that die geometry critically affects stress localization and rivet interlocking, providing guidance for optimizing EMR tooling design to enhance reliability in high-performance aerospace structures.

1. Introduction

Riveting remains one of the most widely used joining methods in the aerospace industry due to its structural reliability, compatibility with composite and metallic materials, and ease of inspection [1]. However, its efficiency can be significantly affected by inadequate geometric design of the rivet or forming tools. Common problems include loss of joint strength, localized stress concentrations, and failure modes such as rivet pullout or fracture of the base material [1,2,3].

Geometric and process factors have a direct influence on joint performance. For example, a non-uniform rivet distribution or poor spacing can induce unbalanced loads and increase the risk of localized failure [1]. Similarly, excessive rivet head protrusion can create high-stress zones in the surrounding material [4].

Particularly relevant in this context is the geometry of the forming die, which determines how the rivet head expands and deforms during the process. Recent studies have shown that small variations in the die angle can significantly alter the quality of the joint: while dies with reduced diameters can promote efficient expansion and better holding power, they can also induce unwanted stress concentrations; on the other hand, more open geometries can reduce localized deformation but compromise interlocking [5,6].

The selection of the rivet material also plays a crucial role. In aerospace applications where lightweight alloys or composites are used, a poor choice can lead to phenomena such as delamination, excessive plastic deformation, or internal fractures in the material layers [7,8,9]. Furthermore, irregular or incomplete finning can result in poor anchorage, making the joint vulnerable under operational load conditions [2,6].

To accurately model these phenomena, several authors have proposed incorporating advanced constitutive laws. In particular, Beecher et al. [10] performed a sensitivity analysis of the Johnson-Cook model for Ti-6Al-4V under aerospace conditions, demonstrating its ability to reproduce plastic responses under severe deformation. Similarly, Tuninetti et al. [11] highlighted that the way in which the material is characterized directly influences the prediction of asymmetric loads in alloys with a hexagonal close-packed structure, such as Ti-6Al-4V, which is especially relevant in dynamic simulations such as electromagnetic riveting (EMR). Recent studies have further reinforced the need for process specific and rate sensitive modeling approaches relevant to high velocity forming operations. Wang et al. [12] demonstrated that coupling a modified Johnson Cook law with a visco plastic self-consistent framework significantly improves finite element predictions of the stress strain response of Ti 6Al 4V under high strain rates, highlighting the importance of accurately representing deformation behavior during rapid loading. Pantale et al. [13] showed that the choice of finite element formulation, including shell, solid, and continuum shell elements, strongly influences predicted thickness evolution and strain distribution in Ti 6Al 4V hot forming simulations. This has important implications for any high deformation analysis where accurate strain and stress gradients are required. Manufacturing route effects also influence mechanical performance. Seo and Park [14] reported that welded and heat treated Ti 6Al 4V exhibits notable variations in hardness and tensile response depending on the post processing method, while Mace et al. [15] documented distinct fretting and fretting corrosion behavior in additively manufactured Ti 6Al 4V arising from differences in surface condition associated with fabrication. Collectively, these findings show that accurate EMR modeling requires not only robust constitutive laws but also careful consideration of material state, fabrication method, and numerical formulation.

Despite significant advances in understanding the mechanical behavior of riveted joints and the increasing adoption of electromagnetic riveting (EMR) in aerospace applications [1,5,6,16], limited research has focused on how die geometry influences the mechanical and thermal evolution of the joint under high-rate forming conditions. Most existing studies have concentrated on optimizing process parameters such as discharge energy, coil configuration, or material response [5,17], while the geometric configuration of the die has often been simplified or assumed constant. Although previous studies [5,6] have highlighted the importance of die angle, a systematic quantitative analysis of its influence on thermo-mechanical coupling responses and stress localization during EMR for Ti-6Al-4V remains lacking. This knowledge gap is particularly relevant for titanium alloys such as Ti-6Al-4V, which exhibit strong strain-rate sensitivity and complex plastic flow behavior under dynamic loading [10,11,18,19,20]. Consequently, there is a need for a systematic numerical assessment that quantifies how variations in die geometry modify the overall mechanical response and thermal stability of EMR joints, thereby providing design-oriented insights for reliable and efficient joining in high-performance aerospace structures.

This study presents a three-dimensional finite element analysis of the electromagnetic riveting (EMR) process for Ti-6Al-4V alloy using ANSYS Explicit Dynamics and the Johnson–Cook constitutive model. The analysis focuses on evaluating the influence of die geometry by comparing three commercial die angles (90°, 70°, and 45°) to determine how geometric variations affect the mechanical evolution of the rivet, stress distribution in the joint, deformation kinematics, and the overall efficiency of the connection. The aim is to establish a scientific basis for selecting suitable die geometries in EMR applications, contributing to the standardization of this advanced joining technique for high-performance aerospace components.

2. Theoretical Mechanics of the EMR Process

The electromagnetic riveting (EMR) process is a high-speed solid-state forming technique governed by the interaction between a transient magnetic field and the induced eddy currents within a conductive driver plate. The physical apparatus consists of a high-energy capacitor bank, a discharge switch, and a working coil that concentrates magnetic flux onto the driver plate (Figure 1). When the capacitor bank discharges, the rapidly varying magnetic field (B) induces eddy currents (J) in the conductive driver plate, generating a repulsive Lorentz force density, $f=J\times B$. This Lorentz-driven impulse accelerates the driver plate downward, and the resulting high-velocity motion is mechanically transmitted through the amplifier to the riveting punch, which then forms the rivet head against the restrictive die. This indirect loading mechanism enables extremely high strain rates without requiring electrical conductivity in the rivet itself.

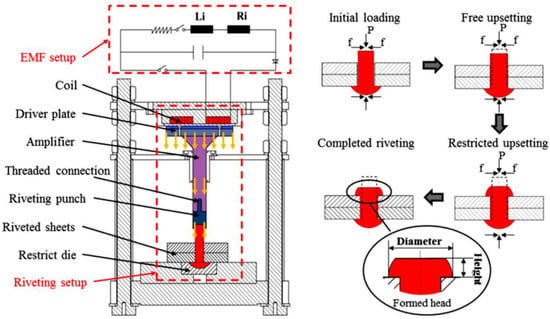
Figure 1. Schematic of the electromagnetic riveting (EMR) system, including the capacitor-driven EMF setup, coil–driver assembly, amplifier, riveting punch, and restricted die, as well as the sequential deformation stages of the rivet head. Reproduced from Qin et al. (2020), Engineering Optimization, 53(5), 770–788 [21]. Taylor & Francis Ltd., Abingdon, UK. Reprinted by permission of the publisher (www.tandfonline.com, accessed on 2 November 2025).

Unlike quasi-static riveting, EMR involves hyper-plastic deformation characterized by strain rates in the order of 10³ s⁻¹ [22]. Under these conditions, the material response is dominated by inertial effects and stress-wave propagation, where the deformation timescale is significantly shorter than the time required for stress equilibrium. Consequently, the rivet head undergoes rapid axial shortening and radial expansion, governed by a constitutive behavior where flow stress is highly sensitive to strain rate.

Thermodynamically, the short duration of the process renders it largely adiabatic, as heat generated during deformation cannot dissipate via conduction. The local temperature rise is driven by three mechanisms: (1) the conversion of plastic work into heat, (2) resistive Joule heating from eddy currents, and (3) frictional heating at the die interface. For titanium alloys like Ti-6Al-4V, the primary thermal driver is plastic work conversion, which is described by the energy conservation relationship in terms temperature increase as ($\Delta T)$ as: $\Delta T={\displaystyle \frac{\beta }{\rho C_p}}\int \sigma d{\epsilon }_p$. The term $C_p$ is the specific heat capacity, $\rho$ the density and $\beta$ is the Taylor-Quinney coefficient (typically 0.9 for Ti-6Al-4V), indicating that 90% of plastic work is converted to thermal energy. This coupled thermo-mechanical response reduces the effective flow stress in the deforming region, facilitating material flow into the die cavity while hardening effects of high strain rates are also present [23].

3. Numerical Method

To numerically analyze the electromagnetic riveting (EMR) process, a three-dimensional model was constructed using the finite element method (FEM). The simulation was performed in ANSYS Workbench, employing the Explicit Dynamics module, specifically designed to address phenomena associated with high strain rates. The model geometry includes two plates of identical thickness, one of which has a countersunk face to facilitate rivet insertion and improve the surface finish in aerodynamic terms by eliminating the exposed rivet head. Both the plates and the rivet were modeled using the titanium alloy Ti-6Al-4V (Ti-Gr5).

The material’s behavior was described using the Johnson-Cook (JC) constitutive model, which considers the dependence of the material’s strength on effective plastic deformation, strain rate, and temperature. As Beecher et al. [10] indicate, this model allows for coupling between plasticity, cumulative damage, and fracture criteria, making it particularly suitable for impact processes such as EMR.

The equations governing the Johnson-Cook model used in this study are as follows:

$$\sigma =\left(A+B\cdot {\dot{\epsilon }}^n\right)\cdot \left(1+C\cdot ln\left({\displaystyle \frac{\dot{\epsilon }}{\dot{{\epsilon }_{ref}}}}\right)\right)\cdot \left({\left(1-\left((T-T_{ref})/(T_{melt}-T_{ref}\right)\right)}^m\right)$$

(1)

$${\epsilon }_f=\left(d_1+d_2\cdot e^{-d_3\eta }\right)\cdot \left(1+d_4\cdot ln\left({\displaystyle \frac{\dot{\epsilon }}{{\dot{\epsilon }}_{ref}}}\right)\right)\cdot \left(1+d_5\cdot (T-T_{ref})/(T_{melt}-T_{ref})\right)$$

(2)

$$D=\int {\displaystyle \frac{1}{{\epsilon }_f}}d\epsilon$$

(3)

where the equivalent Von Mises stress ($\sigma$) is obtained from the equivalent strain ($\epsilon$), the strain rate ($\dot{\epsilon }$) and the temperature ($T$), while the damage is predicted with the D index, based on the cumulative plastic strain ($d\epsilon$) and the fracture strain (${\epsilon }_f$). Subscript ref indicates the reference value of temperature and strain rate.

The model includes variables that depend on the results of a previous characterization, such as the yield strength ($A$), the strain hardening coefficient ($B$), the strain hardening exponent ($n$), the strain rate sensitivity coefficient ($C$), the thermal softening exponent ($m$), and the damage constants ($d_1,d_2,d_3,d_{4}y{d}_5)$. The reliability of the simulation results is grounded in the use of experimentally validated Johnson-Cook parameters for Ti-6Al-4V [18,19], which have been previously shown to accurately predict plastic flow and failure under high-strain-rate conditions similar to EMR. The physical, elastic, plasticity, and damage properties applied to the material model are presented in Table 1 and Table 2.

Table 1. Physical and elastic properties of the Ti-6Al-4V alloy.

Properties	Value
Density (kg/m3)	4430
Modulus of elasticity (GPa)	111
Poisson ratio (-)	0.342

Table 2. Plasticity and damage parameters of the Johnson-Cook model (Tuninetti et al. [18,19]).

Plasticity Parameters		Damage Parameters
A (MPa)	927	d1	0.246
B (MPa)	878	d2	186
C (-)	0.0137	d3	−15.7
m (-)	0.594	d4	0.2582
n (-)	0.795	d5	1.2059

Once the material was defined, the configuration to be used in the simulation was established. As mentioned previously, this consists of two small plates with an equal thickness of 5 mm. These plates represent a local section where a rivet is applied. The model also considers a countersunk rivet with a head diameter of 5 mm and a maximum diameter (at the countersink) of 10 mm. Finally, to complete the model, a riveting die with a countersink angle ($\alpha$) is also considered. A diagram of the modeled configuration is shown in Figure 2.

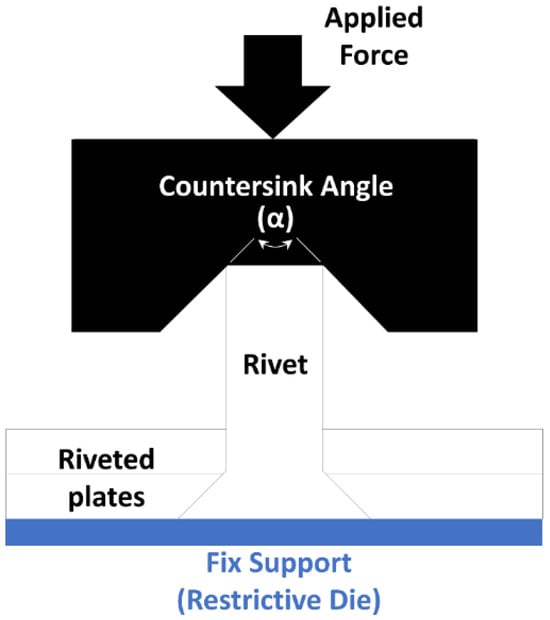
Figure 2. Simplified process configuration.

During the study, three different countersinking angles will be used to determine their influence on the process. Commercial angles of 45°, 70°, and 90° will be studied. The information obtained from this analysis will allow the countersinking angle to be adjusted according to the different requirements of various fuselage components (or other industrial applications) as well as different fuselage types.

3.1. Mesh Configuration

A structured hexahedral mesh strategy was employed for the rivet and plates to ensure accurate computation of the von Mises stress gradients. To capture the high gradients at the contact interface, a localized volumetric mesh refinement technique was applied, ensuring a smooth transition between element sizes. The die was modeled as an analytical rigid body, as its elastic deformation is negligible compared to the rivet plasticity. A mesh convergence study (Figure 3) determined an optimal element size of 0.25 mm in the critical deformation zone, balancing computational cost with stress convergence accuracy.

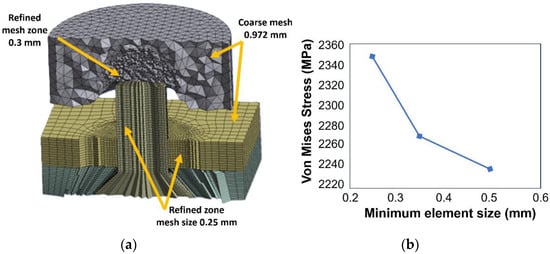
Figure 3. (a) Mesh configuration detail and (b) Mesh convergence.

The mesh quality provided by the software used (ANSYS explicit dynamics) is detailed (Table 3) according to each configuration.

Table 3. Average mesh quality by configuration.

Configuration	Average Mesh Quality
$\alpha =90°$	0.759
$\alpha =70°$	0.766
$\alpha =45°$	0.758

Since the average mesh quality in each configuration is close to 1 and they also exhibit a very low magnitude variation, the meshing is considered validated for each configuration.

3.2. Loading and Boundary Conditions

As detailed in Figure 2, the countersunk head of the rivet is held by a tool during the riveting process, thus restricting its movement (fixed support) during the simulation. For the maximum force provided by the coil, the previously proposed model was considered, which is detailed below.

$${\sigma }_y={\displaystyle \frac{F_{mín}}{A}}$$

(4)

$$F_{mín}{=A\cdot \sigma }_y$$

(5)

$$F=P\cdot F_{mín}=P\cdot {A\cdot \sigma }_y$$

(6)

For this study, an amplification factor $P$ equal to $11.55$ was used, resulting in a force of $210\left(\mathrm{k}\mathrm{N}\right)$, which is proposed after testing several iterations. While the EMR process involves a transient electromagnetic pulse force, this study focuses on the mechanical response at the point of maximum deformation. Therefore, a simplified peak load of 210 kN was applied as a representative constant force to evaluate the comparative influence of die geometry on stress localization.

The loading conditions resulted in peak effective plastic strain rates ranging from 2.0 × 10³ s⁻¹ to 5.5 × 10³ s⁻¹, consistent with the operational window of electromagnetic forming processes. This rapid plastic deformation process is assumed as adiabatic in simulation of EM riveting, with the thermo-mechanical conversion coefficient (Taylor-Quinney) $\beta =0.9$ [20]. For the specific heat capacity $c_p=526{\displaystyle \frac{J}{kg\cdot K}}$ is used as reported at room temperature and frequently used in impact and forming simulations of Ti-6Al-4V [20].

4. Results and Discussion

The simulation was carried out with a total analysis time of 3.5 × 10⁻⁵ s, corresponding to the typical duration of the electromagnetic riveting (EMR) impact event. A frictionless contact condition was defined between the interacting components, as the relative frictional forces were found to be negligible compared to the impact-induced pressures. The outputs included stress, strain, and plastic work distributions for the rivet, die, and plates.

Figure 4 shows the resulting total deformation and final geometry for the three die configurations analyzed: (a–c) total deformation fields for the 90°, 70°, and 45° dies, respectively, and (d–f) the corresponding final shapes of the deformed rivet heads. Under identical loading conditions, all cases exhibit proper plastic deformation and head expansion, indicating a stable forming response. The quality of the formed joint is quantitatively assessed using the diametral ratio (Dₘₐₓ/D₀), defined as the ratio of the final formed head diameter to the initial shank diameter. According to aerospace assembly standards [4,24], a ratio between 1.3 and 1.6 is critical to ensure sufficient interlock without inducing head cracking. The diametral ratios obtained from the simulations for each configuration are summarized in Table 4, confirming that all cases remain within the recommended interval. These results validate that the deformation achieved in the rivet head meets the mechanical and geometric requirements for proper joint formation under high-rate conditions.

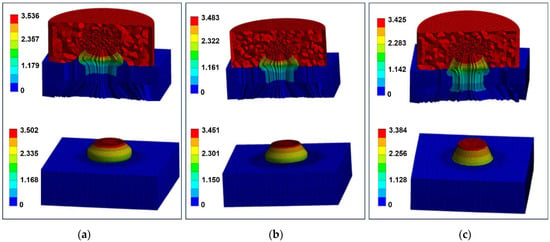
Figure 4. Total deformation (in mm) and final rivet shape for the three die configurations: (a) 1 (90°), (b) 2 (70°), and (c) 3 (45°) showing final shapes of the deformed rivet heads.

Table 4. Relationship between rivet diameters.

Configuration	Diametral Ratio
$\alpha =90°$	1.52968
$\alpha =70°$	1.51066
$\alpha =45°$	1.45496

Therefore, all configurations fall within the acceptable range of 1.40–1.55, which corresponds to the design specifications for proper rivet expansion (Table 4). The small variation among configurations is expected, as no modification was made to the initial rivet geometry. Nevertheless, the stress distribution varies notably with die angle (as discussed in Figure 5), indicating that although the final diametral ratios are similar, the plastic deformation mechanisms leading to those dimensions differ. This highlights that die geometry influences the strain path and local stress concentration, even when the global dimensional outcome remains consistent.

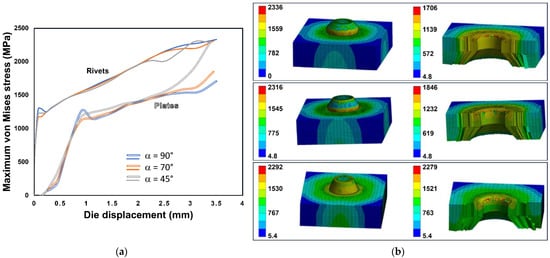
Figure 5. (a) Maximum von Mises equivalent stress (VM) in the rivets and plates for the evaluated die configurations. (b) Stress distribution in the rivet head and adjoining plates (MPa) for die angles of 90°, 70°, and 45°. Larger die angles lead to higher stress concentrations in both the rivet and the plates, indicating the significant influence of die geometry on the mechanical response of the joint under high-rate electromagnetic riveting.

Figure 5 presents a comparison of the von Mises equivalent stress during the high-rate electromagnetic riveting (EMR) process for three die geometrical configurations. In graph (a), it can be observed that the 90° die configuration produces the highest stress values in the rivet, reaching a peak of approximately 2300 MPa, which indicates a more intense localization of plastic deformation under dynamic loading conditions. The 70° configuration exhibits intermediate stress levels, while the 45° configuration shows the lowest values, stabilizing around 1800 MPa. This behavior suggests that die geometry strongly influences the plastic flow generated in the rivet during the high-rate forming event, with the 90° configuration promoting a more pronounced radial expansion. In graph (b), which shows the equivalent stress evolution in the plates, a similar tendency is observed. The 90° configuration induces the highest stress levels in the base material, which could lead to adverse effects such as localized hardening, residual deformations, or even microcrack initiation under repeated high-rate impacts. In contrast, the 45° configuration results in lower stress magnitudes within the plates, indicating a more compliant energy transfer between the rivet and the surrounding material, potentially reducing the risk of structural degradation. The stress contour maps (c–h) confirm these observations, highlighting the localization of stresses at the rivet head and in the contact interface with the upper plate. The 90° configuration displays more extensive and intense stress concentrations, consistent with the higher energy absorption and plastic strain accumulation characteristic of dynamic forming processes. Meanwhile, the 45° configuration presents a more confined and uniform stress distribution, which indicates a smoother deformation mode and a lower degree of plastic strain rate sensitivity. These results indicate that die geometry influences the joint’s mechanical response under high-rate loading, as reflected by changes in stress magnitude and localization in the rivet and plates. Overall, the detected stress patterns suggest potential implications for interlocking efficiency and plate integrity, which should be confirmed in future work through detailed geometric characterization and mechanical testing.

The evolution of axial and radial deformation shows similar overall trends across all configurations (Figure 6), with both components increasing nonlinearly over time due to the high strain-rate loading. However, the magnitude and rate of deformation differ depending on die geometry. The 90° configuration exhibits the highest axial deformation (~3.7 mm), consistent with its larger forming angle and higher stress concentration observed previously. The 70° configuration follows closely, while the 45° configuration shows slightly lower axial deformation, indicating a more restricted plastic flow. In terms of radial deformation, the 45° configuration reaches a lower final expansion and begins to stabilize earlier than the others, confirming that shallower die angles limit lateral material flow. This agrees with the diametral ratios reported in Table 4, where the 45° die produced the smallest final diameter.

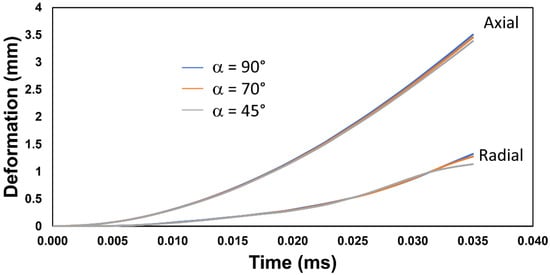
Figure 6. Axial and radial rivet deformation for the three different die angle configurations (α).

These results suggest that, although the final rivet geometries remain within design tolerances, the deformation kinematics and strain-rate response vary significantly with die angle. Future experimental work should involve 3D digital image correlation (DIC) or in situ high-speed optical measurements to validate the predicted axial-radial strain evolution and to quantify the contribution of dynamic effects to the overall deformation process.

Figure 7 illustrates the adiabatic temperature evolution during the high-rate electromagnetic riveting process for the three die configurations. In all cases, the temperature rises nonlinearly over time, driven by the rapid accumulation of plastic work. The 90° die configuration exhibits the most severe heating, reaching a peak of 257 °C, followed by the 70° configuration (247 °C) and the 45° configuration (235 °C). Although the absolute differences are moderate, the trend correlates perfectly with the Von Mises stress distributions observed earlier, confirming that dies inducing sharper stress gradients also promote greater localized heating. Crucially, these temperature magnitudes (approximately 250 °C) confirm that the process is not purely mechanical; it is a coupled thermo-mechanical event. While well below the Beta-transus of Ti-6Al-4V, these temperatures are sufficient to activate thermal softening mechanisms, which compete with strain-rate hardening to facilitate material flow. Future work should incorporate coupled thermomechanical simulations with frictional heating to quantify the additional surface temperature rise, potentially using high-speed infrared thermography to validate these adiabatic predictions.

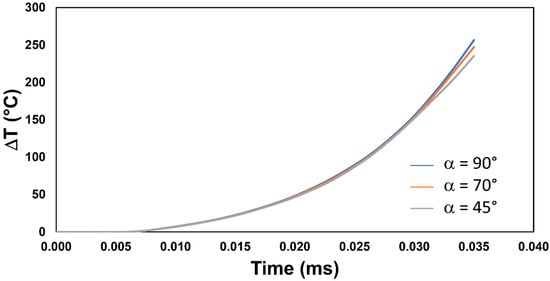
Figure 7. Adiabatic temperature increase in the rivet due to plastic deformation for the three different die angle configurations (α).

Limitations of the Numerical Framework

The interpretation of these results requires the consideration of two specific modeling constraints regarding the loading dynamics and thermal boundary conditions. First, the electromagnetic riveting process is physically governed by a transient, high-frequency magnetic pulse, resulting in a time-dependent force profile (F(t)). In contrast, the current simulation applied a simplified constant load of 210 kN, corresponding to the peak amplitude of the discharge. This boundary condition was deliberately selected to decouple the die geometry effects from the temporal fluctuations of the magnetic field, thereby isolating the stress distribution at the singular moment of maximum deformation. Consequently, the reported stress concentrations represent a static equivalent of the peak forming state rather than the complete inertial response associated with the pulse rise-time.

Furthermore, the thermal analysis was conducted under the assumption of frictionless contact, deriving temperature evolution exclusively from the adiabatic conversion of plastic work. It is acknowledged that interfacial friction constitutes a primary heat source in high-speed forming and its exclusion leads to an underestimation of the total process temperature. As emphasized in recent investigations on heat-resistant aerospace materials [25], friction could further elevate surface temperatures. Therefore, the reported values serve as a baseline for plastic-work-induced heating, representing the internal material state independent of tribological conditions.

5. Conclusions

This work applied the finite element method (FEM) and the Johnson–Cook constitutive model to analyze the influence of die geometry (90°, 70°, and 45°) on the mechanical and thermal behavior of the electromagnetic riveting (EMR) process in Ti-6Al-4V alloy. The findings provide quantitative evidence of how die angle governs plastic flow, stress localization, and energy dissipation in high-strain-rate joining operations.

The simulations confirmed that all configurations produced adequate head formation, satisfying the industrial design criterion of 1.3 ≤ Dₘₐₓ/D₀ ≤ 1.6, which validates the suitability of the process for aerospace-grade rivet expansion. However, despite similar final geometries, the underlying deformation mechanisms differed significantly. The 90° die promoted the highest plastic strain and stress concentration in the rivet head and plates, while the 45° configuration generated a more homogeneous stress distribution with lower radial expansion. This demonstrates that die geometry directly influences the strain path and local energy absorption, even when global dimensions remain constant.

The mechanical response revealed that the maximum Von Mises stress reached approximately 2300 MPa in the 90° configuration, correlating with the greatest plastic work and confirming the sensitivity of Ti-6Al-4V to local stress accumulation under dynamic forming. The thermal analysis revealed that the rapid conversion of plastic work generates localized temperature increases of approximately 250 °C. While this confirms the adiabatic nature of the process, the magnitude is significant enough to activate thermal softening mechanisms, aiding the high-speed deformation of the rivet head. This highlights the necessity of coupled thermo-mechanical modeling for accurate EMR prediction.

The numerical evidence suggests that intermediate die angles (45–70°) provide the most favorable compromise between efficient rivet expansion and controlled stress transfer to the plates. These configurations ensure joint durability while limiting residual stresses and preserving the mechanical properties of the surrounding material.

Future work should focus on experimentally validating the simulated strain-rate effects using 3D digital image correlation (DIC) and high-speed optical diagnostics, as well as on developing coupled thermomechanical models that incorporate frictional and non-adiabatic effects. Finally, future research must extend beyond the transient forming stage to evaluate the long-term fatigue performance of EMR joints. As demonstrated in recent research on assembly defects [26], manufacturing inconsistencies can critically influence fatigue life under random loading. Correlating the die-induced stress concentrations identified in this study with cyclic fatigue behavior will be a key step toward industrial certification.