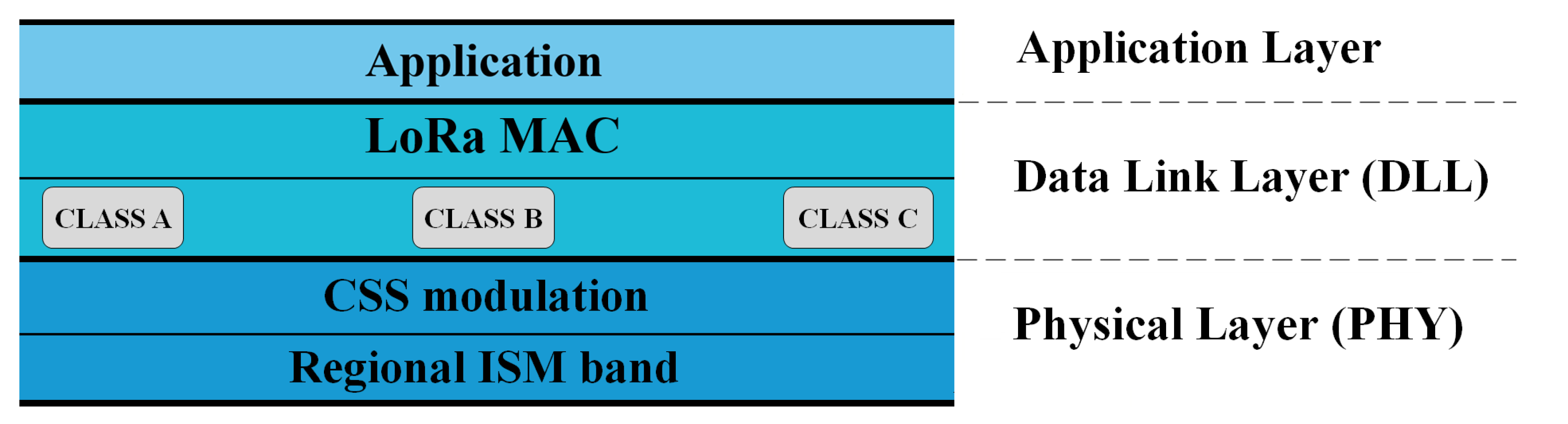
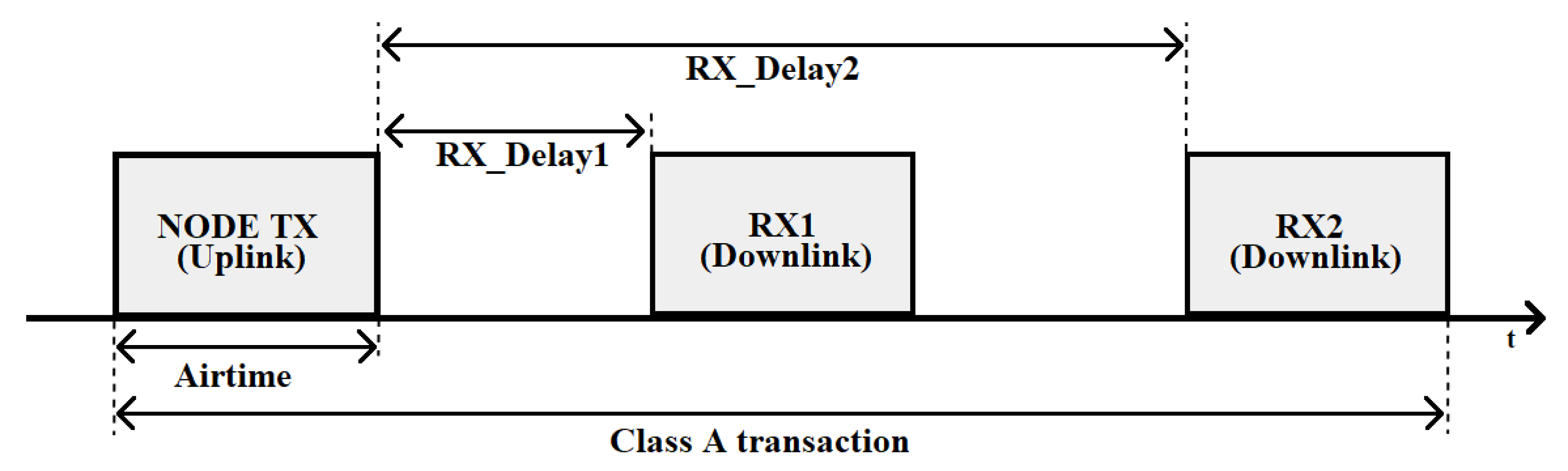
1. Introduction
We are at the dawn of the next generation of the Internet, which will be dominated by trillions of tiny computing devices embedded in everyday objects—the paradigm usually dubbed as Internet-of-Things (IoT). Many communication technologies can be used to interconnect IoT devices, e.g., short-range communication technologies such as Bluetooth, ZigBee, and Z-Wave. However, such technologies face critical challenges in terms of energy, cost, and complexity when applications require covering large geographical areas and feature a large number of devices, due to the need for tricky multi-hop routing in potentially harsh environments. Recent standards/technologies for Low-Power Wide-Area Networks (LPWAN) are an effective way to overcome such challenges and pave the way for new IoT applications that cover wide geographical areas over long distances [
1]. LPWAN technologies such as LoRa (Long Range) [
2], SigFox [
3], Weightless [
4], WAVIoT [
5], and Wi-Fi HaLow [
6] compete for an increasing market share among other IoT technologies, with a projected market worth of 65 Billion USD and smart gas and water metering applications occupying 20% of the LPWAN market by 2025 [
7].
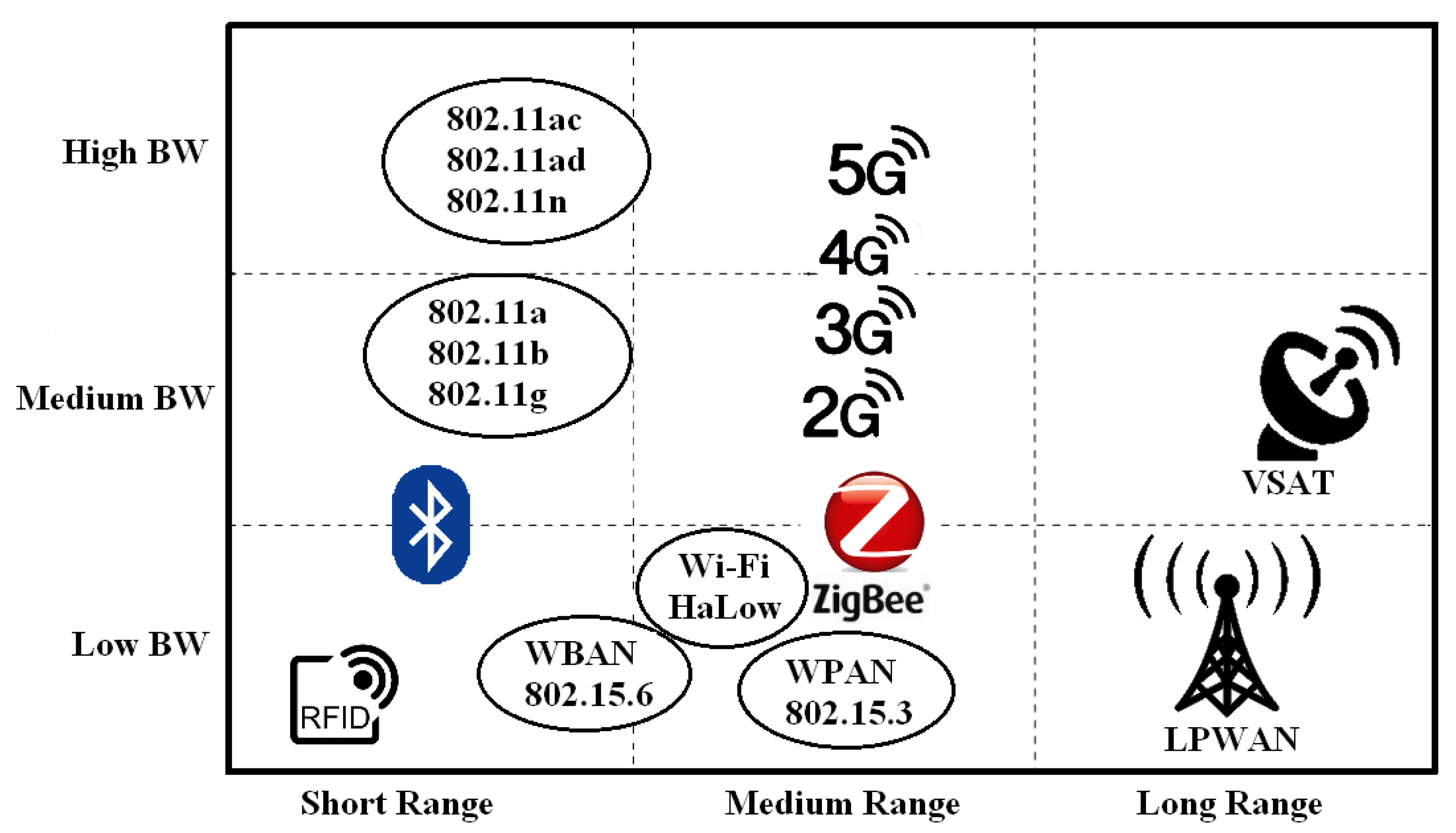
Figure 1 shows how LPWAN compares to other wireless technologies in terms of range and Bandwidth (BW).
This work focuses on LoRa, a proprietary physical layer protocol that affords low-power and long- distance communication through Chirp Spread Spectrum (CSS) modulation. The main advantages of LoRa over other LPWAN technologies are the open-source MAC protocol LoRaWAN specification, low-cost application availability, and community support [
2]. For example, “The Things Network” is a crowd-sourced community from 85 countries building public and global IoT networks based on LoRa [
9].
The configuration of LoRaWAN networks may be a challenging task, especially as the network scales up in the number of nodes. The link layer, LoRa, has some specific radio-related parameters that can be adjusted, such as Carrier Frequency (CF), Spreading Factor (SF), Bandwidth (BW), Transmission Power (TP), and Coding Rate (CR). These parameters can be tuned at a device and/or network level to enhance overall network performance, namely reducing energy consumption, improving radio coverage, and reducing radio interference and error rates. However, despite the increasing adoption of LoRa in IoT applications, the tools, methods, and models available to manage and optimize its performance are still scarce.
In this work, we propose a way to improve the Quality-of-Service (QoS) of LoRaWAN networks, specifically to increase the Data Extraction Rate (DER) and to reduce the number of collisions and energy consumption, through the formulation of a Mixed Integer Linear Programming problem, which generates optimal settings for the Spreading Factor and Carrier Frequency parameters. Our LoRaWAN-based solution takes as input a list of available CF and SF parameters to each node, allowing for pruning settings found to be inadequate (e.g., an SF that is unusable due to distance). The effectiveness of the proposed optimization procedure is demonstrated by simulations, using LoRaSim for different network scales, showing that our solution performs better than standard and other benchmarking radio parameter assignment policies.
We identify the following relevant contributions:
- (i)
definition of a mathematical optimization formulation of the problem of assigning SF and CF parameters according to the traffic characteristics of LoRa end-devices;
- (ii)
definition of an approximation algorithm that leads to results very close to the optimal, but with an execution time that grows much slower as the number of end-devices in the network scales;
- (iii)
approach to implement and integrate the approximation algorithm in LoRaWAN networks and analyze the imposed overhead of the radio parameter assignment scheme to ensure compatibility with the standard protocol;
- (iv)
implementation of the proposed optimization algorithms and of other baseline policies (benchmarks to which our method is compared against in
Section 6), and as well as of the ADR mechanism (not implemented in
LoRaSim) in the
LoRaSim open-source simulator, making our code available to the community [
10]; and
- (v)
Comparative performance analysis of six radio parameter assignment policies, showing the merit of the two proposed parameter assignment methods in relation to the other four policies that we consider as benchmarks.
The remainder of the paper is structured as follows.
Section 2 discusses relevant related work.
Section 3 overviews the characteristics of the LoRa communication protocol that are most relevant within the context of this paper. In
Section 4, we present a method to select optimal values to CF and SF radio parameters, based on a formulation using
Mixed Integer Linear Programming.
Section 5 presents the Approximation Algorithm, which can efficiently produce results very close to the optimal.
Section 6 outlines the simulation setup, the evaluation metrics, and elaborates on the comparative analysis performance of our parameter optimization method against relevant benchmark policies. Finally,
Section 7 concludes the paper by summarizing the main contributions and unveiling future research directions.
2. Related Work
Network performance and scalability are key factors for LoRaWAN network design. These factors are influenced mainly by the correct choice of radio parameters and by environmental conditions [
11]. Several researchers defined a possible formal approach, through the analysis and comparison of performance and scalability of LoRaWAN networks, for the problem of parameter selection. In this section, we outline some relevant works that address these aspects.
The performance analysis of long-range transmission and channel attenuation, made by Petajajarvi [
12], concludes that, in the best scenario, a single gateway configured using SF 12, 125 MHz BW, and data rate of 1.8 kbps, covers an area of 30 km in peripheral urban environments. Additionally, this paper concludes that low values of SF are recommended for urban scenarios due to less interference caused by the Doppler effect. In other work, Petajajarvi [
13] analyzed the performance of LoRa in three experiments. The first and second experiments were performed in a LoRa end-device under the Doppler frequency shift. With TP of 14 dBm and SF12, at least 60% of the packets are received from 30 km distance on the water. The third experiment was performed on an end-device, mounted in a car, configured with a TP of 14 dBm and SF of 12. This work concludes that, in a mobile scenario, the LoRa communication worsens in a displacement speed of end-devices around 40 km/h.
In an indoor environment, Neumann [
14] did a performance analysis of the LoRa network with the parameters throughout RSSI, Signal-to-Noise Ratio (SNR), packet loss, packet error, power consumption, and delay to verify how the average current consumption of one end-device impacts in the performance of LoRa network with one device and one gateway. This study concludes that the data rate affects the packet loss.
The scalability of LoRaWAN networks evaluated in ref. [
15] in the ns-3 simulator, in which the error model is based on interference among various concurrent transmissions, concludes that increasing the gateway density improves the negative effect of restrained downstream in packet delivery ratio of upstream messages.
In ref. [
16], the authors proposed an optimized SF parameter allocation approach, stating that it increases the probability of uplink data delivery by 20–40% at the cost of increasing power consumption by 1–8%, respectively. Due to its relevance in the context of this paper, we considered this algorithm as a benchmark (dubbed “Tiurlikova”) in the comparative performance analysis outlined in
Section 6.
Bakov [
17] measured the limits of a LoRaWAN network, which is about 0.1 51-byte (Frame Payload) in a network with three main channels and six data rates. That corresponds to 5000 end-devices, each node generating two messages per day. A performance analysis conducted in ref. [
18] of LoRaWan end-device using the metrics uplink, throughput, and transmission time concluded that, in terms of LoRaWAN scalability, millions of devices can communicate with a reduced transfer.
Vatcharatiansakul [
19], in a LoRaWAN performance evaluation carried out in internal and external environments, concluded that the LoRa signal range is affected by the properties of the antennas such as antenna gain, directional, and antenna height. Yousuf [
20] measured how internal and external urban environments affect the LoRa signal. In an internal environment of a seven-story building, there was a minimal packet drop. The external coverage depends on the environment. In this experiment performed in a range of 4.4 km, there was 15% of packet drops and the packet size alter the signal range.
Toussaint [
21] evaluated over-the-air performance in a Markov chain model in different traffic conditions, duty cycles, and channel availability. The expected delay and energy consumption of the LoRa network depends on the number of channels, the number of sub-bands, and gateway parameters. Feltrin [
22] characterized experimentally from the link-level viewpoint and evaluated through simulations the capacity of a LoRaWAN gateway to provide communications in large rural environments. In this scenario, a gateway covering an area of 1 km
, the maximum node density is 185 end-devices/hectare. However, using this gateway in an area of 46.5 km
, the maximum density decreased to one node/hectare. To maximize the node density in this large area, four gateways provide 40 end-devices/hectare.
The work of Cattani [
23] presents an analysis of the performance of the LoRa in relation to different configurations of PHY and environmental conditions. The analysis done in a scenario where the network nodes are at the communication limit concludes that it is more efficient to use the faster PHY configuration and higher transmission power than slower configurations that maximize the quality of the link because the faster PHY setting provides 100 times faster effective bit rate than the slower setting scenario, at the cost of a 10% lower average packet reception rate. In addition, the work concludes that environmental factors such as temperature and humidity impact the rate of reception of packets and the intensity of the received signal. In a controlled environment with a temperature of 15
C, an optimal link with 100% Packet Reception Rate becomes unusable at 60
C. Over this temperature range, the received signal strength is reduced by 6 dBm, being 1 dBm per 10
C.
Reynders et al. [
24] analyzed and compared the performance of LoRa networks with a proposed MAC layer two-step lightweight scheduling in ns-3 simulator. The results conclude that, in a scenario with one gateway and 1000 end-devices, the proposed MAC layer reduces the Packet Error Ratio around 20%. In the performance analysis of LoRa network performed in ref. [
25], with Additive white Gaussian noise (AWGN), a frequency selective channel of the Frequency Shift Chirp Modulation (FCSM), and the Frequency-Shift keying modulation (FSK), the authors concluded that the performance of the FCSM and FSK in an AWGN channel are equivalent. However, in a frequency selective channel, the FCSM has a superior performance.
Lim and Han [
26] made a proposal and schema validation to maximize the average Packet Success Probability through SF parameters using MATLAB simulator on Massive Connectivity (MC), respectively. The projected scheme is better for all others MC in relation to Monte Carlo simulations and analysis. For example, in a 2000 end-devices LoRa network, the method provides stability for 810 end-devices, an increase of 22% in MC over the Equal-Area-Based scheme.
Differently from the studies presented, this work proposes to optimize the performance of LoRaWAN networks through a dynamic assignment policy of SF and CF parameters, which is backwards compatible with the standard protocol and ADR mechanism. The proposed policy was compared and analyzed against LoRaWAN’s default assignment policy, and the random, Tiurlikova’s, and equal dynamic assignment policies.
4. MILP Optimization Problem
To increase the performance of the LoRaWAN network through the optimization of radio parameters, we developed a formulation using
Mixed Integer Linear Programming (MILP), a formal mathematical optimization framework. Using MILP provides a mathematical framework that allows solving complex problems by leveraging well-established theory and solution methods. Similar approaches using a MILP formulation in network parameter optimization scenarios can be found in previous work (e.g., [
34,
35]). It is also important to note that the optimization problem is the baseline for the approximation algorithm, allowing us to benchmark the approximation against an optimal solution.
Many objectives can be selected to improve the performance of LoRaWAN networks, e.g., reduce the individual node energy consumption, improve the reliability of data delivery, or improve overall throughput. For the purpose of this work, we aim at improving the amount of successfully delivered messages over a period of time by setting the radio parameters of the LoRaWAN devices in the network. Our performance problem for LoRaWAN, modeled as a MILP problem, assigns values to the CF and SF parameters in order to improve the performance of the network.
Section 4.1 presents general aspects of the MILP,
Section 4.2 introduces the notation and model used, and
Section 4.3 presents our MILP problem formulation.
4.1. Background on Mathematical Optimization
Mathematical optimization has been used in a great number of fields, such as in ref. [
36] for vehicle- control problems, in ref. [
37] for short-term scheduling of resource-constrained multistage flow-shop batch facilities, in ref. [
38] for short-term hydro scheduling and unit commitment with the head-dependent reservoir, and in ref. [
39] for aircraft planning with collision avoidance. Mathematical optimization is also used for automotive applications when optimizing extensibility [
40] or task activation modes [
41]. The problems can be expressed by a set of integer, binary and continuous design variables, design parameters, linear equalities and inequalities representing the constraints on the solution, and a linear objective function. The main advantage consists in the possibility of leveraging a well-established theory and solution methods, which includes the availability of efficient solver engines with controllable solution accuracy and constrained computing time [
38].
Linear Programming is a method for solving design problems using the formal mathematical optimization framework. A MILP optimization problem is given for a set of variables, objective function, and a set of constraints. Solving the problem attempts to find the best solution for the objective function in the set of solutions that satisfies the constraints.
4.2. Notation and Model
Consider a wireless network system with a LoRaWAN gateway and n end-devices. End-devices transmit with an average transmission rate packets/second and an average length of bytes. The time to transmit a packet of length is given by a function , which computes the time to transmit according to parameters SF, CR, BW, and payload size. For the purpose of this model, we assume a fixed BW and CR, which must be taken into account for the airtime computations.
To model our problem as an MILP problem, we define an array of tuples for each end-device, where is a list of available CFs and is a list of available SFs. The lists of SFs and CFs as input allow, e.g., reserving certain for other uses. An example input could be and indicating that the algorithm can use three CFs (868.1, 868.3, and 868.5) and 7–12 SFs in each of these channels. The tuples are arrays of booleans which indicate if an end-device i is using a given or . These are the decision variables of our problem and one of the constraints of our model must restrict the solutions to only having one value of each of the arrays set to true in each end-device, as each end-device can only have one CF and one SF value assigned.
The end-devices of the LoRaWAN networks as with and parameters communicate with gateway G. To increase network performance, multiple indexes are considered: energy consumption of the end-devices, network range, interference reduction, and errors rate. In this case, and are assigned to maximize the probability of success on a single gateway. As an input, to model the LoRaWAN network as MILP, we are given variables where N is equal to the number of end-devices.
4.3. MILP Problem Statement
Considering that SFs are orthogonal with each other, we would like to maximize the probability of success (or minimize the collision probability) for each
pair. Therefore, the decision variables for each node have two Boolean arrays
and
that indicate the
and
of each
N. For example, the following arrays indicate that
is using
and
:
To express this in our MILP model, we define in Equation (
1) the following objective function, which minimizes the difference between the utilization of each
pair, denoted as
, resulting in the minimum load for each
:
where
and
subject to
and
Equation (
2) computes the utilization of the
pair, as defined by Equation (
3), considering the number of end-devices assigned to that pair. The two constraints in Equations (
4) and (
5) limit the assignment
and
such that each end-device is only assigned one
and one
.
Practical Issues: Equation (
3) is the product of two binary variables, which is nonlinear. This can however be made linear given
and the following additional constraints:
This problem can be solved using one of the many state-of-the-art MILP solvers. In our experiments, we used the CPLEX optimizer [
42] due to the set of different options, strategic decomposition, and deactivation of heuristics that reduce the time to solve complex problems [
43].
5. Approximation Algorithm
The ADR mechanism, as described in
Section 3.5, improves the data rate, airtime, and power consumption of each end-device through the TP and
parameters according to
, TP, BW, and SNR. However, the performance of a LoRaWAN network also depends on the occurrence of simultaneous transmissions with the same SF, determined through the two-dimensional coordinates of the end-devices and the LoRaWAN network gateways.
To apply the results obtained through the MILP problem formulation, as described in
Section 4.1, with backward compatibility in LoRaWAN networks, we rely on the ADR mechanism to dynamically adjust the settings of end-devices. As indicated by the standard, only end-devices with a stable RF environment should enable ADR. Our model includes provisions for defining a list of end-devices for which the SF parameter, determined by measurements (which are part of the normal LoRaWAN ADR procedure), can be changed. This is backward compatible with existing LoRaWAN networks and only the LoRa network server needs to be updated to obtain the radio parameters according to our proposed method.
5.1. Description of the Approximation Algorithm
The time to solve MILP problems grows exponentially as the number of end-devices increases. Due to scalability issues, we developed the Approximation Algorithm to provide parameter assignments (Algorithm 3). The approximation is based on a first-fit assignment of the utilization for each
and
combination.
| Algorithm 3: Approximation Algorithm. |
![Jsan 09 00010 i003 Jsan 09 00010 i003]() |
The Approximation Algorithm in Algorithm 3 receives as input the average packet length in bytes (), and the average packet transmission rate (). It also receives two arrays with the available CFs and SFs, with the array being ordered from the SF with the smallest resulting airtime to the largest.
Algorithm 3 starts by creating an array of to hold the utilization of each () pair. Then, the algorithm assigns a CF and SF to each end-device by using a function which takes as input the array and returns a tuple that will result in the lowest utilization increase. That is, it will return the pair that is the . Finally, the algorithm increases the utilization for that pair.
5.2. Backward Compatibility with LoRaWAN
The LoRa Server project [
44] provides a set of open-source applications for building LoRaWAN networks. It is part of a larger project that encompasses a protocol packet forwarder broker for MQTT (LoRa Gateway Bridge), and a compatible application server. The mechanisms provided by LoRa Server allow users to manage the gateways in the LoRa network, the supported applications, and the devices associated with the applications [
44].
Reviewing the documentation for sending LoRa server uplink messages [
45,
46], the way to implement the Approximation Algorithm with backward compatibility with the standard LoRa protocol and its mechanisms, e.g., ADR (as described in
Section 3.5), is to implement the Approximation Algorithm at the LoRa application layer of LoRa and devices. Thus, the application layer determines the
pair individually for each node. The LoRa Server receives as input parameters the
pairs by the application server (that is running the Approximation Algorithm) and transmits to the end-devices in the downlink. Then, the node executes a corresponding application to configure the node parameters.
7. Conclusions and Future Work
We propose a simple yet efficient methodology to improve the performance of LoRaWAN networks by fine-tuning their SF and CF radio parameters, through Mixed Integer Linear Programming optimization approach. This enables the LoRaWAN network designer to choose the best network configuration. Importantly, these parameter assignment policies are backward compatible with the LoRa standard protocol, meaning that they can be implemented in commercial off-the-shelf LoRa devices.
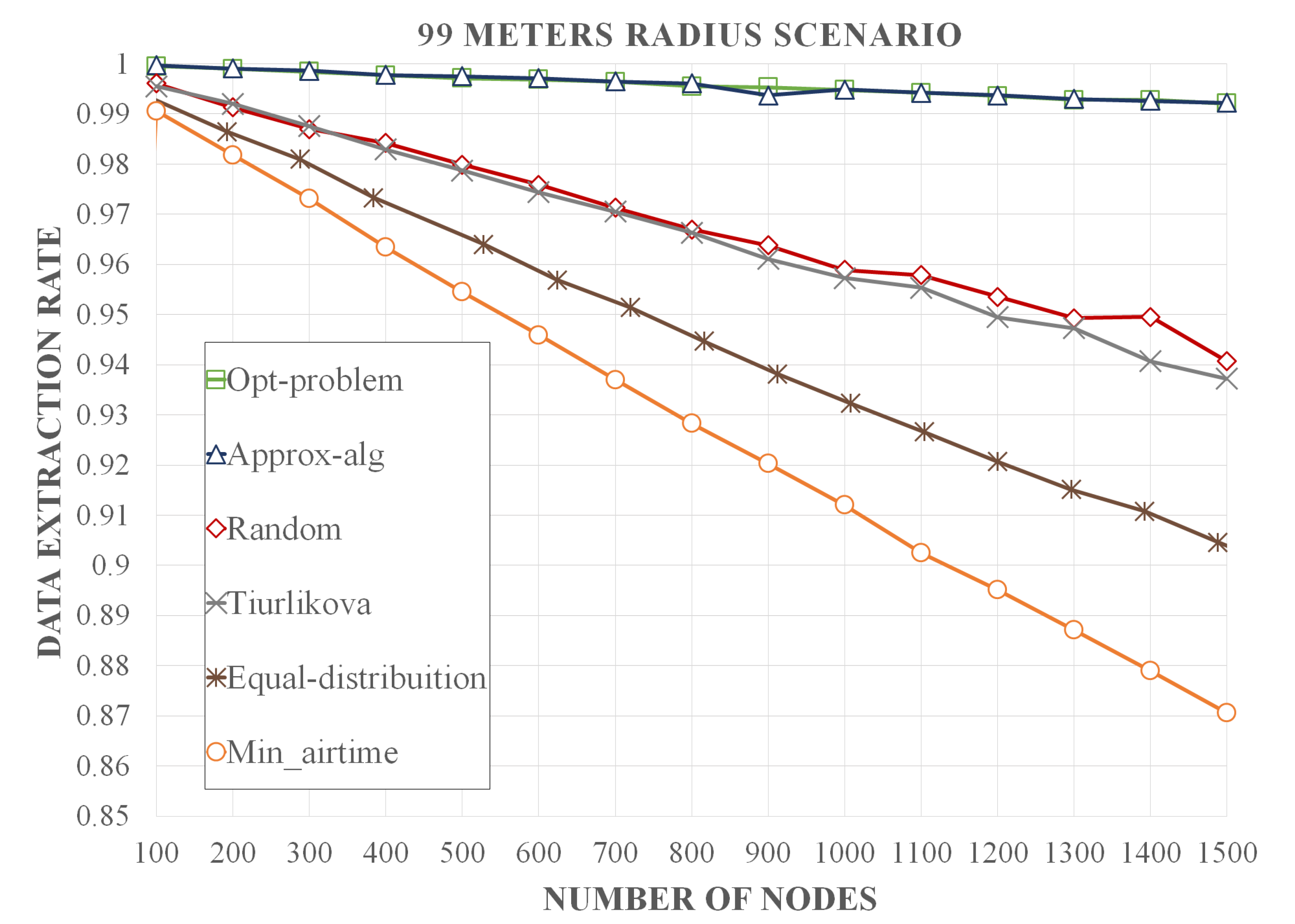
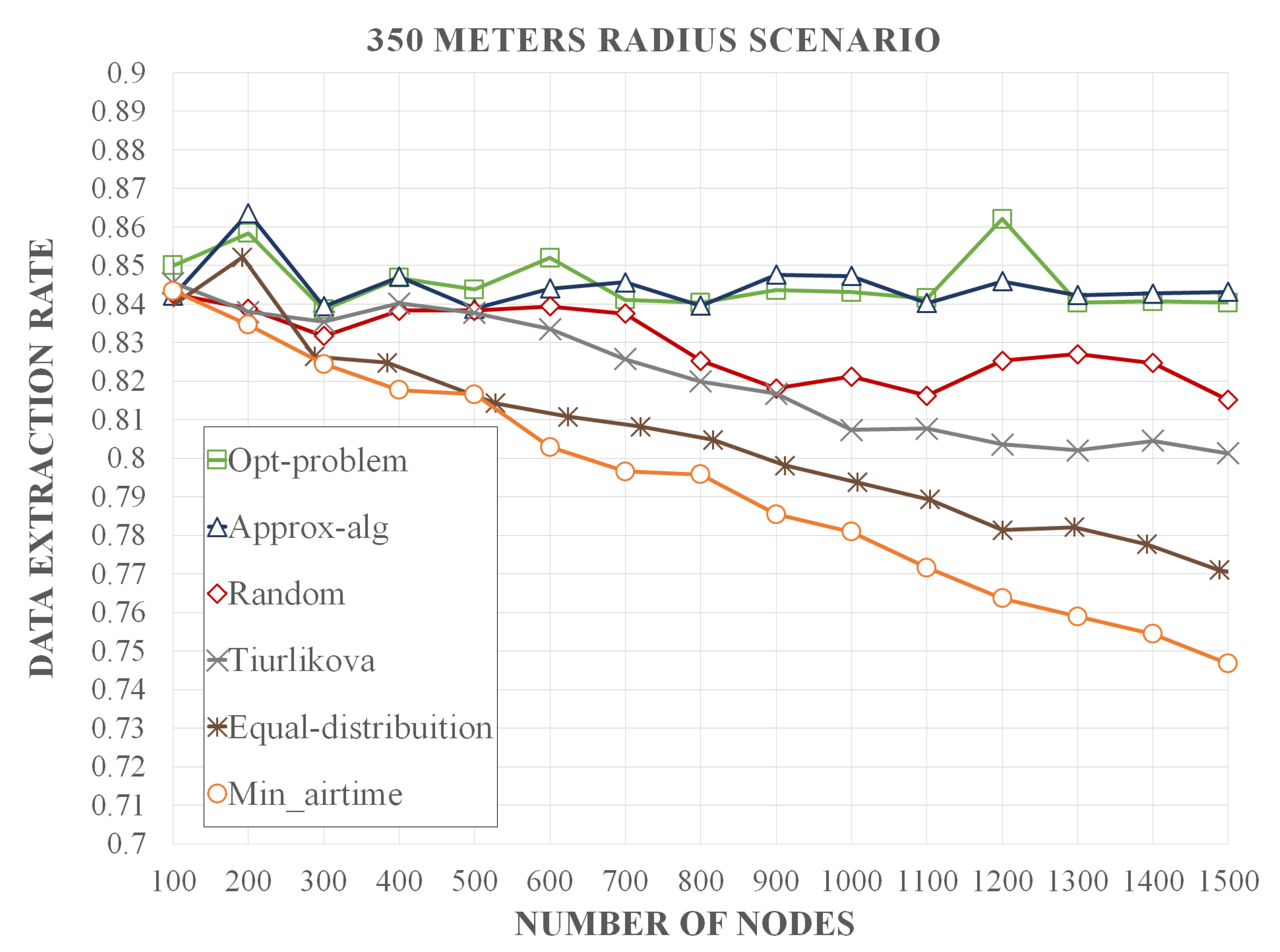
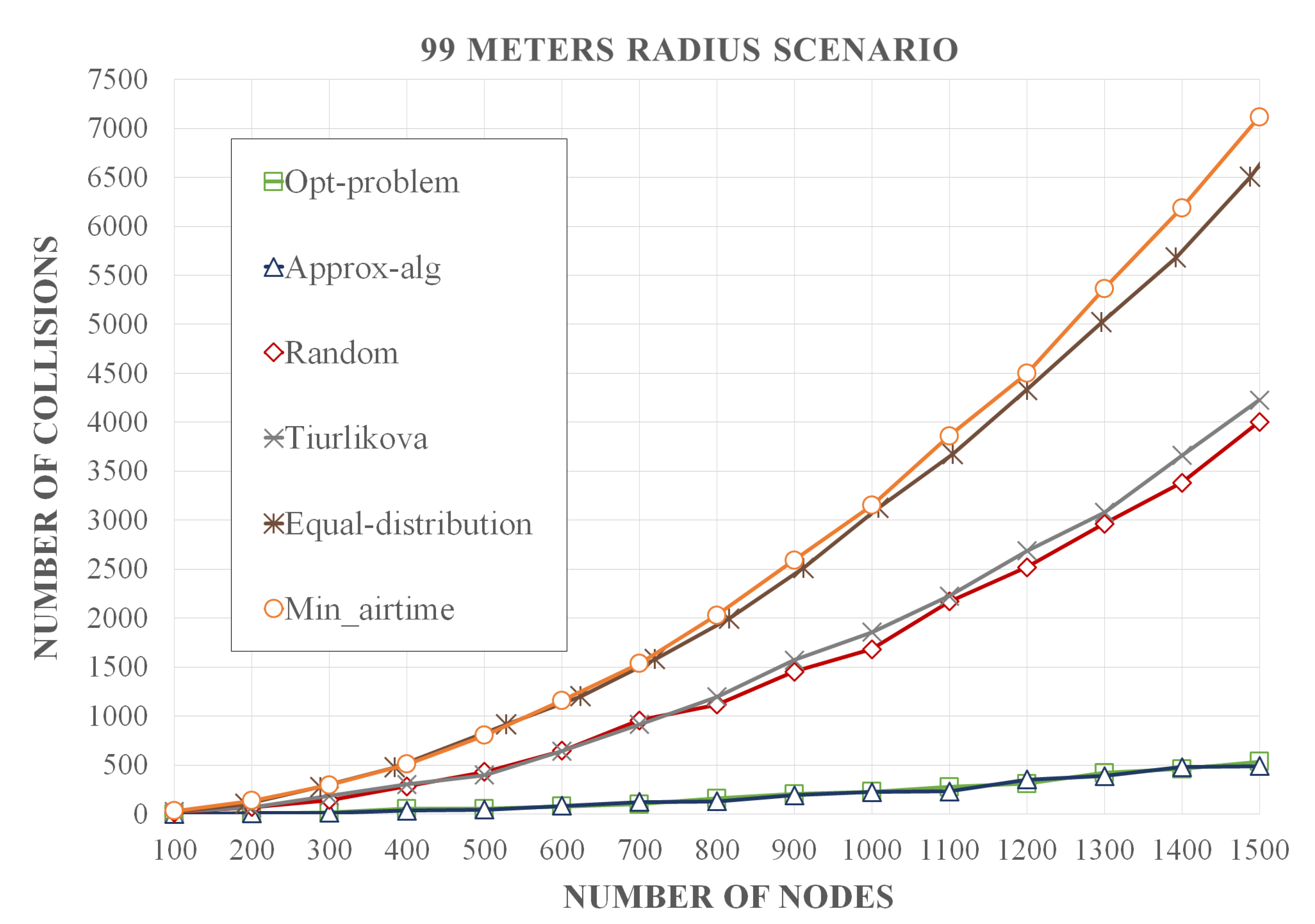
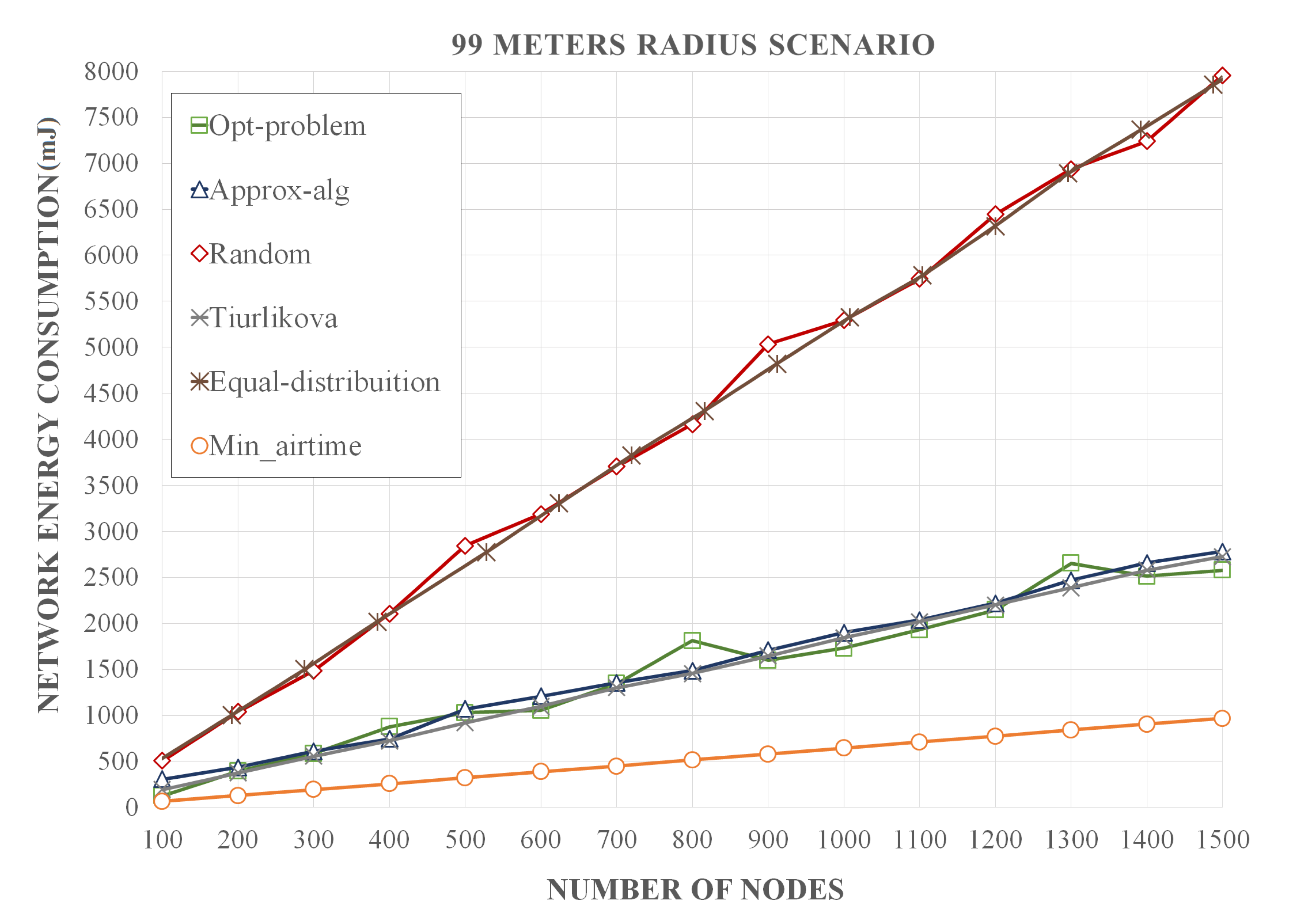
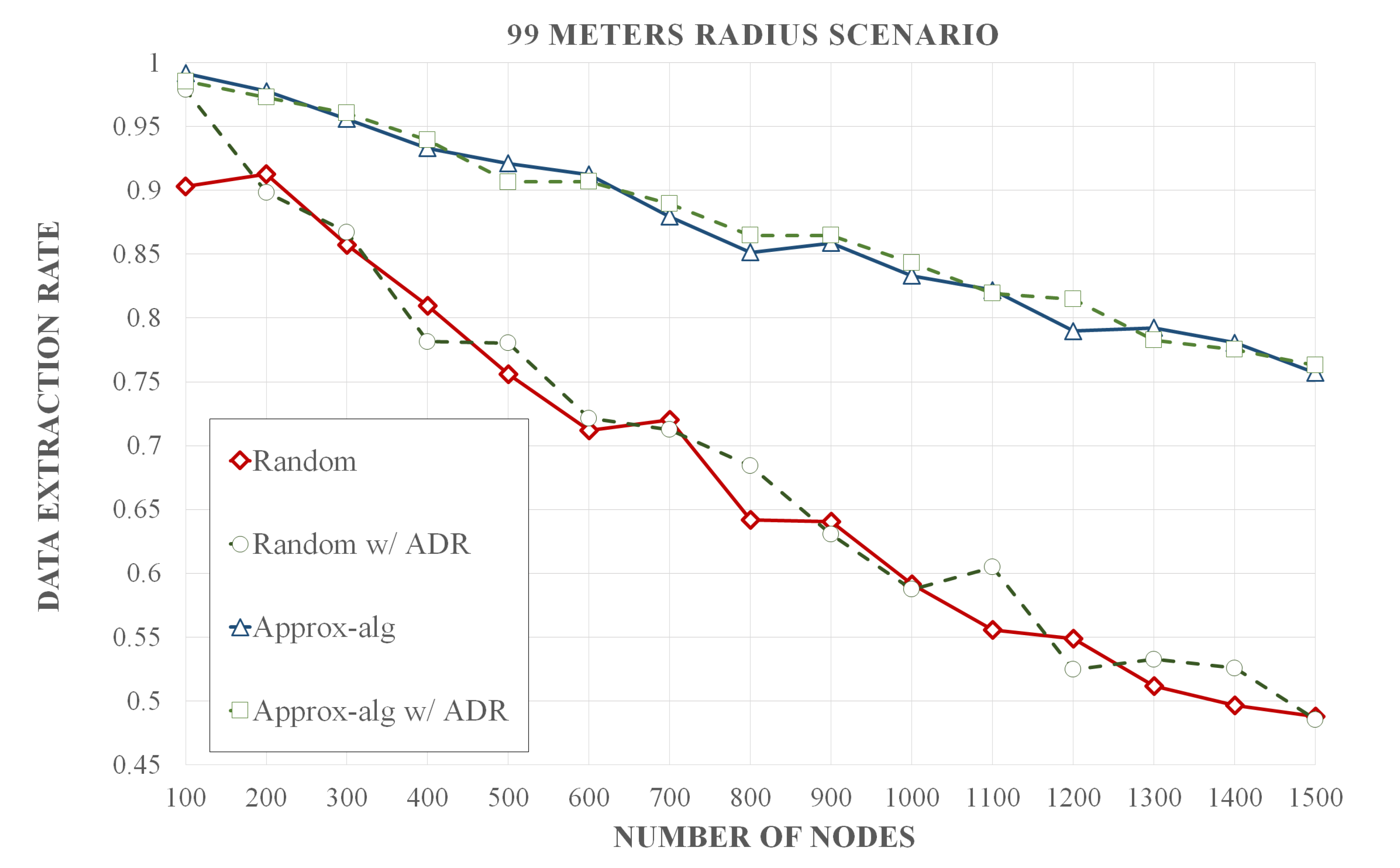
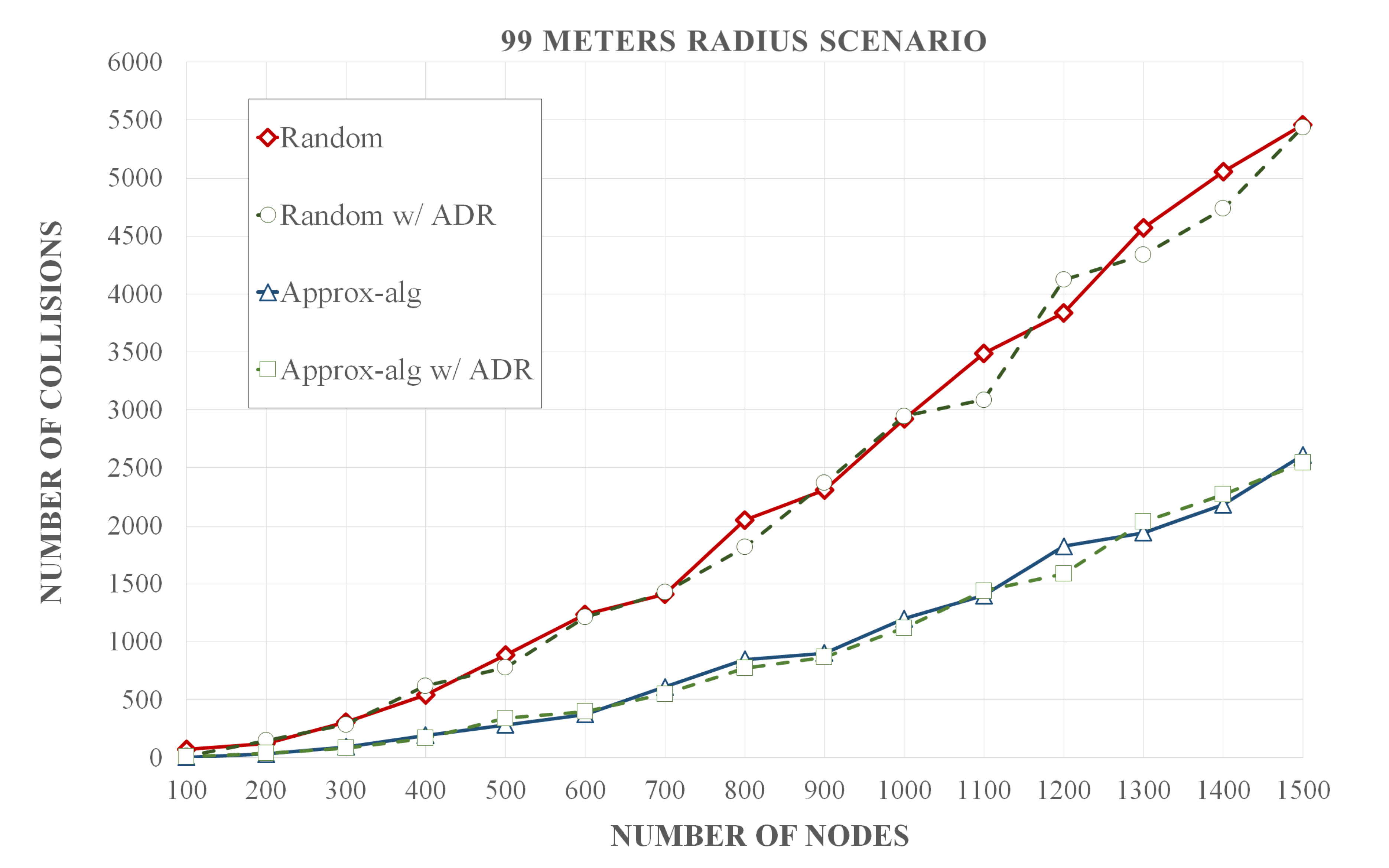
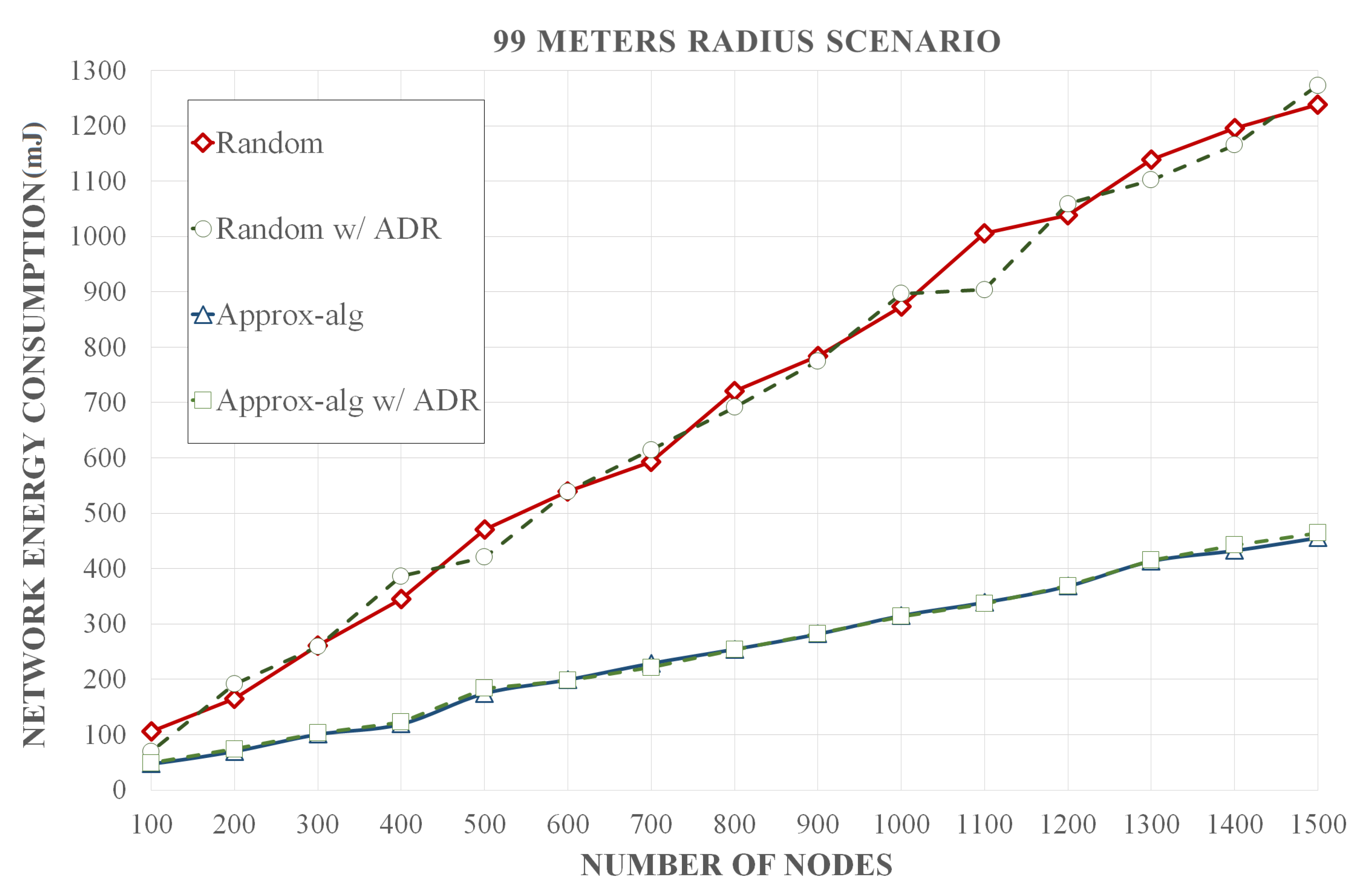
Simulation results show that our methodology optimizes the assignment of CF and SF pairs with an average increase of 6.6% of DER in relation to the standard LoRaWAN assignment, which assigns fixed CF and SF values between the end-devices so that the packets have the minimum air time. In comparison to networks where CF and SF pairs are dynamically assigned by the gateway, there is an increase of 5%, 2.9%, and 1.9% of DER in relation to the Tiurlikova’s, egalitarian, and random distribution, respectively. Furthermore, our method leads to a number of collisions that is 13.3, 12.7, 7.8, and 7.4 times smaller than standard LoRaWAN, egalitarian, Tiurlikova’s, and random distribution, respectively. In relation to the average energy consumption, the scenario with the standard LoRaWAN assignment, whose SF value was set at 7, obtained an energy consumption 2.9 times lower than the proposed optimization. However, our optimization obtained a result similar to Tiurlikova’s method, 3.92 and 2.73 times lower energy consumption than random distribution and egalitarian, respectively.
For future work, we will extend the proposed optimization to support scenarios with longer transmission distance and a larger number of gateways, comparing and analyzing with other allocation methods.