Extraction and Reconstruction of Zebra Crossings from High Resolution Aerial Images

Abstract

In this paper, an automatic approach for zebra crossing extraction and reconstruction from high-resolution aerial images is proposed. In the extraction procedure, zebra crossings are extracted by the JointBoost classifier based on GLCM (Gray Level Co-occurrence Matrix) features and 2D Gabor Features. In the reconstruction procedure, a geometric parameter model based on spatial repeatability relationships is globally fitted to reconstruct the geometric shape of zebra crossings. Additionally, a group of representative experiments is conducted to test the proposed method under interfered conditions, such as zebra crossings covered by pedestrians, shadows and color fading. Furthermore, the performance of the proposed extraction method is compared with the template matching method. Finally, the results show the validation of our proposed method, both in the extraction and reconstruction of zebra crossings.

1. Introduction

Roads and their affiliated features are important man-made objects related to the human daily life. Since the application of remote sensing images, road extraction based on remotely sensed imagery has been researched for decades. The successful approaches for extracting roads have been based on spectral-spatial classification [1] and knowledge-based image analysis methods [2], among others. With the resolution of remotely sensed imagery becoming greater, it is possible to accurately extract the detailed features of affiliated road, such as zebra crossings. Zebra crossings, a type of pedestrian crossing, are used in many places around the world, which is crucial information that is often ignored in geographic data collection [3]. Recently, with the increasing demands of detailed road information stimulated by local accessibility analysis, pedestrian simulation and prediction, and navigation of driverless cars, the extraction of zebra crossings particularly for reconstruction purposes, is becoming an important research topic [4,5,6,7]. High-resolution aerial images are one of the most significant and popular data sources for geographic data retrieval [8,9,10,11,12], and provides further possibilities for zebra crossings extraction and reconstruction.

The extraction of zebra crossings into categorical object instances from aerial images is the first and most critical step for further data processing and reconstruction. Aerial images are mainly used to detect zebra crossings of relatively bigger area to enhance the spatial information of GIS systems. In these studies, the regularity of zebra crossings is utilized to improve their detection rate. In the early 2000s, Chunsun Zhang [13] worked on road extraction, and also on zebra crossing extraction based on the segmentation of the color information and morphological closing for indications of the existence of roads. Tournaire and Paparoditis [14] proposed an automatic approach to detect dashed lines based on stochastic analysis. The core of this approach is the establishment of geometric, radiometric and relational models for dashed line objects. Additionally, Jin et al. [15,16] extracted road markings and zebra crossings based on hierarchical image analyses and 2D Gabor filters [17] in terms of texture features from high-resolution aerial images and obtained moderate results that were effected by shadows.

Beyond the demands of zebra crossing extraction, the reconstruction of zebra crossings with high geometric accuracy is also essential in many practical applications such as traffic simulation, management, maintenance, and updates of cartographic road databases [18,19]. Bahman et al. [19] presented an automatic approach to zebra crossing reconstruction using stereo pairs with geometric constraints of known shape and size. Tournaire and Paparoditis [20] also introduced a method to reconstruct initial zebra crossing models from calibrated mobile images using edge detection, edge chaining, edge matching, and a refining process to optimize the final models. Meanwhile, for the characteristics of invariant objects, zebra crossings are used as ground control objects to provide geo-referencing for mobile mapping systems after they are accurately reconstructed from aerial images [21].

In high-resolution aerial images, the zebra crossings have the following three main characteristics: spectrum, texture and shape. For the first characteristic, the zebra crossings are a sharp contrast with the background. For the second characteristic, the zebra crossings has strong periodic correlation, and simple tuples are always aligned. For the last characteristic, the tuple of the zebra crossings is always a homogenous rectangle or parallelogram. In practice, the images of zebra crossings are often deteriorated due to coverage by cars or pedestrians and shadows, which will affect the spectrum and texture characteristic. Because the texture characteristic is not sensitive to the lighting condition and obscured parts, the shape characteristic performs relatively stably in sample variations. Hence, in this paper, based on the texture characteristics and shape regularity of zebra crossings, we propose a robust algorithm that is capable of extracting and reconstructing zebra crossing from high-resolution aerial images.

The algorithm performs an extraction of the zebra crossings and then reconstructs them. For the extraction step, the JointBoost classifier [22] is used based on their texture patterns described by the gray level co-occurrence matrix (GLCM) [23,24] and a series of 2D Gabor filters [25]. GLCM is one of the texture characteristics descriptors in the space domain, which is simple and effective. The zebra crossings have repetitive properties, which have strong responses in the frequency domain of a series of Gabors filters. For the reconstruction step, we propose a parametrical geometric model to globally describe the shape of zebra crossings. In the model fitting process, we take the zebra crossings’ spatial repeatability into consideration to revise the localized errors caused by the previously mentioned conditions.

This paper is organized as follows: in Section 2, we describe the method for recognizing and reconstructing zebra crossings. The recognition procedure contains the following two components: feature definition and zebra crossing extraction. The reconstruction procedure proposes the parametrical model of zebra crossings and the fitting processing. Section 3 provides validation with several experiments of some images of the zebra crossing obscured by pedestrians, shadows and buses. In the final section, we conclude with comments on the algorithm and future research.

2. Methodology

2.1. Method Overview

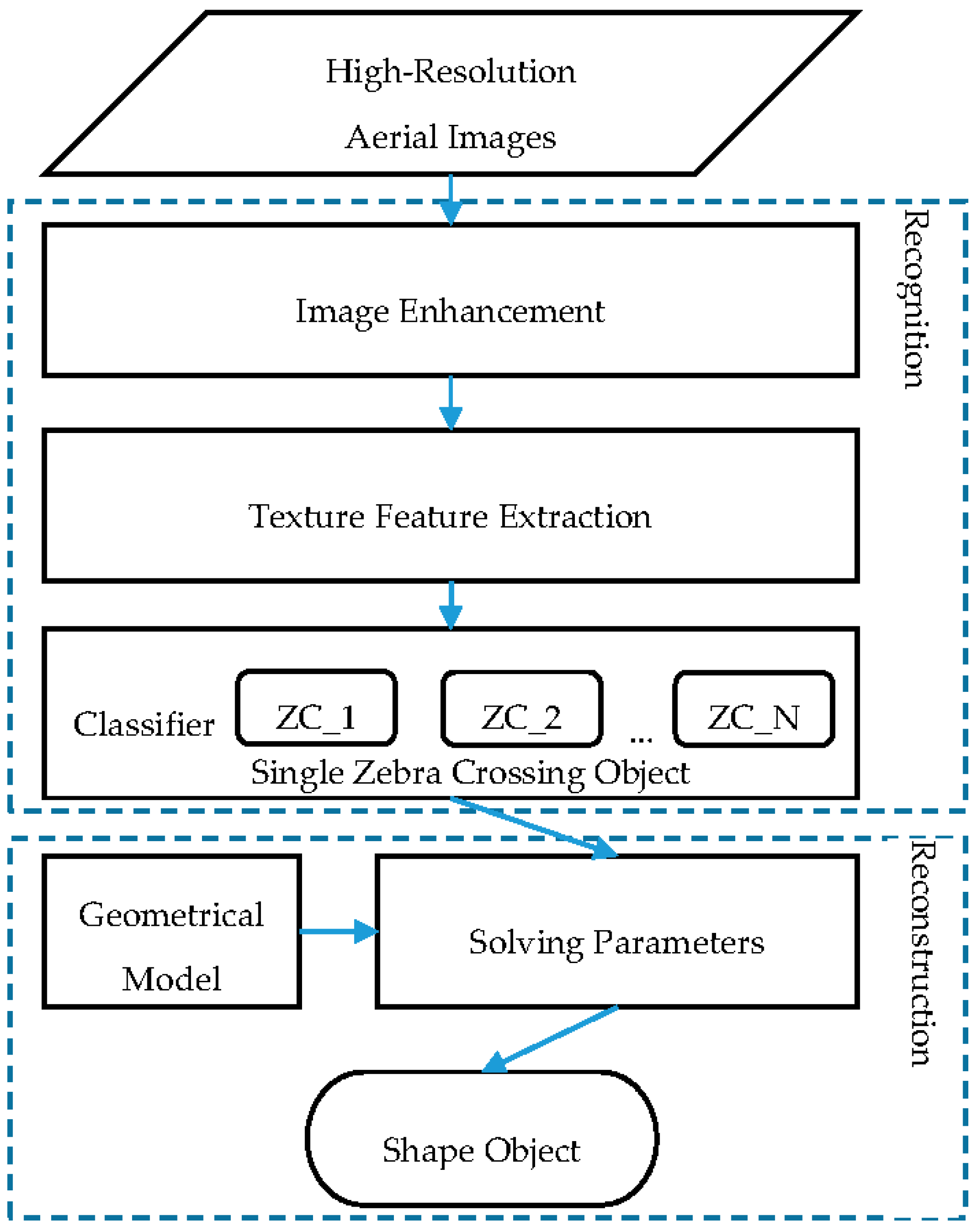
The main approach of our method concentrates on two main phases: zebra crossing recognition and reconstruction; both are depicted in Figure 1. In the first phase, the zebra crossing extraction steps are performed, which include the enhancement of high-resolution imagery, texture feature definition and extraction and a classifier for training and classifying. In the second phase, for every single zebra crossing, the geometrical model is reconstructed by solving a set of predefined parameters using a series of steps.

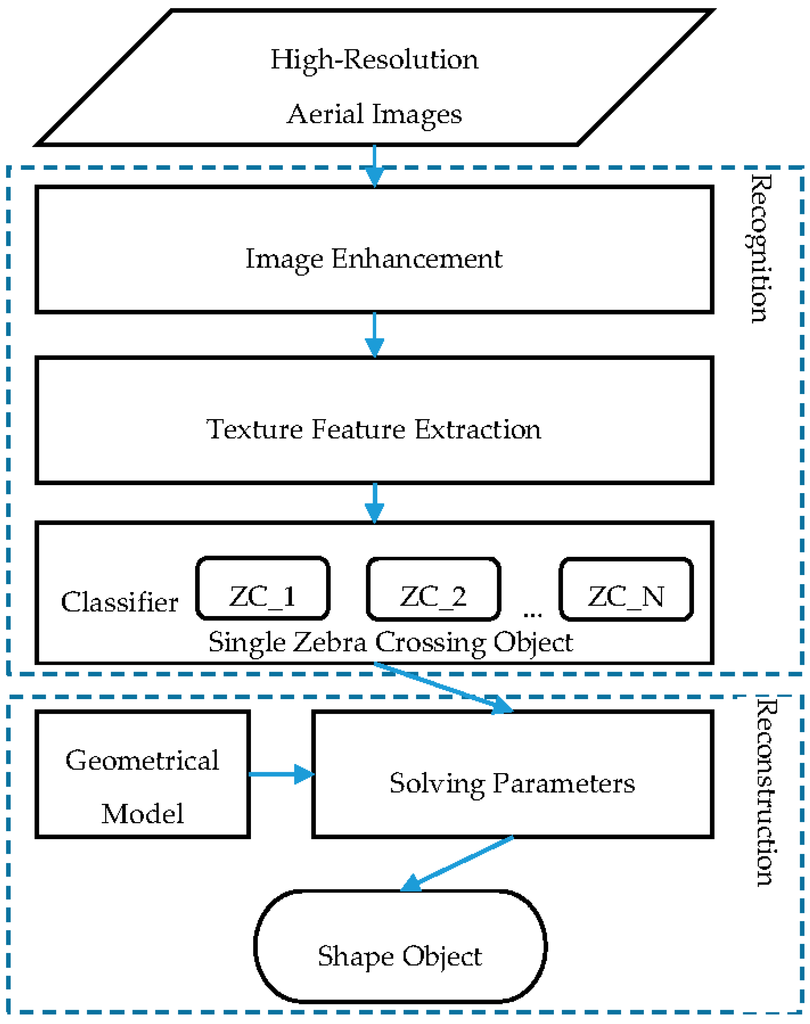
Figure 1. The workflow of the proposed method.

2.2. Zebra Crossing Extraction

This extraction step relies on the JointBoost classifier to distinguish between zebra crossings and their background. As the classification is semi-supervised, we rely solely on the GLCM features and the responses of 2D Gabor filters with multi-scale images.

Before the extraction process, a procedure for image enhancement is performed to optimize the contrast for feature detection as well as to reduce the effects of shadows and white noise in each practical image. The Wallis filter is a local image transform that approximates gray mean and variance of different parts [26]. Namely, it increases the gray contrast of parts where the contrast is small and decreases gray contrast where the contrast is large. Because of the smooth operator introduced when the gray mean and variance are computed, the Wallis filter enhances useful information and suppresses noise simultaneously, expressed as follows.

$$\begin{gathered} f\left(x,y\right)=r_1\times g\left(x,y\right)+r_0 \\ {r}_1=\mathrm{c}\times \frac{s_f}{\mathrm{c}\times s_g+\left(1-\mathrm{c}\right)s_f};r_0=b\times m_f+\left(1-b-r_1\right)m_g \end{gathered}$$

(1)

where $\mathrm{g}\left(x,y\right)$ is the DN (Digital Number) value in the position $\left(x,y\right)$ of original image $\mathrm{g}$, and $f\left(x,y\right)$ is the DN value after the Wallis filter. $r_1$ is a multiplicative coefficient and $r_0$ is an additive coefficient. $m_f$ is the local mean value, and $s_f$ is the variance value to which the original adjusts. $m_g$ is the local mean value, and $s_g$ is the variance value of the original image. $c\in \left[0,1\right]$ is a contrast stretching constant of the image, and $b\in \left[0,1\right]$ is a brightness coefficient. In the Wallis transformation procedure, the original image is divided into blocks, and the image details are enhanced through adjusting the contrast of each small window, as illustrated in Figure 2.

Figure 2. The samples of zebra crossing images before and after the Wallis filter.

2.2.1. Features Definition

GLCM Features

GLCM reflects some comprehensive information of the image texture that considers the direction, distance and gray scale variation of two pixels. Therefore, the size of its dimensions is proportional to the amount of the gray level. With consideration of the balance between the computational efficiency and accuracy, an adequate number of gray levels should be chosen for the statistics of the GLCM. Usually, the 256 grey levels in an image are compressed to save computation time for GLCM [27]. Because the GLCM cannot be used directly as the input features for the classifier, we derive five selection measures from the GLCM for our algorithm.

(1)

Angular Second Moment:

$$\mathrm{ASM}={\displaystyle \sum }_{i=1}^L{\displaystyle \sum }_{j=1}^L{p}^2\left(i,j\right)$$

(2)

where $L$ represents the number of distinct gray levels in the images and $p\left(i,j\right)$ is the (i, j)th entry in the GLCM. This statistic is also called Uniformity, which measures the textural uniformity and disorders.

(2)

Correlation:

$$\mathrm{COR}=({\displaystyle \sum }_{i=1}^L{\displaystyle \sum }_{j=1}^L\left(ij\right)p\left(i,j\right)-u_x{u}_y)/{\mathsf{\sigma }}_x{\mathsf{\sigma }}_y$$

(3)

$$u_x={\displaystyle \sum }_{i=1}^{L}i{\displaystyle \sum }_{j=1}^{L}p\left(i,j\right) u_y={\displaystyle \sum }_{j=1}^{L}j{\displaystyle \sum }_{i=1}^{L}p\left(i,j\right)$$

$${\mathsf{\sigma }}_x^2={\displaystyle \sum }_{i=1}^L{\left(i-u_x\right)}^2{\displaystyle \sum }_{j=1}^{L}p\left(i,j\right) {\mathsf{\sigma }}_y^2={\displaystyle \sum }_{j=1}^L{\left(j-u_y\right)}^2{\displaystyle \sum }_{i=1}^{L}p\left(i,j\right)$$

where $u_x$, $u_y$, ${\mathsf{\sigma }}_x$ and ${\mathsf{\sigma }}_{\mathrm{y}}$ are the means and standard deviations of summarized rows and columns. The correlation feature measures gray-tone linear dependencies in the image.

(3)

Contrast:

$$\mathrm{CON}={\displaystyle \sum }_{i=1}^L{\displaystyle \sum }_{j=1}^L{\left(i-j\right)}^{2}p\left(i,j\right)$$

(4)

This statistic measures the intensity contrast or local variation between a pixel and its neighbor over the whole image.

(4)

Homogeneity:

$$\mathrm{HOM}={\displaystyle \sum }_{i=1}^L{\displaystyle \sum }_{j=1}^{L}p\left(i,j\right)/(1+{\left(i-j\right)}^2)$$

(5)

Homogeneity is also called Inverse Difference Moment (IDM), which measures image homogeneity. The value of $HOM$ is low for inhomogeneous images and has a relatively higher value for homogeneous images.

(5)

Entropy:

$$ENT=-{\displaystyle \sum }_{i=1}^L{\displaystyle \sum }_{j=1}^{L}P\left(i,j\right)log\left\{p\left(i,j\right)\right\}$$

(6)

This statistic measures the disorder or complexity of an image. Inhomogeneous images have low first order entropy, while a homogeneous scene has a high entropy.

To obtain rotation invariable features, we employ the statistical parameters of these five measures, rather than just the GLCM itself, as the features for extraction, including the mean and standard deviation. All of these statistical parameters together are used as the final features for zebra crossing extraction. For simplicity, these parameters are herein called GLCM features.

In general, original images consist of several domains of spatial frequencies. As Figure 3a,b illustrates, it is hard to decouple the zebra crossings from the background of the original images. Fortunately, compared with the background, the zebra crossings with fine edges have higher frequencies, thus a high pass filter is first applied to augment and improve image contrast before a GLCM features computation. Additionally, for the consideration of local scale variation [28,29,30], a DoG (Difference of Gaussians) operator [31] is used which is implemented in the SIFT algorithm [32]. As an example, Figure 4 shows the result of applying a DoG operator with a Gaussian STD $\mathsf{\sigma }=0.5K \left(K=1, 2, 3, 4, 5, 6\right)$ and a $5\times 5$ kernel.

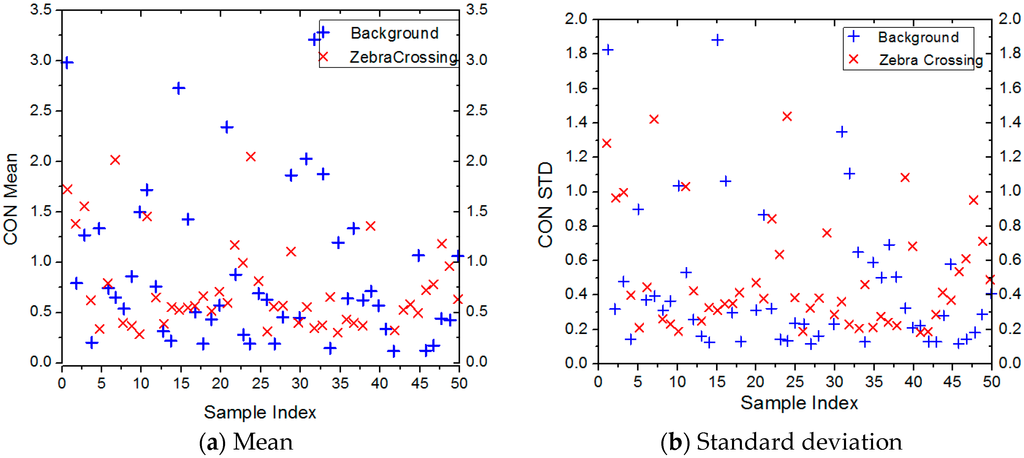
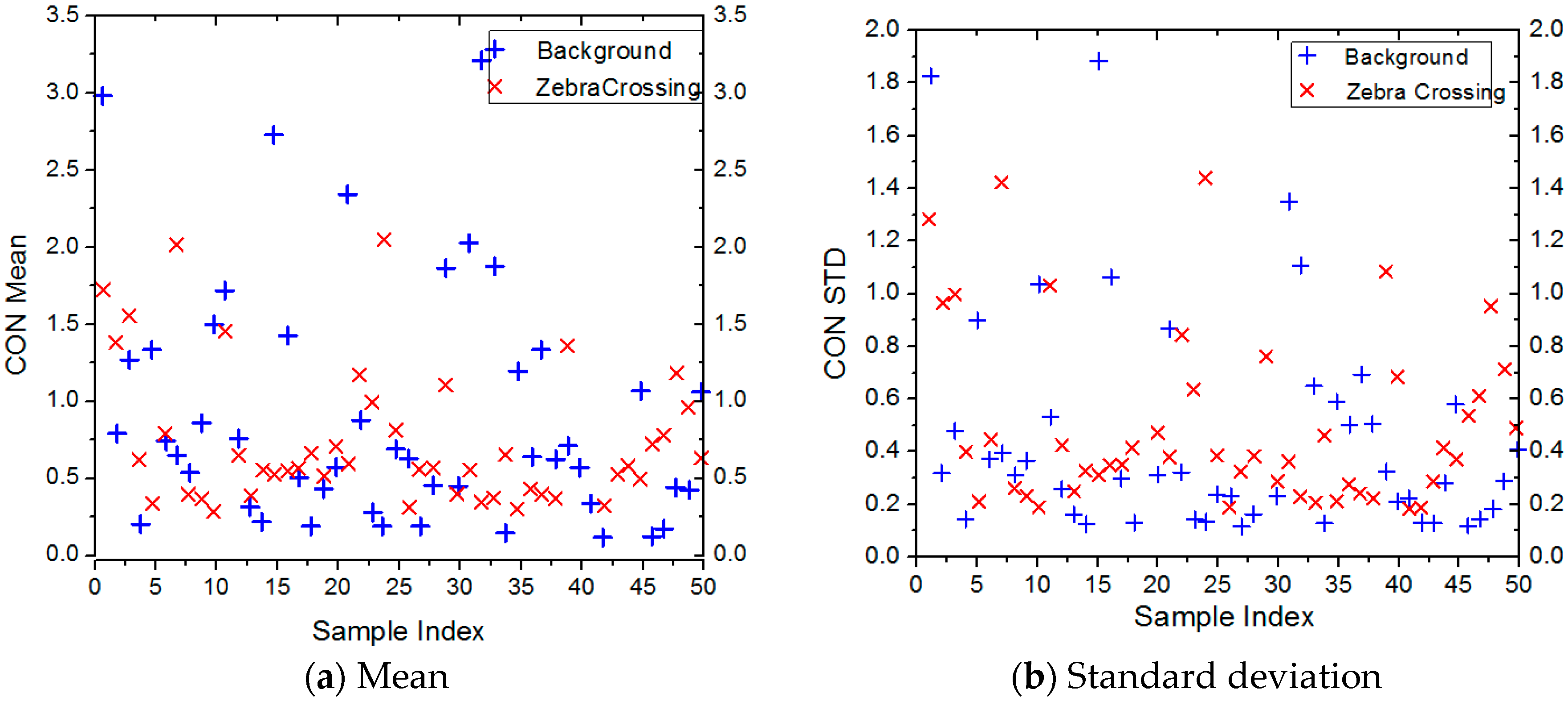
Figure 3. The results of Mean and standard deviation of contrast feature extracted from 50 zebra crossing samples (red crosses) and 50 background samples (blue crosses) based on the original images.

Figure 4. (a) Image after enhancement; (b–f) Image colored by the absolute value of each DoG layer, which are normalized to the range of 0–255.

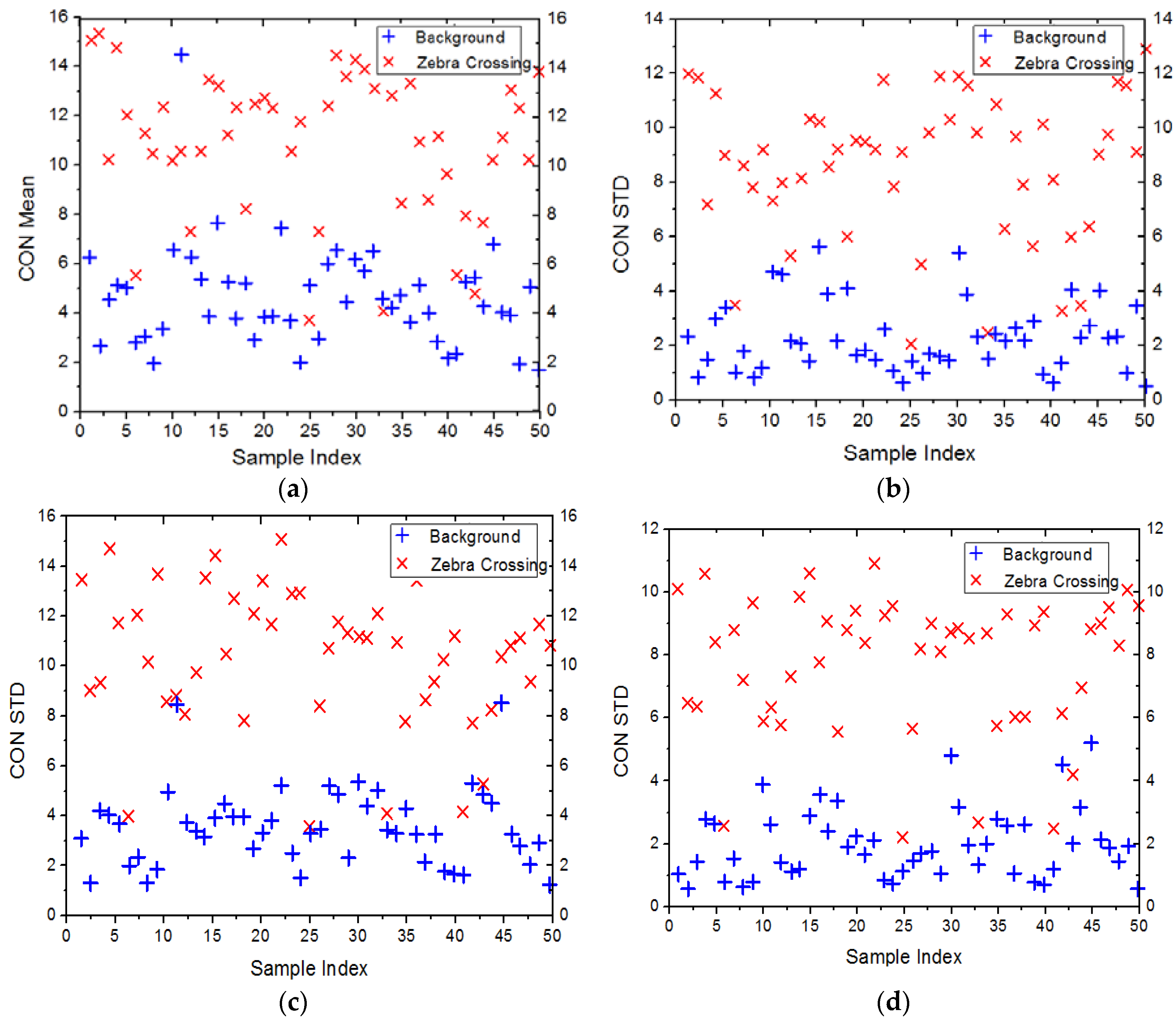
To test the sensitivity of GLCM features at different scales for distinguishing the zebra crossings and background, an experiment is performed by using 50 zebra crossing image samples and 50 background image samples. As an example, Figure 5 shows the mean and standard deviation of the contrast features within the original image and the DoG filtered image in two scales. As we can see, feature segregation of zebra crossings and background samples is significantly superior with DoG filtered results when compared to the original image, which is shown in Figure 3.

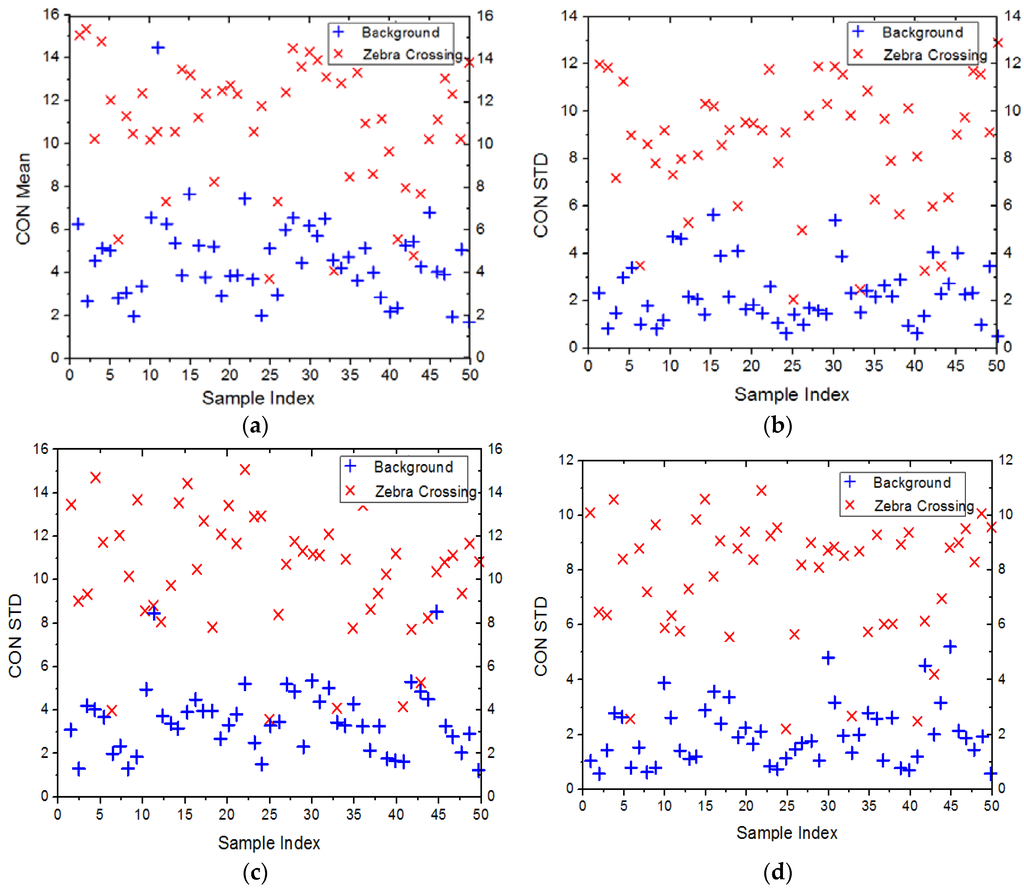
Figure 5. The results of mean and standard deviation of contrast feature extracted from 50 zebra crossing samples (red crosses) and 50 background samples (blue crosses) based on the DoG filtered images at different scales. (a) Mean (G_1.5 − G_1.0); (b) Standard deviation (G_1.5 − G_1.0); (c) Mean (G_2.0 − G_1.5); (d) Standard deviation (G_2.0 − G_1.5).

2D Gabor Feature

A Gabor filter is a linear filter, which is used for edge detection [33]. The 2D Gabor filter extends the properties of the original Gabor filter into two dimensions, and it is able to analyze images of different frequencies, directions and spatial scopes. The 2D Gabor filter performs well in describing image textures with repetitive patterns [34]. The following formula is the description of its kernel function:

$$\begin{gathered} g\left(x,y;\mathsf{\lambda },\mathsf{\theta },\mathsf{\psi },\mathsf{\sigma },\mathsf{\gamma }\right)=\exp \left(-\frac{{x\prime }^2+{\mathsf{\gamma }}^2{y\prime }^2}{2{\mathsf{\sigma }}^2}\right)\exp (i(2\pi \frac{x^{\prime }}{\mathsf{\lambda }}+\mathsf{\psi })) \\ {x}^{\prime }=x\cos \mathsf{\theta }+y\sin \mathsf{\theta } y^{\prime }=-x\sin \mathsf{\theta }+y\cos \mathsf{\theta } \end{gathered}$$

(7)

where $\mathsf{\lambda }$ is the wavelength, $\mathsf{\theta }$ is the direction angle, $\mathsf{\psi }$ is the phase, $\mathsf{\sigma }$ is the variance at the principle direction of the 2D Gaussian function, and $\mathsf{\gamma }$ is the ratio between the two variances of the 2D Gaussian function.

Figure 6 shows the results of applying the Gabor filter with different frequencies to a sample zebra crossing image. It can be clearly observed that, with the application of a low frequency filter, the image becomes globally enhanced, while applying a high frequency filter enhances the detailed information.

Figure 6. Gabor filtered images: (a) is the image after enhancement and (b–d) are the filtered images with the frequency of 2D Gabor filters set to 0.05, 0.08, 0.1, respectively with the direction $\mathsf{\theta }=135°$

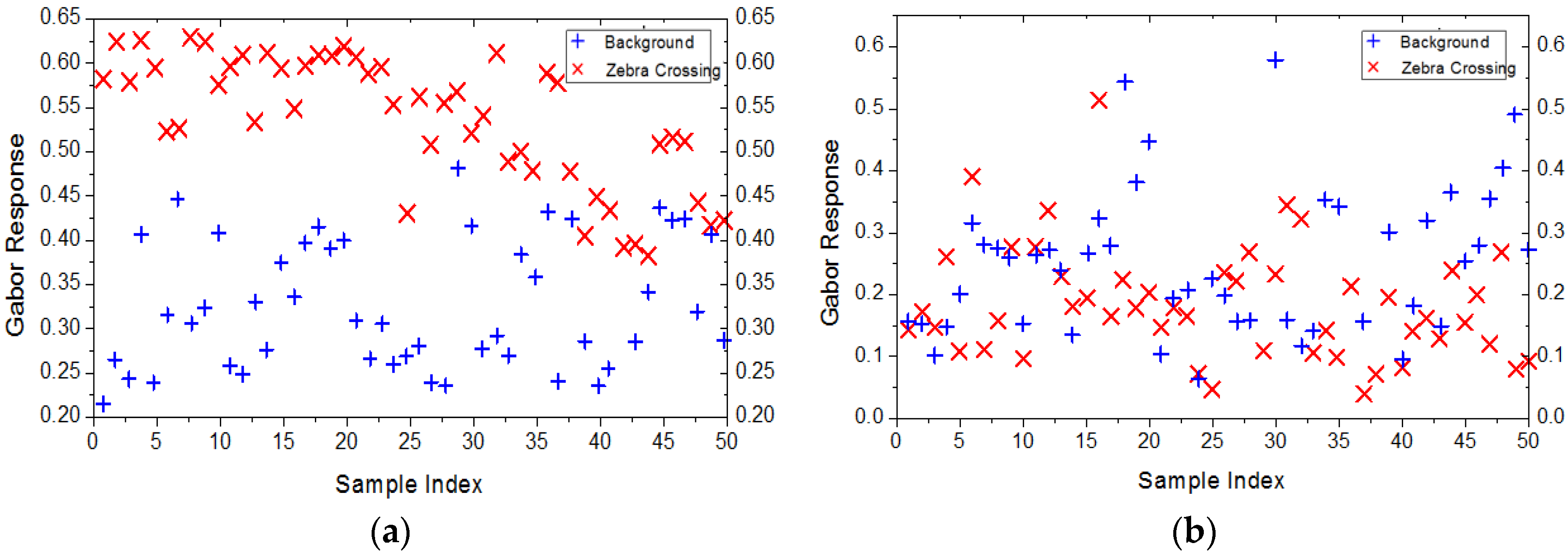
Because the spatial frequency and direction of zebra crossings are arbitrary in the images, three spatial frequency bands and four different directions are assumed based on prior knowledge to cover the spatial frequency and direction of zebra crossings. When the frequency of the filter matches with the spatial frequency of zebra crossing, the magnitude of the response will be large. We take the mean and standard deviation of the response energy in each direction at each spatial frequency as the texture feature. Figure 7 shows the contribution of the feature extracted by two groups of Gabor filters on 50 zebra crossing blocks and 50 background blocks, and the spatial frequency of zebra crossings is near 0.1. It is apparent that the segregation of features extracted by the filters with a frequency of 0.1 is much better than that of the others.

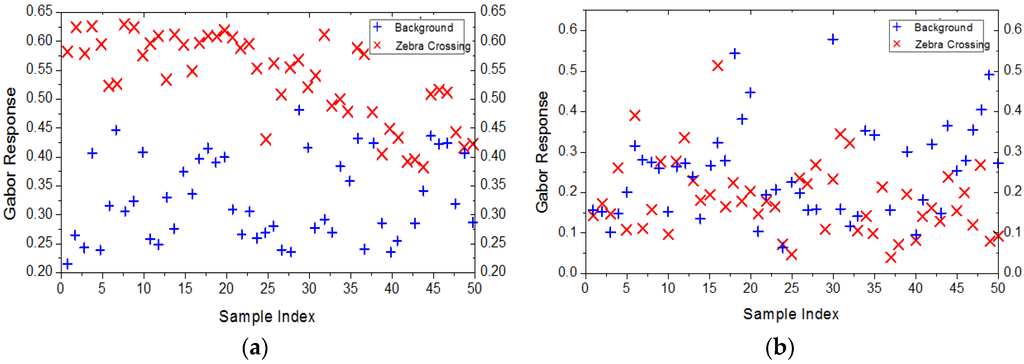
Figure 7. Distribution of the mean feature extracted by two groups of Gabor filters. The frequency of filters used in (a) is 0.1; while it is 0.2 in (b).

2.2.2. Extraction of Zebra Crossings

Principle of JointBoost

JointBoost is an important extension to the boost algorithms, which is powerful and effective for multiclass classification [35,36]. The core idea of JointBoost is to construct a strong classifier out of a series of weak classifiers based on the notion that finding weak classifiers is much easier than finding a strong classifier directly. During the training steps, there are two notable attributes that contribute significantly to the performance of JointBoost. One is that the JointBoost will select the best features for the weak classifiers at each iteration step to ensure minimal errors. This ensures that JointBoost selects the most suitable features for the final classification. The other is that JointBoost can increase the weights of the samples that do not match the classification from the previous iteration step, so the training computation at this step can attach more importance to those samples. This makes the training procedure more effective.

Extraction by JointBoost

The extraction procedure consists of the following two steps: classifier training and zebra crossings extraction. The training samples and the elements for extracting are both based on a small image blocks with a fixed size. Note that this would have been preprocessed before extracting texture features, as introduced in Section 2.2.1.

For the classifier training step, we manually select a set of training samples that include zebra crossings and backgrounds. The samples selected should adequately represent typical zebra crossings and background. Additionally, background samples that are similar to zebra crossings should also be selected, as these samples are significant in improving the performance of the classifier training. Figure 8 is an example of the extraction result. After extraction, several zebra crossing objects are obtained from the target image. Based on those objects, we can reconstruct zebra crossings precisely.

Figure 8. Example of extraction results: (a) The cross marker represents the center of image block which is extracted as a zebra crossing and (b) Outlines of the zebra crossings.

2.3. Zebra Crossing Reconstruction

2.3.1. Geometrical Model

The goal of zebra crossing reconstruction is to find a series of quadrangles that precisely match the edges of zebra crossing stripes. The quadrangle shape of the zebra crossing can then be used to update the GIS database, and provide better landmark representation. In [20], edge detection and edge chaining are introduced for the reconstruction of zebra crossings. Occasionally this method fails due to the edges of the stripes being obscured by pedestrians or cars. However, zebra crossings share a global geometric property of spatial repeatability within a local area, and this principle can be used for the features’ reconstruction.

Obtaining precise stripe edges of zebra crossings is crucial to acquiring global regularities. Because the stripe edges represents the position where the image gradient reaches a local maximum, we can define the Sum of Gradient Edge (SGE) describing the energy of stripe edges as:

$$SGE={{\displaystyle \int }}_{E}g\left(x,y\right)ds$$

(8)

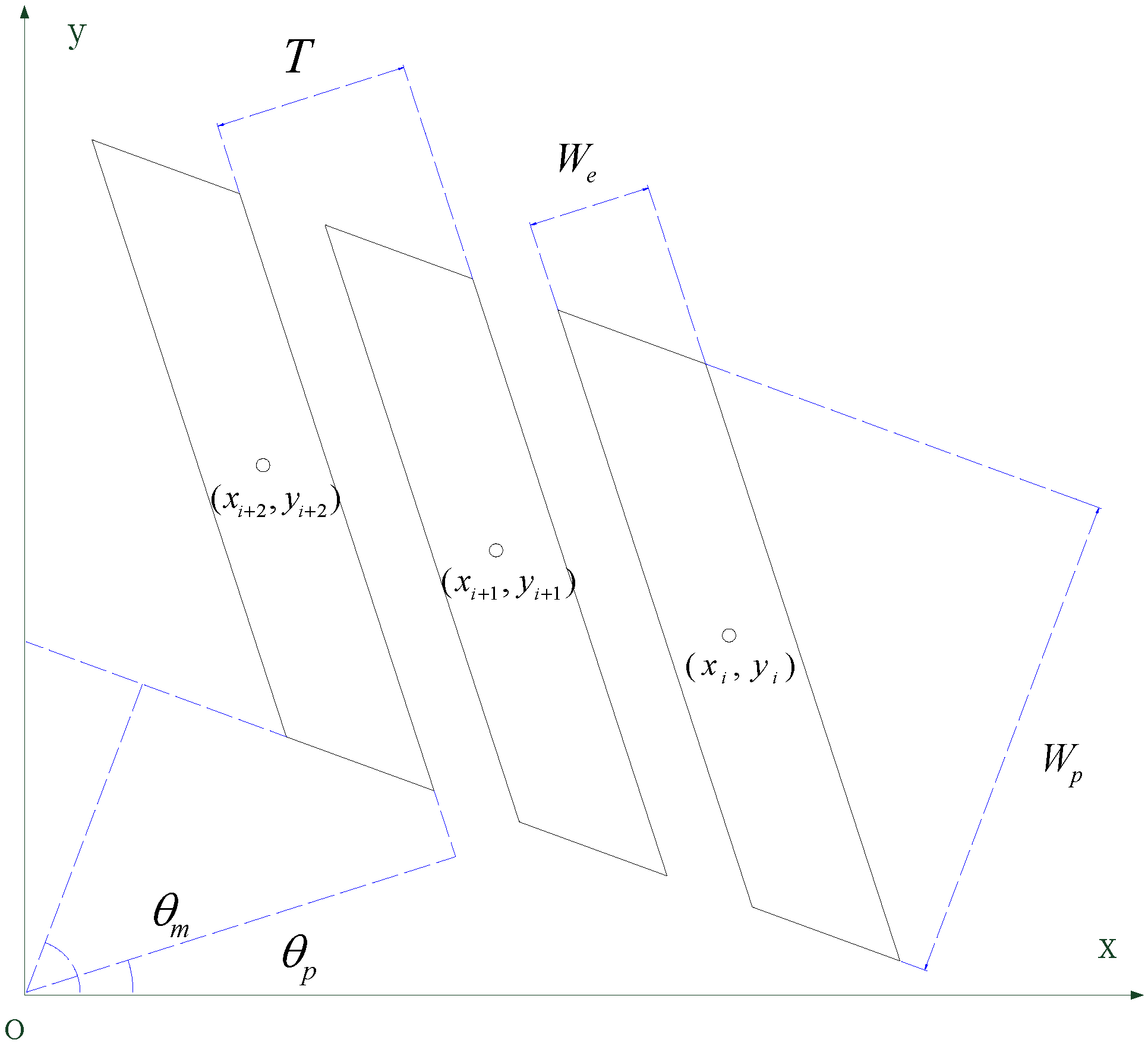
where $g\left(x,y\right)$ is the value of gradient at position $\left(x,y\right)$ and $E$ is defined as a set of positions along the edges of a zebra crossing. The reconstruction of a zebra crossing is essentially a process to reconstruct each stripe’s boundary edges to produce a maximum SGE value. Figure 9 defines a parametrical geometric model to represent the stripes of a zebra crossing.

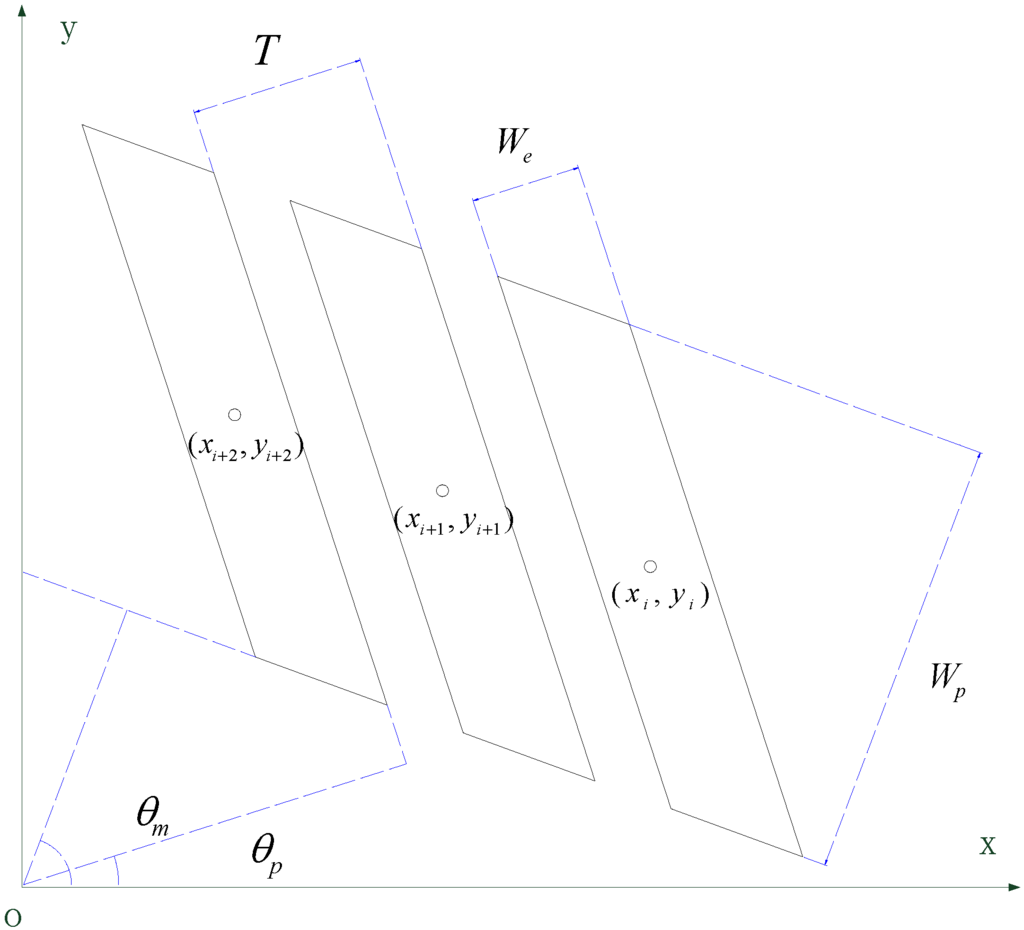
Figure 9. Geometrical model of zebra crossings.

(1)

${\mathsf{\theta }}_m$: the angle of the zebra crossings normal to their principle direction.

(2)

${\mathsf{\theta }}_p$: the angle of the stripes normal to their principle direction.

(3)

$W_p$: the length of the stripe.

(4)

$W_e$: the width of the stripe.

(5)

$T$: the interval of two neighbor stripes.

(6)

${{\displaystyle \cup }}_{i=1}^n\left(x_i,y_i\right)$: the set of center points of the stripes.

It is apparent from the geometry that one stripe can be replaced by four boundary lines. With the center of the stripe denoted as $\left(x_i,y_i\right)$, the function for each of the four lines are:

$$\{\begin{array}{c}{l}_1: x_i\cos {\mathsf{\theta }}_m+y_i\sin {\mathsf{\theta }}_m-\frac{W_p}{2}=0\\ l_2: x_i\cos {\mathsf{\theta }}_m+y_i\sin {\mathsf{\theta }}_m+\frac{W_p}{2}=0\\ l_3: x_i\cos {\mathsf{\theta }}_p+y_i\sin {\mathsf{\theta }}_p-\frac{W_e}{2}=0\\ l_4: x_i\cos {\mathsf{\theta }}_p+y_i\sin {\mathsf{\theta }}_p+\frac{W_e}{2}=0\end{array}$$

(9)

For a stripe’s a center point ($x_i, y_i$), the boundary points of the stripe can be described as:

$$E_e\left(x_i,y_i\right)=\{\left(x,y\right)|\begin{array}{c}[(l_1\left(x,y\right)=0{{\displaystyle \cup }}^{}{l}_2\left(x,y\right)=0){{\displaystyle \cap }}^{}{l}_3\left(x,y\right)l_4\left(x,y\right)\le 0]\\ {{\displaystyle \cup }}^{}[(l_3\left(x,y\right)=0{{\displaystyle \cup }}^{}{l}_4\left(x,y\right)=0){{\displaystyle \cap }}^{}{l}_1\left(x,y\right)l_2\left(x,y\right)\le 0]\end{array}\}$$

(10)

Finally, the set of boundary edge points of all of the stripes will be:

$$E=\underset{i=1}{\overset{N}{{\displaystyle \cup }}}{E}_e\left(x_i,y_i\right)$$

(11)

Thus, if we obtain parameters ${\mathsf{\theta }}_m$, ${\mathsf{\theta }}_p$, $W_p$, $W_e$, and ${{\displaystyle \cup }}_1^N\left(x_i,y_i\right)$, we will be able to establish the geometrical model to describe the set of boundary edge points E In this model, ${{\displaystyle \cup }}_1^N\left(x_i,y_i\right)$ cannot be acquired directly, but every two adjacent center points in ${{\displaystyle \cup }}_1^N\left(x_i,y_i\right)$ have identical intervals of $T$. Thus, ${{\displaystyle \cup }}_1^N\left(x_i,y_i\right)$ are obtained by computing the intersection between the center lines of each stripe and the center line of the zebra crossing. The center lines of each stripe are generated in accordance with parameter $T$.

2.3.2. Solve the Parameters

It is difficult to directly find an appropriate E value to reach the global maximum value of the SGE function. Instead, we first create the initial rough shape of the zebra crossing, then optimize the SGE with a gradient to obtain a precise E. Before computing the original model, the sub-images of the detected zebra crossing are preprocessed into binary images. During preprocessing, histogram equalization, shadow removal and morphological processing are applied to augment the quality of image, as shown in Figure 10.

Figure 10. Example of image preprocessing. (a) is the original image of zebra crossing object; and (b) is the preprocessed image.

Step I:

The Scope

The Hough Transformation (HT) is employed to extract the boundary lines of quadrangular stripes. In some images, the edges along the zebra crossings are blurred, which will introduce inaccuracies to the line detection results. To improve the accuracy of boundary line detection, we separate the procedure into two steps. First, we use HT to detect the boundary lines to obtain initial results. Then, we adjust the direction of the boundary lines by the gradient values of pixels along the detected lines. With this method, we can find the edges of zebra crossing stripes and estimate the scope of the zebra crossing as well as the two angle parameters ${\mathsf{\theta }}_{\mathrm{m}}$ and ${\mathsf{\theta }}_p$. Figure 11 shows the results of the zebra crossing boundary line detection.

Figure 11. Boundary line detection. (a) Depicts the edge lines of stripe widths detected by HT; (b) Depicts the edge lines of stripe lengths detected by HT; (c,d) are the boundary lines of a zebra crossing.

Step II:

The Spatial Repetitive Period

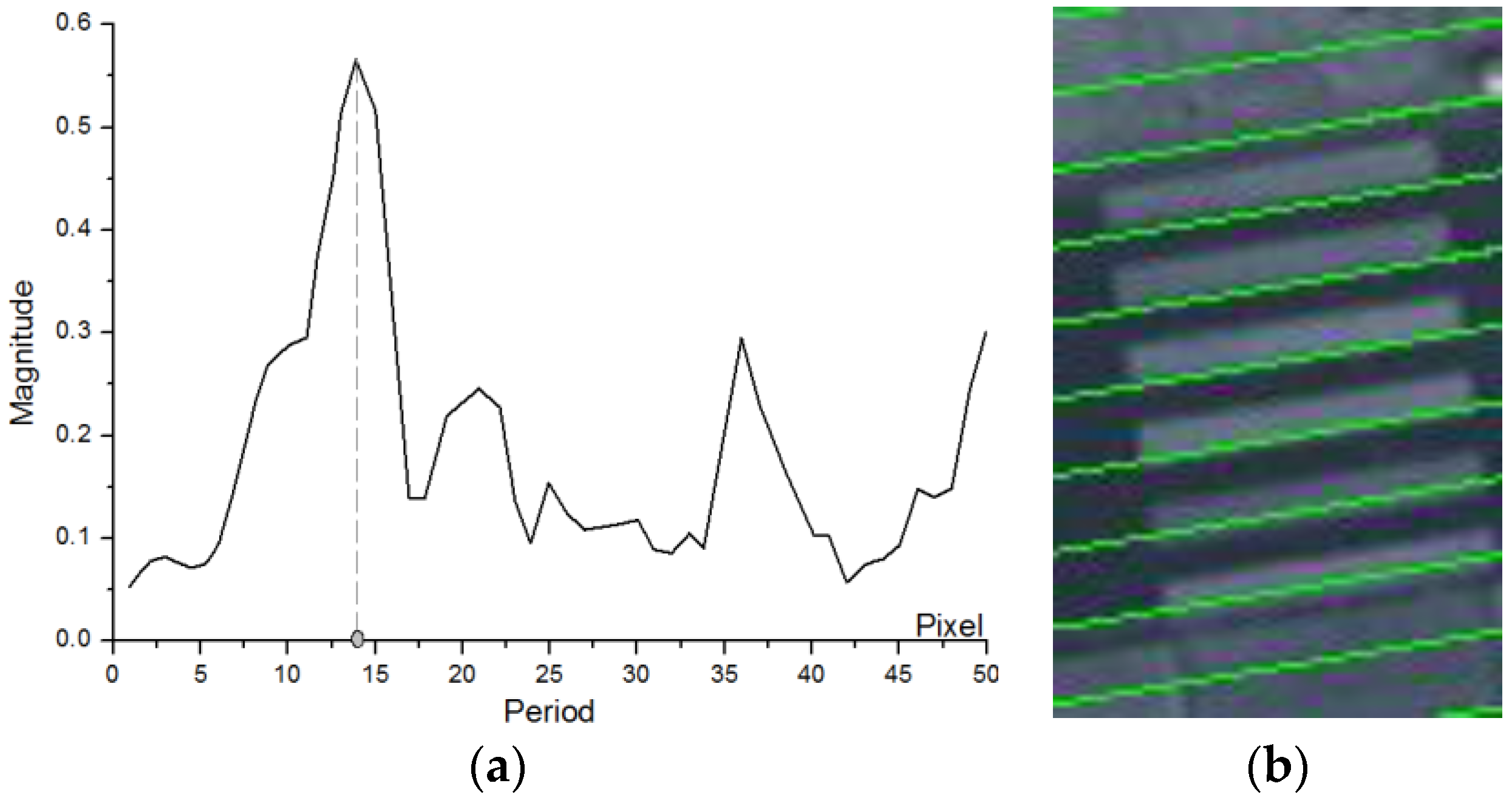
The spatial repetitive period, denoted by T, is a crucial parameter for repetitive regularity. However, the line detection process described in Step I may not cover all the lines, which may lead to the failure of repetitive estimation from the line distance analysis from the perspective of image statistics. The Gabor transform, which is a special case of short time Fourier transform, is good for analysis of non-stable signals which overcomes the space requirement problems that are present with the normal Fourier Transform (FT) [33]. We can transform the image into frequency space to find out the proper T. Figure 12a is an example showing the frequency distribution along the main direction of a zebra crossing. The frequency relative to the peak of the distribution represents the spatial frequency of the zebra crossing, from which we can calculate the spatial period. Figure 12b shows a group of parallel lines generated by this spatial period. Evidently, the results show that not all the lines cover the edges of the stripes precisely, indicating that the spatial period extracted by the Gabor filter is not accurate. Hence, this spatial period can only be used as an initial value that will be adjusted for optimization.

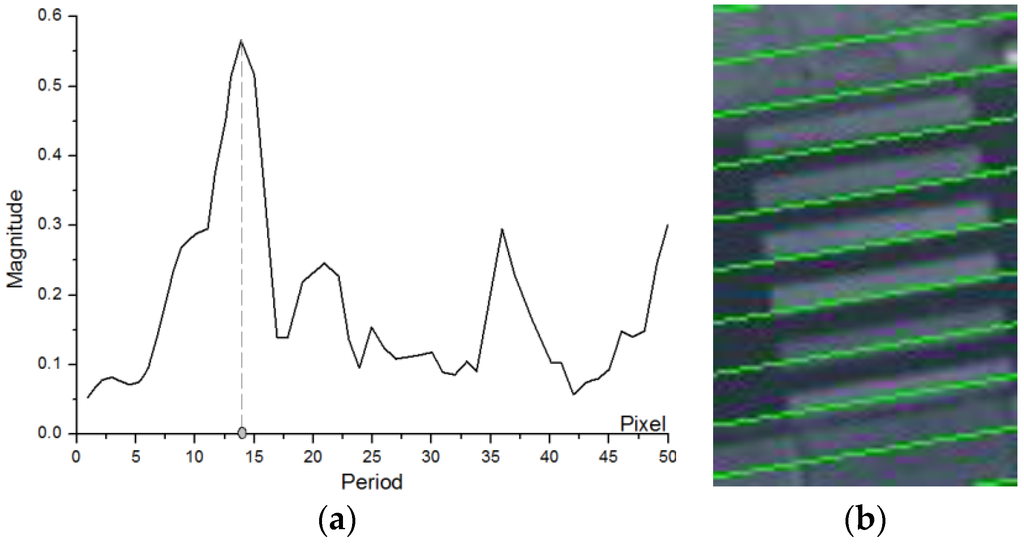
Figure 12. Determining the repetitive pattern of zebra crossing. (a) Frequency distribution on the main direction of zebra crossing; (b) Parallel lines generated representing the spatial period.

Step III:

The Width and Centers

The gradients on the opposite edges of a stripe have opposite directions as shown in Figure 13a,b. Thus, the two groups of lines covering the opposite edges of the stripes can be defined as:

$$L_f=\underset{i=1}{\overset{N}{{\displaystyle \cup }}}\left\{\left(x,y\right)|x\cos {\mathsf{\theta }}_p+y\sin {\mathsf{\theta }}_p-\left({\rho }_f+i{T}_0\right)=0\right\}$$

(12)

$$L_b=\underset{i=1}{\overset{N}{{\displaystyle \cup }}}\left\{\left(x,y\right)|x\cos {\mathsf{\theta }}_p+y\sin {\mathsf{\theta }}_p-\left({\rho }_b+i{T}_0\right)=0\right\}$$

(13)

where $T_0$ is the spatial period obtained in step II, and ${\mathsf{\rho }}_f$, ${\mathsf{\rho }}_b$ are the positions of the first lines among the two groups of lines. The solution of parameters ${\mathsf{\rho }}_f$ and ${\mathsf{\rho }}_b$ are within the range of $\left[0,T_0\right)$. Hence, the parameters can be obtained by enumerating the parameters and those that give a maximal $SGE$ will be selected. With these two groups of parallel lines, the width of the stripe can be described as:

$$W_e^0=\{\begin{array}{c}{\mathsf{\rho }}_f - {\mathsf{\rho }}_b \left({\mathsf{\rho }}_f\ge {\mathsf{\rho }}_b\right)\\ T_0+{\mathsf{\rho }}_f - {\mathsf{\rho }}_b \left({\mathsf{\rho }}_f<{\mathsf{\rho }}_b\right)\end{array}$$

(14)

Figure 13. (a) The gradient of the edges on one side of the stripe; (b) The gradient of edges on the opposite side of the stripe; and (c) The two groups of fitted lines on both sides of the stripes.

For the spatial period with bias, this width is also an approximate value. Figure 13a,b show the two groups of stripe lines. Furthermore, ${{\displaystyle \cup }}_{i=1}^N\left(x,y\right)$ can be calculated using the spatial period, the width of the zebra crossing stripe and its four boundary lines.

Step IV:

Global Optimization

At this point, we have all the parameters needed to generate a geometrical model. Because the main direction is determined by the results of zebra crossing extraction, we only need to optimize the spatial period T and width of stripes W. The SGE function can be described as:

$$SGE=SGE\left(T,W_e\right)$$

(15)

In the optimization, the Gradient Descent method [37] is utilized to optimize those two parameters, which allows the SGE to reach a local maximum. Hence, we change the format into differential model for the Gradient Descent, shown in Equation (16).

$$\nabla SGE=\left[\frac{\partial SGE}{\partial T},\frac{\partial SGE}{\partial W_e}\right]\approx \left[\frac{SGE\left(T,W_{e0}\right)-SGE\left(T_0,W_{e0}\right)}{T-T_0},\frac{SGE\left(T_0,W_e\right)-SGE\left(T_0,W_{e0}\right)}{W_e-W_{e0}}\right]$$

(16)

In the following example, Figure 14b shows two optimized groups of lines, which cover the edges of stripes more accurately than the lines before optimization, as shown in Figure 14a.

Figure 14. (a) Two groups of edge lines before optimization; (b) Lines after optimization; and (c) An example of reconstruction result.

2.3.3. Repair Discontinuities

In some cases, one zebra crossing may be separated into several parts due to obscuring objects such as cars, buses and pedestrians. The connectivity and repetitive pattern are frequently used to address the repairing or merging of the broken zebra crossing justified by the following principles: (1) each part has the same or similar geometry parameters; and (2) the center points of stripes between the two parts should be collinear. From these principles, we define can define the following semantic rules for repairing and merging a zebra crossing:

• Rule 1: The distance of two zebra crossing parts should be smaller than a threshold.
• Rule 2: When fitting the center points to a line, the residual should be smaller than a threshold.
• Rule 3: When selecting two stripe’s center points $p$ and $q$, the distance between $p$ and $q$ should be integral multiples of the repetition period.

For two adjacent zebra crossings, if they follow the conditions listed above, we can combine them into one zebra crossing and re-calculate the parameters of the new zebra crossings.

3. Experiments Section

To test the proposed method, the experiment uses three datasets with different GSD. The first set of test data were collected in Paris, France with a resolution of approximately 0.1 m. The second set of test data were collected in Datong, China with a resolution of approximately 0.05 m. The third set of test data were collected in New York, United States, with a resolution of approximately 0.2 m. The experiments consist of the following two parts: zebra crossing extraction and geometric shape reconstruction.

3.1. Zebra Crossing Extraction

JointBoost is used as the classifier for the extraction of zebra crossing based on texture features of multi-scale GLCM and 2D Gabor. Furthermore, we compare the results of the proposed method to the results of a template matching method. We evaluate the performance of the algorithm with two test data using the same classifier. The training datasets contain 50 positive zebra crossing samples and 150 negative samples. We also use one positive sample as the template to detect the zebra crossing in the template matching method with different threshold.

3.1.1. Experiment I: Zebra Crossing Detection

There are 12 images in three datasets of zebra crossings with different conditions, including features obscuring the zebra crossings as well as color degradation. Figure 15 shows the extraction results of zebra crossings by JointBoost. In Figure 15, all the zebra crossings are detected, despite some disturbances within the image such as color degradation (within the yellow circles) and shadowed zebra crossings (within the red circles).

Figure 15. Extraction results of three datasets by the proposed method.

From these experiments, we find that the performance of JointBoost is good. The JointBoost classifier is built on theories of statistical analysis, which combines many weak classifiers to generate a strong classifier. Each of the weak classifiers is sensitive to a certain feature and statistically defines the possibility of a sample being a zebra crossing or background. Additionally, JointBoost has the ability to select only those features that perform well during classification. JointBoost also utilizes the mis-matched samples to improve the performance of feature extraction, which can help the classifier to differentiate background objects with similar appearances to zebra crossings.

As shown in Table 1, the results are evaluated at the image block level rather than object level. We split the images into 25 × 25 (𝑝𝑖𝑥𝑒𝑙) block and count the number of correctly extracted pixels. Table 1 is the quantitative analysis of the extraction results of these three datasets. In dataset I, there are 472, 439, 398, 143 pixels belonging to zebra crossings, 251, 68, 400, 845 in dataset II, and 352, 468, 395, 368 in dataset III, respectively. By results in dataset I, the correct extraction rates are 90.3%, 87.5%, 94.2%, 83.9%, in dataset II are 98.4%, 91.2%, 82.8%, 69.3%, and they are 80.7%, 83.8%, 81.8%, 88.9% in dataset III. The percentages of omission extraction in dataset I are 9.7%, 12.5%, 5.8%, 16.1%, in dataset II are 1.6%, 8.8%, 17.25%, 30.7%, and in dataset III are 19.3%, 16.2%, 18.2%, 11.1%.

Table 1. The extraction results of three datasets by the proposed method.

	Dataset I (Blocks)				Dataset II (Blocks)				Dataset III (Blocks)
	a	b	c	d	a	b	c	d	a	b	c	d
correct	426	384	375	120	247	62	331	586	284	392	323	327
wrong	14	2	4	3	4	3	55	4	0	9	4	2
omission	46	55	23	23	4	6	69	259	68	76	72	41

3.1.2. Effectiveness of Features

The extraction method relies on GLCM features and 2D Gabor features to make the final classification judgment. To examine the contribution of these two features for extraction, we compare the validation results against the following three conditions: (1) using only GLCM features; (2) using only 2D Gabor features; (3) using both types of features. We tested those conditions on two images to evaluate the contribution of each feature to the final extraction.

In Figure 16, the left column representing image A contains 11 zebra crossings, and the right column representing image B contains 5 zebra crossings. We deliberately selected images with a large difference in color tunes to test the sensitivity of the features detection to the image tone. Image A is a much brighter overall than image B. We trained the JointBoost classifier for each image using the GLCM feature detection method and then again using the 2D Gabor feature detection method. Figure 16a,b show the results extracted by using only GLCM features. Figure 16c,d show the results extracted by using only 2D Gabor features. When compared to the performance of the results based on 2D Gabor features as shown in Figure 16c,d, the results relying on the GLCM feature are less accurate as shown in Figure 16a,b. However, when we use both features together, as shown in shown in Figure 16e,f, it yields better results than anyone based on GLCM or 2D Gabor.

Figure 16. (a,b) are the results under condition 1; (c,d) are the results under condition 2; (e,f) are the results under condition 3.

The algorithm can successfully extract some parts of the zebra crossings, as shown in Figure 16e,f. To give precise information of the effectiveness of each feature, we evaluated the results with the same method in Section 3.1.1. Table 2 is the quantitative analysis of the extraction results of these features. In image A, there are 478 pixels belonging to zebra crossings, and 408 in image B. Using the features of GLCM, 2D Gabor, and a combination of GLCM and 2D Gabor, the correct extraction rates in image A are 66.1%, 70.5% and 77.8%, respectively, and in image B are 77.2%, 87.4%, and 90.3%, respectively. The percentages of omission extraction in image A are 33.9%, 29.5%, and 22.2%, respectively, in image B are 23.0%, 12.6%, and 9.7%, respectively. Although the GLCM is more effective in the zebra crossing extraction, the results are improved with consideration of the 2D Gabor features as well.

Table 2. The comparison of extraction results under three different conditions.

	Image A (478 Blocks)			Image B (382 Blocks)
	GLCM	2D Gabor	Both	GLCM	2D Gabor	Both
correct	316	337	372	294	334	345
wrong	6	1	0	0	4	0
omission	162	141	106	88	48	37

3.2. Geometric Shape Reconstruction

The test images contain significant interference information, which cause difficulties in geometric shape reconstruction. To evaluate the robustness of our method, we test it under various conditions including images containing covered zebra crossings, non-rectangular zebra crossings, color degradation and half-shaded zebra crossing.

3.2.1. Zebra Crossing Covered by Objects

It is possible that stripes are covered by pedestrians, cars or buses, which disturbs the stripe boundaries. After the process of image binarization, these disturbances introduce some small geometric flaws, which breaks the regularity of the stripes. As a consequence, some of the zebra crossings will be broken up into two or more parts. However, the boundary of each stripe can be still recovered based on the global repetitive structure of zebra crossings.

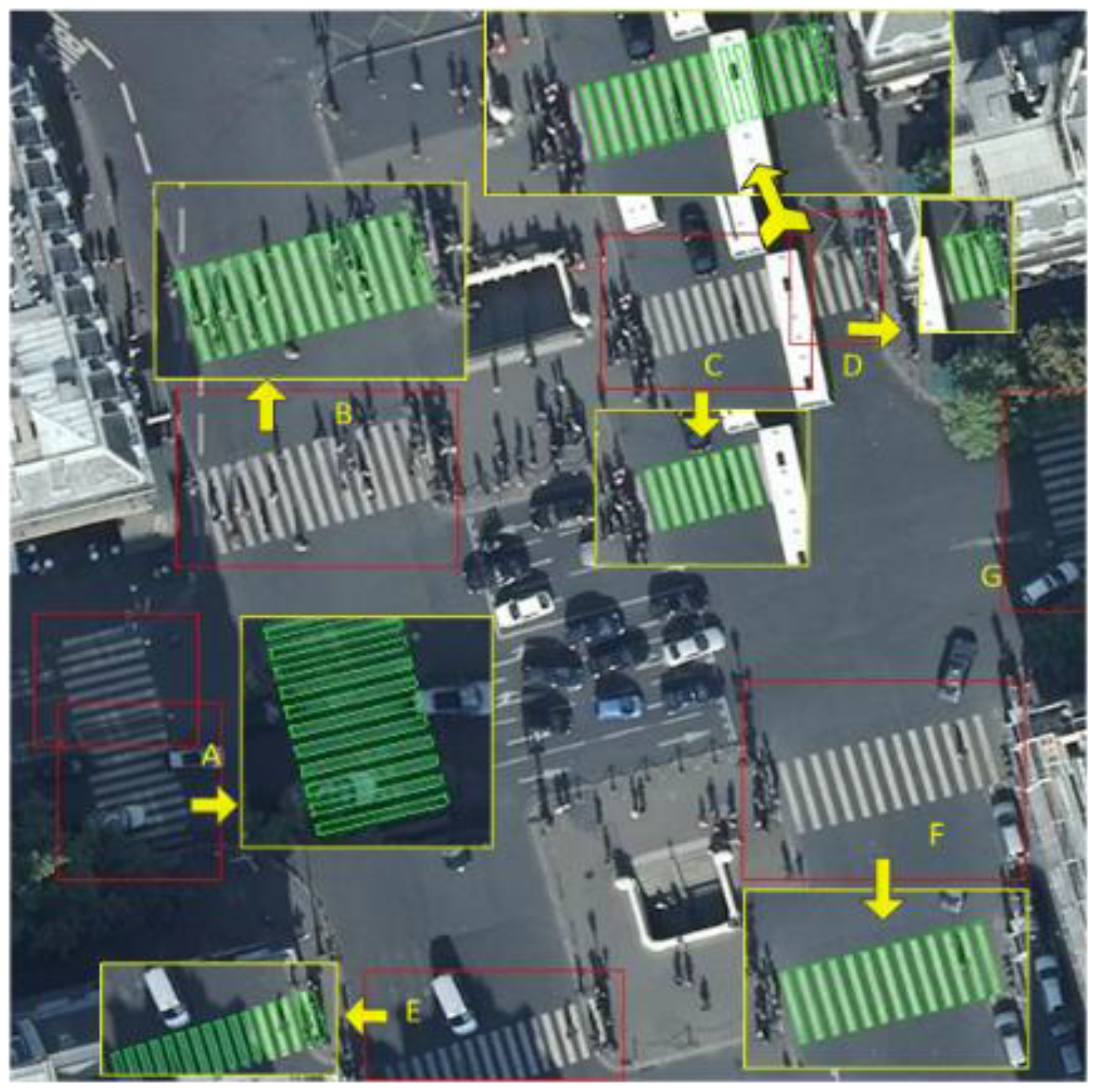
In Figure 17, zebra crossings A, B, and E are the reconstruction results, in which the zebra crossings are covered by buses, pedestrians and shadows. F shows the reconstruction result of a clean zebra crossing. For zebra crossings C and D, which are separated by a bus. They can be jointed into one crossing based on the rules defined in Section 2.3.3, using the principle of spatial repeatability. With respect to image A which contains two zebra crossings, our algorithm extracts them as two standalone zebra crossings, and merges them into one because they are very close and have very similar geometric parameters. The algorithm successfully estimates the geometry parameters and reconstructs zebra crossing E, even though one of its corners does not appear in the image. The algorithm fails in reconstructing zebra crossing G because the area of G is too small for the algorithm to find the correct boundaries.

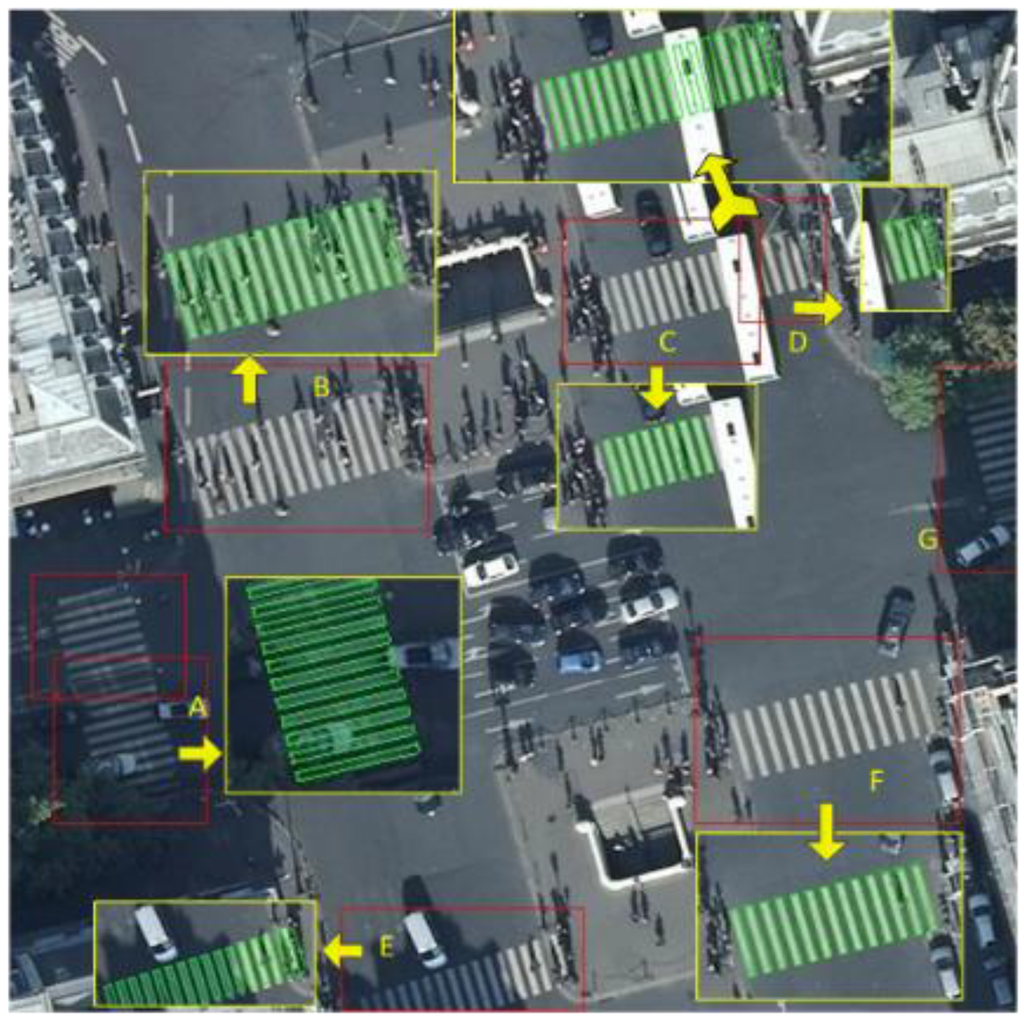
Figure 17. The results of zebra crossing reconstruction in green lines.

3.2.2. Rhomboid Zebra Crossing

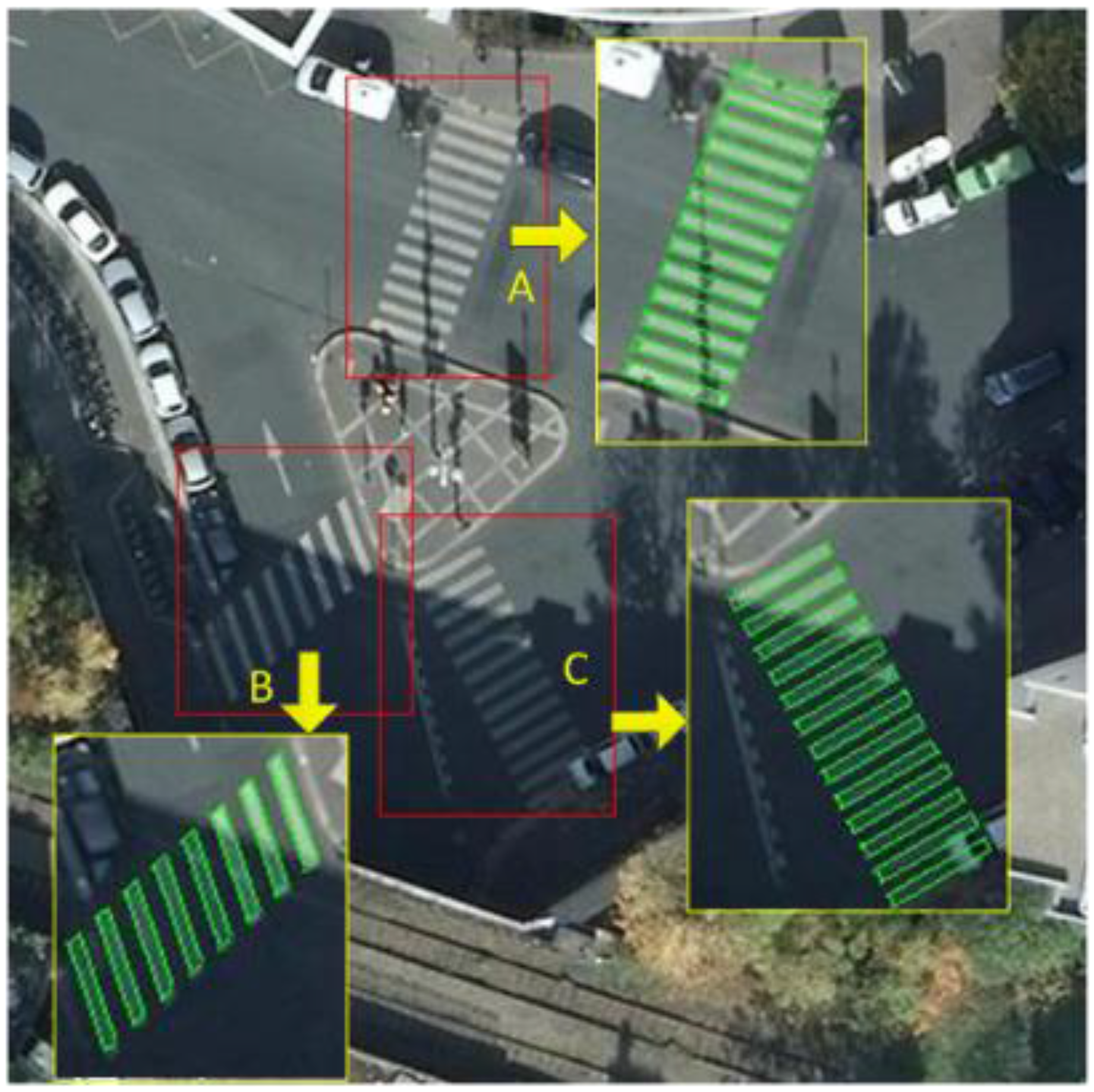
Some zebra crossings are reconstructed as rhomboid shape because of the road orientations, as shown in Figure 18. In our algorithm, Equation (9) also has the ability to describe oblique stripes with the parameters ${\mathsf{\theta }}_m$ and ${\mathsf{\theta }}_p$. The challenge with rhomboid zebra crossings is not in properly fitting parameters but in determining the correct boundary due to the zebra crossing tilt.

Figure 18. Reconstruction results of rhomboid zebra crossings.

3.2.3. Zebra Crossing with Shadow

When considering the effects of shadows, the result of binarization is affected which influences the reconstruction. In our pre-processing step, we transform the image from the RGB space to the HSV space [38] and apply a top-hat transformation [39] to reduce the influence of shadow. This is based on the notion that an image of one zebra crossing should have a similar tone. Next, we apply Otsu’s method [40] to select a proper threshold for image binarization. These pre-processing steps ensures that a stable boundary is obtained for reconstruction.

In Figure 19, (A) is a zebra crossing partially obscured by the shadow of a street lamp; and (B) and (C) are the zebra crossing that are half shaded. Additionally, there are white stripe features similar to the shapes of zebra crossing stripes at the ends of (A) and (B). Our method extracts and reconstructs the main part of the zebra crossings but not the stripes at the ends of the two zebra crossings because the white stripes do not follow the same repetitive regularity of the zebra crossings.

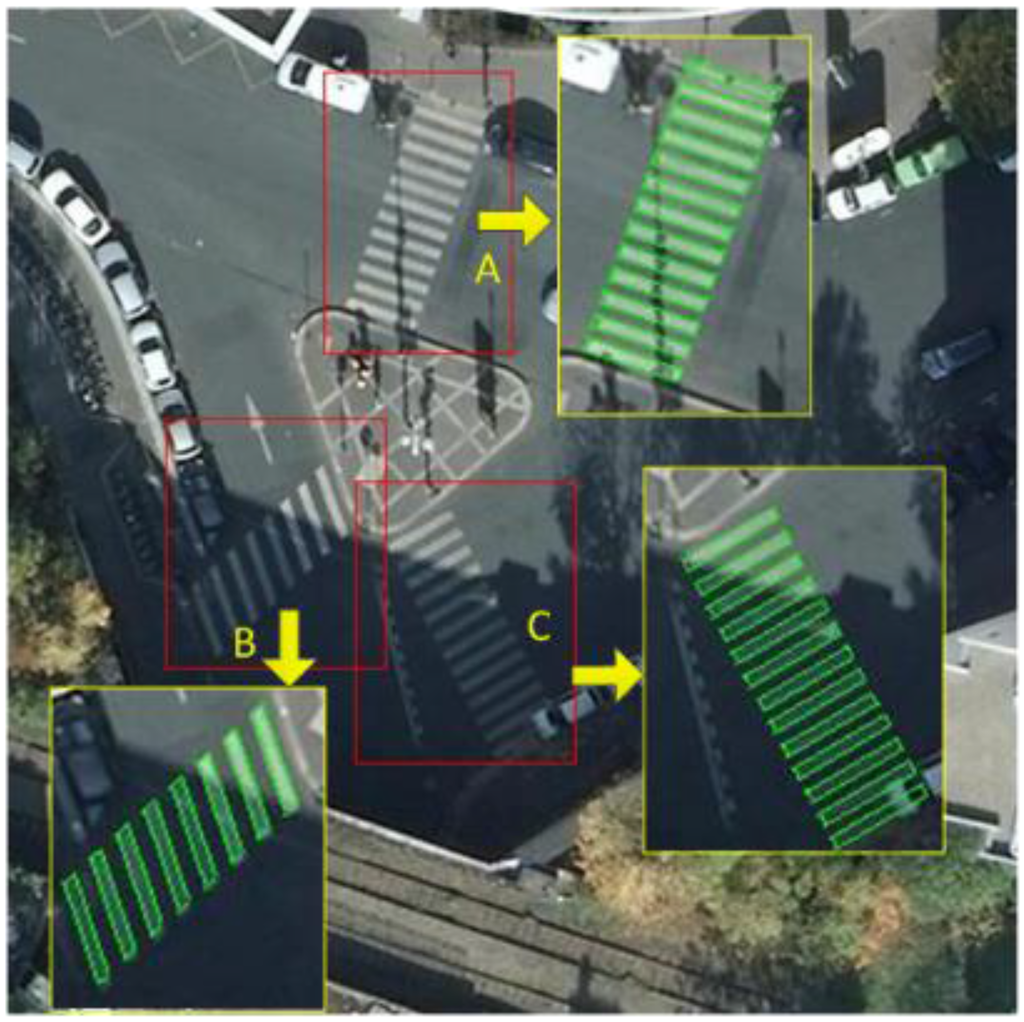
Figure 19. The geometric shape reconstruction of zebra crossing within shadows.

3.2.4. Blurred Zebra Crossing

In the situation where zebra crossings are significantly blurred, the proposed algorithm has difficulties in the extraction and reconstruction procedure. The features calculated from blurred images are unreliable which leads to extraction failure. Furthermore, it also introduces errors in the zebra crossing parameter estimation process for image binarization.

Gray-level stretching in the preprocessing step can improve the image to a certain extent. Figure 20 is the slightly blurred image and its corresponding reconstruction results. Benefiting from our global parameter fitting strategy, the reconstruction compensates for the image blur. However, for seriously affected zebra crossings, our algorithm fails.

Figure 20. Reconstruction of blurred zebra crossing.

4. Discussion and Conclusions

In this paper, we have proposed a new method: (1) the extraction of zebra crossings from high resolution aerial images based on the JointBoost classifier and (2) the reconstruction of the geometric shapes utilizing predefined parameters and the repeatability property. Finally, experiments using several examples are conducted to validate the methodology proposed in this paper. From the experiments, we find that the proposed JointBoost algorithm and the features extracted by the GLCM and 2D Gabor filters are adequate for the extraction of zebra crossings. In the geometric shape reconstruction procedure, a global shape fitting method based on the geometric parameter model and the corresponding spatial repeatability principle are very effective for reconstructing the geometric shape of zebra crossings. This method can effectively reconstruct zebra crossings that have been interfered with by cars, pedestrians or shadows, and this process has been validated by some reconstruction experiments.

During the extraction procedure, scale continues to present a challenge. One classifier usually works well specifically for images with certain spatial resolutions. The GLCM features we used can improve the effectiveness of extraction, but it is difficult to implement a classifier trained from an image of one spatial resolution to process an image of another resolution. If we want improve the feasibility of the classifier, we need to find the key features that are scale independent, or find a solution that adaptively adjusts the parameters according to image resolution and the suitable size of window for feature calculation. Although both proposed methods are very challenging, the problem will be researched as part of our future work.

There are many types of land markings in the world, even zebra crossings have various shapes in different regions. This will limit the application of our algorithm. For example, our algorithm would not be applicable for aerial images of Singapore, where most of the zebra-crossings are square and without repeating stripes. However, we think that the JointBoost classifier can be useful even for other types of land markings, such as in automated image searching for specific content like planes and ships. We will extend our work to improve feature detection as well as developing fitting algorithms suitable for many types of land markings. In future, we will focus on how to reduce the dependency on the parameters tuning of the proposed method, making it applicable in many areas not only aerial high-resolution images.