Abstract
The spectroscopic method for gas temperature determination in argon non-thermal plasmas sustained at atmospheric pressure proposed recently by Spectrochimica Acta Part B 129 14 (2017)—based on collisional broadening measurements of selected pairs of argon atomic lines, has been applied to other pairs of argon atomic lines, and the discrepancies found in some of these results have been analyzed. For validation purposes, the values of the gas temperature obtained using the different pairs of lines have been compared with the rotational temperatures derived from the OH ro-vibrational bands, using the Boltzmann-plot technique.
1. Introduction
Optical emission spectroscopy (OES) techniques based on the analysis of molecular emission spectra are commonly used for gas temperature (Tg) determination of plasmas at atmospheric pressure. The rotational temperature derived from them is considered as a good estimation of the kinetic temperature of the plasma heavy particles [1,2] thanks to the strong coupling between translational and rotational energy states under high-pressure conditions. The emissions of diatomic species, such as OH, N2, N2+, CN, ..., have been traditionally employed with this purpose [3,4,5,6,7,8,9,10], but the use of molecular emission spectroscopy is not always easy for gas temperature measurement in plasmas: overlapping of bands, rotational population distribution of levels having a non-Boltzmann nature, wake emission of rotational bands, among others, can make it difficult to obtain reliable values of gas temperature.
Alternative OES methods for gas temperature determination are needed. In this way, the van der Waals broadening of some atomic lines has been used for this purpose due to its dependence on the plasma gas temperature. For argon plasmas, the 425.9, 522.1, 549.6, and 603.2 nm argon lines have been the most frequently employed [11,12,13,14]. This technique is based on the detection of argon lines not affected by resonance broadening (also related to Tg). It requires the use of additional techniques for simultaneous determination of the electron density [15], as these lines have a non-negligible Stark broadening for electron densities above 1014 cm−3, which needs to be determined. Yubero et al. in [16] proposed a method to circumvent this dependence on electron density by considering pairs of these lines. This method allows for the determination of the gas temperature from the measurements of Lorentzian profiles of some pairs of argon atomic lines, and when applying it, no assumptions on the degree of thermodynamic equilibrium among excited states are needed (unlike methods based on rotational temperature determination).
However, the authors of [16] found a small disagreement in the results from pairs Ar I 603.2 nm/Ar I 522.1nm and Ar I 549.6 nm/Ar I 522.1 nm. In the present work, this disagreement is explained, and other pairs of lines have been employed for the gas temperature determination.
2. Method
This method is valid for plasmas sustained at atmospheric pressure whose line profiles can be fitted to a Voigt function-characterized by a full-width at half-maximum (FWHM), WV-resulting from the convolution of a Gaussian function (WG) with a Lorentzian function (WL) (see, e.g., [17,18]). Indeed, the profiles of atomic lines emitted by plasmas with no presence of magnetic fields result from different broadening mechanisms leading to Gaussian or Lorentzian profile shapes, briefly described below.
The motion of emitting atoms with respect to the detector, with a continuous velocity distribution depending on their temperature, leads to the so called Doppler broadening and a Gaussian-shaped line profile with a FMHW WD (in nm) given by
where λ, Tg, and M are the wavelength (nm), the gas temperature (in K), and the mass of the radiating atom (in a.m.u.), respectively.
The van der Waals broadening is due to the dipole moment induced by neutral perturber atoms interacting with the electric field of the excited emitter atom and generates line profiles with a Lorentzian shape (with an FWHM WW), according to the Lindholm–Foley theory [19].
The resonance broadening of spectral lines is due to dipole–dipole interactions of the emitter with ground-state atoms of the same element [20] and contributes to the Lorentzian part of the profile with an FWHM WR.
The Stark broadening (FWHM WS) of a line is due to interactions of the emitter atom with the surrounding charged particles, perturbing the electric field it experiences. In the case of a non-hydrogenic atom, the profiles of isolated spectral lines broadened by collisions with electrons have a Lorentzian shape. For thermal plasmas with a gas temperature similar to the electron one, the mobility of ions is high and the impact approximation [21] is also valid for ions, being their contribution to the broadening also being Lorentzian. In the ion impact limit, line profiles are symmetric Lorentzian. On the contrary, for plasmas where the ion mobility is small (e.g., plasmas with gas temperature relatively low), a quasistatic approximation is often needed to model the ion broadening in order to explain the slightly asymmetric shape of the profiles. The less dynamical the ions are, the more asymmetric the lines are. The finite lifetime of the excited levels gives rise to natural broadening, which is typically very small (~0.00001 nm) and can be neglected in the case of atmospheric pressure plasma spectroscopy.
Finally, the line profile is also affected by the instrumental function of the spectrometer used for its detection. Usually, this instrumental function can be well approximated by a Gaussian profile with an FWHM WI, as shown in the next section.
Thus, the broadening contributions with a Gaussian shape will lead to a profile with an FWHM (WG) given by
and those having a Lorentzian shape give rise to a profile that is also Lorentzian with an FWHM (WL) given by
The method we propose here only considers atomic lines with a negligible resonance broadening. Thus, the Lorentzian part of a line profile is only due to Stark and van der Waals broadenings, and full width at half maximum of the Lorentzian profile, WL can be written as follows:
Several studies of Stark broadening for atomic and singly charged ion lines [18,22,23,24,25,26] show that Equation (4) can be written as
where parameters and are electronic and ionic contributions to the full-width at half-intensity maximum given for an electron density equal to 1016 cm−3, and ne is the electron density.
In non-thermal-plasmas where Tg is much lower than Te (electron temperature), the ionic contribution can be neglected. Additionally, WS can be considered to have a weak dependence on Te in the small range of electron temperature from 5000 to 10,000 K [22]. In this way, WS depends only on ne and Equation (5) can be approximated as follows:
where .
On the other hand, the van der Waals broadening has a full width at half maximum WW in nm given by Griem [18], which, considering the ideal gas equation N = P/KBTg for the density of perturbers, and where KB is the Boltzmann constant and P is the pressure, can be written as
with C being determined by the type of gas in the discharge and the nature of the atom emitters:
where
is the difference of the squares of coordinate vectors (in a0 units) of the upper and lower level, λ is the wavelength of the observed line in nm, α is the polarizability of perturbers interacting with the excited radiator in cm3, Tg is the temperature of the emitters (coincident with the gas temperature) in K, and µ is the reduced mass of the emitter–perturber pair in a.m.u.
For argon plasma at atmospheric pressure, when considering the van der Waals broadening of argon atomic lines (µ = 19.97 and α = 16.54·10−25 cm3), C can be written as [16]
Thus, the formula for WL given by Equation (3) can be approximately expressed as
The method for gas temperature determination proposed by Yubero et al. in [16] is based on the measurement of the Lorentzian contribution to the entire FWHM for two atomic lines, L1 and L2:
The dependence on the electron density can be eliminated from these expressions, and a linear dependence between the FWHM of the Lorentzian part of the total profile of these two lines, and , is obtained:
Finally, the gas temperature is given by
Thus, as long as the Stark parameters for two lines and their C parameters are known, the gas temperature can be determined from full Lorentzian FWHMs of these lines. Nevertheless, the applicability of this method relies on the knowledge of these parameters, with a certain degree of accuracy. The theoretical estimation of these parameters in the literature can lead to significant errors in gas temperature values.
Concerning this matter, Yubero et al. [16] gather the values of FWHM of the Lorentzian profile of the lines Ar I 603.2 nm, Ar I 549.6 nm, and Ar I 522.1 nm These lines correspond to transitions from high energy levels and exhibit slightly asymmetric profiles [13]. The effect of this asymmetry, not considered in the previous work [16], has been removed from the profiles according to the procedure in [13] (so, only considering the symmetric electron contribution) in order to improve the results of the method. According to this reference, the effect of ions is more important in the right shape of profile. Therefore, only the left part of the profile has been considered to generate the entire profile. Figure 1 shows an example of the symmetrization procedure for the Ar I 522.1 nm line.
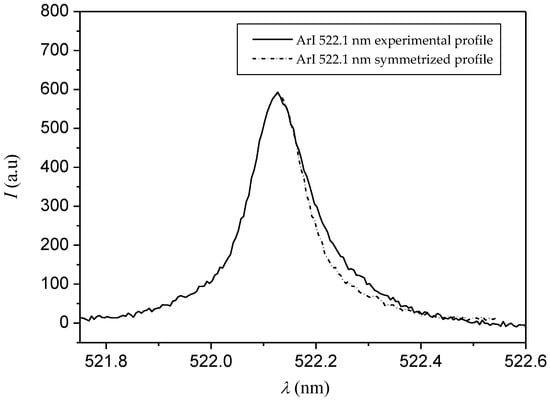
Figure 1.
Symmetrization of Ar I 522.1 nm.
In addition, new Ar I lines at 560.7 nm and 518.8 nm have been included in this work.
Measured values of WL for these lines allow us to obtain Tg using Equation (14), provided the C coefficients and Stark broadening parameters are known. Table 1 includes values of the C coefficients calculated for these lines from Equation (8), and the Stark broadening parameters theoretically determined by Dimitrijević et al. [22] for an electron temperature of 10,000 K.

Table 1.
C coefficients calculated from Equation (8), and the Stark broadening parameters due to electron impacts theoretically determined by Dimitrijević et al. [22] for an electron temperature of 10,000 K and an electron density of 1016 cm−3.
3. Experimental Set-Up
In this work, we measured the gas temperature of an argon microwave (2.45 GHz) induced plasma column sustained at atmospheric pressure and generated inside a quartz tube (with the inner and outer diameters 1.5 mm and 4 mm, respectively), described elsewhere [27]. A similar plasma had been previously characterized in [28], its electron density being of the order of 1014 (cm−3). The electron temperature was estimated to be close to 10,000 K from observed relative populations of the argon excited levels assuming a partial local thermodynamic equilibrium [28].
Figure 2 includes a scheme of the optical detection assembly and data acquisition system to process spectroscopic measurements. A surfaguide was employed as a coupling device, injecting a microwave power of 100 W to the plasma. The argon flow rate was set at 0.5 slm (standard liters per minute) and adjusted with a calibrated mass flow controller.
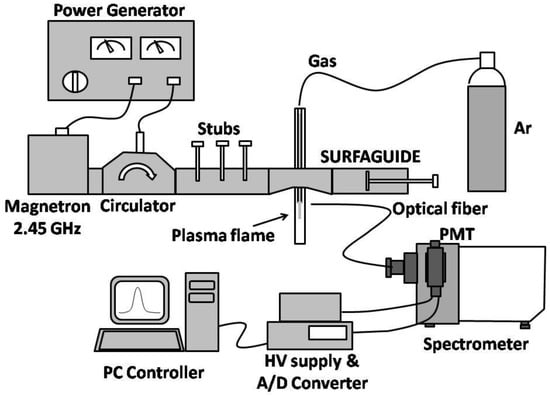
Figure 2.
Scheme of experimental set-up.
Light emission from the plasma was analyzed by using a Czerny–Turner type spectrometer with a 1 m focal length, equipped with a 2400 grooves/mm holographic grating and a photomultiplier (spectral output interval of 200–800 mm) as a detector. The light emitted by the plasma was collected side-on using an optical fiber at different axial positions along the plasma column (z = 4, 8, and 12 cm measured from the end of the column).
The instrumental function of the spectrometer was measured from the FWHM of the line Ne I 632.8 nm emitted by a helium–neon laser (this line is a good choice to make this estimate, as it has a wavelength close to those of the Ar I lines considered in this work). When using equal entrance and exit spectrometer slit widths, this function had an approximately triangular shape, which could be well-fitted with a Gaussian function. In this way, an instrumental broadening width WI = (0.032 ± 0.001) nm was measured when using slit widths of 100 µm.
On the other hand, measurements of the light absorption have shown that the plasma studied can be considered as optically thin in the direction of observation chosen (transversally) for the Ar I lines detected [28,29].
Each Ar I line was measured experimentally several times and was fitted to a Voigt profile. Therefore, the uncertainty of each Voigt FWHM corresponds to the dispersion. The Lorentzian contribution to the entire broadening in each case was obtained from the Voigt FWHM measured for each line using the formula [30,31]
assuming that WG ≈ WI, since, according to Equation (2), the Doppler contribution can be considered as negligible when compared to the instrumental one under the experimental conditions in the plasma studied (Tg ≤ 2500 K, WD ArI ≤ 0.003 nm).
4. Results
Table 2 shows the values of Lorentzian FWHM measured for the different Ar I lines at different positions. For each pair of lines, these values allow for Tg determination using Equation (14), provided C coefficients and Stark broadening parameters given in Table 1.

Table 2.
Lorentzian FWHM of lines Ar I 603.2 nm, Ar I 549.6 nm, Ar I 522.1 nm, Ar I 560.7 nm, and Ar I 518.8 nm measured at different axial plasma positions.
Table 3 shows the Tg values obtained using these parameters for an electron temperature of 10,000 K. These values are also compared with the values obtained using OH ro-vibrational band [13]. Uncertainties in Tg have been obtained from Equation (14) by considering C and WS as theoretical constants and only taking into account uncertainties in the broadenings experimentally measured and errors of approximations used in this method.

Table 3.
Gas temperature obtained using Equation (14) with theoretical Stark broadening parameters at electron temperatures of 10,000 K, and comparison with the one obtained from OH ro-vibrational bands, using the well known Boltzmann plot technique.
Overall, results from the method of pairs of argon lines proposed in this work are in good agreement with those derived from the analysis of OH ro-vibrational band. However, there are some results affected by a very high uncertainty (higher than 50%) corresponding, in some cases, to the Ar I 560.7 nm line. Additionally, there are values lower than the ones obtained from rotational temperature technique corresponding mainly to the 518.8 line.
5. Discussion and Conclusions
In this paper, the OES tool proposed by Yubero et al. in [16] for the determination of the gas temperature in non-thermal plasmas, based on the measurement of the Lorentzian part of the profile of a pair of atomic emission lines, has been improved, as asymmetries of the profiles of these lines have been removed. Compared with the results of [16], better agreement with gas temperatures obtained from OH ro-vibrotional band has been found. We can conclude that symmetrization of the line profile is advisable to obtain good results from this method. Moreover, results from new lines Ar I 560.7 nm and Ar I 518.8 nm have been also included in this paper. As can be seen in Table 3, there are some pairs that do not give accurate results or Tg values with higher uncertainty. They correspond to those cases in which the denominator in Equation (14) is very small, so gas temperature determination becomes very sensitive, giving rise to large errors. Examples of pairs of line giving large errors are Ar I 560.7 nm/Ar I 603.2 nm and Ar I 560.7 nm/Ar I 549.6 nm. This fact does not explain other values that are lower than those obtained from OH ro-vibrotional band. Examples of these pairs of lines are Ar I 518.8 nm/Ar I 603.2 nm, Ar I 518.8 nm/Ar I 549.6 nm, Ar I 518.8 nm/Ar I 522.1 nm, and Ar I 518.8 nm/Ar I 560.7 nm. This could be explained by errors in the theoretical broadening constants given in Table 1.
Although the method has been developed for some pairs of argon lines, it also applies for any pair of atomic lines, as long as they fulfill the following conditions:
(i) Their Stark parameters must be as accurate as possible; (ii) They have a negligible resonance broadening (or they do not have any at all). Choosing lines with an upper or lower level that do not have an electric dipole transition (resonance line) to the ground state is a way to ensure that this condition is satisfied. Additionally, analytical expressions for resonant FWHM in the literature [32,33] can be used to evaluate the importance of this broadening; (iii) Their Stark and van der Waals broadenings should not be very different from each other, so as to avoid large errors in Tg determination (see Equation (14)); this condition applies to plasmas with a relatively low gas temperature (van der Waals broadening not negligible) and moderate electron densities (significant Stark broadening).
The method we propose in this work can be considered a good alternative to the traditional ones based on the measurement of rotational temperatures. In the application of this method, no assumptions on the degree of thermodynamic equilibrium for excited states existing in the plasma are needed, which is its main advantage compared to other methods.
Additionally, as other optical emission spectroscopy techniques, this is a non-plasma diagnosis method, easy to implement.
Acknowledgments
The authors thank the European Regional Development Funds program (EU-FEDER) and the Research Spanish Agency (Agencia Española de Investigación-AEI) of MINECO (project MAT2016-79866-R) for financial support. The authors are also grateful to the Física de Plasmas: Diagnosis, Modelos y Aplicaciones (FQM 136) research group of the Regional Government of Andalusia for technical and financial support.
Author Contributions
All authors contributed equally.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nassar, H.; Pellerin, S.; Mussiol, K.; Martinie, O.; Pellerin, M.N.; Cormier, J.M. N2(+)/N2 ratio and temperature 2 measurements based on the first negative N-2(+) and second positive N-2 overlapped molecular emission spectra. J. Phys. D Appl. Phys. 2004, 37, 1904. [Google Scholar] [CrossRef]
- Britun, N.; Gaillard, M.; Ricard, A.; Kim, Y.M.; Kim, K.S.; Han, H.G. Determination of the vibrational, rotational and electron temperatures in N2 and Ar-N2 rf discharge. J. Phys. D Appl. Phys. 2007, 40, 1022. [Google Scholar] [CrossRef]
- Zhu, X.M.; Chen, W.C.; Pu, Y.K. Gas temperature, electron density and electron temperature measurement in a microwave excited microplasma. J. Phys. D Appl. Phys. 2008, 41, 105212. [Google Scholar] [CrossRef]
- Wang, Q.; Koleva, I.; Donnelly, V.M.; Economou, D.J. Spatially resolved diagnostics of an atmospheric pressure direct current helium microplasma. J. Phys. D Appl. Phys. 2005, 38, 1690. [Google Scholar] [CrossRef]
- Abdallah, M.H.; Mermet, J.M. The Behavior of Nitrogen Excited in an Inductively Coupled Argon Plasma. J. Quant. Spectrosc. Radiat. Transf. 1978, 19, 83–91. [Google Scholar] [CrossRef]
- Laux, C.O.; Spence, T.G.; Kruger, C.H.; Zare, R.N. Optical diagnostics of atmospheric pressure air plasmas. Plasma Sources Sci. Technol. 2003, 12, 125. [Google Scholar] [CrossRef]
- Fantz, U. Emission spectroscopy of molecular low pressure plasmas. Contrib. Plasma Phys. 2004, 44, 508–515. [Google Scholar] [CrossRef]
- Mora, M.; García, M.C.; Jiménez-Sanchidrián, C.; Romero-Salguero, F.J. Transformation of light paraffins in a microwave-induced plasma-based reactor at reduced pressure. Int. J. Hydrog. Energy 2010, 35, 4111–4122. [Google Scholar] [CrossRef]
- Iza, F.; Hopwood, J.A. Rotational, vibrational, and excitation temperatures of a microwave-frequency microplasma. IEEE Trans. Plasma Sci. 2004, 32, 498–504. [Google Scholar] [CrossRef]
- Lombardi, G.; Benedic, F.; Mohasseb, F.; Hassouni, K.; Gicquel, A. Determination of gas temperature and C-2 absolute density in Ar/H-2/CH4 microwave discharges used for nanocrystalline diamond deposition from the C-2 Mulliken system. Plasma Sources Sci. Technol. 2004, 13, 375. [Google Scholar] [CrossRef]
- Christova, M.; Castaños-Martínez, E.; Calzada, M.D.; Kabouzi, Y.; Luque, J.M.; Moisan, M. Electron density and gas temperature from line broadening in an argon surface-wave-sustained discharge at atmospheric pressure. Appl. Spectrosc. 2004, 58, 1032–1037. [Google Scholar] [CrossRef] [PubMed]
- Christova, M.; Gagov, V.; Koleva, I. Analysis of the profiles of the argon 696.5 nm spectral line excited in non-stationary wave-guided discharges. Spectrochim. Acta B 2000, 55, 815–822. [Google Scholar] [CrossRef]
- Yubero, C.; Dimitrijevic, M.S.; García, M.C.; Calzada, M.D. Using the van der Waals broadening of the spectral atomic lines to measure the gas temperature of an argon microwave plasma at atmospheric pressure. Spectrochim. Acta B 2007, 62, 169–176. [Google Scholar] [CrossRef]
- Muñoz, J.; Dimitrijevic, M.S.; Yubero, C.; Calzada, M.D. Using the van der Waals broadening of spectral atomic lines to measure the gas temperature of an argon-helium microwave plasma at atmospheric pressure. Spectrochim. Acta B 2009, 64, 167–172. [Google Scholar] [CrossRef]
- Gigosos, M.A.; Cardeñoso, V. New plasma diagnosis tables of hydrogen Stark broadening including ion dynamics. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 4795. [Google Scholar] [CrossRef]
- Yubero, C.; Rodero, A.; Dimitrijevic, M.; Gamero, A.; García, M.C. Gas temperature determination in an argon non-thermal plasma at atmospheric pressure from broadenings of atomic emission lines. Spectrochim. Acta Part B 2017, 129, 14–20. [Google Scholar] [CrossRef]
- Zaghloul, M.R. On the calculation of the Voigt line profile: A single proper integral with a damped sine integrand MNRAS. Mon. Not. R. Astron. Soc. 2007, 375, 1043–1048. [Google Scholar] [CrossRef]
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Allard, N.; Kielkopf, J. The effect of neutral non resonant collisions on atomic spectral lines. Rev. Mod. Phys. 1982, 54, 1103. [Google Scholar] [CrossRef]
- Griem, H.R. Stark broadening of isolated spectral lines from heavy elements in a plasma. Phys. Rev. 1962, 128, 515–531. [Google Scholar] [CrossRef]
- Konjevic, N. Plasma broadening and shifting of non-hydrogenic spectral lines: Present status and applications. Phys. Rep. 1999, 316, 339–401. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Konjević, N. Stark broadenings of isolated spectral-lines of heavy-elements in plasmas. J. Quant. Spectrosc. Radiat. Transf. 1983, 30, 45–54. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Christova, M.; Sahal-Bréchot, S. Stark broadening of visible Ar I spectral lines. Phys. Scr. 2007, 75, 809–819. [Google Scholar] [CrossRef]
- Christova, M.; Dimitrijević, M.S.; Sahal-Bréchot, S. Stark broadening of Ar I spectral lines emitted in surface wave sustained discharges. Mem. Della Soc. Astron. Ital. Suppl. 2005, 7, 238. [Google Scholar]
- Dimitrijević, M.S. A programme to provide Stark broadening data for stellar and laboratory plasma investigations. Zh. Prikl. Spektrosk. 1996, 63, 810. [Google Scholar]
- Sahal-Bréchot, S. Théorie de l’élargissement et du déplacement des raies spectrales sous l’effect des chocs avec les électrons et les ions dans l’approximation des impacts. Astron. Astrophys. 1959, 1, 91–123. [Google Scholar]
- Moisan, M.; Etermandi, E.; Rostaing, J.C. Excitation System for a Gas Plasma Surface Wave, and Associated Gas Processing System—Has Electromagnetic Material Sleeve Surrounding Gas Circulating Tube (European Patent EP 0874 537 A1). French Patent N. 2,762,748, 1998. [Google Scholar]
- García, M.C.; Rodero, A.; Sola, A.; Gamero, A. Spectroscopic study of a stationary surface-wave sustained argon plasma column at atmospheric pressure. Spectrochim. Acta Part B 2000, 55, 1733–1745. [Google Scholar] [CrossRef]
- Santiago, I.; Christova, M.; García, M.C.; Calzada, M.D. Self-absorbing method to determine the population of the metastable levels in an argon microwave plasma at atmospheric pressure. Eur. Phys. J. Appl. Phys. 2004, 28, 325–330. [Google Scholar] [CrossRef]
- Temme, N.M. Voigt function. In NIST Handbook of Mathematical Functions; Olver Frank, W.J., Lozier, D.M., Boisvert, R.F., Eds.; Cambridge University Press: New York, NY, USA, 2010; ISBN 978-0521192255. [Google Scholar]
- Olivero, J.J.; Longbothum, R.L. Empirical fits to the Voigt line width: A brief review. J. Quant. Spectrosc. Radiat. Transf. 1977, 17, 233–236. [Google Scholar] [CrossRef]
- Ali, A.W.; Giem, H.R. Theory of Resonance Broadening of Spectral Lines by Atom-Atom Impacts. Phys. Rev. 1965, 140, 1044. [Google Scholar] [CrossRef]
- Ali, A.W.; Giem, H.R. Theory of Resonance Broadening of Spectral Lines by Atom-Atom Impacts (ERRATA). Phys. Rev. 1966, 144, 366. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).