Yukawa–Casimir Wormholes in f(Q) Gravity
Abstract
1. Introduction
2. Symmetric Teleparallel Gravity i.e., -Gravity
3. Wormhole Geometry and Solution of Field Equations in Gravity
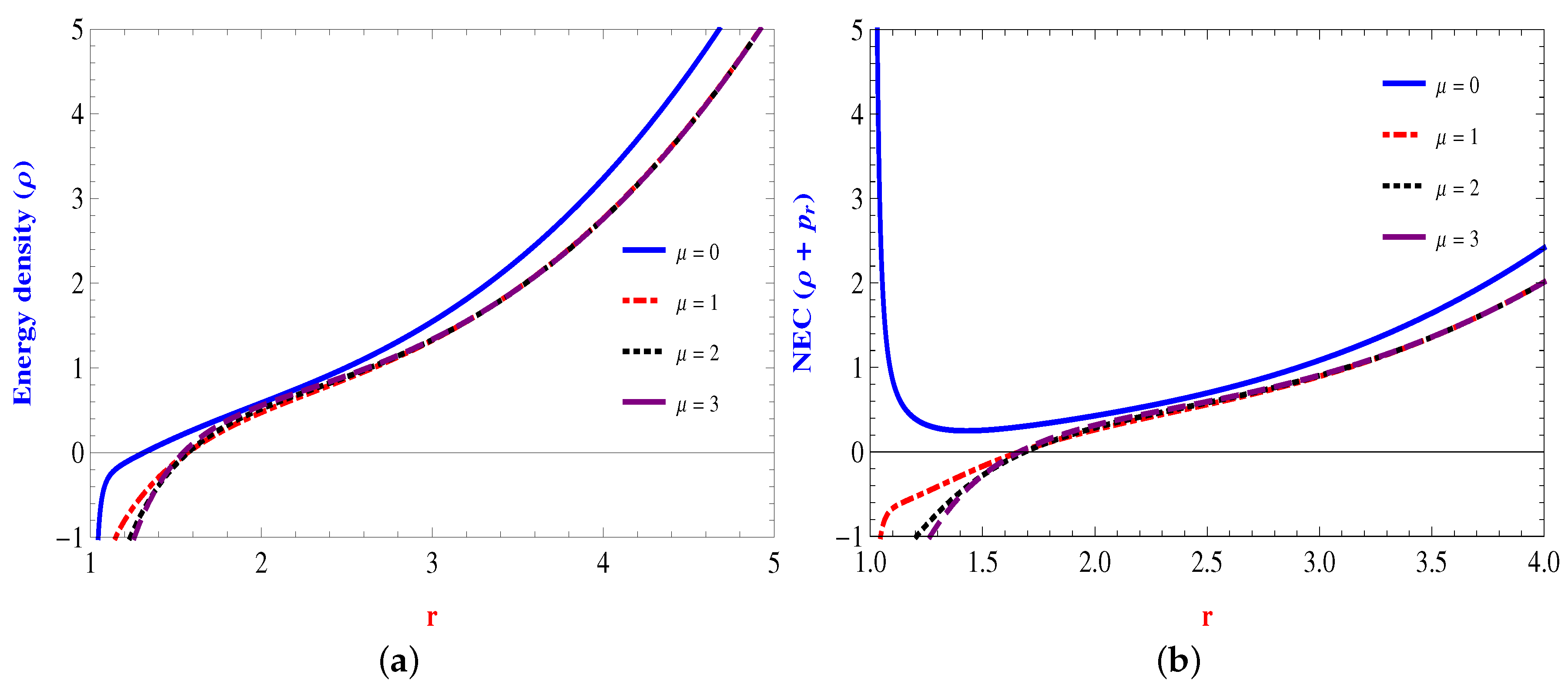
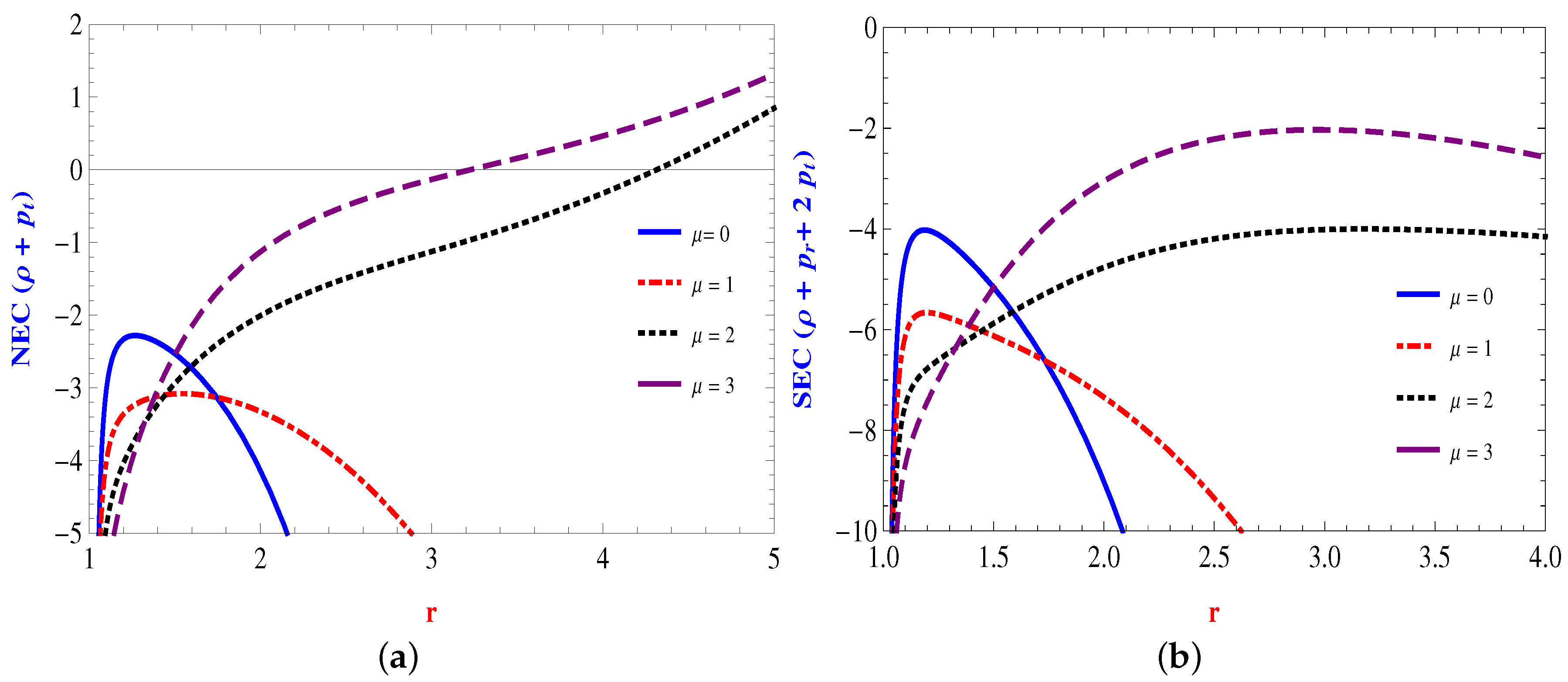
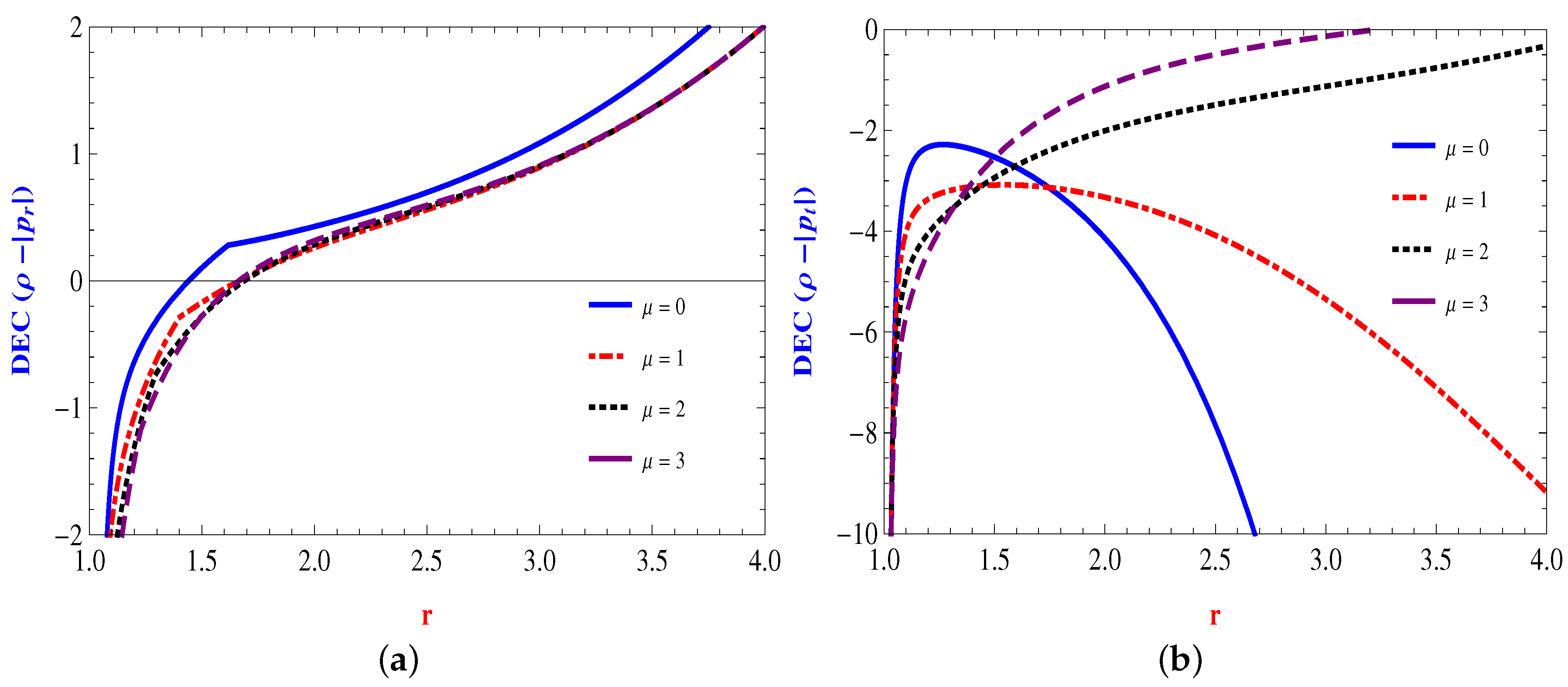
The Energy Conditions
4. The Yukawa–Casimir Wormhole Model
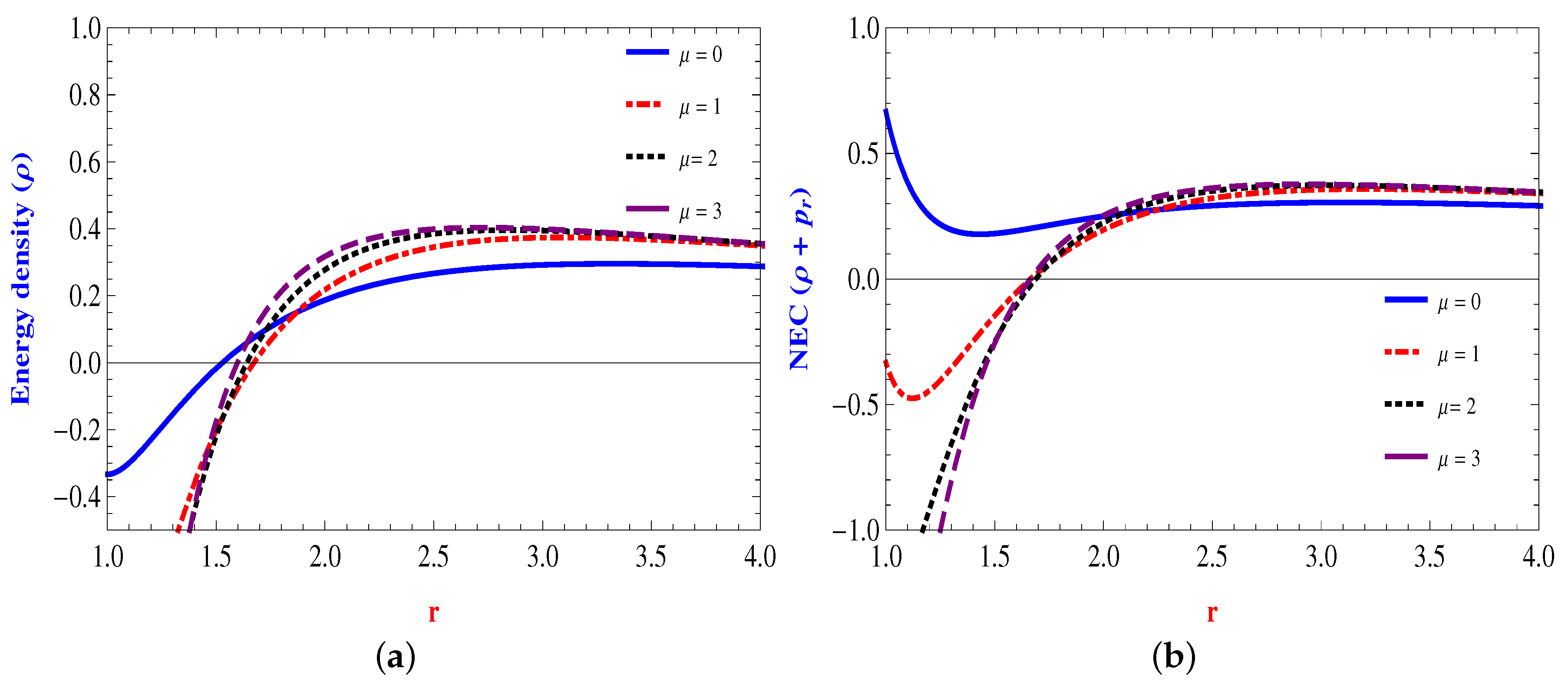
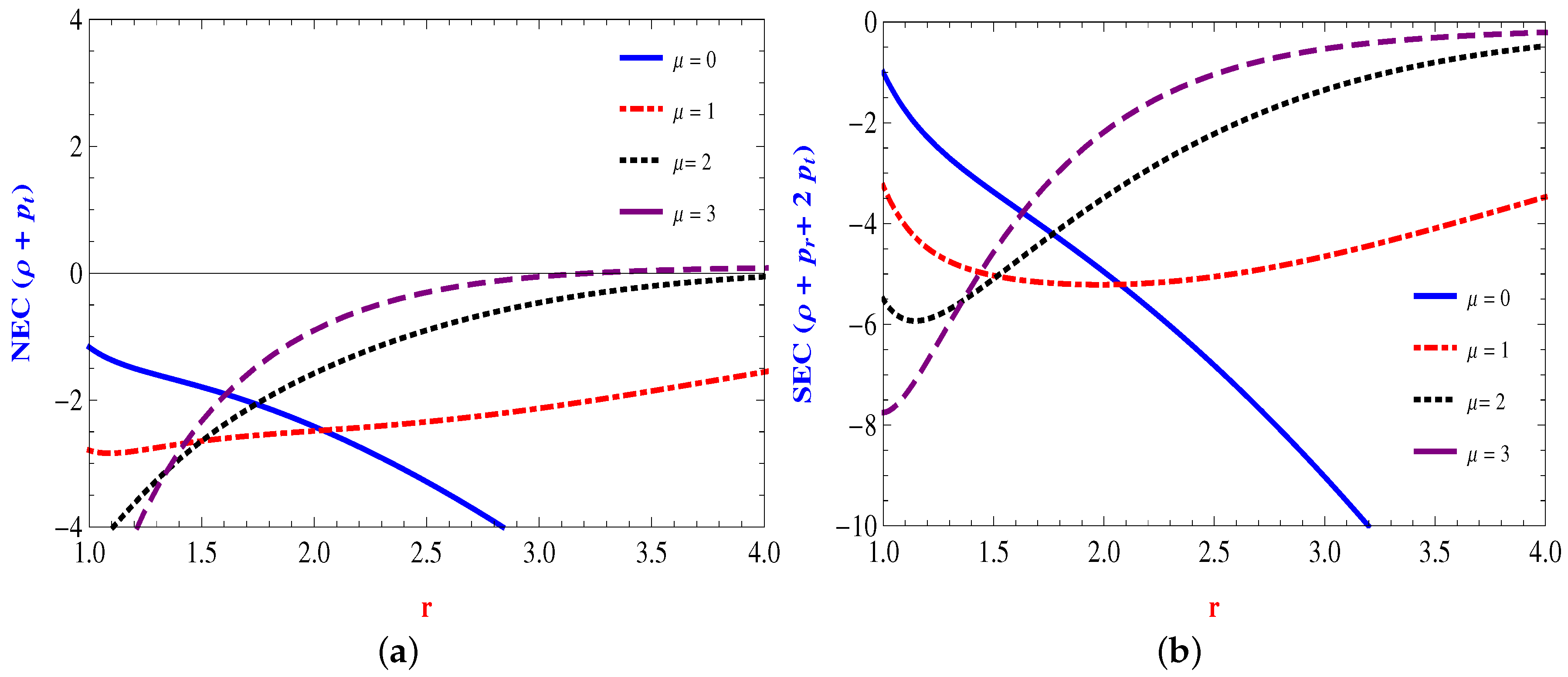
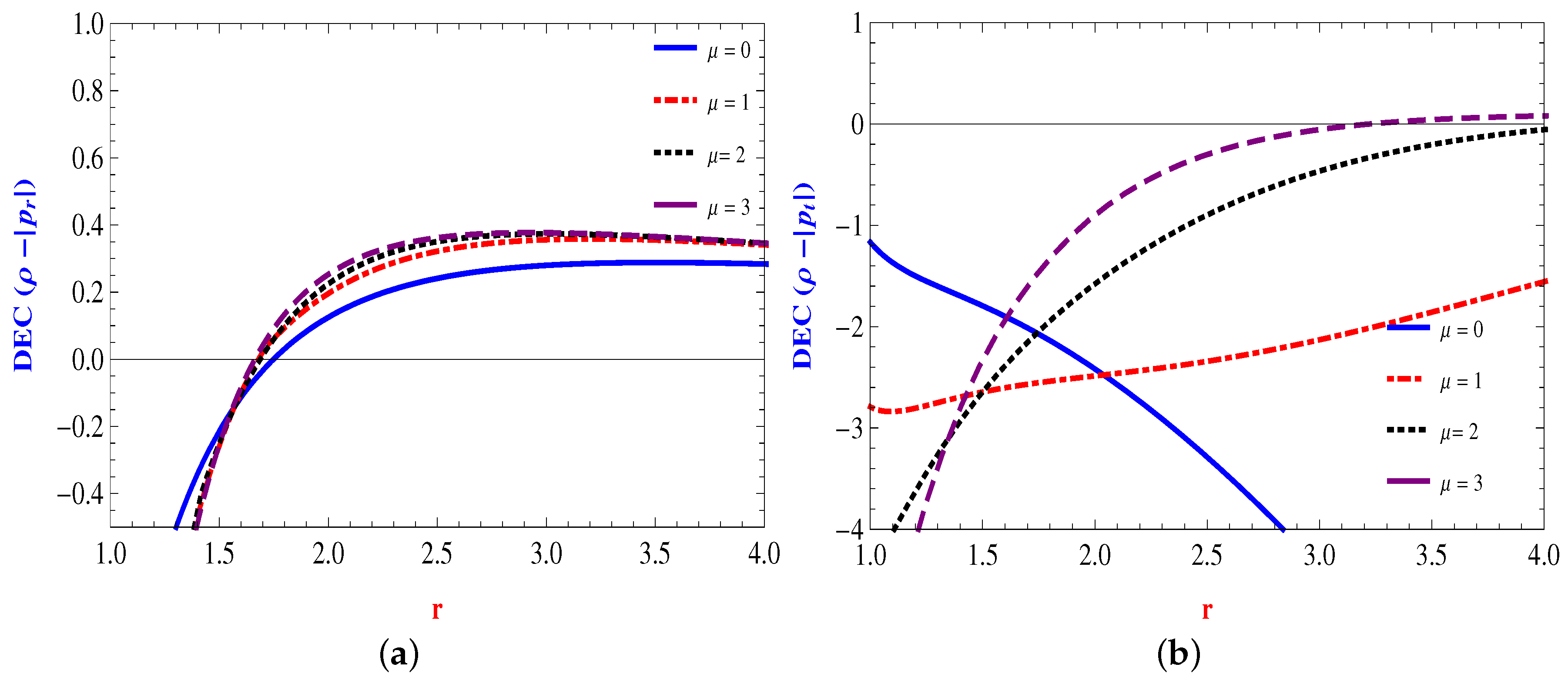
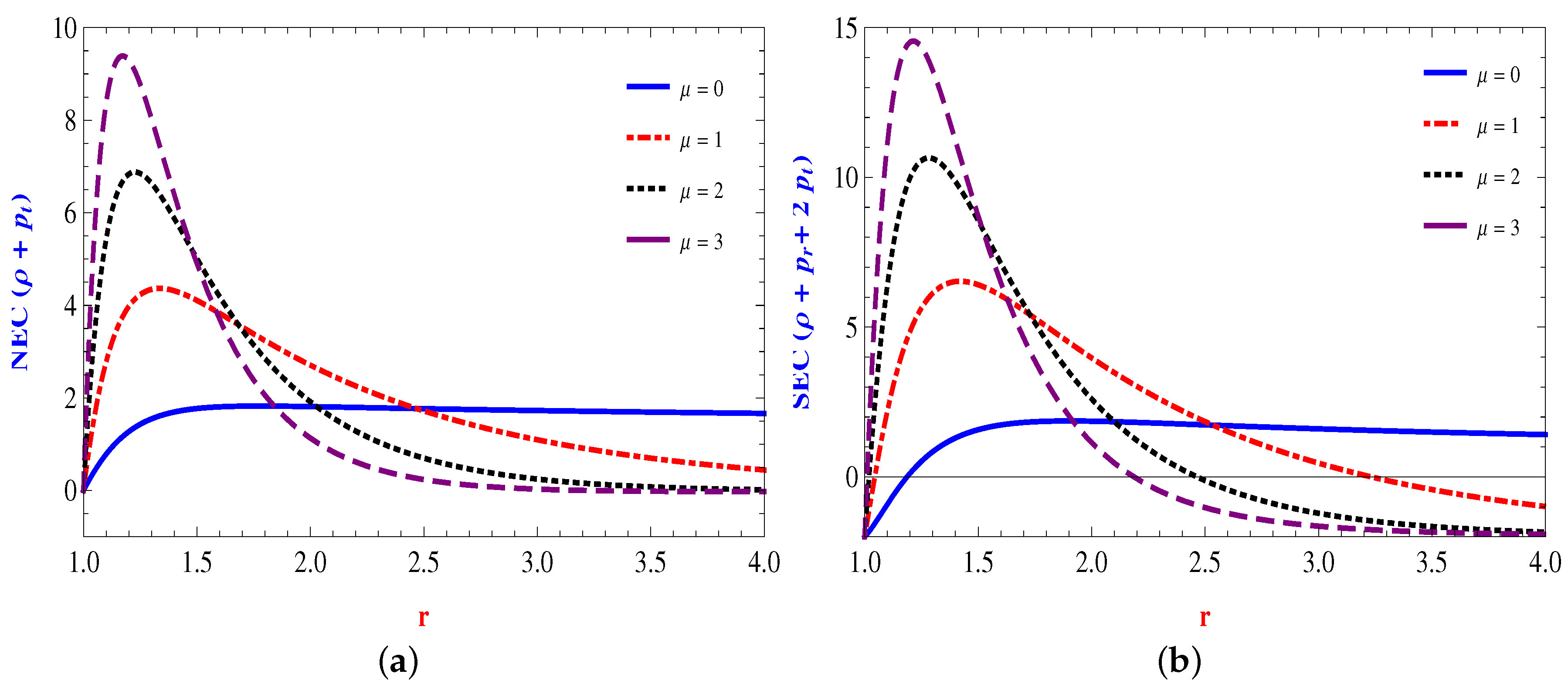
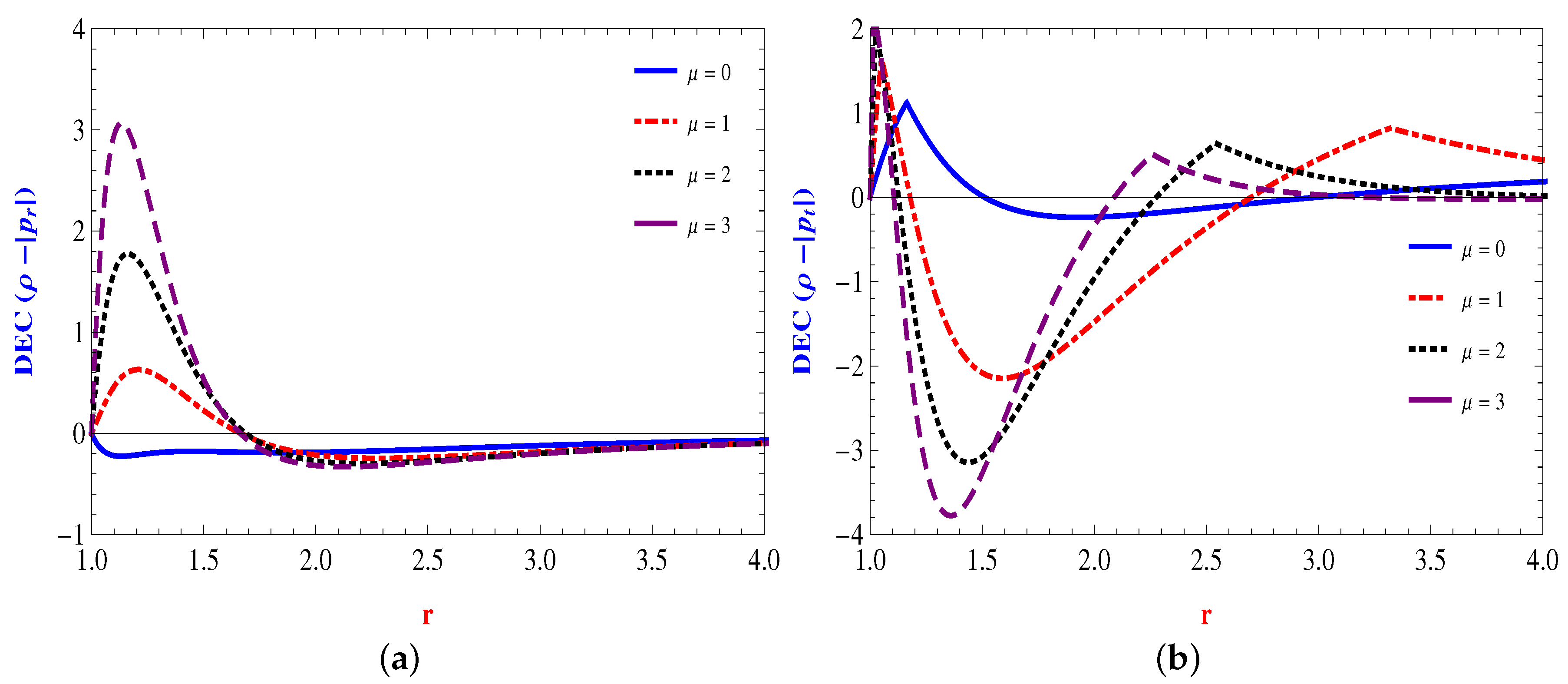
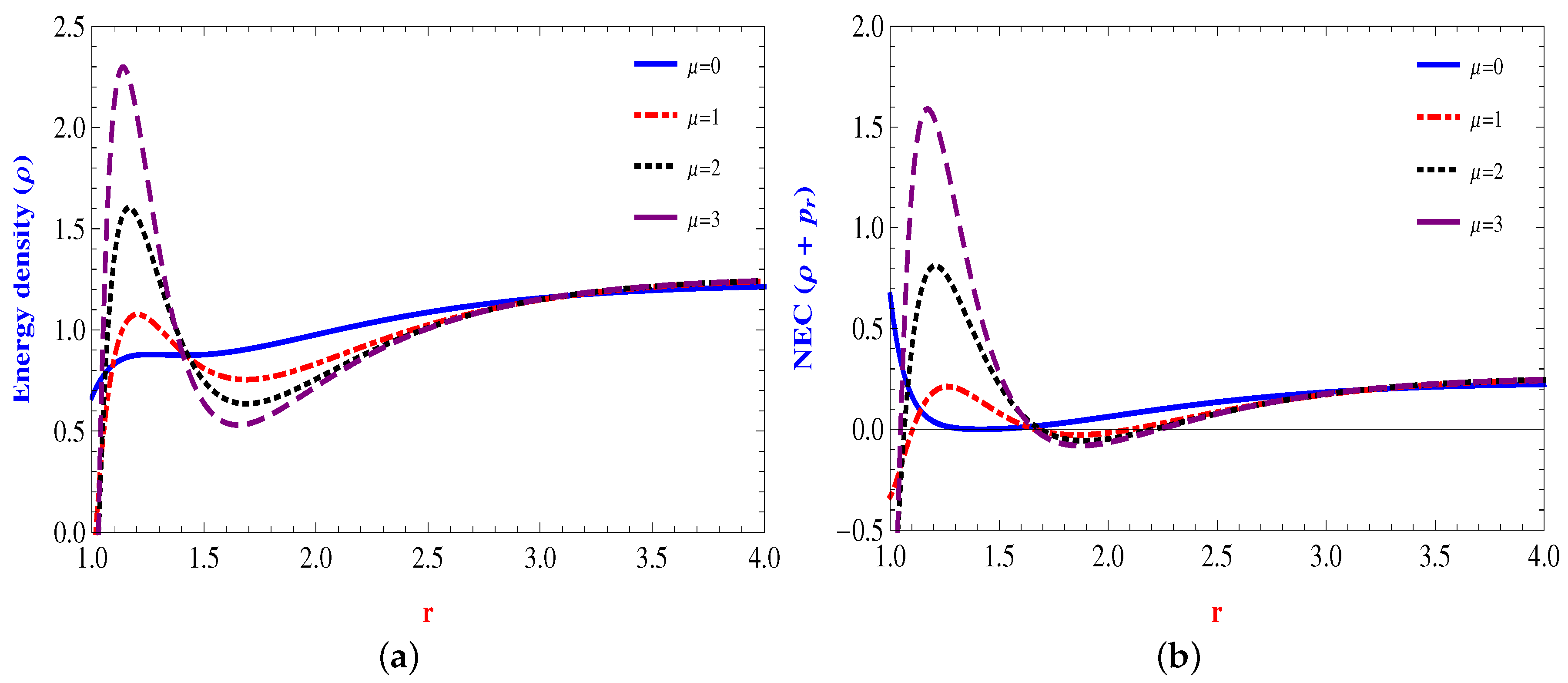
4.1. Linear Form:
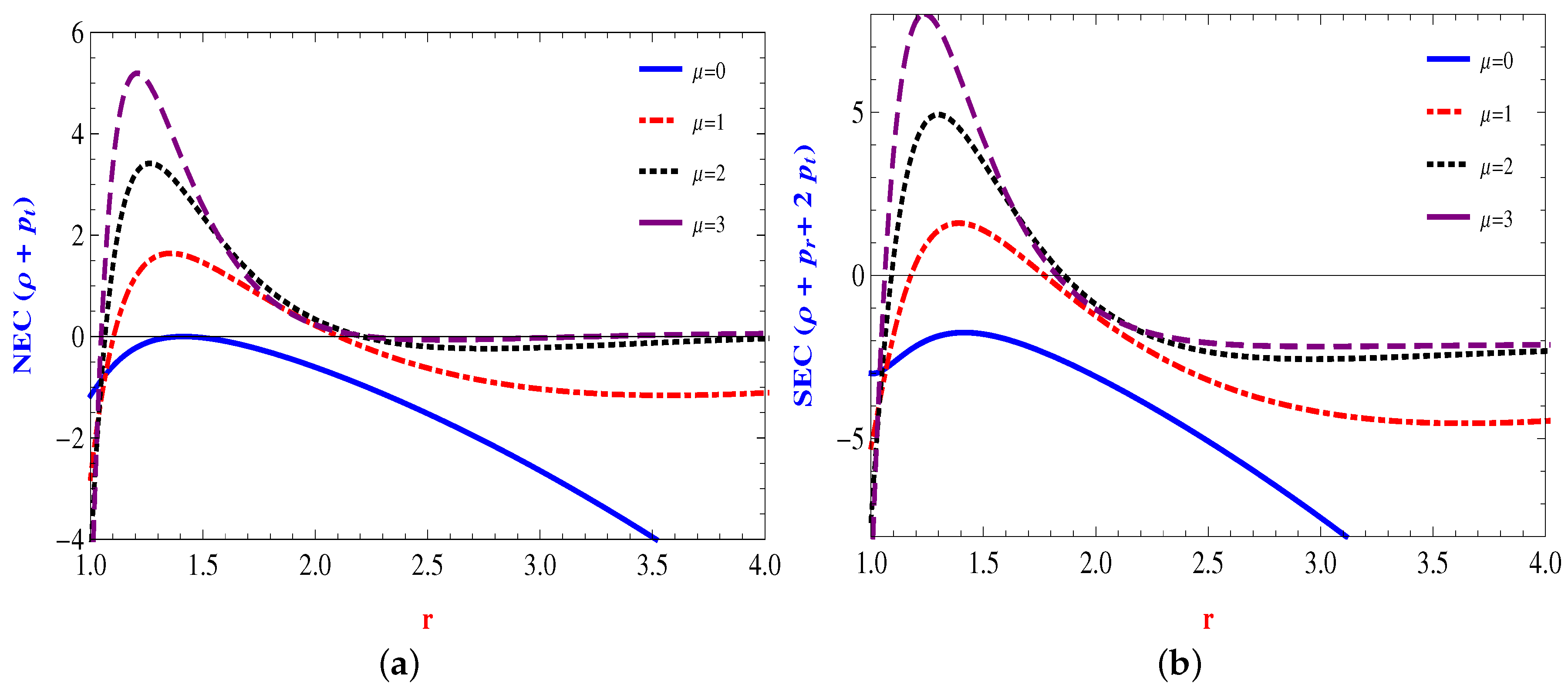
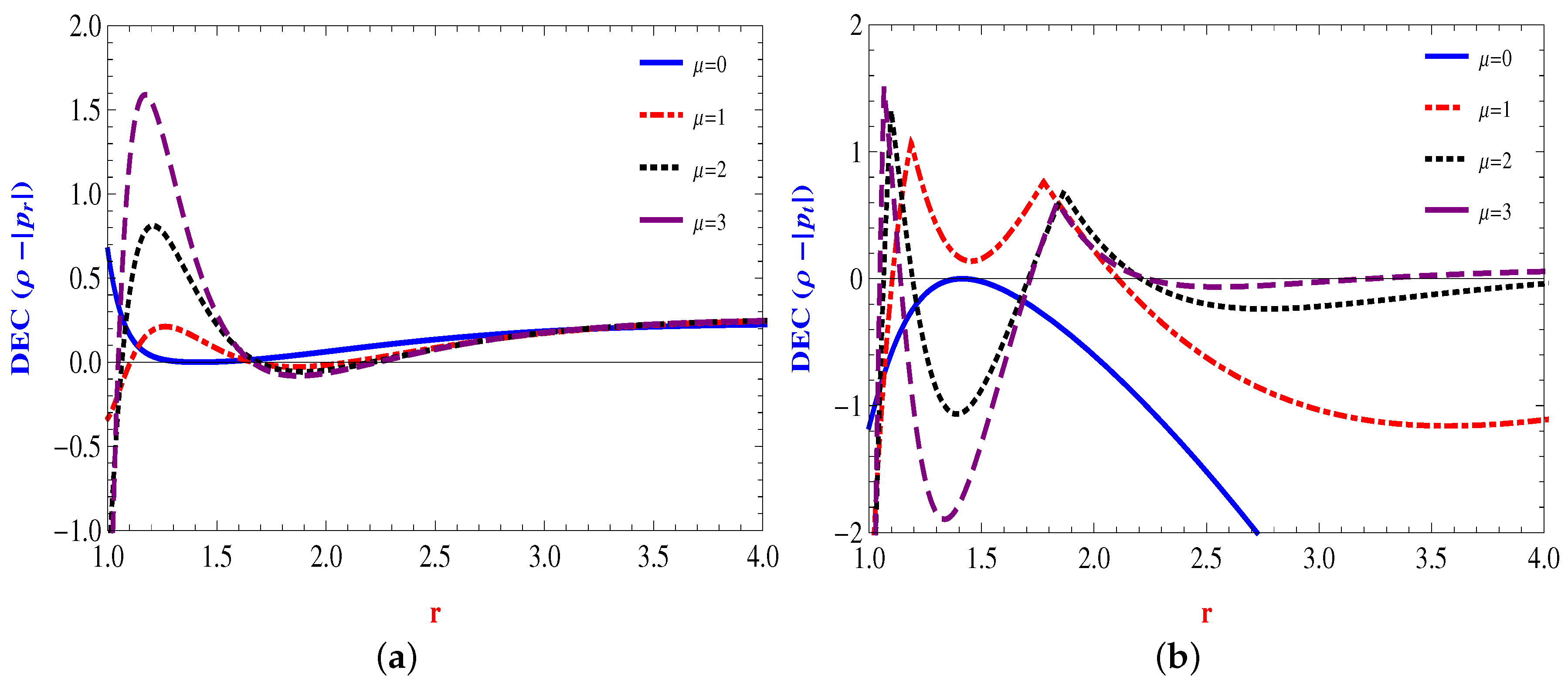
4.2. Power Law Form:
4.3. Quadratic Form:
4.4. Inverse Power Law Form:
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Linear Form: f(Q) = αQ
Appendix A.2. Power Law Form: f(Q) = αQ2 + β
Appendix A.3. Quadratic Form: f(Q) = αQ2 + βQ + γ
Appendix A.4. Inverse Power Law Form: f(Q) = Q +
References
- Shaikh, R.; Banerjee, P.; Paul, S.; Sarkar, T. A novel gravitational lensing feature by wormholes. Phys. Lett. B 2019, 789, 270–275, Erratum in Phys. Lett. B 2019, 791, 422–423. [Google Scholar] [CrossRef]
- Manna, T.; Rahaman, F.; Chowdhury, T. Strong Lensing in the Exponential Wormhole Spacetimes. Available online: http://doi.org/10.2139/ssrn.4349260 (accessed on 26 February 2023).
- Jusufi, K.; Övgün, A.A.B.; Sakallı, I. Gravitational lensing by wormholes supported by electromagnetic, scalar, and quantum effects. Eur. Phys. J. Plus. 2019, 134, 428. [Google Scholar] [CrossRef]
- Flamm, L. Comments on Einstein’s theory of gravity. Phys. Z. 1916, 17, 448. [Google Scholar]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Einstein, A.; Rosen, N. The Particle Problem in the General Theory of Relativity. Phys. Rev. 1935, 48, 73–77. [Google Scholar] [CrossRef]
- Jusufi, K.; Övgün, A. Gravitational Lensing by Rotating Wormholes. Phys. Rev. D 2018, 97, 024042. [Google Scholar] [CrossRef]
- Övgün, A.K.J.; Sakallı, I. Exact traversable wormhole solution in bumblebee gravity. Phys. Rev. D 2019, 99, 024042. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S. Wormholes in space-time and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef]
- Clement, G. The Ellis geometry. Am. J. Phys. 1989, 57, 967. [Google Scholar] [CrossRef]
- Shinkai, H.A.; Hayward, S.A. Fate of the first traversible wormhole: Black hole collapse or inflationary expansion. Phys. Rev. D 2002, 66, 044005. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes, Time Machines, and the Weak Energy Condition. Phys. Rev. Lett. 1988, 61, 1446–1449. [Google Scholar] [CrossRef]
- Kim, S.W.; Thorne, K.S. Do vacuum fluctuations prevent the creation of closed timelike curves? Phys. Rev. D 1991, 43, 3929–3947. [Google Scholar] [CrossRef]
- Visser, M. Lorentzian Wormholes: From Einstein to Hawking; American Institute of Physics: New York, NY, USA, 1995. [Google Scholar]
- Akiyama, K. et al. [Event Horizon Telescope] First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon. Astrophys. J. Lett. 2021, 910, L13. [Google Scholar]
- Blackburn, L.; Doeleman, S.; Dexter, J.; Gómez, J.L.; Johnson, M.D.; Palumbo, D.C.; Weintroub, J.; Bouman, K.L.; Chael, A.A.; Farah, J.R.; et al. Studying Black Holes on Horizon Scales with VLBI Ground Arrays. arXiv 2019, arXiv:1909.01411. [Google Scholar]
- Abuter, R. et al. [GRAVITY] Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2020, 636, L5. [Google Scholar]
- Gourgoulhon, E.; Le Tiec, A.; Vincent, F.H.; Warburton, N. Gravitational waves from bodies orbiting the Galactic Center black hole and their detectability by LISA. Astron. Astrophys. 2019, 627, A92. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific and Virgo]. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Bhattacharya, K.; Majhi, B.R. Fresh look at the scalar-tensor theory of gravity in Jordan and Einstein frames from undiscussed standpoints. Phys. Rev. D 2017, 95, 064026. [Google Scholar] [CrossRef]
- Faraoni, V.; Belknap-Keet, S.D. New inhomogeneous universes in scalar-tensor and f(R) gravity. Phys. Rev. D 2017, 96, 044040. [Google Scholar] [CrossRef]
- Raptis, T.E.; Minotti, F.O. Effects on light propagating in an electromagnetized vacuum, as predicted by a particular class of scalar–tensor theory of gravitation. Class. Quant. Grav. 2013, 30, 235004. [Google Scholar] [CrossRef]
- Genç, O. Some Aspects of Morris-Thorne Wormhole in Scalar Tensor Theory. arXiv 2017, arXiv:1709.06431. [Google Scholar] [CrossRef]
- Jusufi, K.; Banerjee, A.; Ghosh, S.G. Wormholes in 4D Einstein–Gauss–Bonnet gravity. Eur. Phys. J. C 2020, 80, 698. [Google Scholar] [CrossRef]
- Sushkov, S.V. Wormholes supported by a phantom energy. Phys. Rev. D 2005, 71, 043520. [Google Scholar] [CrossRef]
- Wang, D.; Meng, X.H. Wormholes supported by phantom energy from Shan–Chen cosmological fluids. Eur. Phys. J. C 2016, 76, 171. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Moraes, P.H.R.S.; Sahoo, P.; Ribeiro, G. Phantom fluid supporting traversable wormholes in alternative gravity with extra material terms. Int. J. Mod. Phys. D 2018, 27, 1950004. [Google Scholar] [CrossRef]
- Lobo, F.S.N. Phantom energy traversable wormholes. Phys. Rev. D 2005, 71, 084011. [Google Scholar] [CrossRef]
- Shweta, A.K.M.; Sharma, U.K. Traversable wormhole modelling with exponential and hyperbolic shape functions in F(R,T) framework. Int. J. Mod. Phys. A 2020, 35, 2050149. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Sahoo, P.K. Modelling wormholes in f(R,T) gravity. Phys. Rev. D 2017, 96, 044038. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Moraes, P.H.R.S.; Sahoo, P. Wormholes in R2-gravity within the f(R, T) formalism. Eur. Phys. J. C 2018, 78, 46. [Google Scholar] [CrossRef]
- Zubair, M.; Waheed, S.; Mustafa, G.; Ur Rehman, H. Noncommutative inspired wormholes admitting conformal motion involving minimal coupling. Int. J. Mod. Phys. D 2019, 28, 1950067. [Google Scholar] [CrossRef]
- Godani, N.; Samanta, G.C. Gravitational lensing effect in traversable wormholes. Ann. Phys. 2021, 429, 168460. [Google Scholar] [CrossRef]
- Sharma, U.K.; Mishra, A.K. Wormholes Within the Framework of f(R,T) = R + αR2 + λT Gravity. Found. Phys. 2021, 51, 50. [Google Scholar] [CrossRef]
- Mishra, A.K.; Sharma, U.K. Wormhole models in R2-gravity for f(R,T) theory with a hybrid shape function. Can. J. Phys. 2021, 99, 481–489. [Google Scholar] [CrossRef]
- Godani, N.; Samanta, G.C. Deflection angle for charged wormhole in f(R,T) gravity. Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150193. [Google Scholar] [CrossRef]
- Dixit, A.; Chawla, C.; Pradhan, A. Traversable wormholes with logarithmic shape function in f(R, T) gravity. Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150064. [Google Scholar] [CrossRef]
- Mustafa, G.; Tie-Cheng, X.; Ahmad, M.; Shamir, M.F. Anisotropic spheres via embedding approach in R+βR2 gravity with matter coupling. Phys. Dark Univ. 2021, 31, 100747. [Google Scholar] [CrossRef]
- Sushkov, S.V.; Kozyrev, S.M. Composite vacuum Brans-Dicke wormholes. Phys. Rev. D 2011, 84, 124026. [Google Scholar] [CrossRef]
- Godani, N.; Singh, D.V.; Samanta, G.C. Stability of thin-shell wormhole in 4D Einstein–Gauss–Bonnet gravity. Phys. Dark Univ. 2022, 35, 100952. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Sahoo, P.K. Wormholes in exponential f(R,T) gravity. Eur. Phys. J. C 2019, 79, 677. [Google Scholar] [CrossRef]
- Yousaf, Z.; Bhatti, M.Z.; Naseer, T. New definition of complexity factor in f(R,T,RμνTμν) gravity. Phys. Dark Univ. 2020, 28, 100535. [Google Scholar] [CrossRef]
- Samanta, G.C.; Godani, N.; Bamba, K. Traversable wormholes with exponential shape function in modified gravity and general relativity: A comparative study. Int. J. Mod. Phys. D 2020, 29, 2050068. [Google Scholar] [CrossRef]
- Bhatti, M.Z.; Yousaf, Z.; Yousaf, M. Stability of self-gravitating anisotropic fluids in f(R,T) gravity. Phys. Dark Univ. 2020, 28, 100501. [Google Scholar] [CrossRef]
- Rosa, J.L.; Kull, P.M. Non-exotic traversable wormhole solutions in linear f(R,T) gravity. Eur. Phys. J. C 2022, 82, 1154. [Google Scholar] [CrossRef]
- Bhatti, M.Z.; Yousaf, Z.; Yousaf, M. Effects of non-minimally coupled f(R, T) gravity on the stability of a self-gravitating spherically symmetric fluid. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250120. [Google Scholar] [CrossRef]
- Bhatti, M.Z.; Yousaf, Z.; Yousaf, M. Study of nonstatic anisotropic axial structures through perturbation. Int. J. Mod. Phys. D 2022, 31, 2250116. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Wormholes supported by hybrid metric-Palatini gravity. Phys. Rev. D 2012, 86, 127504. [Google Scholar] [CrossRef]
- De Falco, V.; Battista, E.; Capozziello, S.; De Laurentis, M. Reconstructing wormhole solutions in curvature based Extended Theories of Gravity. Eur. Phys. J. C 2021, 81, 157. [Google Scholar] [CrossRef]
- Mustafa, G.; Ahmad, M.; Övgün, A.; Shamir, M.F.; Hussain, I. Traversable Wormholes in the Extended Teleparallel Theory of Gravity with Matter Coupling. Fortsch. Phys. 2021, 69, 2100048. [Google Scholar] [CrossRef]
- Singh, K.N.; Banerjee, A.; Rahaman, F.; Jasim, M.K. Conformally symmetric traversable wormholes in modified teleparallel gravity. Phys. Rev. D 2020, 101, 084012. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Harko, T.; Lobo, F.S.N. Wormhole geometries in modified teleparralel gravity and the energy conditions. Phys. Rev. D 2012, 85, 044033. [Google Scholar] [CrossRef]
- Sengupta, R.; Ghosh, S.; Kalam, M. Lorentzian wormholes supported by tachyon matter. Ann. Phys. 2022, 439, 168778. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Pereira, J.G. Teleparallel Gravity: An Introduction, 13th ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Beltrán Jiménez, J.; Heisenberg, L.; Koivisto, T. Coincident General Relativity. Phys. Rev. D 2018, 98, 044048. [Google Scholar] [CrossRef]
- Lazkoz, R.; Lobo, F.S.N.; Ortiz-Baños, M.; Salzano, V. Observational constraints of f(Q) gravity. Phys. Rev. D 2019, 100, 104027. [Google Scholar] [CrossRef]
- Ayuso, I.; Lazkoz, R.; Salzano, V. Observational constraints on cosmological solutions of f(Q) theories. Phys. Rev. D 2021, 103, 063505. [Google Scholar] [CrossRef]
- de Andrade, V.C.; Guillen, L.C.T.; Pereira, J.G. Gravitational energy momentum density in teleparallel gravity. Phys. Rev. Lett. 2000, 84, 4533–4536. [Google Scholar] [CrossRef]
- Mandal, S.; Sahoo, P.K.; Santos, J.R.L. Energy conditions in f(Q) gravity. Phys. Rev. D 2020, 102, 024057. [Google Scholar] [CrossRef]
- Mandal, S.; Wang, D.; Sahoo, P.K. Cosmography in f(Q) gravity. Phys. Rev. D 2020, 102, 124029. [Google Scholar] [CrossRef]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J.; Rubiera-Garcia, D. Coupling matter in modified Q gravity. Phys. Rev. D 2018, 98, 084043. [Google Scholar] [CrossRef]
- Hassan, Z.; Mandal, S.; Sahoo, P.K. Traversable Wormhole Geometries in f(Q) Gravity. Fortsch. Phys. 2021, 69, 2100023. [Google Scholar] [CrossRef]
- Hassan, Z.; Mustafa, G.; Sahoo, P.K. Wormhole Solutions in Symmetric Teleparallel Gravity with Noncommutative Geometry. Symmetry 2021, 13, 1260. [Google Scholar] [CrossRef]
- Maluf, J.W. The teleparallel equivalent of general relativity. Ann. Phys. 2013, 525, 339–357. [Google Scholar] [CrossRef]
- Sokoliuk, O.; Hassan, Z.; Sahoo, P.K.; Baransky, A. Traversable wormholes with charge and non-commutative geometry in the f(Q) gravity. Ann. Phys. 2022, 443, 168968. [Google Scholar] [CrossRef]
- Mustafa, G.; Hassan, Z.; Sahoo, P.K. Traversable wormhole inspired by non-commutative geometries in f(Q) gravity with conformal symmetry. Ann. Phys. 2022, 437, 168751. [Google Scholar] [CrossRef]
- Sharma, U.K.; Shweta; Mishra, A.K. Traversable wormhole solutions with non-exotic fluid in framework of f(Q) gravity. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250019. [Google Scholar] [CrossRef]
- Plunien, G.; Muller, B.; Greiner, W. The Casimir Effect. Phys. Rep. 1986, 134, 87–193. [Google Scholar] [CrossRef]
- Sparnaay, M. Attractive forces between flat plates. Nature 1957, 180, 334. [Google Scholar] [CrossRef]
- Sparnaay, M. Measurement of attractive forces between flat plates. Physica 1958, 24, 751. [Google Scholar] [CrossRef]
- Lamoreaux, S.K. Demonstration of the Casimir force in the 0.6 to 6 micrometers range. Phys. Rev. Lett. 1998, 78, 5–8, Erratum in Phys. Rev. Lett. 1998, 81, 5475–5476. [Google Scholar] [CrossRef]
- Bressi, G.; Carugno, G.; Onofrio, R.; Ruoso, G. Measurement of the Casimir force between parallel metallic surfaces. Phys. Rev. Lett. 2002, 88, 041804. [Google Scholar] [CrossRef]
- Tripathy, S.K. Modelling Casimir wormholes in extended gravity. Phys. Dark Univ. 2021, 31, 100757. [Google Scholar] [CrossRef]
- Garattini, R. Casimir Wormholes. Eur. Phys. J. C 2019, 79, 951. [Google Scholar] [CrossRef]
- Garattini, R. Yukawa–Casimir wormholes. Eur. Phys. J. C 2021, 81, 824. [Google Scholar] [CrossRef]
- Banerjee, A.; Pradhan, A.; Tangphati, T.; Rahaman, F. Wormhole geometries in f(Q) gravity and the energy conditions. Eur. Phys. J. C 2021, 81, 1031. [Google Scholar] [CrossRef]
- Hassan, Z.; Ghosh, S.; Sahoo, P.K.; Bamba, K. Casimir wormholes in modified symmetric teleparallel gravity. Eur. Phys. J. C 2022, 82, 1116. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Beltrán Jiménez, J.; Heisenberg, L.; Koivisto, T.S.; Pekar, S. Cosmology in f(Q) geometry. Phys. Rev. D 2020, 101, 103507. [Google Scholar] [CrossRef]
- Oliveira, P.H.F.; Alencar, G.; Jardim, I.C.; Landim, R.R. Traversable Casimir Wormholes in D Dimensions. arXiv 2021, arXiv:2107.00605. [Google Scholar] [CrossRef]
- Garattini, R. Generalized Absurdly Benign Traversable Wormholes powered by Casimir Energy. Eur. Phys. J. C 2020, 80, 1172. [Google Scholar] [CrossRef]
- Kontou, E.A.; Sanders, K. Energy conditions in general relativity and quantum field theory. Class. Quant. Grav. 2020, 37, 193001. [Google Scholar] [CrossRef]
- Garattini, R. Self sustained traversable wormholes? Class. Quant. Grav. 2005, 22, 1105–1118. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishra, A.K.; Shweta; Sharma, U.K. Yukawa–Casimir Wormholes in f(Q) Gravity. Universe 2023, 9, 161. https://doi.org/10.3390/universe9040161
Mishra AK, Shweta, Sharma UK. Yukawa–Casimir Wormholes in f(Q) Gravity. Universe. 2023; 9(4):161. https://doi.org/10.3390/universe9040161
Chicago/Turabian StyleMishra, Ambuj Kumar, Shweta, and Umesh Kumar Sharma. 2023. "Yukawa–Casimir Wormholes in f(Q) Gravity" Universe 9, no. 4: 161. https://doi.org/10.3390/universe9040161
APA StyleMishra, A. K., Shweta, & Sharma, U. K. (2023). Yukawa–Casimir Wormholes in f(Q) Gravity. Universe, 9(4), 161. https://doi.org/10.3390/universe9040161





