GEMS Embeddings of Hayward Regular Black Holes in Massless and Massive Gravities

Abstract

After finding a solution for the Hayward regular black hole (HRBH) in massive gravity, we embed the (3+1)-dimensional HRBHs both in massless and in massive gravities into (5+2)- and (6+3)-dimensional Minkowski spacetimes, respectively. Here, massive gravity denotes that a graviton acquires a mass holographically by broken momentum conservation in the HRBH. The original HRBH has no holographically added gravitons, which we call ‘massless’. Making use of newly found embedding coordinates, we obtain desired Unruh temperatures and compare them with the Hawking and local fiducial temperatures, showing that the Unruh effect for a uniformly accelerated observer in a higher-dimensional flat spacetime is equal to the Hawking effect for a fiducial observer in a black hole spacetime. We also obtain freely falling temperatures of the HRBHs in massless and massive gravities seen by freely falling observers, which remain finite even at the event horizons while becoming the Hawking temperatures in asymptotic infinity.

1. Introduction

Black holes are among the most mysterious and fascinating objects in our universe, observationally as well as theoretically. Theoretically, they date back to a century ago, when Schwarzschild found a spherically symmetric vacuum solution of Einstein’s gravitational field equations, and in the same year, Einstein suggested the existence of gravitational waves as a natural outcome of his general relativity. Observationally, precisely a century later, LIGO with Virgo collaboration [1] detected gravitational waves representing the merger of two stellar-mass black holes. In 2019, the Event Horizon Telescope (EHT) [2] finally detected a direct image of a black hole and its event horizon. These remarkable discoveries provide some constraints on the modified theories of gravity, such as the existence of a tight bound on the graviton mass [1], the speed of the gravitational wave [3], black hole parameters and properties [4,5,6], and so on, in light of observational data.

The generalization of the Schwarzschild black hole solution to the electrically charged one [7,8] was done immediately after the work, and the more general and realistic rotating black hole solutions [9,10] were found in the 1960s. However, all of these black hole solutions have a curvature singularity at $r=0$ at which spacetime is geodesically incomplete. According to the singularity theorem proved by Hawking and Penrose [11], singularity is inevitable. Moreover, the usual laws of physics break down at the singularity, and many physicists believe that quantum gravity effects would work near the singularity. Nevertheless, since we do not have a complete quantum gravity theory yet, another line of work to avoid singularity has been pursued on regular black holes. Such works began with Gliner [12] and Sakharov [13], who proposed a way to avoid the singularity in terms of the matter source, which has a de Sitter core with an equation of state $\rho =-p$ at the center of the spacetime. To avoid the singularity problem, Bardeen [14] also proposed a model of a regular black hole obeying the weak energy condition, and thus, the model does not obey at least one condition of the Hawking–Penrose singularity theorem. However, the Bardeen’s regular black hole solution is not an exact solution to Einstein’s equations. After more than three decades, Ayon–Beato and Garcia [15] showed that the Bardeen’s metric could be interpreted as a magnetic solution to Einstein’s equations coupled to nonlinear electrodynamics. Since then, there has been a lot of work on regular black holes, including Dymnikova [16,17], Bronnikov [18], Hayward [19], Ayon–Beato and Garcia [20], and more [21,22,23,24,25,26,27,28,29,30]. These studies have inspired further investigations related to such black holes, for example regarding particle geodesics [31,32,33,34,35,36,37,38,39], the shadows of regular black holes [40,41,42,43], and the quasi-normal modes [44,45,46,47,48]. The thermodynamics and phase transitions for regular black holes have also been studied widely in refs. [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63].

On the other hand, as is well-known, Einstein’s general relativity (GR) is a theory of a massless graviton. However, quantum gravity phenomenology [64] at extreme limits has pushed forward to search for alternatives to GR, one of which is to introduce a massive graviton to GR. Historically, this started with Fierz and Pauli [65], who developed a massive theory by extending GR with a quadratic mass term. However, the theory suffers from the Boulware–Deser ghost problem [66] and the van Dam, Veltman, and Zakharov (vDVZ) discontinuity [67,68] in the massless graviton limit. The vDVZ discontinuity was cured by the Vainshtein mechanism [69]. After half a century, the notorious Boulware–Deser ghost problem was at last solved by de Rham, Gabadadze, and Trolley (dRGT) [70,71] to have a ghost-free massive gravity, which has nonlinearly interacting mass terms constructed from the metric coupled with a symmetric reference metric tensor. These new terms with properly tuned coefficients make it avoid the ghosts order-by-order. To all orders, the complete absence of the Boulware–Deser ghost was subsequently proven by Hassan and Rosen by a Hamiltonian analysis of the untruncated theory [72,73] and by other works [74,75,76,77,78,79]. Since then, the dRGT massive gravity has led to new astronomical and cosmological applications for modified gravity [80,81,82,83,84,85,86,87,88,89], including the black hole shadow [90,91]. In particular, Hendi et al. [92] have obtained a fascinating result allowing for regions with massive parameters by comparing the black hole shadow in the dRGT massive gravity with the EHT data of M87${}^{*}$. On the other hand, Vegh [93] further elaborated on another nonlinear massive gravity with a special singular reference metric and applied it to gauge/gravity duality. The modification in the reference metric in the dRGT massive gravity keeps the diffeomorphism symmetry for coordinates ($t,r$) intact but breaks it in angular directions so that gravitons acquire mass because of broken momentum conservation [94,95,96]. As a result, momentum dissipates as the graviton may behave like a lattice, and it can avoid divergent conductivity. Since then, this Vegh’s type of massive gravity, called holographic massive gravity, has been extensively exploited to investigate many interesting models of gravity [97,98,99,100,101,102,103,104,105,106,107,108,109]. Very recently, we have studied the tidal effects [110] and statistical entropy [111] for the Schwarzschild black hole in holographic massive gravity.

We have also studied the charged BTZ [112] and Schwarzschild black holes [113] in holographic massive gravity in the global embedding Minkowski spacetime (GEMS) scheme. According to the GEMS scheme, any low-dimensional Riemannian manifold can be locally isometrically embedded in a higher-dimensional flat one [114,115,116]. This can make us have a complete analytic extension of manifolds, or we can use it for visualizing or deriving physical properties of the embedded spacetimes, such as a unified description of Hawking [117] and Unruh effects [118]. In this line of work, Deser and Levin [119,120,121] firstly showed that the Hawking temperature for a fiducial observer in a curved spacetime can be considered as the Unruh one for a uniformly accelerated observer in a higher-dimensional GEMS embedded flat spacetime. Since then, there has been much work on the GEMS approach to confirm these ideas in various other spacetimes [122,123,124,125,126,127,128,129,130,131,132,133,134] and an interesting extension to embedding gravity [135,136,137,138]. Later, Brynjolfsson and Thorlacius [139] introduced a local temperature measured by a freely falling observer in the GEMS method. We have also studied various interesting curved spacetimes [140,141] to investigate local temperatures and their equivalences to Hawking ones.

The main goal of this paper is to construct and analyze the GEMS embeddings of spacetimes having regular black holes in massless and massive gravity for which the embeddings are neither found nor even tried at all, as far as we know. Moreover, a recent study on the geodesic completion of a regular black hole [142] supports the needs of the GEMS embeddings of regular black holes. In this respect, it would be interesting to embed a regular black hole with massive gravitons into a higher-dimensional flat spacetime. In this paper, we will consider the Hayward regular black hole (HRBH) in massless gravity as representative of regular black holes and extend it to massive gravity to embed it in higher-dimensional flat spacetimes. Here, the HRBH in massless gravity means the original Hayward black hole, while the HRBH in massive gravity is the one having massive gravitons obtained from the consideration of Vegh’s type of massive gravity. We note that when the Hayward parameter vanishes, the HRBH in massless gravity becomes the Schwarzschild black hole, and when massive gravitons are turned off, the HRBH in massive gravity is reduced to the HRBH in massless gravity.

The remainder of the paper is organized as follows. In Section 2, we newly find solutions to the HRBH in holographic massive gravity. We first briefly summarize the known solution of the HRBH in massless gravity and generalize it to one in holographic massive gravity. Then, we show that the Kretschmann scalar for the HRBH in massive gravity is not regular near $r=0$. In Section 3, we construct the GEMS embeddings of the HRBH both in massless and in massive gravity. As a result, making use of embedding coordinates, we obtain Unruh, Hawking, and freely falling temperatures seen by different observers. Conclusions are drawn in Section 4. Lastly, since embedding coordinates of these regular black holes are very complicated, we list them separately and then show their limits explicitly from the massive to the massless cases in Appendix A.

2. HRBH in Massive Gravity

The (3+1)-dimensional HRBH in holographic massive gravity is described by the action

$$S=\frac{1}{16\pi G}\int d^{4}x\sqrt{-g}\left[\mathcal{R}+\frac{24l^2{m}^2}{{(r^3+2l^{2}m)}^2}+{\tilde{m}}^2\sum _{a=1}^4{c}_a{\mathcal{U}}_a(g_{\mu \nu },f_{\mu \nu })\right],$$

(1)

where $\mathcal{R}$ is the scalar curvature of the metric $g_{\mu \nu }$, m is the black hole mass, l is a length-scale Hayward parameter present in the Hayward solution, $\tilde{m}$ is a graviton mass (in this paper, we shall call it ‘massless’ when $\tilde{m}$ is zero), $c_a$ are the coupling constants, $f_{\mu \nu }$ is a fixed symmetric tensor (usually called the ‘reference metric’), and ${\mathcal{U}}_a$ are symmetric polynomial potentials of the eigenvalue of the matrix ${\mathcal{K}}_{\nu }^{\mu }\equiv \sqrt{g^{\mu \alpha }{f}_{\alpha \nu }}$ given as

$$\begin{array}{ccc}\hfill {\mathcal{U}}_1& =& \left[\mathcal{K}\right],\hfill \\ \hfill {\mathcal{U}}_2& =& {\left[\mathcal{K}\right]}^2-\left[{\mathcal{K}}^2\right],\hfill \\ \hfill {\mathcal{U}}_3& =& {\left[\mathcal{K}\right]}^3-3\left[\mathcal{K}\right]\left[{\mathcal{K}}^2\right]+2\left[{\mathcal{K}}^3\right],\hfill \\ \hfill {\mathcal{U}}_4& =& {\left[\mathcal{K}\right]}^4-6\left[{\mathcal{K}}^2\right]{\left[\mathcal{K}\right]}^2+8\left[{\mathcal{K}}^3\right]\left[\mathcal{K}\right]+3{\left[{\mathcal{K}}^2\right]}^2-6\left[{\mathcal{K}}^4\right].\hfill \end{array}$$

(2)

Here, the square root in $\mathcal{K}$ means ${\left(\sqrt{A}\right)}_{\alpha }^{\mu }{\left(\sqrt{A}\right)}_{\nu }^{\alpha }=A_{\nu }^{\mu }$, and square brackets denote the trace $\left[\mathcal{K}\right]={\mathcal{K}}_{\mu }^{\mu }$. Indices are raised and lowered with the dynamical metric $g_{\mu \nu }$, while the reference metric $f_{\mu \nu }$ is a non-dynamical, fixed symmetric tensor that is introduced to construct nontrivial interaction terms in holographic massive gravity.

Variation of the action (1) with respect to the metric $g_{\mu \nu }$ leads to the equations of motion given by

$$\begin{array}{ccc}\hfill {\mathcal{R}}_{\mu \nu }& -& \frac{1}{2}{g}_{\mu \nu }\left(\mathcal{R}-\frac{24l^2{m}^2}{{(r^3+2l^{2}m)}^2}+{\tilde{m}}^2\sum _{a=1}^4{c}_a{\mathcal{U}}_a\right)\hfill \\ & +& \frac{1}{2}{\tilde{m}}^2\sum _{a=1}^4\left[a{c}_a{\mathcal{U}}_{a-1}{\mathcal{K}}_{\mu \nu }-a(a-1)c_a{\mathcal{U}}_{a-2}{\mathcal{K}}_{\mu \nu }^2+6(3a-8)c_a{\mathcal{U}}_{a-3}{\mathcal{K}}_{\mu \nu }^3-12(a-2)c_a{\mathcal{U}}_{a-4}{\mathcal{K}}_{\mu \nu }^4\right]=0.\hfill \end{array}$$

(3)

with ${\mathcal{U}}_{-a}=0$ and ${\mathcal{U}}_0=1$.

When one considers the spherically symmetric black hole solution ansatz as

$$d{s}^2=-f\left(r\right)d{t}^2+f^{-1}\left(r\right)d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2)$$

(4)

with the following degenerate reference metric

$$f_{\mu \nu }=\mathrm{diag}(0,0,c_0^2,c_0^2{sin}^2\theta ),$$

(5)

one can find

$${\mathcal{K}}_{\theta }^{\theta }={\mathcal{K}}_{\varphi }^{\varphi }=\frac{c_0}{r}.$$

(6)

Note that the choice of the reference metric in Equation (5) preserves general covariance in ($t,r$) but not in the angular directions. This gives the symmetric potentials as

$${\mathcal{U}}_1=\frac{2c_0}{r},{\mathcal{U}}_2=\frac{2c_0^2}{r^2},{\mathcal{U}}_3={\mathcal{U}}_4=0.$$

(7)

Therefore, we see that there are no contributions from the $c_3$ and $c_4$ terms that would appear in (4+1)- and (5+1)-dimensional spacetimes, respectively. Then, we finally obtain the new solution of the HRBH in massive gravity as

$$f\left(r\right)=1-\frac{2m{r}^2}{r^3+2l^{2}m}+2Rr+\mathcal{C}$$

(8)

with graviton mass parameters $R=c_0{c}_1{\tilde{m}}^2/4$ and $\mathcal{C}=c_0^2{c}_2{\tilde{m}}^2$. Note that m is an integration constant related to the mass of the black hole, and $c_0$ is a positive constant. In the limit of $R\to 0$ and $\mathcal{C}\to 0$, it becomes the HRBH in massless gravity, and when $l\to 0$, it is further reduced to the Schwarzschild metric, as expected. On the other hand, when $R\ne 0$ and $\mathcal{C}\ne 0$ with $l=0$, it becomes the Schwarzschild black hole in massive gravity [113].

It is appropriate to comment on the two terms due to massive gravitons. Firstly, the $\mathcal{C}$ term in Equation (8) reminds us of a monopole solution introduced by Barriola and Vilenkin [143], which comes from a topological defect in the early Universe as a result of a gauge symmetry breaking. On the other hand, the R term is not uncommon in gravity theories, which also arises in, for example, the dRGT massive gravity [70,71], conformal gravity [144], and $f\left(R\right)$ gravity [145]. Physically, the linear term in Equation (8) stands for a deviation between the solution and the HRBH spacetime in massless gravity, as modified Newtonian dynamics (MOND) studies deviations of massive bodies in the solar system from the Newtonian mechanics [146]. The linear term also affects the radius of the photon sphere in a black hole, i.e., the size of the shadow, which is smaller than the one in a Schwarzschild spacetime [147]. In addition, Hendi et al. [92] have shown that the black hole shadow in the dRGT massive gravity consistent with EHT data is given for small $R<0.072$ and negative $-0.3<\mathcal{C}<-0.03$ by comparing the black hole shadow with the data of EHT collaboration. We note that the additional $\mathcal{C}$ and R terms in Equation (8) are obtained from the consideration of massive gravitons, while the other theories have different causes.

It is well known that the HRBH solution in massless gravity ($R=0$ and $\mathcal{C}=0$) has two horizons for $m>m_{*}\equiv 3\sqrt{3}l/4$, one for $m=m_{*}$, and none for $m<m_{*}$ [19]. However, for the case of the HRBH in massive gravity, these are modified by R and $\mathcal{C}$. While we find their exact solutions of $f\left(r_H\right)=0$ in the following subsections, we summarize here the number of event horizons of the HRBH in holographic massive gravity according to various values of R and $\mathcal{C}$ in Table 1 and Table 2. In the tables, max(2) and max(3) mean that there exist a maximum of two and three horizons, respectively, satisfying $f\left(r_H\right)=0$ in the given range of R and $\mathcal{C}$. Otherwise, a given number of event horizons are allowed in the range. In order to describe these clearly, as an example, in Figure 1, we have plotted $f\left(r\right)$-graphs for $-1<\mathcal{C}<0$ with R for the case of $m>m_{*}$ where one can see the changes to the number of event horizons according to R and $\mathcal{C}$, respectively.

Table 1. Number of event horizons of the HRBH in holographic massive gravity according to R and $\mathcal{C}$ when $m>m_{*}$. Note that in the table, max(2) and max(3) denote the cases for which a maximum of two or three horizons are formed, respectively, satisfying $f\left(r_H\right)=0$ in the given range.

	$\mathcal{C}<-1$	$\mathcal{C}=-1$	$-1<\mathcal{C}<0$	$\mathcal{C}=0$	$\mathcal{C}>0$
$R>0$	max(3)	max(2)	max(2)	max(2)	max(2)
$R=0$	0	0	2	2	max(2)
$R<0$	0	0	max(3)	max(3)	max(3)

Table 2. Number of event horizons of the HRBH in holographic massive gravity according to R and $\mathcal{C}$ when $m=m_{*}$.

	$\mathcal{C}<-1$	$\mathcal{C}=-1$	$-1<\mathcal{C}<0$	$\mathcal{C}=0$	$\mathcal{C}>0$
$R>0$	1	1	max(2)	0	0
$R=0$	0	0	2	1	0
$R<0$	0	0	max(3)	max(3)	max(3)

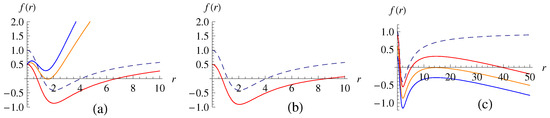
Figure 1. The $f\left(r\right)$-graphs for the third-column case from Table 1 of $-1<\mathcal{C}<0$ and R: (a) for $R>0$, where $(R,\mathcal{C})=(0.01,-0.5),(0.25,-0.5),(0.35,-0.5)$ from top to bottom curves and (b) $R=0$, where $(R,\mathcal{C})=(0,-0.5)$ and (c) $R<0$, where $(R,\mathcal{C})=(-0.01,-0.1),(-0.01,-0.42),(-0.01,-0.7)$ from top to bottom curves. The dashed lines corresponding to $(R,\mathcal{C})=(0,0)$ are for the HRBH in massless gravity with two horizons. Here, we have chosen $m=5\sqrt{3}/4>m_{*}$ and $l=1$.

One can see from Table 1 and Table 2 and Figure 1 that when $m>m_{*}$, it is physically interesting both in all ranges of $\mathcal{C}$ with $R>0$ and all ranges of R with $\mathcal{C}>-1$. In those ranges, there exists not only an outer but also at least one inner event horizon. When $m=m_{*}$, the extremal case for the HRBH in massless gravity, it remains extremal for $\mathcal{C}\le -1$ and $R>0$ in the HRBH in massive gravity. However, for all ranges of R with $-1<\mathcal{C}<0$ and $R<0$ with $\mathcal{C}\ge 0$, it changes to have two or more event horizons. As a result, according to the graviton mass parameters R and $\mathcal{C}$, it is expected that the thermodynamics of the HRBH in massive gravity are differently described compared to those of the HRBH in massless gravity.

On the other hand, from the metric solution (8), one can find that the event horizon $r_H$ determines the mass as

$$m\left(r_H\right)=\frac{(1+\mathcal{C}+2R{r}_H)r_H^3}{2[r_H^2-(1+\mathcal{C}+2R{r}_H)l^2]}.$$

(9)

In Figure 2, we have plotted the mass function by comparing the HRBH in massless gravity with ones in holographic massive gravity. As a result, one can see that for a fixed R (or $\mathcal{C}$), as $\mathcal{C}$ (or R) decreases, the outer event horizon $r_H$ increases in the HRBH in massive gravity.

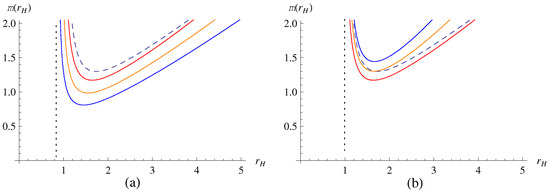
Figure 2. Mass function $m\left(r_H\right)$: (a) $(R,\mathcal{C})=(0,0),(0.01,-0.1),(0.01,-0.2),(0.01,-0.3)$ from top to bottom curves and (b) $(R,\mathcal{C})=(0.01,-0.1),(0,0),(0.03,-0.1),(0.05,-0.1)$ from bottom to top curves. The dashed lines corresponding to $(R,\mathcal{C})=(0,0)$ are for the HRBH in massless gravity.

Finally, it is appropriate to comment on the Kretschmann scalar—which is known to be finite for regular black holes—for the HRBH in massive gravity. First of all, for the HRBH in massless gravity [27], the Kretschmann scalar is given by

$$\begin{array}{c}\hfill {\mathcal{R}}_{\mu \nu \rho \sigma }{\mathcal{R}}^{\mu \nu \rho \sigma }=\frac{48m^2(r^{12}-8l^{2}m{r}^9+72l^4{m}^2{r}^6-16l^6{m}^3{r}^3+32l^8{m}^4)}{{(r^3+2m{l}^2)}^6}.\end{array}$$

(10)

At the center of the spacetime as $r\to 0$, due to the Hayward parameter l, it is finite as

$$\begin{array}{ccc}\hfill {\mathcal{R}}_{\mu \nu \rho \sigma }{\mathcal{R}}^{\mu \nu \rho \sigma }& =& \frac{24}{l^4},\hfill \end{array}$$

(11)

which shows that the HRBH in massless gravity is regular everywhere with no curvature singularity. On the other hand, as $l\to 0$, it becomes

$$\begin{array}{c}\hfill {\mathcal{R}}_{\mu \nu \rho \sigma }{\mathcal{R}}^{\mu \nu \rho \sigma }=\frac{48m^2}{r^6},\end{array}$$

(12)

the Kretschmann scalar of the Schwarzschild spacetime in massless gravity, as expected.

Now, when massive gravitons are introduced as the HRBH in massive gravity having the lapse function (8), we have a new Kretschmann scalar modified by R and $\mathcal{C}$ as

$$\begin{array}{ccc}\hfill {\mathcal{R}}_{\mu \nu \rho \sigma }{\mathcal{R}}^{\mu \nu \rho \sigma }& =& \frac{48m^2(r^{12}-8l^{2}m{r}^9+72l^4{m}^2{r}^6-16l^6{m}^3{r}^3+32l^8{m}^4)}{{(r^3+2m{l}^2)}^6}\hfill \\ & -& \frac{192l^2{m}^{2}R}{r{(r^3+2m{l}^2)}^2}-\frac{16m\mathcal{C}}{r^2(r^3+2m{l}^2)}+\frac{32R^2}{r^2}+\frac{16R\mathcal{C}}{r^3}+\frac{4{\mathcal{C}}^2}{r^4}.\hfill \end{array}$$

(13)

In the massless limit of $R=0$ and $\mathcal{C}=0$, it becomes the Kretschmann scalar (10) of the HRBH in massless gravity. However, near the center as $r\to 0$, the last term in Equation (13) becomes dominant, so it diverges as

$${\mathcal{R}}_{\mu \nu \rho \sigma }{\mathcal{R}}^{\mu \nu \rho \sigma }\sim \frac{4{\mathcal{C}}^2}{r^4}\to \infty .$$

(14)

Thus, the regular structure of the HRBH in massless gravity has been changed to singular due to massive gravitons, though it is less severely divergent than the Schwarzschild case. Note that in the massive Schwarzschild limit as $l\to 0$, the Kretschmann scalar is reduced to

$${\mathcal{R}}_{\mu \nu \rho \sigma }{\mathcal{R}}^{\mu \nu \rho \sigma }=\frac{32R^2}{r^2}+\frac{16R\mathcal{C}}{r^3}+\frac{4{\mathcal{C}}^2}{r^4}-\frac{16m\mathcal{C}}{r^5}+\frac{48m^2}{r^6}.$$

(15)

As a result, we have found that introducing massive gravitons to the HRBH in massless gravity affects the spacetime structure from regular to singular. This singular structure of spacetime can be relieved by enlarging the dimensions of the spacetime according to the well-established GEMS scheme, which we consider in Section 3.

2.1. Solutions of the HRBH in Massless Gravity

Let us first briefly summarize the solutions of the HRBH in massless gravity satisfying $f\left({\tilde{r}}_H\right)=0$ in Equation (8), where ${\tilde{r}}_H$ denotes the horizon radius of the black hole in massless gravity. In the massless case with the graviton mass parameters $R=\mathcal{C}=0$, event horizons can be found from the following cubic equation, rewritten as

$${\tilde{r}}_H^3-2m{\tilde{r}}_H^2+2l^{2}m=0.$$

(16)

By following the general procedure from Equations (32)–(37) presented in the next subsection, one finally gets the solutions of the HRBH in massless gravity as

$$\begin{array}{ccc}\hfill {\tilde{r}}_{H1}& =& \frac{2m}{3}\left[1-2cos\left(\frac{\psi }{3}\right)\right],\hfill \\ \hfill {\tilde{r}}_{H2}& =& \frac{2m}{3}\left[1-2cos\left(\frac{\psi }{3}+\frac{2\pi }{3}\right)\right],\hfill \\ \hfill {\tilde{r}}_{H3}& =& \frac{2m}{3}\left[1-2cos\left(\frac{\psi }{3}+\frac{4\pi }{3}\right)\right],\hfill \end{array}$$

(17)

the behaviors of which are depicted in Figure 3. Here, $cos\psi$ is defined as

$$cos\psi =-1+\frac{27l^2}{8m^2}.$$

(18)

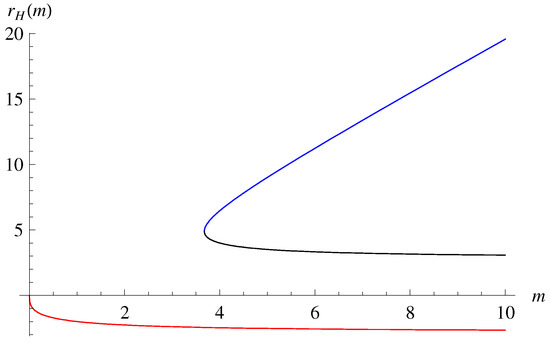
Figure 3. Solutions of the HRBH in massless gravity: the blue curve is for ${\tilde{r}}_{H2}$, the black curve for ${\tilde{r}}_{H3}$, and the red curve for ${\tilde{r}}_{H1}$ with $l=1$. Here, we see that ${\tilde{r}}_{H2}$ corresponds to an outer horizon ($r_{+}$) and ${\tilde{r}}_{H3}$ to an inner horizon ($r_{-}$). The term ${\tilde{r}}_{H1}$ is negative and is thus discarded.

Note that the solutions (17) satisfy the properties

$$\begin{array}{ccc}\hfill {\tilde{r}}_{H1}+{\tilde{r}}_{H2}+{\tilde{r}}_{H3}& =& 2m,\hfill \\ \hfill {\tilde{r}}_{H1}{\tilde{r}}_{H2}+{\tilde{r}}_{H2}{\tilde{r}}_{H3}+{\tilde{r}}_{H3}{\tilde{r}}_{H1}& =& 0,\hfill \\ \hfill {\tilde{r}}_{H1}{\tilde{r}}_{H2}{\tilde{r}}_{H3}& =& -2l^{2}m.\hfill \end{array}$$

(19)

2.2. Solution of the HRBH in Massive Gravity

In this subsection, we newly find general solutions of the HRBH in holographic massive gravity (8) satisfying $f\left(r_H\right)=0$, where $r_H$ denotes the horizon radius of the black hole in massive gravity. First of all, one can rewrite $f\left(r_H\right)=0$ as

$$2R{r}_H^4+(1+\mathcal{C})r_H^3-2m{r}_H^2+4R{l}^{2}m{r}_H+2l^{2}m(1+\mathcal{C})=0,$$

(20)

which is a quartic equation with $R\ne 0$, compared with the cubic one in the previous massless case. After dividing by $2R$ and by introducing a new variable y as

$$y=r_H+\frac{1+\mathcal{C}}{8R},$$

(21)

one can find the standard quartic equation written as

$$y^4+a_1{y}^2+a_{2}y+a_3=0,$$

(22)

where

$$\begin{array}{ccc}\hfill a_1& =& -\frac{m}{R}-\frac{3{(1+\mathcal{C})}^2}{32R^2},\hfill \\ \hfill a_2& =& 2l^{2}m+\frac{(1+\mathcal{C})m}{4R^2}+\frac{{(1+\mathcal{C})}^3}{64R^3},\hfill \\ \hfill a_3& =& \frac{3(1+\mathcal{C})l^{2}m}{4R}-\frac{{(1+\mathcal{C})}^{2}m}{64R^3}-\frac{3{(1+\mathcal{C})}^4}{4096R^4}.\hfill \end{array}$$

(23)

Note that at this stage, one cannot simply take the limit of $R\to 0$ since the coefficients are all divergent. Thus, if one wants to find the limit, Equation (20) should be considered again from the start.

The quartic Equation (22) can be solved by adding and subtracting $x{y}^2+x^2/4$ to Equation (22) as

$$\left(y^4+x{y}^2+\frac{1}{4}{x}^2\right)-x{y}^2-\frac{1}{4}{x}^2+a_1{y}^2+a_{2}y+a_3=0,$$

(24)

which can be rewritten as

$$\begin{array}{ccc}\hfill 0& =& {\left(y^2+\frac{1}{2}x\right)}^2-\left[(x-a_1)y^2-a_{2}y+\left(\frac{1}{4}{x}^2-a_3\right)\right]\hfill \\ & =& {\left(y^2+\frac{1}{2}x\right)}^2-{\left(\sqrt{x-a_1}y-\frac{a_2}{2\sqrt{x-a_1}}\right)}^2+\frac{a_2^2}{4(x-a_1)}-\left(\frac{1}{4}{x}^2-a_3\right).\hfill \end{array}$$

(25)

Thus, if we demand the last two terms to vanish as

$$\frac{a_2^2}{4(x-a_1)}-\left(\frac{1}{4}{x}^2-a_3\right)=0,$$

(26)

one can have

$$\begin{array}{ccc}\hfill 0& =& {\left(y^2+\frac{1}{2}x\right)}^2-{\left(\sqrt{x-a_1}y-\frac{a_2}{2\sqrt{x-a_1}}\right)}^2\hfill \\ & =& \left(y^2-\sqrt{x-a_1}y+\frac{1}{2}x+\frac{a_2}{2\sqrt{x-a_1}}\right)\left(y^2+\sqrt{x-a_1}y+\frac{1}{2}x-\frac{a_2}{2\sqrt{x-a_1}}\right).\hfill \end{array}$$

(27)

These are the products of two quadratic equations whose roots can be easily obtained separately. As a result, we have the following four roots for the quartic Equation (22)

$$\begin{array}{ccc}\hfill y_1=\frac{1}{2}(p_1+p_2),y_2=\frac{1}{2}(p_1-p_2),y_3& =& \frac{1}{2}(-p_1+p_3),y_4=\frac{1}{2}(-p_1-p_3),\hfill \end{array}$$

(28)

with

$$\begin{array}{c}\hfill p_1\equiv {(x_0-a_1)}^{1/2},p_2\equiv {\left(-p_1^2-2a_1-\frac{2a_2}{p_1}\right)}^{1/2},p_3\equiv {\left(-p_1^2-2a_1+\frac{2a_2}{p_1}\right)}^{1/2}.\end{array}$$

(29)

In Equation (29), note that $x_0$ is a root of the cubic Equation (26) rewritten as

$$x^3-a_1{x}^2-4a_{3}x+4a_1{a}_3-a_2^2=0.$$

(30)

Then, we have

$$b_1=-a_1,b_2=-4a_3,b_3=4a_1{a}_3-a_2^2,$$

(31)

where $b_1,b_2$, and $b_3$ are the coefficients of the standard cubic equation of

$$x^3+b_1{x}^2+b_{2}x+b_3=0.$$

(32)

These give us

$$q_1=\frac{9b_1{b}_2-27b_3-2b_1^3}{54},q_2=\frac{3b_2-b_1^2}{9}$$

(33)

to yield

$$\begin{array}{ccc}\hfill q_1& =& 2l^4{m}^2+\frac{3(1+\mathcal{C})l^2{m}^2}{2R^2}-\frac{m^3}{27R^3}+\frac{{(1+\mathcal{C})}^3{l}^{2}m}{8R^3},\hfill \\ \hfill q_2& =& -\frac{(1+\mathcal{C})l^{2}m}{R}-\frac{m^2}{9R^2}.\hfill \end{array}$$

(34)

Now, we define $cos\psi$ [148,149] as

$$cos\psi =\frac{q_1}{{(-q_2^3)}^{1/2}}.$$

(35)

Making use of $q_1$ and $q_2$ in Equation (34), we find

$$\begin{array}{c}\hfill cos\psi =\frac{-8m^3+27{(1+\mathcal{C})}^3{l}^{2}m+324(1+\mathcal{C})l^2{m}^{2}R+432l^4{m}^2{R}^3}{8{[m^2+9(1+\mathcal{C})l^{2}mR]}^{3/2}}.\end{array}$$

(36)

Then, the solutions for the cubic Equation (30) are given by

$$\begin{array}{ccc}\hfill x_1& =& \frac{2}{3R}{[m^2+9(1+\mathcal{C})l^{2}mR]}^{1/2}cos\left(\frac{\psi }{3}\right)-\frac{1}{3R}\left[m+\frac{3{(1+\mathcal{C})}^2}{32R}\right],\hfill \\ \hfill x_2& =& \frac{2}{3R}{[m^2+9(1+\mathcal{C})l^{2}mR]}^{1/2}cos\left(\frac{\psi }{3}+\frac{2\pi }{3}\right)-\frac{1}{3R}\left[m+\frac{3{(1+\mathcal{C})}^2}{32R}\right],\hfill \\ \hfill x_3& =& \frac{2}{3R}{[m^2+9(1+\mathcal{C})l^{2}mR]}^{1/2}cos\left(\frac{\psi }{3}+\frac{4\pi }{3}\right)-\frac{1}{3R}\left[m+\frac{3{(1+\mathcal{C})}^2}{32R}\right].\hfill \end{array}$$

(37)

Thus, making use of these solutions, we finally have the following four roots of the quartic Equation (22) as

$$\begin{array}{ccc}\hfill r_{H1}& =& \frac{1}{2}\left(p_1+p_2-\frac{1+\mathcal{C}}{4R}\right),\hfill \\ \hfill r_{H2}& =& \frac{1}{2}\left(p_1-p_2-\frac{1+\mathcal{C}}{4R}\right),\hfill \\ \hfill r_{H3}& =& \frac{1}{2}\left(-p_1+p_3-\frac{1+\mathcal{C}}{4R}\right),\hfill \\ \hfill r_{H4}& =& \frac{1}{2}\left(-p_1-p_3-\frac{1+\mathcal{C}}{4R}\right),\hfill \end{array}$$

(38)

where

$$\begin{array}{ccc}\hfill p_1& =& {\left(\frac{2}{3R}{[m^2+9(1+\mathcal{C})l^{2}mR]}^{1/2}cos\left(\frac{\psi }{3}\right)+\frac{2}{3R}\left[m+\frac{3{(1+\mathcal{C})}^2}{32R}\right]\right)}^{1/2},\hfill \\ \hfill p_2& =& \left(-\frac{2}{3R}{[m^2+9(1+\mathcal{C})l^{2}mR]}^{1/2}cos\left(\frac{\psi }{3}\right)+\frac{4}{3R}\left[m+\frac{3{(1+\mathcal{C})}^2}{32R}\right]\right.\hfill \\ & & {\left.-2\left\{2l^{2}m+\frac{(1+\mathcal{C})m}{4R^2}+\frac{{(1+\mathcal{C})}^3}{64R^3}\right\}{\left\{\frac{2}{3R}{[m^2+9(1+\mathcal{C})l^{2}mR]}^{1/2}cos\left(\frac{\psi }{3}\right)+\frac{2}{3R}\left[m+\frac{3{(1+\mathcal{C})}^2}{32R}\right]\right\}}^{-1/2}\right)}^{1/2},\hfill \\ \hfill p_3& =& \left(-\frac{2}{3R}{[m^2+9(1+\mathcal{C})l^{2}mR]}^{1/2}cos\left(\frac{\psi }{3}\right)+\frac{4}{3R}\left[m+\frac{3{(1+\mathcal{C})}^2}{32R}\right]\right.\hfill \\ & & {\left.+2\left\{2l^{2}m+\frac{(1+\mathcal{C})m}{4R^2}+\frac{{(1+\mathcal{C})}^3}{64R^3}\right\}{\left\{\frac{2}{3R}{[m^2+9(1+\mathcal{C})l^{2}mR]}^{1/2}cos\left(\frac{\psi }{3}\right)+\frac{2}{3R}\left[m+\frac{3{(1+\mathcal{C})}^2}{32R}\right]\right\}}^{-1/2}\right)}^{1/2}.\hfill \end{array}$$

(39)

Here, we have chosen $x_1$ as $x_0$ in $p_1$.

In Figure 4, we depict a set of solutions for the HRBH in massive gravity for $R=0.01$ and $\mathcal{C}=-0.1$. As explained in Table 1, for the chosen R and $\mathcal{C}$, we expect that there are two event horizons, and Figure 4 shows the same behavior that there are two, i.e., one is an outer $r_{H1}$ and the other is an inner horizon $r_{H2}$. The remaining two, $r_{H3}$ and $r_{H4}$, are of no physical meaning for event horizons since they are negative. In Figure 5, we also draw the solution for the HRBH in massive gravity compared with the HRBH in massless gravity, where one can see how massive gravitons change $r_H\left(m\right)$.

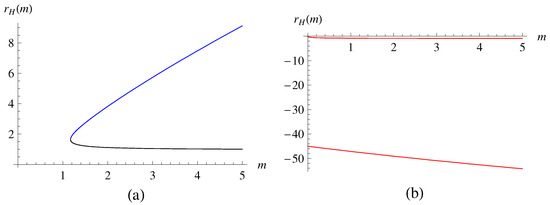
Figure 4. Solutions for the HRBH in massive gravity: (a) The blue curve is for $r_{H1}$ and the black curve is for $r_{H2}$, which correspond to an outer horizon ($r_{+}$) and to an inner horizon ($r_{-}$), respectively. In (b), the curves are for $r_{H3}$ (upper) and $r_{H4}$ (lower), which are negative and are thus discarded. Here, we set $R=0.01$, $\mathcal{C}=-0.1$ with $l=1$.

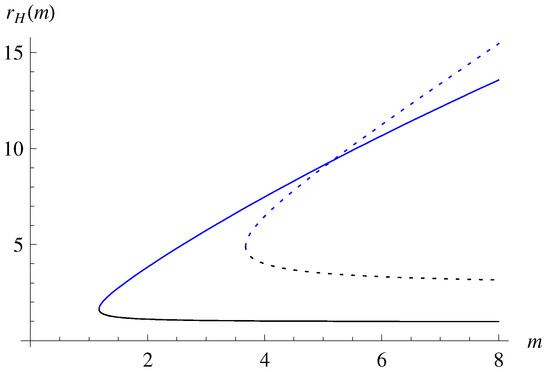
Figure 5. Solutions for the HRBH in massless and massive gravity: the blue and black solid curves are for massive gravity, while the dotted curves are for massless gravity. Here, we set $R=0.01$, $\mathcal{C}=-0.1$ with $l=1$.

Note that $r_{H_i}(i=1,2,3,4)$ in Equation (38) denote the event horizons of the HRBH in holographic massive gravity, while ${\tilde{r}}_{H_i}(i=1,2,3)$ in Equation (17) stand for those of the HRBH in massless gravity. It is also appropriate to comment that it is not possible to directly obtain the solutions of the HRBH in massless gravity by taking $R\to 0$ and $\mathcal{C}\to 0$ from the solutions (38) of the quartic equation. Note that this can be understood due to the fact that they are obtained from the implicit condition of $R\ne 0$ as in Equations (20) and (21).

3. GEMS Embedding of HRBH

3.1. HRBH in Massless Gravity

The (3+1)-dimensional HRBH in massless gravity can be embedded in a (5+2)-dimensional Minkowski spacetime given by

$$d{s}^2={\eta }_{IJ}d{z}^{I}d{z}^J,\mathrm{with}{\eta }_{IJ}=\mathrm{diag}(-1,1,1,1,1,1,-1),$$

(40)

where embedding coordinates are obtained as

$$\begin{array}{ccc}\hfill z^0& =& {\tilde{k}}_H^{-1}{f}^{1/2}\left(r\right)sinh{\tilde{k}}_{H}t,\hfill \\ \hfill z^1& =& {\tilde{k}}_H^{-1}{f}^{1/2}\left(r\right)cosh{\tilde{k}}_{H}t,\hfill \\ \hfill z^2& =& rsin\theta cos\varphi ,\hfill \\ \hfill z^3& =& rsin\theta sin\varphi ,\hfill \\ \hfill z^4& =& rcos\theta ,\hfill \\ \hfill z^5& =& \int \frac{dr}{2{\tilde{k}}_H}{\left(\frac{H_0[r^8{\tilde{r}}_H^{13}+l^4{r}^2{\tilde{r}}_H^9(30r^6+5r^3{\tilde{r}}_H^3+4{\tilde{r}}_H^6)+20l^6{r}^5{\tilde{r}}_H^{10}+l^8{r}^2{\tilde{r}}_H^5(33r^6+6{\tilde{r}}_H^6)+18l^{10}{r}^5{\tilde{r}}_H^6]}{{\tilde{r}}_H^6(r^2{\tilde{r}}_H^2-l^2{H}_0){[r^3({\tilde{r}}_H^2-l^2)+l^2{\tilde{r}}_H^3]}^3}\right)}^{1/2},\hfill \\ \hfill z^6& =& \int \frac{ldr}{2{\tilde{k}}_H}{\left(\frac{H_0[r^5{\tilde{r}}_H^{11}(9r^3+4{\tilde{r}}_H^3)+l^4{r}^2{\tilde{r}}_H^7(46r^6+{\tilde{r}}_H^6)+39l^6{r}^5{\tilde{r}}_H^8+9l^8{r}^2{\tilde{r}}_H^3(r^6+{\tilde{r}}_H^6)]}{{\tilde{r}}_H^6(r^2{\tilde{r}}_H^2-l^2{H}_0){[r^3({\tilde{r}}_H^2-l^2)+l^2{\tilde{r}}_H^3]}^3}\right)}^{1/2},\hfill \end{array}$$

(41)

with

$$\begin{array}{c}\hfill H_0=r^2+r{\tilde{r}}_H+{\tilde{r}}_H^2.\end{array}$$

(42)

In the above embedding functions (41), ${\tilde{k}}_H$ is the surface gravity, which is defined as

$${\tilde{k}}_H={\left.\sqrt{-\frac{1}{2}\left({\nabla }^{\mu }{\xi }^{\nu }\right)\left({\nabla }_{\mu }{\xi }_{\nu }\right)}\right|}_{r={\tilde{r}}_H}=\frac{{\tilde{r}}_H^2-3l^2}{2{\tilde{r}}_H^3},$$

(43)

where ${\xi }^{\mu }$ is a Killing vector, and ${\tilde{r}}_H$ is the event horizon of the HRBH in massless gravity. Note that in the limit of $l\to 0$, $z^6$ vanishes, and $z^5$ becomes

$$z^5=\int \frac{dr}{2{\tilde{k}}_H}{\left(\frac{r^2+r{\tilde{r}}_H+{\tilde{r}}_H^2}{{\tilde{r}}_H{r}^3}\right)}^{1/2}.$$

(44)

Therefore, with $z^0\cdots z^4$ expressed in the same limit, the embedding coordinates (41) are correctly reduced to the well-known (5+1)-dimensional GEMS embeddings of the Schwarzschild black hole [114].

Here, we note that from the original spacetime metric, the Hawking temperature ${\tilde{T}}_H$ seen by an asymptotic observer and a local fiducial temperature measured by an observer who rests at a distance from the black hole are simply found as

$${\tilde{T}}_H=\frac{{\tilde{k}}_H}{2\pi }=\frac{{\tilde{r}}_H^2-3l^2}{4\pi {\tilde{r}}_H^3},$$

(45)

$${\tilde{T}}_{\mathrm{FID}}\left(r\right)=\frac{{\tilde{T}}_H}{\sqrt{f\left(r\right)}}=\frac{({\tilde{r}}_H^2-3l^2){[r^3({\tilde{r}}_H^2-l^2)+l^2{\tilde{r}}_H^3]}^{1/2}}{4\pi {\tilde{r}}_H^3{\left[(r-{\tilde{r}}_H)(r^2{\tilde{r}}_H^2-H_0{l}^2)\right]}^{1/2}},$$

(46)

respectively.

Now, let us consider the Unruh effect in the embedded flat spacetime, which originally states that accelerated observers or detectors with an acceleration a along the x direction by following the trajectory $a^{-2}=x^2-t^2$ measure the Unruh temperature given by $2\pi T=a$ [118]. To apply this to a higher-dimensional flat spacetime, we notice that the static detectors ($r,\theta ,\varphi =\mathrm{constant}$) in the original curved spacetime are described by a fixed point in the ($z^2,z^3,z^4,z^5,z^6$) plane on the GEMS embedded spacetime. Then, an observer who is uniformly accelerated in the (5+2)-dimensional flat spacetime follows a hyperbolic trajectory described by

$$a_7^{-2}={\left(z^1\right)}^2-{\left(z^0\right)}^2=\frac{f\left(r\right)}{{\tilde{k}}_H^2}.$$

(47)

Thus, one can find the Unruh temperature for the uniformly accelerated observer in the (5+2)-dimensional flat spacetime as

$${\tilde{T}}_U=\frac{a_7}{2\pi }=\frac{({\tilde{r}}_H^2-3l^2){[r^3({\tilde{r}}_H^2-l^2)+l^2{\tilde{r}}_H^3]}^{1/2}}{4\pi {\tilde{r}}_H^3{\left[(r-{\tilde{r}}_H)(r^2{\tilde{r}}_H^2-H_0{l}^2)\right]}^{1/2}}.$$

(48)

This corresponds to the fiducial temperature (46) for the observer located at a distance from the HRBH in massless gravity. The Hawking temperature ${\tilde{T}}_H$ seen by an asymptotic observer can be obtained as

$${\tilde{T}}_H=\sqrt{-g_{00}}{\tilde{T}}_U=\frac{{\tilde{k}}_H}{2\pi }.$$

(49)

As a result, one can see that the Hawking effect for a fiducial observer in a black hole spacetime is equal to the Unruh effect for a uniformly accelerated observer in a higher-dimensional flat spacetime.

Now, let us find a freely falling acceleration and corresponding temperature in the (5+2)-dimensional embedded flat spacetime. For an observer who is freely falling from rest $r=r_0$ at $\tau =0$, the equations of motion are

$$\begin{array}{ccc}\hfill \frac{dt}{d\tau }& =& \frac{f^{1/2}\left(r_0\right)}{f\left(r\right)}={\left(1-\frac{2m{r}_0^2}{r_0^3+2l^{2}m}\right)}^{1/2}{\left(1-\frac{2m{r}^2}{r^3+2l^{2}m}\right)}^{-1},\hfill \\ \hfill \frac{dr}{d\tau }& =& -{[f\left(r_0\right)-f\left(r\right)]}^{1/2}=-{\left[\frac{-2m\{r_0^2{r}^2(r-r_0)-2l^{2}m(r^2-r_0^2)\}}{(r_0^3+2l^{2}m)(r^3+2l^{2}m)}\right]}^{1/2},\hfill \end{array}$$

(50)

where the $(-)$ sign is for inward motion. Then, making use of the embedding coordinates in Equation (41) and the geodesic equations in Equation (50), one can explicitly find a freely falling acceleration ${\overline{a}}_7$ in the GEMS embedded (5+2)-dimensional spacetime as

$$\begin{array}{ccc}\hfill {\overline{a}}_7^2& =& \sum _{I=0}^6{\left.{\eta }_{IJ}\frac{d{z}^I}{d\tau }\frac{d{z}^J}{d\tau }\right|}_{r=r_0}\hfill \\ & =& \frac{N_1{N}_2}{4{\tilde{r}}_H^6(r^2{\tilde{r}}_H^2-l^2{H}_0){[r^3({\tilde{r}}_H^2-l^2)+l^2{\tilde{r}}_H^3]}^3},\hfill \end{array}$$

(51)

where

$$\begin{array}{ccc}\hfill N_1& =& r^4{\tilde{r}}_H^6(r+{\tilde{r}}_H)-l^{2}r{\tilde{r}}_H^4{H}_1+l^4{\tilde{r}}_H^2{H}_0{H}_2-3l^6(r-{\tilde{r}}_H)H_0^2,\hfill \\ \hfill N_2& =& r^4{\tilde{r}}_H^6(r^2+{\tilde{r}}_H^2)-l^{2}r{\tilde{r}}_H^4{H}_3+l^4{\tilde{r}}_H^2(r-{\tilde{r}}_H)H_0{H}_2-3l^6{(r-{\tilde{r}}_H)}^2{H}_0^2\hfill \end{array}$$

(52)

with

$$\begin{array}{ccc}\hfill H_1& =& 5r^4+5r^3{\tilde{r}}_H+4r^2{\tilde{r}}_H^2+2r{\tilde{r}}_H^3+2{\tilde{r}}_H^4,\hfill \\ \hfill H_2& =& 7r^3-{\tilde{r}}_H^3,\hfill \\ \hfill H_3& =& 5r^5+r^3{\tilde{r}}_H^2-2r^2{\tilde{r}}_H^3+2{\tilde{r}}_H^5.\hfill \end{array}$$

(53)

Note here that $r_0$ is replaced with r in Equation (51).

According to the Unruh’s prescription, the freely falling acceleration gives us the freely falling temperature measured by the freely falling observer as

$$\begin{array}{ccc}\hfill {\tilde{T}}_{\mathrm{FF}}& =& \frac{{\overline{a}}_7}{2\pi }\hfill \\ & =& \frac{1}{4\pi {\tilde{r}}_H^3}\sqrt{\frac{N_1{N}_2}{(r^2{\tilde{r}}_H^2-l^2{H}_0){[r^3({\tilde{r}}_H^2-l^2)+l^2{\tilde{r}}_H^3]}^3}}.\hfill \end{array}$$

(54)

Making use of the dimensionless parameters $x={\tilde{r}}_H/r$ and $b=l/{\tilde{r}}_H$, the squared freely falling temperature can be written as

$${\tilde{T}}_{\mathrm{FF}}^2=\frac{[1+x-b^2{h}_1+b^4{h}_0{h}_2-3b^6(1-x)h_0^2][1+x^2-b^2{h}_3+b^4(1-x)h_0{h}_2-3b^6{(1-x^3)}^2]}{16{\pi }^2{\tilde{r}}_H^2(1-b^2{h}_0){[1-b^2(1-x^3)]}^3},$$

(55)

where

$$\begin{array}{ccc}\hfill h_0& \equiv & H_0/r^2=1+x+x^2,\hfill \\ \hfill h_1& \equiv & H_1/r^4=5+5x+4x^2+2x^3+2x^4,\hfill \\ \hfill h_2& \equiv & H_2/r^3=7-x^3,\hfill \\ \hfill h_3& \equiv & H_3/r^5=5+x^2-2x^3+2x^5.\hfill \end{array}$$

(56)

As $r\to \infty$, the freely falling temperature ${\tilde{T}}_{\mathrm{FF}}$ is reduced to the Hawking temperature (45). Moreover, as $l\to 0$, it becomes the freely falling temperature of the Schwarzschild black hole as

$$T_{\mathrm{FF}}^{\mathrm{Sch}}=\frac{1}{4\pi {\overline{r}}_H}\sqrt{\frac{r^3+{\overline{r}}_H{H}_0}{r^3}},$$

(57)

where ${\overline{r}}_H=2m$ is the radius of the event horizon of the Schwarzschild black hole. Note also that as $r\to \infty$, $T_{\mathrm{FF}}^{\mathrm{Sch}}$ becomes the Hawking temperature of the Schwarzschild black hole, while as $r\to {\overline{r}}_H$, the freely falling temperature becomes

$$T_{\mathrm{FF}}^{\mathrm{Sch}}\to \frac{1}{2\pi {\overline{r}}_H},$$

(58)

which does not diverge but remains finite at the event horizon.

In Figure 6, we have depicted the ratio of the squared freely falling temperatures to the squared Hawking temperature, ${\tilde{T}}_{\mathrm{FF}}^2/{\tilde{T}}_H^2$. For comparison purposes, it is shown in Figure 6a that the freely falling temperature of the Schwarzschild black hole, which is a prototype of a singular black hole, is finite at the event horizon of $x=1$ ($r={\tilde{r}}_H$), while it becomes the Hawking temperature at asymptotic infinity of $x\to 0$ ($r\to \infty$). On the other hand, as in Figure 6b, for the HRBH in massless gravity, the freely falling temperatures are finite only when $0<b<b_c(\equiv 0.3568)$ at the event horizons, and when $b=b_c$, it vanishes at the event horizon. Meanwhile, the freely falling temperatures become the Hawking temperature at asymptotic infinity. The parameter b also has an upper bound coming from the Hawking temperature (45), which is defined when ${\tilde{r}}_H\ge \sqrt{3}l$ (or $b\le 1/\sqrt{3}=0.5774$) where ${\tilde{T}}_{\mathrm{FF}}^2/{\tilde{T}}_H^2$ diverges. In between $b_c<b<0.5774$, one can see in Figure 6b that the freely falling temperatures of the HRBH behave quite differently from the Schwarzschild singular black hole. They go up and down and then become negative. It is well known that the negativity of squared freely falling temperatures is not entirely prohibited, which means that there is no thermal radiation. This is allowed for a geodesic observer who follows a spacelike motion similar to the case of the Schwarzschild–AdS black hole in massless gravity [113,119,139].

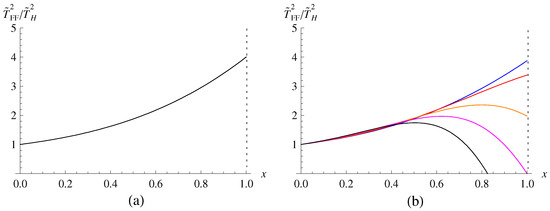
Figure 6. Squared freely falling temperatures ${\tilde{T}}_{\mathrm{FF}}^2/{\tilde{T}}_{\mathrm{H}}^2$ for the HRBH in massless gravity drawn by a dimensionless parameter $x(={\tilde{r}}_H/r)$. (a) The freely falling temperature of the Schwarzschild black hole in massless gravity, which corresponds to $b=0$ (or $l=0$). (b) The freely falling temperatures of the HRBH in massless gravity for $b=0.1\left(\mathrm{blue}\right),0.2\left(\mathrm{red}\right),0.3\left(\mathrm{orange}\right),b_c\left(\mathrm{pink}\right),0.4\left(\mathrm{black}\right)$. Here, the vertical dotted lines are drawn at event horizons.

3.2. HRBH in Massive Gravity

Now, after a lengthy calculation, we newly find that the (3+1)-dimensional HRBH in massive gravity can be embedded in a (6+3)-dimensional Minkowski spacetime as

$$d{s}^2={\eta }_{IJ}d{z}^{I}d{z}^J,\mathrm{with}{\eta }_{IJ}=\mathrm{diag}(-1,1,1,1,1,1,-1,-1,1),$$

(59)

whose embedding coordinates are explicitly written as

$$\begin{array}{ccc}\hfill z^0& =& k_H^{-1}{f}^{1/2}\left(r\right)sinh{k}_{H}t,\hfill \\ \hfill z^1& =& k_H^{-1}{f}^{1/2}\left(r\right)cosh{k}_{H}t,\hfill \\ \hfill z^2& =& rsin\theta cos\varphi ,\hfill \\ \hfill z^3& =& rsin\theta sin\varphi ,\hfill \\ \hfill z^4& =& rcos\theta ,\hfill \\ \hfill z^5& =& \int \frac{dr}{2k_H}{\left[\frac{r^8{r}_H^{12}{H}_5{u}_1+l^2{r}^9{r}_H^{10}{H}_5{u}_2+l^4{r}^2{r}_H^8{H}_5^2{u}_3+2l^6{r}^4{r}_H^6{H}_5^3{u}_4+l^8{r}_H^5{H}_5^4{u}_5+3l^{10}{r}^3{r}_H{H}_5^6{u}_6+9l^{12}{r}_H{H}_5^8{u}_7}{r_H^6[r^2{r}_H^2(H_5+2Rr)-l^2{H}_4{H}_5{H}_6]{[r^3(r_H^2-l^2{H}_5)+l^2{r}_H^3{H}_5]}^3}\right]}^{1/2},\hfill \\ \hfill z^6& =& \int \frac{dr}{2k_H}{\left[\frac{r^8{r}_H^{12}{H}_5{\overline{u}}_1+l^2{r}^9{r}_H^{10}{H}_5{\overline{u}}_2+l^4{r}^2{r}_H^8{H}_5^2{\overline{u}}_3+2l^6{r}^4{r}_H^6{H}_5^3{\overline{u}}_4+l^8{r}_H^5{H}_5^4{\overline{u}}_5+3l^{10}{r}^3{r}_H{H}_5^6{\overline{u}}_6+9l^{12}{r}_H{H}_5^8{\overline{u}}_7}{r_H^6[r^2{r}_H^2(H_5+2Rr)-l^2{H}_4{H}_5{H}_6]{[r^3(r_H^2-l^2{H}_5)+l^2{r}_H^3{H}_5]}^3}\right]}^{1/2},\hfill \\ \hfill z^7& =& \int \frac{ldr}{2k_H}{\left[\frac{r^5{r}_H^{11}{H}_5{v}_1+6l^2{r}^4{r}_H^{11}R{H}_5^2{v}_2+l^{4}r{r}_H^7{H}_5^3{v}_3+l^6{r}^3{r}_H^4{H}_5^4{v}_4+3l^8{r}_H^2{H}_5^6{v}_5+9l^{10}{H}_5^8{v}_6}{r_H^6[r^2{r}_H^2(H_5+2Rr)-l^2{H}_4{H}_5{H}_6]{[r^3(r_H^2-l^2{H}_5)+l^2{r}_H^3{H}_5]}^3}\right]}^{1/2},\hfill \\ \hfill z^8& =& \int \frac{ldr}{2k_H}{\left[\frac{r^5{r}_H^{11}{H}_5{\overline{v}}_1+6l^2{r}^4{r}_H^{11}R{H}_5^2{\overline{v}}_2+l^{4}r{r}_H^7{H}_5^3{\overline{v}}_3+l^6{r}^3{r}_H^4{H}_5^4{\overline{v}}_4+3l^8{r}_H^2{H}_5^6{\overline{v}}_5+9l^{10}{H}_5^8{\overline{v}}_6}{r_H^6[r^2{r}_H^2(H_5+2Rr)-l^2{H}_4{H}_5{H}_6]{[r^3(r_H^2-l^2{H}_5)+l^2{r}_H^3{H}_5]}^3}\right]}^{1/2}.\hfill \end{array}$$

(60)

Here, the surface gravity of the HRBH in massive gravity is given by

$$k_H=\frac{H_5(r_H^2-3l^2{H}_5)}{2r_H^3}+R.$$

(61)

Also, $H_4$, $H_5$, and $H_6$ are defined as

$$\begin{array}{ccc}\hfill H_4& =& 1+\mathcal{C}+2Rr,\hfill \\ \hfill H_5& =& 1+\mathcal{C}+2R{r}_H,\hfill \\ \hfill H_6& =& r^2+r{r}_H+r_H^2,\hfill \end{array}$$

(62)

and $u_i\left({\overline{u}}_i\right)(i=1,2,\cdots ,7)$ and $v_i\left({\overline{v}}_i\right)(i=1,2,\cdots ,6)$ are given in Appendix A. Note that the above GEMS embedding is explicitly carried out under the assumption of $R\ge 0$ and $\mathcal{C}\ge -1$, which is physically much more interesting than other embeddings, as shown in Figure 1 and Figure 2 and Table 1 and Table 2.

It seems appropriate to comment that in the massless gravity limit of $R\to 0$ and $\mathcal{C}\to 0$, $H_4$ and $H_5$ become unity, and $H_6$ becomes $H_0$ in Equation (42). Also, when subtracting the embedding coordinates $z^6$ from $z^5$, the coefficients of $u_i-{\overline{u}}_i(i=1,2,\cdots ,7)$ in the numerator of $z^5-z^6$ are reduced to Equation (A9) in the Appendix A. In the same way, by subtracting the embedding coordinates $z^8$ from $z^7$, the coefficients of $v_i-{\overline{v}}_i$$(i=1,2,\cdots ,6)$ in the numerator of $z^7-z^8$ become Equation (A10). Since $H_6$ is reduced to $H_0$ in the massless limit, one can find that they are exactly the same coefficients in $z^5$ and $z^6$, respectively, of the HRBH in massless gravity in Equations (41). As a result, one can see that when $R\to 0$ and $\mathcal{C}\to 0$, the (6+3)-dimensional embedding coordinates (60) of the HRBH in massive gravity have proper limits of the (5+2)-dimensional ones (41) in massless gravity. Moreover, when one additionally takes the limit of $l\to 0$, $z^7$ and $z^8$ identically vanish, and the combination of $z^5$ and $z^6$ by subtraction is finally reduced to

$$z^5=\int dr\sqrt{\frac{{\overline{r}}_H(r^2+r{\overline{r}}_H+{\overline{r}}_H^2)}{r^3}},$$

(63)

where ${\overline{r}}_H=2m$ is the event horizon of the Schwarzschild black hole. Thus, one can see that the embedding coordinate of $z^5-z^6$ is finally reduced to $z^5$, which is one of the spacelike embedding coordinates of the Schwarzschild black hole in the (5+1)-dimensional GEMS scheme.

Here, we note again that from the original spacetime metric, the Hawking temperature $T_H$ seen by an asymptotic observer can be found as

$$T_H=\frac{H_5(r_H^2-3l^2{H}_5)+2R{r}_H^3}{4\pi r_H^3},$$

(64)

and a local fiducial temperature measured by an observer who rests at a distance from the black hole is given by

$$T_{\mathrm{FID}}\left(r\right)=\frac{T_H}{\sqrt{f\left(r\right)}}=\frac{H_5(r_H^2-3l^2{H}_5){[r^3(r_H^2-H_5{l}^2)+l^2{r}_H^3{H}_5]}^{1/2}}{4\pi r_H^3{\left[H_5(r-r_H)(r^2{r}_H^2-l^2{H}_6)\right]}^{1/2}}.$$

(65)

In the massless limit of $R\to 0$ and $\mathcal{C}\to 0$, one can easily find that it becomes the fiducial temperature (46) since $H_5\to 1$ and $H_6\to H_0$.

On the other hand, in order to investigate the Unruh effect in the GEMS embedded flat spacetime, we note that the static detectors ($r,\theta ,\varphi =\mathrm{constant}$) in the original curved spacetime are described by a fixed point in the ($z^2,z^3,z^4,z^5,z^6,z^7,z^8$) plane on the GEMS embedded spacetime. Then, an observer who is uniformly accelerated in the (6+3)-dimensional flat spacetime follows a hyperbolic trajectory in ($z^0,z^1$) described by

$$a_9^{-2}={\left(z^1\right)}^2-{\left(z^0\right)}^2=\frac{f\left(r\right)}{k_H^2}.$$

(66)

Thus, as before, one can arrive at the Unruh temperature for the uniformly accelerated observer in the (6+3)-dimensional flat spacetime as

$$\begin{array}{c}\hfill T_U=\frac{a_9}{2\pi }=\frac{H_5(r_H^2-3l^2{H}_5){[r^3(r_H^2-H_5{l}^2)+l^2{r}_H^3{H}_5]}^{1/2}}{4\pi r_H^3{\left[H_5(r-r_H)(r^2{r}_H^2-l^2{H}_6)\right]}^{1/2}}.\end{array}$$

(67)

This corresponds to the fiducial temperature for the observer located at a distance from the HRBH in massive gravity. The Hawking temperature $T_H$ seen by an asymptotic observer can be obtained as

$$T_H=\sqrt{-g_{00}}{T}_U=\frac{k_H}{2\pi }.$$

(68)

As a result, one can see that the Hawking effect for a fiducial observer in a black hole spacetime is equal to the Unruh effect for a uniformly accelerated observer in a higher-dimensional flat spacetime.

Now, let us find a freely falling acceleration and corresponding temperature in the (6+3)-dimensional embedded flat spacetime. For an observer who is freely falling from rest $r=r_0$ at $\tau =0$, the equations of motion are

$$\begin{array}{c}\hfill \frac{dt}{d\tau }=\frac{f^{1/2}\left(r_0\right)}{f\left(r\right)}={\left(1-\frac{2m{r}_0^2}{r_0^3+2l^{2}m}+2R{r}_0+\mathcal{C}\right)}^{1/2}{\left(1-\frac{2m{r}^2}{r^3+2l^{2}m}+2Rr+\mathcal{C}\right)}^{-1},\end{array}$$

(69)

$$\begin{array}{c}\hfill \frac{dr}{d\tau }=-{[f\left(r_0\right)-f\left(r\right)]}^{1/2}=-{\left[\frac{-2m\{r_0^2{r}^2(r-r_0)-2l^{2}m(r^2-r_0^2)\}}{(r_0^3+2l^{2}m)(r^3+2l^{2}m)}-2R(r-r_0)\right]}^{1/2}.\end{array}$$

(70)

Then, making use of the embedding coordinates in Equation (60) and the geodesic equations in Equation (69), one can explicitly find a freely falling acceleration $a_9$ in the GEMS embedded (6+3)-dimensional spacetime as

$$\begin{array}{ccc}\hfill {\overline{a}}_9^2& =& \sum _{I=0}^8{\left.{\eta }_{IJ}\frac{d{z}^I}{d\tau }\frac{d{z}^J}{d\tau }\right|}_{r=r_0}\hfill \\ & =& \frac{H_5{N}_3{N}_4}{4r_H^6(r^2{r}_H^2(H_5+2Rr)-l^2{H}_4{H}_5{H}_6){[r^3(r_H^2-l^2{H}_5)+l^2{r}_H^3{H}_5]}^3},\hfill \end{array}$$

(71)

where

$$\begin{array}{ccc}\hfill N_3& \equiv & r^4{r}_H^6(r+r_H)-l^{2}r{r}_H^4{H}_1{H}_5+l^4{r}_H^2{H}_2{H}_5^2{H}_6-3l^6(r-r_H)H_5^3{H}_6^2,\hfill \\ \hfill N_4& \equiv & r^4{r}_H^6[(r^2+r_H^2)H_5+4r^{2}R{r}_H]\hfill \\ & -& l^{2}r{r}_H^4[(5H_5+8R{r}_H)r^5+H_5{r}^3{r}_H^2-2(H_5+4R{r}_H)r^2{r}_H^3+2H_5{r}_H^5]H_5\hfill \\ & +& l^4{r}_H^2(r-r_H)[6H_5{r}^3+(r^3-r_H^3)(1+\mathcal{C}+6R{r}_H)]H_5^2{H}_6\hfill \\ & -& 3l^6{(r-r_H)}^2{H}_5^4{H}_6^2.\hfill \end{array}$$

(72)

One can easily check that in the massless limit of $R\to 0$ and $\mathcal{C}\to 0$, $D_3$ and $D_4$ are reduced to $D_1$ and $D_2$, respectively in Equation (52), and thus, the freely falling acceleration ${\overline{a}}_9^2$ becomes ${\overline{a}}_7^2$ in Equation (51) of the HRBH in massless gravity.

According to the Unruh’s prescription, one can find $T_{\mathrm{FF}}$ measured by the freely falling observer from the freely falling acceleration as

$$T_{\mathrm{FF}}=\frac{{\overline{a}}_9}{2\pi }=\frac{1}{4\pi r_H^3}\sqrt{\frac{H_5{N}_3{N}_4}{(r^2{r}_H^2(H_5+2Rr)-l^2{H}_4{H}_5{H}_6){[r^3(r_H^2-l^2{H}_5)+l^2{r}_H^3{H}_5]}^3}}.$$

(73)

In the massless limit of $R\to 0$ and $\mathcal{C}\to 0$, this is exactly the same as the previous one: the freely falling temperature of the HRBH in massless gravity in Equation (54). Moreover, as $r\to \infty$, the freely falling temperature $T_{\mathrm{FF}}$ is reduced to the Hawking temperature.

Now, making use of the dimensionless parameters $x=r_H/r$, $b=l/r_H$, and $d=R{r}_H$, the squared freely falling temperature can be written as

$$T_{\mathrm{FF}}^2=\frac{x{n}_3{n}_4}{16{\pi }^2{r}_H^2(2d+h_{5}x-b^2{h}_4{h}_5{h}_{6}x){[1-b^2(1-x^3)h_5]}^3},$$

(74)

where

$$\begin{array}{ccc}\hfill n_3& =& 1+x-b^2{h}_1{h}_5+b^4{h}_2{h}_5^2{h}_6-3b^6(1-x)h_5^3{h}_6^2,\hfill \\ \hfill n_4& =& 4d+(1+x^2)h_5-b^2[h_3{h}_5+8d(1-x^3)]h_5+b^4(1-x)[6h_5+(1+\mathcal{C}+6d)(1-x^3)]h_5^2{h}_6-3b^6{(1-x^3)}^2{h}_5^4\hfill \end{array}$$

(75)

with

$$\begin{array}{ccc}\hfill h_4& =& 1+\mathcal{C}+\frac{2d}{x},\hfill \\ \hfill h_5& =& 1+\mathcal{C}+2d,\hfill \\ \hfill h_6& =& 1+x+x^2.\hfill \end{array}$$

(76)

In Figure 7, we have depicted the ratio of the squared freely falling temperatures to the squared Hawking temperature $T_{\mathrm{FF}}^2/T_H^2$ for the HRBH in massive gravity. One can see that at the event horizon, the freely falling temperatures are all finite, while the fiducial temperature diverges [139]. In the limit of $b\to 0$ (or $l\to 0$), which corresponds to the case of the Schwarzschild black hole in massive gravity, the freely falling temperature is reduced to

$$T_{\mathrm{FF}}^2=\frac{x(1+\mathcal{C}+2d)[(1+\mathcal{C}+2d)(1+x+x^2+x^3)+4d(1+x)]}{16{\pi }^2{r}_H^2[(1+\mathcal{C}+2d)x+2d]}.$$

(77)

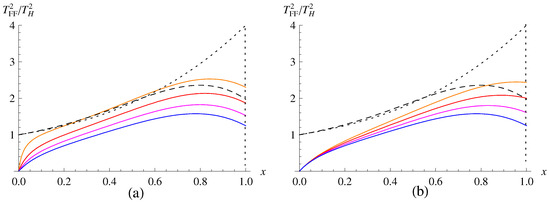
Figure 7. Squared freely falling temperatures $T_{\mathrm{FF}}^2/T_{\mathrm{H}}^2$ for the HRBH in massive gravity drawn by a dimensionless parameter $x(=r_H/r)$. (a) The freely falling temperature of the HRBH in massive gravity for $d=0.01,0.03,0.05,0.07$ from top to bottom with a fixed $\mathcal{C}=-0.1$ and $b=0.3$. (b) The freely falling temperature of the HRBH in massive gravity for $\mathcal{C}=-0.4,-0.3,-0.2,-0.1$ from top to bottom with a fixed $d=0.07$ and $b=0.3$. Here, the dashed black curve is for the HRBH in massless gravity, as in Figure 6, with $b=0.3$, and the dotted black curve is for the Schwarzschild black hole in massless gravity. Also, the vertical dotted lines are drawn at event horizons.

This is exactly the same with $T_{\mathrm{FF}}^2$ in Ref. [113]. Furthermore, in the massless limit of $d\to 0$ (or $R\to 0$) and $\mathcal{C}\to 0$, it becomes

$$T_{\mathrm{FF}}^2=\frac{1+x+x^2+x^3}{16{\pi }^2{r}_H^2}:$$

(78)

the freely falling temperature of the Schwarzschild black hole in massless gravity [139].

4. Discussion

In this paper, we have newly studied the Hayward regular black hole (HRBH) in massive gravity, which is a modification of the HRBH in massless gravity to have nonzero mass of gravitons, as proposed by Vegh in the framework of holography. By solving Einstein’s equations, we have found a solution of the HRBH in massive gravity and analyzed the novel structures of event horizons classified by the graviton mass parameters R and $\mathcal{C}$ qualitatively. Concretely, when $m>m_{*}$, physically interesting ranges of R and $\mathcal{C}$ lie in both all $\mathcal{C}$ with $R>0$ and all R with $\mathcal{C}>-1$. In those ranges, there exist an outer event horizon and at least one inner event horizon. When $m=m_{*}$, which is the extremal case for the HRBH in massless gravity, it remains extremal for $\mathcal{C}\le -1$ and $R>0$. However, for all R with $-1<\mathcal{C}<0$ and $R<0$ with $\mathcal{C}\ge 0$ in the HRBH in massive gravity, it changes to have two or more event horizons. Therefore, according to the specific values in the graviton mass parameters R and $\mathcal{C}$, we expect that the thermodynamics of the HRBH in massive gravity would be different from those of the HRBH in massless gravity. Furthermore, to find full information on event horizons, we have also analytically solved the metric function $f\left(r_H\right)=0$ of the HRBH in massive gravity, which is a non-trivial quartic equation due to massive gravitons, while the HRBH in massless gravity is the cubic equation.

After exploiting the geometric property of the spacetime, we have proceeded to study the GEMS embeddings of the HRBHs in massless and massive gravity, where the former is geodesically incomplete and the latter is singular due to massive gravitons. As a result, we have globally embedded the (3+1)-dimensional HRBH in massless gravity into a (5+2)-dimensional flat Minkowski spacetime and the (3+1)-dimensional HRBH in massive gravity into a much higher (6+3)-dimensional flat Minkowski spacetime, where the difference in embedding dimensions comes from whether or not holographically introduced massive gravitons exist. Furthermore, making use of newly obtained embedding coordinates, we have directly obtained Unruh temperatures and compared them with the Hawking and local fiducial temperatures, showing that the Unruh effect for a uniformly accelerated observer in a higher-dimensionally embedded flat spacetime is equal to the Hawking effect for a fiducial observer in the corresponding curved spacetime. We have also obtained freely falling temperatures of the HRBH in massless and massive gravities seen by freely falling observers following their geodesic trajectories, which remain finite even at the event horizons. These are different from the Hawking temperatures divergent at the event horizons.

Finally, it seems appropriate to comment that the solutions of the HRBH in massless gravity cannot be obtained simply by taking $R\to 0$ and $\mathcal{C}\to 0$ due to their implicit condition of $R\ne 0$, as seen in Equations (20) and (21). On the other hand, the GEMS embedding of the HRBH in massive gravity can be reduced to the corresponding GEMS embedding of the HRBH in massless gravity in the limit of $R\to 0$ and $\mathcal{C}\to 0$ by redefining some embedding coordinates. As a result, when $R\to 0$ and $\mathcal{C}\to 0$, the (6+3)-dimensional embedding coordinates (60) of the HRBH in massive gravity have proper limits of the (5+2)-dimensional ones (41) in massless gravity, which may be a characteristic of the Hayward nonsingular black hole in massive gravity.