Abstract
One of the recent attempts to address the Hubble and tensions is to consider that the Universe started out not as a de Sitter-like spacetime, but rather anti-de Sitter-like. That is, the Universe underwent an “AdS-to-dS” transition at some point. We study the possibility that there are two dark energy fluids, one of which gave rise to the anti-de Sitter-like early Universe. The interaction is modeled by the Lotka–Volterra equations commonly used in population biology. We consider “competition” models that are further classified as “unfair competition” and “fair competition”. The former involves a quintessence in competition with a phantom, and the second involves two phantom fluids. Surprisingly, even in the latter scenario it is possible for the overall dark energy to cross the phantom divide. The latter model also allows a constant w “AdS-to-dS” transition, thus evading the theorem that such a dark energy must possess a singular equation of state. We also consider a “conversion” model in which a phantom fluid still manages to achieve “AdS-to-dS” transition even if it is being converted into a negative energy density quintessence. In these models, the energy density of the late time effective dark energy is related to the coefficient of the quadratic self-interaction term of the fluids, which is analogous to the resource capacity in population biology.
1. Introduction: Cosmology with Sign Switching Dark Energy
The Hubble tension [1,2,3,4] and the tension [5,6,7] in cosmology continue to be highly debated [8,9,10,11,12,13,14,15,16,17]. The former is the mismatch between the locally measured expansion rate and the inferred rate via the cosmic microwave background (CMB), while the latter concerns the measurement of galaxy clusters on a scale of 8 hMpc, which revealed that matter has not clumped as much as expected assuming the concordance CDM cosmology and its parameters constraints given by the CMB data (for a review on these issues, as well as other challenges facing CDM cosmology, see [18]; see [19] for an introduction to various dark energy scenarios). If these effects are real, they could be due to modified gravity or other new physics [20,21].
Note that in the CDM model, the Hubble parameter as a function of the redshift is specified by two constant fitting parameters [22] , or equivalently , as follows:
where A is the term associated with dark energy. The aforementioned tensions could mean that CDM is not correct and thus the “constant” fitting parameters could evolve with redshift (or equivalently, with time). See also [23,24].
Indeed, one of the possible ways to ameliorate these tensions is to consider the possibility that the Universe was originally more anti-de Sitter-(AdS)-like than de Sitter-(dS)-like [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. That is, the physics of dark energy (DE) might be more complicated than we initially expected1. The main idea is to reduce the tension between the higher value of obtained from CMB with the lower value obtained by local measurements, by changing cosmological models either at the recombination epoch or at late time [11]. For example, a phantom energy at late time would accelerate cosmic expansion faster than a cosmological constant would. In addition, Baryon Oscillation Spectroscopic Survey (BOSS) of SDSS-III probing the Ly forest of quasars also indicates preference for a positive dark energy density at late time but a negative one at early time [48]. Future observations such as SKA [49], BINGO [50,51], and Euclid [52] could potentially further constrain this possibility. Another observational support for negative energy density comes from Pantheon+ data of high redshift supernovae [53].
Such a possibility can be realized by simply promoting the cosmological constant to2 , where is the present value of the cosmological constant, and is the value of redshift at which the sign switching abruptly happened [34]. See also [54]. Another model considers a “graduated dark energy” with energy density and pressure satisfying , which provides a continuous transition (controlled by the parameter ) from AdS-like to dS-like Universe [28]. Other options include the possibility that the dark energy sector could consist of a negative cosmological constant and a phantom dark energy [27] or a quintessence [35] (see, however, [55]). A different approach based on fractal modification to the entropy via a running Barrow index [56] could also give rise to an effective sign-changing dark energy [38].
In this work, we shall consider what happens if instead of a scalar field on top of a negative cosmological constant, we have either (1) a quintessence with negative energy density, which competes with a phantom dark energy with a positive energy density3, or (2) a phantom with a negative energy density that competes with another phantom with a positive energy density, or (3) a phantom with positive energy density being converted into a negative energy density quintessence. We shall refer to these scenarios, respectively, as “unfair competition”, “fair competition”, and “conversion” models. This is inspired by the interacting models between dark matter (DM) and dark energy [59,60,61,62,63,64], as well as from biological species interactions. In fact, the connection between these two subjects has been noticed in the literature. For example, [65] Perez et al., as well as Aydiner [66], pointed out that the DM–DE interaction can be re-written as the Lotka–Volterra equation, which is commonly used in population biology to model the interactions between various species. In cosmological contexts, the Lotka–Volterra equation was also studied in [67,68]. In the population model, it is of course required that the numbers of the species involved are non-negative, whereas in our model, the corresponding quantities are the energy densities of the DE fluids, which can be negative by assumption. Indeed, one might expect that if DM is converted into DE at late time, can be increased, while the matter density can be decreased, so that also decreases. This is indeed true for some models, but in others, the tension can in fact worsen [69]. In [70], it is shown that generically, allowing interactions between DE and DM does not allow both the Hubble and tensions to be ameliorated. Somewhat surprisingly, in the same work, it is argued that phantom dark energy with energy flow from the opposite direction, i.e., from DE to DM, is slightly preferred. In this work, we consider the alternative of non-minimal interaction between two DE fields to obtain one effective DE that exhibits sign-switching energy density, which might have a better chance at addressing both tensions simultaneously (as illustrated in [71] with the DE sector consisting of multiple interacting axion-like particle species). Our work is only meant to be an illustration of concept with the simplest models. Some assumptions would need to be relaxed or improved before a more realistic model can be used for data fitting the actual universe.
We will work out the conditions on the interactions between two dark energy fluids (“DE-DE interaction”) in order to obtain a late time accelerated expansion with a very small but positive energy density. In our models, unlike the single fluid models in the literature, neither fluid exhibits any singular behavior in their equation of state, although if the phantom divide is crossed, the combined effective dark energy does exhibit such a singular behavior during the AdS-to-dS transition. Remarkably, we found that in the fair competition model, it is possible for the effective dark energy to cross the phantom divide despite both component fluids satisfying . In addition, in this scenario, there are evolutions that allow AdS-to-dS transition without crossing the phantom divide, which therefore is free of singular behavior in its equation of state. Finally, it is often said that the fact that the dark energy density is extremely small is “unnatural”. We shall see that in the two-fluid model, this value is related to the coefficient of the quadratic self-interaction term of the fluids, which mathematically plays the same role as the resource capacity of a biological population.
2. The Unfair Competition Model
In [65,66], the authors considered a model in which dark energy is being converted into dark matter via
where . Likewise, dark matter can be converted into dark energy with . See [72] for generalizations.
The equations of state considered in [66] are and , i.e., dark matter is a “normal matter” while dark energy is a phantom fluid. Thus, one can define two positive quantities:
Furthermore, assuming that the Hubble parameter is slowly varying (so that and are both approximately constant) and upon introducing4 and , Equation (2) can be re-written as
which is explicitly a Lotka–Volterra equation that describes a predator–prey dynamic with being the “prey” and the “predator”. The system thus displays an oscillatory behavior. Such an interacting model could potentially help to resolve the coincidence problem.
In our case, we have two interacting dark energy fluids, which we will denote by and (despite the notation, they are not constant; the notation is meant to remind us that they are mimicking cosmological constants). Their energy densities would be denoted by and , respectively. The transition from an early time AdS-like Universe to a late time dS-like spacetime thus amounts to becoming subdominant to . Let us first consider an unrealistic model (to be improved upon later) that is analagous to Equation (2), so we can point out the differences:
where . As before, we assume that the late time dark energy is a phantom; thus, . On the other hand5, but with . This is justified by [74,75], in which it was argued that solving both the Hubble and tensions require the overall effective dark energy to cross the phantom divide (if we assume that Newton’s gravitational constant is not varying). See also [76]. This is also similar to the model in [28].
Thus, we define, analogous to Equation (3), two parameters
We assume that both and are constant. Upon introducing the dimensionless quantities and , we obtain the Lotka–Volterra equation of the form
where some of the signs differ from Equation (4) that describes the interacting DM–DE model. In addition, here, we have . This system does not oscillate, but rather there is an attractor and . Note that in contrast to the DM–DE interaction model, it is not quite right to say that is being “converted” into here (a true conversion model will be studied in Section 4), since implies that the interaction term is negative for both x and y. In other words, the two fluids are competing, but unlike two competing species whose birth rates are both positive, x is itself diminishing exponentially due to the “death rate” term , hence the name “unfair competition”. It is clear that the phantom fluid thus dominates over the quintessence. That is, is asymptotically vanishing while becomes large (and eventually diverges) at late time. This is not a desired property since we know from observation that dark energy density is only of the order of .
We can improve upon this model by modifying the term so that
where is a constant. The attractor is then and , so we can prescribe to K the observed value. At this point, this seems rather ad hoc, but later on we will give it a physical interpretation.
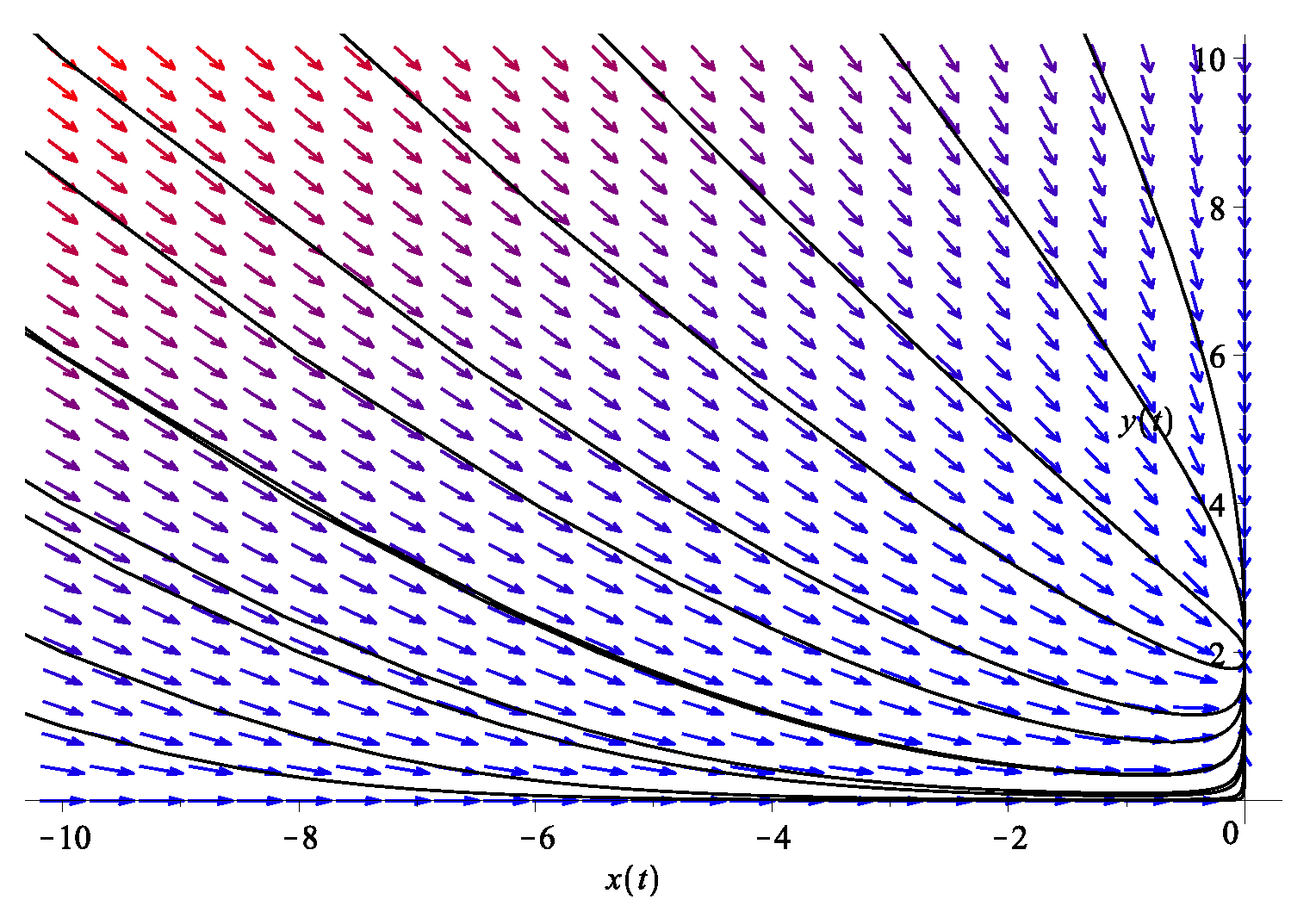
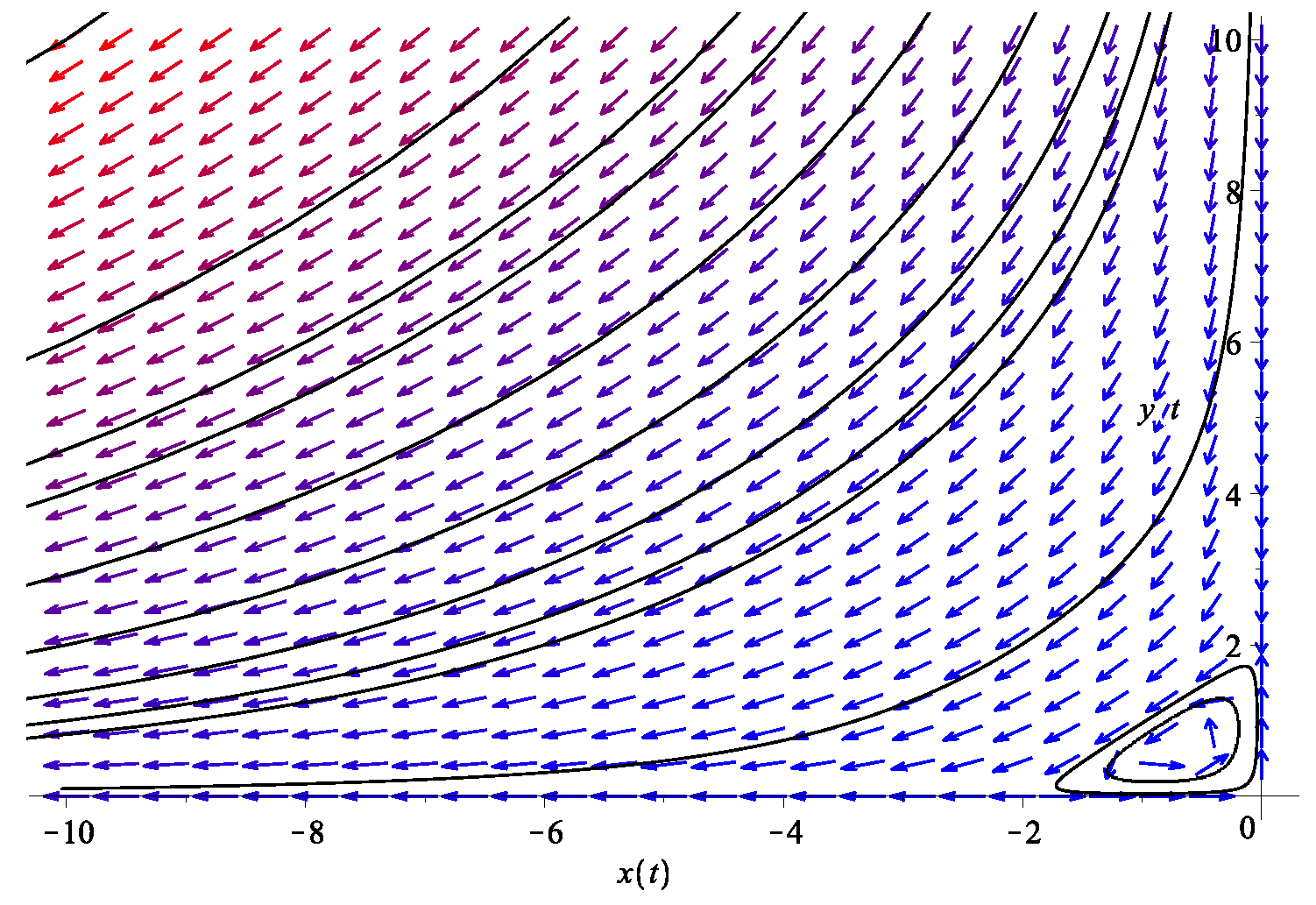
The analogy to population biology can also be made here: with x small at late time, in the absence of term, what we have is analogous to an exponential growth population , whereas Equation (8) corresponds to the logistic model with a resource capacity (or “carrying capacity”) K, so that the actual population size cannot diverge but rather asymptotes to a constant value. Note that since anyway, there is no good reason to add the resource term to in this model. A typical phase diagram is given in Figure 1.
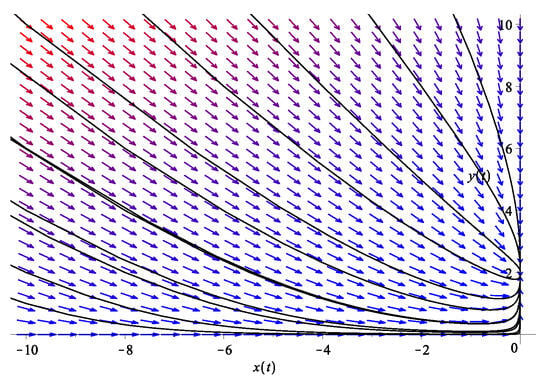
Figure 1.
The phase diagram of the two dark energy fluid model in Equation (8). Here, we use and . The system exhibits a fixed point at .
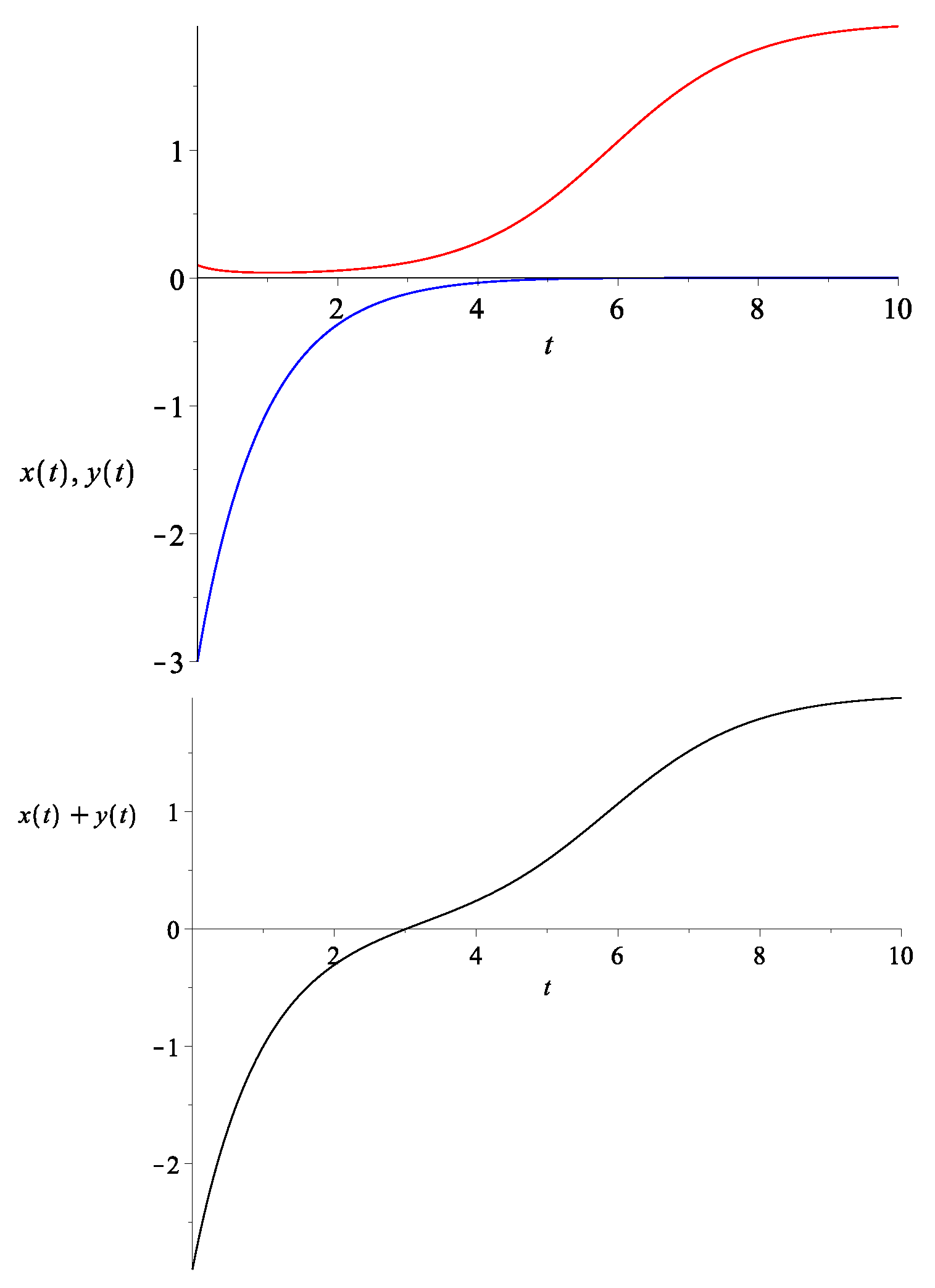
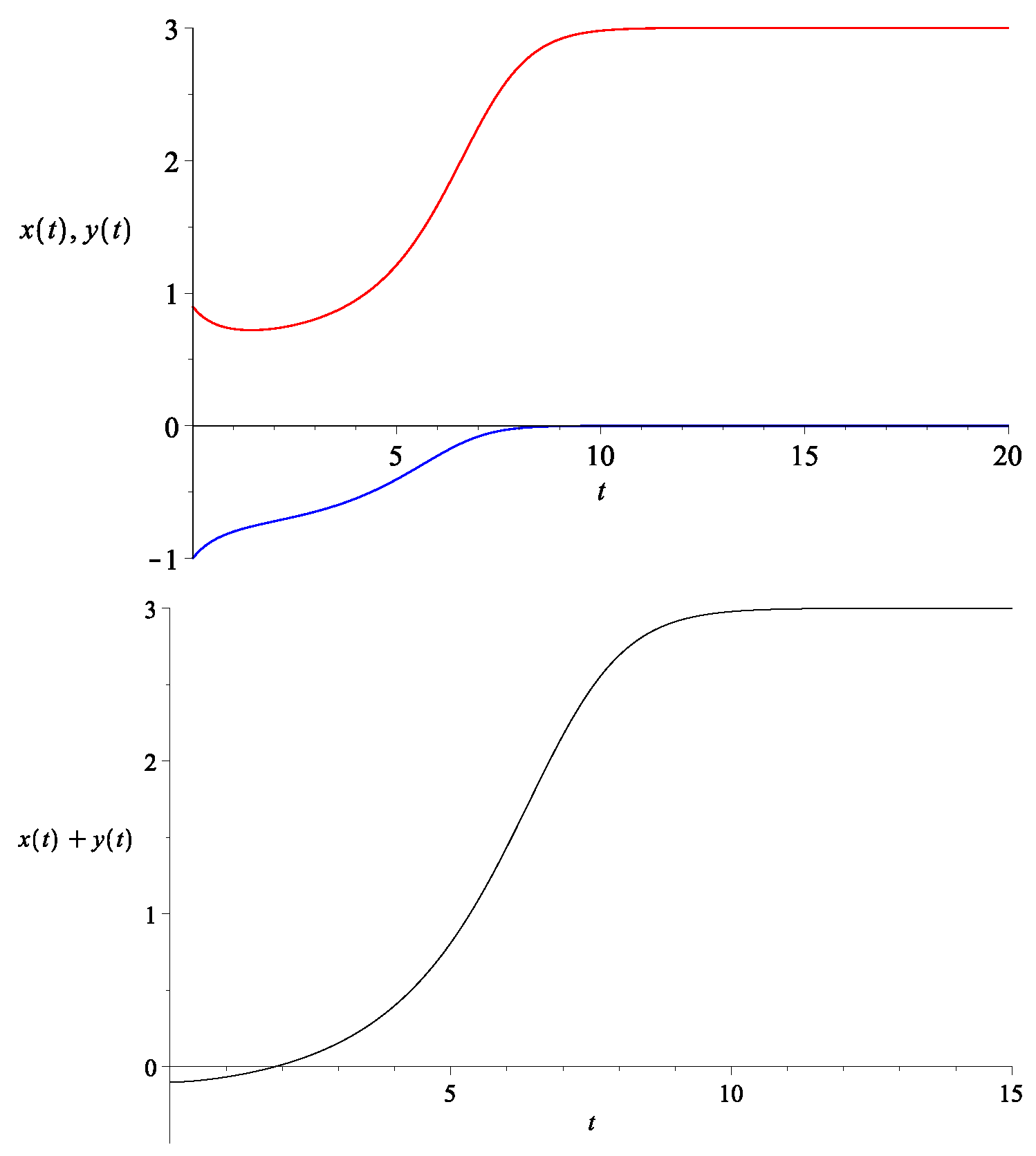
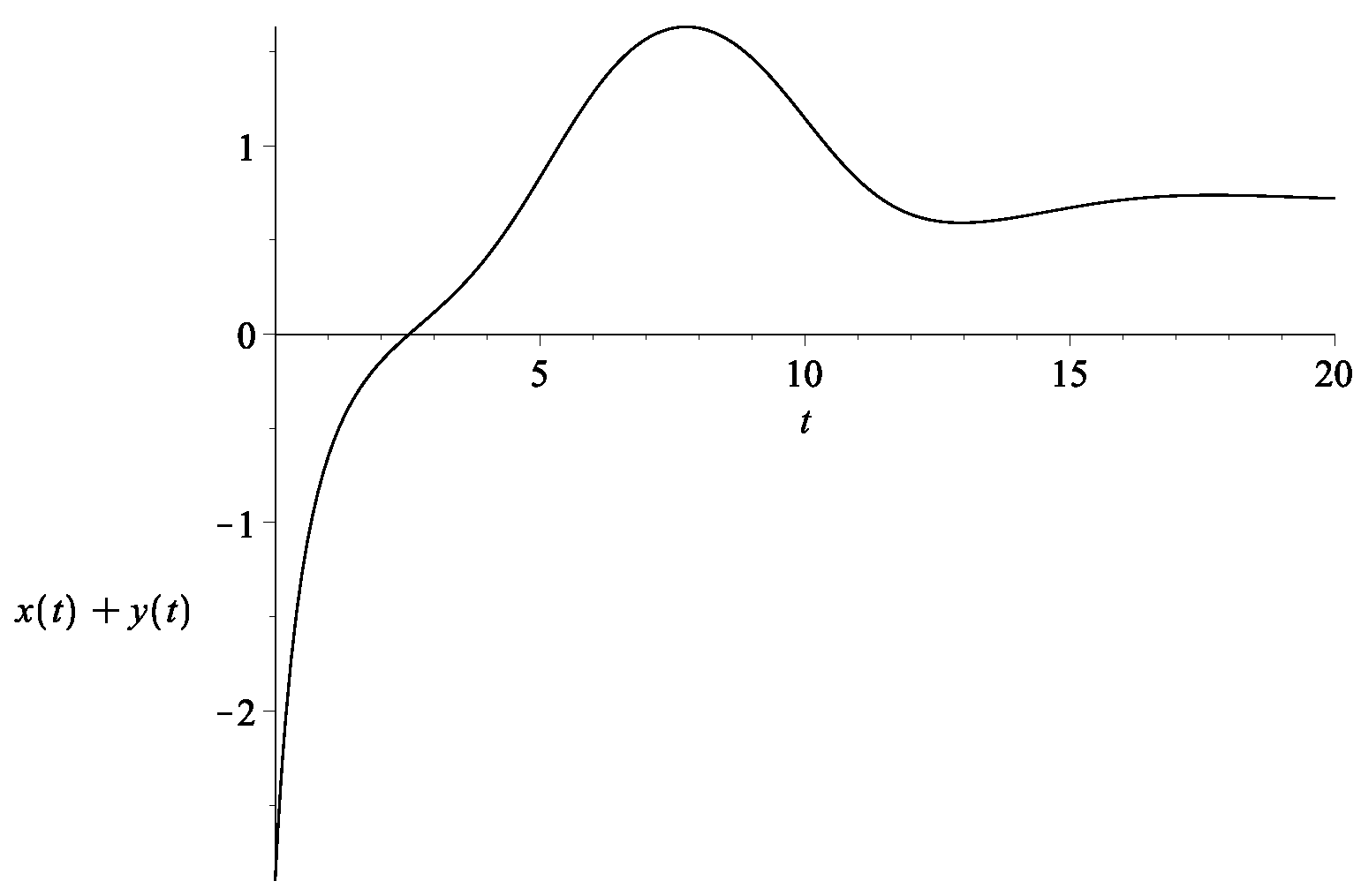
Note that the effective dark energy density is the sum . Thus, in order that this quantity starts out negative, we need the initial condition to satisfy . Then, since the attractor is with , it follows that the continuity must cross over to at some point. The exact profile of or the re-scaled equation would depend on the initial conditions, but the transition from an overall negative energy density to a positive one can be smoother than the model in [28]. One example is given in Figure 2.
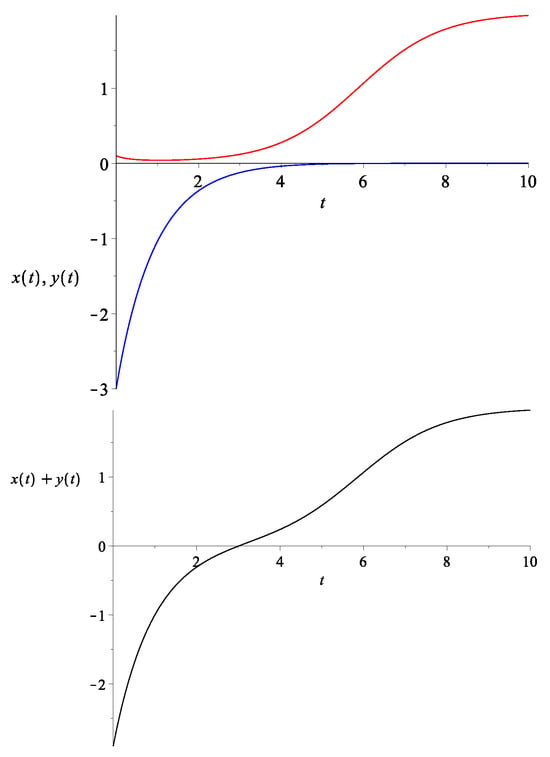
Figure 2.
Top: The evolution of (bottom curve in blue) and (top curve in red) with the initial condition set to be , and with . Bottom: The evolution of , which is essentially the re-scaled version of (in this example, they are in fact equal).
If we know what kind of profile is desired from observational constraints, this would in turn provide us with a mean to choose the coefficients and , as well as the initial conditions of the Lotka–Volterra equation. We also note that the equation of states of both dark energy components are never singular, though the combined effective dark energy density has to pass through , and the effective equation of the state is singular at that point [77]. This can be seen as follows: if we consider the combined fluid to still satisfy the equation of state of the form , where and , then
which implies that the effective varying w is the weighted average:
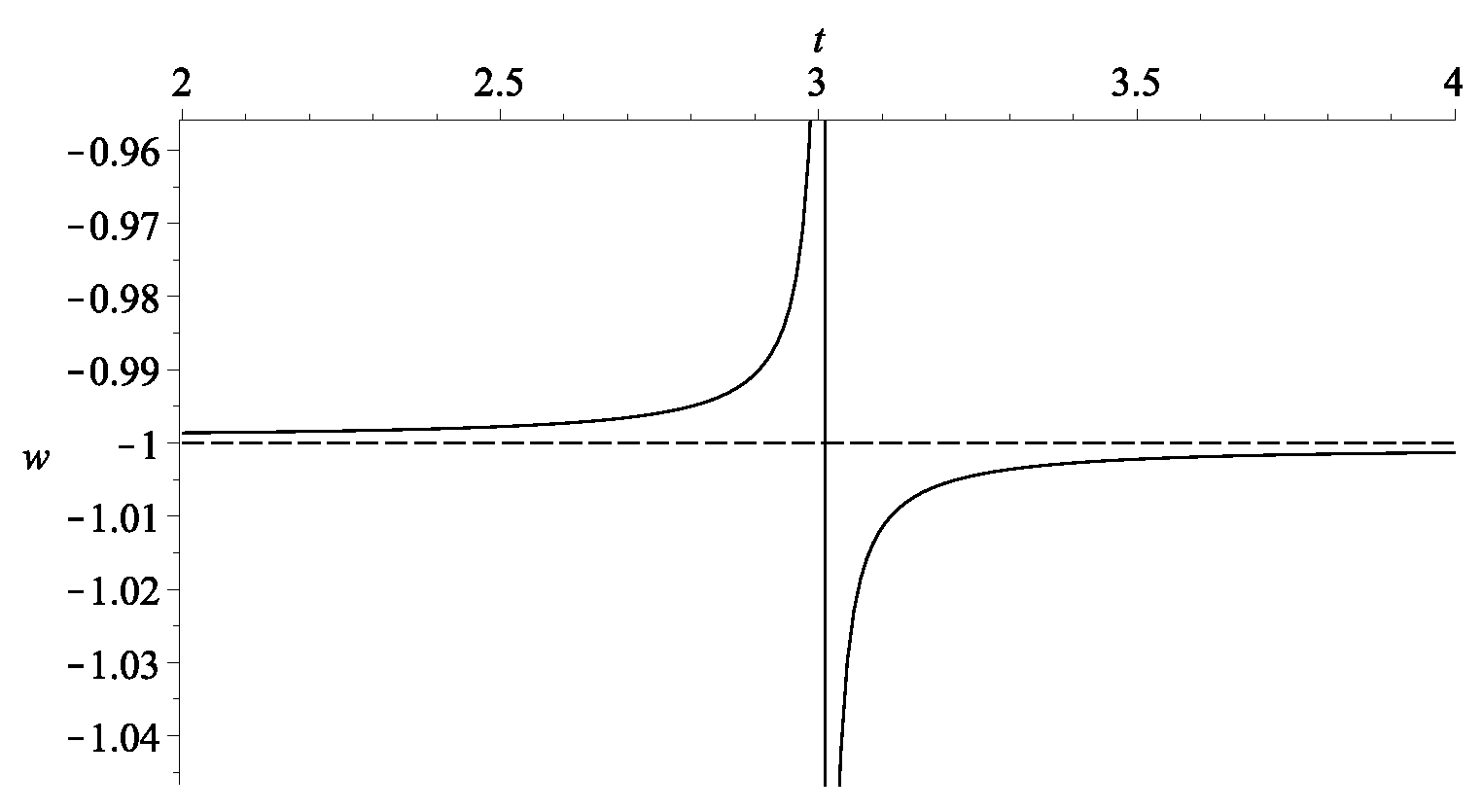
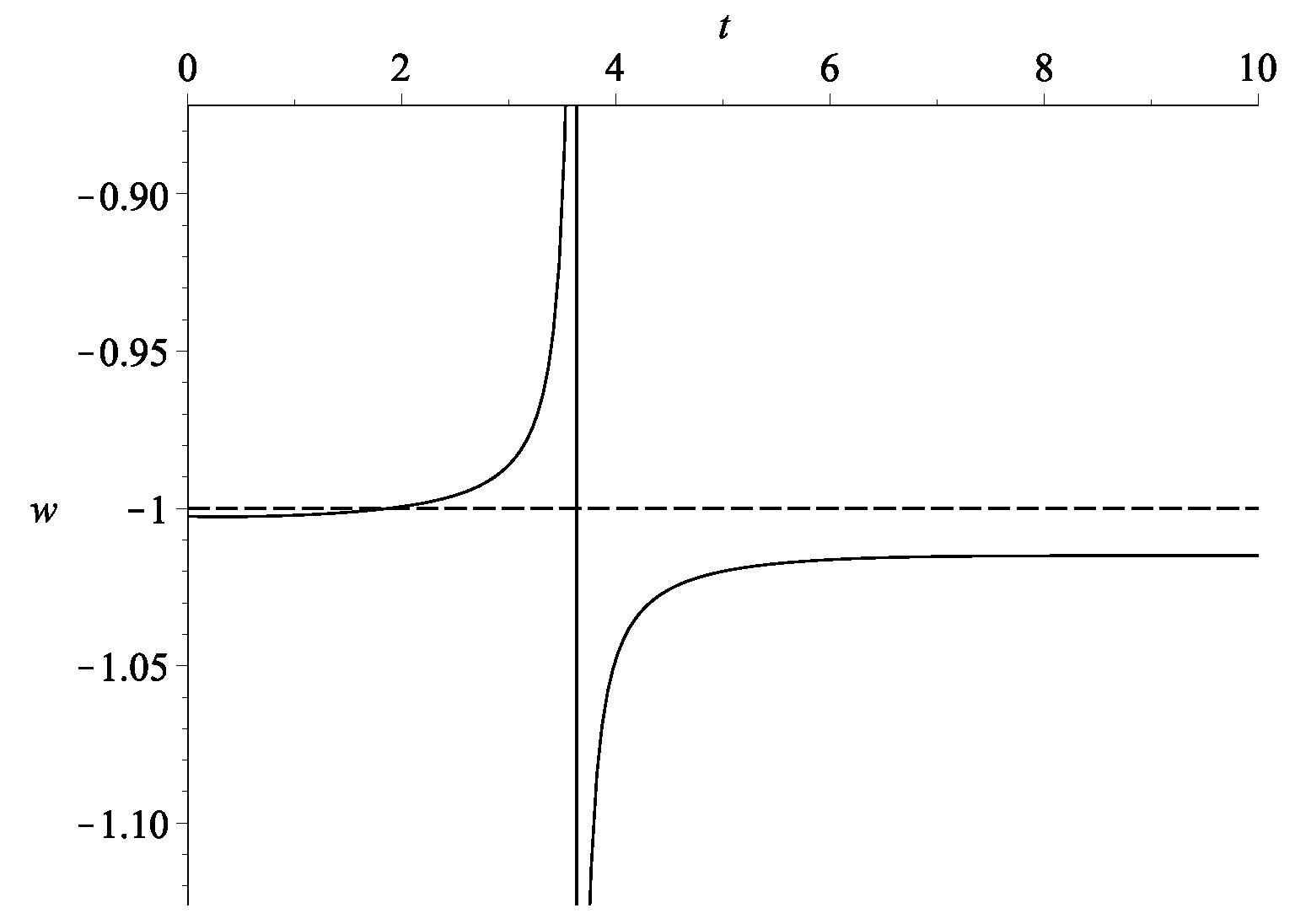
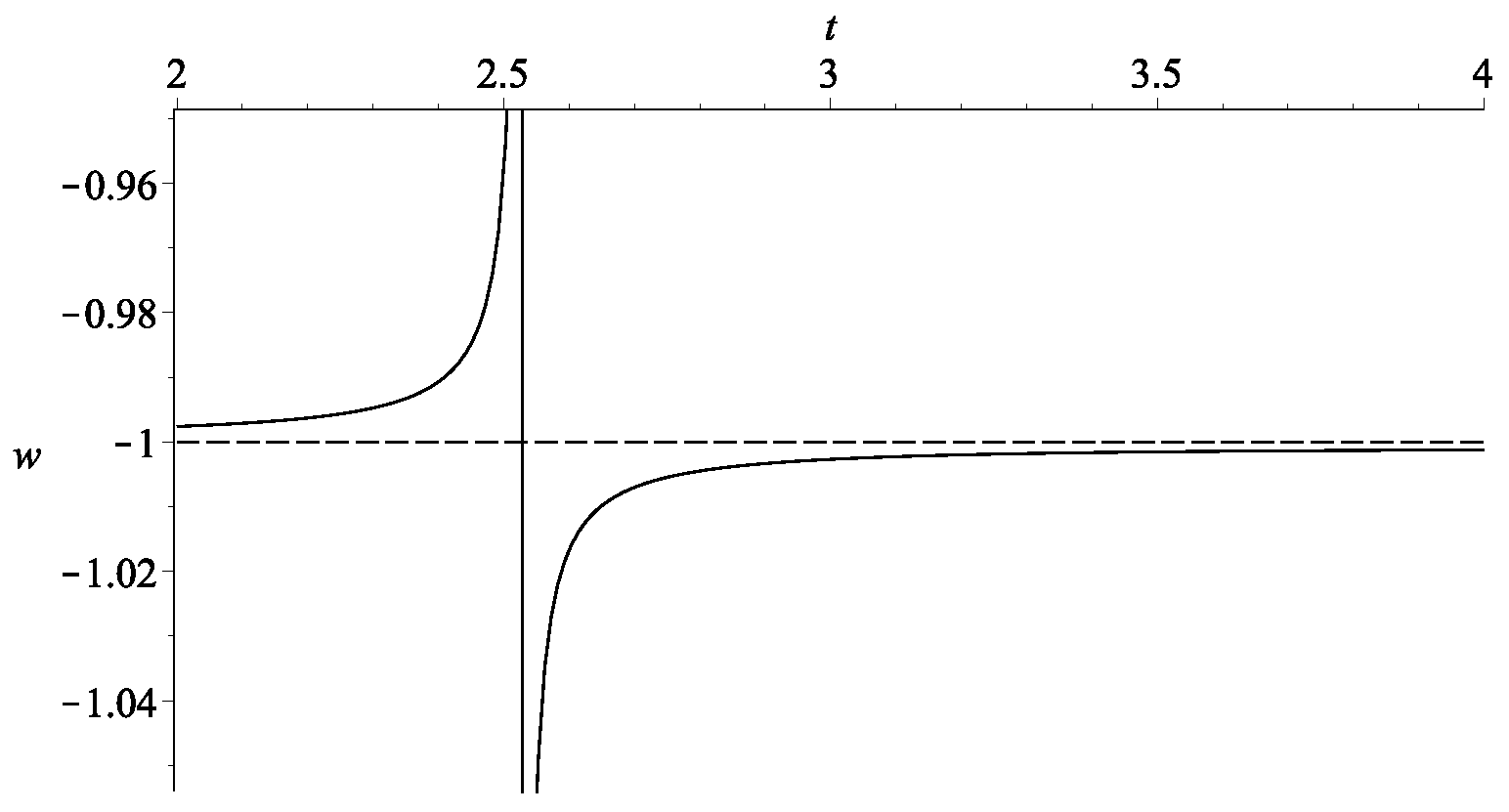
Therefore, evidently when the denominator is zero. Again, the situation is similar to the “graduated dark energy” model of [28], though in that case there is only one dark energy fluid, whose equation of state becomes singular. An example of the evolution of w is shown in Figure 3. Note that the values of and are not freely prescribed since they are constrained by Equation (6), in the sense that once we fix and , the relations between and are also determined. In our example, choosing implies .
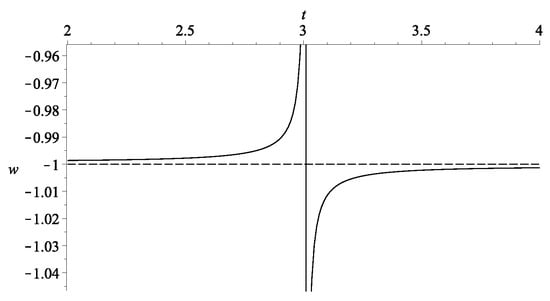
Figure 3.
The evolution of the overall effective w of the example in Figure 2 with and .
We remark that the sign of is not necessarily the same as the sign of . In fact,
Thus, the sign of is the same as the sign of . For simplicity, our example deals with , and the two expressions do have the same sign; furthermore, w is singular when or equivalently at .
3. The Fair Competition Model
In population biology, two species that are very similar (i.e., fulfilling the same ecological niche) will compete for the same resources. To model such a situation, we consider both species to have a positive “birth rate”, so that in this sense, the competition is fair. In place of Equation (8), we have:
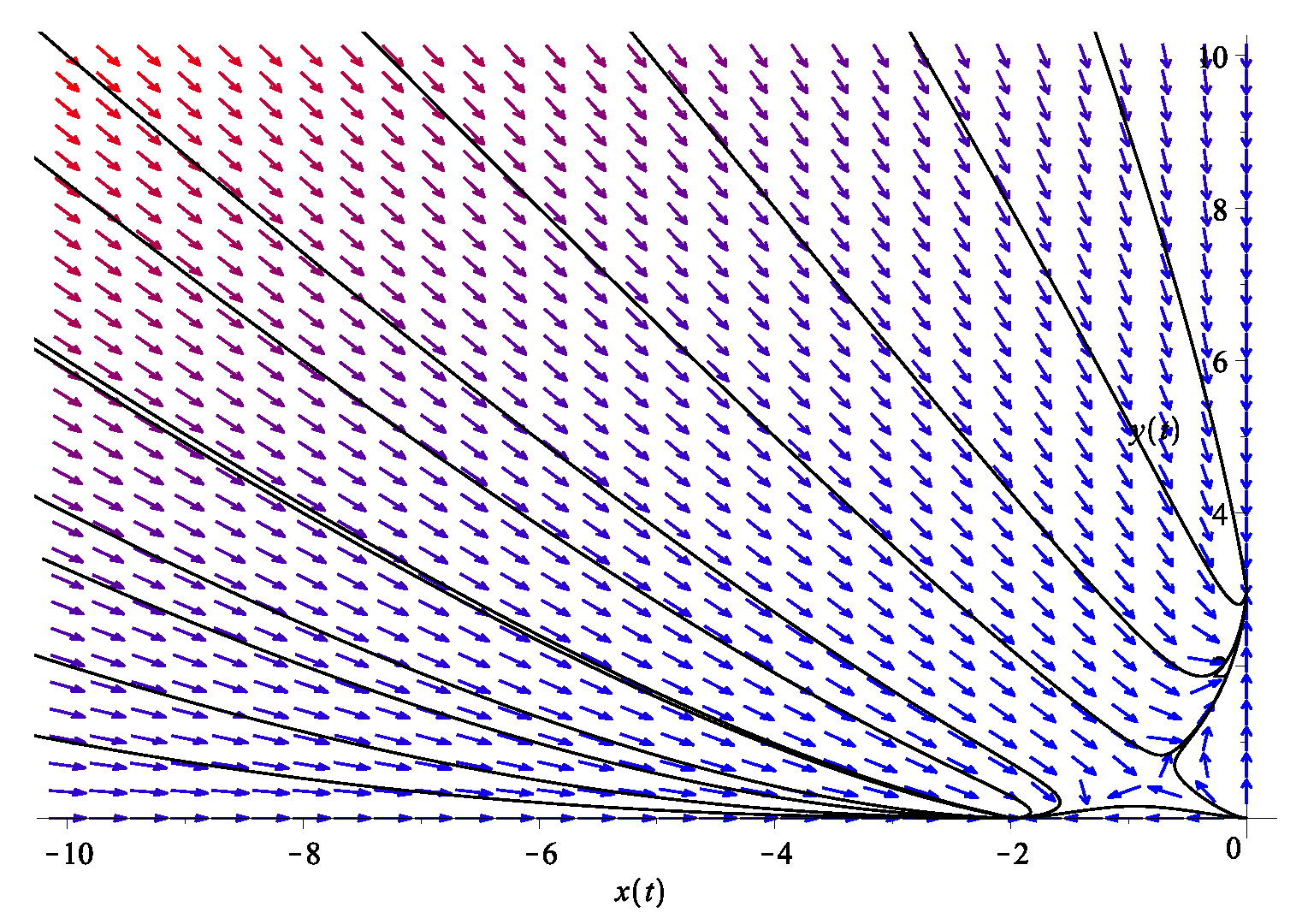
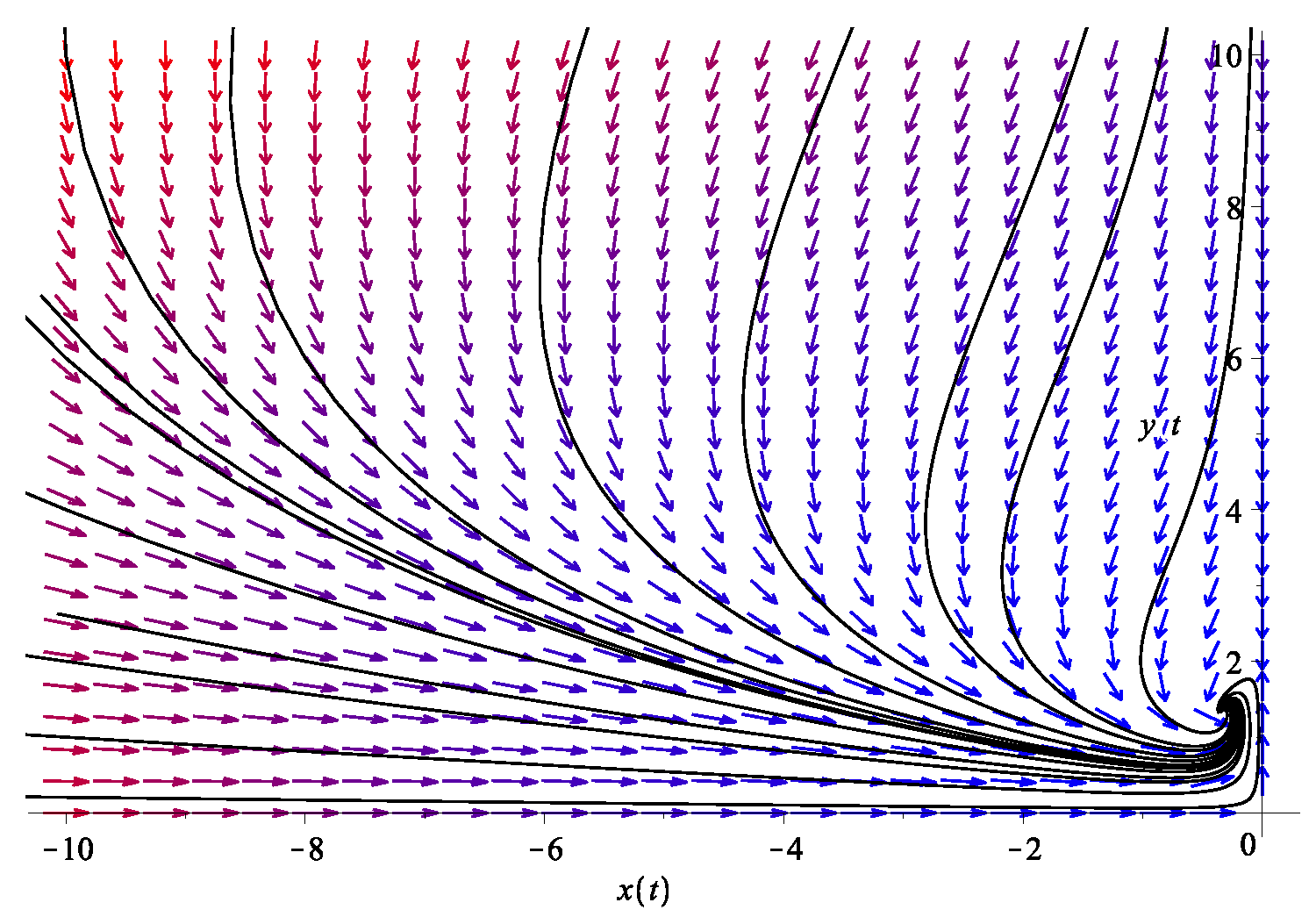
where now . Note the coefficient pre-multiplying is now 1 instead of . Since , we consider the resource term to be instead of , keeping . Note again that “competition” means that the interaction is harmful for both species, so the interaction term is negative for both fluids ( because ). For a fair competition, we also include the carrying capacities and for both fluids, with , both being positive. A typical phase diagram is shown in Figure 4. Two families of flows are observed: those that flow towards and those that flow towards . We are concerned with the latter.
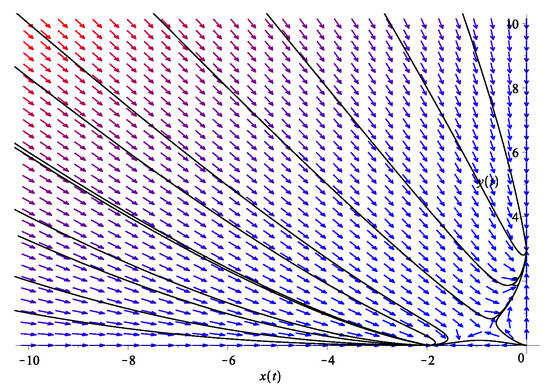
Figure 4.
The phase diagram of the two dark energy fluid model in Equation (12). Here, we use , , and , . The system exhibits trivial fixed points at and , but also notice the existence of a saddle point that “separates” the two families of flow.
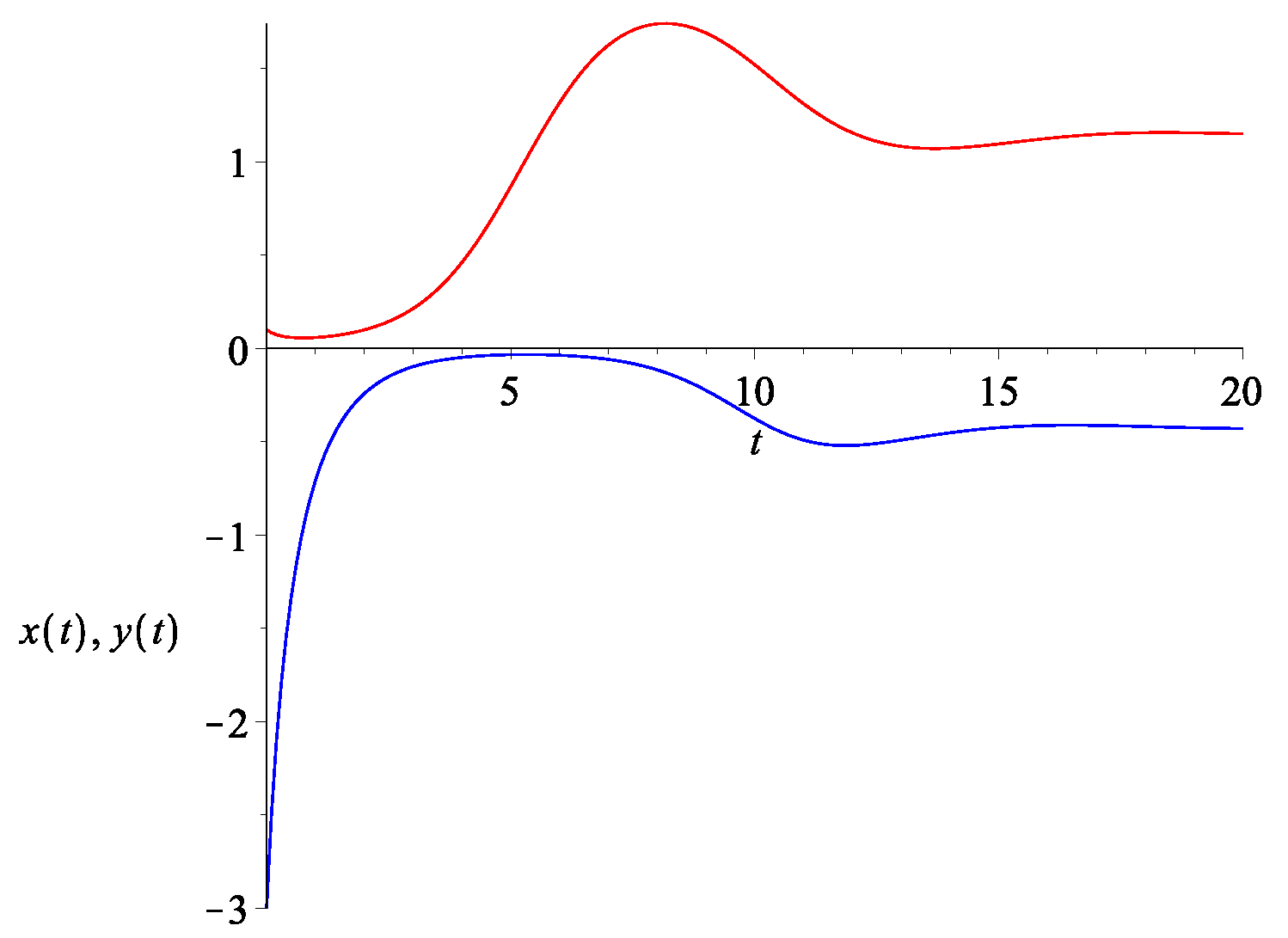
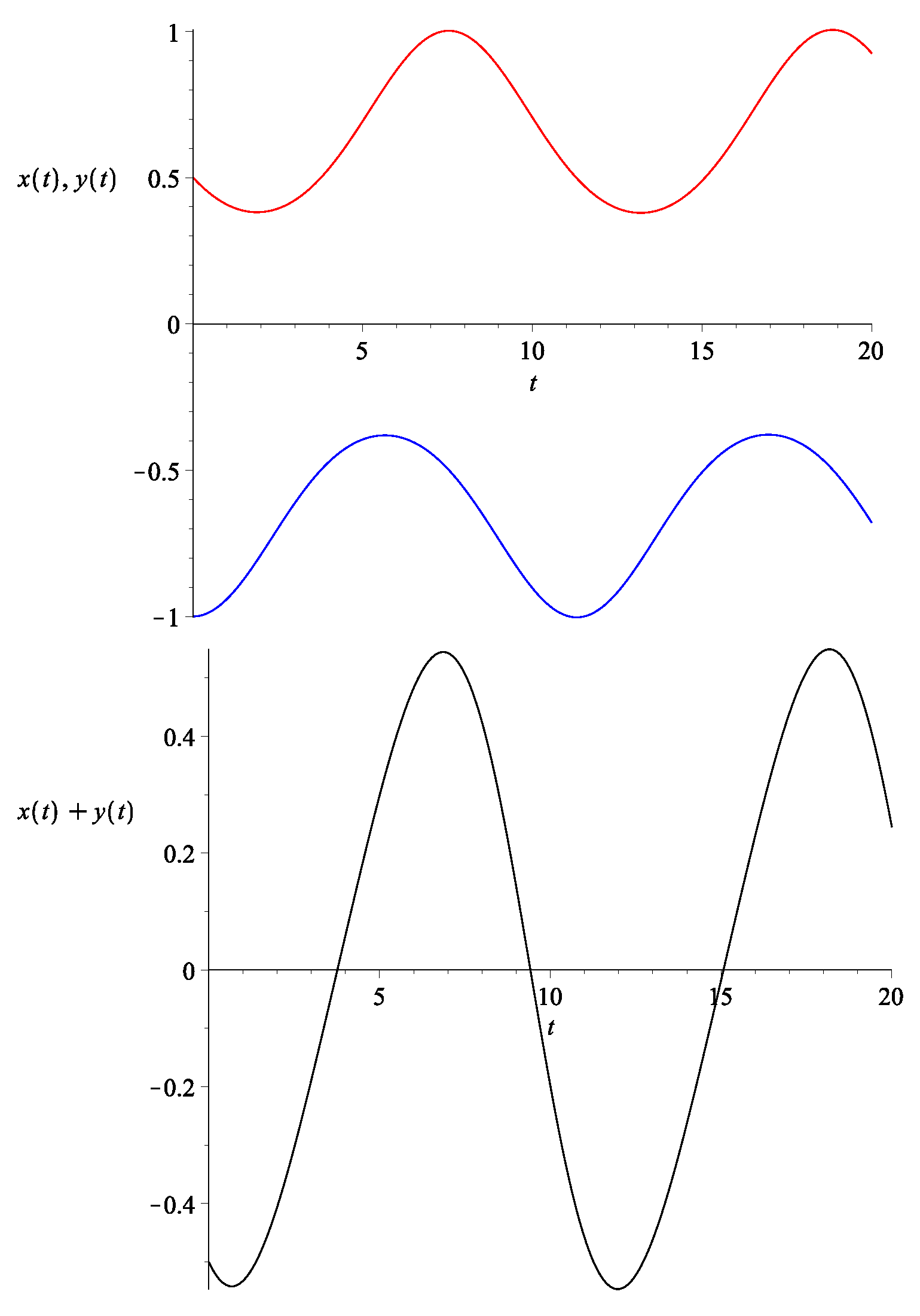
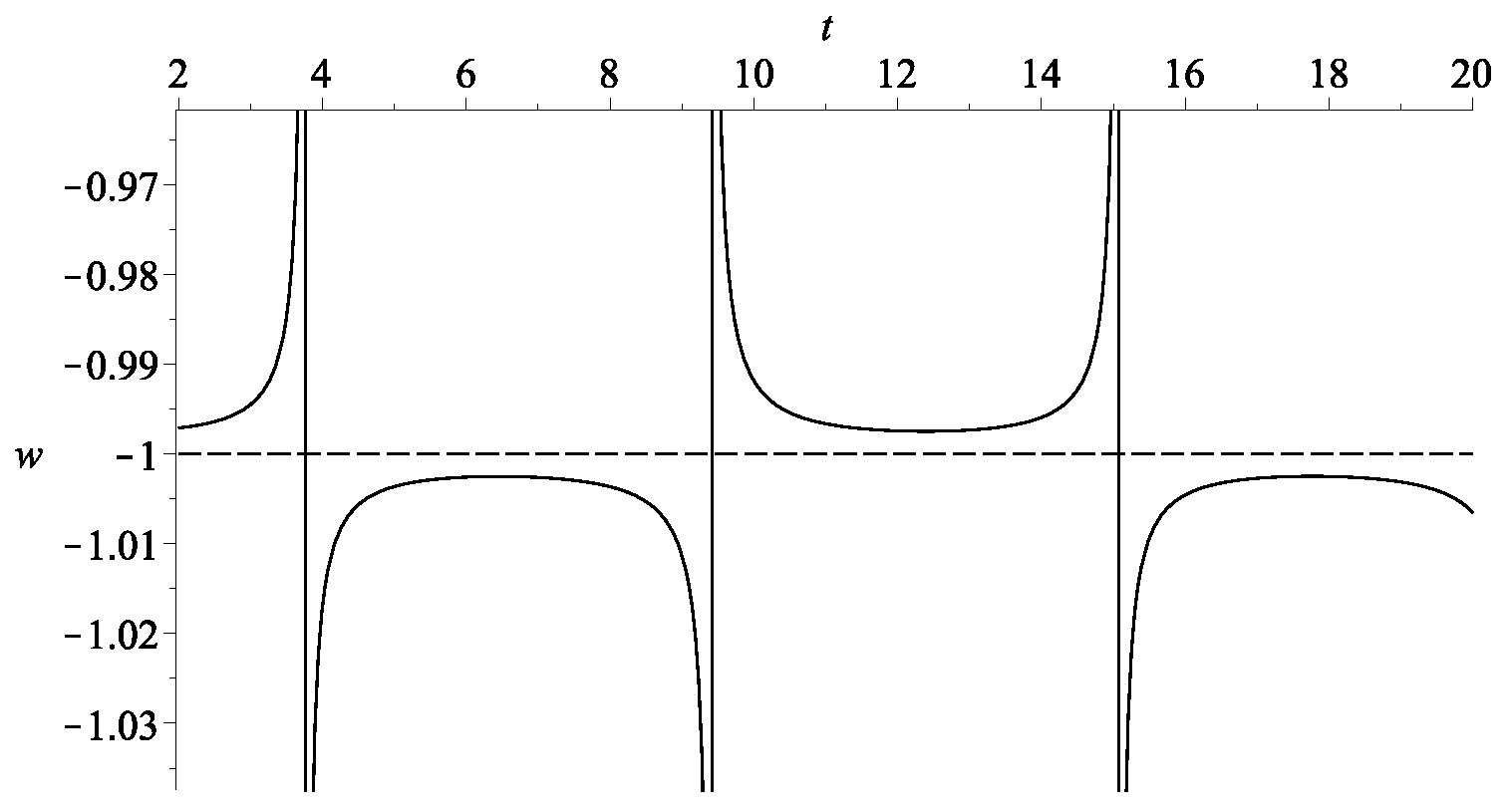
An explicit example of the rescaled energy density x and y as well as their sum are provided in Figure 5. Here, we let and . We can see that changes sign in Figure 6. Now, in this example, since , we cannot directly compare the sign change of to that of the overall dark energy density. However, we note that initially, . Since , it follows that . Thus, it follows that initially. On the other hand, asymptotically, we have as . Equivalently, at late time . Thus, we see that does indeed change the sign., i.e., the Universe transits from AdS-like to dS-like.
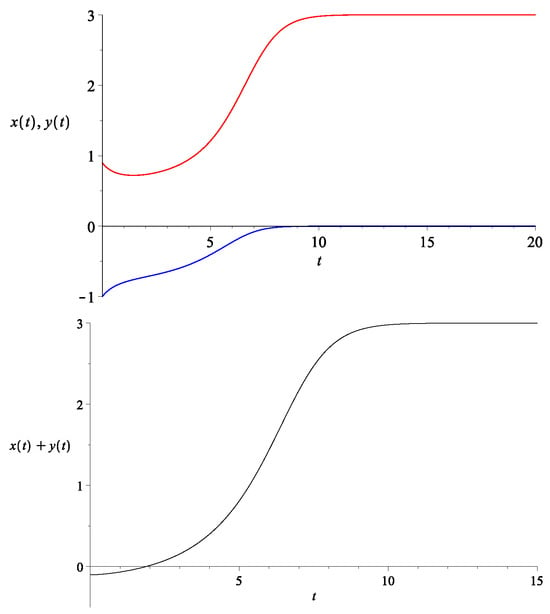
Figure 5.
Top: The evolution of (bottom curve in blue) and (top curve in red) with the initial condition set to be , and with . Bottom: The evolution of , which is essentially the re-scaled version of .
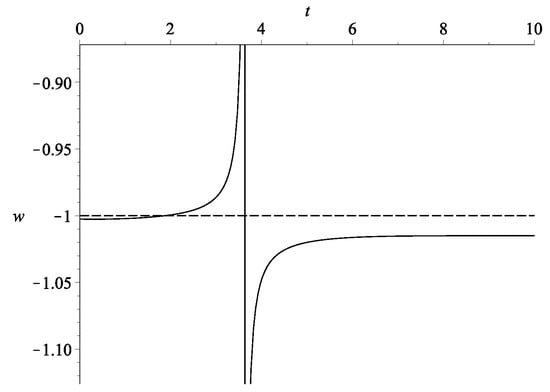
Figure 6.
The evolution of the overall effective w of the example in Figure 5 with and . There are two phantom crossings. The first crossing is smooth and corresponds to the time when . The second crossing is singular and corresponds to . These two conditions are not the same since .
Incidentally, we also note that if is monotonically increasing, then we can give a bound on . To see this, simply observe that
is equivalent to
Given that , this means . Inserting a few terms that cancel each other yields:
Therefore,
If , we can write the last equation as
Likewise, if , we can write
Thus, for example, if (and hence —recall that are positive), and we observe that and x are both monotonicaly increasing, then so must :
The phantom divide can be crossed as shown in Figure 6, where w is given by Equation (10). The values of and are constrained by the defining equations and . With and , if we take , say, then . Note that there are two phantom crossings6 here: the first one occurs without any singularity. From Equation (10), it can be seen that if the denominator is not zero, then such a smooth crossing occurs precisely when . This cannot happen for the unfair competition model as the condition would be instead (which cannot occur since and ). Note that despite the fact that there are two phantom crossings, there is only one AdS-to-dS transition in this example.
Even more surprising is the fact that the overall can stay constant, yet there is still a AdS-to-dS transition. To achieve this we simply need to choose . The plots of and their sum is qualitatively the same as Figure 5 and are thus not shown. However, from the defining relations of and we would have , and so in Equation (10), we obtain
Strictly speaking, during the transition point , which otherwise would give rise to a singular behavior, we obtain an indeterminate form , but both the left and right limit are well defined and equal to , so physically it makes sense to say that for all t. As such, this evades the recent theorem that a sign-changing dark energy must have a singular equation of state [77]. The reason this does not really violate the theorem therein is because the proof in [77] is strictly for DE fluids that obey the usual continuity equation , whereas in our model it can be checked that the combined DE does not satisfy the continuity equation; the “carrying capacity” term K breaks the continuity equation. This is equivalent to saying that . This is not surprising—as we will see in the Section 5, our models have a nontrivial nonlinear self-interaction term that acts as a source term for the continuity equation.
4. The Conversion Model
Given the results above, one might wonder whether the AdS-to-dS transition can still happen if we restrict the growth of by converting it into , or equivalently, by giving an advantage. This is achieved by the following model involving a quintessence and a phantom :
in which we note that the second term of is now instead of . The interaction is therefore beneficial to x but harmful to y. This sounds like the complete opposite of what we wish to achieve (to have being the dominant term at late time). Surprisingly, even in such a scenario, it is possible to have a phantom crossing. The only difference being the attractor is now a stable spiral centered at
as can be seen in the example depicted in Figure 7.
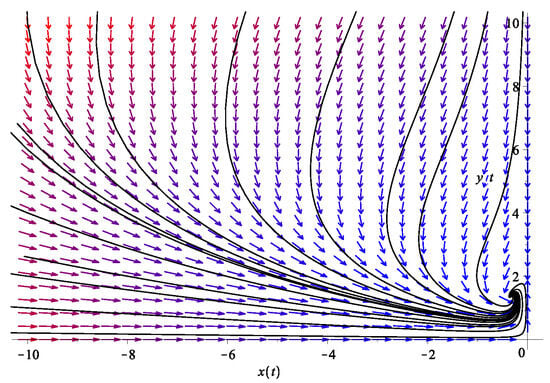
Figure 7.
The phase diagram of the two dark energy fluid model in Equation (21). Here, we use , , and . The system exhibits an attractor fixed point at .
What happens is that, despite the conversion term, can still dominate at late time. After all, we do not need to grow too big. The evolution of and , as well as their sum (which in this example is the same as ), is shown in Figure 8. The phantom crossing is shown in Figure 9.
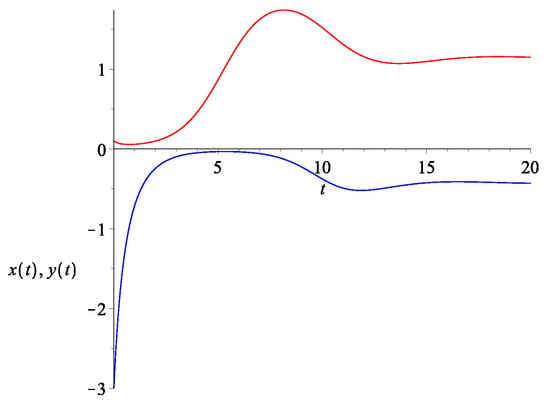
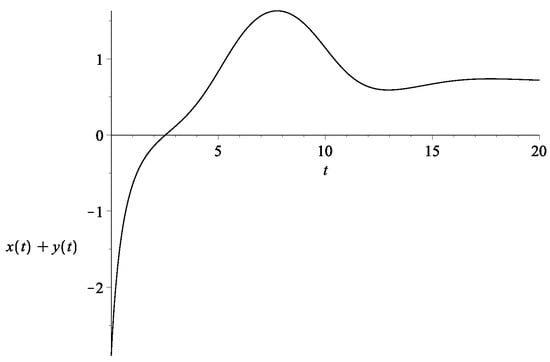
Figure 8.
Top: The evolution of (bottom curve in blue) and (top curve in red) with the initial condition set to be , and with . Bottom: The evolution of , which in this case is the same as the overall .
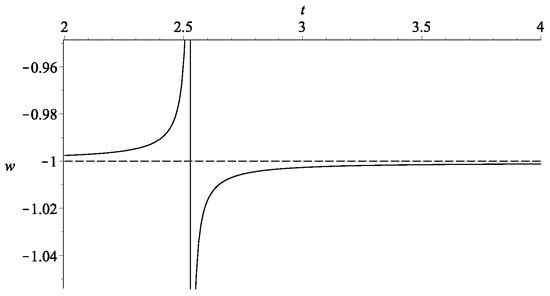
Figure 9.
The evolution of the overall effective w of the example in Figure 8 with and .
The reason we consider a resource term instead of as in the previous section (incidentally, this puts the fixed point outside the physical phase space) is that otherwise, with and the coefficient pre-multiplying being negative (quintessence) instead of positive (phantom), we observe that for “most” initial conditions,
and thus the magnitude of x is increasing and instead of 0, which is not the behavior that we want. This can be seen in Figure 10.
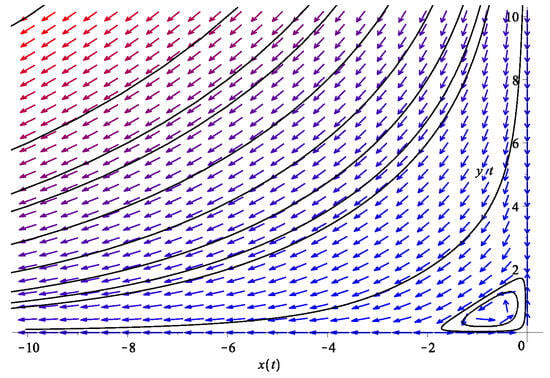
Figure 10.
The phase diagram of the two dark energy fluid model in Equation (21) but with the resource term changed to instead of . Here, we use , . Most trajectories flow towards and . Note, however, the presence of a center surrounded by cyclic flows.
However, even in this scenario, there is one interesting feature worth mentioning. In the neighborhood of the origin, there exists a center around which the flows are cyclic. This implies both x and y, as well as their sum, are oscillatory. As a result, there are multiple (infinitely many) phantom crossings, and infinitely many transitions between AdS-like and dS-like cosmology. These are shown in Figure 11 and Figure 12. Indeed, multiple transition scenarios have been considered in the literature [39].
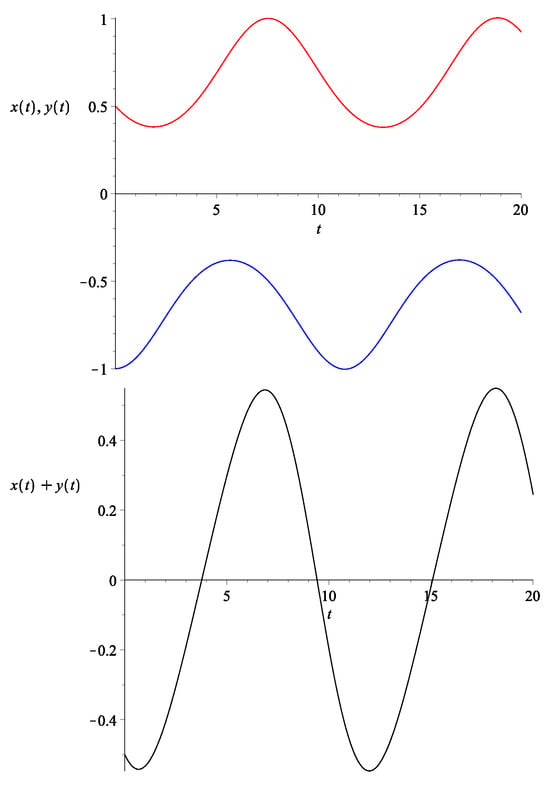
Figure 11.
Top: The evolution of (bottom curve in blue) and (top curve in red) with the initial condition set to be , for the model that corresponds to Figure 10. Bottom: The evolution of , which in this case is the same as the overall .
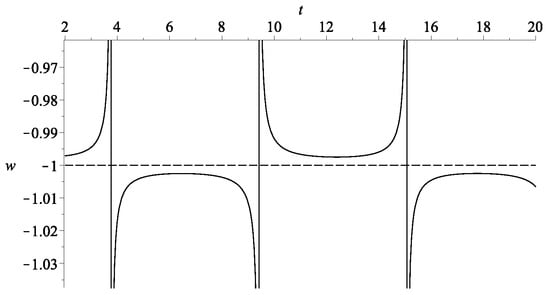
Figure 12.
The evolution of the overall effective w of the example in Figure 11 with and .
5. Discussion: Sign Switching Dark Energy and Naturalness
One of the longstanding questions about dark energy density is why its value is so small, which is some times smaller than the natural scale for a quantum vacuum energy if it is indeed a cosmological constant (for a dynamical field, the problem translates into an extremely light mass of the field). Of course, it is debatable whether this is indeed a problem [78]. In any case, it would be interesting to see what this value corresponds to in the Lotka–Volterra equations in these models.
Take for example, the unfair competition model. We note that the evolution equation for , namely
is equivalent to the following fluid equation:
In other words, the “resource term” in the Lotka–Volterra equation corresponds to a quadratic self-interaction term. How might one interpret this term?
Such a term was also considered in [66,79]. As commented therein, pressure and density may not be linearly related in more complicated and more realistic systems. If we assume for any barotropic fluid to be an analytic function, we can consider equation of state of the form . This is a Taylor expansion of about , or upon re-grouping of terms, the expansion about the present energy density [79,80]. If this is the correct interpretation, then the self-interaction term in Equation (25) can be interpreted as the result of the first order non-linear term in the expansion. However, in a series expansion, typically, the coefficients of the subsequent terms are roughly of the same order of magnitude, so the “natural” expectation is that . Even if and can be very close to , generically we would have the ratio to be of order 1. This means that K being small would typically result in the quadratic coefficient being unnaturally large and dominate over the linear term, which in turn suggests that we should not, in fact, interpret this term as a term in a Taylor series expansion of . Note that if we do not interpret and term as part of a Taylor series, we can still absorb the term as part of the pressure so that . In which case, K is related to the mass scale M of via , see [81,82]; so this is just the aforementioned fact that in the case of dark energy being dynamical, the naturalness problem is its small mass scale. In the conversion model, the situation is similar. The attractor of the spiral is given in Equation (22), in which we see that y and x are both small if and are small. Obviously, our models do not solve the naturalness problem, unless one could explain dynamically why the attractor has such a small value. Perhaps a fundamental understanding of the nature of the phantom fluid or an entropic argument could provide such a mechanism (in the context of cosmological constant, it was argued in [83] that gravitational entropy is maximized by .)
The DM–DE interacting model also has naturalness problem. In this scenario, in addition to the aforementioned mass scale issue, the coincidence problem also enters the discussion. The coincidence problem is the following: why has the DE energy density only recently become comparable to DM energy density? If the two dark sectors interact dynamically and one can convert into another, then it is conceivable that this problem can be resolved. In practice, however, this is not easily achieved and some amount of fine-tuning may be required [84] (though more complicated models like DE coupling to DM inhomogeneities can better accommodate the coincidence problem, as well as other issues like fine-tuning of initial conditions [85]). Interestingly, even in the DM–DE interacting scenario, it was shown in the same work [84] that at least in a general class of models they discussed, DE with a negative energy density (hence AdS-like in our language) in the past is better at resolving the coincidence problem. Indeed, we note that the coincidence problem may be resolved by considering interactions between two DE components. An example is provided by the so-called “cosmon” model [86,87], in which a running cosmological “constant” interacts with another effective DE fluid (the cosmon). Here, it is worth mentioning another interesting proposal, the “running vacuum model” [88], that could potentially solve the Hubble tension, the tension, along with the naturalness problem and the coincidence problem.
To conclude, in this work, motivated by the idea that a sign switching dark energy from an early time AdS-like Universe to a late time dS-like Universe can help to ameliorate the Hubble tension and the tension, we consider a scenario in which the dark energy sector consists of two interacting fluids. We found that AdS-to-dS transition can happen under various models, even if both fluids are phantom, and even if the combined effective dark energy has a constant w. Of course, these are only toy models serve to illustrate the qualitative features. The profiles of these fluids need to be constrained by observations. Still, the possibility that the dark energy sector may contain various interacting components deserves a closer look (see [82,89] for other aspects of self-interacting dark energy) as it can realize many different interesting features.
For generalizations, one could also consider interactions between the two dark energy components with dark matter and/or dark radiation in a more complicated model (a quintom model was considered in [90], with the phantom component interacting with dark matter, but not with the quintessence sector; see also [91]). Another possibility is to consider other forms of interaction terms in place of ; see, for example, [92] and the references therein for the case of DM–DE interaction. Most importantly, more realistic models need to go beyond the assumption that the Hubble parameter is slowly varying when setting up the Lotka–Volterra equations.
Funding
This research was funded by the National Natural Science Foundation of China grant number 11922508.
Data Availability Statement
This research is a theoretical study and has no associated data.
Acknowledgments
Y.C.O. thanks Brett McInnes for useful discussions.
Conflicts of Interest
The author declares no conflict of interest.
Notes
| 1 | Indeed, such a possibility was already considered from other perspectives before the Hubble tension became a serious issue [42,43,44,45,46]. See also the recent work [47]. |
| 2 | Here sgn is the sign function (i.e., it is for positive argument and for negative argument). |
| 3 | The idea that different dark energy components might interact with each other is not new. For example, models in which a quintessence interacts with a Chaplygin gas was considered in [57], in an attempt to explain the coincidence problem [58]. |
| 4 | One can check that in the units in which the speed of light , and have physical dimension , while has dimension ; while and are dimensionless. |
| 5 | In the cosmological case, AdS spacetime has , which is the same as dS spactime. Unlike dS spacetime, however, in AdS spacetime the negative cosmological constant corresponds to a negative energy density but with a positive pressure. Cosmological evolution with negative energy densities was previously studied in details in [73]. |
| 6 | This phantom crossing is achieved by exhibiting a pole/singularity in their equation of state parameter, which is quite different from the more well-known quintom models. |
References
- Bernal, J.L.; Verde, L.; Riess, A.G. The Trouble With H0. arXiv 2016, arXiv:1607.05617. [Google Scholar]
- Verde, L.; Treu, T.; Riess, A.G. Tensions Between the Early and Late Universe. Nat. Astron. 2019, 3, 891–895. [Google Scholar] [CrossRef]
- Valentino, E.D.; Anchordoqui, L.A.; Akarsu, O.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Snowmass2021—Letter of Interest Cosmology Intertwined II: The Hubble Constant Tension. Astropart. Phys. 2021, 131, 102605. [Google Scholar]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the Realm of the Hubble Tension—A Review of Solutions. Class. Quantum Grav. 2021, 38, 153001. [Google Scholar]
- Battye, R.A.; Charnock, T.; Moss, A. Tension Between the Power Spectrum of Density Perturbations Measured on Large and Small Scales. Phys. Rev. D 2015, 91, 103508. [Google Scholar] [CrossRef]
- Benisty, D. Quantifying the S8 Tension With the Redshift Space Distortion Data Set. Phys. Dark Univ. 2021, 1, 100766. [Google Scholar]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, Ö.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Cosmology Intertwined III: fσ8 and S8. Astropart. Phys. 2021, 131, 102604. [Google Scholar]
- Knox, L.; Millea, M. The Hubble Hunter’s Guide. Phys. Rev. D 2020, 101, 043533. [Google Scholar] [CrossRef]
- Rameez, M.; Sarkar, S. Is There Really a Hubble Tension? Class. Quantum Grav. 2021, 38, 154005. [Google Scholar]
- Vagnozzi, S. New Physics in Light of the H0 Tension: An Alternative View. Phys. Rev. D 2020, 102, 023518. [Google Scholar] [CrossRef]
- Benevento, G.; Hu, W.; Raver, M. Can Late Dark Energy Transitions Raise the Hubble Constant? Phys. Rev. D 2020, 101, 103517. [Google Scholar] [CrossRef]
- Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Solomon, R.; Bargiacchi, G.; Capozziello, S.; Dainotti, M.G.; Stojkovic, D. Revealing Intrinsic Flat ΛCDM Biases with Standardizable Candles. Phys. Rev. D 2022, 106, L041301. [Google Scholar] [CrossRef]
- Abdalla, E.; Abellán, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, Ö.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Anchordoqui, L.A.; et al. Cosmology Intertwined: A Review of the Particle Physics, Astrophysics, and Cosmology Associated with the Cosmological Tensions and Anomalies. J. High Energy Astrophys. 2022, 34, 49–211. [Google Scholar]
- Mazo, B.Y.D.V.; Romano, A.E.; Quintero, M.A.C. H0 Tension or M Overestimation? Eur. Phys. J. C 2022, 82, 610. [Google Scholar] [CrossRef]
- Escudero, H.G.; Kuo, J.L.; Keeley, R.E.; Abazajian, K.N. Early or Phantom Dark Energy, Self-Interacting, Extra, or Massive Neutrinos, Primordial Magnetic Fields, or a Curved Universe: An Exploration of Possible Solutions to the H0 and σ8 Problems. Phys. Rev. D 2022, 106, 103517. [Google Scholar] [CrossRef]
- de Sá, R.; Benetti, M.; Graef, L.L. An Empirical Investigation Into Cosmological Tensions. Eur. Phys. J. Plus 2022, 137, 1129. [Google Scholar] [CrossRef]
- Schöneberg, N.; Verde, L.; Gil-Marín, H.; Brieden, S. BAO+BBN Revisited—Growing the Hubble Tension With a 0.7km/s/Mpc Constraint. J. Cosmol. Astropart. Phys. 2022, 11, 039. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An Update. New Astron. Rev. 2022, 95, 101659. [Google Scholar]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark Energy Cosmology: The Equivalent Description via Different Theoretical Models and Cosmography Tests. Astrophys. Space Sci. 2012, 342, 155. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Simone, B.D.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble Constant Tension in the SNe IA Pantheon Sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Simone, B.D.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G.; Bogdan, M.; Ugale, S. On the Evolution of the Hubble Constant With the SNe IA Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030. Galaxies 2022, 10, 24. [Google Scholar] [CrossRef]
- Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Solomon, R.; Dainotti, M.G.; Stojkovic, D. Putting Flat ΛCDM In The (Redshift) Bin. arXiv 2022, arXiv:2206.11447. [Google Scholar]
- Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Solomon, R. High Redshift ΛCDM Cosmology: To Bin or not to Bin? Phys. Dark Univ. 2023, 40, 101216. [Google Scholar] [CrossRef]
- Jia, X.D.; Hu, J.P.; Wang, F.Y. The Evidence for a Decreasing Trend of Hubble Constant. Astron. Astrophys. 2023, 674, A45. [Google Scholar] [CrossRef]
- Dutta, K.; Ruchika; Roy, A.; Sen, A.A.; Sheikh-Jabbari, M.M. Beyond ΛCDM with Low and High Redshift Data: Implications for Dark Energy. Gen. Rel. Grav. 2020, 52, 15. [Google Scholar] [CrossRef]
- Peracaula, J.S.; Gomez-Valent, A.; Perez, J.D. Signs of Dynamical Dark Energy in Current Observations. Phys. Dark Univ. 2019, 25, 100311. [Google Scholar] [CrossRef]
- Visinelli, L.; Vagnozzi, S.; Danielsson, U. Revisiting a Negative Cosmological Constant From Low-Redshift Data. Symmetry 2019, 11, 1035. [Google Scholar] [CrossRef]
- Akarsu, Ö.; Barrow, J.D.; Escamilla, L.A.; Vazquez, J.A. Graduated Dark Energy: Observational Hints of a Spontaneous Sign Switch in the Cosmological Constant. Phys. Rev. D 2020, 101, 063528. [Google Scholar] [CrossRef]
- Ye, G.; Piao, Y.-S. Is the Hubble Tension a Hint of AdS Phase Around Recombination? Phys. Rev. D 2020, 101, 083507. [Google Scholar] [CrossRef]
- Valentino, E.D.; Linder, E.V.; Melchiorri, A. H0 Ex Machina: Vacuum Metamorphosis and Beyond H0. Phys. Dark Univ. 2020, 30, 100733. [Google Scholar] [CrossRef]
- Calderón, R.; Gannouji, R.; L’Huillier, B.; Polarski, D. Negative Cosmological Constant in the Dark Sector? Phys. Rev. D 2021, 103, 023526. [Google Scholar] [CrossRef]
- Lin, W.; Chen, X.; Mack, K.J. Early Universe-Physics Insensitive and Uncalibrated Cosmic Standards: Constraints on ΩM and Implications for the Hubble Tension. Astrophys. J. 2021, 920, 159. [Google Scholar] [CrossRef]
- Cai, R.-G.; Guo, Z.-K.; Wang, S.-J.; Yu, W.-W.; Zhou, Y. No-Go Guide for the Hubble Tension: Late-Time Solutions. Phys. Rev. D 2022, 105, L021301. [Google Scholar] [CrossRef]
- Akarsu, Ö.; Kumar, S.; Ozulker, E.; Vazquez, J.A. Relaxing Cosmological Tensions With a Sign Switching Cosmological Constant. Phys. Rev. D 2021, 104, 123512. [Google Scholar] [CrossRef]
- Sen, A.A.; Adil, S.A.; Sen, S. Do Cosmological Observations Allow a Negative Λ? Mon. Not. R. Astron. Soc. 2022, 518, 1098. [Google Scholar] [CrossRef]
- Cai, R.-G.; Guo, Z.-K.; Wang, S.-J.; Yu, W.-W.; Zhou, Y. No-Go Guide for Late-Time Solutions to the Hubble Tension: Matter Perturbations. Phys. Rev. D 2022, 106, 063519. [Google Scholar] [CrossRef]
- Hu, J.-P.; Wang, F. Revealing the Late-Time Transition of H0: Relieve the Hubble Crisis. Mon. Not. R. Astron. Soc. 2022, 517, 576–581. [Google Scholar] [CrossRef]
- Gennaro, S.D.; Ong, Y.C. Sign Switching Dark Energy from a Running Barrow Entropy. Universe 2022, 8, 541. [Google Scholar] [CrossRef]
- Moshafi, H.; Firouzjahi, H.; Talebian, A. Multiple Transitions in Vacuum Dark Energy and H0 Tension. Astrophys. J. 2022, 940, 2–121. [Google Scholar] [CrossRef]
- Akarsu, Ö.; Kumar, S.; Ozulker, E.; Vazquez, J.A.; Yadav, A. Relaxing Cosmological Tensions With a Sign Switching Cosmological Constant: Improved Results With Planck, BAO and Pantheon Data. Phys. Rev. D 2023, 108, 023513. [Google Scholar] [CrossRef]
- Antonini, S.; Simidzija, P.; Swingle, B.; Raamsdonk, M.V.; Waddell, C. Accelerating Cosmology From Λ<0 Gravitational Effective Field Theory. J. High Energy Phys. 2023, 2023, 203. [Google Scholar]
- Kallosh, R.; Kratochvil, J.; Linde, A.; Linder, E.V.; Shmakova, M. Observational Bounds on Cosmic Doomsday. J. Cosmol. Astropart. Phys. 2003, 2003, 015. [Google Scholar] [CrossRef]
- McInnes, B. Quintessential Maldacena-Maoz Cosmologies. J. High Energy Phys. 2004, 2004, 036. [Google Scholar] [CrossRef]
- Prokopec, T. Negative Energy Cosmology and the Cosmological Constant. arXiv 2011, arXiv:1105.0078. [Google Scholar]
- Biswas, T.; Koivisto, T.; Mazumdar, A. Could Our Universe Have Begun With Negative Lambda? arXiv 2011, arXiv:1105.2636. [Google Scholar]
- Banerjee, S.; Danielsson, U.; Dibitetto, G.; Giri, S.; Schillo, M. Emergent de Sitter Cosmology from Decaying AdS. Phys. Rev. Lett. 2018, 121, 261301. [Google Scholar] [CrossRef] [PubMed]
- Raamsdonk, M.V. Cosmology Without Time-Dependent Scalars Is Like Quantum Field Theory Without RG Flow. arXiv 2022, arXiv:2211.12611. [Google Scholar]
- Delubac, T. et al. [BOSS Collaboration] Baryon Acoustic Oscillations in the Lyα Forest of Boss DR11 Quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef]
- Bacon, D.J. et al. [SKA Collaboration] Cosmology With Phase 1 of the Square Kilometre Array Red Book 2018: Technical Specifications and Performance Forecasts. Publ. Astron. Soc. Austral. 2020, 37, e007. [Google Scholar]
- Abdalla, E. et al. [BINGO Collaboration] The BINGO Project I: Baryon Acoustic Oscillations from Integrated Neutral Gas Observations. Astron. Astrophys. 2022, 664, A14. [Google Scholar] [CrossRef]
- Costa, A.A. et al. [BINGO Collaboration] The BINGO Project VII: Cosmological Forecasts from 21cm Intensity Mapping. Astron. Astrophys. 2022, 664, A20. [Google Scholar] [CrossRef]
- Amendola, L.; Appleby, S.; Avgoustidis, A.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; et al. Cosmology and Fundamental Physics with the Euclid Satellite. Living Rev. Rel. 2018, 21, 2. [Google Scholar] [CrossRef] [PubMed]
- Malekjani, M.; Conville, R.M.; Colgáin, E.Ó.; Pourojaghi, S.; Sheikh-Jabbari, M.M. Negative Dark Energy Density from High Redshift Pantheon+ Supernovae. arXiv 2023, arXiv:2301.12725. [Google Scholar]
- Acquaviva, G.; Akarsu, O.; Katirci, N.; Vazquez, J.A. Simple-Graduated Dark Energy and Spatial Curvature. Phys. Rev. D 2021, 104, 023505. [Google Scholar] [CrossRef]
- Lee, B.-H.; Lee, W.; Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Thakur, S. Is Local H0 At Odds With Dark Energy EFT? J. Cosmol. Astropart. Phys. 2022, 2022, 004. [Google Scholar] [CrossRef]
- Barrow, J.D. The Area of a Rough Black Hole. Phys. Letts. B 2020, 808, 135643. [Google Scholar] [CrossRef]
- Farooq, M.U.; Jamil, M.; Debnath, U. Dynamics of Interacting Phantom and Quintessence Dark Energies. Astrophys. Space Sci. 2011, 334, 243. [Google Scholar] [CrossRef]
- Velten, H.E.S.; von Marttens, R.; Zimdahl, W. Aspects of the Cosmological ‘Coincidence Problem’. Eur. Phys. J. C 2014, 74, 3160. [Google Scholar] [CrossRef]
- Gonzalez, T.; Quiros, I. Exact Models With Non-minimal Interaction Between Dark Matter and (Either Phantom or Quintessence) Dark Energy. Class. Quant. Grav. 2008, 25, 175019. [Google Scholar] [CrossRef]
- Pu, B.-Y.; Xu, X.-D.; Wang, B.; Abdalla, E. Early Dark Energy and Its Interaction With Dark Matter. Phys. Rev. D 2015, 92, 123537. [Google Scholar] [CrossRef]
- Wang, B.; Abdalla, E.; Atrio-Barandela, F.; Pavon, D. Dark Matter and Dark Energy Interactions: Theoretical Challenges, Cosmological Implications and Observational Signatures. Rept. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef]
- Wang, H.; Piao, Y.-S. A Fraction of Dark Matter Faded With Early Dark Energy? arXiv 2022, arXiv:2209.09685. [Google Scholar]
- Yang, W.; Pan, S.; Mena, O.; Valentino, E.D. On the Dynamics of a Dark Sector Coupling. arXiv 2022, arXiv:2209.14816. [Google Scholar] [CrossRef]
- Bernui, A.; Valentino, E.D.; Giarè, W.; Kumar, S.; Nunes, R.C. Exploring the H0 Tension and the Evidence for Dark Sector Interactions From 2D BAO Measurements. Phys. Rev. D 2023, 107, 103531. [Google Scholar] [CrossRef]
- Perez, J.; Füzfa, A.; Carletti, T.; Mélot, L.; Guedezounme, L. The Jungle Universe. Gen. Rel. Grav. 2014, 46, 1753. [Google Scholar] [CrossRef]
- Aydiner, E. Chaotic Universe Model. Sci. Rep. 2018, 8, 721. [Google Scholar] [CrossRef]
- Simon-Petit, A.; Yap, H.-H.; Perez, J. Refinements in the Jungle Universes. arXiv 2016, arXiv:1603.02267. [Google Scholar]
- Haba, Z.; Stachowski, A.; Szydlowski, M. Dynamics of the Diffusive DM–DE Interaction–Dynamical System Approach. J. Cosmol. Astropart. Phys. 2016, 2016, 024. [Google Scholar] [CrossRef]
- Gariazzo, S.; Valentino, E.D.; Mena, O.; Nunes, R.C. Late Time Interacting Cosmologies and the Hubble Constant Tension. Phys. Rev. D 2022, 106, 023530. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Alam, U.; Pandey, K.L.; Das, S.; Pal, S. Are H0 and σ8 Tensions Generic to Present Cosmological Data? Astrophys. J. 2019, 876, 143. [Google Scholar] [CrossRef]
- Mawas, E.; Street, L.; Gass, R.; Wijewardhana, L.C.R. Interacting Dark Energy Axions in Light of the Hubble Tension. arXiv 2021, arXiv:2108.13317. [Google Scholar]
- Cruz, M.; Lepe, S.; Morales-Navarrete, G. Qualitative Description of the Universe in the Interacting Fluids Scheme. Nucl. Phys. B 2019, 943, 114623. [Google Scholar] [CrossRef]
- Saharian, A.A.; Avagyan, R.M.; de Mello, E.R.B.; Kotanjyan, V.K.; Petrosyan, T.A.; Babujyan, H.G. Cosmological Evolution With Negative Energy Densities. Astrophysics 2022, 65, 427. [Google Scholar] [CrossRef]
- Heisenberg, L.; Villarrubia-Rojo, H.; Zosso, J. Simultaneously Solving the H0 and σ8 Tensions With Late Dark Energy. Phys. Dark Univ. 2023, 39, 101163. [Google Scholar] [CrossRef]
- Heisenberg, L.; Villarrubia-Rojo, H.; Zosso, J. Can Late-Time Extensions Solve the H0 and σ8 Tensions? Phys. Rev. D 2022, 106, 043503. [Google Scholar] [CrossRef]
- Valentino, E.D.; Mukherjee, A.; Sen, A.A. Dark Energy With Phantom Crossing and the H0 Tension. Entropy 2021, 23, 404. [Google Scholar] [CrossRef] [PubMed]
- Ozulker, E. Is the Dark Energy Equation of State Parameter Singular? Phys. Rev. D 2022, 106, 063509. [Google Scholar] [CrossRef]
- Bianchi, E.; Rovelli, C. Why All These Prejudices Against a Constant? arXiv 2010, arXiv:1002.3966. [Google Scholar]
- Ananda, K.N.; Bruni, M. Cosmo-Dynamics and Dark Energy With Non-linear Equation of State: A Quadratic Model. Phys. Rev. D 2006, 74, 023523. [Google Scholar] [CrossRef]
- Visser, M. Jerk, Snap, and the Cosmological Equation of State. Class. Quant. Grav. 2004, 21, 2603. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Cheng, H.C.; Luty, M.A.; Mukohyama, S.; Wiseman, T. Dynamics of Gravity in a Higgs Phase. J. High Energy Phys. 2007, 2007, 036. [Google Scholar] [CrossRef]
- Bhattacharya, G.; Mukherjee, P.; Saha, A. On the Self-Interaction of Dark Energy in a Ghost-Condensate Model. arXiv 2013, arXiv:1301.4746. [Google Scholar]
- Boyle, L.; Turok, N. Thermodynamic Solution of the Homogeneity, Isotropy and Flatness Puzzles (And a Clue to the Cosmological Constant). arXiv 2022, arXiv:2210.01142. [Google Scholar]
- Quartin, M.; Calvao, M.O.; Joras, S.E.; Reis, R.R.R.; Waga, I. Dark Interactions and Cosmological Fine-Tuning. J. Cosmol. Astropart. Phys. 2008, 2008, 007. [Google Scholar] [CrossRef]
- Marra, V. Coupling Dark Energy to Dark Matter Inhomogeneities. Phys. Dark Univ. 2016, 13, 25. [Google Scholar] [CrossRef]
- Grande, J.; Sola, J.; Stefancic, H. LXCDM: A Cosmon Model Solution to the Cosmological Coincidence Problem? J. Cosmol. Astropart. Phys. 2006, 2006, 011. [Google Scholar] [CrossRef]
- Grande, J.; Pelinson, A.; Sola, J. Dark Energy Perturbations and Cosmic Coincidence. Phys. Rev. D 2009, 79, 043006. [Google Scholar] [CrossRef]
- Peracaula, J.S. The Cosmological Constant Problem and Running Vacuum in the Expanding Universe. Philos. Trans. R. Soc. Lond. A 2022, 380, 20210182. [Google Scholar] [CrossRef]
- Gonzalez, M.C.; Trodden, M. Field Theories and Fluids for an Interacting Dark Sector. Phys. Rev. D 2018, 97, 043508, Erratum in Phys. Rev. D 2020, 101, 089901. [Google Scholar] [CrossRef]
- Panpanich, S.; Burikham, P.; Ponglertsakul, S.; Tannukij, L. Resolving Hubble Tension with Quintom Dark Energy Model. Chin. Phys. C 2021, 45, 015108. [Google Scholar] [CrossRef]
- Wu, P.; Zhang, S.N. Cosmological Evolution of Interacting Phantom (Quintessence) Model in Loop Quantum Gravity. J. Cosmol. Astropart. Phys. 2008, 2008, 007. [Google Scholar] [CrossRef]
- Bouali, A.; Albarran, I.; Bouhmadi-Lopez, M.; Errahmani, A.; Ouali, T. Cosmological Constraints of Interacting Phantom Dark Energy Models. Phys. Dark Univ. 2021, 34, 100907. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).