Abstract
This paper presents a noncommutative (NC) version of an extended Sáez–Ballester (SB) theory. Concretely, considering the spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric, we propose an appropriate dynamical deformation between the conjugate momenta and, applying the Hamiltonian formalism, obtain deformed equations of motion. In our model, the NC parameter appears linearly in the deformed Poisson bracket and the equations of the NC SB cosmology. When it goes to zero, we get the corresponding commutative counterparts. Even by restricting our attention to a particular case, where there is neither an ordinary matter nor a scalar potential, we show that the effects of the noncommutativity provide interesting results: applying numerical endeavors for very small values of the NC parameter, we show that (i) at the early times of the universe, there is an inflationary phase with a graceful exit, for which the relevant nominal condition is satisfied; (ii) for the late times, there is a zero acceleration epoch. By establishing an appropriate dynamical framework, we show that the results (i) and (ii) can be obtained for many sets of the initial conditions and the parameters of the model. Finally, we indicate that, at the level of the field equations, one may find a close resemblance between our NC model and the Starobinsky inflationary model.
1. Introduction
To overcome the problems of standard cosmology, various alternative theories to general relativity have been established. Among them, the scalar-tensor theories have played a significant role, see, for instance [1,2,3,4,5] and reference therein. In the Sáez–Ballester (SB) scalar-tensor theory [6], in which the scalar field is minimally coupled to gravity, a particular non-canonical kinetic term was added to the Einstein–Hilbert action. The original Lagrangian associated with the SB theory includes the ordinary matter sector, but neither cosmological constant nor a scalar potential have contributed to it. Moreover, we should mention that the SB theory possesses dimensionless parameters n and , in which the latter specifies the strength of the coupling between the gravity and the SB scalar field. To the best of our knowledge, it has not been investigated for which values of the observational limits can be satisfied. The SB theory and its extended versions, in both the classical and quantum levels, have been widely applied to investigate various cosmological problems in either four or arbitrary dimensions [7,8,9,10,11,12,13,14,15,16,17,18].
Another category of alternative theories has arisen due to the incapability of the GR in predicting the effects of some phenomena at the Planck regime [19,20]. Among such theories, one can refer to some approaches to noncommutative (NC) gravity (see, [21,22,23,24,25], and references therein), which has roots in noncommutative geometry and noncommutative quantum field theories. As these frameworks are highly nonlinear, therefore, for investigating effects of noncommutativity on different aspects of the universe, noncommutative cosmology has been proposed, see, for instance [26,27,28]. It has been believed that for constructing noncommutative models, both at the quantum as well as classical regime, cosmology can be considered as an interesting arena [29]. For instance, at the classical regime, by modifying the Poisson brackets of the classical theories, one can obtain noncommutative equations of motion. In these frameworks, by including an NC parameter which is usually interpreted as the Planck (length) constant, the effects of the noncommutativity may assist to resolve a few open problems of cosmology [30,31,32,33,34,35,36].
The main objective of the present work is to establish a noncommutative cosmological model in the context of the SB scalar-tensor theory containing an arbitrary potential. Subsequently, we will study the effects of noncommutativity in a particular case where the ordinary matter, as well as scalar potential, are absent. For such a simple model, we will see that in addition to the NC parameter, the presence of n and the SB coupling parameter are also significant in describing the universe at an early time. Moreover, it is worthy to mention that, if the noncommutativity is present at a small scale, by the UV/IR mixing (which is a feature of the noncommutativity), it can also be observed at late times of the universe.
The paper is outlined as follows. In the next section, considering a spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric as the background geometry and applying the Hamiltonian approach, we will obtain cosmological equations of motion for an extended SB cosmology in the non-deformed case. Then, we propose a general dynamical deformation (noncommutativity) to establish an interesting cosmological scenario. In Section 3, we first obtain analytic exact cosmological solutions for the commutative model. Subsequently, we focus on the NC model and show that, for very small values of the NC parameter, there is an inflationary phase, with graceful exit, at the early time. Moreover, we show that, for our herein NC model, the nominal condition associated with the inflation is satisfied. Furthermore, our numerical endeavors show that the noncommutative effects can also be seen at late times. Concretely, for the latter, we observe that the scale factor increase with zero acceleration. In Section 4, by proposing an appropriate dynamical setting, we show that the above-mentioned results are confirmed. Finally, we present our conclusions in Section 5.
2. A Noncommutative Cosmological Scenario in Sáez–Ballester Theory
We start with the spatially flat FLRW universe
where t is the cosmic time, are the Cartesian coordinates, is the scale factor, and is a lapse function. Let us consider an extended version of the SB Lagrangian density:
where ; n and are dimensionless independent parameters, g denotes the determinant of the metric , R is the Ricci scalar, the Greek indices run from zero to three, and we have assumed the units where . The scalar field is minimally coupled to gravity, is a scalar potential, is the Lagrangian density associated with the ordinary matter, and denotes the covariant derivative.
Substituting the Ricci scalar associated with the metric (1) into (2), we obtain
where a dot denotes a derivative with respect to the time and we have neglected a total time derivative term. It is straightforward to show that the Hamiltonian of the model is given by
where and stand for the momenta conjugates of the scale factor and the scalar field, respectively.
Considering the comoving gauge, i.e., setting , employing the Hamiltonian (4), and admitting the Poisson algebra , , and for the phase space coordinates , we easily obtain:
Using Equations (5)–(8), it is straightforward to obtain the equations of the non-deformed SB cosmological model:
where is the Hubble parameter.
In order to establish an appropriate noncommutative scenario, we would propose a (dynamical) deformation solely between the conjugate momenta as 1
(where is the NC parameter) and leave the other Poisson brackets unchanged.
Under the NC deformation (12), Equations (5) and (7) remain unchanged. However, the equations associated with the momenta, i.e., Equations (6) and (8), are deformed: 2
where we have used
in which h is an arbitrary function of the conjugate momenta.
It is easy to show that the equations of motion associated with our herein NC framework are given by
3. Kinetic Inflation and the Horizon Problem
In this section, let us investigate a very simple set up of our herein NC and commutative models, in which the ordinary matter, as well as the scalar potential, are absent, i.e., and . Therefore, the energy density and pressure reduce to
Using Equations (19)–(21), it is straightforward to show that the conservation equation for the matter (associated with the NC framework) is identically satisfied:
It is important to note that , in Equation (21), depends explicitly on the NC parameter . Although, the NC parameter does not, explicitly, appear in the relations associated with the (or equivalently, ), but we will show that they also depend on the NC parameter, implicitly. The above statements point out that there is no way to specify the commutative sector of any quantity, unless substituting in all the equations of motion.
Substituting into (19), we obtain
where we have assumed . Moreover, assuming , from using Equation (23), we obtain the scale factor as a function of the SB scalar field as 3
where and are integration constants. By substituting (23) and (24) into (19), the wave equation will be a differential equation for the scalar field only:
In what follows, we are going to solve Equation (25) either analytically or numerically, by which we will present analysis for the commutative and NC cosmological models.
3.1. Commutative Case
Let us first investigate the commutative case, which will be required later to compare with the corresponding NC case. Substituting into Equation (25), we can easily obtain an exact solution:
where and are integration constants. Moreover, substituting (26) into the corresponding relation of scale factor in (24), we obtain
which implies that, in the commutative case, the scale factor of the universe decelerates forever. In a particular case where and , the solutions (26) and (27) reduce to the corresponding ones obtained in [39]. Let us abstain from analyzing these results here. However, the behavior of the physical quantities for this case will be described and compared with the corresponding NC model, see, for instance, Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6.

Figure 1.
The behavior of the scalar field and the scale factor (solid curves), their first and second derivatives (dotted and dashed curves, respectively) against cosmic time for the commutative model, for which , (the left panels) and NC model with (the right panels). Moreover, for both the commutative and NC models, we have set , , , , , , . To recognize the quantities with positive and negative values, we have plotted with a red line.

Figure 2.
The behavior of the total kinetic energy (black curves), total pressure (solid blue curve), and NC pressure (dashed blue curve) against cosmic time for the commutative case (upper left panel) and NC case (upper right panel). Moreover, the lower left panel and lower right panel are shown the numerical error concerning satisfying the conservation Equation (22) for the commutative case and NC case, respectively. The values for the initial conditions, parameters and units are equal to the corresponding ones chosen for the Figure 1.

Figure 3.
The behavior of the scalar field and the scale factor against cosmic time for our herein NC model with different values of . The blue, black, and red curves are associated with , , and , respectively. Except (which varies here), the values for the initial conditions, other parameters and units are equal to the corresponding ones chosen for the Figure 1.

Figure 4.
The behavior of the scalar field and the scale factor against cosmic time for our herein NC model with different values of n. The black, blue and red curves are associated with , , and , respectively. Except n (which varies here), the values for the initial conditions, other parameters and units are equal to the corresponding ones chosen for the Figure 1.
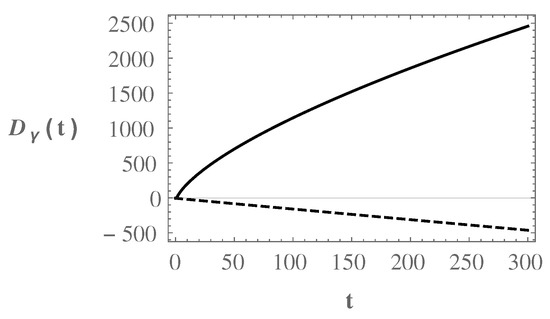
Figure 5.
The time behavior of associated with the commutative model (the dashed curve) and the NC model (the solid curve). The values for the initial conditions, parameters of the model, and units are equal to the corresponding ones chosen for the Figure 1.
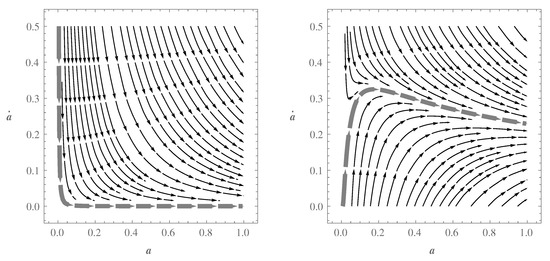
Figure 6.
Phase space portrait for Equation (32). The left and right panels are associated with the commutative case () and noncommutative case (), respectively. We have also assumed , , , and for both of the cases.
3.2. Noncommutative Case
For the NC case, i.e., , it is not feasible to obtain exact solutions for complicated differential Equation (25), analytically. In this respect, let us investigate this case by applying numerical methods. Concretely, assuming , we apply the numerical solution of Equation (25) to plot the physical quantities. In what follows, we will present briefly the consequences of our numerical endeavors, which have been obtained for every proper set of the initial conditions (ICs), the values of the parameters of the model, and the integration constants. We should note that for every set, we have taken very small negative values of the NC parameter. Our results are (see, for instance, Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5):
- In the early times, both the scalar field and the scale factor experience accelerated expansion.
- Thereafter, there is another different phase in which both of them decelerate, see Figure 1.
- At late times, both and asymptotically tend to zero.Up to now, we can conclude that stages 1 and 2 indicate that our NC model may be considered as a successful cosmological inflationary model (see also the discussions will be presented in the following). Concretely, an inflationary phase took place at the earlier times, and afterward, there is a radiation-dominated epoch. Moreover, the effects of the dynamical noncommutativity (12) provide an appropriate transition from the accelerating phase to the decelerating one, which is known as the graceful exit. However, stage (iii) may be interpreted as a quantum gravity footprint as the coarse-grained explanation.
- Let us now analyze the time behavior of the energy density and pressure, see, for instance, the upper right panel of Figure 2. It is seen that always takes positive values such that it increases during the inflationary epoch to reach its maximum value. Soon after exiting from the accelerated phase, it decreases forever. Whilst, both the and always take negative values. In contrast to the , they decrease during the inflationary phase whilst increasing during the radiation-dominated era. They reach their minimum value at the moment of the transition phase.
- In contrast to exact solutions, we should not always expect a numerical solution to satisfy the conservation equation identically. In this regard, it is worth plotting the quantity on the left-hand side of Equation (22) to find out how much disperses from zero (for this we use the numerical solution of Equation (25)). Therefore, for every set of the ICs and the values of the parameters, which have been used to depict the behavior of the quantities, we have checked its corresponding degree of accuracy. Specifically, for every numerical set, we have plotted the corresponding numerical error to be sure that they whether or not satisfy the conservation Equation (22), see, for instance, the lower panels of Figure 2.
- We have also investigated the time behavior of , , their first and second derivatives (with respect to the cosmic time) for different values of the parameters and n, see, for instance, Figure 3 and Figure 4, which show the behavior of and against the cosmic time. Our consequences indicate that, for a specific set of values, by changing the values of (or n) and leaving the others unchanged, there are no perceptible changes in the general behavior of the quantities, which was reported in stages 1 to 5. Notwithstanding, we found that for any t, assuming , the smaller the value of , the larger the values of a and . Moreover, our endeavors have shown that the smaller the value of , the shorter the amount of the interval time of the inflationary epoch. According to Figure 4, an interpretation can also be presented for the case if only n varies.
- Up to now, we have seen that our herein NC model can provide an accelerating phase at early times, and soon after the scale factor can gracefully exit from that accelerating phase and enter to a decelerating phase, which could be assigned to the radiation-dominated era. Therefore, it seems that our model, disregarding the 60 e-fold duration, can be considered as a proper inflationary scenario. Notwithstanding, it has been believed that among the problems associated with the standard cosmology, the horizon problem is the most important one, which should be resolved by a successful inflationary scenario. In this respect, let us investigate only a nominal condition as the key to resolving the horizon problem [40,41]:where denotes the distance a photon has traveledIn order to check satisfaction of the nominal condition (28), we first should obtain . In this respect, for our herein NC, we substitute the relations associated with the scale factor from relations (24) into (29). Therefore, we obtain an integration over with an unknown integrand (as a function of the scalar field), which, in turn, is obtained from (25). Moreover, we should also substitute the Hubble parameter (which can be also obtained from ) from (23) into (28). Consequently, investigating the nominal condition (28) for our herein NC model is not possible unless we obtain from solving (25). However, as mentioned, for the NC case, we have to apply numerical analysis. Our numerical endeavors have shown that condition (28) is satisfied for every set of values that yield the above-mentioned stages 1 to 6, see, for instance, Figure 5.
4. Cosmological Dynamics in Deformed Phase Scenario
It seems that it is impossible to reconstruct the Lagrangian of our NC model. In this respect, let us focus on it at the level of the field equations. Specifically, we can compare the evolution of the scale factor for our herein NC cosmological setting, i.e.,
with that of the Starobinsky inflationary model [42], see Section 5. In order to obtain Equation (30), we have used Equations (18) and (24).
Moreover, in order to confirm the results presented in the previous section, let us provide an appropriate settings for the dynamical system. In this regard, let us rewrite Equation (30) in more convenient form as
Letting , then instead of Equation (31), we have
which is very susceptible to the ICs, values of integration constants ( and ), and the parameters of the model, i.e., , n, and .
Now, by plotting the phase portrait of Equation (32), the difference between the commutative and noncommutative cases are clearly visible. For the former (see the left panel of Figure 6), for all the solutions , it is seen that always decreases while a increases. Whereas, for the latter (see the right panel of the Figure 6), for very small values of the scale factor, we observe an additional interesting behavior for all the solutions . More concretely, during a very short time, increases until it reaches its maximum value. Thereafter, it decreases while the scale factor increases. Finally, depending on the ICs and the values of the parameters of the model, it gets constant values at late times. It is worth noting that Figure 6 includes a vast range of solutions such that the particular solution shown in Figure 1 corresponds to one of the trajectories plotted in Figure 6. This phase portrait, with more complete specifications, certifies the inflationary phase (with a graceful exit) described in the previous section. We should emphasize that our herein NC model, for various sets of the parameters, can yield the interesting results presented within the preceding section. For instance, the Figure 7 shows the phase portrait of Equation (32) with other values of n, and .
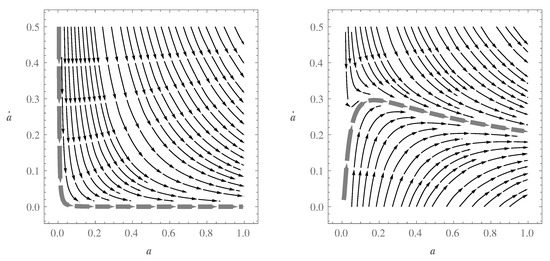
Figure 7.
Phase space portrait for Equation (32). The left and right panels are associated with the commutative case () and noncommutative case (), respectively. We have also assumed , , , and for both of the cases.
5. Conclusions
In this work, by considering the spatially flat FLRW metric and applying the Hamiltonian formalism, we first retrieved the equations of motion associated with a generalized SB theory. Subsequently, by proposing a dynamical deformation between the conjugate momenta (associated with the scale factor and the SB scalar field), in which the deformation parameter appears linearly, we have constructed a noncommutative SB framework, such that in a particular case where , the commutative cosmological model is recovered (see Section 2).
In order to elucidate the kinetic acceleration arisen from our herein NC model, we restricted our attention to a simple case in which not only the scalar potential but also the Lagrangian density associated with the ordinary matter is absent. Then, we have shown that it is straightforward to write the NC Klein–Gordon equation in terms of the only SB scalar field and its time derivatives. It is worthy to note that the NC parameter appears in that wave equation linearly, too.
Subsequently, to do the latter comparison, we first obtained an exact cosmological solution for the standard case. Whilst, concerning the NC model, we found that it is not feasible to obtain an exact analytic solution for the complicated nonlinear differential equation (i.e., the NC Klein–Gordon equation). Therefore, we resorted to applying numerical methods to analyze the time behavior of the physical quantities.
In contrast to the corresponding standard SB model, our numerical endeavors have indicated that our herein simple NC model (in which the NC parameter appears linearly not only in the proposed deformed Poisson bracket but also in the field equations) can provide fascinating aspects. Let us be more precise. We have shown that our NC model yields a kinetic acceleration at early times. Thereafter, the scale factor can exit gracefully from that phase and enter a decelerating one. The latter can be assigned to the radiation-dominated phase. Therefore, we have interpreted this outcome, which is attained due to the presence of the NC effects, as an inflationary phase for the universe at early times and shown that its corresponding expected nominal condition is satisfied. Moreover, at the late times, we also observed the effects of the noncommutativity: we showed that the scale factor increases with constant speed (presence of a zero acceleration epoch), which can be assigned to a coarse-grained explanation.
We have also depicted the time behavior of the NC energy density and NC pressure and then compared them with the corresponding counterparts associated with the non-deformed model. We have shown that the time behavior of the quantities depends not only on the NC parameter but also on the values taken by the parameters and n, as expected.
Finally, we constructed an appropriate dynamical setting by which we easily illustrated the effect of noncommutativity. More concretely, using the same set of ICs and the parameters of the model applied for plotting Figure 1, we have depicted the phase portrait of Equation (32). It is seen that the sole trajectory of that plot corresponds to those of the Figure 1 (for either commutative model or NC model), which confirms all the results of Section 3.2.
Before closing this section, it is worthy to mention a few comments regarding the strengths and shortcomings of our herein NC model:
- In this work, we have investigated the effects of the noncommutativity for a particular case. More concretely, we have restricted our attention to a special case where (i) the ordinary matter and the scalar potential are absent; (ii) a particular dynamical deformation between only the conjugate momenta was proposed. Obviously, by removing either one or more of the above restrictions, one can construct more extended models, which may yield more interesting results. For instance, generalizing this work to an NC model including a non-vanishing scalar potential, but still admitting the other constraints, we can establish NC counterparts for the deformed versions of the Luccin–Mataresse model [43] and the Barrow–Burd–Lancaster–Madsen model [44,45,46], see also [46]. The generalized version of the former and of the latter has been established in the non-deformed phase space in the context of SB theory [47]. Such extended frameworks have been investigated and will be presented within our forthcoming works.
- In comparison with the NC model presented in [48], we observe that in our herein NC model, there are two extra free parameters, i.e., and n, by which one can not only provide different behaviors for the physical quantities but also it may assist to retrieve appropriate values for the e-fold number (which is also one of the essential features of an expected inflationary epoch) to be in agreement with the observational data. In a particular case where and , we recover the corresponding model investigated in [48]. Moreover, in another particular case where and , using transformationwhere and carry the same dimension of , the Lagrangian (2) transforms to the corresponding standard minimally coupled scalar field. Therefore, in the commutative case, we recover the model studied in [48]. However, it is important to note that, under the transformation (33), the deformation (12) is not equivalent to that chosen in [48]. Concretely, the NC case corresponding to will be different from that investigated in [48]. This particular kinetic model was contributed to other extended NC models mentioned in the preceding comment.
- We should emphasize that it is almost impossible to retrieve the Lagrangian associated with our NC model, and therefore, it is a complicated procedure to investigate the quantum features of the model by means of the perturbation analysis. In this respect, at the level of the field equations, we have obtained a proper NC differential equation associated with the evolution of the scale factor. By means of such a procedure as well as by establishing the corresponding dynamical setting, one may probe the possible relations between the parameters appeared in our model (i.e., NC parameter, SB coupling parameter, n and the integration constants) and the quantum corrections observed in the Starobinsky inflationary model to find a feasible correspondence between these scenarios.
Funding
This research received no external funding.
Acknowledgments
I would thank the anonymous reviewers for critical reading of this manuscript and their valuable comments. I acknowledge the FCT grants UID-B-MAT/00212/2020 and UID-P-MAT/00212/2020 at CMA-UBI plus the COST Action CA18108 (Quantum gravity phenomenology in the multi-messenger approach).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations have been used in this manuscript:
| NC | noncommutative |
| SB | Sáez–Ballester |
| FLRW | Friedmann–Lemaître–Robertson–Walker |
Notes
| 1 | Some arguments for such a deformation have been presented in [30]. |
| 2 | In what follows, let us briefly present another approach to obtain the NC field equations, see, for instance, [37,38]. In order to obtain the Hamiltonian corresponding to the NC model, we proceed as follows. (i) All the variables of (4) should be replaced by new ones, for instance, primed variables. (ii) Introducing the only transformation , and assuming that the other primed variables are equal to the corresponding unprimed ones, we can easily recover not only the deformed Poisson bracket (12) but also the NC Hamiltonian. (iii) Finally, using the latter together with usual (standard) Poisson brackets, we can easily obtain the NC counterparts of (5)–(8). |
| 3 | In this work, let us skip the cosmological model corresponding to , see Section 5. |
References
- Faraoni, V. Cosmology in Scalar Tensor Gravity; Kluiwer Academic Publishers: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Dabrowski, M.P.; Denkiewicz, T.; Blaschke, D. The conformal status of ω=-3/2 Brans-Dicke cosmology. Ann. Phys. 2007, 16, 237. [Google Scholar] [CrossRef]
- Quiros, I. Selected topics in scalar–tensor theories and beyond. Int. J. Mod. Phys. D 2019, 28, 1930012. [Google Scholar] [CrossRef]
- Kobayashi, T. Horndeski theory and beyond: A review. Rep. Prog. Phys. 2019, 82, 086901. [Google Scholar] [CrossRef] [PubMed]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Jiménez, J.B.; De Laurentis, M.; Olmo, G.J. Modified Gravity and Cosmology; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Sáez, D.; Ballester, V.J. A simple coupling with cosmological implications. Phys. Lett. A 1986, 113, 467. [Google Scholar] [CrossRef]
- Luis, O.P. Cosmological models in the scalar-tetradic theory A. Astrophys. Space Sci. 1987, 132, 387. [Google Scholar]
- Singh, T.; Agrawal, A.K. Some Bianchi-type cosmological models in a new scalar-tensor theory. Astrophys. Space Sci. 1991, 182, 289. [Google Scholar] [CrossRef]
- Singh, C.P.; Shri, R.A.M. Unified description of early universe in scalar-tensor theory. Astrophys. Space Sci. 2003, 284, 1199. [Google Scholar] [CrossRef]
- Mohanty, G.; Sahoo, R.R.; Mahanta, K.L. Five dimensional LRS Bianchi type-I string cosmological model in Saez and Ballester theory. Astrophys Space Sci. 2007, 312, 321. [Google Scholar] [CrossRef]
- Sabido, M.; Socorro, J.; López, L.A.U. Classical and quantum cosmology of the Sáez-Ballester theory. Fizika B 2010, 19, 177. [Google Scholar]
- Naidu, R.L.; Satyanarayana, B.; Reddy, D.R.K. Bianchi Type-V Dark Energy Model in a Scalar-Tensor Theory of Gravitation. Int. J. Theor. Phys. 2012, 51, 1997. [Google Scholar] [CrossRef]
- Yadav, A.K. Anisotropic massive strings in the scalar-tensor theory of gravitation. Res. Astron. Astrophys. 2013, 13, 772. [Google Scholar] [CrossRef][Green Version]
- Rao, V.U.M.; PapaRao, D.C.; Reddy, D.R.K. Five dimensional FRW cosmological models in a scalar-tensor theory of gravitation. Astrophys. Space Sci. 2015, 357, 164. [Google Scholar] [CrossRef]
- Rao, V.U.M.; Kumari, G.S.; Neelima, D. Bianchi Type-VI0 with Strange Quark Matter Attached to String Cloud in Saez-Ballester Theory of Gravitation. Astrophys. Space Sci. 2012, 337, 499. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Moniz, P.V. Modified Saez–Ballester scalar-tensor theory from 5D space-time. Class. Quantum Grav. 2018, 35, 025004. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Pacheco, R.; Sakellariadou, M.; Moniz, P.V. Late time cosmic acceleration in modified Sáez–Ballester theory. Phys. Dark Universe 2020, 27, 100446. [Google Scholar] [CrossRef]
- Jamil, M.; Ali, S.; Momeni, D.; Myrzakulov, R. Bianchi type I cosmology in generalized Saez–Ballester theory via Noether gauge symmetry. Eur. Phys. J. C 2012, 72, 1998. [Google Scholar] [CrossRef]
- Das, S.; Vagenas, E.C. Universality of quantum gravity corrections. Phys. Rev. Lett. 2008, 101, 221301. [Google Scholar] [CrossRef]
- Bojowald, M. Quantum cosmology: A review. Rep. Prog. Phys. 2015, 78, 023901. [Google Scholar] [CrossRef]
- Garcia-Compean, H.; Obregon, O.; Ramirez, C.; Sabido, M. Noncommutative self-dual gravity. Phys. Rev. D 2003, 68, 044015. [Google Scholar] [CrossRef]
- Giardino, S.; Salzano, V. Cosmological constraints on the Generalized Uncertainty Principle from modified Friedmann equations. arXiv 2006, arXiv:2006.01580. [Google Scholar]
- Harikumar, E.; Rivelles, V.O. Noncommutative gravity. Class. Quantum Grav. 2006, 23, 7551. [Google Scholar] [CrossRef]
- Estrada-Jimenez, S.; Garcia-Compean, H.; Obregon, O.; Ramirez, C. Twisted covariant noncommutative self-dual gravity. Phys. Rev. D 2008, 78, 124008. [Google Scholar] [CrossRef]
- Addazi, A.; Alvarez-Muniz, J.; Batista, R.A.; Amelino-Camelia, G.; Antonelli, V.; Arzano, M.; Asorey, M.; Atteia, J.-L.; Bahamonde, S.; Bajardi, F.; et al. Quantum gravity phenomenology at the dawn of the multi-messenger era: A review. arXiv 2006, arXiv:2111.05659. [Google Scholar] [CrossRef]
- Garcia-Compean, H.; Obregon, O.; Ramirez, C. Noncommutative Quantum Cosmology. Phys. Rev. Lett. 2002, 88, 161301. [Google Scholar] [CrossRef]
- Barbosa, G.D.; Pinto-Neto, N. Noncommutative geometry and cosmology. Phys. Rev. D 2004, 70, 103512. [Google Scholar] [CrossRef]
- Pimentel, L.O.; Mora, C. Noncommutative Quantum Cosmology. Gen. Rel. Grav. 2005, 37, 817. [Google Scholar] [CrossRef]
- Pérez-Payán, S.; Sabido, M.; Yee-Romero, C. Effects of deformed phase space on scalar field cosmology. Phys. Rev. D 2013, 88, 027503. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Farhoudi, M.; Khosravi, N. Horizon problem remediation via deformed phase space. Gen. Rel. Grav. 2011, 43, 2895. [Google Scholar] [CrossRef][Green Version]
- Guzmán, W.; Sabido, M.; Socorro, J. On noncommutative minisuperspace and the Friedmann equations. Phys. Lett. B 2011, 697, 271. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Moniz, P.V. Noncommutative minisuperspace, gravity-driven acceleration, and kinetic inflation. Phys. Rev. D 2014, 90, 083533. [Google Scholar] [CrossRef]
- López, J.L.; Sabido, M.; Yee-Romeroa, C. Phase space deformations in phantom cosmology. Phys. Dark Universe 2018, 19, 104. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Marto, J.; Moniz, P.V. Kinetic inflation in deformed phase space Brans–Dicke cosmology. Phys. Dark Universe 2019, 24, 100269. [Google Scholar] [CrossRef]
- Oliveira-Neto, G.; Marcon, L.F. Complete noncommutativity in a cosmological model with radiation. Eur. Phys. Plus 2021, 136, 584. [Google Scholar] [CrossRef]
- Maldonado, C.; Méndez, F. Bimetric universe with matter. Phys. Rev. D 2021, 103, 123505. [Google Scholar] [CrossRef]
- Djemaï, A.E.F.; Smail, H. On Quantum Mechanics on Noncommutative Quantum Phase Space. Commun. Theor. Phys. 2004, 41, 837. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Ziaie, A.H.; Marto, J.; Moniz, P.V. Gravitational collapse of a homogeneous scalar field in deformed phase space. Phys. Rev. D 2014, 89, 044028. [Google Scholar] [CrossRef]
- Singh, C.P.; Srivastava, M.P. Minimally coupled scalar field cosmology in anisotropic cosmological model. J. Phys. 2017, 88, 22. [Google Scholar] [CrossRef]
- Levin, J.J. Gravity-driven acceleration of the cosmic expansion. Phys. Rev. D 1995, 51, 462. [Google Scholar] [CrossRef]
- Levin, J.J. Kinetic inflation in stringy and other cosmologies. Phys. Rev. D 1995, 51, 1536. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99. [Google Scholar] [CrossRef]
- Lucchin, F.; Mataresse, S. Power-law inflation. Phys. Rev. D 1985, 32, 1316. [Google Scholar] [CrossRef] [PubMed]
- Barrow, J.D.; Burd, A.B.; Lancaster, D. Three-dimensional classical spacetimes. Class. Quantum Grav. 1986, 3, 551. [Google Scholar] [CrossRef]
- Madsen, M.S. An unusual cosmological solution for λφ4 theory with broken symmetry. Gen. Relativ. Gravit. 1986, 18, 879. [Google Scholar] [CrossRef]
- Garcia, A.A.; Carlip, S. n-dimensional generalizations of the Friedmann–Robertson–Walker cosmology. Phys. Lett. B 2007, 645, 101. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Sakellariadou, M.; Moniz, P.V. Geodesic Deviation in Sáez-Ballester Theory. arXiv 2022, arXiv:2203.00766. [Google Scholar]
- Rasouli, S.M.M.; Saba, N.; Farhoudi, M.; Marto, J.; Moniz, P.M. Inflationary universe in deformed phase space scenario. Ann. Phys. 2018, 393, 288. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).