Charged Lepton Flavor Violation at the High-Energy Colliders: Neutrino Mass Relevant Particles
Abstract
1. Introduction
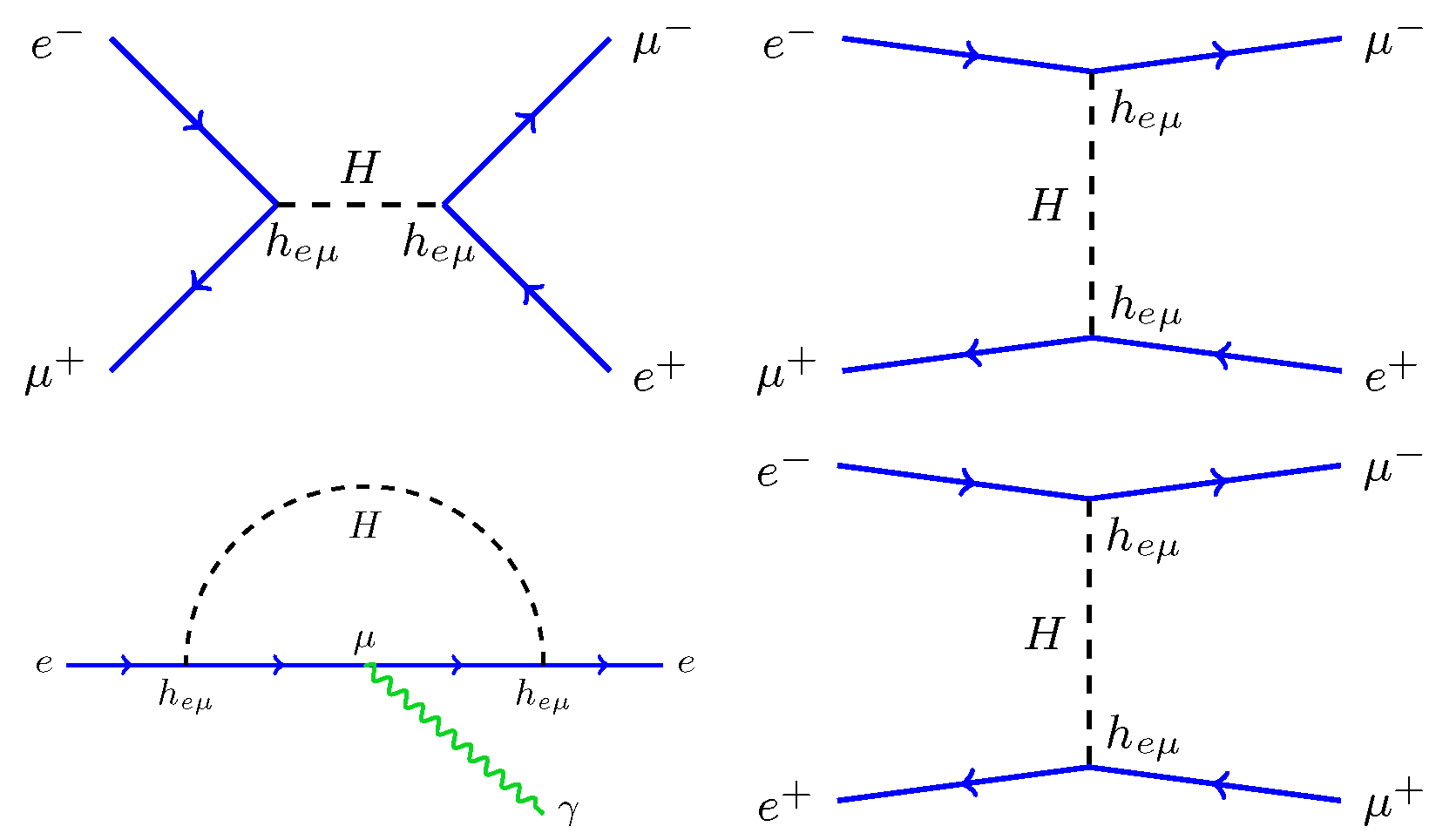
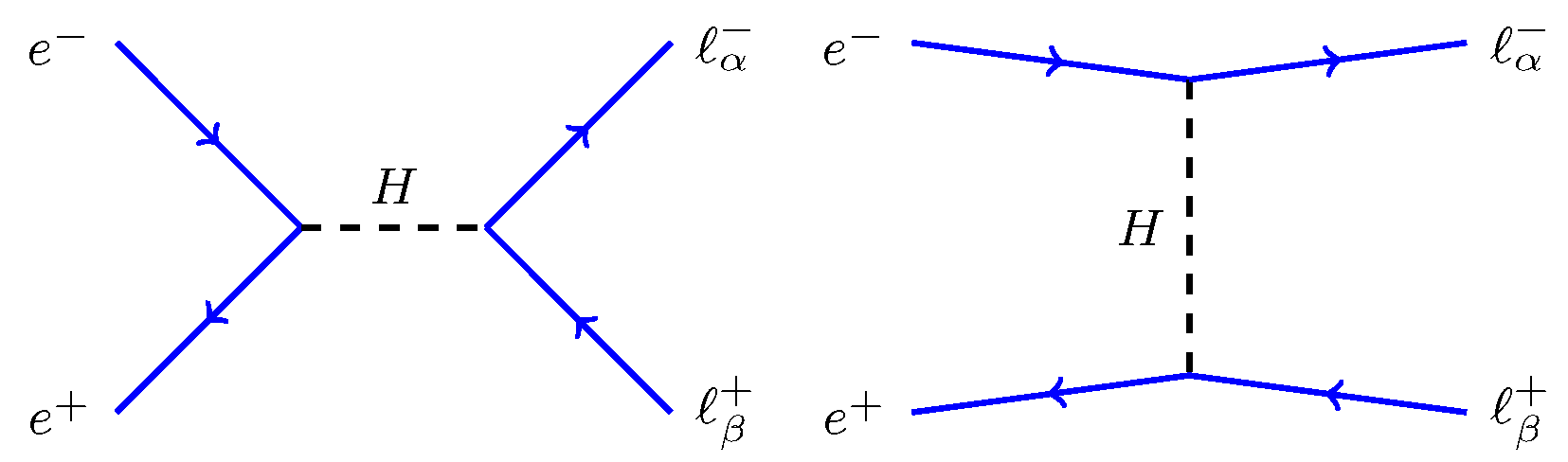
2. BSM Neutral Scalar
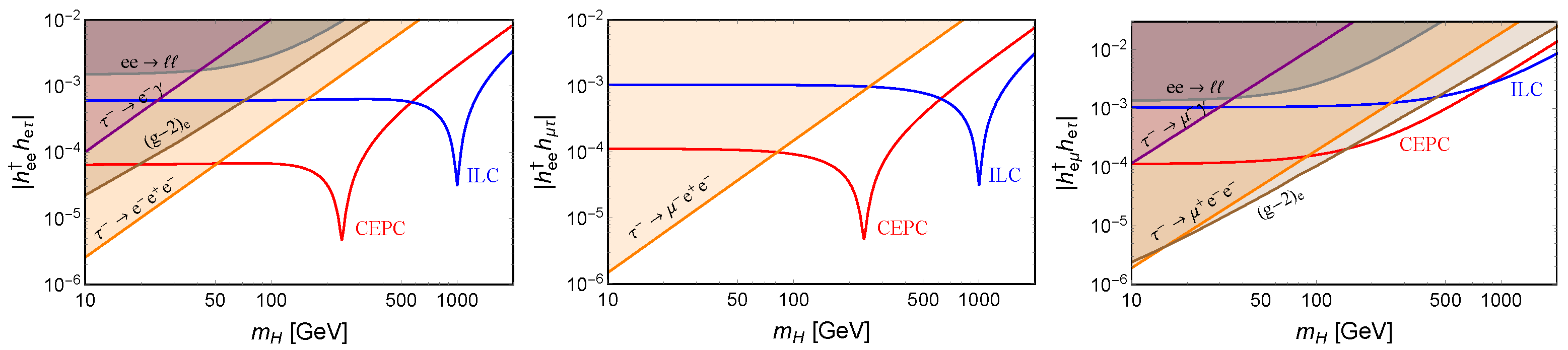
- At future high-energy colliders, high-energy photon beams can be obtained from the back scattering of high-intensity low-energy laser beam off high-energy electron beams [69,70,71], which provides more production channels for the neutral scalar H, e.g., via the process (the corresponding Feynman diagram is similar to the third diagram in Figure 6). These channels are largely complementary to the channels above [58].
- Future high-energy muon colliders can probe larger regions of parameter space for the muon flavor couplings, in particular for the explanation of muon anomaly (see e.g., Ref. [72]).
- The LFV signal due to the scalar H can also be searched for at the hadron colliders, i.e., in the channel at the parton level. As a result of the relatively “dirty” backgrounds at the hadron colliders in particular for the tau leptons, the searches of LFV signals from H is more challenging at the hadron colliders than at the lepton colliders. However, the scalar H can be probed to a larger mass at the hadron colliders (cf. Ref. [73]).
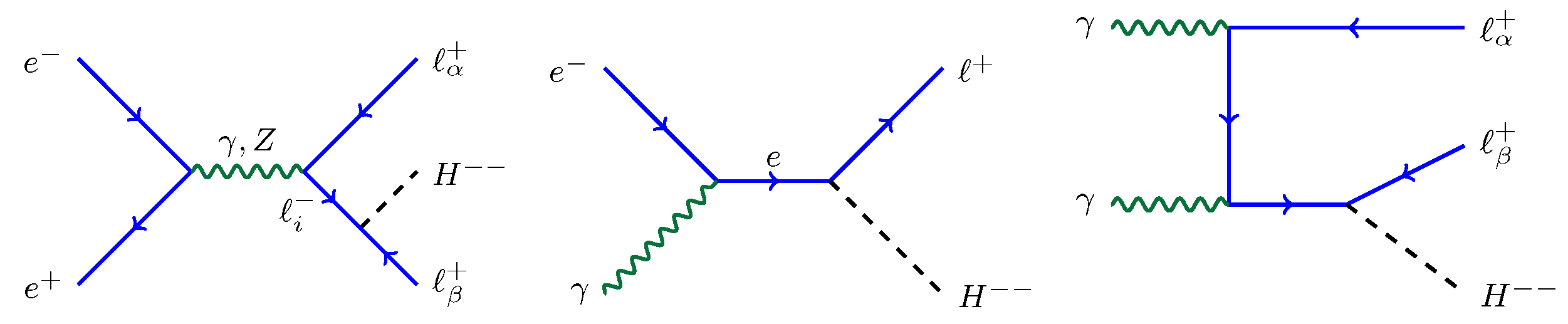
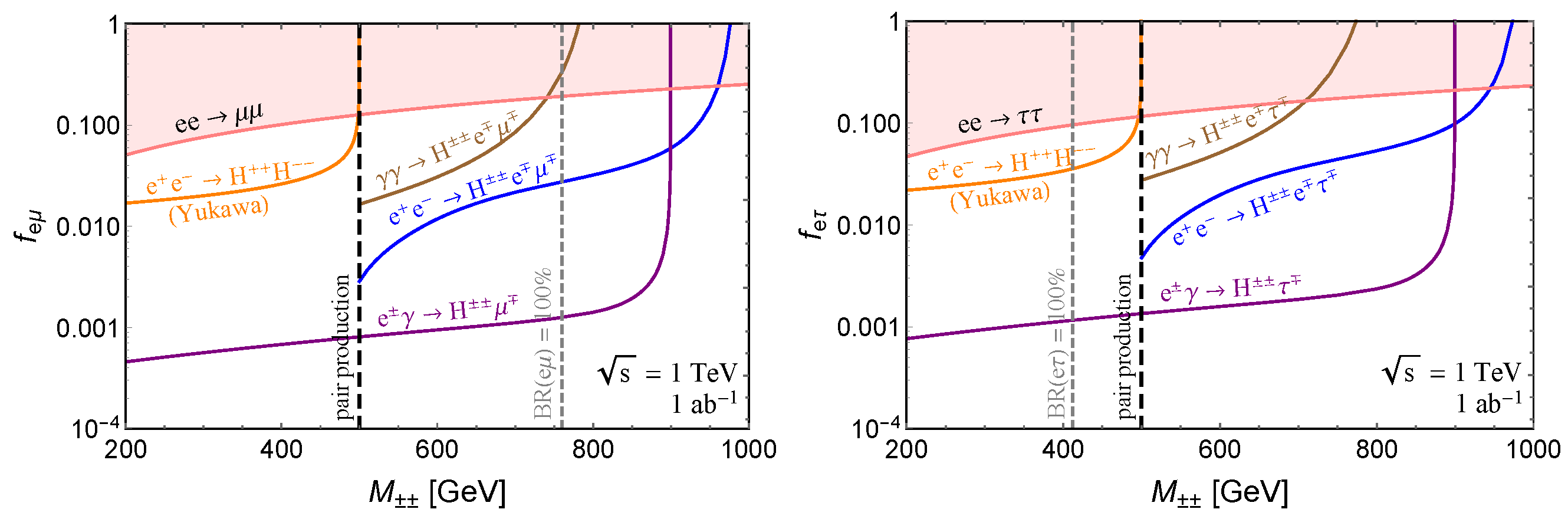
3. Doubly Charged Scalar
- The CLIC energy can go up to 3 TeV, and this will improve significantly the prospects of in both the on-shell and off-shell searches at future lepton colliders.
- The future muon collider will provide more channels for searches of LFV due to the doubly charged scalar, for instance in the processes . Furthermore, the muon collider can explore higher energy scales than the colliders [102].
- For sufficiently small couplings, the doubly charged scalar can be long-lived at the high-energy colliders, which is however largely model dependent. For instance, in some regions of parameter space in the type-II seesaw, the decays are suppressed, respectively, by the tiny active neutrinos and the small vacuum expectation value of the triplet (and the off-shell W bosons), which makes potentially long-lived [90]. The searches of long-lived doubly charged scalar is largely complementary to the searches of prompt signals from decay [103].
- As mentioned above, the doubly charged scalar can be produced at the high-energy colliders via the gauge interactions, e.g., the Drell–Yan process . At future high-energy hadron colliders, the doubly charged scalar can be probed to a higher mass than at the lepton colliders [104]. Though the LFV couplings can not be directly measured in these channels (unless the doubly charged scalar is long-lived at the colliders), the LFV signals at the hadron colliders are largely complementary to the signals in this section at the lepton colliders.
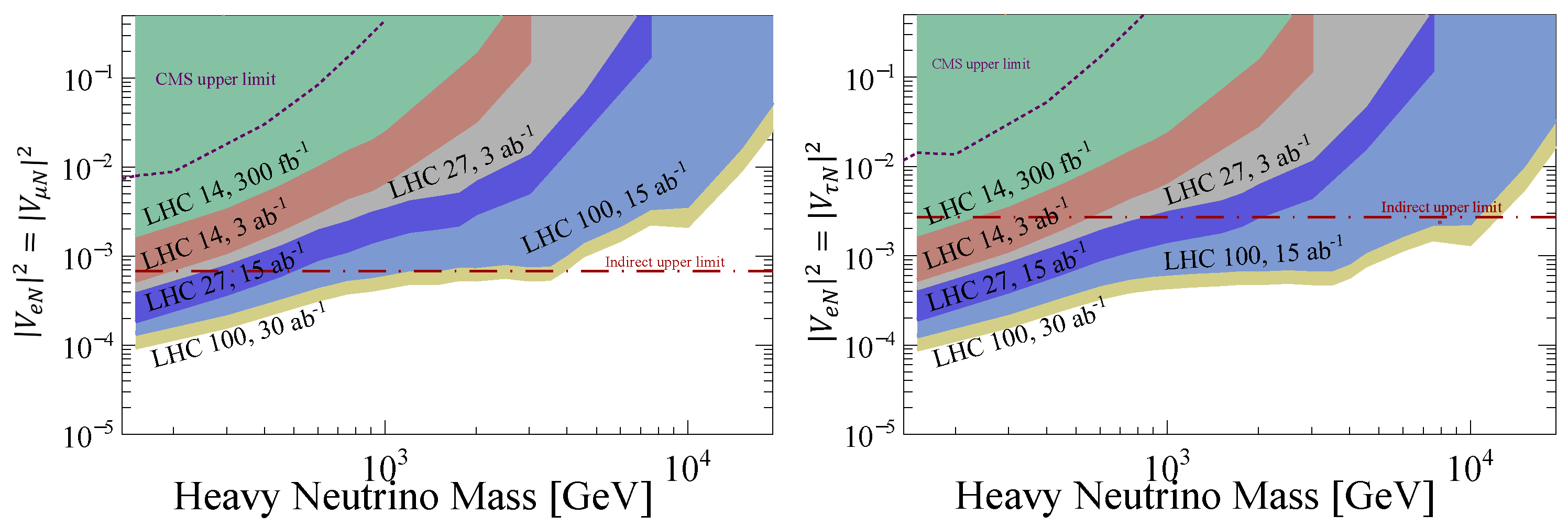
4. Heavy Neutrino
- At lower energies, the charged current Drell–Yan process in Equation (7) will “hadronize” to be semileptonic weak decays of charged mesons, i.e.,with the charged mesons. As at the high energy scale, the heavy neutrino N will induce LFV in meson decays if . LNV decays are also possible if N is a Majorana fermion. It is found that for the mass range of (with the masses of pions and Kaons), the most stringent limit on is from the decay leading to [136]. For (with the B meson mass), the strongest limit is from . In the process (8), if N is on-shell, it can be directly searched via the two-body meson decays, e.g., . The NA62 data have excluded to for MeV [137]. More processes can be found e.g., in Refs. [128,133].
- For neutral mesons , the heavy neutrino will induce LFV leptonic decays at the 1-loop level, i.e., [138]:which can be applied to the LFV leptonic decays of , , , and . Such LFV meson decays are all highly suppressed in the SM, and the mass and heavy-light neutrino mixing are tightly constrained by precision meson data. More details can be found e.g., in Refs. [136,138].
- In the charge lepton sector, if N mixes with two SM neutrino flavors, it will induce extra contribution to the LFV radiative decays of charged leptons and conversion in nuclei. It is found that the most stringent limit is from , which leads to for a 10 GeV N [128].
- For sufficiently light N, it could be long-lived at the high-energy colliders. The corresponding rich phenomenologies can be found e.g., in Refs. [132,133,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174].
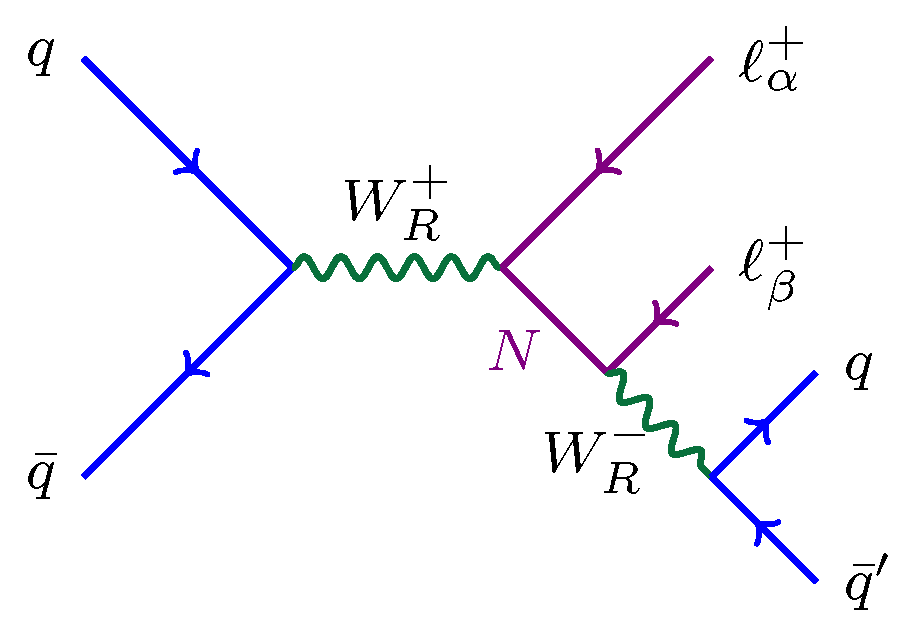
5. Heavy Boson
6. Boson
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
| 1 | |
| 2 | Note that without any details on the couplings of H to the active neutrinos the couplings in Equation (1) are not invariant with respect to the SM group. |
| 3 | |
| 4 | The lepton number of the doubly charged scalar is model dependent: for instance, has lepton number in the type-II seesaw, while in some other models its lepton number can be zero. |
| 5 | In the type-II seesaw, this is not a good approximation, as the leptonic branching fractions are largely determined by the PMNS neutrino mixing matrix, see e.g., Ref. [90]. |
| 6 | |
| 7 |
References
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Lindner, M.; Platscher, M.; Queiroz, F.S. A Call for New Physics: The Muon Anomalous Magnetic Moment and Lepton Flavor Violation. Phys. Rept. 2018, 731, 1–82. [Google Scholar] [CrossRef]
- Jaeckel, J.; Ringwald, A. The Low-Energy Frontier of Particle Physics. Ann. Rev. Nucl. Part. Sci. 2010, 60, 405–437. [Google Scholar] [CrossRef]
- Hewett, J.L.; Weerts, H.; Brock, R.; Butler, J.N.; Casey, B.C.K.; Collar, J.; de Gouvea, A.; Essig, R.; Grossman, Y.; Haxton, W.; et al. Fundamental Physics at the Intensity Frontier. arXiv 2012, arXiv:1205.2671. [Google Scholar]
- Essig, R.; Jaros, J.A.; Wester, W.; Hansson Adrian, P.; Andreas, S.; Averett, T.; Baker, O.; Batell, B.; Battaglieri, M.; Beacham, J.; et al. Working Group Report: New Light Weakly Coupled Particles. arXiv 2013, arXiv:1311.0029. [Google Scholar]
- Beacham, J.; Burrage, C.; Curtin, D.; De Roeck, A.; Evans, J.; Feng, J.L.; Gatto, C.; Gninenko, S.; Hartin, A.; Irastorza, I.; et al. Physics Beyond Colliders at CERN: Beyond the Standard Model Working Group Report. J. Phys. G 2020, 47, 010501. [Google Scholar] [CrossRef]
- Fileviez Perez, P. New Paradigm for Baryon and Lepton Number Violation. Phys. Rept. 2015, 597, 1–30. [Google Scholar] [CrossRef]
- Cai, Y.; Han, T.; Li, T.; Ruiz, R. Lepton Number Violation: Seesaw Models and Their Collider Tests. Front. Phys. 2018, 6, 40. [Google Scholar] [CrossRef]
- Algueró, M.; Capdevila, B.; Descotes-Genon, S.; Masjuan, P.; Matias, J. Are we overlooking lepton flavour universal new physics in b→sℓℓ ? Phys. Rev. D 2019, 99, 075017. [Google Scholar] [CrossRef]
- Datta, A.; Kumar, J.; London, D. The B anomalies and new physics in b→se+e−. Phys. Lett. B 2019, 797, 134858. [Google Scholar] [CrossRef]
- Kumar, J.; London, D. New physics in b→se+e−? Phys. Rev. D 2019, 99, 073008. [Google Scholar] [CrossRef]
- Hurth, T.; Mahmoudi, F.; Santos, D.M.; Neshatpour, S. More indications for lepton nonuniversality in b→sℓ+ℓ−. Phys. Lett. B 2022, 824, 136838. [Google Scholar] [CrossRef]
- London, D.; Matias, J. B Flavour Anomalies: 2021 Theoretical Status Report. arXiv 2021, arXiv:2110.13270. [Google Scholar]
- Aaij, R.; LHCb Collaboration. Test of lepton universality in beauty-quark decays. arXiv 2021, arXiv:hep-ex/2103.11769. [Google Scholar]
- Marciano, W.J.; Mori, T.; Roney, J.M. Charged Lepton Flavor Violation Experiments. Ann. Rev. Nucl. Part. Sci. 2008, 58, 315–341. [Google Scholar] [CrossRef]
- Bernstein, R.H.; Cooper, P.S. Charged Lepton Flavor Violation: An Experimenter’s Guide. Phys. Rept. 2013, 532, 27–64. [Google Scholar] [CrossRef]
- Calibbi, L.; Signorelli, G. Charged Lepton Flavour Violation: An Experimental and Theoretical Introduction. Riv. Nuovo Cim. 2018, 41, 71–174. [Google Scholar] [CrossRef]
- Heeck, J. Interpretation of Lepton Flavor Violation. Phys. Rev. D 2017, 95, 015022. [Google Scholar] [CrossRef]
- Hou, W.S.; Wong, G.G. μ+e−⇆μ−e+ transitions via neutral scalar bosons. Phys. Rev. D 1996, 53, 1537–1541. [Google Scholar] [CrossRef]
- Dev, P.S.B.; Mohapatra, R.N.; Zhang, Y. Lepton Flavor Violation Induced by a Neutral Scalar at Future Lepton Colliders. Phys. Rev. Lett. 2018, 120, 221804. [Google Scholar] [CrossRef]
- Li, T.; Schmidt, M.A. Sensitivity of future lepton colliders to the search for charged lepton flavor violation. Phys. Rev. D 2019, 99, 055038. [Google Scholar] [CrossRef]
- Arganda, E.; Marcano, X.; Mileo, N.I.; Morales, R.A.; Szynkman, A. Model-independent search strategy for the lepton-flavor-violating heavy Higgs boson decay to τμ at the LHC. Eur. Phys. J. C 2019, 79, 738. [Google Scholar] [CrossRef]
- Brignole, A.; Rossi, A. Anatomy and phenomenology of μ–τ lepton flavor violation in the MSSM. Nucl. Phys. B 2004, 701, 3–53. [Google Scholar] [CrossRef][Green Version]
- Harnik, R.; Kopp, J.; Zupan, J. Flavor Violating Higgs Decays. J. High Energy Phys. 2013, 3, 026. [Google Scholar] [CrossRef]
- Blankenburg, G.; Ellis, J.; Isidori, G. Flavour-Changing Decays of a 125 GeV Higgs-like Particle. Phys. Lett. B 2012, 712, 386–390. [Google Scholar] [CrossRef]
- Banerjee, S.; Bhattacherjee, B.; Mitra, M.; Spannowsky, M. The Lepton Flavour Violating Higgs Decays at the HL-LHC and the ILC. J. High Energy Phys. 2016, 7, 1–28. [Google Scholar] [CrossRef]
- Herrero-Garcia, J.; Rius, N.; Santamaria, A. Higgs lepton flavour violation: UV completions and connection to neutrino masses. J. High Energy Phys. 2016, 11, 1–45. [Google Scholar] [CrossRef]
- Chakraborty, I.; Datta, A.; Kundu, A. Lepton flavor violating Higgs boson decay h→μτ at the ILC. J. Phys. G 2016, 43, 125001. [Google Scholar] [CrossRef]
- Chakraborty, I.; Mondal, S.; Mukhopadhyaya, B. Lepton flavor violating Higgs boson decay at e+e− colliders. Phy. Rev. D 2017, 96, 115020. [Google Scholar] [CrossRef]
- Qin, Q.; Li, Q.; Lü, C.D.; Yu, F.S.; Zhou, S.H. Charged lepton flavor violating Higgs decays at future e+e− colliders. Eur. Phys. J. C 2018, 78, 835. [Google Scholar] [CrossRef]
- Lu, M.; Levin, A.M.; Li, C.; Agapitos, A.; Li, Q.; Meng, F.; Qian, S.; Xiao, J.; Yang, T. The physics case for an electron-muon collider. Adv. High Energy Phys. 2021, 2021, 6693618. [Google Scholar] [CrossRef]
- Arganda, E.; Herrero, M.J.; Marcano, X.; Weiland, C. Imprints of massive inverse seesaw model neutrinos in lepton flavor violating Higgs boson decays. Phys. Rev. D 2015, 91, 015001. [Google Scholar] [CrossRef]
- Arganda, E.; Herrero, M.J.; Marcano, X.; Weiland, C. Enhancement of the lepton flavor violating Higgs boson decay rates from SUSY loops in the inverse seesaw model. Phys. Rev. D 2016, 93, 055010. [Google Scholar] [CrossRef]
- Arganda, E.; Herrero, M.J.; Marcano, X.; Morales, R.; Szynkman, A. Effective lepton flavor violating Hℓiℓj vertex from right-handed neutrinos within the mass insertion approximation. Phys. Rev. D 2017, 95, 095029. [Google Scholar] [CrossRef]
- Marcano, X.; Morales, R.A. Flavor techniques for LFV processes: Higgs decays in a general seesaw model. Front. Phys. 2020, 7, 228. [Google Scholar] [CrossRef]
- Dev, P.S.B.; Mohapatra, R.N.; Zhang, Y. Probing the Higgs Sector of the Minimal Left-Right Symmetric Model at Future Hadron Colliders. J. High Energy Phys. 2016, 5, 174. [Google Scholar] [CrossRef]
- Maiezza, A.; Senjanović, G.; Vasquez, J.C. Higgs sector of the minimal left-right symmetric theory. Phys. Rev. D 2017, 95, 095004. [Google Scholar] [CrossRef]
- Bhupal Dev, P.S.; Mohapatra, R.N.; Zhang, Y. Displaced photon signal from a possible light scalar in minimal left-right seesaw model. Phys. Rev. D 2017, 95, 115001. [Google Scholar] [CrossRef]
- Dev, P.S.B.; Mohapatra, R.N.; Zhang, Y. Long Lived Light Scalars as Probe of Low Scale Seesaw Models. Nucl. Phys. B 2017, 923, 179–221. [Google Scholar] [CrossRef]
- Branco, G.C.; Ferreira, P.M.; Lavoura, L.; Rebelo, M.N.; Sher, M.; Silva, J.P. Theory and phenomenology of two-Higgs-doublet models. Phys. Rept. 2012, 516, 1–102. [Google Scholar] [CrossRef]
- Crivellin, A.; Kokulu, A.; Greub, C. Flavor-phenomenology of two-Higgs-doublet models with generic Yukawa structure. Phys. Rev. D 2013, 87, 094031. [Google Scholar] [CrossRef]
- Crivellin, A.; Heeck, J.; Stoffer, P. A perturbed lepton-specific two-Higgs-doublet model facing experimental hints for physics beyond the Standard Model. Phys. Rev. Lett. 2016, 116, 081801. [Google Scholar] [CrossRef] [PubMed]
- Aulakh, C.S.; Mohapatra, R.N. Neutrino as the Supersymmetric Partner of the Majoron. Phys. Lett. B 1982, 119, 136–140. [Google Scholar] [CrossRef]
- Hall, L.J.; Suzuki, M. Explicit R-Parity Breaking in Supersymmetric Models. Nucl. Phys. B 1984, 231, 419–444. [Google Scholar] [CrossRef]
- Ross, G.G.; Valle, J.W.F. Supersymmetric Models Without R-Parity. Phys. Lett. B 1985, 151, 375–381. [Google Scholar] [CrossRef]
- Barbier, R.; Berat, C.; Besancon, M.; Chemtob, M.; Deandrea, A.; Dudas, E.; Fayet, P.; Lavignac, S.; Moreau, G.; Perez, E.; et al. R-parity violating supersymmetry. Phys. Rept. 2005, 420, 1–202. [Google Scholar] [CrossRef]
- Hung, P.Q. A Model of electroweak-scale right-handed neutrino mass. Phys. Lett. B 2007, 649, 275–279. [Google Scholar] [CrossRef]
- Bu, J.P.; Liao, Y.; Liu, J.Y. Lepton Flavor Violating Muon Decays in a Model of Electroweak-Scale Right-Handed Neutrinos. Phys. Lett. B 2008, 665, 39–43. [Google Scholar] [CrossRef]
- Chang, C.F.; Chang, C.H.V.; Nugroho, C.S.; Yuan, T.C. Lepton Flavor Violating Decays of Neutral Higgses in Extended Mirror Fermion Model. Nucl. Phys. B 2016, 910, 293–308. [Google Scholar] [CrossRef][Green Version]
- Hung, P.Q.; Le, T.; Tran, V.Q.; Yuan, T.C. Muon-to-Electron Conversion in Mirror Fermion Model with Electroweak Scale Non-Sterile Right-handed Neutrinos. Nucl. Phys. B 2018, 932, 471–504. [Google Scholar] [CrossRef]
- Baer, H.; Barklow, T.; Fujii, K.; Gao, Y.; Hoang, A.; Kanemura, S.; List, J.; Logan, H.E.; Nomerotski, A.; Perelstein, M.; et al. The International Linear Collider Technical Design Report—Volume 2: Physics. arXiv 2013, arXiv:hep-ph/1306.6352. [Google Scholar]
- Ahmad, M.; Alves, D.; An, H.; An, Q.; Arhrib, A.; Arkani-Hamed, N.; Ahmed, I.; Bai, Y.; Ferroli, R.B.; Ban, Y.; et al. CEPC-SPPC Preliminary Conceptual Design Report 1. Physics and Detector. 2015. Available online: http://cepc.ihep.ac.cn/preCDR/main_preCDR.pdf (accessed on 1 March 2015).
- Bicer, M.; TLEP Design Study Working Group. First Look at the Physics Case of TLEP. J. High Energy Phys. 2014, 1, 164. [Google Scholar] [CrossRef]
- Accomando, E. CLIC Physics Working Group Physics at the CLIC multi-TeV linear collider. In Proceedings of the 11th International Conference on Hadron Spectroscopy, Rio de Janeiro, Brazil, 10 June 2005. [Google Scholar] [CrossRef]
- Willmann, L.; Schmidt, P.V.; Wirtz, H.P.; Abela, R.; Baranov, V.; Bagaturia, J.; Bertl, W.H.; Engfer, R.; Grossmann, A.; Hughes, V.W.; et al. New bounds from searching for muonium to anti-muonium conversion. Phys. Rev. Lett. 1999, 82, 49–52. [Google Scholar] [CrossRef]
- Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA Recommended Values of the Fundamental Physical Constants: 2014. Rev. Mod. Phys. 2016, 88, 035009. [Google Scholar] [CrossRef]
- Abdallah, J.; DELPHI Collaboration. Measurement and interpretation of fermion-pair production at LEP energies above the Z resonance. Eur. Phys. J. C 2006, 45, 589–632. [Google Scholar] [CrossRef]
- Bhupal Dev, P.S.; Mohapatra, R.N.; Zhang, Y. Probing TeV scale origin of neutrino mass at future lepton colliders via neutral and doubly-charged scalars. Phys. Rev. D 2018, 98, 075028. [Google Scholar] [CrossRef]
- Bennett, G.W.; Muon g-2 Collaboration. Final Report of the Muon E821 Anomalous Magnetic Moment Measurement at BNL. Phys. Rev. D 2006, 73, 072003. [Google Scholar] [CrossRef]
- Abi, B.; Muon g-2 Collaboration. Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm. Phys. Rev. Lett. 2021, 126, 141801. [Google Scholar] [CrossRef]
- Bellgardt, U.; SINDRUM Collaboration. Search for the Decay μ+→e+e+e−. Nucl. Phys. B 1988, 299, 1–6. [Google Scholar] [CrossRef]
- Kabachenko, V.V.; Pirogov, Y.F. Studying lepton family violation in lepton lepton collisions. Eur. Phys. J. C 1998, 4, 525–532. [Google Scholar] [CrossRef][Green Version]
- Cho, G.C.; Shimo, H. Search for lepton flavor violation at future lepton colliders. Mod. Phys. A 2017, 32, 1750127. [Google Scholar] [CrossRef]
- Ferreira, P.M.; Guedes, R.B.; Santos, R. Lepton flavour violating processes at the International Linear Collider. Phys. Rev. D 2007, 75, 055015. [Google Scholar] [CrossRef]
- Aranda, J.I.; Flores-Tlalpa, A.; Ramirez-Zavaleta, F.; Tlachino, F.J.; Toscano, J.J.; Tututi, E.S. Effective Lagrangian description of Higgs mediated flavor violating electromagnetic transitions: Implications on lepton flavor violation. Phys. Rev. D 2009, 79, 093009. [Google Scholar] [CrossRef]
- Murakami, B.; Tait, T.M.P. Searching for lepton flavor violation at a future high energy e+e− collider. Phys. Rev. D 2015, 91, 015002. [Google Scholar] [CrossRef]
- Calibbi, L.; Marcano, X.; Roy, J. Z lepton flavour violation as a probe for new physics at future e+e− colliders. Eur. Phys. J. C 2021, 81, 1054. [Google Scholar] [CrossRef]
- Hayasaka, K.; Belle collaboration. Search for Lepton Flavor Violating Tau Decays into Three Leptons with 719 Million Produced Tau+Tau- Pairs. Phys. Lett. B 2010, 687, 139–143. [Google Scholar] [CrossRef]
- Ginzburg, I.F.; Kotkin, G.L.; Serbo, V.G.; Telnov, V.I. Colliding gamma e and gamma gamma Beams Based on the Single Pass Accelerators (of Vlepp Type). Nucl. Instrum. Meth. 1983, 205, 47–68. [Google Scholar] [CrossRef]
- Ginzburg, I.F.; Kotkin, G.L.; Panfil, S.L.; Serbo, V.G.; Telnov, V.I. Colliding gamma e and gamma gamma Beams Based on the Single Pass e+e− Accelerators. 2. Polarization Effects. Monochromatization Improvement. Nucl. Instrum. Meth. A 1984, 219, 5–24. [Google Scholar] [CrossRef]
- Telnov, V.I. Problems of Obtaining γγ and γϵ Colliding Beams at Linear Colliders. Nucl. Instrum. Meth. A 1990, 294, 72–92. [Google Scholar] [CrossRef]
- Capdevilla, R.; Curtin, D.; Kahn, Y.; Krnjaic, G. Discovering the physics of (g-2)μ at future muon colliders. Phys. Rev. D 2021, 103, 075028. [Google Scholar] [CrossRef]
- Iguro, S.; Mohan, K.A.; Yuan, C.P. Detecting a μτ-philic Z’ boson via photon initiated processes at the LHC. Phys. Rev. D 2020, 101, 075011. [Google Scholar] [CrossRef]
- Magg, M.; Wetterich, C. Neutrino Mass Problem and Gauge Hierarchy. Phys. Lett. B 1980, 94, 61–64. [Google Scholar] [CrossRef]
- Schechter, J.; Valle, J.W.F. Neutrino Masses in SU(2) × U(1) Theories. Phys. Rev. D 1980, 22, 2227. [Google Scholar] [CrossRef]
- Cheng, T.P.; Li, L.F. Neutrino Masses, Mixings and Oscillations in SU(2) × U(1) Models of Electroweak Interactions. Phys. Rev. D 1980, 22, 2860. [Google Scholar] [CrossRef]
- Lazarides, G.; Shafi, Q.; Wetterich, C. Proton Lifetime and Fermion Masses in an SO(10) Model. Nucl. Phys. B 1981, 181, 287–300. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Senjanovic, G. Neutrino Masses and Mixings in Gauge Models with Spontaneous Parity Violation. Phys. Rev. D 1981, 23, 165. [Google Scholar] [CrossRef]
- Pati, J.C.; Salam, A. Lepton Number as the Fourth Color. Phys. Rev. D 1974, 10, 275–289, Erratum: Phys. Rev. D 1975, 11, 703–703. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Pati, J.C. A Natural Left-Right Symmetry. Phys. Rev. D 1975, 11, 2558. [Google Scholar] [CrossRef]
- Senjanovic, G.; Mohapatra, R.N. Exact Left-Right Symmetry and Spontaneous Violation of Parity. Phys. Rev. D 1975, 12, 1502. [Google Scholar] [CrossRef]
- Babu, K.S. Model of ‘Calculable’ Majorana Neutrino Masses. Phys. Lett. B 1988, 203, 132–136. [Google Scholar] [CrossRef]
- Crivellin, A.; Ghezzi, M.; Panizzi, L.; Pruna, G.M.; Signer, A. Low- and high-energy phenomenology of a doubly charged scalar. Phys. Rev. D 2019, 99, 035004. [Google Scholar] [CrossRef]
- Aaboud, M.; ATLAS Collaboration. Search for doubly charged Higgs boson production in multi-lepton final states with the ATLAS detector using proton–proton collisions at = 13 TeV. Eur. Phys. J. C 2018, 78, 199. [Google Scholar] [CrossRef] [PubMed]
- CMS Collaboration. A search for doubly-charged Higgs boson production in three and four lepton final states at = 13 TeV, CMS-PAS-HIG-16-036. 2017. Available online: http://cds.cern.ch/record/2242956 (accessed on 25 January 2017).
- Aaboud, M.; ATLAS Collaboration. Search for doubly charged scalar bosons decaying into same-sign W boson pairs with the ATLAS detector. Eur. Phys. J. C 2019, 79, 58. [Google Scholar] [CrossRef] [PubMed]
- Aad, G.; ATLAS Collaboration. Search for doubly and singly charged Higgs bosons decaying into vector bosons in multi-lepton final states with the ATLAS detector using proton-proton collisions at = 13 TeV. J. High Energy Phys. 2021, 6, 146. [Google Scholar] [CrossRef]
- Rizzo, T.G. Doubly Charged Higgs Bosons and Lepton Number Violating Processes. Phys. Rev. D 1982, 25, 1355–1364, Addendum: Phys. Rev. D 1983, 27, 657–659. [Google Scholar] [CrossRef]
- Akeroyd, A.G.; Aoki, M. Single and pair production of doubly charged Higgs bosons at hadron colliders. Phys. Rev. D 2005, 72, 035011. [Google Scholar] [CrossRef]
- Fileviez Perez, P.; Han, T.; Huang, G.Y.; Li, T.; Wang, K. Neutrino Masses and the CERN LHC: Testing Type II Seesaw. Phys. Rev. D 2008, 78, 015018. [Google Scholar] [CrossRef]
- Ferreira, M.M.; de Melo, T.B.; Kovalenko, S.; Pinheiro, P.R.D.; Queiroz, F.S. Lepton Flavor Violation and Collider Searches in a Type I + II Seesaw Model. Eur. Phys. J. C 2019, 79, 955. [Google Scholar] [CrossRef]
- de Melo, T.B.; Queiroz, F.S.; Villamizar, Y. Doubly Charged Scalar at the High-Luminosity and High-Energy LHC. Int. J. Mod. Phys. A 2019, 34, 1950157. [Google Scholar] [CrossRef]
- Padhan, R.; Das, D.; Mitra, M.; Kumar Nayak, A. Probing doubly and singly charged Higgs bosons at the pp collider HE-LHC. Phys. Rev. D 2020, 101, 075050. [Google Scholar] [CrossRef]
- Fuks, B.; Nemevšek, M.; Ruiz, R. Doubly Charged Higgs Boson Production at Hadron Colliders. Phys. Rev. D 2020, 101, 075022. [Google Scholar] [CrossRef]
- Gluza, J.; Kordiaczynska, M.; Srivastava, T. Discriminating the HTM and MLRSM models in collider studies via doubly charged Higgs boson pair production and the subsequent leptonic decays. Chin. Phys. C 2021, 45, 073113. [Google Scholar] [CrossRef]
- Ashanujjaman, S.; Ghosh, K. Revisiting Type-II see-saw: Present Limits and Future Prospects at LHC. arXiv 2021, arXiv:hep-ph/2108.10952. [Google Scholar]
- Lusignoli, M.; Petrarca, S. Exotic Higgs Production AT E+ E− Colliders. Phys. Lett. B 1989, 226, 397–400. [Google Scholar] [CrossRef]
- Barenboim, G.; Huitu, K.; Maalampi, J.; Raidal, M. Constraints on doubly charged Higgs interactions at linear collider. Phys. Lett. B 1997, 394, 132–138. [Google Scholar] [CrossRef]
- Kuze, M.; Sirois, Y. Search for particles and forces beyond the standard model at HERA ep and Tevatron p colliders. Prog. Part. Nucl. Phys. 2003, 50, 1–62, Erratum: Prog. Part. Nucl. Phys. 2004, 53, 583–677. [Google Scholar] [CrossRef]
- Yue, C.X.; Zhao, S. Lepton flavor violating signals of a little Higgs model at the high energy linear e+e− colliders. Eur. Phys. J. C 2007, 50, 897–903. [Google Scholar] [CrossRef]
- Yue, C.X.; Zhao, S.; Ma, W. Single production of the doubly charged scalar in the littlest Higgs model. Nucl. Phys. B 2007, 784, 36–48. [Google Scholar] [CrossRef][Green Version]
- Delahaye, J.P.; Diemoz, M.; Long, K.; Mansoulié, B.; Pastrone, N.; Rivkin, L.; Schulte, D.; Skrinsky, A.; Wulzer, A. Muon Colliders. arXiv 2019, arXiv:physics.acc-ph/1901.06150. [Google Scholar]
- Bhupal Dev, P.S.; Zhang, Y. Displaced vertex signatures of doubly charged scalars in the type-II seesaw and its left-right extensions. J. High Energy Phys. 2018, 10, 199. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Han, T.; Mangano, M.; Wang, L.T. Physics opportunities of a 100 TeV proton–proton collider. Phys. Rept. 2016, 652, 1–49. [Google Scholar] [CrossRef]
- Minkowski, P. μ→eγ at a Rate of One Out of 109 Muon Decays? Phys. Lett. B 1977, 67, 421–428. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Senjanovic, G. Neutrino Mass and Spontaneous Parity Nonconservation. Phys. Rev. Lett. 1980, 44, 912. [Google Scholar] [CrossRef]
- Yanagida, T. Horizontal gauge symmetry and masses of neutrinos. Conf. Proc. C 1979, 7902131, 95–99. [Google Scholar]
- Gell-Mann, M.; Ramond, P.; Slansky, R. Complex Spinors and Unified Theories. Conf. Proc. C 1979, 790927, 315–321. [Google Scholar]
- Glashow, S.L. The Future of Elementary Particle Physics. NATO Sci. Ser. B 1980, 61, 687. [Google Scholar] [CrossRef]
- Mohapatra, R.N. Mechanism for Understanding Small Neutrino Mass in Superstring Theories. Phys. Rev. Lett. 1986, 56, 561–563. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Valle, J.W.F. Neutrino Mass and Baryon Number Nonconservation in Superstring Models. Phys. Rev. D 1986, 34, 1642. [Google Scholar] [CrossRef]
- Bernabeu, J.; Santamaria, A.; Vidal, J.; Mendez, A.; Valle, J.W.F. Lepton Flavor Nonconservation at High-Energies in a Superstring Inspired Standard Model. Phys. Lett. B 1987, 187, 303–308. [Google Scholar] [CrossRef]
- Keung, W.Y.; Senjanovic, G. Majorana Neutrinos and the Production of the Right-handed Charged Gauge Boson. Phys. Rev. Lett. 1983, 50, 1427. [Google Scholar] [CrossRef]
- Datta, A.; Guchait, M.; Pilaftsis, A. Probing lepton number violation via majorana neutrinos at hadron supercolliders. Phys. Rev. D 1994, 50, 3195–3203. [Google Scholar] [CrossRef] [PubMed]
- Dev, P.S.B.; Pilaftsis, A.; Yang, U.K. New Production Mechanism for Heavy Neutrinos at the LHC. Phys. Rev. Lett. 2014, 112, 081801. [Google Scholar] [CrossRef]
- Alva, D.; Han, T.; Ruiz, R. Heavy Majorana neutrinos from Wγ fusion at hadron colliders. J. High Energy Phys. 2015, 2, 072. [Google Scholar] [CrossRef]
- Degrande, C.; Mattelaer, O.; Ruiz, R.; Turner, J. Fully-Automated Precision Predictions for Heavy Neutrino Production Mechanisms at Hadron Colliders. Phys. Rev. D 2016, 94, 053002. [Google Scholar] [CrossRef]
- Dicus, D.A.; Karatas, D.D.; Roy, P. Lepton nonconservation at supercollider energies. Phys. Rev. D 1991, 44, 2033–2037. [Google Scholar] [CrossRef] [PubMed]
- Fuks, B.; Neundorf, J.; Peters, K.; Ruiz, R.; Saimpert, M. Majorana neutrinos in same-sign W±W± scattering at the LHC: Breaking the TeV barrier. Phys. Rev. D 2021, 103, 055005. [Google Scholar] [CrossRef]
- Willenbrock, S.S.D.; Dicus, D.A. Production of Heavy Leptons From Gluon Fusion. Phys. Lett. B 1985, 156, 429–433. [Google Scholar] [CrossRef]
- Dicus, D.A.; Roy, P. Supercollider signatures and correlations of heavy neutrinos. Phys. Rev. D 1991, 44, 1593–1596. [Google Scholar] [CrossRef]
- Hessler, A.G.; Ibarra, A.; Molinaro, E.; Vogl, S. Impact of the Higgs boson on the production of exotic particles at the LHC. Phys. Rev. D 2015, 91, 115004. [Google Scholar] [CrossRef]
- Ruiz, R.; Spannowsky, M.; Waite, P. Heavy neutrinos from gluon fusion. Phys. Rev. D 2017, 96, 055042. [Google Scholar] [CrossRef]
- Pascoli, S.; Ruiz, R.; Weiland, C. Heavy neutrinos with dynamic jet vetoes: Multilepton searches at = 14, 27, and 100 TeV. J. High Energy Phys. 2019, 6, 049. [Google Scholar] [CrossRef]
- Arganda, E.; Herrero, M.J.; Marcano, X.; Weiland, C. Exotic μτjj events from heavy ISS neutrinos at the LHC. Phys. Lett. B 2016, 752, 46–50. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; CMS Collaboration. Search for heavy neutral leptons in events with three charged leptons in proton-proton collisions at = 13 TeV. Phys. Rev. Lett. 2018, 120, 221801. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Martinez, E.; Hernandez-Garcia, J.; Lopez-Pavon, J. Global constraints on heavy neutrino mixing. J. High Energy Phys. 2016, 8, 033. [Google Scholar] [CrossRef]
- Bolton, P.D.; Deppisch, F.F.; Bhupal Dev, P.S. Neutrinoless double beta decay versus other probes of heavy sterile neutrinos. J. High Energy Phys. 2020, 3, 170. [Google Scholar] [CrossRef]
- Aad, G.; ATLAS Collaboration. Search for heavy neutral leptons in decays of W bosons produced in 13 TeV pp collisions using prompt and displaced signatures with the ATLAS detector. J. High Energy Phys. 2019, 10, 265. [Google Scholar] [CrossRef]
- Tumasyan, A.; CMS Collaboration. Search for long-lived heavy neutral leptons with displaced vertices in proton-proton collisions at = 13 TeV. arXiv 2022, arXiv:hep-ex/2201.05578. [Google Scholar]
- Atre, A.; Han, T.; Pascoli, S.; Zhang, B. The Search for Heavy Majorana Neutrinos. J. High Energy Phys. 2009, 5, 030. [Google Scholar] [CrossRef]
- Cottin, G.; Helo, J.C.; Hirsch, M. Displaced vertices as probes of sterile neutrino mixing at the LHC. Phys. Rev. D 2018, 98, 035012. [Google Scholar] [CrossRef]
- Coloma, P.; Fernández-Martínez, E.; González-López, M.; Hernández-García, J.; Pavlovic, Z. GeV-scale neutrinos: Interactions with mesons and DUNE sensitivity. Eur. Phys. J. C 2021, 81, 78. [Google Scholar] [CrossRef]
- De Vries, J.; Dreiner, H.K.; Günther, J.Y.; Wang, Z.S.; Zhou, G. Long-lived Sterile Neutrinos at the LHC in Effective Field Theory. J. High Energy Phys. 2021, 3, 148. [Google Scholar] [CrossRef]
- Zhou, G.; Günther, J.Y.; Wang, Z.S.; de Vries, J.; Dreiner, H.K. Long-lived Sterile Neutrinos at Belle II in Effective Field Theory. arXiv 2021, arXiv:hep-ph/2111.04403. [Google Scholar]
- Hu, S.; Wong, S.M.Y.; Xu, F. Probing Sterile Neutrino via Lepton Flavor Violating Decays of Mesons. arXiv 2019, arXiv:hep-ph/1904.00568. [Google Scholar]
- Cortina Gil, E.; NA62 Collaboration. Search for heavy neutral lepton production in K+ decays. Phys. Lett. B 2018, 778, 137–145. [Google Scholar] [CrossRef]
- Ilakovac, A. Lepton flavor violation in the standard model extended by heavy singlet Dirac neutrinos. Phys. Rev. D 2000, 62, 036010. [Google Scholar] [CrossRef]
- Helo, J.C.; Hirsch, M.; Kovalenko, S. Heavy neutrino searches at the LHC with displaced vertices. Phys. Rev. D 2014, 89, 073005, Erratum: Phys. Rev. D 2016, 93, 099902. [Google Scholar] [CrossRef]
- Izaguirre, E.; Shuve, B. Multilepton and Lepton Jet Probes of Sub-Weak-Scale Right-Handed Neutrinos. Phys. Rev. D 2015, 91, 093010. [Google Scholar] [CrossRef]
- Dube, S.; Gadkari, D.; Thalapillil, A.M. Lepton-Jets and Low-Mass Sterile Neutrinos at Hadron Colliders. Phys. Rev. D 2017, 96, 055031. [Google Scholar] [CrossRef]
- Dib, C.O.; Kim, C.S.; Neill, N.A.; Yuan, X.B. Search for sterile neutrinos decaying into pions at the LHC. Phys. Rev. D 2018, 97, 035022. [Google Scholar] [CrossRef]
- Gago, A.M.; Hernández, P.; Jones-Pérez, J.; Losada, M.; Moreno Briceño, A. Probing the Type I Seesaw Mechanism with Displaced Vertices at the LHC. Eur. Phys. J. C 2015, 75, 470. [Google Scholar] [CrossRef]
- Accomando, E.; Delle Rose, L.; Moretti, S.; Olaiya, E.; Shepherd-Themistocleous, C.H. Novel SM-like Higgs decay into displaced heavy neutrino pairs in U(1)’ models. J. High Energy Phys. 2017, 4, 081. [Google Scholar] [CrossRef]
- Caputo, A.; Hernandez, P.; Lopez-Pavon, J.; Salvado, J. The seesaw portal in testable models of neutrino masses. J. High Energy Phys. 2017, 6, 112. [Google Scholar] [CrossRef]
- Deppisch, F.F.; Liu, W.; Mitra, M. Long-lived Heavy Neutrinos from Higgs Decays. J. High Energy Phys. 2018, 8, 181. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Z.; Wang, L.T. Enhancing Long-Lived Particles Searches at the LHC with Precision Timing Information. Phys. Rev. Lett. 2019, 122, 131801. [Google Scholar] [CrossRef]
- Antusch, S.; Cazzato, E.; Fischer, O. Sterile neutrino searches via displaced vertices at LHCb. Phys. Lett. B 2017, 774, 114–118. [Google Scholar] [CrossRef]
- Kling, F.; Trojanowski, S. Heavy Neutral Leptons at FASER. Phys. Rev. D 2018, 97, 095016. [Google Scholar] [CrossRef]
- Helo, J.C.; Hirsch, M.; Wang, Z.S. Heavy neutral fermions at the high-luminosity LHC. J. High Energy Phys. 2018, 7, 056. [Google Scholar] [CrossRef]
- Jana, S.; Okada, N.; Raut, D. Displaced vertex signature of type-I seesaw model. Phys. Rev. D 2018, 98, 035023. [Google Scholar] [CrossRef]
- Caputo, A.; Hernandez, P.; Kekic, M.; López-Pavón, J.; Salvado, J. The seesaw path to leptonic CP violation. Eur. Phys. J. C 2017, 77, 258. [Google Scholar] [CrossRef]
- Blondel, A.; Graverini, E.; Serra, N.; Shaposhnikov, M. Search for Heavy Right Handed Neutrinos at the FCC-ee. Nucl. Part. Phys. Proc. 2016, 273-275, 1883–1890. [Google Scholar] [CrossRef]
- Antusch, S.; Cazzato, E.; Fischer, O. Displaced vertex searches for sterile neutrinos at future lepton colliders. J. High Energy Phys. 2016, 12, 007. [Google Scholar] [CrossRef]
- Bonivento, W.; Boyarsky, A.; Dijkstra, H.; Egede, U.; Ferro-Luzzi, M.; Goddard, B.; Golutvin, A.; Gorbunov, D.; Jacobsson, R.; Panman, J.; et al. Proposal to Search for Heavy Neutral Leptons at the SPS. arXiv 2013, arXiv:hep-ex/1310.1762. [Google Scholar]
- Abada, A.; Bernal, N.; Losada, M.; Marcano, X. Inclusive Displaced Vertex Searches for Heavy Neutral Leptons at the LHC. J. High Energy Phys. 2019, 1, 093. [Google Scholar] [CrossRef]
- Abada, A.; De Romeri, V.; Monteil, S.; Orloff, J.; Teixeira, A.M. Indirect searches for sterile neutrinos at a high-luminosity Z-factory. J. High Energy Phys. 2015, 4, 051. [Google Scholar] [CrossRef]
- Antusch, S.; Cazzato, E.; Drewes, M.; Fischer, O.; Garbrecht, B.; Gueter, D.; Klaric, J. Probing Leptogenesis at Future Colliders. J. High Energy Phys. 2018, 9, 124. [Google Scholar] [CrossRef]
- Hernández, P.; Jones-Pérez, J.; Suarez-Navarro, O. Majorana vs Pseudo-Dirac Neutrinos at the ILC. Eur. Phys. J. C 2019, 79, 220. [Google Scholar] [CrossRef]
- Abada, A.; Arcadi, G.; Domcke, V.; Drewes, M.; Klaric, J.; Lucente, M. Low-scale leptogenesis with three heavy neutrinos. J. High Energy Phys. 2019, 1, 164. [Google Scholar] [CrossRef]
- Boiarska, I.; Bondarenko, K.; Boyarsky, A.; Eijima, S.; Ovchynnikov, M.; Ruchayskiy, O.; Timiryasov, I. Probing baryon asymmetry of the Universe at LHC and SHiP. arXiv 2019, arXiv:hep-ph/1902.04535. [Google Scholar]
- Lavignac, S.; Medina, A.D. Displaced Vertex signatures of a pseudo-Goldstone sterile neutrino. J. High Energy Phys. 2021, 1, 151. [Google Scholar] [CrossRef]
- Dib, C.O.; Kim, C.S.; Tapia Araya, S. Search for light sterile neutrinos from W± decays at the LHC. Phys. Rev. D 2020, 101, 035022. [Google Scholar] [CrossRef]
- Drewes, M.; Hajer, J. Heavy Neutrinos in displaced vertex searches at the LHC and HL-LHC. J. High Energy Phys. 2020, 2, 070. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Z.; Wang, L.T.; Wang, X.P. Seeking for sterile neutrinos with displaced leptons at the LHC. J. High Energy Phys. 2019, 7, 159. [Google Scholar] [CrossRef]
- Das, A.; Dev, P.S.B.; Okada, N. Long-lived TeV-scale right-handed neutrino production at the LHC in gauged U(1)X model. Phys. Lett. B 2019, 799, 135052. [Google Scholar] [CrossRef]
- Drewes, M.; Giammanco, A.; Hajer, J.; Lucente, M. New long-lived particle searches in heavy-ion collisions at the LHC. Phys. Rev. D 2020, 101, 055002. [Google Scholar] [CrossRef]
- Chiang, C.W.; Cottin, G.; Das, A.; Mandal, S. Displaced heavy neutrinos from Z′ decays at the LHC. J. High Energy Phys. 2019, 12, 070. [Google Scholar] [CrossRef]
- Dib, C.O.; Helo, J.C.; Nayak, M.; Neill, N.A.; Soffer, A.; Zamora-Saa, J. Searching for a sterile neutrino that mixes predominantly with ντ at B factories. Phys. Rev. D 2020, 101, 093003. [Google Scholar] [CrossRef]
- Jones-Pérez, J.; Masias, J.; Ruiz-Álvarez, J.D. Search for Long-Lived Heavy Neutrinos at the LHC with a VBF Trigger. Eur. Phys. J. C 2020, 80, 642. [Google Scholar] [CrossRef]
- Barducci, D.; Bertuzzo, E.; Caputo, A.; Hernandez, P.; Mele, B. The see-saw portal at future Higgs Factories. J. High Energy Phys. 2021, 3, 117. [Google Scholar] [CrossRef]
- Borsato, M.; Cid Vidal, X.; Tsai, Y.; Vázquez Sierra, C.; Zurita, J.; Alonso-Álvarez, G.; Boyarsky, A.; Brea Rodríguez, A.; Buarque Franzosi, D.; Cacciapaglia, G.; et al. Unleashing the full power of LHCb to probe Stealth New Physics. arXiv 2021, arXiv:hep-ph/2105.12668. [Google Scholar] [CrossRef]
- Tastet, J.L.; Ruchayskiy, O.; Timiryasov, I. Reinterpreting the ATLAS bounds on heavy neutral leptons in a realistic neutrino oscillation model. J. High Energy Phys. 2021, 12, 182. [Google Scholar] [CrossRef]
- Liu, W.; Kulkarni, S.; Deppisch, F.F. Heavy Neutrinos at the FCC-hh in the U(1)B–L Model. arXiv 2022, arXiv:hep-ph/2202.07310. [Google Scholar]
- Bray, S.; Lee, J.S.; Pilaftsis, A. Resonant CP violation due to heavy neutrinos at the LHC. Nucl. Phys. B 2007, 786, 95–118. [Google Scholar] [CrossRef]
- Tapia, S.; Vidal-Bravo, M.; Zamora-Saa, J. Discovering heavy neutrino oscillations in rare meson decays at HL-LHCb. arXiv 2021, arXiv:hep-ph/2109.06027. [Google Scholar] [CrossRef]
- Cvetič, G.; Kim, C.S.; Zamora-Saá, J. CP violation in the rare Higgs decays via exchange of on-shell almost degenerate Majorana neutrinos, H→νkNj→νkℓ−U and H→νkNj→νkℓ+D. arXiv 2021, arXiv:hep-ph/2110.08799. [Google Scholar]
- Abada, A.; Hati, C.; Marcano, X.; Teixeira, A.M. Interference effects in LNV and LFV semileptonic decays: The Majorana hypothesis. J. High Energy Phys. 2019, 9, 017. [Google Scholar] [CrossRef]
- Tumasyan, A.; CMS Collaboration. Search for a right-handed W boson and a heavy neutrino in proton-proton collisions at = 13 TeV. arXiv 2021, arXiv:hep-ex/2112.03949. [Google Scholar]
- Nemevšek, M.; Nesti, F.; Popara, G. Keung-Senjanović process at the LHC: From lepton number violation to displaced vertices to invisible decays. Phys. Rev. D 2018, 97, 115018. [Google Scholar] [CrossRef]
- Chauhan, G.; Dev, P.S.B.; Mohapatra, R.N.; Zhang, Y. Perturbativity constraints on U(1)B–L and left-right models and implications for heavy gauge boson searches. J. High Energy Phys. 2019, 1, 208. [Google Scholar] [CrossRef]
- Mitra, M.; Ruiz, R.; Scott, D.J.; Spannowsky, M. Neutrino Jets from High-Mass WR Gauge Bosons in TeV-Scale Left-Right Symmetric Models. Phys. Rev. D 2016, 94, 095016. [Google Scholar] [CrossRef]
- Ferrari, A.; Collot, J.; Andrieux, M.L.; Belhorma, B.; de Saintignon, P.; Hostachy, J.Y.; Martin, P.; Wielers, M. Sensitivity study for new gauge bosons and right-handed Majorana neutrinos in pp collisions at s = 14-TeV. Phys. Rev. D 2000, 62, 013001. [Google Scholar] [CrossRef]
- Aaboud, M.; ATLAS Collaboration. Search for heavy Majorana or Dirac neutrinos and right-handed W gauge bosons in final states with two charged leptons and two jets at = 13 TeV with the ATLAS detector. J. High Energy Phys. 2019, 1, 016. [Google Scholar] [CrossRef]
- Aaboud, M.; ATLAS Collaboration. Search for a right-handed gauge boson decaying into a high-momentum heavy neutrino and a charged lepton in pp collisions with the ATLAS detector at = 13 TeV. Phys. Lett. B 2019, 798, 134942. [Google Scholar] [CrossRef]
- Maiezza, A.; Nemevšek, M.; Nesti, F. Lepton Number Violation in Higgs Decay at LHC. Phys. Rev. Lett. 2015, 115, 081802. [Google Scholar] [CrossRef]
- Nemevšek, M.; Nesti, F.; Vasquez, J.C. Majorana Higgses at colliders. J. High Energy Phys. 2017, 4, 114. [Google Scholar] [CrossRef]
- Cottin, G.; Helo, J.C.; Hirsch, M. Searches for light sterile neutrinos with multitrack displaced vertices. Phys. Rev. D 2018, 97, 055025. [Google Scholar] [CrossRef]
- Cottin, G.; Helo, J.C.; Hirsch, M.; Silva, D. Revisiting the LHC reach in the displaced region of the minimal left-right symmetric model. Phys. Rev. D 2019, 99, 115013. [Google Scholar] [CrossRef]
- Langacker, P.; Plumacher, M. Flavor changing effects in theories with a heavy Z′ boson with family nonuniversal couplings. Phys. Rev. D 2000, 62, 013006. [Google Scholar] [CrossRef]
- Langacker, P. The Physics of Heavy Z′ Gauge Bosons. Rev. Mod. Phys. 2009, 81, 1199–1228. [Google Scholar] [CrossRef]
- del Aguila, F.; de Blas, J.; Perez-Victoria, M. Electroweak Limits on General New Vector Bosons. J. High Energy Phys. 2010, 9, 033. [Google Scholar] [CrossRef]
- de Blas, J.; Lizana, J.M.; Perez-Victoria, M. Combining searches of Z’ and W’ bosons. J. High Energy Phys. 2013, 1, 166. [Google Scholar] [CrossRef]
- Accomando, E.; Becciolini, D.; Belyaev, A.; Moretti, S.; Shepherd-Themistocleous, C. Z′ at the LHC: Interference and Finite Width Effects in Drell-Yan. J. High Energy Phys. 2013, 10, 153. [Google Scholar] [CrossRef]
- Jezo, T.; Klasen, M.; Lamprea, D.R.; Lyonnet, F.; Schienbein, I. NLO+NLL limits on W′ and Z′ gauge boson masses in general extensions of the Standard Model. J. High Energy Phys. 2014, 12, 092. [Google Scholar] [CrossRef]
- Accomando, E.; Coriano, C.; Delle Rose, L.; Fiaschi, J.; Marzo, C.; Moretti, S. Z′, Higgses and heavy neutrinos in U(1)′ models: From the LHC to the GUT scale. J. High Energy Phys. 2016, 7, 086. [Google Scholar] [CrossRef]
- Deppisch, F.; Kulkarni, S.; Liu, W. Heavy neutrino production via Z′ at the lifetime frontier. Phys. Rev. D 2019, 100, 035005. [Google Scholar] [CrossRef]
- Buras, A.J.; Crivellin, A.; Kirk, F.; Manzari, C.A.; Montull, M. Global analysis of leptophilic Z’ bosons. J. High Energy Phys. 2021, 6, 068. [Google Scholar] [CrossRef]
- Bossi, F.; Ciafaloni, P. Lepton Flavor Violation at muon-electron colliders. J. High Energy Phys. 2020, 10, 033. [Google Scholar] [CrossRef]
- Wetterich, C. Neutrino Masses and the Scale of B–L Violation. Nucl. Phys. B 1981, 187, 343–375. [Google Scholar] [CrossRef]
- Buchmuller, W.; Greub, C.; Minkowski, P. Neutrino masses, neutral vector bosons and the scale of B–L breaking. Phys. Lett. B 1991, 267, 395–399. [Google Scholar] [CrossRef]
- Emam, W.; Khalil, S. Higgs and Z-prime phenomenology in B–L extension of the standard model at LHC. Eur. Phys. J. C 2007, 52, 625–633. [Google Scholar] [CrossRef]
- Basso, L.; Belyaev, A.; Moretti, S.; Shepherd-Themistocleous, C.H. Phenomenology of the minimal B–L extension of the Standard model: Z’ and neutrinos. Phys. Rev. D 2009, 80, 055030. [Google Scholar] [CrossRef]
- Fileviez Perez, P.; Han, T.; Li, T. Testability of Type I Seesaw at the CERN LHC: Revealing the Existence of the B–L Symmetry. Phys. Rev. D 2009, 80, 073015. [Google Scholar] [CrossRef]
- Heeck, J. Unbroken B–L symmetry. Phys. Lett. B 2014, 739, 256–262. [Google Scholar] [CrossRef]
- Khalil, S. Low scale B–L extension of the Standard Model at the LHC. J. Phys. G 2008, 35, 055001. [Google Scholar] [CrossRef]
- Huitu, K.; Khalil, S.; Okada, H.; Rai, S.K. Signatures for right-handed neutrinos at the Large Hadron Collider. Phys. Rev. Lett. 2008, 101, 181802. [Google Scholar] [CrossRef]
- Accomando, E.; Delle Rose, L.; Moretti, S.; Olaiya, E.; Shepherd-Themistocleous, C.H. Extra Higgs boson and Z′ as portals to signatures of heavy neutrinos at the LHC. J. High Energy Phys. 2018, 2, 109. [Google Scholar] [CrossRef]
- Dev, P.S.B.; Mohapatra, R.N.; Zhang, Y. Leptogenesis constraints on B–L breaking Higgs boson in TeV scale seesaw models. J. High Energy Phys. 2018, 3, 122. [Google Scholar] [CrossRef]
- Davidson, S.; Lacroix, S.; Verdier, P. LHC sensitivity to lepton flavour violating Z boson decays. J. High Energy Phys. 2012, 9, 092. [Google Scholar] [CrossRef]
- Abada, A.; Bečirević, D.; Lucente, M.; Sumensari, O. Lepton flavor violating decays of vector quarkonia and of the Z boson. Phys. Rev. D 2015, 91, 113013. [Google Scholar] [CrossRef]
- De Romeri, V.; Herrero, M.J.; Marcano, X.; Scarcella, F. Lepton flavor violating Z decays: A promising window to low scale seesaw neutrinos. Phys. Rev. D 2017, 95, 075028. [Google Scholar] [CrossRef]
- Herrero, M.J.; Marcano, X.; Morales, R.; Szynkman, A. One-loop effective LFV Zlklm vertex from heavy neutrinos within the mass insertion approximation. Eur. Phys. J. C 2018, 78, 815. [Google Scholar] [CrossRef]
- Langacker, P.; London, D. Mixing Between Ordinary and Exotic Fermions. Phys. Rev. D 1988, 38, 886. [Google Scholar] [CrossRef]
- Altmannshofer, W.; Chen, C.Y.; Bhupal Dev, P.S.; Soni, A. Lepton flavor violating Z’ explanation of the muon anomalous magnetic moment. Phys. Lett. B 2016, 762, 389–398. [Google Scholar] [CrossRef]
- CMS Collaboration. Search for heavy resonances and quantum black holes in eμ, eτ, and μτ final states in proton-proton collisions at = 13 TeV, CMS-PAS-EXO-19-014. 2021. Available online: http://cds.cern.ch/record/2779023 (accessed on 22 August 2021).
- Dev, P.S.B.; Rodejohann, W.; Xu, X.J.; Zhang, Y. MUonE sensitivity to new physics explanations of the muon anomalous magnetic moment. J. High Energy Phys. 2020, 5, 053. [Google Scholar] [CrossRef]
- Masiero, A.; Paradisi, P.; Passera, M. New physics at the MUonE experiment at CERN. Phys. Rev. D 2020, 102, 075013. [Google Scholar] [CrossRef]
- Carloni Calame, C.M.; Passera, M.; Trentadue, L.; Venanzoni, G. A new approach to evaluate the leading hadronic corrections to the muon g-2. Phys. Lett. B 2015, 746, 325–329. [Google Scholar] [CrossRef]
- Abbiendi, G.; Carloni Calame, C.M.; Marconi, U.; Matteuzzi, C.; Montagna, G.; Nicrosini, O.; Passera, M.; Piccinini, F.; Tenchini, R.; Trentadue, L.; et al. Measuring the leading hadronic contribution to the muon g-2 via μe scattering. Eur. Phys. J. C 2017, 77, 139. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y. Charged Lepton Flavor Violation at the High-Energy Colliders: Neutrino Mass Relevant Particles. Universe 2022, 8, 164. https://doi.org/10.3390/universe8030164
Zhang Y. Charged Lepton Flavor Violation at the High-Energy Colliders: Neutrino Mass Relevant Particles. Universe. 2022; 8(3):164. https://doi.org/10.3390/universe8030164
Chicago/Turabian StyleZhang, Yongchao. 2022. "Charged Lepton Flavor Violation at the High-Energy Colliders: Neutrino Mass Relevant Particles" Universe 8, no. 3: 164. https://doi.org/10.3390/universe8030164
APA StyleZhang, Y. (2022). Charged Lepton Flavor Violation at the High-Energy Colliders: Neutrino Mass Relevant Particles. Universe, 8(3), 164. https://doi.org/10.3390/universe8030164





