Probing Quantum Gravity with Imaging Atmospheric Cherenkov Telescopes
Abstract
| 1 | Introduction and Motivation | 2 | |
| 1.1 | A Proposal to Probe Quantum Gravity | 2 | |
| 1.2 | Modified Photon Dispersion Relation | 3 | |
| 2 | Testing Energy-Dependent Photon Group Velocity | 4 | |
| 2.1 | The First Test with an Imaging Atmospheric Cherenkov telescope | 5 | |
| 2.2 | Fastest Variability in Blazars | 5 | |
| 2.3 | Introducing the Maximum Likelihood Method | 6 | |
| 2.4 | Results from the Maximum Likelihood Method on the Mrk 501 Flare from 2005 | 9 | |
| 2.5 | Sensitivity to the Lorentz Invariance Violation Effects | 9 | |
| 2.6 | Lorentz Invariance Violation Study on the Most Variable Blazar Flare | 10 | |
| 2.7 | Extending to Higher Redshifts | 12 | |
| 2.8 | Exploring Lower Time Variability with the Crab Pulsar Observations by VERITAS | 12 | |
| 2.9 | Applying the Maximum Likelihood Method to the Crab Pulsar with MAGIC | 13 | |
| 2.10 | Lorentz Invariance Violation Study on a New Vela Pulsar | 14 | |
| 2.11 | First Parallel Study of Energy-Dependent Photon Group Velocity and Gamma-ray Absorption on the Same Data Sample | 14 | |
| 2.12 | First Lorentz Invariance Violation Study on a Gamma-Ray Burst Observed with Imaging Atmospheric Cherenkov Telescopes | 15 | |
| 2.13 | Lorentz Invariance Violation on Fermi-LAT Gamma-Ray Bursts | 16 | |
| 3 | Modified Photon Interactions | 19 | |
| 3.1 | Testing Lorentz Invariance Violation with Universe Transparency | 18 | |
| 3.1.1 Influence of Lorentz Invariance Violation on Universe Transparency | 19 | ||
| 3.1.2 Testing Lorentz Invariance Violation on Universe Transparency | 23 | ||
| 3.1.3 The Most Constraining Limits Based on Single Source Analysis | 23 | ||
| 3.1.4 On How the Most Constraining Limits Were Obtained | 24 | ||
| 3.2 | Constraints on Violation of Lorentz Invariance from Atmospheric Showers Initiated by Multi-TeV Photons | 25 | |
| 3.3 | Constraints on Lorentz Invariance Violation Based on Photon Stability | 26 | |
| 4 | Summary and Discussion | 27 | |
| 5 | An Eye on the Future | 30 | |
| 5.1 | Refinement of the Analysis Technique | 30 | |
| 5.2 | Combining Data from Different Sources and Instruments | 31 | |
| 5.3 | Additional and Alternative Lorentz Invariance Violation Effects and Related Phenomena | 33 | |
| 6 | Conclusions | 35 | |
| Abbreviations | 37 | ||
| References | 39 |
1. Introduction and Motivation
1.1. A Proposal to Probe Quantum Gravity
1.2. Modified Photon Dispersion Relation
2. Testing Energy-Dependent Photon Group Velocity
2.1. The First Test with an Imaging Atmospheric Cherenkov Telescope
2.2. Fastest Variability in Blazars
2.3. Introducing the Maximum Likelihood Method
- function is the observed light curve. Here, by taking , it is “corrected” for the potential time delay induced by the LIV effects. In this way, assuming that individual events suffered an energy-dependent time delay, and that no other dispersion effects were present, one obtains a source-intrinsic light curve, often referred to as a light curve template. In practice, there are different ways of obtaining .
- represents the observed spectral distribution of gamma rays. As it will be described in more details in Section 3.1, can be decomposed into a source intrinsic spectrum term and an absorption term. The latter usually implies the absorption of gamma rays on the Extragalactic background light (EBL), as discussed in Section 3.1, but can easily accommodate any additional effect (or modification of this particular one) that can affect the spectral distribution of gamma rays during their propagation towards the detector.
- , contains the information about the energy resolution and the bias of the instrument. is the true energy of a particular event, and is the PDF of being measured as E.
- The final ingredient, represents the collection area (i.e., acceptance) of the instrument expressed in true energy . In the most general case, it can change with time, especially if the data were collected in different observation conditions.
2.4. Results from the Maximum Likelihood Method on the Mrk 501 Flare from 2005
2.5. Sensitivity to the Lorentz Invariance Violation Effects
2.6. Lorentz Invariance Violation Study on the Most Variable Blazar Flare
2.7. Extending to Higher Redshifts
2.8. Exploring Lower Time Variability with the Crab Pulsar Observations by VERITAS
2.9. Applying the Maximum Likelihood Method to the Crab Pulsar with MAGIC
2.10. Lorentz Invariance Violation Study on a New Vela Pulsar
2.11. First Parallel Study of Energy-Dependent Photon Group Velocity and Gamma-ray Absorption on the Same Data Sample
2.12. First Lorentz Invariance Violation Study on a Gamma-ray Burst Observed with Imaging Atmospheric Cherenkov Telescopes
2.13. Lorentz Invariance Violation on Fermi-LAT Gamma-ray Bursts
3. Modified Photon Interactions
3.1. Testing Lorentz Invariance Violation with Universe Transparency
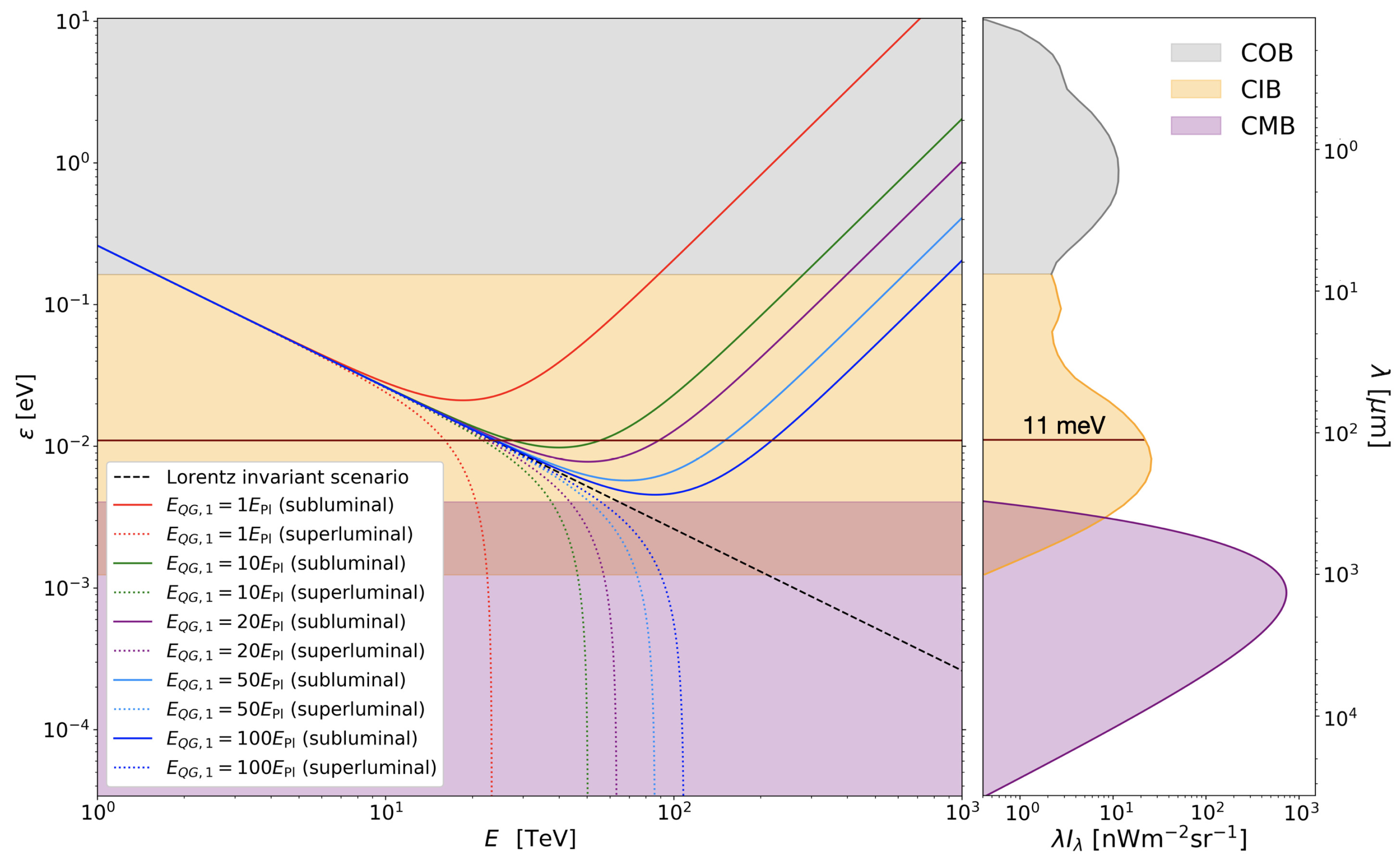
- denotes the energy of an EBL photon in the comoving frame, while is the comoving number density of EBL photons per unit energy.
- The probability of the interaction between a gamma ray and background photons is given by the cross section , where s is the square of the center of mass energy. In the gamma-ray energy range relevant for IACTs, by far the most dominant channel is the Breit–Wheeler process of electron-positron pair creation [107].
- The angle of interaction between a gamma ray and EBL photons is indicated by .
- denotes the EBL energy reaction threshold for electron-positron pair creation, i.e., the minimal energy of an EBL photon, in the comoving frame, necessary for the reaction to take place. Derived from the kinematics laws of special relativity, it can be expressed as:The threshold energy, and its changes due to modifications of the special relativity kinematics, will play a vital role in constraining .
- The final integral accounts for the distance traveled by the gamma ray, assuming flat cosmology:
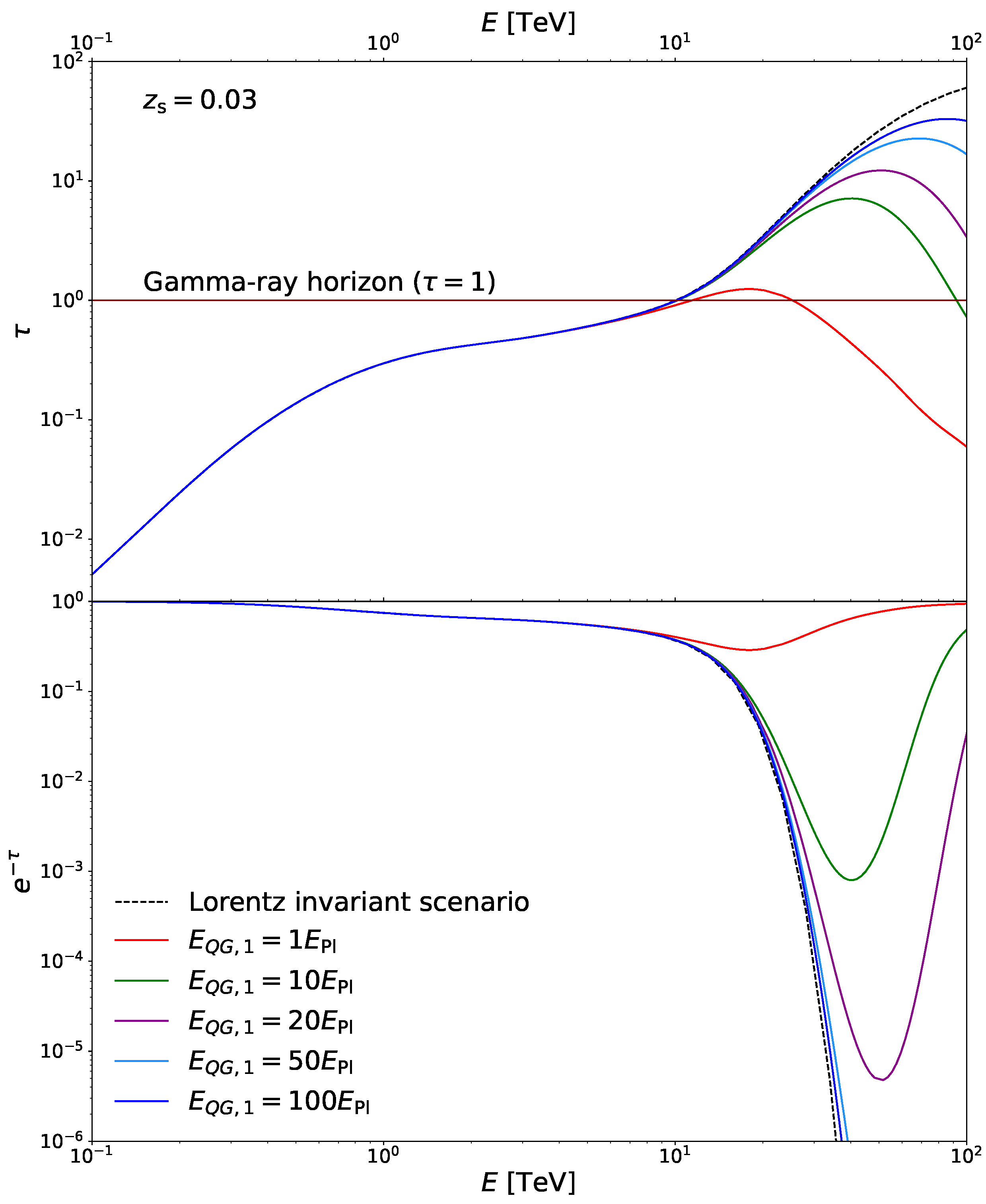
3.1.1. Influence of Lorentz Invariance Violation on Universe Transparency
3.1.2. Testing Lorentz Invariance Violation on Universe Transparency
3.1.3. The Most Constraining Limits Based on Single Source Analysis
3.1.4. On How the Most Constraining Limits Were Obtained
3.2. Constraints on Violation of Lorentz Invariance from Atmospheric Showers Initiated by Multi-TeV Photons
3.3. Constraints on Lorentz Invariance Violation Based on Photon Stability
4. Summary and Discussion
5. An Eye on the Future
5.1. Refinement of the Analysis Technique
5.2. Combining Data from Different Sources and Instruments
5.3. Additional and Alternative Lorentz Invariance Violation Effects and Related Phenomena
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AGN | active galactic nucleus |
| B-H | Bethe–Heitler |
| CMB | cosmic microwave background |
| CTA | Cherenkov Telescope Array |
| C.U. | Crab units |
| CWT | Continuous wavelet transform |
| DisCan | dispersion cancellation |
| DSR | Doubly Special Relativity |
| EBL | extragalactic background light |
| ECF | Energy cost function |
| FACT | First G-APD Cherenkov Telescope |
| GRB | Gamma-ray burst |
| GBM | Gamma-ray Burst Monitor |
| HAWC | High Altitude Water Cherenkov |
| HEGRA | High Energy Gamma Ray Astronomy |
| H.E.S.S. | High Energy Stereoscopic System |
| IACT | imaging atmospheric Cherenkov telescope |
| LAT | Large Area Telescope |
| LHAASO | Large High Altitude Air Shower Observatory |
| LIV | Lorentz invariance violation |
| MAGIC | Major Atmospheric Gamma Imaging Cherenkov |
| MCCF | Modified cross correlation function |
| MD | minimal dispersion |
| ML | maximum likelihood |
| PC | peak comparison |
| probability distribution function | |
| PV | PairView |
| RB | radio background |
| QG | Quantum Gravity |
| SMM | Sharpness maximisation method |
| TS | test statistic |
| VERITAS | Very Energetic Radiation Imaging Telescope Array System |
| VHE | very high energy (100 GeV < E < 100 TeV) |
| 1 | Planck energy GeV, Planck length m, Planck time s. |
| 2 | For a description of GRBs and an overview of observations, we refer the reader to Nava, L. Evolution of GRB observations over the past 30 years, to be printed in this Special Issue |
| 3 | |
| 4 | COST Action CA18108: Quantum gravity phenomenology in the multi-messenger approach (QG-MM, https://qg-mm.unizar.es/, accessed on 15 July 2021) gathers researchers working on the theoretical and phenomenological predictions, and experimental searches for physical phenomena characteristic for of QG. |
| 5 | Note that the time delay can be both positive or negative, depending on whether the behaviour is subluminal or superluminal, respectively. According to the usual convention, a time delay is positive for subluminal behaviour, i.e., photon of a higher energy propagating at a lower speed than a lower energy photon. |
| 6 | Various LIV studies use different values for cosmological parameters. However, given the precision of these studies, their final results are not strongly affected by the differences in the values of the cosmological parameters used, so we will treat them equally in that respect. |
| 7 | The Whipple telescope (https://veritas.sao.arizona.edu/whipple, accessed on 15 July 2021) was the first IACT. It consisted of a single 10 m reflector dish. In operation from 1968 until 2013, it detected the very first TeV gamma-ray source, the Crab nebula [29], and the first AGN detected in the same energy range Mrk 421 [30]. |
| 8 | Not to be confused with the Maximum likelihood (ML) method presented in Section 2.3. |
| 9 | MAGIC ([33,34], https://magic.mpp.mpg.de/, accessed on 15 July 2021) is a system of two semi-identical 17 m reflector dish IACTs. Located in the Roque de los Muchachos Observatory in the Canary island of La Palma, it has been in operation since 2004, first as a single MAGIC-I telescope. MAGIC-II was commissioned in 2009. Since then, MAGIC has been observing as a stereoscopic telescope system. |
| 10 | For a more detailed definition and discussion of , we refer the interested reader to [44]. |
| 11 | For more details on the modelling of these effects in the context of LIV, an interested reader can refer to [45]. |
| 12 | The Fermi Gamma-ray Space Telescope (https://fermi.gsfc.nasa.gov/, accessed on 15 July 2021), formerly known as GLAST, was launched in 2008. |
| 13 | The H.E.S.S. array ([63], https://www.mpi-hd.mpg.de/hfm/HESS/, accessed on 15 July 2021) is located in Khomas Highland plateau of Namibia. It consists of four 12 m telescopes commissioned in 2004. In 2012, the array was extended with a 28 m telescope, which marked the beginning of the H.E.S.S.-II phase. |
| 14 | The Crab nebula is a pulsar wind nebula. It was the first source of gamma rays to be reliably detected with an IACT [29]. It is the brightest steady source of VHE gamma rays, which which is why it is used as a standard candle in gamma astronomy. Gamma-ray flux is often expressed in units of Crab nebula flux (Crab units) in the same energy range. |
| 15 | For details on the absorption of VHE gamma rays on the EBL, see Section 3.1. |
| 16 | The discovery of GRB 180720B by H.E.S.S. [60] was announced after the discovery of GRB 190114C. |
| 17 | CTA ([85], https://www.cta-observatory.org/, accessed on 15 July 2021) is an array of Cherenkov telescopes currently being built in two locations. The approved “Alpha Configuration” in the Southern Site in Paranal Observatory (Chile) will consist of 14 Medium-Sized Telescopes and 37 Small-Sized Telescopes, covering the area of ∼3 km. The Northern Site will be located in the Roque de los Muchachos Observatory (Spain), consisting of four Large-Sized Telescopes and nine Medium-Sized Telescopes, which will cover the area of ∼ km. |
| 18 | Note that this estimate was obtained for a larger number of telescopes in each site compared to the Alpha Configuration. |
| 19 | Considering our focus on research performed the Vasileiou et al. work is strictly speaking out of the scope of this review. However, it derived some interesting results, and other LIV studies are often compared to it, so we will outline its main points. |
| 20 | For a comparison of sensitivities of various current and future instruments see [91] and references therein. |
| 21 | Henceforward, when denoted with prime physical quantity is written in the comoving frame at which the interaction occurs. When prime does not occur, it is written in the observer’s frame of reference. |
| 22 | The HEGRA experiment was a system of five IACTs decommissioned in 2002 [110]. |
| 23 | Modifications of the electron dispersion relation were tested on the 100 MeV synchrotron radiation from the Crab nebula in [112]. The lower limit on for electrons was set to at least seven orders of magnitude above . |
| 24 | Gamma-ray energy range up to 100 TeV was chosen to be compatible with previously published results based on universe transparency to gamma rays. To best of our knowledge there is no publication in which the optical depth behaviour beyond this limit has been investigated. For this reason we departed from the usual energy range used in other figures in this section. |
| 25 | http://tevcat.uchicago.edu/ (accessed on 15 July 2021). |
| 26 | As the name says, HAWC (https://www.hawc-observatory.org/, accessed on 15 July 2021) is a water Cherenkov experiment located in Parque Nacional Pico de Orizaba in Mexico. |
| 27 | LHAASO (http://english.ihep.cas.cn/lhaaso/, accessed on 15 July 2021) is a hybrid detector of cosmic and gamma rays located in Daocheng, Sichuan province, China [137]. |
| 28 | All-sky Medium Energy Gamma-ray Observatory (AMEGO, https://asd.gsfc.nasa.gov/amego/index.html, accessed on 15 July 2021) is a concept for the MeV sky exploration. |
| 29 | Imaging X-ray Polarimetry Explorer (IXPE, https://ixpe.msfc.nasa.gov/index.html, accessed on 15 July 2021). |
References
- Einstein, A. The Foundation of the General Theory of Relativity. Ann. Phys. 1916, 49, 769–822. [Google Scholar] [CrossRef]
- Rovelli, C.; Smolin, L. Loop Space Representation of Quantum General Relativity. Nucl. Phys. B 1990, 331, 80–152. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum gravity. In Philosophy of Physics; Butterfield, J., Earman, J., Eds.; Elsevier: North Holland, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Oriti, D. Space-time geometry from algebra: Spin foam models for nonperturbative quantum gravity. Rep. Prog. Phys. 2001, 64, 1703–1756. [Google Scholar] [CrossRef]
- Niedermaier, M.; Reuter, M. The Asymptotic Safety Scenario in Quantum Gravity. Living Rev. Relativ. 2006, 9, 5–173. [Google Scholar] [CrossRef]
- Ambjorn, J.; Goerlich, A.; Jurkiewicz, J.; Loll, R. Nonperturbative Quantum Gravity. Phys. Rep. 2012, 519, 127–210. [Google Scholar] [CrossRef]
- Horowitz, G.T. Spacetime in string theory. New J. Phys. 2005, 7, 201. [Google Scholar] [CrossRef][Green Version]
- Kostelecky, V.A.; Samuel, S. Spontaneous Breaking of Lorentz Symmetry in String Theory. Phys. Rev. D 1989, 39, 683. [Google Scholar] [CrossRef] [PubMed]
- Gambini, R.; Pullin, J. Nonstandard optics from quantum space-time. Phys. Rev. D 1999, 59, 124021. [Google Scholar] [CrossRef]
- Carroll, S.M.; Harvey, J.A.; Kostelecky, V.A.; Lane, C.D.; Okamoto, T. Noncommutative field theory and Lorentz violation. Phys. Rev. Lett. 2001, 87, 141601. [Google Scholar] [CrossRef] [PubMed]
- Douglas, M.R.; Nekrasov, N.A. Noncommutative field theory. Rev. Mod. Phys. 2001, 73, 977–1029. [Google Scholar] [CrossRef]
- Bird, D.J.; Corbato, S.C.; Dai, H.Y.; Elbert, J.W.; Green, K.D.; Huang, M.A.; Kieda, D.B.; Ko, S.; Larsen, C.G.; Loh, E.C.; et al. Detection of a cosmic ray with measured energy well beyond the expected spectral cutoff due to cosmic microwave radiation. Astrophys. J. 1995, 441, 144–150. [Google Scholar] [CrossRef]
- Halzen, F.; Vázquez, R.A.; Stanev, T.; Vankov, H.P. The highest energy cosmic ray. Astropart. Phys. 1995, 3, 151–156. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abbasi, R.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Amin, N.M.; Andeen, K.; et al. Detection of a particle shower at the Glashow resonance with IceCube. Nature 2021, 591, 220–224, Erratum in 2021, 592, E11. [Google Scholar] [CrossRef]
- Cao, Z.; Aharonian, F.A.; An, Q.; Axikegu; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; et al. Ultrahigh-energy photons up to 1.4 petaelectronvolts from 12 γ-ray Galactic sources. Nature 2021, 594, 33–36. [Google Scholar] [CrossRef]
- Costa, E.; Feroci, M.; Piro, L.; Soffitta, P.; Amati, L.; Cinti, M.N.; Frontera, F.; Zavattini, G.; Nicastro, L.; Palazzi, E.; et al. GRB 970508. IAU Circ. 1997, 6649, 1. [Google Scholar]
- Djorgovski, S.G.; Metzger, M.R.; Kulkarni, S.R.; Odewahn, S.C.; Gal, R.R.; Pahre, M.A.; Frail, D.A.; Feroci, M.; Costa, E.; Palazzi, E. The optical counterpart to the γ-ray burst GRB970508. Nature 1997, 387, 876–878. [Google Scholar] [CrossRef]
- Metzger, M.R.; Djorgovski, S.G.; Kulkarni, S.R.; Steidel, C.C.; Adelberger, K.L.; Frail, D.A.; Costa, E.; Frontera, F. Spectral constraints on the redshift of the optical counterpart to the γ-ray burst of 8 May 1997. Nature 1997, 387, 878–880. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Ellis, J.R.; Mavromatos, N.E.; Nanopoulos, D.V.; Sarkar, S. Tests of quantum gravity from observations of gamma-ray bursts. Nature 1998, 393, 763–765. [Google Scholar] [CrossRef]
- Calcagni, G. Lorentz violations in multifractal spacetimes. Eur. Phys. J. C 2017, 77, 291. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecky, V.A. Lorentz violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef]
- Carroll, S.M.; Field, G.B.; Jackiw, R. Limits on a Lorentz and Parity Violating Modification of Electrodynamics. Phys. Rev. D 1990, 41, 1231. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Mewes, M. Cosmological constraints on Lorentz violation in electrodynamics. Phys. Rev. Lett. 2001, 87, 251304. [Google Scholar] [CrossRef] [PubMed]
- Amelino-Camelia, G. Doubly special relativity. Nature 2002, 418, 34–35. [Google Scholar] [CrossRef] [PubMed]
- Amelino-Camelia, G. Doubly-Special Relativity: Facts, Myths and Some Key Open Issues. Symmetry 2010, 2, 230–271. [Google Scholar] [CrossRef]
- Jacob, U.; Piran, T. Lorentz-violation-induced arrival delays of cosmological particles. JCAP 2008, 1, 031. [Google Scholar] [CrossRef]
- Pfeifer, C. Redshift and lateshift from homogeneous and isotropic modified dispersion relations. Phys. Lett. B 2018, 780, 246–250. [Google Scholar] [CrossRef]
- Rosati, G.; Amelino-Camelia, G.; Marciano, A.; Matassa, M. Planck-scale-modified dispersion relations in FRW spacetime. Phys. Rev. D 2015, 92, 124042. [Google Scholar] [CrossRef]
- Weekes, T.C.; Cawley, M.F.; Fegan, D.J.; Gibbs, K.G.; Hillas, A.M.; Kowk, P.W.; Lamb, R.C.; Lewis, D.A.; Macomb, D.; Porter, N.A.; et al. Observation of TeV gamma rays from the Crab nebula using the atmospheric Cerenkov imaging technique. Astrophys. J. 1989, 342, 379–395. [Google Scholar] [CrossRef]
- Punch, M.; Akerlof, C.W.; Cawley, M.F.; Chantell, M.; Fegan, D.J.; Fennell, S.; Gaidos, J.A.; Hagan, J.; Hillas, A.M.; Jiang, Y.; et al. Detection of TeV photons from the active galaxy Markarian 421. Nature 1992, 358, 477–478. [Google Scholar] [CrossRef]
- Gaidos, J.A.; Akerlof, C.W.; Biller, S.; Boyle, P.J.; Breslin, A.C.; Buckley, J.H.; Carter-Lewis, D.A.; Catanese, M.; Cawley, M.F.; Fegan, D.J.; et al. Extremely rapid bursts of TeV photons from the active galaxy Markarian 421. Nature 1996, 383, 319–320. [Google Scholar] [CrossRef]
- Biller, S.D.; Breslin, A.C.; Buckley, J.; Catanese, M.; Carson, M.; Carter-Lewis, D.A.; Cawley, M.F.; Fegan, D.J.; Finley, J.P.; Gaidos, J.A.; et al. Limits to Quantum Gravity Effects on Energy Dependence of the Speed of Light from Observations of TeV Flares in Active Galaxies. Phys. Rev. Lett. 1999, 83, 2108–2111. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barceló, M.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; et al. The major upgrade of the MAGIC telescopes, Part I: The hardware improvements and the commissioning of the system. Astropart. Phys. 2016, 72, 61–75. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barceló, M.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; et al. The major upgrade of the MAGIC telescopes, Part II: A performance study using observations of the Crab Nebula. Astropart. Phys. 2016, 72, 76–94. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; Becker, J.K.; et al. Variable VHE gamma-ray emission from Markarian 501. Astrophys. J. 2007, 669, 862–883. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; Wiley: New York, NY, USA, 1999. [Google Scholar]
- MAGIC Collaboration; Albert, J.; Aliu, E.; Anderhub, H.; Antonelli, L.A.; Antoranz, P.; Backes, M.; Baixeras, C.; Barrio, J.A.; Bartko, H.; et al. Probing quantum gravity using photons from a flare of the active galactic nucleus Markarian 501 observed by the MAGIC telescope. Phys. Lett. B 2008, 668, 253–257. [Google Scholar] [CrossRef]
- Vasileiou, V.; Jacholkowska, A.; Piron, F.; Bolmont, J.; Couturier, C.; Granot, J.; Stecker, F.W.; Cohen-Tanugi, J.; Longo, F. Constraints on Lorentz Invariance Violation from Fermi-Large Area Telescope Observations of Gamma-ray Bursts. Phys. Rev. D 2013, 87, 122001. [Google Scholar] [CrossRef]
- Barres de Almeida, U.; Daniel, M.K. A Simple Method to Test for Energy-Dependent Dispersion in High Energy Light-Curves of Astrophysical Sources. Astropart. Phys. 2012, 35, 850–860. [Google Scholar] [CrossRef]
- Scargle, J.D.; Norris, J.P.; Bonnell, J.T. An Algorithm for Detecting Quantum Gravity Photon Dispersion in Gamma-ray Bursts: DisCan. Astrophys. J. 2008, 673, 972–980. [Google Scholar] [CrossRef][Green Version]
- Ellis, J.R.; Harries, N.; Meregaglia, A.; Rubbia, A.; Sakharov, A. Probes of Lorentz Violation in Neutrino Propagation. Phys. Rev. D 2008, 78, 033013. [Google Scholar] [CrossRef]
- Martínez, M.; Errando, M. A new approach to study energy-dependent arrival delays on photons from astrophysical sources. Astropart. Phys. 2009, 31, 226–232. [Google Scholar] [CrossRef]
- Wilks, S. The Large-Sample Distribution of the Likelihood Ratio for Testing Composite Hypotheses. Ann. Math. Stat. 1938, 9, 60–62. [Google Scholar] [CrossRef]
- Berge, D.; Funk, S.; Hinton, J. Background Modelling in Very-High-Energy Gamma-ray Astronomy. Astron. Astrophys. 2007, 466, 1219–1229. [Google Scholar] [CrossRef]
- Perennes, C.; Sol, H.; Bolmont, J. Modeling spectral lags in active galactic nucleus flares in the context of Lorentz invariance violation searches. Astron. Astrophys. 2020, 633, A143. [Google Scholar] [CrossRef]
- Aleksić, J.; Antonelli, L.A.; Antoranz, P.; Backes, M.; Baixeras, C.; Barrio, J.A.; Bastieri, D.; Becerra González, J.; Bednarek, W.; Berdyugin, A.; et al. Search for an extended VHE gamma-ray emission from Mrk 421 and Mrk 501 with the MAGIC Telescope. Astron. Astrophys. 2010, 524, A77. [Google Scholar] [CrossRef]
- Abramowski, A.; Aharonian, F.; Ait Benkhali, F.; Akhperjanian, A.G.; Angüner, E.; Anton, G.; Backes, M.; Balenderan, S.; Balzer, A.; Barnacka, A.; et al. Search for Extended gamma-ray Emission around AGN with H.E.S.S. and Fermi-LAT. Astron. Astrophys. 2014, 562, A145. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; Bloom, E.D.; et al. The Search for Spatial Extension in High-latitude Sources Detected by the Fermi Large Area Telescope. Astrophys. J. Suppl. 2018, 237, 32. [Google Scholar] [CrossRef]
- Batista, R.A.; Saveliev, A. The Gamma-ray Window to Intergalactic Magnetism. Universe 2021, 7, 223. [Google Scholar] [CrossRef]
- Sitarek, J.; Bednarek, W. Gamma-rays from the IC e± pair cascade in the radiation field of an accretion disk: Application to CenA. Mon. Not. R. Astron. Soc. 2010, 401, 1983. [Google Scholar] [CrossRef]
- Sitarek, J.; Bednarek, W. Time dependent gamma-ray production in the anisotropic IC e± pair cascade initiated by electrons in active galaxies. Mon. Not. R. Astron. Soc. 2010, 409, 662. [Google Scholar] [CrossRef]
- Aliu, E.; Anderhub, H.; Antonelli, L.A.; Antoranz, P.; Backes, M.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; Becker, J.K.; et al. Observation of Pulsed γ-rays Above 25 GeV from the Crab Pulsar with MAGIC. Science 2008, 322, 1221. [Google Scholar] [CrossRef] [PubMed]
- Abdalla, H.; Aharonian, F.; Ait Benkhali, F.; Angüner, E.O.; Arakawa, M.; Arcaro, C.; Armand, C.; Arrieta, M.; Backes, M.; Barnard, M.; et al. First Ground-based Measurement of Sub-20 GeV to 100 GeV γ-rays from the Vela Pulsar with H.E.S.S. II. Astron. Astrophys. 2018, 620, A66. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Asano, K.; Baack, D.; Babić, A.; Baquero, A.; Barres de Almeida, U.; Barrio, J.A.; et al. Detection of the Geminga pulsar with MAGIC hints at a power-law tail emission beyond 15 GeV. Astron. Astrophys. 2020, 643, L14. [Google Scholar] [CrossRef]
- Spir-Jacob, M.; Djannati-Ataï, A.; Mohrmann, L.; Giavitto, G.; Khelifi, B.; Rudak, B.; Venter, C.; Zanin, R. Detection of sub-100 GeV γ-ray pulsations fromPSR B170644 with H.E.S.S. PoS 2020, ICRC2019, 799. [Google Scholar] [CrossRef]
- Meegan, C.; Lichti, G.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Connaughton, V.; Diehl, R.; Fishman, G.; Greiner, J.; Hoover, A.S.; et al. The Fermi Gamma-ray Burst Monitor. Astrophys. J. 2009, 702, 791–804. [Google Scholar] [CrossRef]
- Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. The Large Area Telescope on the Fermi Gamma-ray Space Telescope Mission. Astrophys. J. 2009, 697, 1071–1102. [Google Scholar] [CrossRef]
- Bhat, P.; Meegan, C.A.; von Kienlin, A.; Paciesas, W.S.; Briggs, M.S.; Burgess, J.M.; Burns, E.; Chaplin, V.; Cleveland, W.H.; Collazzi, A.C.; et al. The Third Fermi gbm Gamma-ray Burst Catalog: The First six Years. Astrophys. J. Suppl. 2016, 223, 28. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. Teraelectronvolt emission from the γ-ray burst GRB 190114C. Nature 2019, 575, 455–458. [Google Scholar] [CrossRef]
- Abdalla, H.; Adam, R.; Aharonian, F.; Ait Benkhali, F.; Angüner, E.O.; Arakawa, M.; Arcaro, C.; Armand, C.; Ashkar, H.; Backes, M.; et al. A very-high-energy component deep in the γ-ray burst afterglow. Nature 2019, 575, 464–467. [Google Scholar] [CrossRef]
- de Naurois, M.; HESS Collaboration. GRB190829A: Detection of VHE gamma-ray emission with H.E.S.S. GRB Coord. Netw. 2019, 25566, 1. [Google Scholar]
- Blanch, O.; Longo, F.; Berti, A.; Fukami, S.; Suda, Y.; Loporchio, S.; Micanovic, S.; Green, J.G.; Pinter, V.; Takahashi, M.; MAGIC Collaboration. GRB 201216C: MAGIC detection in very high energy gamma rays. GRB Coord. Netw. 2020, 29075, 1. [Google Scholar]
- Ashton, T.; Backes, M.; Balzer, A.; Berge, D.; Bolmont, J.; Bonnefoy, S.; Brun, F.; Chaminade, T.; Delagnes, E.; Fontaine, G.; et al. A NECTAr-based upgrade for the Cherenkov cameras of the H.E.S.S. 12-meter telescopes. Astropart. Phys. 2020, 118, 102425. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Behera, B.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; et al. An Exceptional Very High Energy Gamma-ray Flare of PKS 2155-304. Astrophys. J. Lett. 2007, 664, L71–L78. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Barres de Almeida, U.; Bazer-Bachi, A.R.; Becherini, Y.; Behera, B.; Beilicke, M.; Benbow, W.; Bernlöhr, K.; Boisson, C.; et al. Limits on an Energy Dependence of the Speed of Light from a Flare of the Active Galaxy PKS 2155-304. Phys. Rev. Lett. 2008, 101, 170402. [Google Scholar] [CrossRef] [PubMed]
- Li, T.P.; Qu, J.L.; Feng, H.; Song, L.M.; Ding, G.Q.; Chen, L. Timescale analysis of spectral lags. Chin. J. Astron. Astrophys. 2004, 4, 583–598. [Google Scholar] [CrossRef]
- HESS Collaboration; Abramowski, A.; Acero, F.; Aharonian, F.; Akhperjanian, A.G.; Anton, G.; Barnacka, A.; de Barres Almeida, U.; Bazer-Bachi, A.R.; Becherini, Y.; et al. Search for Lorentz Invariance breaking with a likelihood fit of the PKS 2155-304 flare data taken on MJD 53944. Astropart. Phys. 2011, 34, 738–747. [Google Scholar] [CrossRef]
- Abramowski, A.; Aharonian, F.; Ait Benkhali, F.; Akhperjanian, A.G.; Angüner, E.O.; Backes, M.; Balenderan, S.; Balzer, A.; Barnacka, A.; Becherini, Y.; et al. The 2012 flare of PG 1553+113 seen with H.E.S.S. and Fermi-LAT. Astrophys. J. 2015, 802, 65. [Google Scholar] [CrossRef]
- Kaaret, P. Pulsar radiation and quantum gravity. Astron. Astrophys. 1999, 345, L32. [Google Scholar]
- Kaplan, D.L.; Chatterjee, S.; Gaensler, B.M.; Anderson, J. A Precise Proper Motion for the Crab Pulsar, and the Difficulty of Testing Spin-Kick Alignment for Young Neutron Stars. Astrophys. J. 2008, 677, 1201. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. The Australia Telescope National Facility pulsar catalogue. Astron. J. 2005, 129, 1993. [Google Scholar] [CrossRef]
- VERITAS Collaboration; Aliu, E.; Arlen, T.; Aune, T.; Beilicke, M.; Benbow, W.; Bouvier, A.; Bradbury, S.M.; Buckley, J.H.; Bugaev, V.; et al. Detection of Pulsed Gamma Rays Above 100 GeV from the Crab Pulsar. Science 2011, 334, 69. [Google Scholar] [CrossRef]
- Otte, N. Prospects of performing Lorentz invariance tests with VHE emission from Pulsars. In Proceedings of the International Cosmic Ray Conference, Beijing, China, 11–18 August 2011; Volume 7, p. 256. [Google Scholar] [CrossRef]
- Zitzer, B.; VERITAS Collaboration. Lorentz Invariance Violation Limits from the Crab Pulsar using VERITAS. In Proceedings of the International Cosmic Ray Conference, Rio de Janeiro, Brazil, 2–9 July 2013; Volume 33, p. 2768. [Google Scholar]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; et al. Fermi Large Area Telescope Observations of the Crab Pulsar and Nebula. Astrophys. J. 2010, 708, 1254–1267. [Google Scholar] [CrossRef]
- Buccheri, R.; Bennett, K.; Bignami, G.F.; Bloemen, J.B.G.M.; Boriakoff, V.; Caraveo, P.A.; Hermsen, W.; Kanbach, G.; Manchester, R.N.; Masnou, J.L.; et al. Search for pulsed gamma-ray emission from radio pulsars in the COS-B data. Astron. Astrophys. 1983, 128, 245–251. [Google Scholar]
- Ahnen, M.L.; Ansoldi, S.; Antonelli, L.A.; Arcaro, C.; Babić, A.; Banerjee, B.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. Constraining Lorentz invariance violation using the Crab Pulsar emission observed up to TeV energies by MAGIC. Astrophys. J. Suppl. 2017, 232, 9. [Google Scholar] [CrossRef]
- Caraveo, P.A.; De Luca, A.; Mignani, R.P.; Bignami, G.F. The distance to the vela pulsar gauged with hst parallax oservations. Astrophys. J. 2001, 561, 930. [Google Scholar] [CrossRef]
- Chrétien, M.; Bolmont, J.; Jacholkowski, A. Constraining photon dispersion relation from observations of the Vela pulsar with H.E.S.S. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), The Hague, The Netherlands, 30 July–6 August 2015; Volume 34, p. 764. [Google Scholar]
- Anderhub, H.; Backes, M.; Biland, A.; Boccone, V.; Braun, I.; Bretz, T.; Buß, J.; Cadoux, F.; Commichau, V.; Djambazov, L.; et al. Design and operation of FACT—The first G-APD Cherenkov telescope. J. Instrum. 2013, 8, P06008. [Google Scholar] [CrossRef]
- Abdalla, H.; Aharonian, F.; Ait Benkhali, F.; Angüner, E.O.; Arakawa, M.; Arcaro, C.; Armand, C.; Arrieta, M.; Backes, M.; Barnard, M.; et al. The 2014 TeV γ-ray Flare of Mrk 501 Seen with H.E.S.S.: Temporal and Spectral Constraints on Lorentz Invariance Violation. Astrophys. J. 2019, 870, 93. [Google Scholar] [CrossRef]
- Mirzoyan, R.; Noda, K.; Moretti, E.; Berti, A.; Nigro, C.; Hoang, J.; Micanovic, S.; Takahashi, M.; Chai, Y.; Moralejo, A.; MAGIC Collaboration. MAGIC detects the GRB 190114C in the TeV energy domain. GRB Coord. Netw. 2019, 23701, 1. [Google Scholar]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. Bounds on Lorentz invariance violation from MAGIC observation of GRB 190114C. Phys. Rev. Lett. 2020, 125, 021301. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. Observation of inverse Compton emission from a long γ-ray burst. Nature 2019, 575, 459–463. [Google Scholar] [CrossRef]
- Hassan, T.; Arrabito, L.; Bernlöhr, K.; Bregeon, J.; Cortina, J.; Cumani, P.; Di Pierro, F.; Falceta-Goncalves, D.; Lang, R.G.; Hinton, J.; et al. Monte Carlo Performance Studies for the Site Selection of the Cherenkov Telescope Array. Astropart. Phys. 2017, 93, 76–85. [Google Scholar] [CrossRef]
- Inoue, S.; Granot, J.; O’Brien, P.T.; Asano, K.; Bouvier, A.; Carosi, A.; Connaughton, V.; Garczarczyk, M.; Gilmore, R.; Hinton, J.; et al. Gamma-ray Burst Science in the Era of the Cherenkov Telescope Array. Astropart. Phys. 2013, 43, 252–275. [Google Scholar] [CrossRef]
- Greiner, J.; Clemens, C.; Krühler, T.; von Kienlin, A.; Rau, A.; Sari, R.; Fox, D.B.; Kawai, N.; Afonso, P.; Ajello, M.; et al. The redshift and afterglow of the extremely energetic gamma-ray burst GRB 080916C. Astron. Astrophys. 2009, 498, 89–94. [Google Scholar] [CrossRef]
- Olivares, F.; Klose, S.; Kruehler, T.; Greiner, J. GRB 090510: GROND observations. GRB Coord. Netw. 2009, 9352, 1. [Google Scholar]
- Cucchiara, A.; Fox, D.B.; Tanvir, N.; Berger, E. GRB 090902B: Gemini-N absorption redshift. GRB Coord. Netw. 2009, 9873, 1. [Google Scholar]
- D’Elia, V.; Fynbo, J.P.U.; Covino, S.; Goldoni, P.; Jakobsson, P.; Matteucci, F.; Piranomonte, S.; Sollerman, J.; Thöne, C.C.; Vergani, S.D.; et al. VLT/X-shooter spectroscopy of the GRB 090926A afterglow. Astron. Astrophys. 2010, 523, A36. [Google Scholar] [CrossRef]
- CTAO Performance. Available online: https://www.cta-observatory.org/science/ctao-performance/ (accessed on 15 July 2021).
- Kifune, T. Invariance violation extends the cosmic ray horizon? Astrophys. J. Lett. 1999, 518, L21–L24. [Google Scholar] [CrossRef]
- Aloisio, R.; Blasi, P.; Ghia, P.L.; Grillo, A.F. Probing the structure of space-time with cosmic rays. Phys. Rev. D 2000, 62, 053010. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Phenomenology of Planck-scale Lorentz-symmetry test theories. New J. Phys. 2004, 6, 188. [Google Scholar] [CrossRef]
- Gould, R.J.; Schréder, G.P. Pair Production in Photon-Photon Collisions. Phys. Rev. 1967, 155, 1404–1407. [Google Scholar] [CrossRef]
- Stecker, F.W.; de Jager, O.C.; Salamon, M.H. TeV gamma rays from 3C 279 - A possible probe of origin and intergalactic infrared radiation fields. Astrophys. J. Lett. 1992, 390, L49. [Google Scholar] [CrossRef]
- Biteau, J.; Williams, D.A. The extragalactic background light, the Hubble constant, and anomalies: Conclusions from 20 years of TeV gamma-ray observations. Astrophys. J. 2015, 812, 60. [Google Scholar] [CrossRef]
- Abdalla, H.; Böttcher, M. Lorentz Invariance Violation Effects on Gamma–Gamma Absorption and Compton Scattering. Astrophys. J. 2018, 865, 159. [Google Scholar] [CrossRef]
- Hauser, M.G.; Dwek, E. The cosmic infrared background: Measurements and implications. Ann. Rev. Astron. Astrophys. 2001, 39, 249–307. [Google Scholar] [CrossRef]
- Franceschini, A. Photon–Photon Interactions and the Opacity of the Universe in Gamma Rays. Universe 2021, 7, 146. [Google Scholar] [CrossRef]
- Franceschini, A.; Rodighiero, G.; Vaccari, M. The extragalactic optical-infrared background radiations, their time evolution and the cosmic photon-photon opacity. Astron. Astrophys. 2008, 487, 837. [Google Scholar] [CrossRef]
- Domínguez, A.; Primack, J.R.; Rosario, D.J.; Prada, F.; Gilmore, R.C.; Faber, S.M.; Koo, D.C.; Somerville, R.S.; Pérez-Torres, M.A.; Pérez-González, P.; et al. Extragalactic Background Light Inferred from AEGIS Galaxy SED-type Fractions. Mon. Not. R. Astron. Soc. 2011, 410, 2556. [Google Scholar] [CrossRef]
- Gilmore, R.C.; Somerville, R.S.; Primack, J.R.; Dominguez, A. Semi-analytic modeling of the EBL and consequences for extragalactic gamma-ray spectra. Mon. Not. R. Astron. Soc. 2012, 422, 3189. [Google Scholar] [CrossRef]
- Abdalla, H.; Abramowski, A.; Aharonian, F.; Ait Benkhali, F.; Akhperjanian, A.G.; Andersson, T.; Angüner, E.O.; Arakawa, M.; Arrieta, M.; Aubert, P.; et al. Measurement of the EBL spectral energy distribution using the VHE γ-ray spectra of H.E.S.S. blazars. Astron. Astrophys. 2017, 606, A59. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. Measurement of the extragalactic background light using MAGIC and Fermi-LAT gamma-ray observations of blazars up to z = 1. Mon. Not. R. Astron. Soc. 2019, 486, 4233–4251. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Archer, A.; Benbow, W.; Bird, R.; Brill, A.; Brose, R.; Buchovecky, M.; Calderon-Madera, D.; Christiansen, J.L.; Cui, W.; et al. Measurement of the extragalactic background light spectral energy distribution with VERITAS. Astrophys. J. 2019, 885, 150. [Google Scholar] [CrossRef]
- Breit, G.; Wheeler, J.A. Collision of Two Light Quanta. Phys. Rev. 1934, 46, 1087–1091. [Google Scholar] [CrossRef]
- Blanch, O.; Martinez, M. Exploring the gamma ray horizon with the next generation of gamma ray telescopes. Part 1: Theoretical predictions. Astropart. Phys. 2005, 23, 588–597. [Google Scholar] [CrossRef][Green Version]
- Aharonian, F.A.; Akhperjanian, A.G.; Barrio, J.A.; Bernlöhr, K.; Bojahr, H.; Calle, I.; Contreras, J.L.; Cortina, J.; Daum, A.; Deckers, T.; et al. The time averaged TeV energy spectrum of mkn 501 of the extraordinary 1997 outburst as measured with the stereoscopic Cherenkov telescope system of HEGRA. Astron. Astrophys. 1999, 349, 11–28. [Google Scholar]
- Pühlhofer, G.; Bolz, O.; Götting, N.; Heusler, A.; Horns, D.; Kohnle, A.; Lampeitl, H.; Panter, M.; Tluczykont, M.; Aharonian, F.; et al. The technical performance of the HEGRA system of imaging air Cherenkov telescopes. Astropart. Phys. 2003, 20, 267–291. [Google Scholar] [CrossRef]
- Blanch, O.; Lopez, J.; Martinez, M. Testing the effective scale of quantum gravity with the next generation of gamma ray telescopes. Astropart. Phys. 2003, 19, 245–252. [Google Scholar] [CrossRef][Green Version]
- Jacobson, T.; Liberati, S.; Mattingly, D. A Strong astrophysical constraint on the violation of special relativity by quantum gravity. Nature 2003, 424, 1019–1021. [Google Scholar] [CrossRef]
- Protheroe, R.J.; Meyer, H. An infrared background-TeV gamma-ray crisis? Phys. Lett. B 2000, 493, 1–6. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Piran, T. Planck scale deformation of Lorentz symmetry as a solution to the UHECR and the TeV gamma paradoxes. Phys. Rev. D 2001, 64, 036005. [Google Scholar] [CrossRef]
- Jacob, U.; Piran, T. Inspecting absorption in the spectra of extra-galactic gamma-ray sources for insight on Lorentz invariance violation. Phys. Rev. D 2008, 78, 124010. [Google Scholar] [CrossRef]
- Tavecchio, F.; Bonnoli, G. On the detectability of Lorentz invariance violation through anomalies in the multi-TeV γ-ray spectra of blazars. Astron. Astrophys. 2016, 585, A25. [Google Scholar] [CrossRef]
- Madau, P.; Phinney, E.S. Constraints on the Extragalactic Background Light from Gamma-ray Observations of High-Redshift Quasars. Astrophys. J. 1996, 456, 124. [Google Scholar] [CrossRef]
- De Angelis, A.; Galanti, G.; Roncadelli, M. Transparency of the Universe to gamma rays. Mon. Not. R. Astron. Soc. 2013, 432, 3245–3249. [Google Scholar] [CrossRef]
- Batković, I.; De Angelis, A.; Doro, M.; Manganaro, M. Axion-Like Particle Searches with IACTs. Universe 2021, 7, 185. [Google Scholar] [CrossRef]
- Abdalla, H.; Abe, H.; Acero, F.; Acharyya, A.; Adam, R.; Agudo, I.; Aguirre-Santaella, A.; Alfaro, R.; Alfaro, J.; Alispach, C.; et al. Sensitivity of the Cherenkov Telescope Array for probing cosmology and fundamental physics with gamma-ray propagation. JCAP 2021, 2, 48. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Akhperjanian, A.G.; Barrio, J.A.; Bernlöhr, K.; Bolz, O.; Börst, H.; Bojahr, H.; Contreras, J.L.; Cortina, J.; Denninghoff, S.; et al. Reanalysis of the high energy cutoff of the 1997 mkn 501 TeV energy spectrum. Astron. Astrophys. 2001, 366, 62. [Google Scholar] [CrossRef]
- Cologna, G.; Chakraborty, N.; Jacholkowska, A.; Lorentz, M.; Mohamed, M.; Perennes, C.; Romoli, C.; Wagner, S.J.; Wierzcholska, A.; HESS Collaboration; et al. The Exceptional Flare of Mrk 501 in 2014: Combined Observations with H.E.S.S. and FACT. AIP Conf. Proc. 2017, 1792, 050019. [Google Scholar] [CrossRef]
- Fairbairn, M.; Nilsson, A.; Ellis, J.; Hinton, J.; White, R. The CTA Sensitivity to Lorentz-Violating Effects on the Gamma-ray Horizon. JCAP 2014, 6, 5. [Google Scholar] [CrossRef]
- Lang, R.G.; Martínez-Huerta, H.; de Souza, V. Improved limits on Lorentz invariance violation from astrophysical gamma-ray sources. Phys. Rev. D 2019, 99, 043015. [Google Scholar] [CrossRef]
- Rubtsov, G.; Satunin, P.; Sibiryakov, S. Prospective constraints on Lorentz violation from ultrahigh-energy photon detection. Phys. Rev. D 2014, 89, 123011. [Google Scholar] [CrossRef]
- Rubtsov, G.; Satunin, P.; Sibiryakov, S. Constraints on violation of Lorentz invariance from atmospheric showers initiated by multi-TeV photons. JCAP 2017, 5, 49. [Google Scholar] [CrossRef]
- Bethe, H.; Heitler, W. On the Stopping of fast particles and on the creation of positive electrons. Proc. R. Soc. Lond. A 1934, 146, 83–112. [Google Scholar] [CrossRef]
- de Naurois, M.; Rolland, L. A high performance likelihood reconstruction of gamma-rays for Imaging Atmospheric Cherenkov Telescopes. Astropart. Phys. 2009, 32, 231. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.; Beilicke, M.; Bernlöhr, K.; Börst, H.G.; Bojahr, H.; Bolz, O.; Coarasa, T.; Contreras, J.L.; Cortina, J.; et al. The Crab nebula and pulsar between 500-GeV and 80-TeV. Observations with the HEGRA stereoscopic air Cerenkov telescopes. Astrophys. J. 2004, 614, 897–913. [Google Scholar] [CrossRef]
- Abramowski, A.; Aharonian, F.; Ait Benkhali, F.; Akhperjanian, A.G.; Angüner, E.; Anton, G.; Balenderan, S.; Balzer, A.; Barnacka, A.; Becherini, Y.; et al. HESS Observations of the Crab during its March 2013 GeV gamma-ray Flare. Astron. Astrophys. 2014, 562, L4. [Google Scholar] [CrossRef]
- Martínez-Huerta, H.; Pérez-Lorenzana, A. Restrictions from Lorentz invariance violation on cosmic ray propagation. Phys. Rev. D 2017, 95, 063001. [Google Scholar] [CrossRef]
- Astapov, K.; Kirpichnikov, D.; Satunin, P. Photon splitting constraint on Lorentz Invariance Violation from Crab Nebula spectrum. JCAP 2019, 4, 54. [Google Scholar] [CrossRef]
- Albert, A.; Alfaro, R.; Alvarez, C.; Angeles Camacho, J.R.; Arteaga-Velázquez, J.C.; Arunbabu, K.P.; Avila Rojas, D.; Ayala Solares, H.A.; Baghmanyan, V.; Belmont-Moreno, E.; et al. Constraints on Lorentz Invariance Violation from HAWC Observations of Gamma Rays above 100 TeV. Phys. Rev. Lett. 2020, 124, 131101. [Google Scholar] [CrossRef]
- Amenomori, M.; Bao, Y.W.; Bi, X.J.; Chen, D.; Chen, T.L.; Chen, W.Y.; Chen, X.; Chen, Y.; Cirennima; Cui, S.W.; et al. First Detection of Photons with Energy beyond 100 TeV from an Astrophysical Source. Phys. Rev. Lett. 2019, 123, 051101. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Camacho, J.R.A.; Arceo, R.; Arteaga-Velázquez, J.C.; Arunbabu, K.P.; Avila Rojas, D.; et al. Measurement of the Crab Nebula at the Highest Energies with HAWC. Astrophys. J. 2019, 881, 134. [Google Scholar] [CrossRef]
- Satunin, P. New constraints on Lorentz Invariance violation from Crab Nebula spectrum beyond 100 TeV. Eur. Phys. J. C 2019, 79, 1011. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, M.J.; Chen, S.Z.; Hu, H.B.; Liu, C.; Liu, Y.; Ma, L.L.; Ma, X.H.; Sheng, X.D.; Wu, H.R.; et al. Introduction to Large High Altitude Air Shower Observatory (LHAASO). Chin. Astron. Astrophys. 2019, 43, 457–478. [Google Scholar] [CrossRef]
- LHAASO Collaboration. Exploring Lorentz Invariance Violation from Ultra-high-energy Gamma Rays Observed by LHAASO. arXiv 2021, arXiv:2106.12350. [Google Scholar]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. MAGIC very large zenith angle observations of the Crab Nebula up to 100 TeV. Astron. Astrophys. 2020, 635, A158. [Google Scholar] [CrossRef]
- D’Amico, G.; Terzić, T.; Strišković, J.; Doro, M.; Strzys, M.; van Scherpenberg, J. Signal estimation in On/Off measurements including event-by-event variables. Phys. Rev. D 2021, 103, 123001. [Google Scholar] [CrossRef]
- Nogués, L.; Lin, T.T.Y.; Perennes, C.; Gent, A.E.; Bolmont, J.; Gaug, M.; Jacholkowska, A.; Martinez, M.; Otte, A.N.; Wagner, R.; et al. First combined studies on Lorentz Invariance Violation from observations of astrophysical sources. In Proceedings of the 35th International Cosmic Ray Conference (ICRC2017), Busan, Korea, 12–20 July 2017; Volume 301, p. 646. [Google Scholar]
- Ellis, J.R.; Mavromatos, N.E.; Nanopoulos, D.V. Quantum gravitational diffusion and stochastic fluctuations in the velocity of light. Gen. Relativ. Gravit. 2000, 32, 127–144. [Google Scholar] [CrossRef]
- Vasileiou, V.; Granot, J.; Piran, T.; Amelino-Camelia, G. A Planck-scale limit on spacetime fuzziness and stochastic Lorentz invariance violation. Nat. Phys. 2015, 11, 344–346. [Google Scholar] [CrossRef]
- Bolmont, J. Is the Speed of Light in Vacuum Really Constant? Habilitation à Diriger des Recherches. Habilitation Thesis, UPMC, Paris, France, 2016. [Google Scholar]
- Kostelecky, V.A.; Mewes, M. Astrophysical Tests of Lorentz and CPT Violation with Photons. Astrophys. J. Lett. 2008, 689, L1–L4. [Google Scholar] [CrossRef]
- Kislat, F.; Krawczynski, H. Planck-scale constraints on anisotropic Lorentz and CPT invariance violations from optical polarization measurements. Phys. Rev. D 2017, 95, 083013. [Google Scholar] [CrossRef]
- Friedman, A.S.; Gerasimov, R.; Leon, D.; Stevens, W.; Tytler, D.; Keating, B.G.; Kislat, F. Improved constraints on anisotropic birefringent Lorentz invariance and CPT violation from broadband optical polarimetry of high redshift galaxies. Phys. Rev. D 2020, 102, 043008. [Google Scholar] [CrossRef]
- Toma, K.; Mukohyama, S.; Yonetoku, D.; Murakami, T.; Gunji, S.; Mihara, T.; Morihara, Y.; Sakashita, T.; Takahashi, T.; Wakashima, Y.; et al. Strict Limit on CPT Violation from Polarization of Gamma-ray Burst. Phys. Rev. Lett. 2012, 109, 241104. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Mewes, M. Constraints on relativity violations from gamma-ray bursts. Phys. Rev. Lett. 2013, 110, 201601. [Google Scholar] [CrossRef] [PubMed]
- Gotz, D.; Laurent, P.; Antier, S.; Covino, S.; D’Avanzo, P.; D’Elia, V.; Melandri, A. GRB 140206A: The most distant polarized Gamma-ray Burst. Mon. Not. R. Astron. Soc. 2014, 444, 2776–2782. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Mewes, M. Electrodynamics with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2009, 80, 015020. [Google Scholar] [CrossRef]
- De Angelis, A.; Tatischeff, V.; Tavani, M.; Oberlack, U.; Grenier, I.; Hanlon, L.; Walter, R.; Argan, A.; von Ballmoos, P.; Bulgarelli, A.; et al. The e-ASTROGAM mission. Exp. Astron. 2017, 44, 25–82. [Google Scholar] [CrossRef]

| ∝ | ||||
| ∝ |
| Effect | Source | Type | Distance | Method | [GeV] | [GeV] | Instr. | Ref. | Sec. |
|---|---|---|---|---|---|---|---|---|---|
| Time delay | Mrk 421 | AGN | band comparison | Whipple | [32] | Section 2.1 | |||
| Time delay | Mrk 501 | AGN | ECF | MAGIC | [37] | Section 2.2 | |||
| Time delay | Mrk 501 | AGN | ML | MAGIC | [42] | Section 2.4 | |||
| Time delay | PKS 2155-304 | AGN | MCCF | H.E.S.S. | [65] | Section 2.6 | |||
| CWT | |||||||||
| Time delay | PKS 2155-304 | AGN | ML | H.E.S.S. | [67] | Section 2.6 | |||
| Time delay | GRB 090510 | GRB | PV, SMM, | LAT | [38] | Section 2.13 | |||
| and ML | |||||||||
| Time delay | Crab | Pulsar | kpc | PC | VERITAS | [73] | Section 2.8 | ||
| DisCan | [74] | ||||||||
| Time delay | PG 1553+113 | AGN | ML | H.E.S.S. | [68] | Section 2.7 | |||
| Time delay | Vela | Pulsar | kpc | ML | H.E.S.S. | [79] | Section 2.10 | ||
| Universe transparency | Multiple (30) | AGN | TS | Multiple | [97] | Section 3.1.2 | |||
| Bethe–Heitler | Crab | Nebula | kpc | ML | HEGRA | [126] | Section 3.2 | ||
| H.E.S.S. | |||||||||
| Time delay | Crab | Pulsar | kpc | PC | MAGIC | [77] | Section 2.9 | ||
| ML | |||||||||
| Time delay | Mrk 501 | AGN | ML | H.E.S.S. | [81] | Section 2.11 | |||
| Universe transparency | TS | Section 3.1.3 | |||||||
| Universe transparency | Multiple (6) | AGN | TS | Multiple | [124] | Section 3.1.4 | |||
| Photon decay | Multiple (4) | Galactic | kpc | TS | HAWC | [133] | Section 3.3 | ||
| Photon splitting | |||||||||
| Time delay | GRB 190114C | GRB | ML | MAGIC | [83] | Section 2.12 | |||
| Photon decay | J2032+4102 | Stellar | kpc | TS | LHAASO | [138] | Section 3.3 | ||
| Photon splitting | cluster |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terzić, T.; Kerszberg, D.; Strišković, J. Probing Quantum Gravity with Imaging Atmospheric Cherenkov Telescopes. Universe 2021, 7, 345. https://doi.org/10.3390/universe7090345
Terzić T, Kerszberg D, Strišković J. Probing Quantum Gravity with Imaging Atmospheric Cherenkov Telescopes. Universe. 2021; 7(9):345. https://doi.org/10.3390/universe7090345
Chicago/Turabian StyleTerzić, Tomislav, Daniel Kerszberg, and Jelena Strišković. 2021. "Probing Quantum Gravity with Imaging Atmospheric Cherenkov Telescopes" Universe 7, no. 9: 345. https://doi.org/10.3390/universe7090345
APA StyleTerzić, T., Kerszberg, D., & Strišković, J. (2021). Probing Quantum Gravity with Imaging Atmospheric Cherenkov Telescopes. Universe, 7(9), 345. https://doi.org/10.3390/universe7090345






