Origin of Low- and High-Energy Monopole Collectivity in 132Sn
Abstract
1. Introduction
2. The FRSA Model
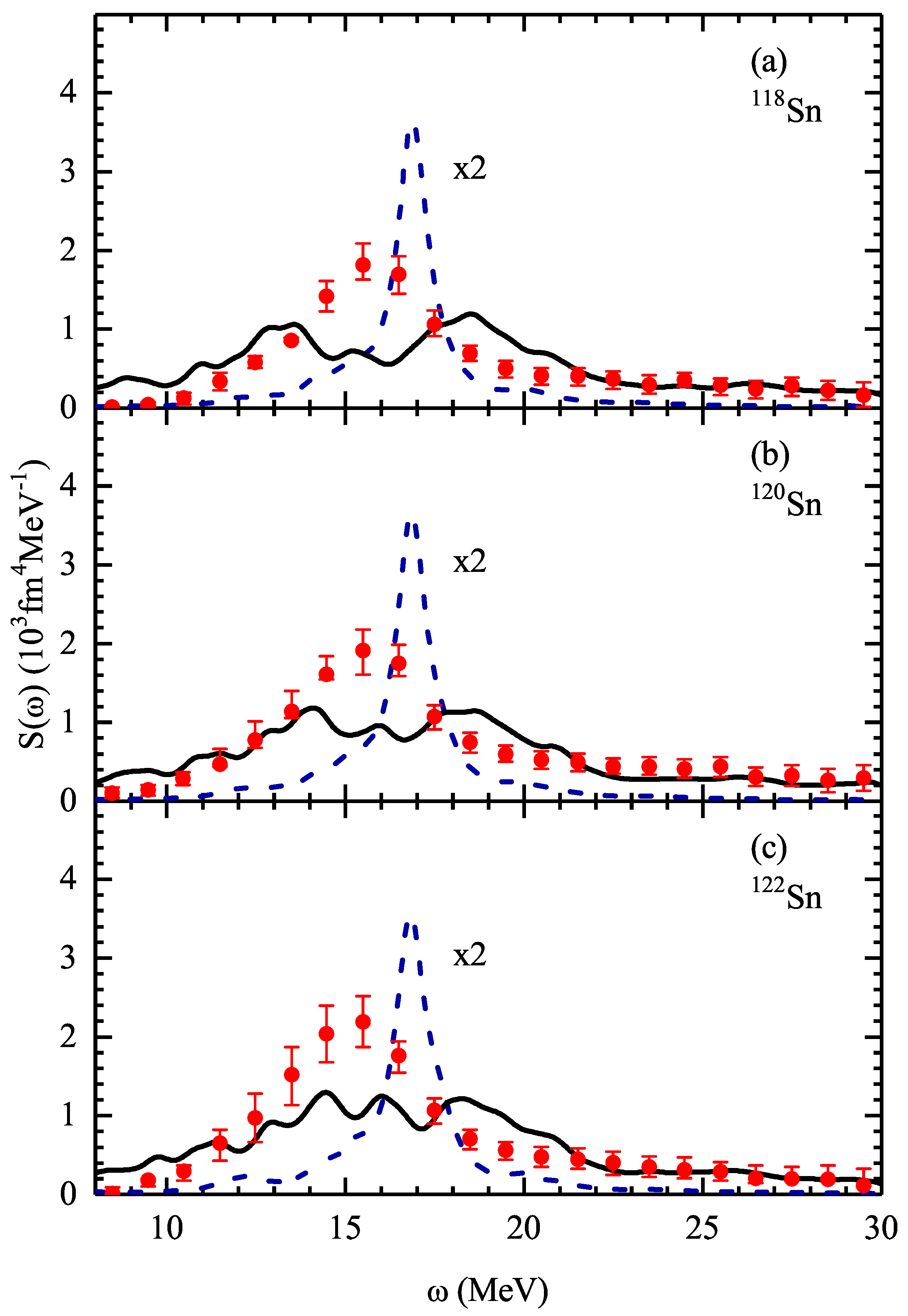
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blaizot, J.P. Nuclear compressibilitles. Phys. Rep. 1980, 64, 171–248. [Google Scholar] [CrossRef]
- Baron, E.; Cooperstein, J.; Kahana, S. Type-II supernovae in 12M⊙ and 15M⊙ stars: The equation of state and general relativity. Phys. Rev. Lett. 1985, 55, 126–129. [Google Scholar] [CrossRef] [PubMed]
- Bethe, H.A. Supernova mechanisms. Rev. Mod. Phys. 1990, 62, 801–866. [Google Scholar] [CrossRef]
- Glendenning, N.K. Neutron-star masses as a constraint on the nuclear compression modulus. Phys. Rev. Lett. 1986, 57, 1120–1123. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron star structure and the equation of state. Astrophys. J. 2001, 550, 426–442. [Google Scholar] [CrossRef]
- Youngblood, D.H.; Clark, H.L.; Lui, Y.-W. Incompressibility of nuclear matter from the giant monopole resonance. Phys. Rev. Lett. 1999, 82, 691–694. [Google Scholar] [CrossRef]
- Youngblood, D.H.; Lui, Y.-W.; Clark, H.L.; John, B.; Tokimoto, Y.; Chen, X. Isoscalar E0–E3 strength in 116Sn, 144Sm, 154Sm, and 208Pb. Phys. Rev. C 2004, 70, 034315. [Google Scholar] [CrossRef]
- Lui, Y.-W.; Youngblood, D.H.; Tokimoto, Y.; Clark, H.L.; John, B. Giant resonances in 112Sn and 124Sn: Isotopic dependence of monopole resonance energies. Phys. Rev. C 2004, 70, 014307. [Google Scholar] [CrossRef]
- Li, T.; Garg, U.; Liu, Y.; Marks, R.; Nayak, B.K.; Madhusudhana Rao, P.V.; Fujiwara, M.; Hashimoto, H.; Kawase, K.; Nakanishi, K.; et al. Isotopic dependence of the giant monopole resonance in the even-A 112–124Sn isotopes and the asymmetry term in nuclear incompressibility. Phys. Rev. Lett. 2007, 99, 162503. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Garg, U.; Liu, Y.; Marks, R.; Nayak, B.K.; Madhusudhana Rao, P.V.; Fujiwara, M.; Hashimoto, H.; Nakanishi, K.; Okumura, S.; et al. Isoscalar giant resonances in the Sn nuclei and implications for the asymmetry term in the nuclear-matter incompressibility. Phys. Rev. C 2010, 81, 034309. [Google Scholar] [CrossRef]
- Patel, D.; Garg, U.; Itoh, M.; Akimune, H.; Berg, G.P.A.; Fujiwara, M.; Harakeh, M.N.; Iwamoto, C.; Kawabata, T.; Kawase, K.; et al. Excitation of giant monopole resonance in 208Pb and 116Sn using inelastic deuteron scattering. Phys. Lett. B 2014, 735, 387–390. [Google Scholar] [CrossRef]
- Garg, U.; Colò, G. The compression-mode giant resonances and nuclear incompressibility. Prog. Part. Nucl. Phys. 2018, 101, 55–95. [Google Scholar] [CrossRef]
- Giai, N.V.; Sagawa, H. Monopole and dipole compression modes in nuclei. Nucl. Phys. A 1981, 371, 1–18. [Google Scholar] [CrossRef]
- Agrawal, B.K.; Shlomo, S. Consequences of self-consistency violations in Hartree-Fock random-phase approximation calculations of the nuclear breathing mode energy. Phys. Rev. C 2004, 70, 014308. [Google Scholar] [CrossRef]
- Colò, G.; Giai, N.V.; Meyer, J.; Bennaceur, K.; Bonche, P. Microscopic determination of the nuclear incompressibility within the nonrelativistic framework. Phys. Rev. C 2004, 70, 024307. [Google Scholar] [CrossRef]
- Terasaki, J.; Engel, J. Self-consistent description of multipole strength: Systematic calculations. Phys. Rev. C 2006, 74, 044301. [Google Scholar] [CrossRef]
- Paar, N.; Vretenar, D.; Khan, E.; Colò, G. Exotic modes of excitation in atomic nuclei far from stability. Rep. Prog. Phys. 2007, 70, 691–793. [Google Scholar] [CrossRef]
- Li, J.; Colò, G.; Meng, J. Microscopic linear response calculations based on the Skyrme functional plus the pairing contribution. Phys. Rev. C 2008, 78, 064304. [Google Scholar] [CrossRef]
- Khan, E. Role of superfluidity in nuclear incompressibilities. Phys. Rev. C 2009, 80, 011307(R). [Google Scholar] [CrossRef]
- Cao, L.-G.; Sagawa, H.; Colò, G. Microscopic study of the isoscalar giant monopole resonance in Cd, Sn, and Pb isotopes. Phys. Rev. C 2012, 86, 054313. [Google Scholar] [CrossRef]
- Yüksel, E.; Khan, E.; Bozkurt, K. The soft giant monopole resonance as a probe of the spin-orbit splitting. Eur. Phys. J. A 2013, 49, 124. [Google Scholar] [CrossRef]
- Khan, E.; Paar, N.; Vretenar, D.; Cao, L.-G.; Sagawa, H.; Colò, G. Incompressibility of finite fermionic systems: Stable and exotic atomic nuclei. Phys. Rev. C 2013, 87, 064311. [Google Scholar] [CrossRef]
- Hamamoto, I.; Sagawa, H. Self-consistent Hartree-Fock and RPA Green’s function method indicate no pygmy resonance in the monopole response of neutron-rich Ni isotopes. Phys. Rev. C 2014, 90, 031302(R). [Google Scholar] [CrossRef]
- Péru, S.; Berger, J.F.; Bortignon, P.F. Giant resonances in exotic spherical nuclei within the RPA approach with the Gogny force. Eur. Phys. J. A 2005, 26, 25–32. [Google Scholar] [CrossRef][Green Version]
- Gambacurta, D.; Grasso, M.; De Donno, V.; Co’, G.; Catara, F. Second random-phase approximation with the Gogny force: First applications. Phys. Rev. C 2012, 86, 021304(R). [Google Scholar] [CrossRef]
- Péru, S.; Martini, M. Mean field based calculations with the Gogny force: Some theoretical tools to explore the nuclear structure. Eur. Phys. J. A 2014, 50, 88. [Google Scholar] [CrossRef]
- Piekarewicz, J. Self-consistent description of nuclear compressional modes. Phys. Rev. C 2001, 64, 024307. [Google Scholar] [CrossRef]
- Ma, Z.-Y.; Wandelt, A.; Giai, N.V.; Vretenar, D.; Ring, P.; Cao, L.-G. Collective multipole excitations in a microscopic relativistic approach. Nucl. Phys. A 2002, 703, 222–239. [Google Scholar] [CrossRef]
- Vretenar, D.; NikŠić, T.; Ring, P. A microscopic estimate of the nuclear matter compressibility and symmetry energy in relativistic mean-field models. Phys. Rev. C 2003, 68, 024310. [Google Scholar] [CrossRef]
- Drożdż, S.; Nishizaki, S.; Speth, J.; Wambach, J. The nuclear response within extended RPA theories. Phys. Rep. 1990, 197, 1–65. [Google Scholar] [CrossRef]
- Kamerdzhiev, S.; Speth, J.; Tertychny, G. Microscopic analysis of the breathing mode in 40Ca and 58Ni. Eur. Phys. J. A 2000, 7, 483–490. [Google Scholar] [CrossRef]
- Litvinova, E.; Ring, P.; Tselyaev, V. Particle-vibration coupling within covariant density functional theory. Phys. Rev. C 2007, 75, 064308. [Google Scholar] [CrossRef]
- Tselyaev, V.; Speth, J.; Krewald, S.; Litvinova, E.; Kamerdzhiev, S.; Lyutorovich, N.; Avdeenkov, A.; Grümmer, F. Description of the giant monopole resonance in the even-A 112–124Sn isotopes within a microscopic model including quasiparticle-phonon coupling. Phys. Rev. C 2009, 79, 034309. [Google Scholar] [CrossRef]
- Severyukhin, A.P.; Åberg, S.; Arsenyev, N.N.; Nazmitdinov, R.G. Spreading widths of giant resonances in spherical nuclei: Damped transient response. Phys. Rev. C 2017, 95, 061305(R). [Google Scholar] [CrossRef]
- Li, B.-A.; Xie, W.-J. Differential analysis of incompressibility in neutron-rich nuclei. arXiv 2021, arXiv:2102.10683. [Google Scholar]
- Blomqvist, J. The 3−⊗3− two-phonon quartet and the proton pairing vibration in 208Pb. Phys. Lett. B 1970, 33, 541–544. [Google Scholar] [CrossRef]
- Igo, G.J.; Barnes, P.D.; Flynn, E.R. Mixing of two-particle, two-hole states in Pb. Phys. Rev. Lett. 1970, 24, 470–473. [Google Scholar] [CrossRef]
- Julin, R.; Kantele, J.; Kumpulainen, J.; Luontama, M.; Passoja, A.; Trzaska, W.; Verho, E.; Blomqvist, J. E0 study of 0+ states near 5 MeV in Pb. Phys. Rev. C 1987, 36, 1129–1131. [Google Scholar] [CrossRef]
- Heusler, A.; Faestermann, T.; Hertenberger, R.; Wirth, H.-F.; von Brentano, P. Identification of the 0+ proton pairing vibration state in the doubly magic nucleus 208Pb by particle spectroscopy. Phys. Rev. C 2015, 91, 044325. [Google Scholar] [CrossRef]
- Lanza, E.G.; Andrés, M.V.; Catara, F.; Chomaz, P.; Volpe, C. Role of anharmonicities and nonlinearities in heavy ion collisions a microscopic approach. Nucl. Phys. A 1997, 613, 445–471. [Google Scholar] [CrossRef][Green Version]
- Ponomarev, V.Y.; von Neumann-Cosel, P. Fragmentation of the two-octupole phonon multiplet in 208Pb. Phys. Rev. Lett. 1999, 82, 501–504. [Google Scholar] [CrossRef]
- Yeh, M.; Garrett, P.E.; McGrath, C.A.; Yates, S.W.; Belgya, T. Two-phonon octupole excitation in 208Pb. Phys. Rev. Lett. 1996, 76, 1208–1211. [Google Scholar] [CrossRef]
- Severyukhin, A.P.; Åberg, S.; Arsenyev, N.N.; Nazmitdinov, R.G.; Pichugin, K.N. Random matrix analysis of the monopole strength distribution in 208Pb. Phys. At. Nucl. 2016, 79, 835–841. [Google Scholar] [CrossRef]
- Fogelberg, B.; Hellström, M.; Jerrestam, D.; Mach, H.; Blomqvist, J.; Kerek, A.; Norlin, L.O.; Omtvedt, J.P. Detailed spectroscopy of the doubly closed shell nucleus 132Sn: First observation of octupole collectivity. Phys. Rev. Lett. 1994, 73, 2413–2416. [Google Scholar] [CrossRef]
- Severyukhin, A.P.; Voronov, V.V.; Giai, N.V. Effects of phonon-phonon coupling on low-lying states in neutron-rich Sn isotopes. Eur. Phys. J. A 2004, 22, 397–403. [Google Scholar] [CrossRef]
- Giai, N.V.; Stoyanov, C.; Voronov, V.V. Finite rank approximation for random phase approximation calculations with Skyrme interactions: An application to Ar isotopes. Phys. Rev. C 1998, 57, 1204–1209. [Google Scholar] [CrossRef]
- Severyukhin, A.P.; Voronov, V.V.; Giai, N.V. Effects of the particle-particle channel on properties of low-lying vibrational states. Phys. Rev. C 2008, 77, 024322. [Google Scholar] [CrossRef]
- Severyukhin, A.P.; Arsenyev, N.N.; Pietralla, N. Proton-neutron symmetry in 92Zr, 94Mo with Skyrme interactions in a separable approximation. Phys. Rev. C 2012, 86, 024311. [Google Scholar] [CrossRef]
- Severyukhin, A.P.; Arsenyev, N.N.; Pietralla, N.; Werner, V. Impact of variational space on M1 transitions between first and second quadrupole excitations in 132,134,136Te. Phys. Rev. C 2014, 90, 011306(R). [Google Scholar] [CrossRef]
- Giai, N.V.; Sagawa, H. Spin-isospin and pairing properties of modified Skyrme interactions. Phys. Lett. B 1981, 106, 379–382. [Google Scholar] [CrossRef]
- Bartel, J.; Quentin, P.; Brack, M.; Guet, C.; Håkansson, H.-B. Towards a better parametrisation of Skyrme-like effective forces: A critical study of the SkM force. Nucl. Phys. A 1982, 386, 79–100. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities part II. Nuclear far form stabilities. Nucl. Phys. A 1998, 635, 231–256, Erratum in 1998, 643, 441. [Google Scholar] [CrossRef]
- Severyukhin, A.P.; Arsenyev, N.N.; Borzov, I.N.; Sushenok, E.O. Multi-neutron emission of Cd isotopes. Phys. Rev. C 2017, 95, 034314. [Google Scholar] [CrossRef]
- Soloviev, V.G. Theory of Atomic Nuclei: Quasiparticles and Phonons; Institute of Physics: Bristol, UK, 1992. [Google Scholar]
- Voronov, V.V.; Karadjov, D.; Catara, F.; Severyukhin, A.P. Ground state correlations beyond random phase approximation and collective excitations. Phys. Part. Nucl. 2000, 31, 452–470. [Google Scholar]
- Colò, G.; Bortignon, B.F.; Sarchi, D.; Khoa, D.T.; Khan, E. Giai, N.V. Excited states of neutron-rich nuclei: Mean field theory and beyond. Nucl. Phys. A 2003, 722, 111c–116c. [Google Scholar] [CrossRef]
- Rosiak, D.; Seidlitz, M.; Reiter, P.; Naïdja, H.; Tsunoda, Y.; Togashi, T.; Nowacki, F.; Otsuka, T.; Colò, G.; Arnswald, K.; et al. Enhanced quadrupole and octupole strength in doubly magic 132Sn. Phys. Rev. Lett. 2018, 121, 252501. [Google Scholar] [CrossRef]
- Benito, J.; Fraile, L.M.; Korgul, A.; Piersa, M.; Adamska, E.; Andreyev, A.N.; Álvarez-Rodríguez, R.; Barzakh, A.E.; Benzoni, G.; Berry, T.; et al. Detailed spectroscopy of doubly magic 132Sn. Phys. Rev. C 2020, 102, 014328. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Warr, N.; Fransen, C.; Boukharouba, N.; Werner, V.; Yates, S.W.; Weil, J.L.; McEllistrem, M.T. Three-phonon excitations in 124Sn. Nucl. Phys. A 2005, 747, 206–226. [Google Scholar] [CrossRef]




| Energy (MeV) | (W.u.) | Structure | ||
|---|---|---|---|---|
| SLy4 | 4.5 | 6.9 | 61% | |
| 33% | ||||
| 5.5 | 28.0 | 12% | ||
| 12% | ||||
| 16% | ||||
| 11% | ||||
| 5.1 | 11.3 | 66% | ||
| 19% | ||||
| 6.9 | 8.5 | 85% | ||
| SkM | 4.3 | 6.0 | 70% | |
| 25% | ||||
| 4.6 | 22.0 | 22% | ||
| 14% | ||||
| 11% | ||||
| 10% | ||||
| 4.8 | 9.5 | 75% | ||
| 13% | ||||
| 5.5 | 4.9 | 92% | ||
| SGII | 4.3 | 7.0 | 63% | |
| 27% | ||||
| 4.5 | 27.5 | 16% | ||
| 12% | ||||
| 11% | ||||
| 11% | ||||
| 4.8 | 13.3 | 49% | ||
| 24% | ||||
| 13% | ||||
| 6.2 | 10.6 | 75% |
| Energy (MeV) | (W.u.) | |||||||
|---|---|---|---|---|---|---|---|---|
| Expt. | Theory | Expt. | Theory | |||||
| SLy4 | SkM | SGII | SLy4 | SkM | SGII | |||
| 4.04 | 4.4 | 4.0 | 3.8 | 6.8 | 5.6 | 6.3 | ||
| 4.35 | 5.2 | 4.2 | 3.8 | 26.2 | 20.1 | 24.1 | ||
| 4.42 | 5.0 | 4.6 | 4.4 | 11.2 | 9.0 | 12.3 | ||
| 4.94 | 6.9 | 5.5 | 6.0 | – | 8.5 | 4.8 | 9.7 | |
| Energy (MeV) | Structure | NEWSR Fraction | |||||
|---|---|---|---|---|---|---|---|
| A | B | A | B | A | B | ||
| SLy4 | 8.8 | 8.7 | 96 | 93 | 1.1% | 1.6% | |
| 10.0 | 9.9 | 61 | 49 | 5.0% | 6.0% | ||
| +27 | +34 | ||||||
| 10.4 | 10.4 | 55 | 47 | 3.2% | 1.9% | ||
| +37 | +43 | ||||||
| SkM | 8.1 | 8.0 | 46 | 42 | 6.5% | 7.8% | |
| +39 | +38 | ||||||
| 8.6 | 8.6 | 52 | 59 | 1.9% | 1.6% | ||
| +43 | +36 | ||||||
| 9.6 | 9.6 | 94 | 92 | 0.2% | 0.2% | ||
| SGII | 7.7 | 7.6 | 62 | 60 | 10.2% | 11.4% | |
| +17 | +16 | ||||||
| 8.5 | 8.5 | 80 | 81 | 0.3% | 0.3% | ||
| +19 | +18 | ||||||
| 9.5 | 9.5 | 93 | 92 | 0.2% | 0.2% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arsenyev, N.N.; Severyukhin, A.P. Origin of Low- and High-Energy Monopole Collectivity in 132Sn. Universe 2021, 7, 145. https://doi.org/10.3390/universe7050145
Arsenyev NN, Severyukhin AP. Origin of Low- and High-Energy Monopole Collectivity in 132Sn. Universe. 2021; 7(5):145. https://doi.org/10.3390/universe7050145
Chicago/Turabian StyleArsenyev, Nikolay N., and Alexey P. Severyukhin. 2021. "Origin of Low- and High-Energy Monopole Collectivity in 132Sn" Universe 7, no. 5: 145. https://doi.org/10.3390/universe7050145
APA StyleArsenyev, N. N., & Severyukhin, A. P. (2021). Origin of Low- and High-Energy Monopole Collectivity in 132Sn. Universe, 7(5), 145. https://doi.org/10.3390/universe7050145






