Abstract
In this paper, we investigate the motion of a classical spinning test particle in a background of a spherically symmetric black hole based on the novel four-dimensional Einstein–Gauss–Bonnet gravity [D. Glavan and C. Lin, Phys. Rev. Lett. 124, 081301 (2020)]. We find that the effective potential of a spinning test particle in this background could have two minima when the Gauss–Bonnet coupling parameter is nearly in a special range (M is the mass of the black hole), which means a particle can be in two separate orbits with the same spin-angular momentum and orbital angular momentum, and the accretion disc could have discrete structures. We also investigate the innermost stable circular orbits of the spinning test particle and find that the corresponding radius could be smaller than the cases in general relativity.
1. Introduction
As the most successful gravitational theory, general relativity (GR) can explain the relation between geometry and matter. One of the most impressive results derived from GR is black hole solutions. As vacuum solutions of strong gravitational systems, black holes have lots of interesting characters, for examples, a binary black hole system can produce gravitational waves [1,2,3,4,5], and a black hole can act as an accelerator of particles [6,7]. However, we should note that, even though GR is so powerful and can be used to explain many phenomena, there are still some problems that cannot be interpreted by GR. Therefore, it is believed that there should be a more fundamental theory beyond GR.
It is well-known that the existence of a singularity located inside a black hole leads to geodesics incompleteness [8,9]. To overcome the problem of singularity, several quantum theories of gravity have been proposed, like the superstring/M theory and the extension of such theories. With the help of the perturbation approximation of these theories, the Gauss–Bonnet (GB) term was found as the next leading order term [10,11,12], and this term has ghost-free combinations and does not add higher derivative terms into the gravitational field equations [13]. The GB term appears in D-dimensional spacetime as follows
where D is the number of the spacetime dimensions, is the GB coupling parameter with mass dimension , and the GB invariant is defined as
Many black hole solutions of GB gravity in have been derived, such as the vacuum case [14], Einstein-Maxwell fields with a GB term [15,16], and anti-de Sitter (AdS) case [17]. In four-dimensional spacetime, the GB term does not make contributions to the gravitational dynamics, which makes the four-dimensional minimally coupled GB gravity is hard to obtain. However, very recently, D. Glavan and C. Lin [18] proposed a novel four-dimensional Einstein–Gauss–Bonnet (EGB) gravity that bypasses the Lovelock theorem by adopting an artful coupling constant . It takes the contributions from the Gauss–Bonnet term into the dynamics of the four-dimensional spcaetime. The same idea about rescaling the coupling constant has been already introduced in Ref. [19].
In this novel four-dimensional EGB gravity, the GB invariant term does not affect the properties of the massless graviton and a four-dimensional static and spherically symmetric black hole solution was obtained. The stability and shadow of this four-dimensional EGB black hole have been studied in Ref. [20], where the quasinormal modes of a scalar, electromagnetic, and gravitational perturbations were studied. The solutions of a charged black hole [21] and spinning black hole [22] have also been obtained, and a constraint to the GB parameter was first given in Ref. [22] in terms of the shadow of the rotating black hole. Inspired by the novel four-dimensional EGB gravity, the novel four-dimensional Einstein–Lovelock gravities are also proposed [23,24]. Note that the way of rescaling coupling constant is based on the limit of in a higher D-dimensional spacetime, where the limit is not continuous due to the parameter D—the number of dimensions—a new way for the dimensional-regularization is proposed [25]. Apart from the discontinuousness of the dimension, there are also several works [26,27,28,29,30,31,32,33,34,35,36] pointing out that this novel four-dimensional EGB gravity [18] will cause problems at the level of action and equation of motion and give the improved four-dimensional EGB gravity. However, the Schwarzchild black hole solution in this novel four-dimensional EGB gravity [18] is the same as the result in the improved four-dimensional EGB gravity, which means the properties of the black hole still deserve to be investigated.
It is known that a massless or massive particle can orbit around a central black hole and the motion depends on the geometry of the central black hole. The innermost stable circular orbit (ISCO) of the test particle is the last stable circular orbit, and when a particle is in the location with a radius less than the ISCO, it will plunge into the black hole. Therefore the information of the ISCO and the motion of the test particle in the background black hole could give us some properties of the accretion disc and the corresponding radiation spectrum [37]. In Ref. [38], the authors extended the range of the GB coupling parameter for the black hole solution to (M is the mass of the black hole) and investigated the shadow and ISCO of a spinless test particle. They found that a positive (or negative) GB coupling parameter will reduce (or increase) the ISCO radius. It is shown that the spin of a test particle can also reduce or increase the ISCO radius of a test particle in the background of a black hole in GR [39]. Inspired by the effects of the four-dimensional GB term and the non-vanishing spin on the motion of the test particle, it is necessary to investigate the motion of a spinning test particle and the corresponding ISCO in this novel four-dimensional EGB black hole. In this paper, we will investigate the motion of a spinning test particle in the background of the novel four-dimensional EGB black hole and show how the ISCO of the spinning test particle is changed. For simplicity, we only consider the motion of a spinning test particle in the equatorial plane.
This paper is organized as follows. In Section 2, we use the MPD equation to obtain the four-momentum and four-velocity of a spinning test particle in the novel four-dimensional EGB black hole background. In Section 2.2, we study the motion of the spinning test particle and give the relations between the motion of the spinning test particle and the properties of the four-dimensional EGB black hole. Finally, a brief summary and conclusion are given in Section 3.
2. Motion of a Spinning Test Particle in a Four-Dimensional EGB Black Hole
2.1. Four-Momentum and Four-Velocity of the Spinning Test Particle
In this part, we will solve the equations of motion for a spinning test particle in the novel four-dimensional EGB black hole background. Firstly, let us review the solution of the four-dimensional EGB black hole. The action of the D-dimensional EGB gravity is described by
where is the gravitational constant and will be set as in this paper. The GB term does not contribute to the dynamics of the four-dimensional spacetime because it is a total derivative. Recently, by rescaling the coupling parameter as
and taking the limit , Glaan and Lin [18] obtained the four-dimensional novel EGB gravity. The four-dimensional static spherically symmetric black hole solution was found [18]
where M is the mass of the black hole and the coupling parameter [38]. Solving , one can get two black hole horizons
In fact, the above solution (5)–(7) was also found in gravity with a conformal anomaly in Ref. [40] and was extended to the case with a cosmological in Ref. [41].
For a spinning test particle, its motion will not follow the geodesics because of the spin-curvature force . The equations of motion for the spinning test particle are described by the Mathisson-Papapetrou-Dixon (MPD) equations [42,43,44,45,46,47,48,49,50] under the “pole–dipole” approximation, and the four-velocity and the four-momentum are not parallel [46,51] due to the spin-curvature force. The MPD equations are
where , , and are the four-momentum, spin tensor, and tangent vector of the spinning test particle along the trajectory, respectively. Note that the MPD equations are not uniquely specified and we should use a spin-supplementary condition to determine them. This spin-supplementary condition is related to the center of mass of the spinning test particle with different observers [52,53,54,55,56]. In this paper, we choose the Tulczyjew spin-supplementary condition [57]
and the four-momentum satisfies
which makes sure that the spinning test particle stays timelike along the trajectory, where m is the mass of the test particle. On the contrary, the four-velocity would be superluminal [46,51] when the spin of the test particle is too large. Actually, this superluminal behavior comes from the ignorance of the “multi-pole” effects. When such effects are considered, the superluminal problem can be avoided [58,59,60,61,62]. For the properties of the spinning test particle in different black hole backgrounds, see Refs. [39,55,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84].
For the equatorial motion of the spinning test particle with spin-aligned or anti-aligned orbits, the four-momentum and spin tensor should satisfy and . The non-vanishing independent variables for the equatorial orbits are , , , and . After adopting the spin-supplementary condition (10), we have [47]
Substituting Equation (12) into the following equation
and using Equation (11), we get the component of spin tensor
The non-vanishing components of the spin tensor in the four-dimensional EGB black hole background are
where the parameter s is the spin angular momentum of the test particle and the spin direction is perpendicular to the equatorial plane.
Due to the existence of the spin-curvature coupling term, the conserved quantities of the spinning test particle are modified. The relation between a killing vector field and the conserved quantity is [46,47]
where the semicolon denotes the covariant derivative. For simplicity, we only consider the motion in the equatorial plane. Then in the spherically-symmetric EGB black hole with the metric (5), we have the conserved energy with a timelike killing vector and the conserved total angular momentum with a spacelike killing vector [47], they are
Here, the parameters are defined as , , and (we set ), where e, m, and j are the energy, mass, and total angular momentum of the spinning test particle, respectively. Note that we have used the relations and for the two Killing vectors.
Solving Equations (11), (17) and (18), we get the non-vanishing components of the four-momentum:
and
where the function . We can solve the four-velocity by using the equations of motion (8) and (9) and the components of in (15) [82,85]
Finally, the non-vanishing components of the four-velocity are
where the functions , , , , , and are defined as
We can set the affine parameter as coordinate time and choose because the trajectories of the test particle are independent of the affine parameter [45,56]. Then the orbital frequency parameter [45,56]. Then the orbital frequency parameter of the test particle is
where the dot means .
2.2. Circular Orbits of Spinning Test Particle
The motion of a test particle in a central field can be determined with the help of the effective potential in the Newtonian dynamics [86,87]. We can use the same method to solve the motion of a test particle in the black hole background in GR. We can prove that the radial velocity is parallel to the radial momentum [88], therefore the effective potential of the spinning test particle can be solved by using the form of (21) [79]. We decompose the (21) as [68,79]
where the functions A, B, and C are
and
where the function is
The effective potential of the test particle is defined by the positive square root of Equation (33)
The positive square root corresponds to the four-momentum pointing toward future, while the negative one corresponds to the past-pointing four-momentum [89]. When the spin of the test particle is zero, it reduces to
Note that for the four-dimensional Schwarzchild black hole in GR, the function .
The properties of a test particle in a central field are mainly determined by the effective potential. Thus, the effects on the motion of a spinning test particle can be derived based on how the effective potential depends on the GB coupling parameter and the spin angular momentum . We plot some shapes of the effective potential (38) in Figure 1. We can see that the radii of the extreme points become smaller when the coupling parameter and become larger when the parameter . The extreme points of the effective potential mean a test particle could move in circular orbits, noting that the orbit at the maximum (minimum) point is unstable (stable). These phenomena mean that a positive GB coupling parameter induces the attractive effect and a negative one results in the repulsive effect on the motion of the test particle.
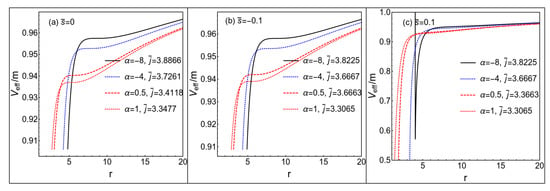
Figure 1.
The effective potential for a spinning test particle in the four-dimensional Einstein–Gauss–Bonnet (EGB) black hole background. The parameters are set as and .
In addition to the attractive or repulsive effects on the motion of the test particle, some more interesting results are found when we check the shapes of the effective potential in the parameter space . We find that the effective potential has two minima when the GB coupling parameter is in a special range. When the test particle moves in stable circular orbits [79], the radial velocity should be zero
and the the radial acceleration vanishes
The conditions and mean that the energy of the particle should equal to the minimum of the effective potential.
Therefore, when the effective potential of a spinning test particle has two minima, there will be two stable circular orbits for the particle with a spin angular momentum and an orbital angular momentum. This is a new feature for the motion of a spinning test particle in four-dimensional EGB black hole background. We plot the effective potential with two minima in Figure 2, where the corresponding two separate orbits of the spinning test particle with and are still given. The case of a spinning test particle can posses two stable circular orbits only happens when with a special range for . We give the numerical results in Figure 3 and find that the range of is nearly in .
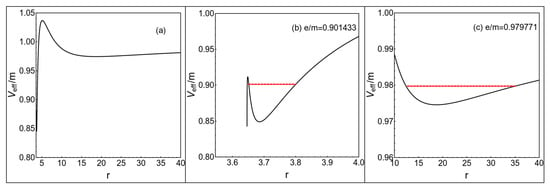
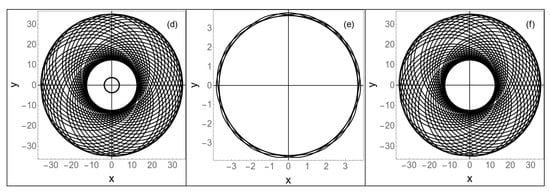
Figure 2.
Plots of the effective potential and orbits for a spinning test particle with , , and . Here . Subfigures (b,c) are the two minima of the effective potential shown in subfigure (a). Subfigures (e,f) are two separate orbits around the two minima of the effective potential shown in subfigure (d), and they are related to the effective potential in subfigures (b,c). The values of the red dashed line in subfigures (b,c) stand for the energy of the test particle. The range of the red dashes in the radial direction stands for the radial range that the test particle can move in, see the corresponding orbits in subfigures (e,f). The test particles on the two orbits have the same spin and orbital angular momentum. The parameters are set as and .
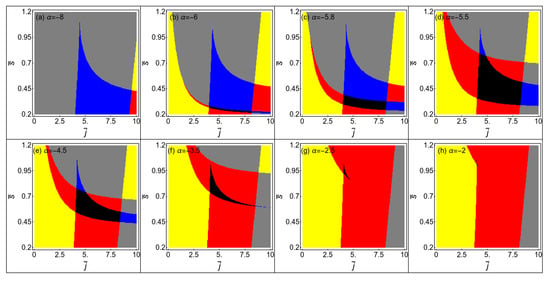
Figure 3.
Plots of the parameter space describing whether a spinning test particle have two stable circular orbits with the same spin and the same total angular momentum . The parameters are set as and . In the black and blue regions, the effective potential has two minima corresponds two stable circular orbits. In the red region the effective potential has one minimum and the test particle has one stable circular orbit. In the gray and yellow regions, the test particle has no stable circular orbits.
We have mentioned that the MPD equations of the spinning test particle is obtained under the “pole–dipole” approximation, which will lead the four-velocity transform from timelike to spacelike if the particle spin is too large. In order to make sure the motion of the spinning test particle is timelike, we adopt the superluminal constraint [68]
By using the superluminal constraint and circular orbit conditions (40) and (41) of the spinning test particle, we obtain the parameter space in Figure 4, which describes whether the motion on a circular orbit is timelike or spacelike. By comparing the results in Figure 3 and in Figure 4, we confirm that the motion of the particle in the two separate stable orbits is timelike. We know that the effects from the GB term on the motion of the test particle can be attractive or repulsive, where a positive (or negative) GB coupling parameter leads to an attractive (or repulsive) force. The spin–curvature force can also be attractive or repulsive. When the effects induced by the GB term and the spin–curvature force exist simultaneously, the total attractive or negative force will be enhanced or weakened. It will change the shapes of the regions in .
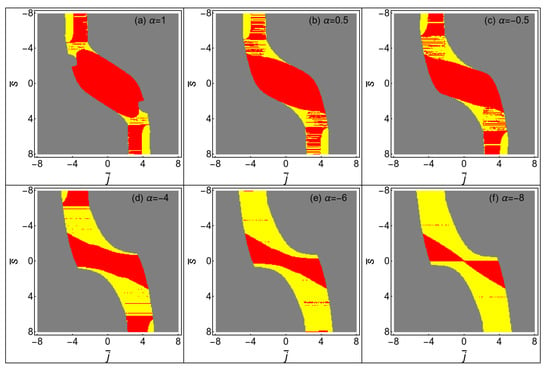
Figure 4.
Properties of circular orbits for the spinning test particle in the four-dimensional GB black hole background. Here is the orbital angular momentum. The parameters are set as and . In the gray region, the test particle can have timelike circular orbits. In the red and yellow regions, the test particle does not have stable timelike circular orbits. In the yellow region, the motion of the test particle is spacelike and unphysical.
Next, we will investigate the ISCO of the spinning test particle. The ISCO of the test particle locates at the position where the maximum and minimum of the effective potential merge. Thus, the effective potential of the test particle at the ISCO should satisfy
By using Equations (40), (41) and (43), we can derive the ISCO of the test particle. In Ref. [38], the authors showed that the radius of the ISCO for a spinless test particle varies in the form of
This result was derived under the linear approach with a small around 0. Obviously, the ISCO of a spinless test particle can be larger or smaller due to the existence of the GB term. This phenomenon is consistent with the behavior of the effective potential, see the subfigure (a) in Figure 1.
When the test particle possesses a non-vanishing spin, the contribution of the spin-curvature force should affect the properties of the motion. The relation between the effective potential and the spin of the test particle is still shown in Figure 1. We give the numerical results of the ISCO in Figure 5. Note that there is a jump behavior for the ISCO parameters in the subfigure (e) in Figure 5, which is induced by the fact that the effective potential has two minima. Because we use the position where the maximum and minimum of the effective potential merge to locate the ISCO and our step length of spin is not small enough to cover the change of the ISCO parameters. We summarize how the ISCO of the spinning test particle depends on the spin and GB coupling parameter as follows:
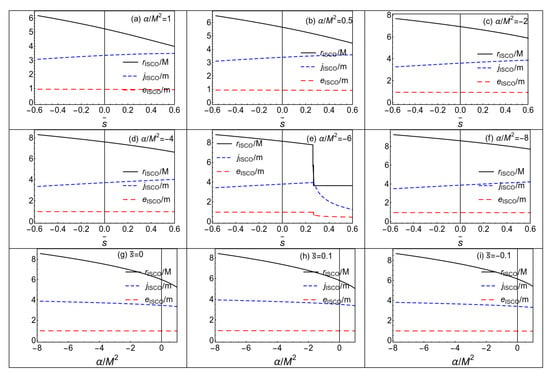
Figure 5.
The ISCO parameters of the spinning test particle with different values of . The parameters are set as and .
- For the ISCO of the spinning test particle in four-dimensional EGB black hole, the corresponding radius and angular momentum decrease with the spin when the GB coupling parameter is fixed. When the effect from the GB term is considered, the radius of the ISCO will be smaller than the case of the Schwarzchild black hole in GR, and the Gauss–Bonnet term does not change the laws of the ISCO with spin.
- When the spin of the test particle is fixed, the radius and angular momentum of the ISCO decrease with the GB coupling parameter and this behavior is almost the same as the results of the spinless case in Ref. [38].
3. Summary
In this paper, we investigated the motion of a spinning test particle in the equatorial plane of the four-dimensional novel EGB black hole. We solved the four-momentum and four-velocity of the spinning test particle and investigated the properties the ISCO. We found that the ISCO of the spinning test particle has similar behavior as the case of a spinning test particle in GR. The GB term and spin parameter can reduce or increase the radius of the ISCO. The new feature for the spinning test particle in the four-dimensional EGB black hole is that the test particle could have two separate stable orbits with the same spin and same total angular momentum when the GB coupling parameter is in a special range . Due to the fact that the motion of the spinning test particle will be superluminal when the spinning is too large, we also gave the superluminal constraint on the four-velocity of the spinning test particle in the circular orbits and confirmed that the motion of the spinning test particle that can move at two seperate orbits is timelike. It means that there will be a discrete gravitational radiation spectrum when a spinning test particle is inspiraling into a four-dimensional EGB black hole, and the corresponding accretion disc could have discrete structures, which provides a possible way to test and constraint the four-dimensional EGB gravity.
Author Contributions
The authors have contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (Grants No. 11875151, No. 11705070, No. 11522541, and No. 11675064). Y.P. Zhang was supported by a scholarship granted by the Chinese Scholarship Council (CSC: 201806180036).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abbott, B.; Jawahar, S.; Lockerbie, N.; Tokmakov, K. [LIGO Scientific Collaboration and Virgo Collaboration]. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.; Jawahar, S.; Lockerbie, N.; Tokmakov, K. [LIGO Scientific Collaboration and Virgo Collaboration]. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B. [LIGO Scientific Collaboration and Virgo Collaboration]. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. [LIGO Scientific Collaboration and Virgo Collaboration]. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.; Jawahar, S.; Lockerbie, N.; Tokmakov, K. [LIGO Scientific Collaboration and Virgo Collaboration]. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Banados, M.; Silk, J.; West, S.M. Kerr Black Holes as Particle Accelerators to Arbitrarily High Energy. Phys. Rev. Lett. 2009, 103, 111102. [Google Scholar] [CrossRef]
- Wei, S.-W.; Liu, Y.-X.; Guo, H.; Fu, C.-E. Charged spinning black holes as Particle Accelerators. Phys. Rev. D 2010, 82, 103005. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse and space-time singularities. Phys. Rev. Lett. 1965, 14, 57. [Google Scholar] [CrossRef]
- Hawking, S.W.; Penrose, R. The Singularities of gravitational collapse and cosmology. Proc. R. Soc. Lond. A 1970, 314, 529–548. [Google Scholar]
- Gross, D.J.; Witten, E. Superstring Modifications of Einstein’s Equations. Nucl. Phys. B 1986, 277, 1–10. [Google Scholar] [CrossRef]
- Gross, D.J.; Sloan, J.H. The Quartic Effective Action for the Heterotic String. Nucl. Phys. B 1987, 291, 41–89. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O. Maximally Symmetric Cosmological Solutions of higher curvature string effective theories with dilatons. Phys. Lett. B 1996, 368, 198–201. [Google Scholar] [CrossRef]
- Zwiebach, B. Curvature Squared Terms and String Theories. Phys. Lett. B 1985, 156, 315–317. [Google Scholar] [CrossRef]
- Boulware, D.G.; Deser, S. String-generated gravity models. Phys. Rev. Lett. 1985, 55, 2656–2660. [Google Scholar] [CrossRef]
- Wiltshire, D.L. Spherically symmetric solutions of Einstein-Maxwell theory with a Gauss-Bonnet term. Phys. Lett. B 1986, 169, 36–40. [Google Scholar] [CrossRef]
- Wiltshire, D.L. Black holes in string-generated gravity models. Phys. Rev. D 1988, 38, 2445. [Google Scholar] [CrossRef] [PubMed]
- Cai, R.-G. Gauss-Bonnet black holes in AdS spaces. Phys. Rev. D 2002, 65, 084014. [Google Scholar] [CrossRef]
- Glavan, D.; Lin, C. Einstein-Gauss-Bonnet Gravity in Four-Dimensional Spacetime. Phys. Rev. Lett. 2020, 124, 081301. [Google Scholar] [CrossRef]
- Cognola, G.; Myrzakulov, R.; Sebastiani, L.; Zerbini, S. Einstein gravity with Gauss-Bonnet entropic corrections. Phys. Rev. D 2013, 88, 024006. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zinhailo, A.F. Quasinormal modes, stability and shadows of a black hole in the novel 4D Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2003.01188. [Google Scholar]
- Fernandes, P.G.S. Charged Black Holes in AdS Spaces in 4D Einstein Gauss-Bonnet Gravity. Phys. Lett. B 2020, 805, 135468. [Google Scholar] [CrossRef]
- Wei, S.-W.; Liu, Y.-X. Testing the nature of Gauss-Bonnet gravity by four-dimensional rotating black hole shadow. arXiv 2020, arXiv:2003.07769. [Google Scholar]
- Konoplya, R.A.; Zhidenko, A. Black holes in the four-dimensional Einstein-Lovelock gravity. arXiv 2020, arXiv:2003.07788. [Google Scholar] [CrossRef]
- Casalino, A.; Colleaux, A.; Rinaldi, M.; Vicentini, S. Regularized Lovelock gravity. arXiv 2020, arXiv:2003.07068. [Google Scholar]
- Ai, W.-Y. A note on the novel 4D Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2004.02858. [Google Scholar]
- Bonifacio, J.; Hinterbichler, K.; Johnson, L.A. Amplitudes and 4D Gauss-Bonnet Theory. Phys. Rev. D 2020, 102, 024029. [Google Scholar] [CrossRef]
- Metin, G.; Sisman, T.C.; Tekin, B. Is there a novel Einstein-Gauss-Bonnet theory in four dimensions? arXiv 2020, arXiv:2004.03390. [Google Scholar]
- Hennigar, R.A.; Kubiznak, D.; Mann, R.B.; Pollack, C. On Taking the D→4 limit of Gauss-Bonnet Gravity: Theory and Solutions. J. High Energy Phys. 2020, 2020, 27. [Google Scholar] [CrossRef]
- Aoki, K.; Gorji, M.A.; Mukohyama, S. A consistent theory of D→4 Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2005.03859. [Google Scholar]
- Shu, F.-W. Vacua in novel 4D Einstein-Gauss-Bonnet Gravity: Pathology and instability? arXiv 2020, arXiv:2004.09339. [Google Scholar]
- Mahapatra, S. A note on the total action of 4D Gauss-Bonnet theory. arXiv 2020, arXiv:2004.09214. [Google Scholar]
- Tian, S.-X.; Zhu, Z.-H. Comment on “Einstein-Gauss-Bonnet Gravity in Four-Dimensional Spacetime”. arXiv 2020, arXiv:2004.09954. [Google Scholar]
- Arrechea, J.; Delhom, A.; Jiménez-Cano, A. Yet another comment on four-dimensional Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2004.12998. [Google Scholar]
- Lu, H.; Pang, Y. Horndeski Gravity as D→4 Limit of Gauss-Bonnet. arXiv 2020, arXiv:2003.11552. [Google Scholar]
- Kobayashi, T. Effective scalar-tensor description of regularized Lovelock gravity in four dimensions. J. Cosmol. Astropart. Phys. 2020, 2020, 013. [Google Scholar] [CrossRef]
- Fernandes, P.G.S.; Carrilho, P.; Clifton, T.; Mulryne, D.J. Derivation of Regularized Field Equations for the Einstein-Gauss-Bonnet Theory in Four Dimensions. Phys. Rev. D 2020, 102, 024025. [Google Scholar] [CrossRef]
- Page, D.N.; Thorne, K.S. Disk-accretion onto a black hole. Time-averaged structure of accretion disk. Astrophys. J. 1974, 191, 499–506. [Google Scholar] [CrossRef]
- Guo, M.-Y.; Li, P.-C. The innermost stable circular orbit and shadow in the novel 4D Einstein-Gauss-Bonnet gravity. Eur. Phys. J. C 2020, 80, 588. [Google Scholar] [CrossRef]
- Suzuki, S.; Maeda, K. Innermost stable circular orbit of a spinning particle in Kerr space-time. Phys. Rev. D 1998, 58, 023005. [Google Scholar] [CrossRef]
- Cai, R.-G.; Cao, L.-M.; Ohta, N. Black Holes in Gravity with Conformal Anomaly and Logarithmic Term in Black Hole Entropy. J. High Energy Phys. 2010, 2010, 082. [Google Scholar] [CrossRef]
- Cai, R.-G. Thermodynamics of Conformal Anomaly Corrected Black Holes in AdS Space. Phys. Lett. B 2014, 733, 183–189. [Google Scholar] [CrossRef]
- Mathisson, M. New mechanics of material systems. Acta Phys. Pol. 1937, 6, 163. [Google Scholar]
- Papapetrou, A. Spinning test-particles in general relativity. I. Proc. R. Soc. Lond. A 1951, 209, 248–258. [Google Scholar]
- Corinaldesi, E.; Papapetrou, A. Spinning test-particles in general relativity. II. Proc. R. Soc. Lond. A 1951, 209, 259–268. [Google Scholar]
- Dixon, W.G. Dynamics of extended bodies in general relativity II. Moments of the charge-current vector. Proc. R. Soc. Lond. A 1970, 319, 509–547. [Google Scholar]
- Hojman, S.A. Electromagnetic and Gravitational Interactions of a Spherical Relativistic Top. Unpublished Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1975. [Google Scholar]
- Hojman, R.; Hojman, S. Spinning Charged Test Particles in a Kerr-Newman Background. Phys. Rev. D 1977, 15, 2724. [Google Scholar] [CrossRef]
- Mashhoon, B.; Singh, D. Dynamics of Extended Spinning Masses in a Gravitational Field. Phys. Rev. D 2006, 74, 124006. [Google Scholar] [CrossRef]
- Zalaquett, N.; Hojman, S.A.; Asenjo, F.A. Spinning massive test particles in cosmological and general static spherically symmetric spacetimes. Class. Quant. Grav. 2014, 31, 085011. [Google Scholar] [CrossRef]
- Uchupol, R.; Sarah, J.V.; Scott, A.H. Gyroscopes orbiting black holes: A frequency-domain approach to precession and spin-curvature coupling for spinning bodies on generic Kerr orbits. Phys. Rev. D 2016, 94, 044008. [Google Scholar]
- Armaza, C.; Banados, M.; Koch, B. Collisions of spinning massive particles in a Schwarzschild background. Class. Quantum Gravity 2016, 33, 105014. [Google Scholar] [CrossRef]
- Wald, R.M. Gravitational spin interaction. Phys. Rev. D 1972, 6, 406–413. [Google Scholar] [CrossRef]
- Lukes-Gerakopoulos, G.; Seyrich, J.; Kunst, D. Investigating spinning test particles: Spin supplementary conditions and the Hamiltonian formalism. Phys. Rev. D 2014, 90, 104019. [Google Scholar] [CrossRef]
- Filipe, L.; Costa, O.; Lukes-Gerakopoulos, G.; Semerák, O. On spinning particles in general relativity: Momentum-velocity relation for the Mathisson-Pirani spin condition. Phys. Rev. D 2018, 97, 084023. [Google Scholar]
- Lukes-Gerakopoulos, G.; Harms, E.; Bernuzzi, S.; Nagar, A. Spinning test-body orbiting around a Kerr black hole: Circular dynamics and gravitational-wave fluxes. Phys. Rev. D 2017, 96, 064051. [Google Scholar] [CrossRef]
- Lukes-Gerakopoulos, G. Time parameterizations and spin supplementary conditions of the Mathisson- Papapetrou-Dixon equations. Phys. Rev. D 2017, 96, 104023. [Google Scholar] [CrossRef]
- Tulczyjew, W. Motion of multipole particles in general relativity theory. Acta Phys. Pol. 1959, 18, 393. [Google Scholar]
- Deriglazov, A.A.; Ramírez, W.G. Mathisson-Papapetrou-Tulczyjew-Dixon (MPTD) equations in ultra-relativistic regime and gravimagnetic moment. Int. J. Mod. Phys. D 2016, 26, 1750047. [Google Scholar] [CrossRef]
- Deriglazov, A.A.; Ramírez, W.G. Ultrarelativistic Spinning Particle and a Rotating Body in External Fields. Adv. High Energy Phys. 2016, 2016, 1376016. [Google Scholar] [CrossRef]
- Ramírez, W.G.; Deriglazov, A.A. Relativistic effects due to gravimagnetic moment of a rotating body. Phys. Rev. D 2017, 96, 124013. [Google Scholar] [CrossRef]
- Deriglazov, A.A.; Ramírez, W.G. Recent progress on the description of relativistic spin: Vector model of spinning particle and rotating body with gravimagnetic moment in General Relativity. Adv. Math. Phys. 2017, 2017, 7397159. [Google Scholar] [CrossRef]
- Steinhoff, J.; Puetzfeld, D. Multipolar equations of motion for extended test bodies in general relativity. Phys. Rev. D 2010, 81, 044019. [Google Scholar] [CrossRef]
- Han, W.-B. Gravitational Radiations from a Spinning Compact Object around a supermassive Kerr black hole in circular orbit. Phys. Rev. D 2010, 82, 084013. [Google Scholar] [CrossRef]
- Harms, E.; Lukes-Gerakopoulos, G.; Bernuzzi, S.; Nagar, A. Spinning test body orbiting around a Schwarzschild black hole: Circular dynamics and gravitational-wave fluxes. Phys. Rev. D 2016, 94, 104010. [Google Scholar] [CrossRef]
- Mukherjee, S.; Nayak, K.R. Off-equatorial stable circular orbits for spinning particles. Phys. Rev. D 2018, 98, 084023. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, W.-B. Innermost stable circular orbits of charged spinning test particles. Phys. Lett. B 2019, 789, 393. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevado, H.; Ruffini, R. Equatorial circular orbits of neutral test particles in the Kerr Newman spacetime. Phys. Rev. D 2013, 88, 024042. [Google Scholar] [CrossRef]
- Zhang, Y.-P.; Wei, S.-W.; Guo, W.-D.; Sui, T.-T.; Liu, Y.-X. Innermost stable circular orbit of spinning particle in charged spinning black hole background. Phys. Rev. D 2018, 97, 084056. [Google Scholar] [CrossRef]
- Stuchlík, Z. Equilibrium of spinning test particles in the Schwarzschild-de Sitter spacetimes. Acta Phys. Slov. 1999, 49, 319. [Google Scholar]
- Stuchlík, Z.; Ková, J. Equilibrium conditions of spinning test particles in Kerr-de Sitter spacetimes. Class. Quant. Grav. 2006, 23, 3935. [Google Scholar] [CrossRef]
- Plyatsko, R.; Fenyk, M.; Panat, V. Highly relativistic spin-gravity-Λ coupling. Phys. Rev. D 2017, 96, 064038. [Google Scholar] [CrossRef]
- Plyatsko, R.; Panat, V.; Fenyk, M. Nonequatorial circular orbits of spinning particles in the Schwarzschild-de Sitter background. Gen. Relat. Grav. 2018, 50, 150. [Google Scholar] [CrossRef]
- Han, W.-B. Dynamics of extended bodies with spin-induced quadrupole in Kerr spacetime: Generic orbits. Gen. Relat. Grav. 2017, 49, 48. [Google Scholar] [CrossRef][Green Version]
- Warburton, N.; Osburn, T.; Evans, C.R. Evolution of small-mass-ratio binaries with a spinning secondary. Phys. Rev. D 2017, 96, 084057. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, W.-B. Energy extraction of a spinning particle via the super Penrose process from an extremal Kerr black hole. Phys. Rev. D 2018, 97, 064024. [Google Scholar] [CrossRef]
- Mukherjee, S. Collisional Penrose process with spinning particles. Phys. Lett. B 2018, 778, 54–59. [Google Scholar] [CrossRef]
- Faye, G.; Blanchet, L.; Buonanno, A. Higher-order spin effects in the dynamics of compact binaries. I. Equations of motion. Phys. Rev. D 2006, 74, 104033. [Google Scholar] [CrossRef]
- Witzany, V.; Steinhoff, J.; Lukes-Gerakopoulos, G. Hamiltonians and canonical coordinates for spinning particles in curved space-time. Class. Quantum Gravity 2019, 36, 075003. [Google Scholar] [CrossRef]
- Jefremov, P.I.; Tsupko, O.Y.; Bisnovatyi-Kogan, G.S. Innermost stable circular orbits of spinning test particles in Schwarzschild and Kerr space-times. Phys. Rev. D 2015, 91, 124030. [Google Scholar] [CrossRef]
- Toshmatov, B.; Malafarina, D. Spinning test particle in the γ space-times. Phys. Rev. D 2019, 100, 104052. [Google Scholar] [CrossRef]
- Nucamendi, U.; Becerril, R.; Sheoran, P. Bounds on spinning particles in their innermost stable circular orbits around rotating braneworld black hole. Eur. Phys. J. C 2020, 80, 35. [Google Scholar] [CrossRef]
- Zhang, Y.-P.; Gu, B.-M.; Wei, S.-W.; Yang, J.; Liu, Y.-X. Charged spinning black holes as accelerators of spinning particles. Phys. Rev. D 2016, 94, 124017. [Google Scholar] [CrossRef]
- Conde, C.; Galvis, C. Properties of the Innermost Stable Circular Orbit of a spinning particle moving in a rotating Maxwell-dilaton black hole background. Phys. Rev. D 2019, 99, 104059. [Google Scholar] [CrossRef]
- Liu, Y.-L.; Zhang, X.-D. Maximal efficiency of the collisional Penrose process with spinning particles in Kerr-Sen black hole. Eur. Phys. J. C 2020, 80, 31. [Google Scholar] [CrossRef]
- Hojman, S.A.; Asenjo, F.A. Can gravitation accelerate neutrinos? Class. Quantum Gravity 2013, 30, 025008. [Google Scholar] [CrossRef]
- Kaplan, S.A. On crcular orbits in Einstein’s Gravitation Theory. J. Exp. Theor. Phys. 1949, 19, 951. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon: Oxford, UK, 1993. [Google Scholar]
- Zhang, Y.-P.; Wei, S.-W.; Amaro-Seoane, P.; Yang, J.; Liu, Y.-X. Motion deviation of test body induced by spin and cosmological constant in extreme mass ratio inspiral binary system. Eur. Phys. J. C 2019, 79, 856. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Freeman: New York, NY, USA, 1973; p. 911. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).