Abstract
In this paper, we use a three flavor non-local Nambu–Jona-Lasinio (NJL) model, an improved effective model of Quantum Chromodynamics (QCD) at low energies, to investigate the existence of deconfined quarks in the cores of neutron stars. Particular emphasis is put on the possible existence of quark matter in the cores of rotating neutron stars (pulsars). In contrast to non-rotating neutron stars, whose particle compositions do not change with time (are frozen in), the type and structure of the matter in the cores of rotating neutron stars depends on the spin frequencies of these stars, which opens up a possible new window on the nature of matter deep in the cores of neutron stars. Our study shows that, depending on mass and rotational frequency, up to around 8% of the mass of a massive neutron star may be in the mixed quark-hadron phase, if the phase transition is treated as a Gibbs transition. We also find that the gravitational mass at which quark deconfinement occurs in rotating neutron stars varies quadratically with spin frequency, which can be fitted by a simple formula.
1. Introduction
Exploring the properties of compressed baryonic matter, or, more generally, strongly interacting matter at high densities and/or temperatures has become a forefront area of modern physics [1,2,3]. Experimentally, the properties of such matter are being probed with the Relativistic Heavy Ion Collider RHIC at Brookhaven and the Large Hadron Collider (LHC) at Cern. Great advances in our understanding of such matter are expected from the next generation of heavy-ion collision experiments at FAIR (Facility for Antiproton and Ion Research, GSI), NICA (Nucloton-based Ion Collider fAcility, JINR), and, at lower energies, from radioactive beam facilities such as FRIB at MSU.
The universe was filled with hot and dense baryonic matter shortly after the Big Bang. Today, such matter is being created in the universe in the final stages of catastrophic stellar events (e.g., core-collapse supernovae, gamma-ray bursts) and exists permanently inside of neutron stars. Depending on mass and rotational frequency, gravity compresses the matter in the core regions of neutron stars to densities that are several times higher than the density of ordinary atomic nuclei [4,5,6,7,8,9,10,11,12]. At such huge densities atoms themselves collapse, and atomic nuclei are squeezed so tightly together that new particle states may appear and novel states of matter, foremost quark matter, may be created. This feature makes neutron stars superb astrophysical laboratories for a wide range of physical studies [4,5,6,7,9,11,13,14]. With observational data accumulating rapidly from both orbiting and ground based observatories spanning the spectrum from X-rays to radio wavelengths, there has never been a more exiting time than today to study neutron stars. The Hubble Space Telescope and X-ray satellites such as Chandra and XMM-Newton, for instance, have proven especially valuable. New astrophysical instruments such as the Five hundred meter Aperture Spherical Telescope (FAST), the square kilometer Array (skA), Fermi Gamma-ray Space Telescope (formerly GLAST), Astrosat, ATHENA (Advanced Telescope for High ENergy Astrophysics), and the Neutron Star Interior Composition Explorer (NICER) promise the discovery of tens of thousands of new neutron stars. In particular, the NICER mission is expected to open up a window on the inner workings of neutron stars, as this mission is dedicated to the study of extraordinary gravitational, electromagnetic, and nuclear physics environments embodied by neutron stars.
In this paper, we use a non-local extension of the SU(3) Nambu–Jona-Lasinio (NJL) model to investigate the possible existence of deconfined quarks in the cores of neutron stars. Investigations of dense neutron star matter based on the non-local SU(2) version of the NJL model have been carried out in Refs. [15,16].
The possible existence of such matter inside of neutron stars has already been suggested in the 1970s [17] but has remained an open issue ever since, as QCD cannot be solved for dense astrophysical matter with the tools usually employed by relativistic quantum field theories. We put particular emphasis on the possible existence of quark matter inside of rotating neutron stars, known as pulsars. In contrast to non-rotating neutron stars, whose core compositions do not change with time (are frozen in), the type and structure of the matter in the cores of rotating neutron stars depends on the spin frequencies of these stars, which could give rise to observable astrophysical signals of quark deconfinement [18,19,20,21,22].
A histogram of the rotational frequencies of 2510 observed pulsars is shown in Figure 1. This number is expected to increase dramatically once new instruments such as FAST and skA come into operation.
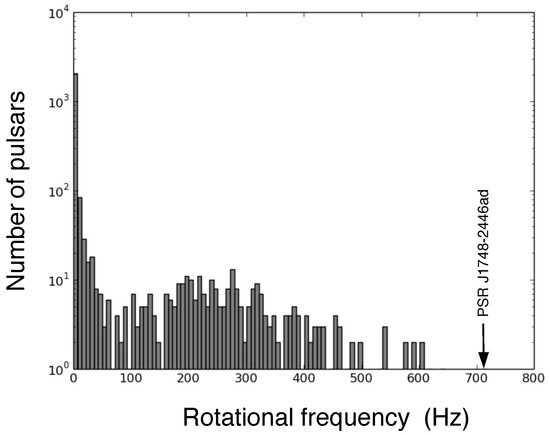
Figure 1.
Histogram for the frequencies of all 2510 pulsars which have frequency data in version 1.53 of The Australia Telescope National Facility Pulsar Catalog [23,24]. The most rapidly rotating neutron star observed to date is the pulsar J1748-2446ad, which rotates at a frequency of 716 Hz [25] (rotational period of 1.4 milliseconds).
The paper is organized as follows. In Section 2 we introduce the nuclear equations of state (EoS) that were used to model the properties of (non) rotating neutron stars. The treatment of rotating neutron stars in the framework of general relativity theory is discussed in Section 3. The results of our investigations are presented in Section 4. A brief discussion of the results in provided in Section 5.
2. Models for the Nuclear Equations of State
2.1. Hadronic Matter
In the most primitive conception, the matter in the core of a neutron star is constituted from neutrons. At a slightly more accurate representation, the cores consist of neutrons and protons whose electric charge is balanced by leptons (). Other particles, like hyperons () and the Δ resonance, may be present if the Fermi energies of these particles become large enough so that the existing baryon populations can be rearranged and a lower energy state be reached. To model this hadronic phase, we make use of the relativistic mean-field (RMF) approximation, in which the interactions between baryons are described by the exchange of scalar (σ), vector (ω), and isovector (ρ) mesons [26]. The standard mean-field Lagrangian is given by [4,5,27,28,29,30].
with the meson-baryon vortices given by
The σ and ω mesons in Equation (1) are responsible for nuclear binding while the ρ meson is required to obtain the correct value for the empirical symmetry energy. The cubic and quartic σ terms in Equation (1) are necessary, at the relativistic mean-field level, to obtain the empirical incompressibility of nuclear matter [28,29]. The field tensors and are defined as and .
The parameters (i.e., coupling constants) of the theory must reproduce the bulk properties of infinite nuclear matter at saturation density, . These are the binding energy , effective nucleon mass , nuclear incompressibility K, and the symmetry energy and its density derivative L. Of the six, the values of K, , and L carry some uncertainty. The K value is believed to lie in the range between about 220 and 260 MeV [31], or between 250 and 315 MeV, as recently suggested in Reference [32]. The values for and L are in the ranges of 29 to 35 MeV and 43 to 70 MeV, respectively [33,34,35]. We have chosen two parameter sets, denoted GM1 and DD2, which approximately cover the uncertainties in the nuclear matter properties just above. They are listed in Table 1.

Table 1.
Properties of infinite nuclear matter at saturation density computed for parameter sets GM1 [36] and DD2 [37]. Shown are the saturation density , energy per nucleon , nuclear incompressibility K, effective nucleon mass , asymmetry energy , and the density derivative of the symmetry energy, L.
The coupling constants associated with GM1 are , , , , and [36].
The field equations for the baryon fields , which follow from Equation (1), are given by [4,5,8,27].
In the standard RMF limit, the meson fields of Equations (4)–(6) simplify to [4,5,8,27].
where , , and denote the mean-field limits of σ, ω, and , respectively, and the effective baryon masses are given by . and denote the spin respectively isospin of a baryon of type B, and stands for the number density of baryon B.
In addition to the standard RMF theory discussed just above, we also consider a lagrangian where the meson-baryon vortices (where ) of Equation (2) are no longer constant but rather depend on density [38,39,40]. In that case the values of the vortices are derived from relativistic Dirac-Brueckner calculations of nuclear matter, which use one-boson-exchange interactions as an input. A characteristic feature of the density-dependent theory is the occurrence of rearrangement terms in the expression for the baryon chemical potential, which leads to a more complex condition for chemical equilibrium compared to the standard RMF approximation [40]. The parameter set of the density-dependent (DD) treatment adopted in this paper is denoted DD2 (), where a vanishing vector coupling constant among quarks has been chosen [37]. For DD2, the coupling constants at saturation density are , , and [37], which lead to the saturation properties of infinite nuclear matter shown in Table 1.
The equation of state of the standard mean-field treatment (for the DD formalism, see References [39,40,41,42]) is obtained by solving Equations (7)–(9) together with the charge conservation conditions (baryonic, electric) given by [4,5,27].
where is the total baryonic density and and are the electric charges of baryons and leptons, respectively. Particles in the hadronic phase are subject to the chemical equilibrium condition
where is the chemical potential and is the baryon number of baryon B. and denote the linearly independent chemical potentials of neutrons and electrons, respectively, which reflect baryon number and electric charge conservation on neutron star matter. New baryon or lepton states are populated when the right side of Equation (11) is greater than the particle’s chemical potential. The baryonic and leptonic number densities ( and ) are both given by . The unknowns of the theory are the meson mean-fields (σ, ω, ρ), and the neutron and electron fermi momenta (, ). Finally, the energy density and pressure of the hadronic phase are given by [4,5,27].
2.2. Deconfined Quark Phase
A popular model widely used to describe deconfined 3-flavor (up, down, strange) quark matter is the Nambu–Jona-Lasinio model [43,44,45,46,47]. Here we use a non-local extension of this model (n3NJL) [48,49], whose effective action is given by
where , is the current quark mass matrix, () denote the Gell-Mann matrices–generators of SU(3), and 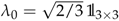 . The currents and are given by
where is a form factor responsible for the non-local character of the interaction. Finally, the constants in the t’Hooft term accounting for flavor-mixing are defined by
. The currents and are given by
where is a form factor responsible for the non-local character of the interaction. Finally, the constants in the t’Hooft term accounting for flavor-mixing are defined by
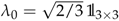 . The currents and are given by
. The currents and are given by
The current quark mass of up and down quarks and the coupling constants and H in Equation (14), have been fitted to the pion decay constant, , and meson masses , , and , as described in [50,51]. The result of this fit is MeV, MeV, , . The strange quark current mass is treated as a free parameter and was set to MeV. The strength of the vector interaction is expressed in terms of the strong coupling constant . To account for the uncertainty in the theoretical predictions for the ratio , we treat the vector coupling constant as a free parameter [52,53,54], which varies from 0 to .
For the mean-field approximation, the thermodynamic potential following from of Equation (14) is given by
where , , and are the quark scalar, vector, and auxiliary mean fields, respectively. Moreover, is given by and we have defined . The momentum dependent quark masses are given by . The quantities are the Gaussian form factors, responsible for the nonlocal nature of the interaction among quarks [49]. The auxiliary mean fields are given by
The vector interactions taken into account in the treatment shift the quark chemical potentials as and . The scalar and vector mean fields are obtained by minimizing the grand thermodynamic potential, and . Finally, the quark number densities are obtained from .
To determine the equation of state one must solve a nonlinear system of equations for the fields and , and the neutron and electron chemical potentials and . This system of equations consists of the mean field equations
with cyclic permutations over the quark flavors, , and the baryonic and electric charge conservation equations and , respectively. Finally, the pressure and energy density are given by
and
where was chosen by the condition that vanishes at [48,49].
2.3. Quark-Hadron Mixed Phase
To model the mixed phase region of quarks and hadrons in neutron stars, we use the Gibbs condition for phase equilibrium between hadronic (H) and quark (Q) matter,
where and denote the pressures of hadronic matter and quark matter, respectively [55,56]. The quantity in Equation (22) stands collectively for the field variables (, , ) and Fermi momenta (, ) that characterize a solution to the equations of confined hadronic matter (Section 2). We use the symbol to denote the volume proportion of quark matter, , in the unknown volume V. By definition, χ varies between 0 and 1, depending on how much confined hadronic matter has been converted to quark matter. Equation (22) is to be supplemented with the conditions of global baryon charge conservation and global electric charge conservation. The global conservation of baryon charge is expressed as [55,56].
where and denote the baryon number densities of the quark phase and hadronic phase, respectively. The global neutrality of electric charge is given by [55,56].
with and denoting the electric charge densities of the quark phase and hadronic phase, respectively. We have chosen global rather than local electric charge neutrality. Local NJL studies carried out for local electric charge neutrality have been reported recently in References [57,58,59,60].
In Figure 2, we show the GM1 and DD2 equations of state (EoS) used in this work to study the quark-hadron composition of rotating neutron stars. The solid dots mark the beginning and the end of the quark-hadron mixed phases for these equations of state. Since the Gibbs condition is used to model the quark-hadron phase transition, pressure varies monotonically with the proportion of the phases in equilibrium. This would not be the case if the Maxwell construction were used to model the phase equilibrium between quarks and hadrons, in which case the pressure throughout the mixed phase is constant. For that reason, the mixed phase would strictly be excluded from neutron stars, but small cores made entirely of quark matter may still be possible in neutron stars close the maximum-mass model (see, for instance, Refrences [61,62], and references therein).
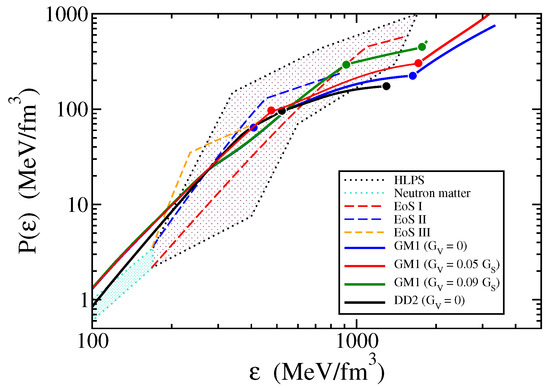
Figure 2.
Comparison of the equations of state used in this work, GM1 and DD2, with models recently suggested in the literature (see text for details). The solid dots mark the beginning and the end of the quark-hadron mixed phases for GM1 and DD2. The repulsive interaction among quarks is controlled by the vector coupling constant, .
A Maxwell-like phase transition is generally supported by larger surface tensions, σ, of quark matter (see, however, Reference [63]). Values of have recently been suggested in the literature [64,65,66,67,68], but its actual value is an open issue.
The GM1 and DD2 equations of state are compared in Figure 2 with models for the equation of state that have recently been suggested in the literature. ’HLPS’ and ’Neutron matter’ show the constraints on the equation of state established by Hebeler, Lattimer, Pethick, and Schwenk [33,69]. The curves labeled ’EoS I’, ’EoS II’, and ’EoS III’ show the compact star matter equations of state determined by Kurkela et al. [70], which are based on an interpolation between the regimes of low-energy chiral effective theory and high-density perturbative QCD. One sees that the GM1 and DD2 models are well within these limits. The only difference concerns the behavior of the equation of state at sub-nuclear densities (labeled “Neutron matter” in Figure 2), where our models provide slightly more pressure. This, however, does in no way impact the results for the quark-hadron compositions shown in Section 4, because of the large masses of these stars.
Figure 3 shows the gravitational mass versus central neutron stars density (left panel) and gravitational mass versus radius of non-rotating neutron stars for the equations of state discussed in this section. The maximum masses of these neutron stars are between 1.9 and . Stellar rotation, which will be discussed in the next section, increases the masses of these stars to values that are between 2.2 and , while their central densities drops by around 20%.
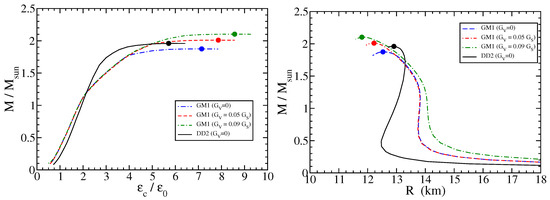
Figure 3.
Mass–central density (left) and mass–radius relationships of non-rotating neutron stars for the nuclear equations of state (EoS) used in this work. ( MeV/fm denotes the density of infinite nuclear matter).
3. Treatment of Rotating Neutron Stars in General Relativity Theory
The fact that rotation deforms neutron stars, stabilizes them against collapse, and drags along the local inertial frames inside and outside of them so that they co-rotate with the stars, renders the construction of models of rotating neutron stars very complicated. A line element which accounts for these three features has the form [5,71,72,73,74,75]
where ν, ψ, μ and λ denote metric functions and ω is the angular velocity of the local inertial frames. All these quantities depend on the radial coordinate r, the polar angle θ, and implicitly on the star’s angular velocity Ω. The metric functions and the frame dragging frequencies are to be computed from Einstein’s field equation,
where denotes the energy momentum tensor of the stellar matter, whose equation of state is given by . The other quantities in Equation (26) are the Ricci tensor , the curvature scalar R, and the metric tensor, . No simple stability criteria are known for rapidly rotating stellar configurations in general relativity. However, an absolute limit on rapid rotation is set by the onset of mass shedding from the equator of a rotating star. The corresponding rotational frequency is known as the Kepler frequency, . In classical mechanics, the expression for the Kepler frequency, determined by the equality between the centrifugal force and gravity, is readily obtained as . Its general relativistic counterpart is given by [5,71].
which is to be evaluated self-consistently at the equator of a rotating neutron star. The Kepler period follows from Equation (27) as . For typical neutron star matter equations of state, the Kepler period obtained for neutron stars is typically around 1 ms. [5,8,71,72]. An exception to this are strange quark matter stars. Since they are self-bound, they tend to possess smaller radii than conventional neutron stars, which are bound by gravity only. Because of their smaller radii, strange stars can withstand mass shedding from the equator down to periods of around 0.5 ms [76,77].
A mass increase of up to % is typical for rotation at . Because of rotation, the equatorial radii increase by several kilometers, while the polar radii become smaller by several kilometers. The ratio between both radii is around 2/3, except for rotation close to the Kepler frequency. The most rapidly rotating, currently known neutron star is pulsar PSR J1748-2446ad, which rotates at a period of 1.39 ms (719 Hz) [25], well below the Kepler frequency for most neutron star equations of state. Examples of other rapidly rotating neutron stars are PSRs B1937+21 [78] and B1957+20 [79], whose rotational periods are 1.58 ms (633 Hz) and 1.61 ms (621 Hz), respectively.
The density change in the core of a neutron star whose frequency varies from can be as large as 60% [5,8]. This suggests that rotation may drive phase transitions or cause significant compositional changes of the matter in the cores of neutron stars [4,5,8].
4. Results
For each equation of state, a numerical code, based on Hartle’s rotation formalism [80,81,82], was used to predict the percentage of the mass made up by deconfined quark matter over a wide range of frequencies and gravitational masses. Figure 4 and Figure 5 show the composition of rotating neutron stars based on the lagrangian of Equation (1). As can be seen, the quark-hadron mixed phase as well as several different hyperon species are successively spun out of the neutron star if the rotation rate increases toward the Kepler frequency. Non-rotating neutron stars posses the most complex compositions, since they are the most dense members of the rotational sequence. The compositions shown in Figure 5 are snapshots taken from movies (see ”Supplementary Materials” at the end of the paper) showing the entire rotational evolution of this neutron star all the way from zero frequency to .
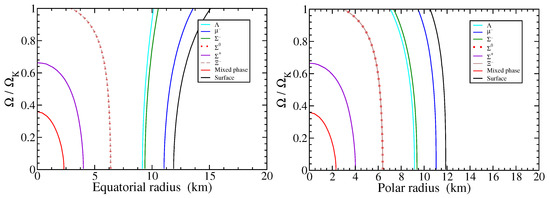
Figure 4.
Particle populations inside of rotating neutron stars, in equatorial (left) and polar (right) directions, computed for the GM1 EoS. The vector interaction among quarks is . The stellar frequency, Ω, ranges from zero to the Kepler frequency, Hz. The gravitational mass of the non-rotating star is , which increases to for rotation at .
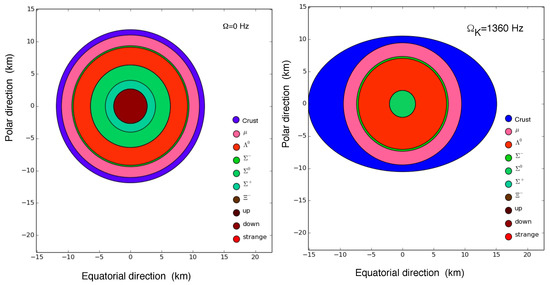
Figure 5.
Change of the interior composition of a 2 neutron star caused by rotation, computed for the GM1 EoS. The vector interaction among quarks is . The star on the left (right) hand-side is non-rotating (rotating at the Kepler frequency, ). The baryon number of both stars is the same ().
A heat map showing the quark-hadron content of rotating neutron stars computed for the GM1 () equation of state is shown in Figure 6. As can be seen in this figure, up to 8% of the total gravitational mass of these neutron stars exists in the form a mixed quark-hadron phase. Lines of constant baryon number are also depicted on the figures as white lines, labeled with the logarithm of the star’s baryon number. These lines were included to give a sense of the path that a secluded neutron star would be expected to take through as it spins down.
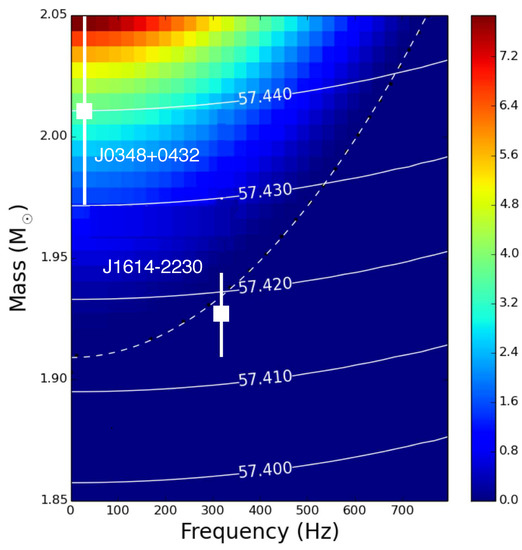
Figure 6.
Heat map showing the percent (column on the right) of total mass of a neutron star made up of deconfined quark matter, as predicted by the GM1 () EoS. The white solid lines show the rotational evolution of neutron stars with constant baryon numbers A (the reported figures being ). Also shown are the observed masses of pulsars J1614-2230 and J0348+0432 and the trend line (dashed white) fit, which separates confined from deconfined matter. A fit of the trend line is given by Equation (28).
By parsing out the maximum frequency where deconfined quark matter is expected to exist at the center of the neutron star for a given mass it is possible to get a curve through the gravitational mass–frequency diagram for the threshold above which one can expect to find deconfined quarks. These threshold frequencies for each mass were fit to determine a (quadratic) function for the curve. The fit equation, depicted as a dashed white line in Figure 6, was found to have the form
where M is the neutron star’s gravitational mass in solar masses, Ω its rotational frequency, and a and c are parameters determined through fitting. The values for a and c can be found in Table 2.

Table 2.
Parameters for the empirical deconfinement threshold curve for each equation of state (EoS) with the form shown in Equation (28).
Figure 6 allows one to estimate the amount of quark-hadron matter that may exist in the cores of neutron stars that have both a measured frequency and mass, as illustrated for pulsars PSR J1614-2230 (, rotational frequency Hz) [83,84] and PSR J0348+0432 (, Hz) [85,86] in Figure 6. According to this calculation, up to around 7% of the mass of PSR J0348+0432 could be in the mixed quark-hadron phase, while the core of the more rapidly rotating pulsars PSR J1614-2230 may be hovering right at the quark deconfinement density.
5. Discussion and Summary
The type and structure of the matter in the cores of rotating neutron stars (pulsars) depends on the spin frequencies of these stars [5,8,87], which opens up a new window on the nature of matter deep in their cores. We find that, depending on mass and rotational frequency, up to around 8% of the mass of massive neutron stars may be in the mixed quark-hadron phase, if the quark-hadron phase transition is Gibbs-like. Examples of such stars are pulsars PSR J1614-2230 with a gravitational mass of [84] and PSR J0348+0432 with a mass of [85,86] (Figure 6). Pure quark matter in the centers of neutron stars is not obtained for any of the models for the nuclear equation of state studied in this work. We also find that the gravitational mass at which quark deconfinement occurs in rotating neutron stars varies quadratically with spin frequency, which can be fitted by a simple quadratic formula.
Our view of the interior composition of pulsars has changed dramatically since their first discovery almost 50 years ago. It has also become clear during that time period that all the ambient conditions that characterize pulsars tend to the extreme, making pulsars almost ideal astrophysical laboratories for a broad range of physical studies. Owing to the unprecedented wealth of high-quality data on pulsars provided by radio telescopes, X-ray satellites–and soon the latest generation of gravitational-wave detectors–it seems within reach to decipher the inner workings of pulsars, and to explore the phase diagram of cold and ultra-dense hadronic matter from astrophysics.
Supplementary Materials
Several movies showing the changing particle compositions inside of rotating neutron stars are available online at http://www-rohan.sdsu.edu/∼fweber/Mellinger/Compositions.html.
Acknowledgments
This work is supported through the U.S. National Science Foundation under Grants PHY-1411708 and DUE-1259951. Additional computing resources are provided by the Computational Science Research Center and the Department of Physics at San Diego State University. Milva G. Orsaria thanks the financial support from American Physical Society’s International Research Travel Award Program. Gustavo A. Contrera, and Milva G. Orsaria acknowledge financial support from CONICET and UNLP (Project identification code 11/G140 and 11/X718), Argentina.
Author Contributions
The authors contributed equally to the theoretical and numerical aspects of the work presented in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Friman, B.; Höhne, C.; Knoll, J.; Leupold, S.; Randrup, J.; Rapp, R.; Senger, P. (Eds.) The CBM Physics Book; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2011; Volume 814.
- Blaschke, D.; Aichelin, J.; Bratkovskaya, E.; Friese, V.; Gazdzicki, M.; Randrup, J.; Rogachevsky, O.; Teryaev, O.; Toneev, V. Topical Issue on Exploring Strongly Interacting Matter at High Densities—NICA White Paper. Eur. Phys. J. A 2016, 52, 267. [Google Scholar] [CrossRef]
- Bass, S.; Caines, H.; Cole, B.A.; Dunlop, J.; Hemmick, T.K.; Morrison, D.; Putschke, J.; Salur, S.; Schenke, B.; Solz, R.A.; et al. Hot and Dense QCD Matter. Community White Paper. Available online: http://www.bnl.gov/npp/ (accessed on 10 October 2016).
- Glendenning, N.K. Compact Stars, Nuclear Physics, Particle Physics, and General Relativity, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Weber, F. Pulsars as Astrophysical Laboratories for Nuclear and Particle Physics; High Energy Physics, Cosmology and Gravitation Series; IOP Publishing: Bristol, UK, 1999. [Google Scholar]
- Baldo, M.; Burgio, F. Microscopic Theory of the Nuclear Equation of State and Neutron Star Structure. In Physics Of Neutron Star Interiors; Blaschke, D., Glendenning, N.K., Sedrakian, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 578, pp. 1–29. [Google Scholar]
- Lattimer, J.M.; Prakash, M. Neutron Star Structure and the Equation of State. Astrophys. J. 2001, 550, 426–442. [Google Scholar] [CrossRef]
- Weber, F. Strange Quark Matter and Compact Stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Page, D.; Reddy, S. Dense Matter in Compact Stars: Theoretical Developments and Observational Constraints. Ann. Rev. Nucl. Part. Sci. 2006, 56, 327–374. [Google Scholar] [CrossRef]
- Klähn, T.; Blaschke, D.; Typel, S.; van Dalen, E.N.E.; Faessler, A.; Fuchs, C.H.; Gaitanos, T.; Grigorian, H.; Ho, A.; Kolomeitsev, E.E.; et al. Constraints on the high-density nuclear equation of state from the phenomenology of compact stars and heavy-ion collisions. Phys. Rev. C 2006, 74, 035802. [Google Scholar] [CrossRef]
- Sedrakian, A. The physics of dense hadronic matter and compact. stars. Prog. Part. Nucl. Phys. 2007, 58, 168–246. [Google Scholar] [CrossRef]
- Klähn, T.; Blaschke, D.; Sandin, F.; Fuchs, C.H.; Faessler, A.; Grigorian, H.; Röpke, G.; Trümper, J. Modern compact star observations and the quark matter equation of state. Phys. Lett. B 2007, 654, 170–176. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Becker, W. (Ed.) Neutron Stars and Pulsars, Astrophysics and Space Science Library; Springer: New York, NY, USA, 2009; Volume 357.
- Grigorian, H.; Blaschke, D.; Aguilera, D.N. Hybrid stars with color superconductivity within a nonlocal chiral quark model. Phys. Rev. C 2004, 69, 065802. [Google Scholar] [CrossRef]
- Blaschke, D.B.; Gómez Dumm, D.; Grunfeld, A.G.; Klähn, T.; Scoccola, N.N. Hybrid stars within a covariant, nonlocal chiral quark model. Phys. Rev. C 2007, 75, 065804. [Google Scholar] [CrossRef]
- Fritzsch, H.; Gell-Mann, M.; Leutwyler, H. Advantages of the Color Octet Gluon Picture. Phys. Lett. 1973, 47, 365–368. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Pei, S.; Weber, F. Signal of Quark Deconfinement in the Timing Structure of Pulsar Spin-Down. Phys. Rev. Lett. 1997, 79, 1603–1606. [Google Scholar] [CrossRef]
- Chubarian, E.; Grigorian, H.; Poghosyan, G.; Blaschke, D. Deconfinement transition in rotating compact stars. Astron. Astrophys. 2000, 357, 968–976. [Google Scholar]
- Glendenning, N.K.; Weber, F. Signal of Quark Deconfinement in Millisecond Pulsars and Reconfinement in Accreting X-ray Neutron Stars. In Physics Of Neutron Star Interiors; Blaschke, D., Glendenning, N.K., Sedrakian, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 578, pp. 305–332. [Google Scholar]
- Glendenning, N.K.; Weber, F. Phase Transition and Spin Clustering of Neutron Stars in X-Ray Binaries. Astrophys. J. 2001, 559, 119–122. [Google Scholar] [CrossRef]
- Poghosyan, G.; Grigorian, H.; Blaschke, D. Population Clustering as a Signal for Deconfinement in Accreting Compact Stars. Astrophys. J. 2001, 551, 73–76. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. The Australia Telescope National Facility Pulsar Catalogue. Astron. J. 2005, 129, 1993–2006. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. ATNF Pulsar Catalogue: Version 1.53. 2005. Available online: http://www.atnf.csiro.au/research/pulsar/psrcat/ (accessed on 23 September 2015).
- Hessels, J.W.T.; Ransom, S.M.; Stairs, I.H.; Freire, P.C.C.; Kaspi, V.M.; Camilo, F. A Radio Pulsar Spinning at 716 Hz. Science 2006, 311, 1901–1904. [Google Scholar] [CrossRef] [PubMed]
- Walecka, J.D. A theory of highly condensed matter. Ann. Phys. 1974, 83, 491–531. [Google Scholar] [CrossRef]
- Glendenning, N.K. Neutron stars are giant hypernuclei? Astrophys. J. 1985, 293, 470–493. [Google Scholar] [CrossRef]
- Boguta, J.; Bodmer, A.R. Relativistic calculation of nuclear matter and the nuclear surface. Nucl. Phys. 1977, 292, 413–428. [Google Scholar] [CrossRef]
- Boguta, J.; Rafelski, J. Thomas Fermi model of finite nuclei. Phys. Lett. 1977, 71, 22–26. [Google Scholar] [CrossRef]
- Boguta, J.; Stöcker, H. Systematics of nuclear matter properties in a non-linear relativistic field theory. Phys. Lett. 1983, 120, 289–293. [Google Scholar] [CrossRef]
- Shlomo, S.; Kolomietz, V.M.; Coló, G. Deducing the nuclear-matter incompressibility coefficient from data on isoscalar compression modes. Eur. Phys. J. A 2006, 30, 23–30. [Google Scholar] [CrossRef]
- Stone, J.R.; Stone, N.J.; Moszkowski, S.A. Incompressibility in finite nuclei and nuclear matter. Phys. Rev. C 2014, 89, 044316. [Google Scholar] [CrossRef]
- Krüger, T.; Tews, I.; Hebeler, K.; Schwenk, A. Neutron matter from chiral effective field theory interactions. Phys. Rev. C 2013, 88, 025802. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Steiner, A.W. Constraints on the symmetry energy using the mass-radius relation of neutron stars. Eur. Phys. J. A 2014, 50, 40. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lee, J. Symmetry energy II: Isobaric analog states. Nucl. Phys. A 2014, 922, 1–70. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Moszkowski, S.A. Reconciliation of neutron-star masses and binding of the Λ in hypernuclei. Phys. Rev. Lett. 1991, 67, 2414–2417. [Google Scholar] [CrossRef] [PubMed]
- Typel, S.; Ropke, G.; Klähn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Brockmann, R.; Toki, H. Relativistic density-dependent Hartree approach for finite nuclei. Phys. Rev. Lett. 1992, 68, 3408–3411. [Google Scholar] [CrossRef] [PubMed]
- Lenske, H.; Fuchs, C.H. Rearrangement in the density dependent relativistic field theory of nucle. Phys. Lett. B 1995, 345, 355–360. [Google Scholar] [CrossRef]
- Hofmann, F.; Keil, C.M.; Lenske, H. Application of the density dependent hadron field theory to neutron star matter. Phys. Rev. C 2001, 64, 025804. [Google Scholar] [CrossRef]
- Fuchs, C.H.; Lenske, H.; Wolter, H.H. Density dependent hadron field theory. Phys. Rev. C 1995, 52, 3043. [Google Scholar] [CrossRef]
- Typel, S.; Wolter, H.H. Relativistic mean field calculations with density-dependent meson-nucleon coupling. Nucl. Phys. A 1999, 656, 331–364. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Klevansky, S.P. The Nambu—Jona-Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 1992, 64, 649–708. [Google Scholar] [CrossRef]
- Vogl, U.; Weise, W. The Nambu and Jona-Lasinio model: Its implications for Hadrons and Nuclei. Prog. Part. Nucl. Phys. 1991, 27, 195–272. [Google Scholar] [CrossRef]
- Buballa, M. NJL-model analysis of dense quark matter. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Orsaria, M.; Rodrigues, H.; Weber, F.; Contrera, G.A. Quark-hybrid matter in the cores of massive neutron stars. Phys. Rev. D 2013, 87, 023001. [Google Scholar] [CrossRef]
- Orsaria, M.; Rodrigues, H.; Weber, F.; Contrera, G.A. Quark deconfinement in high-mass neutron stars. Phys. Rev. C 2014, 89, 015806. [Google Scholar] [CrossRef]
- Contrera, G.A.; Gomez Dumm, D.; Scoccola, N.N. Nonlocal SU(3) chiral quark models at finite temperature: The role of the Polyakov loop. Phys. Lett. B 2008, 661, 113–117. [Google Scholar] [CrossRef]
- Contrera, G.A.; Gomez Dumm, D.; Scoccola, N.N. Meson properties at finite temperature in a three flavor nonlocal chiral quark model with Polyakov loop. Phys. Rev. D 2010, 81, 054005. [Google Scholar] [CrossRef]
- Sasaki, C.; Friman, B.; Redlich, K. Quark Number Fluctuations in a Chiral Model at Finite Baryon Chemical Potential. Phys. Rev. D 2007, 75, 054026. [Google Scholar] [CrossRef]
- Fukushima, K. Phase diagrams in the three-flavor Nambu-Jona-Lasinio model with the Polyakov loop. Phys. Rev. D 2008, 77, 114028, Erratum in 2008, 78, 039902. [Google Scholar] [CrossRef]
- Bratovic, N.M.; Hatsuda, T.; Weise, W. Role of Vector Interaction and Axial Anomaly in the PNJL Modeling of the QCD Phase Diagram. Phys. Lett. B 2013, 719, 131–135. [Google Scholar] [CrossRef]
- Glendenning, N.K. First-order phase transitions with more than one conserved charge: Consequences for neutron stars. Phys. Rev. D 1992, 46, 1274–1287. [Google Scholar] [CrossRef]
- Glendenning, N.K. Phase transitions and crystalline structures in neutron star cores. Phys. Rep. 2001, 342, 393–447. [Google Scholar] [CrossRef]
- Bonanno, L.; Sedrakian, A. Composition and stability of hybrid stars with hyperons and quark color-superconductivity. Astron. Astrophys. 2012, 539, A16. [Google Scholar] [CrossRef]
- Masuda, K.; Hatsuda, T.; Takatsuka, T. Hadron-quark crossover and massive hybrid stars with strangeness. Astrophys. J. 2013, 764, 12. [Google Scholar] [CrossRef]
- Masuda, K.; Hatsuda, T.; Takatsuka, T. Hadron–quark crossover and massive hybrid stars. Prog. Theor. Exp. Phys. 2013, 7, 073D01. [Google Scholar] [CrossRef]
- Lenzi, C.H.; Lugones, G. Hybrid Stars in the Light of the Massive Pulsar PSR J1614-2230. Astrophys. J. 2012, 759, 57. [Google Scholar] [CrossRef]
- Ranea-Sandoval, I.F.; Han, S.; Orsaria, M.O.; Contrera, G.A.; Weber, F.; Alford, M.G. Constant-sound-speed parametrization for Nambu–Jona-Lasinio models of quark matter in hybrid stars. Phys. Rev. C 2016, 93, 045812. [Google Scholar] [CrossRef]
- Contrera, G.A.; Orsaria, M.; Ranea-Sandoval, I.F.; Weber, F. Hybrid Stars in the Framework of different NJL Models. arXiv 2016. [Google Scholar]
- Voskresensky, D.N.; Yasuhira, M.; Tatsumi, T. Charge screening in hadron–quark mixed phase. Phys. Lett. B 2002, 541, 93–100. [Google Scholar] [CrossRef]
- Yasutake, N.; Lastowiecki, R.; Benic, S.; Blaschke, D.; Maruyama, T.; Tatsumi, T. Finite-size effects at the hadron-quark transition and heavy hybrid stars. Phys. Rev. C 2014, 89, 065803. [Google Scholar] [CrossRef]
- Palhares, L.F.; Fraga, E.S. Droplets in the cold and dense linear sigma model with quarks. Phys. Rev. D 2010, 82, 125018. [Google Scholar] [CrossRef]
- Pinto, M.B.; Koch, V.; Randrup, J. Surface tension of quark matter in a geometrical approach. Phys. Rev. C 2012, 86, 025203. [Google Scholar] [CrossRef]
- Mintz, B.W.; Stiele, R.; Ramos, R.O.; Schaffner-Bielich, J. Phase diagram and surface tension in the three-flavor Polyakov-quark-meson model. Phys. Rev. D 2013, 87, 036004. [Google Scholar] [CrossRef]
- Spinella, W.M.; Weber, F.; Contrera, G.A.; Orsaria, M.G. Neutrino emissivity in the quark-hadron mixed phase of neutron stars. Eur. Phys. J. A 2016, 52, 61. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef]
- Kurkela, A.; Fraga, E.S.; Schaffner-Bielich, J.; Vuorinen, A. Constraining neutron star matter with Quantum Chromodynamics. Astrophys. J. 2014, 789, 127. [Google Scholar] [CrossRef]
- Friedman, J.L.; Ipser, J.R.; Parker, L. Rapidly rotating neutron star models. Astrophys. J. 1986, 304, 115–139. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M.; Masak, D.; Yahil, A. Rapidly rotating pulsars and the equation of state. Astrophys. J. 1990, 355, 241–254. [Google Scholar] [CrossRef]
- Salgado, M.; Bonazzola, S.; Gourgoulhon, E.; Haensel, P. High precision rotating netron star models 1: Analysis of neutron star properties. Astron. Astrophys. 1994, 291, 155–170. [Google Scholar]
- Cook, G.B.; Shapiro, S.L.; Teukolsky, S.A. Rapidly rotating polytropes in general relativity. Astrophys. J. 1994, 422, 227–242. [Google Scholar] [CrossRef]
- Cook, G.B.; Shapiro, S.L.; Teukolsky, S.A. Rapidly rotating neutron stars in general relativity: Realistic equations of state. Astrophys. J. 1994, 424, 823–845. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Weber, F. Nuclear solid crust on rotating strange quark stars. Astrophys. J. 1992, 400, 647–658. [Google Scholar] [CrossRef]
- Glendenning, N.K. Limiting rotational period of neutron stars. Phys. Rev. D 1992, 46, 4161–4168. [Google Scholar] [CrossRef]
- Backer, D.C.; Kulkarni, S.R.; Heiles, C.; Davis, M.M.; Goss, W.M. A millisecond pulsar. Nature 1982, 300, 615–618. [Google Scholar] [CrossRef]
- Fruchter, A.S.; Stinebring, D.R.; Taylor, J.H. A millisecond pulsar in an eclipsing binary. Nature 1988, 333, 237–239. [Google Scholar] [CrossRef]
- Hartle, J.B. Slowly Rotating Relativistic Stars. I. Equations of Structure. Astrophys. J. 1967, 150, 1005. [Google Scholar] [CrossRef]
- Hartle, J.B.; Thorne, K.S. Slowly Rotating Relativistic Stars. II. Models for Neutron Stars and Supermassive Stars. Astrophys. J. 1968, 153, 807–834. [Google Scholar] [CrossRef]
- Weber, F.; Glendenning, N.K. Application of the improved Hartle method for the construction of general relativistic rotating neutron star models. Astrophys. J. 1992, 390, 541–549. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ranson, S.M.; Roberts, M.S.E.; Hessels, J.W.T. Shapiro delay measurement of a two solar mass neutron star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Lynch, R.S.; Boyles, J.; Ransom, S.M.; Stairs, I.H.; Lorimer, D.R.; McLaughlin, M.A.; Hessels, J.W.T.; Kaspi, V.M.; Kondratiev, V.I.; Archibald, A.M. The Green Bank Telescope 350 MHz drift-scan survey II: data analysis and the timing of 10 new pulsars, including a relativistic binary. Astrophys. J. 2013, 763, 81. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A massive pulsar in a compact relativistic binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Stejner, M.; Weber, F.; Madsen, J. Signature of deconfinement with spin-down compression in cooling hybrid stars. Astrophys. J. 2009, 694, 1019–1033. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).