Gauge-Invariant Gravitational Wave Polarization in Metric f(R) Gravity with Cosmological Implications

Abstract

We develop a fully gauge-invariant analysis of gravitational-wave polarizations in metric $f\left(R\right)$ gravity with a particular focus on the modified Starobinsky model $f\left(R\right)=R+\alpha R^2-2\mathsf{\Lambda }$, whose constant-curvature solution $R_d=4\mathsf{\Lambda }$ provides a natural de Sitter background for both early- and late-time cosmology. Linearizing the field equations around this background, we derive the Klein–Gordon equation for the curvature perturbation $\delta R$ and show that the scalar propagating mode acquires a mass $m_{\psi }^2=1/\left(6\alpha \right)$, highlighting how the same scalar degree of freedom governs inflationary dynamics at high curvature and the propagation of gravitational waves in the current accelerating Universe. Using the scalar–vector–tensor decomposition and a decomposition of the perturbed Ricci tensor, we obtain a set of fully gauge-invariant propagation equations that isolate the contributions of the scalar, vector, and tensor modes in the presence of matter. We find that the tensor sector retains the two transverse–traceless polarizations of General Relativity, while the scalar sector contains an additional massive scalar propagating degree of freedom, which manifests through breathing and longitudinal tidal responses depending on the wave regime and detector frame. Through the geodesic deviation equation—computed both in a local Minkowski patch and in fully covariant de Sitter form—we independently recover the same polarization content and identify its tidal signatures. The resulting framework connects the extra scalar polarization to cosmological observables: the massive scalar propagating mode sets the range of the fifth force, influences the time evolution of gravitational potentials, and affects the propagation and dispersion of gravitational waves on cosmological scales. This provides a unified, gauge-invariant link between gravitational-wave phenomenology and the cosmological implications of metric $f\left(R\right)$ gravity.

1. Introduction

The study of gravitational wave (GW) polarizations provides a powerful way to distinguish General Relativity (GR) from alternative theories of gravity [1]. In the classic classification by Eardley, Lee, and Lightman using the Newman–Penrose (NP) formalism [2], a general metric theory of gravity may contain up to six possible GW polarization states. This framework has since been extensively developed and applied to a wide class of modified gravity theories, both at the level of fundamental classification and in the context of detector response and observational constraints [1,3,4,5]. In GR only two of these, the familiar tensor “plus” (⊕) and “cross” (⊗) modes, are present, corresponding to the two radiative degrees of freedom (DoF) of the metric. Extensions of GR often introduce additional scalar and/or vectorial modes whose presence modifies the relative displacement of freely-falling test particles.

A particularly well-known example is Brans–Dicke theory [6], in which the scalar field gives rise to an additional transverse breathing mode. More generally, recent analyses using both the NP formalism and the irreducible (3 + 1) decomposition [7,8] have confirmed that the number of NP polarization states does not necessarily coincide with the number of radiative DoF in a theory. This mismatch appears naturally in scalar–tensor theories and in metric $f\left(R\right)$ gravity, where the Ricci scalar perturbation introduces a new massive scalar propagating mode that obeys a Klein–Gordon equation with an effective mass $m_{\psi }$ [9,10,11]. For massless propagation, this scalar mode produces a single independent polarization: a transverse breathing distortion of a ring of test particles. When the scalar mode is massive ($m_{\psi }\ne 0$), however, the scalar sector induces a mixture of transverse breathing and longitudinal motion along the propagation direction; these two NP amplitudes are not independent but jointly encode a single scalar radiative DoF. Thus, metric $f\left(R\right)$ gravity contains three radiative DoF but may exhibit up to four NP polarization amplitudes in the massive case.

It is important to note recent discussions regarding the interpretation of NP quantities in theories containing massive modes. For gravitational waves whose group velocity differs from the speed of light, some NP components that vanish in GR no longer vanish identically, raising subtleties concerning the mapping between NP scalars and physical polarizations [2]. This occurs because nonluminal propagation renders the wave vector non-null, so the standard NP null tetrad cannot be aligned with the direction of propagation, and the usual decoupling between radiative and non-radiative components breaks down [3,4,7]. These issues do not invalidate the NP approach but motivate complementary gauge-invariant formalisms.

Several modified gravity models exhibit similar features. In modified Gauss–Bonnet gravity $f\left(G\right)$, for example, tensor waves propagate as in GR while an additional massive scalar mode appears [12]. In massive gravity theories studied via Bardeen variables [13], a normally non-radiative scalar mode becomes dynamical, constituting the helicity-0 component of a massive graviton. By contrast, quadratic theories such as Einstein–Dilaton–Gauss–Bonnet and dynamical Chern–Simons gravity can display the same polarization content as GR in their linearized limit [14]. Extensions involving explicit matter–geometry couplings, including $f(R,T)$ and $f(R,T^{\varphi })$ gravity [15], further illustrate the subtlety of polarization counting. Although $f(R,T)$ and $f\left(R\right)$ gravity share the same far-field polarization structure in vacuum ($T=0$), their source-dependent dynamics differ. The $f(R,T^{\varphi })$ theory, involving an additional scalar $\varphi$, leads to distinguishable polarization patterns even in vacuum. These analyses also emphasize that the scalar mode $\psi$ belonging to $f\left(R\right)$ gravity must be clearly distinguished from any additional matter scalar $\varphi$.

Gravitational radiation in linearized metric $f\left(R\right)$ gravity has been studied in both power-series models:

$$f\left(R\right)=\sum _{n=0}^N{a}_n{R}^n,$$

(1)

and in specific subclasses such as the Starobinsky model. Solar-system tests constrain viable metric $f\left(R\right)$ models to reproduce light deflection very close to the GR value (post-Newtonian parameter $\mathsf{\Gamma }\simeq 1$), typically via a sufficiently heavy or screened scalar degree of freedom, although other post-Newtonian effects (e.g., perihelion precession) can still differ in some regimes [16]. Studies of waveform phases in extreme-mass-ratio inspirals suggest that deviations from GR may be detectable in some regimes. Polarization analyses performed in both $f\left(R\right)$ and Horndeski theories [4] highlight the challenge of detecting longitudinal scalar modes with laser interferometers, whereas Pulsar Timing Arrays may offer greater sensitivity. The mixed longitudinal–breathing nature of the massive scalar propagating mode has been explicitly confirmed using the geodesic deviation equation [17]. Additional applications of $f\left(R\right)$ gravity include the study of gravitational radiation from white dwarfs with sub- and super-Chandrasekhar masses, where all relevant polarization amplitudes were estimated using Green-function methods [18].

A de Sitter background is particularly well motivated for analyzing the propagation of tensor and scalar modes in metric $f\left(R\right)$ gravity. It provides an excellent approximation to late-time cosmic acceleration driven by dark energy and also captures the quasi-exponential “slow-roll” inflationary phase in the early Universe. (Here, “slow-roll” refers to the regime in which the inflaton’s kinetic energy remains small compared to its potential energy, yielding an almost constant Hubble parameter.) Background curvature affects dispersion relations, mode mixing, and asymptotic behavior of gravitational waves, which motivates studying the massive scalar mode and tensor modes directly on de Sitter space [19,20]. Because GR with a cosmological constant supports only two tensor polarizations, de Sitter space provides a clean setting for isolating any additional modes arising from $f\left(R\right)$ gravity and for providing a common constant-curvature background on which the tensor and scalar modes can be analyzed across cosmological epochs, even though the physical mechanisms and energy scales governing inflation and late-time acceleration are distinct.

The structure of this paper is as follows. In Section 2, we derive the field equations of metric $f\left(R\right)$ gravity on a de Sitter background and obtain the Klein–Gordon equation for the extra scalar mode with mass $m_{\psi }$. Section 3 develops the perturbation of the Ricci tensor, and the resulting linearized field equations. Section 4 performs the (3 + 1) irreducible decomposition into scalar, vector, and tensor sectors. In Section 5, we specialize to the model $f\left(R\right)=R+\alpha R^2-2\mathsf{\Lambda }$ and present its explicit linearized dynamics. Section 6 identifies the gauge-invariant Bardeen variables and derives the physical polarization content. Finally, in Section 7, we verify these results using the geodesic deviation equation, demonstrating that the obtained polarization modes are physically realized in the relative acceleration of freely falling test particles.

2. Field Equations of Metric $\mathit{f}\left(\mathit{R}\right)$ Gravity on a de Sitter Background

In metric $f\left(R\right)$ gravity, the Einstein–Hilbert Lagrangian density R is replaced by a general function $f\left(R\right)$:

$$S={\displaystyle \frac{1}{2\kappa }}\int d^{4}x\sqrt{-g}f\left(R\right)+S_m[g_{\mu \nu },{\mathsf{\Psi }}_m],$$

(2)

where $S_m$ is the matter action, ${\mathsf{\Psi }}_m$ collectively denotes the matter fields, and

$$\kappa \equiv 8\pi G=2M_{\mathrm{Pl}}^{-2}$$

(3)

in terms of the reduced Planck mass $M_{\mathrm{Pl}}$ (we use units $c=1$). Varying (2) with respect to the metric and following, e.g., [21], one obtains the metric $f\left(R\right)$ field equations:

$$f^{\prime }\left(R\right)R_{\mu \nu }-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }f\left(R\right)+\left(g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu }\right)f^{\prime }\left(R\right)=\kappa T_{\mu \nu },$$

(4)

where $f^{\prime }\left(R\right)\equiv df/dR$, $\square \equiv g^{\rho \sigma }{\nabla }_{\rho }{\nabla }_{\sigma }$, and

$$T_{\mu \nu }=-{\displaystyle \frac{2}{\sqrt{-g}}}{\displaystyle \frac{\delta \left(\sqrt{-g}{S}_m\right)}{\delta g^{\mu \nu }}}$$

(5)

is the matter stress–energy tensor. In vacuum we set $T_{\mu \nu }=0$ and (4) reduces to the following:

$$f^{\prime }\left(R\right)R_{\mu \nu }-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }f\left(R\right)+\left(g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu }\right)f^{\prime }\left(R\right)=0.$$

(6)

Taking the trace of (4) yields the scalar (trace) equation

$$3\square f^{\prime }\left(R\right)+R{f}^{\prime }\left(R\right)-2f\left(R\right)=\kappa T,$$

(7)

where $T\equiv g^{\mu \nu }{T}_{\mu \nu }$. In vacuum, it is as follows:

$$3\square f^{\prime }\left(R\right)+R{f}^{\prime }\left(R\right)-2f\left(R\right)=0.$$

(8)

The trace equation will be the starting point for identifying the massive scalar propagating mode (the “scalaron”) and its effective mass.

2.1. $f\left(R\right)$ Gravity, Scalar–Tensor Form, and the Chameleon Mechanism

The field Equation (4) contain higher derivatives of the metric through $\square f^{\prime }\left(R\right)$ and ${\nabla }_{\mu }{\nabla }_{\nu }{f}^{\prime }\left(R\right)$. A useful way to expose the extra scalar degree of freedom and to analyze screening—namely, the suppression of scalar-mediated fifth forces in high-density environments via an environment-dependent effective mass—is to recast metric $f\left(R\right)$ gravity as a scalar–tensor theory via a conformal transformation (see, e.g., [10,11]).

Define

$$F\left(R\right)\equiv f^{\prime }\left(R\right)>0,F\left(R\right)=exp\left(-{\displaystyle \frac{2\beta \varphi }{M_{\mathrm{Pl}}}}\right),$$

(9)

where $\varphi$ is a scalar field. (Our sign convention for $\varphi$ follows from this definition; flipping $\varphi \to -\varphi$ maps to the alternative convention commonly used in the literature.) In metric $f\left(R\right)$ gravity the coupling parameter is fixed to $\beta =1/\sqrt{6}$, reflecting the universal strength of the scalar coupling to matter. We then introduce the conformal transformation:

$${\overline{g}}_{\mu \nu }=F\left(R\right)g_{\mu \nu }=exp\left(-{\displaystyle \frac{2\beta \varphi }{M_{\mathrm{Pl}}}}\right)g_{\mu \nu },$$

(10)

which maps the Jordan frame metric $g_{\mu \nu }$ to the Einstein frame metric ${\overline{g}}_{\mu \nu }$. In the Jordan frame, matter is minimally coupled to $g_{\mu \nu }$ and freely falling test particles follow geodesics of $g_{\mu \nu }$. In the Einstein frame, the gravitational sector takes the Einstein–Hilbert form plus a canonical scalar field, while matter acquires a $\varphi$-dependent non-minimal coupling with respect to the Einstein-frame metric ${\overline{g}}_{\mu \nu }$.

In terms of ${\overline{g}}_{\mu \nu }$ and $\varphi$, the action (2) becomes the following:

$$S=\int d^{4}x\sqrt{-\overline{g}}\left[{\displaystyle \frac{M_{\mathrm{Pl}}^2}{2}}\overline{R}-{\displaystyle \frac{1}{2}}{\overline{g}}^{\mu \nu }{\overline{\nabla }}_{\mu }\varphi {\overline{\nabla }}_{\nu }\varphi -V\left(\varphi \right)\right]+S_m\left(A^2\left(\varphi \right){\overline{g}}_{\mu \nu },{\mathsf{\Psi }}_m\right),$$

(11)

where ${\overline{\nabla }}_{\mu }$ and $\overline{R}$ are the covariant derivative and Ricci scalar of ${\overline{g}}_{\mu \nu }$, and

$$A^2\left(\varphi \right)=F^{-1}\left(R\right)=exp\left(+{\displaystyle \frac{2\beta \varphi }{M_{\mathrm{Pl}}}}\right)$$

(12)

is the conformal factor relating the Einstein and Jordan metrics in the matter sector. The scalar potential is as follows:

$$V\left(\varphi \right)={\displaystyle \frac{M_{\mathrm{Pl}}^2}{2}}{\displaystyle \frac{RF\left(R\right)-f\left(R\right)}{F^2\left(R\right)}}={\displaystyle \frac{1}{\kappa }}{\displaystyle \frac{R{f}^{\prime }\left(R\right)-f\left(R\right)}{f^{\prime 2}\left(R\right)}}.$$

(13)

The corresponding Einstein-frame field equations can be written as follows:

$$\begin{array}{cc}\hfill {\overline{G}}_{\mu \nu }& ={\displaystyle \frac{1}{M_{\mathrm{Pl}}^2}}\left(T_{\mu \nu }^{\left(\varphi \right)}+T_{\mu \nu }^{\left(m\right)}\right),\hfill \\ \hfill \overline{\square }\varphi & =V^{\prime }\left(\varphi \right)-{\displaystyle \frac{\beta }{M_{\mathrm{Pl}}}}{T}^{\left(m\right)},\hfill \end{array}$$

(14)

where $T_{\mu \nu }^{\left(\varphi \right)}$ is the scalar-field stress tensor and $T_{\mu \nu }^{\left(m\right)}$ is the Einstein-frame matter tensor. For a spatially homogeneous scalar field $\varphi =\varphi \left(t\right)$ in a spatially flat FRW background, this equation reduces to the standard cosmological Klein–Gordon equation:

$$\ddot{\varphi }+3H\dot{\varphi }+V^{\prime }\left(\varphi \right)={\displaystyle \frac{\beta }{M_{\mathrm{Pl}}}}{T}^{\left(m\right)},$$

(15)

which in the vacuum limit ($T^{\left(m\right)}=0$) becomes the following:

$$\ddot{\varphi }+3H\dot{\varphi }+V^{\prime }\left(\varphi \right)=0,$$

(16)

which is the equation solved in inflationary and background cosmological applications [10,22,23]. This equation illustrates that the same $f\left(R\right)$ action admits de Sitter solutions in both high- and low-curvature regimes at the level of the underlying action. This unification is purely formal: the corresponding solutions arise from parametrically distinct operators and operate at vastly different energy scales. In particular, the $R^2$ term governs early-time inflationary dynamics, while late-time cosmic acceleration is controlled by the effective cosmological constant. The scalar degree of freedom associated with the $R^2$ term is therefore relevant only at inflationary curvatures and is decoupled from late-time gravitational-wave phenomenology.

2.2. Jordan vs. Einstein Frame in Practice

The Jordan frame is the one in which matter is minimally coupled and experimental observables (such as test-particle trajectories and detector responses) are most directly interpreted. The Einstein frame is mathematically convenient for analyzing the dynamics of the extra scalar degree of freedom and for discussing stability, screening mechanisms, and cosmological evolution. Physical predictions are frame-independent provided one consistently transforms both the metric and matter variables. In this paper, we perform the gravitational-wave analysis in the Jordan frame (where the Bardeen variables and metric perturbations are defined), while the Einstein-frame description is used only to clarify the scalar–tensor structure and the chameleon mechanism.

2.3. Chameleon Mechanism in $f\left(R\right)$ Gravity

We briefly summarize the chameleon mechanism here for completeness, as it plays no direct role in the gravitational-wave polarization analysis carried out in later sections.

The additional scalar degree of freedom in metric $f\left(R\right)$ gravity mediates a universal fifth force [10,11] through its coupling to the trace of the matter stress–energy tensor. The scalar field $\varphi$ in (11) couples universally to matter via $A^2\left(\varphi \right){\overline{g}}_{\mu \nu }$ and can mediate this fifth force unless its effective mass becomes large in high-density environments. The chameleon mechanism exploits the density dependence of the effective potential:

$$V_{\mathrm{eff}}\left(\varphi \right)=V\left(\varphi \right)+\rho A\left(\varphi \right),A\left(\varphi \right)=exp\left(+{\displaystyle \frac{\beta \varphi }{M_{\mathrm{Pl}}}}\right),$$

(17)

where $\rho$ is the local matter density. In regions of high density, $V_{\mathrm{eff}}$ develops a minimum at which the effective mass

$$m_{\mathrm{eff}}^2\left(\rho \right)\equiv {\left.{\displaystyle \frac{d^2{V}_{\mathrm{eff}}}{d{\varphi }^2}}\right|}_{{\varphi }_{\min }\left(\rho \right)}$$

(18)

is large, so that the scalar-mediated force is short-ranged and consistent with local tests of gravity. In low-density environments (cosmological scales) the minimum shifts and $m_{\mathrm{eff}}$ can become small enough for the scalar to drive cosmic acceleration or leave imprints on structure formation [24,25,26].

For an $f\left(R\right)$ model to exhibit viable chameleon behavior, the scalar potential $V\left(\varphi \right)$ derived from (13) must satisfy certain conditions in at least part of field space:

$$V^{\prime }\left(\varphi \right)<0,V^{″}\left(\varphi \right)>0,V^{‴}\left(\varphi \right)<0,$$

(19)

which translate into nontrivial constraints on the form of $f\left(R\right)$ and its derivatives [25]. This ensures that the scalar field can be heavy in high-density regions while remaining light enough on cosmological scales to influence late-time acceleration.

2.4. Slow-Roll Inflation and Scalaron Dynamics in the Einstein Frame

We summarize the inflationary dynamics here only to establish notation and to clarify the origin of the scalar mass scale; no perturbative or polarization analysis is performed in this subsection. The scalar–tensor reformulation of metric $f\left(R\right)$ gravity introduced above provides a natural framework for discussing early-Universe inflation driven by the scalaron. When written in the Einstein frame, the scalar field $\varphi$ obeys the field equation obtained by varying the Einstein-frame action (11) is as follows:

$$\overline{\square }\varphi =V^{\prime }\left(\varphi \right),$$

(20)

where $V\left(\varphi \right)$ is given in Equation (13). For a spatially homogeneous scalar field $\varphi =\varphi \left(t\right)$ evolving in a spatially flat FLRW background, $d{\overline{s}}^2=-d{t}^2+a^2\left(t\right)d{\overrightarrow{x}}^2$, this equation reduces to the standard cosmological Klein–Gordon equation [10,22,23]:

$$\ddot{\varphi }+3H\dot{\varphi }+V^{\prime }\left(\varphi \right)=0,$$

(21)

where $H=\dot{a}/a$. The background expansion is governed by the Friedmann equation:

$$3M_{\mathrm{Pl}}^2{H}^2={\displaystyle \frac{1}{2}}{\dot{\varphi }}^2+V\left(\varphi \right).$$

(22)

Inflation occurs when the potential dominates the kinetic energy and the field slowly rolls along $V\left(\varphi \right)$. This is quantified by the slow-roll parameters:

$$ϵ\left(\varphi \right)\equiv {\displaystyle \frac{M_{\mathrm{Pl}}^2}{2}}{\left({\displaystyle \frac{V^{\prime }\left(\varphi \right)}{V\left(\varphi \right)}}\right)}^2,\eta \left(\varphi \right)\equiv M_{\mathrm{Pl}}^2{\displaystyle \frac{V^{″}\left(\varphi \right)}{V\left(\varphi \right)}},$$

(23)

where inflation requires $ϵ\ll 1$ and $\left|\eta \right|\ll 1$. Under these conditions, Equation (21) reduces to the familiar slow-roll equation:

$$3H\dot{\varphi }\simeq -V^{\prime }\left(\varphi \right),$$

(24)

and the Hubble parameter satisfies $H^2\simeq V\left(\varphi \right)/\left(3M_{\mathrm{Pl}}^2\right)$.

For the Starobinsky-type models considered in this work, the potential $V\left(\varphi \right)$ possesses a nearly flat region at large curvature ($R\gg \mathsf{\Lambda }$), ensuring that the slow-roll conditions (23) are naturally satisfied. In this regime, the scalaron behaves as an inflaton with an effective mass $m_{\varphi }^2\simeq V^{″}\left(\varphi \right)$, and the inflationary predictions coincide with those of the well-known $R+\alpha R^2$ model [9,27]. Observationally, the slow-roll phase gives rise to a nearly scale-invariant spectrum of primordial curvature perturbations and a suppressed tensor-to-scalar ratio, in excellent agreement with current CMB constraints.

Although slow-roll inflation operates at curvature scales far above those relevant for present-day gravitational-wave detectors, the same underlying extra scalar degree of freedom of $f\left(R\right)$ gravity governs both regimes. In the inflationary context this degree of freedom is commonly referred to as the scalaron, while at the level of linear perturbations it appears as a propagating massive scalar mode. In particular, the mass of the scalar perturbation at the de Sitter solution,

$$m_{\psi }^2={\displaystyle \frac{1}{3}}\left[{\displaystyle \frac{f^{\prime }\left(R_d\right)}{f^{″}\left(R_d\right)}}-R_d\right],$$

(25)

controls the propagation of the scalar polarization of gravitational waves. The scalar mass scale $m_{\psi }$ that appears in the perturbative analysis of gravitational waves is inherited from this inflationary sector, but its physical effects are confined to the appropriate energy regime.

2.5. de Sitter Solutions and Cosmological Implications

We are particularly interested in constant-curvature de Sitter solutions and small perturbations around them. For a vacuum constant-curvature background with $R=R_d=\mathrm{const}$ and $T=0$, the trace Equation (8) reduces to the following algebraic condition:

$$R_d{f}^{\prime }\left(R_d\right)-2f\left(R_d\right)=0.$$

(26)

Any function $f\left(R\right)$ that admits a solution of (26) possesses a de Sitter solution with curvature $R_d$. (Anti–de Sitter solutions correspond to constant-curvature solutions with $R_d<0$ and must be analyzed separately.) For the modified Starobinsky model

$$f\left(R\right)=R+\alpha R^2-2\mathsf{\Lambda },$$

(27)

the de Sitter curvature $R_d$ is determined by

$$R_d(1+2\alpha R_d)-2(R_d+\alpha R_d^2-2\mathsf{\Lambda })=0,$$

(28)

which yields the exact solution $R_d=4\mathsf{\Lambda }$.1 Thus, constant-curvature solutions in $f\left(R\right)$ gravity provide a common geometric setting in which both early-time inflationary and late-time accelerating backgrounds arise from the same action, even though their physical realizations and observational consequences are entirely distinct. In the present work, these solutions serve as the natural background for our gravitational-wave polarization analysis.

It is important to emphasize that, although both the inflationary and late-time accelerating phases correspond to de Sitter solutions of the underlying $f\left(R\right)$ theory, they arise from fundamentally different terms in the action. Inflation is driven by the $R^2$ correction and is characterized by a scalar mass scale m∼${10}^{13}\mathrm{GeV}$, as fixed by CMB observations of the scalar amplitude and tensor-to-scalar ratio in the Starobinsky model. By contrast, the present cosmic acceleration is controlled by the effective cosmological constant $\mathsf{\Lambda }$, corresponding to a dark-energy scale ${\mathsf{\Lambda }}^{1/4}$∼${10}^{-12}\mathrm{GeV}$.

As a consequence, these two regimes are widely separated and effectively decoupled. Gravitational waves observed at astrophysical frequencies (f∼10–${10}^3\mathrm{Hz}$, corresponding to $E_{\mathrm{GW}}$∼${10}^{-22}\mathrm{GeV}$) probe energies many orders of magnitude below the inflationary scalar mass. The scalar polarization associated with the $R^2$ term is therefore negligible for present-day gravitational-wave observations.

In the remainder of this paper, we will work in the Jordan frame and treat the extra propagating scalar mode directly in terms of the curvature perturbation $\delta R$. To avoid confusion of notation, we will use:

• $\varphi$ for the Einstein-frame scalar field entering the scalar–tensor and inflationary description in this subsection; and
• $\delta R$ (or, equivalently, a canonically normalized scalar perturbation $\psi$ with mass $m_{\psi }$) for the extra propagating scalar mode that appears in the linearized Jordan-frame field equations and in the Bardeen-variable analysis.

2.6. Metric Perturbations Around a de Sitter Background

We now consider small perturbations around a background solution $g_{\mu \nu }$ which solves the vacuum field Equation (6). In particular, we will later specialize to a de Sitter background satisfying (26). The perturbed metric is written as follows:

$$g_{\mu \nu }⟶{\tilde{g}}_{\mu \nu }=g_{\mu \nu }+h_{\mu \nu },{\tilde{g}}^{\mu \nu }=g^{\mu \nu }-h^{\mu \nu }+\mathcal{O}\left(h^2\right),$$

(29)

where indices on $h_{\mu \nu }$ are raised and lowered with the background metric $g_{\mu \nu }$.

To linear order, the curvature quantities and the function $f\left(R\right)$ expand as follows:

$$\begin{array}{cc}\hfill \tilde{R}& =R+\delta R+\mathcal{O}\left(h^2\right),\hfill \\ \hfill \tilde{f}\left(R\right)& =f\left(R\right)+f^{\prime }\left(R\right)\delta R+\mathcal{O}\left(h^2\right),\hfill \\ \hfill {\tilde{f}}^{\prime }\left(R\right)& =f^{\prime }\left(R\right)+f^{\prime \prime }\left(R\right)\delta R+\mathcal{O}\left(h^2\right),\hfill \end{array}$$

(30)

where R is the background Ricci scalar and $\delta R$ is its perturbation.

It is convenient to separate background and perturbed covariant derivatives. Denoting by ${\tilde{\nabla }}_{\mu }$ the covariant derivative associated with ${\tilde{g}}_{\mu \nu }$ and by ${\nabla }_{\mu }$ the one associated with $g_{\mu \nu }$, the difference between them acting on a generic tensor ${T^{{\nu }_1\dots {\nu }_k}}_{{\rho }_1\dots {\rho }_l}$ is (see, e.g., [28])

$${\tilde{\nabla }}_{\mu }{T^{{\nu }_1\dots {\nu }_k}}_{{\rho }_1\dots {\rho }_l}={\nabla }_{\mu }{T^{{\nu }_1\dots {\nu }_k}}_{{\rho }_1\dots {\rho }_l}+\sum _i{C^{{\nu }_i}}_{\mu \sigma }{T^{{\nu }_1\dots \sigma \dots {\nu }_k}}_{{\rho }_1\dots {\rho }_l}-\sum _j{C^{\sigma }}_{\mu {\rho }_j}{T^{{\nu }_1\dots {\nu }_k}}_{{\rho }_1\dots \sigma \dots {\rho }_l},$$

(31)

where the connection difference ${C^{\rho }}_{\mu \nu }$ is

$${C^{\rho }}_{\mu \nu }={\displaystyle \frac{1}{2}}{\tilde{g}}^{\rho \sigma }\left({\nabla }_{\mu }{\tilde{g}}_{\nu \sigma }+{\nabla }_{\nu }{\tilde{g}}_{\mu \sigma }-{\nabla }_{\sigma }{\tilde{g}}_{\mu \nu }\right).$$

(32)

All quantities without tildes refer to the background metric. These relations allow one to express perturbed curvature tensors and the perturbed trace equation in terms of $h_{\mu \nu }$ and $\delta R$.

Varying the vacuum trace Equation (8) and keeping terms linear in the perturbations yields the following:

$$\begin{array}{cc}0& =\delta \left[\square f^{\prime }\left(R\right)+{\displaystyle \frac{1}{3}}R{f}^{\prime }\left(R\right)-{\displaystyle \frac{2}{3}}f\left(R\right)\right]\hfill \\ \hfill & =\left[\square f^{″}\left(R\right)+f^{″}\left(R\right)\square -{\displaystyle \frac{1}{3}}\left(f^{\prime }\left(R\right)-R{f}^{″}\left(R\right)\right)\right]\delta R\hfill \\ \hfill & -\left[h^{\mu \rho }{\nabla }_{\mu }+{\displaystyle \frac{1}{2}}{g}^{\mu \nu }{g}^{\rho \sigma }\left({\nabla }_{\mu }{h}_{\nu \sigma }+{\nabla }_{\nu }{h}_{\mu \sigma }-{\nabla }_{\sigma }{h}_{\mu \nu }\right)\right]\left(f^{″}\left(R\right){\partial }_{\rho }R\right),\hfill \end{array}$$

(33)

where we have used (30) and (31). Equation (33) is valid for a general background.

For the de Sitter backgrounds of interest in this work, the Ricci scalar is constant,

$$R=R_d=\mathrm{const},$$

(34)

so that ${\nabla }_{\mu }R=0$ and $f^{\prime }\left(R_d\right)$, $f^{″}\left(R_d\right)$ are constants. In this case the second line of (33) vanishes, $\square f^{″}\left(R_d\right)=0$, and we obtain the simplified scalar perturbation equation

$$\left[\square -{\displaystyle \frac{1}{3}}\left({\displaystyle \frac{f^{\prime }\left(R_d\right)}{f^{″}\left(R_d\right)}}-R_d\right)\right]\delta R=0,$$

(35)

or, equivalently,

$$\left(\square -m_{\psi }^2\right)\delta R=0,$$

(36)

with

$$m_{\psi }^2={\displaystyle \frac{1}{3}}\left[{\displaystyle \frac{f^{\prime }\left(R_d\right)}{f^{″}\left(R_d\right)}}-R_d\right].$$

(37)

Here, $m_{\psi }$ is the effective mass of the scalar propagating mode associated with the curvature perturbation $\delta R$ in the de Sitter background. Equation (36) is a Klein–Gordon equation for $\delta R$ and describes the propagation of a massive scalar mode in addition to the usual tensor modes of general relativity. In later sections, we will relate $\delta R$ to a gauge-invariant Bardeen combination and denote the corresponding massive scalar propagating mode by $\psi$.

2.7. Cosmological Interpretation of $m_{\psi }$

The mass scale $m_{\psi }^{-1}$ determines the range of the scalar-mediated interaction and the characteristic dispersion of the scalar polarization of gravitational waves in a de Sitter background. On sub-horizon scales with $k\gg a{m}_{\psi }$, the scalar mode behaves effectively massless and can, in principle, contribute to additional polarization signatures. On scales $k\ll a{m}_{\psi }$, the mode is strongly suppressed, consistent with local gravity constraints.

For the modified Starobinsky model (27), one finds $m_{\psi }^2=1/\left(6\alpha \right)$, independent of $R_d$. This identifies the scalar mass scale that governs inflationary dynamics; however, at late times the corresponding mode is parametrically heavy and effectively decoupled from gravitational-wave propagation. Thus, while the same $f\left(R\right)$ action admits scalar excitations in both regimes, their physical relevance is restricted to the appropriate energy scales.

The detailed decomposition of the metric perturbations into scalar, vector, and tensor Bardeen variables, and the identification of the corresponding polarization modes, will be carried out in the following sections.

Throughout this work, we distinguish between matter anisotropic stress and the effective geometric anisotropic stress induced by the scalar degree of freedom. Statements about $\mathsf{\Phi }=\mathsf{\Psi }$ apply only when both contributions vanish.

3. Perturbations of the Ricci Tensor $\mathit{\delta }{\mathit{R}}_{\mathit{\mu }\mathit{\nu }}$ and Scalar Dynamics in $\mathit{f}\left(\mathit{R}\right)$ Gravity

The evolution of cosmological perturbations in $f\left(R\right)$ gravity influences both the expansion history of the Universe and the propagation of gravitational waves across different cosmological epochs [29]. To understand how the gravitational field responds to small deviations from a background metric—whether a cosmological FRW background, a black hole spacetime, or, as in this work, a de Sitter background—it is necessary to compute the perturbation of curvature quantities. Since the Ricci tensor enters directly in the field equations, its perturbation represents the leading-order correction to the spacetime curvature and is essential for identifying the massive scalar propagating mode present in $f\left(R\right)$ theories.

Furthermore, gauge transformations in $f\left(R\right)$ gravity are complicated by the presence of higher derivatives of R. A fully gauge-invariant description of perturbations therefore requires determining how the scalar curvature perturbation $\delta R$ interacts with metric perturbations $h_{\mu \nu }$ through $\delta R_{\mu \nu }$. This provides a crucial intermediate step on the way to constructing the gauge-invariant Bardeen potentials in later sections.

To obtain the perturbed field equation, we expand the metric as $g_{\mu \nu }=g_{\mu \nu }^d+h_{\mu \nu }$ and linearize each term of the $f\left(R\right)$ field Equation (6). Using $\delta f=f^{\prime }\left(R_d\right)\delta R$ and $\delta f^{\prime }=f^{″}\left(R_d\right)\delta R$, and recalling that $R_d$ is constant, the variation of covariant derivative terms such as ${\nabla }_{\mu }{\nabla }_{\nu }{f}^{\prime }\left(R\right)$ must be treated carefully. In general,

$$\delta \left({\nabla }_{\mu }{\nabla }_{\nu }{f}^{\prime }\right)={\nabla }_{\mu }{\nabla }_{\nu }\delta f^{\prime }-\left(\delta {\mathsf{\Gamma }}_{\mu \nu }^{\lambda }\right){\nabla }_{\lambda }{f}^{\prime }.$$

(38)

However, on a constant-curvature de Sitter background one has

$${\nabla }_{\lambda }{f}^{\prime }\left(R_d\right)=0,$$

(39)

so the connection-variation term vanishes identically. As a result, at linear order

$$\delta \left({\nabla }_{\mu }{\nabla }_{\nu }{f}^{\prime }\right)={\nabla }_{\mu }{\nabla }_{\nu }\delta f^{\prime }.$$

(40)

After accounting for this simplification, the variation of $(g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu })f^{\prime }$ yields the operator $(g_{\mu \nu }^d\square -{\nabla }_{\mu }{\nabla }_{\nu })\delta f^{\prime }$.

Perturbing the vacuum field Equation (6) using a de Sitter background ($R=R_d=\mathrm{const}$) yields the linearized equation

$$f^{\prime }\left(R_d\right)\delta R_{\mu \nu }+R_{\mu \nu }^d\delta f^{\prime }\left(R_d\right)-{\displaystyle \frac{1}{2}}\left[g_{\mu \nu }^d\delta f\left(R_d\right)+h_{\mu \nu }f\left(R_d\right)\right]+\left(g_{\mu \nu }^d\square -{\nabla }_{\mu }{\nabla }_{\nu }\right)\delta f^{\prime }\left(R_d\right)=0,$$

(41)

where $g_{\mu \nu }^d$ is the background de Sitter metric.

To obtain (41), we decompose the metric as

$$g_{\mu \nu }=g_{\mu \nu }^d+h_{\mu \nu },$$

(42)

with indices on $h_{\mu \nu }$ raised and lowered using $g_{\mu \nu }^d$. Since de Sitter space is a constant-curvature solution of metric $f\left(R\right)$ gravity, the background satisfies

$${\nabla }_{\mu }{f}^{\prime }\left(R_d\right)=0,$$

(43)

which follows directly from the constancy of $R_d$. This condition reflects the fact that $f^{\prime }\left(R_d\right)$ is a nonzero constant fixed by the chosen $f\left(R\right)$ model and represents the effective gravitational coupling on the background.

The nonperturbed trace Equation (8) evaluated on a constant-curvature vacuum background yields the algebraic de Sitter condition (26) which determines the allowed background curvature $R_d$ of the $f\left(R\right)$ theory. Using the de Sitter condition (26) in the background field Equation (6) and using $R=R_d$ and $T_{\mu \nu }=0$ gives

$$R_{\mu \nu }^d{f}^{\prime }\left(R_d\right)-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }^{d}f\left(R_d\right)=0,$$

(44)

which implies

$$R_{\mu \nu }^d={\displaystyle \frac{1}{2}}{\displaystyle \frac{f\left(R_d\right)}{f^{\prime }\left(R_d\right)}}{g}_{\mu \nu }^d.$$

(45)

Using (48) once more yields

$$R_{\mu \nu }^d={\displaystyle \frac{1}{4}}{R}_d{g}_{\mu \nu }^d,$$

(46)

showing that the background is an Einstein space and, in fact, maximally symmetric.

Dividing (41) by $f^{\prime }\left(R_d\right)$ and substituting $\delta f=f_d^{\prime }\delta R$ and $\delta f^{\prime }=f_d^{″}\delta R$ gives

$$\begin{array}{c}\hfill \delta R_{\mu \nu }+\left({\displaystyle \frac{f_d^{″}}{f_d^{\prime }}}{R}_{\mu \nu }^d-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }^d\right)\delta R-{\displaystyle \frac{1}{2}}{\displaystyle \frac{f_d}{f_d^{\prime }}}{h}_{\mu \nu }+{\displaystyle \frac{f_d^{″}}{f_d^{\prime }}}\left(g_{\mu \nu }^d\square -{\nabla }_{\mu }{\nabla }_{\nu }\right)\delta R=0.\end{array}$$

(47)

At this stage, it is important to clarify the fate of the algebraic term $-{\displaystyle \frac{1}{2}}{\displaystyle \frac{f_d}{f_d^{\prime }}}{h}_{\mu \nu }$ appearing in Equation (47). On a constant–curvature de Sitter background, the trace condition (8) implies

$${\displaystyle \frac{f_d}{f_d^{\prime }}}={\displaystyle \frac{R_d}{2}},$$

(48)

so that this contribution may be written as $-(R_d/4)h_{\mu \nu }$. This term is proportional to the background curvature scale and contains no derivatives. For gravitational waves of wavelength $\lambda \ll H_d^{-1}$, corresponding to the local inertial (short–wavelength) limit relevant for detector-scale propagation, such curvature-suppressed algebraic terms do not contribute to the dynamical wave equation. They may therefore be consistently neglected, or equivalently absorbed into the background de Sitter curvature. With this understanding, the linearized field equation reduces to Equation (51).

To evaluate (51), we recall the general linearized Ricci tensor [28,30]

$$\delta R_{\mu \nu }={\displaystyle \frac{1}{2}}\left(-\square h_{\mu \nu }-{\nabla }_{\mu }{\nabla }_{\nu }h+{\nabla }^{\rho }{\nabla }_{\mu }{h}_{\rho \nu }+{\nabla }^{\rho }{\nabla }_{\nu }{h}_{\rho \mu }\right)+\mathcal{O}\left(h^2\right),$$

(49)

where $h\equiv {h^{\rho }}_{\rho }$.

One may therefore work in a local inertial frame in which the background metric is approximately Minkowskian, $g_{\mu \nu }\simeq {\eta }_{\mu \nu }$, and background-curvature contributions to the wave equation are suppressed by $\mathcal{O}(H_d/\omega )$.

$$g_{\mu \nu }\simeq {\eta }_{\mu \nu },$$

(50)

while still retaining the nonzero constants $f_d^{\prime }$ and $f_d^{″}$. In this limit, curvature-suppressed algebraic terms proportional to $h_{\mu \nu }$ do not contribute to the dynamical propagation of high-frequency gravitational waves.

Under this approximation, (47) reduces to

$$\delta R_{\mu \nu }-{\displaystyle \frac{1}{2}}{\eta }_{\mu \nu }\delta R+{\displaystyle \frac{f_d^{″}}{f_d^{\prime }}}({\eta }_{\mu \nu }\square -{\partial }_{\mu }{\partial }_{\nu })\delta R=0.$$

(51)

The linearized scalar curvature is

$$\delta R\equiv R\left[h\right],$$

(52)

and the linearized Einstein tensor reduces to

$$\delta G_{\mu \nu }=\delta R_{\mu \nu }-{\displaystyle \frac{1}{2}}{\eta }_{\mu \nu }\delta R\left[h\right].$$

(53)

Substituting (52) and (53) into (51) yields the perturbed field equation

$$\delta G_{\mu \nu }+{\displaystyle \frac{1}{3m_{\psi }^2}}({\eta }_{\mu \nu }\square -{\partial }_{\mu }{\partial }_{\nu })\delta R=0,$$

(54)

where the effective scalar mass $m_{\psi }$ arises from the trace of the linearized field equations and is given by (37). In the Minkowski limit $(R_d\to 0)$, this reduces to

$$m_{\psi }^2={\displaystyle \frac{1}{3}}{\displaystyle \frac{f_d^{\prime }}{f_d^{″}}}.$$

(55)

Once the effective scalar mass $m_{\psi }^2$ is identified, its physical meaning becomes transparent by considering a Fourier (plane-wave) decomposition of the gauge-invariant variables. In a constant-curvature background, linear perturbations admit the ansatz $X(t,\mathbf{x})=X_k{e}^{-i(\omega t-\mathbf{k}·\mathbf{x})}$, which diagonalizes the spatial Laplacian. Substituting this into the Klein–Gordon–type equation $(\square -m_{\psi }^2)\delta R=0$ yields the dispersion relation ${\omega }^2=k^2+m_{\psi }^2$. Thus the extra scalar mode propagates as a massive mode, in contrast to the transverse tensor polarizations, which remain massless. This plane-wave form clarifies how the additional scalar polarization arises in metric $f\left(R\right)$ gravity.

Thus, the scalar curvature perturbation $\delta R$ propagates as a massive mode with dispersion relation ${\omega }^2=k^2+m_{\psi }^2$. In the following sections we relate this mode to gauge-invariant variables and identify its physical polarization content.

4. 3 + 1 Decomposition and the Scalar, Vector, and Tensor Modes of $\mathit{f}\left(\mathit{R}\right)$ Gravity

4.1. Conventions

Throughout the manuscript, we use the metric signature $(-,+,+,+)$ and define the d’Alembertian by $\square \equiv g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu }$. In Appendix A we show the calculation for the d’Alembertian in de–Sitter (curved) spacetime. In a local inertial frame, $\square =-{\partial }_t^2+{\nabla }^2$. Our curvature conventions are

$${R^{\rho }}_{\sigma \mu \nu }={\partial }_{\mu }{\mathsf{\Gamma }}_{\nu \sigma }^{\rho }-{\partial }_{\nu }{\mathsf{\Gamma }}_{\mu \sigma }^{\rho }+{\mathsf{\Gamma }}_{\mu \lambda }^{\rho }{\mathsf{\Gamma }}_{\nu \sigma }^{\lambda }-{\mathsf{\Gamma }}_{\nu \lambda }^{\rho }{\mathsf{\Gamma }}_{\mu \sigma }^{\lambda }$$

(56)

and

$$R_{\mu \nu }={R^{\rho }}_{\mu \rho \nu }.$$

(57)

In this section we analyze the scalar, vector, and tensor perturbations of the metric using the standard scalar–vector–tensor (SVT) decomposition. As discussed in Section 2, gravitational waves detected at astrophysical scales propagate on a spacetime whose curvature radius is much larger than their wavelength. Therefore, for the purpose of the 3 + 1 decomposition we work in the local Minkowski limit of the de Sitter background,

$$g_{\mu \nu }\approx {\eta }_{\mu \nu },$$

(58)

while retaining the constant background quantities $f_d^{\prime }$, $f_d^{″}$, and the mass $m_{\psi }$ of the massive scalar propagating mode. For the scalar sector we work in the longitudinal (Newtonian) gauge, in which the metric perturbations are encoded in the gauge-invariant Bardeen potentials $\mathsf{\Phi }$ and $\mathsf{\Psi }$.

4.2. Scalar Mode

The 00 component of the linearized Einstein tensor in the longitudinal gauge is

$$\delta G_{00}=-2{\nabla }^2\mathsf{\Phi }.$$

(59)

The 00 component of the perturbed $f\left(R\right)$ field Equation (54) then takes the form

$$\delta G_{00}-{\displaystyle \frac{1}{3m_{\psi }^2}}{\nabla }^2\delta R=0.$$

(60)

Substituting (59) into (60) yields

$$\begin{array}{c}\hfill -2{\nabla }^2\mathsf{\Phi }-{\displaystyle \frac{1}{3m_{\psi }^2}}{\nabla }^2\delta R=0,\end{array}$$

(61)

so that

$$2\mathsf{\Phi }+{\displaystyle \frac{\delta R}{3m_{\psi }^2}}=0,$$

(62)

and, therefore,

$$\mathsf{\Phi }=-{\displaystyle \frac{\delta R}{6m_{\psi }^2}}.$$

(63)

The traceless spatial components $(i\ne j)$ encode the anisotropy (slip) relation. In metric $f\left(R\right)$ gravity, even when the matter anisotropic stress vanishes, the perturbation $\delta \left({\nabla }_i{\nabla }_j{f}^{\prime }\right)$ contributes an effective anisotropic stress term. Since $\delta f^{\prime }\left(R\right)=f^{″}\left(R_d\right)\delta R$, the off-diagonal scalar sector contains terms of the form ${\partial }_i{\partial }_j\delta f^{\prime }\left(R\right)\propto f^{″}\left(R_d\right){\partial }_i{\partial }_j\delta R$, so that generically $\mathsf{\Phi }-\mathsf{\Psi }\ne 0$ when the scalar mode is active. In the no-slip sector (e.g., when the effective anisotropic source vanishes), one recovers $\mathsf{\Phi }=\mathsf{\Psi }$.

$$\mathsf{\Phi }=-{\displaystyle \frac{\delta R}{6m_{\psi }^2}}.$$

(64)

Thus, when the scalar curvature perturbation $\delta R$ is dynamically excited, it directly sources the scalar metric sector even in the absence of matter anisotropic stress. The 00 equation fixes the Newtonian potential $\mathsf{\Phi }$ in terms of $\delta R$, while the traceless spatial equations determine the gravitational slip $\mathsf{\Phi }-\mathsf{\Psi }$ through the effective anisotropic stress generated by the scalar degree of freedom. Only in the vacuum no-slip limit—when the scalar mode does not source the traceless sector—does one recover $\mathsf{\Phi }=\mathsf{\Psi }$. In a cosmological context, this structure links the additional scalar gravitational-wave polarization to the scalar sector of cosmological perturbations and to the scalar mass $m_{\psi }$ on a de Sitter background.

It is worth noting that the expression (64) and the mass parameter $m_{\psi }^2$ used in this local 3 + 1 analysis correspond to the short-wavelength, locally Minkowskian limit of a de Sitter background. In this regime the curvature radius $H^{-1}$ is much larger than the gravitational-wave wavelength, and terms proportional to the background curvature $R_d$ are negligible. Consequently, in the $R_d\to 0$ (locally Minkowskian) limit the scalar mass reduces to (55). In a fully global de Sitter treatment, however, the effective mass contains an additional curvature contribution and takes the form (37). Thus the local vacuum 3 + 1 decomposition used here captures the correct propagation physics for gravitational waves measured in a local inertial frame, while the global de Sitter mass governs the long-wavelength, cosmological evolution of the scalar mode.

4.3. Vector Modes

Vector perturbations appear in the $0i$ components of the metric as divergence-free vectors. The gauge-invariant combination is [31,32]

$$V_i\equiv S_i-F_i^{\prime },{\partial }^i{V}_i=0,$$

(65)

where $S_i$ enters the $g_{0i}$ component and $F_i$ the vector part of the spatial metric.

In the vector sector all scalar perturbations vanish; so, in particular,

$$\delta R=0.$$

(66)

The linearized Ricci tensor reduces to [7,8]

$$\delta R_{0i}=-{\displaystyle \frac{1}{2}}{\nabla }^2{V}_i.$$

(67)

The perturbed field equations in vacuum imply

$$\delta G_{0i}=\delta R_{0i}=0,$$

(68)

and, hence,

$${\nabla }^2{V}_i=0.$$

(69)

Under localized boundary conditions this yields $V_i=0$. As in general relativity, no vector modes propagate in vacuum metric $f\left(R\right)$ gravity.

4.4. Tensor Modes

We now examine the transverse–traceless (TT) tensor perturbations $h_{ij}^{TT}$. The spatial components of the perturbed $f\left(R\right)$ field equations take the form

$$\delta G_{ij}+{\displaystyle \frac{1}{3m_{\psi }^2}}({\delta }_{ij}\square -{\partial }_i{\partial }_j)\delta R=0.$$

(70)

The SVT decomposition of the perturbed Ricci tensor is [7,8,31,33]

$$\delta R_{ij}=-{\partial }_i{\partial }_j(\mathsf{\Phi }+\mathsf{\Psi })-{\delta }_{ij}(-\ddot{\mathsf{\Phi }}+{\nabla }^2\mathsf{\Phi })-{\displaystyle \frac{1}{2}}({\partial }_i{\dot{V}}_j+{\partial }_j{\dot{V}}_i)-{\displaystyle \frac{1}{2}}\square h_{ij}^{TT}.$$

(71)

In the pure tensor sector,

$$\mathsf{\Phi }=\mathsf{\Psi }=0,V_i=0,\delta R=0.$$

Equation (71) reduces to

$$\delta R_{ij}=-{\displaystyle \frac{1}{2}}\square h_{ij}^{TT}.$$

(72)

The term $({\delta }_{ij}\square -{\partial }_i{\partial }_j)\delta R$ in (70) has no TT projection and therefore drops out. Substituting into (70) yields

$$\square h_{ij}^{TT}=0.$$

(73)

Thus, the tensor modes in metric $f\left(R\right)$ gravity propagate exactly as in GR: they satisfy the standard wave equation, travel at the speed of light, and possess only two transverse-traceless polarization states. All deviations from GR in gravitational-wave propagation therefore originate exclusively from the massive scalar propagating mode.

5. Analyzing a Specific $\mathit{f}\left(\mathit{R}\right)$ Model

We now specialize the general discussion of Section 2 and Section 3 to a concrete and widely studied model. One of the simplest and most successful choices is the Starobinsky model

$$f\left(R\right)=R+\alpha R^2+O\left(R^3\right),$$

(74)

which provides a purely geometric mechanism for early-Universe inflation and introduces an additional scalar degree of freedom through the higher-curvature term [9,27]. In this framework, inflation is driven by the $R^2$ correction itself, rather than by an independent inflationary field, with the parameter $\alpha$ setting the characteristic inflationary scale and controlling the amplitude of primordial fluctuations [34,35].

For the truncated model (74), the first and second derivatives of $f\left(R\right)$ are

$$f^{\prime }\left(R\right)\approx 1+2\alpha R,$$

(75)

$$f^{″}\left(R\right)\approx 2\alpha .$$

(76)

We will use the vacuum field Equation (6) and their trace (8) specialized to the model (74).

5.1. Constant-Curvature Backgrounds and the Need for a Modified Starobinsky Model

For the following analysis, refer to the vacuum field equation in $f\left(R\right)$ gravity (6) and the corresponding trace Equation (8). We seek constant-curvature vacuum solutions with $R=R_d=\mathrm{const}$. For such backgrounds, the trace equation reduces to the algebraic de Sitter condition (26) (see Section 2). Substituting the Starobinsky form (74) into (26) yields the unique solution

$$R_d=0.$$

(77)

Thus, within the pure Starobinsky model (74), Minkowski spacetime is the only constant-curvature vacuum solution. In particular, there is no nontrivial de Sitter background with $R_d>0$ that could describe an exponentially expanding late-time Universe.

From a cosmological standpoint this limitation motivates extending the model to include a vacuum-energy contribution. We therefore adopt the modified Starobinsky model

$$f\left(R\right)=R+\alpha R^2-2\mathsf{\Lambda },$$

(78)

which supplements the inflationary $R+\alpha R^2$ sector with a cosmological constant term. In this model the quadratic curvature term governs early-time inflation [9], while the constant contribution $-2\mathsf{\Lambda }$ drives late-time accelerated expansion [11,36].

For the modified model, the constant-curvature condition (48) yields

$$R_d=4\mathsf{\Lambda }.$$

(79)

This solution defines a de Sitter background on which we will linearize the field equations. As shown in Section 3, a constant-$R_d$ background of this type satisfies $R_{\mu \nu }=\frac{1}{4}{R}_d{g}_{\mu \nu }$; so, the spacetime is an Einstein space, characterized by $R_{\mu \nu }\propto g_{\mu \nu }$. This geometric notion should be distinguished from the Einstein frame discussed in Section 2.1, which is obtained from the Jordan frame by a conformal transformation.

5.2. Einstein-Frame Potential and Stability Around the de Sitter Point

In Section 2.1 we reviewed the scalar–tensor (Einstein-frame) representation of metric $f\left(R\right)$ gravity. For the modified Starobinsky model

$$f\left(R\right)=R+\alpha R^2-2\mathsf{\Lambda },$$

(80)

the Einstein-frame scalar potential is

$$V\left(\varphi \right)={\displaystyle \frac{M_{\mathrm{Pl}}^2}{2}}{\displaystyle \frac{\alpha R^2+2\mathsf{\Lambda }}{{(1+2\alpha R)}^2}},$$

(81)

where the scalar field $\varphi$ is related to the curvature through the conformal relation

$$f^{\prime }\left(R\right)=1+2\alpha R=exp\left(-{\displaystyle \frac{2\beta \varphi }{M_{\mathrm{Pl}}}}\right),$$

(82)

with $\beta$ defined as in Section 2.1. Equation (82) implicitly defines $R=R\left(\varphi \right)$.

5.3. Chain Rule and Curvature Derivatives

Using (82), the derivative of R with respect to $\varphi$ is

$${\displaystyle \frac{dR}{d\varphi }}=-{\displaystyle \frac{2\beta }{M_{\mathrm{Pl}}}}{\displaystyle \frac{f^{\prime }\left(R\right)}{f^{″}\left(R\right)}}=-{\displaystyle \frac{\beta }{\alpha M_{\mathrm{Pl}}}}(1+2\alpha R),$$

(83)

where we used $f^{″}\left(R\right)=2\alpha$. All derivatives of $V\left(\varphi \right)$ follow from repeated application of the chain rule $d/d\varphi =(dR/d\varphi )d/dR.$

5.4. First Derivative

Differentiating (81) with respect to R gives

$${\displaystyle \frac{dV}{dR}}={\displaystyle \frac{M_{\mathrm{Pl}}^2}{2}}{\displaystyle \frac{(1+2\alpha R)(R-4\mathsf{\Lambda })}{{(1+2\alpha R)}^3}}.$$

(84)

Using (83), the first derivative of the potential becomes

$$V^{\prime }\left(\varphi \right)=-{\displaystyle \frac{\beta M_{\mathrm{Pl}}}{2\alpha }}{\displaystyle \frac{R-4\mathsf{\Lambda }}{(1+2\alpha R)}}.$$

(85)

Thus $V^{\prime }\left(\varphi \right)=0$ precisely at

$$R=R_d=4\mathsf{\Lambda },$$

(86)

corresponding to the de Sitter background.

5.5. Second Derivative

Applying the chain rule once more yields

$$V^{″}\left(\varphi \right)={\displaystyle \frac{{\beta }^2}{\alpha }}{\displaystyle \frac{1-2\alpha R+16\alpha \mathsf{\Lambda }}{{(1+2\alpha R)}^2}}.$$

(87)

Evaluating this at the de Sitter point gives

$$V^{″}\left({\varphi }_d\right)={\displaystyle \frac{{\beta }^2}{\alpha (1+8\alpha \mathsf{\Lambda })}}>0(\alpha >0),$$

(88)

showing that the de Sitter configuration corresponds to a local minimum of the Einstein-frame potential and is therefore linearly stable.

5.6. Third Derivative

For completeness, the third derivative of the potential is

$$V^{‴}\left(\varphi \right)={\displaystyle \frac{2{\beta }^3}{\alpha M_{\mathrm{Pl}}}}{\displaystyle \frac{32\alpha \mathsf{\Lambda }-2\alpha R+3}{{(1+2\alpha R)}^2}},$$

(89)

which is nonvanishing and controls the leading self-interactions of the scalar mode around the de Sitter minimum. Equation (89) is fully consistent with the explicit expression obtained by direct differentiation in the Einstein frame.

5.7. Stability Interpretation

The conditions

$$V^{\prime }\left({\varphi }_d\right)=0,V^{″}\left({\varphi }_d\right)>0$$

(90)

establish that the modified Starobinsky model admits a stable de Sitter vacuum solution in metric $f\left(R\right)$ gravity. The corresponding scalar degree of freedom has positive mass squared in the Einstein frame, in agreement with the Jordan frame perturbative analysis of Section 3.

The full chameleon mechanism discussed in Section 2.1 requires including the matter coupling through the conformal factor $A\left(\varphi \right)$ and analyzing the density dependence of the effective potential $V_{\mathrm{eff}}\left(\varphi \right)=V\left(\varphi \right)+\rho A\left(\varphi \right)$. For the present discussion, it is sufficient to note that the vacuum Einstein-frame potential $V\left(\varphi \right)$ derived from the modified Starobinsky model admits a stable de Sitter minimum within metric $f\left(R\right)$ gravity. The resulting density-dependent scalar mass and screening behavior are encoded in the same Einstein-frame structure already introduced in Section 2.1.

5.8. Trace Perturbations and the Scalar Mass

We now extract the scalar mass $m_{\psi }$ for the modified Starobinsky model by specializing the general expression obtained earlier. We decompose the curvature scalar as

$$R=R_d+\delta R,$$

(91)

where $R_d$ is the constant-curvature de Sitter background.

We therefore use the de Sitter solution $R_d=4\mathsf{\Lambda }$ of the modified Starobinsky model as the background for the linearized and polarization analyses that follow.

We now specialize to the modified Starobinsky model,

$$f\left(R\right)=R+\alpha R^2-2\mathsf{\Lambda }.$$

(92)

For this choice, one finds

$$f^{\prime }\left(R_d\right)=1+2\alpha R_d,f^{″}\left(R_d\right)=2\alpha .$$

(93)

Substituting these expressions into Equation (8) yields

$$\left(\square -{\displaystyle \frac{1}{6\alpha }}\right)\delta R=0,$$

(94)

so that the scalar curvature perturbation satisfies a Klein–Gordon equation with mass

$$m_{\psi }^2={\displaystyle \frac{1}{6\alpha }},$$

(95)

independent of the background curvature $R_d$.

For the modified Starobinsky model, the de Sitter background curvature is fixed by the cosmological constant through

$$R_d=4\mathsf{\Lambda },$$

(96)

while the mass of the additional scalar degree of freedom is controlled entirely by the quadratic coupling $\alpha$,

$$m_{\psi }^{-1}=\sqrt{6\alpha }.$$

(97)

From a cosmological perspective, $\alpha$ determines the range and dispersion scale of the scalar polarization of gravitational waves when the scalar mode is dynamically excited, whereas $\mathsf{\Lambda }$ fixes the asymptotic de Sitter curvature. This clean separation of roles will be important when we discuss the propagation of the scalar mode and its potential observational signatures in de Sitter cosmology.

6. SVT Decomposition of the Perturbed Ricci Tensor in Metric $\mathit{f}\left(\mathit{R}\right)$ Gravity

In this section, we revisit the $(3+1)$ decomposition in the presence of matter sources. Instead of starting from the vacuum perturbed field Equation (54), we now consider the linearized field equations of the modified Starobinsky model in a nearly Minkowski background, including the stress–energy tensor $T_{\mu \nu }$:

$$\delta G_{\mu \nu }+2\alpha \left({\eta }_{\mu \nu }\square -{\partial }_{\mu }{\partial }_{\nu }\right)\delta R=\kappa T_{\mu \nu },$$

(98)

where $\alpha >0$ is the $R^2$ coupling, $\delta R$ is the scalar curvature perturbation, and ${\eta }_{\mu \nu }$ is the background Minkowski metric. Using the relation

$$m_{\psi }^2={\displaystyle \frac{1}{6\alpha }},$$

(99)

the term proportional to $\alpha$ can also be written as $(1/3m_{\psi }^2)({\eta }_{\mu \nu }\square -{\partial }_{\mu }{\partial }_{\nu })\delta R$, in agreement with the vacuum analysis.

The Klein–Gordon equation for the massive extra scalar mode (94) in vacuum generalizes in the presence of matter to

$$(\square -m_{\psi }^2)\delta R=m_{\psi }^2\kappa T,$$

(100)

or equivalently

$$\square \delta R=m_{\psi }^2(\delta R+\kappa T),$$

(101)

where $T\equiv {\eta }^{\mu \nu }{T}_{\mu \nu }$ is the trace of the stress–energy tensor. Equation (100) shows that $\delta R$ behaves as a massive scalar field (the massive scalar propagating mode) sourced by the trace T; in the limit $T\to 0$ we recover the vacuum equation.

Using the definition of the Einstein tensor in the flat background,

$$\delta G_{\mu \nu }=\delta R_{\mu \nu }-{\displaystyle \frac{1}{2}}{\eta }_{\mu \nu }\delta R,$$

(102)

and eliminating $\square \delta R$ via (101), the linearized field Equation (98) may be written as

$$\delta R_{\mu \nu }-{\displaystyle \frac{1}{2}}{\eta }_{\mu \nu }\delta R+{\displaystyle \frac{1}{3}}{\eta }_{\mu \nu }(\delta R+\kappa T)-2\alpha {\partial }_{\mu }{\partial }_{\nu }\delta R=\kappa T_{\mu \nu },$$

(103)

or, equivalently,

$$\delta R_{\mu \nu }-\left({\displaystyle \frac{1}{6}}{\eta }_{\mu \nu }+2\alpha {\partial }_{\mu }{\partial }_{\nu }\right)\delta R=\kappa \left[T_{\mu \nu }-{\displaystyle \frac{1}{3}}{\eta }_{\mu \nu }T\right].$$

(104)

Equations (103) and (104) are the starting point for the $(3+1)$ decomposition with matter: the left-hand side contains the usual Ricci-tensor perturbation corrected by the massive scalar propagating mode $\delta R$, while the right-hand side involves the traceless combination $T_{\mu \nu }-{\eta }_{\mu \nu }T/3$.

6.1. Irreducible SVT Decomposition of the Metric and Matter

Following [8,13], the SVT decomposition of the metric perturbation $h_{\mu \nu }$ in a nearly Minkowski background reads

$$\begin{array}{cc}\hfill h_{00}& =2\psi ,\hfill \end{array}$$

(105)

$$\begin{array}{cc}\hfill h_{0i}& ={\beta }_i+{\partial }_i\gamma ,\hfill \end{array}$$

(106)

$$\begin{array}{cc}\hfill h_{ij}& =-2\varphi {\delta }_{ij}+\left({\partial }_i{\partial }_j-{\displaystyle \frac{1}{3}}{\delta }_{ij}{\nabla }^2\right)\lambda +{\displaystyle \frac{1}{2}}\left({\partial }_i{ϵ}_j+{\partial }_j{ϵ}_i\right)+h_{ij}^{TT},\hfill \end{array}$$

(107)

where we have defined the new quantities $\psi ,{\beta }_i,\gamma ,\varphi ,{ϵ}_i,\lambda ,h_{ij}^{TT}$ with the assumption that $h_{\mu \nu }\to 0$ as $r\to \infty$. The transverse and traceless conditions are

$$\begin{array}{cc}\hfill {\partial }^i{\beta }_i& =0,\hfill \end{array}$$

(108)

$$\begin{array}{cc}\hfill {\partial }^i{ϵ}_i& =0,\hfill \end{array}$$

(109)

$$\begin{array}{cc}\hfill {\partial }^i{h}_{ij}^{TT}& =0,\hfill \end{array}$$

(110)

$$\begin{array}{cc}\hfill {\delta }^{ij}{h}_{ij}^{TT}& =0.\hfill \end{array}$$

(111)

In both [8] and in our earlier Bardeen-variable work we have shown how the variables $\psi ,{\beta }_i,\gamma ,\varphi ,{ϵ}_i,\lambda ,h_{ij}^{TT}$ transform under a gauge transformation generated by ${\xi }^a$ with ${\xi }^a\to 0$ as $r\to \infty$. Such transformations are parametrized as

$${\xi }^a=({\xi }^0,{\xi }^i)=(A,B^i+{\partial }^{i}C),$$

(112)

with ${\partial }_i{B}^i=0$. Following the same procedure as in [8], one obtains the gauge-invariant scalar and vector combinations

$$\begin{array}{cc}\hfill \mathsf{\Phi }& \equiv -\varphi -{\displaystyle \frac{1}{6}}{\nabla }^2\lambda ,\hfill \end{array}$$

(113)

$$\begin{array}{cc}\hfill \mathsf{\Psi }& \equiv -\psi +\dot{\gamma }-{\displaystyle \frac{1}{2}}\ddot{\lambda },\hfill \end{array}$$

(114)

$$\begin{array}{cc}\hfill V_i& \equiv {\beta }_i-{\displaystyle \frac{1}{2}}{\dot{ϵ}}_i,{\partial }_i{V}^i=0.\hfill \end{array}$$

(115)

In metric $f\left(R\right)$ gravity, the traceless spatial field equation generally fixes the gravitational slip $\mathsf{\Phi }-\mathsf{\Psi }$ through an effective geometric anisotropic-stress term proportional to $\delta f^{\prime }\left(R\right)=f^{″}\left(R_d\right)\delta R$, so the condition $\mathsf{\Phi }=\mathsf{\Psi }$ should only be imposed in a genuine no-slip sector. The tensor perturbation $h_{ij}^{TT}$ is already gauge invariant.

We can perform a similar SVT decomposition of the matter stress–energy tensor $T_{\mu \nu }$ on the right-hand side of the field equations. We write

$$\begin{array}{cc}\hfill T_{00}& =\rho ,\hfill \end{array}$$

(116)

$$\begin{array}{cc}\hfill T_{0i}& =S_i+{\partial }_{i}S,\hfill \end{array}$$

(117)

$$\begin{array}{cc}\hfill T_{ij}& =-P{\delta }_{ij}+{\sigma }_{ij}+({\partial }_i{\sigma }_j+{\partial }_j{\sigma }_i)+\left({\partial }_i{\partial }_j-{\displaystyle \frac{1}{3}}{\delta }_{ij}{\nabla }^2\right)\sigma ,\hfill \end{array}$$

(118)

where $\rho$, S, $S_i$, P, $\sigma$, ${\sigma }_i$, and ${\sigma }_{ij}$ are new scalar, vector, and tensor quantities with the constraints

$$\begin{array}{cc}\hfill {\partial }_i{S}^i& =0,\hfill \end{array}$$

(119)

$$\begin{array}{cc}\hfill {\partial }^i{\sigma }_i& =0,\hfill \end{array}$$

(120)

$$\begin{array}{cc}\hfill {\partial }^i{\sigma }_{ij}& =0,\hfill \end{array}$$

(121)

$$\begin{array}{cc}\hfill {\delta }^{ij}{\sigma }_{ij}& =0,\hfill \end{array}$$

(122)

along with boundary conditions $S\to 0,{\sigma }_i\to 0,\sigma \to 0,{\nabla }^2\sigma \to 0$ as $r\to \infty$ (spatial infinity). The overall minus sign in the isotropic part $-P{\delta }_{ij}$ in (118) will be tracked explicitly in the relations obtained from stress–energy conservation below.

The conservation law

$${\partial }^{\mu }{T}_{\mu \nu }=0,$$

(123)

determines relations between $\rho$, S, $S_i$, P, $\sigma$, ${\sigma }_i$, and ${\sigma }_{ij}$. In the nearly Minkowski background used throughout this section, we have ${\partial }^{\mu }=(-{\partial }_0,{\partial }^i)$; so, (123) reads

$$-{\partial }_0{T}_{0\nu }+{\partial }^i{T}_{i\nu }=0.$$

(124)

As a useful special case (and for later physical interpretation), we note that a perfect fluid at rest in Minkowski space has

$$T_{\mu \nu }=\left[\begin{array}{cccc}\rho & 0& 0& 0\\ 0& -P& 0& 0\\ 0& 0& -P& 0\\ 0& 0& 0& -P\end{array}\right],$$

(125)

so that $T_{0i}=0$ and $T_{ij}=-P{\delta }_{ij}$. Comparing with (117) and (118), this corresponds to vanishing momentum and anisotropic-stress components ($S_i=0$, $S=0$, ${\sigma }_i=0$, $\sigma =0$, ${\sigma }_{ij}=0$), while retaining the scalars $\rho$ and P. In particular, the trace is

$$T=\rho -3P.$$

(126)

The $\nu =0$ component of (123) gives

$$\dot{\rho }={\partial }^i{T}_{i0}={\partial }^i{T}_{0i}={\nabla }^{2}S,$$

(127)

where we have used (117) and the constraint (119). For $\nu =i$, it is convenient to separate the two pieces entering $-{\partial }_0{T}_{0i}+{\partial }^j{T}_{ji}=0$. First, taking a spatial derivative of (118) yields

$${\partial }^j{T}_{ji}=-{\partial }_{i}P+{\displaystyle \frac{2}{3}}{\nabla }^2{\partial }_i\sigma +{\nabla }^2{\sigma }_i+{\partial }^j{\sigma }_{ji},$$

(128)

and the constraints (120) and (121) imply ${\partial }^j{\sigma }_{ji}=0$. Second, taking a time derivative of (117) gives

$${\partial }_0{T}_{0i}={\dot{S}}_i+{\partial }_i\dot{S}.$$

(129)

Stress–energy conservation for $\nu =i$ then combines (128) and (129) as

$${\partial }_i\left(-P-\dot{S}+{\displaystyle \frac{2}{3}}{\nabla }^2\sigma \right)-{\dot{S}}_i+{\nabla }^2{\sigma }_i=0,$$

(130)

where we used ${\partial }^j{\sigma }_{ji}=0$.

Taking one more spatial derivative of (130) and applying the constraints on ${\sigma }_i$ and $S_i$, we obtain

$${\nabla }^2\left[-P-\dot{S}+{\displaystyle \frac{2}{3}}{\nabla }^2\sigma \right]=0.$$

(131)

Applying the boundary condition at spatial infinity for S, P, and ${\nabla }^2\sigma$ (which also guarantees the uniqueness of the decomposition), we conclude that

$$-P-\dot{S}+{\displaystyle \frac{2}{3}}{\nabla }^2\sigma =0.$$

(132)

Inserting this condition into (130) gives

$${\nabla }^2{\sigma }^i={\dot{S}}^i.$$

(133)

Equation (132) can also be rewritten as

$${\nabla }^2\sigma ={\displaystyle \frac{3}{2}}\dot{S}-{\displaystyle \frac{3}{2}}P.$$

(134)

Equations (127), (133) and (134) are the required set of differential equations that relate the newly defined irreducible matter variables $\rho$, $S_i$, S, P, $\sigma$, ${\sigma }_i$, and ${\sigma }_{ij}$. These results match Equation (23) of [37], up to differences in notation.

6.2. (3 + 1) Decomposition of the Perturbed Ricci Tensor

In $f\left(R\right)$ gravity, the field equations contain higher-order derivatives of the metric through their dependence on the Ricci scalar R. Unlike in General Relativity, where the Einstein tensor $G_{\mu \nu }$ alone determines the dynamics, $f\left(R\right)$ theories introduce a massive scalar propagating mode, associated with the scalar curvature perturbation $\delta R$. To fully understand how this scalar mode interacts with the usual scalar, vector, and tensor components of the metric perturbation, it is necessary to go beyond the standard metric decomposition and analyze the perturbation of the Ricci tensor $\delta R_{\mu \nu }$ itself.

By expressing $\delta R_{\mu \nu }$ in terms of the gauge-invariant Bardeen variables and the scalar curvature perturbation, we obtain a set of decoupled differential equations that reveal how each mode behaves in the presence of matter. This decomposition provides a more complete and transparent description of the linearized dynamics in $f\left(R\right)$ gravity and is particularly useful for identifying modifications to gravitational-wave propagation and structure formation due to the extra scalar mode.

Following the approach in [8], the components of the Einstein tensor $G_{\mu \nu }$ were decomposed in GR to obtain a set of differential equations for the perturbation of the Einstein tensor in terms of the Bardeen variables. In the case of $f\left(R\right)$ gravity, we instead decompose the perturbed Ricci tensor $\delta R_{\mu \nu }$ in terms of the Bardeen variables, to obtain a new set of differential equations. We work entirely in terms of the gauge-invariant vector perturbation $V_i$ (defined in Section 6.1), which is transverse, ${\partial }^i{V}_i=0$; in particular, all intermediate gauge-dependent vector potentials are absorbed into $V_i$ and do not appear in the final expressions for $\delta R_{\mu \nu }$. The components of $\delta R_{\mu \nu }$ are

$$\begin{array}{cc}\hfill \delta R_{00}& ={\nabla }^2\mathsf{\Psi }-{\displaystyle \frac{3}{2}}\ddot{\mathsf{\Phi }},\hfill \end{array}$$

(135)

$$\begin{array}{cc}\hfill \delta R_{0i}& =-{\displaystyle \frac{1}{2}}{\nabla }^2{V}_i-{\partial }_i\dot{\mathsf{\Phi }},\hfill \end{array}$$

(136)

$$\begin{array}{cc}\hfill \delta R_{ij}& =-{\partial }_{(i}{\dot{V}}_{j)}-{\partial }_i{\partial }_j\left(\mathsf{\Phi }+{\displaystyle \frac{1}{2}}\mathsf{\Psi }\right)-{\displaystyle \frac{1}{2}}\square h_{ij}^{TT}-{\delta }_{ij}\left(-\ddot{\mathsf{\Phi }}+{\nabla }^2\mathsf{\Phi }\right).\hfill \end{array}$$

(137)

In terms of these Bardeen variables $\mathsf{\Phi },\mathsf{\Psi },V_i$, the field equation in the form of Equation (104) can be recast into a set of differential equations, each corresponding to a component of $\delta R_{\mu \nu }$. For example, the 00 component of (104) takes the form

$$\delta R_{00}-{\displaystyle \frac{1}{6m_{\psi }^2}}\left(m_{\psi }^2{\eta }_{00}+2{\partial }_0{\partial }_0\right)\delta R=\kappa \left(T_{00}-{\displaystyle \frac{1}{3}}{\eta }_{00}T\right).$$

(138)

Substituting the expression for $\delta R_{00}$ from Equation (135), using ${\eta }_{00}=-1$ and $T=\rho -3P$, we obtain

$${\nabla }^2\mathsf{\Psi }-{\displaystyle \frac{3}{2}}\ddot{\mathsf{\Phi }}+{\displaystyle \frac{1}{6}}\delta R-{\displaystyle \frac{1}{3m_{\psi }^2}}\ddot{\delta R}=\kappa \left({\displaystyle \frac{4}{3}}\rho -P\right),$$

(139)

which gives the corresponding differential equation for the 00 component of $\delta R_{\mu \nu }$.

Next, we consider the differential equations corresponding to the $0i$ component of the perturbation of the Ricci tensor. Equation (104) gives

$$\delta R_{0i}-{\displaystyle \frac{1}{6m_{\psi }^2}}\left(m_{\psi }^2{\eta }_{0i}+2{\partial }_0{\partial }_i\right)\delta R=\kappa \left(T_{0i}-{\displaystyle \frac{1}{3}}{\eta }_{0i}T\right).$$

(140)

Substituting the expression (136) for $\delta R_{0i}$ in Equation (140), Equation (117) for $T_{0i}$, and using ${\eta }_{0i}=0$, we obtain

$$-{\displaystyle \frac{1}{2}}{\nabla }^2{V}_i-{\partial }_i\dot{\mathsf{\Phi }}-{\displaystyle \frac{1}{3m_{\psi }^2}}{\partial }_0{\partial }_i\delta R=\kappa (S_i+{\partial }_{i}S).$$

(141)

At spatial infinity ($r\to \infty$), we impose $S\to 0$, so that ${\partial }_{i}S\to 0$, and similarly ${\partial }_i\dot{\mathsf{\Phi }}\to 0$ and ${\partial }_0{\partial }_i\delta R\to 0$. Under these conditions Equation (141) reduces to

$${\nabla }^2{V}_i=-2\kappa S_i.$$

(142)

Separating the longitudinal and transverse parts of (141) and comparing the coefficients of ${\partial }_i$ yields

$$\dot{\mathsf{\Phi }}+{\displaystyle \frac{1}{3m_{\psi }^2}}\dot{\delta R}=-\kappa S.$$

(143)

Equations (142) and (143) are the differential equations based on the $0i$ component of $\delta R_{\mu \nu }$ in terms of the Bardeen variables and the massive scalar propagating mode.

Finally, we consider the $ij$ component of the perturbation of the Ricci tensor, which is

$$\delta R_{ij}-{\displaystyle \frac{1}{6m_{\psi }^2}}\left(m_{\psi }^2{\eta }_{ij}+2{\partial }_i{\partial }_j\right)\delta R=\kappa \left(T_{ij}-{\displaystyle \frac{1}{3}}{\eta }_{ij}T\right).$$

(144)

Substituting the expression (137) for $\delta R_{ij}$ and Equation (118) for $T_{ij}$ into Equation (144), and equating coefficients of the independent SVT pieces, we obtain

$$\begin{array}{cc}\hfill -{\partial }_{(i}{\dot{V}}_{j)}& =\kappa {\partial }_{(i}{\sigma }_{j)},\hfill \end{array}$$

(145)

$$\begin{array}{cc}\hfill -{\displaystyle \frac{1}{2}}\square h_{ij}^{TT}& =\kappa {\sigma }_{ij},\hfill \end{array}$$

(146)

$$\begin{array}{cc}\hfill -{\displaystyle \frac{1}{2}}\square {\delta }_{ij}\mathsf{\Phi }-{\displaystyle \frac{1}{3}}{\partial }_i{\partial }_j\delta R& =\kappa \left(-{\displaystyle \frac{1}{3}}{\delta }_{ij}{\nabla }^2\sigma -{\displaystyle \frac{1}{3}}{\eta }_{ij}T\right).\hfill \end{array}$$

(147)

These equations imply

$$\begin{array}{cc}\hfill {\dot{V}}_i& =\kappa {\sigma }_i,\hfill \end{array}$$

(148)

$$\begin{array}{cc}\hfill \square h_{ij}^{TT}& =-2\kappa {\sigma }_{ij},\hfill \end{array}$$

(149)

$$\begin{array}{cc}\hfill \mathsf{\Psi }+{\displaystyle \frac{1}{2}}\mathsf{\Phi }+{\displaystyle \frac{1}{3m_{\psi }^2}}\delta R& =-\kappa \sigma ,\hfill \end{array}$$

(150)

and, using $T=\rho -3P$,

$$\square \mathsf{\Phi }+{\displaystyle \frac{1}{3}}\delta R={\displaystyle \frac{2}{3}}\kappa \left({\nabla }^2\sigma -\rho \right).$$

(151)

Equations (148)–(151) are the set of differential equations corresponding to the $ij$ component of $\delta R_{\mu \nu }$ in terms of the Bardeen variables and the matter SVT variables. These results are consistent with those derived in [37], up to differences in notation.

6.3. Cosmological Interpretation of the SVT Equations with the Extra Scalar Degree of Freedom

The system of Equations (139), (142), (143), and (148)–(151) allows a direct physical interpretation in cosmology once the background is promoted from Minkowski to a slowly varying FLRW or de Sitter spacetime.

The $\delta R_{00}$ Equation (139) is a modified Poisson-type equation: the gravitational potential $\mathsf{\Psi }$ is sourced not only by the energy density $\rho$ but also by pressure P, time derivatives of the potential $\mathsf{\Phi }$, and the dynamics of the scalar curvature perturbation $\delta R$ [38,39]. In GR, the corresponding equation at linear order would involve essentially the Laplacian of $\mathsf{\Psi }$ sourced only by $\rho$, with no extra scalar degree of freedom contribution. This modification leads to a scale- and time-dependent effective gravitational coupling, which directly affects the growth of cosmological structure and can be constrained by large-scale structure and weak-lensing surveys.

The $\delta R_{0i}$ sector separates into a transverse (vector) part and a longitudinal (scalar) part. The transverse part, Equation (142) together with Equation (148), shows that vector perturbations $V_i$ are sourced by the transverse momentum density $S_i$ and anisotropic stress ${\sigma }_i$, just as in GR. Thus, $f\left(R\right)$ gravity does not introduce new propagating vector modes at linear order. The longitudinal scalar Equation (143), however, contains the time derivative of the additional scalar degree of freedom $\dot{\delta R}$, modifying the time evolution of $\mathsf{\Phi }$ relative to GR. The time dependence of the gravitational potentials is directly probed by the integrated Sachs–Wolfe (ISW) effect and cross-correlations of CMB maps with large-scale structure.

The $\delta R_{ij}$ equations show that the tensor sector, Equation (149), obeys a wave equation structurally identical to that of GR, but with a source from anisotropic stress. In $f\left(R\right)$ gravity, the background scalar degree of freedom and the modified expansion history can nevertheless change the amplitude damping and effective propagation of gravitational waves over cosmological distances, providing an additional channel to test modifications of gravity with standard sirens.

Finally, the scalar sector of the perturbed field equations provides a direct window into one of the characteristic phenomenological signatures of modified gravity. In linear cosmological perturbation theory, scalar metric perturbations are described by the gauge-invariant Bardeen potentials $\mathsf{\Phi }$ and $\mathsf{\Psi }$, which coincide in General Relativity in the absence of matter anisotropic stress. Their inequality, $\mathsf{\Phi }\ne \mathsf{\Psi }$, is commonly referred to as gravitational slip and signals a departure from GR caused either by imperfect fluids or by additional gravitational degrees of freedom [39,40].

In metric $f\left(R\right)$ gravity, the scalar part of the $\delta R_{ij}$ equations, Equations (150) and (151), reveals that gravitational slip can arise even in the absence of matter anisotropic stress when the scalar curvature perturbation $\delta R$ is dynamically sourced. In metric $f\left(R\right)$ gravity, the scalar field induces an effective (geometric) anisotropic stress through $\delta f^{\prime }=f^{″}\delta R$, so that $\mathsf{\Phi }\ne \mathsf{\Psi }$ even when ${\sigma }^{\left(m\right)}=0$.

In the vacuum limit $\rho =P=\sigma =0$, Equations (150) and (151) reduce directly to Equation (84) of Ref. [7], confirming consistency with the standard result that no gravitational slip occurs in vacuum metric $f\left(R\right)$ gravity.

It is important to emphasize, however, that, in a vacuum, where matter sources vanish and the scalar curvature perturbation obeys its homogeneous Klein–Gordon equation, metric $f\left(R\right)$ gravity does not generate gravitational slip in the pure vacuum sector where the scalar mode is not excited. In this limit, one recovers $\mathsf{\Phi }=\mathsf{\Psi }$, in agreement with Equation (87) of Ref. [7]. The appearance of a nonzero gravitational slip therefore reflects the dynamical excitation of the scalar degree of freedom, rather than a purely vacuum effect.

In the presence of matter perturbations, the difference between the two scalar potentials is instead sourced by $\delta R$, reflecting the presence of the additional propagating scalar mode. This modification of the relation between $\mathsf{\Phi }$ and $\mathsf{\Psi }$ is a characteristic phenomenological signature of $f\left(R\right)$ models and can be observationally constrained through joint analyses of galaxy clustering, redshift-space distortions, and weak gravitational lensing [39,41]. The full SVT decomposition of $\delta R_{\mu \nu }$ thus provides a unified framework for linking the gauge-invariant scalar dynamics of the theory to observable effects in both gravitational-wave physics and cosmology.

7. Geodesic Deviation Method to Find the Polarization Content

The geodesic deviation equation relates the Riemann curvature tensor to the relative acceleration of neighboring geodesics and therefore provides a direct probe of gravitational-wave polarizations in a given theory of gravity [30,42]. In this section, we use the geodesic deviation equations to identify the polarization modes of gravitational waves in our specific metric $f\left(R\right)$ model,

$$f\left(R\right)=R+\alpha R^2-2\mathsf{\Lambda },$$

(152)

for which the scalar curvature perturbation $\delta R$ obeys the massive Klein–Gordon equation

$$\left(\square -m_{\psi }^2\right)\delta R=0,m_{\psi }^2={\displaystyle \frac{1}{6\alpha }},$$

(153)

on a de Sitter background. The scalar perturbation $\delta R$ corresponds to the extra scalar degree of freedom, in addition to the usual tensor modes of GR.

We first work in the local Minkowski patch of the de Sitter background, which is appropriate for interferometric detectors whose size is much smaller than the background curvature radius. We then show how the same polarization structure appears when the calculation is formulated fully on a de Sitter FRW background.

7.1. Local Minkowski Patch of de Sitter

The general geodesic deviation equation is

$${\displaystyle \frac{D^2{\xi }^{\mu }}{d{\tau }^2}}=-{R^{\mu }}_{\alpha \nu \beta }{\xi }^{\nu }{\displaystyle \frac{d{x}^{\alpha }}{d\tau }}{\displaystyle \frac{d{x}^{\beta }}{d\tau }},$$

(154)

where ${\xi }^{\mu }$ is the separation vector between neighboring geodesics and $\tau$ is proper time. For gravitational-wave detectors, we work in the weak-field, slow-motion limit: the detector is at rest in the chosen coordinates and far from the source, so

$${\displaystyle \frac{d{x}^i}{d\tau }}\ll {\displaystyle \frac{d{x}^0}{d\tau }}\Rightarrow {\displaystyle \frac{d{x}^{\mu }}{d\tau }}\approx (1,0,0,0),$$

(155)

and we can identify proper time with coordinate time,

$$\tau \simeq t.$$

(156)

In this regime, the covariant derivatives in (154) reduce to ordinary time derivatives, and the spatial components of the geodesic deviation equation become

$${\ddot{\xi }}_i=-R_{i0j0}{\xi }^j,$$

(157)

where overdots denote derivatives with respect to t.

In linearized gravity, the Riemann tensor is

$$R_{\mu \nu \rho \sigma }={\displaystyle \frac{1}{2}}\left({\partial }_{\rho }{\partial }_{\nu }{h}_{\mu \sigma }+{\partial }_{\sigma }{\partial }_{\mu }{h}_{\nu \rho }-{\partial }_{\sigma }{\partial }_{\nu }{h}_{\mu \rho }-{\partial }_{\rho }{\partial }_{\mu }{h}_{\nu \sigma }\right),$$

(158)

where $h_{\mu \nu }$ is the metric perturbation on the local Minkowski background ${\eta }_{\mu \nu }$. We decompose $h_{\mu \nu }$ into a transverse-traceless tensor part $h_{\mu \nu }^{TT}$ and a scalar part associated with the scalar curvature perturbation $\delta R$.

For the scalar mode, in a convenient gauge compatible with the Newtonian (longitudinal) gauge used in Section 4, the scalar perturbation can be chosen proportional to the background metric:

$$h_{\mu \nu }^{\left(s\right)}=C\delta R{\eta }_{\mu \nu },$$

(159)

where C is an overall constant that only rescales the amplitude and does not affect the polarization pattern. For simplicity, we set $C=1$ below. Equivalently, one may view this as choosing a convenient representative of the scalar sector that reproduces the correct nonvanishing components of the tidal tensor $R_{i0j0}$ implied by the field equations, rather than as a unique metric reconstruction. This choice is a convenient representative scalar-sector gauge that reproduces the correct tidal (polarization) pattern of the massive scalar mode; it should not be interpreted as a unique reconstruction of $h_{\mu \nu }$ from $\delta R$ in an arbitrary gauge.

• Explicitly,

$$\begin{array}{cc}\hfill h_{00}^{\left(s\right)}& =-\delta R,\hfill \end{array}$$

(160)

$$\begin{array}{cc}\hfill h_{0i}^{\left(s\right)}& =0,\hfill \end{array}$$

(161)

$$\begin{array}{cc}\hfill h_{ij}^{\left(s\right)}& =\delta R{\delta }_{ij}.\hfill \end{array}$$

(162)

Substituting into the expression for the Riemann tensor and focusing on $R_{i0j0}$, we find

$$R_{i0j0}=-{\displaystyle \frac{1}{2}}\left({\partial }_0{\partial }_0{h}_{ij}+{\partial }_i{\partial }_j{h}_{00}\right)=-{\displaystyle \frac{1}{2}}\left({\delta }_{ij}\ddot{\delta R}-{\partial }_i{\partial }_j\delta R\right).$$

(163)

Now, consider a scalar wave propagating along the $+z$ direction,

$$\delta R=\delta R(t,z).$$

(164)

In the transverse directions x and y,

$${\partial }_x\delta R={\partial }_y\delta R=0,$$

(165)

so that

$$R_{x0x0}=R_{y0y0}=-{\displaystyle \frac{1}{2}}\ddot{\delta R}.$$

(166)

In the longitudinal direction,

$$R_{z0z0}=-{\displaystyle \frac{1}{2}}\left(\ddot{\delta R}-{\partial }_z^2\delta R\right).$$

(167)

Using the massive Klein–Gordon equation for the extra scalar mode in the local Minkowski patch,

$$\left(\square -m_{\psi }^2\right)\delta R=0,$$

(168)

which implies

$$\ddot{\delta R}={\partial }_z^2\delta R-m_{\psi }^2\delta R,$$

(169)

we obtain

$$\begin{array}{cc}\hfill R_{x0x0}& =R_{y0y0}=-{\displaystyle \frac{1}{2}}\left({\partial }_z^2\delta R-m_{\psi }^2\delta R\right),\hfill \end{array}$$

(170)

$$\begin{array}{cc}\hfill R_{z0z0}& =+{\displaystyle \frac{1}{2}}{m}_{\psi }^2\delta R.\hfill \end{array}$$

(171)

For a monochromatic plane wave

$$\begin{array}{cccc}\hfill \delta R(t,z)& =A{e}^{i(k_{z}z-\omega t)},\hfill & \hfill & (\mathrm{the}\mathrm{physical}\mathrm{field}\mathrm{is}\mathrm{the}\mathrm{real}\mathrm{part}),\hfill \end{array}$$

(172)

$$\begin{array}{cc}\hfill {\omega }^2& =k_z^2+m_{\psi }^2.\hfill \end{array}$$

(173)

The tidal components become

$$\begin{array}{cc}\hfill R_{x0x0}& =R_{y0y0}=+{\displaystyle \frac{1}{2}}{\omega }^2\delta R,\hfill \end{array}$$

(174)

$$\begin{array}{cc}\hfill R_{z0z0}& =+{\displaystyle \frac{1}{2}}{m}_{\psi }^2\delta R.\hfill \end{array}$$

(175)

The geodesic deviation equations

$${\ddot{\xi }}_i=-R_{i0j0}{\xi }^j$$

(176)

then give

$$\begin{array}{cc}\hfill \ddot{X}& =-{\displaystyle \frac{1}{2}}{\omega }^2\delta RX,\hfill \end{array}$$

(177)

$$\begin{array}{cc}\hfill \ddot{Y}& =-{\displaystyle \frac{1}{2}}{\omega }^2\delta RY,\hfill \end{array}$$

(178)

$$\begin{array}{cc}\hfill \ddot{Z}& =-{\displaystyle \frac{1}{2}}{m}_{\psi }^2\delta RZ.\hfill \end{array}$$

(179)

These equations show that the extra scalar degree of freedom induces both a transverse breathing mode (in the X and Y directions) and a longitudinal mode (in the Z direction). This is precisely the expected polarization content for a massive scalar mode.

In pure GR, where only the transverse-traceless tensor $h_{ij}^{TT}$ is present, $\delta R=0$ and the scalar-induced contributions vanish; only the familiar ⊕ and ⊗ tensor modes remain. In metric $f\left(R\right)$ gravity, the nonzero $\delta R$ generates additional breathing and longitudinal polarizations on top of the GR tensor modes.

7.2. Geodesic Deviation on a de Sitter FRW Background

We now sketch how the same polarization structure arises when the calculation is performed directly on the de Sitter background without passing explicitly to a Minkowski patch. In spatially flat FRW coordinates, the de Sitter metric can be written as

$$d{s}^2=-d{t}^2+a^2\left(t\right){\delta }_{ij}d{x}^{i}d{x}^j,a\left(t\right)=e^{H_{d}t},$$

(180)

with constant Hubble parameter $H_d=\sqrt{R_d/12}$ in four dimensions.

We consider small perturbations around this background in Newtonian gauge. Restricting initially to the scalar sector, the perturbed metric takes the form

$$d{s}^2=-(1+2\mathsf{\Phi })d{t}^2+a^2\left(t\right)(1-2\mathsf{\Psi }){\delta }_{ij}d{x}^{i}d{x}^j,$$

(181)

where the 00 field equation fixes the Newtonian potential in terms of the scalar curvature perturbation, while the traceless spatial equations determine the gravitational slip $\mathsf{\Phi }-\mathsf{\Psi }$ (see Section 4). In particular,

$$\mathsf{\Phi }=-{\displaystyle \frac{\delta R}{6m_{\psi }^2}}.$$

(182)

The equality $\mathsf{\Phi }=\mathsf{\Psi }$ is recovered in the sector where the slip source vanishes (e.g., in the corresponding vacuum limit of the SVT system); when the scalar sector sources the traceless spatial equations, one generically has $\mathsf{\Phi }-\mathsf{\Psi }\ne 0$.

Thus, the additional scalar degree of freedom is encoded in the scalar metric sector, with $\mathsf{\Phi }$ fixed by $\delta R$ and the slip $\mathsf{\Phi }-\mathsf{\Psi }$ determined by the traceless spatial equations. To relate the geodesic deviation equation to the detector frame, it is convenient to introduce an orthonormal tetrad adapted to a comoving observer. To first order in the perturbations one may take

$$\begin{array}{cc}\hfill {e_{\widehat{0}}}^{\mu }& =(1-\mathsf{\Phi },0,0,0),\hfill \end{array}$$

(183)

$$\begin{array}{cc}\hfill {e_{\widehat{i}}}^{\mu }& ={\displaystyle \frac{1+\mathsf{\Psi }}{a\left(t\right)}}{{\delta }_i}^{\mu },\hfill \end{array}$$

(184)

so that physical (proper) spatial separations are measured with hatted indices. In the short-wavelength, locally inertial limit used below, the $\mathcal{O}(\mathsf{\Phi },\mathsf{\Psi })$ corrections in the tetrad only affect higher-order terms and may be neglected when identifying the polarization pattern. In this orthonormal frame the geodesic deviation equation takes the form

$${\displaystyle \frac{d^2{\xi }^{\widehat{i}}}{d{t}^2}}=-{R^{\widehat{i}}}_{\widehat{0}\widehat{j}\widehat{0}}{\xi }^{\widehat{j}}.$$

(185)

The tidal tensor splits naturally into a background de Sitter contribution and a perturbation induced by scalar and tensor modes,

$${R^{\widehat{i}}}_{\widehat{0}\widehat{j}\widehat{0}}={R^{\widehat{i}}}_{\widehat{0}\widehat{j}\widehat{0}}{|}_{\mathrm{dS}}+\delta {R^{\widehat{i}}}_{\widehat{0}\widehat{j}\widehat{0}}.$$

(186)

For the spatially flat de Sitter background, the nonvanishing Christoffel symbols are ${{\mathsf{\Gamma }}^0}_{ij}=a\dot{a}{\delta }_{ij}$ and ${{\mathsf{\Gamma }}^i}_{0j}=H_d{{\delta }^i}_j,$ which follow directly from the FRW line element. From these, the coordinate-basis Riemann component relevant for geodesic deviation is

$${R^i}_{0j0}=-{\displaystyle \frac{\ddot{a}}{a}}{{\delta }^i}_j.$$

(187)

For exact de Sitter expansion $a\left(t\right)=e^{H_{d}t}$, one has $\ddot{a}/a=H_d^2$, yielding

$${R^i}_{0j0}{|}_{\mathrm{dS}}=-H_d^2{{\delta }^i}_j.$$

(188)

Projecting onto the orthonormal tetrad,

${R^{\widehat{i}}}_{\widehat{0}\widehat{j}\widehat{0}}={e^{\widehat{i}}}_k{e_{\widehat{j}}}^{\ell }{R^k}_{0\ell 0},$ the factors of $a\left(t\right)$ from the tetrads cancel those implicit in the metric, leaving

$${R^{\widehat{i}}}_{\widehat{0}\widehat{j}\widehat{0}}{|}_{\mathrm{dS}}=-H_d^2{{\delta }^i}_j.$$

(189)

We now include perturbations. Restoring both scalar and tensor modes, the perturbed FRW metric may be written as

$$d{s}^2=-(1+2\mathsf{\Phi })d{t}^2+a^2\left(t\right)\left[(1-2\mathsf{\Psi }){\delta }_{ij}+h_{ij}^{\mathrm{TT}}(t,\overrightarrow{x})\right]d{x}^{i}d{x}^j,$$

(190)

where $h_{ij}^{\mathrm{TT}}$ denotes the transverse–traceless tensor perturbation. Introducing the Minkowski metric ${\eta }_{\mu \nu }=\mathrm{diag}(-1,1,1,1)$, all perturbations can be collected into a single tensor

$$h_{00}=2\mathsf{\Phi },h_{0i}=0,h_{ij}=-2\mathsf{\Psi }{\delta }_{ij}+h_{ij}^{\mathrm{TT}},$$

(191)

so that the metric assumes the conformal form

$$g_{\mu \nu }(t,\mathbf{x})=a^2\left(t\right)\left[{\eta }_{\mu \nu }+h_{\mu \nu }(t,\mathbf{x})\right].$$

(192)

Expanding the Riemann tensor to first order, $R_{\mu \nu \rho \sigma }=R_{\mu \nu \rho \sigma }^{\left(0\right)}+\delta R_{\mu \nu \rho \sigma }\left[h\right],$ the linearized part depends only on derivatives of $h_{\mu \nu }$. In the short-wavelength (locally inertial) limit relevant for detector-scale physics, the wave-induced part of the tidal tensor is dominated by derivatives of the perturbations rather than by derivatives of the scale factor. In this regime, after projecting onto the comoving orthonormal tetrad, the perturbative contribution satisfies

$$\delta {R^{\widehat{i}}}_{\widehat{0}\widehat{j}\widehat{0}}=\delta R_{i0j0}^{\left(\mathrm{Mink}\right)}{|}_{\begin{array}{c}\mathrm{physical}\\ \mathrm{wavenumber}\end{array}}+\mathcal{O}\left({\displaystyle \frac{H_d}{\omega }}\right),$$

(193)

where $\delta R_{i0j0}^{\left(\mathrm{Mink}\right)}$ is the Minkowski-patch tidal matrix computed in Section 7.1.

Therefore, for the massive scalar propagating mode, we can directly carry over the Minkowski polarization pattern; cosmological expansion produces the usual redshift/dilution of amplitudes but does not change the mode content. With careful attention to the overall sign, one finds

$$\begin{array}{cc}\hfill \delta {R^{\widehat{x}}}_{\widehat{0}\widehat{x}\widehat{0}}& =\delta {R^{\widehat{y}}}_{\widehat{0}\widehat{y}\widehat{0}}=+{\displaystyle \frac{1}{2a^2}}{\omega }^2\delta R,\hfill \end{array}$$

(194)

$$\begin{array}{cc}\hfill \delta {R^{\widehat{z}}}_{\widehat{0}\widehat{z}\widehat{0}}& =+{\displaystyle \frac{1}{2a^2}}{m}_{\psi }^2\delta R,\hfill \end{array}$$

(195)

for a monochromatic mode, and similarly for a generic wave packet using the Klein–Gordon Equation (168). The tidal amplitudes are diluted by cosmological expansion (and redshifted relative to local physical frequencies), while the polarization pattern is unchanged.

The geodesic deviation equations for physical separations ${\xi }^{\widehat{i}}$ are, therefore,

$$\begin{array}{cc}\hfill {\ddot{\xi }}^{\widehat{X}}& =\left[H_d^2-\delta {R^{\widehat{x}}}_{\widehat{0}\widehat{x}\widehat{0}}\right]{\xi }^{\widehat{X}},\hfill \end{array}$$

(196)

$$\begin{array}{cc}\hfill {\ddot{\xi }}^{\widehat{Y}}& =\left[H_d^2-\delta {R^{\widehat{y}}}_{\widehat{0}\widehat{y}\widehat{0}}\right]{\xi }^{\widehat{Y}},\hfill \end{array}$$

(197)

$$\begin{array}{cc}\hfill {\ddot{\xi }}^{\widehat{Z}}& =\left[H_d^2-\delta {R^{\widehat{z}}}_{\widehat{0}\widehat{z}\widehat{0}}\right]{\xi }^{\widehat{Z}}.\hfill \end{array}$$

(198)

The background term encodes the isotropic de Sitter tidal contribution, while the wave-induced part reproduces the same transverse breathing and longitudinal pattern as in the local Minkowski analysis. Thus, cosmological expansion modifies amplitudes but does not change the polarization content.

7.3. Polarization Classification via $R_{i0j0}$

The geodesic deviation equations derived above show explicitly that the additional scalar degree of freedom in our $f\left(R\right)$ model produces both breathing and longitudinal motion of test particles. For completeness, we now review a more formal method to classify the polarization modes using the components of $R_{i0j0}$, following [2,43].

In a local inertial (Minkowski) patch of the spacetime, the perturbed metric may be written in terms of scalar, vector, and tensor perturbations as

$$d{s}^2=-(1+2\mathsf{\Phi })d{t}^2+2E_{i}dtd{x}^i+\left[(1-2\mathsf{\Psi }){\delta }_{ij}+h_{ij}^{TT}\right]d{x}^{i}d{x}^j,$$

(199)

where $\mathsf{\Phi }$ and $\mathsf{\Psi }$ are the scalar Bardeen potentials, $E_i$ encodes the vector (shear) perturbations, and $h_{ij}^{TT}$ is the transverse–traceless tensor mode. In metric $f\left(R\right)$ gravity the traceless spatial field equations determine the gravitational slip $\mathsf{\Phi }-\mathsf{\Psi }$; one has $\mathsf{\Phi }=\mathsf{\Psi }$ only in a genuine no-slip sector (e.g., when the effective geometric anisotropic-stress source proportional to $\delta f^{\prime }=f^{″}\left(R_d\right)\delta R$ vanishes) (see Section 4 and Section 7). The Riemann tensor components entering the geodesic deviation equation are

$$R_{i0j0}=-{\partial }_i{\partial }_j\mathsf{\Phi }+{\displaystyle \frac{1}{2}}\left({\partial }_0{\partial }_j{E}_i+{\partial }_0{\partial }_i{E}_j\right)+{\delta }_{ij}{\partial }_0^2\mathsf{\Psi }-{\displaystyle \frac{1}{2}}{\partial }_0^2{h}_{ij}^{TT}.$$

(200)

The six possible GW polarization modes can be encoded by writing the tidal tensor $R_{i0j0}$ as a symmetric $3\times 3$ matrix,

$$R_{i0j0}=\left[\begin{array}{ccc}{P}_4+P_6& P_5& P_2\\ P_5& -P_4+P_6& P_3\\ P_2& P_3& P_1\end{array}\right],$$

(201)

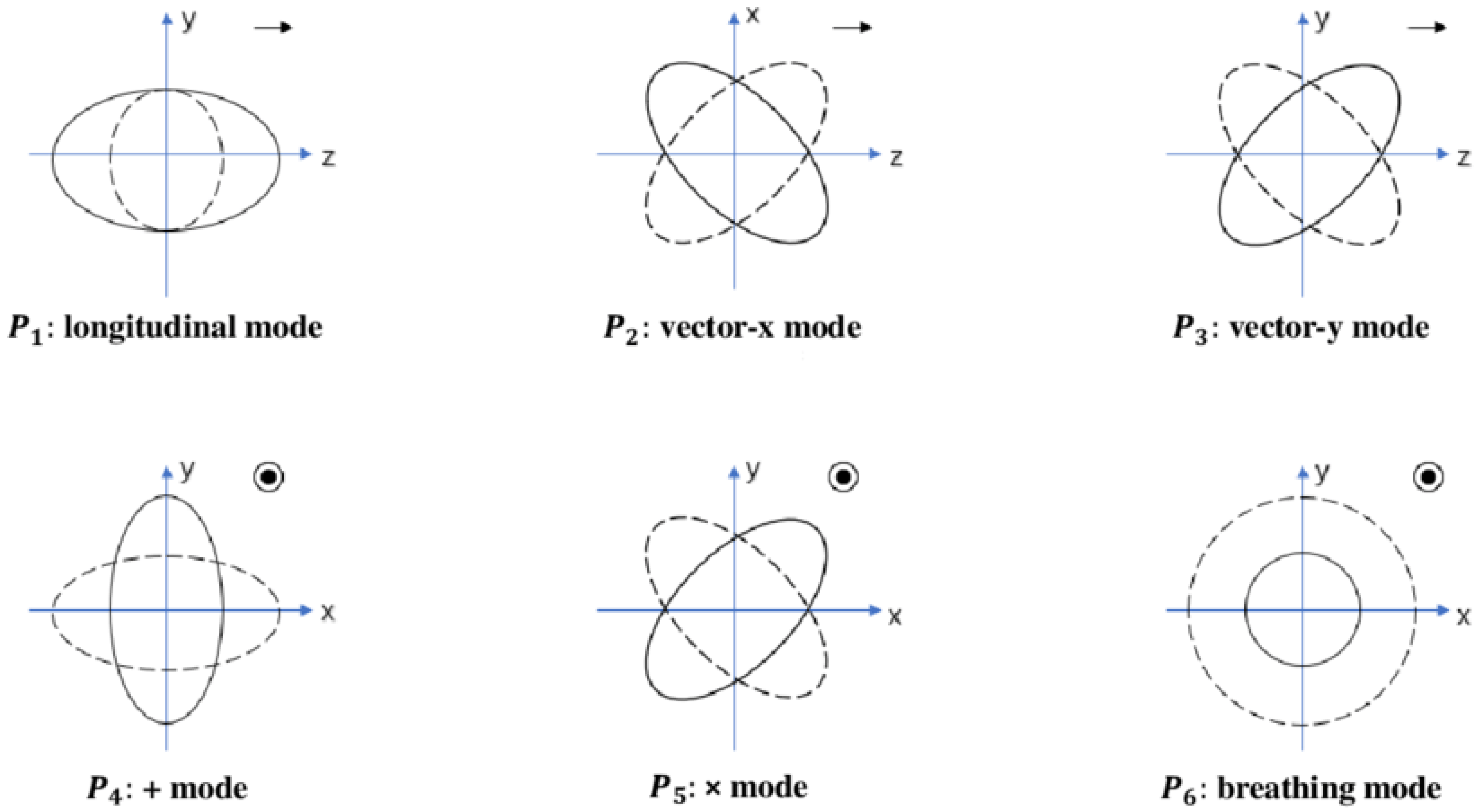
where $P_1,\dots ,P_6$ are the six independent polarization amplitudes (scalar longitudinal, two vector modes, two tensor modes, and scalar breathing). They correspond to the six standard polarization patterns shown in Figure 1.2

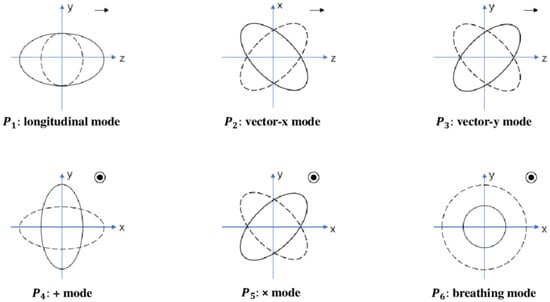
Figure 1. Six polarization modes of gravitational waves.

For a plane wave propagating along the z direction, comparison of (200) with the matrix form (201) yields

$$\begin{array}{cc}\hfill P_1& =-{\partial }_3{\partial }_3\mathsf{\Phi }+{\partial }_0^2\mathsf{\Psi },\hfill \end{array}$$

(202)

$$\begin{array}{cc}\hfill P_2& ={\displaystyle \frac{1}{2}}{\partial }_0{\partial }_3{E}_1,\hfill \end{array}$$

(203)

$$\begin{array}{cc}\hfill P_3& ={\displaystyle \frac{1}{2}}{\partial }_0{\partial }_3{E}_2,\hfill \end{array}$$

(204)

$$\begin{array}{cc}\hfill P_4& =-{\displaystyle \frac{1}{2}}{\partial }_0^2{h}_{11}^{TT},\hfill \end{array}$$

(205)

$$\begin{array}{cc}\hfill P_5& =-{\displaystyle \frac{1}{2}}{\partial }_0^2{h}_{12}^{TT},\hfill \end{array}$$

(206)

$$\begin{array}{cc}\hfill P_6& ={\partial }_0^2\mathsf{\Psi }.\hfill \end{array}$$

(207)

Here, $E_1$ and $E_2$ encode the vector (shear) polarizations, $h_{ij}^{TT}$ represents the usual ⊕ and ⊗ tensor modes, and $\mathsf{\Phi },\mathsf{\Psi }$ are the scalar Bardeen potentials.

In metric $f\left(R\right)$ gravity, there are no additional propagating vector degrees of freedom beyond GR; in a vacuum, the vector sector is non-radiative; so, the vector GW polarizations are absent and $P_2=P_3=0$. The tensor modes $P_4$ and $P_5$ coincide with those of GR and correspond to the ⊕ and ⊗ polarizations. The remaining scalar modes are encoded in $P_1$ (longitudinal, involving $\mathsf{\Phi }$ and $\mathsf{\Psi }$) and $P_6$ (breathing, involving $\mathsf{\Psi }$ in this SVT parametrization). In metric $f\left(R\right)$ gravity, the 00 equation fixes $\mathsf{\Phi }$ in terms of the scalar curvature perturbation, while the traceless spatial equations determine the slip $\mathsf{\Phi }-\mathsf{\Psi }$ (see Section 4). In particular, one may write

$$\mathsf{\Phi }=-{\displaystyle \frac{\delta R}{6m_{\psi }^2}},$$

(208)

while $\mathsf{\Psi }$ differs from $\mathsf{\Phi }$ by a slip term set by the scalar sector. Consequently, when the massive scalar mode is dynamically excited, both $P_1$ and $P_6$ are generically nonzero, confirming the presence of longitudinal and breathing scalar polarizations in addition to the two tensor polarizations.

In summary, the geodesic deviation analysis—both in the local Minkowski patch and on the full de Sitter background—shows that the metric $f\left(R\right)$ model $f\left(R\right)=R+\alpha R^2-2\mathsf{\Lambda }$ supports:

• Two massless tensor modes $(\oplus ,\otimes )$, identical to those of GR;
• One massive scalar mode (the massive scalar propagating mode), which decomposes into a transverse breathing polarization and a longitudinal polarization along the propagation direction.

This pattern agrees with the general expectation for metric $f\left(R\right)$ gravity and provides the polarization content against which current and future GW observations can test this class of models.

8. Conclusions and Future Outlook

In this work, we developed a unified and fully gauge-invariant analysis of gravitational-wave polarizations in metric $f\left(R\right)$ gravity, with particular emphasis on the modified Starobinsky model $f\left(R\right)=R+\alpha R^2-2\mathsf{\Lambda }.$ Working on a constant-curvature de Sitter background, we reformulated the linearized field equations in terms of Bardeen gauge-invariant variables and the scalar curvature perturbation $\delta R$, thereby making the massive scalar propagating mode manifest. By deriving the Klein–Gordon equation for $\delta R$ directly from the perturbed trace equation, we verified that the scalar mode behaves as a massive propagating field with mass $m_{\psi }^2=1/\left(6\alpha \right)$ on the de Sitter background. This establishes the scalar curvature perturbation $\delta R$ as the source of the additional breathing and longitudinal polarizations absent in General Relativity.

We complemented the Bardeen-variable analysis with a full $(3+1)$ decomposition of the perturbed Ricci tensor, including the presence of matter sources. This approach revealed explicitly how scalar, vector, and tensor perturbations enter the modified field equations and how the scalar sector departs from its GR behavior. In particular, the decomposition demonstrated that (i) the vector sector remains nondynamical and identical to that of GR, (ii) the tensor sector continues to satisfy the standard transverse–traceless wave equation, and (iii) all modifications are encoded in the scalar sector through the dynamical curvature perturbation $\delta R$. The resulting coupled equations for $\mathsf{\Phi }$, $\mathsf{\Psi }$, and $\delta R$ illustrate the origin of the gravitational slip, modified Poisson equation, and scale-dependent evolution of cosmological perturbations characteristic of $f\left(R\right)$ models.

A complementary geodesic-deviation analysis was carried out in both the local-Minkowski patch of de Sitter spacetime and in the fully covariant de Sitter background. In both cases, the tidal tensor $R_{i0j0}$ depends on the scalar curvature perturbation $\delta R$ and yields the characteristic polarization pattern: two tensor modes (⊕ and ⊗), a breathing mode, and a longitudinal mode. This agrees with the general classification of metric theories admitting up to six polarizations and verifies, by two independent methods, that metric $f\left(R\right)$ gravity contains the two tensor polarizations of GR together with one additional propagating massive scalar degree of freedom, which manifests as breathing and longitudinal responses depending on the detector frame and wave regime.

From a cosmological perspective, the Compton wavelength $m_{\psi }^{-1}$ associated with the extra scalar sets a characteristic scale for departures from GR in linear perturbations (up to environmental screening effects), separating GR-like behavior on sufficiently small scales from modified dynamics on larger scales. Because the same massive scalar propagating mode controls the late-time background evolution, the growth rate of structure, and the propagation of gravitational waves, future multi-probe observations—combining large-scale structure, weak lensing, CMB anisotropies, pulsar-timing arrays, and gravitational-wave observatories—provide a coherent program for testing the viability of $f\left(R\right)$ gravity on both astrophysical and cosmological scales.

Future Outlook

Several natural extensions follow from the framework developed here:

• Beyond de Sitter backgrounds: The methods employed here can be generalized to slowly evolving FLRW backgrounds, permitting a direct link between gravitational-wave propagation and the time dependence of the mass $m_{\psi }$ of the massive scalar propagating mode in realistic cosmologies.
• Mode mixing and GW propagation: A next step is the study of mode mixing between the tensor and scalar sectors, including amplitude damping and potential dispersion effects in late-time, low-density environments.
• Constraints from forthcoming surveys: Current and future missions (Euclid, LSST, SKA, LISA, pulsar-timing arrays) will significantly improve constraints on gravitational slip, the mass of the scalar mode, and the scale-dependent growth of cosmological perturbations. The gauge-invariant formalism presented here is well suited for connecting theoretical predictions with these upcoming datasets.
• Extension to broader modified-gravity families: The techniques developed in this paper—decomposition of the perturbed Ricci tensor, isolation of the massive scalar propagating mode, fully covariant GW polarization extraction, and geodesic-deviation analysis—can be applied to more general higher-curvature theories such as $f\left(G\right)$ gravity, scalar–tensor Horndeski theories, and Einstein–dilaton–Gauss–Bonnet models.

Overall, the combination of gauge-invariant SVT analysis, Ricci-tensor decomposition, and geodesic deviation provides a robust framework for identifying and interpreting the polarization content of gravitational waves in metric $f\left(R\right)$ gravity. This establishes a consistent pathway for future observational tests capable of distinguishing GR from its simplest and most theoretically motivated extensions.