A Comparative X-ray Diffraction Study and Ab Initio Calculation on RU60358, a New Pyrethroid

Fodil Hamzaoui; Abdelkader Chouaih; Philippe Lagant; Ouassila Belarbi; Gérard Vergoten

doi:10.3390/i7080255

,

and

¹

Laboratoire SEA2M, Département de Chimie, Université de Mostaganem, 27000 Mostaganem, Algeria

²

UMR CNRS 8576 Glycobiologie Structurale et Fonctionnelle, Université des Sciences et Technologies, 59655 Villeneuve d’Ascq, France

^*

Author to whom correspondence should be addressed.

Int. J. Mol. Sci.2006, 7(8), 255-265;https://doi.org/10.3390/i7080255

Version Notes

Order Reprints

Abstract

The crystal structure of RU60358, C₂₀H₂₁NO₃, has been determined using X-ray diffraction to establish the configuration and stereochemistry of the molecule around the C15-C16 triple bond. The compound crystallises in the orthorhombic space group P2₁2₁2₁, a = 7.7575, b = 11.3182, c = 21.3529Å, V = 1874.80Å3 and Z = 4. The structure has been refined to a final R = 0.068 for the observed structure factors with I ≥ 3σ (I). The refined structure was found to be significantly non planar. A comparative study, using the ab initio calculations of the structure at B3LYP/6-31G** levels of theory, shows good geometrical agreement with the X-ray diffraction data. Standard deviations between the calculated and experimental bond values have been shown to be 0.01 Å and 0.5° for bond angles. Vibrational wavenumbers were obtained from a normal mode analysis using the ab initio calculations.

Keywords:

X-ray diffraction; Ab initio calculation; organic compounds; pyrethroid.

1. Introduction

The structures of pyrethroids compounds obtained from experimental X-ray diffraction data has been investigated by several authors [1,2,3,4]. Considerable progress has been made in relating the structure of pyrethroids with their biological activity, but improvement of such concepts requires reliable information on molecular shape (configuration, bond lengths and angles and conformation). Biological activity in pyrethroids is related to molecular structure and depends strongly on the stereochemistry adopted by the asymmetric centers [5,6,7]. In this context the compound RU60358 appears as an useful intermediate in the synthesis of some pyrethroid insecticides [8]. The study of the conformation of this molecule may yield information about the mechanism of its biological activity [9,10]. In this paper, we propose a comparative study between the experimental X-ray diffraction data and the optimized geometry predicted from ab initio molecular orbital calculations performed on the compound RU60358. Vibrational wavenumbers were then consequently predicted and correct assignments obtained.

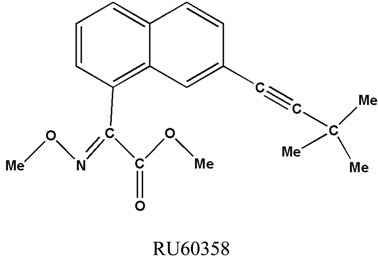
2. Results and discussion

2.1. Description of the crystal structure

The displacement ellipsoid plot with the numbering scheme for the title compound is shown in Figure 1. Figure 2 shows a perspective view of the crystal packing in the unit cell. Selected X-ray diffraction data summarize bond lengths in Table 1 and bond angles in Table 2.

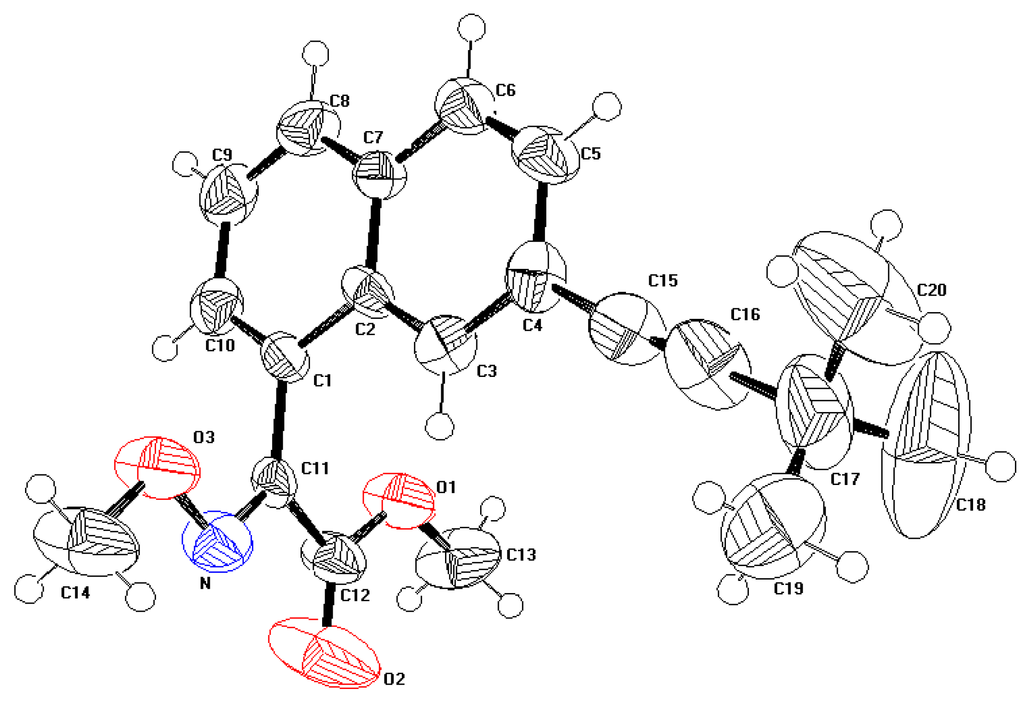
Figure 1. Perspective view of the molecule showing the atom-labelling scheme. Displacement ellipsoids are drawn at the 50% probability level and H atoms are shown as small spheres of arbitrary radii.

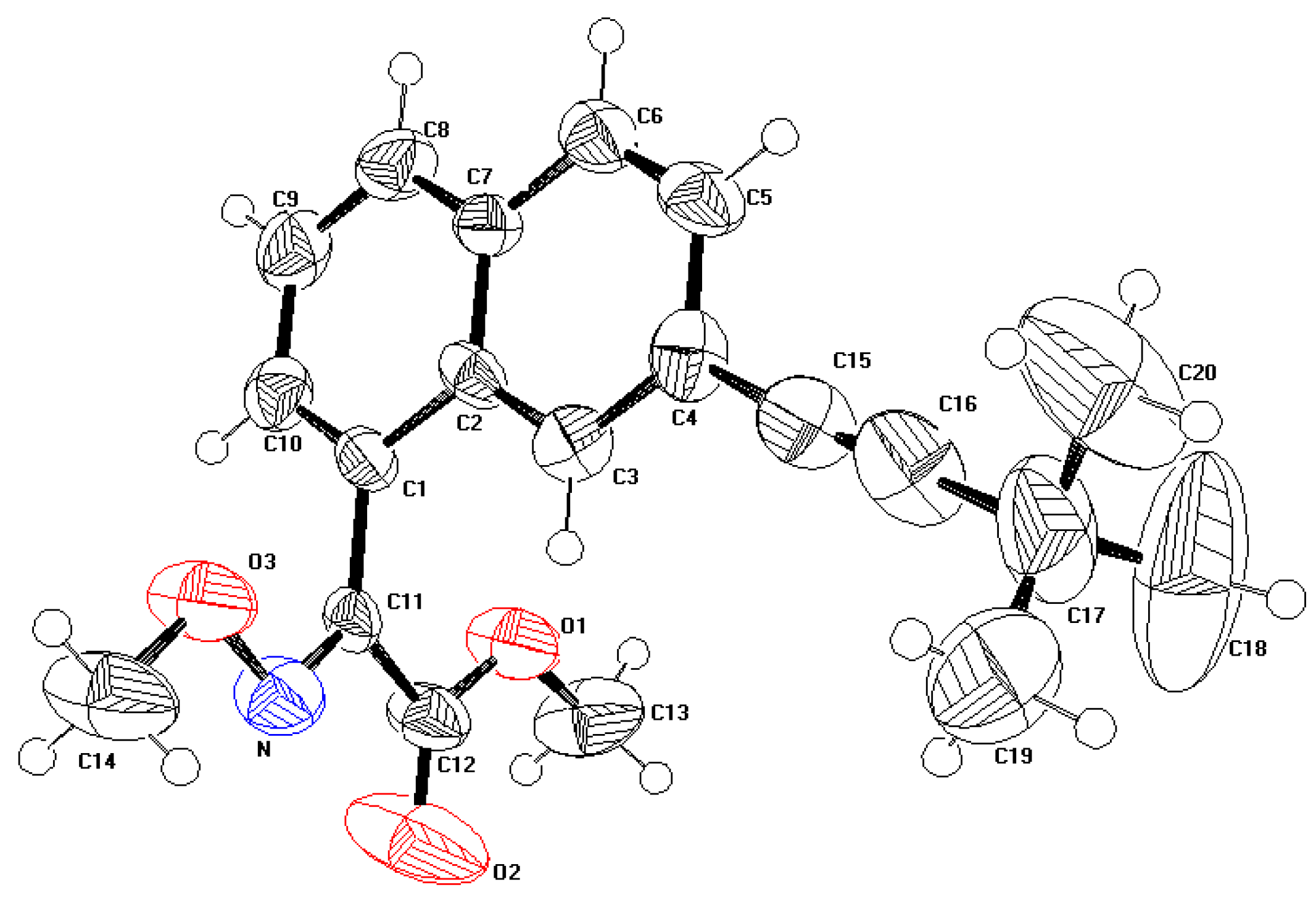
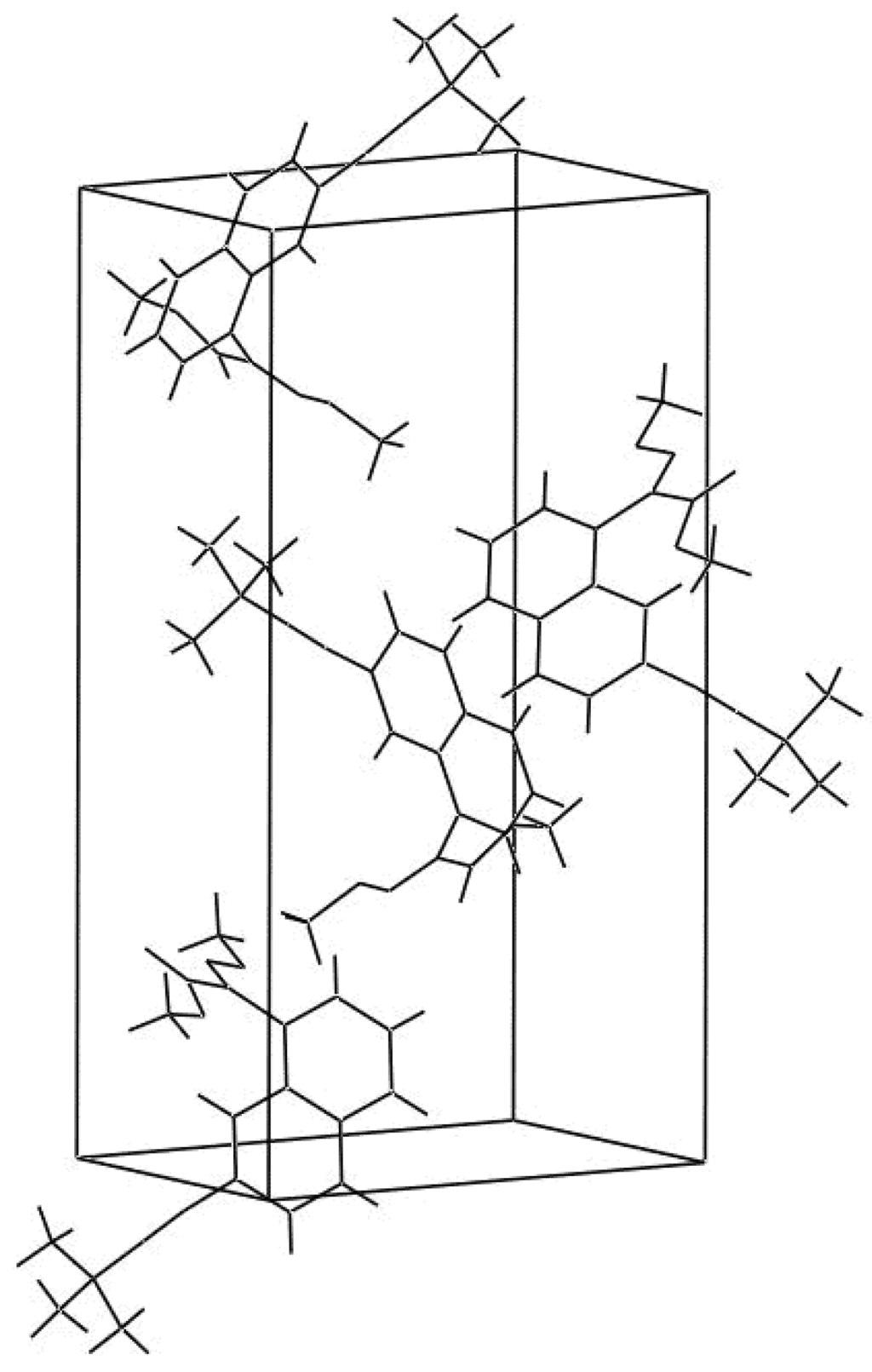
Figure 2. A perspective view of the crystal packing in the unit cell.

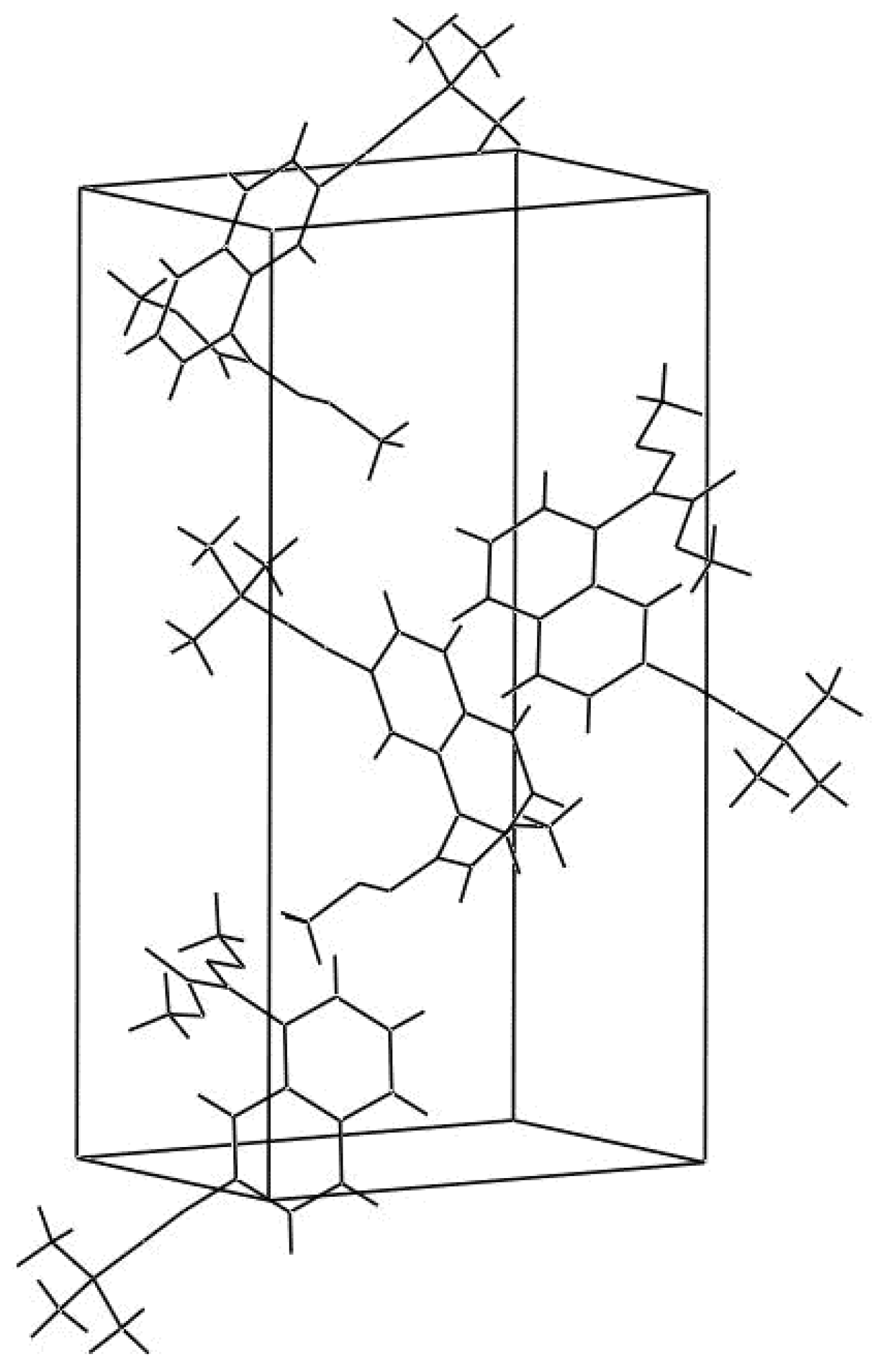
Table 1. Selected bond distances (Å) by X-ray and theoretical calculations

**Table 1.** Selected bond distances (Å) by X-ray and theoretical calculations
Atom 1	Atom 2	Distance (Å)
Atom 1	Atom 2	X-ray	B3LYP/6-31G**
C1	C2	1.395 (10)	1.433
C1	C10	1.395 (11)	1.381
C1	C11	1.474 (12)	1.472
C2	C3	1.410 (09)	1.416
C2	C7	1.395 (11)	1.433
C3	C4	1.395 (13)	1.388
C4	C5	1.395 (10)	1.428
C4	C15	1.429 (10)	1.428
C5	C6	1.395 (10)	1.371
C6	C7	1.395 (09)	1.422
C7	C8	1.395 (11)	1.418
C8	C9	1.395 (11)	1.375
C9	C10	1.395 (09)	1.412
C11	N	1.278 (13)	1.290
C11	C12	1.514 (15)	1.497
C12	O1	1.292 (10)	1.351
C12	O2	1.152 (10)	1.210
C13	O1	1.439 (12)	1.436
N	O3	1.376 (09)	1.374
C14	O3	1.427 (11)	1.467
C15	C16	1.163 (13)	1.213
C16	C17	1.467 (12)	1.459
C17	C18	1.439 (12)	1.548
C17	C19	1.469 (11)	1.541
C17	C20	1.531 (13)	1.549

Table 2. Selected bond angles (°) by X-ray and theoretical calculations

**Table 2.** Selected bond angles (°) by X-ray and theoretical calculations
Atom 1	Atom 2	Atom 3	Angle (°)
Atom 1	Atom 2	Atom 3	X-ray	B3LYP/6-31G**
C2	C1	C10	120.0 (8)	119.8
C2	C1	C11	123.5 (5)	121.1
C10	C1	C11	116.2 (8)	119.1
C1	C2	C3	120.2 (6)	122.6
C1	C2	C7	120.0 (7)	118.5
C3	C2	C7	119.8 (7)	118.7
C2	C3	C4	120.0 (5)	121.5
C3	C4	C5	120.0 (5)	119.2
C3	C4	C15	122.1 (6)	120.9
C5	C4	C15	117.9 (8)	119.9
C4	C5	C6	120.0 (8)	120.4
C5	C6	C7	120.4 (7)	121.2
C2	C7	C6	119.8 (9)	118.8
C2	C7	C8	120.0 (5)	119.6
C6	C7	C8	120.2 (6)	121.6
C7	C8	C9	120.0 (5)	120.6
C8	C9	C10	120.0 (7)	120.1
C16	C17	C19	111.5 (9)	109.4
C16	C17	C20	107.7 (9)	109.3
C18	C17	C19	110.5 (8)	109.7
C18	C17	C20	107.3 (5)	109.6
C19	C17	C20	107.2 (4)	109.5
C1	C10	C9	120.0 (6)	121.2
C1	C11	N	126.9 (8)	125.7
C1	C11	C12	121.6 (5)	121.4
N	C11	C12	111.5 (4)	112.9
C12	O1	C13	117.0 (9)	115.0
N	O3	C14	108.5 (5)	109.2
C11	N	O3	110.8 (7)	112.6
C11	C12	O1	110.6 (7)	110.5
C11	C12	O2	126.0 (9)	125.7
O1	C12	O2	123.4 (5)	123.8
C4	C15	C16	174.8 (9)	180.5
C15	C16	C17	179.3 (6)	180.1
C16	C17	C18	112.6 (7)	109.6

2.2. Optimized geometry

Calculated geometric parameters at B3LYP/6-311G** are equally displayed into Table 1 and Table 2. From the theoretical values, it is noteworthy that most of the optimized bond lengths have slightly larger values than the corresponding experimental ones, due to the fact that theoretical calculations imply isolated molecules in gaseous phase state while experimental results refer to molecules in the solid state. Comparing theoretical bond angles with those given in experimental data, the B3LYP calculated values correlate in a good agreement. In spite of the differences, calculated geometric parameters represent a good approximation and can provide a starting point to calculate other parameters, such as vibrational wavenumbers, as will be described below.

2.3. Vibrational wavenumbers

The theoretically derived DFT vibrational wavenumbers corresponding to the optimized geometry can be expressed in the more convenient internal coordinate space for a description of the potential energy distribution (PED) via the Redong Program [11]. This algorithm uses least square methods to fit the theoretical vibrational wavenumbers to the experimental ones by introducing scaling factors associated to the various types of force constants.

Table 3 displays the potential energy distribution among internal coordinates obtained for the scaled DFT normal modes analysis (scaling factor = 0.962). This last value is currently recommended to obtain correct vibrational wavenumbers and adequate assignments of the PED [12].

The νC=N stretching mode of the imine part is generally observed in the 1665-1675 cm-1 range by Raman spectroscopy. The presence of neigbouring aryl groups lowers this value by 10-20 cm-1. Using a general scaling factor of 0.962 leads to the 1594 cm^-1 DFT theoretical wavenumber (1657 cm^-1 without scaling). This assignment is in accordance with the Raman wavenumbers as reported by Dollish et al. [13]. The imine moiety participates also to Raman bands around 1274 cm^-1, presently calculated at 1266 cm^-1. Other vibrational modes of interest implying the imine group are predicted to occur at 314 cm^-1 (δ(N-O-CH₃), at 971.6 cm^-1 (νN-O) and at 997 cm^-1 for the (νO-CH₃) stretching mode.

The alkyne νCΞC stretching mode displays intense Raman bands in the 2220-2240 cm^-1 range. The DFT corresponding wavenumber is obtained presently at 2243 cm^-1. Keeping the same 0.962 scaling factor, the δC-CΞC in plane bending mode is predicted to occur at 474.6 cm^-1, this frequency being quite comparable to the experimental range centered at 484 cm^-1[13].

The ester group gives a predicted DFT νC=O stretching mode located at 1749 cm^-1 corresponding to current experimental bands obtained in the 1730-1750 cm^-1 range. The associated νC-O stretching mode is predicted at 1215 cm^-1, this value appearing quite consistent with experimental data (1200-1220 cm^-1). The in plane δ(O-C=O) bending mode is observed in the 750-775 cm^-1 range using Raman spectroscopy and the DFT derived corresponding wavenumber is obtained here at 752 cm^-1. The δ(C-C=O) and δ(C-O-CH₃) in plane bending motions are predicted to stand at 374 and 298 cm^-1 respectively, these two wavenumbers being very close to the experimental data (300-340 cm^-1).

For the aromatic part of the molecule, we can observe a rough accordance between the DFT predicted wavenumbers (and corresponding vibrational assignments) and the experimental data obtained from vibrational analyses on benzene derivatives [14]. The pyrethoid molecule displays numerous and complex mixings of vibrational modes between the two rings and their substituents.

The ν8 degenerate (8a, 8b) mode (in Wilson’s notation) [14] implying νCA-CA ring stretching motions is generally observed around 1596 cm^-1. DFT calculations predict contributions from these two modes at 1558 and in the1582-1594 cm^-1 range.

νCA-CA and δCH modes related to the δ₁₉ degenerate mode [14] give rise to experimental vibrational bands around 1485 cm^-1. The DFT derived 1484.6 cm^-1 wavenumber corresponds correctly to such an assignment.

The mode 4 of benzene generally gives rise to weak Raman and strong IR bands. This out of plane mode (γCH) is generally observed to occur around 693 cm^-1. The DFT wavenumber obtained presently at 738 cm^-1 could correspond to this mode.

The intense νCA-CA (ν₁ in Wilson’s notation) ring stretching mode appears in Raman spectra at 992 cm^-1. This mode has been identified as being slightly dependent of δCH bending motions. Due to large mixings of vibrational motions taking place between the two rings, an attempt in the assignment of this mode from DFT calculation is given here at 971.6 cm^-1.

From DFT vibrational analyses, out of plane γCH motions display in and out of phase motions depending on the ring. These modes are predicted at 819 and 825 cm^-1. Other contributions to the out of plane motions have been also obtained theoretically at 887 and 933 cm^-1. An attempt to assign these wavenumbers to the ν5, 10a and 10b normal modes as observed for benzene derivatives [13,14,15] remains however difficult.

Table 3. Normal modes analysis of RU60358 from DFT (RB3LYP/6-31G (d, p).

**Table 3.** Normal modes analysis of RU60358 from DFT (RB3LYP/6-31G (d, p).
ν (cm^-1)*	Assignments	ν (cm^-1)*	Assignments
10.6	τ_C17C_T, τ_C1C11, δ_C4,C15,C16	702.1	ν_CACA, ν_C1C11, δ_CACACA, δ_C_T,O,_N
13.8	τ_C1C11	723.4	νs_{CT(CH3)3 (tBu)}
24.7	τ_C11C12	738.1	γ_CAH, γ_CACA, τ_CACA
30.9	δ_CA,C4,C15	749.6	γ_C12=O2, γ_C11_N, δ_C12=O2
35.4	τ_C4C15, τ_C1C2, δ_C15,C16,C17	752.2	γ_C12=O2, δ_C12=O2, δ_C12O1C_T, ν_C12O1
61.9	τ_C1C11, τ_C1CA, τ_C4C15	778.7	γ_CAH, γ_C1C11, γ_CACA
67.2	τ_N_O, γ_C11_N	819.0	γ_CAH^#, γ_CACA
98.1	τ_C14O, τ_N_O	825.3	δ_{CACACA(ring 1)}, γ_CAH^##, ν_CACA
102.4	δ_C15,C16,C17, τ_C6C7	832.4	δ_CACACA, ν_C16C17, ν_C17C_T
108.4	δ_C12,C11,N, τ_O1_C13, δ_C1,C11,C12	873.0	γ_C3H, τ_CACA
112.8	τ_O1C13	887.1	γ_{CAH(ring 1)}
129.4	δ_C4,C15,C16, τ_O1C12	897.4	ν_O3N, ν_O3C_T, ν_O1C12, ν_O1C_T,ν_C17C_T
158.9	τ_C2C7, τ_C2C3, τ_C7C8	897.8	ν_C17C_T, ρ_(tBu)
163.6	τ_O1_C12, τ_O3_C14, τ_O_N	899.7	ν_C17C_T
173.9	τ_O_N, δ_C4,C15,C16, τ_O3C14	926.0	ν_C17C_T, ν_N_O3, ν_C4CA, δ_CACACA
185.2	τ_C6C7, τ_C1C2, τ_C4C15	933.0	γ_{CAH( all rings)}
218.6	ν_C4C15, ν_C16C17, δ_C3,C4,C5	933.8	ρ_(tBu)
221.9	τ_{C17CH3 (tBu)}	942.9	γ_{CAH(all rings)}
246.0	δ_C12,O1,C13, δ_O1,C12,C11, τ_C4C15	971.6	ν_O3_N, ν_CACA, δ_CACACA, δ_CAH, δ_C11,_N,O3
269.5	τ_C17CH3_(tBu)	996.9	ν_C_TO1, ν_O3CT
276.5	τ_C17CH3_(tBu)	1013.9	ρ_(tBu)
279.4	δ_C12,O1,C13, ν_C1C11, δ_C1,C11,C12	1014.1	ρ_(tBu)
297.8	τ_C11_N, δ_C12,O1,C13, τ_O1C12	1045.1	ν_CACA, ν_O3CT, ν_O3_N
314.3	δ_C14,O,_N, ν_C1C11, τ_C11_N, δ_CACACA	1060.2	ν_O3CT, ν_CACA, ν_O3_N
332.4	δ_C_T,C17,C_T_(tBu)	1095.2	ν_C12O1, ν_C_TO1, δ_C11,_N,O3, ν_O3CT
336.7	δ_C_T,C17,C_T_(tBu)	1130.9	ρ_C14H3
357.3	δ_C_T,C17,C_T_(tBu), δ_C1,C2,C3, δ_C6,C7,C8	1133.8	ρ_C13H3
367.4	ν_C11C12, δ_C11,_N,O, δ_C12,C11,_N	1134.5	δ_CAH, ν_{CACA(ring 2)}
373.6	δ_C11,C12,O2, δ_C12,O1,C13	1148.6	δ_CAH, ν_{CACA(ring 1)}
387.9	τ_C4C15, τ_C4CA, γ_C6C7	1163.1	ρ_C13H3
424.2	δ_C_T,C17,C_T_(tBu)	1172.1	ρ_C14H3
425.2	τ_CACA, γ_CAH	1181.6	ρ_(tBu)
474.6	δ_C4,C15,C16, δ_C16,C17,C_T, γ_C-_N	1183.4	ρ_(tBu)
501.5	δ_C16,C17,C_T, δ_CA,C4,C15, δ_CACACA	1184.8	ν_O1C12, ρ_C14H3, ν_C4C15, ρ_C13H3, ρ_(tBu)
512.7	δ_C16,C17,C_T, δ_C15,C16,C17, τ_CACA	1196.4	ν_CACA, δ_CAH
528.1	γ_CACA, τ_CACA, γ_C1C11, δ_C_14,O3,_N	1215.3	δ_CAH, ν_O1C12
545.3	τ_C4C15, δ_C15,C16,C17, δ_C16,C17,C_T,τ_CACA, γ_C4C15	1241.2	δ_CAH_{(ring 2)}
550.4	δ_C4,C15,C16, δ_C16,C17,CT	1266.0	ν_C11C12, ν_C1C11, ν_O1C12, δ_{CAH(ring 1)}
583.3	τ_C11_N, ν_C16C17, δ_CA,C1,C11, γ_C11_N, γ_C12=O2	1270.9	ν_C16C17, ν_C4C15, δ_{CAH(ring 1)}
590.2	γ_C11_N, τ_C11C12, γ_C12=O2, g _C4C15	1303.8	ν_CACA, δ_CAH
616.1	δ_CACACA, δ_C_T,O,_N, ν_C17C_T	1352.3	ν_CACA
652.7	γ_C4C15, γ_C1C11, τ_CACA, γ_CAH	1353.7	ds_CH3_(tBu)
1354.4	ds_CH3_(tBu)	2243.4	ν_C15C16
1364.7	ν_CACA, δ_CAH	2925.2	ν_{sCH3 (tBu)}
1384.7	δ_sCH3_(tBu)	2925.8	ν_sCH3_(tBu)
1416.2	δ_sC14H3	2931.6	ν_sC14H3
1421.4	δ_sC13H3	2931.8	ν_sC14H3, ns_CH3_(tBu)
1423.3	δ_sC13H3	2947.1	ν_sC13H3
1433.6	δ_aCH3_(tBu)	2996.8	ν_aCH3_(tBu)
1434.7	δ_aC14H3	2997.4	ν_aCH3_(tBu)
1436.2	ν_CACA, δ_CAH	3002.5	ν_{aCH3 (tBu)}
1437.8	δ_aC13H3	3006.2	ν_aC14H3
1443.9	δ_{aCH3 (tBu)}	3006.8	ν_aCH3_(tBu)
1444.4	δ_aCH3_(tBu)	3010.2	ν_aCH3_(tBu)
1451.5	δ_aC13H3	3010.9	ν_aCH3_(tBu)
1456.3	δ_aCH3_(tBu)	3020.7	ν_aC13H3
1456.8	δ_aCH3_(tBu)	3041.2	ν_aC14H3
1457.4	δ_aC14H3	3054.8	ν_aC13H3
1474.6	δ_aCH3_(tBu)	3056.3	ν_{CAH(all rings)}
1484.6	ν_CACA, δ_CAH	3059.4	ν_{CAH(all rings)}
1557.7	ν_CACA, δ_CAH	3068.8	ν_{CAH(ring 1)}
1582.1	ν_C11_N, ν_CACA	3083.6	ν_{CAH(ring 1)}
1593.9	ν_C11_N, ν_CACA	3087.9	ν_{CAH(ring 2)}
1609.1	ν_CACA	3096.9	ν_{CAH(ring 2)}
1749.0	ν_C12=O2

(tBu) : Tertiobutyl group. ring 1 is defined by atoms C₁, C₂, C₇, C₈, C₉ and C₁₀. ring 2 is defined by atoms C₂, C₃, C₄, C₅, C₆ and C₇^#CA-H out of plane bending (in phase in each ring but out of phase between rings)^##CA-H out of plane bending in phase for both rings. ν : stretching modes (νs : symmetric, νa : antisymmetric)δ : in plane valence angle bending, (δs : symmetric, δa : antisymmetric). τ, γ, ρ : torsion, out of plane wagging and rocking deformations respectively(*scaled vibrational frequencies originate from application of a general scaling factor (0.962) applied to all types of internal force constants).

3. Experimental Section

3.1 X-ray structure determination

A needle-shaped crystal of dimensions 0.32 ´ 0.27 ´ 0.10 mm was mounted on a Philips Enraf Nonius four-circle diffractometer. Data were collected with MoKa radiation. Intensities for 3082 reflections were measured by the w/2q scan method, scan width = 1.4°, scan speed 0.02°s-1 and 0 < h < 10, 0 < l < 15, 0 < k < 30. Lattice parameters from 25 reflections (2 < q < 30). Three standard reflections monitored every two hours, no significant variation was observed. The data were corrected for Lorentz and Polarization effects, but not for absorption or extinction. The structure was determined by considering 1583 reflections with I ≥ 3σ(I).

The structure was solved by direct methods implemented in Shelxs [16]. A Fourier synthesis revealed the complete structure, which was refined by full-matrix least squares. All non-H atoms refined anisotropically. The H atoms were located from a difference Fourier map and included in the refinement with the isotropic temperature factor of the carrier atom. Fig. 1 shows the atomic numbering of the molecule.

The final least-squares cycle using Shelxl [17] gave R = 0.068 for all reflections with I ≥ 3σ(I), wR = 6.8%, S = 1.25, w =1. (Δρ)_min= -0.271 eÅ^-3 , (Δρ)_max = 0.380 eÅ^-3.

Atomic scattering factors for heavy atoms were taken from International Tables for X-ray Crystallography [18] while the factors for H were those of Stewart, Davidson & Simpson [19]. A summary of the key crystallographic information is given in Table 4.

Crystallographic data has been deposited with the Cambridge Crystallographic Data Centre with the deposition number CCDC 272 478. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.

3.2. Computational methods

Molecular modeling, geometry optimizations, harmonic wavenumbers for the normal modes of vibration and force field in cartesian coordinates were calculated on RU60358 using the Density Functional Theory and the B3LYP [20,21] (Becke’s three parameter Hybrid Functional using the LYP correlation Functional) functional together with the 6-31G(d,p) basis set. Such combination is being used with good results for organic molecules [22] and hydrogen-bonded systems [23,24,25], and represents a good compromise between economy of computational resources, accuracy and applicability to many-atoms molecules. All the calculations were made with the Gaussian 03 set of programs [26]. Ab initio geometry optimization on RU60358 was performed starting from the geometry found in the X-ray refinement.

Table 4. Crystallographic data and experimental details for C₂₀H₂₁NO₃

**Table 4.** Crystallographic data and experimental details for C₂₀H₂₁NO₃
Crystal data
Formula	C₂₀H₂₁NO₃
Molecular weight	323.34
Crystal system	Orthorhombic
Space group	P2₁2₁2₁
Unit cell determination	Least-squares fit from 25 reflections (2° < q < 30°)
a (Å)	7.7575
b (Å)	11.3182
c (Å)	21.3529
V (Å³)	1874.80
Z	4
d_calc(g. cm^-3)	1.16
mu (mm^-1)	0.077
Crystal colour	Colourless
Crystal size	0.32 ´ 0.27 ´ 0.10 ( mm)
Experimental data
Technique	Four circles diffractometer, CAD4 Enraf Nonius kappa geometry
	Graphite oriented monochromator : Moka
	λ = 0.71070 Å, ω/2q scan
Scanning range for θ	2.04 ¾ 29.96
Number of reflections measured	3082
Number of reflections observed	1583 (I ≥ 3σ(I)criterion)
Limiting indices	h 0 ® 10
	k 0 ® 15
	l 0 ® 30
T (K)	293
Refinement data
Refinement method	Full-matrix least-squares on F
Final R indices	R=0.068, wR=0.068
S	1.249
H atoms	constrained refinement
Parameters	224
(Δ/σ)_max	0.380
(Δρ)_min	-0.271 eÅ^-3
(Δρ)_max	0.380 eÅ^-3
Extinction	No extinction correction applied

References

Baert, F.; Guelzim, A. X-ray Structure of the Pyrethroid Insecticide { 1R-[1 α(S*),2α] }-2-(2,2-Dichlorovinyl)-3,3-dimethylcyclopropanecarboxylic Acid Cyano(3-phenoxyphenyl)methyl Ester (RU 24501). Acta Cryst. C 1991, 47, 606–608. [Google Scholar] [CrossRef]
Baert, F.; Guelzim, A.; Germain, G. Structure of Two Pyrethroid Insecticides: Acrynathryn (RU 38702) and a Derivative (RU 38181). Acta Cryst. C 1991, 47, 768–771. [Google Scholar] [CrossRef]
Hamzaoui, F.; Lamiot, J.; Baert, F. X-ray Structure of a New Pyrethroid RU 52259. Acta Cryst. C 1993, 49, 818–820. [Google Scholar] [CrossRef]
Hamzaoui, F.; Baert, F. A New Pyrethroid Insecticide RU41414. Acta Cryst. C 1996, 52, 689–690. [Google Scholar] [CrossRef]
Tessier, J. Recent Advances in the Chemistry of Insect Control; Janes, N.F., Ed.; The Royal Society of Chemistry: London, 1985; pp. 26–52. [Google Scholar]
Tessier, J.; Teche, A.; Demoute, J. P. Pesticide Chemistry: Human Welfare and the Environment; Miyamoto, J., Kearney, P.C., Eds.; Pergamon Press: Oxford, New York, 1983; Vol. 1, pp. 95–100. [Google Scholar]
Tessier, J.; Teche, A.; Demoute, J. P. Proceedings of the 5^th IUPAC International Congress of Pesticide Chemistry; Miyamoto, J., Kearney, P.C., Eds.; Pergamon Press: Oxford, New York, 1983; pp. 197–202.
Babin, D.; Demassey, J.; Demoute, J. P.; Dutheil, P.; Terrie, I.; Tessier, J. A New Way toward Zα,β Unsaturated Esters: A Pyrethroid Application. J. Org. Chem. 1992, 57, 584–589. [Google Scholar] [CrossRef]
Elliott, M. The Relationship between the Structure and the Activity of Pyrethroids. Bull. Wld Hlth Org. 1970, 44, 315–324. [Google Scholar]
Elliott, M.; Farnham, A. W.; Janes, N. F.; Needham, P. H.; Pulman, D. A. Insecticidal Activity of the Pyrethrins and Related Compounds. Pestic. Sci. 1975, 6, 537–542. [Google Scholar] [CrossRef]
Allouche, A.; Pourcin, J. Ab initio calculation of vibrational force fields: Determination of non-redundant symmetry coordinates by least-square component analysis. Spectrochim. Acta, Part A 1993, 49, 571–580. [Google Scholar] [CrossRef]
Pulay, P. Possibilities and limitations of ab initio calculation of vibrational spectra. J. Mol. Struct. 1995, 347, 293–308. [Google Scholar] [CrossRef]
Dollish, F. R.; Fateley, W. G.; Bentley, F. F. Characteristic Raman Frequencies of Organic Compounds; John Wiley& Sons: New York, 1974. [Google Scholar]
Varsányi, G.; Szöke, S. Vibrational Spectra of Benzene Derivatives; Academic Press: New York, 1969. [Google Scholar]
Wilson, E. B., Jr. The Normal Modes and Frequencies of Vibration of the Regular Plane Hexagon Model of the Benzene Molecule. Phys. Rev. 1934, 45, 706–714. [Google Scholar] [CrossRef]
Sheldrick, G.M. SHELXS97: Program for crystal structure determination; University of Göttingen: Germany, 1997. [Google Scholar]
Sheldrick, G. M. SHELXL97: Program for crystal structure determination; University of Göttingen: Germany, 1997. [Google Scholar]
Brown, P. J.; Fox, A. G.; Maslen, E. N.; O'Keefe, M. A.; Willis, B. T. M. International Tables for X-ray Crystallography; Wilson, A. J.C., Prince, E., Eds.; Kluwer Academic Publishers: Dordrecht, 1999; Vol. C, pp. 548–589. [Google Scholar]
Stewart, R. F.; Davidson, E. R.; Simpson, W. T. Coherent X-Ray Scattering for the Hydrogen Atom in the Hydrogen Molecule. J. Chem. Phys. 1965, 42, 3175–3187. [Google Scholar] [CrossRef]
Becke, A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
Lee, C.; Yang, W.; Parr, R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar]
Rauhut, G.; Pulay, P. Transferable scaling factors for density functional derived vibrational force fields. J. Phys. Chem. 1995, 99, 3093–3100. [Google Scholar] [CrossRef]
Gómez Marigliano, A. C.; Varetti, E. L. Self-Association of Formamide in Carbon Tetrachloride Solutions: An Experimental and Quantum Chemistry Vibrational and Thermodynamic Study. J. Phys. Chem. A 2002, 106, 1100–1106. [Google Scholar] [CrossRef]
Gómez Marigliano, A.C.; Varetti, E.L. Unpublished results.
Sim, F.; St.-Amant, A.; Papai, I.; Salahub, D. R. Gaussian density functional calculations on hydrogen-bonded systems. J. Am. Chem. Soc. 1992, 114, 4391–4400. [Google Scholar] [CrossRef]
Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, J. A., Jr.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C.; Pople, J. A. Gaussian 03, Revision A.1. Gaussian, Inc.: Pittsburgh PA, 2003. [Google Scholar]