Design and Evaluation of Cell Interaction Based Vedic Multiplier Using Quantum-Dot Cellular Automata

Abstract

A multiplier is one of the main units for digital signal processing and communication systems. In this paper, a high speed and low complexity multiplier is designed on the basis of quantum-dot cellular automata (QCA), which is considered promising nanotechnology. We focus on Vedic multiplier architectures according to Vedic mathematics from ancient Indian sculptures. In fact, an adder is an important block in the design of almost all types of multipliers and a ripple carry adder is used to design simple multiplier implementations. However, a high-speed multi-bit multiplier requires high-speed adder owing to carry propagation. Cell-interaction-based QCA adders have better improvements over conventional majority-gate-based adders. Therefore, a two-bit Vedic multiplier is proposed in QCA and it is used to implement a four-bit form of the multiplier. The proposed architecture has a lower cell count and area compared to other existing structures. Moreover, simulation results demonstrate that the proposed design is sustainable and can be used to realize complex circuit designs for QCA communication networks.

1. Introduction

High energy consumption is one of the major limitations for transistor-based complementary metal-oxide-semiconductor (CMOS) technology. This limitation cannot be solved completely by scaling down the size of the transistor. Quantum-dot cellular automata (QCA) [1], a type of self-reproduction cellular automata [2,3,4], is one remarkable nanotechnology that can be a possible solution to solve this problem. The energy efficiency and high-speed switching features of this technology is great motivation for developing this paradigm [5,6,7,8,9].

In this technology, logical states can be represented by two antipodal polarization levels in a QCA cell configuration. The square-shaped cell includes a pair of electrons with four quantum dots. QCA offers a new computation method and is based on the fundamental principle of quantum confinement [10,11,12].

There are some challenges for the physical implementation of a QCA cell at room temperature. In previous experiments, the cells were found to operate only at cryogenic temperatures. Recently, the fabrication of a QCA cell using the nano-damascene process has been successful [13]. This potentially enables the room temperature operation of QCA-based circuits.

Array multipliers have been extensively investigated in QCA technology. However, there are also mathematical operations using the Vedic method that are very fast and require less hardware architecture. This can be used to improve the computational speed of processors. A huge number of adders are used to perform partial product addition for higher order multiplications. This method of multiplication is based on 16 Vedic sutras and describes the natural ways of solving a whole series of mathematical problems [14,15,16].

In this paper, a new design for a two-bit multiplier using QCA technology is presented. We also propose a half adder for the implementation of a Vedic multiplier. It is implemented using a cell-interaction-based exclusive-OR (XOR) structure [17]. Meanwhile, the energy dissipation of the proposed half adder is also analyzed. The proposed half adder plays an important role in the implementation of the two-bit Vedic multiplier design. On the basis of this two-bit multiplier, a four-bit Vedic multiplier design is proposed. Simulations and a comparison with prior designs are conducted with the simulation tool QCADesigner 2.0.3 and QCAPro. The proposed designs have a lower cell count, smaller area, lower latency, and smaller energy consumption features in comparison.

This paper is organized as follows. Section 2 introduces the basic concepts of QCA. In Section 3, the proposed designs, 2 × 2 and 4 × 4 Vedic multipliers are presented with their implementations in QCA. The simulations and comparison are discussed in Section 4, with a brief explanation of the analysis. Finally, Section 5 concludes the paper.

2. Related Works

2.1. Basic QCA

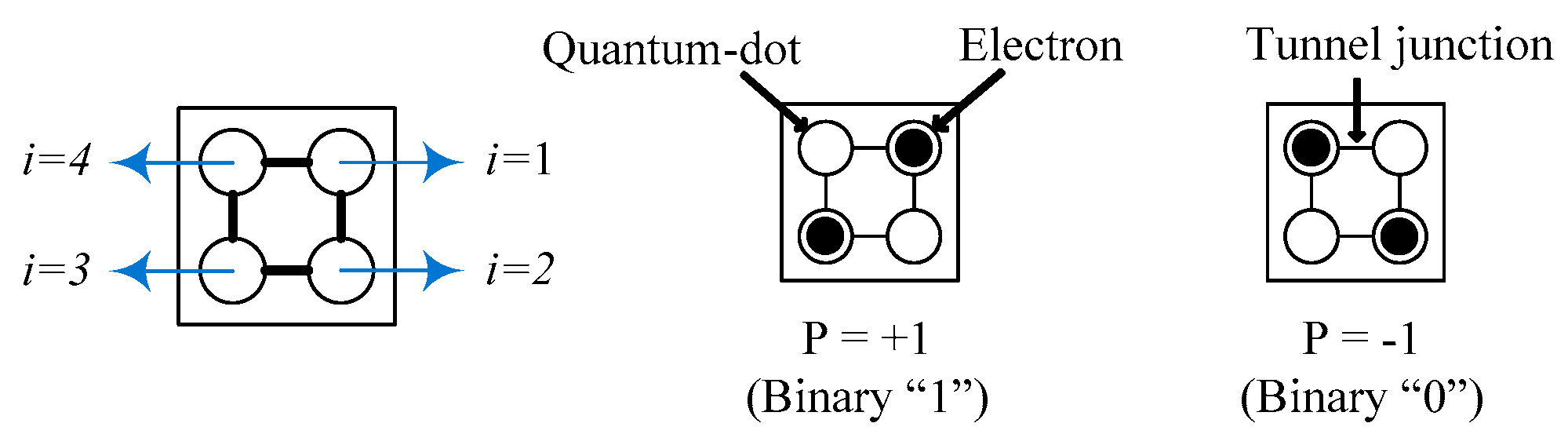
The basic element of QCA is a cell that holds quantum dots and two excess electrons. The positions of the electrons in a cell are a logical state. The cell has a square-shaped nanostructure that contains four quantum dots and two electrons, as shown in Figure 1. The electrons can move through a tunnel junction owing to their Coulombic repulsion. The existing Coulombic interaction between the electrons forces them to occupy positions at opposite corners of the cell by the concept of polarization. As a result, two stable states (binary zero and one) are represented in the cell [18,19,20]. Polarization, P, is determined by one of two diagonals depending on the distribution of charges, and the value is measured [18]. If the cell specifies ρ_i as the electron density of the i-th point for the four points i = 1 to 4 clockwise from the top right, then P is defined as follows.

P = ((ρ₁ + ρ₃) − (ρ₂ + ρ₄))/(ρ₁ + ρ₂ + ρ₃ + ρ₄)

(1)

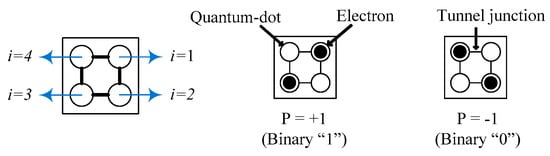
Figure 1. QCA cell with two possible polarizations.

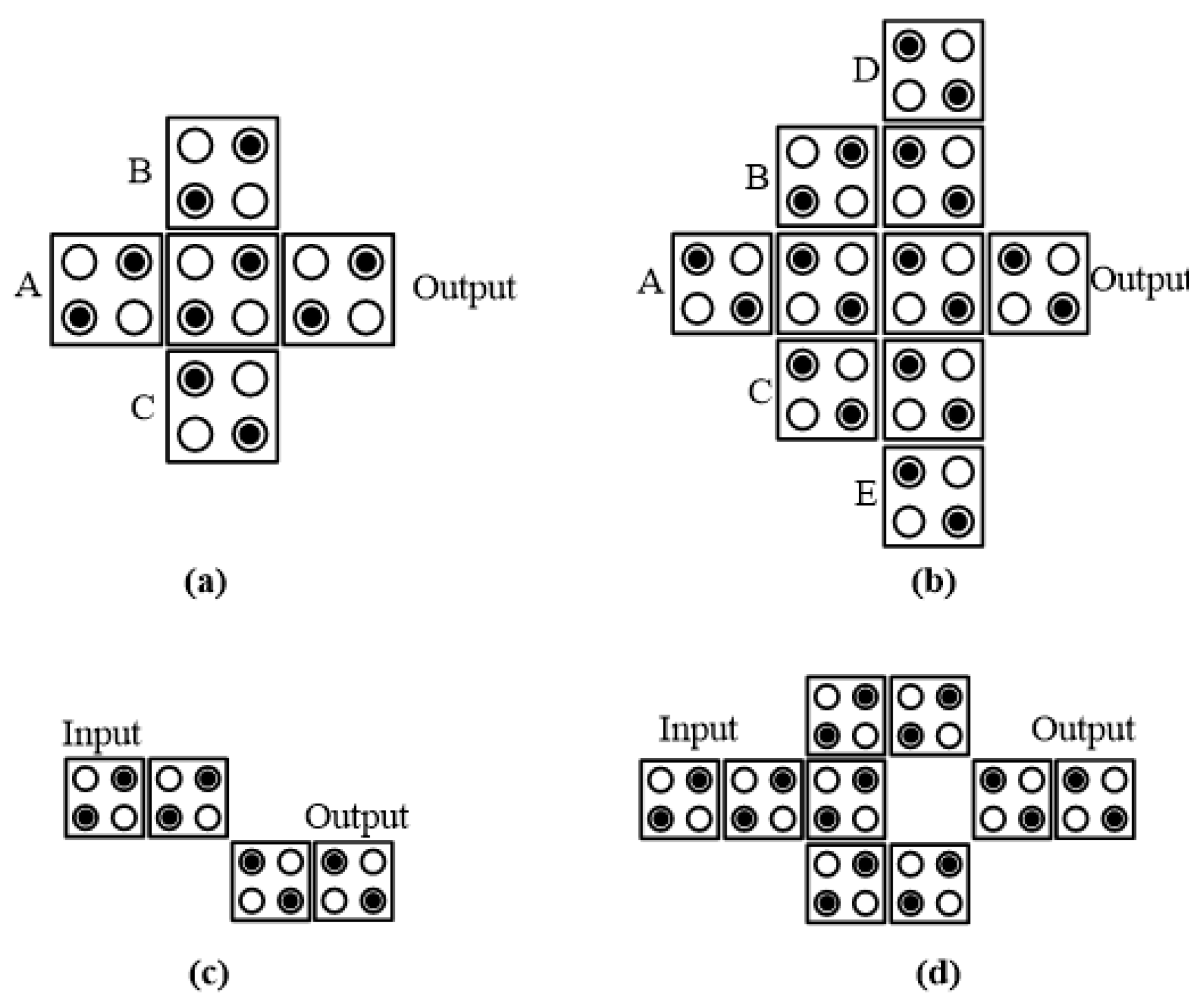
The binary information is propagated by the neighboring cell interaction along a line of QCA cells owing to the high nonlinearity. This is called a QCA standard wire as shown in Figure 2a. Coulombic interaction acts not only on one cell, but also on neighboring cells, making it easy to make QCA wires by sequentially arranging cells. Therefore, information is transmitted without current flow. In this technology, the basic logic components, an inverter and a majority gate, can be implemented on the basis of the mutual interaction between cells. The majority gate can be three- and five-input majority gates. The three-input majority gate is defined as follows.

M(A,B,C) = AB + BC + AC

(2)

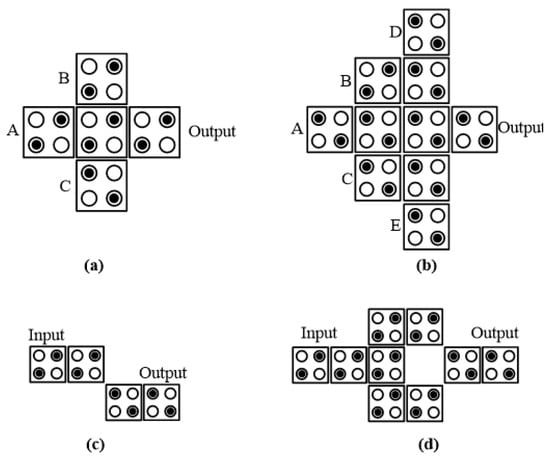
Figure 2. Quantum-dot cellular automata (QCA) basics: (a) wire; (b) three-input majority gate; (c) five-input majority gate; (d) simple inverter; and (d) robust inverter.

As shown in Figure 2b, the three-input majority gate is composed of five cells, and logical two-input AND and OR can be implemented using this majority gate, by setting one arbitrary input cell to binary “0” and “1”, respectively as follows.

M(A,B,0) = AB
M(A,B,1) = A + B

(3)

As an innovative structure, the five-input majority gate consists of 10 cells, and designs based on this majority gate are efficient in terms of the area compared to traditional ones [21]. It can be a multi-functional structure and expressed as follows and shown in Figure 2c.

M(A,B,C,D,E) = ABC + ABD + ABE + ACD + ACE + ADE + BCD + BCE + BDE + CDE

(4)

Two types of inversion operation are actualized by placing the cells diagonally, as illustrated in Figure 2d,e. In Figure 2, the red long two-way arrows indicate the parts where Coulombic repulsion was applied well, and the blue short two arrows indicate the parts that were not applied due to the surrounding repulsive forces.

2.2. QCA Clocking

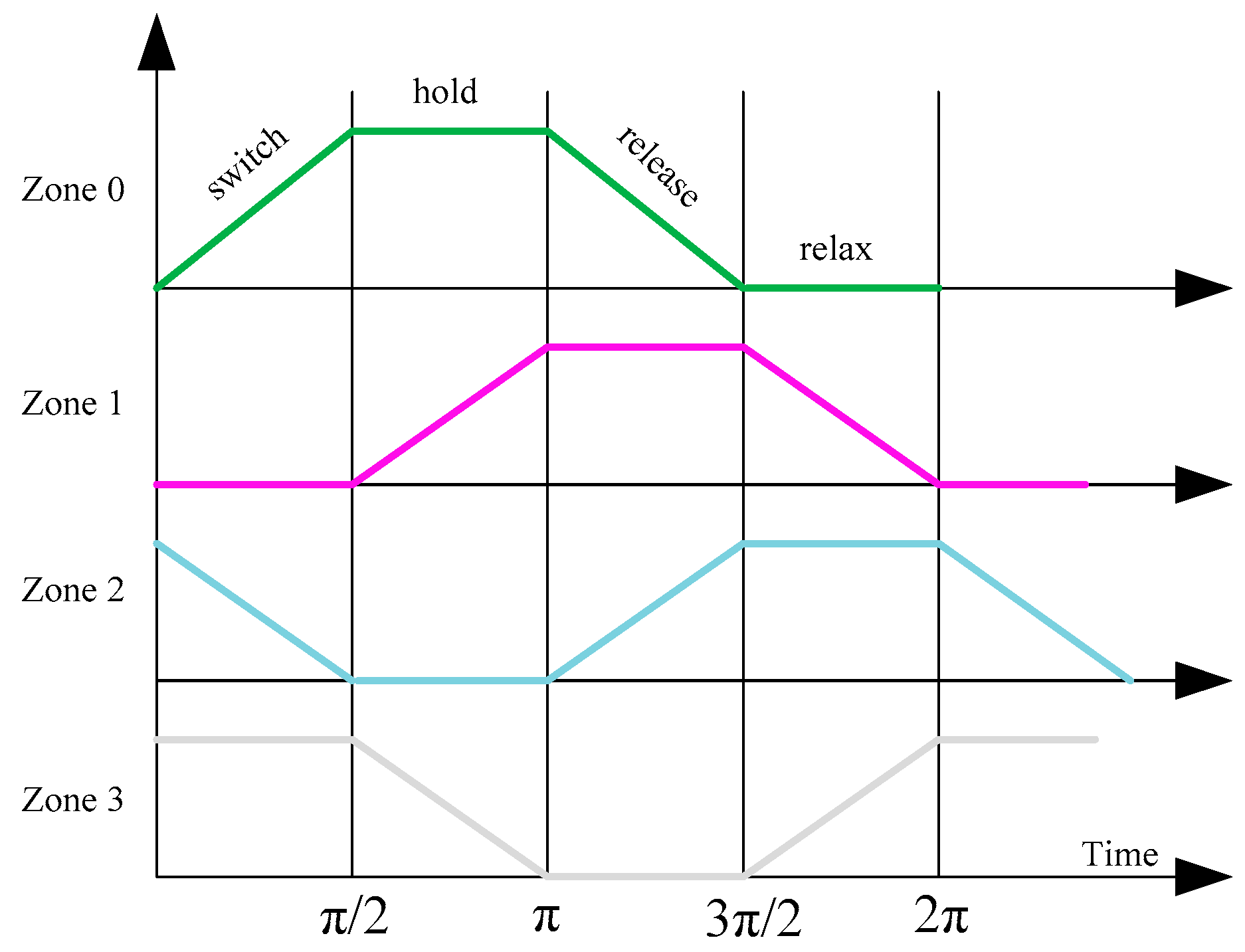
The QCA frequency plays a crucial role in signal energy recovery and solving the thermodynamic problem in large-scale QCA circuits based on four clearly defined and π/2 interval clock pulses, as shown in Figure 3. The clock is used as an inter-dot barrier controller.

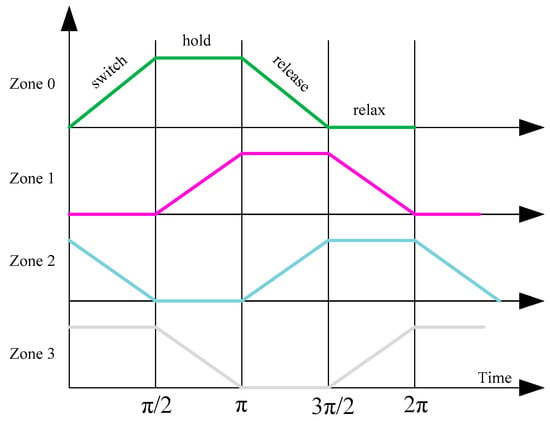
Figure 3. Four distinct QCA clock stages.

In each QCA clock zone, there are four synchronization phases: Switch, hold, release, and relax. When the inter-dot barrier is high, the cells are held in the hold phase, and when the barrier is low, the cells remain in the relax phases. When the inter-dot barrier is changed, e.g., from low to high or from high to low, the cells are stored in the switch or release phase, respectively. A signal transition occurs during the switching phase. QCA synchronization also serves as an energy source [22,23,24].

2.3. Wire Crossing in QCA

Four types of implementations can be used for the physical fabrication of QCA, such as metal-dot, semiconductor, molecular, and magnetic QCA implementations. If material production can be efficiently addressed, the next practical problem for a QCA circuit is its operating temperature (7K). This temperature is considered to be extremely low, and a QCA circuit needs to be optimized for room-temperature operation [25].

Cross-over technology is also considered as one of the problems in QCA technology. According to this concept, there are three types of cross methods: Coplanar, multi-layered, and logical crossover. The coplanar intersection of a wire is carried out using an inverter chain. The inverter chain represents a line of rotating (45˚) cells. A multi-layered crossover is a stereoscopic structure, which is built of several layers. The logical intersection of the wires is updated on the basis of QCA synchronization; namely, the cells in the switch and hold phases can cross cells in the release and relax phases, respectively [26,27,28]. The logical method of crossing wires is more reliable and tolerant than other crossover methods in the modelling process.

3. The Proposed Structures

3.1. Half Adder for the Multiplier

As mentioned, most half-adder designs in QCA are equation-based structures, namely, a combination of inverter and majority gates. It is also possible to implement a QCA half adder using an XOR gate. Several QCA XOR designs have been proposed [17,29,30].

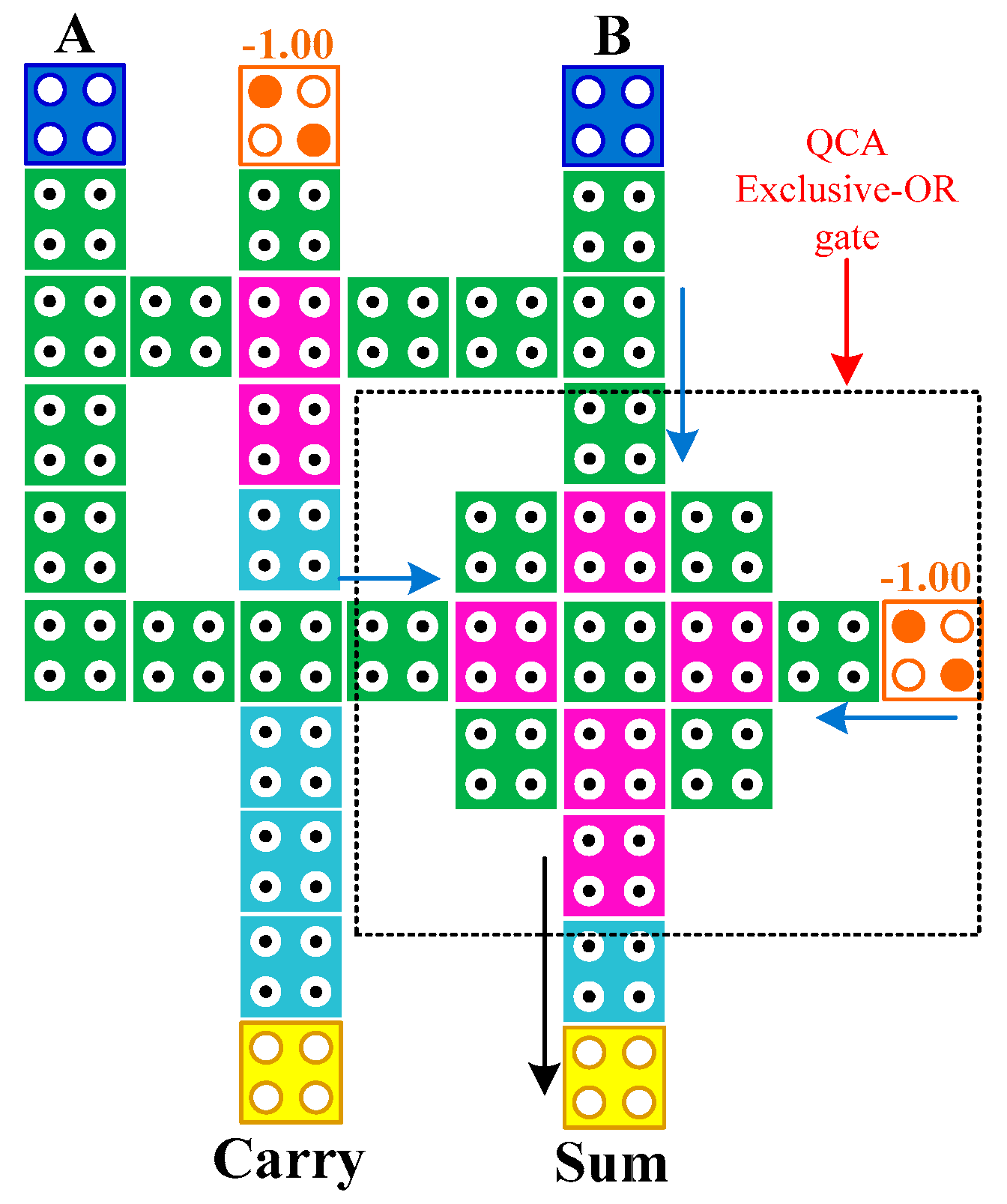
We use cell-interaction-based XOR [17]. The QCA design of the proposed half adder is presented in Figure 4. The proposed structure consists of one XOR gate and one three-input majority gate with two fixed cells to a value of zero which are drawn in orange color. Consequently, the proposed half adder is also considered as a structure based on cell interaction.

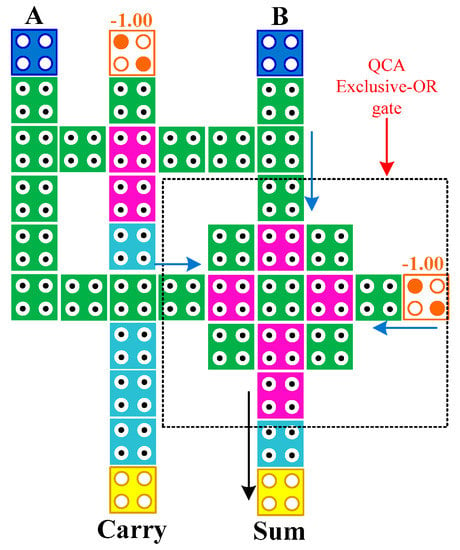
Figure 4. The proposed half adder.

The design is composed of 39 cells and the output is generated after three clock phases. The truth table of the half adder is summarized in Table 1, and it is defined as follows:

Sum = A⨁B
Carry out = M(A,B,0)

(5)

Table 1. Truth table of half adder.

Input		Output
A	B	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

3.2. The 2 × 2 Bit Vedic Multiplier

This section focuses on a method of Vedic multiplication called, Urdhva-Tiryakbhyam (UT)—vertically and crosswise, which can be used for both decimal and binary multiplication [14,15,16]. This method is an algorithm that can be used to multiply the number N × N. The Vedic multiplier does not depend on the processor’s clock frequency since the sums and their partial products are calculated in parallel. This means that it is possible to reduce the energy dissipation using a Vedic multiplier and increase the speed of multiplication.

The multiplication of ax + b and cx + d in Vedic mathematics is based on the UT sutra exactly; the resulting expression is derived as acx² + (ad + bc)x + bd. The principles of the UT sutra are as follows:

• The coefficient of x² indicates the vertical multiplication of a and c.
• The coefficient of x expresses cross-wise multiplication of a with d and b with c, along with the addition of both outputs.
• The constant is the vertical multiplication of b and d.

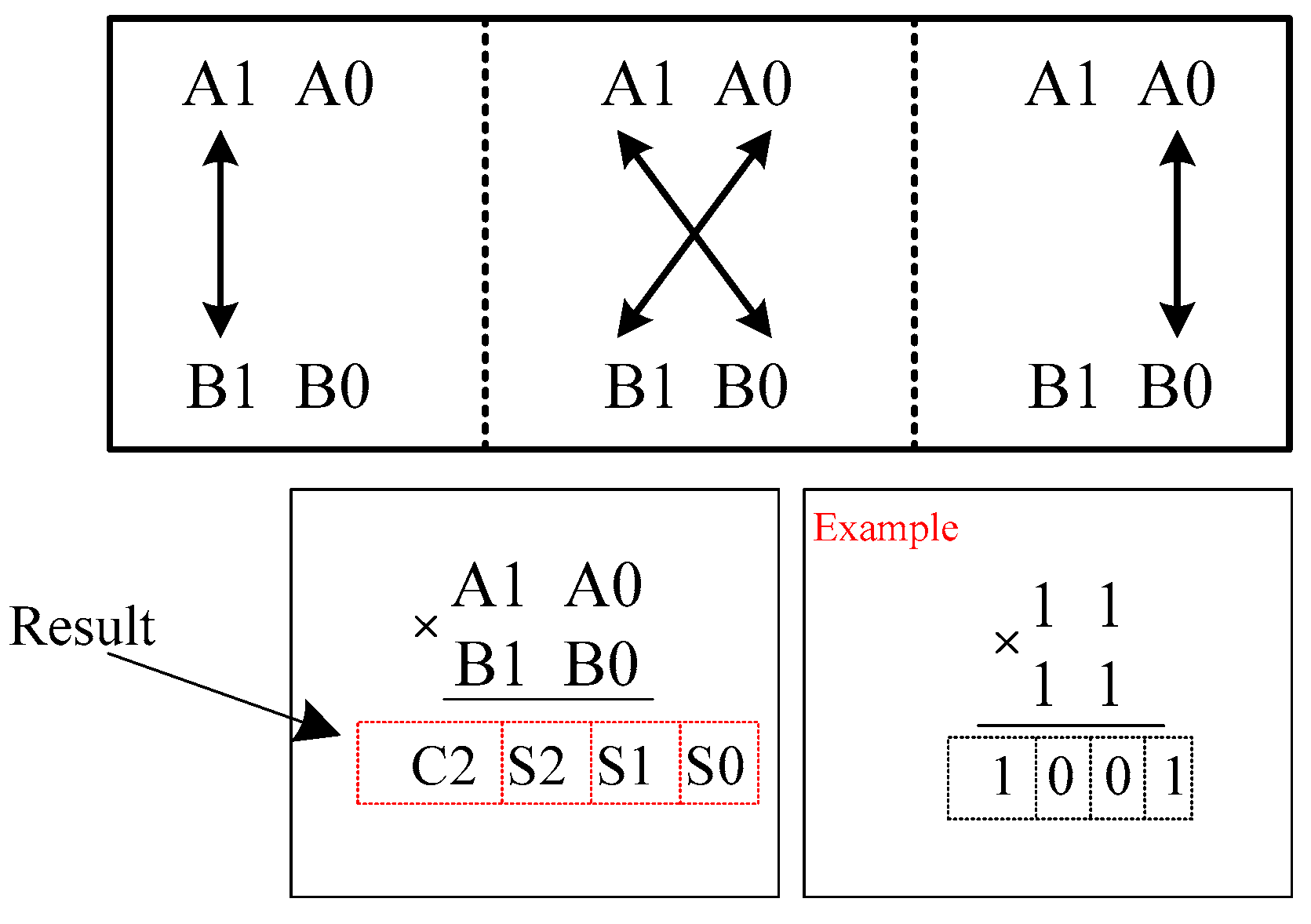
It is easy to explain the algorithm by multiplying 2 × 2 bits. The two-bit binary numbers A = [A₁A₀] and B = [B₁B₀] are obtained, as shown in Figure 5. First, the least significant bit (LSB) of the first binary code ‘A’, namely (A₀), is multiplied by the LBS ‘B’, namely (B₀). The generated product (A₀B₀) is stored for the next as the LSB of final result. Table 2 is for the simulation of 2 × 2 Vedic multiplier.

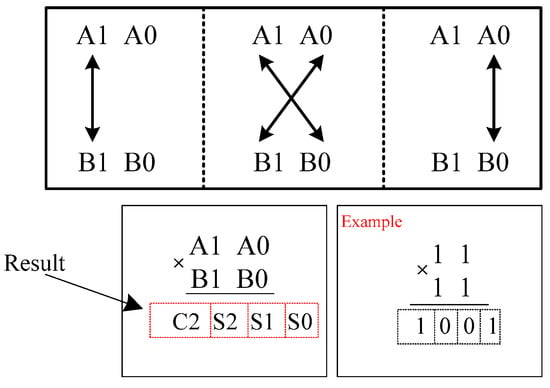
Figure 5. Multiplication steps of 4 × 4 Vedic multiplier.

Table 2. Operation of the 2 × 2 Vedic multiplier.

A1	A0	B1	B0	Output
1	1	1	1	1001
1	1	0	1	0011
1	0	0	1	0010
0	1	0	1	0001

The multiplication of A₀ and B₀ requires one AND gate. The first step is the crosswise multiplication of the numbers A and B, and this requires two AND gates. The second step is actualized as follows: The LSB of the number A is multiplied with the most significant bit (MSB) of the number B, namely (A₀ × B₁), and at the same time the MSB of the number A is multiplied with the LSB of the number B, namely (A₁ × B₀). These generated products are added [(A₀ × B₁) + (A₁ × B₀)] using a half adder. The generated two-bit result [C₁S₁] from the first half adder is considered as that (S₁) for the second bit of the final product, and (C₁) is saved as a pre-carry for the next step. In the last step, the MSB of the number A (A₁) is multiplied with the MSB of the number B(B₁) and the result (A₁ × B₁) is added to the pre-carry (C₁) via a second half adder. The two-bit result [C₂S₂] is obtained from the second half adder; namely (S₂) and (C₂) are the third and fourth bits, respectively, of the final product. Finally, the four-bit number [C₂S₂S₁S₀] is formed as an output. The block diagram of the 2 × 2 bit Vedic multiplier is shown in Figure 6 and the definition is as follows:

S₀ = A₀B₀
C₁S₁ = A₁B₀ + A₀B₁
C₂S₂ = C₁ + A₁B₁

(6)

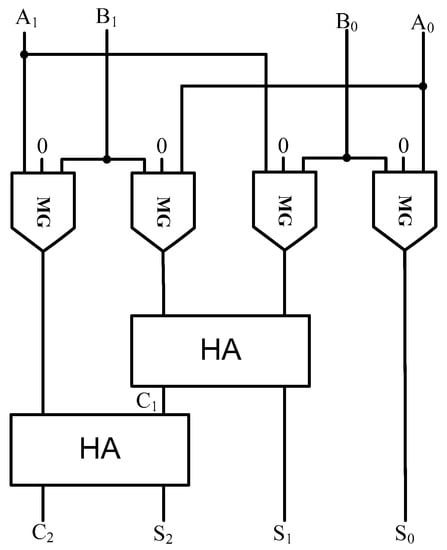
Figure 6. The method of the two-bit Vedic multiplier.

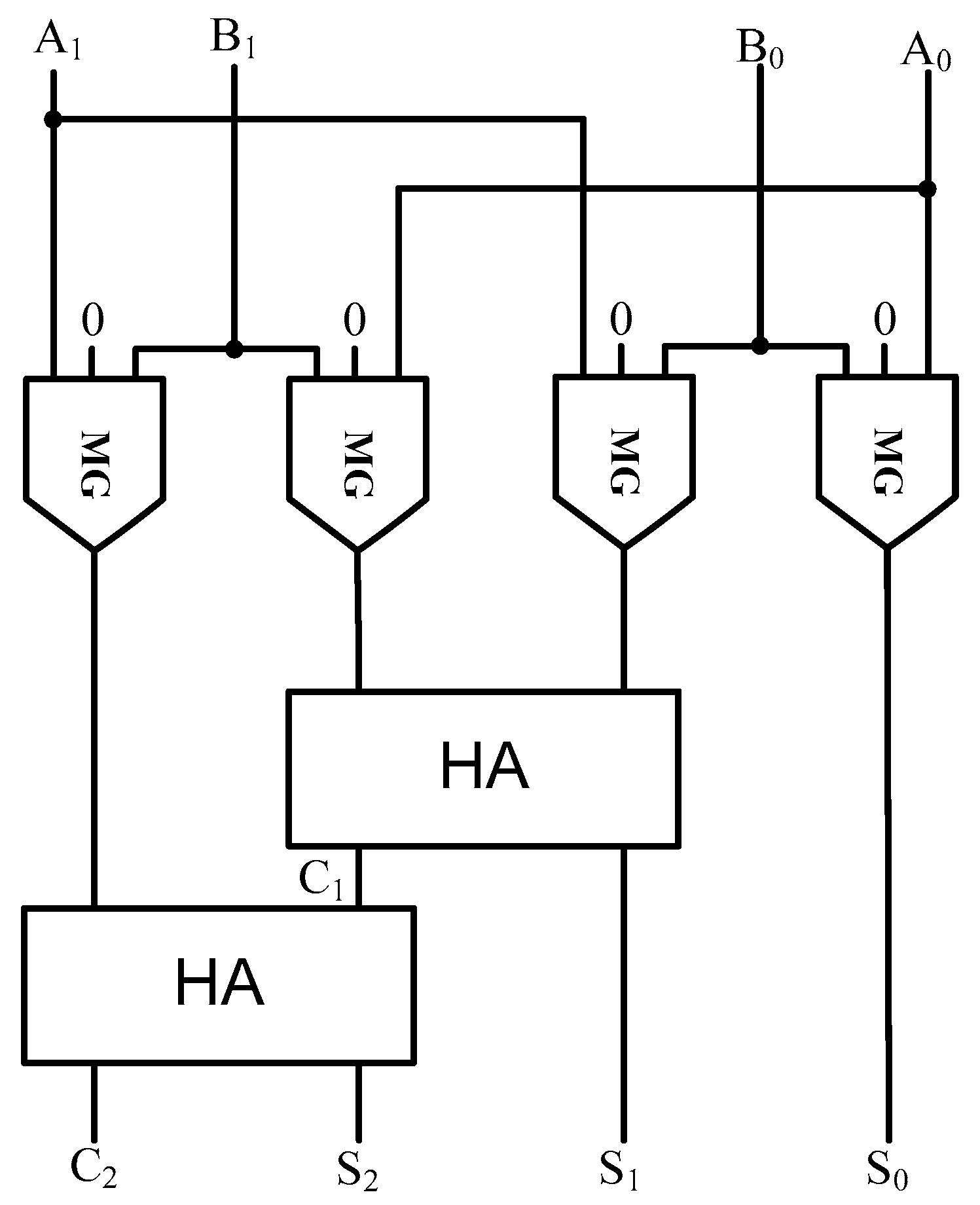
The 2 × 2 bit Vedic multiplier has been designed in QCA on the basis of the block diagram in Figure 7. Logical wire-crossing is extensively used to cross the wires, as illustrated in Figure 8. There is a total of two half adders and four AND gates in the proposed structure. As mentioned in the previous section, the half adder is designed as a low complexity structure. Hence, the proposed 2 × 2 Vedic multiplier is also a coplanar design.

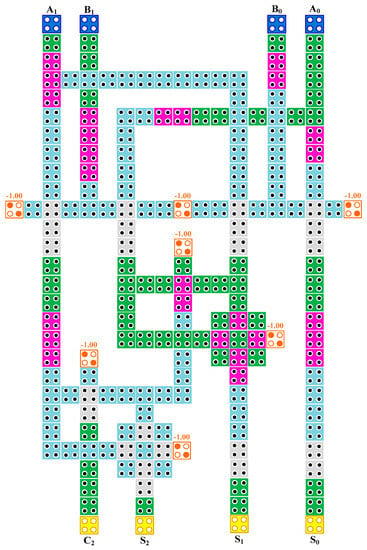
Figure 7. QCA design of the proposed 2 × 2 Vedic multiplier.

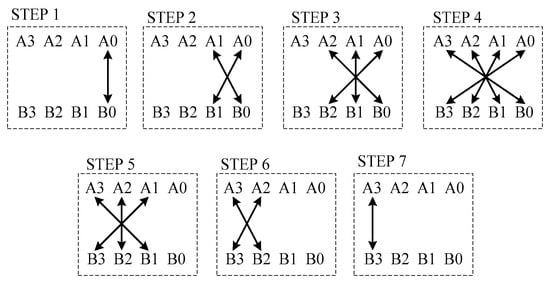
Figure 8. Multiplication steps of 4 × 4 Vedic multiplier.

3.3. The 4 × 4 Bit Vedic Multiplier

A Vedic multiplier applies bit-wise multiplication with simultaneous product term finding and its column-wise addition. This is one of the best standards for the algorithm of fast multiplication. The main advantage of this Vedic multiplier is that we can calculate partial products and sums, which must be fulfilled simultaneously.

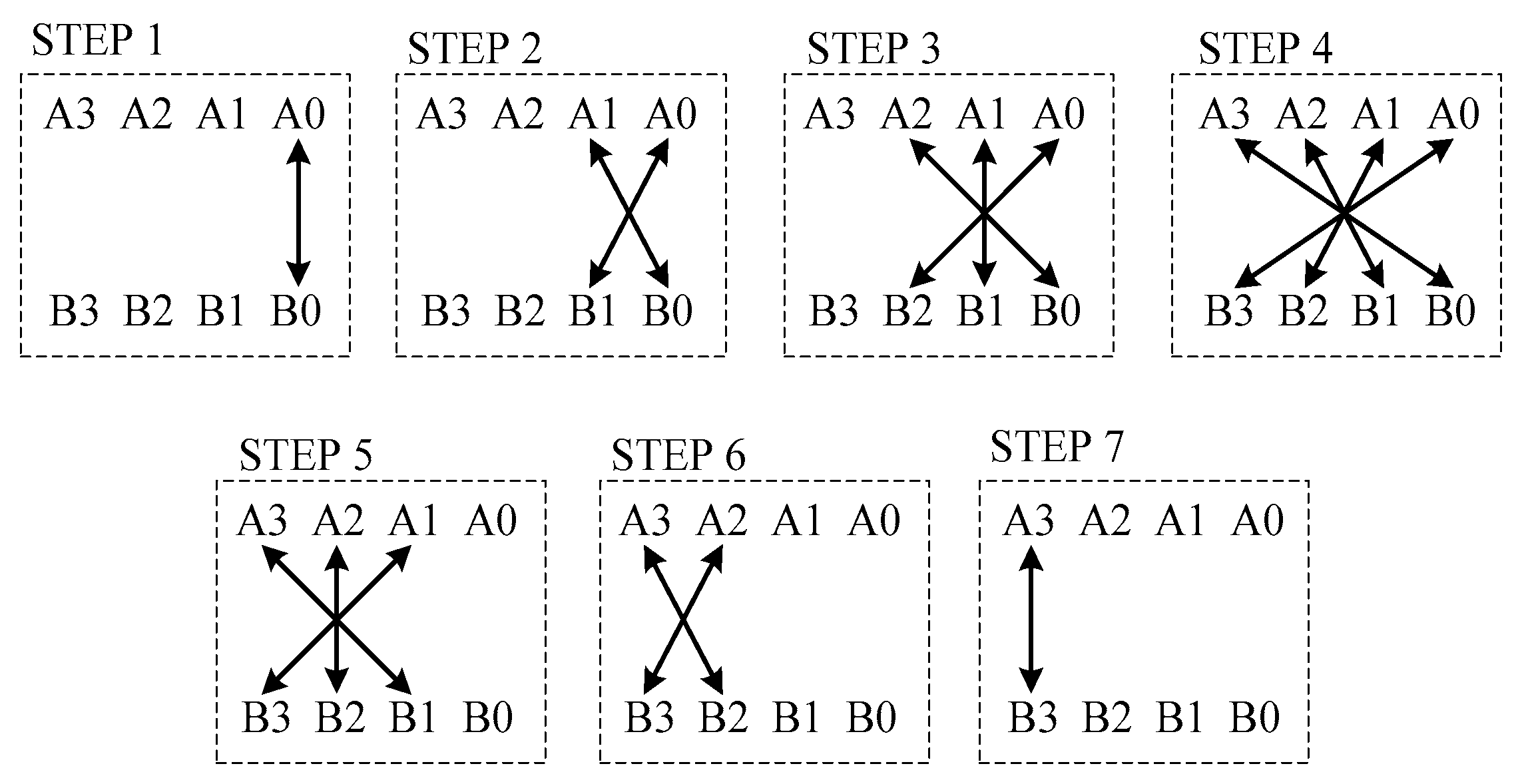
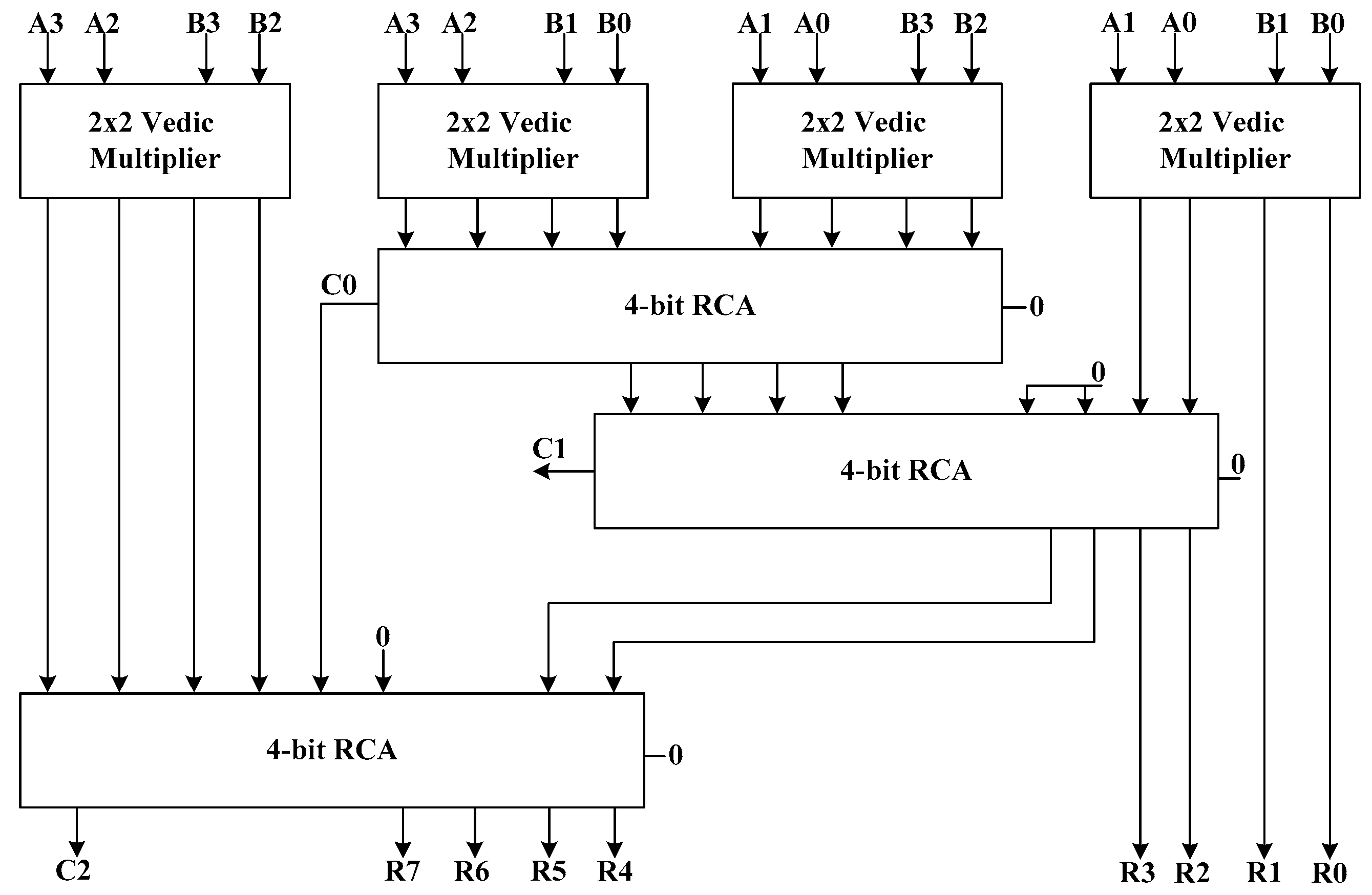
This section focuses on a 4 × 4 Vedic multiplier architecture. In this algorithm, two four-digit numbers: A = [A₃A₂A₁A₀] and B = [B₃B₂B₁B₀] are obtained for clear explanation. In the first step, the LSB of number A is multiplied with the LSB of number B to generate the LSB of the final product. The rest of the steps are similar to the procedure of the 2 × 2 multiplier. The procedure of the 4 × 4 Vedic multiplier steps is explained using line diagram, as illustrated in Figure 9, and RCA full adder in Figure 10.

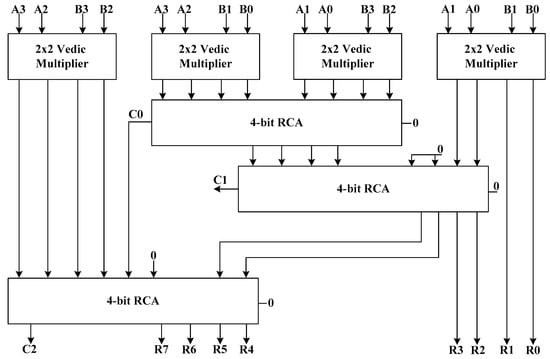
Figure 9. Block diagram of 4 × 4 Vedic multiplier.

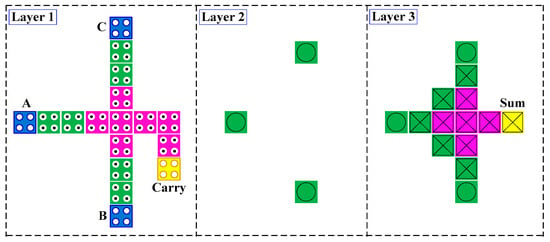
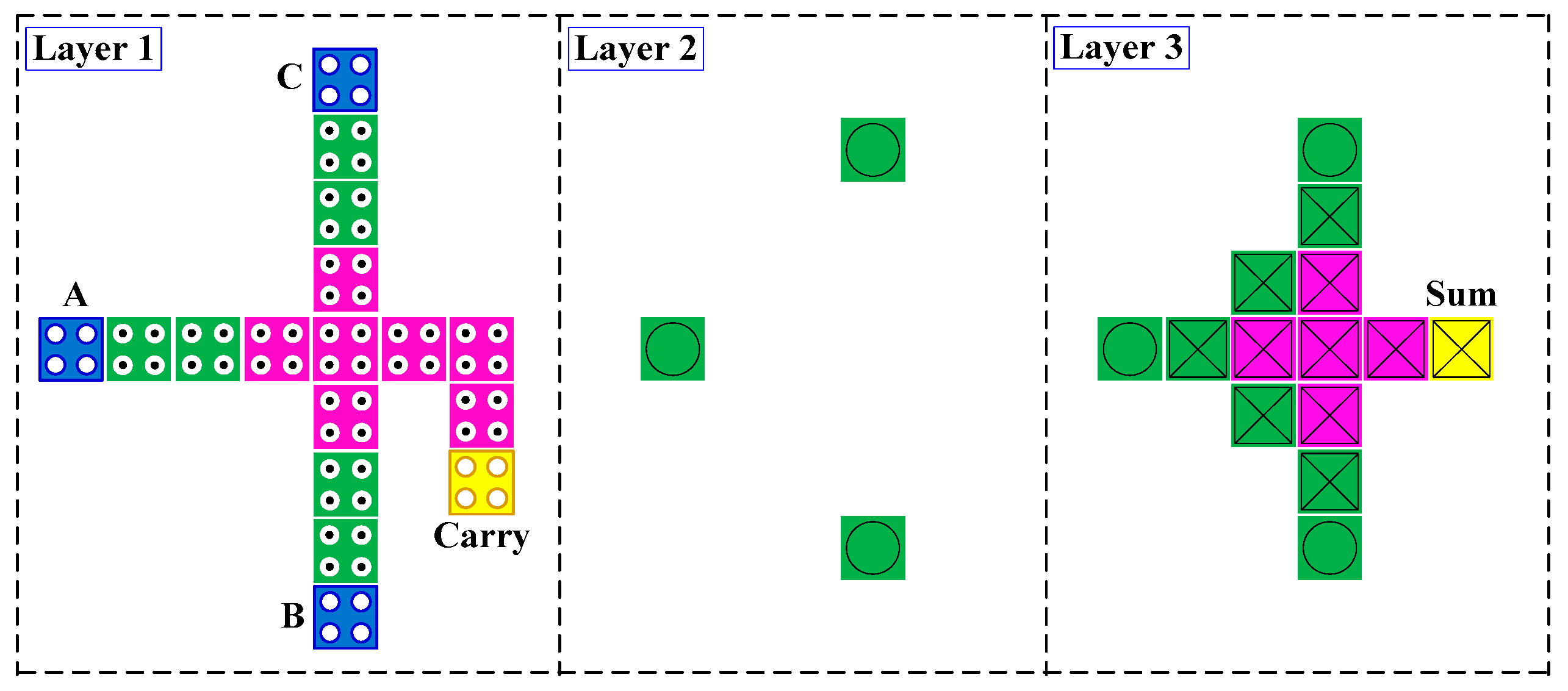
Figure 10. Full adder for designing ripple carry adder (RCA).

By the general concept, the generated carry (C_n) is forwarded to the next step in each step. The process goes on until the last step. The outputs C₆ and S₆ are taken at the last step. Finally, all of the generated results are obtained as form of [C₆ S₆ S₅ S₄ S₃ S₂ S₁ S₀]. The process is defined as follows:

S₀ = A₀B₀
C₁S₁ = A₁B₀ + A₀B₁
C₂S₂ = C₁ + A₀ B₂ + A₂ B₀ + A₁ B₁
C₃S₃ = C₂ + A₀ B₃ + A₃ B₀ + A₁B₂ + A₂B₁
C₄S₄ = C₃ + A₁B₃ + A₃B₁ + A₂B₂
C₅S₅ = C₄ + A₃B₂ + A₂B₃
C₆S₆ = C₅ + A₃B₃

(7)

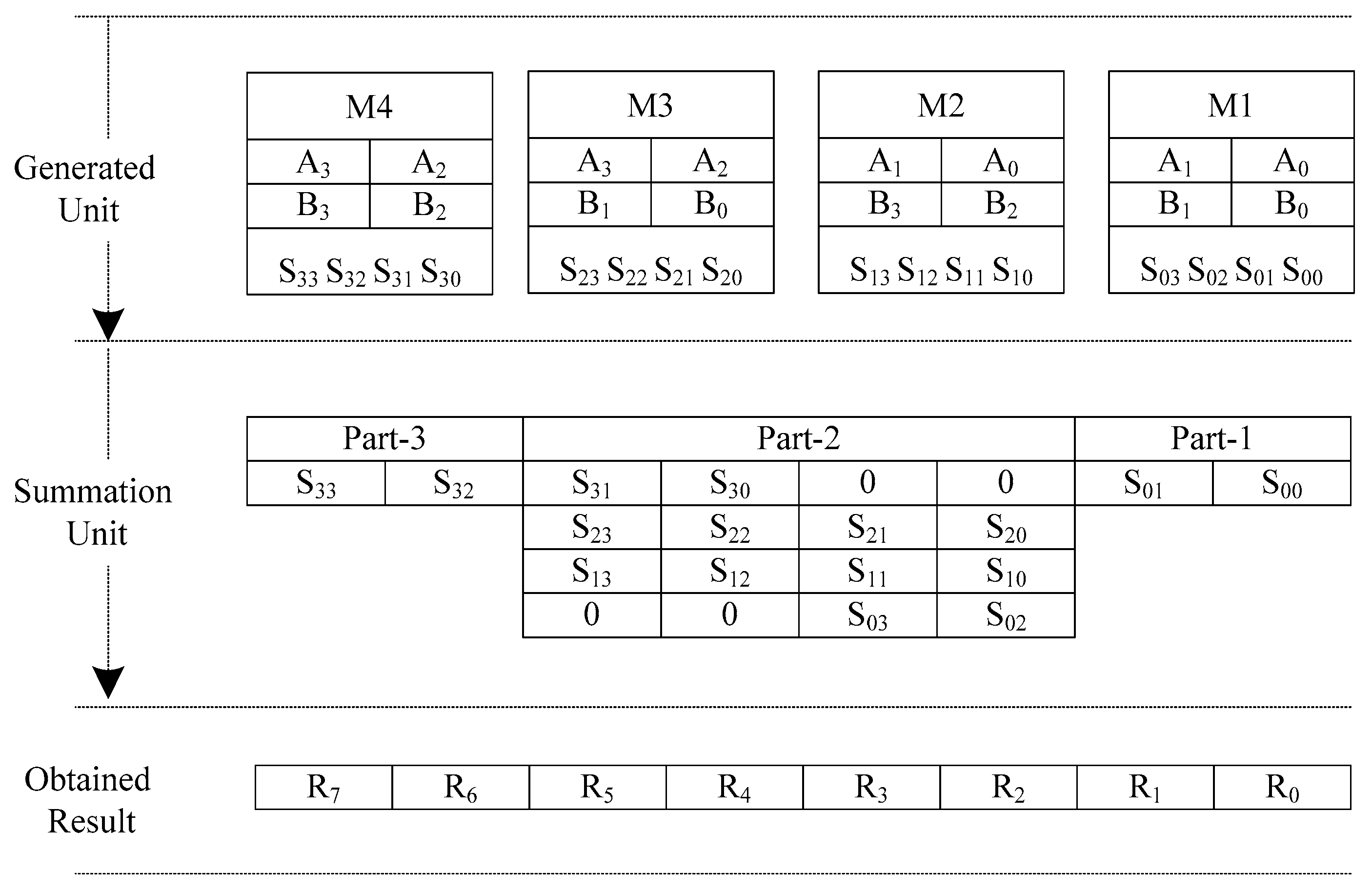
The design of the 4 × 4 Vedic multiplier architecture using the 2 × 2 Vedic multiplier improves the complexity of the operation. Four 2 × 2 Vedic multipliers (M1, M2, M3, and M4) perform multiplication operation between the defined inputs and produce sixteen products (S₀₀, S₀₁…S₃₂, S₃₃). The products obtained from the generated unit are placed in three particular positions, i.e., part-one, part-two, and part-three. Part-one includes the last two bits of the M1 result (S₀₁ S₀₀) and part-three contains the primary two bits of the M4 result (S₃₃ S₃₂). However, part-two is a multi-operative part of the summation unit that performs the main cross-wise multiplication for the 4 × 4 architecture of the Vedic multiplier. There are ‘0’ values in part-two in some cases wherever required, as shown in Figure 11. The final result is obtained after calculating the summation unit in the form [R₇R₆R₅R₄R₃R₂R₁R₀].

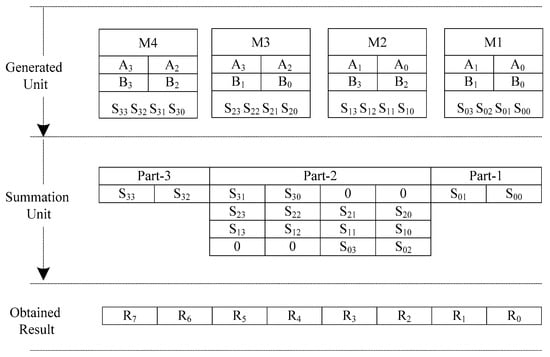
Figure 11. Calculation Process of 4 × 4 Vedic multiplier.

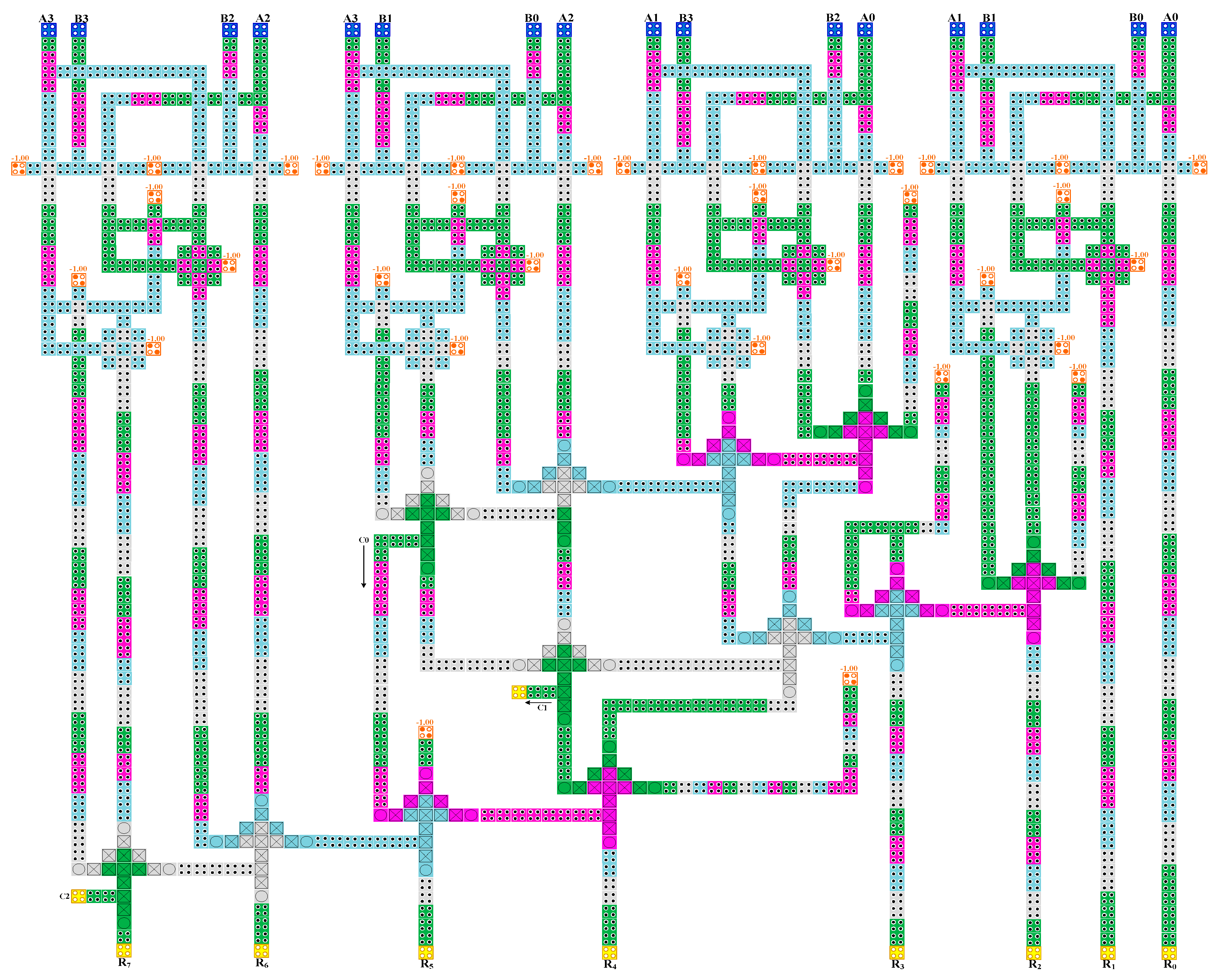
A block diagram of the 4 × 4 Vedic multiplier is shown in Figure 9. The basic building block of the 4 × 4 Vedic multiplier is a 2 × 2 Vedic multiplier. The architecture is composed of four 2 × 2 multipliers and three 4-bit ripple carry adder (RCA) designs. The partial products generated from the 2 × 2 multipliers are forwarded to the adders to perform addition. The results obtained from the first RCA are transmitted to the next RCA, and there exist two zero inputs for the second RCA. In some cases, zero inputs are given to some RCAs wherever required. On the basis of the block diagram in Figure 9, the 4 × 4 Vedic multiplier is developed in QCA. As shown in Figure 12, the proposed multiplier design is constructed using logical and multi-layered wire-crossing techniques. The structure is well pipelined within 5.25 clock cycle.

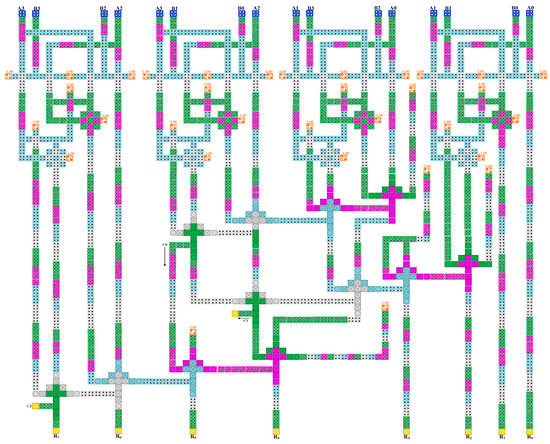
Figure 12. Design of the proposed 4 × 4 Vedic multiplier.

The existing one-bit full adder [31] is used to create RCA designs. This is a multi-layered structure consisting of a majority gate that is placed at the layer of the main cells and an XOR gate that is located on the top layer of the cell in the QCADesigner tool. This means that summation by the full adder is performed using an XOR gate, along with the carry which is obtained serially from the majority gates, as shown in Figure 10. The four-bit RCA design is implemented for the proposed 4 × 4 Vedic multiplier by sequentially connecting the one-bit full adders. Note that other types of adders can be used to help to improve the speed of the addition operation.

In this hierarchical design, a multi-layered technique is used for only the full adder structures. The rest of the structure has been designed as a coplanar architecture. As crossover type in the design, logical crossover is extensively used. The whole architecture would be a coplanar layout if the full adder is changed with a coplanar one.

4. Simulation Results and Analyses

In this section, we report the results of a structural analysis of the proposed designs, and energy dissipation analysis for the proposed half adder.

4.1. Structural Analysis

The proposed designs are simulated with the QCADesigner tool version 2.0.3 [32], which is a well-aimed simulation tool for QCA circuits. QCA circuits are simulated using the bistable approximation and coherence vector simulation engines. The simulation parameters are listed in Table 3.

Table 3. Simulation parameters.

Parameters	Bistable Approximation	Coherence Vector
Cell size	18 nm	18 nm
Dot diameter	5 nm	5 nm
Cell separation	2 nm	2 nm
Layer separation	11.5 nm	11.5 nm
Clock high	9.8×10−22 J	9.8×10−22 J
Clock low	3.8×10−23 J	3.8×10−23 J
Clock shift	0	0
Clock amplitude factor	2.0	2.0
Relative permittivity	12.9	12.9
Radius of effect	65 nm	80 nm

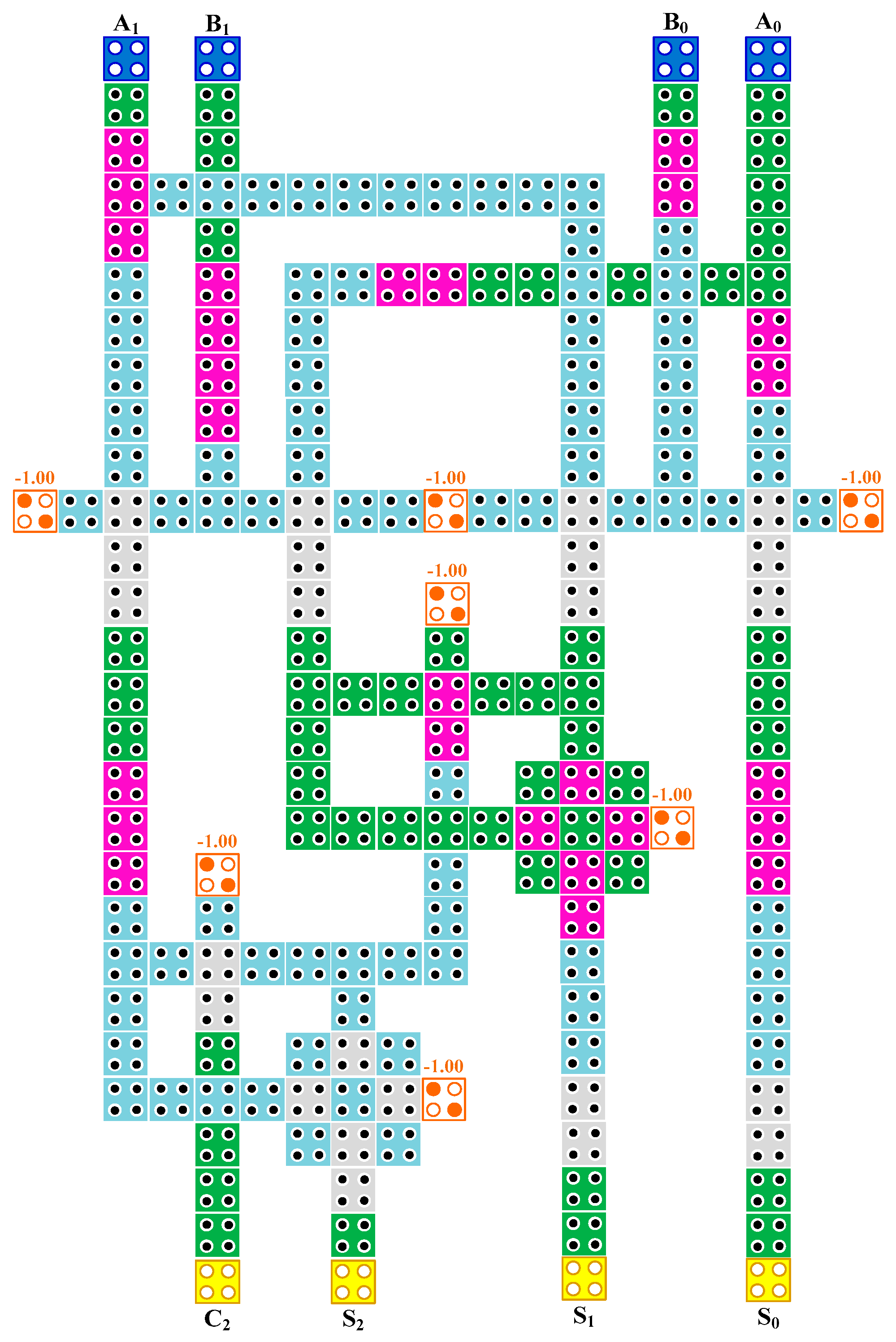
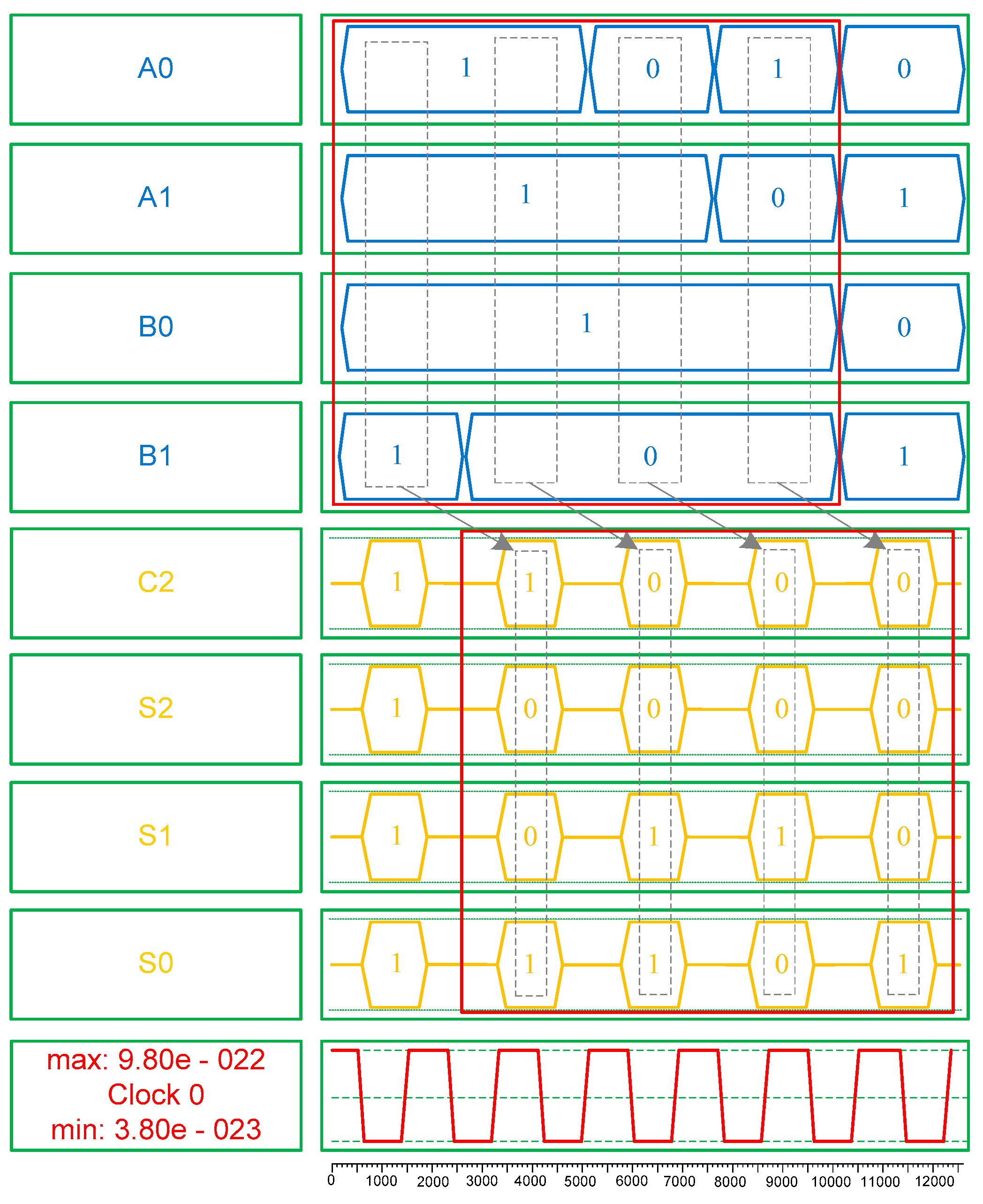
Figure 13 shows a simulation result of the proposed 2 × 2 Vedic multiplier. The simulation results confirm that the binary numbers obtained from the simulation match the values in Table 2. This is explained as follows; the input-output value is shown in the red rectangles in Figure 13; namely, multiplication of the binary number ‘11’ (A₁ A₀) by ‘11’ (B₁ B₀) is equal to the binary number ‘1001’ (C₂ S₂ S₁ S₀). It is clearly seen that the first dashed-line-based rectangle in the input is generated correctly below the first dashed-line-based rectangle in the output, and so on, as shown in Figure 13.

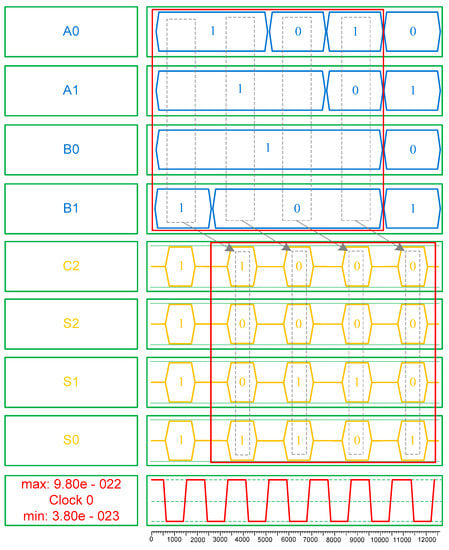
Figure 13. The simulation result of the proposed 2 × 2 bit multiplier.

The 4 × 4 Vedic multiplier architecture was designed on the basis of the proposed Vedic 2 × 2 multiplier. In the designs, we use a logical intersection scheme, because of the reliable and stable signal propagation throughout the QCA wires.

A multi-layered cross-over technique is used only in the full adder. The proposed designs have been compared with previous multiplier designs. In this comparison, QCA parallel 4 × 4 multipliers have been also chosen for comparison with the Vedic multipliers. The comparison results are summarized in Table 4, in terms of the cell count, total area, and latency.

Table 4. Comparison of QCA multipliers.

Circuit	Cell Count	Area	Delay	Cross-Over
4 × 4Array I [33]	2956	5.18	14	Multilayer
4 × 4Array II [33]	3738	6.02	14	Multilayer
4 × 4 Dadda [34]	3384	7.51	12	Coplanar
4 × 4 Wallace [34]	3295	7.39	10	Coplanar
4 × 4 Vedic [35]	1955	2.25	4.25	Multilayer
4 × 4 Proposed	1726	1.74	5.25	Multilayer
2 × 2 Proposed	194	0.17	2.25	Coplanar

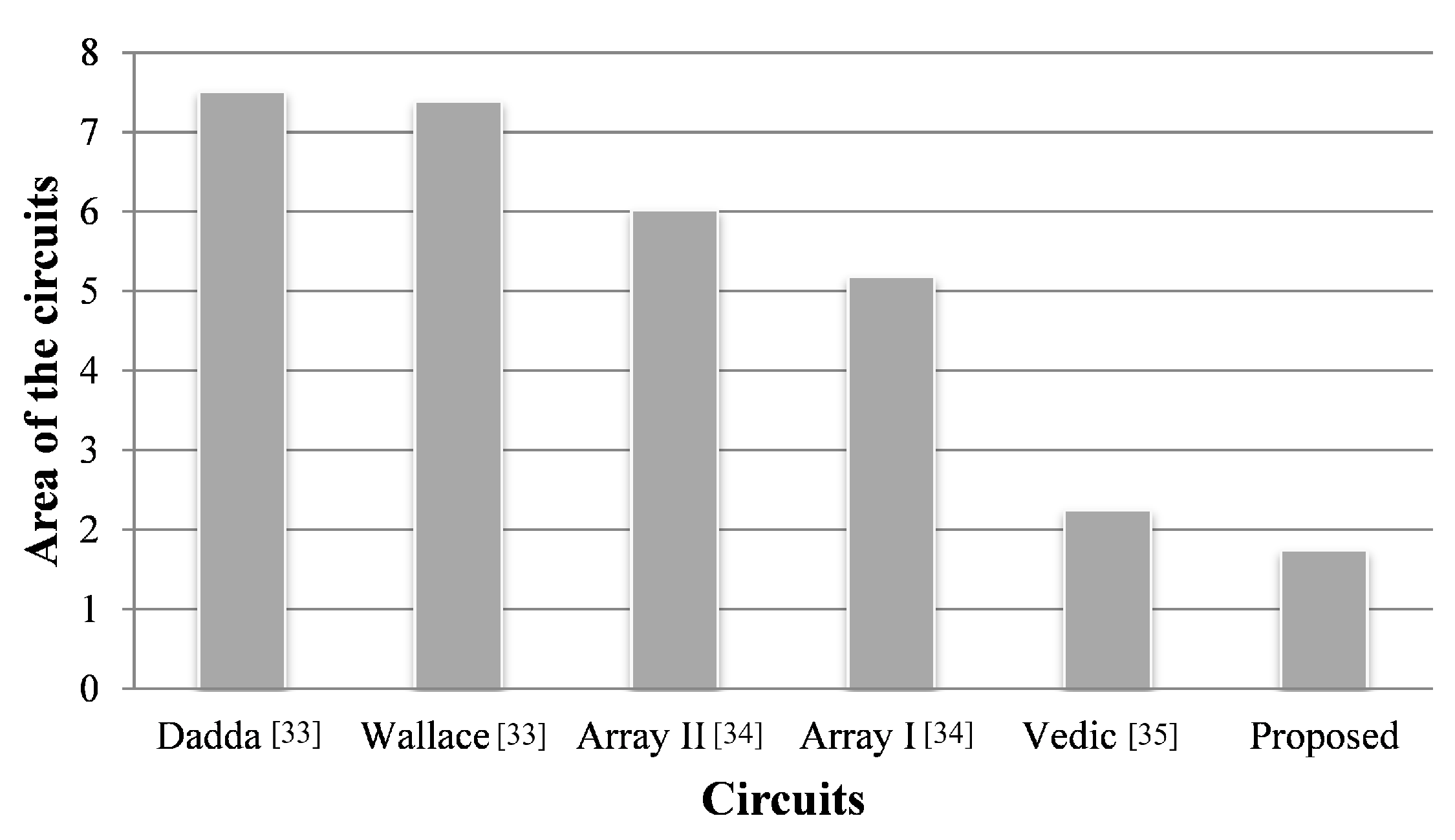
According to the comparison, the proposed designs have achieved significant improvements. The chart in Figure 14 indicates that the proposed 4 × 4 Vedic multiplier has great achievements in terms of the area in comparison to previously designed QCA multipliers [33,34,35].

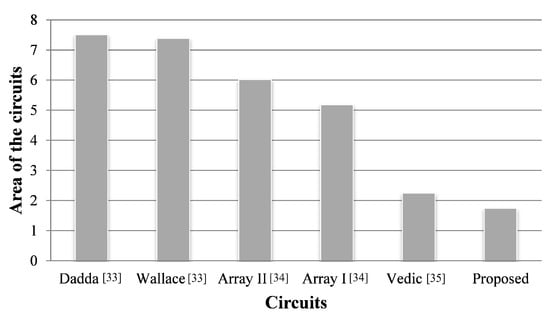
Figure 14. Area comparison of QCA 4 × 4 multipliers.

Note that the QCA multipliers have been implemented using the cell-interaction XOR structures to attain reliable results in the simulation, because, the cell-interaction based XOR gate has improvements over conventional AND-OR-INVERTER-based ones in all aspects.

4.2. Energy Dissipation Analysis

In order to estimate the energy dissipation, the QCAPro [36] tool has been utilized. The energy dissipation is analyzed by considering three different energy levels (0.5 E_k, 1.0 E_k, and 1.5 E_k) at a temperature of 2 K. The dissipated energy is measured on the basis of the Hamiltonian matrix using the HartreeFock approximation concerning the Columbic interaction between the cells and defined as follows.

$$H=\left[\begin{array}{cc}\frac{-E_k}{2}{\displaystyle \sum }_i{C}_i{f}_{i,j}& -\gamma \\ -\gamma & \frac{E_k}{2}{\displaystyle \sum }_i{C}_i{f}_{i,j}\end{array}\right]=\left[\begin{array}{cc}\frac{-E_k}{2}\left(C_{j-1}+C_{j+1}\right)& -\gamma \\ -\gamma & \frac{E_k}{2}\left(C_{j-1}+C_{j+1}\right)\end{array}\right]$$

(8)

In the above equation, polarization of i-th juxtaposed cell is represented by $C_i$ and the geometrical factor identifying electrostatic interaction between cells i and j is represented by $f_{i,j}$ due to geometrical distance where $E_k$ is the kink energy between the cells. This kink energy is related to the energy cost of two cells with the opposite polarization γ—the electron tunneling energy inside the cell, which is controlled by the clock. We have evaluated the energy dissipation of the proposed half adder using the adequate energy estimation tool QCAPro. As given in Table 5, Table 6 and Table 7, the average leakage energy, switching energy, and circuit energy dissipation, respectively, for the three different tunneling energy levels are calculated at a temperature of 2 K.

Table 5. Leakage energy analysis at T = 2 K.

Designs	0.5 Ek (eV)	1.0 Ek (eV)	1.5 Ek (eV)
[7]	0.03	0.08	0.14
[15]	0.02	0.06	0.10
[29]	0.01	0.04	0.07
Proposed	0.01	0.03	0.06

Table 6. Switching energy analysis at T = 2 K.

Designs	0.5 Ek (eV)	1.0 Ek (eV)	1.5 Ek (eV)
[7]	0.09	0.08	0.06
[15]	0.08	0.07	0.06
[29]	0.06	0.05	0.04
Proposed	0.04	0.04	0.03

Table 7. Energy dissipation analysis at T = 2 K.

Designs	0.5 Ek (eV)	1.0 Ek (eV)	1.5 Ek (eV)
[7]	0.12	0.15	0.20
[15]	0.10	0.12	0.15
[29]	0.07	0.09	0.12
Proposed	0.06	0.08	0.10

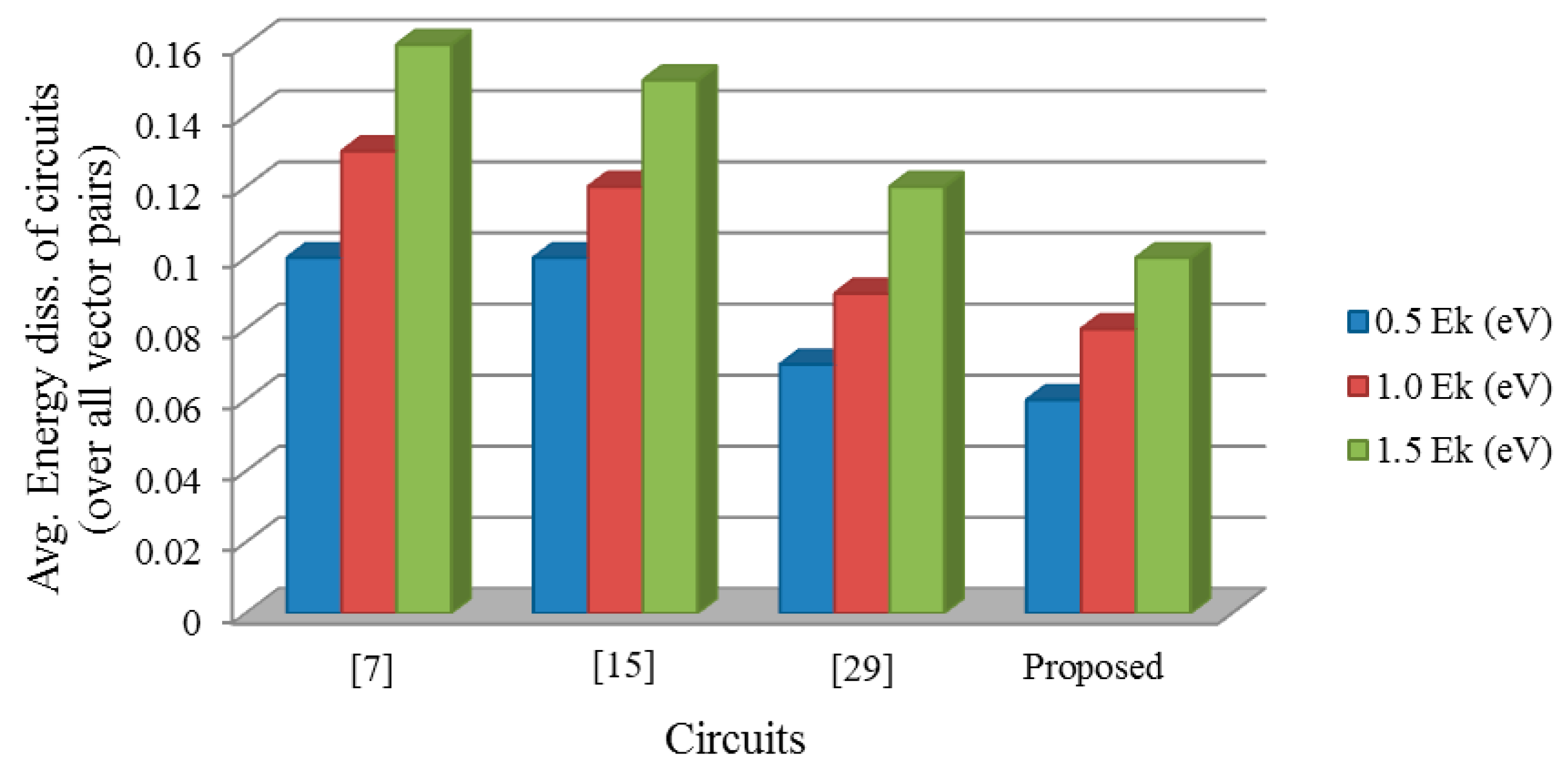
The obtained results are compared to the previous designs in [7,15,29] according to the metrics. Figure 15 shows the considerable optimization of the proposed design with regards to the average energy dissipation. According to the chart in Figure 15, the proposed half adder design consumes the lowest amount of energy compared to previous designs.

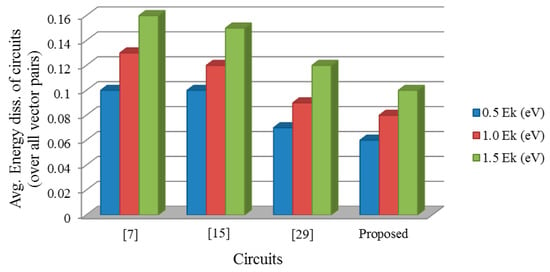
Figure 15. The average energy dissipation of the half adders for various tunneling energy levels.

5. Conclusions

In this paper, a technique for designing Vedic multiplier with cell-interaction QCA structures based on QCA technology is presented. First, a coplanar 2 × 2 Vedic multiplier has been designed and simulated with QCADesigner. The energy dissipation was also calculated for the circuit by QCAPro. Then, the architecture of a 4 × 4 Vedic multiplier has been designed by applying the 2 × 2 Vedic multiplier. The proposed QCA layouts have been compared with prior works in terms of the cell count, area, and latency. A comparison demonstrated that the proposed structures are implemented with significant improvements. According to this study, the use of the cell-interaction technique and clock-zone-based crossover can considerably improve the performance of the final structure.