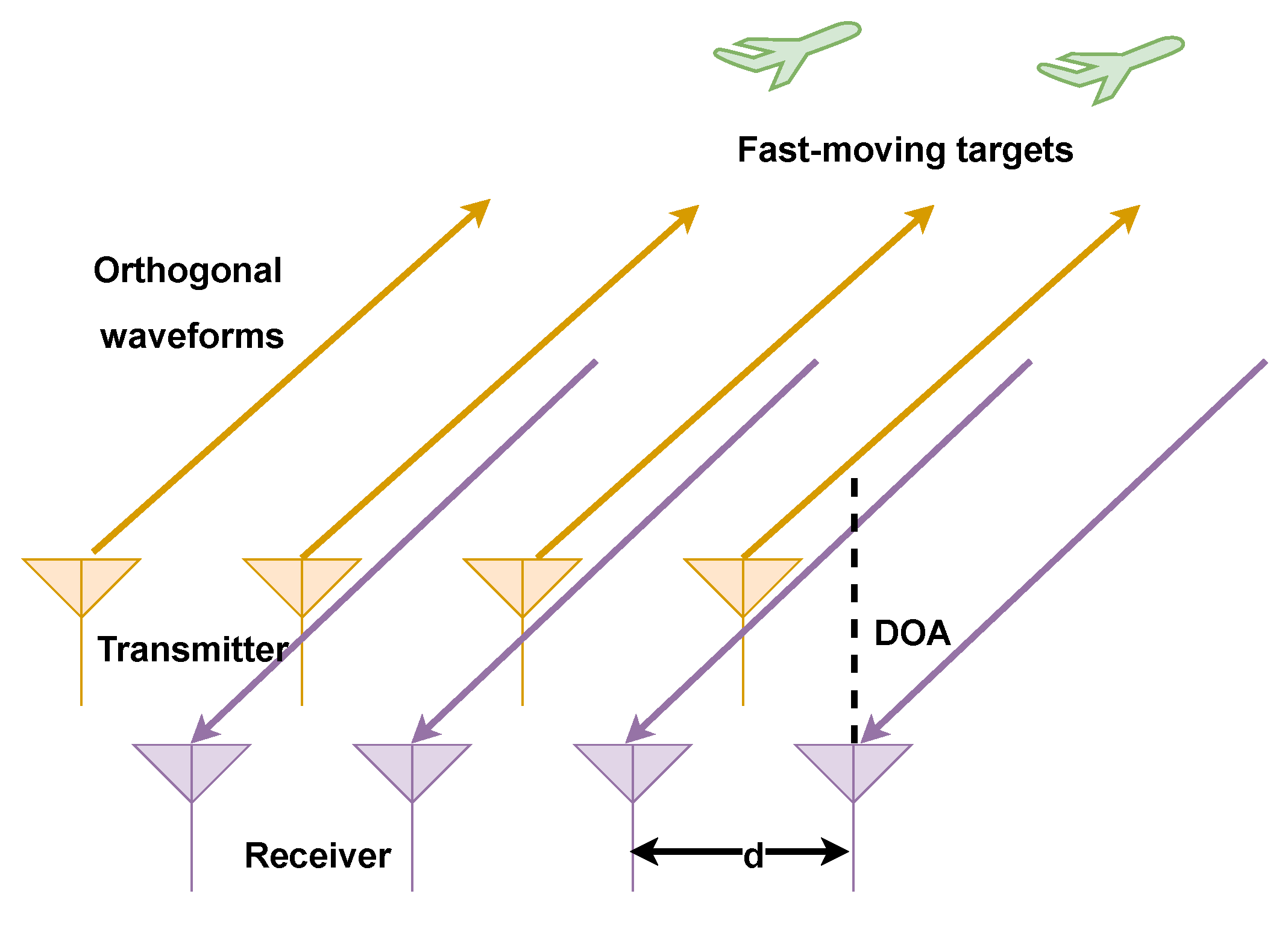
1. Introduction
Multiple-input and multiple-out (MIMO) radar systems [
1,
2,
3] transmit orthogonal waveforms, and the corresponding matched filters are used in the receiver to distinguish the orthogonal waveforms. Then, the virtual aperture is provided in the MIMO radar system and improves the radar performance in the target detection, estimation, and tracking [
4,
5]. The MIMO radar systems usually have two types: the colocated MIMO radar with the distance between antennas being comparable with the wavelength [
6,
7], and the distributed MIMO radar having larger distance between antennas [
8,
9,
10]. Compared with the distributed MIMO radar, the colocated MIMO radar has better characteristics in terms of system synchronization and waveform diversity [
11]. Therefore, in this paper, the colocated MIMO radar is used to estimate the direction of arrival (DOA).
In the DOA estimation problem, many methods have been proposed for decades [
12,
13]. For only one target, interferometer methods using different phases among antennas achieve excellent performances for DOA estimation. Notably, the interferometer methods have lower computational complexity and can be realized in the field-programmable gate array (FPGA) easily [
14,
15]. However, the interferometer methods can only estimate one target [
16]. In the scenario with more than one target, early methods are based on the discrete Fourier transform (DFT) [
17,
18], where the DOA estimation problem is similar to the frequency estimation from the samples in the time domain. However, the resolution of the DFT-based methods is limited by Rayleigh criteria, and the targets in the same beam cannot be distinguished. To break through the Rayleigh criteria, the
super-resolution methods have been proposed. The most famous methods are the ones based on the subspace theory. For example, the multiple signal classification (MUSIC) method is based on the noise subspace [
19,
20] using the eigenvalue decomposition [
21]; Root-MUSIC [
22] avoids the peak searching to find the DOA; the estimation of signal parameters via the rotational invariant techniques (ESPRIT) method uses the rotational invariant feature to estimate the DOA from the signal subspace [
23,
24,
25]. In the subspace-based methods, the subspaces are estimated from the received signals with multiple snapshots. For the MUSIC method, more than 3000 snapshots are used to estimate the covariance matrix, so with the pulse repetition interval (PRI) being 1 ms, more than 3 s are needed to estimate the DOA. For a fast-moving target, the target will move more than 1000 m in 3 s. Therefore, the subspace-based methods are not suitable for the DOA estimation in the scenario with fast-moving targets.
To improve the DOA estimation performance with fewer samples, the compressed sensing (CS)-based methods have been proposed [
26,
27], where the target sparsity in the spatial domain is exploited and transforms the problem of the DOA estimation to that of sparse reconstruction [
28,
29,
30]. In the sparse reconstruction methods, the orthogonal matching pursuits (OMP) [
31], stagewise OMP (StOMP), etc., are widely used. To further improve the performance, a sparse Bayesian learning (SBL)-based method has been proposed in [
27,
32]. However, the SBL-based methods usually have high computational complexity. In the sparse reconstruction method, a dictionary matrix is formulated by discretizing the spatial domain into grids, which will introduce an
off-grid error and limit the improvement of the DOA estimation. Hence, the off-grid methods have been proposed by a one-order Taylor expansion, such as in [
3,
33]. Moreover, an atomic norm-based method is also given in [
34,
35], where a semidefinite programming (SDP)-based method is formulated to solve the atomic norm minimization problem.
In this paper, the DOA estimation problem is investigated in the colocated MIMO radar system, and the fast-moving targets are considered. The system model with moving targets is first formulated. Then, To exploit the target sparsity in the spatial domain, an SBL-based method is proposed to estimate the DOA. Since the performance of the SBL-based method is limited by the off-grid problem, we combine the SBL with the Kalman filter and propose an SBL Kalman filter (SBLKF) method, where the temporal correlation of DOA is exploited for the moving targets. Furthermore, simulation results are also given for the proposed method and compared with the existing methods.
The remainder of this paper is organized as follows. The MIMO radar system model for moving targets is formulated in
Section 2. A DOA estimation method, combined with the SBL and KF for the fast-moving targets, is proposed in
Section 3. Simulation results are given in
Section 4.
Section 5 concludes the paper.
3. DOA Estimation Method
3.1. Sparse Bayesian Learning-Based DOA Estimation
To estimate the DOA during the
p-th pulse, the target sparsity in the spatial domain can be exploited to improve the estimation performance. First, the sparse system model will be formulated. A dictionary containing all possible steering vectors for target DOAs can be expressed as
where
Q denotes the number of columns in the dictionary matrix
. The spatial is descretized into
Q angles, and formulates a vector
Hence, the
q-th column in the dictionary matrix
is
where
is the
q-th discrete DOA.
Then, the system model in (
6) can be rewritten as the following sparse model
where the vector
is a sparse vector denoting the scattering coefficients, and the positions of non-zero entries indicate the corresponding DOAs. For example, if the
q-th discrete angle
is equal to the DOA
, i.e.,
, we have
.
To reconstruct the sparse vector
in (
16), a SBL-based method is proposed in this paper, and we first show the probability density function (PDF) of AWGN (
) as
where the noise variance
is usually unknown, and we define the precision of noise variance as
. Then,
follows a Gamma distribution as
where
and
are the hyperparameters, and the Gamma function is defined as
To simplify the analysis, as the Gamma distribution is a conjugate prior of the Gaussian distribution, we assume that the target scattering coefficients
follow the following Gaussian distribution:
where the covariance matrix
is a diagonal matrix
. Similarity, the variances of the entries in the sparse vector
can also described by a Gamma distribution
where we define
.
g and
h are the hyperparameters of
.
Therefore, the DOA estimation problem with the unknown noise variance can be described by a problem to maximize the posterior probability, which is expressed as
Then, for the sparse vector , the estimated mean and variance can be obtained by the following theorem.
Theorem 1. With the received signal in (16) and the Gaussian distribution assumption in (20), the mean and variance of are, respectively, Proof. To estimate the mean and variance of the sparse vector, we first formulate the joint distribution
as
Then, with the joint distribution
, the posterior for
is obtained as
where
can be obtained as
and
is obtained as
Substitute (
27) and (
28) into (
26), and we can find that the sparse vector
follows the Gaussian distribution. The mean and variance can be obtained as
□
From Theorem 1, we find how to estimate the mean and variance of the sparse vector , but the unknown parameters including and are still unknown. The expectation-maximum (EM)-based method is used to estimate these unknown parameters, and can be obtained by the following theorem.
Theorem 2. The unknown parameters β and γ in Theorem 1 can be obtained by the EM-based method as Proof. The likelihood function for the unknown parameters
and
can be expressed as
Therefore, for the noise precision
, we can simplify the likelihood function by ignoring terms independent thereof in (
33) as
Then, the noise precision can be estimated by maximizing the likelihood function
. Set
, and the estimated noise precision is
Similarity, for the precision
, we have the following likelihood function
By setting
, we can estimate the
q-th entry in
as
□
The details for the sparse reconstruction using the SBL-based method are shown in Algorithm 1. Using the proposed method, the DOA can be estimated. Moreover, the movements of targets can be exploited to improve the estimation performance further.
3.2. The KF-Combined SBL Estimation Method
For the far-field targets, the movement of targets are stationary, and cannot change significantly. Thus, the KF can be used to improve further the DOA estimation performance when combined with the SBL-based estimation method, the movement model in (
12), and the estimated DOA
obtained by Algorithm 1.
During the
p-th pulse, the estimated target state is denoted as
where the estimated state
for the
k-th target has the DOA and acceleration information. Then, the transition matrix for all the targets can be expressed as
| Algorithm 1 The SBL-based DOA estimation method. |
- 1:
Input: the received signal during the p-th pulse, the dictionary matrix , the hyperparameters , , g, and h. - 2:
Initialization: set the values of hyperparameters as , and the number of iterations is . - 3:
for to do - 4:
Estimate the mean and variance as
- 5:
Estimate the precision of noise variance as
- 6:
Estimate the q-th precision of sparse vector as
- 7:
end for - 8:
Estimate the DOA by peak-searching the spatial spectrum using the mean and variance . - 9:
Output: the estimated DOA .
|
The predicted target state using the KF method can be obtained as
and the estimated state during the
-th pulse is
where
is the estimated DOA using the SBL-based method in Algorithm 1, and
is the DOA obtained from the predicted target state
. The matrix
is obtained as
where
is the noise covariance in the measurement,
,
is the noise covariance of state movement, and
. The matrix
is a measurement matrix, and is expressed as
Then, with the KF theory, the details for the sparse DOA estimation method are shown in Algorithm 2. In
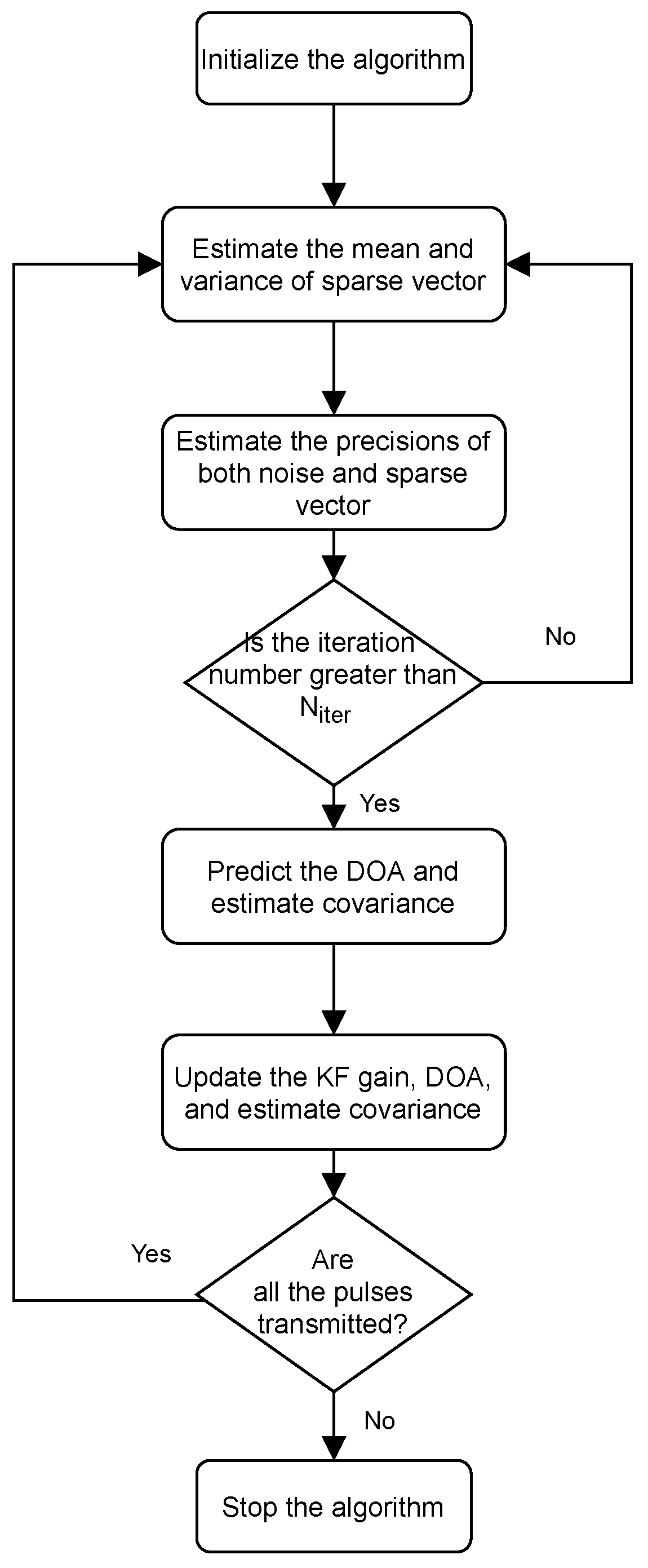
Figure 2, the flow chart of the proposed method is shown, and two main steps, including the SBL-based sparse reconstruction and the KF-based prediction, are combined in the proposed method. Hence, better DOA estimation performance can be achieved, especially for the fast-moving targets.
| Algorithm 2 The KF-based sparse DOA estimation method. |
- 1:
Input: the estimated DOA () using Algorithm 1 during the -th pulse. - 2:
During the -th pulse: - 3:
Predict the DOA from the p-th pulse as
- 4:
Predict the estimate covariance as
- 5:
- 6:
Update the estimated DOA as
- 7:
Update the estimate covariance as
- 8:
Output: the estimated DOA as .
|
Additionally, the proposed method can also deal with the off-grid problem caused by the discretized grids in the sparse reconstruction method. In the SBL-based reconstruction step, the on-grid DOAs are estimated. To further improve the estimation performance, the KF-based method is combined to predict the DOAs, so the off-grid errors can be reduced. For example, when the ground-truth DOA is °, the traditional SBL method cannot breakthrough the resolution of grid size. The estimated DOA using the SBL method can be 30° or 31° with the grid size being 1°. However, when the proposed method is used, the resolution can be less than 1° when the KF is combined with the SBL method. Therefore, the proposed method can solve the off-grid problem.
3.3. Computational Complexity
The computational complexity can be estimated from the two main steps of the proposed method. In the SBL-based reconstruction step, we can find that the computational complexities in the mean and variance are and , respectively. The computation complexity for the precision estimation is . Additionally, in the KF-based step, the computational complexity is .
Since the number of antennas is much lower than that of discretized grids in the practically MIMO radar system, i.e., , and the number of targets is also much lower than that of Q, i.e., , we can find that the computational complexity of the proposed method is .
4. Simulation Results
In this section, the simulation results are given to show the performance of the proposed method in the DOA estimation. The proposed method was carried out in a PC with Intel i7 processor and 16 GB RAM. The proposed method is also available online (
https://drive.google.com/drive/folders/1eHSYMnwEGy2kf_2NXZSmdbuK4lyIrSEt?usp=sharing).The simulation parameters are shown in
Table 1. The targets have movements with constant speed, and the DOA is described as
where we can choose the speed
as
.
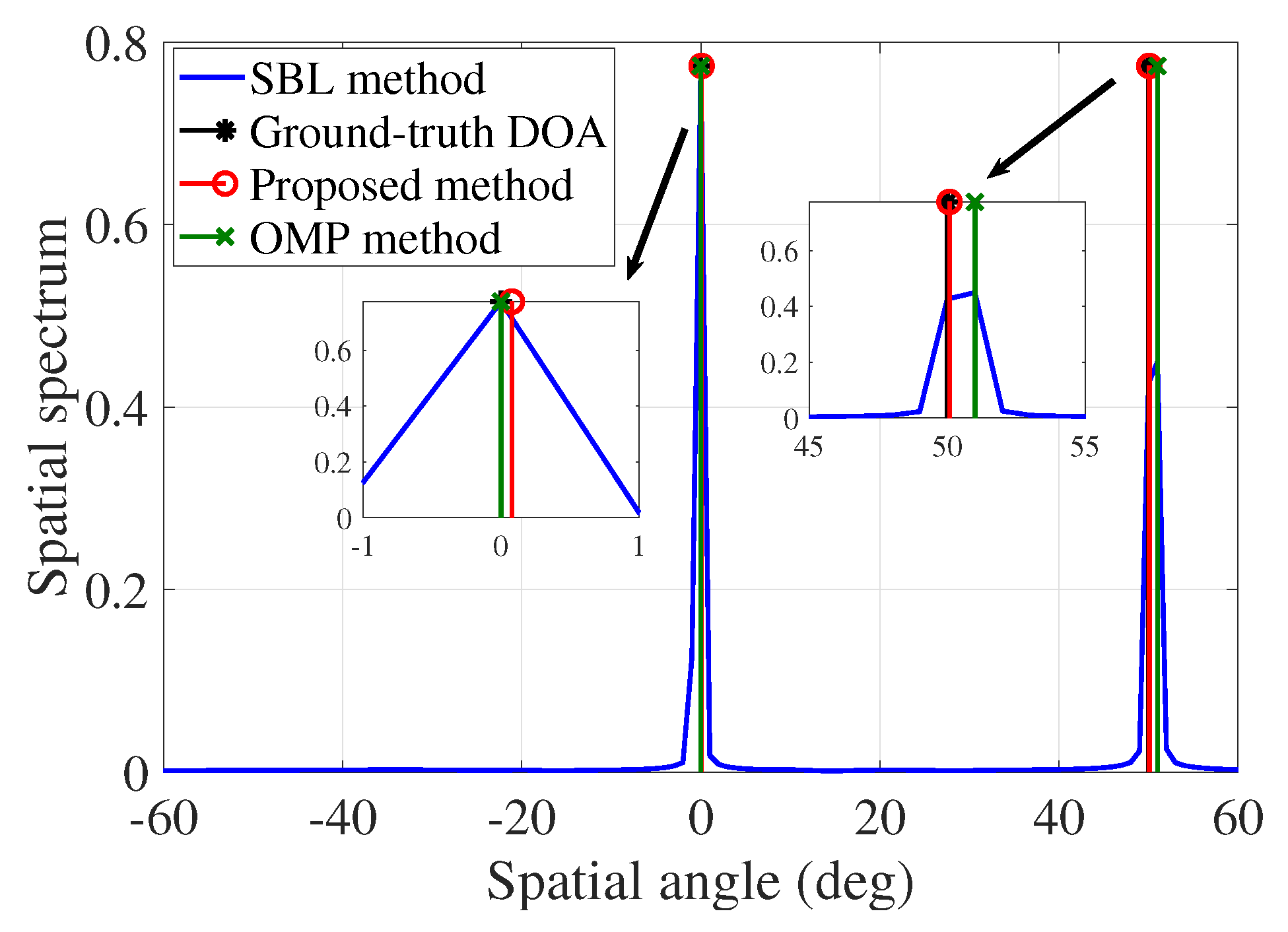
During the 100-th pulse, the ground-truth DOAs are 0° and 50°, as shown in
Figure 3, and we use 3 methods to estimate the DOA:
SBL method: The method is proposed in [
3,
27,
32,
33], where the SBL theory is exploit to reconstruct the sparse vector. The better estimation performance can be achieved, but with higher computational complexity.
OMP method: The method is widely used in the sparse reconstruction theory, and has lower computational complexity. However, this method cannot have better estimation performance in the scenario with a coherent dictionary matrix.
Proposed method: This is the method proposed in this paper, where both the SBL and KF are combined. Hence, the off-grid problem can be solved, and better DOA estimation performance can be achieved.
As shown in
Figure 3, all three methods can find the two targets. The root mean square error (RMSE) in degrees is used to measure the DOA estimation performance, and is defined as
We found that the RMSEs of the SBL method, the OMP method, and the proposed method were , , and . Hence, the best estimation performance was achieved by the proposed method. Additionally, we found that compared with the grid size 1°, the RMSE in degrees () of the proposed method is much less than the gird size, so the off-grid problem is solved.
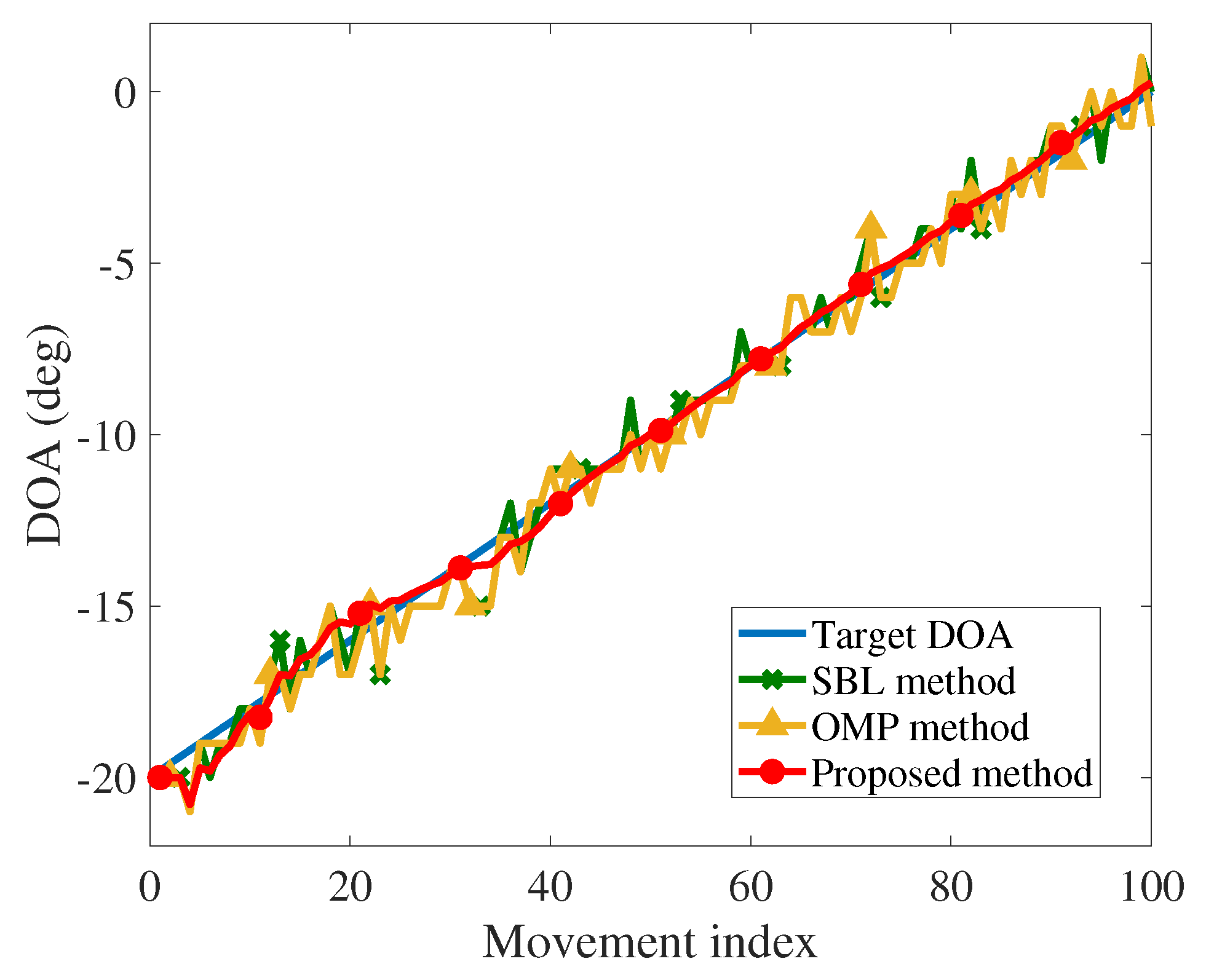
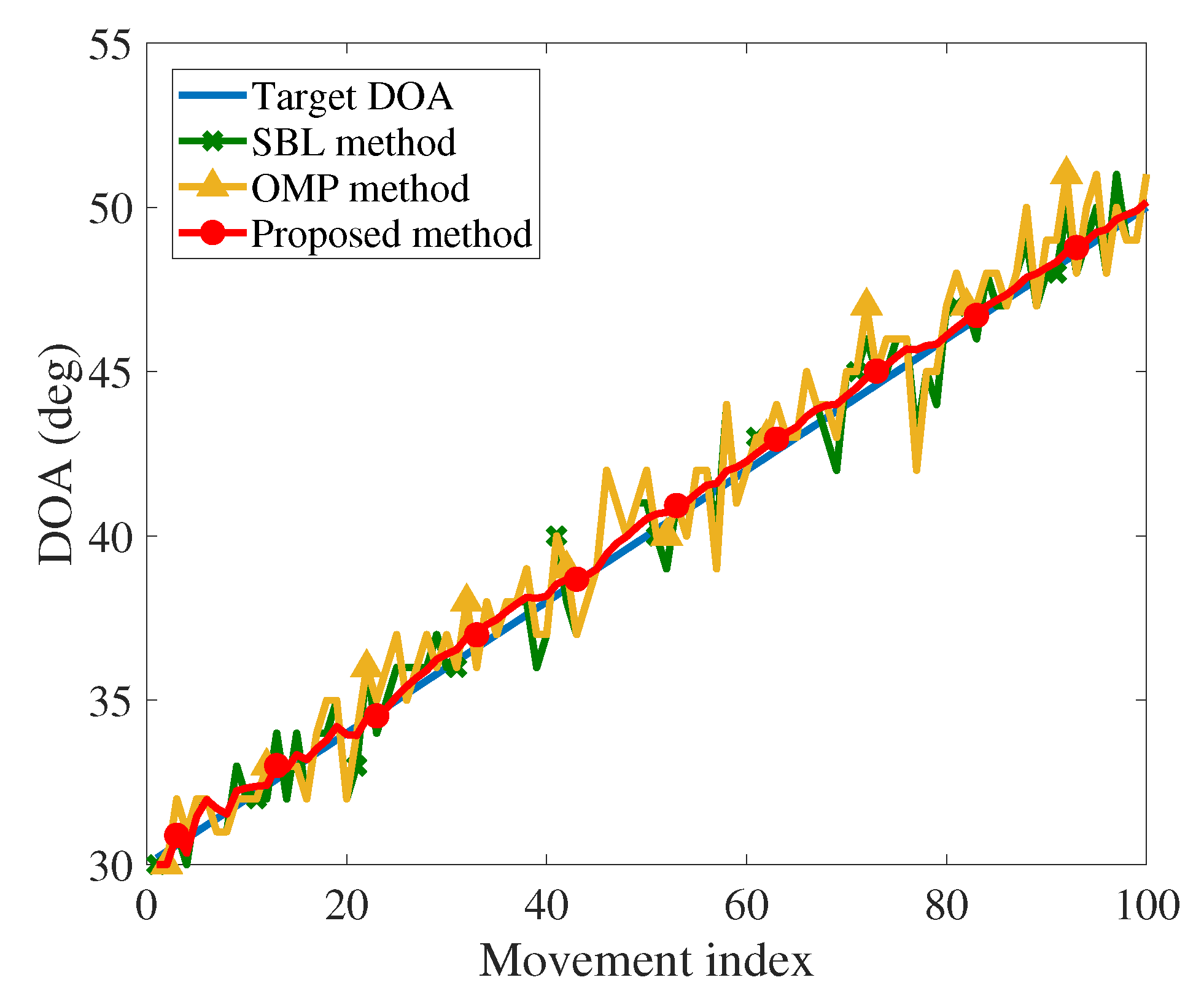
For the DOA estimation with a moving target,
Figure 4 and
Figure 5 show the estimation results for the first and second targets, respectively. We use three methods to track the target movement, and the proposed method can more precisely track the moving DOA, compared with SBL and OMP methods. The corresponding RMSEs of DOA estimation with a moving target are shown in
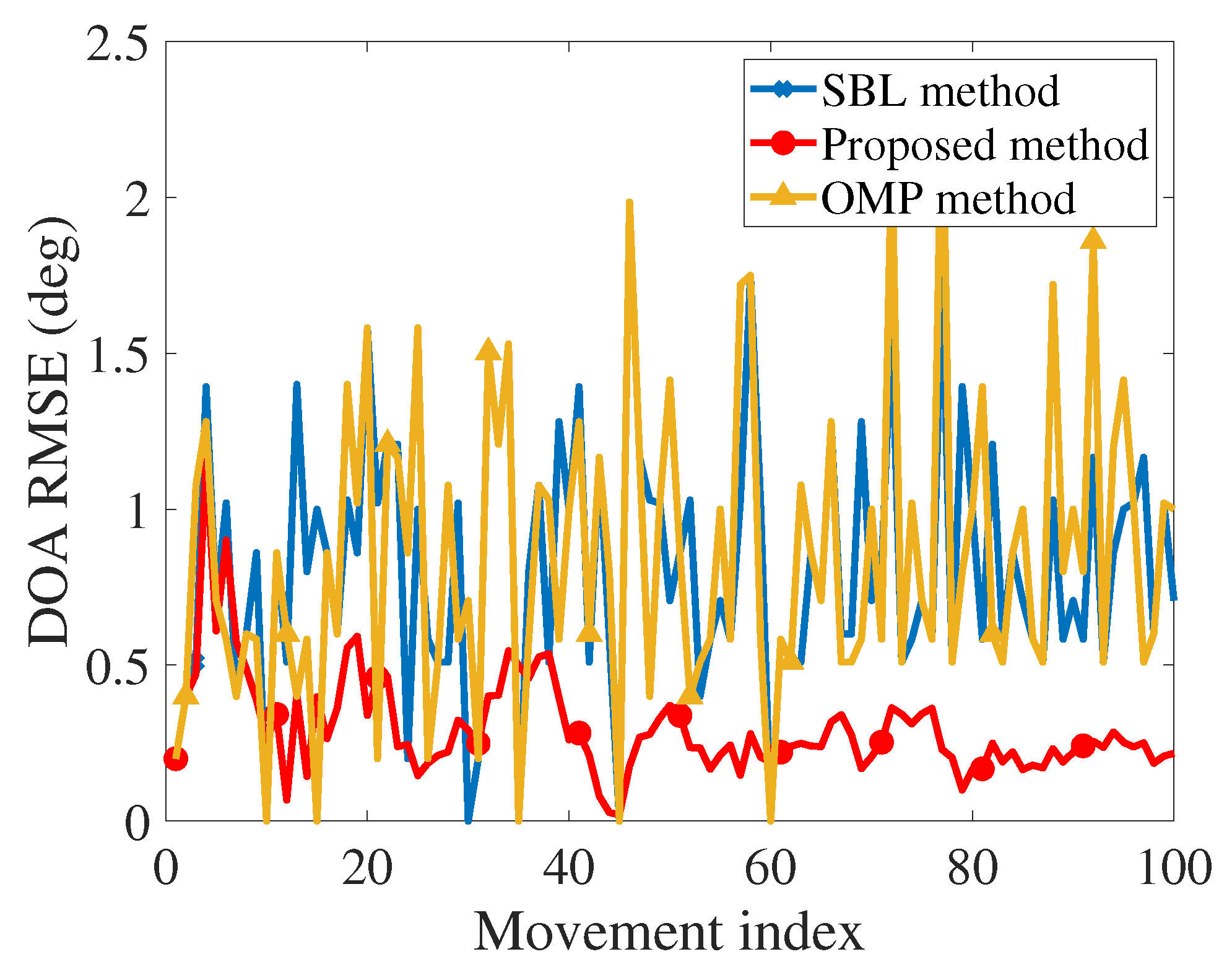
Figure 6, where the proposed method has relatively lower RMSE with the increasing index of movement. However, for the SBL and OMP methods, the performance cannot be improved using the historical information of the estimated DOA. Therefore, with more estimation information, the DOA estimation performance can be further improved using the proposed method.
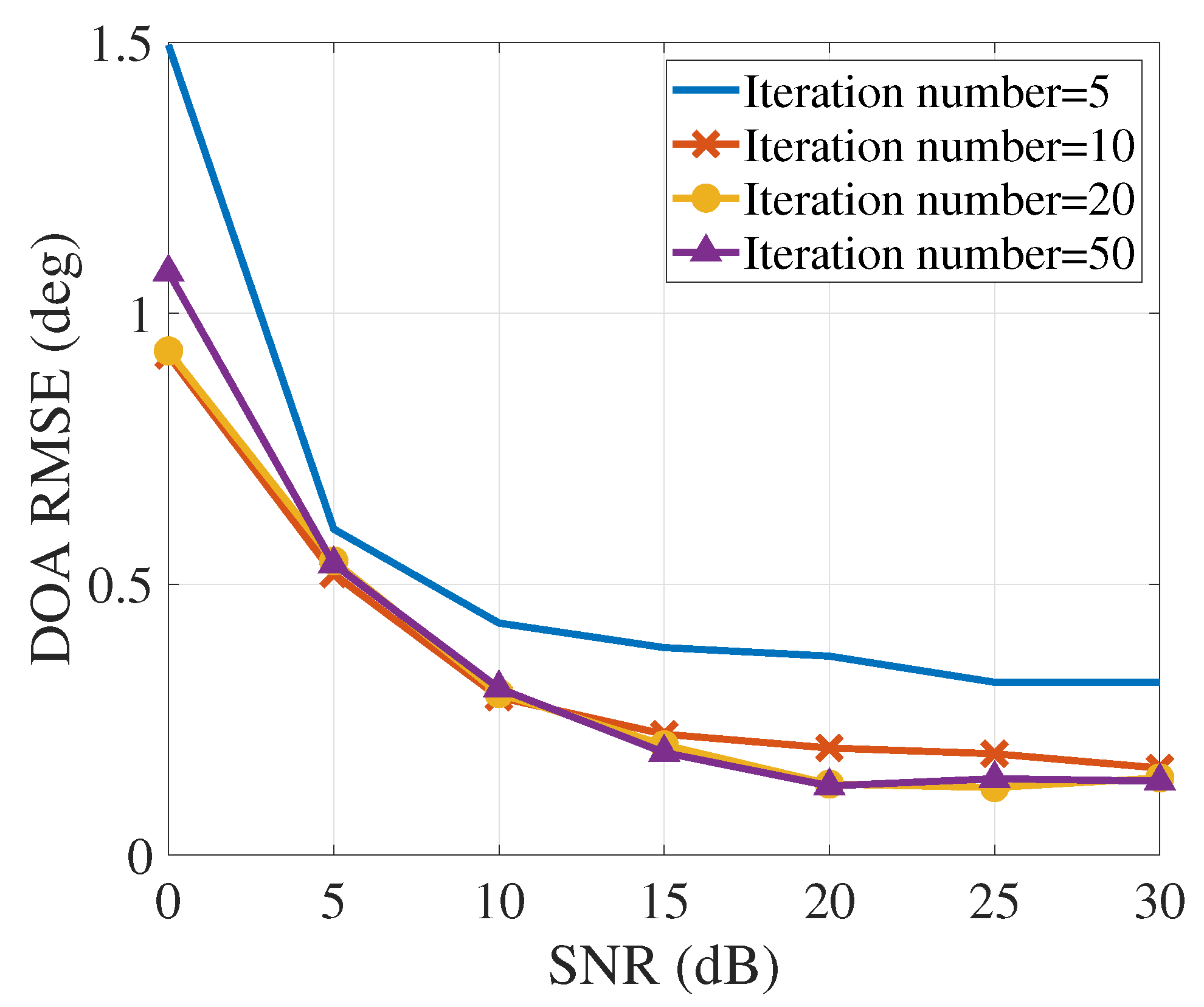
In the proposed method, Algorithm 1 uses the iterations to estimate the DOA during the
p-th pulse, so we show the DOA estimations with different numbers of iterations in
Figure 7. We can find that when the number of iteration is greater than 20, the same DOA estimation performance is achieved. Hence, in the following simulations, the number of iterations is chosen as
. Moreover, when
dB, we have acceptable performance (
) of the DOA estimation, so we choose
in the following simulations.
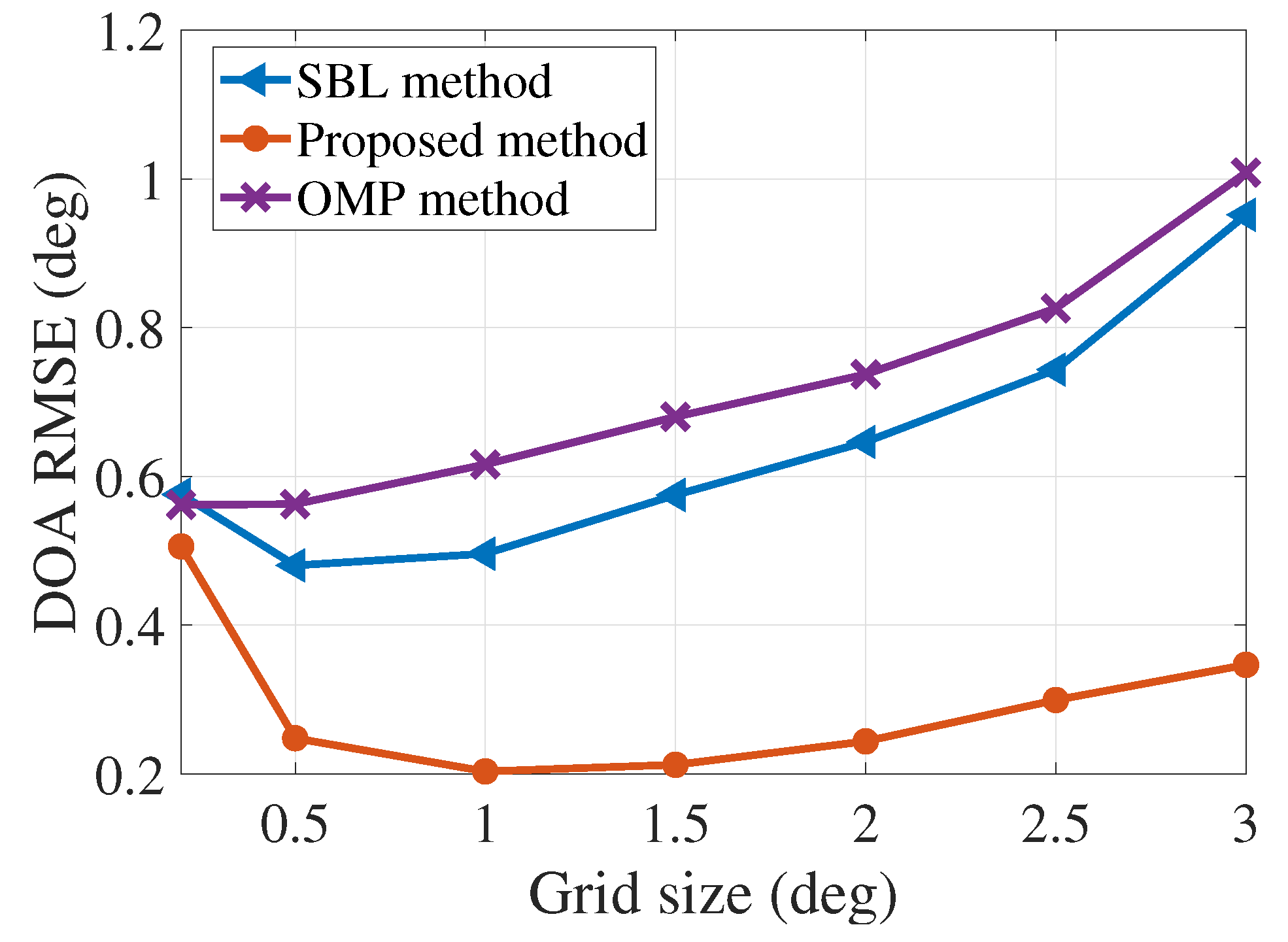
For the sparse reconstruction method, the dictionary matrix
is formulated, so the grid size is essential to controlling the performance of sparse reconstruction. In
Figure 8, the DOA estimation performance with different grid sizes is shown; we choose the grid sizes as
,
, 1°,
, 2°,
, and 3°. The SBL, OMP, and proposed methods are compared in the scenario with different grid sizes. We can find that when the grid size is less than
, the coherence between the adjacent columns in the dictionary matrix is higher, so the sparse reconstruction performance is worse. When the grid size is larger than 2°, the DOA estimation performance is also worse with the additional off-grid problem. As a trade-off between the dictionary size and the reconstruction performance, we choose the grid size as 1° in the following simulations. Under this condition, the RMSE of the DOA estimation using the proposed method is about
and much less than the grid size 1°.
Then, the DOA estimation performances using the SBL, OMP, and proposed methods are shown in
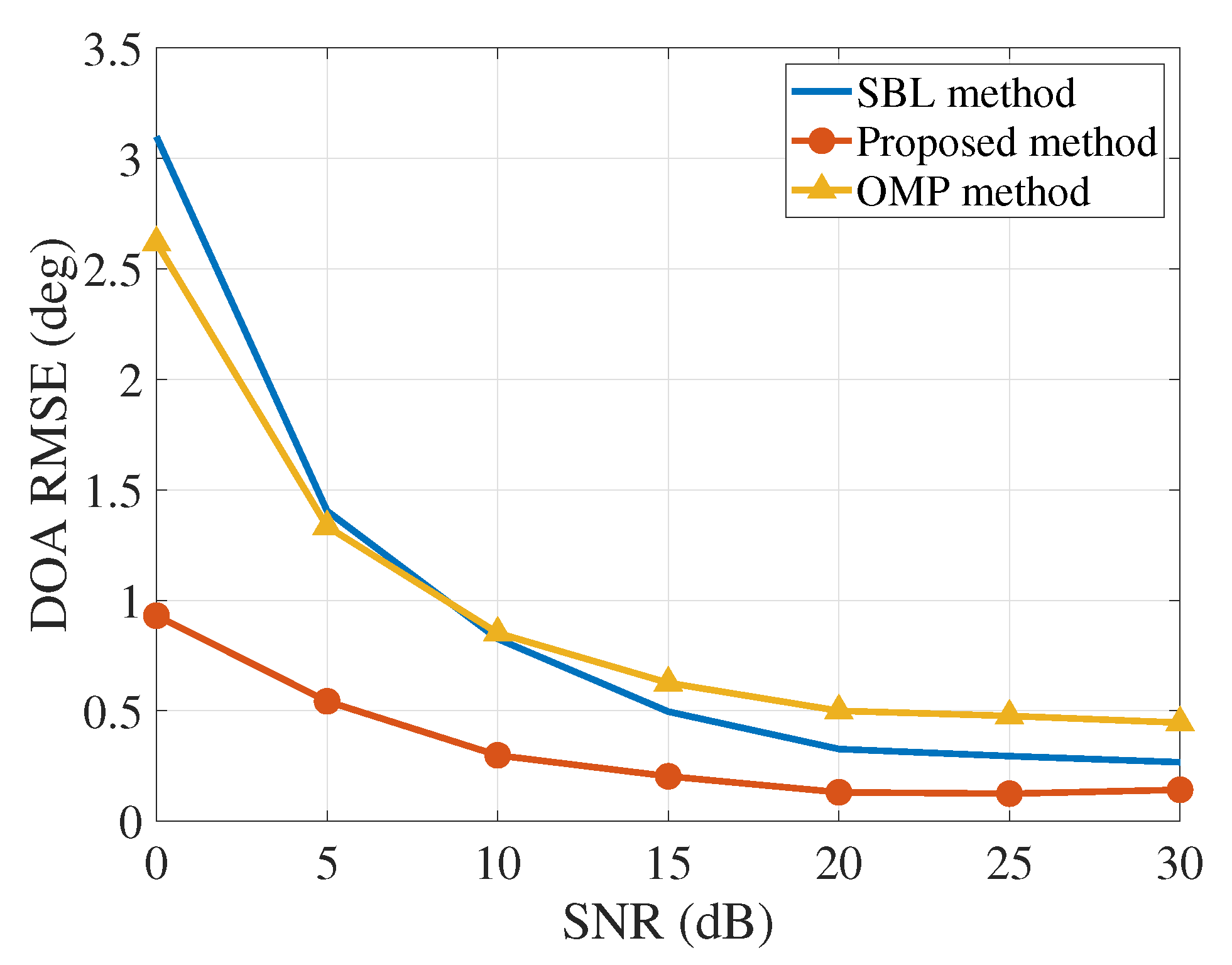
Figure 9 with different SNRs. As shown in
Figure 9, the proposed method achieves the best estimation performance from 0 dB to 30 dB. The SBL method has better performance than the OMP method but also has higher computational complexity. Additionally, in the scenario with worse SNR (
dB), the performance improvement is more significant.
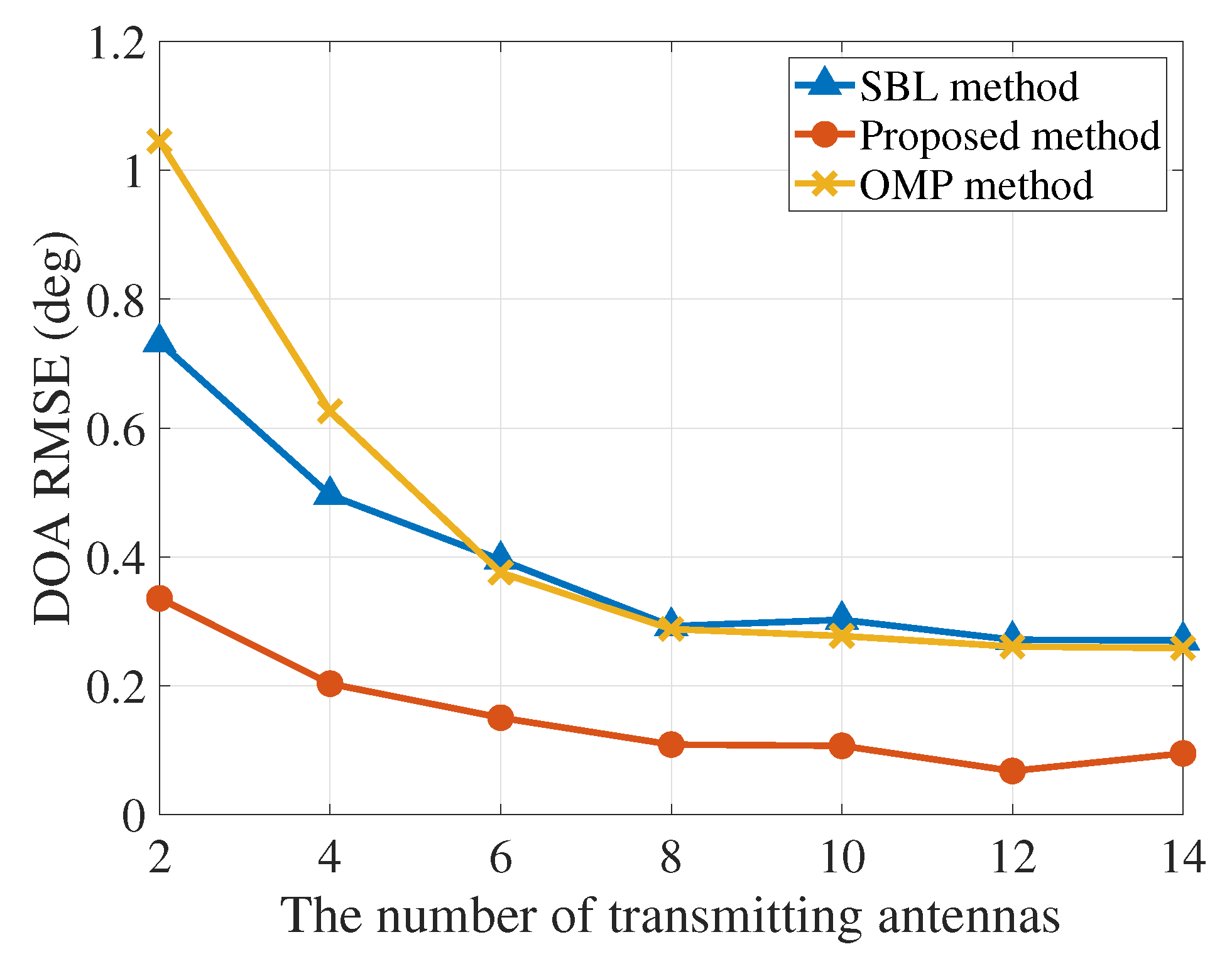
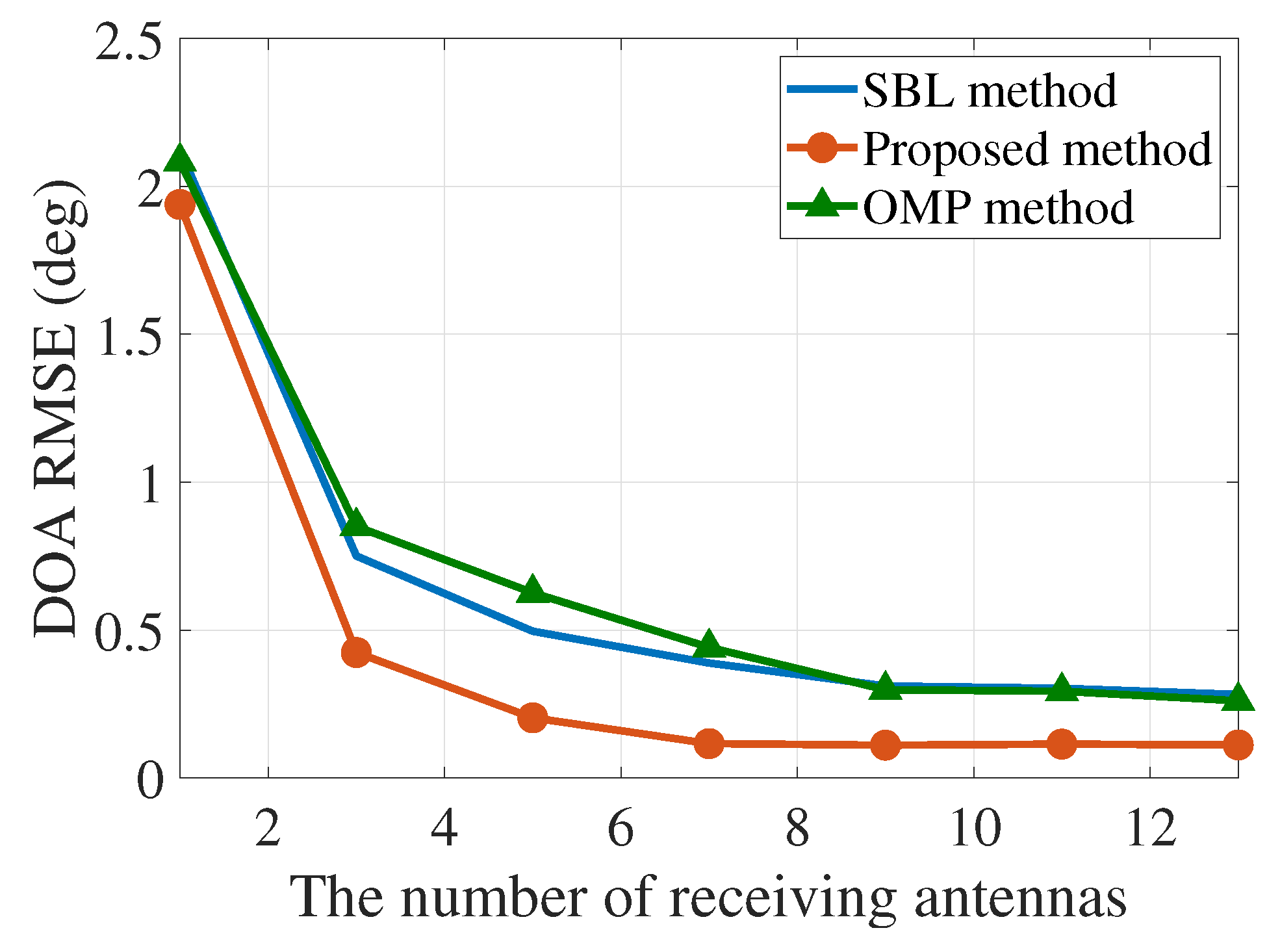
The DOA estimation performance with different numbers of the transmitting and receiving antennas is also shown in
Figure 10 and
Figure 11, respectively. We can find that the estimation performance is improved with more antennas. However, with the limit of the grid size, the estimation performance cannot be improved significantly when the number of transmitting antennas is higher than 8 and that of receiving antennas greater than 7. Compared with the SBL and OMP methods, the proposed method can achieve better DOA estimation performance. When the grid size is large (i.e., greater than 2°), we can find that the RMSE of the DOA estimation using the proposed method is
, which is much lower than the SBL and OMP methods, as shown in
Figure 8. Additionally, the computational time with the 2° grid size is also half of the one with the grid size being 1°.
Finally, the computational complexity is investigated. As shown in
Table 2, we show the computation time of the SBL, OMP, and proposed methods with different grid sizes. The proposed method has higher computational complexity than SBL and OMP methods but is comparable with the SBL method. For the computational time, the grid size controls the total computational time. Additionally, the relative time is also added, where we normalized the relative time of the proposed method as
. Hence, the computational complexity of the proposed method is acceptable.