Abstract
It is usual in literature that power sharing among grid-forming sources of an isolated microgrid obeys their energy rating, instead of economic agreements between stakeholders, and circulating energy among them is usually avoided. However, these energy interchanges make strong sense and classical power sharing methods must be reformulated in the context of prosumer-based microgrids. This paper proposes a secondary control method for a prosumer-based low-voltage nanogrid that allows for energy interchange between prosumers, where storage systems, together with PV generators, are the controllable grid-forming sources. A power flow technique adapted to islanded microgrids is used for secondary control algorithm and the whole hierarchical control strategy for the prosumer converter is simulated and validated. This hierarchical control consists of three stages: tertiary control plans the energy interchange among prosumers, secondary obtains different voltage and power setpoints for each of the grid-forming sources, and, finally, primary control guarantees stable voltage and frequency values within the nanogrid with droop rules. Inner control loops for the power converter are also defined to track setpoints and assure stable performance. Simulation tests are carried out, which prove the stability of the proposed methods and the accuracy of the setpoint tracking.
1. Introduction
These days, it is generally accepted that microgrids are a key structure to integrate Distributed Generation (DG) and energy storage into the smart grids [1,2,3,4]. Hierarchical control for microgrids constitutes a trade-off between the accuracy of centralized control techniques and the flexibility and resilience that are presented by the distributed control ones [2]. Under this control scheme, primary control assures power balance within the microgrid, when it is islanded, usually by means of well-known droop rules, at the cost of frequency and voltage deviations; secondary control is responsible for restoring frequency and voltage to reference values and tertiary control (sometimes only present in grid-connected situation) performs economic optimization, according to energy price, energy efficiency targets, or agreements between stakeholders [3].
Under current European Energy Policies [5], renewable energy penetration and energy efficiency must be significantly improved during the next decades. An increase in the use of DG and Energy Storage Systems (ESS) and a transformation of classical consumers in the so-called prosumers is required to accomplish this objective. These prosumers interchange energy bidirectionally with the main power system and with other neighboring prosumers [6]. Energy trading has attracted the attention of researcher during the last years, although most of the works are focused on energy interchange between microgrids. For example, [7] proposes a supply-demand model as a market framework to optimize energy interchange between islanded microgrids. The authors in [8] go further with incentive mechanism for energy interchange between microgrids that addresses the coupling between this purpose and internal energy sharing within each microgrid. Other authors, like [9], address the energy trading issue between producers in a community microgrid. A new concept of Collaborative Energy Economy is introduced and discussed in [10], as an attempt to emulate the well-known collaborative platforms already working in sectors, such as mobility or house-renting. Under this concept, prosumers participate in a local or community energy market to both buy and sell energy to other prosumers, with the aim of maximizing their profits, within the concept of Peer-to-Peer (P2P) energy trading. Currently, many papers address the challenge of P2P trading within microgrids [11,12], but they usually deal with the algorithm for the economic trading. There is a lack of research regarding how the Distributed Energy Resources (DER) of a microgrid can follow the power setpoints derived from P2P contracts jointly with hierarchical control usually applied in islanded grid mode. More specifically, the following assumptions are usual in the microgrid control literature [2,3]:
- Grid-forming DERs, i.e., those DERs responsible for keeping proper and stable frequency and voltage values within the microgrid, are connected (either directly or through radial feeders) to the same Point of Common Coupling (PCC), where the loads are also connected [13]. In this case, voltage setpoint is the same for every DER and virtual impedance is usually required to decouple Active Power-Frequency and Reactive Power-Voltage dependence relationships.
- Power sharing obeys to individual energy ratings, thus avoiding circulating currents among DERs. Therefore, power interchange due to economic agreements is usually discarded in isolated mode.
Moreover, most recent and complete overview on secondary control for AC microgrids [4] assigns to this control stage the mission of obtaining a correction term for the droop controller of islanded microgrids in such a way that, after a finite time period, both the frequency and voltage amplitude reach their respective reference values. These reference values are the same for every grid-forming DERs of the microgrid, according to the desired values in the common PCC. Under this premise, the active and reactive power of loads are shared among DERs, but no power interchange is allowed in the steady state among them. Therefore, collaborative economy and P2P agreements are not possible in those islanded microgrids.
However, in a microgrid or nanogrid composed by several prosumers, DG and loads (and ESS, if they are included) are located together in each load bus of the nanogrid. There is not a common PCC, whose voltage is the common voltage setpoint, and circulating currents among prosumers cannot be avoided, but they are even desirable to accomplish with collaborative energy trading. In this context, different voltage setpoints are required for each DER, along with different power setpoints. Power flow equations must be considered within the microgrid to assure the technical feasibility of the adopted solution to address this challenge.
The strategy presented in [14] develops an optimization method to obtain different voltage and reactive power setpoints for each of the agents of a microgrid. Only voltage control is performed in this paper, whereas frequency control is assumed to be performed by other DERs. The power flow equations within the microgrid are also considered as constraints for the method. However, both voltage and reactive power setpoints obey to the objective to improve accuracy in the setpoint accomplishments, according to DER rating and voltage and power allowed range. Therefore, neither tertiary control nor active/reactive power interchange among DERs are considered in this control technique. On the other hand, [15] proposes a hierarchical control scheme for islanded microgrids in which estimations of the average values of power flows between neighboring DERs are used to control the power and frequency. This proposal decentralizes secondary control and, therefore, improves the resilience in case of communication faults, but it requires continuous updating of measured voltage and current values and calculated power and frequency, with the consequent computational cost.
The main contributions of this paper can be summarized, as follows:
- P2P energy trading between prosumers is addressed in islanded microgrids, from the point of view of the voltage and power setpoint generation and how the DER converter can follow them. Power flow among prosumers is guaranteed due to different voltage setpoint in each prosumer’s load bus.
- A novel secondary control based on power flow algorithm in microgrids is proposed to reach classical secondary control target as well as allow energy interchange between DERs.
- A residential nanogrid is simulated with all the necessary control loops to perform hierarchical control, starting from previously mentioned setpoints.
The nanogrid under study consists of two residential prosumers, both with PV generation and battery ESS systems, which are connected to their load buses by means of a single-phase converter. A two-wire cable connects load bus of both prosumers. The nanogrid operates islanded from the main grid.
2. Proposed Control Strategy
A hierarchical control structure is proposed in this paper, which improves the structures that are generally accepted in literature [2]. Three stages, which range from the outer and slower control loop to the inner and faster one, are considered:
- Tertiary control aims to optimize the energy use inside the nanogrid. Starting from generation and demand forecasting, demand and storage systems are managed at this stage to match power and energy balance in the isolated nanogrid with optimal resource exploitation. Energy interchange among the resources within the nanogrid presents a clear importance when it is grid-connected, with the aim of obtaining economic advantages and improving self-consumption and self-sufficiency. Another scenario for this tertiary control is P2P energy interchange, which schedules energy sharing under agreement in both grid-connected and isolated situation.
- Secondary control determines the electrical magnitude setpoints for the DERs. In the context of isolated nanogrids, the target of this stage is usually to restore the voltage and the frequency in a unique PCC, with a power-sharing strategy that aimed at using the available resources to keep secure and stable electrical conditions, without considering the economic or agreement-based energy interchange among DERs. In this paper, the P2P energy interchange concept is taken into account at this control stage to allow for complying with economic or energy agreements among different prosumers.
- Primary control acts automatically to obtain stable frequency and voltage magnitudes when power balance mismatching occurs due to unexpected changes in demand or generation. A decentralized droop control is the most frequently used strategy for this stage, whose formulation strongly depends on the resistive/inductive character of the system.
These three control stages are described below, although secondary control draws most of the attention in this paper.
2.1. Nanogrid Tertiary Control
This control stage constitutes the Energy Management System (EMS) of the nanogrid. It makes special sense when the nanogrid is grid-connected and the energy flows with the main grid are intended to be scheduled to achieve economic advantages and to shave power peaks, to improve self-consumption and self-sufficiency rates inside the nanogrid or to accomplish with P2P interchange agreements. However, an energy management procedure is also important in islanded nanogrids, to assure power balance with the highest benefit for the nanogrid stakeholders and with an optimal resource exploitation. These targets usually to active power interchanges among the prosumers or with the main grid (when grid-connected). It is desirable that power generated by PV installations is mostly used to improve self-consumption and reduce energy that is generated from polluting sources. Therefore, in this paper, it is assumed that PV generator is working at Maximum Power Point (MPP) regime unless surplus energy is produced. In that case, generated power is curtailed and the PV generator moves to the Reference Power Point (RPP) mode (see [16] for further explanation).
Similarly, demand is assumed to be managed according to a valid Demand Side Management (DSM) technique, like that proposed in [17]. Therefore, each battery charging/discharging power is obtained from the nanogrid power balance and the sharing method selected. An example of tertiary control for batteries in microgrids of prosumers can be seen in [18].
After this tertiary control stage, active power hourly setpoints are obtained for both PV generator and battery. Assuming that they are connected to prosumer’s load bus by means of a common power converter, the setpoint for the output active power of the converter after tertiary control is obtained in (1) for each hour t of the day.
On the other hand, reactive power should not circulate among different DERs of the nanogrid, as it would produce higher losses and voltage drops than necessary. Therefore, the reactive power setpoint for each converter of the nanogrid is also obtained in (1).
where:
- PG-TERCi: hourly average active power setpoint for tertiary control (W)
- QG-TERCi: hourly average reactive power setpoint for tertiary control (VAr)
- PGi: hourly average forecasted PV generation power, once curtailed (W)
- PBi: hourly average scheduled battery power (positive values when charging, negative when discharging) (W)
- QDi: hourly average forecasted reactive power demanded by load in bus i (VAr)
2.2. Nanogrid Secondary Control
Starting from hourly setpoints of the tertiary control, secondary control must provide active and reactive power and voltage setpoints for the converter output, with higher time resolution. The objective of secondary control is usually to restore frequency and voltage values in the nanogrid within proper values, once primary control has changed the values to stabilize them after unexpected changes in generated or demanded power values. In this paper, one-minute resolution time has been selected for secondary control. A demanding communication system is not required with this resolution time. Battery power (PB0i) is obtained by linear interpolation between consecutive hourly scheduled power values, whereas the generated (PG0i) and demanded (PD0i) power values are both measured and values of the previous minute are used to obtain secondary control setpoints. In the case of communication fault, measured values can be substituted by an interpolation of forecasted values, with the consequent decrease in accuracy, which will be compensated by primary control.
Unlike those works in which every grid-forming converters are connected to the same PCC and voltage setpoints for them are equal, multi-bus prosumer nanogrids require different voltage setpoints for each bus, according to pursued power input and the output of each prosumer and power flow constraints due to nanogrid configuration and impedance between buses. Active and reactive power setpoints in secondary control are changed according to a droop technique, and they must assure consistent behavior with voltage setpoints and power flows. Therefore, a power flow algorithm for islanded microgrids is used in this paper to obtain both power and voltage setpoints. As updating of initial values is done once a minute, during the minute the nanogrid can be considered as a quasi-static system.
Power flow algorithms for islanded microgrids can be found in literature [19], although they usually aim to analyze the microgrid, instead of obtain control setpoints. Several differences exist between this problem and classical power flow problem in bulk power systems:
- There is no slack bus in microgrids, as there is not a bus with a powerful generation capacity that assures stable frequency and provides power losses. Two kind of buses are usual in microgrids: PQ (load or grid-following generation buses) and droop buses (this is a new kind of bus, which shares the responsibility to keep stable and proper frequency values).
- Frequency value of the system is not guaranteed, but it is a variable of the problem.
- Active and reactive power generation is governed by droop rules.
2.2.1. Element Modelling for Power Flow Algorithm
The lines in nanogrids are short. Consequently, shunt admittance can be neglected according to the so-called short line model. Only series impedance is considered (2).
where:
- Rij: line resistance (Ω)
- Xij: line reactance (Ω)
- Lij: line inductance (H)
- f: nanogrid frequency (Hz)
Regarding loads, active and reactive power demanded depend on the voltage and frequency in the connection bus. The degree of this dependence varies with the kind of load. A general model for linear loads can be obtained from (3).
where:
- PD-SECi: active power demand estimation for secondary control (W)
- QD-SECi: reactive power demand estimation for secondary control (VAr)
- Ui: RMS value of the voltage in bus i (V)
- Un: rated voltage (230 V in low-voltage single-phase systems)
- fn: rated frequency (50 Hz)
- α, β: active and reactive exponents
- kpf, kqf: sensitivity factors of active and reactive power to frequency (pu/pu)

Table 1.
Exponents and sensitivity factors of active and reactive power to voltage and frequency.
The modelling of a generating unit differs depending on its grid-following or grid-forming character. Generators that do not control voltage or frequency act as PQ buses and load model with the proper sign criterion is valid for them. However, generators that are responsible to control voltage and frequency of the microgrid respond to droop rules: (4) for mainly-inductive grids and (5) for mainly-resistive grids [22].
where:
- PG-SECi: active power setpoint for the converter output, for secondary control (W)
- QG-SECi: reactive power setpoint for the converter output, for secondary control (VAr)
- mp, mq, kp, kq: droop coefficients
Droop coefficients control P or Q variations with voltage and frequency. They are usually obtained, starting from extreme values of proper ranges of voltage, frequency, and active and reactive power, although some authors propose their adjustment as a function of battery SoC [23,24].
2.2.2. Power Flow Algorithm Formulation
The authors in [19] develop the algorithm for three-phase systems, with independent equations for each phase and imposing balanced voltage in droop buses. In this paper, the model in [19] is reformulated for single-phase microgrids.
The power flow equations are similar to the classical power flow algorithm for bulk power systems. Net injected active (PSECi) and reactive (QSECi) power in bus i are calculated in (6).
with:
- USECi, δSECi: RMS value (V) and phase angle (rad) of i-bus voltage
- Yik, γik: magnitude (S) and phase angle (rad) of ik-element of Ybus admittance matrix
The equations to solve for each bus are (7) for PQ buses (unknown variables USECi and δSECi) and (8) for droop buses (unknown variables PSECi, QSECi, USECi and δSECi). One of the droop buses acts as phase angle reference (δSEC1 = 0), whereas frequency f is an unknown variable. Therefore, the same number of equations and variables are provided.
In this paper, resistive grids have been assumed and the trust-region Newton method has been selected to solve the problem, as suggested in [19,25].
Therefore, secondary control provides power and voltage setpoints in each prosumer’s load bus (Figure 1), according to initial agreed power flows and voltage and frequency control within the nanogrid.
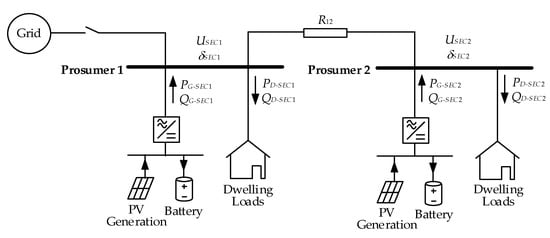
Figure 1.
Secondary control setpoints in the nanogrid.
2.3. Nanogrid Primary Control
The primary control acts in each prosumer converter, which intends to follow power and voltage setpoints obtained in secondary control, but it makes adjustments to dynamically stabilize the frequency and voltage in a decentralized procedure. Figure 2 shows the electric scheme of the converter AC filter, where the power and voltage magnitudes are also depicted.
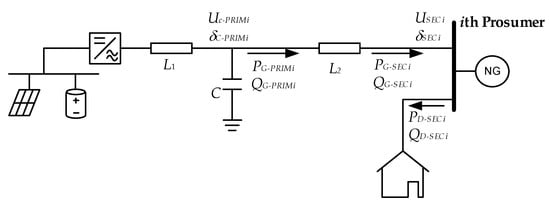
Figure 2.
Converter magnitudes for primary control.
Inductances L1 and L2 and capacitance C constitute the LCL output filter of the converter. Setpoints in prosumer’s load bus have been provided by secondary control. Primary control firstly obtains setpoints for capacitor voltage and the power injected in L2, necessary to perform primary control.
Equation (9) allows for obtaining the voltage setpoint for the capacitor (Uc-PRIMi, δc-PRIMi) and the active and reactive power setpoints (PG-PRIMi, QG-PRIMi) in the input terminal of reactance L2.
In (9), iL2 is the current in the filter inductance L2 and * denotes complex conjugate.
A droop control is added to keep frequency and voltage stable, besides the required inner voltage and current control loops for following these setpoints. In this case, the impedance between the filter capacitor and the load bus is mainly inductive, therefore the droop condition is that of (4). Droop control obtains corrected setpoints of capacitor voltage uci_ref, according to measured values and droop characteristic in (4):
where:
- uci-ref: reference voltage signal in the filter capacitor of the ith converter
- Uci-ref: RMS value of uci-ref (V)
- θci-ref: angle signal of uci-ref
- Pi: measured active power in the filter reactance L2 of the ith converter (W)
- Qi: measured reactive power in the filter reactance L2 of the ith converter (VAr).
Droop constants both in secondary and primary control have been obtained, starting from extreme values of the proper range of frequency (±1 Hz) and voltage (±7% rated voltage), according to Spanish regulation [26], and from the available capacity of each prosumer’s resources (while considering PV generation, battery charge/discharge maximum power, and SoC).
It is worth noting that droop rules have been split into two stages (one in secondary control through the resistive line between prosumers and another one in primary control through the inductive filter). Therefore, decoupling between active/reactive power and frequency/voltage is assured and virtual impedance is not required.
2.4. Power Converter Inner Voltage and Current Control Loops
Proportional-resonant (PR) controllers have been selected for both control loops, since they can track sinusoidal references with zero steady-state error and present high disturbance rejection capability [27]. At the same time, these controllers perform with constant switching frequency in comparison with another non-linear alternatives as hysteresis or predictive controllers [28]. Besides, PR controllers do not include any parameter of the plant in the feedback loop and they also reduce the computational burden (PR works in the αβ-stationary reference frame, avoiding dq-rotational transformation [29]). The ideal transfer function of a PR controller is shown in (11):
where ωn is the reference angular frequency, in this case, 2π50 rad/s.
The converter voltage controller obtains a reference current according to the error between reference and measured values of capacitor voltage. A PR controller has been used for this loop, with kP-PR = 0.001 and kR-PR = 100, as was previously mentioned.
Finally, the current controller compares reference and measured values of the converter output current and it obtains the modulating signal for the converter switching by means of another PR controller with kP-PR = 20 and kR-PR = 2000. The voltage and the current PR controller coefficients were both tuned by means of the guidelines provided in [30].
Figure 3 depicts these control loops, where uci is the measured voltage signal in the filter capacitor of the ith converter and iL1 is the current in the inverter-side reactance of the LCL filter.
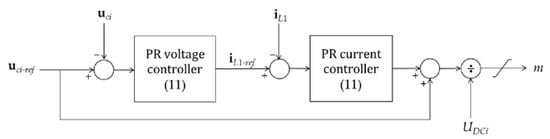
Figure 3.
Converter inner control loops.
From the obtained modulating signal, the switching signals for the converter gates S1–S4 (see Figure 5) are generated by means of the Sinusoidal Pulse Width Modulation (SPWM) technique.
2.5. Battery DC/DC Converter Control Loop
The last controller is that of the DC/DC converter that connects the battery to the DC-link. This converter has two simultaneous targets: keeping power values according to scheduled setpoints and controlling a constant value for the voltage of the converter DC-link. Two terms for the battery current are obtained to address both of the targets. The first one is obtained in (12) from the expected power of the converter, which was provided by the PV generator and the battery voltage. The second term adjusts the current to keep DC-bus voltage stable around 400 V (Figure 4). This second term is also responsible to cover the converter losses and the mismatch between power setpoint and actual values.
where:
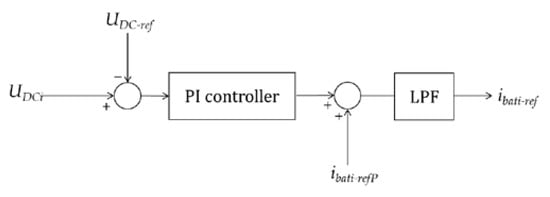
Figure 4.
Battery control loop.
- ibati-ref: reference charging current for the ith battery (A)
- ibati-refP: power-reference charging current for the ith battery (A)
- UDC-ref: reference value for the DC-link voltage of the ith converter (V)
- UDCi: measured value for the DC-link voltage of the ith converter (V)
- ipvi: measured value for the ith PV generator current (A)
- ubati: measured value for the battery voltage (V)
A dead-beat technique is used to control the battery current, according to (13) [31].
where:
- dbati: duty cycle for the ith battery DC/DC converter
- ibati: measured value for the battery current (A)
- Lbat: filter inductance (H)
- Rbat: filter resistance (Ω)
- Ts: sampling period (s)
A Pulse Width Modulation (PWM) technique is used to convert this duty cycle to switching signals for the converter gates S5–S6 (see Figure 5).
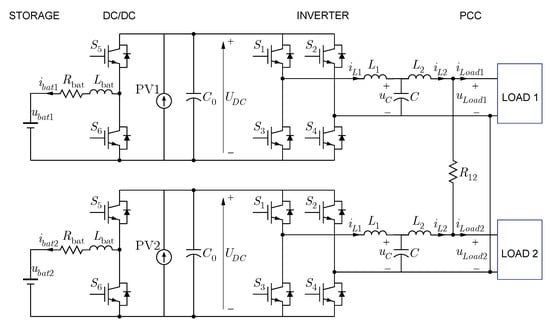
Figure 5.
Nanogrid simulation model.
3. Case Study and Simulation Parameters
As was previously described, the nanogrid in this study consists of two prosumers, each of them having PV generation, battery ESS, and dwelling loads. Their load buses are connected by a 6 mm2 cross-section, 20 m long two-wire cable. As PV generation is not the matter of study in this work, it has been modelled as a DC current source that is assumed to be working at MPP at each house. However, battery ESS consists of a battery source and a DC/DC converter, whose control strategy has been discussed in Section 2.3. A common inverter connects both PV generation and ESS to the load bus of each prosumer. The nanogrid is islanded, i.e., it is disconnected from the main grid. Figure 5 depicts the nanogrid schematic and Table 2 shows the simulation parameters. It can be observed that the droop constants used in primary control are the same or proportional (scaled for stability reasons) to those of secondary control, but changing the relationship between Reactive Power-Frequency and Active Power-Voltage (in resistive line between prosumers for secondary control) and between Active Power-Frequency and Reactive Power-Voltage (in inductive filter for primary control).

Table 2.
Simulation parameters.
In the test performed, firstly, the ESS charges the inverter DC-link up to a stable voltage of 400 V. Subsequently, the inverter is connected and the reference values for the different control loops are generated (Table 3 shows the initial values of power demand forecast and setpoints obtained from secondary control. Constant power load model has been used, with zero value for exponents and sensitivity factors, according to (3)). It can be observed that active power setpoint of each converter does not match demand power of its prosumer. The reason lies on the droop rule used in secondary control for power sharing, according to available energy resources of each prosumer (8).

Table 3.
Initial and updated power and voltage setpoints from secondary control.
The last control connected is the droop control, which adjusts active and reactive power with the aim of keeping stable frequency and voltage values. The PV current source is connected once the converter is supplying the load using only the ESS as a source, supplying part of the demanded load (each prosumer’ PV installations is assumed to produce 200 W).
As it was described in the previous section, secondary control has provided a set of power and voltage setpoints to each converter, which start from the tertiary control strategy and the power flow rules within the nanogrid. It is assumed at the beginning of the test that the demanded load and PV generation have been properly forecasted, and the nanogrid converters are operating at the rated frequency and planned voltage. Afterwards, an unplanned change in load occurs, which increases the active power of prosumer 1 in 100 W and reactive power of prosumer 2 in 30 VAr. Consequently, droop control acts by slightly moving frequency and voltage from planned values.
Once the secondary control loop reaches a new cycle, updated setpoints are sent to both prosumers’ converters (updated values in Table 3). These new setpoints are obtained, starting from the last PV generation and load measurements. In this test it is assumed that these measured loads match actual loads. Therefore, both of the converters reach their respective power and voltage setpoints and frequency and voltage are restored to planned values. In the other case, droop control should have kept a slight deviation in frequency and voltage magnitude until correct setpoint had been received.
4. Simulation Results and Discussion
The nanogrid in Figure 5 has been simulated by means of Matlab/Simulink®. Table 4 depicts the time sequence of the simulation. It is the same for both prosumers.

Table 4.
Time sequence of the nanogrid simulation.
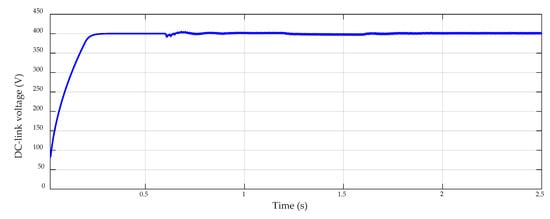
Figure 6.
DC-link voltage.
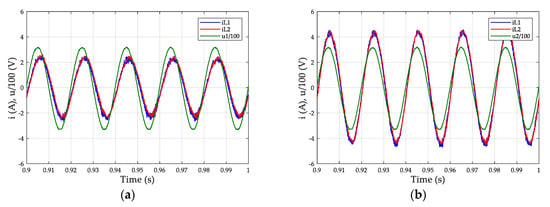
Figure 7.
Voltage in the load bus and current in both reactances of converter LCL filter: (a) Prosumer 1; (b) Prosumer 2.
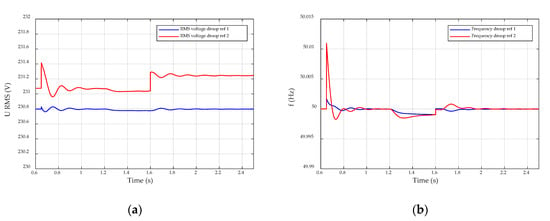
Figure 8.
Droop control performance: (a) Voltage droop reference in the filter capacitor; and, (b) Frequency droop reference.
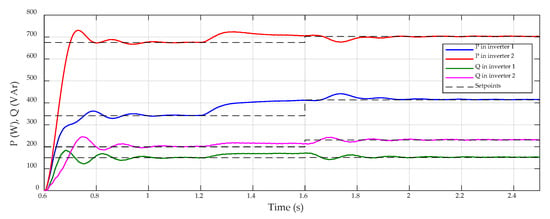
Figure 9.
Active and reactive power output in both inverters, calculated from measured voltage and current values.
Figure 6 shows the evolution of DC-link voltage with time, in converter of prosumer 1. The same behavior is observed in the other converter. At the beginning, the control loop of battery DC/DC converter charges the DC-link capacitor to a stable voltage of 400 V. After 0.6 s, the connection of the inverter produces a slight oscillation in DC-link voltage, but its value keeps very close to 400 V. The rest of the simulation shows how this voltage is corrected to 400 V after each event.
Figure 7 depicts the voltage in the load bus and currents in both reactances of the LCL filter of both converters, once the converter and the PV have been connected and before the load change. Voltage is scaled by a factor 100 for better visibility. As can be seen, the current in L2 is a filtered version of current in L1. They are both quite sinusoidal and their amplitude and phase-shift are consistent with the power setpoints of each converter.
Voltage setpoint in the filter capacitor and frequency, both being obtained after droop correction (10), are shown in Figure 8. It can be observed how both of the parameters suffer from an initial transitory change at 0.65 s, when droop control is activated. After a short transient, they reach a stable value matching initial setpoints. At 1.2 s, when the loads change, frequency and voltage both slightly change their values according to droop rules. Once the secondary control setpoints are updated (1.6 s), rated frequency and new voltage setpoints are reached and kept stable after a short time period. Anyway, voltage and frequency deviations are both low enough for the nanogrid to properly work, even before the secondary control updating. Therefore, if high unexpected changes occur in generation or demand, or a communication fault avoid setpoint updating, the nanogrid can securely work until the abnormal situation is corrected.
Finally, Figure 9 shows the measured active and reactive power of both prosumers’ inverters. The power values are calculated from measured voltage in filter capacitors (uci) and measured current in filter L2 reactances (iL2). Setpoints for active and reactive powers in primary control (PG-PRIMi and QG-PRIMi) are also depicted in the dashed line in the figure, under their calculated values. It can be observed that the calculated power values reach their initial setpoints once the inverter is connected, after a short transient period. Subsequently, loads change starting from 1.2 s of simulation and droop control shares increment in both active and reactive powers, pushing the calculated powers aside from setpoints. Once the setpoints are updated (1.6 s), the calculated power values reach again their new setpoints with a proper accuracy.
The dynamic performance of controllers shows a proper combination of fast and low-oscillating response (after each change, new stable power values are reached after 0.2–0.3 s) and a negligible steady-state error, as can be observed in the power values in Figure 9. Regarding dynamic response of voltage and current signals, Figure 10 shows, as an example, a detail of the transient in voltage in the load bus and current in the outer filter reactance of prosumer 2, when the voltage and control loops are activated. It can be observed that the transient in voltage is fast and accurate, whereas current signal presents a low amplitude oscillation, consistent with transient observed in power values (Figure 9). However, neither high frequency oscillations nor sudden peaks are observed.
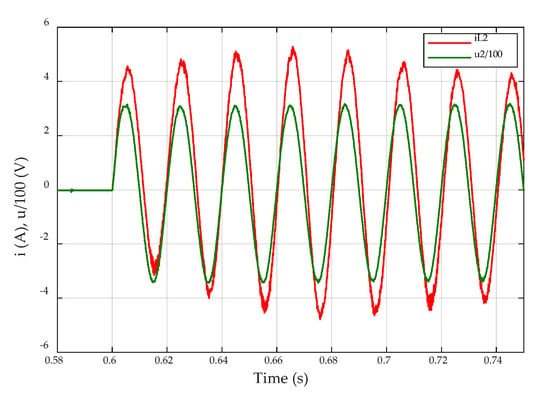
Figure 10.
Detail of voltage and current transient in the converter output of prosumer 2.
5. Conclusions and Future Works
This paper proposes and validates a hierarchical control scheme for prosumer nanogrids, which includes a novel secondary control strategy to allow for energy interchange between prosumers, aligned with P2P trading. Under the proposed secondary control, setpoints for active and reactive power and voltage in each prosumer load bus are generated to allow for energy interchange between them. Simultaneously, power flow equations, frequency reference value and power sharing based on droop rules are considered in the secondary control algorithm. All of the control loops that are required to manage a prosumer converter to connect both PV generation and battery ESS are designed and tested. Simulation results show a proper performance of the control loops, a very accurate tracking of the power and voltage setpoints and a very stable behavior of the voltage and the frequency within the nanogrid, even after unexpected changes in loads. Power flow between prosumers can be controlled, according to P2P agreements or other economic strategies, as a different controlled voltage value is obtained in each prosumer’s load bus.
Future steps to continue this research project are the adaptation of the control scheme to grid-connected situation and seamless transition between both states. In addition, experimental tests are planned to demonstrate the method validity in actual lab conditions.
Author Contributions
Conceptualization, E.R.-C. and M.-I.M.M.; methodology, E.G.-R. and M.R.-C.; validation, C.R.-C., E.G.-R. and M.R.-C.; formal analysis, E.G.-R., E.R.-C. and F.B.-G.; investigation, E.R.-C.; writing—original draft preparation, E.G.-R.; writing—review and editing, C.R.-C. and F.B.-G.; supervision, A.M.-M.; project administration, E.G.-R.; funding acquisition, C.R.-C., E.G.-R., E.R.-C., F.B.-G. and M.-I.M.M. All authors have read and agree to the published version of the manuscript.
Funding
This research was funded by the Spanish Agencia Estatal de Investigación (AEI), Fondo Europeo de Desarrollo Regional (FEDER), grant number TEC2016-77632-C3-1-R (AEI/FEDER, UE). Junta de Extremadura (Regional Government) also co-supported this work under the program “Ayudas Talento (TA18003)”.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Acronyms | |
| DER | Distributed Energy Resource |
| DG | Distributed Generation |
| DSM | Demand Side Management |
| EMS | Energy Management System |
| ESS | Energy Storage System |
| MPP | Maximum Power Point |
| PCC | Point of Common Coupling |
| PR | Proportional-Resonant |
| PV | Photovoltaic |
| PWM | Pulse Width Modulation |
| RPP | Reference Power Point |
| SoC | State of Charge |
| Variables | |
| C | Capacitance of the LCL Filter |
| C0 | Capacitance of the DC-link capacitor |
| dbati | Duty Cycle of the ith Prosumer’s Battery Converter |
| f | Frequency |
| fn | Rated Frequency |
| ibati | Charging Current of the ith Prosumer’s Battery |
| ibati-ref | Reference Charging Current of the ith Prosumer’s Battery |
| ibati-refP | Power-Reference Charging Current of the ith Prosumer’s Battery |
| iL1 | Current Signal in the Inner Filter Reactance of the ith Prosumer |
| iL1-ref | Reference Current Signal in the Inner Filter Reactance of the ith Prosumer |
| iL2 | Current Signal in the Outer Filter Reactance of the ith Prosumer |
| ipvi | Current of the ith Prosumer’s PV Generation System |
| kp | P-U Droop Coefficient |
| kpf | Sensitivity Factor of Active Power Load to Frequency |
| kP-PR | Proportional-Term Constant of Proportional-Resonant Controllers |
| kq | Q-f Droop Coefficient |
| kqf | Sensitivity Factor of Reactive Power Load to Frequency |
| kR-PR | Resonant-Term Constant of Proportional-Resonant Controllers |
| L1 | Converter-Side Inductance of the LCL Filter |
| L2 | Grid-Side Inductance of the LCL Filter |
| Lbat | Inductance of the Battery Filter |
| Lij | Line Inductance of Feeder Between ith and jth Prosumers |
| mp | P-f Droop Coefficient |
| mq | Q-U Droop Coefficient |
| PB0i | 1 Minute-Resolution Interpolation of PBi |
| PBi | Charging Power of the ith Prosumer’s Battery |
| PD0i | Last-Minute Measured Active Power Demand of the ith Prosumer |
| PDi | Hourly Average Active Power Demand Forecasting of the ith Prosumer |
| PD-SECi | Active Power Estimation of the ith Prosumer’s Demand, for Secondary Control |
| PG0i | Last-Minute Measured Power PV Generation of the ith Prosumer |
| PGi | Hourly Average Power PV Generation Forecasting of the ith Prosumer |
| PG-PRIMi | Active Power Setpoint for the ith Converter Output, in Primary Control |
| PG-SECi | Active Power Setpoint for the ith Converter Output, in Secondary Control |
| PG-TERCi | Active Power Setpoint for the ith Converter Output, in Tertiary Control |
| Pi | Measured Active Power in the Outer Filter Reactance of the ith Converter |
| PSECi | Net Injected Active Power in the ith bus, in Secondary Control |
| QDi | Hourly Average Reactive Power Demand Forecasting of the ith Prosumer |
| QD-SECi | Reactive Power Estimation of the ith Prosumer’s Demand, for Secondary Control |
| QG-PRIMi | Reactive Power Setpoint for the ith Converter Output, in Primary Control |
| QG-SECi | Reactive Power Setpoint for the ith Converter Output, in Secondary Control |
| QG-TERCi | Reactive Power Setpoint for the ith Converter Output, in Tertiary Control |
| Qi | Measured Reactive Power in the Outer Filter Reactance of the ith Converter |
| QSECi | Net Injected Reactive Power in the ith bus, in Secondary Control |
| Rbat | Resistance of the Battery Filter |
| Rij | Line Resistance of Feeder Between ith and jth Prosumers |
| SG-PRIMi | Complex Power Setpoint for the ith Converter Output, in Primary Control |
| SG-SECi | Complex Power Setpoint for the ith Converter Output, in Secondary Control |
| t | Time |
| Ts | Sampling Period |
| ubati | Voltage of the ith Prosumer’s Battery |
| uci | Voltage Signal in the Filter Capacitor of the ith Converter |
| Uci | RMS Value of the Voltage in the Filter Capacitor of the ith Converter |
| uci-ref | Reference Voltage Signal in the Filter Capacitor of the ith Converter |
| Uci-ref | Reference RMS Value for the Voltage in the Filter Capacitor of the ith Converter |
| Uc-PRIMi | RMS Value of the Voltage Signal in the Filter Capacitor of the ith Converter, in Primary Control |
| uc-PRIMi | Voltage Signal in the Filter Capacitor of the ith Converter, in Primary Control |
| Udci | Voltage in DC-Bus of the ith Converter |
| Udc-ref | Reference Voltage of DC-Bus |
| Ui | RMS Value of the Voltage in the ith bus |
| ui | Voltage Signal in the ith bus |
| Un | Rated Voltage |
| uSECi | Reference Voltage Signal in the ith bus, in Secondary Control |
| USECi | RMS Value of the Voltage in the ith bus, in Secondary Control |
| Xij | Line Reactance of Feeder Between ith and jth Prosumers |
| Yik | Module of the ik-element of the system admittance matrix |
| Zij | Line Impedance of Feeder Between ith and jth Prosumers |
| α | Sensitivity exponent of Active Power Load to Voltage |
| β | Sensitivity exponent of Reactive Power Load to Voltage |
| δc-PRIMi | Phase Angle of the Voltage in the Filter Capacitor of the ith Converter, in Primary Control |
| δSECi | Phase Angle of the Voltage in the ith bus, in Secondary Control |
| γik | Phase Angle of the ik-element of the system admittance matrix |
| θci-ref | Reference Angle Signal of the Voltage in the Filter Capacitor of the ith Converter |
| ωn | Reference Angular Frequency |
References
- Vasquez, J.C.; Guerrero, J.; Miret, J.; Castilla, M.; De Vicuna, L.G. Hierarchical Control of Intelligent Microgrids. IEEE Ind. Electron. Mag. 2010, 4, 23–29. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled DC and AC microgrids—A general approach towards standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Lu, J.; Zhang, X.; Koh, L.H.; Su, M.; Guerrero, J.M.; Hai, K.L. Distributed Hierarchical Control of AC Microgrid Operating in Grid-Connected, Islanded and Their Transition Modes. IEEE Access 2018, 6, 77388–77401. [Google Scholar] [CrossRef]
- Khayat, Y.; Guerrero, J.M.; Bevrani, H.; Shafiee, Q.; Heydari, R.; Naderi, M.; Dragicevic, T.; Simpson-Porco, J.W.; Dorfler, F.; Fathi, M.; et al. On the Secondary Control Architectures of AC Microgrids: An Overview. IEEE Trans. Power Electron. 2019. [Google Scholar] [CrossRef]
- European Commission. The Strategic Energy Technology (SET) Plan. At the Heart of Energy Research & Innovation in Europe. Available online: https://setis.ec.europa.eu/publications/set-plan-implementation-progress-reports/strategic-energy-technology-set-plan-heart-of (accessed on 29 November 2019).
- Gao, C.; Xu, D.; Miao, L.; Yu, X. A redundant parallel control strategy of multiple PCS (power conversion system) for microgrid in islanded operation. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 3147–3151. [Google Scholar]
- Gregoratti, D.; Matamoros, J. Distributed energy trading: The multiple-microgrid case. IEEE Trans. Ind. Electron. 2015, 62, 2551–2559. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Incentivizing energy trading for interconnected microgrids. IEEE Trans. Smart Grid 2018, 9, 2647–2657. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Zhang, C.; Thomas, L.; Cheng, M.; Jenkins, N. Peer-to-peer energy trading in a community microgrid. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Baez-Gonzalez, P.; Rodriguez-Diaz, E.; Vasquez, J.C.; Guerrero, J.M. Peer-to-peer energy market for community microgrids [Technology leaders]. IEEE Electrif. Mag. 2018, 6, 102–107. [Google Scholar] [CrossRef]
- Neagu, B.C.; Grigoraş, G.; Ivanov, O. An efficient peer-to-peer based blockchain approach for prosumers energy trading in microgrids. In Proceedings of the 2019 8th International Conference on Modern Power Systems (MPS), Cluj Napoca, Romania, 21–23 May 2019; pp. 1–4. [Google Scholar]
- Paudel, A.; Beng, G.H. A hierarchical peer-to-peer energy trading in community microgrid distribution systems. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–9 August 2018; pp. 1–5. [Google Scholar]
- Ramos-Ruiz, J.A.; Enjeti, P.; Xie, L. Peer-to-peer energy transaction in microgrids with power electronics enabled angle droop control. In Proceedings of the 2018 IEEE Electronic Power Grid (eGrid), Charleston, SC, USA, 12–14 November 2018; pp. 1–6. [Google Scholar]
- Yang, X.; Du, Y.; Su, J.; Chen, X.; Chang, L. An optimal secondary voltage control strategy for islanded microgrid. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 2880–2885. [Google Scholar]
- Hashmi, K.; Khan, M.M.; Xu, J.; Shahid, M.U.; Habib, S.; Faiz, M.T.; Tang, H. A quasi-average estimation aided hierarchical control scheme for power electronics-based islanded microgrids. Electronics 2019, 8, 39. [Google Scholar] [CrossRef]
- Barrero-González, F.; Miñambres-Marcos, V.; Guerrero-Martínez, M.A.; Romero-Cadaval, E.; Milanes-Montero, M.; González-Romera, E. Photovoltaic converter with smart grid functions. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 6–8 June 2016; pp. 1–6. [Google Scholar]
- Garrido-Zafra, J.; Moreno-Munoz, A.; Gil-de-Castro, A.; Palacios-Garcia, E.J.; Moreno-Moreno, C.D.; Morales-Leal, T.A. Novel direct load control testbed for smart appliances. Energies 2019, 12, 3336. [Google Scholar] [CrossRef]
- Ruiz-Cortés, M.; González-Romera, E.; Amaral-Lopes, R.; Romero-Cadaval, E.; Martins, J.; Milanés-Montero, M.I.; Barrero-González, F. Optimal charge/discharge scheduling of batteries in microgrids of prosumers. IEEE Trans. Energy Convers. 2019, 34, 468–477. [Google Scholar] [CrossRef]
- Abdelaziz, M.M.A.; Farag, H.E.; El-Saadany, E.F.; Mohamed, Y.A.I. A novel and generalized three-phase power flow algorithm for islanded microgrids using a newton trust region method. IEEE Trans. Power Syst. 2013, 28, 190–201. [Google Scholar] [CrossRef]
- Price, W.W.; Casper, S.G.; Nwankpa, C.O.; Bradish, R.W.; Chiang, H.-D.; Concordia, C.; Staron, J.V.; Taylor, C.W.; Vaahedi, E.; Wu, G. Bibliography on load models for power flow and dynamic performance simulation. IEEE Trans. Power Syst. 1995, 10, 523–538. [Google Scholar]
- Arguence, O.; Raison, B.; Cadoux, F. Comments on “Impact of Load Frequency Dependence on the NDZ and Performance of the SFS Islanding Detection Method”. IEEE Trans. Ind. Electron. 2017, 64, 7277–7279. [Google Scholar] [CrossRef]
- VanDoorn, T.L.; Vasquez, J.C.; De Kooning, J.; Guerrero, J.M.; Vandevelde, L. Microgrids: Hierarchical Control and an Overview of the Control and Reserve Management Strategies. IEEE Ind. Electron. Mag. 2013, 7, 42–55. [Google Scholar] [CrossRef]
- Ghanbari, N.; Bhattacharya, S. SoC balancing of different energy storage systems in DC microgrids using modified droop control. In Proceedings of the 2018 IEEE Industrial Electronics Conference (IECON), Washington, DC, USA, 21–23 October 2018; pp. 1–6. [Google Scholar]
- Gkavanoudis, S.I.; Oureilidis, K.O.; Demoulias, C.S. An adaptive droop control method for balancing the SoC of distributed batteries in AC microgrids. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; pp. 1–6. [Google Scholar]
- Li, C.; Chaudhary, S.K.; Savaghebi, M.; Vasquez, J.C.; Guerrero, J.M. Power Flow Analysis for Low-Voltage AC and DC Microgrids Considering Droop Control and Virtual Impedance. IEEE Trans. Smart Grid 2017, 8, 2754–2764. [Google Scholar] [CrossRef]
- Spanish Ministry of Economy. Royal Decree 1955/2000 of 1 December, which Regulates the Activities of Transport, Distribution, Marketing, Supply and Installations of Electricity Authorization Procedures. Available online: http://www.omie.es/files/tr_rd_1955-2000_de_1_diciembre.pdf (accessed on 17 December 2019).
- Zmood, D.N.; Holmes, D.G. Stationary frame current regulation of PWM inverters with zero steady-state error. IEEE Trans. Power Electron. 2003, 18, 814–822. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEE Proc. Electr. Power Appl. 2006, 153, 750. [Google Scholar] [CrossRef]
- Husev, O.; Roncero-Clemente, C.; Makovenko, E.; Pimentel, S.P.; Vinnikov, D.; Martins, J. Optimization and Implementation of the Proportional-Resonant Controller for Grid-Connected Inverter With Significant Computation Delay. IEEE Trans. Ind. Electron. 2020, 67, 1201–1211. [Google Scholar] [CrossRef]
- Milanes-Montero, M.I.; Barrero-González, F.; Pando-Acedo, J.; Gonzalez-Romera, E.; Romero-Cadaval, E.; Moreno-Muñoz, A. Smart Community Electric Energy Micro-Storage Systems With Active Functions. IEEE Trans. Ind. Appl. 2018, 54, 1975–1982. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).