Abstract
As safety-critical systems, grid cyber-physical systems (GCPSs) are required to ensure the safety of power-related systems. However, in many cases, GCPSs may be subject to uncertain and nondeterministic environmental hazards, as well as the variable quality of devices. They can cause failures and hazards in the whole system and may jeopardize system safety. Thus, it necessitates safety analysis for system safety assurance. This paper proposes an architecture-level safety analysis approach for GCPSs applying the probabilistic model-checking of stochastic games. GCPSs are modeled using Architecture Analysis and Design Language (AADL). Random errors and failures of a GCPS and nondeterministic environment behaviors are explicitly described with AADL annexes. A GCPS AADL model including the environment can be regarded as a game. To transform AADL models to stochastic multi-player games (SMGs) models, model transformation rules are proposed and the completeness and consistency of rules are proved. Property formulae are formulated for formal verification of GCPS SMG models, so that occurrence probabilities of failed states and hazards can be obtained for system-level safety analysis. Finally, a modified IEEE 9-bus system with grid elements that are power management systems is modeled and analyzed using the proposed approach.
1. Introduction
To improve system quality and reduce cost, power systems are evolving to smart grids which can be seen as GCPSs [1]. A GCPS, obtaining the information from sensors and sending the data/command to actuators, is an integration of the computing system and the physical process under control. With the information transmitted through the communication, a GCPS has the ability to calculate, control and monitor the whole system to ensure system safety.
The interdependency between cyber systems and physical processes in GCPSs has been considered by many researchers. The errors and failures can propagate from cyber systems to physical processes or vice versa. Huang et al. [2,3] study the system robustness of a GCPS for cascading failures between the computational network and physical network. Rahnamay-Naeini and Hayat [4] model and analyze the cascading failures and effects of interdependence on system reliability. The robustness [2,3,5,6], reliability [4] and security [7,8,9] of GCPSs have been analyzed in numerous papers. It necessitates to perform safety assessment for power grids [10,11]. In this paper, we focus on system safety of GCPSs. The internal random errors, error/failure propagations between components, error behaviors and hazard behaviors will be modeled in a GCPS model for safety analysis.
GCPSs must interact with the changing environment (such as the lightning strike and high temperature, etc.) which is uncertain and nondeterministic. In most cases, contingencies caused by the environment can occur randomly. If a contingency has happened to be occurring, the environment may nondeterministically continue to disturb the system or recover to the normal state. Hence, a GCPS is inevitable to be subject to environmental hazards. Furthermore, the quality of devices and subsystems is variable, which may lead to system hazards and jeopardize system safety. As a safety-critical system, if a GCPS fails, it will result in economic loss and even cause casualties. Consequently, system safety of such GCPSs must be ensured by all means.
In this paper, an architecture-level safety analysis approach for GCPSs is proposed. Based on model-based methods, GCPSs are described as a hierarchical model using AADL [12] which supports safety analysis [13,14,15,16,17]. AADL describes uncertain behaviors of devices by means of probability distributions. Nondeterministic behaviors inside of components are specified in error models [18] of an AADL model. Through the extension of the AADL semantics, the environment behaviors are modeled using an abstract component and error behaviors, meanwhile the physical process is described using AADL components and interactions. The error propagations between cyber systems and physical processes are modeled by error models. Hazard behaviors in a GCPS AADL model are specified using hazard models [13,14]. Then, we formulate formal semantics for AADL models including error models and hazard models, and make rules to transform GCPS AADL models to SMGs [19,20,21]. SMGs can be regarded as a generalization of Markov Decision Processes (MDPs), and nondeterministic choices are under the control of several distinct players. MDPs are a generalization of Discrete-Time Markov Chains (DTMCs), and nondeterministic behaviors are under the control of the system itself. DTMCs can merely specify stochastic behaviors. SMGs are capable of naturally modeling GCPSs in the game-theoretic view, because a GCPS with the external environment is a game that distinguishes between controllable behaviors in the system and uncontrollable behaviors in the environment. This kind of environment may give rise to the disturbance for a GCPS. The system competes with the environment to ensure the safe execution. To verify the correctness of these rules, the completeness and consistency are proved. Safety requirements are represented as probabilistic property formulae with temporal logic. At last, using a probabilistic model-checking tool, occurrence probabilities of failed states and hazards can be calculated through probabilistic model-checking for system-level safety analysis.
The rest of this paper is organized as follows. Section 2 introduces some preliminaries about AADL and the model-checking of SMGs. Section 3 highlights our safety analysis framework including building a GCPS AADL model, transforming AADL models to SMG models, generating property formulae for safety requirements and verifying property formulae for safety analysis. Section 4 formulates the formal semantics for a GCPS AADL model, provides model transformation rules from AADL models to SMG models and proves the correctness of model transformation rules. Section 5 provides the case study for the application of the proposed approach. The related work is presented in Section 6 and Section 7 describes the conclusion and future work.
2. Preliminaries
2.1. AADL
The AADL [12] is designed for the specification of distributed computer systems. The AADL model is a hierarchical model, which contains software components (such as the thread, process, and data components, etc.), execution platform components (such as the processor, memory, bus and device components, etc.), composite and generic components (i.e., system and abstract components) and component interactions (such as port connections and data access, etc.). Three port types are supported, i.e., data, event and event data. To better support safety and reliability analysis, AADL has powerful extendability. Specifically, the Error Model Annex (EMA) [18] and Hazard Model Annex (HMA) [13,14], as sublanguages, have extended AADL core language to specify safety requirements, errors and hazards. EMA can specify the component error behavior for each component, error propagations between components, composite error behavior for a component in terms of its subcomponents, and error behavior state machines including error states, error events and transitions for components. Since it does not consider hazard behaviors, we use HMA to compensate the weakness of EMA. HMA can specify hazard sources, hazard propagations from hazard sources to hazards with the triggering condition, hazard transitions between hazards with the triggering condition, and hazard behavior machines to define hazard information including hazards, hazard triggers, severity levels, and hazard transitions. The triggering condition can be a hazard trigger or a logical combination of hazard triggers.
2.2. Model Checking of Stochastic Multi-Player Games
Probabilistic model-checking provides a means to describe and analyze the system that exhibits stochastic behaviors, and it can quantitatively deal with probability properties. SMGs [19,20,21] can not only model random behaviors but also competitive behaviors. The players in SMGs can either collaborate or compete in order to achieve a particular goal. In this paper, competitive stochastic systems are expressed as turn-based SMGs. In each state of an SMG model, only one player can choose between several actions, and the outcome of actions can be probabilistic.
Definition 1.
SMG: A (turn-based) stochastic multi-player game (SMG) is a tuple , where: Π is a finite set of players; S is a finite, non-empty set of states; A is a finite, non-empty set of actions; is a partition of S; is a (partial) transition function; is a finite set of atomic propositions; and is a labelling function.
For each state , the set of available actions is expressed by . We assume that for all s. The choice of an action to take in s is under the control of a single player . Once a player selects an action a, the successor state is chosen according to the probabilistic distribution .
The temporal logic, Probabilistic Alternating-time Temporal Logic with Rewards (rPATL) [19], is employed to express quantitative properties of SMGs. rPATL is able to describe that a coalition of players has a strategy to satisfy the requirement, such as the probability threshold for the occurrence probability of an event. For instance, there are four players in the system, and a typical probability property is <<player1, player2>> Pmax<=0.05 [ F<=60 terminating ], i.e., “can players 1 and 2 collaborate so that the maximal probability of the system terminating within 60 s is at most 0.05, whatever players 3 and 4 do?”
To verify an SMG model, Kwiatkowska et al. [22] provide a tool, PRISM-games, to model and verify SMGs. PRISM-games is a probabilistic model-checker for modeling and analyzing SMGs. STORM [23] is the new model-checker and provides solvers for stochastic games which are used in the abstraction-refinement engine, but it does not support stochastic games as input models. The description language, PRISM-games language, is an extended PRISM language with new semantics for the game theory. In this paper, an SMG model described by the PRISM-games language is named as a PRISM-games model. A PRISM-games model is a combination of players, modules, global variables, constants and formulas. A player includes modules and actions. A module contains commands and local variables. A module can access local variables of other modules, but cannot modify them. A command is composed by an action, a guard and one or more transitions. For instance, [a] s>0 & n=1 -> 0.1:(n=2)+0.9:(n=0); is a command, where a is an action for the synchronization between modules, s>0 & n=1 is the guard that is the condition for the execution of this command, and 0.1:(n=2) and 0.9:(n=0) are transitions. Each transition has a probability value and an update, for example, 0.1 is a probability corresponding to the update n=2 in the transition 0.1:(n=2). Constants can be integers, doubles or booleans. A formula comprises a name and an expression. The formula name can be used as shorthand for the expression to avoid duplication of codes.
3. Approach
The proposed safety analysis framework for GCPSs is presented in Figure 1 including four steps. Firstly, the specification of a GCPS is described using AADL, and safety requirements related to errors and hazards are specified using EMA and HMA with randomization and nondeterminism. Secondly, the proposed approach will integrate the probabilistic model-checking of SMGs with safety analysis. Thus, transforming AADL models to PRISM-games models is required to obtain SMG models for our model-based analysis approach. Thirdly, according to error models and hazard models, property formulae of a GCPS should be generated for checking whether safety requirements are satisfied by the system model. At last, we can verify property formulae for a GCPS and obtain safety analysis results. The detailed explanation is provided in the following four sections.
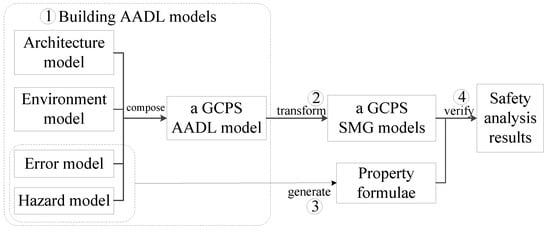
Figure 1.
Proposed safety analysis framework for GCPSs.
3.1. Building AADL Models for GCPSs
The power system is always described as a single line diagram. A modified, redrawn and relabeled IEEE 9-bus power system [24] with power management systems (PMSs) is shown in Figure 2. It is a GCPS. The bus in this figure represents a node and it is different with the bus component in AADL models. This GCPS has three buses (bus1, bus2 and bus3), which are managed by PMSs (PMS1, PMS2 and PMS3), respectively. A PMS contains some hardware devices such as sensors and line breakers, etc. It can sample data, receive commands from the control center, and control line breakers. Here, a PMS is considered as a whole and the internal structure is not specified at the architecture level. In this GCPS, there are three generators (G1, G2 and G3) used to supply the power. Black lines between buses and generators are power transmission lines (TL1, TL2 and TL3). Additionally, there exists a control center system to control this GCPS. PMSs and generators can send and receive the information to the control center.
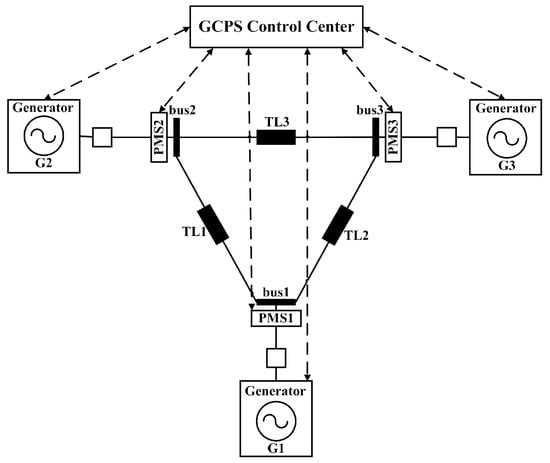
Figure 2.
A modified, redrawn and relabeled IEEE 9-bus system with grid elements that are PMSs.
To perform safety analysis for a GCPS at the architecture level, a GCPS should be described as an AADL model. Generators are described using AADL device components. Transmission lines take charge of power transmission and are important constituent parts of a GCPS. Based on electrical characteristics of transmission lines, they have the impedance and they are modeled as resistances in Figure 2. Thus, transmission lines are seen as devices and they are specified as device components in AADL models, so that we can build error models and hazard models for them. Each PMS is described as a system component. The power transmission between generators and PMSs in a GCPS is described using the AADL component connection between event ports. The connections for power transmission should bind to AADL buses representing transmission lines. The connections in the cyber system should bind to AADL buses representing data lines. The control center system is modeled as an upper-level system and seen as a GCPS system component, which contains all subcomponents of a GCPS except the environment. Then, an AADL architecture model of a GCPS system can be built. For example, an AADL model of the GCPS system (Figure 2) is provided in Figure 3. Based on aforementioned modeling method, the G1, G2 and G3 devices in Figure 2 are corresponding to three generators in Figure 3. Similarly, the PMS1, PMS2 and PMS3 systems are corresponding to three PMSs. The TL1, TL2 and TL3 devices are corresponding to three transmission lines. There are also two buses, a transmission line (TL) and a data line (DL). The control center system is modeled as a system component GCPSsys, which contains these subcomponents, so that the GCPSsys can communicate with generators, PMSs and transmission lines through the hierarchical structure in the AADL model.
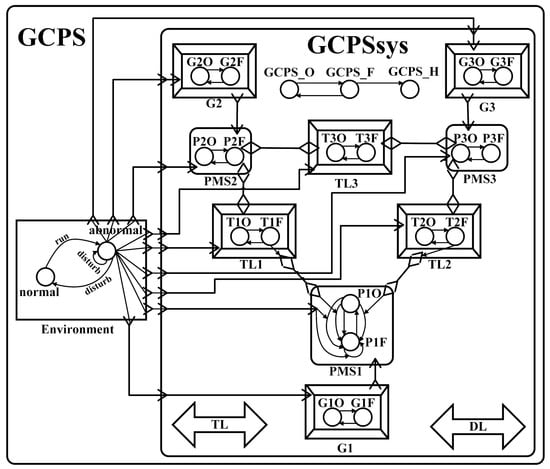
Figure 3.
An AADL model of a GCPS with the environment.
For safety analysis of a GCPS AADL model, error behaviors and hazard behaviors should be built using EMA and HMA. Each error state is part of total state of a component. It may lead to its subsequent failure. And a failure can result in hazards or propagate to the connected components. A hazard is a real or potential condition due to the failure. The evolvement between error states or hazards is described using error transitions or hazard transitions, respectively. The failure propagation between components is expressed with error propagations. The evolvement from the failure to the hazard can be described with hazard propagations. An AADL model without the environment can be obtained by combining an architecture model, error models and hazard models. A power system and a cyber system are constructed in a single AADL model so that it is easier to understand the whole GCPS and it is more convenient for further analysis when the system architecture is changed. For example, error behaviors and hazard behaviors of a GCPS (Figure 2) are shown in Figure 3. The cycles denote error states or hazards. The lines with arrows between error states or hazards are error transitions or hazard transitions, respectively. The line with arrows from error states to hazards are hazard propagations. In the GCPSsys system component, GCPS_O (O denotes an operational state) and GCPS_F (F denotes a failed state) are error states, and GCPS_H (H denotes a hazard) is a hazard. Because the detailed hazard model of GCPSsys is complex, only part of that is shown in Figure 3 and we will introduce the complete hazard model in Section 5. For example, in the subcomponent PMS1, its state can evolve from P1O to P1F and from P1F to P1O. It can also be triggered by an incoming propagation point so that its state may change from P1O to P1F and from P1F to P1F. All generators, PMSs and TLs can be triggered by an incoming propagation point from environment, but to make this AADL model clear, these error transitions are not drawn in Figure 3.
In this paper, the environment will be considered for the analysis of external contingencies. We utilize an abstract component to specify the external environment. The effects of the environment on a GCPS are described with connections between event ports. EMA and HMA are employed to describe environmental behaviors, which can be random and nondeterministic behaviors. Thus, a complete GCPS AADL model will be built by combining an architecture model, error models, hazard models and the environment component. For example, an environment component with error models is presented in the left of Figure 3. The state transition from normal to abnormal represents a contingency from the environment occurs randomly during the normal execution of the GCPSsys. The environment’s state is abnormal, it means a contingency has occurred. The state transition from abnormal to abnormal represents that this contingency gives rise to the continuous disturbance to the GCPSsys. The state transition from abnormal to normal represents that this contingency disturbs the GCPSsys and recover to normal. The latter two state transitions occur nondeterministically. While one of these two transitions is occurring, the environment can propagate an error to connected components and affects the GCPSsys, for example, the outgoing propagation point of environment can trigger error transitions in PMS1 (from P1O to P1F and from P1F to P1F).
3.2. Transforming AADL Models to SMG Models
This paper will apply the model-checking of SMGs for safety analysis. The approach is based on modelling a GCPS and its environment as two players of an SMG model. The game-theoretic view of a GCPS and the environment is described as follows,
Definition 2.
The SMG model specification of a GCPS and its environment is an SMG , where:
- is the set of players formed by a GCPS and its environment.
- is the set of states, where and are sets of states owned by the system and the environment players, respectively, and .
- is the set of actions, where and are sets of actions controlled by the system and the environment players, respectively. In this paper, for all commands, actions are and .
- is a (partial) transition function based on error transitions, hazard transitions, error propagations and hazard propagations.
- is a set of all the predicates that are built over state variables including error states and hazards.
- is a labelling function for hazard sources.
The formal model of a GCPS including the environment is described using PRISM-games language [22]. Model transformation from a GCPS AADL model to a PRISM-games model makes it possible to get a GCPS SMG model and propose a model-based safety analysis approach based on the model-checking of SMGs. It is an important contribution of this paper. The detailed transformation rules are provided in Section 4.2.
3.3. Generating Property Formulae
The purpose of using probabilistic model-checking is to calculate occurrence probabilities of error states and hazards, and quantitatively perform safety analysis for a GCPS. Many safety standards use occurrence probabilities for quantitative analysis of system safety. Occurrence probabilities of failed states (represented using error states) and hazards can help to analyze system safety of a GCPS, which is a safety-critical system. The hazards and failed states are contained in safety requirements and they are focused in safety analysis. Thus, we formulate formulae for property specification of failed states and hazards using the temporal logic rPATL. The formula for a hazard is shown in Formula (1), where represents the GCPS, represents the maximal occurrence probability, represents a hazard of a component, F represents the future and 3600 is the number of iterations in an hour. The occurrence probability is required to be maximal since the behaviors of an SMG model can be nondeterministic. Formula (1) means that “what is the maximal occurrence probability when the system is at the state within 3600 steps (1 h) against the environment?” In this formula, the system does not collaborate with the environment, because a GCPS competes with the environment to ensure that it is at operational state. Similarly, a formula for a failed state is formulated by replacing in Formula (1) with a failed state.
3.4. Verifying Property Formulae for Safety Analysis
With an SMG model of a GCPS AADL model and the property formulae for failed states and hazards, we can verify safety requirements for a GCPS. Occurrence probabilities of hazards will be obtained through formal verification. So a safety analysis table can be generated including component names, failed states, hazards and their occurrence probabilities.
4. Model Transformation
We build an AADL model based on a GCPS architecture model including its environment with error models and hazard models. The formal semantics of a GCPS AADL model is first provided in Section 4.1, model transformation rules are explained in Section 4.2, and the completeness and consistency of model transformation rules are proved in Section 4.3.
4.1. Formalization of AADL Models
The formalization of an AADL model is divided into six parts including basic elements, error transitions (ETs), error propagations (EPs), composite error behaviors (CEBs), hazard propagations (HPs) and hazard transitions (HTs). Basic elements are constituent elements of other parts. The relationship between ETs, EPs, CEBs, HPs and HTs in an AADL model is shown in Figure 4. ETs are internal behaviors of components, System1 and System2. EPs are propagations between ETs of connected components (System1 and System2). CEBs are behaviors of a composite component, PowerSystem, whose state is affected by its subcomponents, two systems. ETs are also allowed to be established in a composite component. HTs are hazard behaviors of a component. HPs are the evolvement from CEBs or ETs to HTs.
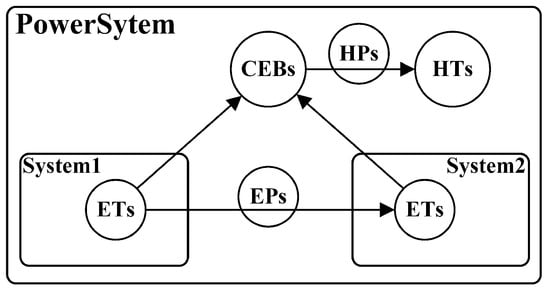
Figure 4.
The relationship between constituent parts of an AADL model.
4.1.1. Basic Elements of an AADL Model
Basic elements of an AADL model contain error states, error events, hazards, hazard triggers and hazard sources. The formal semantics of them is defined as follows.
Definition 3.
Each element of an AADL component is defined as a tuple:
- , where: S is a finite set of error states; is an initial error state; is a finite set of atomic propositions built over error states.
- , where: A is a finite set of actions based on error events in the triggered condition; For a probabilistic error transition function , is established based on probabilities of error events.
- , where: S is a finite set of hazards; is a finite set of atomic propositions built over hazards.
- A is a finite set of actions based on hazard triggers in the triggered condition; is a probabilistic hazard transition function and is established based on probabilities of hazard triggers;
- , where: S is a finite set of hazard sources; is a finite set of atomic propositions built over hazard sources; is a labelling function.
Some parts of , , , and are not explained since they are empty and have no effect on the formal semantics.
4.1.2. Other Five Constituent Parts of an AADL Model
An error propagation is designed to specify under what conditions an error propagation occurs on an outgoing error propagation point. The conditions are composed by error states and the errors on incoming error propagation points. Error propagations between two components are based on connections between two components and propagations in two components.
Definition 4.
EP Error propagations (EPs) between two components are defined as a tuple , where: S is a finite set of error states and states of outgoing propagation points; is an initial error state; A is a finite set of actions based on the triggered condition including error events and ingoing propagation points; is a (partial) probabilistic error transition function and is established based on probabilities of error events; is a finite set of atomic propositions built over error states and outgoing propagation points; is a labelling function.
Definition 5.
ET Error transitions (ETs) of an AADL component are defined as a tuple , where: S is a finite set of error states; is an initial error state; A is a finite set of actions based on the triggered condition including error events and ingoing propagation points; is a (partial) probabilistic error transition function and is established based on probabilities of error events; is a finite set of atomic propositions built over error states; is a labelling function.
Definition 6.
CEB Composite error behaviors (CEBs) of an AADL component are defined as a tuple , where: S is a finite set of error states including error states of subcomponents; is empty; A is empty; is an error transition function and is equal to 1; is a finite set of atomic propositions built over error states; is a labelling function.
Definition 7.
HP Hazard propagations (HPs) of an AADL component are defined as a tuple , where: S is a finite set of hazard sources and hazards; is empty; A is a finite set of actions built based on hazard triggers; is a (partial) probabilistic hazard propagation function and is established based on probabilities of hazard triggers; is a finite set of atomic propositions built over hazard sources and hazards; is a labelling function.
Definition 8.
HT Hazard transitions (HTs) of an AADL component are defined as a tuple , where: S is a finite set of hazards; is empty; A is a finite set of actions built based on hazard triggers; is a probabilistic hazard transition function and is established based on probabilities of hazard triggers; is a finite set of atomic propositions built over hazards; is a labelling function.
4.2. Model Transformation Rules
This section provides rules for the model transformation. We first propose basic rules for the transformation of basic elements in an AADL model. Then, rules to transform ETs, HTs, EPs, CEBs and HPs are formalized, respectively. At last, rules to transform logical operators and primitives are presented. They are important tools for expressing the combination of error states, error events, hazard sources or hazard triggers.
4.2.1. Basic Rules
As shown in Table 1, five basic rules are presented. Each component implementation is encoded as a module (see first row). Error states and hazards of a component are encoded as an integer variable (see second row) and each value is corresponding to an error state or a hazard. The initial value of this variable is 0, which is corresponding to an initial error state (see third row). Error events and hazard triggers are encoded using the probability distributions, i.e., the probability value p is encoded as a double constant for an error event or a hazard itself, and is for the opposite aspect that is encoded as true (see fourth row). Each hazard source corresponds to an error state or an error event, so a hazard source is encoded as a formula which represents a value of its corresponding error state or error event, as shown in the fifth row.

Table 1.
Basic rules for the model transformation.
Definition 9.
Rules for Basic Elements: Transformation rules from basic elements to the PRISM-games language (an SMG model) are defined as a tuple , where can be error states , error events , hazards , hazard triggers or hazard sources , and is a set of the corresponding PRISM-games elements. includes rules: , , , , and , which are defined as follows:
- , where is a set of error states in a component, and is a local variable. The value range of this variable is corresponding to the number of error states. Each value represents an error state and 0 is for an initial error state.
- , where is a set of error events, and is a set of probability values for transitions in commands. Each probability value is defined as a double constant.
- , where is a set of hazards in a component, and is equal to of the same component. The value range of is added with the the number of hazards. Each added value represents a hazard.
- , where is a set of hazard triggers, and is a set of probability values for transitions in commands. Each probability value is defined as a double constant.
- , where is a set of hazard sources, and is a set of formulae. Each formula represents a variable with the value of the corresponding state of an error state or a probability value of an error event.
4.2.2. Rules for Error Propagations
Connections (including data, event and event data connections) build the link between components, and provide conditions for the data, command and event transmission. In an error model, an error is propagated to the connected component through error propagations based on connections. For instance, an error propagation from TL1 to PMS1 in Figure 3 is based on the event port connection. Since the semantics of connections is included in error propagations, we only need to transform each error propagation to PRISM-games language.
Rules for error propagations are defined as , which can be categorized into , and . If an error propagation is not triggered by the interference by the environment, we will provide two kinds of rules for the transformation of an error propagation, and , as follows.
Definition 10.
Rules for error propagations that are not from the environment are defined as a tuple or , where is an error propagation.
- 1.
- For , is a corresponding command of . The source error state and the triggered condition of is encoded as the guard. If error events are included in the triggered condition, they are transformed to a probability value for a transition of the command. The outgoing propagation point in the destination of is encoded as a local variable (0 denotes no error, 1 denotes an error). The value 1 is assigned to this variable as an update of a transition for the command. This variable with value 1 will be used as the triggered condition by other components.
- 2.
- If the triggered condition of does not contain incoming propagation points, is better than . is the value of the state variable that is corresponding to the source error state of . The probability values of error events in the triggered condition is added to . The variable corresponding to the source error state will be used as the triggered condition by other components.
Error propagations are designed for the propagation of errors and propagated errors can be used as the triggered condition of error transitions or error propagations in the connected component. encodes an error propagation as the destination of for the triggered condition. directly uses the value of the source state variable for the triggered condition. Both and can implement the same function. However, can reduce the complexity of the transformed SMG model. For instance, as shown in Figure 3, an error propagation from T1F (a failed state) of TL1 to PMS1 and it causes an error transition from P1O to P1F. According to , this error propagation is encoded as “TL1s=1” in the guard of a command at line 9 of Figure 5. Since its triggered condition is empty, it is not transformed to a command. Similarly, “TL2s=1” at line 10 of Figure 5 is for an error propagation from TL2 to PMS1. Moreover, according to , the outgoing propagation point of TL1 in Figure 3 is transformed to a variable TL1Out at line 5 of Figure 6. A command at line 10 of Figure 6 is transformed from this error propagation. The source error state T1F in TL1 component is encoded as the guard and the value 1 is assigned to the variable TL1Out.

Figure 5.
The PRISM-games model of PMS1 system component.

Figure 6.
The PRISM-games model of TL1 device component.
If an error propagation is triggered by the interference from the environment, it is transformed to the action disturb for affected error transitions to synchronize with the environment, as follows.
Definition 11.
Rules for error propagations from the environment are defined as a tuple , where is an error propagation propagated from the environment. is an action, that’s, disturb, which will be used in the affected error transitions.
For example, the error propagation from abnormal in the environment component to the outgoing propagation point to error transitions in the PMS1 component in Figure 3. This error propagation is encoded as an action disturb, which will be used in the commands corresponding to affected error transitions in the PMS1 component. This action disturb is the link between commands.
4.2.3. Rules for Error Transitions and Hazard Transitions
Error transitions and hazard transitions are for the evolvement between error states or hazards. Each error transition is transformed to a command, as follows.
Definition 12.
Rules for error transitions are defined as a tuple , where is an error transition and is a command.
- 1.
- If is not related to the environment component, the source error state and triggered condition of are transformed to the guard, the destination error state is transformed to a transition t, and error events are transformed to a probability for the transition t. If there are no error events in an error transition, the probability is 1. If there are outgoing propagation points, their corresponding variables should be recovered in the recovered error transition.
- 2.
- Additionally, if is an error transition specifying the occurrence of interference in the environment component, the action of the command is disturb which will synchronize with the affected error transitions in GCPSs.
- 3.
- Moreover, if is an error transition in a component of a GCPS and it is affected by the incoming propagation point from the environment, the action of the command is disturb which will synchronize with the error transitions in the environment. This action is transformed from the error propagation between the environment and a component of a GCPS. If a component does not has error transitions caused by the environment, a command from true to true with the action disturb should be added to this component.
If is not related to the environment, it is transformed according to the first rule of Definition 12. For example, if an error propagation from T1F to PMS1 in TL1 of Figure 3 is transformed according to in Definition 10, error transitions in TL1 are transformed to commands at lines 8–9 of Figure 6, and error propagations in PMS1 are transformed to commands at lines 7–10 of Figure 5. If that error propagation from T1F to PMS1 in TL1 is transformed according to in Definition 10, error transitions of TL1 are transformed to commands at lines 8 and 11 of Figure 6, and error transitions of PMS1 are transformed to lines 7–8 and 11–12 of Figure 5. The command at line 11 of Figure 6 is corresponding to the recovered error transition, so it also should recover the variable for an outgoing propagation point in the transition of this command.
The error transition from abnormal to abnormal or from abnormal to normal in the environment of Figure 3 is the occurrence of interference. It will disturb GCPSsys through error propagations and event port connections. For example, an error propagation from abnormal state of environment component to PMS1 is encoded as an action disturb based on Definition 11. Based on the second and third rules of Definition 10, this action is added to commands at lines 5 and 6 of Figure 7 and lines 5–6 of Figure 5. These commands are transformed from ETs. Moreover, since error transitions of GCPSsys are not caused by the environment, a command at line 11 of Figure 8 is added for the synchronization between modules.

Figure 7.
The PRISM-games model of environment component.

Figure 8.
The PRISM-games model of GCPSsys system component.
Similarly, a hazard transition is transformed to a command, as follows.
Definition 13.
Rules for a hazard transition are defined as a tuple , where is a hazard transition and is a command. The source hazard is transformed to the guard, the destination hazard is transformed to a transition t, and hazard triggers are transformed to a probability for the transition t. If there are not hazard triggers, the probability is 1.
4.2.4. Rules for Logical Operators and Primitives
The logical operators And and Or in EMA and HMA can be directly replaced by PRISM language. EMA also has primitives such as Ormore and Orless, which can be encoded by combining And and Or operators. For instance, a condition expression 1 Ormore (state1, state2) means if one or more than one states are true, the value of this expression is true. It can be converted to the logical expression state1 Or state2 Or (state1 And state2).
Definition 14.
Rules for logical operators and primitives are defined as a tuple , where is a composition through logical operators and/or primitives, and is a composition through logical operators. For logical operators, it is one-to-one mapping between and . For primitives, Ormore and Orless are encoded by combining And and Or operators.
4.2.5. Rules for Composite Error Behaviors
Composite error behaviors of a component are expressed in terms of error states of its subcomponents. A composite error behavior is transformed to a command whose destination state will occur with the probability 1 if the source state is satisfied.
Definition 15.
Rules for composite error behaviors are defined as a tuple , where is a composite error behavior, and is a command. The combination of error states of subcomponents are transformed to the guard and the destination error state is encoded as a transition of this command.
4.2.6. Rules for Hazard Propagations
The hazard source is used as the link between an error model and a hazard model [13]. A hazard propagation is the evolvement from one or several hazard sources to a hazard with the triggered condition. The condition is a logical combination of hazard triggers. The source of a hazard propagation is encoded using rules for logical operators in Section 4.2.4. The triggered condition is transformed based on the probability distribution of hazard triggers. The hazard in the destination is represented with a hazard variable. For example, a hazard propagation “StateAnd(state thread1Failed, state thread2Failed)-[ht]->h” is encoded as a command “[] s_t1=1 & s_t2=1 -> 0.1:(hazardVar’=1) + 0.9:true;”, where the occurrence probability value of ht is 0.1, hazard sources thread1Failed and thread2Failed are corresponding to the value 1 of two error state variables in thread1 and thread2, respectively, and the hazard h is corresponding to the value 1 of a hazard variable hazardVar.
Definition 16.
Rules for hazard propagations are a tuple , where is a hazard propagation and is a command. A combination of hazard sources is transformed to the guard, the destination hazard is transformed to a transition t, and hazard triggers are transformed to a probability for the transition t. If there are not hazard triggers, the probability is 1.
4.3. Completeness and Consistency of Model Transformation Rules
A GCPS AADL model has been divided into six parts, as presented in Section 4.1. Each part has at least one corresponding model transformation rule. Following rules in Definitions 9–16 for the model transformation from a GCPS AADL model to an SMG model in PRISM-games language, we prove the completeness and semantic consistency of model transformation rules as follows.
Theorem 1.
(Completeness 1) Let A be an AADL model of a GCPS and its environment, be the transformed PRISM-games model (SMG model), and be the set of transformation rules. If , there exists a rule such that .
Proof.
Recall that , , . We have formulated model transformation rules for all parts of a GCPS AADL model. Some part has more than one transformation rule. The rule set can transform all parts of A to elements of . Therefore, for any , there exists a model transformation rule , such that . □
Theorem 2.
(Completeness 2) Let A be an AADL model of a GCPS and its environment, be the transformed PRISM-games model (an SMG model), and be the set of transformation rules. Given and , if and are equivalent, there exists a rule such that .
Proof.
Recall that , , . is transformed from each part of A based on the rules in . The source part of a GCPS AADL model is equivalent to the target part of a PRISM-games model. Therefore, for any and , if and are equivalent, there exists a model transformation rule , such that . □
Theorem 3.
(Consistency) Let A be an AADL model of a GCPS and its environment, be the transformed PRISM-games model (an SMG model), and be the set of transformation rules. If both and can used for the transformation of . and are equivalent.
Proof.
Recall that , , , and can be , or . Both and can be applied to transform to ( and , respectively), as shown in Definition 10. As the explanation in Section 4.2.2, is equivalent to , that’s, is equivalent to . Other transformation rules in are designed for each different part of a GCPS AADL model and they cannot transform the same part. Therefore, if both and can used for the transformation of (here, , and must be , and , respectively), is equivalent to , that’s, and are equivalent. □
5. Case Study
To assess the applicability of the proposed approach, we use a GCPS as an illustrated example. The architecture model, error model and hazard model are built for this system. Base on model transformation rules, a GCPS AADL model is transformed to a GCPS SMG model described with PRISM-games language. Property formulae for safety requirements are generated. We also show the results of the verification via model-checking of SMGs for safety analysis.
5.1. A GCPS, Its AADL Model and Transformed SMG Model
The AADL model of a GCPS for illustration is shown in Figure 3. The architecture model of this GCPS system, the environment component and their error models have been introduced in Section 3.1. Every failed ET (from an operational state to a failed state) and recovered ET (from a failed state to an operational state) is triggered by an error event with the probability and (one hour), respectively. In this section, we will introduce CEBs, hazard sources, HPs and HTs of GCPSsys system component.
The error state of a composite component is expressed in terms of its subcomponents’ error states, that’s, the system-level state is affected by its subcomponents. The GCPSsys has two error states, GCPS_O and GCPSsys_F. There are two CEBs in GCPSsys. First, when one of PMSs fails, GCPSsys fails. Second, when one of the generators fails, GCPSsys fails. These two CEBs use OR logical operator to combine error states. According to model transformation rules in Definition 15, two CEBs are encoded as two commands at lines 14 and 15 of Figure 8.
Each failed state of PMSs, generators and GCPSsys system is a hazard source. These hazard sources are encoded as formulae at lines 1–3 of Figure 8. These hazard sources can lead to hazards through HPs. When two of PMSs fail or GCPSsys system state fails, the dangerous overvoltage may occur as a hazard (OverVoltage) triggered by a hazard trigger ht1. OverVoltage will lead to a hazard EquipDamage (equipment damage) triggered by a hazard trigger ht2. When two of generators fail, the power is not enough for users and may affect the normal production process as a hazard (LowPower) triggered by a hazard trigger ht3. Assuming that occurrence probabilities of hazard triggers is . According to model transformation rules in Definition 16, two HBs are encoded as two commands at lines 16 and 18 of Figure 8. A HT is encoded as a command at line 17.
A GCPS is always working in a harsh environment which may cause a failure and a hazard. There are some contingencies to express hazardous factors such as high temperatures, etc. We assume that a contingency will occur one time every day. So the occurrence probability of a contingency is . As shown in Figure 3, contingencies from environment may affect PMSs, generators and TLs and they may fail with the probability . The environment is transformed a module, as shown in Figure 7.
Based on transformation rules in Section 4.2, a GCPS AADL model is transformed to a complete SMG model. Two players of this SMG model are shown in Figure 9. The environment component is encoded as the environment module, which is regarded as a player env, as shown at lines 5–7. Other modules are composed as a player sys, as shown at lines 2–4. The action disturb is controlled by the environment, so it is contained in the env player. The action run is contained in the sys player.

Figure 9.
Part of the transformed SMG model of an aircraft power system.
5.2. Results
All experiments were run on a virtual machine with the Intel(R) Core(TM) i5-7500 CPU@3.40GHz and 14GB RAM. The explicit computation engine of PRISM is selected for our experiments. Java heap space is set to 10GB RAM, which is the upper memory limit for Java virtual machine (JVM) to execute PRISM. Termination epsilon is set to . The number of states and transitions of the transformed SMG model are 5120 and 16437230.
According to Formula (1), property formulae can be formulated for failed states and hazards, including GCPSsysFailed, OverVoltage, LowPower and EquipDamage. For example, a property formula for GCPSsysFailed is presented in Formula (2), where “” is corresponding to GCPSsysFailed (see line 10 of Figure 8). Using the PRISM-games tool, we verify property formulae for a complete transformed SGM model to obtain occurrence probabilities. Safety analysis results are shown in Table 2. We can see that GCPSsys’s failure may occur with a large probability at the system-level. The occurrence probabilities of hazards are smaller. They can used to decide if the design of a GCPS is feasible and it satisfies safety requirements. If a probability is too large, the GCPS architecture model should be modified or the failed probabilities of subcomponents should be lowered.

Table 2.
Verification results for a GCPS.
5.3. Discussion
In the aforementioned GCPS AADL model, probabilities of error states and hazards are calculated for the occurrence in an hour. The number of iteration is 3600 and the time resolution is 1 s. The time resolution value discretizes the occurrence of error events and hazard triggers. It can not only determine the number of iterations, but also has an impact on the accuracy of occurrence probabilities of failed states and hazards. We perform an experiment by changing the time resolution and discretizing the corresponding occurrence probabilities of error events and hazard triggers. Time resolution values are 10,000 ms, 1000 ms, 100 ms and 10 ms. Corresponding numbers of iterations are 360, 3600, 36,000 and 360,000, which are used for the underlying bonded model-checking algorithms. The results are provided in Table 3. From these probabilities and required calculation time, we can see that smaller time resolution values can obtain higher accuracy, but they require much more time. The overhead of doing more iterations maybe time-consuming for engineers. It may outweigh the advantage in accuracy.

Table 3.
Effects of time resolution on probabilistic results and calculation time.
6. Related Work
AADL supports safety analysis of distributed complex safety-critical systems. In the Correctness, Modeling and Performance of Aerospace Systems (COMPASS) [15,16], an extended variant of AADL, the System-Level Integrated Modeling (SLIM) language, is used for safety analysis using Fault Tree Analysis (FTA), Failure Mode and Effects Analysis (FMEA) and Timed Failure Propagation Graphs (TFPG). COMPASS applies Markov Reward Model Checker (MRMC) [25], a probabilistic model-checker, for performability analyses. MRMC is able to analyze discrete-time and continuous-time Markov reward models, but it cannot analyze stochastic games models. Morozov et al. [26] provide a method only for the stochastic error propagation analysis, however, the nondeterminism is not considered. They transform AADL models to formal Dual-graph Error Propagation Models (DEPMs) for reliability analysis. In papers [13,14], authors propose an architecture-based hazard analysis approach using AADL. This approach can provide component-level and system-level safety analysis results including hazard sources, hazard trigger mechanisms, severities and probability levels. They also design the HMA to improve the modeling capability of AADL for hazard analysis. To ensure the correctness of occurrence probabilities of hazards, they prove the semantic preservation of the model transformation between AADL models and Deterministic Stochastic Petri Net (DSPN) models that is used for quantitative computation. In paper [17], they integrate the quantitative verification of Continuous Time Markov Chains (CTMCs) with safety analysis for AADL models. Additionally, a safety-based software reconfiguration method [27] is proposed based on AADL with EMA and HMA. These existing AADL-based safety analysis methods cannot be directly applied for GCPSs with the physical process. Because AADL semantics needs to be extended to support GCPSs modeling including physical processes and computing systems. In this paper, the environment is also described in a GCPS AADL model. Like AADL, UML is a commonly used modeling language. Bernardi et al. [28] propose the Dependability Analysis Modeling (DAM) profile. They define a Dependability Analysis (DA) domain model, the aim of which is to provide the basis for adding a dependability profile to the Modeling and Analysis of Real Time and Embedded systems (MARTE). Although it supports several dependability analysis, such as reliability, safety and availability analysis, it cannot describe random hazard behaviors and express the semantics of stochastic game.
Cascading failures in GCPSs have attracted more and more attention. Many papers focus on system robustness. In our approach, they are specified in error propagations between cyber components, physical components and their interactions for system safety. For the impact of interdependencies on infrastructures through networks, an interdependent Markov-chain framework [4] is proposed to model cascading failures in interdependent infrastructures with the ultimate goal of predicting their resilience to cascading failures and to describe effects of interdependencies on system reliability. It is able to predict behaviors of interdependent systems at the system-level. Since the cyber-physical interdependence can make a GCPS more robust and resilient and more fragile to cascading failures, wei et al. [5] analyze advantages and disadvantages of the interdependence, perform theoretical analysis and show its effects through system-level simulations. Qi et al. [29] propose an interaction model for simulation and mitigation of cascading failures. The interaction between component failures is quantified by calculating the probability that a component failure causes another. Modern systems should be described as interdependent networks and a failure of a node may lead to cascading failures. So, Buldyrev et al. [6] propose a framework to understand the robustness of interacting networks. Huang et al. [2] study the system robustness of smart grid for two types of cascading failures, interdependence cascading failures and load propagation cascading failures. They [3] also analyze the system robustness and effects of cascading failures caused in the interdependency between physical-resource and computational-resource networks, e.g., smart power grids. Cyber-contingencies may result in inappropriate control commands and further affect the physical power system, so Xin et al. [30] abstract the cyber network of a hierarchical control system as a directed graph and describe the connectivity with a node-branch incidence matrix. Cyber-contingencies are described for cyber-contingency assessment.
There are also many papers for security analysis of GCPSs. Vellaithurai et al. [7] propose a security-oriented stochastic risk management technique for calculation of cyber-physical security indices. Wadhawan et al. [8] consider false data injection detection on transmission lines of a GCPS and present a detection framework. Xun et al. [9] provide a comprehensive study of smart grid security against cyber-physical attacks and describe a risk assessment methodology.
It is significant to ensure that a complete GCPS model can meet safety requirements. Qin et al. [31] present a formal modeling and verification approach for the flexible load control process of GCPSs with differential dynamic logic theories. The model is constructed using HybridUML and it is verified through an automatic hybrid reasoning tool. Nguyen et al. [11] propose a two-phase load management scheme for a power grid. It allows not only customers to curtail demands if there exist no immediate safety concerns, but also the grid to perform load shedding for safety assurance when it is at a vulnerable state.
Our architecture-based approach shown in Figure 1 applies model-checking of SMGs to analyze a GCPS. Firstly, stochastic and nondeterministic behaviors are described using AADL. The whole GCPS including the external environment is modeled as an SMG model to express that the system competes with the environment. Then, the model transformation and the generation of property formulae can be implemented as an automatic tool. Finally, the formal verification is supported by PRISM-games for analyzing system-level safety which is not considered by many papers.
7. Conclusions and Future Work
This paper proposes a model-based safety analysis for GCPSs using probabilistic model-checking of SMGs. AADL is used to build the model for a GCPS including the environment. Since a system may suffer stochastic faults and nondeterministic external hazards, a probabilistic model-checking technique is applied to capture stochastic and nondeterministic characteristics. Meanwhile, we employ SMGs to model the system and the environment as two players that compete for a particular goal. To integrate SMGs into safety analysis, formal semantics of AADL models is defined and model transformation rules are provided to obtain SMG models from GCPS AADL models. Moreover, the completeness and consistency of model transformation rules is proved to ensure the correctness of rules. Finally, we use a GCPS to demonstrate the applicability of the proposed approach.
In the future, we will consider to extend AADL to describe the detailed physical process of GCPSs, for example, the changing process of the electric power supply of generators. We also plan to look into more involved analysis techniques (such as MDPs and Petri-nets) for safety analysis and compare their performance. Additionally, we will work on the applicability of our approach to the larger GCPSs.
Author Contributions
Conceptualization, X.W. and Y.D.; methodology, X.W. and Y.D.; software, X.W.; validation, X.W., Y.D., P.S. and M.X.; formal analysis, X.W.; investigation, X.W. and P.S.; resources, X.W., P.S., and M.X.; data curation, X.W.; writing–original draft preparation, X.W.; writing–review and editing, X.W. and Y.D.; visualization, X.W. and M.X.; supervision, Y.D. and X.W.; project administration, X.W.; funding acquisition, Y.D.; All of the authors approved the final version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China under Grant No. 2017YFB0903000, the National Science Foundation of China under Grant No. 61772423, and the Aviation Science Foundation of China under Grant No. 2016ZC31003.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yu, X.; Xue, Y. Smart grids: A cyber–physical systems perspective. Proc. IEEE 2016, 104, 1058–1070. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, C.; Zhu, T.; Nayak, A. Cascading failures in smart grid: Joint effect of load propagation and interdependence. IEEE Access 2015, 3, 2520–2530. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, C.; Stojmenovic, M.; Nayak, A. Characterization of cascading failures in interdependent cyber-physical systems. IEEE Trans. Comput. 2015, 64, 2158–2168. [Google Scholar] [CrossRef]
- Rahnamay-Naeini, M.; Hayat, M.M. Cascading Failures in Interdependent Infrastructures: An Interdependent Markov-Chain Approach. IEEE Trans. Smart Grid 2016, 7, 1997–2006. [Google Scholar] [CrossRef]
- Wei, M.; Lu, Z.; Tang, Y.; Lu, X. How Can Cyber-Physical Interdependence Affect the Mitigation of Cascading Power Failure? In Proceedings of the IEEE INFOCOM 2018-IEEE Conference on Computer Communication, Honolulu, HI, USA, 16–19 April 2018; pp. 2501–2509. [Google Scholar]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- Vellaithurai, C.; Srivastava, A.; Zonouz, S.; Berthier, R. CPIndex: Cyber-Physical Vulnerability Assessment for Power-Grid Infrastructures. IEEE Trans. Smart Grid 2015, 6, 566–575. [Google Scholar] [CrossRef]
- Xun, P.; Zhu, P.; Zhang, Z.; Cui, P.; Xiong, Y. Detectors on Edge Nodes against False Data Injection on Transmission Lines of Smart Grid. Electronics 2018, 7, 89. [Google Scholar] [CrossRef]
- Wadhawan, Y.; AlMajali, A.; Neuman, C. A Comprehensive Analysis of Smart Grid Systems against Cyber-Physical Attacks. Electronics 2018, 7, 249. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Nguyen, H.H.; Tan, R.; Yau, D.K. Safety-assured collaborative load management in smart grids. In Proceedings of the 2014 ACM/IEEE International Conference on Cyber-Physical Systems (ICCPS), Berlin, Germany, 14–17 April 2014; pp. 151–162. [Google Scholar]
- SAE International. AS5506C—(R) Architecture Analysis and Design Language (AADL); SAE International: Warrendale, PA, USA, 2017. [Google Scholar]
- Wei, X.; Dong, Y.; Li, X.; Wong, W.E. Architecture-level hazard analysis using AADL. J. Syst. Softw. 2018, 137, 580–604. [Google Scholar] [CrossRef]
- Wei, X.; Dong, Y.; Yang, M.; Hu, N.; Ye, H. Hazard analysis for AADL model. In Proceedings of the 2014 IEEE 20th International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA), Chongqing, China, 20–22 August 2014; pp. 1–10. [Google Scholar] [CrossRef]
- Bozzano, M.; Cimatti, A.; Katoen, J.P.; Nguyen, V.Y.; Noll, T.; Roveri, M. Safety, Dependability and Performance Analysis of Extended AADL Models. Comput. J. 2011, 54, 754–775. [Google Scholar] [CrossRef]
- Bozzano, M.; Bruintjes, H.; Cimatti, A.; Katoen, J.P.; Noll, T.; Tonetta, S. The COMPASS 3.0 Toolset. In Proceedings of the fifth International Symposium on Model-Based Safety and Assessment (IMBSA 2017), Trento, Italy, 11–13 September 2017. [Google Scholar]
- Wei, X.; Dong, Y.; Ye, H. QaSten: Integrating Quantitative Verification with Safety Analysis for AADL Model. In Proceedings of the 2015 International Symposium on Theoretical Aspects of Software Engineering (TASE), Nanjing, China, 12–14 September 2015; pp. 103–110. [Google Scholar] [CrossRef]
- SAE International. (R) SAE Architecture Analysis and Design Language (AADL) Annex Volume 1: Annex E: Error Model Annex; SAE International: Warrendale, PA, USA, 2015. [Google Scholar]
- Simaitis, A. Automatic Verification of Competitive Stochastic Systems. Ph.D. Thesis, Department of Computer Science, University of Oxford, Oxford, UK, 2014. [Google Scholar]
- Svoreňová, M.; Kwiatkowska, M. Quantitative verification and strategy synthesis for stochastic games. Eur. J. Control 2016, 30, 15–30. [Google Scholar] [CrossRef]
- Kwiatkowska, M. Model Checking and Strategy Synthesis for Stochastic Games: From Theory to Practice. In Proceedings of the 43rd International Colloquium on Automata, Languages, and Programming (ICALP 2016), Rome, Italy, 12–15 July 2016. [Google Scholar]
- Kwiatkowska, M.; Parker, D.; Wiltsche, C. PRISM-games 2.0: A Tool for Multi-Objective Strategy Synthesis for Stochastic Games. In Proceedings of the 22nd International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS’16), Eindhoven, The Netherlands, 2–8 April 2016. [Google Scholar]
- Dehnert, C.; Junges, S.; Katoen, J.P.; Volk, M. A storm is coming: A modern probabilistic model-checker. In Proceedings of the International Conference on Computer Aided Verification, Heidelberg, Germany, 24–28 July 2017; Springer: Cham, Switzerland, 2017; pp. 592–600. [Google Scholar]
- WSCC 9-Bus System. Available online: http://icseg.iti.illinois.edu/wscc-9-bus-system/ (accessed on 10 September 2018).
- Markov Reward Model Checker. Available online: http://www.mrmc-tool.org/trac/ (accessed on 1 February 2019).
- Morozov, A.; Mutzke, T.; Ren, B.; Janschek, K. AADL-based stochastic error propagation analysis for reliable system design of a medical patient table. In Proceedings of the 2018 Annual Reliability and Maintainability Symposium (RAMS), Reno, NV, USA, 22–25 January 2018; pp. 1–7. [Google Scholar]
- Dong, Y.; Wei, X.; Xiao, M. Overview: System Architecture Virtual Integration based on an AADL Model. In Symposium on Real-Time and Hybrid Systems; Springer: Cham, Switzerland, 2018; pp. 105–115. [Google Scholar]
- Bernardi, S.; Merseguer, J.; Petriu, D. An UML Profile for Dependability Analysis and Modeling of Software Systems; Technical Report RR-08-05; University of Zaragoza: Zaragoza, Spain, 2008. [Google Scholar]
- Qi, J.; Sun, K.; Mei, S. An interaction model for simulation and mitigation of cascading failures. IEEE Trans. Power Syst. 2015, 30, 804–819. [Google Scholar] [CrossRef]
- Xin, S.; Guo, Q.; Sun, H.; Zhang, B.; Wang, J.; Chen, C. Cyber-physical modeling and cyber-contingency assessment of hierarchical control systems. IEEE Trans. Smart Grid 2015, 6, 2375–2385. [Google Scholar] [CrossRef]
- Qin, B.; Liu, D.; Cao, M.; Zou, J. Formal modeling and verification of flexible load control for power grid CPS based on differential dynamic logic. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).