Abstract
This paper addresses the real-time optimization problem of the message-chain structure to maximize the throughput in data communications based on half-duplex command-response protocols. This paper proposes a new variant of the particle swarm optimization (PSO) algorithm to resolve real-time optimization, which is implemented on field programmable gate arrays (FPGA) to be performed faster in parallel and to avoid the delays caused by other tasks on a central processing unit. The proposed method was verified by finding the optimal message-chain structure much faster than the original PSO, as well as reliably with different system and algorithm parameters.
1. Introduction
Data communications with half-duplex command-response protocols generally consist of a commander controlling the transmission line and response terminals responding to the commander. In the MIL-STD-1553B data communication system [1], which is a well-known military communication platform using a serial data bus, it consists of a bus controller (BC) as the commander and remote terminals (RTs) as the response terminals. In the physical layer, the properties of the electrical design inevitably limit the bit rate of the data bus to 1 Mbps. Besides, in the application layer, since the communication protocol is generally determined based on messages that consist of a set of words composed of multiple bits [2], it is hard to use the full bandwidth. Therefore, the structure of message-chains for the BC and the RTs should be carefully determined to maximize the data throughput with consideration of the limited bit rate and insufficient bandwidth.
Data throughput can be improved by simply increasing the number of messages within a given transmission duration in the message-chain structure of the BC. However, the excessive increase in the number of messages with a fixed transmission duration may cause the loss of data in the RTs because the data in receiving buffers may be rewritten by the currently receiving data before the previously received data processing is finished. Therefore, to achieve high data throughput without data loss, the number of messages and the transmission period in the structure of message-chains should be carefully determined.
Zhang et al. [3] improved the data throughput in MIL-STD-1553B communication systems with a heuristic algorithm rearranging the components of the command table based on the number of command or data words. However, they did not consider the processing time in the RT, which affects the reliability of the data communications. Kim et al. [4] presented and analyzed the whole timing diagram between the BC and the RT. They found that when multi-message chains and double buffers were used for the communication system, the data throughput can be improved. However, the message-chain structure in their approach was empirically determined. One can consider optimization algorithms such as the least square methods. Recently, sampling-based optimization algorithms, which are particle swarm optimization (PSO) [5] and its variants [6,7,8], have been widely used because of their convenience and good performance in spite of nonlinear system constraints.
However, optimization algorithms may be faced with much computation time because of a large number of samples, which means that the computation time should be reduced significantly to be applied to real-time systems. In this work, the optimization process needs to be conducted in real-time to find the optimal message-chain structure as fast as possible with different system parameters. Liu et al. [9] proposed real-time approaches for the PSO applied to identify and cancel the current harmonics in power systems. However, since their approach was based on the limited number of particles, it cannot be applied to more complex optimization problems, requiring more number of particles.
To reduce computation time, the PSO was recently implemented on field-programmable gate arrays (FPGA) in various fields. Gao et al. [10] proposed an FPGA implementation method of the PSO to quickly select and update the coefficients of adaptive infinite impulse response (IIR) filters. In addition, Gupta and Mehra [11] implemented the modified PSO algorithm on an FPGA for fast unknown system identification, selecting and updating the coefficients of adaptive infinite impulse response (IIR) filters. Vasumathi and Moorthi [12] developed the hybrid adaptive neural network and the PSO and implemented it on a Spartan 3E FPGA to accelerate the computation speed for real-time processing. Morsi et al. [13] implemented the PSO algorithm on an FPGA to quickly compute the structural similarity (SSIM) index between the target image and the candidate region. They showed that the results of their implementation, which is a combination of software and hardware, were better than the results of the software-only implementation. Trimeche et al. [14] implemented the PSO on FPGA for a multi-input multi-output (MIMO) detection system. Their work was able to reduce the computational complexity of the maximum likelihood estimation in an MIMO detection system.
This paper proposes a new variant of the PSO for real-time optimization, which is conducted on FPGA to find the optimal number of messages and the transmission period in the message-chain structure. The original PSO is modified to be properly implemented on FPGA by synthesizable hardware description language (HDL) codes. Consequently, the contributions of this paper are as follows. First, the proposed approach can find the optimal number of messages and the transmission period without data loss in the structure of message-chains for data communication systems with half-duplex command-response protocols. Second, the proposed approach can be conducted in real-time, despite the high computation load of the PSO. To the best of our knowledge, PSO to optimize the message-chain structure in data communication systems with half-duplex command-response protocols has never been implemented on FPGA. The main notations used in this paper are summarized in Table 1.

Table 1.
The main notations in this paper.
This remainder of this paper is organized as follows: Section 2 defines and formulates the optimization problem of message-chain structures in half-duplex command-response protocols. Section 3 describes the proposed approach, which is a real-time PSO algorithm on FPGA. Section 4 gives the evaluation of the performance of the proposed approach with various algorithm parameters and system conditions. The real-time capability of the proposed approach implemented on FPGA is then verified by successfully finding the optimal message-chain structure. Finally, Section 5 offers the conclusions.
2. Optimization Problem of Message-Chain Structures
The formulation of the optimization problem depends on a specific data communication system. In our previous work [15], for the offline optimization of the MC structure, we analyzed its timing diagram between the BC and the RT, as shown in Figure 1. At every transmission period (TBC), the BC transmits an MC, which consists of a certain number of messages, NBC. In each MC, the time assigned to each message is called the message gap time (tMG), including the inter-message gap time (tIMG), which separates messages.
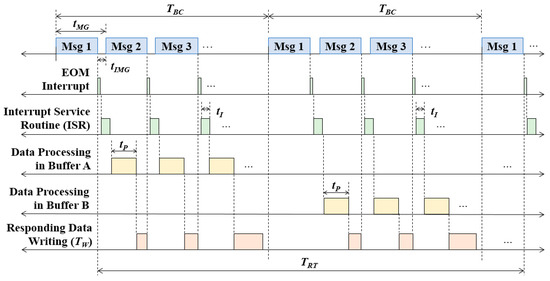
Figure 1.
The timing diagram of data processing in the RT with double buffers for the received message-chains from the BC.
The whole required time in the RT (TRT) is analyzed with the following factors: the processing time for an interrupt service routine (tI) and the received data (tP), the total writing time for responding to messages (TW), and the total processing time for high-priority tasks (TH). The most important point in the RT is to design a structure for MC, which can finish the whole processing for the current MC before receiving the next MC at the same buffer. Since TW is considered to be of two types—tW1 and tW2, which are the average writing times before and after completing the data reception from the BC—it can be computed as follows:
where NRD is the number of response messages that should be written at the buffers in the RT for each message from the BC, and , which is the number of messages on processing in the RT before completing the data reception from the BC. Then, the total required time in the RT, TRT, can be obtained as follows:
To avoid data loss caused by rewriting the buffer containing the current MC by the next MC transmitted for the same buffer, the relation between TRT and TBC is established as follows:
Additionally, the transmission margin for unexpected situations in the BC, which is the time margin from the end of the current MC to the beginning of the next MC, is considered as an optimization constraint because it has been heuristically determined. The additional constraint for the transmission margin, α, in the BC can be formulated as follows:
where . The larger α means more transmission margin. Finally, the upper limits of TBC and NBC are determined according to system requirements and applied to the PSO algorithm.
3. Real-Time PSO on FPGA
To resolve the real-time optimization problem, we propose a new FPGA-based real-time PSO (FRPSO), which is a hardware-friendly variant of the original PSO using the hardware resources of FPGAs for parallel processing. The main differences between the original PSO and FRPSO are summarized in Table 2. The main advantage of FRPSO is the parallelizability with look-up tables (LUTs), which is more flexible and scalable than CPU cores.

Table 2.
The main differences between the original PSO and FRPSO.
3.1. Particle and Swarm Definition
In FRPSO, the particle and swarm are newly defined for efficient FPGA implementation for fixed-point addition, subtraction, multiplication, and division. In addition, the particle swarm with particles is rearranged with groups. The n-th particle of the m-th group at the i-th iteration is defined as where n = 1, …, and m = 1, …, , and and denote and , respectively. Each of them consists of two 15-bit fixed-point vectors, as shown in Figure 2. The first bit is a sign bit. The number of integer bits was determined by the search space for the optimization problem. As the maximum configuration of the search space was 15, according to system requirements, we need at least four bits to represent it. The same number of dummy bits as the integer bits was required for fixed-point multiplication. The number of decimal bits was closely related to the resolution of the optimization results. In this work, the minimum number of decimals bits to obtain appropriate results was six.
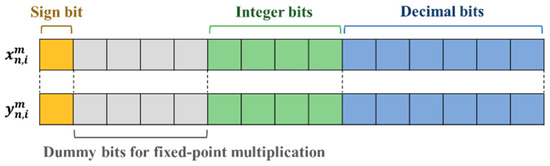
Figure 2.
The concept of fixed-point particle definition in FRPSO.
The concept of particle swarm definition and grouping for parallel processing on FPGAs in FRPSO is shown in Figure 3. The particle swarm at the initial step is generally defined as shown in Figure 3a; the positions of the particles have been sequentially updated as iteration goes, which requires much computation time. In FRPSO, the particle swarm at the initial step is defined with several groups, as shown in Figure 3b, and the position update of the particles can be conducted in a partially parallel manner as iteration goes, which can significantly reduce computation time. FRPSO is different from the existing multi-swarm-based PSO variants [16]. The particles within a swarm in their work cannot move into the areas of other swarms while the particles that belong to different groups in FRPSO can move anywhere in the given search space, as shown in Figure 3c. In addition, FRPSO can be applied to multi-swarm-based approaches if they need parallelization to reduce computation time.
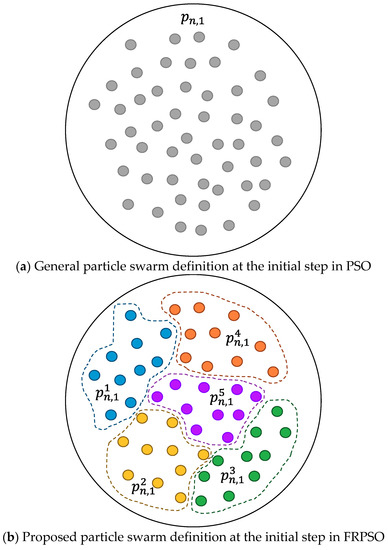

Figure 3.
The concept of the particle swarm definition and grouping for parallel processing on FPGAs in FRPSO.
3.2. FPGA Structure
The FPGA structure of FRPSO is shown in Figure 4, and the pseudo-code of FRPSO is described in Table 3. At every rising edge of the clock produced by phase-locked loop (PLL), FRPSO is conducted with two counters: the clock counter (CC) to control algorithm processes and the particle number counter (PNC) to differentiate particles in each particle set. In states with dependency among particles, as both CC and PNC are used, FRPSO is performed partially in parallel. However, in states without dependency among particles, as only the CC is used, FRPSO is performed entirely in parallel. The states before decision on termination of iterations are conducted with the NG groups of particles in parallel. The multiplication and division are conducted by FixedP_Mul and FixedP_Div, respectively. The core algorithm of FRPSO is conducted in PSO_CORE, which consists of more logic blocks than the original PSO. This is because FRPSO should be implemented with the consideration of avoiding the data loss caused by clock sharing for variable updates among logic blocks with data dependency. For example, if a logic block has variables, which may be rewritten for updates in the same clock, it should be divided by multiple logic blocks and processed independently.
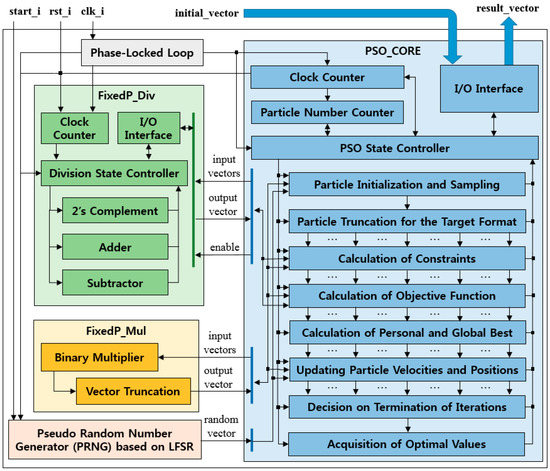
Figure 4.
The FPGA structure of the proposed method.

Table 3.
The pseudo-code of FRPSO.
3.3. Core Algorithm
The core algorithm of FRPSO is conducted as follows. First, NP particles are initialized and randomly sampled by the pseudo random number generator (PRNG) based on the linear feedback shift register (LFSR) within the defined search space. As PRNG produces an 8-bit random vector at every clock, the position of each particle is acquired by combining with multiple vectors and truncated for the target format. Next, the particle evaluation state is conducted by three separate states to avoid wrong updates of errors and best particles. The two constraints, (3) and (4), for each can be rewritten by:
where and are the mean and standard deviation of , and and are the mean and standard deviation of .
As the variations of and are not negligible, their mean and three-sigma standard deviations are used. Then, the objective function is calculated as follows:
where is the weighting factor, which was set to 0.5 in this work. Next, and which are respectively the personal best and the global best are selected to minimize from the history of the n-th particle of the m-th group and throughout all particles, respectively. Next, the velocity and position of the n-th particle of the m-th group at the i + 1 iteration are respectively updated as follows:
where is a constriction factor which is set to 0.2, and and are control factors for relative attraction to and , which are commonly set to 1.9, and is an unit random vector. After the last iteration, the optimal and are finally acquired by at the last iteration.
4. Implementation, Simulations, and Evaluations
4.1. Implementation
FRPSO was implemented on Xilinx FPGA Kintex-7 with synthesizable VHDL codes. The simulations and evaluations of the implemented FRPSO were conducted by Xilinx Vivado. The synthesis and implementation with 90 MHz PLL clocks was successfully completed. The utilization and timing results are summarized in Table 4 and Table 5, respectively.

Table 4.
The utilization results of the post-implementation of FRPSO with 200 particles and 20 groups.

Table 5.
The timing results of the post-implementation of FRPSO with 200 particles and 20 groups.
4.2. Simulation Results
For simulations, we chose 200 particles, because the minimum number of particles that can consistently show optimal results was 200. It is well known that the more the number of particles, the better will be the optimization performance of the original PSO and its variant, including FRPSO. Therefore, we can expect good results from FRPSO with more number of particles. The number of groups indicates how FRPSO processes are parallelized. The more groups, the more parallelized processes and the smaller computation time. In this work, the number of groups was empirically chosen to properly show that the computation time of FRPSO on FPGAs is much smaller than the original PSO on CPUs. Obviously, if FRPSO is implemented with groups over 20, the computation time decreases.
The whole simulation result of FRPSO with 200 particles in 20 groups when the design margin α = 0 is as shown in Figure 5, Pg1 and Pg2, respectively, indicate NBC and TBC and successfully converge the optimal configuration of fixed-point binary vectors. px1_psetm and px2_psetm represent the two-dimensional positions of the particles in the m-th group, respectively. The whole particle positions according to iterations and the final global best position are shown in Figure 6. The particles were successfully converged to the final global best.
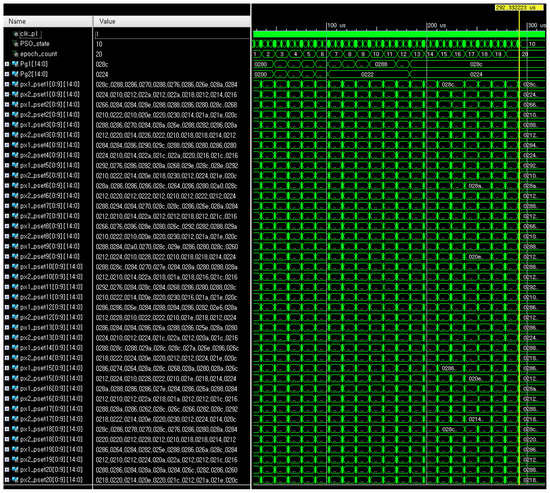
Figure 5.
The simulation result of FRPSO with 200 particles in 20 groups when α = 0.
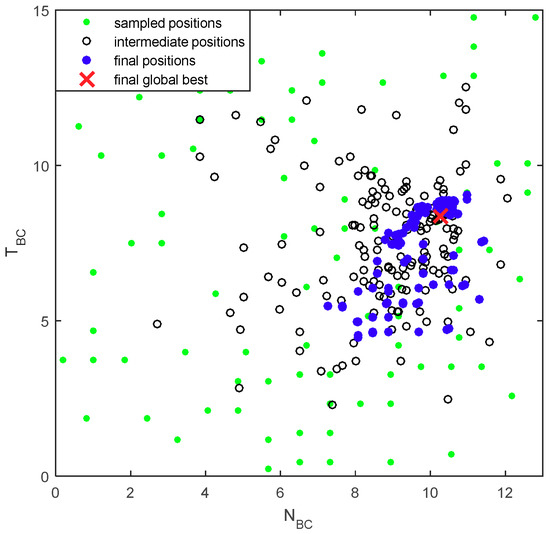
Figure 6.
Whole particle positions according to iterations and the final global best position.
The trajectories of the particle positions in different groups are shown in Figure 7. The particles in each group were successfully converged to the final global best. The sampled particles represented by green dots from the uniform distribution on the given search space have moved to the global best position represented by red cross as the iteration goes. FRPSO processed and updated the positions of the particles in different groups in parallel.
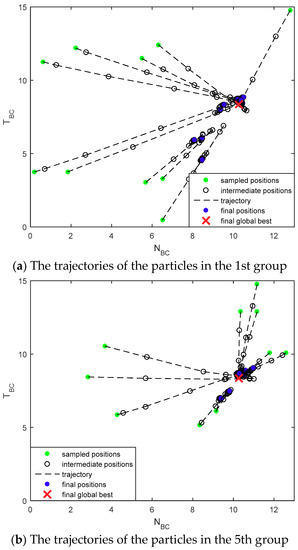
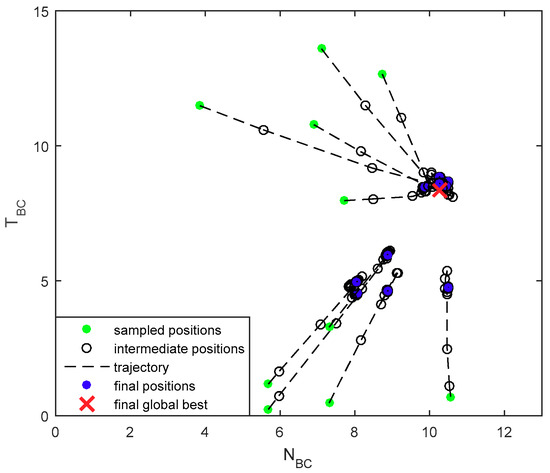
Figure 7.
The trajectories of the particles in different groups.
4.3. Evaluations
The evaluations of FRPSO were also conducted by Xilinx Vivado with 90 MHz PLL clocks. The results according to the number of particles used in FRPSO are summarized in Table 6, which indicates that FRPSO can find the optimal NBC and TBC even though the number of particles varies between 200 and 440. Under 200 particles, the optimization results of FRPSO were not consistent. Over 440 particles, FRPSO could not be implemented on Xilinx FPGA Kintex-7 due to the lack of LUTs. If FPGAs with more LUTs are used, FRPSO will be successfully implemented.

Table 6.
The optimization results of FRPSO according to the number of particles.
For a more detailed evaluation, the optimization results of FRPSO with 200 particles according to α were analyzed, as shown in Figure 8. FRPSO successfully found optimal configurations according to α, which indicates that it can be applied to different systems with different requirements. Note that the optimal throughput with optimal configuration decreases as α increases, which indicates that users should carefully design the BC by considering the trade-off relation between the maximum throughput and transmission margin.
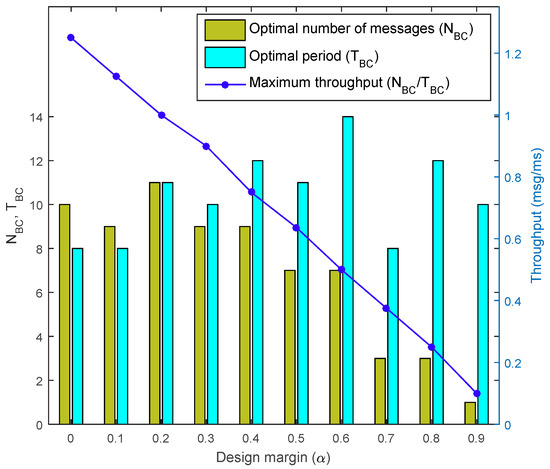
Figure 8.
Optimization results by FRPSO according to α.
To show how FRPSO reduces computational time, the processing times of FRPSO were compared with those of the original PSO and its parallelized version with a GPU (Graphics Processing Unit) according to NP, as shown in Figure 9. The processing time of the original PSO and its parallelized version with the GPU were acquired by a desktop computer with 2.3 GHz CPU clocks and NVIDIA GeForce GTX 750. The parallelized PSO with the GPU was implemented with NVIDIA CUDA Toolkit 10.0, which was mainly conducted on CPU. Obviously, the processing time of FRPSO were smaller than those of both the original PSO and its parallelized version with the GPU with the same optimization results. The increase amounts of processing time for FRPSO according to NP were also smaller than those of the original PSO and its parallelized version with the GPU. This is because FRPSO is designed to be conducted in parallel, using the resources of FPGAs. Moreover, if the number of particles is fixed, the computation time of FRPSO is consistent because the processing lines on FPGAs are physically allocated and connected, while the original PSO is affected by other communication tasks on CPU. Therefore, FRPSO benefits task scheduling in real-time systems because of fast computation time and independency from other tasks.
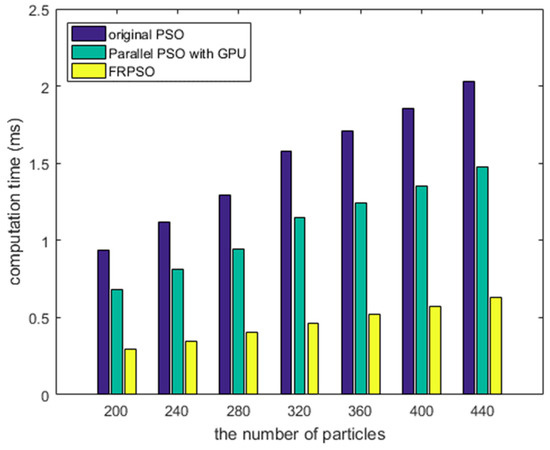
Figure 9.
The comparison results of the processing times between the original PSO, its parallelized version with a GPU, and FRPSO.
The utilization results of FRPSO according to NP are shown in Figure 10. When FRPSO used 440 particles, the utilization result of the LUTs, which are the critical hardware resource in FPGA, was 93.61%, as described in Figure 10, and the computation time of the proposed method was about 0.6307 ms, as described in Figure 9. This means that FRPSO is fast enough to be conducted in real time, even though critical hardware resources are considerably utilized. The LUT was the main factor to affect the implementation availability of FRPSO. The LUTRAM and the FF also increase as NP increases, but they were not significant to affect the implementation availability of FRPSO. The DSP, BUFG, IO, and PLL were consistent regardless of NP. The utilization results of FPGA resources can be affected by variable definitions, algorithm structures, and logics. Note that the variable definitions, structure, and logic of FRPSO was designed to be parallelized and applied to real-time optimization by reducing computation time with FPGA resources. Because particle positions in FRPSO were defined and calculated with 15-bit fix-point vectors, quantization errors occurred between the particle positions in the original PSO and FRPSO; they were evaluated by mean squared errors according to epochs as shown in Figure 11, which was not significant. Besides, in this work, since the final results were used as rounded values, small quantization errors did not affect FRPSO’s performance.
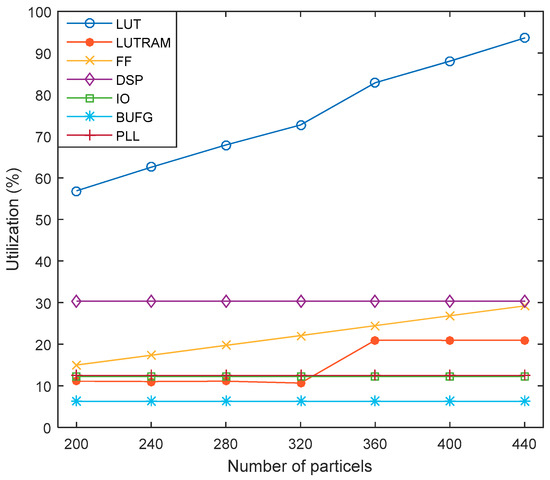
Figure 10.
The comparison results of the computation times between the original PSO and FRPSO.
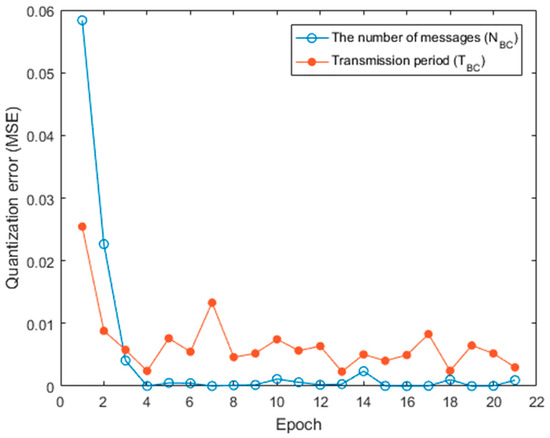
Figure 11.
Quantization errors between particle positions in the original PSO and FRPSO.
In summary, this work is focused on the extension of the original PSO to the real-time optimization problem in data communications with half-duplex command-response protocols. The contributions of this work are as follows. First, the original PSO on CPU to find the optimal message-chain structure was hardware-friendly modified and implemented on FPGA. Second, since the proposed new variant of the PSO is parallelized with hardware resources on FPGA, its computation time is much smaller than the original PSO. Third, as the proposed variant is conducted on FPGA, it can avoid conflicts with other tasks on CPU. In future, we will conduct further research to generalize FRPSO for data throughput maximization in other platforms such as multi-to-multi serial communication systems and wireless communication systems [17,18,19,20,21].
5. Conclusions
This paper proposed FRPSO, which is a hardware-friendly variant of the original PSO, to optimize the message-chain structure in real-time. FRPSO was implemented and conducted on FPGA with synthesizable HDL codes. The simulation and evaluation results showed that FRPSO can successfully offer optimal configuration with much smaller computation time than the original PSO. In addition, its performance was consistent in spite of different system and algorithm parameters. The implementation availability of FRPSO according to the number of particles was also evaluated and analyzed with FPGA resources. Consequently, FRPSO is good for real-time optimization of the message-chain structure in half-duplex command-response data communications.
Author Contributions
All authors contributed the present paper with the same effort in describing the problem, finding available literatures, and writing the paper. H.L. designed and implemented the proposed method to resolve the problem.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- MIL-STD-1553B NOTICE II; Department of Defense: Washington, DC, USA, 1986.
- MIL-STD-1553B Designer’s Guide; Data Device Corporation: Bohemia, NY, USA, 1998.
- Zhang, J.; Liu, M.; Shi, G.; Pan, W. A MIL-STD-1553B bus command optimization algorithm based on load balance. Appl. Mech. Mater. 2012, 130–134, 3839–3842. [Google Scholar] [CrossRef]
- Kim, K.P.; Ahn, K.-H.; Kwon, Y.-S.; Yun, S.-J.; Lee, S.-H. Analysis and implementation of high speed data processing technology using multi-message chain and double buffering method with MIL-STD-1553B. J. Korea Inst. Mil. Sci. Technol. 2013, 16, 422–429. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Lee, H.C.; Park, S.K.; Choi, J.S.; Lee, B.H. PSO-FastSLAM: An improved FastSLAM framework using particle swarm optimization. In Proceedings of the IEEE International Conference Systems, Man, and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 2763–2768. [Google Scholar]
- Zhang, J.; Ni, L.; Xie, C.; Tan, Y.; Tang, Z. AMT-PSO: An adaptive magnification transformation based particle swarm optimizer. IEICE Trans. Inf. Syst. 2011, E94-D, 786–797. [Google Scholar] [CrossRef]
- Ishikawa, K.; Hayashi, N.; Takai, S. Consensus-based distributed particle swarm optimization with event-triggered communication. IEICE Trans. Fundam. Commun. Comput. Sci. 2018, E101-A, 338–344. [Google Scholar] [CrossRef]
- Liu, W.; Chung, I.; Liu, L.; Leng, S.; Cartes, D.A. Real-time particle swarm optimization based current harmonic cancellation. Eng. Appl. Artif. Intell. 2011, 24, 132–141. [Google Scholar] [CrossRef]
- Gao, Z.; Zeng, X.; Wang, J.; Liu, J. FPGA implementation of adaptive IIR filters with particle swarm optimization algorithm. In Proceedings of the ICCS 2008. 11th IEEE Singapore International Conference on Communication Systems, Guangzhou, China, 19–21 November 2008; pp. 1364–1367. [Google Scholar]
- Gupta, L.; Mehra, R. Modified PSO based Adaptive IIR Filter Design for System Identification on FPGA. Int. J. Comput. Appl. 2011, 22, 1–7. [Google Scholar] [CrossRef]
- Vasumathi, B.; Moorthi, S. Implementation of hybrid ANN–PSO algorithm on FPGA for harmonic estimation. Eng. Appl. Artif. Intell. 2012, 25, 476–483. [Google Scholar] [CrossRef]
- Morsi, N.N.; Abdelhalim, M.B.; Shehata, K.A. FPGA Implementation of PSO-Based Object Tracking System Using SSIM. In Proceedings of the International Conference on Micro-electronics, Beirut, Lebanon, 15–18 December 2013; pp. 1–4. [Google Scholar]
- Trimeche, A.; Sakly, A.; Mtibaa, A. Implementation of PSO algorithm for MIMO detection system in FPGA. Int. J. Electron. 2018, 105, 42–57. [Google Scholar] [CrossRef]
- Lee, H.C.; Kim, K.P.; Kwon, Y.S. Efficient and reliable bus controller operation with particle swarm optimization in MIL-STD-1553B. In Proceedings of the Asia-Pacific International Sym. Aerospace Technology, Seoul, Korea, 16–18 October 2017; pp. 1433–1440. [Google Scholar]
- Blackwell, T.; Branke, J. Multi-swarm optimization in dynamic environments. In Proceedings of the Workshops on Applications of Evolutionary Computing, Coimbra, Portugal, 5–7 April 2004; pp. 489–500. [Google Scholar]
- Vamvakas, P.; Tsiropoulou, E.E.; Papavassiliou, S. A user-centric economic-driven paradigm for rate allocation in non-orthogonal multiple access wireless systems. EURASIP J. Wirel. Commun. Netw. 2018, 129, 1–14. [Google Scholar] [CrossRef]
- Tan, C.W.; Chiang, M.; Srikant, R. Fast algorithms and performance bounds for sum rate maximization in wireless networks. IEEE/ACM Trans. Netw. 2013, 21, 706–719. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, Y.; Li, G. Robust rate maximization for heterogeneous wireless networks under channel uncertainties. Sensors 2018, 18, 639. [Google Scholar] [CrossRef] [PubMed]
- Tsiropoulou, E.E.; Vamvakas, P.; Papavassiliou, S. Joint utility-based uplink power and rate allocation in wireless networks: A non-cooperative game theoretic framework. Phys. Commun. 2013, 9, 299–307. [Google Scholar] [CrossRef]
- Bi, S.; Zhang, Y.J. Computation rate maximization for wireless powered mobile-edge computing with binary computation offloading. IEEE Trans. Wirel. Commun. 2018, 17, 4177–4190. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).