Abstract
This work presents a multi-objective approach for scheduling energy consumption in data centers considering traditional and green energy data sources. This problem is addressed as a whole by simultaneously scheduling the state of the servers and the cooling devices, and by scheduling the workload of the data center, which is comprised of a set of independent tasks with due dates. Its goal is to simultaneously minimize the energy consumption budget of the data center, the energy consumption deviation from a reference profile, and the amount of tasks whose due dates are violated. Two multi-objective evolutionary algorithms hybridized with a greedy heuristic are proposed and are enhanced by applying simulated annealing for post hoc optimization. Experimental results show that these methods are able to reduce energy consumption budget by about 60% while adequately following a power consumption profile and providing a high quality of service. These results confirm the effectiveness of the proposed algorithmic approach and the usefulness of green energy sources for data center infrastructures.
1. Introduction
Energy consumption in data centers has become a critical matter, especially to large providers like Google, Facebook, and Amazon among others. The Internet industry requires more and bigger data centers to sustain its growth, but the amount of energy required for their operation has become an issue for economic and environmental reasons. In 2005, data centers accounted for around 0.5% of the total world energy consumption, while in the year 2010, it reached an estimate of 1.3%. With an estimated annual growth rate of more than 16%, forecasts are grim [1,2]. By the year 2030, the worst-case scenario estimates the electricity consumption from data centers will reach up to 13% of the total world energy [3].
Significant efforts have been made to address the aforesaid energy issues with different approaches and techniques [4,5]. Many traditional energy saving methods focus on lowering energy consumption when computing resources are idle, or reducing the system performance when executing non-critical computing tasks, or scheduling the computational load when energy is cheaper [6,7,8,9]. These methods are helpful, but their effectiveness is limited because they usually lower the quality of service delivered by the data center. More recently, advances in renewable energy sources—known as green energy—have provided new ways to reduce energy consumption and the environmental impact of data centers [10]. The use of green energy sources has empowered energy saving methods, enabling the scheduling of computational workload when green energy is available. Nevertheless, this remains a challenging approach since green energy sources are unreliable and depend on uncontrollable external conditions such as sun irradiation and wind velocity. Because of their unreliability, most data centers must consider a hybrid energy approach, with green energy combined with traditional energy—known as brown energy—to avoid energy outages.
When optimizing energy consumption in data centers, most approaches focus on optimizing Central Processing Units (CPUs) and cooling devices that are the most power hungry components in data centers. CPUs are, by far, the most power hungry components, using an estimated 46% of the total power consumption of a data center. The second most power hungry components are cooling devices, such as air conditioning systems, which consume an estimated of 15% of the total power. Despite the fact that cooling devices consume less energy than CPUs, they are a key focus when addressing energy consumption since they are the most inefficient components and the best candidates for improvement [11].
This work presents a multi-objective problem formulation for optimizing the energy consumption of data centers that are powered by hybrid energy. The problem formulation addresses the scheduling of computational load and cooling devices in a data center in order to minimize its energy consumption budget, minimize the deviation of its energy consumption from a reference consumption profile, and maximize the Quality of the Service (QoS) provided to its users. Two Multi-Objective Evolutionary Algorithms (MOEAs) are applied for effectively solving the scheduling problem: the Non-dominated Sorting Genetic Algorithm, version II (NSGA-II) [12] and the Epsilon-Variable Multi-Objective Genetic Algorithm (ev-MOGA) [13]. Experimental results show the proposed approach reduces energy consumption budget by about 60% while maintaining QoS over 95% and a deviation from a reference power profile of about 3%, all this compared to a traditional business as the usual data center scenario.
This work is an extension of our previous work [14]. This work further extends [14] by applying ev-MOGA and comparing its accuracy with NSGA-II when addressing the proposed problem. In addition to this, a larger and more diverse set of problem instances are evaluated and a more thorough multi-objective experimental analysis with statistical support is provided.
This article is organized as follows: Section 2 briefly reviews the most relevant and recently published work. Section 3 defines the scheme of the data center model. Section 4 presents the problem formulation. Section 5 describes the proposed MOEA designed for solving the problem. Section 6 reports and discusses the results of the experimental evaluation. Finally, Section 8 presents conclusions and future work.
2. Related Work
Many articles in the literature address the energy efficiency problem in data centers. Next, some of the latest and most relevant ones are presented.
Goiri et al. [8] propose GreenSlot, a single-objective greedy heuristic for scheduling computational load in data centers powered by green and brown energy. The aim of GreenSlot is to schedule a set of independent parallel computing tasks using the minimum amount of traditional energy while also meeting all task deadlines. Although GreenSlot takes into consideration a hybrid energy source, it uses brown energy just as a backup for when it cannot meet all deadlines using green energy alone. Furthermore, Goiri at al. use a realistic energy forecast model based on historical data to predict the availability of green energy. Goriri et al. show GreenSlot can reduce energy cost by up to 39% when compared to conventional schedulers. The work from Goriri et al. is different from ours mainly in that they address a single-objective problem considering QoS as a constraint, and because they do not consider cooling devices as energy consuming components nor temperature as an operative constraint.
Lei et al. [9] address the energy efficiency problem in data centers by scheduling a set of independent tasks with deadlines to be executed in a system with Dynamic Voltage Frequency Scaling (DVFS) and powered by hybrid energy. The scheduler uses DVFS for reducing energy consumption when executing tasks with loose deadlines. In this formulation, a task can be rejected when its deadline cannot be met. Lei et al. formulate a multi-objective problem and propose two MOEA for solving it, optimizing four objectives: (i) maximizing green energy usage; (ii) minimizing the finishing time of the whole schedule; (iii) minimizing the total energy consumption; and (iv) minimizing the task rejection rate. Then, the proposed MOEAs are compared with each other using a simple multi-objective metric. Although Lei et al. argue that these results confirm the effectiveness of their approach, the amount of energy consumption saved when using it is not clear. This work is different from the work of Lei et al. in that, in our work, the temperature of the data center is a constraint and cooling devices are considered when computing the energy consumption. In addition, a thorough multi-objective analysis is performed in our work and statistical confidence results are presented.
Peng et al. [15] deal with the scheduling of resources in multiple data centers powered by hybrid energy. The aim of this problem is to allocate virtual machines to physical machines in order to satisfy the computing demand while minimizing total energy cost and considering quality of service as a constraint. Peng et al. propose a single-objective formulation for addressing this problem and present an evolutionary algorithm for solving it. Peng et al. report that this approach reduces energy cost between 8% and 10% when compared to traditional allocation schemes. Once more, the work from Peng et al. is different from ours in that, in our work, a multi-objective problem is addressed and the scheduling of cooling devices and the temperature of the data center as a constraint are both considered.
In our previous work [14], a data center powered by hybrid energy was modeled, considering cooling devices and internal data center temperature. The multi-objective scheduling problem of minimizing the energy budget, maximizing the QoS, and meeting a brown energy consumption threshold is addressed, constrained to the operative temperature of the data center. The scheduling problem consisted of scheduling a set of independent computing tasks with due dates into a set of computing resources. An improved scheduling algorithm is proposed by hybridizing NSGA-II with a Local Search (LS) operator in order to exploit the most promising solutions. Experimental results show that this approach is able to reduce the energy budget by about 30% when compared to traditional schedulers. This work extends our previous work [14] by comparing evMOGA—a novel state of the art MOEA—with NSGA-II, our previously proposed approach. The experimental analysis is improved by increasing the number and diversity of evaluated problem instances and by performing a more thorough experimental analysis presenting multi-objective metrics, providing statistical confidence.
3. The Data Center Energy- and QoS-Aware Model
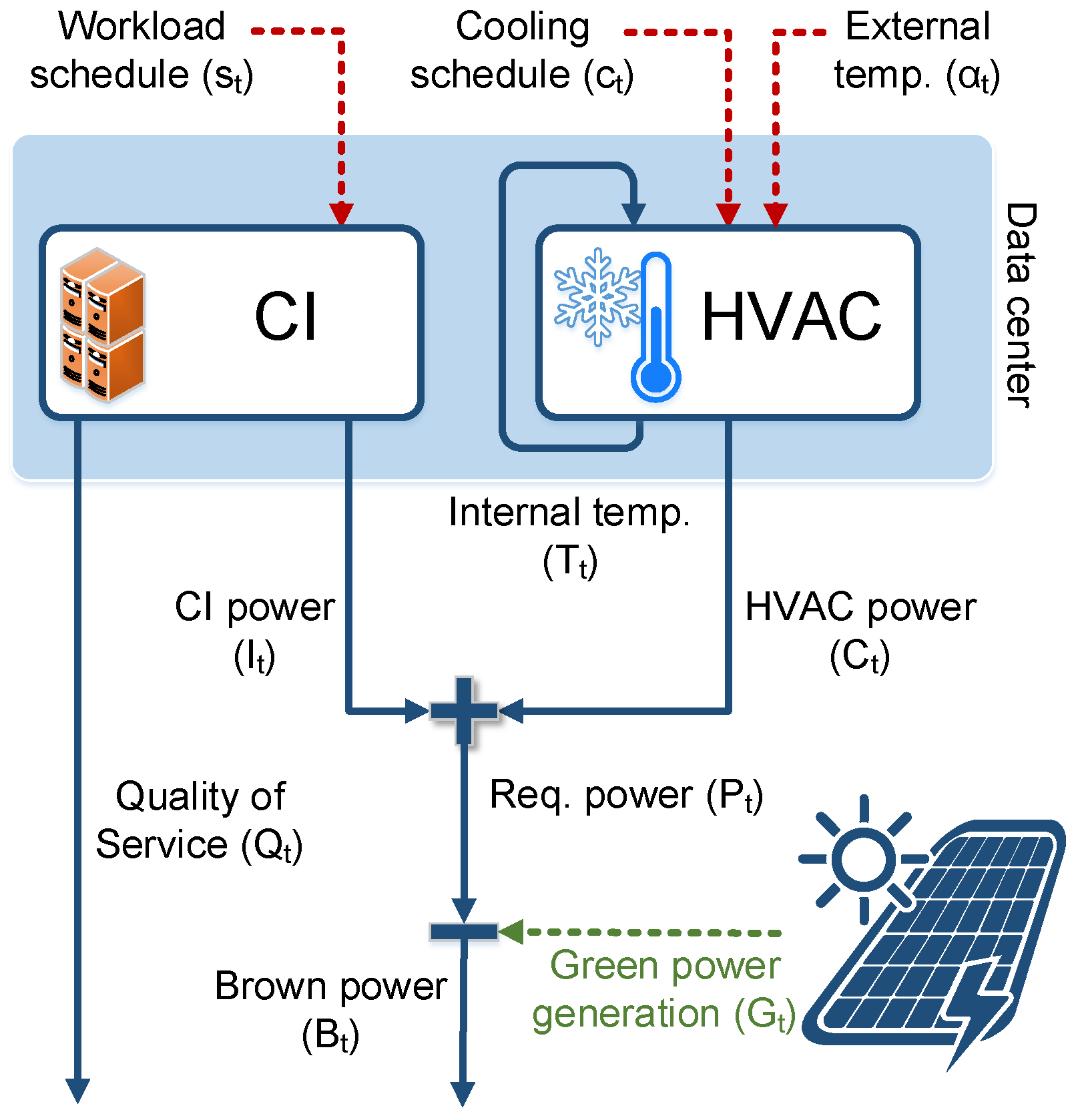
The proposed data center model is based on the one proposed in [16] and further extended in [14]. Figure 1 shows the schema of the data center model.
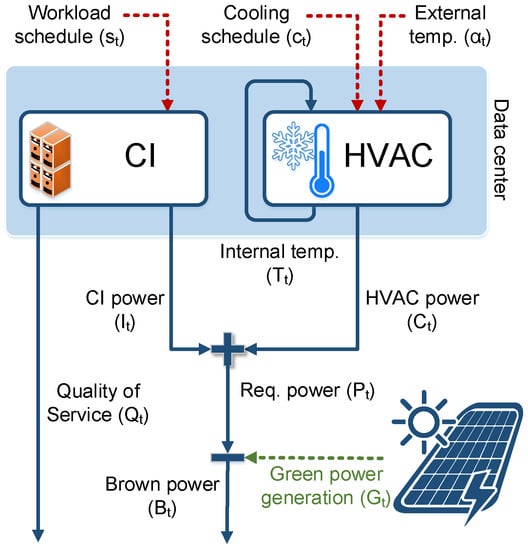
Figure 1.
Data center scheme considering energy consumption and quality of service.
This model is comprised of two main components: the Heating, Ventilation and Air Conditioning (HVAC) component and the Computing Infrastructure (CI) component. The HVAC component represents the cooling devices, while the CI component represents the computing resources of the data center (i.e., the servers). A simple but realistic energy model is considered where each server may be either in the executing state, in the idle state, or in the sleep state. Every time a server executes a task, it is considered to be at peak performance, thus consuming the maximum amount of energy for the server. When a server is on but not executing a task, it is considered to be idle and consuming a lower amount of energy. Finally, a server may be in sleep state and consuming a minimum amount of energy. Formally, the total energy consumption of the CI component () is calculated as , where is the total energy consumption of servers that are executing a task, of which are in idle state, and of which are in sleep state.
The data center is controlled by two input variables: task schedule () and cooling schedule (). The task schedule defines the allocation of tasks to computing resources in the CI component for each time unit. Likewise, the cooling schedule defines the cooling strategy of the HVAC component for each time unit.
Furthermore, two non-controllable input variables are considered: external temperature () and green energy availability (). These variables are external and are not controllable by the scheduling algorithm. The external temperature variable, , represents the temperature outside the data center at each time unit. This temperature affects the effectiveness of the free cooling method. While the green energy availability variable, , represents the amount of energy generated by the renewable energy source for each time unit.
Finally, three output variables are defined for the model: (i) the amount of overdue time required for task completion (); (ii) the internal temperature variable () which is the temperature inside the data center; and (iii) which is the energy required by the HVAC component, and which is the energy required by the CI component. Hence, the total power required by the data center () is the sum of the power required by the HVAC and the CI components. Similarly, the total amount of traditional energy required by the data center () is the difference between the required power () and the amount of green power available ().
The computing workload of the data center is comprised of a set of independent tasks with due dates. For a task, its due date is its expected or desired completion time. In this approach, the QoS of the system is measured by the total amount of additional time, over the due date, required by the system to complete the execution of all tasks. It is key to consider a QoS-related objective when reducing energy consumption since the latter, most likely, will affect the QoS provided to the final users.
The variable schedules the HVAC while considering two cooling methods: air conditioning and free cooling. Both of these methods are widely used cooling methods [11]. The air conditioning mode uses the conventional Computer Room Air Conditioning (CRAC) unit which can take on and off values. The free cooling mode uses a fan system to inject air from the outside into the data center, and it can take fan speed values between 1 and 100. Hence, the energy consumption of the HVAC component at time t () is defined as shown in Equation (1):
The energy consumption of the air conditioning () is fixed, and is between 0 and the maximum fan energy consumption. Because the cooling mode directly affects the temperature in the data center, the Auto-Regressive eXogenous (ARX) model presented in [17] is used for modeling . This model estimates the internal temperature of the data center taking into account the air conditioning, fan speed, outside temperature, and data center load.
4. The Problem Formulation
The data center must execute N tasks in a time horizon of K time units. The problem formulation consists of finding a schedule of computing tasks () and cooling resources () such that: it minimizes the difference between the energy consumption of the data center () with respect to a predefined reference profile (), minimizes the energy budget, and minimizes the total overdue time of the tasks. Furthermore, the problem is subject to the internal temperature of the data center () which must be kept below its maximum operative value ().
Each task is an atomic unit which cannot be interrupted; once started, it must be executed to completion. Moreover, each task i should be completed before its due date for the data center to deliver the optimum QoS level. With representing the finishing time of task i and representing the brown energy cost at time t, optimization goals of this problem can be formally defined as presented in Equation (2):(3) and (4).
Equation (2) defines the objective of minimizing the deviation of the power consumption of the data center with respect to the reference power profile . Equation (3) defines the objective of minimizing the total monetary cost of the energy consumption of the system. Finally, Equation (4) defines the objective of minimizing the total overdue time required for completing the execution of all tasks.
5. Multi-Objective Evolutionary Scheduling for Energy-Aware Data Centers
Evolutionary algorithms are iterative stochastic optimization methods inspired in the evolution of the species and the natural selection process [18]. Algorithm 1 presents the general schema of an evolutionary algorithm. At each iteration, the evolutionary algorithm stochastically applies a set of evolutionary operators to a population of candidate solutions to the optimization problem. These evolutionary operators combine and mutate solutions in the population, producing new solutions that compete with each other to survive the selection process and remain in the population. The recombination operator exploits known solutions by producing new solutions with the best characteristics of solutions already in the population. On the other hand, the mutation operator explores the solution landscape searching for solutions with new characteristics by applying small perturbations to known solutions. These methods have been successfully applied for solving optimization, search, and learning problems in many application domains.
Multi-Objective Evolutionary Algorithms (MOEAs) are evolutionary algorithms that deal with more than one simultaneous optimization objective. Unlike single objective optimization methods, MOEAs are able to compute a set of trade-off solutions in a single execution thanks to their population-based approach. However, an MOEA must maintain a adequate balance between optimizing each objective as much as possible, and sampling a diverse and homogeneously distributed Pareto front.
In this work, NSGA-II [19] and ev-MOGA [20] are applied for addressing the proposed scheduling problem. These MOEA are entrusted with planning the state of servers and the cooling devices. On top of these MOEA, two hybridization mechanisms are further applied. The first mechanism consists of applying a greedy scheduling heuristic during the evolutionary process for reducing the dimension of the problem search space. This greedy heuristic receives a server and cooling schedule, and computes a scheduling for the task workload. The second mechanism consists of applying Simulated Annealing (SA) as a post hoc optimization procedure. That is, once the evolutionary process has finished, the SA is applied for further improving the accuracy of the solutions computed by the MOEAs. Next, the proposed algorithmic approach is described in detail.
| Algorithm 1 General schema of an evolutionary algorithm | |
| ▹ create the initial population of parents | |
| ▹ evaluate population of parents | |
| while stopping condition is not met do | |
| ▹ select parents to evolve | |
| ▹ recombine parents and create offspring | |
| ▹ mutate offspring | |
| ▹ evaluate population of offspring | |
| ▹ new population with the best individuals | |
| end while | |
5.1. Solution Representation
For representing the problem solution, a time discretization approach is applied using a time horizon of time steps. For each time step, the solution encodes the number of active servers and the state of the cooling devices.
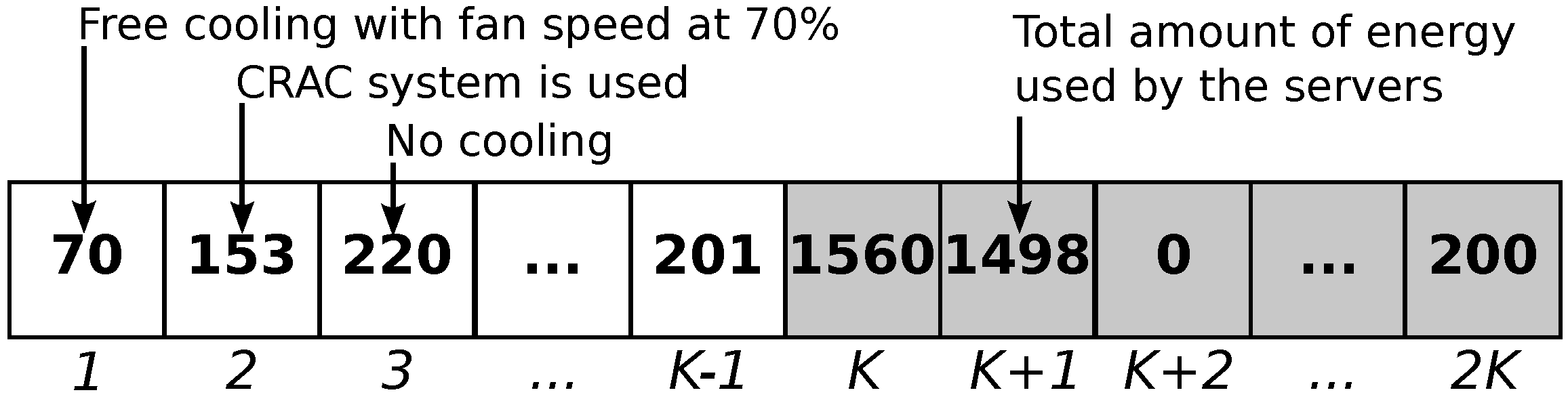
The active servers are encoded directly with their total power consumption in Watts. Hence, an integer vector of size K is used, with values ranging from 0 up to , where is the power consumed when all servers are active. Similarly, the state of the cooling devices is encoded as an integer vector of size K with each value representing three states in the interval . A value v in the interval represents the free cooling being used with a fan speed of v. On the other hand, a value v in the interval represents the CRAC being used. Finally, a value v in the interval means that all cooling devices are off.
Considering both encodings, the complete solution representation is an integer vector of size where the cooling devices are encoded in the first K integers of the representation, and the server state is encoded in the last K elements of the representation. This representation was previously introduced in [17]. Figure 2 shows the representation of a sample solution.

Figure 2.
Representation of a sample solution.
5.2. Initial Population
Each solution of the initial population is created randomly using the following criteria. With probability , the new solution is created totally at random. That is, each value of the solution encoding is chosen randomly following a uniform distribution in the whole range of valid values. Otherwise, the new solution is created randomly in a high energy subspace of the solution space. For this, each value of the encoding is chosen in the upper 20% of the range of valid values. This technique allows us to provide the MOEA with a greater number of feasible solutions in the initial population.
5.3. Evolutionary Operators for NSGA-II
NSGA-II is a well-known MOEA proposed by Deb [19]. In this work, the NSGA-II implementation previously proposed in [14] is applied for addressing the scheduling problem since it proved to be accurate and efficient. Next, the recombination and mutation operators for the NSGA-II are presented.
5.3.1. Recombination Operator
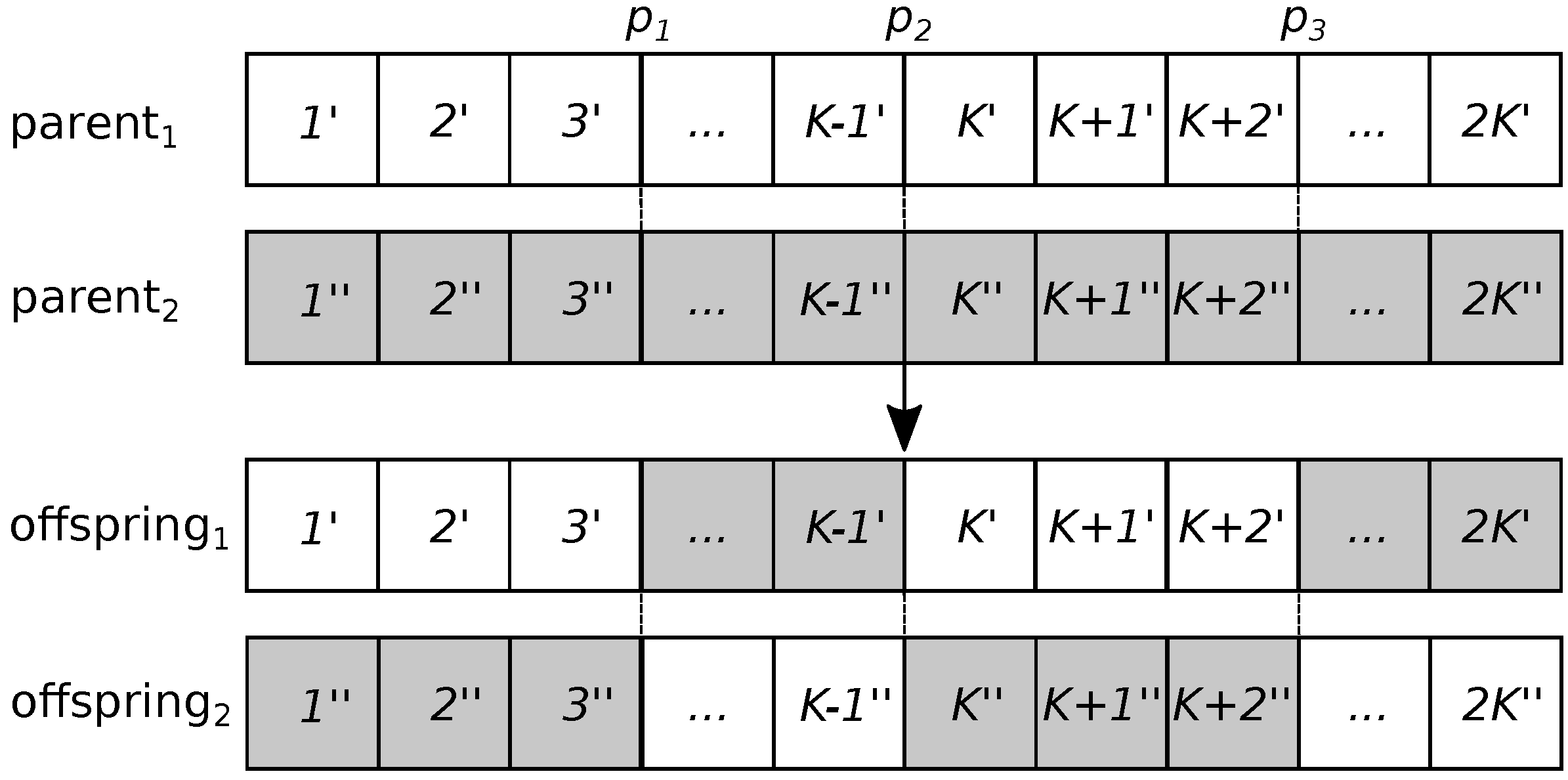
A three-point operator is defined for the recombination operator. This operator starts by selecting three points: . Point is selected randomly following a uniform distribution in the interval . Point is always K, and point is . By defining to always be K, it is asserted that cooling and server power values at each time step from each parent are inherited together by the offspring. For example, the value at position is always inherited with position , each corresponding to cooling and server power values at time step 1. Figure 3 shows how this operator works.
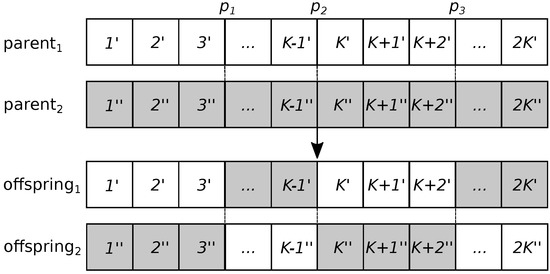
Figure 3.
Example of the three point recombination operator for the Non-dominated Sorting Genetic Algorithm, version II (NSGA-II).
5.3.2. Mutation Operator
The mutation operator is applied individually to each integer in the solution encoding but uses two different approaches, one for the cooling state part of the solution and another for the server power part. For the cooling state part (i.e., the first K elements in the encoding), a differential approach is applied. This approach works as follows. For mutating an integer value v, a random value is selected, and the mutated value of v is computed as . For the server power part of the encoding (i.e., elements to ), a simple uniform mutation is applied, such that the value of is a random value between 0 (i.e., when all servers are off) and (i.e., when all servers are on).
5.4. Evolutionary Operators for ev-MOGA
The ev-MOGA was proposed by Martínez et al. [20] to address the shortcomings of many MOEAs. In this work, ev-MOGA uses the exact same mutation operator as NSGA-II. This mutation operation proved to be useful and adapted adequately for ev-MOGA. On the other hand, a linear recombination is used for the recombination of an operator, as recommended by the original ev-MOGA implementation. This latter operator is detailed next.
5.4.1. Recombination Operator
For the recombination operation, a linear recombination method is applied such that parents and are recombined to produce offspring and as shown in Equation (5) and (6):
where α is a random vector in the space and ⊗ is the element-wise multiplication of two vectors. Finally, all values of and are rounded to their nearest integer value to satisfy the encoding.
5.4.2. Fitness Functions
The fitness functions that guide the evolutionary process are identical to the ones defined in Equation (2), (3) and (4). Because the MOEA solution encodes the cooling and server power, it alone is sufficient for computing Equation (2) and (3). However, because it does not include task scheduling information, it is not possible to compute Equation (4).
For computing Equation (4), the Best Fit Hole (BFH) algorithm is used as a subordinate greedy scheduling heuristic for computing a task-to-server scheduling. Next, the BFH task-scheduling heuristic is presented in detail.
5.4.3. Greedy Task Scheduling Heuristic
The Best Fit Hole (BFH) heuristic is applied for task scheduling [7]. This heuristic works by applying a backfilling approach and keeping track of holes in the schedule when servers are idle. Tasks are assigned, one by one, to the hole that satisfies their due date and minimizes the difference between its execution time and the hole duration (i.e., it best fits the task). If no hole satisfies the deadline constraint of a task, then that task is scheduled at the end of the server that can execute it faster. Algorithm 2 shows the schema of the BFH scheduler.
| Algorithm 2 Schema of the Best Fit Hole (BFH) scheduling heuristic | |
| ▹ queue of tasks | |
| ▹ set of holes | |
| while do | |
| ▹ get the first task and remove it from the set | |
| ▹ get holes which may accommodate the task | |
| ▹ get holes which satisfy the due date of the task | |
| if then | |
| ▹ get hole with smallest length | |
| ▹ remove hole from set and update remaining hole time | |
| else | |
| end if | |
| end while | |
5.5. Simulated Annealing for Post Hoc Optimization
Simulated Annealing (SA) is a metaheuristic introduced by Kirkpatrick et al. [21]. In this work, it is applied as a post hoc optimization for further improving the solutions computed by the MOEA. A similar post hoc approach proved to be very effective in significantly improving QoS in [14].
Since SA works with a single solution, it is executed separately from each non-dominated solution computed by the MOEA. On top of that, SA is a single objective optimization method and cannot deal with multiple objectives. For this reason, it is applied multiple times (N) for each solution. Each time, the SA randomly chooses an optimization objective to be improved. Algorithm 3 shows the schema for applying the post hoc optimization. Dominance is used as an acceptance criterion, that is, a new solution is accepted only when it dominates the current solution. The neighborhood for the SA is constructed using a simple task moving operation which moves one task from its current machine to a new machine in some arbitrary position.
| Algorithm 3 Schema for post hoc optimization using Simulated Annealing (SA) | |
| ▹ set of solutions computed by the MOEA | |
| ▹ set of improved solutions | |
| while do | |
| for do | |
| ▹ applies simulated annealing to s | |
| if dominates s then | ▹ evaluates Pareto dominance |
| end if | |
| end for | |
| end while | |
6. Experimental Evaluation
In this section, the experimental evaluation of the proposed algorithmic solutions is presented. It introduces the problem instances created for assessing the efficacy of the proposed algorithms and the parameter setting of each algorithm.
6.1. Problem Instances
A set of realistic problem instances is created to evaluate the proposed algorithmic approach. For all these problem instances, a scheduling horizon of time steps is defined and a rescheduling policy is considered. Every K time steps or when a new task arrives, the scheduling algorithm is executed and all queued tasks are rescheduled. This is a realistic time horizon with an adequate compromise of time ahead scheduling and rescheduling frequency. An external temperature of 25 °C is considered, an initial internal temperature of 26.5 °C, and a maximum operative temperature of 27 °C. The data center simulates the Parasol data center presented in [8]. This data center consists of 64 low-power servers with Intel Atom processors. Each server consumes 30 W when executing at peak performance, 22 W in idle state, and only 3 W in sleep state. The CRAC system consumes 2.3 kW and the free cooling system up to 410 W.
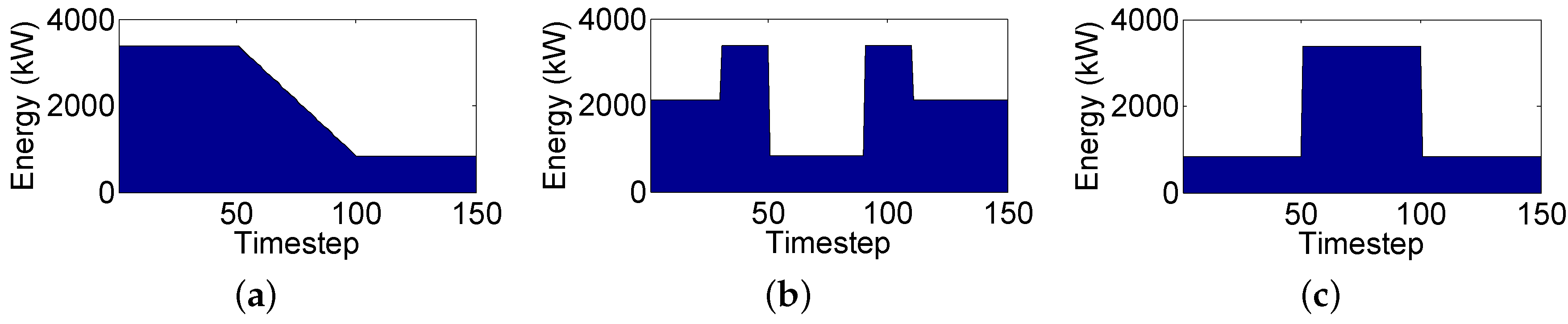
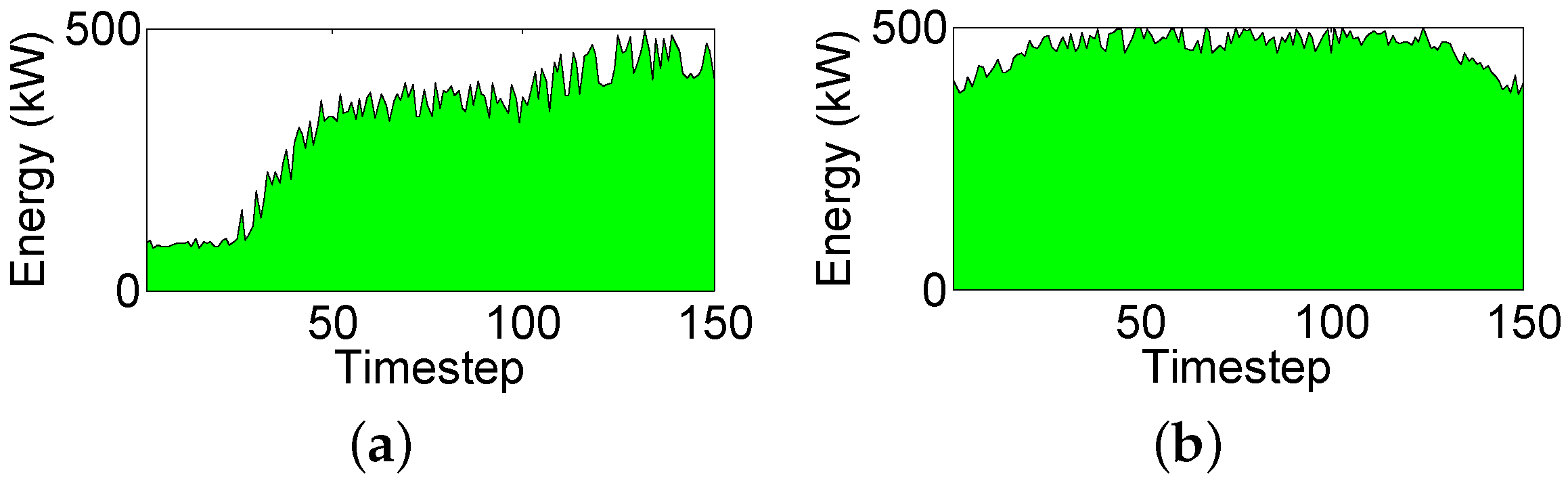
Considering all the above, small, medium, and large workloads are defined comprised of 200, 300 and 400 tasks, respectively. Three different workload instances are created for each size totaling nine different workload instances. For the reference power profile, , three different configurations are considered. These configurations represent a fairly heterogeneous spectrum of scenarios with varying reference profiles. Figure 4 shows all three reference power profiles. Regarding the green power generation, an array of three solar panels are simulated, each one capable of producing up to 0.5 kW. Three different green power profiles are considered for these solar panels. The first one, , is shown in Figure 5a and represents a morning power generation profile. This profile represents a scenario that starts with low energy generation and gradually increases energy generation as midday approaches. Profile , which corresponds to a midday power generation profile, is shown in Figure 5b. This profile represents the maximum energy generation profile with peak solar irradiation. Finally, profile equals a null green power generation representing a nighttime environment. This profile is not even shown, as no energy is generated during the night. All three of these power profiles were generated using historical solar irradiation information from [8].
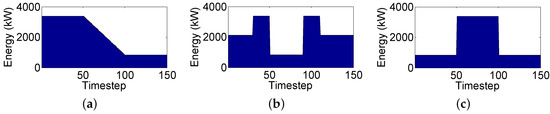
Figure 4.
Power reference profiles. (a) profile A; (b) profile B; and (c) profile C.
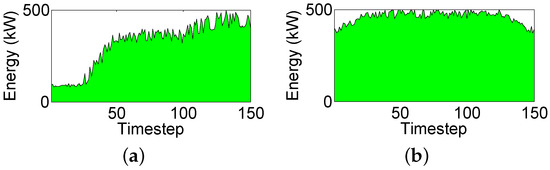
Figure 5.
Green power generation profiles. (a) morning profile (); and (b) midday profile ().
In total, 81 different instances are created considering a wide range of different scenarios.
6.2. Parameter Settings
In this work, NSGA-II is configured with a population size of , a recombination probability of , and a mutation probability of . On the other hand, ev-MOGA is configured with a P population size of and a G population size of . A mutation probability of and a recombination probability of . These settings are heavily based on the values proposed originally by [19,20]. Both MOEAs were configured with a stopping criterion () of 1000 generations for keeping the algorithms within reasonable execution times.
As for the post hoc optimization, SA is configured to be executed times for each non-dominated MOEA solution. The initial temperature of SA was configured as , the stopping temperature () as , and the cooling schedule () as . These settings are heavily based on the values originally proposed by [21]. Table 1 summarizes NSGA-II, ev-MOGA and SA settings.

Table 1.
Parameter settings for Non-dominated Sorting Genetic Algorithm version II (NSGA-II), Epsilon-Variable Multi-Objective Genetic Algorithm (ev-MOGA) and simulated annealing (SA).
7. Experimental Results and Discussion
This section presents and discusses the experimental results computed by both algorithmic approaches, the one based on NSGA-II and the one based on ev-MOGA. First, the efficacy of these approaches is studied by comparing their accuracy at optimizing the objectives and at sampling the Pareto front. After that, the best approach is compared with a traditional business-as-usual scenario where no power optimization is performed and no green power source is available. This business-as-usual scenario is a typical scenario in many small- and medium-sized data centers.
7.1. NSGA-II and ev-MOGA Comparison
The hypervolume metric is applied for comparing the NSGA-II and ev-MOGA approaches. The hypervolume metric was introduced by Zitzler and Thiele [22] and is the most used metric for comparing multiobjective optimization results [23]. This metric works by constructing a hypercube for each solution i in the Pareto front Q. Each hypercube is defined with a reference point W and solution i as corners of the diagonal of the hypercube. The reference point W is arbitrary but may be easily constructed using the worst computed values for each objective function. Finally, the hypervolume () is computed as the union of all hypercubes such that a larger hypervolume is always preferable. Equation (7) shows how hypervolume is calculated:
The hypervolume metric considers both the convergence and the diversity of a Pareto front providing an all-around quantitative value. In this work, the relative hypervolume metric is reported for readability. The relative hypervolume is computed as , where is the hypervolume of the best known approximation to the true Pareto front.
For the comparison study, a total of 30 independent executions were performed for each algorithm and for each problem instance. Table 2 shows the average and standard deviation of the relative hypervolume computed by each algorithm grouped by workload size and by green power profile. The Kruskal–Wallis test [24] is used to provide statistical confidence in the comparison. Statistically significant differences are presented in bold font.

Table 2.
Average and standard deviation of the relative hypervolume (RHV) computed by each algorithm for each workload size and green power generation profile.
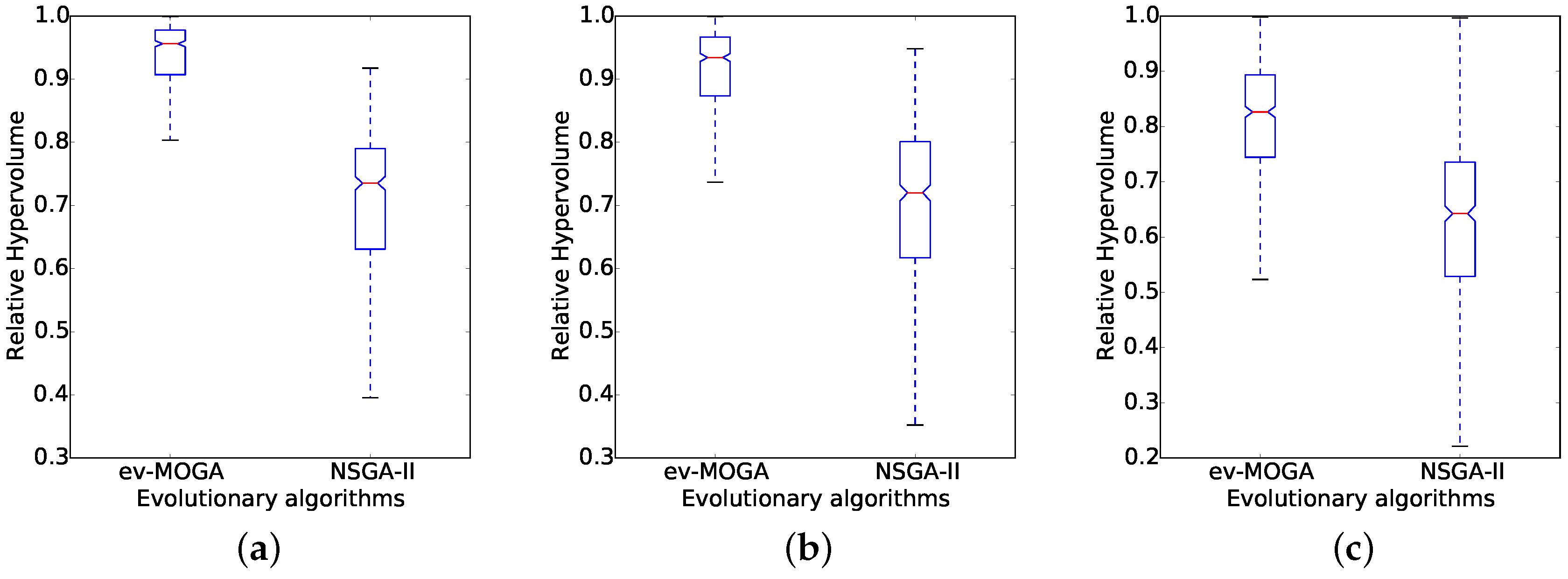
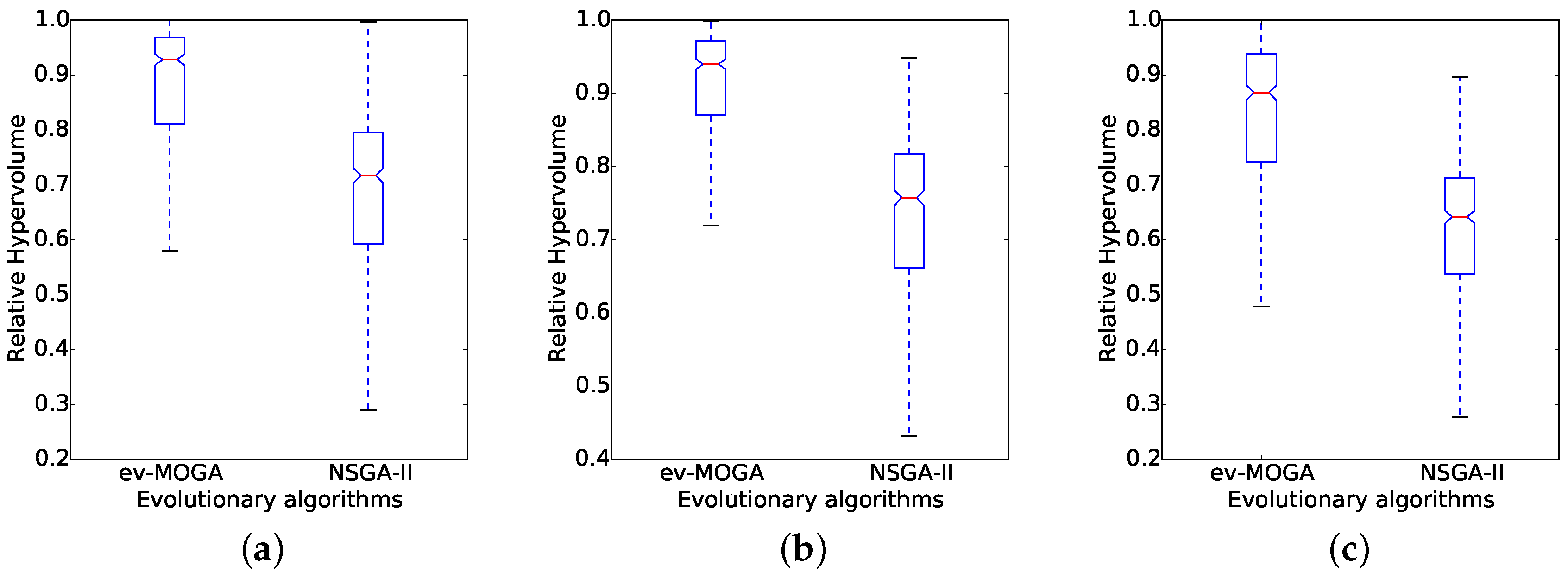
Overall results show ev-MOGA computes consistently better solutions than NSGA-II for all scenarios. Figure 6 and Figure 7 present box plots for RHV results aggregated by dimension and by green power profile. For all scenarios, ev-MOGA presents a higher median RHV and a better reliability supported by lower dispersion values.
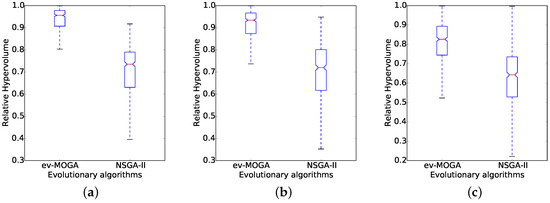
Figure 6.
Relative hypervolume computed by Epsilon-Variable Multi-Objective Genetic Algorithm (ev-MOGA) and Non-dominated Sorting Genetic Algorithm version II (NSGA-II) for each workload size. (a) small workload size; (b) medium workload size; and (c) large workload size.
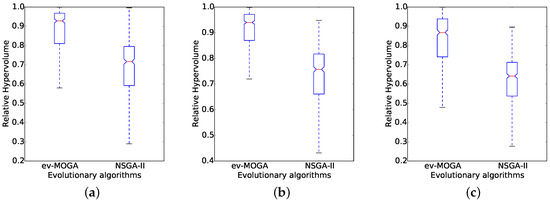
Figure 7.
Relative hypervolume computed by Epsilon-Variable Multi-Objective Genetic Algorithm (ev-MOGA) and Non-dominated Sorting Genetic Algorithm version II (NSGA-II) for each green energy profile. (a) morning profile (); (b) midday profile (); and (c) night profile ().
Next, the best aggregated results computed by each algorithm are analyzed, that is, the best approximation to the true Pareto front computed by each algorithm. Table 3 presents the best aggregated RHV values for each algorithm, for each workload size, and for each green power profile. Results show ev-MOGA is significantly better than NSGA-II for all problem instances with small- and medium-sized workloads. In particular, for small-sized workloads, ev-MOGA is always able to compute the best approximation to the true Pareto front without fail. Results are more contested for the large-sized workloads where ev-MOGA is significantly better than NSGA-II in just one out of three scenarios.

Table 3.
Average and standard deviation of the relative hypervolume (RHV) for the best aggregated Pareto front computed by each algorithm for each workload size and green power generation profile.
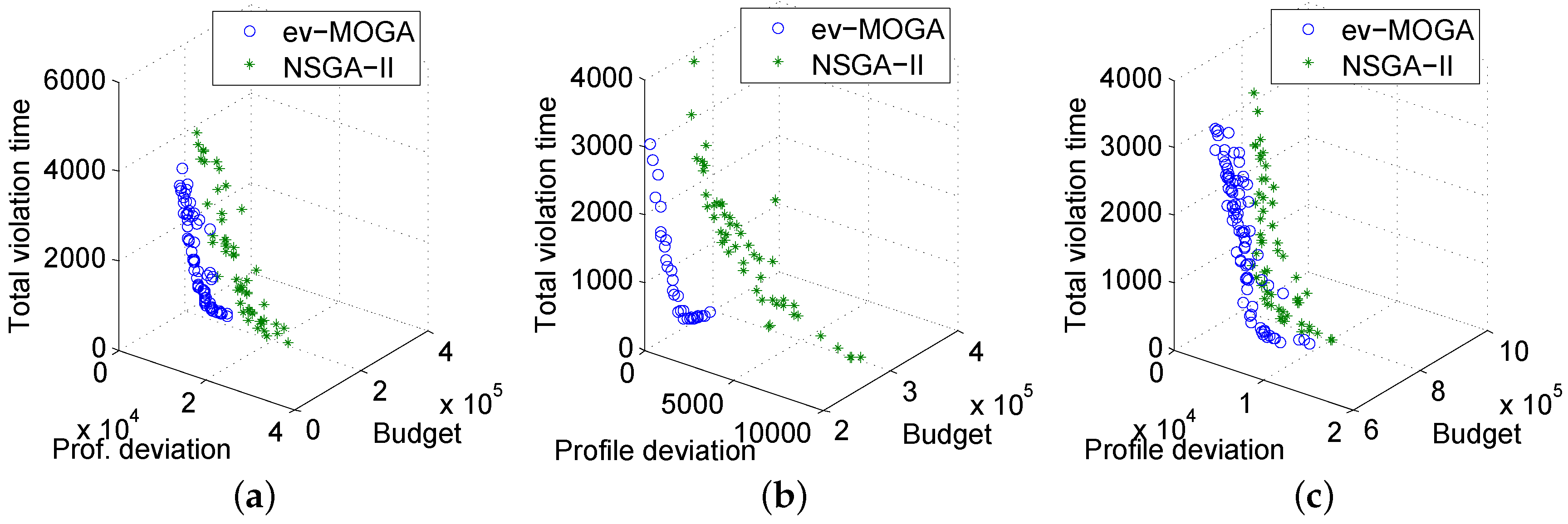
Figure 8a–c show a sample of the best aggregated Pareto front for each algorithm and for each green power profile for a medium-sized workload. In summary, ev-MOGA proved to be more accurate than NSGA-II in nearly all of the considered problem instances.
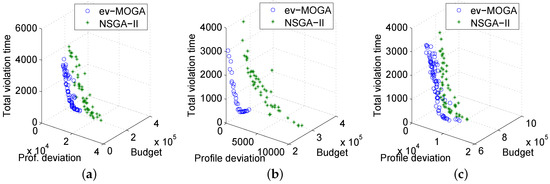
Figure 8.
Best aggregated Pareto front computed by each algorithm for medium-sized workloads and for each green energy profile. (a) morning profile (); (b) midday profile (); and (c) night profile ().
7.2. Comparison of ev-MOGA with the Business-as-Usual Approach
The business-as-usual scenario represents a real-world scenario where no green power source is available and where servers are never in sleep state. For this comparison, just solutions with a relative QoS of 95% or greater are considered. This is a realistic scenario since providing a low QoS is not desirable for most data centers. The relative QoS value is computed as the total amount of overdue time relative to the sum of execution time required by all tasks. Hence, a schedule with a relative QoS of 95% means it requires just 5% of additional overdue time for task execution.
Table 4 shows the average and standard deviation for the relative budget reduction computed by ev-MOGA over the business-as-usual scenario for each workload size and each green power profile with QoS of over 95%. On top of that, it also shows the average and standard deviation for the relative deviation from the reference power profile, with the deviation from the reference power profile being calculated as the total amount of energy required that surpasses the reference profile, relative to the total amount of energy specified in the reference profile.

Table 4.
Average and standard deviation for the relative budget reduction over the business-as-usual scenario (BAU), and relative deviation from the reference power computed by ev-MOGA for quality of service over 95%.
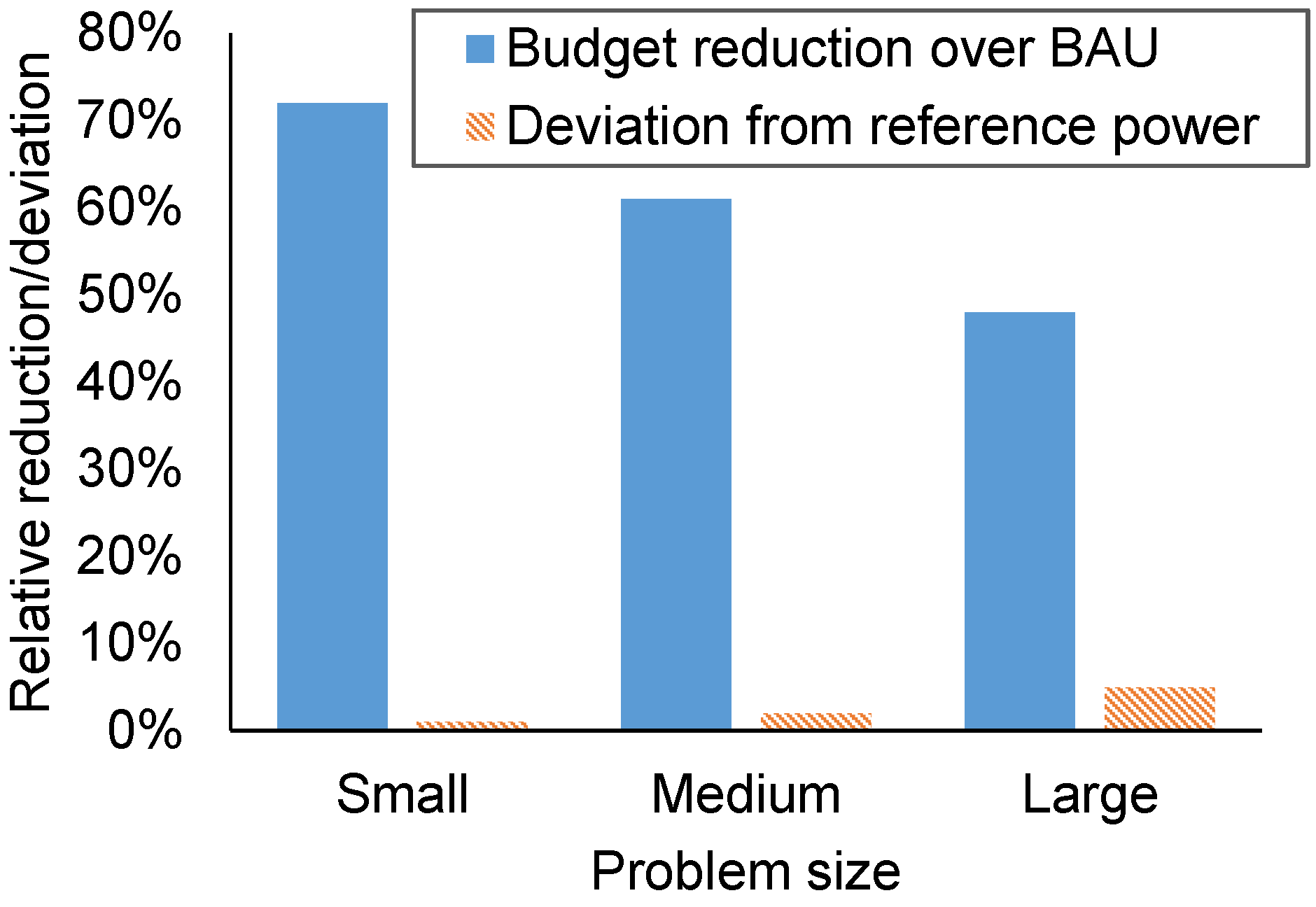
Results show that ev-MOGA is able to compute a large budget reduction, up to 83%, with a small relative deviation from the power reference profile, lower than 5% in most scenarios. As expected, the larger reductions are computed for the morning and midday green power profile ( and ), with an average reduction of 68%. Budget reduction is much lower for the nighttime green power profile (), with an average reduction of 46%, which accounts for just the server state and cooling device planning. These results show the effectiveness of considering green energy sources for data center infrastructures, reducing the energy budget by an average of 22%. Figure 9 shows the average budget reduction and relative power reference deviation for the solutions computed by ev-MOGA when compared to the business-as-usual scenario.
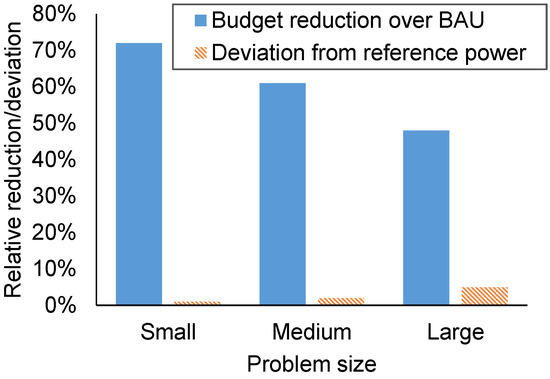
Figure 9.
Average relative budget improvement over business-as-usual scenario and relative deviation from power reference computed by ev-MOGA for a relative quality of service over 95%
8. Conclusions
This work addresses the problem of controlling power consumption in data centers considering both traditional and renewable energy sources. This scheduling problem consists of simultaneously scheduling the states of the servers and the cooling devices of the data center, and the scheduling of tasks to be executed in the data center. A mathematical formulation is proposed for this problem, taking into account a desired reference power consumption profile, the overall electricity budget, and the QoS provided to its users.
A fully Pareto-oriented methodology is applied for solving this problem, and two multi-objective evolutionary algorithms—NSGA-II and ev-MOEA—are presented. Both are hybridized with a greedy scheduling algorithm and a simulated annealing algorithm. In the proposed schema, the multi-objective evolutionary algorithms schedule the server and cooling devices, while the greedy heuristic schedules the execution of tasks. On top of that, simulated annealing is used as a post hoc optimization mechanism and it is executed at the very last moment.
A small low-power data center is modeled for the experimental, taking into account the heat dissipation of its servers and the effectiveness of its cooling devices. A wide set of problem instances are constructed considering different power profiles, green power generation profiles, and workloads of tasks. First, NSGA-II and ev-MOEA approaches are compared using a Pareto-aware methodology to determine the best evolutionary approach. Next, the best approach is compared with a business-as-usual scenario with no scheduling of server or cooling devices, and with just a traditional energy source.
Results show the ev-MOGA approach is significantly more accurate than the NSGA-II approach for all of the problem instances, improving accuracy of the schedules by about 18% in average. When comparing ev-MOGA with the business-as-usual scenario, only schedules with high QoS values are considered, since low QoS values are certainly not desirable for most real-world data centers. In these high-QoS scenarios, ev-MOGA proved to be very effective, computing average budget reductions ranging from 33% up to 83%, depending on the workload size and green power generation profile. Furthermore, these reductions are obtained with an average deviation from the reference power profile of just about 3%.
These results confirm the effectiveness of the proposed approach and the usefulness of considering renewable energy sources for data center infrastructures. The main lines of future work include extending the experimental analysis and improving the efficiency of the proposed methods. The experimental analysis is to be improved by considering larger data center infrastructures and a wider range of green power generation profiles. At the same time, improving the efficiency and efficacy of the proposed methods is equally important and is certainly necessary in order to address larger problem instances.
Acknowledgments
The work of Santiago Iturriaga and Sergio Nesmachnow is partly supported by Agencia Nacional de Investigación e Innovación (ANII) and Programa de Desarrollo de las Ciencias Básicas (PEDECIBA), Uruguay. The "Solar Panel" icon is by Maurizio Fusilo from the Noun Project.
Author Contributions
Both authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Koomey, J. Worldwide electricity used in data centers. Environ. Res. Lett. 2008, 3, 1–8. [Google Scholar] [CrossRef]
- Koomey, J. Growth in Data Center Electricity Use 2005–2010; Analytic Press: Burlingame, CA, USA, 2011. [Google Scholar]
- Andrae, A.S.; Edler, T. On global electricity usage of communication technology: Trends to 2030. Challenges 2015, 6, 117–157. [Google Scholar] [CrossRef]
- Dayarathna, M.; Wen, Y.; Fan, R. Data Center Energy Consumption Modeling: A Survey. IEEE Commun. Surv. Tutor. 2016, 18, 732–794. [Google Scholar] [CrossRef]
- Zhang, W.; Wen, Y.; Wong, Y.; Toh, K.; Chen, C.H. Towards Joint Optimization over ICT and Cooling Systems in Data Centre: A Survey. IEEE Commun. Surv. Tutor. 2016, 18, 1–22. [Google Scholar] [CrossRef]
- Nesmachnow, S.; Dorronsoro, B.; Pecero, J.E.; Bouvry, P. Energy-Aware Scheduling on Multicore Heterogeneous Grid Computing Systems. J. Grid Comput. 2013, 11, 653–680. [Google Scholar] [CrossRef]
- Dorronsoro, B.; Nesmachnow, S.; Taheri, J.; Zomaya, A.; Talbi, E.G.; Bouvry, P. A hierarchical approach for energy-efficient scheduling of large workloads in multicore distributed systems. Sustain. Comput. 2014, 4, 252–261. [Google Scholar] [CrossRef]
- Goiri, I.; Haque, M.; Le, K.; Beauchea, R.; Nguyen, T.; Guitart, J.; Torres, J.; Bianchini, R. Matching renewable energy supply and demand in green datacenters. Ad Hoc Netw. 2015, 25, 520–534. [Google Scholar] [CrossRef]
- Lei, H.; Wang, R.; Zhang, T.; Liu, Y.; Zha, Y. A multi-objective co-evolutionary algorithm for energy-efficient scheduling on a green data center. Comput. Oper. Res. 2016, 75, 103–117. [Google Scholar] [CrossRef]
- Wang, L.; Khan, S.U. Review of performance metrics for green data centers: A taxonomy study. J. Supercomput. 2013, 63, 639–656. [Google Scholar] [CrossRef]
- Barroso, L.A.; Clidaras, J.; Höelzle, U. The Datacenter As a Computer: An Introduction to the Design of Warehouse-Scale Machines, 2nd ed.; Morgan and Claypool Publishers: San Rafael, CA, USA, 2013. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Herrero, J.M.; Reynoso-Meza, G.; Martínez, M.; Blasco, X.; Sanchis, J. A Smart-Distributed Pareto Front Using the ev-MOGA Evolutionary Algorithm. Int. J. Artif. Intell. Tools 2014, 23, 1–22. [Google Scholar] [CrossRef]
- Iturriaga, S.; Nesmachnow, S. Multiobjective scheduling of green-powered datacenters considering QoS and budget objectives. In Proceedings of the Innovative Smart Grid Technologies Latin America, Montevideo, Uruguay, 5–7 October 2015; pp. 570–573.
- Peng, Y.; Kang, D.K.; Al-Hazemi, F.; Youn, C.H. Energy and QoS aware resource allocation for heterogeneous sustainable cloud datacenters. Opt. Switch. Netw. 2016. [Google Scholar] [CrossRef]
- Nesmachnow, S.; Perfumo, C.; Goiri, Í. Holistic multiobjective planning of datacenters powered by renewable energy. Clust. Comput. 2015, 18, 1379–1397. [Google Scholar] [CrossRef]
- Nesmachnow, S.; Perfumo, C.; Goiri, I. Controlling datacenter power consumption while maintaining temperature and QoS levels. In Proceedings of the IEEE 3rd International Conference on Cloud Networking, Luxembourg, 8–10 October 2014; pp. 242–247.
- Yu, X.; Gen, M. Introduction to Evolutionary Algorithms; Springer: New York, NY, USA, 2012. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; J. Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Martínez-Iranzo, M.; Herrero, J.M.; Sanchis, J.; Blasco, X.; García-Nieto, S. Applied Pareto multi-objective optimization by stochastic solvers. Eng. Appl. Artif. Intell. 2009, 22, 455–465. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Zitzler, E.; Thiele, L. Multiobjective Optimization Using Evolutionary Algorithms—A Comparative Case Study. In Proceedings of the 5th International Conference on Parallel Problem Solving from Nature—PPSN V, Amsterdam, The Netherlands, 27–30 September 1998; Springer: London, UK, 1998; pp. 292–304. [Google Scholar]
- Riquelme, N.; Lücken, C.V.; Baran, B. Performance metrics in multi-objective optimization. In Proceedings of the Latin American Computing Conference, Arequipa, Peru, 9–23 October 2015; pp. 1–11.
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).