Abstract
Fairness is becoming indispensable for ethical machine learning (ML) applications. However, it remains a challenge to identify unfairness if there are changes in the distribution of underlying features among different groups and machine learning outputs. This paper proposes a novel fairness metric framework considering multiple attributes, including ML outputs and feature variations for bias detection. The framework comprises two principal components, comparison and aggregation functions, which collectively ensure fairness metrics with high adaptability across various contexts and scenarios. The comparison function evaluates individual variations in the attribute across different groups to generate a fairness score for an individual attribute, while the aggregation function combines individual fairness scores of single or multiple attributes for the overall fairness understanding. Both the comparison and aggregation functions can be customized based on the context for the optimized fairness evaluations. Three innovative comparison–aggregation function pairs are proposed to demonstrate the effectiveness and robustness of the novel framework. The novel framework underscores the importance of dynamic fairness, where ML systems are designed to adapt to changing societal norms and population demographics. The new metric can monitor bias as a dynamic fairness indicator for robustness in ML systems.
1. Introduction
The widespread use of machine learning (ML) algorithms in fields like forensic analysis has raised concerns about potential biases introduced into decision-making processes, stemming from both the algorithms themselves and the data used to train them [1,2,3,4]. Early detection and mitigation of bias are essential to maintain the accuracy and reliability of predictions [5,6]. There are various methods addressing fairness in machine learning, including in-processing techniques that incorporate fairness criteria during model development. Critical to evaluating these fairness-conscious ML models are varied benchmark datasets [7]. Specifically, fairness-aware ML often relies on tabular data, using Bayesian networks to examine how attributes, particularly protected and class attributes, interrelate [8,9]. Additionally, research has investigated deep generative models for generating unbiased data, supported by a range of fairness metrics [10]. This underscores the significance of comprehensive benchmarks in assessing the effectiveness of fairness interventions. Furthermore, fairness metrics effectively address fairness concerns and play an important role in bias detection [11,12]. They are a set of numerical measures that detect the presence of bias in a machine learning model. The machine learning literature offers different fairness metrics, including equalized odds [13], equal opportunity [13], demographic parity [14,15,16,17], fairness through awareness [14,15] or unawareness [15], counterfactual fairness [15], and the FairCanary Quantile Demographic Disparity (QDD) metric [18]. The concept of “group” refers to divisions or categorizations of individuals based on shared characteristics, such as gender, age, or other demographics. These groups are often defined based on protected attributes that are legally recognized and considered sensitive. Many existing fairness metrics cannot identify unfairness if there are changes in the distribution of underlying features among different groups. Even a slight shift in the distribution of underlying features can render fairness metrics unreliable and unable to identify bias. Because of this major limitation, fairness metrics should consider the change of underlying feature distributions to address bias in predictions effectively. This paper introduces Quantile Multi-Attribute Disparity (QMAD), a novel fairness metric designed to address these challenges by considering the complex distributions of continuous attributes and adapting to dynamic environments. Unlike traditional metrics, QMAD accounts for concept drift, ensuring robustness and interpretability in assessing fairness across demographic groups as shown in Figure 1. Its empirical validation demonstrates superior performance compared to existing metrics, making it a valuable tool for ensuring fairness in ML systems operating in evolving data landscapes.
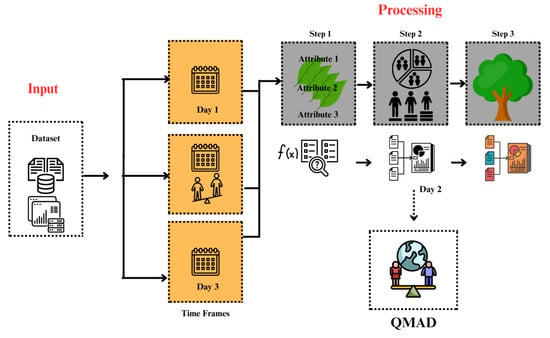
Figure 1.
Overview of the QMAD framework. It evaluates fairness dynamically over time and across multiple attributes using comparison and aggregation functions. It supports auditing in both synthetic and real-world scenarios.
The major contributions of this paper are summarized below:
- A novel fairness metric framework is proposed that considers multiple attributes, including machine learning outputs and feature variations for bias detection and quantification.
- The two key components of comparison and aggregation functions introduced in the framework allow the novel fairness metric to be highly adaptable to variations of contexts and scenarios.
- Three innovative comparison–aggregation function pairs are proposed to demonstrate the effectiveness and robustness of the novel fairness metric framework.
The remaining of this paper is organized as follows. The related work is reviewed in Section 2. The preliminary key concepts used in this paper are introduced in Section 3. The novel fairness metric framework is then proposed in Section 4. Section 5 introduces three pairs of comparison and aggregation functions used to verify the configuration flexibility of the proposed framework as well as datasets and models used in the experiment. Section 6 presents detailed experimental results to demonstrate the effectiveness of the proposed fairness metric framework. We discuss the advantages and limitations of the proposed framework in Section 8. Finally, the conclusion and future work are presented in Section 9.
2. Related Work
The research in the field of fairness of machine learning systems offers various techniques to identify and mitigate the unfair behavior of ML systems. Unfairness in any ML system can stem from biased data encoding or discriminatory ML algorithms. Numerous approaches exist for recognizing bias in data. Moreover, considerable ML research is dedicated to enhancing the fairness of ML algorithms.
Research on fairness in machine learning addresses techniques to identify and mitigate unfair behavior from biased data or discriminatory algorithms. While “fairness through awareness” [14] proposes continual adjustments to fairness criteria, it faces challenges such as reliance on sensitive attributes, potential ethical concerns, and computational demands that limit scalability and real-time application. Another approach to ensuring fairness in machine learning is to enhance the robustness of algorithms towards bias. Ref. [19] proposed a novel method to identify bias in training data using counterfactual thinking. Their framework, CFSA, ranks training samples based on their likelihood of introducing bias, suggesting the removal of these samples and their replacement with synthetic ones. However, CFSA’s effectiveness relies on the training data covering the entire sample space, which is rare in real-world scenarios, highlighting the continued need for techniques to detect unfairness in machine learning systems.
On the other hand, the work of [20] discusses the long-term impacts of implementing fairness constraints in machine learning systems. A key limitation is the focus on theoretical outcomes without extensive practical validation, which might not capture all real-world complexities and unintended consequences of applying fairness interventions over time. Another approach to ensure the fairness of a machine learning system is to make ML algorithms more robust towards bias. Ref. [21] proposed a concept of robustness bias, which makes ML algorithms fairer by choosing a robust decision boundary. This strategy demonstrates respectable effectiveness in enhancing the fairness of machine learning algorithms.
Although these approaches have made substantial contributions to the fairness literature, their design can lead to incomplete assessments and insufficient mitigation of real-world bias, where multiple and intersecting sources of unfairness are often present. QMAD directly addresses this gap by supporting fairness auditing, enabling a more comprehensive and context-sensitive evaluation framework. Despite the existence of various methods for detecting bias at both the data and algorithmic levels, the likelihood of machine learning systems exhibiting unfairness remains substantial. Hence, there exists a need for a fairness metric that can flag bias in predictions across groups even with underlying feature distribution drifts.
Fairness Monitoring
Fairness monitoring addresses the crucial need to ensure algorithms make equitable decisions. Among the variety of approaches developed to monitor and enhance fairness, each comes with its unique set of strengths and limitations. This section will focus on the recent fairness monitoring approaches with their limitations. Rampisela et al. [22] critically examine existing evaluation measures of individual item fairness in recommender systems, pointing out limitations that may affect the interpretation, computation, or comparison of recommendations based on exposure-based fairness measures. This highlights a crucial limitation in fairness monitoring: the complexity and potential inadequacy of fairness metrics to account for nuanced user–item interactions within recommender systems, potentially leading to oversimplified assessments of fairness. Despite its promise for dynamic interactions, a notable limitation is the potential computational overhead and the complexity of implementing such real-time monitoring in diverse operational environments without impacting system performance, as shown in Table 1.

Table 1.
Comparison of fairness metrics on key capabilities. ✓ indicates that the capability is supported; ✗ indicates it is not supported.
3. Preliminary
In this study, we evaluate a variety of conventional fairness metrics commonly employed in previous research. Table 2 illustrates several popular conventional fairness metrics utilized in prior studies, along with their respective capabilities for handling continuous machine learning (ML) output and consideration of feature distributions. Notably, our analysis reveals that all conventional fairness metrics, with the exception of FairCanary QDD, fail to account for continuous ML output and feature distributions.

Table 2.
Fairness metrics in machine learning.
Statistical Parity Difference quantifies the discrepancy in the rates at which distinct groups receive positive outcomes. A value nearing 0 suggests equitable predictions, while a considerable deviation from 0 signifies unfair predictions for the monitored group. Rather than comparing continuous outputs, this metric typically contrasts the frequencies of distinct outcomes across different groups [26].
Disparate Impact compares the percentage of positive outcomes between two groups, the monitored and reference groups. It evaluates the ratio of positive outcomes received by different groups to the ratio of negative outcomes. A deviation from 1 in the Disparate Impact ratio indicates potential unfair predictions, mainly used for discrete outcomes and considered an important measure of fairness [27].
Empirical Difference Fairness assesses model fairness by measuring differences in the probability distribution of its predictions between protected and reference groups. Significant differences from zero indicate bias within the model. However, it can be computationally intensive and requires a large sample size for accurate estimation [25].
Consistency measures how similar labels are for similar instances, based on the comparison of model classifications for a given data point to its k-nearest neighbours. Any significant deviation from 1 indicates an unfair prediction [28].
FairCanary is a Quantile Demographic Disparity (QDD) metric crafted to assess and monitor fairness in machine learning models with continuous outputs. It calculates expected prediction values across multiple groups and compares the mean prediction across bins for different groups to quantify fairness. However, FairCanary may fail to identify unfairness if the underlying feature distribution varies across bins.
4. Adaptable Fairness Metric Framework
This paper proposes an adaptable fairness metric framework to detect biases in a machine learning pipeline even when the distribution of features changes over different time frames. This is important as changes in feature distributions may introduce unexpected unfairness in the system. Our proposed metrics compare both the ML predictions and feature distributions across different time frames, introducing a fairness score that is resilient to changes in the features used for prediction. This score can be deployed to a bias monitor system to continuously monitor the system and avoid any potential unfairness. The proposed metric can detect any bias in the system as well as the features responsible for the bias. We can then send this information back to the data collection or data wrangling stage, providing feedback to guide further data collection or data wrangling efforts. This helps reduce bias and ensure fairness in the system. The life cycle of a typical machine learning system includes data collection, data wrangling, data modeling, data validation, and monitoring. The proposed metric is specifically designed for the monitoring stage in the life cycle of the machine learning system (QMAD; see Figure 2).
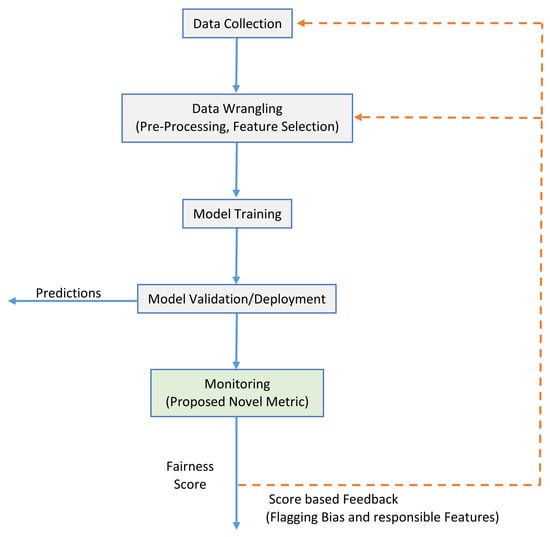
Figure 2.
Our new metric within the life cycle of an ML system.
Let us begin by presenting our QMAD metric framework. To clarify QMAD, we first define the attribute samples. Considering there are two groups, G1 and G2, let the samples of an attribute a be and for G1 and G2, respectively. This attribute can be either the prediction result or the features of the data used for prediction. If a is the attribute of prediction results, the two distributional prediction results p can be represented as and for G1 and G2, respectively. Similarly, let the two distributional samples of a specific feature f of G1 and G2 be and , respectively. Inspired by the quantile binning method used in [18], we divide and into B bins of equal size, N1 and N2 for groups G1 and G2, respectively. The attribute samples of groups G1 and G2 in a selected bin b are presented as and , respectively. Our novel metric consists of two primary components: (1) the comparison function and (2) the aggregation function. The comparison function evaluates the variation in the distribution of a selected bin b across group G1 and group G2 and generates a comparison score as shown in the following Equation (1):
where and are the attribute samples of groups G1 and G2, respectively, in a selected bin b. represents the corresponding created comparison score. The aggregation function, on the other hand, combines both the comparison scores of a single attribute and the comparison scores of all attributes. To calculate the comparison scores of an attribute a, the aggregation function is defined as shown in Equation (2):
where FA is the aggregation function that takes list of as input and produces output , which represents the metric value for attribute a. is obtained from the previous comparison function and indicates the fairness score of attribute a across groups G1 and G2 in bin b. The value of b ranges from 1 to B, where B represents the total number of bins. Our fairness metric QMAD takes into account the distributions of various attributes, including features and predictions. We can apply function FA to these attributes to calculate a final fairness score for all of them as shown in Equation (3):
The aggregation function FA takes a list of as its input, which is the fairness score of attribute a created using Equation (2), and produces the M, which is the aggregated metric value for all the attributes. Here, a is the set of attributes of interest.It is worth noting that QMAD is considered a framework of fairness because it allows users to select the appropriate comparison and aggregation functions based on their machine learning system context while ensuring effectiveness. For instance, the QDD metric proposed in [18] can be viewed as a special instance of QMAD. QDD utilizes expected values to quantify the difference in demographic distributions of a sample dataset and a reference dataset. Hence, the expected value serves as the comparison score. QDD only takes into account ML prediction as the only intended attribute, which means that it only aggregates the comparison scores of prediction in different bins. Additionally, it uses the arithmetic mean to average the comparison across different bins. Therefore, QDD can be presented in a QMAD format as shown in Equations (4) and (5):
The details of the QMAD fairness score calculation can be found in Algorithm 1.
| Algorithm 1 QMAD fairness score calculation. |
| Input: FC, FA, , , B, A Output: M
|
5. Experiment
The QMAD framework allows for the customization of its two main components—the comparison and aggregation functions—to achieve the most optimized combination. In our experiment, we tested three pairs of comparison and aggregation functions to verify the configuration flexibility of QMAD. These pairs will be introduced in Section 5.1 and be used for both synthetic and real dataset evaluations. Our goal is to evaluate the effectiveness and robustness of QMAD by testing it on both synthetic and real-world data. We start with a synthetic dataset based on [18] but with modifications focusing on the regression problem [8]. This test is presented in Section 5.2. Next, we evaluate QMAD on the UCI Adult Dataset [29], a widely used real-world dataset for evaluating fairness algorithms on classification problems. This test is presented in Section 5.3. Our aim is to verify the utility of QMAD in a real-world environment and extend its application to classification problems. For both synthetic and real-world datasets, our objective is to determine if QMAD could detect bias and then compare its performance with five benchmarks: Statistical Parity Difference [23], Disparate Impact [13], Empirical Difference Fairness [25], Consistency [25], and the QDD Metric [18].
5.1. Comparison–Aggregation Functions Evaluated
One of the main benefits of QMAD is its ability to allow users to choose different comparison and aggregation functions. To test its versatility and effectiveness, we evaluate three pairs of comparison functions (FC) and aggregation functions (FA) pairs. The first pair uses the ratio of mean (ROM) as the comparison function, and the arithmetic mean as the aggregation function, which we name the ROM–Arithmetic pair. For the second evaluation, we opt for the Kolmogorov–Smirnov Test (KSTest) as the comparison function and harmonic mean as the aggregation function, which we name the KSTest–Harmonic pair. Lastly, in the third evaluation, we chose the Anderson-Darling Test (ADTest) as the comparison function and harmonic mean as the aggregation function, which we named the ADTest-Harmonic pair. ROM and arithmetic mean have been commonly used in previous research for the comparison of two distributions. They offer advantages such as the ability to combine and compare distributions across varied measurement scales and faster processing compared to other comparison functions. By using ROM as a comparison function, the results of the comparison of different distributions are of the same scale, which can then be combined using an arithmetic mean as an aggregation function. Furthermore, considering the nature of a large number of instance tests for fairness, statistical approaches are a natural option to evaluate the effectiveness of our approach. The KSTest and ADTest are popular non-parametric statistical tests for comparing distributions without assuming specific underlying distributions and are robust against outliers. However, the choice of comparison–aggregation functions should be tailored to the use case, distribution characteristics, and implementation ease. To ensure score interpretability during multi-attribute aggregation, QMAD could optionally apply normalization to intermediate comparison scores Ca,b and attribute-level fairness scores Ma. If raw comparison metrics differ in scale or direction (e.g., distance vs. p-value), normalization aligns them to a comparable reference frame (e.g., [0, 1]), and aggregation weights can be adjusted accordingly.
5.1.1. ROM–Arithmetic Pair
In the evaluation of the ROM–Arithmetic pair, we adopt the ratio of the means as the comparison function. This means that Ca,b can be computed using the following Equation (6):
In this context, is the expected value of attribute a of data in group in bin b. Similarly, is the expected value of attribute a of data in group in bin b. If is significantly smaller than , then the value of will be smaller and the value of will be larger. As a result, the value of will be larger. The same applies when is larger than .
To summarize, a larger value of indicates a larger difference between the distributions of and . To aggregate the values, we use the arithmetic mean as the function. This means that for each attribute a, we sum up all the values of in different bins and divide by the total number of bins. The formula for calculating is shown in Equation (7):
In our experiment, we will evaluate the fairness score across different attributes, including prediction and data features. Therefore, we need to aggregate the of different attributes a from an attribute set A as shown in Equation (8):
Here, represents the attribute number in the given attribute set A. Please note that as inferred above, a larger value of indicates a significant difference between the distribution of and that of , and the arithmetic mean is a monotonically increasing function. Therefore, larger values of M and indicate a greater difference between these two distributions and suggest a significant bias in the data.
5.1.2. KSTest–Harmonic Pair
The Kolmogorov–Smirnov test is a statistical method used to determine if two continuous probability distributions are equal or different [30,31]. There are two types of KS tests: the one-sample KS test and the two-sample KS test. The one-sample test is used to compare a sample with a reference probability distribution, while the two-sample test is used to compare the probability distribution of two samples. For our KSTest–Harmonic pair evaluation, we choose the two-sample KS test as the comparison function because we need to compare the difference between the probability distribution of and . We assign the p-value of the KS test of and to the value of . Therefore, can be defined as shown in Equation (9):
Here, applying the Kolmogorov–Smirnov test on and yields a p-value, represented by . In statistical testing, a p-value less than 5% is typically considered significant, and smaller p-values indicate greater significance. Therefore, a smaller value for Ca,b suggests a more significant difference between the distributions of and .
We used the harmonic mean to aggregate Ca,b values for attribute a and generate metric value Ma for that attribute. Therefore, the value of Ma can be calculated as shown in Equation (10):
In our study, we are interested in the effects on fairness from both the prediction and data features, so we use the harmonic mean to aggregate the Ma of different attributes. The final metric value M can be calculated as shown in Equation (11):
It is important to note that the harmonic mean is also a monotonically increasing function. Therefore, a smaller harmonic mean M indicates that the values in the list of Ma are also smaller compared to those in the list of larger values. Similarly, if the harmonic mean Ma value is smaller, the list of also has smaller values. Therefore, a smaller M indicates that the list of has smaller values. However, smaller indicates a more significant difference between the probability distribution of and , as we have already inferred. Therefore, a small M indicates a significant difference between the distribution of and in KSTest–Harmonic pair evaluation. This is different from the meaning of the M value in ROM–Arithmetic evaluation, where a larger M value indicates a more significant difference between the distribution of and . However, the M values in the following ADTest–Harmonic evaluation have the same meaning as described here because the is also a p-value of a statistic test.
5.1.3. ADTest–Harmonic Pair
The evaluation of the ADTest–Harmonic pair is similar to that of the KPTest–Harmonic pair. The only difference is that we use the Anderson-Darling test [32], which is another popular statistical test to measure the difference between two attributes, as the comparison function. The reason why we used two robust statistical tests is to study their efficiency in bias detection. However, we still use the harmonic mean as the aggregation function. Therefore, similar to the KPTest–Harmonic pair evaluation, the p-value of ADTest is assigned to in the following manner Equation (12):
We can define and M as shown in Equation (10) and Equation (11), respectively. Therefore, we will not repeat them here. It is important to note that represents the p-value of statistics, and in addition to that, we use the harmonic mean as the aggregation function. Thus, smaller values of M indicate a more significant difference between the distribution of and . This evaluation is similar to that in the KSTest–Harmonic pair. We summarise the calculation formulas in this section in Table 3 to enhance understanding of the three comparison function and aggregation function pairs evaluated.

Table 3.
Comparison functions and aggregation functions evaluated.
5.2. Synthetic Data Test on Regression
5.2.1. Synthetic Dataset
We use the synthetic dataset generated in [18] in our study. The reason for selecting this particular dataset from [18] is twofold. Firstly, our primary aim is to showcase the QMAD’s ability to detect bias in feature distributions that other existing fairness metrics cannot detect. For this purpose, we choose to use QDD, which is used in [18], as one of our benchmark comparisons. And it provides a controlled environment to inject measurable biases into features and predictions, allowing for fine-grained validation of QMAD’s detection sensitivity. To maintain consistency in our comparison, we select the same dataset that is used in [18]. Secondly, we chose this dataset to evaluate the effectiveness of QMAD in continuous output models. The dataset is used in [18] to predict the salaries of job seekers using regression, which is appropriate for our requirements. Therefore, data for three distinct groups are constructed through a methodology that involves random sampling from the distributions of individual features specific to each group. To simulate skewed data scenarios, synthetic bias is intentionally introduced into one of these groups. Furthermore, to enable detailed comparative analysis, the dataset within each group is segmented into bins. This binning process divides the group’s data points into distinct subsets, each with equal cardinality. Specifically, with a bin size of b, the first b data points are allocated to “Bin-1”, the subsequent b points to “Bin-2”, and so forth, continuing this pattern for the remainder of the data. An overview of the features, their values, and distributions in the dataset is provided in Table 4. In [18], the authors simulated continuous time frames by creating unbiased data for 3 days, consisting of 20,000 samples each, for day 1, day 2, and day 3. These days are considered as the target group. On each day, the education feature followed the distribution of 80% “GRAD” and 20% “POST-GRAD” for both males and females, as presented in Table 4. To introduce bias into the data, the authors set all females’ education as “GRAD” on day 2. In addition to the three days’ data, the authors created a reference dataset consisting of 10,000 samples without any bias. This reference group serves as a standard to compare the target group with.

Table 4.
Features, values, and their distribution used in the dataset [18].
5.2.2. Bias Injection
The QMAD is proposed to measure the impact of injected biases on model performance. To test the effectiveness of QMAD, we introduced new biases into the data of day 2 by modifying the distribution of two features, “Location” and “Relevant Experience”. Firstly, we changed the distribution of “Location” for all females on day 2 from 70% “Springfield” and 30% “Centerville” to 85% “Springfield” and 15% “Centerville”. This is a significant distribution shift, and we wanted to see if QMAD could detect it. Additionally, we introduced a small data distribution shift to verify that QMAD could also detect such a shift. To do this, we selected only 50% of the females on day 2 and increased their “Relevant Experience” value by 30%.
5.2.3. Regression Models Evaluated
As part of our testing process, we evaluate two different regression models on synthetic data, one linear regression model and one decision tree regressor model. We begin by testing the linear regression model used in [18] to predict the starting salary of job seekers based on their resume features such as education, location and relevant experiences. The model has learned the relationship between these features and the job seeker’s salary Equation (13):
To evaluate QMAD’s ability to work with various regression models, we train a decision tree regressor model in addition to the linear regression model. The decision tree regressor is trained using the reference dataset provided in [18]. We use the linear regression model and the decision tree regressor model to predict salaries based on the sample dataset spanning three days. We then compare the features and predictions of the sample dataset against the reference dataset using three comparison and aggregation function pairs. It should be noted that we deliberately introduce bias into the data for day 2, which we expect to yield a greater difference in the sample dataset compared to day 1 and day 3. As a result, we are able to detect the bias on day 2.
5.3. Real-World Data Test on Classification
In this section, we evaluate the performance of QMAD on real-world data. Since we assessed the performance of regression in the previous section, we concentrate on QMAD’s classification performance in this subsection.
5.3.1. UCI Adult Dataset
The UCI Adult Dataset [29] is derived from the 1994 Census database of America. It is commonly used for predicting whether an employee’s annual income exceeds USD 50K, making it a typical classification problem. For this reason, we have selected the UCI Adult Dataset for our study. The dataset consists of 14 features, of which we have only focused on 8 in our study. It offers a real-world testbed with demographic richness and relevance, enabling us to evaluate QMAD’s robustness in high-stakes fairness contexts aligned with existing benchmarks.
5.3.2. Bias Injection
To evaluate approaches on real-world datasets, we create 4 days’ data to mimic real-world time frames: day 1, day 2, day 3, and day 4. For each day, we randomly selected 20,000 samples from the UCI Adult Dataset. As a result, data within these groups are also divided into bins for granular comparative analysis. This binning follows the previous synthetic dataset, whereby data points are segmented into subsets equally, ensuring a consistent framework for comparison across all groups. We aim to inject bias into day 2 and day 3. Education and marital status heavily affect salary, so we focus on biasing these two features. On day 2, we modified only the “Education” feature. We set all females as not having attended college while all males had attended college. To introduce more bias on day 3 and to check whether QMAD could quantify the injected bias properly, we inject bias into both “Education” and “Marital_status” features. On day 3, we set all females’ education as not having attended college and their marital status as married, while all males’ education is set as having attended college, and their marital status is set as unmarried. We expect QMAD to detect and quantify the injected bias on day 2 and day 3, respectively. This four-day dataset is used as the target group, while the original data in the UCI Adult Dataset are used as the reference group.
5.3.3. Classification Model Evaluated
In our study, we choose the decision tree classifier as our classification model. It is a simple yet effective model widely used in real-world applications. To train this model, we use the real-world dataset of the UCI Adult Dataset, which we split into 80% training data and 20% testing data. To obtain accurate classification results, we conduct hyperparameter tuning through cross-validations. In particular, we focus on two important parameters for decision tree classifiers: “max_depth” and “min_samples_leaf”. After hyperparameter tuning, we set “max_depth” to 10 and “min_samples_leaf” to 50 in our study. After training the decision tree classifier, we use it to generate predictions based on the four-day data. We calculate the QMAD value of target groups and reference groups using three different comparison and aggregation function pairs. This calculation is performed for both the feature distribution and the prediction distribution.
6. Experiment Results
In this section, first, we present the evaluation results of the synthetic data, followed by the evaluation results of the real-world data. For each dataset, we demonstrate QMAD’s ability to detect bias and then the comparison of its performance with other benchmarks, Further experimental details and figures are provided in the Supplementary Materials. The implementation code is available upon request from the corresponding author.
6.1. Synthetic Data Evaluation Result
Bias Detection
Table 5 and Figure 3 show the QMAD’s bias detection ability on synthetic data. Let us take a look at the ROM–Arithmetic result pair. The aggregation function can aggregate either the metric for one attribute or the M metric for all attributes. Please note that the aggregation score in the ROM–Arithmetic result is the final M that aggregates the metric of data features and prediction. The comparison function is the ratio of mean, which means that a larger value indicates a larger difference and vice versa. We used linear regression and decision tree regressor to predict the salary. Both the linear regression and decision tree regressor aggregation scores successfully detected bias because their values (0.1239 and 0.1238) were larger than those of day 1 and day 3. Similarly, we can find that the score of features injected with bias can also detect bias on day 2. For example, the score of education (0.5103) is larger than those of day 1 and day 3 because it was injected with bias by the authors of [18]. We have injected bias into the job location and relevant experience features. This can be verified by the score of “job_location” and “relevant_experience”, which have values larger than those of day 1 and day 3. Regarding the KPSTest–Harmonic pair result, it is important to note that the aggregate score, which is denoted as , only aggregates all the for salary prediction results. This is because the score here is represented as a p-value, which indicates whether the target group and reference group are significantly different if it is less than 5%. For instance, the scores of linear regression prediction and decision tree regressor prediction (0.0061 and 0.0024) are less than 5%, which is sufficient to detect any bias. Additionally, the score of the injected features “job_location” and “education” can also identify any bias on day 2. However, the score of “relevant_exp” is not less than 5%, even though its score of 0.0911 is smaller than those of day 1 and day 3. This may indicate that the 30% increase in relevant experience for females is not significant enough to detect any bias. The ADTest–Harmonic pair is similar to the KPSTest–Harmonic pair, as both the aggregated score and the features’ score can detect any bias.

Table 5.
Bias detection results on the synthetic dataset. Bias is introduced into Day 2 data. Female education is set to graduate, job location distribution changes from 70%:30% to 85%:15%, and relevant experience is increased by 30%.
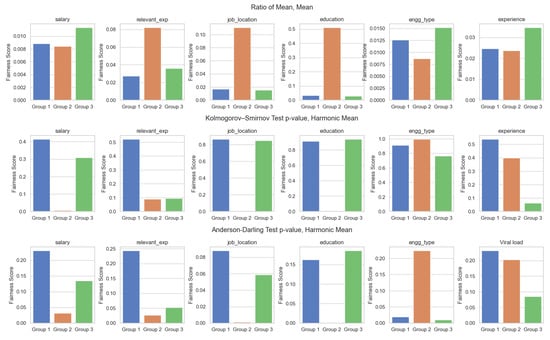
Figure 3.
Experimental results for the synthetic dataset.
6.2. Real-World Data Evaluation Result
Bias Detection
In Table 6 and Figure 4, Figure 5 and Figure 6 we can see the bias detection capability of QMAD using the three comparison–aggregation function pairs. To better understand the scores, let us review the bias injected in the UCI adult dataset. We injected bias into the education feature on day 2, where all female candidates were set to not having attended college, while all male candidates were set to having attended college. On day 3, we injected bias into both education and marital status features, where all female candidates were set to not having attended college and were all married, while all male candidates were set to having attended college and were unmarried. The higher score in the ROM–Arithmetic pair indicates bias detected, while the lower score in the KPTest–Harmonic and ADTest–Harmonic pair, and the score less than 5%, indicates the bias detected. All the aggregated scores across ROM–Arithmetic, KPTest–Harmonic, and ADTest–Harmonic can detect the bias on day 2 and day 3, as highlighted in Table 6. In addition to the bias detection, we are also interested in the bias quantification.

Table 6.
Bias detection results on the real-world dataset. Bias is introduced in data collected on Day 2 and Day 3. On Day 2, all female participants were recorded as not having attended college, while all male participants were recorded as having attended college. On Day 3, all female participants were again recorded as not having attended college, and their marital status was set as married, while all male participants were recorded as having attended college and being unmarried.
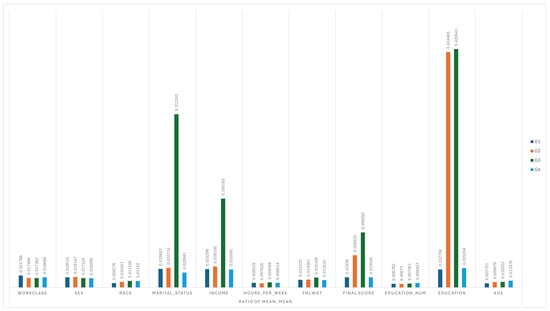
Figure 4.
Ratio of Means across Groups for Each Attribute.
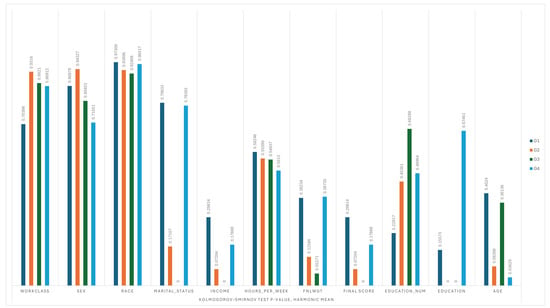
Figure 5.
Kolmogorov-Smirnov Test, Harmonic Mean of p-values across Groups.
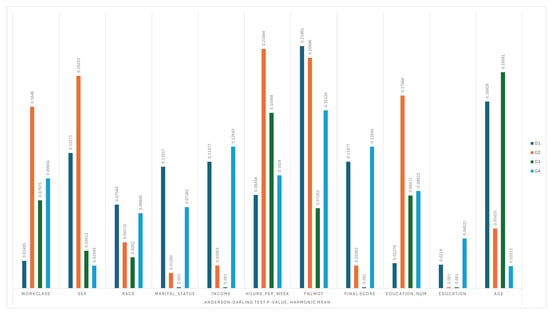
Figure 6.
Anderson-Darling Test, Harmonic Mean of p-values across Groups.
Let us focus on the ROM–Arithmetic pair result first. Both aggregation scores on day 2 and day 3 are larger than those on day 1 and day 4, indicating that the bias in day 2 and day 3 is detected. Furthermore, the score on day 2 is less than that on day 3, meaning that day 3 has a more significant bias than day 2. This is reasonable because we only injected bias into education on day 2 but injected bias into both education and marital status on day 3. Hence, QMAD can not only detect the bias but also quantify it. The same applies to the KPTest–Harmonic pair result and ADTest–Harmonic pair result, with the only difference being that the score value on day 2 is larger than that on day 3 because the score is the p-value, where a smaller value indicates a more significant deviation. Moving on to biased feature detection, we can see that QMAD can detect biased education on day 2 and biased education and marital status on day 3 across all three comparison pairs. However, we surprisingly found that QMAD also wrongly detected marital status and race on day 2 and race and sex on day 3. This may be due to the ADTest–Harmonic pair being more sensitive to minor differences. One reason may be attributed to the sensitivity of the ADTest–Harmonic pair, which is designed to detect even small distributional discrepancies. While this sensitivity supports high recall in bias detection, it also introduces the potential for false positives. To explain this in real-world settings, not all biases are injected deliberately or known a priori. QMAD’s ability to flag these attributes highlights its strength in detecting potential distributional shifts, which may otherwise go unnoticed. For example, marital status may be entangled with education or income levels, and race distribution may shift subtly due to sampling variability across time frames. We now view them as early warnings, as shown in Table 7, which can guide further causal or statistical investigation.

Table 7.
Analysis of QMAD flagging results for selected attributes. ✓ A indicates the presence of the condition; a ✗ indicates its absence.
However, we will leave this finding for further investigation in future work. Overall, from the experiment results, we can safely conclude that QMAD can effectively detect bias and also quantify it.
7. Benchmark Comparison
7.1. Benchmark Comparison on the Synthetic Dataset
To verify QMAD’s bias detection ability, we also compare its performance with other bias detection benchmarks, such as Statistical Parity Difference, Disparate Impact, Empirical Difference Fairness, and Consistency. The comparison results are presented in Table 8. We apply these fairness metrics to the synthetic data of three created days to check if they can detect the bias on day 2. From our experimental results based on their metric definition, we found that none of them can detect the bias on day 2. We test both linear regression and decision tree regressor, but only the linear regression result is used in Table 8 as QMAD’s performance. We observed that all of our tested comparison–aggregation function pairs can detect the bias on day 2. This is already verified in Table 3 (bias detection results on the synthetic dataset) in the main paper. These results indicate that QMAD’s performance is significantly better than the tested benchmarks.

Table 8.
Metric comparison results on the synthetic dataset. Only QMAD can detect bias on Day 2, while all other metrics cannot.
7.2. Benchmark Comparison on the Real-World Dataset
Table 9 displays the comparison of QMAD’s performance against existing benchmark metrics. In Table 9, we demonstrate that QMAD is able to successfully identify both the minor bias on day 2 and the larger bias on day 3. Statistical Parity Difference, on the other hand, fails to detect bias on both days. Similarly, Disparate Impact and Empirical Difference Fairness are able to detect the larger bias on day 3 but fail to identify the smaller bias on day 2, indicating that these metrics may only be sensitive to obvious bias and not smaller bias.

Table 9.
Metric comparison results on the real world dataset. QMAD accurately identifies bias on Days 2 and 3. However, Statistical Parity Difference fails to detect any bias on these days. Disparate Impact and Empirical Difference Fairness detect larger biases on Day 3 but miss smaller biases on Day 2. While Consistency detects bias on both Day 2 and Day 3, it also falsely identifies Days 1 and 4 as biased, making it an inaccurate metric.
The Consistency score being less than one indicates bias. Therefore, Consistency is able to detect the bias on both days 2 and 3. However, Consistency incorrectly flagged days 1 and 4 as having bias, which is inaccurate. Hence, Consistency results cannot be considered accurate. From this comparison, we can conclude that QMAD’s performance in real-world data classification tasks is significantly better than that of existing benchmark metrics.
7.3. Choice of Comparison–Aggregation Function Pair
The goal of the comparison function is to give a similarity or dissimilarity score for the distribution across groups. It aims to encode how different the predictions (or features) are across groups. The aggregation function combines the scores generated by the comparison function across various bins and distributions, considering model features if applicable. It is crucial to select an aggregation function that aligns with the chosen comparison function. The proposed novel metric offers flexibility in selecting these functions to suit specific requirements and use cases. For example, to compare the distribution of a categorical feature that takes on (0, 1) values, the chi-squared test can be used. Users can choose from a wide range of comparison functions based on the underlying distribution. Based on the used comparison function, the results need to be aggregated across bins and then across distributions (if multiple distributions are compared) using the appropriate aggregation technique. For example, if a statistical test is used to compare the distributions and the resulting p-value is reported, the p-values across bins and distributions cannot be combined using the mean as they are probabilities.
FairCanary used the difference in means as the comparison function. Since FairCanary did not utilize multiple distributions (features), the QDD Metric did not require combining scores across distributions. Thus, a simple mean as the aggregation function sufficed (the difference in means across distributions is reported in the quantity’s scale and thus cannot be combined using a simple mean). As the proposed novel metric combines comparison scores across different distributions, we introduced a new comparison function, the ratio of mean, which calculates the ratio of mean values for the two groups and hence is scale-agnostic. The comparison scores are then combined using the mean as an aggregation function across bins and distributions. We propose two more novel comparison–aggregation function pairs based on statistical tests. Various statistical tests exist for comparing two distributions, each with its own underlying assumptions and limitations. For example, a Z-test or t-test can be used to compare the mean of a sample to a specified constant mean when the variance of the sample is known. To use the Z-test as the comparison function, the mean and variance should be known, and the data should be normally distributed. A t-test can be used if the variance is unknown and the sample size is small. Given the limitations and assumptions inherent in statistical tests, careful consideration is essential when selecting the appropriate test for comparison purposes. To combine the test results (p-value), simple averaging cannot be used. Fisher’s method and the harmonic mean are two commonly used approaches to combine p-values from multiple statistical tests into an overall measure of significance. Fisher’s method combines the logarithms of individual p-values and sums them up, resulting in a statistic that follows a chi-square distribution. In contrast, the harmonic mean of p-values is calculated by taking the reciprocal of the average of the reciprocals of the individual p-values. Fisher’s method can be sensitive to extremely small p-values and may inflate the overall significance if not used cautiously. On the other hand, the harmonic mean is more conservative and less affected by extremely small p-values. It provides a more robust measure of significance, particularly when dealing with a small number of tests or when individual p-values are highly skewed. Hence, the harmonic mean is chosen as the preferred aggregation function when a statistical test is used as the comparison function.
When selecting the appropriate statistical test as the comparison function, it is crucial to consider several criteria. The choice of test is strongly influenced by the underlying distribution of the data. Non-parametric tests are preferred when population parameters are unknown. We considered various statistical tests, including the two-sample t-test, Mann–Whitney U test, and Brunner–Munzel test, as potential comparison functions for evaluation alongside the chosen test. The two-sample t-test is a parametric statistical test commonly used to compare the means of two independent groups. It assumes that the data are normally distributed and have equal variances between the two groups being compared. Additionally, the t-test is sensitive to outliers, and if outliers are present in the data, they can significantly affect the results. The Mann–Whitney U test is a non-parametric statistical test used to compare two independent groups. It is robust to violations of normality and suitable for ordinal or continuous data. However, it may not be appropriate or provide meaningful results in certain scenarios, such as violations of the independence assumption, differences in the shape or variability of distributions between groups, non-continuous data, and small sample sizes. Moreover, extreme outliers or skewness in the data can affect the validity of the results obtained. The Brunner–Munzel test is a non-parametric method used to test the null hypothesis that the probability of one randomly selected value being greater than another is equal. This test is similar to the Mann-Whitney U test but differs in that it does not assume equal variances, though the test results could still be affected by the extreme outliers or skewness in the data. The results of these tests on the Synthetic Dataset are shown in Table 10.

Table 10.
Other metric test results on the Synthetic Dataset using linear regression. Comparison functions include t-test, Mann–Whitney U test, and Brunner–Munzel test. A p-value below 0.05 indicates bias at 95% confidence.
Apart from the two-sample t-test, the rest of the comparison functions fail to flag bias in the group. While the t-test effectively identifies bias, its reliance on the assumption of normal distributions limits its suitability as a comparison function. In contrast, the proposed comparison functions (Kolmogorov–Smirnov test and Anderson-Darling test) are non-parametric, devoid of specific underlying distribution assumptions, and demonstrate robustness against outliers.
8. Discussion and Limitations
To demonstrate the working of the novel proposed metric and how good it is compared with respect to other existing ones, a comparison is performed with Statistical Parity Difference [25], Disparate Impact, Empirical Difference Fairness [25], and Consistency [25]. Most of the previous metrics do not support continuous prediction output, and they lack the inclusion of feature drift. Due to the non-consideration of feature drift, all these metrics fail to detect bias in prediction when the underlying feature distribution changes. This study has led to several significant findings that contribute to our understanding of fairness metrics. Firstly, for any fairness metric to effectively address bias in predictions across groups, it must take the underlying feature distributions into account. This result is particularly noteworthy as it aligns with our original hypothesis, suggesting that if there is a slight drift in the underlying feature distribution across groups, the fairness metrics based on the comparison of predictions will be deemed unreliable and may fail to capture the bias. The potential impact of our work on general research, particularly in the field of machine learning and ML fairness, can be substantial and multifaceted. We focus on adaptability to data distribution changes, consideration of feature variation, equitable treatment across groups, and robustness to skewness and imbalance. We suggest that the results of the novel metric should be used as an indicator of biases in the ML system, and any action should be taken after further analyzing the underlying discrepancies. Apart from this, the proposed metric, used with other fairness measures, may improve the ML system’s ability to detect unfairness. The limitation of the proposed framework is the lack of automation of the selection for the function pairs. This will be one of our future works.
Additionally, we observed that enhancing bias identification in machine learning models, particularly in the context of fairness metrics, is a crucial area of research. The approach of using underlying feature distributions challenges existing approaches in continuous output prediction. These findings collectively provide new insights into model robustness to the real data distribution.
The role of using underlying feature distributions in enhancing bias identification can offer a more nuanced and dynamic approach to bias detection. First, unlike one-shot fairness assessments, variation of feature distributions can continuously monitor prediction outputs for signs of bias, adapting to changes in data patterns over time.
The adaptability of the proposed metric to accommodate additional context-aware comparison and aggregation functions as needed is a significant advantage of our approach. This flexibility allows end users to tailor the metric by defining customized comparison–aggregation functions aligned with their use cases’ specific requirements. Such customization enhances the robustness of the metric, ensuring that it can effectively address the unique challenges and nuances of different scenarios. This capability not only improves the precision of the metric but also its applicability across a wide range of domains, making it a versatile tool in the realm of machine learning.
Our work contributes in several significant ways:
- Our approach underscores the importance of dynamic fairness, where ML systems are designed to adapt to changing societal norms and population demographics. By integrating this adaptability, our work encourages the development of ML systems that remain fair and unbiased over time, reducing the risk of perpetuating or exacerbating existing biases.
- By emphasizing the need to consider a wide range of feature variations, including both obvious and subtle factors, our work advocates for more inclusive and comprehensive fairness assessments and ensures that AI systems are fair and equitable for diverse groups, accounting for multi-dimensionality that might otherwise be overlooked.
- By focusing on the robustness of ML systems to skewed and imbalanced datasets, our work addresses a significant challenge in real-world data. This aspect is particularly impactful as it guides researchers and practitioners in developing ML models that are not only fair in ideal conditions but also maintain their fairness in less-than-ideal, real-world scenarios.
Further enhancements to the metric are well-thought-out and address some crucial aspects of bias detection and fairness evaluation in machine learning systems. Adding comparison–aggregation function pairs and tailoring them to specific ML tasks and use cases is a strategic move. This customization allows for more precise and relevant fairness evaluations, as different ML applications may have unique fairness considerations and requirements. By this, we can ensure that the metric is not only universal but also adaptable to the specific nuances of different applications. Developing comparison functions that not only detect biases but also quantify their direction and magnitude is a significant advancement. This enhancement would enable a deeper understanding of how and to what extent biases affect model predictions. Incorporating feature-level analysis into this framework further enriches the metric, allowing for a more granular understanding of bias sources. The results of our novel metric can be used as an initial indicator rather than a definitive conclusion, which is a prudent approach. It emphasizes the need for a comprehensive analysis where anomalies and discrepancies in data distributions are manually reviewed, especially for flagged features. This step is vital for understanding the root causes of detected biases and for developing more targeted interventions.
9. Conclusions and Future Work
The proposed novel metric does a fair job of flagging biases when existing classic algorithms fail. It demonstrates the ability to identify instances of unfairness when metrics like Statistical Parity Difference, Disparate Impact, Empirical Difference Fairness, and Consistency fail to flag the bias. Due to its flexibility to include underlying feature attributes in analysis, the metric can even flag the slightest biases in any ML system. Apart from this, this flexibility provides insights into the robustness of our fairness metric, and it is highly configurable as it can accommodate further pairs of comparison and aggregation functions based on the need. Overall, our work paves the way for a more sensitive analysis of fairness problems in computer vision and the related unfairness mitigation methods, providing reliable tools for future evaluations.
Fairness evaluation, especially across sensitive societal contexts, cannot be reliably automated without risking misleading or inappropriate conclusions. Different applications (e.g., health vs. finance vs. criminal justice) require different fairness definitions, statistical assumptions, and interpretive norms, which cannot be universally encoded in an automated pipeline. QMAD is designed to offer modular flexibility, allowing practitioners and domain experts to tailor the metric according to the nature of the dataset (e.g., balanced vs. skewed), the protected attribute types (continuous vs. categorical), and the evaluation goal (bias detection vs. bias quantification). However, while QMAD is modular by design, the framework favours manual selection of comparison-aggregation pairs to ensure alignment with the ethical, contextual, and statistical considerations of the target domain. This approach supports more nuanced and trustworthy fairness auditing than fully automated solutions, which risk masking or misrepresenting bias. Moreover, automation in fairness metrics can foster false confidence and misrepresentation of bias, especially if underlying assumptions (e.g., distribution shape, feature importance, or causal structure) are violated. QMAD intentionally avoids this by enabling transparent, interpretable, and domain-informed configurations. As our empirical framework and use-case mapping show, different contexts demand different statistical treatments, and each comparison–aggregation pair evaluated was selected with a specific application scenario in mind. In Table 11 presents a mapping between common machine learning use cases (e.g., binary classification, skewed regression, and fairness monitoring) and the function pair most appropriate for robust bias detection in that setting. This helps practitioners select the most suitable configuration based on the statistical characteristics of their problem.

Table 11.
Recommended comparison and aggregation functions across use cases: an evidence-based guideline for choosing appropriate function pairs per use case. This further supports that fairness metrics must be context-sensitive and cannot be rigidly automated without compromising interpretability or accuracy.
However, in future work, we plan to mitigate flagging non-injected attributes as biased; we propose using stability analysis across bootstrapped samples or time frames to filter out inconsistent alerts. In this light, QMAD is intended to prioritize sensitivity over automation, with the understanding that domain expertise or pipeline heuristics can help refine the signal-to-noise ratio.
Moreover, as QMAD is designed to detect even subtle disparities, we aim to integrate bootstrapped stability checks or multiple testing corrections to prevent over-alerting in noisy datasets. Future versions may incorporate causal structure awareness and support fairness tracking over continuous, non-discrete time frames or policies.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/electronics14081627/s1.
Author Contributions
Writing—review & editing, D.A.A., J.Z., Y.D., J.W., X.J.G. and F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article and Supplementary Materials.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan, A. A survey on bias and fairness in machine learning. ACM Comput. Surv. (Csur) 2021, 54, 1–35. [Google Scholar] [CrossRef]
- Angerschmid, A.; Zhou, J.; Theuermann, K.; Chen, F.; Holzinger, A. Fairness and explanation in AI-informed decision making. Mach. Learn. Knowl. Extr. 2022, 4, 556–579. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Z.; Xiao, C.; Chen, F. Does a Compromise on Fairness Exist in Using AI Models? In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Perth, Australia, 5–8 December 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 191–204. [Google Scholar]
- Jui, T.D.; Rivas, P. Fairness issues, current approaches, and challenges in machine learning models. Int. J. Mach. Learn. Cybern. 2024, 15, 3095–3125. [Google Scholar] [CrossRef]
- Chaudhari, B.; Agarwal, A.; Bhowmik, T. Simultaneous Improvement of ML Model Fairness and Performance by Identifying Bias in Data. arXiv 2022, arXiv:2210.13182. [Google Scholar]
- Schelter, S.; Biessmann, F.; Januschowski, T.; Salinas, D.; Seufert, S.; Szarvas, G. On Challenges in Machine Learning Model Management. IEEE Data Eng. Bull. 2015, 38, 50–60. [Google Scholar]
- Villar, D.; Casillas, J. Facing Many Objectives for Fairness in Machine Learning. In Proceedings of the International Conference on the Quality of Information and Communications Technology, Online, 8–10 September 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 373–386. [Google Scholar]
- Le Quy, T.; Roy, A.; Iosifidis, V.; Zhang, W.; Ntoutsi, E. A survey on datasets for fairness-aware machine learning. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2022, 12, e1452. [Google Scholar] [CrossRef]
- Caton, S.; Haas, C. Fairness in machine learning: A survey. Acm Comput. Surv. 2024, 56, 1–38. [Google Scholar] [CrossRef]
- Teo, C.T.; Cheung, N.M. Measuring fairness in generative models. arXiv 2021, arXiv:2107.07754. [Google Scholar]
- Wan, M.; Zha, D.; Liu, N.; Zou, N. Modeling techniques for machine learning fairness: A survey. arXiv 2021, arXiv:2111.03015. [Google Scholar] [CrossRef]
- Hort, M.; Chen, Z.; Zhang, J.M.; Harman, M.; Sarro, F. Bias Mitigation for Machine Learning Classifiers: A Comprehensive Survey. ACM J. Responsib. Comput. 2024, 1, 11. [Google Scholar] [CrossRef]
- Hardt, M.; Price, E.; Srebro, N. Equality of Opportunity in Supervised Learning. In Advances in Neural Information Processing Systems (NeurIPS); Curran Associates, Inc.: Red Hook, NY, USA, 2016; Volume 29, pp. 3315–3323. [Google Scholar]
- Dwork, C.; Hardt, M.; Pitassi, T.; Reingold, O.; Zemel, R. Fairness through awareness. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, Cambridge, MA, USA, 8–10 January 2012; pp. 214–226. [Google Scholar]
- Di Stefano, P.G.; Hickey, J.M.; Vasileiou, V. Counterfactual fairness: Removing direct effects through regularization. arXiv 2020, arXiv:2002.10774. [Google Scholar]
- Franklin, J.S.; Bhanot, K.; Ghalwash, M.; Bennett, K.P.; McCusker, J.; McGuinness, D.L. An Ontology for Fairness Metrics. In Proceedings of the 2022 AAAI/ACM Conference on AI, Ethics, and Society, Oxford, UK, 19–21 May 2021; Association for Computing Machinery: New York, NY, USA, 2022; pp. 265–275. [Google Scholar]
- Franklin, J.S.; Powers, H.; Erickson, J.S.; McCusker, J.; McGuinness, D.L.; Bennett, K.P. An Ontology for Reasoning About Fairness in Regression and Machine Learning. In Proceedings of the Knowledge Graphs and Semantic Web; Ortiz-Rodriguez, F., Villazón-Terrazas, B., Tiwari, S., Bobed, C., Eds.; Springer: Cham, Switzerland, 2023; pp. 243–261. [Google Scholar]
- Ghosh, A.; Shanbhag, A.; Wilson, C. Faircanary: Rapid continuous explainable fairness. In Proceedings of the 2022 AAAI/ACM Conference on AI, Ethics, and Society, Oxford, UK, 19–21 May 2021; Association for Computing Machinery: New York, NY, USA, 2022; pp. 307–316. [Google Scholar]
- Wang, Z.; Zhou, Y.; Qiu, M.; Haque, I.; Brown, L.; He, Y.; Wang, J.; Lo, D.; Zhang, W. Towards Fair Machine Learning Software: Understanding and Addressing Model Bias Through Counterfactual Thinking. arXiv 2023, arXiv:2302.08018. [Google Scholar]
- Liu, L.T.; Dean, S.; Rolf, E.; Simchowitz, M.; Hardt, M. Delayed impact of fair machine learning. In Proceedings of the International Conference on Machine Learning, PMLR, Macau, China, 26–28 February 2018; pp. 3150–3158. [Google Scholar]
- Nanda, V.; Dooley, S.; Singla, S.; Feizi, S.; Dickerson, J.P. Fairness through robustness: Investigating robustness disparity in deep learning. In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency, Virtual Event, 3–10 March 2021; pp. 466–477. [Google Scholar]
- Rampisela, T.V.; Maistro, M.; Ruotsalo, T.; Lioma, C. Evaluation measures of individual item fairness for recommender systems: A critical study. ACM Trans. Recomm. Syst. 2024, 3, 1–52. [Google Scholar] [CrossRef]
- Feldman, M.; Friedler, S.A.; Moeller, J.; Scheidegger, C.; Venkatasubramanian, S. Certifying and removing disparate impact. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 259–268. [Google Scholar]
- Bellamy, R.K.E.; Dey, K.; Hind, M.; Hoffman, S.C.; Houde, S.; Kannan, K.; Lohia, P.; Martino, J.; Mehta, S.; Mojsilović, A.; et al. AI Fairness 360: An extensible toolkit for detecting and mitigating algorithmic bias. IBM J. Res. Dev. 2019, 63, 4.1–4.15. [Google Scholar] [CrossRef]
- Bellamy, R.K.; Dey, K.; Hind, M.; Hoffman, S.C.; Houde, S.; Kannan, K.; Lohia, P.; Martino, J.; Mehta, S.; Mojsilovic, A.; et al. AI Fairness 360: An extensible toolkit for detecting, understanding, and mitigating unwanted algorithmic bias. arXiv 2018, arXiv:1810.01943. [Google Scholar]
- Selbst, A.D.; Boyd, D.; Friedler, S.A.; Venkatasubramanian, S.; Vertesi, J. Fairness and Abstraction in Sociotechnical Systems. In Proceedings of the FAT* ’19: Conference on Fairness, Accountability, and Transparency, Atlanta, GA, USA, 29–31 January 2019. [Google Scholar]
- Barocas, S.; Hardt, M.; Narayanan, A. Fairness and Machine Learning: Limitations and Opportunities; MIT Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Zemel, R.; Wu, Y.; Swersky, K.; Pitassi, T.; Dwork, C. Learning fair representations. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 16–21 June 2013; pp. 325–333. [Google Scholar]
- Becker, B.; Kohavi, R. UCI Adult Dataset. In Proceedings of the UCI Machine Learning Repository; University of California, Irvine, CA, USA. 1996. Available online: https://archive.ics.uci.edu/dataset/2/adult (accessed on 1 January 2025).
- An, K. Sulla determinazione empirica di una legge didistribuzione. Giorn. Dell’inst. Ital. Degli Att. 1933, 4, 89–91. [Google Scholar]
- Smirnov, N. Table for estimating the goodness of fit of empirical distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Stephens, M.A. EDF statistics for goodness of fit and some comparisons. J. Am. Stat. Assoc. 1974, 69, 730–737. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).