Design and Real-Time Control of an Electric Furnace with Three-Dimensional Heating

Abstract

Currently, heating in electric ovens is generally achieved using heaters placed on the top and bottom surfaces. In some advanced ovens, heaters are installed on the back surface, allowing 3D heating. However, in these ovens, temperature measurements are obtained from a single point, making the temperature control unreliable. Additionally, this type of oven cannot provide homogeneous heating since it lacks heaters on the left, right, or front surfaces. In this study, a unique electric oven equipped with heaters and temperature sensors was designed and produced on all six surfaces. To model its performance, the heating behavior of the oven was derived using the Ziegler–Nichols tangent method, and the gain factors for the proportional (P), proportional-integral (PI), and proportional-integral-derivative (PID) controllers were determined. Subsequently, real-time digital control of the oven was performed using on-off, P, PI, and PID controllers, which ensured a comprehensive evaluation of the oven’s control performance. The experimental results showed that homogeneous heating could only be achieved when all panels were energized. Additionally, the PI and PID controllers stabilized the system with a maximum steady-state error of 1.3 °C in all cases, demonstrating the accuracy of the derived system model and adequacy of the implemented control system.

1. Introduction

Electric furnaces are frequently used in industry and in daily life. Generally, the heating process in these furnaces is performed by taking measurements from single point heaters placed on the lower and upper surfaces of the furnace. Therefore, it cannot be determined whether the thermal distribution in the inner chamber of the furnace is homogeneous. A considerable amount of literature has been published on the heating of electric furnaces. In one of these studies, the temperature distribution in electric furnaces is modeled as first-order plus delay (FOPDT) [1,2,3]. In line with this model, although different techniques are used for temperature control of the device, proportional-integral-derivative (PID) control stands out because of its simplicity, performance, and stability [4,5,6,7]. In [8], a system model of an electric furnace was proposed, and simulation studies of classical PID and fractional-order PID control methods were conducted according to this system model. Furnace temperature control using three PID tuning techniques, namely Ziegler–Nichols (ZN), Cohen–Coon (CC) and Chien, Hrones and Reswick (CHR) of the PID parameters was proposed in [9]. In [10], temperature control of the heat pump solar-assisted drying system was carried out using a PID controller. The operating stability of the system was investigated by drying red pepper. In [11], traditional PID controllers, intelligent control techniques, such as fuzzy PID, fuzzy self-adjusting PID, fuzzy immunity PID, and expert PID, were compared to eliminate the large overshoot and large swing problem in furnace temperature control. In [12], an adaptive fuzzy control technique was used to control the temperature of the electric furnace. The efficiency of the technique used was compared with that of classical PID and traditional fuzzy controller techniques. In [13], a proportional integral (PI) controller was used to control an inter-heated thermal turbine. The gain parameters K_p and K_i of the PI controller were adjusted using particle swarm optimization (PSO). In [14], temperature control of an electric furnace was performed using a fuzzy PID controller. The performance of the applied control technique was compared to that of a traditional PID controller. A linear low-order model for the temperature control of a tempering furnace was proposed in [15], and a model predictive control was applied. To validate the performance of the proposed model and adaptive observer-based model predictive control, simulation studies were performed, and their performance was compared with that of a PI controller and a nonlinear model predictive controller. Temperature control of biofuel furnaces was realized in [16] using a PID controller. In this study, the K_p, K_i, and K_d parameters were determined using a trial-and-error method. The optimum K_p, K_i, and K_d weighting factors were determined based on the system control performance, steady-state error, overshoot size, rise time, and settling time, respectively. An adaptive fuzzy PID controller for a resistive furnace system was designed in [17] by combining the simple nature of PID control with the strong reasoning of fuzzy rules. The efficiency of the proposed method was compared with that of a conventional PID controller. In [18], a heat pump solar collector dryer was designed and controlled using a PID controller. In this study, temperature control, with an accuracy of approximately ±0.369 °C, was performed at a reference temperature of 40 °C. In [19], temperature control of a glass melting furnace was carried out for a television picture tube. A hybrid control system was proposed as a control method that combines a fuzzy logic controller and a PI controller. The proposed hybrid controller was implemented in a real production furnace at the Samsung–Corning Company, Suwon, Korea, and its performance was investigated. Although different control theories for furnace temperature control have been proposed in these studies, none of them have investigated the homogeneity of the thermal distribution in the heater chamber of furnaces.

In the literature, the distribution of thermal changes in heater chambers of different furnace types has been investigated. In [20], three-dimensional temperature measurement of a gas-fired pilot tube furnace was performed. The temperature distribution of the furnace was determined using the DRESOR method based on radiation image processing technology, with the help of four flame image detectors placed in the heater chamber. The accuracy of the measurement results was compared with the data obtained using the thermocouples. In [21], a three-dimensional temperature distribution in large-scale boiler furnaces was visualized. Radiative energy images were obtained using cameras placed around the furnace. A modified Tikhonov regularization method was proposed to obtain a three-dimensional temperature distribution using these data. In [22], a one-dimensional mathematical model describing the gas flow of a tunnel kiln, heat transfer between the brick and air, and evaporation of bound water in the brick was proposed, and simulation studies were conducted. In [23], a new tomography detector was proposed to determine the three-dimensional flame temperature distribution in a furnace. The proposed sensor was used to detect the three-dimensional temperature distribution of semi-industrial fuel-oil flames. The performance results of the proposed sensor were compared with those obtained using color pyrometry. In [24], the temperature change in an aluminum melting furnace was observed using optical sensors. A light-receiving camera was placed in the upper part of the oven. Using this camera, a new method that allows the user to objectively evaluate the melting process in a furnace was proposed. In [25], a three-dimensional temperature distribution was observed in a tangentially fired furnace. Flame images inside the furnace were measured at different angles using a camera placed inside the furnace. To determine the three-dimensional thermal distribution in the inner chamber of the furnace with minimum error, the measurements obtained from different angles were combined with the proposed solution algorithm. The efficiency and applicability of the proposed algorithm were verified through experimental tests. In [26], the three-dimensional homogeneous thermal change in reflow furnaces, depending on the internal convectional coefficient, was investigated. A three-dimensional internal convection coefficient map of the reflow oven was obtained from the data obtained using the measuring probes. Based on this map, the convection efficiency of the heater chamber of the reflow brazing furnace was investigated. The results of these studies indicate that previous approaches, which applied heating from a single region, failed to achieve a homogeneous temperature distribution in the heater chamber of the furnace.

This study sets out to design, produce, and control a three-dimensional electric furnace. The heaters and PT100 temperature sensors were located on all six inner surfaces of the oven to achieve homogeneous heat distribution in the chamber. PID control of the heaters on the entire surface was performed separately with the help of the driver cards. Thus, the heating process along the x-, y-, and z-axes of the furnace was conducted in three dimensions. The system model of the furnace and K_p, K_i, and K_d parameters were determined using the ZN method. The on-off, proportional (P), proportional plus integral (PI), and proportional plus integral plus derivative (PID) control methods were applied to the furnace. The time responses of the applied control techniques such as overshoot, rise time, offset error, integration of absolute error (IAE), integration of square error (ISE), integration of time-weighted absolute error (ITAE), and integration of time-weighted square error (ITSE) metrics were calculated and analyzed. In addition, the noise originating from the network was minimized by applying zero-crossing circuits to the driver unit. The results of the experimental studies indicated that a homogeneous thermal distribution was achieved in the heater chamber of the furnace within an acceptable error range. There are several important areas where this study makes an original contribution to the heating control system of electric furnaces:

• An original oven equipped with heaters and temperature sensors on six surfaces was designed and modeled, and temperature was controlled.
• Temperature measurements were performed at six different points inside the oven, and each heater on the six surfaces of the oven was controlled separately.
• It was demonstrated that homogeneous heating is not possible in electric ovens unless heaters are present on all six surfaces and the temperature of each heater is individually controlled.
• The heaters were switched at zero crossings of the main voltage to prevent sudden surges in current and noise generation on the mains.

The remaining part of the paper proceeds as follows: Section 2 contextualizes the research by introducing the implemented oven and explaining the applied methods. Section 3 includes a discussion of the findings based on experimental results. The final section provides a summary and critique of the findings.

2. Materials and Methods

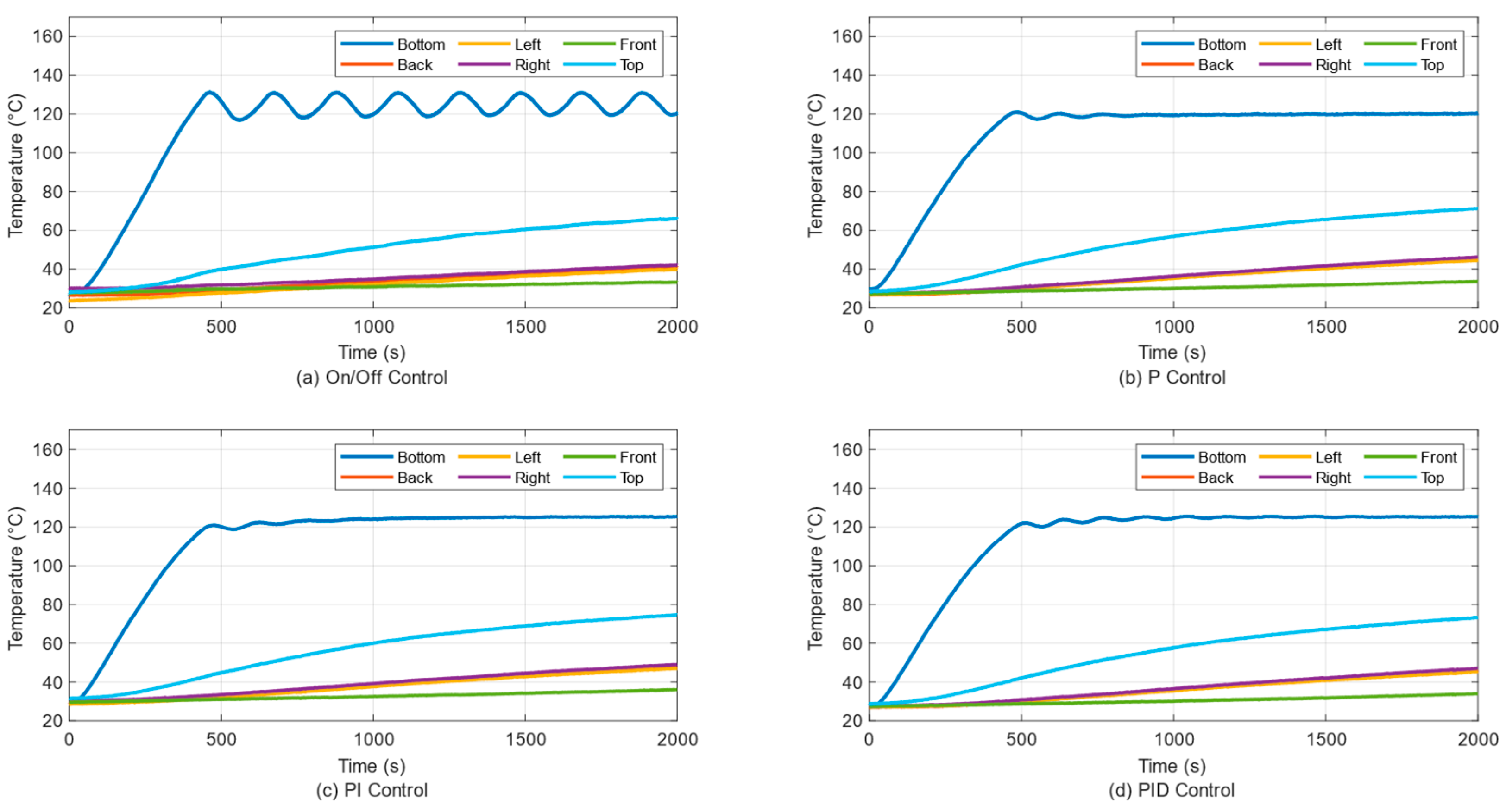
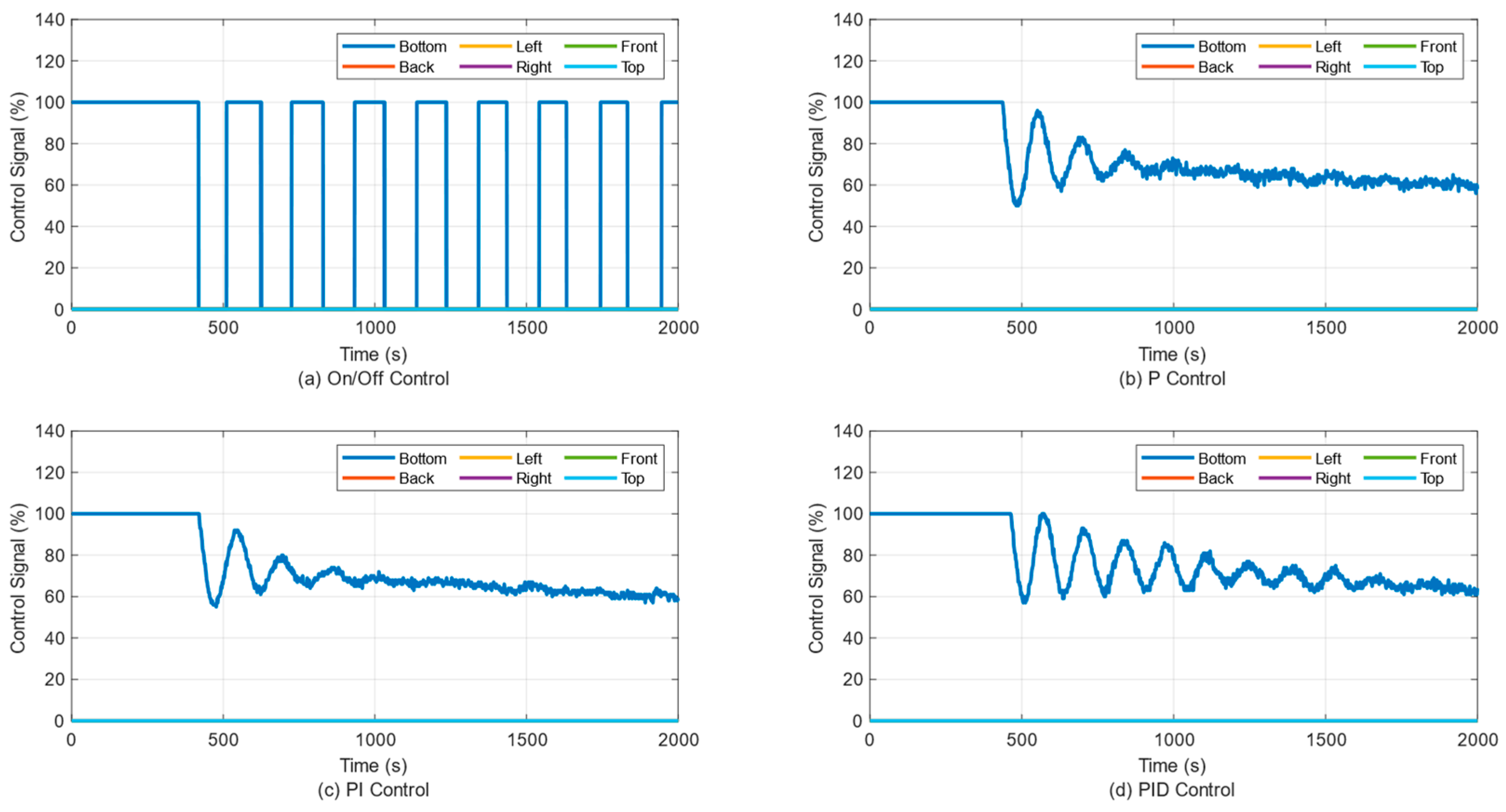
2.1. The On-Off Control

The on-off control system is the simplest control method, and it is frequently encountered in industry and our daily lives [27]. This system is used in heaters, air conditioners, ovens, combined boilers, and many other devices. In the on-off control technique, a set point is determined according to the state of the system to be operated. If the system has a value below this set point, it continues to operate. If the system produces a value greater than the set point, it stops working and attempts to fix the system at the set point [28]. There are no intermediate values for an ideal on-off control system. In other words, the system oscillates at a set point and performs continuous opening and closing operations. This results in a reduction in the life of the system used during the continuous opening and closing process, as well as of the components that make up the system. For this reason, a band gap or hysteresis below and above the system set value is generated, and the system is prevented from being continuously on and off [29]. Thus, more accurate operation of the system is ensured, and the durability of the system units is extended. This control system can also be used to control parameters, such as temperature, pressure, speed, acceleration, and position.

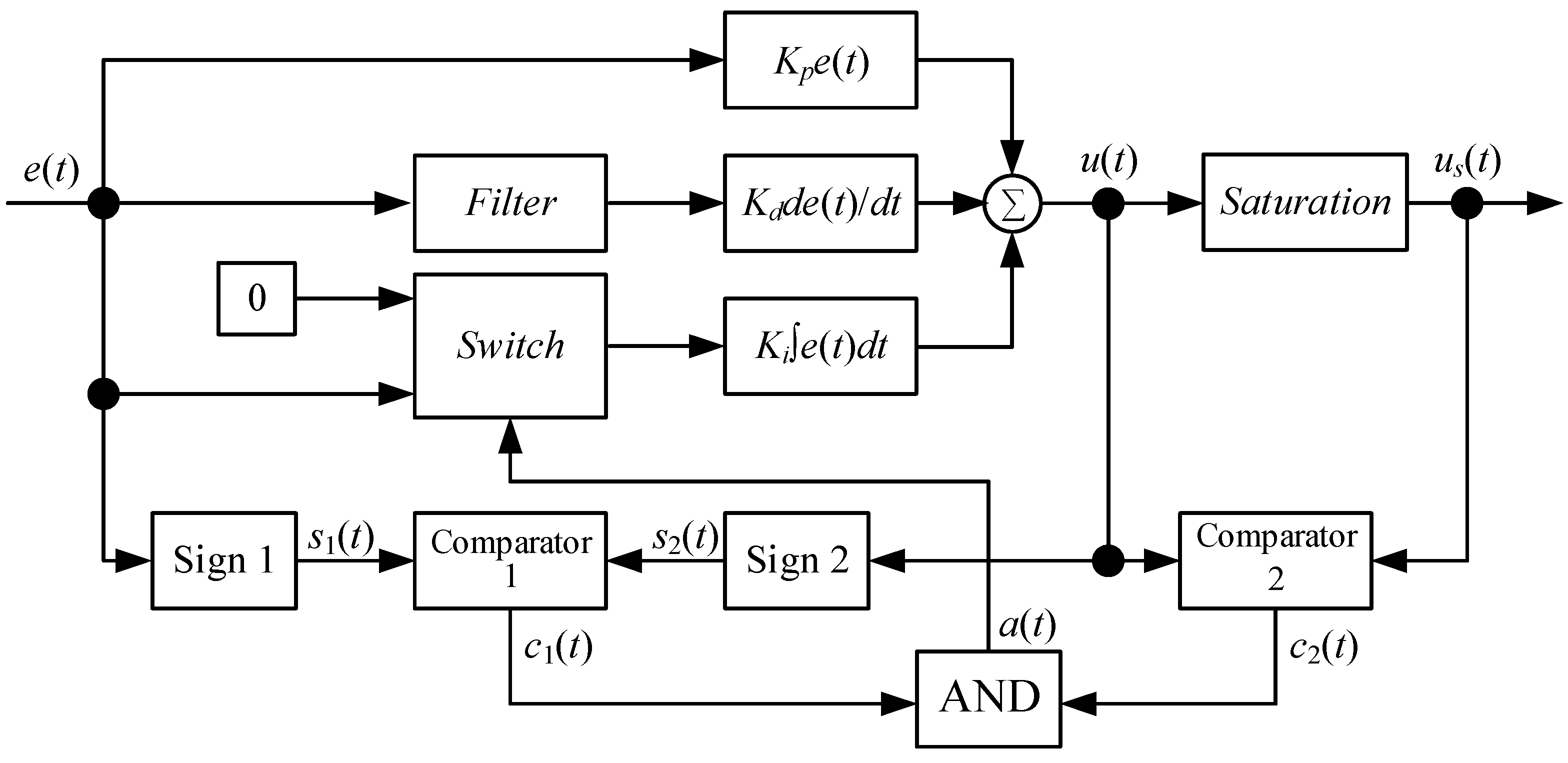
2.2. PID Control

PID control is widely used in control systems because of its sensitivity and practicality. It is commonly employed to stabilize unstable systems [30]. In this control method, the control signal is obtained by combining three proportional, derivative, and integral actions [31]. Here, an integral action is used to minimize and eliminate the offset error in large changes in the system. Derivative actions are generally used to reduce errors that occur during sudden changes. Thus, the error is maintained within the desired limits by using PID control in situations that may occur in the system [32]. Figure 1 shows a block diagram of the PID with an anti-windup and derivative filter.

Figure 1. Block diagram of the PID controller with anti-windup and derivative filter.

In Figure 1, $e\left(t\right)$ represents the error signal, $u\left(t\right)$ the control signal, $u_s\left(t\right)$ the saturated control signal, $s_1\left(t\right)$ the sign of the system error, $s_2\left(t\right)$ the sign of the control signal, $c_1\left(t\right)$ the output of the first comparator, $c_2\left(t\right)$ the output of the second comparator, and $a\left(t\right)$ the output of the logical AND operation [33,34]. When the system output is noisy, this noise is transferred to the error signal. The derivative component of the PID controller amplifies the noise carried by the error signal and adds it to the control signal. This situation leads to a degradation in the stability of the system. In Figure 1, a low-pass filter is added to the input of the derivative component to minimize the effect of noise in the system output and sudden changes at the setpoint on the control signal. In addition, the signs of the error and control signals were first compared to prevent the integral component of the controller from saturating. If the signs of these two signals are the same, the output of the first comparator is logical-1 ($c_1\left(t\right)=1$); otherwise, it is logical-0 ($c_1\left(t\right)=0$). Subsequently, the second comparator monitors whether the control signal has reached saturation. When the control signal is not saturated ($u\left(t\right)=u_s\left(t\right)$), the comparator output is logical-0 ($c_2\left(t\right)=0$). However, when the control signal reaches saturation ($u\left(t\right)\ne u_s\left(t\right))$, the comparator output becomes logical-1 ($c_2\left(t\right)=1)$. The outputs of the comparators are connected to the input of the logical AND operator, and the output of the AND operator is connected to the input of the switch. In the case of saturation, when the error and control signals have the same sign and the control signal reaches saturation, the operator output is logical-1 ($a\left(t\right)=1)$. In this case (clamping), the switch connects the input of the integral component to zero. In other cases, since the output of the AND operator is logical-0, an error signal is applied to the integrator input. The use of a derivative filter and integrator anti-windup in the PID controller enhances the performance of the controller and stability of the system.

2.3. Error Area Based Performance Criteria

The error area is defined as the area between the system response curve and the reference curve. The commonly used criteria for error areas in the literature are presented in Equations (1)–(4).

$$Integration of Absolute Error \left(IAE\right):{\int }_0^T\left|e\left(t\right)\right|dt$$

(1)

$$Integration of Square Error \left(ISE\right):{\int }_0^T{e}^2\left(t\right)dt$$

(2)

$$Integration of Time Weighted Absolute Error \left(ITAE\right):{\int }_0^{T}t\left|e\left(t\right)\right|dt$$

(3)

$$Integration of Time Weighted Square Error \left(ITSE\right):{\int }_0^T{t.e}^2\left(t\right)dt$$

(4)

where t is the time, T is the period, and |.| shows the absolute values.

2.4. General Description of the System

A block diagram of the digitally controlled electric furnace is presented in Figure 2. The furnace consisted of three main components: mechanical, electrical, and software. The mechanical components included the outer main body of the oven, heaters, and sensors. The electrical unit consisted of a microcontroller card, zero-crossing detection circuit, analog digital converter (ADC) card, and driver circuits. The software component included control software running on a laptop computer and embedded software running on the microcontroller.

Figure 2. General block diagram of the system.

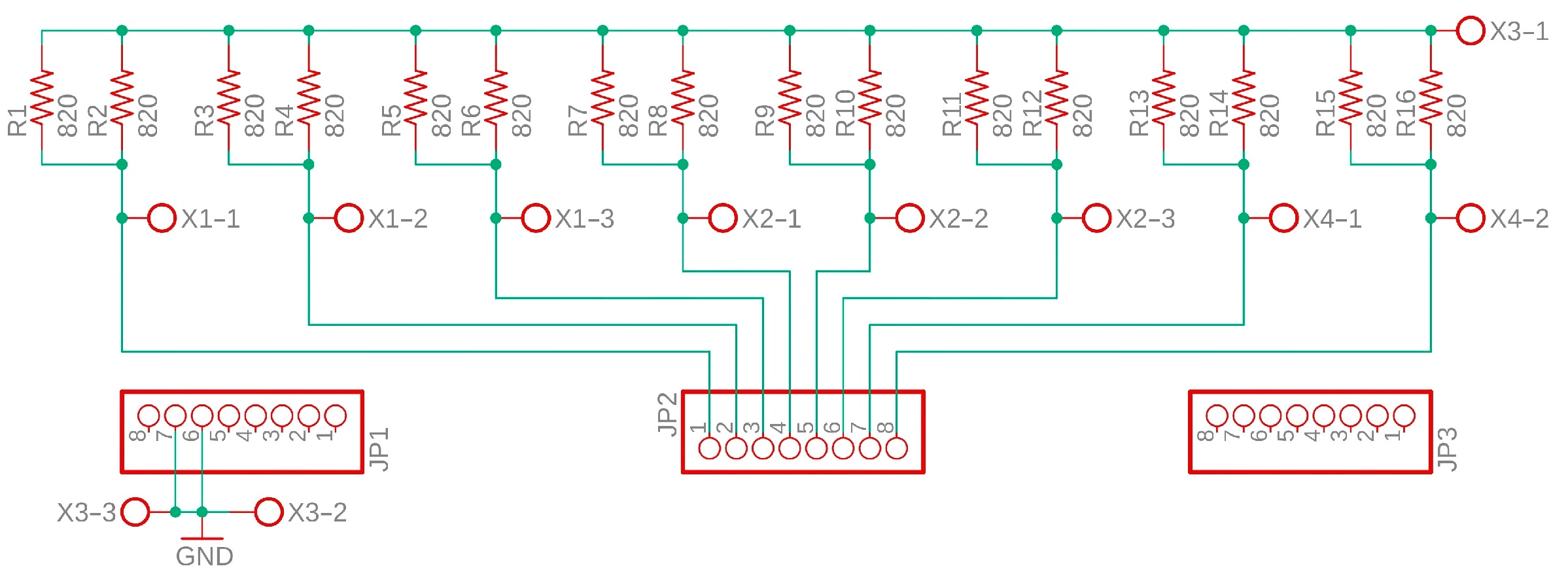
2.5. Mechanical Part

The mechanical component of the electric furnace was produced in three stages. In the first stage, the main body of the furnace was constructed as a cube measuring 60 cm × 60 cm × 60 cm, composed of four aluminum profiles measuring 60 cm × 5 cm × 5 cm and twelve profiles measuring 50 cm × 5 cm × 50 cm. Subsequently, the panels of the electric furnace were formed using aluminum plates measuring 60 cm × 60 cm, with each panel consisting of five layers. The first layer included an aluminum plate measuring 45 cm × 45 cm × 0.3 cm, designed to radiate heat generated by the resistance element. The second layer contained a 375 W heater (Baykal Rezistans Ltd. Co., Sakarya, Türkiye) and a PT100 temperature sensor (JUMO Process Control, Inc., Syracuse, NY, USA). The third layer consisted of another aluminum plate measuring 45 cm × 45 cm × 0.3 cm, which was fixed to the second layer with a copper spacer measuring 2 cm in height. The fourth layer was filled with rock wool, measuring 2.2 cm thick, capable of withstanding temperatures up to 750 °C to provide thermal insulation. Finally, a fifth layer comprised an aluminum plate measuring 60 cm × 60 cm × 0.3 cm, forming the outer surface of the oven. The mechanical assembly of the electric furnace was completed by combining these panels and components. Figure 3 provides a general view of the oven.

Figure 3. General view of the oven system.

2.6. Electrical Part

The electrical component consisted of three basic components. The first is the converter unit, which converts analog data received from the sensors to digital data. The second part is the zero-crossing detection circuit, which enables the driver board to trigger. The last unit was the heater driver board.

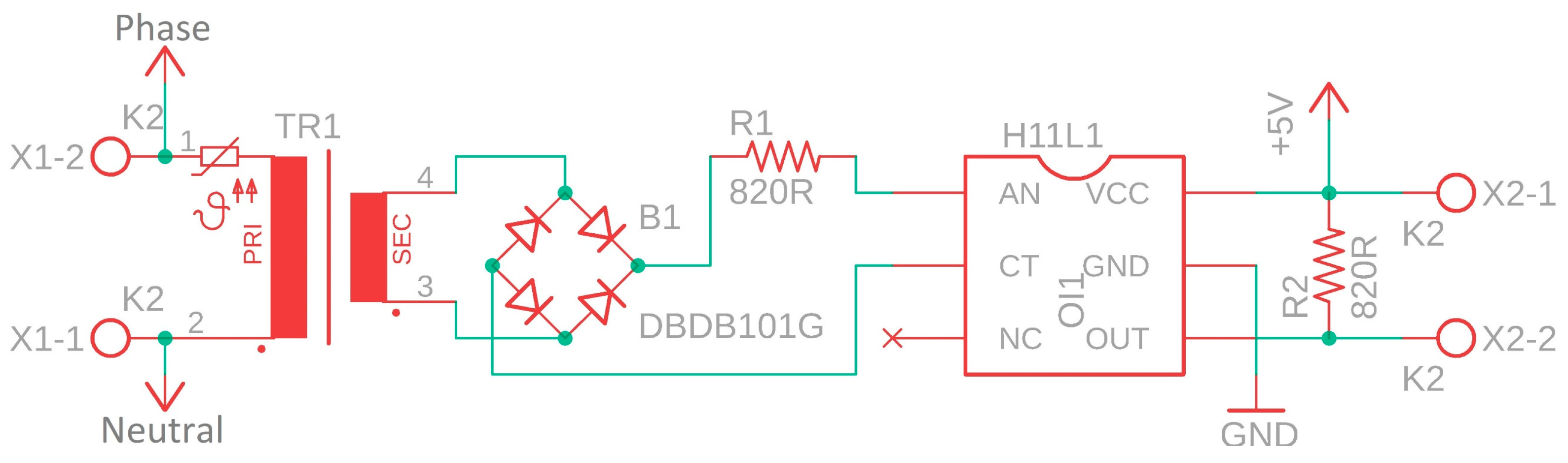
2.6.1. Analog Digital Converter Card

The ADC card digitally converted the temperature detected by the PT100 sensor. Temperature variations in the resistors led to changes in the resistance of the PT100 sensor. These resistance changes were converted into voltage changes by using the ADC interface card. Subsequently, this voltage change was digitized using an Arduino Mega microcontroller card and transferred to a laptop via the USB port. A schematic diagram of the ADC interface card is shown in Figure 4.

Figure 4. Schematic of ADC board.

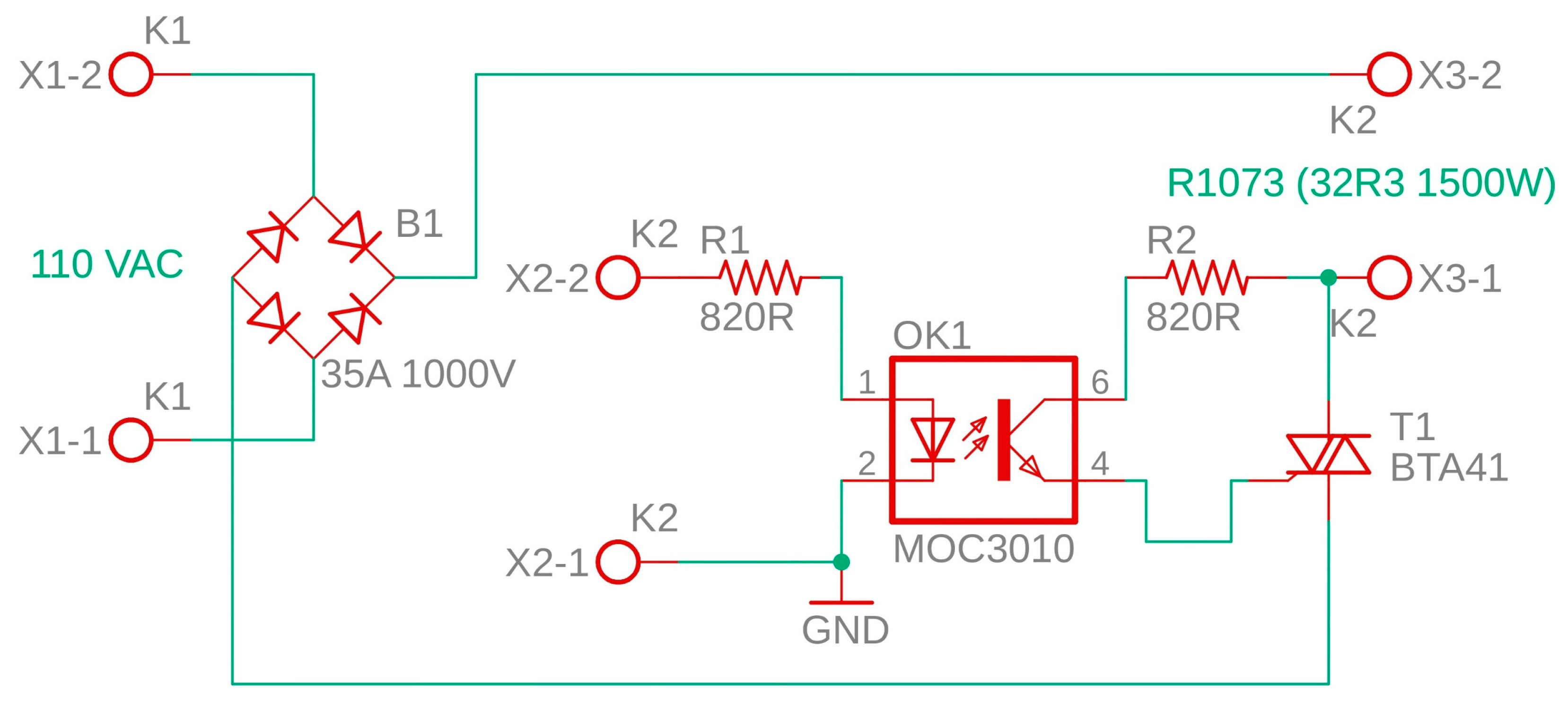
2.6.2. Zero-Crossing Detection Circuit

Resistance heaters with a power of 375 W were placed on each surface of the electric furnace to ensure homogeneous heating. The resistance heaters were independently controlled by pulse-width-modulated (PWM) trigger signals. Trigger signals were provided by a microcontroller card in 1 ms steps in a 100 ms period. The trigger signal and zero-crossing detection circuit were operated simultaneously to prevent interference from potential disturbances in the network. A schematic of the zero-crossing circuit is shown in Figure 5. Zero-crossings of the network frequency were detected using an H11L1 integrated circuit. The supply voltage required for the operation of H11L1 is provided by a 2 W transformer, 1.5 A bridge diode, and a 12 VDC supply regulated by an LM7805 linear voltage regulator and its peripheral components. The H11L1 generates a pulse with an amplitude of 5 V and a width of 500 μs for each zero crossing.

Figure 5. Schematic of the zero-crossing detection circuit.

With the zero-crossing detection circuit, the triac was always placed into conduction or occlusion at zero crossings. Thus, the current at the time of switching became zero, and soft switching was performed. Otherwise, excessive currents could be drawn instantaneously during the furnace operation, and noise would be generated at the network voltage.

Driver Circuit

The implemented driver circuit consisted of a 35 A 1000 V rectifier bridge diode, an MOC3010 optically isolated triac driver, and a BTA41 triac. After the main voltage was rectified using the bridge diode, it was applied to the input end of the resistance. The output end of the heater was connected to a 41 A 600 V triac with a dynamic resistance of 10 mΩ. The trigger signal from the controller card was applied to BTA41 through MOC3010 optically insulated triac driver integration. Thus, the heater operated at different power levels using a trigger signal. A schematic of the driver circuit is shown in Figure 6.

Figure 6. Schematic of driver circuit.

The main control panel of the electric furnace was realized by combining a microcontroller card, ADC card, zero-crossing detection circuit, and driver cards. Figure 7 shows the control panel.

Figure 7. General view of the main control panel.

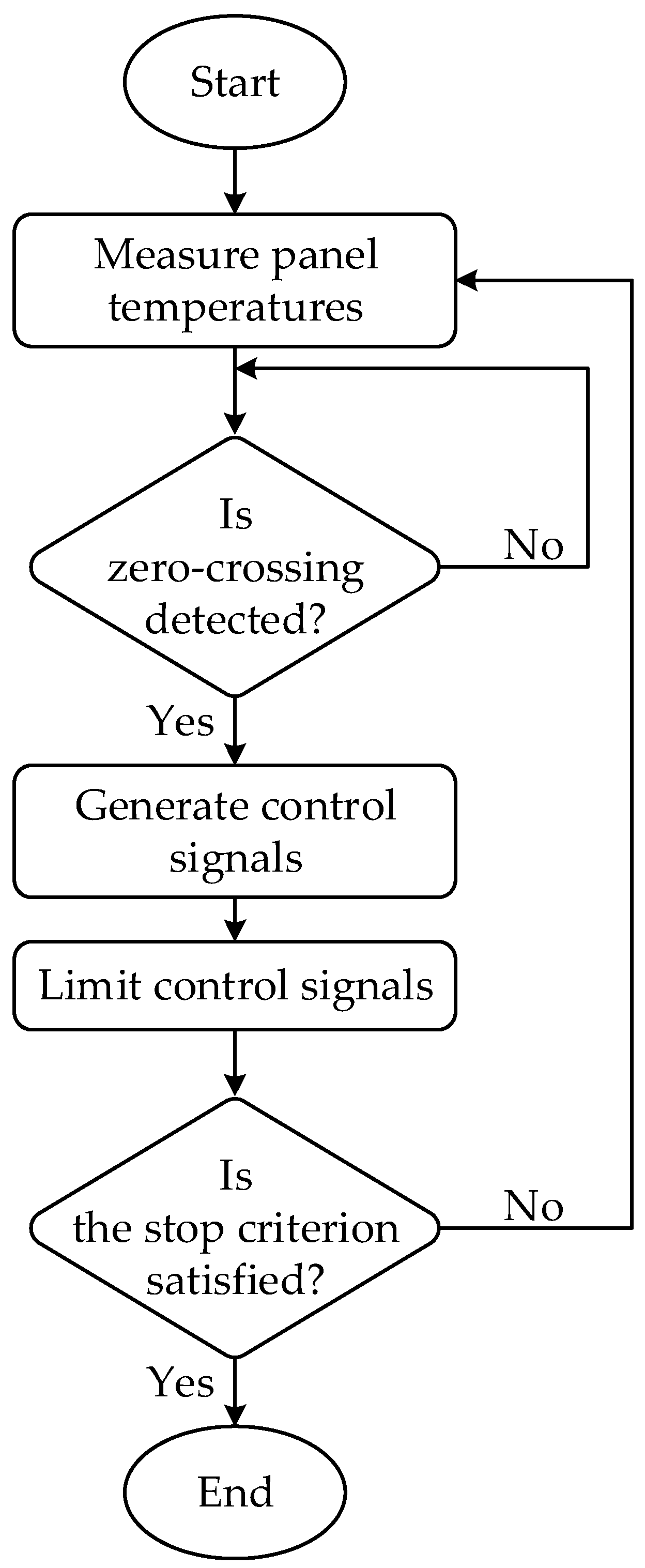
2.7. Software Part

The software part consisted of programs on a laptop and controller card. These programs enabled real-time temperature control of the electric furnace using on-off, P, PI, and PID control methods.

2.7.1. Control Software

The control software received the real-time temperature data for each panel from the microcontroller card via the USB port and calculated the instantaneous error by comparing it with the specified reference temperatures. The temperature error was applied as an input to the on-off, P, PI, and PID controllers, and the duty ratios required for each heater were calculated. The duty ratios were between 0% and 100% with a resolution of 1%. These values were then transmitted to the controller card via the USB port, with this process occurring every second.

2.7.2. Controller Software

The control card functioned as a data capture interface between the computer and controlled system. It generated control signals and triggers driver circuits based on the duty values received from the computer and the output of the zero-crossing detection circuit. Additionally, it measured the panel temperatures and transmitted them to a computer in real time.

Figure 8 shows a flowchart of the main control program. The main control program consisted of five components. These are:

Figure 8. Flowchart of the main control program.

Measurement: The resistance change in the PT100 sensors on each panel was converted into a voltage change using an ADC card. These analog temperature voltages were sampled and digitized 100 times per second, as defined in Equation (5). The average temperature was then used to obtain the digital temperature of each panel. This process acted as a derivative filter for the derivative component of the PID controller. In this way, the high-frequency components of the noise on the controlled variable, and therefore, on the error signal, were filtered. Thus, the disruptive effect of the measurement noise on the stability of the system, caused by the derivative controller, was minimized.

$$y[k]={\displaystyle \frac{1}{N}}\sum _{i=0}^{N-1}y\left(k\times T_s+i\times T_{so}\right)$$

(5)

where $y\left[k\right]$ is the panel temperature, N is the number of samples, k is the sample index, i is the oversampling index, and $T_{so}$ is the oversampling period. $T_s=1 \mathrm{s}$ and $T_{so}=1 \mathrm{m}\mathrm{s}$ were selected. In this case, the temperature of each panel was sampled 100 times within 100 ms.

Synchronization: To prevent the proposed electric furnace from generating noise on the grid during operation, the heaters on the panels were powered on and off at the zero crossings of the main voltage. The output of the zero-crossing detection circuit was connected to the digital input of the microcontroller board. Upon detecting the zero crossing, the controller applied control signals to the driver circuits, thereby synchronizing the control signals with the mains voltage.

Control: The control signal for each panel was determined based on the selected control method (on-off, P, PI, or PID). The temperatures of the six panels were maintained at the reference values using six independent control loops. In the on-off control, control signals were generated using Equation (6):

$$\begin{gathered} y\left[k\right]<r\left[k\right]-ϵ then u\left[k\right]=logic-1 \\ y\left[k\right]>r\left[k\right]+ϵ then u\left[k\right]=logic-0 \end{gathered}$$

(6)

where $u\left[k\right]$ is the control signal, and $ϵ$ is the threshold, which is set to $ϵ=1 °\mathrm{C}$.

In the P-controller, the error signals were obtained using Equation (7), and the control signals were determined using Equation (8):

$$e\left[k\right]=r\left[k\right]-y\left[k\right]$$

(7)

$$u\left[k\right]=K_p\times e\left[k\right]$$

(8)

where $e\left[k\right]$ is the temperature control error, and $K_p$ is the proportional gain.

In the PI controller, the control signals were obtained using Equation (9):

$$u\left[k\right]=K_p\times e\left[k\right]+K_i\times \sum _{i=0}^k(e\left[k\right]\times T_s)$$

(9)

where $K_i$ denotes the integral gain. The anti-windup method, shown in Figure 1, was used for the integral action of the PI controller.

In the PID controller, the control signals were generated using Equations (10) and (11):

$$u\left[k\right]=K_p\times e\left[k\right]+K_i\times \sum _{i=0}^k(e\left[k\right]\times T_s)+{\displaystyle \frac{K_d}{T_s}}\times (e_f\left[k\right]-e_f\left[k-1\right])$$

(10)

$$e_f\left[k\right]=0.0969e_f\left[k-1\right]+0.00155e\left[k\right]+0.00155e[k-1]$$

(11)

where $K_d$ is the derivative gain, $e\left[k\right]$ is the current value of the system error, $e\left[k-1\right]$ is the value of the system error in the previous sample, $e_f\left[k\right]$ is the current value of the filtered error signal, $e_f\left[k-1\right]$ is the value of the filtered error signal in the previous sample, and $k$ is the sample index. The anti-windup strategy shown in the block diagram in Figure 1 was used for the integral action of the PID controller. Additionally, to prevent the noise in the temperature measurements from adversely affecting the system, a first-order Butterworth filter, defined in Equation (11), was used in the derivative action of the PID controller.

Saturation: The control signal was a positive integer that varied between zero and 100. The control signal was limited to within this range by using Equation (12).

$$\begin{gathered} u\left[k\right]<0 then u_s\left[k\right]=0 \\ u\left[k\right]>100 then u_s\left[k\right]=100 \end{gathered}$$

(12)

Termination: The temperature control continued until the stop condition was satisfied. The stop condition was determined by the maximum number of samples, and temperature control was terminated when $k=2000$.

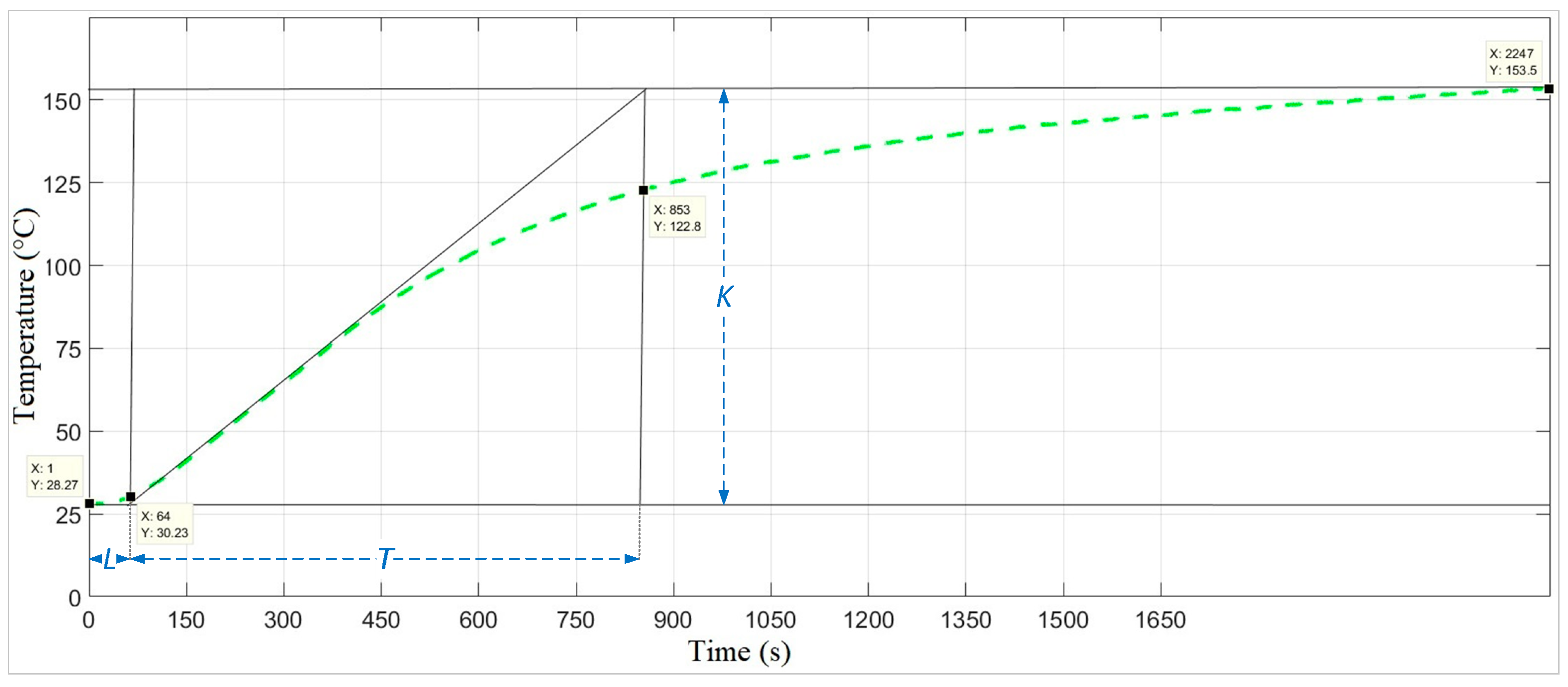
2.8. System Modeling and Determination of PID Parameters

The designed electric furnace was a first order plus dead time (FOPDT) system. Ziegler–Nichols step response method was used in modeling the furnace. In the system modeling, a unit step function was first applied to the system input. The system model was determined from the obtained output signal using the Ziegler–Nichols step response method. Figure 9 shows the output response of the system. Equation (13) was used when modeling the system using the Ziegler–Nichols step response method:

$$G(s)={\displaystyle \frac{K\times e^{-Ls}}{Ts+1}}$$

(13)

where K is the steady-state gain, L is the time delay, and T is the time constant. From the graph in Figure 8, K = 125.23, T = 789, and L = 64 are obtained. Using these values, the system model was determined, as given in Equation (14).

$$G(s)={\displaystyle \frac{125.23\times e^{-64s}}{789s+1}}$$

(14)

Figure 9. Step response of the system.

PID parameters were obtained using these coefficients (K, T, and L), as listed in Table 1.

Table 1. PID parameters found by the Ziegler–Nichols tangent method.

Controller	${\mathit{K}}_{\mathit{p}}$	${\mathit{K}}_{\mathit{i}}$	${\mathit{K}}_{\mathit{d}}$
P	${\displaystyle \frac{T}{L}}=12.3281$	$\infty$	$0$
PI	$0.9{\displaystyle \frac{T}{L}}=11.0953$	${\displaystyle \frac{{0.3K}_p}{L}}=0.0520$	$0$
PID	$1.2{\displaystyle \frac{T}{L}}=14.7937$	${\displaystyle \frac{K_p}{2L}}=0.1156$	${0.5K}_{p}L=473.4000$

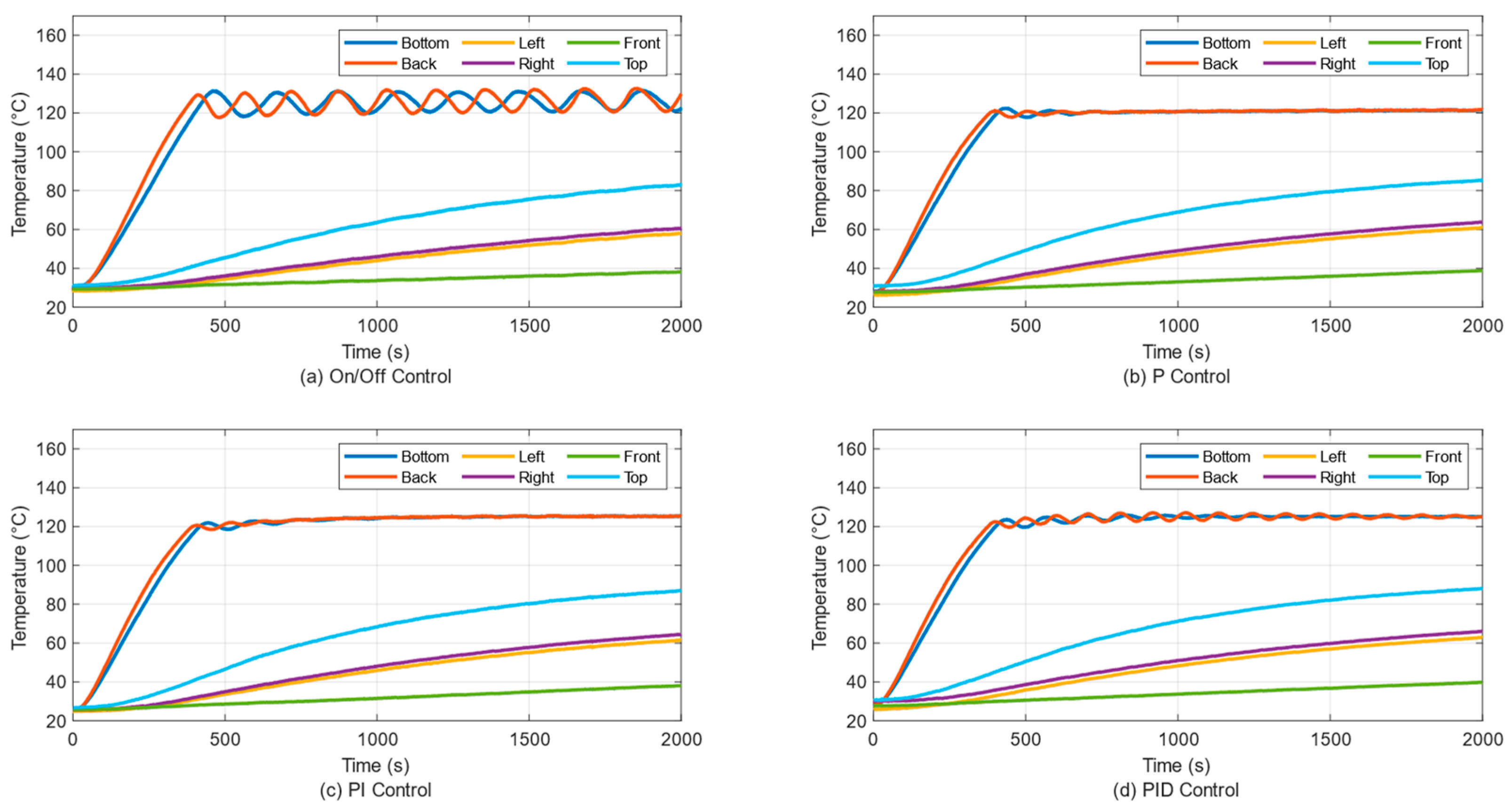
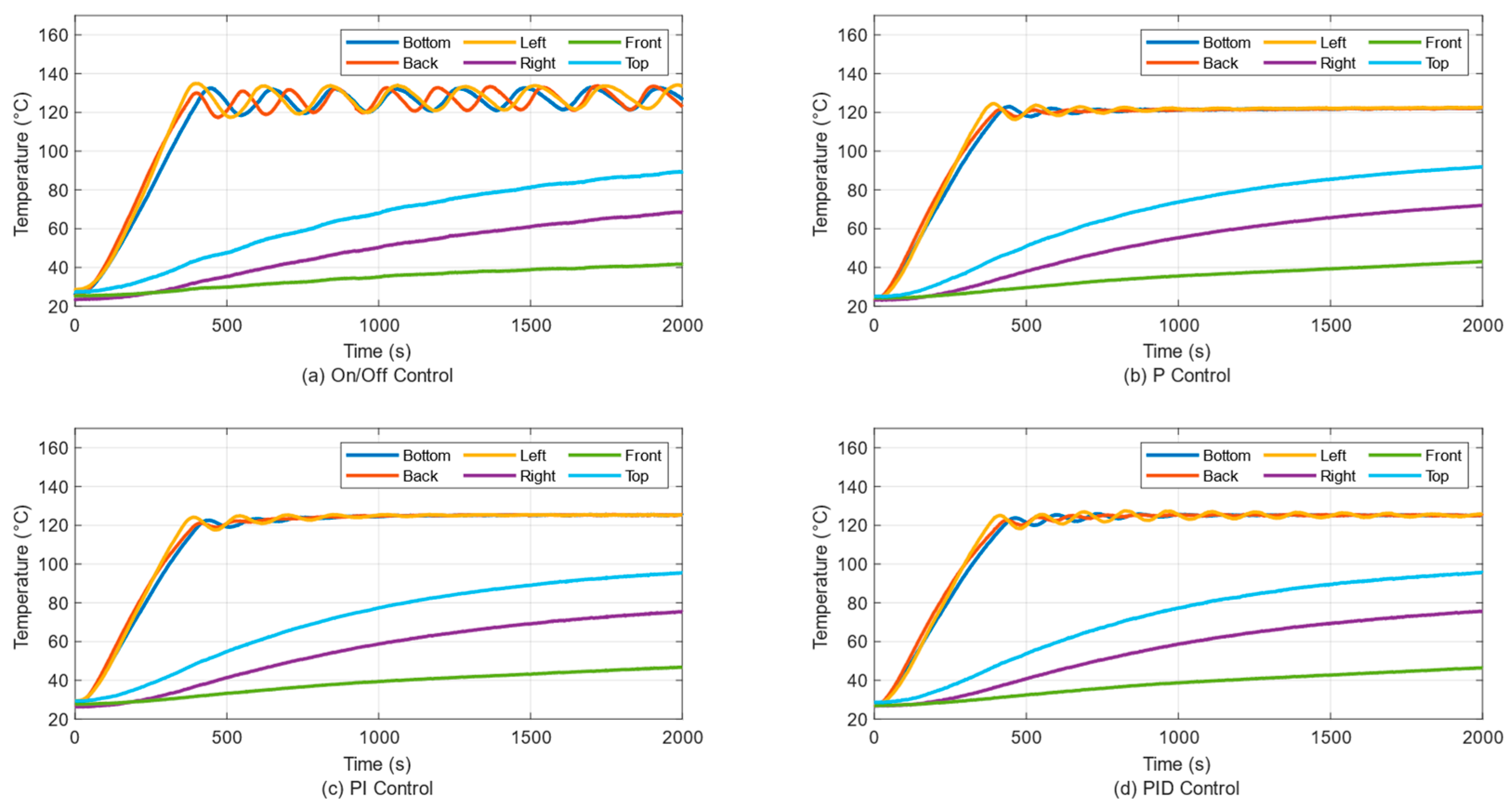
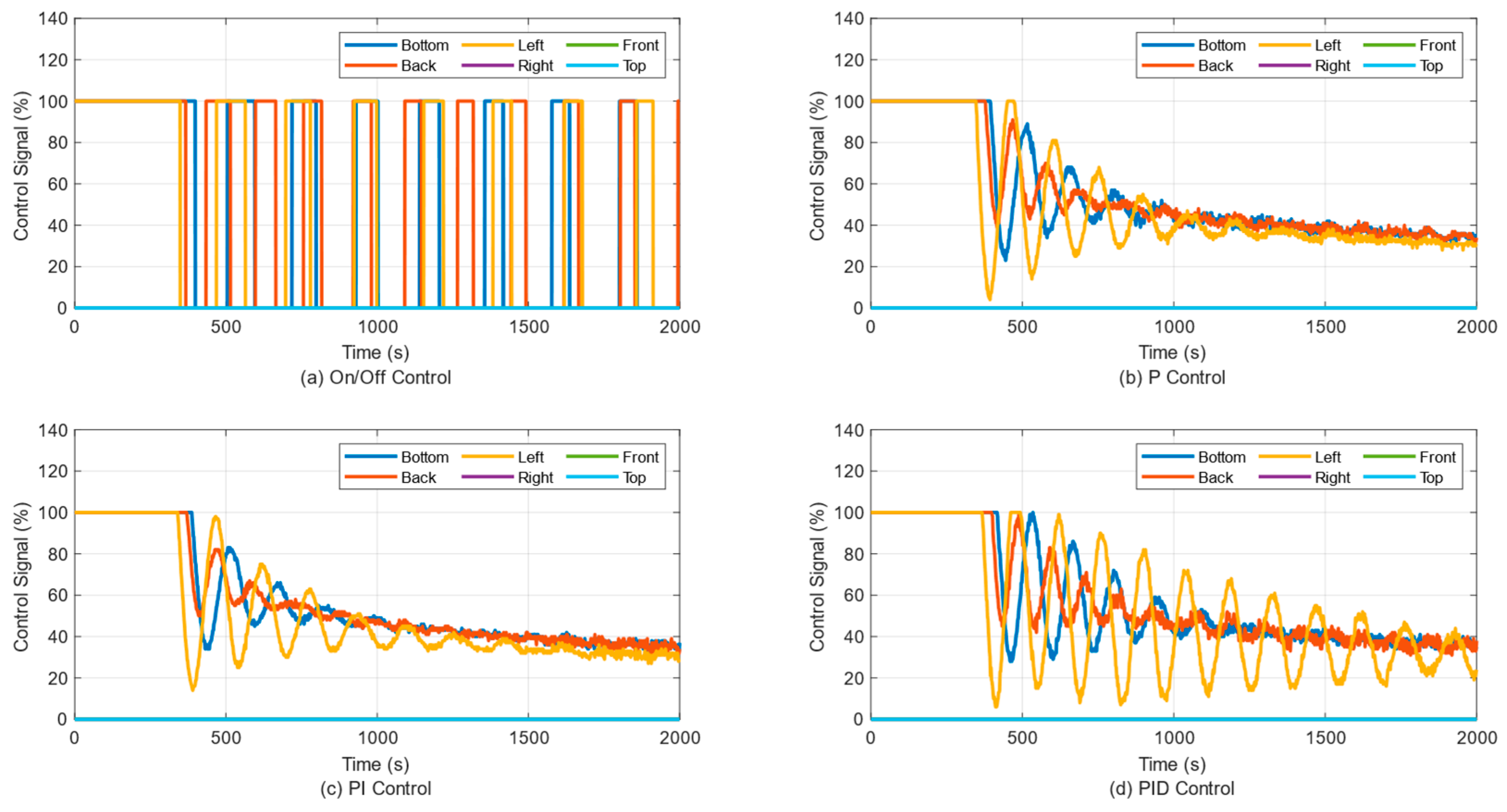
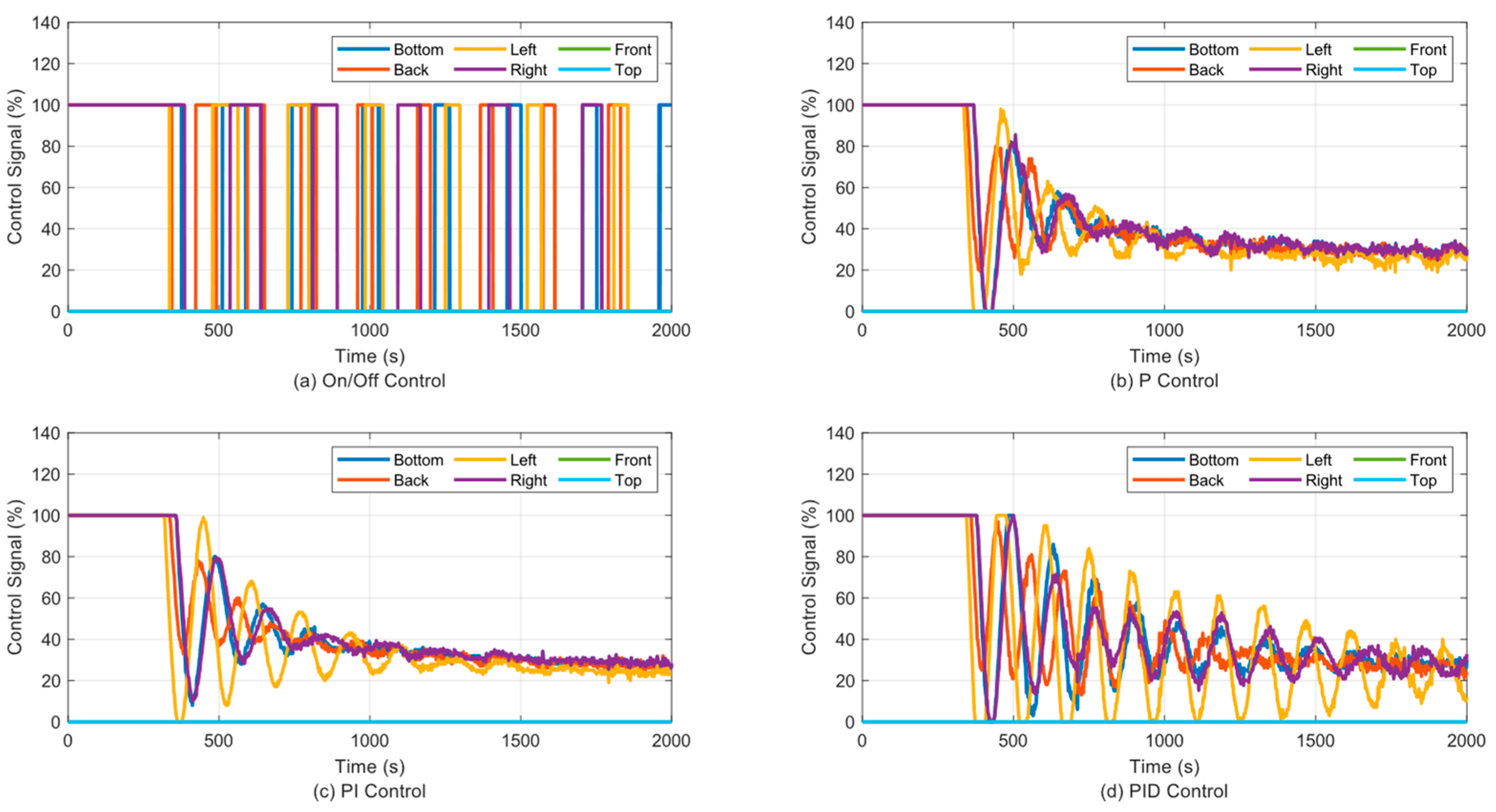
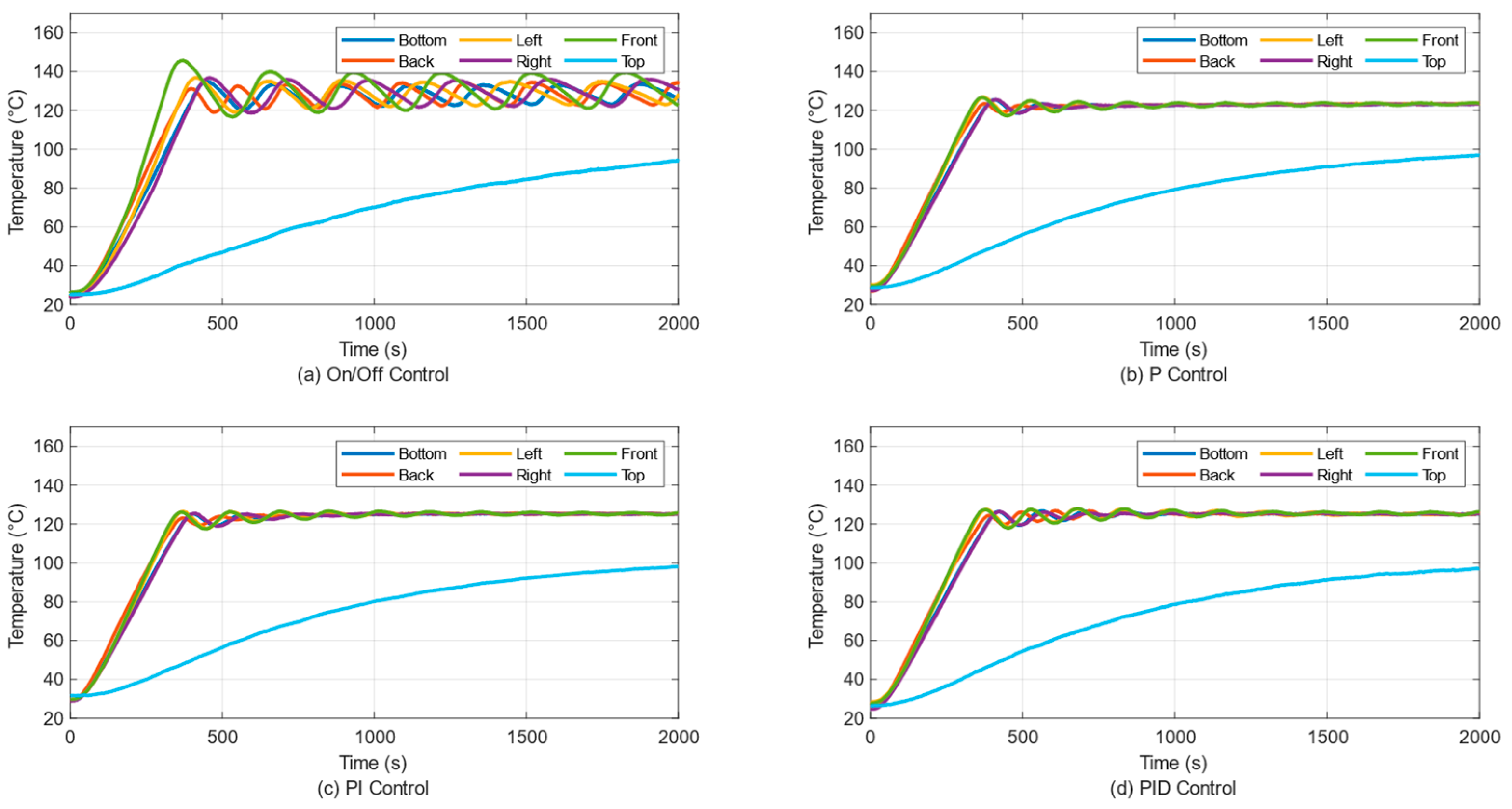
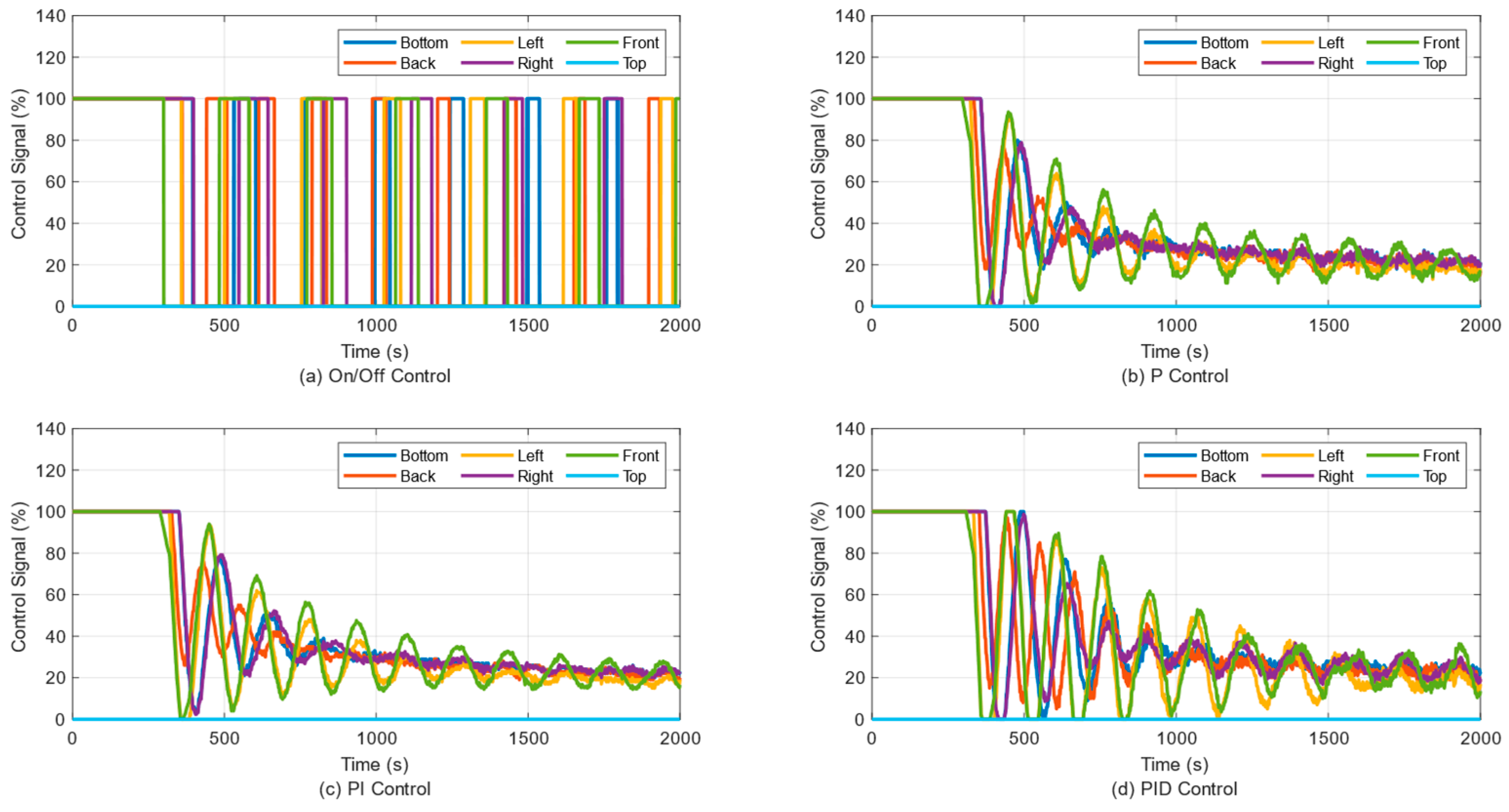
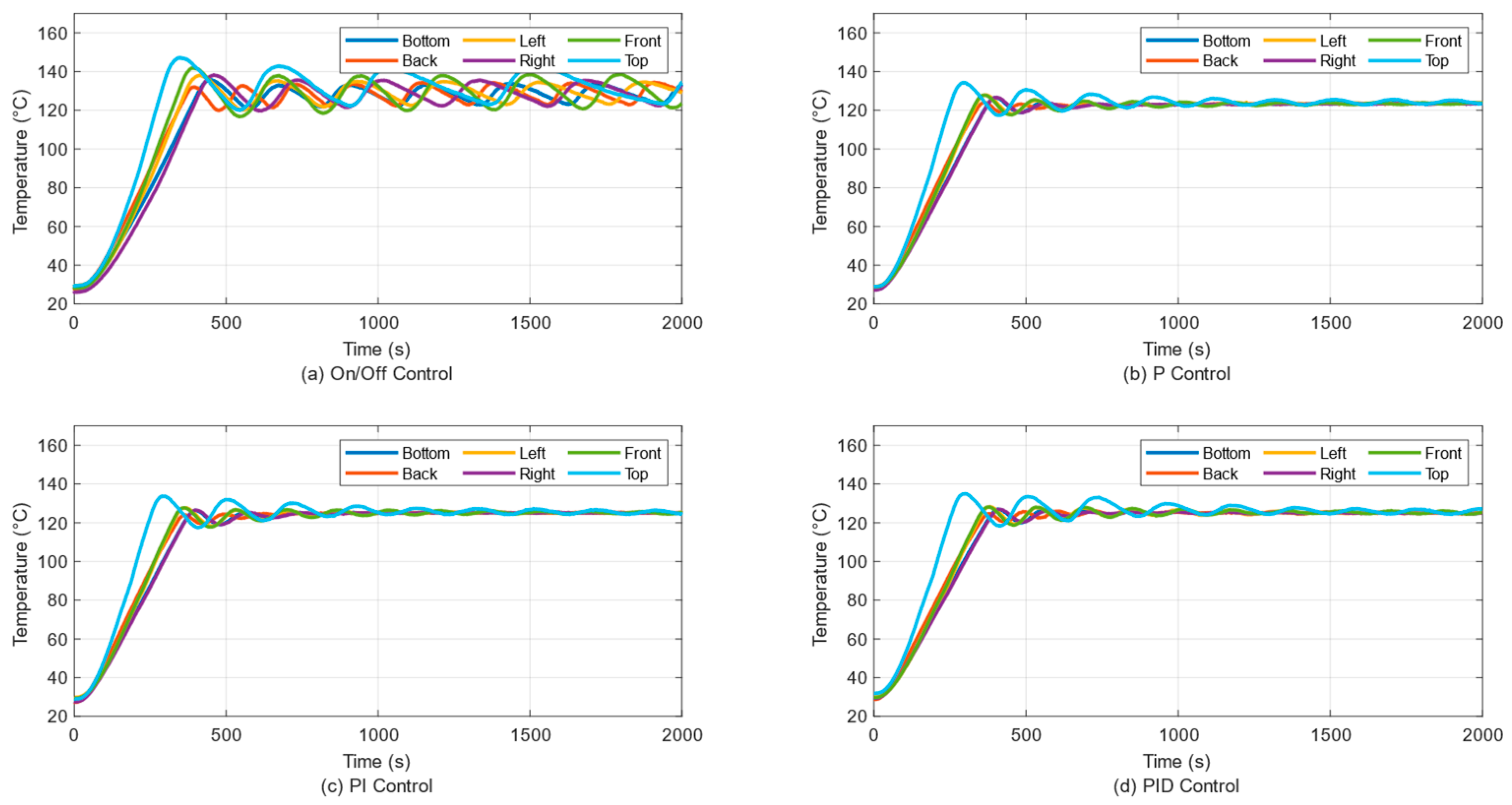
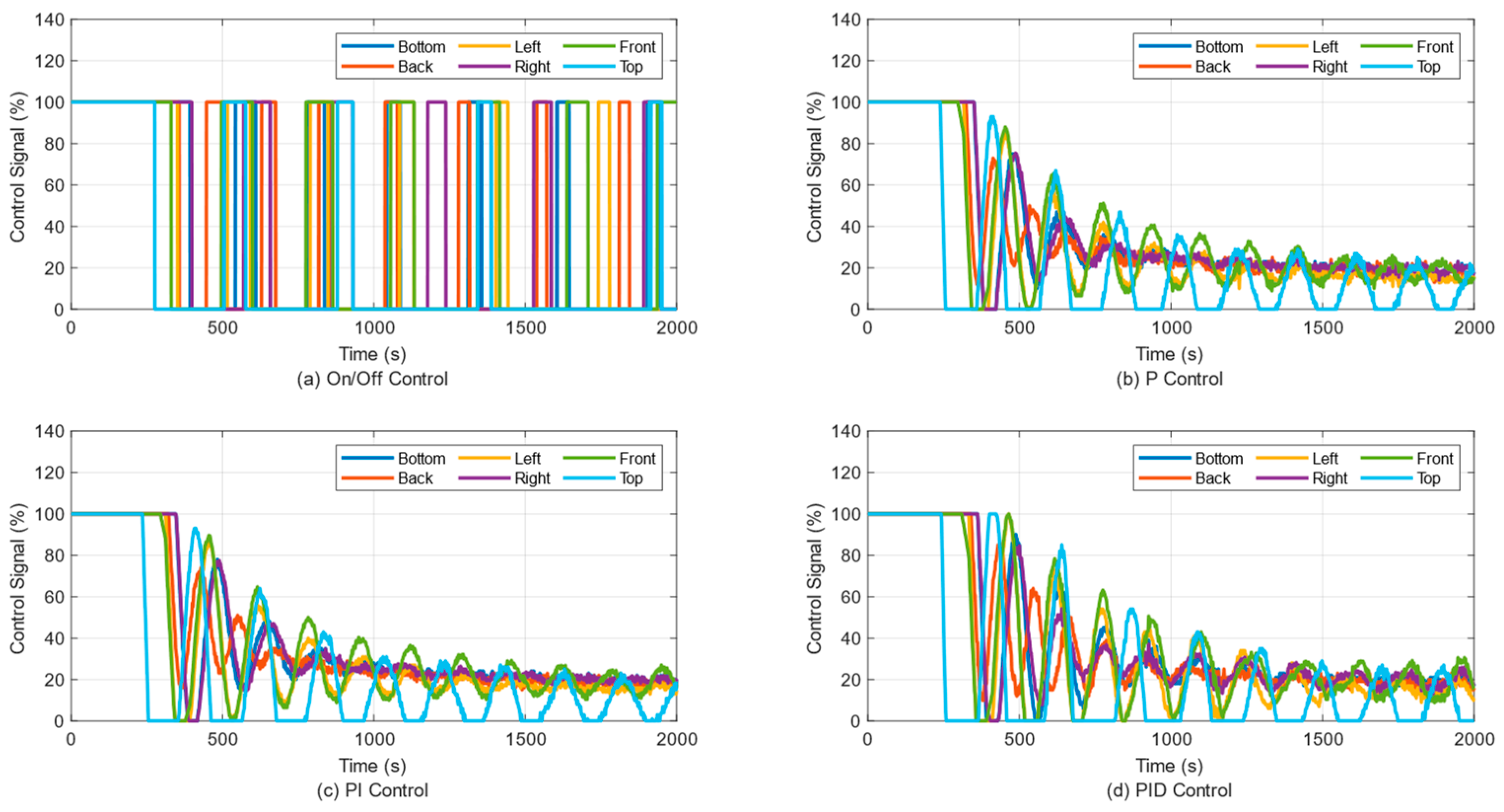
3. Results

In this section, the temperature control of the furnace designed for three-dimensional heating was presented, along with the obtained results. The reference temperature was set to 125 °C, and the gain factors of the P, PI, and PID controllers were considered, as shown in Table 1.

3.1. Temperature Control of a Single Panel

In this section, only the bottom panel was energized in the experimental results given. The temperature variations of the six panels are shown in Figure 10, and the control signals applied to the panels are shown in Figure 11. In Figure 10, it can be observed that, when the on-off control was applied, the panel temperature fluctuated around the reference temperature line. Additionally, it was observed that the P controller produced a steady-state error, whereas the steady-state error was significantly reduced by the PI and PID controllers.

Figure 10. Temperature change over time for a single panel.

Figure 11. Change in control signal over time for a single panel.

In Figure 10, it can be observed that, when only the bottom panel is energized, the temperatures of the other panels also change. In Figure 10, the temperatures of the right, left, front, and rear panels increased by less than 20 °C. However, the temperature of the top panel increased by approximately 50 °C. This was due to an increase in the heated air. In addition, the temperature distributions of the panels indicate that homogeneous heating is not possible with a single panel.

The performance metrics of the four control methods are presented in Table 2. For each control method, the error-area-based performance metrics (IAE, ISE, ITAE, and ITSE) were calculated and are listed in the table. As shown in Table 2, the lowest time rise was obtained with the on-off controller. This was because the bottom panel operated at full power until it reached the reference temperature. However, this led to an overshoot of 9.1877%. In addition, the system was stabilized in the shortest time with the P controller, and the least steady-state error was obtained with the PID controller. Finally, in terms of the performance criteria based on the error area, the best performance was achieved with the PI controller.

Table 2. Bottom panel temperature control performance values for a single panel case.

Metric.	On-off	P	PI	PID
Overshoot (%)	9.1877	0.5738	0.1117	0.3437
Settling Time (s)	-	575.1781	763.4308	721.9968
Rise Time (s)	351.1147	377.6131	397.2166	420.2006
Offset Error (°C)	-	4.7967	−0.3167	−0.1633
IAE	2.9070 × 104	3.0936 × 104	2.4179 × 104	2.4923 × 104
ISE	1.6953 × 106	1.5468 × 106	1.4908 × 106	1.6038 × 106
ITAE	1.0439 × 107	1.3410 × 107	4.7162 × 106	4.6175 × 106
ITSE	2.1521 × 108	2.1815 × 108	1.6447 × 108	1.8295 × 108

3.2. Temperature Control of Two Panels

The temperature changes in the panels when the bottom and back panels were energized are shown in Figure 12, and the control signals are shown in Figure 13. It was observed that, with the on-off control, the panel temperatures oscillated around the reference temperature, and the system did not stabilize. Additionally, it was found that the P controller stabilized the system but produced an offset error. Finally, this error was reduced to a negligible level when using the PI and PID controllers.

Figure 12. Temperature changes over time for two panels.

Figure 13. Change in control signal over time for the two panels.

When the bottom and rear panels were energized, the PI and PID controllers maintained temperature control at the reference value, as shown in Figure 12. Due to its greater geometric distance from the energized panels, the front panel experienced the least temperature change (less than 10 °C). The right and left panels, equidistant from the bottom and rear panels, respectively, showed a moderate temperature change (less than 35 °C). The top panel, owing to the rising heated air, experienced the most significant temperature change (less than 60 °C).

When two panels were energized, the temperature distribution inside the furnace was more homogeneous compared to when only one panel was energized, as presented in Figure 12. However, a significant temperature difference remained between the energized and non-energized panels, indicating that homogeneous heating was not achievable with only two panels.

As shown in Table 3 and Table 4, the lowest rise time was obtained with the P control. Additionally, in the on-off control, the overshoot at the panel temperatures exceeded 2%. Furthermore, the system stabilized in the shortest time with the P controller, and the least steady-state error was obtained with the PID controller. Finally, based on the error area criteria, the best temperature control performance was achieved using the PID controller.

Table 3. Bottom panel temperature control performance values for two panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	7.9623	0.7906	0.2714	0.5996
Settling Time (s)	-	532.1878	708.5739	654.1841
Rise Time (s)	357.5858	349.3789	376.0623	360.8522
Offset Error (°C)	-	3.5967	−0.3233	−0.1267
IAE	2.7860 × 104	2.8045 × 104	2.3880 × 104	2.2017 × 104
ISE	1.5948 × 106	1.4974 × 106	1.5620 × 106	1.4328 × 106
ITAE	9.6852 × 106	1.0698 × 107	4.3631 × 106	3.6342 × 106
ITSE	1.9986 × 108	1.8212 × 108	1.6442 × 108	1.4559 × 108

Table 4. Back panel temperature control performance values for two panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	2.3372	0.1973	0.3433	1.6223
Settling Time (s)	-	574.0770	695.5740	865.1587
Rise Time (s)	345.8092	323.5204	347.9466	334.2511
Offset Error (°C)	-	3.2300	−0.3967	−0.0967
IAE	2.6053 × 104	2.6270 × 104	2.2011 × 104	2.2007 × 104
ISE	1.4452 × 106	1.3633 × 106	1.4109 × 106	1.2948 × 106
ITAE	9.6810 × 106	1.0155 × 107	3.8344 × 106	4.1931 × 106
ITSE	1.7072 × 108	1.5396 × 108	1.3410 × 108	1.2013 × 108

3.3. Temperature Control of Three Panels

In the three-panel scenario, the bottom, back, and left panels were energized, and the temperature changes in the panels are shown in Figure 14, with the control signals presented in Figure 15. As with the single-panel and two-panel cases, the on-off controller caused the panel temperatures to oscillate around the reference value and failed to stabilize the system. Similarly, the P controller stabilized the system but produced a steady-state error. Finally, the PI and PID controllers, owing to their integral action, stabilized the system, with the steady-state error reduced to a negligible level. When the three panels were energized, the bottom, rear, and left panels reached the reference temperatures using the PI and PID controllers, as shown in Figure 14. Additionally, the front panel experienced minimal temperature change, the right panel experienced moderate temperature change, and the top panel underwent the greatest temperature change. However, a significant temperature difference remained between the energized and non-energized panels, indicating that homogeneous heating could not be achieved.

Figure 14. Temperature changes over time for the three panels.

Figure 15. Change in control signal over time for the three panels.

As shown in Table 5, Table 6 and Table 7, the lowest rise time was achieved with the on-off control for the back panel and P control for the bottom and left panels. Additionally, the P controller stabilized the system in the shortest time, and while the PID controller resulted in the smallest steady-state error. Based on the error area criteria, the PI controller exhibited the best performance.

Table 5. Bottom panel temperature control performance values for three panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	5.0079	0.7614	0.4558	0.6073
Settling Time (s)	-	673.1897	691.6205	682.4102
Rise Time (s)	361.9082	361.0085	368.9795	385.9637
Offset Error (°C)	-	2.8500	−0.2567	−0.1467
IAE	2.9077 × 104	2.8227 × 104	2.3052 × 104	2.3477 × 104
ISE	1.7029 × 106	1.6412 × 106	1.4952 × 106	1.5553 × 106
ITAE	1.0770 × 107	9.5687 × 106	4.0620 × 106	4.0002 × 106
ITSE	2.1882 × 108	1.9083 × 108	1.5704 × 108	1.6778 × 108

Table 6. Back panel temperature control performance values for three panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	8.8262	0.1718	0.2074	0.6003
Settling Time (s)	-	599.1459	630.2504	608.6277
Rise Time (s)	314.2285	341.1530	353.6272	365.1283
Offset Error (°C)	-	2.7033	−0.4200	−0.1333
IAE	2.6803 × 104	2.6719 × 104	2.1614 × 104	2.3477 × 104
ISE	1.5256 × 106	1.5022 × 106	1.3764 × 106	1.4116 × 106
ITAE	1.0314 × 107	9.2219 × 106	3.7212 × 106	3.5097 × 106
ITSE	1.8406 × 108	1.6386 × 108	1.3303 × 108	1.3969 × 108

Table 7. Left panel temperature control performance values for three panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	1.0405	1.8136	0.2393	1.5447
Settling Time (s)	-	766.1138	786.7241	1035.9697
Rise Time (s)	337.9090	321.5296	328.6221	346.8321
Offset Error (°C)	-	2.5367	−0.3733	−0.6700
IAE	2.8455 × 104	2.6468 × 104	2.1456 × 104	2.3239 × 104
ISE	1.5978 × 106	1.6014 × 106	1.4222 × 106	1.5214 × 106
ITAE	1.1433 × 107	8.5275 × 106	3.5903 × 106	4.7296 × 106
ITSE	2.0922 × 108	1.7149 × 108	1.3841 × 108	1.5530 × 108

3.4. Temperature Control of Four Panels

Regarding the bottom, back, left, and right panels energized, the temperature changes of the panels are shown in Figure 16, while the control signals are illustrated in Figure 17. In the on-off control, the temperatures of the four energized panels oscillated around the reference temperature. In contrast to the PI, and PID controls, the temperatures of the bottom, rear, left, and right panels reached the reference temperature with a lower steady-state error at 1 °C.

Figure 16. Temperature changes over time for the four panels.

Figure 17. Change in control signal over time for the four panels.

In Figure 16, the four energized panels reached the reference temperature with the P, PI, and PID controls. However, the front panel temperature was lower (less than 20 °C), and the upper panel was significantly affected (less than 75 °C) compared to the four energized panels. Additionally, there was a significant temperature difference between the four energized panels and two non-energized panels. Therefore, homogeneous heating could not be achieved using the four panels.

Table 8, Table 9, Table 10 and Table 11 indicate that the P controller stabilized the system in the shortest time, and the lowest offset error was obtained with the PI and PID controllers. Additionally, in terms of error-area-based performance metrics, PI control was the most successful control method.

Table 8. Bottom panel temperature control performance values for four panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	9.2270	2.4462	0.2476	1.4728
Settling Time (s)	-	538.1967	664.1534	650.8365
Rise Time (s)	335.8857	341.8926	344.7341	356.7687
Offset Error (°C)	-	2.3400	−0.2667	−0.0567
IAE	2.8414 × 104	2.5661 × 104	2.2098 × 104	2.3463 × 104
ISE	1.6260 × 106	1.4961 × 106	1.4898 × 106	1.6311 × 106
ITAE	1.0624 × 107	8.0850 × 106	3.5290 × 106	3.9511 × 106
ITSE	2.0860 × 108	1.6332 × 108	1.4974 × 108	1.6815 × 108

Table 9. Back panel temperature control performance values for four panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	7.0701	0.7673	0.2474	1.2218
Settling Time (s)	-	578.1557	588.5704	671.8252
Rise Time (s)	307.4825	317.3479	323.5048	335.9518
Offset Error (°C)	-	2.3600	−0.2833	−0.2833
IAE	2.6463 × 104	2.3921 × 104	2.0421 × 104	2.3463 × 104
ISE	1.4541 × 106	1.3506 × 106	1.3455 × 106	1.4751 × 106
ITAE	1.0846 × 107	7.5748 × 106	3.1565 × 106	3.3550 × 106
ITSE	1.8298 × 108	1.3625 × 108	1.2351 × 108	1.3856 × 108

Table 10. Left panel temperature control performance values for four panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	4.0446	3.1756	0.7587	1.7480
Settling Time (s)	-	633.7487	637.0141	1320.1805
Rise Time (s)	321.3823	314.7711	307.9014	328.5658
Offset Error (°C)	-	2.1100	−0.2067	−0.8933
IAE	2.8611 × 104	2.4332 × 104	2.0504 × 104	2.3473 × 104
ISE	1.5536 × 106	1.4393 × 106	1.3774 × 106	1.6043 × 106
ITAE	1.2279 × 107	7.2434 × 106	3.2667 × 106	4.8083 × 106
ITSE	2.1493 × 108	1.5034 × 108	1.2792 × 108	1.5809 × 108

Table 11. Right panel temperature control performance values for four panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	9.2256	2.6484	0.2572	1.5360
Settling Time (s)	-	546.6014	678.8034	644.2474
Rise Time (s)	353.7195	343.8626	348.8171	358.3697
Offset Error (°C)	-	2.3987	−0.2647	0.1333
IAE	3.2484 × 104	2.5915 × 104	2.2580 × 104	2.3782 × 104
ISE	1.8800 × 106	1.4969 × 106	1.5453 × 106	1.6627 × 106
ITAE	1.3662 × 107	8.1811 × 106	3.6565 × 106	4.1673 × 106
ITSE	2.7877 × 108	1.6724 × 108	1.5647 × 108	1.7326 × 108

3.5. Temperature Control of Five Panels

The temperature changes of the panels when the bottom, back, left, and right, and front panels were energized are shown in Figure 18, while the control signals applied to the panels are shown in Figure 19. Similarly, under the on-off control, the panel temperatures fluctuated around the reference temperature, and the system did not stabilize. However, with PI, and PID control, the panel temperatures approached the reference value with a steady-state error of less than 0.4 °C, achieving system stability.

Figure 18. Temperature changes over time for the five panels.

Figure 19. Change in control signal over time for the five panels.

The five energized panels increased the temperature of the unenergized top panel from 27 to 97 °C. However, this value remained significantly below the reference temperature, and homogeneous heating could not be achieved with the five energized panels.

In Table 12, Table 13, Table 14, Table 15 and Table 16, considering the error-area-based performance criteria, the PI controller demonstrated the best performance. Additionally, the temperature control stabilized in the shortest time with the P controller, as shown in Table 12 and Table 16. Moreover, the lowest offset error was achieved with the PI and PID controllers, as listed in Table 12, Table 13, Table 14, Table 15 and Table 16.

Table 12. Bottom panel temperature control performance values for five panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	6.8864	1.9232	0.3118	1.3189
Settling Time (s)	-	518.4043	649.5157	651.8311
Rise Time (s)	361.1103	335.5157	337.8383	352.1654
Offset Error (°C)	-	1.7033	−0.1700	−0.0967
IAE	3.0045 × 104	2.4512 × 104	2.1267 × 104	2.2727 × 104
ISE	1.7934 × 106	1.4813 × 106	1.4161 × 106	1.5761 × 106
ITAE	1.1215 × 107	6.8247 × 106	3.3421 × 106	3.6055 × 106
ITSE	2.3592 × 108	1.5542 × 108	1.4015 × 108	1.6089 × 108

Table 13. Back panel temperature control performance values for five panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	0.3358	0.0809	0.3033	1.3092
Settling Time (s)	-	572.0462	572.8060	669.4066
Rise Time (s)	349.0101	313.1541	313.5342	330.0963
Offset Error (°C)	-	1.3733	−0.3067	−0.2667
IAE	2.7857 × 104	2.2924 × 104	1.9485 × 104	2.2727 × 104
ISE	1.6099 × 106	1.3583 × 106	1.2718 × 106	1.4347 × 106
ITAE	1.0980 × 107	6.3262 × 106	2.9511 × 106	3.1997 × 106
ITSE	2.0345 × 108	1.3066 × 108	1.1359 × 108	1.3316 × 108

Table 14. Left panel temperature control performance values for five panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	7.2330	2.5981	1.0467	2.0366
Settling Time (s)	-	632.6726	641.9243	764.0194
Rise Time (s)	333.7219	305.3322	308.9633	315.4245
Offset Error (°C)	-	1.4267	−0.1967	−0.2900
IAE	3.0573 × 104	2.2663 × 104	2.0556 × 104	2.1643 × 104
ISE	1.8010 × 106	1.3821 × 106	1.3776 × 106	1.4480 × 106
ITAE	1.2116 × 107	5.9261 × 106	3.3005 × 106	3.8630 × 106
ITSE	2.4449 × 108	1.3561 × 108	1.2931 × 108	1.3910 × 108

Table 15. Right panel temperature control performance values for five panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	4.8207	2.0111	0.3861	0.8887
Settling Time (s)	-	526.5578	678.6200	652.6726
Rise Time (s)	377.7083	338.5213	340.4289	355.8225
Offset Error (°C)	-	1.7053	−0.1560	−0.3767
IAE	3.3652 × 104	2.4921 × 104	2.1695 × 104	2.3098 × 104
ISE	1.9995 × 106	1.5238 × 106	1.4555 × 106	1.6224 × 106
ITAE	1.4221 × 107	6.9302 × 106	3.4691 × 106	3.7520 × 106
ITSE	3.0393 × 108	1.6159 × 108	1.4632 × 108	1.6738 × 108

Table 16. Front panel temperature control performance values for five panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	18.9718	2.5273	0.8612	1.4391
Settling Time (s)	-	786.5390	794.1063	1072.0829
Rise Time (s)	273.6282	299.9921	303.6485	313.5332
Offset Error (°C)	-	1.3440	−0.6680	−1.2393
IAE	3.2293 × 104	2.2771 × 104	2.0684 × 104	2.1786 × 104
ISE	1.6467 × 106	1.3837 × 106	1.3584 × 106	1.4502 × 106
ITAE	1.6360 × 107	6.1959 × 106	3.7315 × 106	4.1781 × 106
ITSE	2.8573 × 108	1.3555 × 108	1.2596 × 108	1.3788 × 108

3.6. Temperature Control of Six Panels

Regarding all energized panels, the change in panel temperatures over time is shown in Figure 20, while the control signals are illustrated in Figure 21. Since the panels had a disruptive effect on each other, when all the panels were energized, the oscillations in the panel temperatures and control signals increased. Additionally, it took more time for the system to reach a steady state. These negative effects can be minimized by using advanced control algorithms. In practice, due to the non-homogeneous heating of electric furnaces, the temperature difference inside the furnace can rise to dozens of degrees. Considering this situation, it is clear that the performance of the applied control algorithm and system is within acceptable limits. The on-off controller could not stabilize the system, causing the panel temperatures to oscillate around the reference value. In contrast, the PI and PID controllers stabilized the system and reduced the steady-state error to below 1 °C. Figure 20 clearly shows that homogeneous heating can only be achieved when all panels are energized.

Figure 20. Temperature changes over time for the six panels.

Figure 21. Change in control signal over time for the six panels.

In Table 17, Table 18, Table 19, Table 20, Table 21 and Table 22, it can be observed that when the P controller was used, the electric oven was controlled with the lowest settling time, and the least offset error was obtained with the PI controller. In addition, considering the error-area-based performance criteria, the PI and PID controllers provide better performance.

Table 17. Bottom panel temperature control performance values for six panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	1.8538	2.5022	1.0712	1.5750
Settling Time (s)	-	516.0430	651.8739	642.2717
Rise Time (s)	379.0619	330.6310	334.5555	340.7141
Offset Error (°C)	-	1.5000	−0.1167	−0.1200
IAE	2.9482 × 104	2.3987 × 104	2.1419 × 104	2.1322 × 104
ISE	1.7019 × 106	1.4859 × 106	1.4589 × 106	1.4212 × 106
ITAE	1.0993 × 107	6.2694 × 106	3.2829 × 106	3.3071 × 106
ITSE	2.2735 × 108	1.5309 × 108	1.4408 × 108	1.4269 × 108

Table 18. Back panel temperature control performance values for six panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	3.7426	0.3235	0.4960	0.8309
Settling Time (s)	-	551.8600	561.9304	550.2113
Rise Time (s)	331.9288	303.5585	308.8958	319.2715
Offset Error (°C)	-	1.3367	−0.1100	−0.2100
IAE	2.7348 × 104	2.1961 × 104	1.9600 × 104	2.1322 × 104
ISE	1.5091 × 106	1.3254 × 106	1.3197 × 106	1.3137 × 106
ITAE	1.1283 × 107	5.6469 × 106	2.8590 × 106	2.8361 × 106
ITSE	1.9778 × 108	1.2350 × 108	1.1753 × 108	1.2061 × 108

Table 19. Left panel temperature control performance values for six panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	6.9812	3.4452	2.1416	2.4416
Settling Time (s)	-	635.3010	645.1251	633.5759
Rise Time (s)	331.6767	300.3843	302.6602	316.0528
Offset Error (°C)	-	1.2867	−0.2267	−0.3500
IAE	2.9958 × 104	2.2312 × 104	2.0346 × 104	2.1098 × 104
ISE	1.6442 × 106	1.4115 × 106	1.3761 × 106	1.4021 × 106
ITAE	1.2769 × 107	5.3787 × 106	3.1734 × 106	3.5626 × 106
ITSE	2.3502 × 108	1.3630 × 108	1.2817 × 108	1.3539 × 108

Table 20. Right panel temperature control performance values for six panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	4.0322	2.6106	1.1817	1.4640
Settling Time (s)	-	522.3131	529.8595	521.9867
Rise Time (s)	384.8076	332.1441	335.9745	343.9082
Offset Error (°C)	-	1.5020	−0.1220	−0.1573
IAE	3.2640 × 104	2.4271 × 104	2.1685 × 104	2.1595 × 104
ISE	1.9175 × 106	1.5144 × 106	1.4886 × 106	1.4567 × 106
ITAE	1.2911 × 107	6.3480 × 106	3.3314 × 106	3.3939 × 106
ITSE	2.8184 × 108	1.5736 × 108	1.4837 × 108	1.4806 × 108

Table 21. Front panel temperature control performance values for six panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	14.9077	3.3296	2.0154	2.1409
Settling Time (s)	-	789.0030	785.0673	783.4679
Rise Time (s)	299.0711	296.7176	299.5336	311.3349
Offset Error (°C)	-	1.2433	−0.2893	−0.4360
IAE	3.1624 × 104	2.2443 × 104	2.0666 × 104	2.1266 × 104
ISE	1.6508 × 106	1.4034 × 106	1.3701 × 106	1.3920 × 106
ITAE	1.5089 × 107	5.7110 × 106	3.6616 × 106	3.9728 × 106
ITSE	2.6743 × 108	1.3542 × 108	1.2672 × 108	1.3334 × 108

Table 22. Top panel temperature control performance values for six panel cases.

Metric	On-Off	P	PI	PID
Overshoot (%)	9.6546	8.8242	7.5569	6.2170
Settling Time (s)	-	1137.7823	1541.7901	1905.0788
Rise Time (s)	270.7276	227.7468	228.0005	235.2037
Offset Error (°C)	-	1.5733	0.4567	−0.9933
IAE	3.2113 × 104	1.8598 × 104	1.8538 × 104	1.9302 × 104
ISE	1.5196 × 106	1.1489 × 106	1.1376 × 106	1.0898 × 106
ITAE	1.6927 × 107	4.1039 × 106	4.1215 × 106	5.1115 × 106
ITSE	3.0048 × 108	8.9667 × 108	8.8455 × 108	9.1754 × 108

4. Conclusions

In modern electric ovens, heating is generally performed by placing heaters on the top and bottom surfaces. In some special ovens, a heater is placed on the back surface of the oven to provide three-dimensional heating. However, homogeneous heating cannot be achieved when heaters are placed on the top, bottom, and back surfaces of an electric oven. Additionally, since the oven temperature is measured from a single point, and the top, bottom, and back heaters are energized according to the same control signal, the temperature control error in such ovens can reach dozens of degrees Celsius. In this study, unlike similar studies, the design, analysis, production, and control of an innovative electric oven equipped with heaters and temperature sensors on six surfaces were carried out. The temperature of each of the six heaters on the six surfaces of the oven was measured separately and energized according to the six different control signals. Consequently, the temperature of each panel was maintained at the set reference temperature. The temperature control of the implemented unique oven was conducted using on-off, P, PI, and PID controllers. The oven heating model was derived using the Ziegler–Nichols tangent method. Using this system model, the gain factors of P, PI, and PID controllers were calculated and optimized. The experimental results demonstrated the accuracy of the obtained system model and optimized gain factors.

When the experimental results were examined, it was observed that, with on-off control, the panel temperature fluctuated around the reference value, and the system could not reach stability. In contrast, the system achieved stability with the P, PI, and PID controllers. The P controller generally produced a steady-state error, whereas the PI and PID controllers reduced the steady-state error to below 0.7 °C in the case of one, two, and three energized panels, and to below 1.3 °C in the case of four, five, and six energized panels.

The temperature control of the implemented oven was carried out for one, two, three, four, five, and six panels. The experimental results revealed that homogeneous heating was not possible unless all six panels were energized, and temperature control was applied. Therefore, it is not possible to achieve homogeneous heating with modern electric ovens that provide three-dimensional heating, as used today. This result is a novel contribution to the literature.

Finally, each of the six heaters were energized and de-energized at the zero crossings of the mains voltage. By switching the heaters when the main voltage was 0 V, the sudden surges in current from the mains and noise generation on the mains were prevented.

The system model of the implemented furnace and gain factors of the PID controller were obtained using the Ziegler–Nichols open-loop method. In future studies, the system model can be derived using linear system identification methods, such as autoregressive-moving average, autoregressive moving average with exogenous variables, and output error models, or nonlinear system identification methods, such as artificial neural networks, fuzzy jogic models, and support vector machines. Subsequently, the PID weighting factors can be optimized using metaheuristic optimization methods. Furthermore, a PT100 temperature sensor was used for the temperature measurements in the furnace. To reduce the effects of contact and cable resistance on the temperature measurement, a PT1000 temperature sensor can be used, and a low-noise operational amplifier circuit can be implemented to improve measurement accuracy. Finally, when multiple panels were energized in this study, they were powered simultaneously and de-energized based on the control signal. To obtain a more homogeneous current from the grid, a power management strategy can be applied to energize the panels sequentially in each control cycle.