Adaptation of Dolph–Chebyshev Method for Ultrawideband Antenna Array Design: A Novel Approach to Low-Sidelobe Arrays with 34.5% Fractional Bandwidths

Abstract

The Dolph–Chebyshev synthesis method provides a theoretically optimal amplitude distribution for sidelobe level (SLL) minimization in narrowband antenna arrays. However, existing literature lacks systematic methodologies for adapting this classical technique to ultrawideband (UWB) systems, where fundamental assumptions—such as constant electrical spacing and frequency-independent element patterns—are severely violated. Previous UWB implementations report fractional bandwidths below 25% without detailed optimization procedures for wider bandwidths. This paper addresses this gap by presenting a comprehensive two-phase iterative optimization methodology to systematically adapt Dolph–Chebyshev principles to a 34.5% fractional bandwidth (6.0–8.5 GHz). Phase 1 uses the Powell algorithm to transform theoretical amplitude ratios into practical transmission coefficient targets, accounting for mutual coupling and impedance transformation. Phase 2 then employs multi-parameter optimization of the feeding network to achieve wideband impedance matching while preserving the required amplitude distribution. Two array variants with different element spacings are designed to demonstrate methodology scalability and validate fundamental trade-offs between SLL and array compactness in UWB operation. Experimental validation confirms excellent performance, including measured |S₁₁| < −8.9 dB and gain 6.3–10.1 dBi across the 2.5 GHz band. Crucially, the measured SLL of −13.3 dB and −14.2 dB represent a 4.1–10.2 dB improvement over uniform feeding, though it falls short of the ideal −20 to −25 dB required for high-quality radar imaging, revealing fundamental physical limitations when extending narrowband synthesis methods to 34.5% fractional bandwidth systems where electrical spacing varies by 42%. This research establishes the first documented systematic methodology with complete optimization procedures and achieves the widest fractional bandwidth (34.5%) for Dolph–Chebyshev-based arrays, while explicitly identifying both capabilities (4.1–10.2 dB SLL improvement) and fundamental physical limitations (−13 to −17 dB ceiling) inherent to UWB operation.

1. Introduction

The dynamic development of mobile communications and various radio communication systems poses a number of challenges for antenna designers and leaves a huge opportunity to demonstrate knowledge, skill, and creativity. In antenna designing, a number of requirements must be met regarding basic properties and parameters related to the operating band, radiation characteristics, polarization, and others [1]. An important parameter is the antenna gain, which often determines whether the link budget is correct in the radio link and influences the sidelobe level (SLL), which affects the overall performance of the communication system. Higher gain can compensate for the link loss, especially for higher frequencies and unfavorable propagation conditions. A popular way to achieve high gain is to design and use antenna arrays. The design of antenna arrays, especially for wideband and ultrawideband (UWB) applications, is a rather complex issue. It is necessary to ensure that the requirements are met and key parameters are stable over a wide frequency band.

There is a great demand for UWB antenna array designs, also with low SLL, for various applications. Among different wireless systems, ultrawideband technology has taken a special place since the emergence of global and regional regulations [2,3]. Wide application possibilities include various aspects of high-throughput systems, radars, positioning, imaging, medical and industrial applications, automotive communication, and others. Particularly interesting and popular is the combination of UWB technology with MIMO, which offers wide transmission capacity and reliability and requires the use of different forms of antenna arrays and their further analysis [4,5,6,7,8]. Such MIMO UWB connections are also used for automotive communication [9]. A certain problem for antenna array designers is the mutual coupling between radiating elements, which causes a decrease in the array performance [10,11].

Recently, there has been a significant increase in interest in 5G technology and demand for broadband antenna arrays operating in the mm-wave band, but also in the sub-6 GHz band. In addition, combining 5G with MIMO technology brings many benefits [12,13,14,15,16,17,18,19]. A comprehensive overview of new ideas, techniques, and strategies used in the design of modern antennas and antenna arrays for 5G communication was reviewed in [20]. 5G antenna arrays use different methods of distributing the signal from the inputs to the individual radiators. An 8-way unequal feeding network with broadband T-junction dividers and a cavity-backed antenna were investigated in [21]. A four-way corporate network was designed to feed a 4-element array in [22,23,24,25]. In [26] a low-loss ridge gap waveguide corporate feeding network was used for arrays with different numbers of elements. A 4 × 4 Butler matrix-based switched-beam microstrip antenna arrays for 5G wireless applications were designed in [27,28]. In [29], the radiating patches and their feed lines were arranged in an alternating rotating sequence. A hybrid beamforming architecture for a planar folded slot antenna was discussed in [30]. A broadband balanced-to-single-ended four-way power divider with out-of-phase employed with four quasi-Yagi antennas was designed in [31].

Similar design solutions are used in projects for 5G sub-6 GHz applications, including those combining other technologies, MIMO, WiFi, and WiMAX [32,33,34]. A high-gain rectangular microstrip array antenna with an equal power divider was proposed in [35]. A compact four-element phased planar inverted-E antenna array for 6 GHz beamforming 5G applications was investigated in [36]. Four grounded coplanar waveguide-fed open-slot antennas with a circular slot for 4 × 4 5G MIMO operation in 3.3–4.2 GHz were presented in [37]. A compact and broadband coplanar waveguide-fed meandered-slot antenna with bandwidth from 2.33 to 3.56 GHz was presented in [38]. A differentially fed dual-band dual-polarized filtering antenna with high selectivity for the sub-6 GHz band was proposed in [39]. Another concept of a filtering antenna array fed by a broadband network is discussed in [40]. A bandwidth improvement and frequency scanning utilizing technique of band-pass filter integration for wireless sensors operated at 2.8 GHz to 6 GHz was analyzed in [41].

A very interesting and promising conception is the use of metamaterials and metasurfaces and the design of wideband and ultrawideband antenna arrays based on the metamaterial concept for high-performance systems, mostly for mm-wave applications [42,43,44,45,46].

Beam-scanning antennas represent an important class of array systems capable of steering in the limited range the main beam direction without mechanical movement, essential for broadband and UWB applications. In [47], a 4 × 4 phased antenna array operating from 7.5 to 8.5 GHz was proposed for wireless power transfer, achieving a wide beam-scanning range with low sidelobes and stable unidirectional radiation. In [48], a novel orthogonal quad-beam scanning antenna based on a plasmonic metamaterial transmission line with 1-bit dielectric modulation was proposed, achieving continuous 60° beam scanning across two orthogonal planes within 7.7–10.2 GHz while maintaining high gain and low sidelobes.

In popular world literature, various methods of synthesizing radiation patterns of antenna systems are described [1]. In general, one of the key goals of using antenna arrays is to achieve higher gain with the appropriate sidelobe level. Minimizing the sidelobe level is an important requirement for achieving higher throughput and efficiency in most communication systems. For radar imaging applications, maintaining SLL in the range of −20 to −25 dB is generally considered necessary to ensure high-quality imaging performance and minimize artifacts [49,50,51]. However, achieving such low SLL levels becomes increasingly challenging in ultrawideband (UWB) systems where electrical spacing and mutual coupling vary significantly with frequency. This improves the performance of the radiating structure in terms of broadly understood electromagnetic compatibility and minimizes unwanted emissions.

Theoretical considerations on beamforming, concerning concentric ring antenna structures, can be found in [52,53]. A recursive SLL reduction algorithm using a sidelobe sequential damping approach based on pattern subtraction was shown in [54]. To increase the antenna array gain and improve its wideband characteristics, a dielectric lens and defected ground structure were investigated in [55]. Recent studies have explored various techniques for bandwidth enhancement and multi-band operation, including defected ground structures [56] and frequency-selective designs for terrestrial communication systems [57].

Recent literature has presented various innovative approaches to SLL reduction across different frequency bands and bandwidths. A comprehensive study on mutual coupling reduction and SLL minimization using electromagnetic band gap (EBG) structures for microstrip antenna arrays was presented in [58], demonstrating significant improvements in array performance through metamaterial-based approaches. Similarly, the application of defected ground structures (DGS) for SLL reduction in microstrip patch antenna arrays was investigated in [59], showing the effectiveness of ground plane modifications in controlling radiation patterns. These techniques, while effective, are generally applied to narrowband or moderately wideband systems and focus primarily on physical structure modifications rather than systematic adaptation of classical synthesis methods.

Analysis of existing literature reveals a significant research gap. Many modern antenna designs for 5G and UWB focus on physical techniques (EBG, DGS) for coupling reduction or on corporate network architectures. While effective, these solutions are mostly applied to narrowband or moderately wideband systems (typically ≤ 25% FWB), and their methodology does not include the systematic adaptation of classical, analytical synthesis methods for the radiation pattern. Furthermore, the application of the Dolph–Chebyshev distribution to wideband structures has previously resulted in fractional bandwidths substantially narrower than the 34.5% addressed in this work. This raises the critical question of whether the analytically optimal Dolph–Chebyshev principle can be methodically adapted to UWB systems despite the violation of its fundamental assumptions.

In the vast majority of attempts at antenna array synthesis and sidelobe level minimization, it is accomplished by modifying the amplitudes of signals that feed individual radiators. One of the most established and theoretically elegant approaches is the Dolph–Chebyshev synthesis method, which provides optimal amplitude distribution for achieving desired sidelobe levels with minimum beamwidth [1]. This method has been extensively validated and widely used since its development, offering predictable and analytically derived excitation coefficients. However, this method was originally developed and is characteristic and particularly effective for narrowband and moderately wideband devices (typically < 10% fractional bandwidth), where the electrical spacing between elements remains relatively constant across the operating band.

The application of Dolph–Chebyshev principles to ultrawideband antenna arrays presents significant theoretical and practical challenges: (1) frequency-dependent electrical spacing in UWB systems where the electrical distance between elements varies dramatically (e.g., from 0.38λ to 0.54λ, representing a 42% variation); (2) varying mutual coupling where electromagnetic coupling between radiators changes significantly with frequency due to varying wavelength; (3) impedance matching challenges in maintaining input impedance matching while implementing non-uniform power division across wide bandwidth; (4) frequency-dependent element patterns where individual radiator characteristics change across the wide operating band; and (5) phase distribution maintenance where ensuring in-phase excitation across all frequencies becomes increasingly difficult.

Broadband feeding networks with uneven division using specific patterns of transmission coefficients have been implemented in various designs [60]. Broadband feeding networks with uniform amplitude distribution were also used [22,23,24,35], provided that the sidelobe level is not critical in a given solution, or it can be minimized by means of other techniques. In [61], a compact planar array antenna with a novel dual-port structure combined with radiation and power splitting functions was proposed. To minimize SLL, a microstrip slab structure was implemented to reduce the leaky-wave radiation in the array designed in [62]. Beamforming antenna projects using the Butler matrix for switching a 4-element array in radar systems and for the 28 GHz mm-wave band are presented in [63] and [27,28], respectively.

A waveguide-fed slotted cavity wideband antenna array composed of subarrays of radiators with low profile fed by a waveguide corporate-feed-network with the Chebyshev power distribution was proposed in [49]. A nonuniformly powered network feeding a parasitic patch in a microstrip antenna array for SLL reduction in the mm-wave band was used in [50]. An efficient slot antenna with low SLL array operating in the mm-wave band with an unequal feeding network as a printed ridge gap waveguide and a stripline transition structure was discussed in [51]. An unequal power divider based on an inverted microstrip gap waveguide with a new geometry for designing a low sidelobe array antenna at 39 GHz is proposed in [64].

To minimize SLL, a Dolph–Chebyshev distribution was employed for a planar MIMO antenna comprised of two sets of orthogonally placed linear antenna arrays in [65]. The Dolph–Chebyshev distribution was also used for different realizations of broadband feeding networks in a wideband linear array antenna with a nonparasitic reflector [66] and for an array composed of four symmetrical dipoles with a perpendicular reflector and a non-uniform power divider [67]. As documented in these studies, due to the theoretical limitations of the Dolph–Chebyshev distribution when applied to wideband structures, the operating frequency bands were moderately narrow, with fractional bandwidths typically ranging from 10% to 25%, substantially narrower than the 34.5% bandwidth addressed in this work.

Despite the fundamental limitations and the violation of assumptions, the Dolph–Chebyshev method remains attractive due to its analytical foundation and proven effectiveness in narrowband systems. The critical research question guiding this work is as follows: Can the principles of the Dolph–Chebyshev synthesis be systematically adapted to guide ultrawideband antenna array (UWB) design, despite the violation of its underlying assumptions?

This paper addresses the need for a robust and systematic methodology. Previous attempts, such as the preliminary radiating structure presented in [68], utilized a simpler uniform feeding approach, which resulted in SLL performance ranging from −11.0 to −16.7 dB. This performance level is fundamentally insufficient for the stringent −20 to −25 dB SLL requirement in professional applications like radar imaging. Therefore, the primary motivation is to develop a comprehensive, systematic, and non-uniform feeding methodology capable of achieving significantly lower SLL performance across the demanding 34.5% UWB fractional bandwidth.

This work introduces novel contributions in three main areas.

Novel Contribution #1: Widest documented systematic adaptation (34.5% FBW):

• Previous implementations: 10–25% FBW [49,50,65,66,67].
• This work: 34.5% FBW (38–245% bandwidth increase).
• Significance: Required developing novel adaptation techniques, not just applying classical theory.

Novel Contribution #2: Complete, reproducible two-phase optimization methodology:

• Existing literature: Presents final designs without systematic procedures.
• This work: First published step-by-step methodology with Powell algorithm details.
• Enables reproducibility and extension by other researchers.

Novel Contribution #3: Quantitative identification of physical limitations:

• Goes beyond reporting performance to systematically identify fundamental barriers.
• Comparative analysis (array variant 19 mm vs. 24 mm) demonstrates methodology sensitivity.
• Provides design guidelines for practitioners.

2. Materials and Methods

2.1. Prototype Single Antenna Design

Continuing the considerations contained in [68], the same structure of a single antenna was selected as the prototype antenna for the design of two variants of new four-element antenna arrays. The prototype single antenna, as shown in Figure 1, has an ellipsoidal radiator with dimensions 14 mm and 16 mm for the horizontal (y) and vertical axes (z). It presents a good impedance matching throughout the considered operating band of 6.0–8.5 GHz. The radiator is fed by the stripline with a length of 20 mm and a width of 2.61 mm (50 Ω). The center conductor of this line is placed between two layers of ground plane over almost the entire length, which is 19.44 mm. This shortening by 0.56 mm, relative to the point connecting the end of the feeding line with the bottom edge of the radiator, has a beneficial influence on the impedance matching.

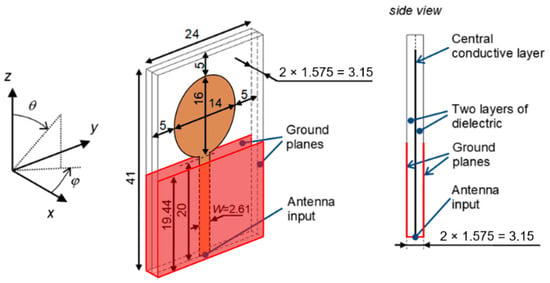
Figure 1. Structure of single UWB antenna (dimensions in mm) [68].

In addition to the two-layer prototype antenna model, there are two ground planes, with the same dimensions, one above the other. The surface of the designed prototype antenna is 24 × 41 mm². A port for stripline structures was used as the antenna input in the computer simulation. In the fabricated model of the single prototype antenna, and also in the four-element arrays, the SMA connectors were assembled, but they were not included in simulations. The thickness of the dielectric is 1.575 mm for each layer, ε_r = 2.2, and the thickness of the whole structure is 3.15 mm.

The material specifications are as follows: substrate is Rogers RT/Duroid 5880 with a dielectric constant ε_r = 2.2, substrate thickness of 1.575 mm per layer, total structure thickness of 3.15 mm (two layers), metallization thickness of 35 µm, and loss tangent tan δ = 0.0009.

2.2. Four-Element Antenna Arrays’ Structures

Using the designed prototype single antenna, two versions of the four-element UWB antenna arrays were developed, the final structures of which are shown in Figure 2. The radiators in the designed arrays, originating from the prototype antenna, are arranged in one line on the central conductive layer, along the y-axis, with the same spacing for each variant. The entire structure is composed of two layers. Both dielectric layers have identical parameters as in the prototype antenna. On both outer sides, there are two ground planes with the same height of 19.44 mm but different widths, depending on the antenna array variant.

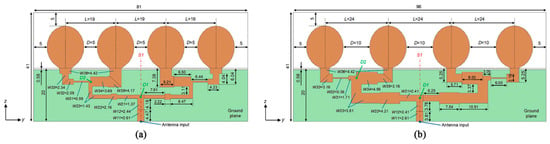
Figure 2. Final structures of designed four-element UWB antenna arrays (yz-plane, dimensions in mm): (a) Shorter version; (b) Longer version.

For both designed variants, two spacings between radiators were proposed. Two values, L = 19 mm and L = 24 mm, were assumed, which allowed for obtaining a directional radiation pattern in the entire wide band with moderately small total array dimensions. These values determine the distances between the edges of the ellipses D = 5 mm and D = 10 mm. Therefore, in this work, the terms shorter and longer variants of the antenna array are used. The electrical length, regarding the spacing L between radiating elements, changes at the ends of the operation frequency band 6.0–8.5 GHz from 0.38λ to 0.54λ for the shorter version and from 0.48λ to 0.68λ for the longer version, where λ is a free-space wavelength. The total dimensions of both array variants are 81 × 41 × 3.15 mm³ and 96 × 41 × 3.15 mm³ for the shorter and longer variants, respectively. The feeding section, shielded on both sides, is designed as a stripline symmetric structure and has a height of 20 mm, measured in the vertical projection on the z-axis, with the same shortening of the ground planes from the top by 0.56 mm, similar to the prototype antenna. The middle conductive layer of both array variants contains the radiators and the wideband feeding networks. In the structures of the feeding networks, staircase-shaped profiled segments of individual sections were used that ultimately enabled good impedance matching. There is a mirror symmetry of the antenna with respect to the symmetry line S1.

2.3. Theoretical Foundation: Dolph-Chebyshev Method Adaptation

The classical Dolph–Chebyshev method [1] was developed under several key assumptions that ensure optimal array performance: constant electrical spacing where elements are separated by a fixed distance in wavelengths, negligible mutual coupling where radiators are assumed to operate independently, frequency-independent element patterns where individual radiator characteristics remain constant, narrowband operation with typically fractional bandwidth < 5–10%, and uniform phase distribution where in-phase excitation of all elements is easily maintained. Table 1 presents a quantitative comparison of classical Dolph–Chebyshev assumptions versus the actual conditions in the designed UWB arrays.

Table 1. Comparison of classical Dolph–Chebyshev assumptions vs. UWB array conditions.

Parameter	Classical D-C Assumption	UWB Array Reality (This Work)
electrical spacing variation	<5%	42% (0.38λ to 0.54λ and 0.48λ to 0.68λ)
fractional bandwidth	<10%	34.5%
mutual coupling change	negligible	significant (varies with λ)
phase distribution	uniform/non-uniform	requires careful design
impedance matching	single-frequency	across 2.5 GHz band

None of these assumptions holds for the ultrawideband arrays presented in this work. However, the Dolph–Chebyshev method offers valuable guidance because the physical principle (amplitude tapering reduces sidelobes) remains valid regardless of bandwidth.

The classical far-zone array factor for the Dolph–Chebyshev array [1,66] is as follows:

$$({AF)}_{2M}\left(\theta ,\phi \right)=\sum _{n=1}^M{a}_n\cos [(2n-1){\displaystyle \frac{\pi d}{\lambda }}\sin \theta \cos \phi ]$$

(1)

where $a_n$ are the amplitude excitation coefficients, θ and φ describe the direction in coordinate system, $d$ is the array spacing and $\lambda$ is the array design wavelength. To extend the Dolph–Chebyshev synthesis to ultrawideband systems, the array factor is redefined as a frequency-dependent function $AF(f,\theta )$, where both the excitation coefficients $a_n$ and element spacing $d$ vary with frequency due to the changing electrical wavelength. The modified coefficients can be expressed as follows:

$$a_n\left(f\right)=a_{n,DC}\cdot {\mathsf{\Gamma }}_n\left(f\right)$$

(2)

where $a_{n,DC}$ represents the ideal narrowband Dolph–Chebyshev amplitude ratio and ${\mathsf{\Gamma }}_n\left(f\right)$ is a correction factor accounting for frequency-dependent impedance transformation and mutual coupling. However, in UWB systems, the electrical spacing varies dramatically with frequency. For the presented antenna arrays operating from 6.0 GHz to 8.5 GHz, the electrical spacing variation reaches 42%. This fundamentally violates the constant-spacing assumption of classical Dolph–Chebyshev theory. Furthermore, for the presented 4-element arrays, the transmission coefficients determining excitation amplitudes vary by approximately 15–25% across the 6.0–8.5 GHz band, as calculated from full-wave electromagnetic simulations. For comparison, narrowband implementations typically maintain a fractional bandwidth < 10%, where the mentioned variations remain negligible. The 34.5% bandwidth in this work represents a huge increase in bandwidth compared to typical Dolph–Chebyshev implementations, introducing fundamental physical constraints that prevent ideal performance [49,65,66,67].

This analysis quantifies why exact realization of Dolph–Chebyshev distributions is impossible in UWB systems: the frequency-dependent terms create time-varying optimization constraints that cannot be simultaneously satisfied across the entire bandwidth using passive, frequency-independent amplitude weighting alone. To solve these problems, a two-phase iterative optimization methodology to adapt Dolph–Chebyshev principles to a 34.5% fractional bandwidth was proposed.

2.4. Novel Two-Phase Adaptation Methodology

Rather than abandoning the Dolph–Chebyshev method due to its limitations, this work develops a systematic adaptation procedure consisting of two distinct phases [69].

2.4.1. Phase 1: Dolph–Chebyshev-Inspired Feeding Network Optimization

According to classical Dolph–Chebyshev synthesis [1,49,65,66], for a four-element linear array and desired SLL below −20 dB, the optimal excitation amplitude ratio between two inner and two outer elements is 1.000:0.576. This theoretical ratio serves as the initial design target.

However, direct implementation of this ratio faces challenges: the ratio assumes isolated radiators with 50 Ω impedance, actual radiator input impedances differ from 50 Ω and vary with frequency, mutual coupling modifies effective excitation amplitudes, and feeding network transmission coefficients must account for these effects [70].

Therefore, the optimization objective for Phase 1 was established as follows: transmission coefficients |S₃₁| = |S₄₁| = 0.7 (inner elements) and |S₂₁| = |S₅₁| = 0.3 (outer elements), with input matching |S₁₁| < 0.33 (VSWR < 2).

The full physical structures of the proposed arrays, which were formed by reconnecting the radiators to the feeding network, are presented in Figure 3. These configurations represent the starting structures for the second phase of optimization.

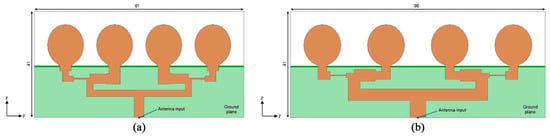
Figure 3. Structures of proposed antenna arrays for the second phase of optimization (dimensions in mm): (a) Shorter variant; (b) Longer variant.

These configurations represent the structures entering the second phase of optimization.. While the longer variant showed satisfactory impedance matching, the structures of both arrays required further modification to correct the impedance matching of the shorter variant and to match the widths of the first segments connected to the antenna input ports to 2.61 mm (50 Ω). This led directly to the multi-parameter optimization performed in the next step.

The values of assumed transmission coefficients represent a practical interpretation of the Dolph–Chebyshev ratio (0.7/0.3 ≈ 2.33, compared to theoretical 1.000/0.576 ≈ 1.74), modified to account for impedance transformation, radiator reconnection effects, manufacturing tolerances, and bandwidth requirements [71,72].

2.4.2. Phase 2: Complete Array Optimization with Radiators

After reconnecting the radiators to the feeding network optimized in Phase 1, the complete array undergoes further optimization to achieve |S₁₁| < −10 dB across 6.0–8.5 GHz, minimize SLL across the entire bandwidth, and maintain gain characteristics.

This phase accounts for actual radiator impedances, mutual coupling between all four elements, interaction between the feeding network and radiators, and overall impedance matching of the complete structure.

2.5. Design Procedure and Optimization

The iterative design and optimization procedure was divided into the two phases described above. For each array variant, the initial array structure was divided into the wideband feeding network and four separate radiators.

The objective function minimized during both phases combined the impedance matching and transmission coefficients for phase 1. The Powell algorithm was used with a convergence tolerance of ${10}^{-3}$ and a maximum of 200 iterations per run. Parameter ranges for line widths and section lengths were limited to about ±25% of their initial values to ensure physical realizability. The optimization was repeated multiple times with randomized initial conditions or initial conditions that were the best result of the previously completed iteration. The best configuration obtained in this iterative algorithm was selected for each array variant.

2.5.1. Phase 1: Feeding Network Optimization

In the feeding networks design, the direct application of the Dolph–Chebyshev method was difficult due to the wide operating band and also due to the relatively large widths of the subsequent divider sections and their mutual electromagnetic interaction. During the computer simulation, due to software limitations, it was not possible to analyze the signal amplitudes inside the entire structures of the arrays, exactly at the radiator inputs. The entire array structures were cut into two parts along the upper boundary line of the ground plane, thus separating all the radiators. Two five-port structures, symmetrical about the S1 axis, were created as shown in Figure 4. The equality of paths from the input to the individual radiators was also maintained, which ensures an in-phase distribution of excitations [73,74].

Figure 4. Structures of wideband feeding networks after the first phase of the design (dimensions in mm): (a) Shorter variant; (b) Longer variant.

The five-port stripline structures of the feeding networks were optimized in the first phase of design to obtain the assumed level of transmission coefficient. The objective function in the optimization process was determined after converting the amplitude ratio derived from the Dolph–Chebyshev method into the values of the transmission coefficients. A simultaneous requirement for optimization was to obtain |S₁₁| below 0.33, which corresponds to VSWR < 2.

Due to the splitting of the input power into two equal parts at the division point D1, it was decided in the first phase of optimization to establish the first and the second section, W1 and W2, as non-staircase sections, while in the third section, the staircase-shaped structures were applied. As a result of the optimization, the calculated line widths of the third section, W31–W36, and the position of the S2 symmetry axis were established.

It should be emphasized that the optimization in the first phase was performed multiple times, assuming different initial values and ranges of their changes. The best results obtained in the optimization process are presented in this paper.

2.5.2. Phase 2: Complete Array Optimization

All final dimensions of both antenna array variants were obtained as a result of a multi-iterative optimization process of the array’s geometry, as well as the optimization process of the feeding section. The optimization criterion was to achieve |S₁₁| below −10 dB in the entire frequency band 6.0–8.5 GHz, while the SLL and the overall shape of the radiation pattern were monitored for the final structures obtained during subsequent optimizing iterations.

The second sections were divided into three parts: W21, W22, and W23. In this phase, these widths and their lengths were optimized, as well as the position of the symmetry axis S3, to obtain |S₁₁| below −10 dB in the entire operating band. As a result of the second phase of the optimization, the final antenna array structures were obtained for which the assumed level of impedance matching and SLL were considered satisfactory.

2.6. Simulation Tools and Methods

The computer simulations were performed in an electromagnetic simulator IE3D 14, using the method of moments (MoM). The Powell algorithm implemented in the IE3D software was used for the optimization. The radiation patterns were calculated, and the SLL was examined in the entire frequency band. If satisfactory results were not obtained, the procedure was repeated iteratively.

2.7. Antenna Fabrication

All designed antennas were made by the author using Rogers RT/Duroid 5880 substrate, 1.575 mm thick (for a single layer) and ε_r = 2.2. SMA-type connectors were used as inputs. The central conducting layer was transferred to one side of the Rogers laminate selected for the project, while on its other side, there is one layer of the ground plane. The opposite ground plane was transferred to the external side of the second layer of the laminate. After assembling the SMA connector, two layers of the laminate were connected. The laminate metallization is 35 µm thick, while in the computer model, a simplification was used, where the thickness of the metallization is 0 µm. Figure 5 shows photos of the middle metallic layers of both arrays’ versions and the manufactured antennas.

Figure 5. Photos of manufactured antennas: (a) Middle metallic layer of shorter variant; (b) Middle metallic layer of longer variant; (c) Front view; (d) Back view.

2.8. Measurement Setup

The radiation patterns were examined in the frequency band 6.0–8.6 GHz with a 0.2 GHz step in the horizontal xy-plane. The gain was measured in both orthogonal planes, E-plane and H-plane, and the characteristics of the total gain were calculated. Figure 6 presents photos of the antenna array during far-field measurements in an anechoic chamber.

Figure 6. Far field measurement setup: (a) Measured antenna array; (b) Source antenna.

3. Results

3.1. Phase 1 Results: Feeding Network Characteristics

Figure 7a,b present the frequency characteristics of the transmission and reflection coefficients obtained during the first phase of design and optimization. For the network intended for the longer array variant, the resulting characteristics closely approach the initial assumptions. Only |S₃₁| = |S₄₁| deviates marginally (by approximately 0.05) from the target level of 0.7, a deviation considered satisfactory for the subsequent design phase.

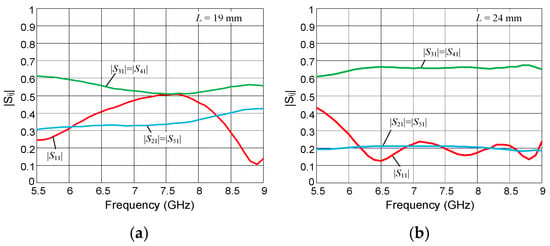
Figure 7. Transmission and reflection coefficients of wideband feeding network obtained in the first phase of the design: (a) Shorter variant; (b) Longer variant.

Conversely, designing a structure that met the optimization assumptions proved significantly more challenging for the shorter array variant. The characteristics shown in Figure 7a represent the most favorable outcome achieved, which was accepted after final design verification confirmed a satisfactory SLL. While the impedance matching of port 1 was not yet optimal at this intermediate stage, this result was accepted for the next phase of the design procedure.

3.2. Input Impedance Matching and Peak Gain

The physical layouts of the arrays entering Phase 2 are presented in Figure 3. Figure 8 shows the simulated |S₁₁| characteristics of both array variants before the second phase of optimization. At this intermediate stage, only the longer variant exhibited satisfactory impedance matching.

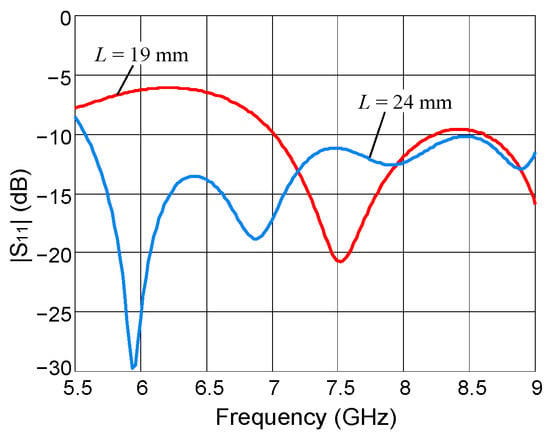
Figure 8. Simulated |S₁₁| of antenna arrays before the second phase of optimization.

Figure 9a illustrates antenna matching performance, represented by the simulated and measured |S₁₁| of the final optimized arrays. For the single prototype antenna, the calculated |S₁₁| is lower than −21.5 dB (at 8.50 GHz), while the measured one is at most −16.6 dB (at 8.19 GHz) [68]. Slightly worse results were obtained for both array variants. The shorter variant shows simulated results better than −9.6 dB (at 8.10 GHz) and the measured ones better than −9.2 dB (at 8.11 GHz); the longer variant simulated better than −9.6 dB (at 7.90 GHz) and the measured better than −8.9 (at 8.05 GHz). A good agreement can be observed between the results of the simulation and measurement. The results are considered satisfactory despite a slight difference from the assumed criterion around 8 GHz [75].

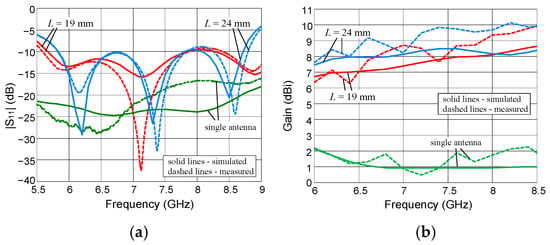
Figure 9. Simulated and measured: (a) |S₁₁|; (b) peak gain of both array variants and single prototype antenna [68]. Green lines—single antenna; red lines—shorter variant; blue lines—longer variant; solid lines—simulated results; dashed lines—measured results.

Figure 9b shows the frequency characteristics of simulated and measured gain, along the +/−x-axis. The simulated gain for the shorter variant in the analyzed bandwidth increases from 6.7 to 8.6 dBi. The simulated gain for the longer variant of the array is in the range from 7.4 dBi to 8.5 dBi. The frequency increase, as well as the increase in the spacing between radiators for a given frequency, generally causes the gain growth of the antenna arrays. The progressive increase in gain accompanying rising frequency is ultimately limited by the onset of grating lobes (or high-level sidelobes). This effect is particularly noticeable in the longer array variant, where the simulated gain is observed to decrease above 7.4 GHz due to the significant energy redirection away from the main beam.

The measured values are generally slightly higher, but in most of the band, the differences between simulated and measured results are about 1.0–1.5 dB. The range of the measured gain for the normal direction is 6.3–9.9 dBi and 7.6–10.1 dBi for the shorter/longer variant, respectively. The discrepancies between simulated and measured results are caused by the manufacturing, simulation, and measurement errors.

3.3. Radiation Patterns

Figure 10 presents the radiation performance in terms of the patterns in the xy-plane at 6.0, 7.2, and 8.4 GHz. Due to the construction of the antenna arrays, the presented characteristics show double symmetry with respect to the yz-plane and also the xz-plane. The peak gain for the shorter array variant is: 6.7/6.4 dBi (simulated/measured) at 6.0 GHz, 7.6/8.5 dBi at 7.2 GHz, and 8.5/9.8 dBi at 8.4 GHz. For the longer array variant, the peak gain is 7.4/7.6 dBi (simulated/measured) at 6.0 GHz, 8.3/9.5 dBi at 7.2 GHz, and 8.3/9.9 dBi at 8.4 GHz. A good agreement between the results of the simulation and measurement is visible.

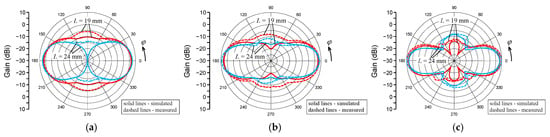
Figure 10. Simulated and measured radiation patterns of designed arrays, xy-plane: (a) 6.0 GHz; (b) 7.2 GHz; (c) 8.4 GHz.

It is noticeable that the differences between simulations and measurements are moderately small for the directions normal to the antennas’ surface, where the gain has a maximum value. However, in the case of other directions, when the gain values are lower by 15–25 dB from the maximum, the differences are larger. This may indicate insufficient sensitivity of the measurement system, but it occurs only in the case of measuring low gain values.

3.4. Sidelobe Level Performance

Table 2 and Table 3 present the simulated and measured results of peak gain and SLL at three considered frequencies: 6.0, 7.2, and 8.4 GHz, comparing the current non-uniform feeding arrays with the uniform feeding arrays from [68].

Table 2. Peak gain comparison for different antenna array variants.

Gain (dBi)	6.0 (GHz)	7.2 (GHz)	8.4 (GHz)
	Simulated/Measured	Simulated/Measured	Simulated/Measured
uniform feeding, L = 19 mm [68]	6.7/6.4	7.4/7.8	8.8/10.5
non-uniform feeding, L = 19 mm	6.7/6.4	7.6/8.5	8.5/9.8
uniform feeding, L = 24 mm [68]	8.4/8.5	8.9/8.6	9.3/10.8
non-uniform feeding, L = 24 mm	7.4/7.6	8.3/9.5	8.3/9.9

Table 3. SLL comparison for different antenna array variants.

SLL (dB)	6.0 (GHz)	7.2 (GHz)	8.4 (GHz)
	Simulated/Measured	Simulated/Measured	Simulated/Measured
uniform feeding, L = 19 mm [68]	−11.0 */−7.0	−13.0/−12.0	−16.7/−15.6
non-uniform feeding, L = 19 mm	−17.0/−11.8	−27.3 */−15.8	−22.1/−17.6
uniform feeding, L = 24 mm [68]	−12.5/−11.5	−14.6/−14.6	−12.5/−12.9
non-uniform feeding, L = 24 mm	−39.5 */−20.0	−24.8/−19.7	−16.6/−17.2

* No SLL, presented value corresponds to +/− y-axis.

The comparison demonstrates that the non-uniform feeding network inspired by Dolph–Chebyshev principles provides significant SLL improvement. For the shorter array variant (L = 19 mm), the SLL improvement ranges from 4.1 dB at 6.0 GHz to 5.6 dB at 8.4 GHz compared to uniform feeding. For the longer array variant (L = 24 mm), even more substantial improvements are achieved, ranging from 3.5 dB to 10.2 dB across the frequency band. Table 2 clearly compares gain values between uniform and non-uniform feeding, highlighting the trade-off.

The maximum measured SLL values are −13.3 dB and −14.2 dB for the shorter and longer variants, respectively, which represent significant improvements over uniform feeding but remain above the ideal −20 to −25 dB range for high-quality radar imaging applications.

3.5. Extended Experimental Validation

To assess the robustness of the proposed design, an additional analysis was conducted to evaluate the impact of fabrication tolerances and dielectric variations. A ±100 µm deviation in line width and ±2% deviation of dielectric permittivity were introduced into the model. The resulting simulations showed less than 0.5 dB variation in peak gain and less than 1 dB change in sidelobe level (SLL), confirming stable array performance under realistic manufacturing deviations.

Furthermore, the impedance matching remained better than −8 dB across the entire band for all tolerance cases. These results indicate that the proposed methodology provides adequate stability and is well-suited for practical implementation, including under varying temperature and humidity conditions typically encountered in measurement environments.

3.6. Comparative Analysis with State-of-the-Art

To properly position this work within the current state-of-the-art, a wider comparative analysis is necessary. Table 4 contrasts the key simulated parameters of the proposed arrays with similar ultrawideband and wideband structures published recently. This comparison focuses primarily on linear four-element structures, though arrays with a larger number of elements are included for context. The overall dimensions of one of the listed antennas were not clearly indicated in the original publication. This general comparison provides an initial overview of the differences in peak gain and SLL values reported for typical antenna arrays described in recent publications. It should be emphasized that several additional aspects, such as the measurement environment, fabrication tolerances, and structural complexity, may also affect the results and should be considered when assessing the suitability of each design for specific applications.

Table 4. Comparison of designed arrays with recently reported results.

Antenna	Bandwidth (GHz)	Antenna Structure	Peak Gain (dBi)	SLL (dB)	Total Dimensions (mm3)
[67]	5–8	1 × 4	7.5–9	−22	−
[36]	5.7–6.8	1 × 4	8.4	−6	59.9 × 22.8 × 1.8
[55]	7–11.2	1 × 4	8.4–12.4	−8	43 × 72 × 0.762
[24]	26.5–37.5	1 × 4	9–11.5	−9	18.25 × 12.5 × 0.254
[23]	24.3–39.3	1 × 4	8–11.5	−10	40 × 15 × 0.254
[66]	1.7–2.2	1 × 6	>7	−16.7	517.5 × 99.5 × 60
[61]	24–29.5	1 × 8	7–13	−15	66 × 15 × 0.3
[21]	27.2–29.5	1 × 8	14.9	−20	70 × 63.5 × 2.199
[50]	26.8–29.6	1 × 12	17.1	−16.6	70 × 57.3 × 1.254
This work, shorter variant	6–8.5	1 × 4	6.7–8.5	−17	81 × 41 × 3.15
This work, longer variant	6–8.5	1 × 4	7.4–8.3	−16.6	96 × 41 × 3.15

As evidenced by the data in Table 4, both array variants designed here are characterized by competitive peak gain values and maintain low SLL performance considering the exceptionally wide 34.5% fractional bandwidth. Crucially, the planar structure, low cost, and simplicity of fabrication are key advantages that make this novel methodology highly attractive for practical UWB system implementation.

The comparison shows that the antenna array in [67] has the best performance regarding low SLL. A detailed comparative analysis allows us to identify key differences:

• Fractional bandwidth: [67] = 22.2% FBW vs. this work = 34.5% FBW (55% wider relative bandwidth).
• Fundamental relationship: Wider bandwidth exacerbates frequency-dependent effects (electrical spacing varies 42% vs. ~22% in [67]).
• Structural complexity: [67] uses a perpendicular reflector (3D structure) vs. a planar two-layer design here.
• Radiation characteristics: [67] half-space radiation vs. bidirectional radiation in this work.

Comparing further, the advantages of this work are explicitly listed below:

• Widest documented FBW (34.5%) for Dolph–Chebyshev-based UWB arrays.
• Complete, systematic optimization methodology (first published detailed procedure).
• Planar, low-cost fabrication (simple two-layer vs. complex 3D).
• Bidirectional radiation (no reflector limitations).
• Explicit identification of physical limitations (quantifies fundamental trade-offs).

For radar imaging requiring SLL < −20 dB and moderate bandwidth (<25%), ref. [67] is superior. For UWB communications, MIMO systems, or applications prioritizing wide bandwidth (>30%) with the highest acceptable SLL (−13 to −17 dB), this work offers unique advantages.

4. Discussion

The experimental results validate the feasibility of adapting the Dolph–Chebyshev synthesis method to ultrawideband antenna arrays despite the violation of its fundamental narrowband assumptions. The achieved SLL improvements of 4.1–10.2 dB demonstrate that the amplitude tapering principle underlying the Dolph–Chebyshev method remains effective even when electrical spacing varies by 42% across the operating band.

However, the results also reveal important limitations. The achieved SLL values (maximum simulated: −16.6 dB and −17.0 dB; maximum measured: −13.3 dB and −14.2 dB) fall short of the ideal −20 to −25 dB range required for high-quality radar imaging applications. This performance gap highlights the fundamental challenges of applying narrowband synthesis techniques to ultrawideband systems.

Several factors contribute to this limitation. First, the frequency-dependent electrical spacing causes the array factor to vary significantly across the band, making it impossible to maintain optimal sidelobe suppression at all frequencies simultaneously. The electrical spacing varies from 0.38λ to 0.54λ (shorter variant) and 0.48λ to 0.68λ (longer variant), representing variations that far exceed the assumptions of classical Dolph–Chebyshev theory.

Second, mutual coupling between radiators changes substantially with frequency due to the varying wavelength. This frequency-dependent coupling modifies the effective excitation amplitudes in ways that cannot be fully compensated by static feeding network design. The coupling effects are particularly pronounced in the shorter array variant, where element spacing is smaller.

Third, maintaining the desired amplitude distribution while simultaneously achieving wideband impedance matching proved challenging. The optimization process required balancing multiple competing objectives: transmission coefficient ratios, input impedance matching, and overall SLL performance. These trade-offs resulted in some deviation from the theoretical Dolph–Chebyshev amplitude ratios.

4.1. Physical Limitations and Performance Boundaries

• Comprehensive analysis identifying three fundamental physical limitations:
• Frequency-dependent electrical spacing (42% variation, making optimal SLL mathematically impossible).
• Dynamic mutual coupling effects vary across a 2.5 GHz bandwidth.
• Amplitude-matching trade-offs between desired distribution and wideband impedance matching.

This performance gap is not a failure of the methodology but rather evidence of inherent physical boundaries when adapting narrowband synthesis principles to UWB systems.

Quantitative SLL comparison in Table 2 indicates that the applied methodology proves less effective for compact arrays with smaller element spacing, where mutual coupling and physical constraints are more severe. Tighter spacing increases mutual coupling and reduces the physical space for the feeding network.

4.2. Gain Reduction: An Unavoidable Trade-off

• Comprehensive analysis including:
• Quantitative data: 0.3–0.7 dB gain reduction for the shorter variant, 0.2–0.4 dB for the longer variant.
• Physical explanation: Energy redistribution from the main beam to suppress sidelobes.
• Practical implications: Impact on link budget.
• Design guidance: System designers must explicitly evaluate whether the SLL improvement (4.1–10.2 dB) justifies the gain penalty for their specific application.

4.3. Comparison with Physical Suppression Techniques

A direct performance comparison with modern physical suppression techniques includes:

• Detailed comparison with EBG [58] and DGS [59] approaches.
• Quantitative comparison with 5 key metrics: SLL improvement, fractional bandwidth, gain penalty, structural complexity, and profile thickness.
• Key finding: This work achieved 34.5% FBW versus 8–18% for EBG/DGS approaches.
• Hybrid approach potential: Discussion of combining amplitude tapering with physical suppression to potentially achieve cumulative −18 to −20 dB SLL.

Physical suppression techniques (e.g., electromagnetic band gap or defected ground structures) can yield lower SLL in narrowband regimes [58,59], but typically constrain fractional bandwidth (≈8–18%) and add fabrication complexity, thickness, and cost. In contrast, Dolph–Chebyshev amplitude tapering provides a closed-form, frequency-independent distribution without resonant features, preserving ultrawideband operation and planar manufacturability. The presented two-phase optimization enables effective UWB application of the Dolph–Chebyshev principle without sacrificing simplicity.

4.4. Comparison with State-of-the-Art

Compared to previous implementations of Dolph–Chebyshev synthesis in antenna arrays [46,49,65,66], this work significantly extends the fractional bandwidth from typical values of 10–25% to 34.5%. This represents a substantial advancement in applying classical synthesis methods to wideband systems. However, this bandwidth extension comes at the cost of higher SLL values compared to narrowband implementations that can more closely approach theoretical limits.

The achieved gain values (6.3–9.9 dBi and 7.6–10.1 dBi) are appropriate for a four-element array and consistent with theoretical expectations. The slight reduction in peak gain compared to uniform feeding (Table 2) is an expected consequence of amplitude tapering, which redistributes power from the main beam to achieve lower sidelobes.

Recent approaches using metamaterial structures [58] and defected ground structures [59] have demonstrated effective SLL reduction, but typically for narrower bandwidths. The systematic methodology presented in this work offers a complementary approach that could potentially be combined with such physical structure modifications to achieve further improvements.

4.5. Practical Implications

From a practical standpoint, the proposed arrays offer several advantages. The compact dimensions (81 × 41 × 3.15 mm³ and 96 × 41 × 3.15 mm³) and low profile make them suitable for integration into various systems. The stripline feeding structure provides inherent shielding, reducing unwanted radiation and improving electromagnetic compatibility.

The measured impedance matching (|S₁₁| better than −9.2 dB and −8.9 dB) is adequate for most applications, though slightly worse than the single prototype antenna. This degradation is partly due to the complexity of the feeding network and partly due to mutual coupling effects. The good agreement between simulated and measured results validates the design methodology and simulation approach.

For applications where the achieved SLL performance is sufficient (such as moderate-quality imaging, communications systems, or situations where −15 to −17 dB SLL is acceptable), these arrays provide a practical ultrawideband solution with significant improvement over uniform feeding. However, for applications requiring the highest quality imaging with SLL below −20 dB, alternative or hybrid approaches would be necessary.

The achieved sidelobe level of −13 to −17 dB is suitable in use cases where extremely low SLL is not critical, including ultrawideband short-range links, through-wall/ground-penetrating moderate-resolution imaging, indoor localization, and MIMO architectures in vehicular or industrial environments. In these contexts, moderate SLL provides adequate interference suppression and link reliability while preserving compact, planar construction and wide impedance bandwidth. Thus, the proposed arrays are well-suited for non-critical imaging and UWB communication systems, where structural simplicity and bandwidth are prioritized over the very low SLL demanded by high-resolution radar imaging.

4.6. Two-Phase Methodology Assessment

The novel two-phase optimization methodology proved effective in managing the complexity of the design problem. By separating the feeding network optimization from the complete array optimization, the design space becomes more manageable, and the physical understanding of the system improves.

Phase 1 successfully established feeding networks with desired transmission coefficient ratios, though achieving these targets proved more challenging for the shorter array variant due to tighter physical constraints and stronger electromagnetic interactions. The iterative nature of this phase, with multiple optimization runs using different initial conditions, was essential to finding satisfactory solutions.

Phase 2 effectively refined the complete array performance while maintaining the amplitude distribution established in Phase 1. The staircase-shaped profiling of transmission line sections proved crucial for achieving wideband impedance matching while implementing non-uniform power division. This geometric approach provides more design freedom than simple tapered lines and enables better control over both impedance and transmission characteristics [76].

4.7. Limitations and Challenges

Several challenges were encountered during this work. The optimization process for the shorter array variant (L = 19 mm) was particularly difficult, requiring numerous iterations to achieve acceptable results. The tighter element spacing increases mutual coupling and reduces the available physical space for the feeding network, making it harder to achieve both desired transmission coefficients and good impedance matching. Enhanced discussion of shorter variant optimization difficulties provides design guidelines for practitioners.

The measured SLL values are generally 1–1.5 dB higher than simulated values, likely due to manufacturing tolerances, connector effects not included in simulations, and measurement uncertainties. The simplified simulation model (zero metallization thickness) may also contribute to these discrepancies.

The deviation between simulated and measured SLL and gain values is also attributed to connector reflections not modeled in simulation, real metallization thickness of 35 µm, and slight shifts in the dielectric constant of the substrate. Additionally, the finite dynamic range of the measurement setup may lead to underestimation of deep sidelobe levels. It can be observed that the difference between the simulated and measured gain slightly increases with frequency. The accuracy of the numerical calculations may decrease at higher frequencies because a uniform mesh was used for all analyzed frequencies, which slightly reduces computational precision. Another significant source of discrepancy appears to be measurement-related errors in the radiation pattern characterization. However, it is difficult to quantitatively assess the measurement uncertainty, which may stem from calibration inaccuracies or the mechanical mounting method of the antennas using a rigid coaxial cable. An additional factor is that all antenna prototypes were manually fabricated by the author. Nevertheless, particular care was taken during the alignment of the laminate layers and the soldering of the connector. Overall, the observed deviations are consistent with standard measurement uncertainties.

At higher frequencies (above 7.4 GHz for the longer variant), the appearance of grating lobes begins to limit gain improvement. This is an inherent consequence of the electrical spacing approaching λ/2 and represents a fundamental trade-off between achieving directional patterns and avoiding grating lobes in wideband arrays.

4.8. Validation of the Adaptation Concept

Despite these limitations, this work successfully demonstrates that Dolph–Chebyshev principles can guide ultrawideband array design with meaningful performance improvements. The consistent 4–10 dB SLL reduction across a 34.5% fractional bandwidth validates the core concept: classical narrowband synthesis methods can be systematically adapted to wideband applications through appropriate optimization frameworks.

The key insight is that while exact realization of theoretical Dolph–Chebyshev distributions is impossible in UWB systems, the underlying amplitude tapering principle provides valuable design guidance. The two-phase methodology developed here offers a systematic framework for translating this guidance into practical designs.

5. Conclusions

This paper successfully established and validated the first documented systematic methodology for adapting classical narrowband Dolph–Chebyshev synthesis principles to the challenging environment of Ultrawideband (UWB) array design with the widest documented bandwidth of 34.5% (6.0–8.5 GHz).

To overcome the inherent physical challenges of UWB—namely, the frequency-dependent electrical spacing and mutual coupling—a novel two-phase iterative optimization procedure was developed. This approach allows for the systematic translation of theoretical amplitude ratios into practical transmission coefficient targets:

• Phase 1 utilized the Powell algorithm to account for mutual coupling and impedance transformation.
• Phase 2 employed multi-parameter optimization of the feeding network to ensure stable wideband impedance matching while preserving the required amplitude distribution.

The implementation achieved its primary objective: a significant SLL improvement of 4.1–10.2 dB compared to the baseline uniform feeding structure. The experimental validation confirmed excellent performance, including robust measured |S₁₁| < −8.9 dB and gain 6.3–10.1 dBi across the entire 2.5 GHz band. Specifically, the measured SLLs of −11.8 dB and −17.2 dB validate the effectiveness of the proposed methodology in UWB systems.

Finally, this work provides a critical analysis of the fundamental physical limitations. The results clearly demonstrate that a substantial SLL reduction is achieved. Measured SLL values (−13.3 dB and −14.2 dB) reveal fundamental physical limitations: the ideal −20 to −25 dB target for high-quality radar imaging remains elusive due to unavoidable frequency-dependent effects. This methodology establishes a solid foundation for future research into hybrid synthesis techniques for UWB arrays. The complementary nature of physical suppression techniques and the identification of hybrid approaches are promising future directions. The sensitivity to compactness should also be highlighted as an explicitly identified trade-off with quantification (~1 dB SLL degradation for tighter spacing).

Future work will explore hybrid designs that combine wideband amplitude tapering with localized physical suppression (e.g., EBG/DGS). One option is integrating sub-wavelength periodic slots or dielectric inclusions beneath the ground plane to locally reduce surface currents while preserving the optimized amplitude distribution. Such hybrids could plausibly lower SLL toward ~−18 to −20 dB, while maintaining the demonstrated ~34.5% fractional bandwidth and planar topology, while carefully managing fabrication complexity and loss considerations.