A Unified Design Methodology for Front-End RF/mmWave Receivers

Abstract

In this work, a unified design methodology for front-end RF/mmWave receivers is presented, aiming to significantly accelerate the design procedure of the front-end RF blocks in complex RX/TX chain implementations. The proposed design methodology is based on optimization loops with well-defined cost functions so as to minimize the design iterations that may be encountered during specification tuning. As proof of concept, two essential RF blocks widely used in RF receivers, a low-noise amplifier (LNA) and a voltage-controlled oscillator (VCO), were designed using the proposed unified methodology with a 65 nm RF-CMOS processing node. Finally, the derived designs were compared to similar designs in the literature, proving that the proposed unified methodology is capable of synthesizing RF/mmWave LNAs and VCOs with industry-standard specifications within a significantly faster time frame.

1. Introduction

The complexity of high-performance RX/TX chips is growing rapidly as specifications become stricter in order to fulfill application demands. This complexity directly translates into time-consuming design cycles of each individual block that synthesizes a receiver/transmitter system, as illustrated in Figure 1. In order to accelerate the design cycle in RF/mmWave blocks, the desire for a unified methodology that exploits well-defined cost functions and is capable of dividing the design procedure into discrete steps has arisen. However, all of the attention has been paid to well-known baseband linear circuits, such as operational amplifiers (OpAmps) and transconductance amplifiers (OTAs) [1,2,3,4], while some attention has also been paid to RF/mmWave blocks, such as low-noise amplifiers (LNAs) and voltage-controlled oscillators (VCOs) [4,5,6,7] that can be used in the receiver system.

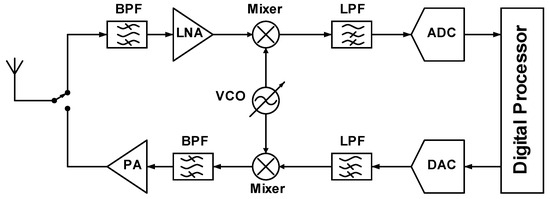
Figure 1. RF/mmWave circuit blocks that synthesize a full RX/TX system.

In this work, a unified design methodology for LNAs and VCOs is proposed and well-defined algorithms and cost functions are utilized to synthesize algorithm-based design procedures with adaptive specifications according to the targeted application. The proposed methodology includes two fully detailed design methodologies for both LNA and VCO designs and analytical algorithms are provided so as to accelerate the design procedure for both RF circuit blocks in a time-conservative manner. The proposed algorithms were written in order to be used in an automated design framework since they utilize well-defined cost functions during each iteration.

This work is divided into sections as follows. Section 2 is devoted to the network theory for both of the circuits being tested in order to derive the needed cost functions for each design methodology, including impedance matching and LC tank characterization. In Section 3, the analytical design methodologies, which utilize the aforementioned cost functions, are presented and discussed along with their respective algorithms. Finally, Section 4 is devoted to the simulation results of the circuits as derived from the proposed methodology. The provided simulation results include process–voltage–temperature (PVT) analysis and post-layout simulations of each circuit block along with their respective layout footprints. A qualitative comparison of each circuit with the literature was carried out, proving the effectiveness of the proposed methodology by synthesizing LNAs and VCOs with competitive performance metrics.

2. From Network Theory to Cost Functions

The algorithms proposed for both the LNA and VCO design methodologies are based on well-defined cost functions derived from RF network theory. Hence, basic definitions of network theory, such as scattering parameters (S-parameters), impedance parameters (Z-parameters), and admittance parameters (Y-parameters), should be extracted for the parameters as this is beneficial when defining the essential cost functions of each circuit undergoing testing.

2.1. LNA Transistor Sizing Using the $N{F}_{MIN}$ Parameter

Transistor sizing is a delicate procedure in which every transistor’s optimum widths and lengths are chosen according to the desired specifications. However, since transistor sizing also affects the input impedance of a circuit, such as an LNA, this procedure should be performed before the actual input/output impedance matching procedure. Hence, a difficult-to-solve design loop exists between optimum transistor sizing and impedance matching. These time-consuming iterations can be efficiently solved by monitoring the minimum noise figure ($N{F}_{MIN}$) of the system.

In general, an LNA’s noise figure defines its ability to amplify the desired signal without significantly amplifying the noise. By selecting the DC bias points, the transistor sizing, and the impedance matching, low-noise performance can be achieved. The noise figure of a two-port network has a matching-dependent term and a matching-independent term, the latter of which is the $N{F}_{MIN}$ cost function, and can be expressed as follows:

$$NF=N{F}_{MIN}+{\displaystyle \frac{R_N}{G_S}}{\left|Y_S-Y_{S,opt}\right|}^2$$

(1)

where $R_N$ is the equivalent noise resistance and $G_S$ is the source conductance of the two-port network being tested [8,9,10]. $Y_S$ and $Y_{S,opt}$ are the source and the optimum source admittance, respectively. When the input impedance of the two-port network undergoing testing is matched with the source impedance $(Y_S=Y_{S,opt})$, the matching-dependent term is zero and the noise of the network is determined solely from the $N{F}_{MIN}$ term.

The optimum transistor sizing can be calculated by monitoring the $N{F}_{MIN}$ parameter, which serves as a well-defined cost function for solving the sizing optimization problem. The $N{F}_{MIN}$ is matching-independent, and thus, the gate and source degeneration inductors have no effect on it. The input transistor mostly determines the $N{F}_{MIN}$, which depends upon the DC operating point of the input transistor, its sizing and the operating frequency. By monitoring the $N{F}_{MIN}$ cost functions with respect to the input transistor’s sizing and bias voltage, this cost function will be minimized at the optimum transistor sizing and DC operating point of the circuit, as presented in Figure 2.

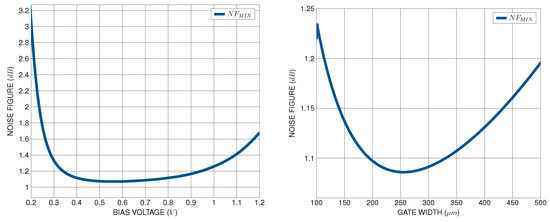
Figure 2. $N{F}_{MIN}$ cost function with respect to input transistor sizing and bias voltage.

2.2. LNA Impedance Matching Using the S-Parameters

Achieving high-input impedance matching is an important requirement in LNA design. Proper matching ensures optimal power transfer between the source and the amplifier, while simultaneously minimizing wave reflection. In radio frequency (RF) circuits, impedance mismatches can result in substantial power losses and wave reflections, leading to a reduction in system efficiency and overall performance. Typically, RF antennas have a characteristic impedance of $50\Omega$, necessitating the input impedance $Z_{IN}$ of the LNA to match this value [11]. To address this, a small-signal analysis approach is utilized to derive the conditions for impedance matching, using a simple cascoded LNA design with source degeneration, as illustrated in Figure 3.

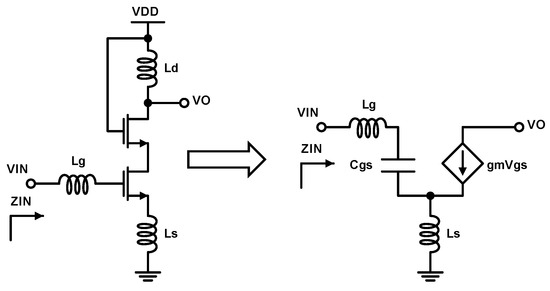
Figure 3. Small-signal representation of a cascoded LNA with source degeneration.

The input impedance of the LNA, denoted as $Z_{IN}$, is derived as follows:

$$Z_{IN}={\displaystyle \frac{V_{IN}}{I_{IN}}}=j\omega L_G+{\displaystyle \frac{V_S+V_{GS}}{I_{IN}}},V_{GS}={\displaystyle \frac{I_{IN}}{j\omega C_{GS}}}$$

(2)

where $V_S$ and $V_{GS}$ represent the source and gate-source voltage of the input transistor, respectively, while $I_{IN}$ denotes the input current. The source current can be obtained as:

$$I_S=I_{IN}+g_m\times V_{GS}=I_{IN}\left(1+{\displaystyle \frac{g_m}{j\omega C_{GS}}}\right)$$

(3)

where $g_m$ is the transconductance of the input transistor. From the above equation, the source voltage $V_S$ is derived as:

$$V_S=I_{IN}\left(1+{\displaystyle \frac{g_m}{j\omega C_{GS}}}\right)\times j\omega L_S$$

(4)

By combining (1)–(3), the following expression for the input impedance is derived:

$$Z_{IN}={\displaystyle \frac{g_m\times L_S}{C_{GS}}}+j\left[\omega \left(L_S+L_G\right)-{\displaystyle \frac{1}{\omega C_{GS}}}\right]$$

(5)

In order to achieve input impedance matching, the real part of $Z_{IN}$ should be equal to $50\Omega$, while the imaginary part should be zero. Setting the imaginary component equal to zero yields the resonance condition for the circuit, which is defined by the operating frequency. Hence, the two essential cost functions for the LNA input impedance matching, along with the LNA’s forward gain expression, are as follows:

$$Re\left(Z_{IN}\right)={\displaystyle \frac{g_m\times L_S}{C_{GS}}}$$

(6)

$$Im\left(Z_{IN}\right)=0\Rightarrow \omega \left(L_S+L_G\right)-{\displaystyle \frac{1}{\omega C_{GS}}}=0\Rightarrow f_0={\displaystyle \frac{1}{2\pi }}\times \sqrt{{\displaystyle \frac{1}{C_{GS}\left(L_S+L_G\right)}}}$$

(7)

$$Z_{\mathit{OUT}}=g_{m\left(M2\right)}{r}_{O\left(M2\right)}{r}_{O\left(M1\right)}||{\displaystyle \frac{1}{j\omega C_{GS}}}||j\omega L_D\hspace{1em},\hspace{1em}{A}_V=g_m\times Z_{\mathit{OUT}}$$

(8)

The above cost functions can be simplified by exploiting the S-parameter Smith chart representation of the equivalent LNA’s two-port network. S-Parameters are fundamental in the analysis and design of high-frequency circuits, since they provide a compact and effective means of characterizing the behavior of network components by describing the relationship between incident and reflected signals at each port. The S-parameter matrix is an $N\times N$ matrix, where N is the number of network ports undergoing testing. The relationship between the reflected and incident power waves and the scattering parameter matrix of a two-port network, depicted in Figure 4, can be expressed as follows [12,13]:

$$\left(\begin{array}{c}{b}_2\\ b_1\end{array}\right)=\left(\begin{array}{cc}{S}_{11}& S_{12}\\ S_{21}& S_{22}\end{array}\right)\left(\begin{array}{c}{a}_1\\ a_2\end{array}\right)$$

(9)

$$S_{11}={\displaystyle \frac{b_1}{a_1}}{|}_{a_2=0}{S}_{21}={\displaystyle \frac{b_2}{a_1}}{|}_{a_2=0}{S}_{22}={\displaystyle \frac{b_2}{a_2}}{|}_{a_1=0}{S}_{12}={\displaystyle \frac{b_1}{a_2}}{|}_{a_1=0}$$

(10)

where $a_1$, $b_1$, $a_2$ and $b_2$ are the electric fields of the microwave signals entering/leaving the network input/output port, respectively.

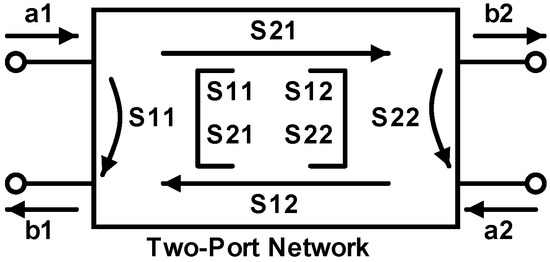
Figure 4. Two-port network versus scattering parameters.

S-parameters aid in quantifying key performance metrics, while their respective Smith chart representation significantly simplifies the impedance matching procedure. The input reflection coefficient $\left(S_{11}\right)$ describes the impedance mismatches between the source and load impedances and should be minimized to ensure maximum power transfer, thus reducing signal loss. When $S_{11}$ or $S_{22}$ parameters are transferred to the Smith chart, the S-parameters are translated into Z-parameters for the input and output impedance matching, respectively. The forward gain coefficient $\left(S_{21}\right)$ represents the gain of the network, the reverse isolation parameter $\left(S_{12}\right)$ is indicative of the signal that travels from the output back to the input and the output reflection coefficient $\left(S_{22}\right)$ describes the output impedance matching, i.e., the portion of the signal at the output that is reflected from the next stage circuitry.

The Smith chart is a widely used graphical tool to solve complex transmission line and impedance matching problems [14]. As illustrated in Figure 5, the red grid of the Smith chart corresponds to the impedance, where the blue grid corresponds to the admittance of a two-port network. The input impedance matching procedure, using the S-parameters Smith chart representation, is depicted in Figure 5. The points that fulfill the two well-defined cost functions for the input impedance matching, (5) and (6), can be found by sweeping the gate and source degeneration inductors $L_G$ and $L_S$, respectively, at the targeted frequency. At these two points, for a given input transistor sizing, the values of the gate and source degeneration inductors $L_G$ and $L_S$ can be calculated at a specific frequency of interest.

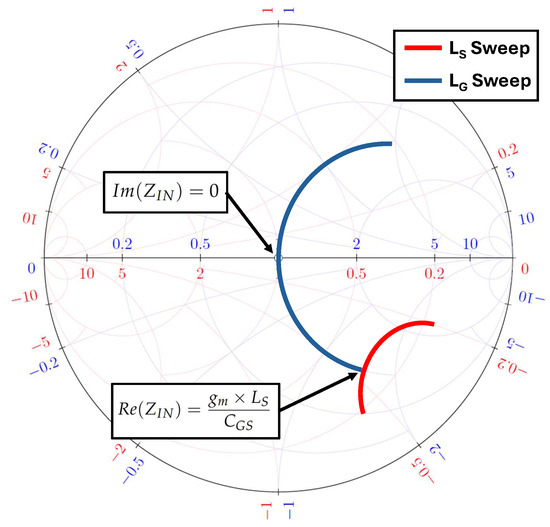
Figure 5. Impedance matching cost functions fulfillment points using Smith chart representation.

2.3. VCO LC-Tank Characterization Using the Z-Parameters

Voltage-controlled oscillators (VCOs) are essential components in wireless communication systems, playing a critical role in the RF transceiver chain. They generate the local oscillation signal essential for the entire system’s operation. Consequently, any deficiencies or suboptimal design in a VCO can impact the following stages of the transceiver. As an example, the phase noise and tuning range of a VCO significantly influence the noise performance of the entire system [15,16]. Additionally, designing a VCO presents the challenge of creating a reliable and efficient circuit while ensuring precision and accuracy. VCOs are designed to produce a continuous periodic signal whose frequency can be controlled by a DC voltage. Although the system incorporates negative feedback, the phase shift of the oscillator at a specific frequency introduces an additional 180 degrees, resulting in a total phase shift of 360 degrees, which creates positive feedback.

The core of the VCO circuit being tested is the LC tank resonator, depicted in Figure 6. The inductor and the capacitor are passive components that form the LC tank, capable of storing and releasing energy in the form of electric or magnetic fields. This energy exchange occurs at a frequency known as the resonance frequency of the tank. In an ideal world, this periodic exchange would continue indefinitely, without requiring additional circuitry. However, due to the non-idealistic manufacturing of passive components, the LC tank introduces a parallel parasitic resistance $R_P$. As a result, the amplitude of the periodic oscillation will eventually decay to zero.

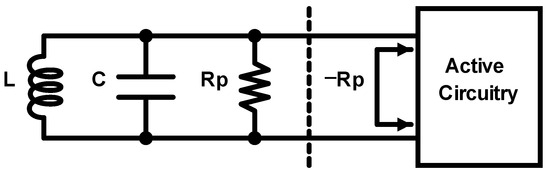
Figure 6. LC lossless tank illustration using active circuitry to compensate tank losses.

In order to have a self–sustained oscillation, additional active circuitry should be designed so as to replenish the energy losses of the tank. This active circuit should exhibit an input resistance equal and opposite to the parasitic resistance of the LC-tank, $-R_P$, to compensate for the energy losses [17,18,19]. The VCO architecture, along with its corresponding small-signal equivalent one-port network, is illustrated in Figure 7. Small-signal analysis is carried out to extract the essential cost function of the VCO that leads to sustainable oscillation at the frequency of interest. By considering the LC tank as a one-port network, the impedance of the tank $Z_{IN}$ can be expressed as follows:

$$\frac{V_X}{I_X}=-(\frac{1}{g_{m1}}+\frac{1}{g_{m2}})\Rightarrow \frac{V_X}{I_X}=-\frac{2}{g_m}$$

(11)

assuming that the two cross-coupled transistors, both NMOS and PMOS, have the same transconductance.

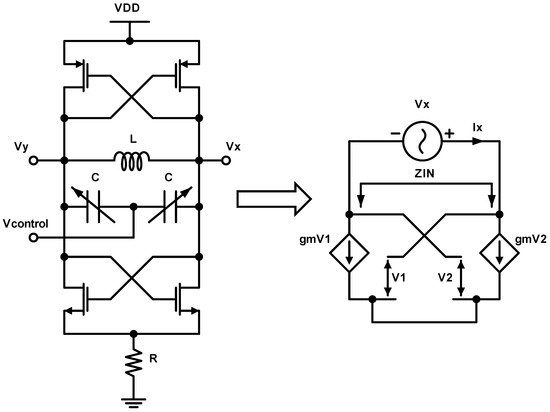
Figure 7. Cross-coupled LC VCO architecture and its negative resistance small-signal equivalent circuit.

Since the circuit being tested is a complementary LC VCO that uses both NMOS and PMOS devices, the contribution of both cross-coupled transistor pairs should be considered. By choosing the appropriate device parameters for both NMOS and PMOS devices to have the same transconductance, the overall negative resistance of the active circuitry can be expressed as follows:

$$Z_{IN}={\displaystyle \frac{V_X}{I_X}}=-{\displaystyle \frac{1}{g_m}}$$

(12)

Hence, in order to compensate for the parasitic resistance of the LC tank, the transconductances of both NMOS and PMOS of the cross-coupled LC VCO should satisfy the self-sustained oscillation criterion below:

$$g_m\ge {\displaystyle \frac{1}{R_P}}$$

(13)

The resonance frequency of the LC-tank depends on the inductance and the capacitance of the tank as derived by the following equation:

$${\omega }_{OSC}={\displaystyle \frac{1}{\sqrt{L(C_{VAR}+C_P)}}}$$

(14)

where $C_{VAR}$ is the varactor’s capacitance value at a given control voltage, while $C_P$ is the overall parasitic capacitance of the LC-tank and the cross-coupled transistor pairs. By varying the varactor capacitance $C_{VAR}$, the oscillation frequency can be tuned according to the application needs. By increasing the control voltage, a monotonic decrease in the capacitance occurs and the oscillation frequency therefore increases.

To fully characterize the LC tank of the VCO undergoing testing, impedance parameters or Z-Parameters are utilized, offering significant insights about the LC-tank resonance frequency and its parasitic resistance $R_P$. In general, the Z-Parameters are extracted using the equivalent two-port network of a circuit, as depicted in Figure 8. Similarly, the Z-parameter matrix is an $N\times N$ matrix, where N is the number of the network ports under test. The relationship between the input/output voltages with respect to the input/output currents and the impedance parameter matrix of a two-port network can be expressed as follows [20,21]:

$$\left(\begin{array}{c}{V}_1\\ V_2\end{array}\right)=\left(\begin{array}{cc}{Z}_{11}& Z_{12}\\ Z_{21}& Z_{22}\end{array}\right)\left(\begin{array}{c}{I}_1\\ I_2\end{array}\right)$$

(15)

$$Z_{11}={\displaystyle \frac{V_1}{I_1}}{|}_{I_2=0}{Z}_{21}={\displaystyle \frac{V_2}{I_1}}{|}_{I_2=0}{Z}_{22}={\displaystyle \frac{V_2}{I_2}}{|}_{I_1=0}{Z}_{12}={\displaystyle \frac{V_1}{I_2}}{|}_{I_1=0}$$

(16)

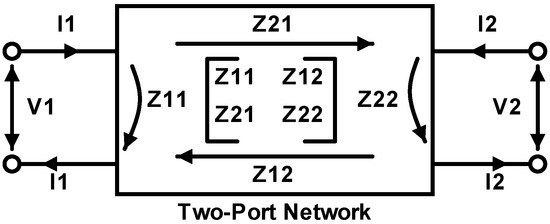
Figure 8. Z-Parameter definitions using a two-port network.

Hence, by monitoring the $Z_{11}$-Parameters of the equivalent one-port network of the LC-tank, the ratio of the voltage across the tank to the current flowing into the tank can be extracted with respect to frequency. The LC resonators exhibit a purely resistive behavior at the resonance frequency, where the imaginary part is zeroed out, as illustrated graphically in Figure 9. At the frequency of 5 GHz, the LC-tank undergoing testing resonates and the imaginary part of the $Z_{11}$-Parameter becomes zero, leading to a purely resistive behavior of the LC-tank impedance. Hence, the maximum of the real part of $Z_{11}$-Parameter is the parasitic resistance $R_P$ of the LC-tank and, to compensate for this resistance, the active circuit transconductances should be tuned accordingly. Thus, the VCO cost function for oscillation is expressed, using Z-Parameters, as follows:

$$g_m\ge {\displaystyle \frac{1}{max\left(Re\left(Z_{11}\right)\right)}}$$

(17)

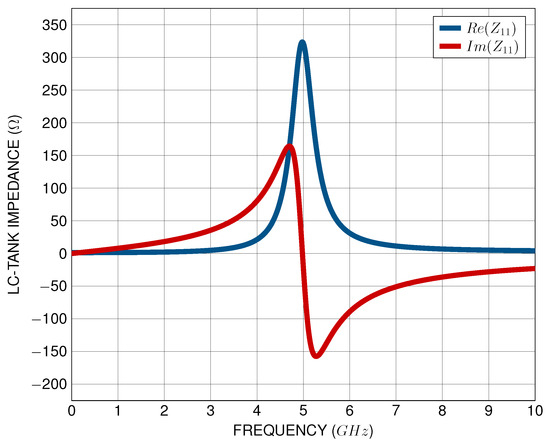
Figure 9. LC-tank $Z_{11}$-Parameters with respect to frequency.

2.4. Inductor Characterization Using the Y-Parameters

In both test cases, inductors were utilized so as to match the input impedance of the LNA or to resonate at the desired operating frequency the LC-tank of the VCO. These inductors were pre-characterized by the respective foundry, providing programmable cells (PCELLs) for each inductor geometry. In these PCELLs, the inductance and quality factor are calculated on the fly using call-back functions developed by the foundry. However, this is a back-end operation, and the user only has access to the geometry parameters of the inductor, e.g., number of turns, turn width, turn spacing, and inner diameter.

By utilizing the Y-Parameters, inductor characterization becomes a front-end process, providing useful insights to the designer. Both the inductance and quality factor of the inductor, regardless of its geometry, can be extracted using Y-Parameters. Y-Parameters are extracted using the same two-port network depicted in Figure 8 considering variables $I_1$ and $I_2$ as dependent, and $V_1$ and $V_2$ as independent. Thus, the Y-Parameter matrix is again an $N\times N$ matrix, where N represents the number of ports, which describes the relationship between the input/output currents with respect to the input/output voltages, as expressed below [22,23]: 

$$\left(\begin{array}{c}{I}_1\\ I_2\end{array}\right)=\left(\begin{array}{cc}{Y}_{11}& Y_{12}\\ Y_{21}& Y_{22}\end{array}\right)\left(\begin{array}{c}{V}_1\\ V_2\end{array}\right)$$

(18)

$$Y_{11}={\displaystyle \frac{I_1}{V_1}}{|}_{V_2=0}{Y}_{21}={\displaystyle \frac{I_2}{V_1}}{|}_{V_2=0}{Y}_{22}={\displaystyle \frac{I_2}{V_2}}{|}_{V_1=0}{Y}_{12}={\displaystyle \frac{I_1}{V_2}}{|}_{V_1=0}$$

(19)

The quality factor Q of the inductor plays a critical role in RF circuits/hl, especially in LNA and VCO designs. In LNA schemes, the high-quality factor of the output inductor load leads to higher gain but lower 3 dB gain bandwidth [24] since the gain of tuned amplifiers is proportional to $\propto Q$. Moreover, the quality factor of the inductor load also determines the output impedance of the LNA, which should be matched to the input impedance of the next-stage circuitry. On the other hand, in VCO schemes, phase noise is proportional to $\propto 1/Q^2$, and hence, the high-quality factor of the LC-tank inductor leads to low phase noise [25,26]. Therefore, the task of finding the best possible inductor geometry can be solved using Y-Parameters in the inductor testbench depicted in Figure 10, extracting the inductance and quality factor with respect to frequency, as illustrated in Figure 11.

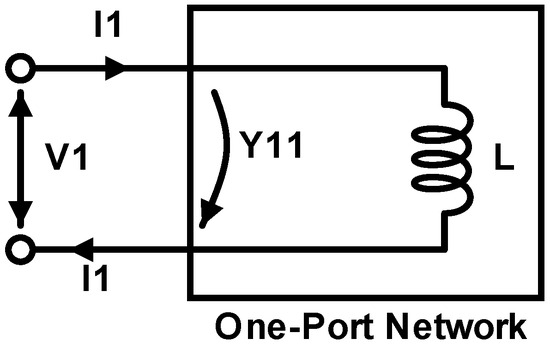
Figure 10. Inductor one-port network for Y-parameter characterization.

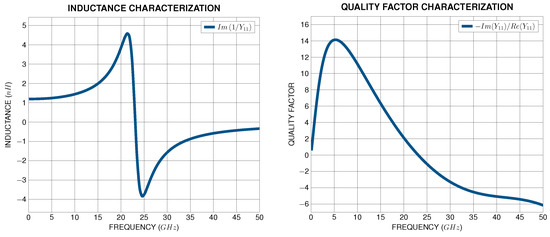
Figure 11. Inductor characterization using Y-Parameters.

In order to obtain well-defined cost functions regarding inductor characterization, the inductance and quality factor of the inductor undergoing testing should be expressed with respect to Y-parameters, as follows:

$$L\left(f\right)={\displaystyle \frac{Im\left(\frac{1}{Y_{11}}\right)}{2\pi \times f}},Q\left(f\right)={\displaystyle \frac{-Im\left(Y_{11}\right)}{Re\left(Y_{11}\right)}}$$

(20)

To construct the cost function for solving the optimal inductor geometry problem, the dynamic geometry parameters of the inductor being tested should be defined. Since the quality factor of an inductor is the ratio of the stored and dissipated energy, the geometry parameters that significantly impact the quality factor are the number of turns $NT$ and the inner diameter $ID$ of the inductor. Therefore, by monitoring the quality factor at the desired frequency of operation $f_0$, the optimal inductor cost function can be expressed as follows:

$$Q{(ID,NT)}_{@f_0}=max\left({\displaystyle \frac{-Im\left(Y_{11}\right)}{Re\left(Y_{11}\right)}}\right)$$

(21)

while its graphical illustration is presented in Figure 12. The inductor PCELL limits of the inner diameter and the number of turns were used as limits of search for deriving the behavior of the optimal Q cost function. Upon completion of this search, the optimal Q cost function returns the inner diameter $ID$ and number of turns $NT$ that define the geometry of the inductor being tested at which the maximum quality factor is achieved.

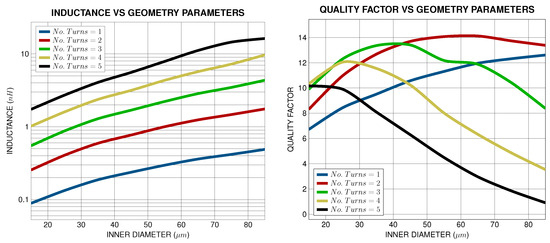
Figure 12. Optimum search cost function with respect to geometry parameters at $f_0=5$ GHz.

3. From Cost Functions to Design Methodologies

Having defined the essential cost functions of each circuit, detailed design methodologies are synthesized. Each design methodology developed in this work is based on the corresponding cost functions that adequately describe the circuits undergoing testing. In the LNA scheme, scattering and impedance parameters are utilized for the input impedance matching of the LNA, while the minimum noise figure $N{F}_{MIN}$ parameter is employed for the transistor sizing. In the VCO scheme, the impedance and admittance parameters are employed for the LC-tank and optimal inductor characterizations, respectively. For the VCO’s transistor sizing, the boundary condition for oscillation cost function $g_m\ge 1/max\left(Re\left(Z_{11}\right)\right)$ is used where the Z-Parameters are exploited.

3.1. LNA Design Methodology

The proposed methodology for designing an LNA is outlined with a flowchart and a pseudo-code, as depicted in Figure 13 and Algorithm 1, respectively, offering a structured framework for achieving the desired performance specifications. The design process begins with defining key specifications and the transistor PDK limits. The specifications include the operating frequency $f_0$, the target input reflection coefficient $S_{11-SPEC}$, the desired forward gain $S_{21-SPEC}$, and the noise figure $N{F}_{SPEC}$ of the LNA being tested.

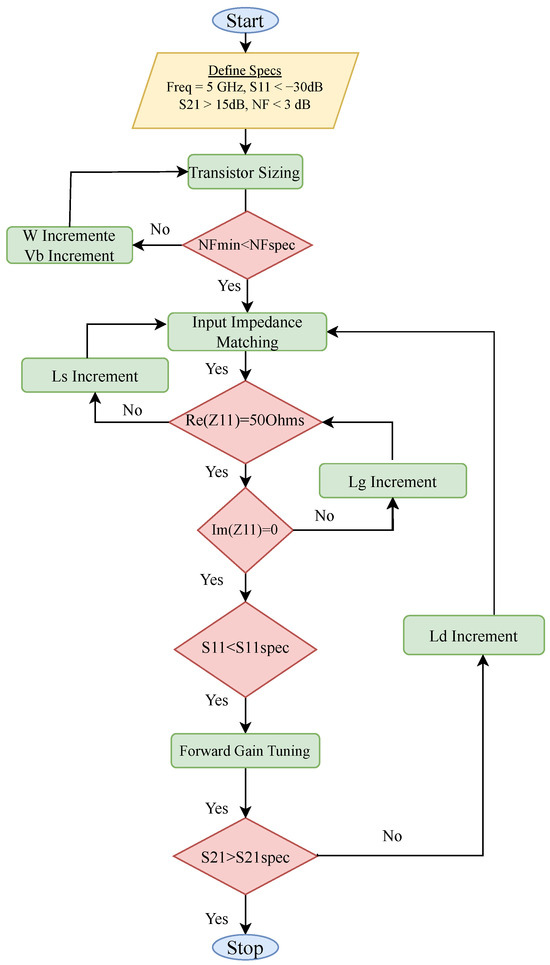
Figure 13. LNA design methodology flowchart.

The first phase involves transistor sizing, which directly impacts the noise figure. The transistor’s width and the bias voltage are adjusted to ensure that the minimum noise figure $N{F}_{MIN}$ value does not exceed the target noise figure $N{F}_{SPEC}$ value. As evident from Figure 2, the $N{F}_{MIN}$ parameter exhibits a minimum value within a specific range of transistor widths and bias points, which scale with power consumption. As the transistor width increases, transconductance $g_m$ and gate-to-source capacitance $C_{GS}$ increase. Therefore, based on (6) and (7), careful selection of the transistor width is necessary to achieve the minimum $N{F}_{MIN}$ value while also enabling input impedance matching to $50\Omega$. If the condition $N{F}_{MIN}\le N{F}_{SPEC}$ is not met, adjustments are systematically applied to the transistor’s width and bias point until the noise specifications are satisfied. If not, the transistor sizing at the absolute minimum of the $N{F}_{MIN}$ parameter should be returned, thus breaking the transistor sizing procedure loop.

Algorithm 1 LNA Design Methodology

1: Define Min and Max values according to PDK limits:   2:    Transistor min Channel Width → $W_{MIN}$   3:    Transistor min Channel Length → $L_{MIN}$   4:     5: Define LNA Specifications and Parameters:   6:    Operating Frequency → $f_0$   7:    Voltage Supply → $V_{DD}$   8:    Bias Voltage → $V_B$   9:    Gate Inductor → $L_G$ 10:    Source Degeneration Inductor → $L_S$ 11:    Input Impedance Matching → $S_{11-SPEC}$ 12:    Forward Gain → $S_{21-SPEC}$ 13:    Noise Figure → $N{F}_{SPEC}$ 14:   15: LNA Cost Functions: 16: $•N{F}_{min}(W,V_B,f_0)$: Returns the minimum Noise Figure for a given transistor width W, monitored at the $f_0$ frequency while applying a $V_B$ biasing. 17: $•Re\left(Z_{11}(f_0,X)\right)$: Returns the real part of the input impedance at the specified frequency $f_0$, sweeping the parameter X. 18: $•Im\left(Z_{11}(f_0,X)\right)$: Returns the imaginary part of the input impedance at the specified frequency $f_0$, sweeping the parameter X. 19:   20: Main Optimization Algorithm: 21: while (TRUE) { 22:   // Transistor Sizing 23:   for $\left(W_N=W_{MIN}:W_{MAX}\right)$ loop { 24:      for $\left(V_B=0:V_{DD}\right)$ loop { 25:          $W=min\left(N{F}_{min}(W_N,f_0,V_B)\right)$ 26:          if ($N{F}_{min}\le N{F}_{SPEC}$) return W and $V_B$ }} 27:   // Input Impedance Matching 28:   while $\left(Re\left(Z_{11}\right)\ne 50\right)$ { 29:      for $\left(L_S=L_{MIN}:L_{MAX}\right)$ loop { 30:          $Re\left(Z_{IN}\right)=Re\left(Z_{11}(f_0,L_S)\right)$ 31:          if $\left(Re\left(Z_{IN}\right)=50\right)$ return $L_S$ break}} 32:   while $\left(Im\left(Z_{11}\right)\ne 0\right)$ { 33:      for $\left(L_G=L_{MIN}:L_{MAX}\right)$ loop { 34:          $Im\left(Z_{IN}\right)=Im\left(Z_{IN}(f_0,L_G)\right)$ 35:          if $\left(Im\left(Z_{11}\right)=0\right)$ return $L_G$ break}} 36:   if $\left(S_{11}>S_{11-SPEC}\right)$ { 37:      go to Input Impedance Matching } 38:   // Forward Gain Tuning 39:   else if $\left(S_{21}<S_{21-SPEC}\right)$ { 40:      for $\left(L_D=L_{MIN}:L_{MAX}\right)$ loop { 41:          while $\left(S_{11}>S_{11-SPEC}\right)$ { 42:            if $\left(S_{21}\ge S_{21-SPEC}\right)$ return $L_D$ break }}} 43: end

Once the noise performance is optimized, attention shifts to achieving proper input impedance matching. This requires ensuring that the real part of the input impedance $Re\left(Z_{11}\right)$ equals the antenna impedance of $50\Omega$, to enable maximum power transfer and minimal reflection. If $Re\left(Z_{11}\right)\ne 50$, the source degeneration inductance $L_S$ is incrementally adjusted until this condition is met. Simultaneously, the imaginary component of the input impedance should satisfy the condition $Im\left(Z_{11}\right)=0$ by tuning the gate inductance $L_G$. Together, these adjustments ensure that the amplifier’s input is optimally matched to the source impedance. The iterative tuning process continues until the input reflection coefficient is less than or equal to the target $S_{11-SPEC}$. This ensures that the amplifier achieves high efficiency and minimal signal loss at the interface with no wave reflections back to the antenna.

Following the impedance matching stage, forward gain optimization is performed in order to tune the amplifier’s gain to the desired value, dictated by the $S_{21-SPEC}$ specification. If the achieved gain is less than the specified $S_{21-SPEC}$, the load inductance $L_D$ is incrementally increased, affecting the amplifier’s gain. However, any adjustments to $L_D$ inherently alter the input impedance matching, as illustrated in Figure 14, necessitating a repetition of the input impedance matching process so as to maintain the input matching criteria. This iterative loop of gain enhancement and impedance re-tuning ensures that the forward gain meets $S_{21-SPEC}$ without compromising other performance metrics of the LNA. The methodology terminates once all design specifications are fulfilled, resulting in a robust and efficient LNA design.

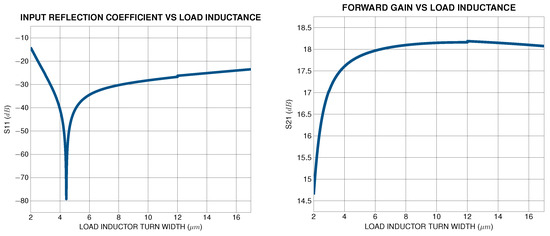
Figure 14. Load inductor tuning has an impact on both input reflection coefficient and forward gain.

3.2. VCO Design Methodology

The proposed VCO methodology is outlined again using a flowchart and a pseudo-code representation of the developed methodology, as depicted in Figure 15 and Algorithm 2, respectively. The design process begins with defining key specifications and the PDK limits of the respective models, used in the design. The specifications include the oscillation frequency $f_0$, the target output voltage swing $V_{OUT}$, and the phase noise performance $P{N}_0$, while maintaining the power consumption of the VCO $<1$ mW.

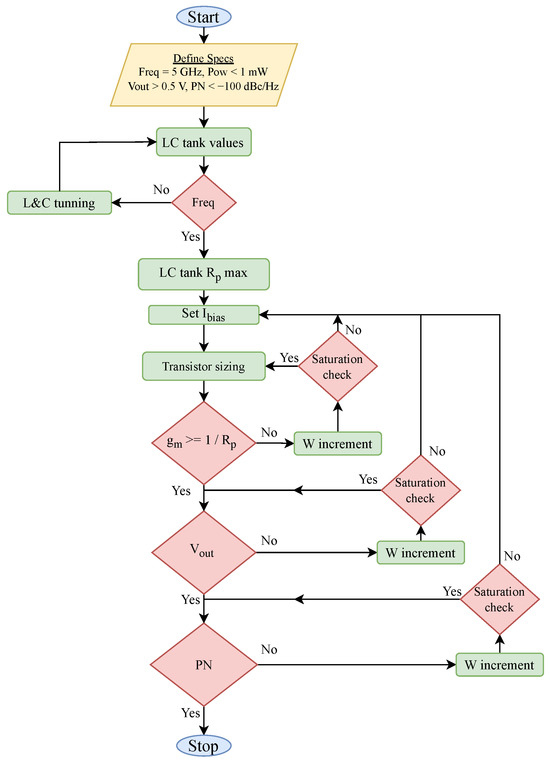
Figure 15. VCO design methodology flowchart.

The first step, which involves defining the desired performance specifications, is performed focusing on synthesizing high-performance VCO designs with industry-standard specifications. After setting the initial conditions, the methodology moves to the LC-tank characterization of the VCO. Two processes were included during the execution of the LC-tank characterization: the optimum Q-factor inductor search, which is performed using the $Q{(ID,NT)}_{@f_0}$ cost function, and the LC-tank tuning process via searching the optimum varactor value with which the LC-tank will resonate at the desired frequency of $f_0$. Finally, the LC-tank characterization procedure finishes by calculating the overall parasitic resistance $R_P$ of the LC-tank using the Z-parameters of its respective one-port network.

Based on the specified requirements and the desired power consumption, the bias current of the VCO is defined. In the topology being tested, the VCO’s biasing is performed utilizing a resistor, simplifying the circuit and improving the phase noise performance [27]. The bias current emerges as a critical factor influencing key performance metrics of the VCO, such as output voltage amplitude and phase noise [28]. It is prudent to prioritize setting the bias current, especially when the VCO has a stringent power budget. This approach reduces the number of iterations required in the following stages, speeding up the process of achieving the final specifications. Notably, the output voltage amplitude is directly proportional to the bias current, and this relationship can be expressed as follows:

$$V_{out}=2\times \left({\displaystyle \frac{4}{\pi }}\times R_P\times I_B\right)$$

(22)

An essential feature of the complementary cross-coupled LC VCO aids in demonstrating this dependency; the presence of both NMOS and PMOS transistors, along with the circuit’s symmetrical structure, results in a doubled output voltage amplitude for the same bias current [29].

Following the bias definition stage, transistor sizing is performed followed by three consecutive decision loops. Every loop tunes the respective performance metric based on the defined specifications and the required conditions that guarantee oscillation. Initially, the transistors are sized according to the boundary condition for oscillation (17). If this condition is true, the oscillation will occur and the algorithm moves on to the next procedure, which is the output voltage amplitude evaluation. If the output voltage swing is lower than the specified specification, a width increment for both NMOS and PMOS devices is performed, leading to an increase in the transistors’ transconductance to surpass the inverse of the parallel resistance of the tank $1/R_P$. It should be noted that the width is increased for both NMOS and PMOS devices, with the aim of keeping the transconductance of both the same. For the process node used in this study, the width ratio is evaluated as $W_N/W_P\approx 1/3$.

Algorithm 2 VCO Design Methodology

1: Define Min and Max values according to PDK limits:   2:    Transistor min Channel Width → $W_{MIN}$   3:    Transistor min Channel Length → $L_{MIN}$   4:    Minimum Inductor Inner Diameter → $I{D}_{MIN}$   5:    Maximum Inductor Inner Diameter → $I{D}_{MAX}$   6:    Minimum Inductor Turns → $N{T}_{MIN}$   7:    Maximum Inductor Turns → $N{T}_{MAX}$   8:    MOS VARACTOR min Capacitance → $C_{MIN}$   9:    MOS VARACTOR max Capacitance → $C_{MAX}$ 10:   11: Define VCO Specifications and Parameters: 12:    NMOS and PMOS Width ratio for equal $g_m$ → $1/3$ 13:    Operating Frequency → $f_0$ 14:    Voltage Supply → $V_{DD}$ 15:    Bias Current → $I_B$ 16:    Output Amplitude Swing → $V_0$ 17:    Phase Noise → $P{N}_0$ 18:   19: VCO Cost Functions: 20: $•Q{(ID,NT)}_{@f_0}$: Returns the Quality Factor of the LC-tank inductor for specific inner diameter $ID$ and specific number of turns $NT$, monitored at the $f_0$ frequency. 21: $•max\left(Re\left(Z_{11}\right)\right)$: Returns the maximum real part of the input impedance with respect to frequency. 22: $•L{(ID,NT)}_{@f_0}$: Returns the Inductance of the inductor with specific geometry parameters (inner diameter $ID$ and number of turns $NT$) at the specified frequency $f_0$. 23:   24: Main Optimization Algorithm: 25: while (TRUE) { 26:   // Optimum Inductor Search 27:   for $\left(NT=N{T}_{MIN}:N{T}_{MAX}\right)$ loop { 28:      for $\left(ID=I{D}_{MIN}:I{D}_{MAX}\right)$ loop { 29:        $Q_{OPT}=max\left(Q{(ID,NT)}_{@f_0}\right)$ 30:        return $I{D}_{OPT}=ID$ and $N{T}_{OPT}=NT$ } 31:      return $L_{OPT}=L{(I{D}_{OPT},N{T}_{OPT})}_{@f_0}$ } 32:   // LC-Tank Tuning and Characterization 33:   for $\left(C_{TANK}=C_{MIN}:C_{MAX}\right)$ loop { 34:      if ($1/(2\pi \sqrt{L_{OPT}\times C_{TANK}}=f_0$) { 35:        return $C_{TANK}$ } 36:      return $R_P=max(Re\left(Z_{11}\right)$} 37:   // Transistor Sizing 38:   define $I_B$ 39:   while (TRUE) { 40:      for $\left(W=W_{MIN}:W_{MAX}\right)$ loop { 41:        if ($g_m\ge 1/R_P$) { 42:         if (SATURATION CHECK = TRUE) { 43:           return $W_{OPT}=W$ break } } } 44:         else go to define $I_B$ } 45:   // Output Voltage Swing Tuning 46:   while (TRUE) { 47:      for $\left(W=W_{OPT}:W_{MAX}\right)$ loop { 48:        if ($V_{OUT}\ge V_0$) { 49:         if (SATURATION CHECK = TRUE) { 50:           return $W_{OPT}=W$ break } } } 51:         else go to define $I_B$ } 52:   // Phase Noise Tuning 53:   while (TRUE) { 54:      for $\left(W=W_{OPT}:W_{MAX}\right)$ loop { 55:        if ($PN\le P{N}_0$) { 56:         if (SATURATION CHECK = TRUE) { 57:           return $W_{OPT}=W$ break } } } 58:         else go to define $I_B$ } 59: end

In the current topology, resistor-based biasing is employed to set the bias current, rather than using a simple current mirror. However, this approach results in poorly defined current, as it depends on the sizing of the transistors. This dependence arises because the resistor-based configuration does not precisely regulate the current. Consequently, the amplitude of the output voltage can be adjusted by modifying the sizing of the transistors. This relationship underscores the importance of transistor sizing when it comes to achieving the desired output voltage characteristics. If the desired specification is not met, the algorithm returns to the bias current definition procedure to change the bias current of the circuit, thus changing the biasing resistor value.

Finally, the phase noise of the oscillator is evaluated. At this point of the methodology, and taking all the previous steps into consideration, it is possible that the phase noise requirements are met anyway. Nevertheless, few iterations can be made so as to further decrease the phase noise through a loop that increases the width of the transistors, increasing their transconductance. Concluding the description of the presented methodology, it is important to highlight the function of the nested loops present in the three final consecutive iterations, where the circuit’s performance is evaluated. These nested loops are performed extremely fast since they exploit well-defined cost functions about each metric, while they ensure that the transistors remain in the desired region of operation. During the optimization process, if the methodology detects that the transistors have shifted out of the saturation region, it takes corrective action. This correction involves returning to the bias current adjustment step and, by regulating the bias current, the methodology can effectively push the transistors back into the saturation region, ensuring proper operation.

4. From Design Methodologies to RF Circuit Implementations

Concluding this work, the proposed methodology is applied to derive full circuit implementations of an LNA and a VCO with industry-standard specifications. The selected architectures for the circuit test cases are a single-stage cascoded with source degeneration LNA and a cross-coupled LC-VCO, respectively. Both architectures are synthesized for an operating frequency of 5 GHz, with a 65 nm RF-CMOS processing node. The target specifications of each RF circuit are summarized in Table 1 and Table 2, respectively.

Table 1. LNA design specifications.

Specification	Value
Operating Frequency $f_0$	5 GHz
Input Reflection Coefficient ($S_{11}$)	≤−30 dB
Output Reflection Coefficient ($S_{22}$)	≤−10 dB
Forward Gain ($S_{21}$)	≥15 dB
Reverse Isolation ($S_{12}$)	≤−20 dB
Noise Figure ($NF$)	≤3 dB

Table 2. VCO design specifications.

Specification	Value
Operating Frequency $f_0$	5 GHz
Frequency Tuning Range $(f_0/\Delta f)$	≥10%
Output Voltage Swing ($V_{OUT}$)	≥$0.5V_{p-p}$
Phase Noise ($P{N}_0$)	≤−100 dBc/Hz
Power Consumption ($P_D$)	≤1 mW

4.1. LNA Implementation

The common source cascoded LNA topology, which was designed with a 65 nm RF-CMOS process, is illustrated in Figure 16. This LNA topology is commonly used in RF systems due to its ability to provide good input matching, high forward gain, and low noise performance. Also, due to its simplicity, this design has a low silicon footprint. The transistor $M_1$ is the main amplifying component, and the RF signal is applied to its gate. Hence, this gate impedance should be matched to the impedance of the antenna utilizing the $L_S$ and $L_G$ inductors. The transistor $M_2$ provides a stable bias current to $M_1$, and it is used to improve the gain and the output impedance of the circuit while providing higher isolation between input and output ports. Finally, the capacitors $C_1$, $C_2$ are DC blocking capacitors, while the resistor R is used for biasing the gate of $M_1$, setting the operating point of the transistor.

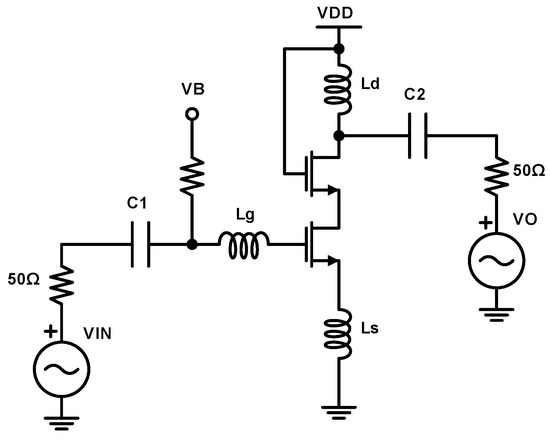
Figure 16. Common source cascoded LNA architecture.

By applying the proposed methodology, the synthesized LNA design parameters are summarized in Table 3. The physical design of the synthesized LNA is depicted in Figure 17, while its S-Parameter performance, pre- and post-layout, is illustrated in Figure 18. Furthermore, the noise performance, the stability factor $K_f$ and the $1^{ST}$- and $3^{RD}$-order intercept points ($I{P}_1$ and $I{P}_3$) are also extracted and graphically illustrated in Figure 18 and Figure 19, respectively. Also, to further validate the synthesized design, PVT analysis is performed and the LNA performance across PVT corners is summarized in Table 4. It should be noted here that the stability factor $K_f$ is calculated using the expression below, utilizing only the Y-Parameters of the LNA being tested [30,31]:

$$K_f={\displaystyle \frac{2Re\left(Y_{11}\right)Re\left(Y_{22}\right)-Re\left(Y_{12}{Y}_{21}\right)}{|Y_{12}{Y}_{21}|}}$$

(23)

Table 3. LNA design parameters.

Parameter	Value
Operating Frequency	5 GHz
Supply Voltage $V_{DD}$	1.2 V
Bias Voltage $V_B$	550 mV
${\left({\displaystyle \frac{W}{L}}\right)}_{M1}$ (μm)	$276/0.06$
${\left({\displaystyle \frac{W}{L}}\right)}_{M2}$ (μm)	$390/0.08$
Gate Inductance $L_G$	3 nH
Source Degeneration Inductance $L_S$	170 pH
Load Inductance $L_D$	2.4 nH

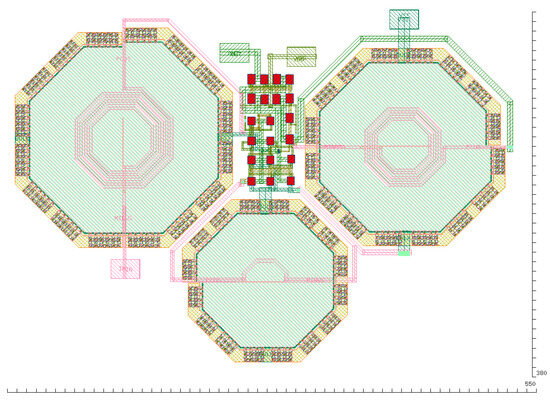
Figure 17. Physical design of the synthesized LNA.

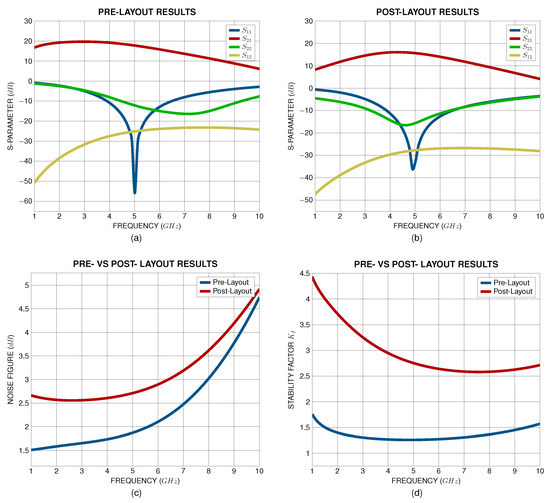
Figure 18. (a) Pre-layout and (b) post-layout S-Parameter, (c) noise figure performance and (d) stability factor of the synthesized LNA.

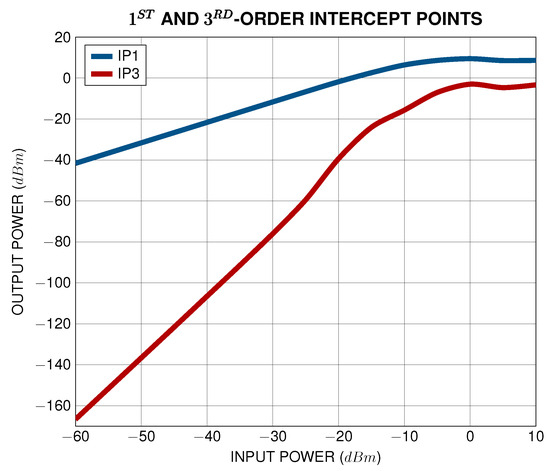
Figure 19. $1^{ST}$ and $3^{RD}$-order intercept points of the synthesized LNA.

Table 4. LNA design performance across process–temperature–voltage (PVT) corners.

Parameter	TT (${\mathit{T}}_{\mathit{A}}=27$ °C)	SS (${\mathit{T}}_{\mathit{A}}=80$ °C)	FF (${\mathit{T}}_{\mathit{A}}=0$ °C)
$V_{DD}$ (V)	1.2	1.1	1.3
$V_B$ (V)	0.55	0.5	0.6
$S_{11}$ (dB)	−46.9	−27.4	−30
$S_{21}$ (dB)	17.8	16.9	18.3
$S_{22}$ (dB)	−12.1	−15	−10.9
$S_{12}$ (dB)	−25	−23.7	−25.2
$NF$ (dB)	1.9	2.2	1.7
$IP1$ (dBm)	−14	−14.75	−13.5
$IP3$ (dBm)	2.5	0.7	3.8

The pre-layout simulation for the input reflection coefficient achieves a minimum value of approximately −43 dB at the operating frequency, while the post-layout results show a degraded value of −36 dB, attributed to parasitic elements introduced during the layout implementation. The LNA demonstrates a peak gain of 17.8 dB in the pre-layout simulation scheme, which is reduced to 15.5 dB during post-layout simulations due to resistive losses in the interconnects. For the output reflection coefficient, a minor deviation is observed between pre- (−12.1 dB) and post-layout (−15 dB) results, with both coefficients (pre- and post-layout) fulfilling the output impedance matching specification. Furthermore, both simulation results of the reverse isolation parameter $S_{12}$ exhibit good performance, with values below −25 dB, indicating negligible feedback paths from output to input ports.

The noise figure ($NF$) of the amplifier is simulated at 1.9 dB, at the operating frequency of the LNA, in the pre-layout simulation scheme. In the post-layout simulations, however, an increase of 0.6 dB was observed, resulting in a noise figure of 2.5 dB. This increase is due to the increase in the matching-dependent parameter of the noise figure expression (1) since the input matching was slightly altered due to the layout parasitics. Despite this, the NF remains within acceptable levels for high-performance LNA designs. The stability factor $K_f$ of the LNA is kept above 1 at the frequencies of interest, confirming an unconditionally stable design [32].

It is worth mentioning that the LNA design synthesized using the proposed methodology exhibits a high power consumption of 22 mW (post-layout) and more power-efficient designs could be synthesized that achieve the targeted specifications. During the transistor sizing, the methodology determines the optimum transistor width and bias point that enable the circuit to achieve the minimum possible noise figure. However, having as reference Figure 2, there is a range of transistor widths and biasing points where the LNA exhibits low noise with $N{F}_{MIN}\le 1.2$ dB. Hence, the biasing points and the transistor widths can be easily tuned according to the available power budget. The algorithms converge to the optimal value of noise figure achievable by the circuit, at the expense of power consumption.

In order to prove that the synthesized LNA, using the proposed methodology, has industry-standard performance, a literature comparison was carried out, extracting a Figure of Merit (FoM) for each implementation according to the expression below [33]:

$$Fo{M}_1={\displaystyle \frac{S_{21}\left(\mathrm{dB}\right)\times IP3\left(\mathrm{dBm}\right)\times f_0\left(\mathrm{GHz}\right)}{|NF-1| \times P_{DC}\left(\mathrm{mW}\right)\times Area\left({\mathrm{mm}}^2\right)}}$$

(24)

The literature comparison is presented in Table 5, along with the respective $FoMs$ for each circuit. The designed LNA, using the proposed methodology, proved to be a high-performance and low-noise implementation compared to implementations found in the literature, while exhibiting the highest third-order intersect point. This comparison conclusively proves the efficiency of the proposed methodology in the task of synthesizing high-performance LNAs.

Table 5. Literature comparison of LNA implementations versus the LNA synthesized using the proposed methodology.

Parameter	[34] **	[35] *	[36] *	[37] *	[38] **	This Work *
Technology Process	22 nm	180 nm	130 nm	180 nm	65 nm	65 nm
Supply Voltage (V)	1	1.8	1.2	1.2	1.2	1.2
Frequency Range (GHz)	2.1–5.2	5–6	5.6–6	2.45	0.5–7	4–6.5 a
$S_{11}$ (dB)	<−10	$-10.8$	<−30	$-15.2$	<−12	$-33$
$S_{22}$(dB)	$NR$ b	$-23.3$	$NR$	$-2.2$	$NR$	$-15.5$
$S_{21}$ (dB)	12.7–15.7	14.9–15.4	17–25	13	16.8	15.6
$NF$ (dB)	1.5–2	1.6–1.8	2.6–2.9	2.5	2.9–3.8	2.7
$IP3$ (dBm)	$-6$	$-3$	$-3.8$	$0.84$	$-4.5$	$2.5$
Power (mW)	16	14.9	10.5	3.2	11.3	22
Silicon Area (mm2)	0.38	0.26	0.29	0.79 c	0.044	0.21
$Fo{M}_1$	8.44	23.42	19.54	17.3	38.4	34.7

^a Evaluated for frequencies at which $S_{11}\le -10$ dB; ^b Not Recorded; ^c Including Pads; * Simulation Results; ** Measurement Results.

4.2. VCO Implementation

The cross-coupled LC VCO, which was designed using a 65 nm RF-CMOS process, is illustrated in Figure 20. The complementary LC VCO architecture offers some advantages over a simpler design. This architecture provides two active circuits that replenish the lost energy of the tank; thus, the bias current is reused in this circuit by the PMOS devices, providing higher effective transconductance. Also, this architecture provides the advantage of producing twice the voltage swing for a given bias current and inductor design geometry. Lastly, it can maintain the output common-mode level at approximately equal to $V_{DD}/2$ if necessary. The design and LC tank parameters are extracted using the proposed methodology, and they are summarized in Table 6. The inductor’s and varactor’s parameters are also presented along with the extracted parallel resistance of the LC-tank exploring Z parameters, resulting in a parasitic resistance of $R_P=320\Omega$.

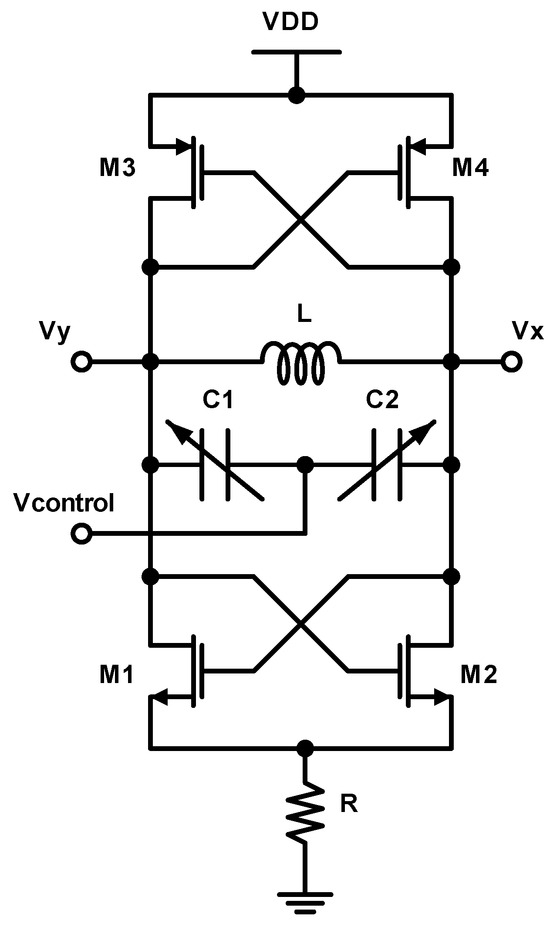
Figure 20. Cross-coupled LC VCO architecture.

Table 6. VCO design parameters.

Parameter	Value
Supply Voltage $V_{DD}$	1.2 V
Inductance L	5 nH
Inductor Width	5 μm
Inductor Inner Diameter $ID$	65 μm
Inductor Number of Turns $NT$	2
LC-Tank Parasitic Resistance $R_P$	$320\Omega$
${\left({\displaystyle \frac{W}{L}}\right)}_{M1,M2}$ (μm)	$14/0.08$
${\left({\displaystyle \frac{W}{L}}\right)}_{M3,M4}$ (μm)	$42/0.08$
Biasing Resistance R	$600\Omega$

The physical design of the synthesized VCO is depicted in Figure 21, while its frequency tuning range, its phase noise performance, and output transient signals in pre- and post-layout simulation schemes and the output frequency spectrum are illustrated in Figure 22, respectively. Moreover, to further validate the synthesized VCO design across process, temperature, and voltage corners, a PVT analysis is performed and the VCO performance is summarized in Table 7. It should be noted here that the synthesized design achieves the desired specifications only in the typical corner scenario since the algorithm used the typical models of the design components. Both LNA and VCO algorithms can use a model other than the typical one during their execution so as to achieve the desired specification in the worst case scenario. The proposed methodology has been meticulously applied to ensure that the power consumption of the circuit remains at 0.9 mW, using a supply voltage of $V_{DD}=1.2$ V. Moreover, the ratio of the widths of the PMOS and NMOS transistors is kept fixed and equal to $1/3$, ensuring equal transconductance for both NMOS and PMOS devices.

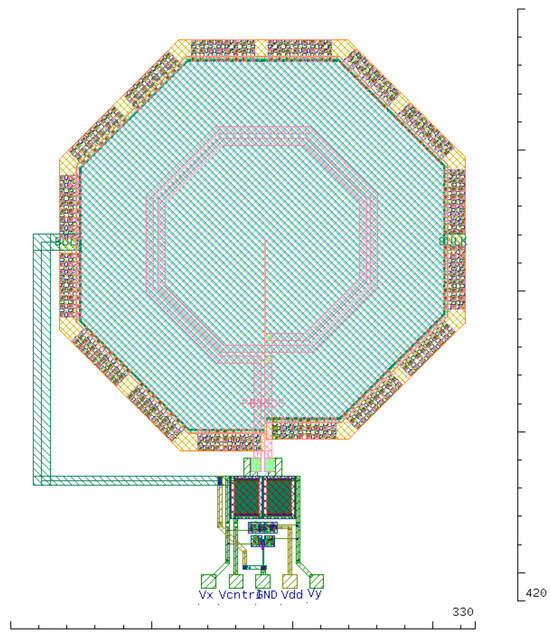
Figure 21. Physical design of the synthesized VCO.

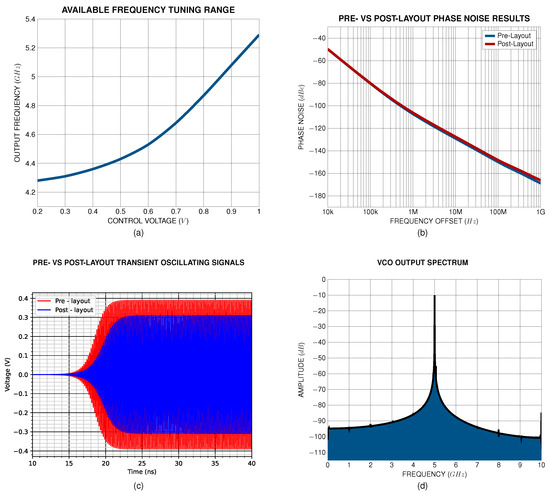
Figure 22. (a) Available frequency tuning range, pre- and post-layout; (b) phase noise performance; (c) output transient signals and (d) output frequency spectrum of the synthesized VCO.

Table 7. VCO design performance across process–temperature–voltage (PVT) corners.

Parameter	TT (${\mathit{T}}_{\mathit{A}}=27$ °C)	SS (${\mathit{T}}_{\mathit{A}}=80$ °C)	FF (${\mathit{T}}_{\mathit{A}}=0$ °C)
$V_{DD}$ (V)	1.2	1.1	1.3
$f_0$ (GHz) a	5	5.4	4.8
Freq. Range (GHz)	4.3–5.3	5–5.6	4.2–5
$f_0/\Delta f$ (%)	20	11	17
$P{N}_0$ (dBc/Hz)	−107.2	−100.9	−110.8
$V_{OUT}\left(V_{p-p}\right)$	0.78	0.3	1.1
$P_D$ (mW)	0.92	0.47	1.64

^a Evaluated for $V_{CONTROL}=0.875$ V.

The VCO design, implemented using the proposed methodology, achieves good phase noise performance of −106 dBc/Hz, evaluated at 1 MHz offset from the carrier frequency, while maintaining low power consumption. The tuning range of the oscillator extends up to 1 GHz, reaching $20\%$ tunable range, having as reference the center frequency of 5 GHz. Also, this tuning range ensures adaptability to process, voltage, and temperature (PVT) variations. Regarding the output signal swing, lower control voltages, and hence lower frequencies, lead to output amplitude degradation. This is a well-studied phenomenon, known as amplitude variation with frequency tuning, originating from the increased capacitance that is presented to the tank with low control voltages [39]. The parallel resistance $R_P$ also degrades in proportion to $\propto {\omega }^2$, and thus, amplitude variation is observed.

In the same manner, to prove that the synthesized VCO, using the proposed methodology, has industry-standard performance, a literature comparison is carried out, extracting another Figure of Merit (FoM) for each implementation according to the expression below [26]:

$$Fo{M}_2=PNOISE(dBc/Hz)-20log\left({\displaystyle \frac{f_0}{\Delta f}}\right)+10log\left({\displaystyle \frac{P_{DC}\left(mW\right)}{1mW}}\right)$$

(25)

The literature comparison is presented in Table 8, along with the respective $FoMs$ for each circuit. The VCO design, synthesized using the proposed methodology, proved to be a high-performance, low-power, and low-area implementation concerning other counterparts, found in the literature. Hence, using the proposed methodology, a low-phase-noise LC VCO can be efficiently synthesized, keeping optimum power consumption and low silicon footprint.

Table 8. Literature comparison of VCO implementations versus the VCO synthesized using the proposed methodology.

Parameter	[40] *	[41] **	[42] *	[43] **	[44] *	This Work *
Technology Process	130 nm	28 nm	65 nm	65 nm	180 nm	65 nm
Supply Voltage (V)	0.5	1.1	1.2	0.55	1.8	1.2
Frequency (GHz)	3.85–4.99	4.5–6.7	0.82–2.06	6.8–7.66	3.85–5.23	4.3–5.3
Tuning Range $(\%)$	22.8	39.3	89	12	31	20
Phase Noise (dBc/Hz) a	−120.8	−105.9	−127	−117.5	−115.3	−106.1
Power (mW)	0.7	4.35	5.3	5	4.5	0.85
Silicon Area (mm2)	0.18	0.17	$NR$ b	0.21	0.95	0.12
$Fo{M}_2$	−195.4	−172.1	−185.4	−187.2	−180.6	−180.8

^a Evaluated at 1 MHz offset; ^b Not Recorded; * Simulation Results; ** Measurement Results.

5. Conclusions and Future Work

In this work, a unified design methodology for front-end RF/mmWave receivers was proposed, focusing on the task of synthesizing low-noise amplifiers (LNAs) and voltage-controlled oscillators (VCOs) with industry-standard performance. The proposed methodology exploits scattering, impedance, and admittance parameters so as to derive well-defined cost functions that aid the design procedure, while also accelerating the design cycle of the circuit undergoing testing. From the well-defined cost function, two design algorithms were developed discretizing the design steps and calculating the component values of each circuit according to the given specifications. Hence, the design cycle of LNAs and VCOs was devised into well-defined steps with low design iteration loops, needed for the optimization of the circuit, while achieving the desired performance. For the proof of concept, two RF circuit blocks, an LNA and a VCO, most commonly used in RF/mmWave receiver systems, were synthesized using the proposed methodology, with a 65 nm RF-CMOS processing node. The derived circuits were compared to those found in the literature, proving the efficiency of the proposed methodology in the task of synthesizing LNAs and VCOs with industry-standard performance, in a time-conservative manner.

As a future work, the proposed algorithms will be tailored accordingly so as to be able to run using the Python interface while simultaneously exploiting the advantages of the SpectreRF simulator. Hence, the design methodology will be fully automated, with call-back functions and procedures, dictated by the proposed cost functions and algorithms, presented in this work. Due to the linear behavior of the LNAs and VCOs that the proposed methodology addresses, some of the procedures can be easily surpassed by means of Machine Learning (ML) frameworks, focusing on pre-characterizing the design space and minimizing the iteration loops included within each methodology algorithm. In this way, the design methodology will be fully automated, while the run time will eventually shrink to a few seconds or hours, for the entire design of the front-end RF/mmWave blocks under development.