DVIOR: Dynamic Vertical and Low-Intensity Outlier Removal for Efficient Snow Noise Removal from LiDAR Point Clouds in Adverse Weather

Abstract

With the advancement of autonomous driving technology, the performance of LiDAR in adverse weather conditions has garnered increasing attention. Traditional denoising algorithms, including intensity-based methods like LIOR (a representative intensity-based filter that relies solely on signal intensity), have limited effectiveness in handling snow noise, especially in removing dynamic noise points and distinguishing them from environmental features. This paper proposes a Dynamic Vertical and Low-Intensity Outlier Removal (DVIOR) algorithm, specifically designed to optimize LiDAR point cloud data under snowy conditions. The DVIOR algorithm, as an extension of intensity-based filtering augmented with vertical height information, dynamically adjusts filter parameters by combining the height and intensity information of the point cloud, effectively filtering out snow noise while preserving environmental features. In our experiments, the DVIOR algorithm was evaluated on several publicly available adverse weather datasets, including the Winter Adverse Driving Scenarios (WADS), the Canadian Adverse Driving Conditions (CADC), and the Radar Dataset for Autonomous Driving in Adverse weather conditions (RADIATE) datasets. Compared with both the mainstream dynamic distance–intensity hybrid algorithm in recent years, Dynamic Distance–Intensity Outlier Removal (DDIOR), and the representative intensity-based filter LIOR, DVIOR achieved notable improvements: it gained a 10.2-point higher F1-score than DDIOR and an 11.8-point higher F1-score than LIOR (79.00) on the WADS dataset. Additionally, DVIOR performed excellently on the CADC and RADIATE datasets, achieving F1-scores of 87.35 and 86.68, respectively—representing an improvement of 19.82 and 36.9 points over DDIOR and 4.67 and 17.95 points over LIOR (82.68 and 68.73). These results demonstrate that the DVIOR algorithm outperforms existing methods, including both distance–intensity hybrid approaches and intensity-based filters like LIOR, in snow noise removal, particularly in complex snowy environments.

1. Introduction

In recent years, the rapid development of LiDAR technology has significantly enhanced the accuracy and resolution of remote sensing data, making it indispensable in areas such as environmental monitoring, urban planning, and autonomous driving [1,2,3]. LiDAR technology uses laser beams to measure distances to objects, generating high-density point cloud data that provides robust support for precise analysis and decision making. However, despite LiDAR’s outstanding performance in many applications, its performance under snowfall conditions significantly deteriorates [4,5,6,7,8]. Snowflakes, as dynamic noise sources, interfere with LiDAR detection results, as illustrated in Figure 1. This phenomenon is especially critical in autonomous driving systems. Most current autonomous driving perception algorithms are developed and benchmarked in clear weather, leading to unstable performance in snowy or other harsh weather conditions [9,10]. In real driving scenarios, snow noise can be misinterpreted as road obstacles, increasing the risk of accidents and posing severe safety hazards. Even minor sensor errors can lead to serious traffic accidents, endangering human lives. Therefore, improving the performance of LiDAR systems in snow and other adverse weather conditions is a key challenge for enhancing the safety of autonomous driving systems.

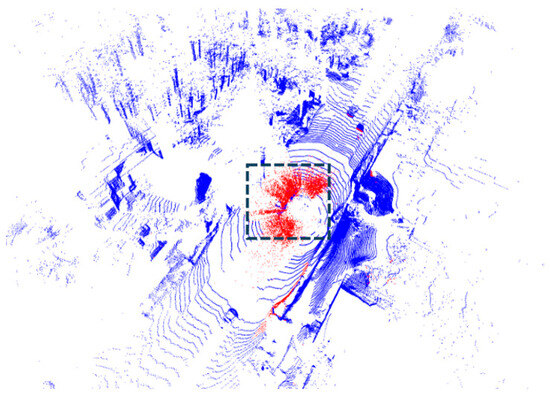
Figure 1. Vehicles in the black frame line are covered due to the red snow noise.

In adverse weather conditions, the impact of snow noise on LiDAR point cloud data is significant. Traditional denoising algorithms perform well in filtering static noise but struggle when dealing with highly dynamic noise sources such as snowflakes. This type of noise not only misleads perception systems by falsely identifying snow noise as obstacles but can also lead to the loss of environmental features, thus affecting the decision-making accuracy of autonomous driving systems. Therefore, efficiently removing snow noise from LiDAR point clouds while preserving essential environmental features has become a critical challenge for current autonomous driving perception systems [11,12].

To solve the problem of removing more snow noise points (recall) while retaining necessary environmental features (precision) with stronger robustness, we propose a new Dynamic Vertical and Low-Intensity Outlier Removal (DVIOR) algorithm. DVIOR particularly considers the vertical characteristics of snow noise and the low-intensity values of snowflakes, effectively filtering snow noise from LiDAR point clouds while preserving environmental features. Our method performs well on the WADS [13], CADC [14], and RADIATE [15] datasets, dynamically adapting to different noise conditions and significantly improving the reliability of LiDAR-based remote sensing applications. The main contributions of this paper are summarized as follows:

(1)

To address the key challenge that existing LiDAR snow noise removal methods struggle to balance snow noise elimination and environmental feature preservation (a critical bottleneck for autonomous driving perception accuracy in adverse weather), this study focuses on the unmet demand for robust dynamic filtering and establishes a targeted technical framework that integrates snow noise characteristics with point cloud spatial attributes;

(2)

According to the characteristics of snow noise points, a dynamic filter DVIOR is proposed, which combines the distance, height, and intensity of the point cloud;

(3)

Experiments on the MSP (WADS, CADC, RADIATE) datasets demonstrate that DVIOR outperforms DDIOR, with F1-scores exceeding DDIOR by 10.20, 19.82, and 36.9, respectively.

2. Related Works

2.1. Datasets

The WADS [13] dataset stands out as a key multimodal resource for studying adverse winter driving conditions. Collected in the “snow belt” region of Michigan’s Upper Peninsula, it features extensive LiDAR point cloud data captured during extreme winter weather scenarios, including heavy snowfall, snow-covered roads, and icy conditions. A notable aspect of the WADS dataset is its provision of point-level annotated LiDAR scans alongside data from other sensors such as cameras and radar. With over 26 TB of multimodal data, including more than 7 GB of LiDAR point cloud data (approximately 3.6 billion points), it serves as a rich resource for evaluating LiDAR performance in harsh winter conditions, making it ideal for testing snow noise removal algorithms.

In contrast, the CADC [14] dataset focuses on capturing sensory data in adverse Canadian driving conditions, encompassing LiDAR, camera, and radar data recorded during snowy and rainy weather. Although CADC primarily provides bounding box annotations for object detection rather than point-level snow noise labels, it remains an important dataset for investigating the performance of autonomous driving systems in cold weather.

The RADIATE [15] dataset emphasizes the collection of radar and LiDAR data under adverse weather conditions to support the development of autonomous perception systems capable of operating in complex environments. The LiDAR data in RADIATE include recordings captured during various weather conditions, such as rain, fog, and snow. Similar to CADC, RADIATE primarily provides bounding box annotations for object detection tasks, but it also contains substantial noise points within its LiDAR data. This dataset is particularly useful for examining the generalization capabilities of noise removal algorithms and testing their robustness across different weather scenarios. Alongside CADC, the DENSE [16] dataset (a European project focusing on developing and enhancing the safety of autonomous vehicles in severe environments) is another valuable resource. It collects multisensory data, including LiDAR and radar, under various adverse weather conditions such as rain, snow, fog, and low light, aiming to enhance perception systems for autonomous vehicles in harsh environments. The combination of diverse weather conditions and complex urban environments in CADC and DENSE makes them both useful tools for testing noise removal algorithms, particularly in preserving environmental features and managing dynamic noise points.

The MSP [17] dataset represents a filtered and reconstructed LiDAR point cloud dataset that integrates existing snowy LiDAR datasets, including CADC and RADIATE. MSP provides point-level annotations for snow noise points in the LiDAR point clouds from these datasets, creating a hybrid snow point cloud dataset. This offers a solid foundation for the development of precise noise removal algorithms and is especially suitable for statistical analysis and performance evaluation, effectively validating the performance of various algorithms in real-world snowy scenarios. Table 1 shows the characteristics of the various datasets.

Table 1. Lidar dataset comparison for adverse weather.

Dataset	Channels	Features	Sensors	Weather Conditions	Annotations	Data Size
DENSE	32 channels	Focus on enhancing perception systems for autonomous driving in severe conditions	LiDAR, Radar, Cameras	Snow, Rain, Fog, Low Light	Primarily bounding boxes for object detection	Approx. 8 TB
CADC	32 channels	Canadian winter conditions, urban/rural driving environments	LiDAR, Radar, Cameras	Snow, Rain	Bounding boxes for object detection	200 GB+
RADIATE	64 channels	Adverse weather focus, complex environments	LiDAR, Radar, Cameras	Rain, Snow, Fog, Low Light	Bounding boxes for object detection	Approx. 400 GB
WADS	32 channels	Collected in extreme winter conditions in Michigan’s Upper Peninsula	LiDAR, Radar, Cameras	Heavy Snowfall, Icy Roads, Snow-Covered Roads	Point-level LiDAR annotations	26 TB (7 GB LiDAR, 3.6 billion points)

2.2. Filter

Although many algorithms have been proposed for removing LiDAR noise, each with its own strengths, there are still significant limitations when dealing with complex and dynamic environments. For example, commonly used algorithms like Statistical Outlier Removal (SOR) and Radius Outlier Removal (ROR) [18] typically identify and filter out noise points by detecting local density differences in the point cloud. However, these methods struggle to handle dynamic noise sources, especially unevenly distributed noise like snowflakes, because they rely on fixed filtering radii or thresholds, which are not well-suited for the rapidly changing and randomly distributed noise caused by snow.

To improve the filtering performance, some studies have proposed dynamically adjustable filtering methods. For instance, Dynamic Radius Outlier Removal (DROR) [19] adjusts the filtering radius dynamically based on the distance between each point and the LiDAR sensor, which partly addresses the limitations of fixed-radius methods. In light snowfall and simpler noise scenarios, DROR can significantly enhance noise removal. However, as snowfall intensity increases or noise point distribution becomes more complex, the performance of DROR starts to decline noticeably, particularly in distant scenes where important environmental information is often lost.

To tackle this issue, researchers have introduced Dynamic Statistical Outlier Removal (DSOR) [13], which not only takes point cloud distance information into account but also incorporates statistical analysis to assess the distribution of noise points at different distances. DSOR performs well in removing snow noise from distant scenes and achieves a high recall rate in more severe snowfall conditions. Nevertheless, while DSOR is effective in long-range scenarios, its performance in short-range environments remains limited.

Following DSOR, Low-Intensity Outlier Removal (LIOR) [10] was proposed to specifically address noise points with very low reflectivity, such as those generated by snowflakes. LIOR effectively filters out low-intensity noise points from the point cloud, particularly in scenarios where snowflakes cause significant interference. However, LIOR also faces challenges in maintaining a balance between precision and recall in dynamic environments, as it struggles with the rapid changes in noise characteristics that occur in adverse weather conditions.

Among dynamic hybrid filtering methods for snow noise removal, Dynamic Distance–Intensity Outlier Removal (DDIOR) [20] is a mainstream representative in recent years. This method combines point cloud distance and reflectance intensity information to quickly and effectively eliminate snow noise while preserving some environmental features. However, DDIOR still lacks adaptability in diverse environments. Its filtering strategy may lead to either over-filtering or under-filtering in certain extreme weather or complex terrain conditions, resulting in the loss of environmental information or the incomplete removal of noise.

Deep learning-based snow noise removal methods, combined with a Weather Recognition Network (WeatherNet) [21], can dynamically adjust the filtering parameters of noise removal algorithms based on real-time weather conditions, thereby enhancing adaptability in complex environments. This approach can significantly improve the accuracy and reliability of noise removal. However, its limitations include the need for a large amount of high-quality annotated data and the requirement for further validation of the model’s generalization capability in extreme weather conditions. This may result in suboptimal performance of the algorithm in certain specific environments.

3. Method

In adverse weather conditions, LiDAR point clouds are affected to varying degrees. Rain and fog, for example, cause laser signals to scatter and attenuate, leading to degraded point cloud data quality [22]. Snowflakes not only scatter laser signals but may also adhere to the LiDAR sensor, further reducing signal strength. The current mainstream approach (DSOR, DDIOR, LIOR, WeatherNet) typically considers factors such as the density, distance, and reflectance intensity of snowflakes but often neglects the vertical characteristics of snow noise points, specifically their height information [23]. This section will detail the characteristics of snow noise data and the implementation process of the DVIOR filter. Figure 2 shows the DVIOR framework.

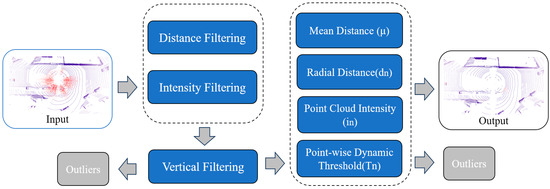
Figure 2. Process of DVIOR algorithm; red is snow.

3.1. Characteristics of Snow Noise

During snowfall, the intensity values of snow noise points are usually low, reflecting the weak reflective ability of snowflakes to laser signals [24]. At the same time, the spatial distribution of snow noise points tends to be disordered, often appearing in a random scatter pattern, making it difficult to form the regular shapes seen in real objects. Additionally, the height values of snow noise points show significant fluctuations, with a high degree of randomness, resulting in large differences from the ground or object surface heights. These noise points are typically concentrated near the sensor, as snowflakes are more likely to interact with the laser at short distances [25,26]. On the other hand, the distance measurements of snow noise points often contain errors, as the laser sensor struggles to accurately distinguish between snowflakes and real objects, leading to inaccuracies in measurements. The distribution and density of snow noise points are also influenced by dynamic changes in weather conditions, showing temporal instability, which leads to noticeable differences in noise characteristics at different times of data collection [27,28,29]. These characteristics present significant challenges for processing point cloud data and impact the final perception accuracy.

Therefore, snow noise points are analyzed in detail in this paper. Several main datasets for adverse weather conditions include DENSE, CADC, RADIATE, and WADS, but DENSE, CADC, and RADIATE only provide bounding box annotations without fine-grained labels for snow noise points, complicating the statistical analysis. Sun et al. introduced the MSP [17] dataset, which filters and reconstructs existing snowy LiDAR datasets, labeling snow points in each point cloud frame to form a hybrid snow point cloud dataset.

This paper selected three representative winter adverse weather datasets—WADS, CADC, and RADIATE—as raw data sources to analyze the characteristics of snow noise in these datasets. As shown in Figure 3, the number of LiDAR points decreases with increasing scan distance, and most snow noise points are concentrated near the LiDAR sensor, within a radial distance of 50 m, with intensity below 0.4 and an absolute height within 5 m. Based on these characteristics, the DVIOR filter is designed.

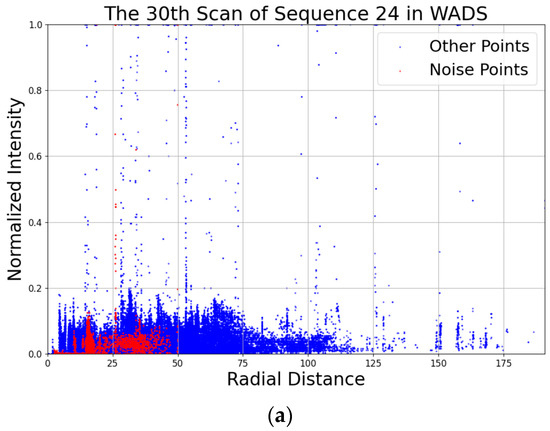
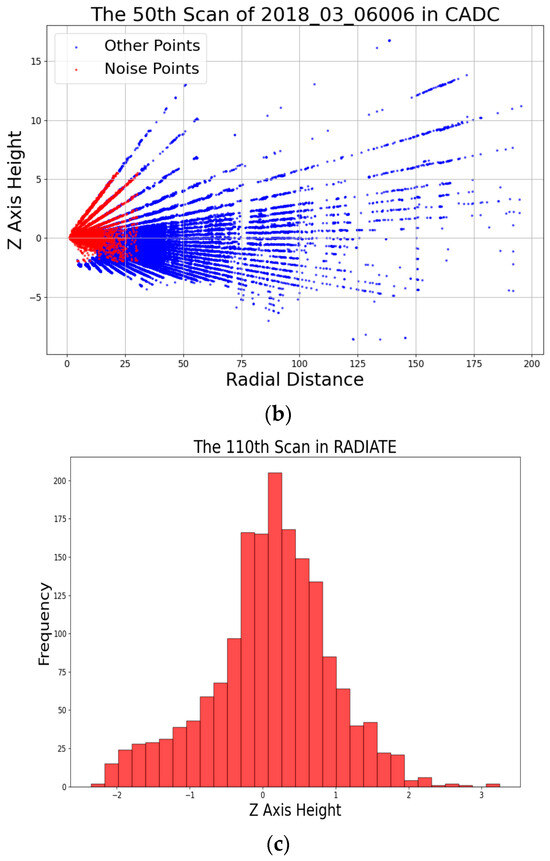
Figure 3. (a) Intensity distribution of snow noise points in the 30th scan of sequence 24 from the WADS dataset. (b) z-axis height distribution of snow noise points in the 50th scan of sequence 006 from the CADC dataset. (c) Frequency of z-axis height occurrences for snow noise points in the 110th scan from the RADIATE dataset. Red is snow noise; blue is non-noise points. All distance and height values are in meters.

3.2. DVIOR

DVIOR algorithm is designed to effectively tackle the challenge of snow noise in LiDAR point clouds, particularly in adverse weather conditions. Unlike conventional methods, DVIOR focuses on the unique characteristics of snow noise, such as its low intensity and its concentration in vertical regions of the point cloud. By dynamically adjusting filter parameters based on the height, intensity, and distance of the points, DVIOR achieves more accurate removal of noise while preserving critical environmental features.

One of the key innovations of DVIOR lies in its ability to adapt the filtering process according to the spatial and intensity distribution of the snow noise. This adaptive approach ensures that snowflakes, which typically exhibit low intensity and are often located close to the LiDAR sensor, are correctly identified and filtered out, minimizing the impact on the surrounding environment and ensuring a higher fidelity of the resulting point cloud.

The DVIOR algorithm can be broken down into several distinct steps. The first step is to separate the snow noise points around the sensor, using multiple threshold conditions to filter out some snow points. For each point $P_n=(x_n,y_n,z_n)$, we have the following:

$$D=d_{max}\times \alpha$$

(1)

where $d_{max}=\mathrm{m}\mathrm{a}\mathrm{x}\left\{d_n=\sqrt{x_n^2+y_n^2+z_n^2}\right\}$, with n = 1, …, i being the maximum radial distance, and $\alpha$ is the distance coefficient set to 0.1. For points where $d_n$ < $d_{max}\times \alpha$, we further check if $\left|Z_n\right|<{\displaystyle \frac{Z_{max}}{2}}$ and $i_n<0.1$, and if both conditions hold, we filter out these low-intensity points near the sensor. The remaining points are processed in the next step.

The second step applies dynamic filtering to the remaining points based on their intensity and distance from the LiDAR:

$$T_n=\mu \times r\times [0.1\times (i_n+{\displaystyle \frac{r}{d}}\left)\right]$$

(2)

where $\mu$ is the mean distance, $i_n$ is the point’s intensity, $r$ is the distance to the LiDAR, and $d$ is the radial distance. As the ratio of $r$ to $d$ increases, $d$ decreases, indicating a lower height point cloud, resulting in a more conservative filter. Conversely, when $d$ increases, the filter becomes more aggressive.

After dynamic filtering, we obtain the snow-free point cloud with rich environmental features. Algorithm 1 presents the pseudocode for DVIOR.

Algorithm 1: Dynamic Vertical and Low-Intensity Outliers Removal

Input: Point Cloud $P=p_n;p_n=\left(x_n;y_n;z_n;i_n\right);$ $n=1,\dots ,N$; $K=\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{b}\mathrm{o}\mathrm{r}\mathrm{s}$ Output:  Outliers (O)  Filtered point cloud (F)

1: P ← KdTree; 2: for $p_n\in$ P do 3: $d_n$ = $\sqrt{x_n^2+y_n^2+z_n^2}$ 4:  if $d_n<d_{max}\times \alpha$ then 5:   if ${|Z}_n|<{\displaystyle \frac{Z_{max}}{2}}\&i_n<0.1$ then 6:    O ← $p_n$ 7:   else 8:    F ← $p_n$ 9:   end if 10:     end if 11:     end for 12:     for $p_i\in$ F do 13:     mean_distances ← nearestKSearch(K) 14:     calculate: mean(μ) ← mean_distances 15:     distance ← $\sqrt{x_i^2+y_i^2+z_i^2}$ 16:     r ← $\sqrt{x_i^2+y_i^2}$ 17:    calculate: $T_n\leftarrow \mu \times r\times [0.1\times (i_n+{\displaystyle \frac{r}{d}}\left)\right]$ 18:     if mean_distances < $T_n$ then 19:       F ← $p_i$ 20:     else 21:       O ← $p_i$ 22:     end if 23:     end for 24:     return F, O

4. Experimental Results and Analysis

This paper’s experiments were conducted on the WADS and MSP datasets (which include CADC and RADIATE). These datasets provide point-level annotations, facilitating statistical results. All experiments were performed on a laptop equipped with an Intel i7-12650H CPU and 16 GB of RAM.

4.1. Qualitative Evaluation

In this part, we qualitatively evaluate the filtering effect of the DVIOR algorithm. DDIOR is a widely used baseline for dynamic hybrid filtering in recent studies, an extension of DSOR that incorporates intensity and distance factors. To clarify the parameter settings for subsequent quantitative and qualitative evaluations, we first note that the K-Nearest Neighbors (KNN) algorithm is used in this study to search for local adjacent points in the LiDAR point cloud. This algorithm identifies the k closest points to a target point, and the “number of neighbors k” (a core parameter of KNN) directly affects the filtering granularity—too small a k may lead to over-filtering of valid points, while too large a k may miss snow noise. Since the DDIOR and LIOR algorithms are not open source, we implemented them ourselves for further analysis. The parameter values for the number of neighbors k were set to 5, and the dynamic distance coefficient ${\alpha }_r$ was set according to the original paper. The details are shown in Table 2.

Table 2. Parameters of each de-snowing method.

Algorithm	Parameters	Values
DSOR	k for KNN search	5
	the global threshold constant	0.01
	the range multiplicative factor	0.05
LIOR	searching radius	0.1 m
	min. number of neighbors	3
	snow detection range	71.235 m
	intensity threshold constant	0.066
DDIOR	k for KNN search	5
DVIOR	k for KNN search	5
	distance threshold	intensity threshold
	intensity threshold	1.0

The experimental results are presented in Figure 4, which shows the original point cloud, the point cloud processed by DDIOR, and the point cloud processed by DVIOR. On the whole, DVIOR preserves environmental features well while removing snow noise points. In contrast, while removing a large number of noise points, DDIOR is often accompanied by the loss of part of the environmental features, especially in long-distance or high noise density scenes; its filtering effect is not ideal. Although DDIOR was able to remove most of the close snow noise points, some noise remained in the regions with high noise density. By dynamically adjusting the filter parameters, DVIOR can further remove these difficult noise points while effectively preserving environmental features such as trees and buildings.

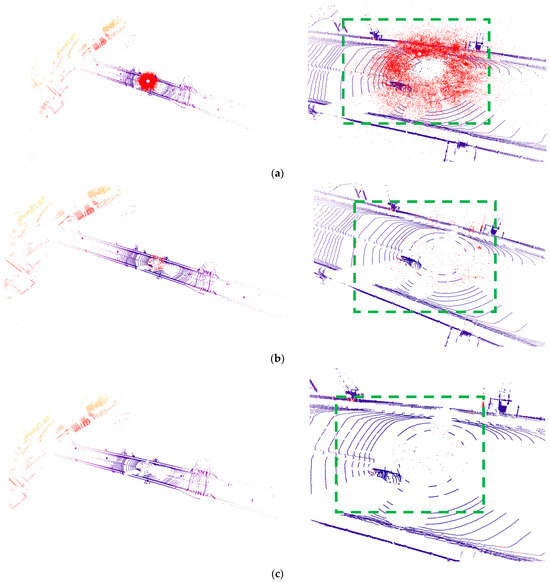
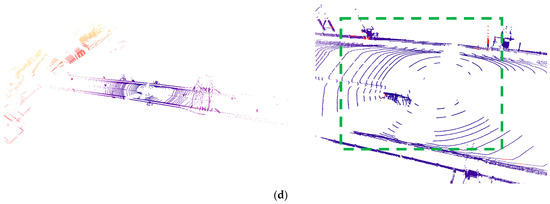
Figure 4. From top to bottom, (a) is the original point cloud, (b) is LIOR, (c) is DDIOR, and (d) is DVIOR. The left is the visualization result of the overall filtering effect, the right is the visualization result of the local amplification filtering effect, and red is the snow noise point. It can be seen from the figure that DVIOR effectively filters out the vehicle noise from the snow noise (the green box marked with a frame).

In terms of local details, DVIOR performs particularly well. Especially in long-distance point cloud data, DDIOR tends to misjudge some environmental points with lower intensity as noise points, thus filtering them out. However, DVIOR successfully avoids this problem by combining the height information and intensity features of the point cloud, ensuring the integrity of the environmental features at a long distance. This advantage is particularly important in applications such as autonomous driving that require high accuracy of environment perception, since subtle features in the environment play a key role in path planning and obstacle identification.

4.2. Quantitative Evaluation

This paper uses precision and recall analysis to quantitatively evaluate the proposed method. The essence of snow noise removal in adverse weather conditions is to remove more snow noise points (high recall) while preserving environmental features (high precision). An overly conservative filter may increase precision but reduce recall, meaning fewer snow noise points are removed. Conversely, an overly aggressive filter may increase recall but reduce precision, as more environmental features are lost along with the snow noise points. To balance these two factors and assess the performance of the algorithm, we used the F1-score as the main evaluation metric. Furthermore, we conducted ablation experiments on the DVIOR algorithm and obtained the data without considering the vertical characteristics of the z-axis. Precision, recall, and F1-score are defined as follows:

$$Precision={\displaystyle \frac{TP}{TP+FP}},Recall={\displaystyle \frac{TP}{TP+FN}}$$

(3)

$$F1={\displaystyle \frac{2}{\frac{1}{Precision}+\frac{1}{Recall}}}$$

(4)

where TP represents true positives (snow noise points correctly removed from the original point cloud), FP represents false positives (non-snow noise points incorrectly removed), and FN represents false negatives (snow noise points left in the point cloud after filtering). Precision, recall, and F1-score are calculated as the average values of 100 frames from 10 sequences for the WADS and CADC datasets, while for RADIATE, they are calculated as the average values of 500 frames.

Table 3 provides a quantitative comparison of DSOR, DDIOR, LIOR, DVIOR, DVIOR (no z-axis), and WeatherNet on the WADS, CADC, and RADIATE datasets. Firstly, on the WADS dataset, DVIOR achieves an F1-score of 90.80, significantly higher than DDIOR’s 80.60, LIOR’s 79.00, and DVIOR’s (no z-axis) 78.07—a 12.73-point improvement over the z-axis-free variant. As a filter that extends intensity-based denoising by incorporating vertical Z-value, DVIOR outperforms LIOR while also surpassing DDIOR and its own z-axis-free version. Specifically, DVIOR’s precision reached 86.02 compared to DDIOR’s 69.87, LIOR’s 80.90, and DVIOR’s (no z-axis) 64.73; this gap confirms that the vertical Z-value effectively reduces the misclassification of low-intensity environmental points (e.g., distant tree branches or road curbs) as noise, a flaw that plagues the z-axis-free variant. Furthermore, DVIOR’s recall was 96.25—slightly lower than DVIOR’s (no z-axis) 98.33, but far higher than LIOR’s 78.10—demonstrating that z-axis integration balances noise capture and feature preservation, whereas the z-axis-free version sacrifices precision for overly high recall. In comparison, while DDIOR also has a high recall (95.23), its disadvantage in precision results in a lower overall F1-score. Furthermore, although the accuracy of WeatherNet is higher than that of DVIOR, its recall rate and F1-score are not better than those of DVIOR. In other words, WeatherNet removes fewer snow noise points, which may improve the accuracy. Moreover, applying deep learning methods to autonomous driving systems is a challenge.

Table 3. Quantitative comparison on de-snowing.

Dataset	Method	Precision	Recall	F1-Score
WADS [13]	DSOR	65.07	95.60	77.43
	LIOR	80.90	78.10	79.00
	DDIOR	69.87	95.23	80.60
	WeatherNet	94.88	85.13	89.74
	DVIOR	86.02	96.25	90.80
	DVIOR (no z-axis)	64.73	98.33	78.07
CADC [14]	DSOR	71.55	96.01	81.74
	LIOR	76.64	89.75	82.68
	DDIOR	51.96	98.60	67.53
	DVIOR	83.92	91.07	87.35
	DVIOR (no z-axis)	75.72	91.65	82.92
RADIATE [15]	DSOR	29.43	99.19	45.39
	LIOR	56.73	86.66	68.73
	DDIOR	36.04	80.40	49.78
	DVIOR	78.93	96.11	86.68
	DVIOR (no z-axis)	59.33	96.88	73.60

The experimental results on the CADC dataset further confirmed that DVIOR achieved an F1-score of 87.35, significantly higher than DDIOR’s 67.53, LIOR’s 82.68, and DVIOR’s (no z-axis) 82.92. As an extension of intensity-based approaches with vertical Z-value integration, DVIOR outperforms both DDIOR, LIOR, and its z-axis-free counterpart here. In this dataset, DVIOR’s precision was 83.92, while DDIOR’s was only 51.96, LIOR’s was 76.54, and DVIOR’s (no z-axis) was 75.72. This indicates that the vertical Z-value is critical for distinguishing high-altitude snow noise from elevated environmental features (e.g., street lamps or building eaves)—a task the z-axis-free variant fails to complete, leading to lower precision. DVIOR also exhibited strong recall, reaching 91.07—comparable to DVIOR’s (no z-axis) 91.65 and higher than LIOR’s 89.75—adapting well to the more complex noise distribution conditions present in the CADC dataset.

In the RADIATE dataset, DVIOR’s performance was particularly outstanding, achieving an F1-score of 86.68 compared to DDIOR’s 49.78, LIOR’s 68.73, and DVIOR’s (no z-axis) 73.60—representing a 36.9 improvement over DDIOR and a 13.08-point improvement over the z-axis-free variant. As a method that augments intensity-based filtering with vertical Z-value, DVIOR distinguishes itself in handling high-noise-density scenarios, where the z-axis-free variant struggles. In the experiments on this dataset, DVIOR’s precision was 78.93, whereas DDIOR only reached 36.04, LIOR reached 56.73, and DVIOR (no z-axis) only reached 59.33. This result illustrates that the vertical Z-value helps DVIOR effectively distinguish dense snow noise from low-intensity environmental points (e.g., asphalt textures or small obstacles), while the z-axis-free variant succumbs to ambiguity and over-filters valid points. DVIOR also maintained an advantage in recall, with a rate of 96.11—slightly lower than DVIOR’s (no z-axis) 96.88 but still exceeding LIOR’s 86.66—ensuring that the majority of snow noise points were accurately identified and removed.

In summary, DVIOR—an extension of intensity-based filtering enhanced by vertical Z-value—demonstrated exceptional denoising capabilities across the WADS, CADC, and RADIATE datasets, surpassing DDIOR (a distance–intensity hybrid), LIOR (a representative intensity-based filter), and DVIOR (no z-axis) in core metrics such as precision and F1-score. The consistent performance gap between DVIOR and its z-axis-free variant confirms that integrating vertical Z-value with intensity information provides complementary spatial context: it avoids the precision loss of the z-axis-free version (caused by misclassifying environmental points as noise) while retaining high recall, addressing a key limitation of pure intensity-based methods. Additionally, DVIOR exhibited stability under varying noise densities and distance conditions. This indicates that DVIOR is effective in removing noise points while maintaining a high degree of environmental feature retention, making it suitable for point cloud data processing tasks in various challenging weather conditions. The improvements over LIOR and DVIOR (no z-axis) further validate the necessity of the vertical Z-value as DVIOR’s core innovation.

5. Conclusions

This paper introduces the DVIOR algorithm, which effectively removes snow noise from LiDAR point clouds under adverse weather conditions, providing more reliable data for autonomous driving applications. As an extension of intensity-based filtering augmented with vertical Z-value, DVIOR demonstrates significant advantages over both traditional distance/intensity hybrid algorithms (e.g., DSOR, DDIOR) and representative intensity-based methods (e.g., LIOR). It excels particularly in filtering low-intensity, high-concentration snow noise points in long-range and heavy snowfall scenarios. Across the WADS, CADC, and RADIATE datasets, DVIOR achieves precisions of 86.02%, 83.92%, and 78.93%, respectively—outperforming LIOR (a typical intensity-based filter) in preserving environmental features while removing noise, as LIOR relies solely on intensity and often struggles with misclassifying scene points or incompletely capturing snow noise.

Experimental results show that on the WADS dataset, DVIOR outperforms DDIOR by 10.20 points in F1-score, DSOR by 13.37 points, and LIOR by 11.80 points. In the CADC dataset, DVIOR’s F1-score (87.35) surpasses DDIOR (67.53), DSOR (81.74), and LIOR (82.68)—with DVIOR striking a better balance between precision and recall than LIOR when facing complex noise distributions. For the RADIATE dataset, DVIOR’s F1-score (86.68) exceeds DDIOR (49.78), DSOR (45.39), and LIOR (68.73)—proving superior at distinguishing noise from environmental points under high noise density, where LIOR’s pure intensity-based approach leads to greater ambiguity. Thus, DVIOR proves more effective in snow noise removal across diverse environments.

In future work, DVIOR can be further optimized to handle a wider range of adverse weather conditions (e.g., rain, fog) and be adapted to various sensor systems. Moreover, dynamically integrating vertical and intensity characteristics of point clouds for adaptive filtering is a promising direction to enhance LiDAR systems’ performance in complex environments. This research lays the foundation for advancing autonomous driving technology by improving point cloud reliability in challenging weather.