A Multi-Agent Deep Reinforcement Learning Anti-Jamming Spectrum-Access Method in LEO Satellites

Abstract

Low-Earth-orbit (LEO) satellite networks face significant vulnerabilities to malicious jamming and co-channel interference, compounded by dynamic topologies, resource constraints, and complex electromagnetic environments. Traditional anti-jamming approaches lack adaptability, centralized intelligent methods incur high overhead, and distributed intelligent methods fail to achieve global optimization. To address these limitations, this paper proposed a value decomposition network (VDN)-based multi-agent deep reinforcement learning (DRL) anti-jamming spectrum access approach with a centralized training and distributed execution architecture. Following offline centralized ground-based training, the model was deployed distributedly on satellites for real-time spectrum-access decision-making. The simulation results demonstrate that the proposed method effectively balances training costs with anti-jamming performance. The method achieved near-optimal user satisfaction (approximately 97%) with minimal link overhead, confirming its effectiveness for resource-constrained LEO satellite networks.

1. Introduction

Low-Earth-orbit (LEO) satellites offer significant advantages, including low-latency communication, high data rates, and wide geographical coverage capabilities [1,2]. These attributes make their application a powerful supplement to terrestrial networks [3,4], and they have broad application prospects [5]. In recent years, the global deployment of LEO constellations (e.g., Starlink, OneWeb, and Kuiper) has been rapidly expanding in both speed and scale [6]. However, the inherent exposure of satellites and their reliance on open wireless channels make them susceptible to external malicious jamming and internal co-channel interference. Consequently, developing effective anti-jamming techniques is critical to ensure communication security. However, dynamic topologies [7], limited resources [8], and complex electromagnetic conditions [9] in LEO networks pose significant challenges to achieving this goal.

Extensive research has been dedicated to anti-jamming technologies. Overall, the existing approaches can be divided into two categories: traditional anti-jamming technologies and intelligent anti-jamming technologies.

1.1. Traditional Anti-Jamming Techniques

Direct-sequence spread spectrum (DSSS) and frequency-hopping spread spectrum (FHSS) constitute the foundational techniques for anti-jamming communications [10]. The authors of [11] proposed the Turbo iterative acquisition algorithm based on factor graph modeling of time-varying Doppler rate to address the challenges of DSSS signal acquisition in highly mobile satellite communications. Ref. [12] proposed random differential DSSS based on the traditional DSSS technology, which can effectively alleviate reactive jamming attacks. FHSS uses pre-shared pseudorandom sequences to switch communication frequencies. Ref. [13] proved that the performance of FHSS signals is superior to that of DSSS signals, and FHSS signals are suitable for application in military satellite communication. The authors of [14] achieved a stable connection and good anti-jamming ability by applying adaptive frequency hopping technology. Ref. [15] proposed dynamic spectrum-access technology (DSA) based on cognitive database control, and it achieved co-channel sharing between non-terrestrial networks and terrestrial networks. The authors of [16] presented anti-jamming technologies in the time and transform domains and further investigated spatial-domain techniques, space–time processing, and adaptive beamforming based on array antennas. However, these methods typically rely on predefined rules or static configurations. Although effective in stable environments, their fixed strategies lack adaptability in high-mobility LEO satellite networks with dynamic uncertainties.

1.2. Intelligent Anti-Jamming Techniques

Intelligent anti-jamming techniques can explore the environment through trial-and-error, enabling them to learn to make robust and adaptive anti-jamming decisions under highly dynamic and uncertain conditions [17]. The adaptive learning capabilities, ability to handle complex high-dimensional state spaces, and innovative distributed/collaborative learning paradigms of these intelligent technologies overcome traditional bottlenecks and address anti-jamming challenges in satellite communications [18,19]. The authors of [20] proposed a decentralized federated learning-assisted deep Q-network (DQN) algorithm to determine collaborative anti-jamming strategies for UAV pairs. In  [21], an energy-saving and anti-jamming communication framework of a UAV cluster based on multi-agent cooperation was constructed. Ref. [22] introduced a deep reinforcement learning (DRL)-based dynamic spectrum-access method with accelerated convergence where soft labels replace conventional reward signals; it reduced iteration counts. Ref. [23] proposed an intelligent dynamic-spectrum anti-jamming communication approach based on DRL, and it improved in a trial-and-error manner to adapt to the dynamic nature of jamming. Ref. [24] proposed a collaborative multi-agent layered Q learning (MALQL)-based anti-jamming communication algorithm to reduce the high dimensionality of the action space. Ref. [25] proposed a multi-agent proximal policy optimization (MAPPO) algorithm to optimize a collaborative strategy for multiple UAVs regarding transmission power and flight trajectory. The authors of [26] designed a deep recurrent Q-network (DRQN) algorithm and an intelligent anti-jamming decision algorithm, which improved throughput and convergence performance. However, centralized intelligent anti-jamming architectures incur high computational overhead and complexity, while distributed intelligent anti-jamming architectures fail to converge to globally optimal solutions. Consequently, neither approach is suitable for resource-constrained LEO satellite networks.

To address the aforementioned issues, this paper proposes a value decomposition network (VDN)-based multi-agent DRL method that applies a centralized training and distributed execution architecture. This method achieves global optimization during training and local decision-making during execution, which has certain advantages in terms of performance improvement and cost reduction. The main contributions of this paper are as follows:

• A VDN-based multi-agent DRL method is proposed to solve the anti-jamming spectrum-access problem. This method adopts an “offline centralized training–online distributed execution” architecture. After offline training on the ground, the model is deployed onto satellites to enable real-time anti-jamming spectrum-access decisions based on local observations.
• During training, the parameter-sharing mechanism is employed to reduce communication overhead significantly. During execution, the incremental update mechanism is employed to enhance model adaptability.
• The simulation results prove the proposed method’s effectiveness. It balances performance and cost better than fully centralized training and independent distributed training.

The rest of the paper is organized as follows. The system model and problem construction are outlined in Section 2. Section 3 proposes a multi-agent deep reinforcement learning algorithm. Section 4 presents the simulation results and discussion. Section 5 concludes this paper. The main notations employed in the paper are shown in Table 1.

Table 1. Main notations.

Notation	Description
$LE{O}_k$	The kth LEO satellite
$U_n$	The nth user of LEO satellites
$l_n\left(t\right)$	The downlink accessed by $U_n$ at time slot t
$l_m\left(t\right)$	The downlink accessed by $U_m$ at time slot t
$i_n^m\left(t\right)$	The interference link from $l_m\left(t\right)$ to $U_n$ at time slot t
$i_n^j\left(t\right)$	The jamming link from the jamming satellite to $U_n$ at time slot t
$I_n^m\left(t\right)$	The co-channel interference from $l_m\left(t\right)$ to $U_n$ at time slot t
$I_n^j\left(t\right)$	Jamming from the jamming satellite to $U_n$ at time slot t
${\theta }_n^m\left(t\right)$	The off-axis angle from the $l_m\left(t\right)$ to $U_n$ at time slot t
${\theta }_n^j\left(t\right)$	The off-axis angle from the center of the jamming beam to $U_n$ at time slot t
$B_f$	Channel bandwidth
$p_j$	The beam power of jamming satellite
$p_l$	The beam power of LEO satellites
$h_n^j\left(t\right)$	The channel gain of link $i_n^j\left(t\right)$
$h_n^m\left(t\right)$	The channel gain of link $i_n^m\left(t\right)$
$h_n\left(t\right)$	The channel gain of link $l_n\left(t\right)$
$r_n\left(t\right)$	The transmission rate of user $U_n$ at time slot t
$s_n\left(t\right)$	The satisfaction of user $U_n$ at time slot t

2. System Model and Problem Construction

2.1. System Model

As shown in Figure 1, there is a jamming satellite and an LEO constellation. Region S is the area jointly covered by jamming satellite and LEO satellites, and users are randomly distributed within region S. The jamming satellite applies randomized frequency suppression jamming to the satellite downlinks. The frequency variations follow a Markov probability matrix. Jamming strategies are formulated by the ground control center and distributed to jamming satellites. The LEO satellites are equipped with multibeam phased array antennas that can dynamically adjust the beam frequency for anti-jamming, and user communication quality is maintained uninterrupted.

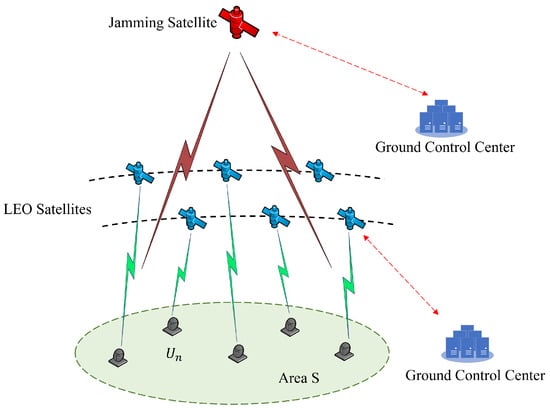
Figure 1. Anti-jamming communication scenario.

The set of LEO satellites is denoted as $\begin{array}{c}LEO=\{{LEO}_1,{LEO}_2,\cdots ,{LEO}_K\}\end{array}$; the set of users is denoted as $\begin{array}{c}U=\{U_1,U_2,\cdots ,U_N\}\end{array}$. Each satellite has B beams, and each beam serves one user. The set of available channels for each beam is denoted as $\begin{array}{c}{F}_L=\{f_1,f_2,\cdots ,f_M\}\end{array}$, and each channel bandwidth is $B_f$. The jamming channel set is $F_J=F_L$, and the beam power of the jamming satellite and LEO satellites are denoted as $p_j$ and $p_l$, respectively.

At each time slot, jamming satellite switches channels based on Markov probability matrix, and LEO satellites decide the optimal spectrum-access scheme for the downlinks based on real-time environment sensing and historical data analysis. This paper focuses on dynamic spectrum-access strategies for LEO satellite downlinks in malicious jamming environments, aiming to reduce interference and improve user satisfaction.

2.2. Propagation Model

According to ITU-R S.672 [27], the gain of jamming satellite transmitting antenna is

$$G_J\left({\theta }_n^j\left(t\right)\right)=\left\{\begin{array}{cc}{G}_{J_{max}},\hfill & {\theta }_n^j\left(t\right)\le {\theta }_{J_b},\hfill \\ G_{J_{max}}-3{\left({\displaystyle \frac{{\theta }_n^j\left(t\right)}{{\theta }_{J_b}}}\right)}^2,\hfill & {\theta }_{J_b}<{\theta }_n^j\left(t\right)\le 2.58{\theta }_{J_b},\hfill \\ G_{J_{max}}-20,\hfill & 2.58{\theta }_{J_b}<{\theta }_n^j\left(t\right)\le 6.32{\theta }_{J_b}\hfill \\ G_{J_{max}}-25log({\displaystyle \frac{{\theta }_n^j(t)}{{\theta }_{J_b}}}),\hfill & 6.32{\theta }_{J_b}<{\theta }_n^j\left(t\right)\le {\theta }_1,\hfill \\ 0,\hfill & {\theta }_1<{\theta }_n^j\left(t\right),\hfill \end{array}\right.$$

(1)

where $G_{J_{max}}$ is the maximum gain of jamming satellite transmitting antenna, and ${\theta }_n^j\left(t\right)$ is the off-axis angle of the center of the jamming beam in the $U_n$ direction. ${\theta }_{J_b}$ is half the 3 dB beamwidth ${\theta }_{J_{3dB}}$, and ${\theta }_1$ denotes the value obtained when the fourth line of Equation (1) is equal to 0.

According to ITU-R S.1528 [28], the gain of LEO satellite transmitting antenna is

$$G_L\left({\theta }_n^m\left(t\right)\right)=\left\{\begin{array}{cc}{G}_{L_{max}},\hfill & {\theta }_n^m\left(t\right)\le {\theta }_{L_b},\hfill \\ G_{L_{max}}-3{\left({\displaystyle \frac{{\theta }_n^m\left(t\right)}{{\theta }_{L_b}}}\right)}^2,\hfill & {\theta }_{L_b}<{\theta }_n^m\left(t\right)\le Y,\hfill \\ G_{L_{max}}+L_s-25log({\displaystyle \frac{{\theta }_n^m\left(t\right)}{Y}}),\hfill & Y<{\theta }_n^m\left(t\right)\le Z,\hfill \\ L_F,\hfill & Z<{\theta }_n^m\left(t\right),\hfill \end{array}\right.$$

(2)

where $G_{L_{max}}$ is the maximum gain of LEO satellite transmitting antenna, and ${\theta }_n^m\left(t\right)$ is the off-axis angle of the link $l_m\left(t\right)$ in the $U_n$ direction. ${\theta }_{L_b}$ is half the 3 dB beamwidth ${\theta }_{L_{3dB}}$, $L_s=-6.75 \mathrm{d}\mathrm{B}$ is main beam and proximal paraflap mask intersection, and $L_F=0$ dBi is near-axis paravalve level. Parameters Y and Z are denoted as

$$Y=1.5{\theta }_{L_b},Z=Y\times {10}^{0.04(G_{L_{max}}+L_s-L_F)}.$$

(3)

According to ITU-R S.465 [29], the gain of user receiving antenna is

$$G_U\left({\theta }_m^n\left(t\right)\right)=\left\{\begin{array}{cc}{G}_{U_{max}},\hfill & {\theta }_m^n\left(t\right)\le {\theta }_{min},\hfill \\ 32-25log\left({\theta }_m^n\left(t\right)\right),\hfill & {\theta }_{min}<{\theta }_m^n\left(t\right)\le {48}^{\circ },\hfill \\ -10,\hfill & {48}^{\circ }<{\theta }_m^n\left(t\right),\hfill \end{array}\right.$$

(4)

where $G_{U_{max}}$ is the maximum gain of user receiving antenna, and ${\theta }_m^n\left(t\right)$ is the off-axis angle of the link $l_n\left(t\right)$ in the $U_m$ direction. The parameter ${\theta }_{min}$ is denoted as

$${\theta }_{min}=\left\{\begin{array}{cc}max(1^{\circ },100\lambda /D),\hfill & D/\lambda \ge 50,\hfill \\ max(2^{\circ },144D/{\lambda }^{-1.09}),\hfill & \mathrm{else},\hfill \end{array}\right.$$

(5)

where D is the circular equivalent diameter of antenna, and $\lambda$ is the wavelength.

As shown in Figure 2, users are disrupted in two ways:

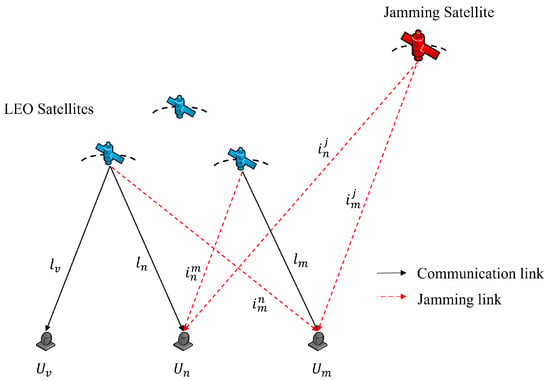
Figure 2. Interference model.

➀ Malicious jamming from jamming satellite:

$$I_n^j\left(t\right)=p_j{\delta }_n^j\left(t\right)h_n^j\left(t\right).$$

(6)

where the channel gain $h_n^j\left(t\right)$ is

$$h_n^j\left(t\right)={\displaystyle \frac{G_J\left({\theta }_n^j\left(t\right)\right)G_U\left({\theta }_j^n\left(t\right)\right)}{{\left(\frac{4\pi d_n^j\left(t\right)}{\lambda }\right)}^2}},$$

(7)

and the function ${\delta }_n^j\left(t\right)$ is

$${\delta }_n^j\left(t\right)=\left\{\begin{array}{cc}1,\hfill & a_j\left(t\right)=a_n\left(t\right),\hfill \\ 0,\hfill & a_j\left(t\right)\ne a_n\left(t\right).\hfill \end{array}\right.$$

(8)

where $G_J\left({\theta }_n^j\left(t\right)\right)$ is antenna gain of the jamming satellite in the $U_n$ direction, $G_U\left({\theta }_j^n\left(t\right)\right)$ is antenna gain of user in the jamming satellite direction, and $d_n^j\left(t\right)$ is distance of the link $i_n^j\left(t\right)$.

➁ Co-channel interference from other beams of the LEO satellites:

$$I_n^m\left(t\right)=\sum _{m=1,m\ne n}^N{p}_l{\delta }_n^m\left(t\right)h_n^m\left(t\right).$$

(9)

where the channel gain $h_n^m\left(t\right)$ is

$$h_n^m\left(t\right)={\displaystyle \frac{G_L\left({\theta }_n^m\left(t\right)\right)G_U\left({\theta }_m^n\left(t\right)\right)}{{\left(\frac{4\pi d_n^m\left(t\right)}{\lambda }\right)}^2}},$$

(10)

and $G_L\left({\theta }_n^m\left(t\right)\right)$ is antenna gain of the link $l_m\left(t\right)$ in the $U_n$ direction, $G_U\left({\theta }_m^n\left(t\right)\right)$ is antenna gain of the link $l_n\left(t\right)$ in the $U_m$ direction, and $d_n^m\left(t\right)$ is distance of the link $i_n^m\left(t\right)$.

Consequently, the transmission rate of user $U_n$ is

$$r_n\left(a_n^t\right)=B_f{log}_2(1+{\displaystyle \frac{p_l{h}_n\left(t\right)}{I_n^j\left(t\right)+I_n^m\left(t\right)+N_n\left(t\right)}}),$$

(11)

where $N_n\left(t\right)$ is the system noise, $h_n\left(t\right)$ is the channel gain, and its expression is

$$h_n\left(t\right)={\displaystyle \frac{G_{L_{max}}{G}_{U_{max}}}{{\left(\frac{4\pi d_n\left(t\right)}{\lambda }\right)}^2}},$$

(12)

where $d_n\left(t\right)$ is distance of the link $l_n\left(t\right)$.

In order to capture the user’s individualized needs and preferences, perceived satisfaction [30] is introduced with the following expression:

$$s_n\left(a_n^t\right)={\displaystyle \frac{1}{1+exp(-c(r_n\left(a_n^t\right)-r_n^{th}))}},$$

(13)

where $a_n^t$ is the spectrum selection of user $U_n$ at time slot t, $r_n^{th}$ is transmission rate threshold, and the parameter c modulates the slope of the demand utility curve, reflecting the sensitivity of the $s_n\left(a_n^t\right)$ to deviations from the rate threshold. Higher values of the $s_n\left(a_n^t\right)$ indicate superior user satisfaction with communication services, whereas lower values signify that the system fails to adequately meet service requirements.

2.3. Problem Construction

This paper aims to determine optimal spectrum-access strategies for LEO satellites to maximize average user satisfaction over T periods while maximizing anti-jamming performance. The optimization problem can be formulated as follows:

$$\begin{array}{cc}\hfill P:& \underset{a_n^t,\forall n,t}{max}\mathbb{E}\left[\sum _{t=1}^T\sum _{n=1}^N{s}_n\left(a_n^t\right)\right]\hfill \end{array}$$

(14a)

$$\begin{array}{c}s.t.{\mathrm{C}}_1:r_n\left(a_n^t\right)\ge r_n^{th},\forall t\in \left\{1,\cdots ,T\right\}\hfill \end{array}$$

(14b)

$$\begin{array}{cc}\hfill & {\mathrm{C}}_2:T\in {\mathbb{N}}^{+}\cup \{\infty \} \hfill \end{array}$$

(14c)

$$\begin{array}{cc}\hfill & {\mathrm{C}}_3:a_n^t\in F_L \hfill \end{array}$$

(14d)

In this optimization problem, ${\mathrm{C}}_1$ indicates that the transmission rate must be greater than a threshold to ensure normal communication, ${\mathrm{C}}_2$ indicates that the time horizon is either finite or infinite, and ${\mathrm{C}}_3$ indicates that the spectrum accessed by the user $U_n$ at time slot t must be within the orthogonal frequency band. The model not only takes into account the immediate user needs but also optimizes the overall user satisfaction over a longer period of time.

The optimization problem P is a non-convex nonlinear program [31]. According to [32,33], this problem is generally NP-hard, and it is difficult to find the optimal solution. Although convex optimization, heuristic, or game-theoretic approaches may attain suboptimal solutions, they typically require global information collection. This makes them impractical for resource-constrained LEO satellites with strict real-time requirements [34]. Since the dynamic spectrum-access problem satisfies the characteristics of the Markov decision process (MDP), the multi-agent DRL solution is introduced in detail subsequently.

3. The Proposed Multi-Agent Deep Reinforcement Learning Method

This section first presents the multi-agent MDP [35] formulation for multi-user anti-jamming spectrum access. Subsequently, the process of VDN-based multi-agent DRL is detailed.

3.1. Multi-Agent MDP Problem Formulation

In this paper, each satellite operates as an agent that observes local environmental states and selects actions per time slot. With all agents collaboratively maximizing the long-term cumulative reward, this constitutes a fully cooperative multi-agent task modeled as an MDP, mathematically expressed as $(\mathcal{S},\mathcal{A},\mathcal{F},\mathcal{R},\gamma )$, where $\mathcal{S}$ is the set of environment state, $\mathcal{A}$ is the the set of action, $\mathcal{F}$ is the state transition probability function, $\mathcal{R}$ is the reward function, and $\gamma$ is the discount factor; its values range from 0 to 1. Specifically, key parameters for the multi-user scenario are formally defined as follows:

• State: The state of the environment $s^t$ is the global information of all users, which can be formed as follows:

  $$s^t=(s_1^t,s_2^t,\cdots ,s_N^t),$$

  (15)

  where each $s_n^t$ contains self-satisfaction, current jamming, and current co-channel interference.
• Action: The action is the spectrum-access strategy for all users at time slot t, which can be formed as follows:

  $$a^t=(a_1^t,a_2^t,\cdots ,a_N^t),$$

  (16)

  where $a_n^t$ is the spectrum-access strategy of user n.
• Reward: The agents can obtain immediate rewards after taking actions, which can be formed as follows:

  $$r^t=\sum _{n=1}^N{s}_n\left(a_n^t\right).$$

  (17)
• State–action value function: The state–action value function is the discounted reward obtained by taking action $a_n^t$ in state $s_n^t$, which can be formed as follows:

  $$Q_n\left(s_n^t,a_n^t\right)=\underset{a_n}{max}\mathbb{E}\left[r^t+\gamma r^{t+1}\right],$$

  (18)

  where $a_n$ is the action set of agent n over period T, $a_n=\left\{a_n^1,a_n^2,\cdots ,a_n^T\right\}$, $r^{t+1}$ is long-term reward, and $\mathbb{E}\left[·\right]$ is the expectation. The agent’s goal is to learn the optimal strategy that maximizes the long-term reward.

3.2. Multi-Agent DRL Algorithm Design

Centralized multi-agent DRL methods require global information and incur high computational overhead. Conversely, distributed multi-agent DRL approaches relying on local observations fail to converge to optimal solutions. To overcome these limitations, the VDN [36] algorithm is adopted for multi-satellite anti-jamming spectrum access. This approach implements a centralized training and distributed execution framework. Global information is utilized during offline training, while local observations are required during online execution. The overall structure of the proposed algorithm is shown in Figure 3.

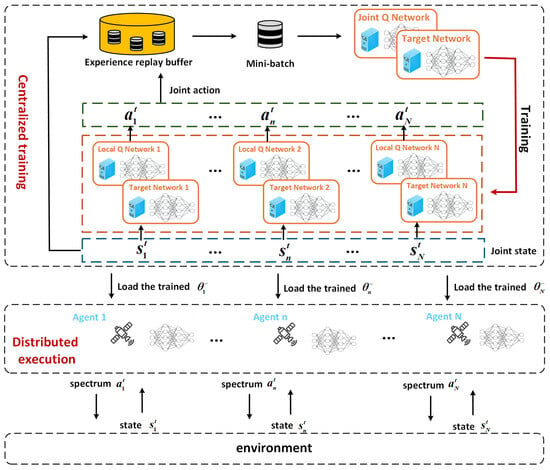
Figure 3. The overall architecture of the proposed algorithm.

3.2.1. The Offline Centralized Training Phase

The core idea of the VDN algorithm is to decompose the joint action-value function $Q_{tot}(s^t,a^t;\theta )$ of a multi-agent system into the sum of the local action-value functions $Q_n(s_n^t,a_n^t;{\theta }_n)$ of the individual agent, and it is denoted as

$$Q_{tot}\left(s^t,a^t;\theta \right)=\sum _{n=1}^N{Q}_n\left(s_n^t,a_n^t;{\theta }_n\right),$$

(19)

where $s^t$ is joint state, $a^t$ is joint action, and ${\theta }_n$ is parameter of local Q-network of the agent n. This decomposition allows the agent to independently select actions based on their local observations during the execution phase while optimizing the strategy through a global temporal difference (TD) objective during the centralized training phase. During the training process, the agent n selects action according to the $ϵ$-greedy strategy, and it is denoted as

$$a_n^t=\left\{\begin{array}{cc}\mathrm{random}{a}_n^t,\hfill & \mathrm{with}\mathrm{probability}ϵ,\\ \underset{a_n^t}{argmax}{Q}_n\left(s_n^t,a_n^t;\theta \right),\hfill & \mathrm{with}\mathrm{probability}1-ϵ.\end{array}\right.$$

(20)

The VDN network architecture is shown in Figure 4. After approximating the joint Q-value $Q_{tot}(s^t,a^t;\theta )$, the VDN updates the network parameters by minimizing the global reward-based TD error, and the loss function is defined as

$$L\left(\theta ,{\theta }_n\right)=\sum _{i\in \mathcal{B}}\left[{(y_i^{tot}-Q_{tot}\left(s_i,a_i;\theta \right))}^2\right],$$

(21)

where $\mathcal{B}$ denotes the mini-batch set sampled from the replay buffer, and $y_i^{tot}$ is target value denoted as

$$y_i^{tot}=r_i+\gamma \underset{a_{i+1}}{argmax}{Q}_{tot}^{-}\left(s_{i+1},a_{i+1};{\theta }^{-}\right),$$

(22)

where $r_i$ is global immediate reward, $\gamma$ is discount factor, and $s_{i+1}$ and $a_{i+1}$ denote the next joint state and joint action, respectively.

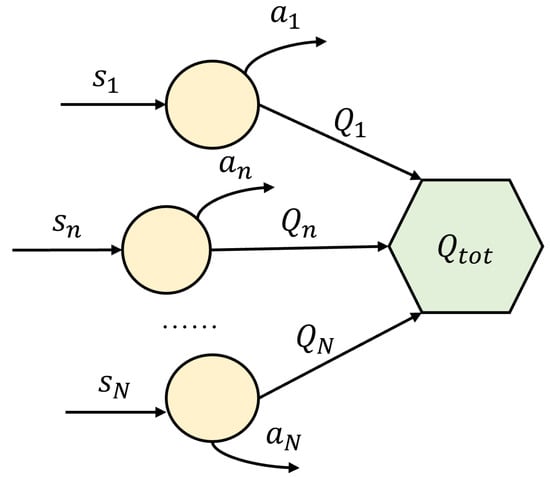
Figure 4. The structure of the VDN.

The gradient of the loss function $L\left(\theta ,{\theta }_n\right)$ is backpropagated through $Q_{tot}$ to each local Q function $Q_n$, which in turn updates its parameters ${\theta }_n$. This optimization process ensures that the local Q-network parameters of each agent are updated from the perspective of global returns. In order to improve learning efficiency, reduce computational and storage overheads, and facilitate collaboration among the agents, the algorithm employs a parameter-sharing mechanism.

After the centralized training phase is completed, the optimized model parameters ${\theta }_n^{-}$ are uploaded to the satellite agent to support subsequent distributed autonomous operation. Algorithm 1 describes the centralized training process in detail.

Algorithm 1 Offline Centralized Training Algorithm

1: Initialize: network parameter ${\theta }_n,\theta$, target network parameter ${\theta }_n^{-},{\theta }^{-}$, replay buffer $\mathcal{D}$, mini-batch size $\mathcal{B}$, and exploration probability $ϵ$   2: for episode = 1 to M do   3:       Initial environment, observe states s   4:       for t = 1 to T do   5:           for agent = 1 to N do   6:              Select action $a_n^t$ according to local state $s_n^t$ and $ϵ$-greedy strategy as shown in Equation (20)   7:           end for   8:           Central node calculates additive joint Q-value according to Equation (19)   9:           Execute joint action $a^t=(a_1^t,a_2^t,\cdots ,a_N^t)$; observe reward $r^t$ and next state $s^{t+1}$ 10:           Store experience $(s^t,a^t,r^t,s^{t+1})$ in replay buffer $\mathcal{D}$ 11:       end for 12:       if $\left|\mathcal{D}\right|>\left|\mathcal{B}\right|$ then 13:           Central node sample a $\mathcal{B}$ mini-batch experience from replay buffer $\mathcal{D}$ 14:           Compute loss according to Equations (21) and (22) 15:       end if 16:       Use gradient descent to minimize losses; update parameter $\theta ,{\theta }_n$ 17:       Update the target network parameters softly every C episode: $${\theta }^{-}=\tau \theta +(1-\tau ){\theta }^{-},{\theta }_n^{-}=\tau {\theta }_n^{-}+(1-\tau ){\theta }_n^{-}$$ (23) 18: end for 19: Upload trained parameters ${\theta }_n^{-}$ to satellite agents

3.2.2. The Online Distributed Execution Phase

Each satellite agent loads the trained agent network ${\theta }_n^{-}$. Satellite agent determines the optimal spectrum access by independently selecting the action that maximizes their local Q value $Q_n(s_n^t,a_n^t;{\theta }_n^{-})$ based only on their local observations.

An incremental parameter update mechanism is introduced to adapt to dynamic satellite network environment. Each agent continuously collects execution experiences, storing them in a local replay buffer. Periodically, new experiences from this buffer are utilized to refine pretrained network parameters ${\theta }_n$ through local loss computation and stochastic gradient descent. This online adaptation accommodates environmental dynamics while avoiding complete retraining. Algorithm 2 describes the distributed execution process in detail.

Algorithm 2 Online Distributed Execution Algorithm

1: Initialize: Load trained parameter ${\theta }_n^{-}$   2: for each time slot t do   3:       for each agent n do   4:             Observe current state $s_n^t$   5:             Select action $a_n^t=\underset{a_n^t}{argmax}{Q}_n\left(s_n^t,a_n^t;{\theta }_n^{-}\right)$   6:             Execute action $a_n^t$; observe local reward $r_n^t$ and next state $s_n^{t+1}$   7:             Store experience $(s_n^t,a_n^t,r_n^t,s_n^{t+1})$ in replay buffer   8:       end for   9:       Periodically incremental updates using new experience in replay buffer 10: end for

3.2.3. Complexity Analysis

The computational complexity of the proposed method is analyzed from two key phases: centralized training and distributed execution.

Centralized Training Phase: Each agent’s local Q-network performs forward propagation with complexity $\mathcal{O}(L_f·D^2)$, where $L_f$ is the number of layers in forward propagation, and D is the dimension of hidden layers in the neural network. For N agents, the total forward complexity per time slot is $\mathcal{O}(N·L_f·D^2)$. For each mini-batch, backpropagation of the TD error involves computing gradients across all layers, with per-sample complexity $\mathcal{O}(L_b·D^2)$, where $L_b$ is the number of layers in backpropagation. For a mini-batch of size $\left|\mathcal{B}\right|$, the total backpropagation complexity per episode is $\mathcal{O}\left(\right|\mathcal{B}|·L_b·D^2)$. Combining forward and backward operations over T time slots, the training complexity is $\mathcal{O}(T·[N·L_f·D^2+\left|\mathcal{B}\right|·L_b·D^2\left]\right)$. The parameter-sharing mechanism reduces the parameter space from $\mathcal{O}(N·D^2)$ to $\mathcal{O}\left(D^2\right)$, significantly lowering computational costs.

Distributed Execution Phase: Each satellite agent requires only $\mathcal{O}(L_f·D^2)$ per time slot to compute $Q_n(s_n^t,a_n^t)$ and select actions locally. The incremental update further adapts to environmental dynamics with minimal overhead $\mathcal{O}\left(\right|\mathcal{L}|·L_b·D^2)$, where $\left|\mathcal{L}\right|$ is the size of the local replay buffer. Therefore, the overall complexity of per time slot is $\mathcal{O}(L_f·D^2+|\mathcal{L}|·L_b·D^2)$.

4. Simulation Results and Performance Analysis

4.1. Simulation Parameters

In this section, the performance of the proposed multi-agent DRL algorithm is evaluated. The simulated scenario consists of one jamming satellite and an LEO Walker constellation, with ten users randomly distributed within the jamming satellite’s beam coverage. Detailed simulation parameters are documented in Table 2. All the simulations are executed on a computer equipped with a 2.7 GHz Intel Core Ultra 9 CPU, 32 GB RAM, and NVIDIA 5070Ti GPU. Algorithm framework parameters are summarized in Table 3.

Table 2. Parameters of constellation.

Parameter	Jamming Satellite	LEO Satellite
Orbital altitude	35,786 km	550 km
Beam power	45 dBw	15 dBw
Beam bandwidth	200 MHz	200 MHz
Beam radius	200 km	50 km
Frequency range	10.7–12.7 GHz	10.7–12.7 GHz
Frequency channels	4	4
Channel noise	−100 dBm	−100 dBm
Spectrum switching	Markov probability matrix	intelligent

Table 3. Parameters of algorithm framework.

Parameter	Value
Learning rate	0.001
Replay buffer size $\mathcal{D}$	10,000
Mini-batch size $\mathcal{B}$	64
Initial exploration rate	0.1
Final exploration rate	0.01
Discount factor $\gamma$	0.99
Optimizer	Adam

In this paper, we compare the proposed method with the following three different methods:

• Centralized Training Execution (CTE) [37]: The CTE method employs a fully centralized architecture during both training and execution phases. It requires continuous global information interaction and incurs high communication overhead.
• Non-Cooperative Independent Learning (NIL) [38]: In the NIL method, each agent independently optimizes strategies without coordination mechanisms or information sharing.
• Random Action Selection (RAS): The RAS method is a benchmark strategy without learning ability, and each agent randomly selects actions.

4.2. Convergence Analysis

Figure 5 illustrates the convergence of the proposed method through episode reward and loss. The reward values in Figure 5a increase during training and stabilize after 200 episodes, while the loss values in Figure 5b exhibit progressive reduction. These observations validate the proposed method’s convergence.

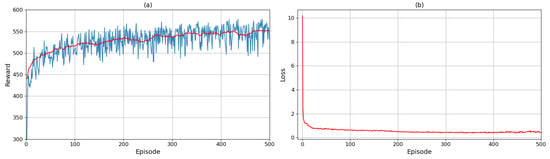
Figure 5. An illustration of (a) reward and (b) loss during the training process.

Figure 6 compares convergence among different methods, with the vertical axis denoting the satisfaction index. Evidently, the CTE method demonstrates superior convergence performance due to its global information awareness; its practical application is significantly constrained by satellite network communication and computational resources. The proposed method achieves approximately 97% of CTE’s convergence performance without excessive link overhead. It validates the effectiveness of the proposed method. The NIL method achieves a fully independent decision-making training mode, but the convergence performance is significantly reduced due to the lack of a cooperation mechanism. The RAS method has the worst performance due to its lack of learning ability.

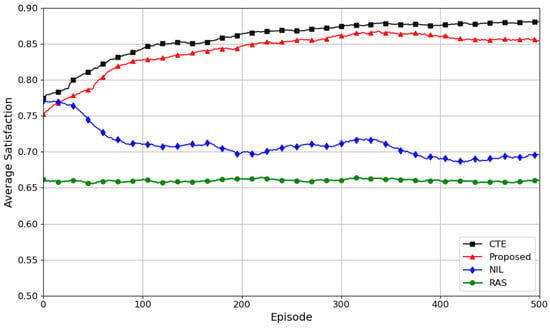
Figure 6. Convergence comparison of different methods.

4.3. Performance Analysis

4.3.1. Jamming Avoidance

Table 4 and Table 5, respectively, present the channel selection of users and the jammer during initial and convergence episodes. Each row corresponds to a distinct time slot. As shown in Table 4, the users exhibit random channel selection during the initial exploration, resulting in significant channel overlap with jammer transmissions. In contrast, Table 5 demonstrates users’ effective avoidance of jammed channels after convergence. This comparative analysis confirms the proposed algorithm’s efficacy in achieving near-optimal jamming avoidance.

Table 4. Channel selection in the initial episode.

	User 1	User 2	User 3	User 4	User 5	User 6	User 7	User 8	User 9	User 10	Jammer
t = 10	3	3	3	4	3	4	4	3	4	3	4
t = 20	3	3	4	3	4	3	4	3	4	3	4
t = 30	4	3	3	3	3	3	3	4	3	3	4
t = 40	3	2	3	3	3	3	3	3	3	3	3
t = 50	3	4	3	4	3	4	3	3	3	4	2

Table 5. Channel selection in the convergence episode.

	User 1	User 2	User 3	User 4	User 5	User 6	User 7	User 8	User 9	User 10	Jammer
t = 10	1	1	4	2	4	1	4	2	4	2	3
t = 20	2	2	1	2	3	1	2	3	2	2	4
t = 30	3	4	4	1	4	3	3	4	3	4	2
t = 40	4	3	3	1	3	3	4	3	4	1	2
t = 50	3	2	3	3	1	2	3	1	1	3	4

Figure 7 illustrates the users’ channel selection over 12 time slots after algorithm convergence under sweep jamming. It is obvious that the proposed method remains effective under sweep jamming, and users can thus avoid the channel selected by the jammer.

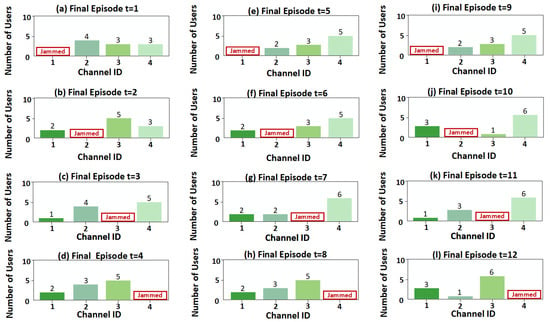
Figure 7. The channel selection under sweep jamming.

4.3.2. User Satisfaction

Figure 8 illustrates the impact of number of agents on user satisfaction. As number of agents increases, average satisfaction decreases for all the methods. The CTE method achieves the highest satisfaction. However, its computational costs rise significantly with user scaling. The NIL method reduces costs but causes frequent spectrum collisions from insufficient information exchange, so it has lower satisfaction. The proposed method maintains moderate satisfaction levels. Malicious jamming and computational costs are reduced through collaborative decisions. Thus, the proposed method is more suitable for spectrum management in LEO dynamic networks.

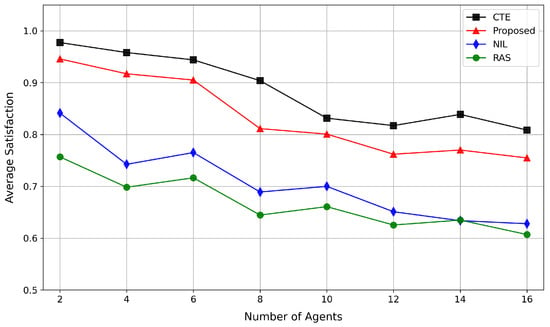
Figure 8. Impact of number of agents on user satisfaction.

4.3.3. Network Fairness

Inspired by [39], to better demonstrate the effectiveness of the proposed method, the user fairness index is introduced as follows:

$$J={\displaystyle \frac{{\left({\sum }_{n\in N}{s}_n\right)}^2}{N{\sum }_{n\in N}{\left(s_n\right)}^2}},$$

(24)

where N is the number of users, $s_n$ is the satisfaction of user $U_n$. It is evident that, the closer the fairness index is to 1, the better the network fairness.

Figure 9 illustrates the impact of number of agents on network fairness. The fairness index exhibits a declining trend across all the methods with an increasing number of agents. Among them, the CTE method demonstrates the best fairness index, while the proposed method’s fairness index is slightly inferior to CTE. In contrast, due to a lack of coordination among agents, NIL exhibits a relatively poor fairness index. RAS achieves the worst fairness index owing to its lack of learning ability.

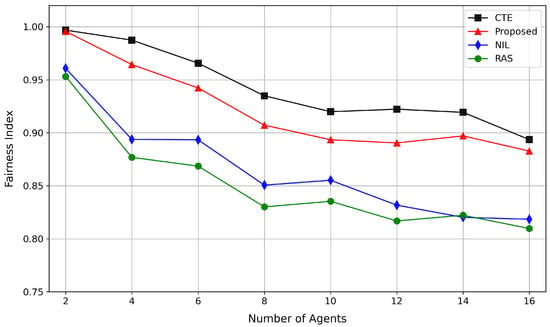
Figure 9. Impact of number of agents on network fairness.

5. Conclusions

A VDN-based multi-agent DRL method is proposed for anti-jamming spectrum access in LEO satellite networks. To enhance training efficiency and minimize communication overhead, a centralized training with distributed execution architecture is adopted. Following offline centralized training, the network is distributedly deployed on LEO satellites to enable real-time spectrum-access decision-making. Parameter sharing is employed to accelerate convergence and reduce complexity, while incremental updates enhance model adaptability. The simulation results demonstrate improvements in jamming avoidance and user satisfaction, along with reduced computational overhead. Therefore, this approach provides an effective solution for dynamic anti-jamming spectrum access in resource-constrained LEO satellite networks. Future work will explore multi-domain joint anti-jamming technologies and integrate them with physical layer security techniques to further enhance resilience against evolving jamming threats.