ADMM-Based Two-Tier Distributed Collaborative Allocation Planning for Shared Energy Storage Capacity in Microgrid Cluster
Abstract
1. Introduction
- (1)
- Current research on capacity planning for microgrid clusters with SES predominantly focuses on the overall operational status of the system and the minimization of total power costs; however, there is a lack of comprehensive investigation into the coordinated operational mechanisms across microgrids. They have not considered the energy interaction and flow between the various entities in a microgrid cluster, making it difficult to balance the operating costs of each microgrid.
- (2)
- Many scholars examining SES capacity allocation focus solely on the revenue and costs of shared energy storage operators and microgrid clusters collectively, neglecting the operational costs of individual entities within the microgrid cluster. This oversight leads to conclusions that diverge from the actual operational conditions of microgrid clusters.
2. Model of Microgrid Cluster
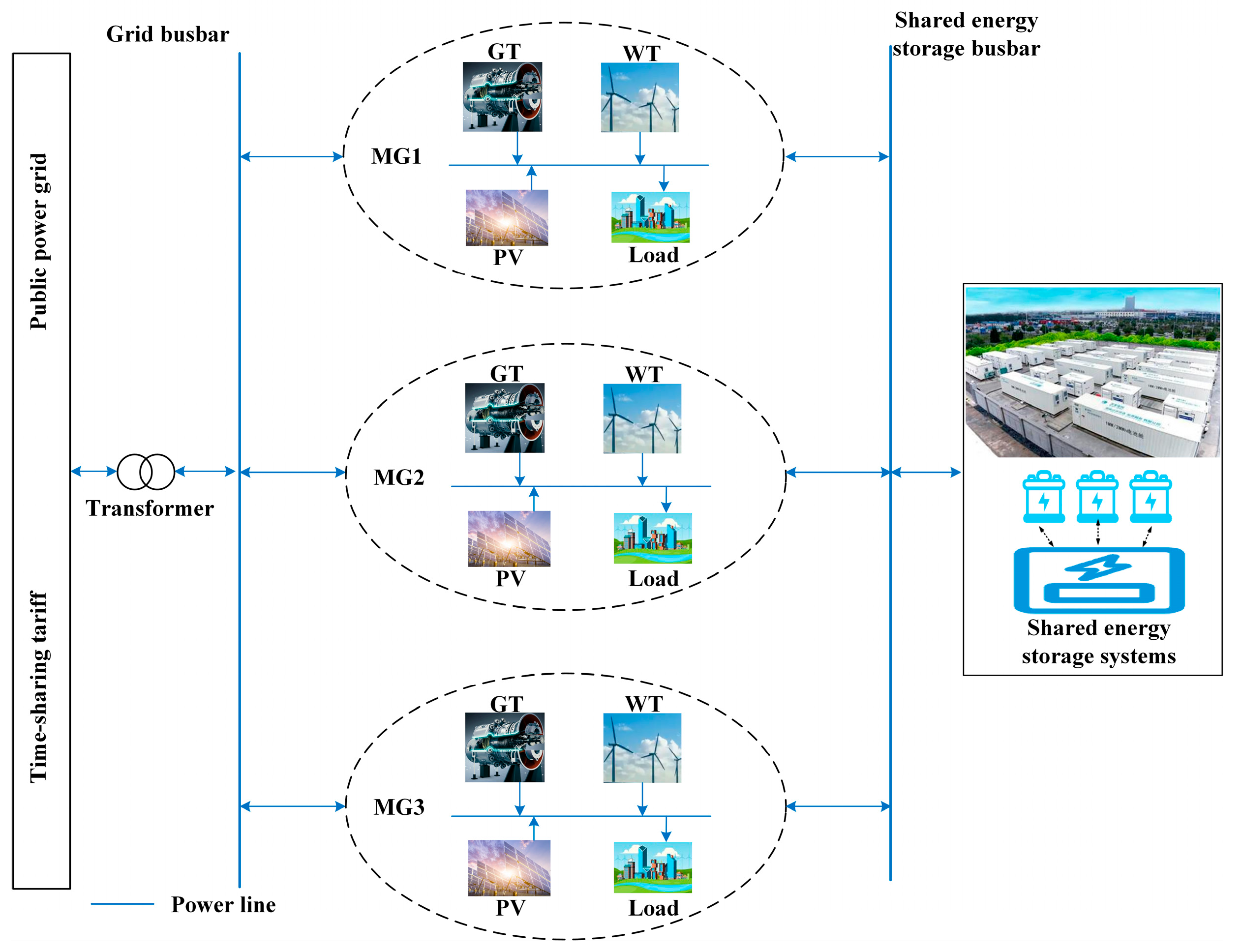
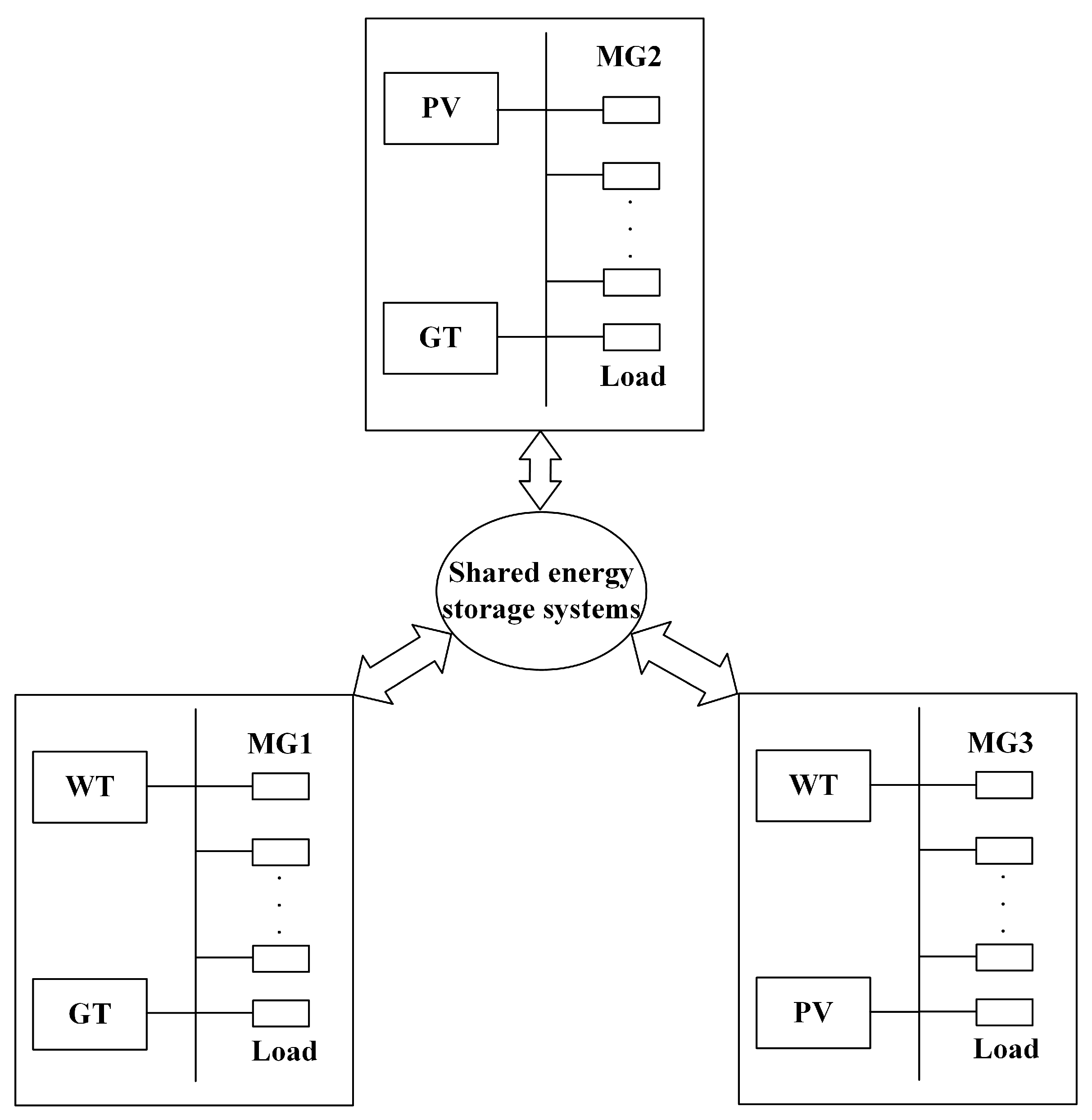
2.1. Typical Physical Architecture of Microgrid Cluster
2.2. Mathematical Model of Microgrid Cluster
- (1)
- Mathematical Model of WT
- (2)
- Mathematical Model of PV
- (3)
- Mathematical model of GT
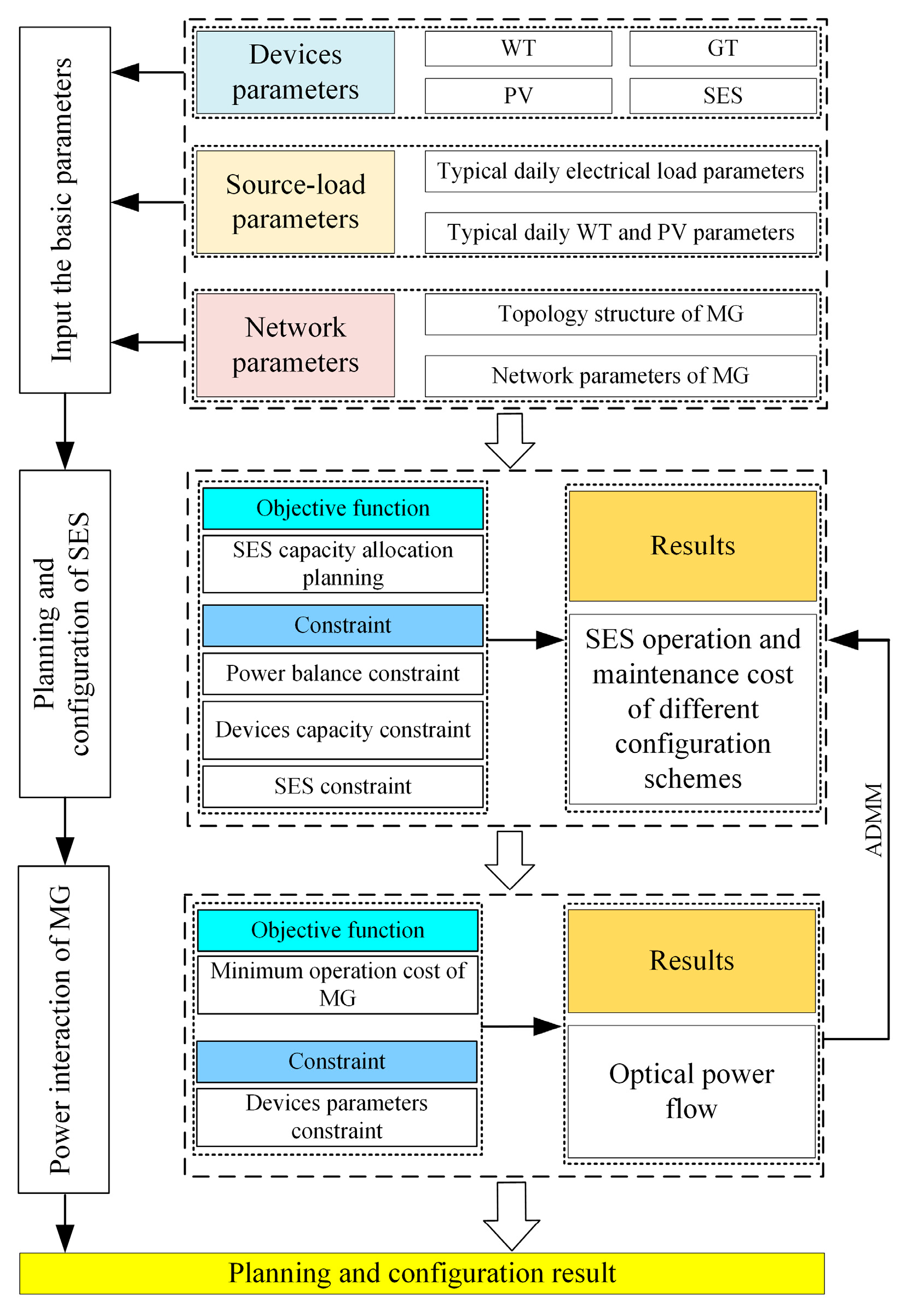
3. SES Bi-Layer Optimal Configuration Model
3.1. SES Capacity Configuration Model of Upper Layer
3.1.1. Objective Function
3.1.2. Constraint Function
- (1)
- SES rated capacity, rated power constraints
- (2)
- Energy storage device constraints
- (3)
- Energy storage charging and discharging power constraints
- (4)
- SES bus interaction power constraints
3.2. Optimization Operation Model of Lower Layer
3.2.1. Objective Function
- (1)
- Microgrid source-side generation costs
- (2)
- SES charge and discharge costs
- (3)
- Microgrid load-side energy costs
3.2.2. Constraint Function
- (1)
- Microgrid power balance constraints
- (2)
- Microgrid constraints on selling and purchasing electricity from external grids
3.3. Model Solving Algorithms
3.3.1. ADMM Fundamentals
3.3.2. Model and Algorithm
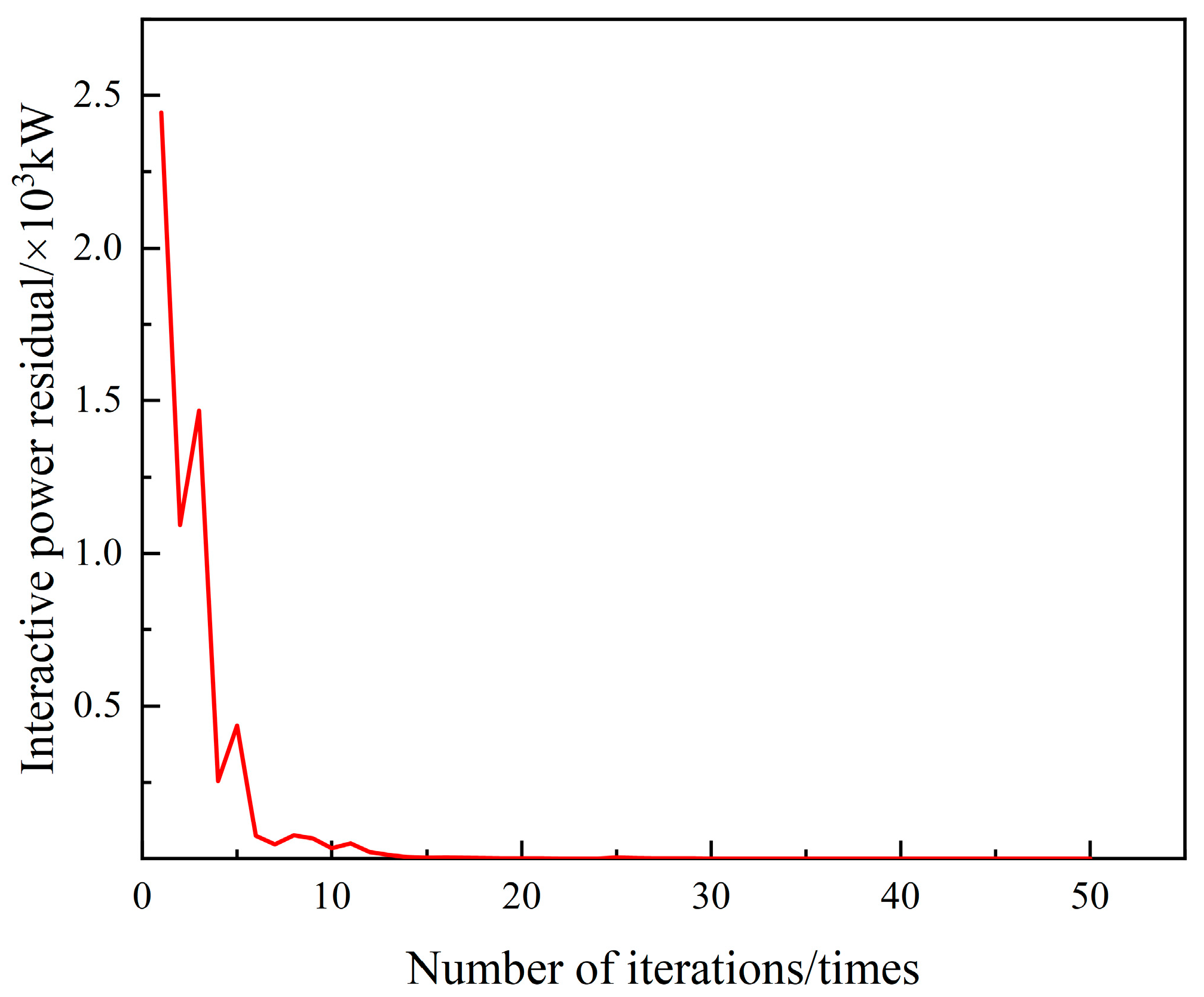
3.3.3. Convergence Criterion
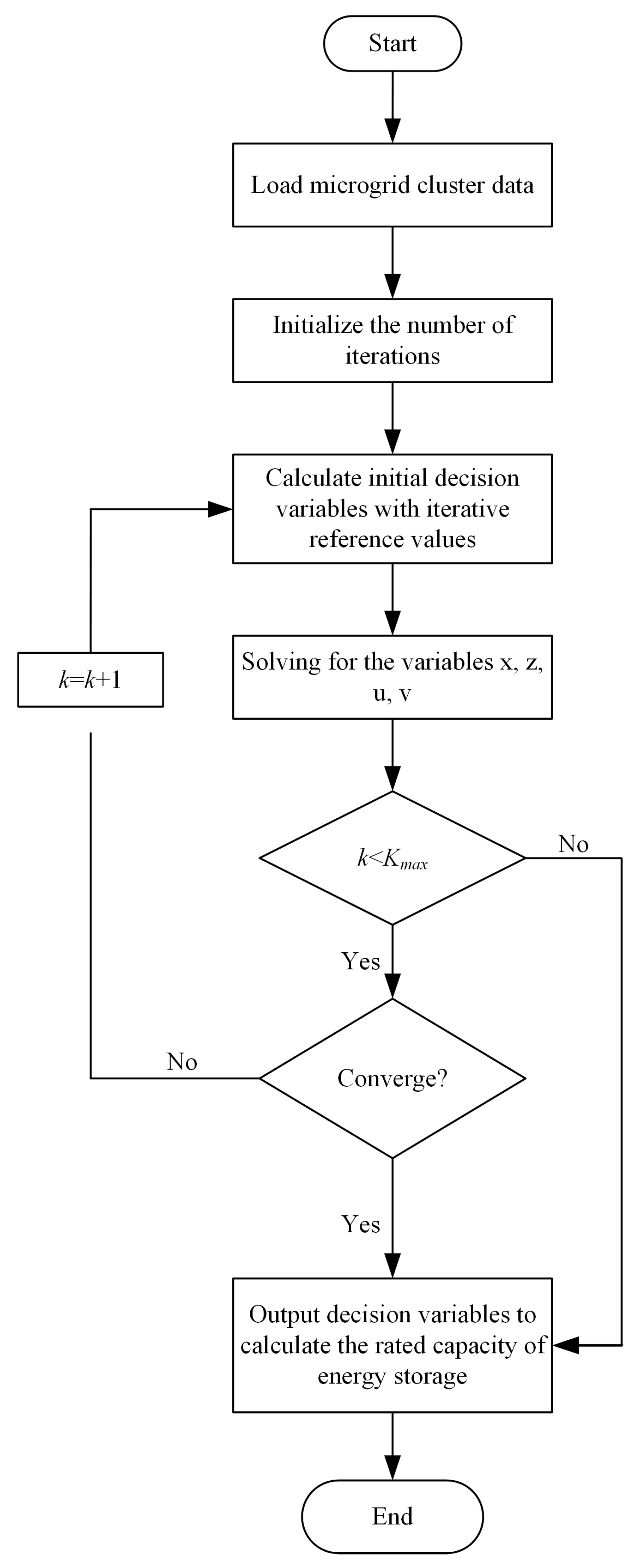
3.4. SES Capacity Allocation Planning Solution Process
- (1)
- Step 1: Load the data of microgrid typical scene output and load, and initialize the settings of parameters such as εabs, εrel, K, and so on.
- (2)
- Step 2: Make the number of iterations k = 1 and calculate the interaction power Pi,ex of neighboring microgrids through the SES bus and the reference value of the interaction power Pi,ex_ref of the SES bus.
- (3)
- Step 3: Construct the augmented Lagrangian function, solve for the variables x, z, u, v by iteration, and update the decision variables Pses and Pex.
- (4)
- Step 4: Judge whether the original residuals and pairwise residuals satisfy the condition or the number of iterations k = Kmax, then stop the iteration and output the optimization results; otherwise, make k = k + 1 and return to step 2 to continue the iteration.
4. Case Study
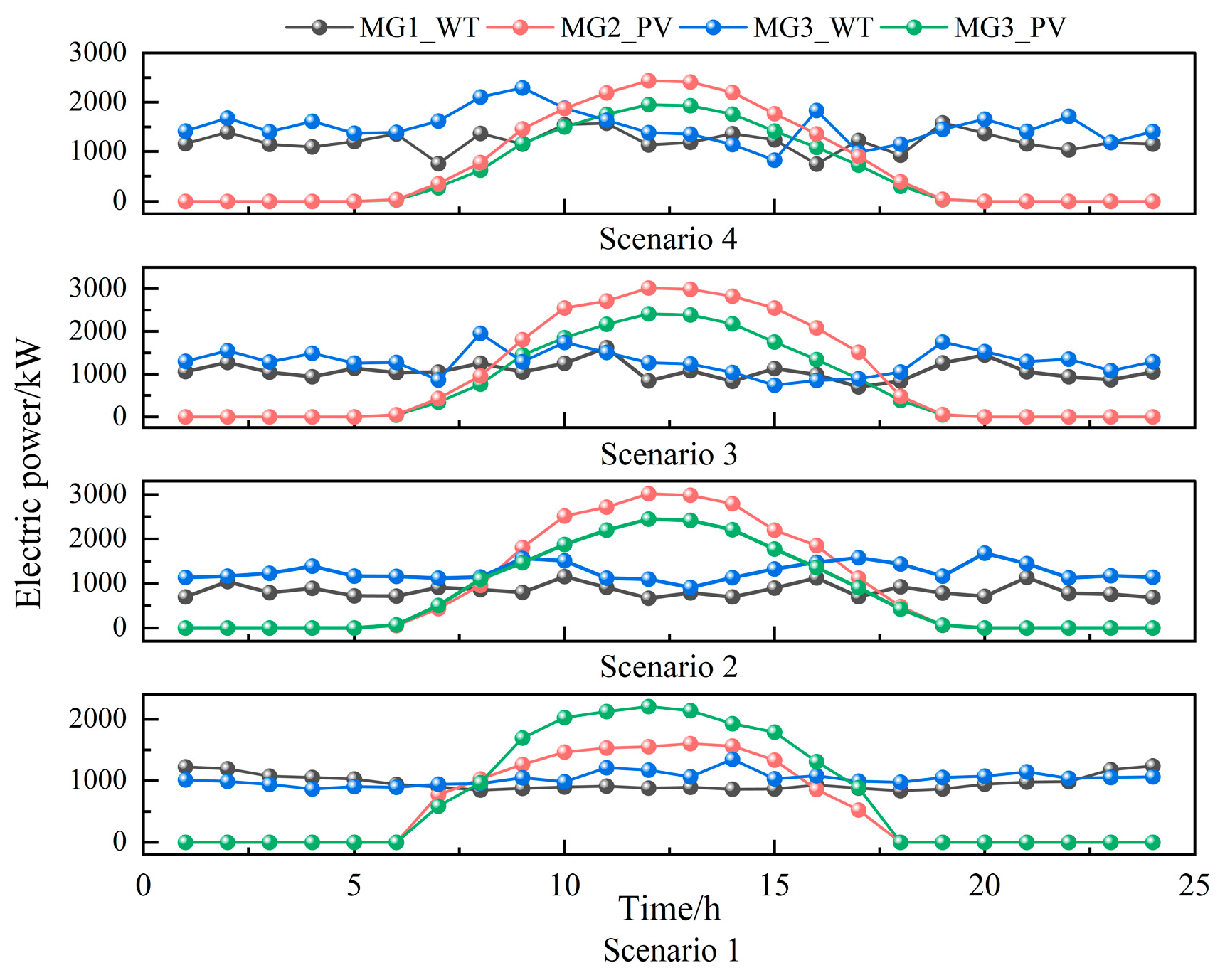
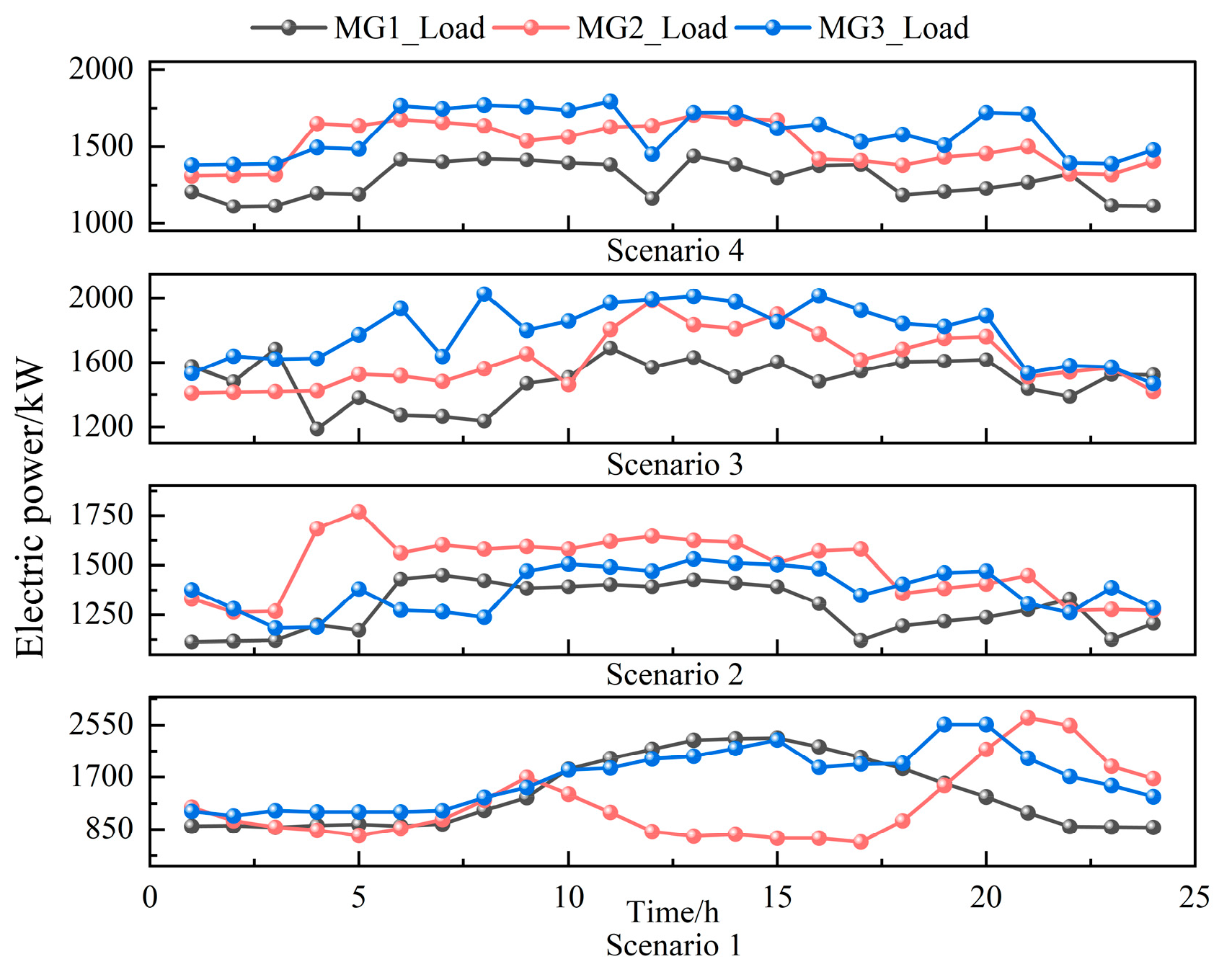
4.1. Case System Overview
- (1)
- Step 1: Input typical daily wind and solar radiation, load, and other data.
- (2)
- Step 2: Fit and calculate data such as wind power output and load demand based on probability density functions to generate raw data curves.
- (3)
- Step 3: Based on the Monte Carlo method, random sampling simulations are performed to generate multiple discrete scenario curves.
- (4)
- Step 4: Calculate the probability distance between scenarios and reduce the number of scenarios to ultimately determine the typical daily power curves for four different scenarios.
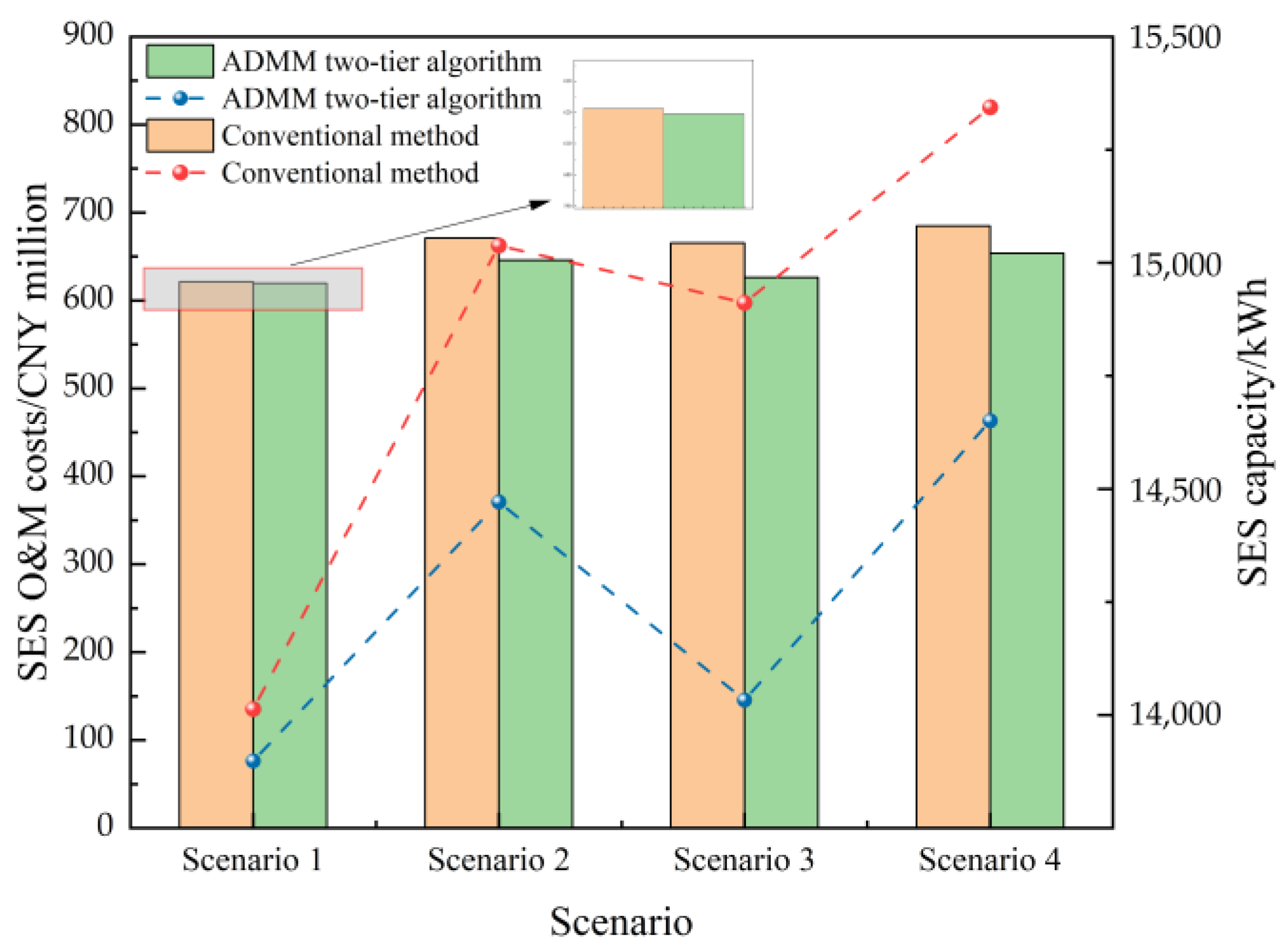
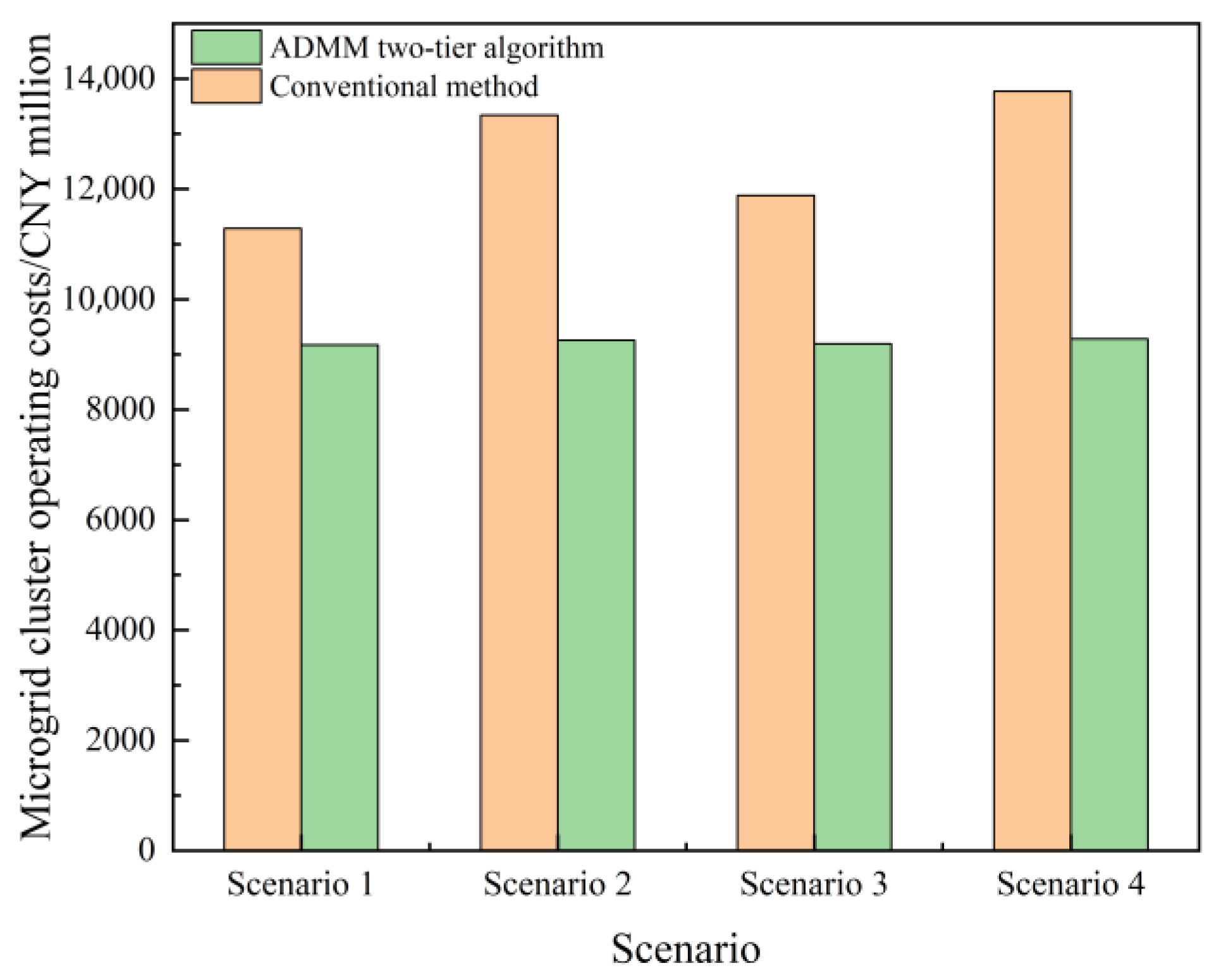
4.2. SES Capacity Allocation Planning
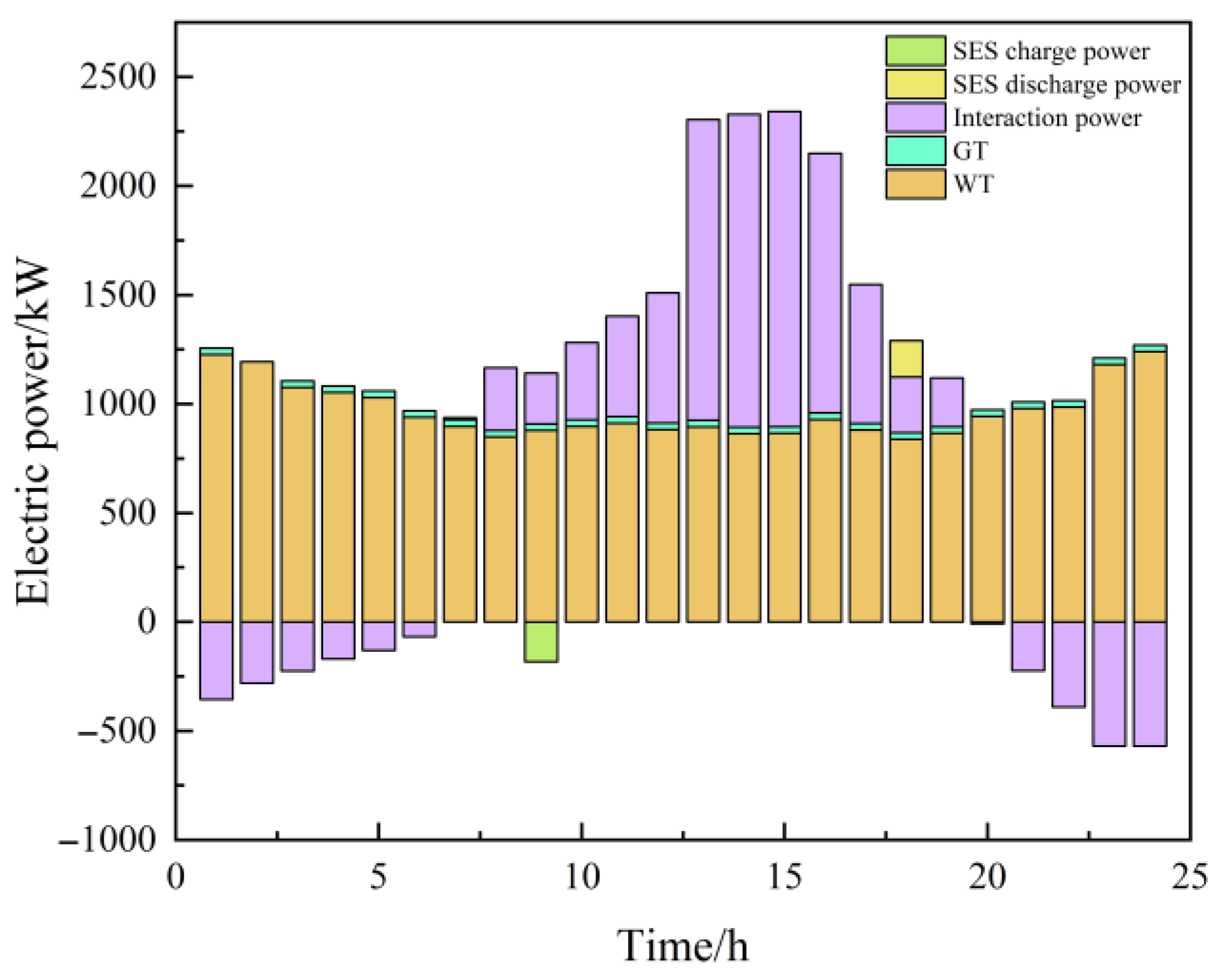
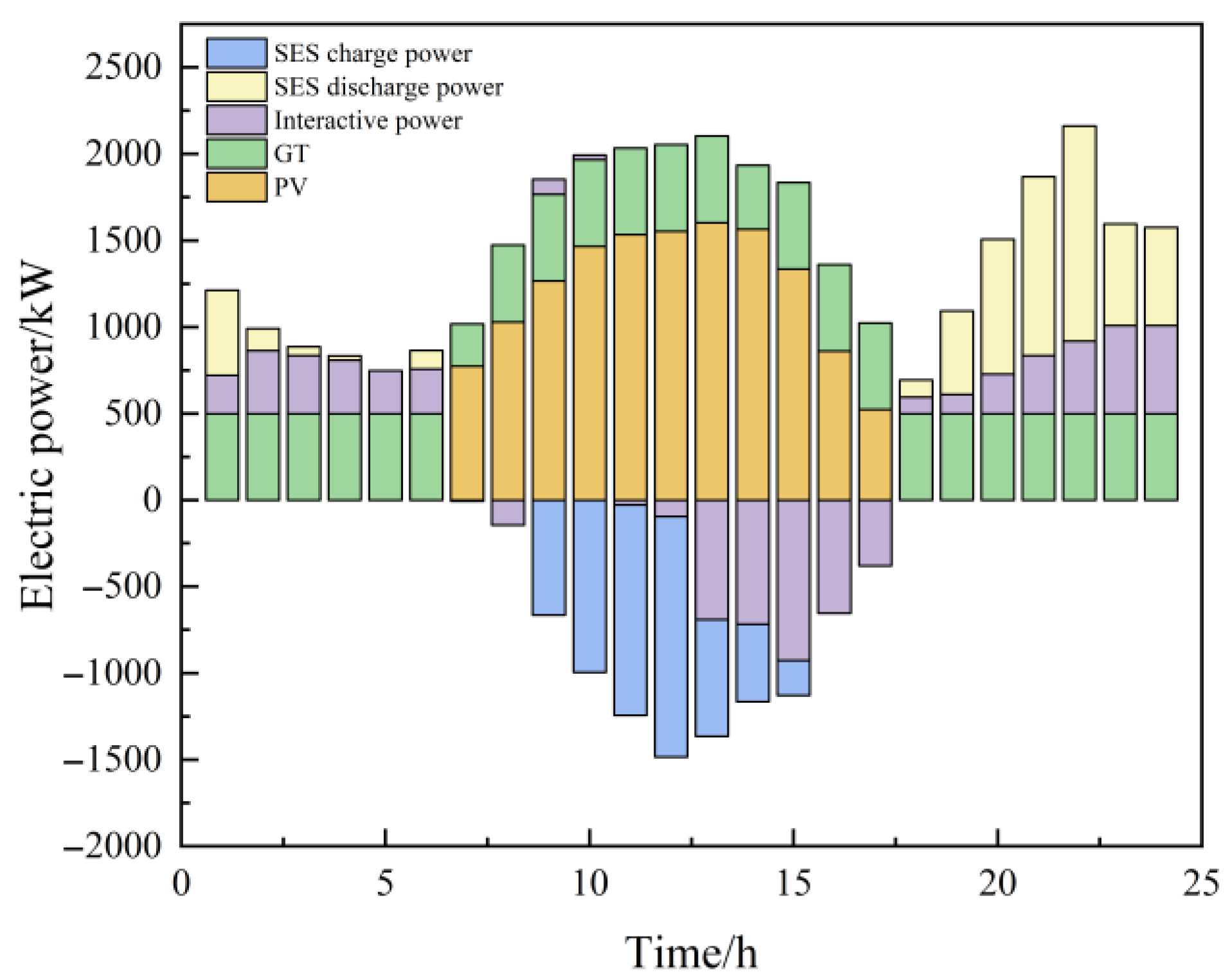
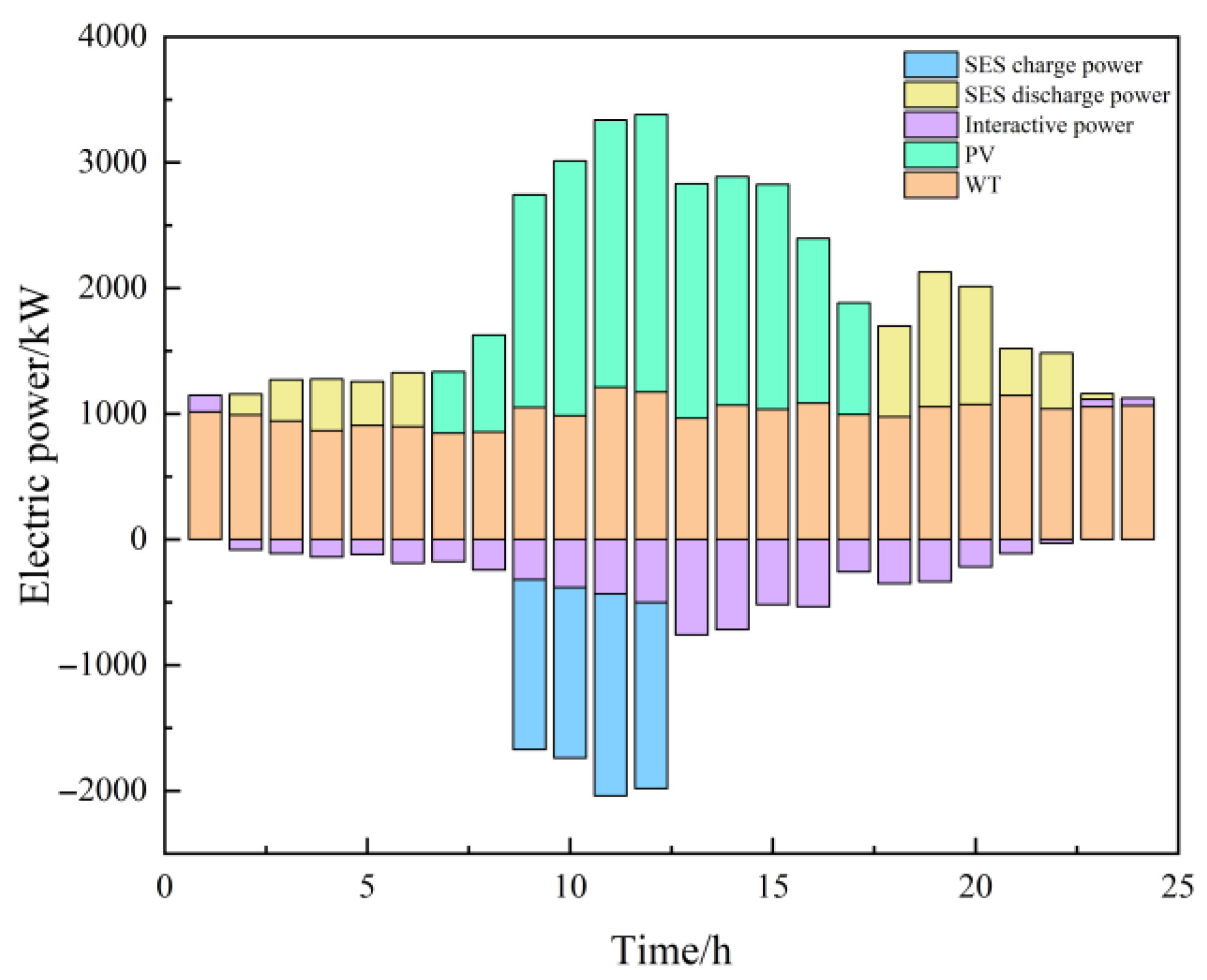
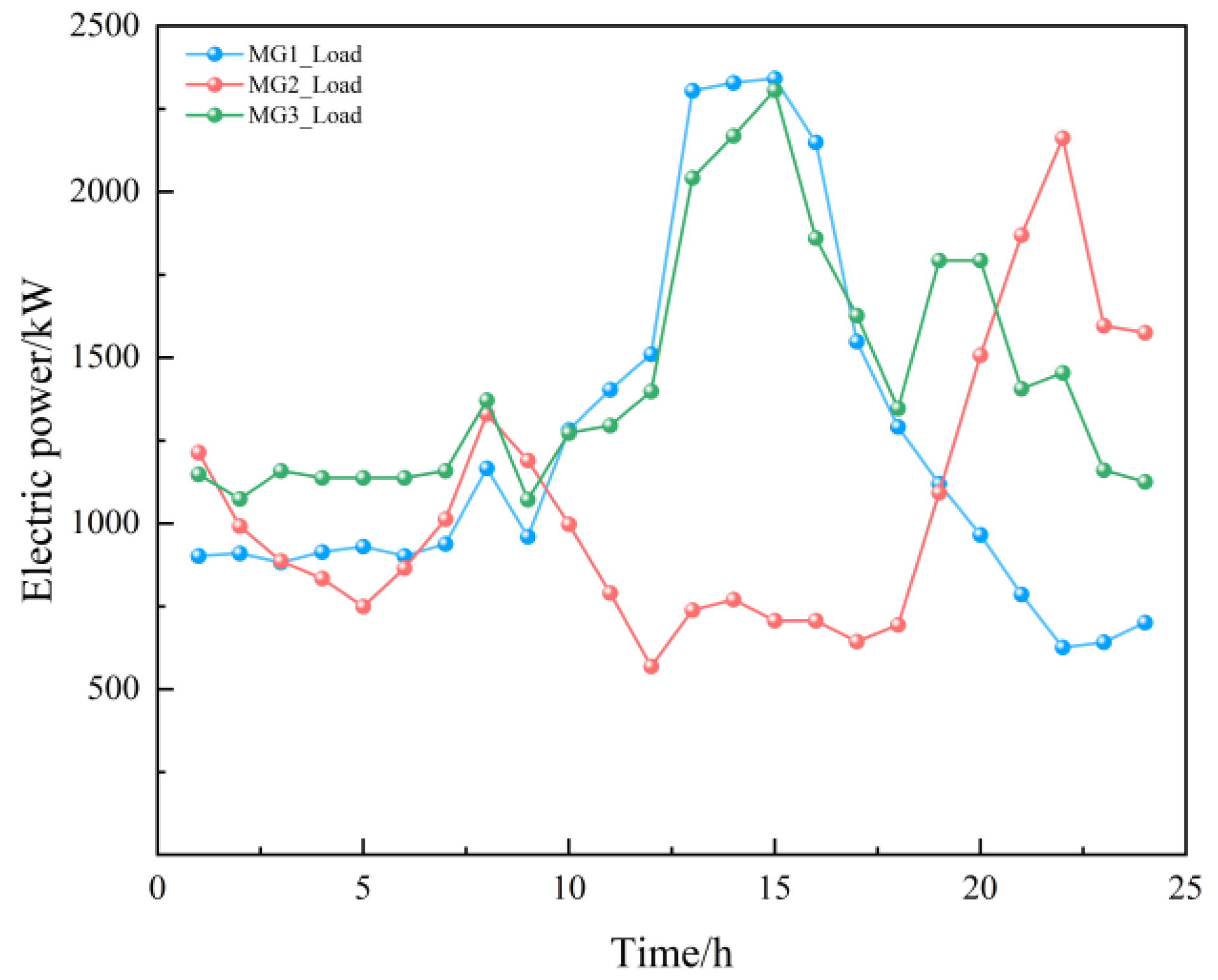
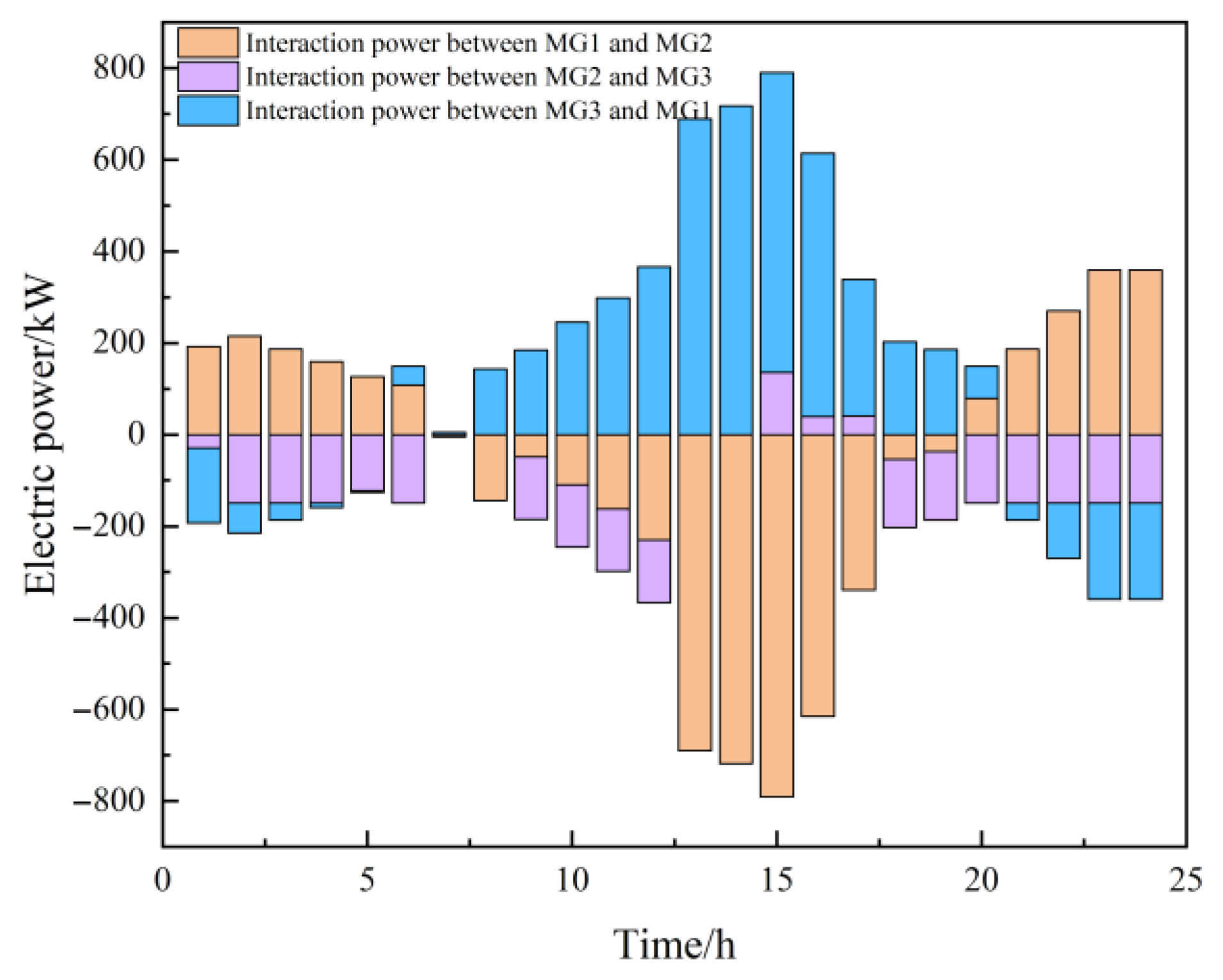
4.2.1. Microgrid Energy Flow Analysis
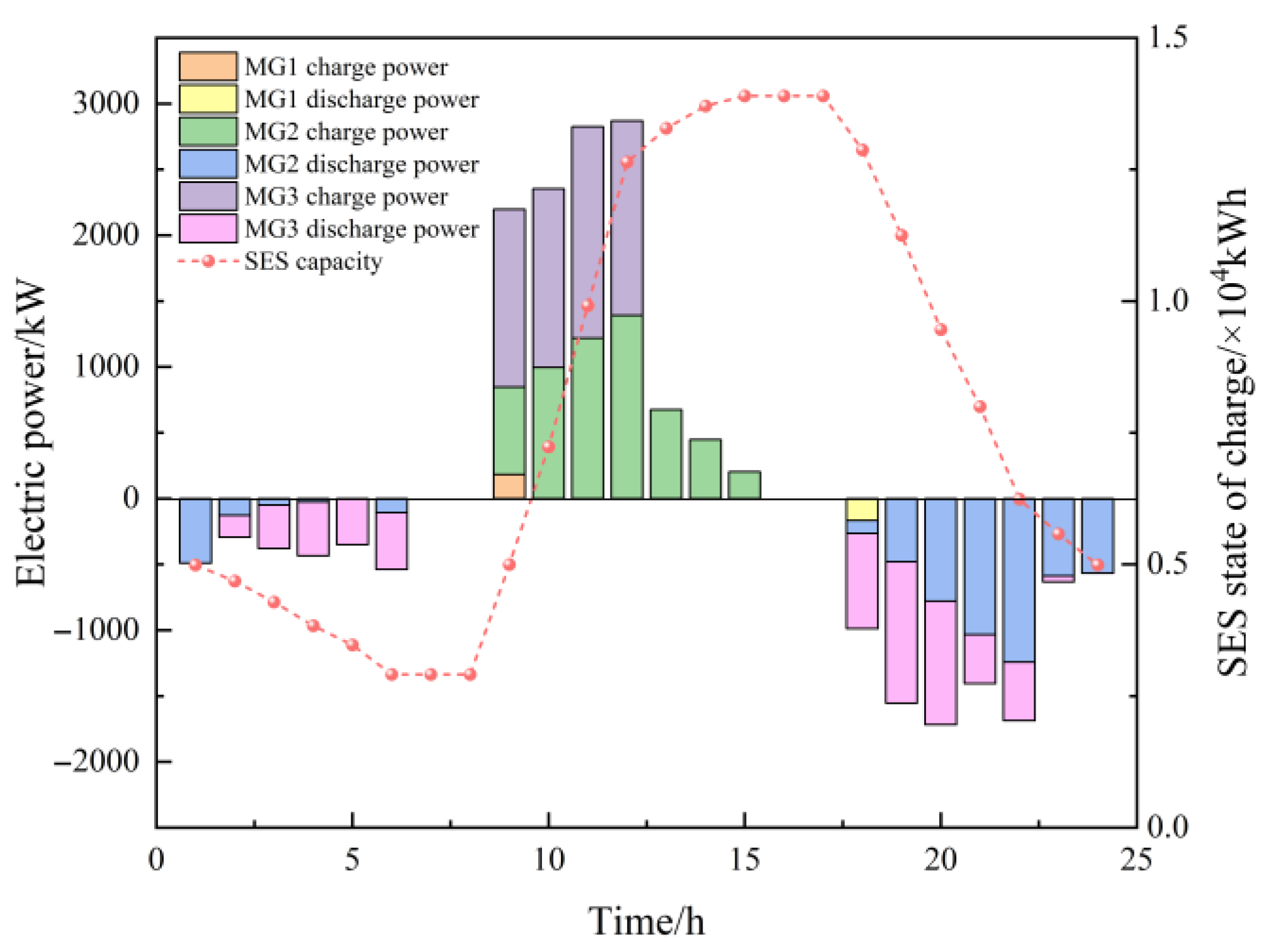
4.2.2. Energy Flow Analysis of the SES System
5. Conclusions and Future Work
- (1)
- Constructing a cooperative operation model of a microgrid cluster containing SES and proposing a microgrid energy dispatch strategy based on the ADMM algorithm by considering the operating costs of each entity within the microgrid cluster, the total operating cost of the system was significantly reduced.
- (2)
- The introduction of the new SES energy storage technology improves the system operation flexibility through the time-space transfer mechanism of energy, optimizes the load power and energy flow distribution characteristics of the microgrid cluster, and thus reduces the system operation cost in the whole life cycle.
- (3)
- Based on the two-layer optimal configurational model solution analysis, we obtain the SES configuration scheme, the minimized operational and maintenance investment costs parameter, and the energy interaction mechanism of the microgrid cluster, etc. The effectiveness of the method proposed in this paper compared to traditional shared energy storage configuration methods was verified in different scenarios, significantly enhancing the reliability of the power supply in a microgrid cluster.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Solanki, B.; Raghurajan, A.; Bhattacharya, K.; Cañizares, C. Including smart loads for optimal demand response in integrated energy management systems for isolated microgrids. IEEE Trans. Smart Grid 2015, 8, 1739–1748. [Google Scholar] [CrossRef]
- Roy, K.; Mandal, K.; Mandal, A. Modeling and managing of micro grid connected system using improved artificial bee colony algorithm. Int. J. Electr. Power Energy Syst. 2016, 75, 50–58. [Google Scholar] [CrossRef]
- Huang, S.; Abedinia, O. Investigation in economic analysis of microgrids based on renewable energy uncertainty and demand response in the electricity market. Energy 2021, 225, 120247. [Google Scholar] [CrossRef]
- Wu, Q.; Xie, Z.; Ren, H.; Li, Q.; Yang, Y. Optimal trading strategies for multi-energy microgrid cluster considering demand response under different trading modes: A comparison study. Energy 2022, 254, 124448. [Google Scholar] [CrossRef]
- Chen, Z.; Fan, F.; Tai, N.; Hu, Y.; Li, R. Coordinated energy dispatch and flexibility support for microgrid cluster using rule-based Stackelberg gaming approach. IEEE Trans. Ind. Appl. 2023, 60, 1564–1575. [Google Scholar] [CrossRef]
- Bui, V.; Hussain, A.; Kim, H. A multiagent-based hierarchical energy management strategy for multi-microgrids considering adjustable power and demand response. IEEE Trans. Smart Grid 2016, 9, 1323–1333. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, L.; Liao, S.; Xu, J.; Cheng, F. Hierarchical scheduling method for distribution network-microgrid clusters considering flexible grouping. Int. J. Electr. Power Energy Syst. 2025, 169, 110797. [Google Scholar] [CrossRef]
- Cunha, P.; Saavedra, O.; Ribeiro, L.; Oliveira, D. Cluster operation of microgrids: Assessing economic and resilience gains. Electr. Power Syst. Res. 2025, 239, 111220. [Google Scholar] [CrossRef]
- Gbadega, P.; Sun, Y.; Balogun, O. Optimized energy management in Grid-Connected microgrids leveraging K-means clustering algorithm and Artificial Neural network models. Energy Convers. Manag. 2025, 336, 119868. [Google Scholar] [CrossRef]
- Rajaei, A.; Fattaheian-Dehkordi, S.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. Decentralized transactive energy management of multi-microgrid distribution systems based on ADMM. Int. J. Electr. Power Energy Syst. 2021, 132, 107126. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, P.; Wu, D.; Liu, Z.; Ge, H.; Zhang, S.; Yang, X. A new collaborative optimization method for a distributed energy system combining hybrid energy storage. Sustain. Cities Soc. 2021, 75, 103330. [Google Scholar] [CrossRef]
- Yong, X.; Wu, Y.; Zhou, J.; Tao, Y.; Chen, W. Prospects and barriers analysis framework for the development of energy storage sharing. Sustain. Cities Soc. 2023, 89, 104368. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Wang, Y.; Xiong, H.; Ding, X.; Guo, C. Pricing method of electric-thermal heterogeneous shared energy storage service. Energy 2023, 281, 128275. [Google Scholar] [CrossRef]
- Siqin, T.; He, S.; Hu, B.; Fan, X. Shared energy storage-multi-microgrid operation strategy based on multi-stage robust optimization. J. Energy Storage 2024, 97, 112785. [Google Scholar] [CrossRef]
- Xie, T.; Ma, K.; Zhang, G.; Zhang, K.; Li, H. Optimal scheduling of multi-regional energy system considering demand response union and shared energy storage. Energy Strategy Rev. 2024, 53, 101413. [Google Scholar] [CrossRef]
- Li, P.; Li, Y.; Li, Z.; Jia, Q. Multi-time scale game dispatching strategy for microgrid cluster with shared energy storage considering demand response uncertainty. Energy 2025, 328, 136568. [Google Scholar] [CrossRef]
- Cao, W.; Xiao, J.; Cui, S.; Liu, X. An efficient and economical storage and energy sharing model for multiple multi-energy microgrids. Energy 2022, 244, 123124. [Google Scholar] [CrossRef]
- Chen, B.; Li, Z.; Liu, B.; Fan, H.; Zhong, Q. Dynamic cooperative scheduling and adaptive benefit allocation for multi-microgrid systems with shared energy storage under source-load uncertainty. J. Energy Storage 2025, 128, 117213. [Google Scholar] [CrossRef]
- Yang, X.; Yi, X.; Wang, H.; Li, L. Shared energy storage with multi-microgrids: Coordinated development and economic-social-environmental comprehensive assessment under supply–demand uncertainties. Renew. Energy 2025, 249, 123101. [Google Scholar] [CrossRef]
- Wen, Y.; Ding, R.; Liang, Y.; Chen, J. Multi-microgrid shared energy storage operation optimization strategy based on a mixed game theory. Electr. Power Syst. Res. 2025, 246, 111643. [Google Scholar] [CrossRef]
- Li, J.; Liu, D.; Jiang, S.; Wu, L. Optimal configuration of shared energy storage system in microgrid cluster: Economic analysis and planning for hybrid self-built and leased modes. J. Energy Storage 2024, 104, 114624. [Google Scholar] [CrossRef]
- Li, J.; Zhao, Z.; Wang, X.; Zhu, X.; Liu, H.; Zhao, Z.; Zhou, H.; Li, Z.; Li, C. Optimized configuration of shared energy storage in renewable energy power plants considering multiple master-slave game pricing modes. J. Energy Storage 2025, 115, 116012. [Google Scholar] [CrossRef]
- Li, J.; Liu, D.; Wang, J.; Bao, G.; Shi, M. Collaborative configuration optimization of renewable energy generation capacity for islanded microgrid clusters: A decision-making framework based on multi-criteria flexible interaction and shared mobile energy storage. Energy 2025, 333, 137448. [Google Scholar] [CrossRef]
- He, Y.; Zhang, Y. Optimal configuration of shared energy storage for multi-microgrid systems: Integrating battery decommissioning value and renewable energy economic consumption. Energy Convers. Manag. 2025, 343, 120156. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alter-nating direction method of multipliers. Found. Trends® Mach. Learn. 2021, 3, 1–122. [Google Scholar]
- Goh, H.; Shi, S.; Liang, X.; Zhang, D.; Dai, W.; Liu, H.; Wong, S.; Kurniawan, T.; Goh, K.; Cham, C. Optimal energy scheduling of grid-connected microgrids with demand side response considering uncertainty. Appl. Energy 2022, 327, 120094. [Google Scholar] [CrossRef]
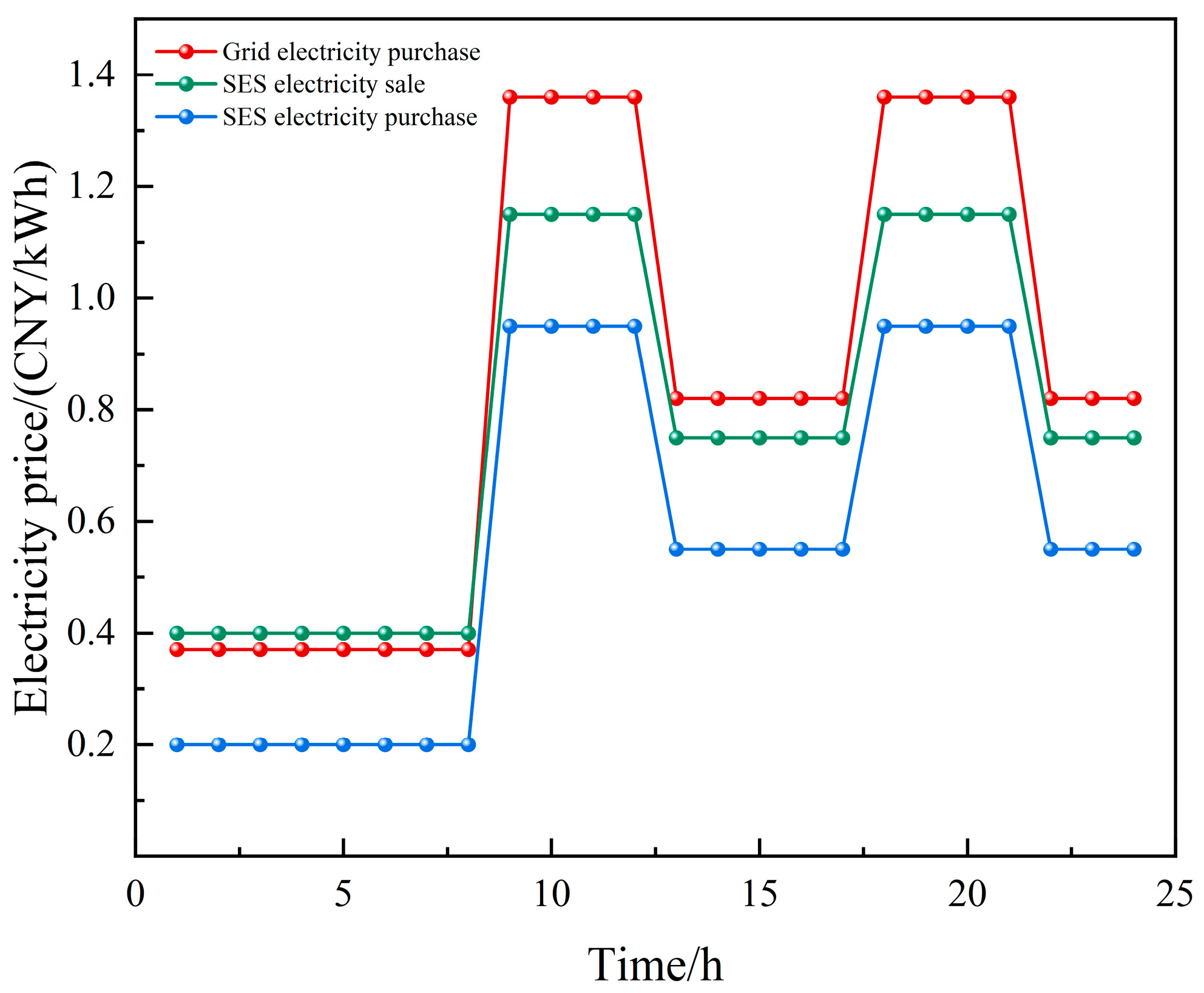
| Time Period | Electricity Price CNT/(kW·h) | ||
|---|---|---|---|
| Grid Power Sales | SES Power Sales | SES Power Purchase | |
| 08:00–12:00 | 1.36 | 1.15 | 0.95 |
| 17:00–21:00 | |||
| 12:00–17:00 | 0.82 | 0.75 | 0.55 |
| 21:00–24:00 | |||
| 00:00–08:00 | 0.37 | 0.40 | 0.20 |
| Subject | Unit | Cost |
|---|---|---|
| The first microgrid operating | CNY million | 3446.66 |
| The second microgrid operating | CNY million | 1226.54 |
| The third microgrid operating | CNY million | 4498.85 |
| SES capacity | kW·h | 13,898.72 |
| SES Rating power | kW | 2869.35 |
| SES O and M | CNY million | 619.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Zhang, X.; Wang, S.; Zhao, W. ADMM-Based Two-Tier Distributed Collaborative Allocation Planning for Shared Energy Storage Capacity in Microgrid Cluster. Electronics 2025, 14, 3234. https://doi.org/10.3390/electronics14163234
Feng J, Zhang X, Wang S, Zhao W. ADMM-Based Two-Tier Distributed Collaborative Allocation Planning for Shared Energy Storage Capacity in Microgrid Cluster. Electronics. 2025; 14(16):3234. https://doi.org/10.3390/electronics14163234
Chicago/Turabian StyleFeng, Jiao, Xiaoming Zhang, Shuhan Wang, and Wei Zhao. 2025. "ADMM-Based Two-Tier Distributed Collaborative Allocation Planning for Shared Energy Storage Capacity in Microgrid Cluster" Electronics 14, no. 16: 3234. https://doi.org/10.3390/electronics14163234
APA StyleFeng, J., Zhang, X., Wang, S., & Zhao, W. (2025). ADMM-Based Two-Tier Distributed Collaborative Allocation Planning for Shared Energy Storage Capacity in Microgrid Cluster. Electronics, 14(16), 3234. https://doi.org/10.3390/electronics14163234





