Stable Throughput Analysis of Heterogeneous Hybrid FSO/RF Networks with Cognitive Radio Capability

Abstract

This study explores the potential of heterogeneous hybrid Free Space Optical (FSO) and Radio Frequency (RF) cognitive networks, which feature both cooperative and economic systems. The cooperative system is defined as a heterogeneous network where the hybrid FSO/RF node possesses dedicated RF resources and shares these resources to create additional transmission opportunities. In contrast, the low-cost economic system consists of a heterogeneous network where only an RF node has RF resources, and the hybrid node shares these resources. We provide a comprehensive analysis for each system, employing stay-and-switch (SAS) and simultaneous multipacket transmission (SMT) methods to ensure a thorough understanding of its performance. As a performance measure, we investigate the stability region of the proposed cognitive and economic systems and devise a reference system without cognitive capability for comparison. Numerical evaluations indicate that the cooperative system using SMT typically outperforms the reference system, increasing stability throughput by up to 52%. However, this advantage diminishes when SAS is used or in rainy conditions. The economic model shows performance levels comparable to the reference model, particularly when incoming traffic is low and when SAS is implemented in clear or hazy environments.

1. Introduction

Free-space optical (FSO) communication has emerged as one of the most promising technologies for high-capacity wireless links due to its unique features, including extensive bandwidth, lack of licensing requirements, robust security, and other advantageous properties that make it an attractive option for numerous applications [1]. However, FSO communication is particularly vulnerable to performance degradation caused by atmospheric turbulence, pointing errors, and adverse weather conditions, which can significantly impact its reliability and stability [2,3]. To mitigate these limitations, hybrid FSO/RF systems—integrating FSO links with radio frequency (RF) channels—have been extensively investigated. In such systems, the RF channel is typically reserved as a backup for instances when the FSO link experiences a failure, providing a layer of resilience. However, this backup-only approach results in the underutilization of RF resources, which are often left idle when the FSO link is operational.

Previous research, including the work presented in [4,5], underscores the underutilization of RF resources in hybrid FSO/RF frameworks. To address this issue, recent studies have proposed alternative configurations, such as a “Shared RF” setup, that allow RF resources to be dynamically shared between FSO/RF pairs depending on link quality. This study introduces two novel system configurations that enable dynamic RF allocation in response to real-time FSO performance. The first variant involves two hybrid FSO/RF pairs, where the primary pair (pair 1) holds RF resources that the secondary pair (pair 2) can use when they are temporarily unutilized by pair 1. The second variant involves two FSO/RF pairs each with dedicated RF frequencies ( $f_1$ and $f_2$) that are shared based on threshold signal-to-noise ratios (SNRs). In this configuration, each pair transmits over the FSO link if the SNR is above a specific threshold and switches to the RF link when the FSO SNR falls below the threshold, optimizing resource utilization while enhancing overall system performance.

The existing literature presents a range of strategies aimed at improving the reliability of hybrid FSO/RF systems, broadly classified into three categories: hard switching, soft switching, and multiplexing. Hard switching schemes involve selecting either the FSO or RF link based on channel conditions, typically with feedback signals sent from the destination to the source to optimize the link selection [6,7,8,9,10,11,12,13]. In soft switching schemes, which are more complex, the system utilizes joint coding or the maximum ratio combining (MRC) of FSO and RF signals to enhance performance under variable channel conditions [14,15,16,17,18,19,20]. Multiplexing schemes, in contrast, allow multiple signals to be transmitted over FSO and RF links simultaneously, leveraging the distinct strengths of both channels [21,22]. Each of these switching schemes offers specific benefits, from maximizing link availability to optimizing the efficient use of resources.

For hard-switching schemes, various hybrid FSO/RF systems have been developed to select the FSO or RF channel with the highest SNR, thus reducing the outage probability and error rates under different environmental conditions [6,7,8,9,10,11,12,13]. Systems that incorporate decode-and-forward relays or multi-input–multi-output (MIMO) configurations have shown enhanced resilience by dynamically selecting FSO or RF channels according to channel state information [9,10]. In contrast, soft-switching schemes rely on MRC to combine FSO and RF signals, thus minimizing the impact of atmospheric interference on signal quality [16,19]. This study extends these approaches by analyzing configurations that focus on spectral efficiency, aiming to maximize data throughput by optimizing channel selection within hybrid FSO/RF frameworks.

Multiplexing-based approaches also play a significant role, especially in systems with finite buffer sizes. These systems are designed to support simultaneous signal transmissions across FSO and RF links, storing data packets in buffers for optimized relay to the appropriate channel based on SNR thresholds [21,22,23]. By employing relay selection mechanisms, these systems seek to optimize buffer size to reduce data loss, improve throughput, and manage latency. Our work further explores buffer management in hybrid FSO/RF systems, identifying the optimal buffer size required to ensure effective data transmission under dynamic, bursty arrival rates.

The inclusion of cognitive capability in FSO/RF systems has also been investigated in several studies [24,25,26]. These studies primarily focus on transmitted packet delays as a performance metric across different network and operational settings: utilizing multiple FSO channels [24], offloading packets based on the buffer states of FSO and RF channels [25], and aggregating RF channels for macro and small cells [26]. The previous research has indicated that the packet delay becomes infinite when the arrival rate exceeds a certain threshold. In this study, we aim to analyze the stability region of combined FSO and RF traffic, which ensures the packet delays remain finite in various cognitive FSO/RF system settings. To the best of our knowledge, no prior study has specifically analyzed the stability region of cognitive FSO/RF systems.

This study proposes a heterogeneous hybrid FSO/RF system structured around cognitive and economic frameworks. In the cognitive system, FSO and RF channels operate as a heterogeneous network with distinct RF resources shared dynamically to provide additional transmission opportunities. The economic system (placing the proposed system in currently practical environments), in contrast, restricts RF resources exclusively to RF links, allowing hybrid FSO/RF systems to access RF resources only when the FSO link is degraded. By employing both a stay-and-switch (SAS) method and a simultaneous multipacket transmission (SMT) strategy, this study investigates the stability region as a performance metric. The stability region is defined by the range of data arrival rates that maintain finite queue lengths across hybrid FSO/RF and RF links, offering a valuable indicator of network performance under bursty data traffic and probabilistic interference conditions. This analysis provides insights into network stability, highlighting the significance of stability regions as a measure of performance. By applying the static domain concept in [27], this work explores throughput within interaction queues, advancing our understanding of how hybrid FSO/RF systems can be optimized for robust, high-performance wireless communication. The key contributions of this study are summarized as follows:

• This study presents a cognitive hybrid FSO/RF system model and its operational scenarios consisting of cooperative and economic mode operations. In addition, a reference mode of operation is also defined to evaluate the performance of the proposed usages.
• For each operational scenario, this study conducts thorough stability analyses for two transmission strategies (i.e., SAS and SMT transmissions), and obtains the respective stable throughput. Furthermore, a hybrid SAS and SMT transmission is investigated for the cooperative mode and the stable throughput is also obtained.
• This study illustrates and compares the performance of the proposed methods through numerical evaluations. The data used in the simulation are sources from various relevant studies in the literature. The advantages of the proposed system are assessed against the reference system. The numerical results indicate that the cooperative system utilizing SMT generally outperforms the reference system, achieving an increase in stable throughput of up to 52%. However, this advantage diminishes when the SAS strategy is employed. The low-cost economic model demonstrates performance levels comparable to the reference model, particularly under conditions of low incoming traffic and when SAS is applied in clear or hazy environments.

The remainder of this paper is organized as follows: Section 2 presents the system models considered in this study, which define the heterogeneous hybrid network operations, including the cooperative, economic, and reference systems. Additionally, it defines a physical-layer signal representation to be used in the subsequent analysis and introduces the concept of queue stability. Section 3 analyzes the stable throughput for the reference system in SAS and SMT modes, respectively. Section 4 presents the stable throughput of the cooperative system, addressing both SAS and SMT modes. Additionally, this section investigates a hybrid SAS and SMT application and provides an analytical expression for stable throughput. In Section 5, we obtain the stable throughput of the economic system. Section 6 includes numerical evaluations alongside the analytical results for stable throughputs, offering comparisons between the proposed systems. Finally, Section 7 summarizes the main findings of the study. Appendix A provides the expressions for the rate of successful packet transmissions used in the stability analysis of the cooperative system.

2. System Models

2.1. Network Model

We consider a network with two transmitter–receiver pairs, as depicted in Figure 1. One pair (the upper pair in the figure) is communicating only through an RF channel(s) ($\mathtt{RO}$). The other uses hybrid FSO and RF channels ($\mathtt{HY}$). We investigate three different operating scenarios of the network according to the level of cooperation between $\mathtt{RO}$ and $\mathtt{HY}$ pairs: a non-cooperative reference model (Figure 1a, referred to as REF in this paper), a cooperative model (Figure 1b, referred to as COG in this paper), and an economic cooperative model (Figure 1c, referred to as ECO in this paper). In the non-cooperative model that is used as a reference, both $\mathtt{RO}$ and $\mathtt{HY}$ have their own RF frequency (denoted by $f_1$ and $f_2$, respectively) and $\mathtt{HY}$, in addition, has an optical channel $f_0$. $\mathtt{RO}$ and $\mathtt{HY}$ send packets independently. $\mathtt{HY}$ uses RF channel $f_2$ as a backup of the optical channel $f_0$ (referred to as stay-and-switching (SAS) in this paper). In SAS, $\mathtt{HY}$ uses $f_2$ only when the quality of $f_0$ drops below a certain level. However, we also investigate simultaneous multipacket transmission (SMT) in which HY tries to transmit packets simultaneously through both $f_2$ and $f_0$ to enhance the throughput compared to SAS.

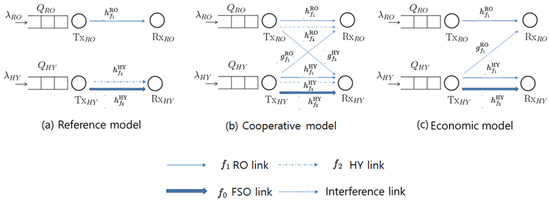
Figure 1. The heterogeneous hybrid FSO/RF systems considered in this study.

In the cooperative model, both $\mathtt{RO}$ and $\mathtt{HY}$ have cognitive radio capability (CR). $\mathtt{RO}$ and $\mathtt{HY}$ can sense and borrow to temporarily use $f_2$ and $f_1$, respectively, if the channels are idle. In SAS, the borrowing is for backup, and sensing is needed when the assigned channel(s) fails. In SMT, on the other hand, borrowing is used to improve throughput, and sensing is performed every time to determine whether the channel is idle. In the economic cooperative model, $f_1$ frequencies allocate to $\mathtt{RO}$, but $f_2$ frequencies do not allocate to $\mathtt{HY}$ due to lack of frequency resources. $\mathtt{HY}$ has CR and can operate in either SAS or SMT. In the cooperative models, $\mathtt{RO}$ and $\mathtt{HY}$ cannot send packets independently since the sensing can fail. Then, interference may occur by sending packets through the falsely borrowed channel.

Each transmitter of $\mathtt{RO}$ and $\mathtt{HY}$ has a buffer of infinite capacity to store their incoming packets, respectively. Time is slotted, the transmission of each packet is assumed to take one-time slot, and the transmissions in $\mathtt{RO}$ and $\mathtt{HY}$ are assumed to be synchronized. The packet arrival processes are independent and jointly strictly stationary with mean ${\lambda }_{\mathtt{RO}}$ (packets per slot) and ${\lambda }_{\mathtt{HY}}$ for $\mathtt{RO}$ and $\mathtt{HY}$, respectively. In addition, $Q_{\mathtt{RO}}$ and $Q_{\mathtt{HY}}$ denote their respective queue lengths.

2.2. Physical Layer Model

As shown in Figure 1, let $h_i^j$ denote the channel between communicating pair $j\in \{\mathtt{RO},\mathtt{HY}\}$ over the frequency channel $i\in \{f_0,f_1,f_2\}$. When a pair j is communicating on an RF channel, but the other pair k with CR falsely senses it to be idle, k may send a signal using the channel and cause interference at the receiver of j. Interfering channel from the transmitter of k to the receiver of the other pair j over channel l is denoted by $g_l^j$. The FSO channel is assumed not to be borrowed. And, thus $l\in \{f_1,f_2\}$. We assume that RF propagation over any transmitter–receiver pair is an independent stationary Rayleigh flat-fading channel and FSO link is an independent stationary Gamma–Gamma atmospheric turbulence-induced fading.

Let $x_i^j$ denote a transmit signal, with $E\left[\right|x_i^j{|}^2]=1$, between communication pair $j\in \{\mathtt{RO},\mathtt{HY}\}$ over frequency channel $i\in \{f_0,f_1,f_2\}$. And let $P_i^j$ denote transmitting power of $x_i^j$. Let ${\theta }_i^j$ be a binary variable that indicates whether an interfering signal exits at the receiver of j (${\theta }_i^j=1$) or not (${\theta }_i^j=0$). Since the FSO channel is not rented, ${\theta }_i^j=0$ if $i=f_0$. Then, the received signal for pair j over channel i is

$$\begin{array}{c}\hfill y_i^j=\sqrt{P_i^j}{h}_i^j{x}_i^j+{\theta }_i^j\sqrt{P_i^k}{g}_i^j{x}_i^k+n_i^j,\end{array}$$

(1)

where $h_i^j$ and $g_i^j$ are independently and identically distributed according to $CN(0,{\sigma }_i^j)$ and $CN(0,{\widehat{\sigma }}_i^j)$, respectively. k ($k\ne j,k\in \{\mathtt{RO},\mathtt{HY}\}$) denotes an interfering transmitter, and $n_i^j$ is an additive white Gaussian noise (AWGN) at the receiver of j. Hereafter, we assume that the AWGN at each receiver is independently and identically distributed according to $CN(0,N_0)$.

Then, the SNR or signal-to-interference-plus-noise ratio (SINR) is given by

$$\begin{array}{c}\hfill {\gamma }_i^j={\displaystyle \frac{P_i^j{\left|h_i^j\right|}^2}{N_0+{\theta }_i^j{P}_i^k{\left|g_i^j\right|}^2}}.\end{array}$$

(2)

We assume that a receiving node can decode a packet successfully if the received SNR or SINR is greater than or equal to a certain threshold ${\delta }_i^j$. Let $s_{i\in \{f_1,f_2\},j\in \{\mathtt{RO},\mathtt{HY}\}}$ denote the probability of successfully decoding a packet without interference $({\theta }_i^j=0)$ through the RF link $i\in \{f_1,f_2\}$, and it is given by

$$\begin{array}{c}\hfill s_{i,j}=Pr({\gamma }_i^j>{\delta }_i^j|{\theta }_i^j=0)=exp\left(-{\displaystyle \frac{N_0{\delta }_i^j}{P_i^j{\sigma }_i^j}}\right).\end{array}$$

(3)

And let $s_{i,j}^I$ denote the probability of successfully decoding a packet with interference $({\theta }_i^j=1)$, and it given by

$$\begin{array}{c}\hfill s_{i,j}^I=Pr({\gamma }_i^j>{\delta }_i^j|{\theta }_i^j=1)={\displaystyle \frac{P_i^j{\sigma }_i^j}{P_i^j{\sigma }_i^j+P_i^k{\widehat{\sigma }}_i^j}}exp\left(-{\displaystyle \frac{N_0{\delta }_i^j}{P_i^j{\sigma }_i^j}}\right).\end{array}$$

(4)

Let $s_{f_0}^{HY}$ denote the probability of successfully decoding a packet through an FSO link, and it is given by

$$\begin{array}{c}\hfill s_{f_0,HY}={\displaystyle \frac{{\xi }^2}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}}{G}_{2,4}^{4,0}\left[\alpha \beta o{\delta }_{f_0}^{HY}/\eta |\begin{array}{cccc}1& {\xi }^2+1& & \\ 0& {\xi }^2& \alpha & \beta \end{array}\right],\end{array}$$

(5)

where $\alpha$, $\beta$, and $\xi$ are the turbulence parameters, and ${\delta }_{f_0}^{\mathtt{HY}}$ and $\eta$ are the target SNR of FSO link and average SNR of FSO link and $o={\xi }^2/({\xi }^2+1)$ and $\Gamma (·)$ and $G_{a,b}^{c,d}(·)$ are gamma function and Meijer’s G-function, respectively.

2.3. Queue Stability

Let the number of packets stored in the buffer at transmitter j be $Q_j$. This buffer receives one packet at an average arrival rate of ${\lambda }_j$. Let ${\mu }_{j,n}$ represent the average service rate when the transmitter j simultaneously services n packets. The packets stored in $Q_j$ increase by 1 at a rate of ${\lambda }_j$ or decrease by n at a rate of ${\mu }_{j,n}$. We model the buffer of hybrid FSO/RF as a discrete-time $M/M^{\left[B\right]}/1$ queue, where buck services $B=2$ [28,29]. Let ${\pi }_l$ denote the steady-state probability that buffers j stores l packet and N is a maximum number of simultaneous services packets. In this case, ${\pi }_n$ can be expressed as follows.

$$\begin{array}{c}\hfill {\pi }_0{\lambda }_j=\sum _{n=1}^N{\pi }_n{\mu }_{j,n}+{\pi }_1{\mu }_{j,2}+{\pi }_1{\mu }_{j,3}+2{\pi }_2{\mu }_{j,3},\end{array}$$

(6)

$$\begin{array}{c}\hfill {\pi }_l{\lambda }_j=\sum _{n=1}^N{\pi }_{l+n}{\mu }_{j,n}.\end{array}$$

(7)

The average service rate consists of the scenarios where the communication pair of the borrowed frequency is idle ($Q_k=0$) and when it is active ($Q_k\ne 0$). Let the probability of successfully delivering n packets when $Q_k=0$ and $Q_k\ne 0$ be $v_{j,n,0}$ and $v_{j,n,1}$, respectively. In this case, the average service rate can be expressed as follows.

$$\begin{array}{c}\hfill {\mu }_{j,n}=Pr(Q_k=0)v_{j,n,0}+Pr(Q_k\ne 0)v_{j,n,1},\end{array}$$

(8)

where Pr(A) denotes the probability of state A.

For queues where the arrival and service processes are jointly strictly stationary and ergodic, Loynes’ theorem [30] states that the queue at each transmitting node is stable if and only if the average arrival rate is strictly less than the average service rate. Based on Loynes’ theorem, let us define that a queue is stable if $Pr(Q_k=0)>0$. Moreover, a system is said to be stable if and only if all the queues are stable.

Our goal is to obtain the stable throughput of the proposed COG and ECO and compare them with that of REF. We investigate how much throughput improvement occurs through the proposed cooperative method, which depends on various network and physical layers parameters. Among the parameters, we mainly focus on the effect of the turbulent FSO channel conditions.

3. Stable Throughput of Reference System (REF)

With REF model, both $\mathtt{RO}$ pair and $\mathtt{HY}$ pair have licensed RF $f_1$ and $f_2$, respectively. It is assumed that each transmitter has no CR and uses its frequency only. Therefore, there is no interference signal caused by borrowing the frequency, and accordingly, $v_{j,n,0}=v_{j,n,1}$ holds.

3.1. Stay and Switch Mode

We set the switching threshold for FSO as ${\delta }_{f_0}^{HY}$. In this system, $N=1$ and $v_{j,1,0}=v_{j,1,1}$ is given by

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},1,0}& =& s_{f_0,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill v_{\mathtt{RO},1,0}& =& s_{f_1,\mathtt{RO}}.\hfill \end{array}$$

(10)

The respective service rate of $\mathtt{RO}$ and $\mathtt{HY}$ dose not interact then the $Pr(Q_j=0)=1-{\displaystyle \frac{{\lambda }_j}{{\mu }_{j,1}}}$ and the stable region is given by

$$\begin{array}{c}\hfill R_{REF,\mathrm{SAS}}=\{{\lambda }_{\mathtt{HY}},{\lambda }_{\mathtt{RO}}|{\lambda }_{\mathtt{HY}}<{\mu }_{\mathtt{HY},1},{\lambda }_{\mathtt{RO}}<{\mu }_{\mathtt{RO},1}\}.\end{array}$$

(11)

3.2. Simultaneous Multipacket Transmission

In this system, $N=2$ for $\mathtt{HY}$ and $N=1$ for $\mathtt{RO}$, and $v_{j,1,0}=v_{j,1,1}$ is given by

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},1,0}& =& s_{f_0,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}},\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},2,0}& =& s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}.\hfill \end{array}$$

(13)

The state transition diagram is shown in Figure 2. The balance equation for $Q_{HY}$ is as follows:

$$\begin{array}{ccc}& \dots & \\ \hfill {\pi }_n({\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2})+{\pi }_{n+1}{\mu }_{\mathtt{HY},2}& =& {\pi }_{n-1}{\lambda }_{\mathtt{HY}},\hfill \\ & \dots & \end{array}$$

(14)

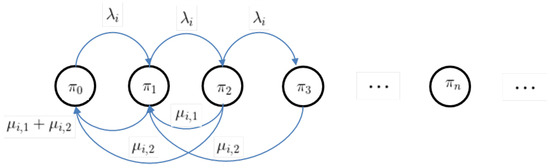
Figure 2. The buffer state transition diagram with one- or two-packet service in a single time slot.

Simple manipulation of this system of equations provides a new representation that will be useful for deriving an explicit expression of the desired distribution. Rearranging Equation (14), we have

$$\begin{array}{ccc}\hfill {\pi }_n& =& {\pi }_{n-1}{\displaystyle \frac{{\lambda }_{\mathtt{HY}}-{\psi }_{n-1}}{{\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2}}},\hfill \end{array}$$

(15)

where ${\psi }_n={\displaystyle \frac{{\pi }_{n+2}{\mu }_{\mathtt{HY},2}}{{\pi }_n}}$. If ${\psi }_0={\psi }_1={\psi }_2...=\psi$, then we have a closed form of $\psi$ such that

$$\begin{array}{ccc}\hfill \psi & =& {\displaystyle \frac{2{\lambda }_{\mathtt{HY}}+\frac{{({\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2})}^2}{{\mu }_{\mathtt{HY},2}}}{2}}-{\displaystyle \frac{\sqrt{4{\lambda }_{\mathtt{HY}}\frac{{({\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2})}^2}{{\mu }_{\mathtt{HY},2}}+\frac{{({\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2})}^4}{{\mu }_{\mathtt{HY},2}^2}}}{2}}.\hfill \end{array}$$

(16)

With $\psi$ in Equation (16), the probability of $Q_{\mathtt{HY}}=0$ is given by

$$\begin{array}{c}\hfill Pr(Q_{\mathtt{HY}}=0)={\pi }_0={\displaystyle \frac{{\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2}-{\lambda }_{\mathtt{HY}}+\psi }{{\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2}}}..\end{array}$$

(17)

The service rate of $Q_{\mathtt{RO}}$ is the same to (10). Then, the stable region is finally obtained by

$$\begin{array}{c}\hfill R_{REF,\mathrm{SMT}}=\{{\lambda }_{\mathtt{HY}},{\lambda }_{\mathtt{RO}}|{\lambda }_{\mathtt{HY}}<{\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2}+\psi ,{\lambda }_{\mathtt{RO}}<{\mu }_{\mathtt{RO}}\}.\end{array}$$

(18)

4. Stable Throughput of Cooperative System (COG)

With this model, both $\mathtt{RO}$ pair and $\mathtt{HY}$ pair have licensed a RF $f_{\mathtt{RO}}$ and $f_{\mathtt{HY}}$, respectively. RF part of $\mathtt{RO}$ and $\mathtt{HY}$ pair being capable of performing CR functions. The RF part uses the other pairs of licensed RF with spectrum sensing with CR capability.

4.1. Stay and Switch Mode

In this system, $N=1$ and the success rates of packet transmission for $j\in \{\mathtt{RO},\mathtt{HY}\}$$v_{j,1,0}$ and $v_{j,1,1}$ expressions are given in Appendix A.1, where $p_{d,\mathtt{HY}}$ and $p_{f,\mathtt{HY}}$ are detection and false alarm probabilities of $\mathtt{HY}$ transmitter, respectively.

The average service rate of ${\mu }_{j,1}$ is given in (8) with $v_{j,1,0}$ and $v_{j,1,1}$ in (A1)–(A4). In that model, the average service rate depends on the probability of the buffer state of the pair borrowing the frequency. In this case, the domain system is used to find a stable region. In the domain system, one buffer is always filled with packets, and the average service rate does not depend on the probability of the buffer state.

The first dominant system is identical to the original system, except that the RF transmitter transmits a dummy packet whenever $Q_{\mathtt{RO}}$ empties. All other assumptions remain unchanged in the dominant system. Let ${\mu }_{\mathtt{HY}}^{\left(1\right)}$ and ${\mu }_{\mathtt{RO}}^{\left(1\right)}$ be the service rates of $Q_{\mathtt{RO}}$ and $Q_{\mathtt{HY}}$ in first dominant system, respectively, then they are given by

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{HY}}^{\left(1\right)}& =& v_{\mathtt{HY},1},\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{RO}}^{\left(1\right)}& =& \left(1-{\displaystyle \frac{{\lambda }_{\mathtt{HY}}^{\left(1\right)}}{{\mu }_{\mathtt{HY}}^{\left(1\right)}}}\right)v_{\mathtt{RO},0}+{\displaystyle \frac{{\lambda }_{\mathtt{HY}}^{\left(1\right)}}{{\mu }_{\mathtt{HY}}^{\left(1\right)}}}{v}_{\mathtt{RO},1}.\hfill \end{array}$$

(20)

Thus, the stable region for the first dominant system is obtained by

$$\begin{array}{c}\hfill R_{COG,\mathrm{SAS}}^{\left(1\right)}=\{{\lambda }_{\mathtt{HY}}^{\left(1\right)},{\lambda }_{\mathtt{RO}}^{\left(1\right)}|{\lambda }_{\mathtt{HY}}^{\left(1\right)}<{\mu }_{\mathtt{HY}}^{\left(1\right)},{\lambda }_{\mathtt{RO}}^{\left(2\right)}<\mu {\mathtt{RO}}^{\left(2\right)}\}.\end{array}$$

(21)

The second dominant system is identical to the original system, except that the $\mathtt{HY}$ transmitter transmits a dummy packet whenever $Q_{\mathtt{HY}}$ empties. All other assumptions remain unchanged in the dominant system. Let ${\mu }_{\mathtt{HY}}^{\left(2\right)}$ and ${\mu }_{\mathtt{RO}}^{\left(2\right)}$ be the service rates of $Q_{\mathtt{RO}}$ and $Q_{\mathtt{HY}}$ in second dominant system, respectively, then they are expressed as

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{RO}}^{\left(2\right)}& =& v_{\mathtt{RO},1},\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{HY}}^{\left(2\right)}& =& \left(1-{\displaystyle \frac{{\lambda }_{\mathtt{RO}}^{\left(2\right)}}{{\mu }_{\mathtt{RO}}^{\left(2\right)}}}\right)v_{\mathtt{HY},0}+{\displaystyle \frac{{\lambda }_{\mathtt{RO}}^{\left(2\right)}}{{\mu }_{\mathtt{RO}}^{\left(2\right)}}}{v}_{\mathtt{HY},1}.\hfill \end{array}$$

(23)

Thus, the stable region for the second dominant system is obtained by

$$\begin{array}{c}\hfill R_{COG,\mathrm{SAS}}^{\left(2\right)}=\{{\lambda }_{\mathtt{HY}}^{\left(2\right)},{\lambda }_{\mathtt{RO}}^{\left(2\right)}|{\lambda }_{\mathtt{HY}}^{\left(2\right)}<{\mu }_{\mathtt{HY}}^{\left(2\right)},{\lambda }_{\mathtt{RO}}^{\left(2\right)}<\mu {\mathtt{RO}}^{\left(2\right)}\}.\end{array}$$

(24)

Finally, the stable region for COG with SAS is given by

$$\begin{array}{c}\hfill R_{COG,\mathrm{SAS}}=\{R_{COG,\mathrm{SAS}}^{\left(1\right)}\cup R_{COG,\mathrm{SAS}}^{\left(2\right)}\}.\end{array}$$

(25)

4.2. Simultaneous Multipacket Transmission Mode

In this system, $N=3$ for $\mathtt{HY}$ and $N=2$ for $\mathtt{RO}$, and the success rates of packet transmission for $j\in \{\mathtt{RO},\mathtt{HY}\}$$v_{j,n,0}$ and $v_{j,n,1}$ expressions are given in Appendix A.2, then we have the service rate ${\mu }_{j,n}$ which is given in (8).

Referring to the state transition diagram presented by Figure 3, the balance equation of $Q_{\mathtt{HY}}$ is given in (6) and (7). A simple manipulation of the above balance equations gives

$$\begin{array}{ccc}\hfill {\pi }_{\mathtt{HY},l}& =& {\pi }_{\mathtt{HY},l-1}{\displaystyle \frac{{\lambda }_{\mathtt{HY}}-\frac{{\pi }_{\mathtt{HY},2}({\mu }_{\mathtt{HY},2}+{\mu }_{\mathtt{HY},3})}{{\pi }_{\mathtt{HY},l-1}}-\frac{{\pi }_{\mathtt{HY},l+2}{\mu }_{\mathtt{HY},1}}{{\pi }_{\mathtt{HY},l-2}}}{{\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2}+{\mu }_{\mathtt{HY},3}}}={\pi }_{\mathtt{HY},l-1}{\displaystyle \frac{{\lambda }_{\mathtt{HY}}-{\psi }_{\mathtt{HY},l-1}}{{\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2}+{\mu }_{\mathtt{HY},3}}},\hfill \end{array}$$

(26)

If ${\psi }_{\mathtt{HY},0}={\psi }_{\mathtt{HY},1}={\psi }_{\mathtt{HY},2}...={\psi }_{\mathtt{HY}}$, then ${\psi }_{\mathtt{HY}}$ with $0<{\psi }_{\mathtt{HY}}<1$ is a solution of

$$\begin{array}{ccc}& & ({\lambda }_{\mathtt{HY}}-{\psi }_{\mathtt{HY}}){({\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2}+{\mu }_{\mathtt{HY},3})}^3+({\mu }_{\mathtt{HY},2}+{\mu }_{\mathtt{HY},3})({\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2}+{\mu }_{\mathtt{HY},3})({\lambda }_{\mathtt{HY}}-{\psi }_{\mathtt{HY}})\hfill \\ & & +{\mu }_{\mathtt{HY},3}{({\lambda }_{\mathtt{HY}}-{\psi }_{\mathtt{HY}})}^3-{\lambda }_{\mathtt{HY}}{({\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2}+{\mu }_{\mathtt{HY},3})}^3=0.\hfill \end{array}$$

(27)

With ${\psi }_{\mathtt{HY}}$ in Equation (27), the probability of $Q_{\mathtt{HY}}=0$ is obtained by

$$\begin{array}{c}\hfill Pr(Q_{\mathtt{HY}}=0)=1-{\displaystyle \frac{{\lambda }_{\mathtt{HY}}-{\psi }_{\mathtt{HY}}}{{\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2}+{\mu }_{\mathtt{HY},3}}}.\end{array}$$

(28)

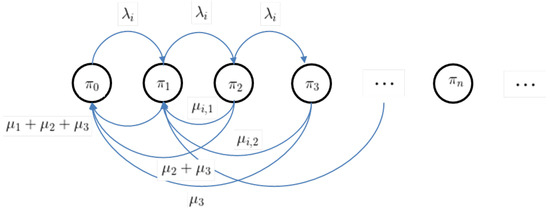
Figure 3. The buffer state transition diagram with up to three-packet service in a single time slot.

The $\mathtt{RO}$ system now transmits one or two packets in a single time slot, the state transition diagram of which is given in Figure 2. The balance equations of $Q_{\mathtt{RO}}$ are the same to the equations in (14) by replacing ${\mu }_{\mathtt{HY},1}$, ${\mu }_{\mathtt{HY},2}$ with ${\mu }_{\mathtt{RO},1}$, ${\mu }_{\mathtt{RO},2}$, respectively.

Thus, in the first dominant system, the service rates for $Q_{\mathtt{HY}}$ and $Q_{\mathtt{RO}}$ are obtained by

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{HY},n\in \{1,2,3\}}^{\left(1\right)}& =& v_{\mathtt{HY},n,1},\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{RO},l\in \{1,2\}}^{\left(1\right)}& =& \left(1-{\displaystyle \frac{{\lambda }_{\mathtt{HY}}^{\left(1\right)}-{\psi }_{\mathtt{HY}}^{\left(1\right)}}{{\mu }_{\mathtt{HY},1}^{\left(1\right)}+{\mu }_{\mathtt{HY},2}^{\left(1\right)}+{\mu }_{\mathtt{HY},3}^{\left(1\right)}}}\right)v_{\mathtt{RO},l,0}+{\displaystyle \frac{{\lambda }_{\mathtt{HY}}^{\left(1\right)}-{\psi }_{\mathtt{HY}}^{\left(1\right)}}{{\mu }_{\mathtt{HY},1}^{\left(1\right)}+{\mu }_{\mathtt{HY},2}^{\left(1\right)}+{\mu }_{\mathtt{HY},3}^{\left(1\right)}}}{v}_{\mathtt{RO},l,1},\hfill \end{array}$$

(30)

where ${\psi }_{\mathtt{HY}}^{\left(1\right)}$ is obtained by a solution of the equation given similar to (27). The equation should be reconstructed by replacing ${\mu }_{\mathtt{HY},1}$, ${\mu }_{\mathtt{HY},2}$, ${\mu }_{\mathtt{HY},3}$, and ${\lambda }_{\mathtt{HY}}$ with ${\mu }_{\mathtt{HY},1}^{\left(1\right)}$, ${\mu }_{\mathtt{HY},2}^{\left(1\right)}$, ${\mu }_{\mathtt{HY},3}^{\left(1\right)}$, and ${\lambda }_{\mathtt{HY}}^{\left(1\right)}$, respectively.

The stable region for the first dominant system $R_{COG,\mathrm{SMT}}^{\left(1\right)}$ can now be expressed by

$$\begin{array}{c}\hfill R_{COG,\mathrm{SMT}}^{\left(1\right)}=\{{\lambda }_{\mathtt{HY}}^{\left(1\right)},{\lambda }_{\mathtt{RO}}^{\left(1\right)}|{\lambda }_{\mathtt{HY}}^{\left(1\right)}<{\mu }_{\mathtt{HY},1}^{\left(1\right)}+{\mu }_{\mathtt{HY},2}^{\left(1\right)}+{\mu }_{\mathtt{HY},3}^{\left(1\right)}+{\psi }_{\mathtt{HY}}^{\left(1\right)},{\lambda }_{\mathtt{RO}}^{\left(1\right)}<{\mu }_{\mathtt{RO},1}^{\left(1\right)}+{\mu }_{\mathtt{RO},2}^{\left(1\right)}+{\psi }_{\mathtt{RO}}^{\left(1\right)}\}.\end{array}$$

(31)

In the second dominant system, the service rates $Q_{\mathtt{RO}}$ and $Q_{\mathtt{HY}}$ are given by

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{RO},l\in \{1,2\}}^{\left(2\right)}& =& v_{\mathtt{RO},l,1},\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{HY},n\in \{1,2,3\}}^{\left(2\right)}& =& \left(1-{\displaystyle \frac{{\lambda }_{\mathtt{RO}}^{\left(2\right)}-{\psi }_{\mathtt{RO}}^{\left(2\right)}}{{\mu }_{\mathtt{RO},1}^{\left(2\right)}+{\mu }_{\mathtt{RO},2}^{\left(2\right)}}}\right)v_{\mathtt{HY},n,0}+{\displaystyle \frac{{\lambda }_{\mathtt{RO}}^{\left(2\right)}-{\psi }_{\mathtt{RO}}^{\left(2\right)}}{{\mu }_{\mathtt{RO},1}^{\left(2\right)}+{\mu }_{\mathtt{RO},2}^{\left(2\right)}}}{v}_{\mathtt{HY},n,1}.\hfill \end{array}$$

(33)

The stable region for the second dominant system $R_{COG,\mathrm{SMT}}^{\left(2\right)}$ now can be expressed by

$$\begin{array}{c}\hfill R_{COG,\mathrm{SMT}}^{\left(2\right)}=\{{\lambda }_{\mathtt{HY}}^{\left(2\right)},{\lambda }_{\mathtt{RO}}^{\left(2\right)}|{\lambda }_{\mathtt{HY}}^{\left(2\right)}<{\mu }_{\mathtt{HY},1}^{\left(2\right)}+{\mu }_{\mathtt{HY},2}^{\left(2\right)}+{\mu }_{\mathtt{HY},3}^{\left(2\right)}+{\psi }_{\mathtt{HY}}^{\left(2\right)},{\lambda }_{\mathtt{RO}}^{\left(2\right)}<{\mu }_{\mathtt{RO},1}^{\left(2\right)}+{\mu }_{\mathtt{RO},2}^{\left(2\right)}+{\psi }_{\mathtt{RO}}^{\left(2\right)}\}.\end{array}$$

(34)

Thus, the stable region for the cooperative system with SMT is obtained by

$$\begin{array}{c}\hfill R_{COG,\mathrm{SMT}}=\{R_{COG,\mathrm{SMT}}^{\left(1\right)}\cup R_{COG,\mathrm{SMT}}^{\left(2\right)}\}.\end{array}$$

(35)

4.3. A Hybrid Combination of SMT and SAS

In this subsection, we analyze the stability region of a hybrid cooperative system in which the $\mathtt{RO}$ system operates as SMT and $\mathtt{HY}$ system as SAS. In this case, during a single time slot, $\mathtt{RO}$ transmits up to two packets at the same time, and $\mathtt{HY}$ transmits a single packet. Then, we have $v_{j,n,0}$ and $v_{j,n,1}$ for (A15)–(A18) and (A19) and (A20) in Appendix A.3; then, we have the service rate of ${\mu }_{j,1}$ which is given in (8).

In the first dominant system, the service rates for $Q_{\mathtt{HY}}$ and $Q_{\mathtt{RO}}$ are then given by

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{HY}}^{\left(1\right)}& =& v_{\mathtt{HY},1,1},\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{RO},l\in \{1,2\}}^{\left(1\right)}& =& \left(1-{\displaystyle \frac{{\lambda }_{\mathtt{HY}}^{\left(1\right)}}{{\mu }_{\mathtt{HY}}^{\left(1\right)}}}\right)v_{\mathtt{RO},l,0}+{\displaystyle \frac{{\lambda }_{\mathtt{HY}}^{\left(1\right)}}{{\mu }_{\mathtt{HY}}^{\left(1\right)}}}{v}_{\mathtt{RO},l,1}.\hfill \end{array}$$

(37)

The stable region for the first dominant system $R_{COG,\mathrm{VS}}^{\left(1\right)}$ (hereafter, the subscript $\mathrm{VS}$ is used to denote the hybrid cooperative system considered in this subsection) can thus be expressed by

$$\begin{array}{c}\hfill R_{COG,\mathrm{VS}}^{\left(1\right)}=\{{\lambda }_{\mathtt{HY}}^{\left(1\right)},{\lambda }_{\mathtt{RO}}^{\left(1\right)}|{\lambda }_{\mathtt{HY}}^{\left(1\right)}<{\mu }_{\mathtt{HY}}^{\left(1\right)},{\lambda }_{\mathtt{RO}}^{\left(1\right)}<{\mu }_{\mathtt{RO},1}^{\left(1\right)}+{\mu }_{\mathtt{RO},2}^{\left(1\right)}+{\psi }_{\mathtt{RO}}^{\left(1\right)}\},\end{array}$$

(38)

where ${\psi }_{\mathtt{RO}}^{\left(1\right)}$ is obtained by replacing ${\mu }_{\mathtt{HY},1}^{\left(1\right)}$, ${\mu }_{\mathtt{HY},2}^{\left(1\right)}$, and ${\lambda }_{\mathtt{HY}}^{\left(1\right)}$ for $\psi$ given in Equation (16) with ${\mu }_{\mathtt{RO},1}$, ${\mu }_{\mathtt{RO},2}$, and ${\lambda }_{\mathtt{RO}}$, respectively.

In the second dominant system, the service rates $Q_{\mathtt{RO}}$ and $Q_{\mathtt{HY}}$ are given by

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{RO},l\in \{1,2\}}^{\left(2\right)}& =& v_{\mathtt{RO},l,1},\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill {\mu }_{\mathtt{HY}}^{\left(2\right)}& =& \left(1-{\displaystyle \frac{{\lambda }_{\mathtt{RO}}^{\left(2\right)}-{\psi }_{\mathtt{RO}}^{\left(2\right)}}{{\mu }_{\mathtt{RO},1}^{\left(2\right)}+{\mu }_{\mathtt{RO},2}^{\left(2\right)}}}\right)v_{\mathtt{HY},1,0}+{\displaystyle \frac{{\lambda }_{\mathtt{RO}}^{\left(2\right)}-{\psi }_{\mathtt{RO}}^{\left(2\right)}}{{\mu }_{\mathtt{RO},1}^{\left(2\right)}+{\mu }_{\mathtt{RO},2}^{\left(2\right)}}}{v}_{\mathtt{HY},1,1},\hfill \end{array}$$

(40)

respectively. The stable region for the second dominant system $R_{COG,\mathrm{VS}}^{\left(2\right)}$ can now be obtained by

$$\begin{array}{ccc}\hfill R_{COG,\mathrm{VS}}^{\left(2\right)}& =& \{{\lambda }_{\mathtt{HY}}^{\left(2\right)},{\lambda }_{\mathtt{RO}}^{\left(2\right)}|{\lambda }_{\mathtt{HY}}^{\left(2\right)}<{\mu }_{\mathtt{HY},1}^{\left(2\right)}+{\mu }_{\mathtt{HY},2}^{\left(2\right)}+{\mu }_{\mathtt{HY},3}^{\left(2\right)}+{\psi }_{\mathtt{HY}}^{\left(2\right)},\hfill \\ & & {\lambda }_{\mathtt{RO}}^{\left(2\right)}<{\mu }_{\mathtt{RO},1}^{\left(2\right)}+{\mu }_{\mathtt{RO},2}^{\left(2\right)}+{\psi }_{\mathtt{RO}}^{\left(2\right)}\}.\hfill \end{array}$$

(41)

Finally, the stable region for the hybrid cooperative system is obtained by

$$\begin{array}{c}\hfill R_{COG,\mathrm{VS}}=\{R_{COG,\mathrm{VS}}^{\left(1\right)}\cup R_{COG,\mathrm{VS}}^{\left(2\right)}\}.\end{array}$$

(42)

5. Stable Throughput of Economic System Model

In this section, we assume that only the $\mathtt{RO}$ pair has licensed radio frequency RF $f_1$. It is also assumed that only the $\mathtt{HY}$ transmitter has the CR and can access $f_1$ with spectrum sensing. Since $\mathtt{HY}$ does not allocate $f_2$, we set the transmission success probabilities $s_{f_2,j}$, $s_{f_2,j}^I$ to zero.

5.1. Stay and Switch Mode

The success rate of single packet $v_{j,1,0}$$v_{j,1,0}$ can be obtained from Equations (A1)–(A4). The average service rate of ${\mu }_{j,1}$ is given in (8). The stability region can be similarly obtained from $R_{COG,\mathrm{SAS}}$ given in (25).

5.2. Simultaneous Multipacket Transmission Mode

The success rate of n packets $v_{j,n,0}$ and $v_{j,n,1}$ can be obtained from Equations (A5), (A6) and (A9) and $v_{\mathtt{RO},2,0}=v_{\mathtt{RO},2,1}=0$, $v_{\mathtt{HY},3,0}=v_{\mathtt{HY},3,1}=0$, since $s_{f_2,j}=s_{f_2,j}^I=0$. The average service rate of ${\mu }_{j,1}$ is given in (8).

In the first dominant system, the service rates for $Q_{\mathtt{HY}}$ and $Q_{\mathtt{RO}}$ are given (29) and (30) with $s_{f_2,j}=s_{f_2,j}^I=0$. The stable region for the first dominant system $R_{ECO,\mathrm{SMT}}^{\left(1\right)}$ thus can be expressed by

$$\begin{array}{c}\hfill R_{ECO,\mathrm{SMT}}^{\left(1\right)}=\left\{{\lambda }_{\mathtt{HY}}^{\left(1\right)},{\lambda }_{\mathtt{RO}}^{\left(1\right)}|{\lambda }_{\mathtt{HY}}^{\left(1\right)}<{\mu }_{\mathtt{HY},1}+{\mu }_{\mathtt{HY},2}+{\psi }^{\left(1\right)},{\lambda }_{\mathtt{RO}}^{\left(1\right)}<{\mu }_{\mathtt{RO}}^{\left(1\right)}\right\}.\end{array}$$

(43)

In the second dominant system, the service rates for $Q_{\mathtt{HY}}$ and $Q_{\mathtt{RO}}$ are given (32) and (33) with $s_{f_2,j}=s_{f_2,j}^I=0$. The stable region for the second dominant system $R_{ECO,\mathrm{SMT}}^{\left(2\right)}$ thus can be expressed by

$$\begin{array}{c}\hfill R_{ECO,\mathrm{SMT}}^{\left(2\right)}=\left\{{\lambda }_{\mathtt{HY}}^{\left(2\right)},{\lambda }_{\mathtt{RO}}^{\left(2\right)}|{\lambda }_{\mathtt{HY}}^{\left(2\right)}<{\mu }_{\mathtt{HY},1}^{\left(2\right)}+{\mu }_{\mathtt{HY},2}^{\left(2\right)}+{\psi }^{\left(2\right)},{\lambda }_{\mathtt{RO}}^{\left(1\right)}<{\mu }_{\mathtt{RO}}^{\left(1\right)}\right\}.\end{array}$$

(44)

Finally, the stable region for the economic system with SMT is given by

$$\begin{array}{c}\hfill R_{ECO,\mathrm{SMT}}=\{R_{ECO,\mathrm{SMT}}^{\left(1\right)}\cup R_{ECO,\mathrm{SMT}}^{\left(2\right)}\}.\end{array}$$

(45)

6. Numerical Results

In the simulation, the FSO link and RF parameter values are computed as follows [31]:

$$\begin{array}{ccc}\hfill \alpha & =& {\left(e^{{\displaystyle \frac{0.49{\xi }^2}{{(1+0.18d^2+0.56{\xi }^{12/5})}^{7/6}}}}\right)}^{-1},\hfill \end{array}$$

(46)

$$\begin{array}{ccc}\hfill \beta & =& {\left(e^{{\displaystyle \frac{0.51{\xi }^2{(1+0.69{\xi }^{12/5})}^{-5/6}}{{(1+0.9d^2+0.62d^2{\xi }^{12/5})}^{5/6}}}}\right)}^{-1},\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill \xi & =& \sqrt{0.5c_n^2{k}^{7/6}{z}^{11/6}},\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill k& =& 2\pi /{\lambda }_{f_0},\hfill \end{array}$$

(49)

where $\xi$ and z are the waver number of RF links and the distance between the FSO transmitter and the receiver. We assume a point receiver, i.e., $D<<z$, leading to $d=0$ [32]. The average SNR of FSO is given by [33,34]

$$\begin{array}{c}\hfill \overline{{\gamma }_{f_0}^{\mathtt{HY}}}={\displaystyle \frac{\eta P_{f_0}^{\mathtt{HY}}{P}_{LO,f_0}^{\mathtt{HY}}}{{\sigma }_{f_0}^{\mathtt{HY}}}},\end{array}$$

(50)

where $\eta$, $P_{f_0}^{\mathtt{HY}}$,${\sigma }_{f_0}^{\mathtt{HY}}$, and $P_{LO,f_0}^{\mathtt{HY}}={\alpha }_{l}z$ are the responsivity of the FSO receiver, transmit power of the FSO transmitter, noise variance at the FSO receiver, and an attenuation factor by distance, respectively. The values of FSO parameters used in the simulation are summarized in Table 1 [34,35,36].

Table 1. Simulation parameters for FSO systems.

FSO Parameter	Symbol	Value
Wavelength	${\lambda }_{f_0}$	1550 nm
Photo detector diameter	D	0.2 m
Transmit power	$P_{f_0}^{\mathtt{HY}}$	20 dBm
Responsivity	$\eta$	0.5
Noise variance	${\sigma }_{f_0}^{\mathtt{HY}}$	$5\times {10}^{-12}$
Clear air	$C_n^2$	$5\times {10}^{-14}$
	${\alpha }_l$	0.43 dB/Km
Haze	$C_n^2$	$1.7\times {10}^{-14}$
	${\alpha }_l$	4.2 dB/Km
Moderate rain	$C_n^2$	$5\times {10}^{-15}$
	${\alpha }_l$	5.8 dB/Km

For the desired channel $h_i^j$, we assumed the channel power ${\sigma }_i^j$ for $CN(0,{\sigma }_i^j)$ as

$$\begin{array}{c}\hfill {\sigma }_i^j={\displaystyle \frac{G_T{G}_R}{P_{PL,RF}{P}_{oxy}}},\end{array}$$

(51)

where $G_T$, $G_R$, $P_{PL,RF}$, $P_{oxy}$ is the transmit and receive antenna gains, pathloss, and an attenuation factor for oxygen. The pathloss and attenuation factor for oxygen is given by [36]

$$\begin{array}{c}\hfill P_{PL,RF}=20{log}_{10}\left(4\pi z{f}_{RF}\right),\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}{P}_{oxy}={\alpha }_{oxy}z.\end{array}$$

(52)

For the interfering channel $g_i^j$, we assumed the channel power ${\widehat{\sigma }}_i^j$ for $CN(0,{\widehat{\sigma }}_i^j)$ as

$$\begin{array}{c}\hfill {\widehat{\sigma }}_i^j={\displaystyle \frac{G_T{G}_R}{P_{PL,RF}^I{P}_{oxy}^I}},\end{array}$$

(53)

where $P_{PL,RF}^I$, $P_{oxy}^I$ is the pathloss and the attenuation factor for oxygen between interfering links, which is given by

$$\begin{array}{c}\hfill P_{PL,RF}^I=20{log}_{10}\left(4\pi z^I{f}_{RF}\right),\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}{P}_{oxy}^I={\alpha }_{oxy}{z}^I,\end{array}$$

(54)

where $z^I$ is the distance between interfering links. The value of the RF parameters used in the simulation is summarized in Table 2 [36].

Table 2. Simulation parameters for RF systems.

RF Parameter	Symbol	Value
Antenna type	-	omnidirectional
Carrier frequency	$f_{RF}$	60 GHz
Bandwidth	W	250 MHz
Transmit power	$P_{RF}$	15 dBm
Transmit antenna gain	$G_T$	43 dBi
Receive antenna gain	$G_R$	43 dBi
Noise variance	${\sigma }_{N0,RF}$	−91 dBm
Receiver noise figure	$N_{r,RF}$	5 dB
Oxygen attenuation	${\alpha }_{oxy}$	15.1 dB/Km

Figure 4 illustrates the stable regions for the SAS when the distance is set to $z=z^I=3000 \mathrm{m}$. In this scenario, we have $s_{f_1,\mathtt{RO}}=s_{f_2,\mathtt{RO}}=s_{f_1,\mathtt{HY}}=s_{f_2,\mathtt{HY}}=0.6581$, and $s_{f_1,\mathtt{RO}}^I=s_{f_2,\mathtt{RO}}^I=s_{f_1,\mathtt{HY}}^I=s_{f_2,\mathtt{HY}}^I=0.2389$; while $s_{f_0\mathtt{HY}}$ takes on the values of 1, 0.7308, and 0, respectively. Under clear air conditions, a hybrid FSO/RF pair can effectively transmit signals through the FSO link, leaving the $f_2$ channel idle. Consequently, the RF pair remains unaffected by the hybrid FSO/RF pair, resulting in no change in the performance related to ${\lambda }_{\mathtt{RO}}$. In hazy conditions, the cooperative case achieves a higher ${\lambda }_{\mathtt{RO}}$ compared to the reference case (REF) when ${\lambda }_{\mathtt{HY}}$ is between 0 and 0.875. However, REF surpasses the cooperative case with a higher ${\lambda }_{\mathtt{RO}}$ in the range of $0.875$–$0.905$ of ${\lambda }_{\mathtt{HY}}$. Beyond this point, the cooperative case regains a higher ${\lambda }_{\mathtt{RO}}$.

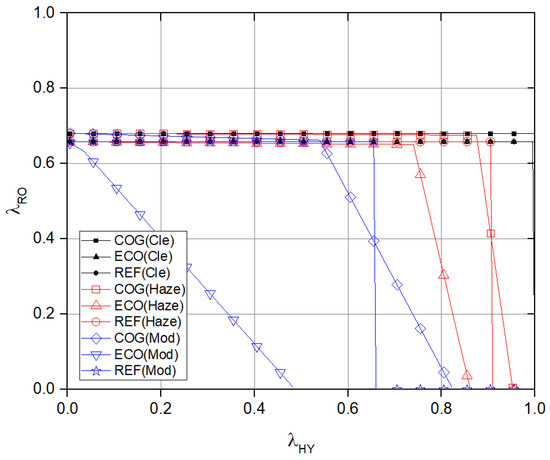
Figure 4. Comparison of stable regions for stay-and-switching transmission for $z=z^I=3000$ m.

When ${\lambda }_{\mathtt{HY}}<0.875$, there is a reduced chance of interference from the RF pair on the hybrid FSO/RF pair, leading to a greater opportunity to access the idle channel of $f_2$. This results in a higher ${\lambda }_{\mathtt{HY}}$ compared to REF. However, within the range of $0.875<{\lambda }_{\mathtt{HY}}<0.905$, the likelihood of interference with the hybrid FSO/RF pair increases, diminishing the opportunity to access the idle channel of $f_2$, which leads to a lower ${\lambda }_{\mathtt{HY}}$ than REF. Once ${\lambda }_{\mathtt{HY}}>0.905$, the hybrid FSO/RF pair in the REF case fails to reach a stable region. In contrast, the cooperative case enables the hybrid FSO/RF pair to achieve a stable region by accessing the $f_1$ frequency. Under moderate rain conditions, the results indicate a lower ${\lambda }_{\mathtt{HY}}$. The economic system presents an equal (in clear conditions) or smaller stable region than the REF across clear, haze, and moderate rain conditions.

Figure 5 compares the stable regions for SAS with $z=3000$ m and $z^I=2500$ m. Under these conditions, we have $s_{f_1,\mathtt{RO}}=s_{f_2,\mathtt{RO}}=s_{f_1,\mathtt{HY}}=s_{f_2,\mathtt{HY}}=0.6581$ and $s_{f_1,\mathtt{RO}}^I=s_{f_2,\mathtt{RO}}^I=s_{f_1,\mathtt{HY}}^I=s_{f_2,\mathtt{HY}}^I=0.0141$. Despite the low probability of success with the interference signal, the REF does not cause any performance changes due to interference signals with each other. However, COG and ECO, which can generate interference signals, experience a slight performance degradation. When $z^I=2500$ m, both COG and ECO show a decrease in ${\lambda }_{\mathtt{RO}}$ compared to the scenario where $z^I=3000$ m, as the magnitude of the interference signal between $\mathtt{RO}$ and $\mathtt{HY}$ increases. This leads to a reduction in ${\lambda }_{\mathtt{RO}}$ of 0.007% to 1.47% across all tested FSO link environments compared to the $z^I=3000$ m scenario. Consequently, under haze conditions, the area where the cooperative case yields ${\lambda }_{\mathtt{RO}}$ higher than REF is reduced to ranges of 0–0.870 and 0.905–0.952.

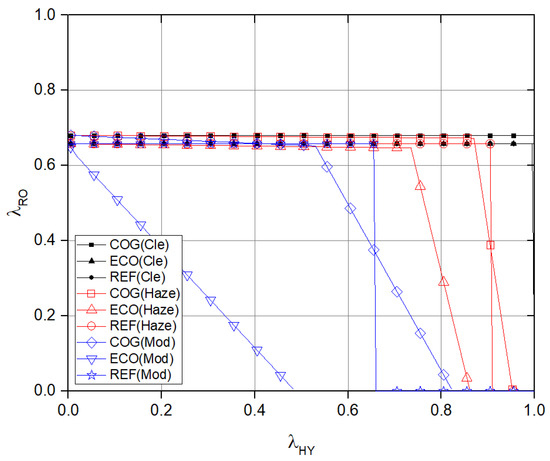
Figure 5. Comparison of the stable regions for stay-and-switching transmission with $z=3000$ m, $z^I=2500$ m.

Figure 6 illustrates the stability regions for the SMP with $z=z^I=3000 \mathrm{m}$. Under clear air conditions, the stability region of the cooperative and economic system decreases as ${\lambda }_{\mathrm{HY}}$ increases. In the SMP, the hybrid FSO/RF pair within the cooperative and economic system seeks to access the $f_1$ frequency for additional transmissions, even when the HY successfully sends packets through the FSO link. As a result, the stability region of the cooperative and economic system diminishes with increasing ${\lambda }_{\mathrm{HY}}$ in clear air conditions. In the cooperative system, the RF pair can maintain stability with ${\lambda }_{\mathrm{RO}}\le 1$ as long as ${\lambda }_{\mathrm{HY}}<0.335$. When ${\lambda }_{\mathrm{HY}}<0.335$, the RF pair experiences less interference from the hybrid FSO/RF pair and has a greater chance of accessing the idle channel at $f_2$. Consequently, the average number of service packets for the RF pair exceeds 1. Similar trends are observed under haze and moderate rain conditions.

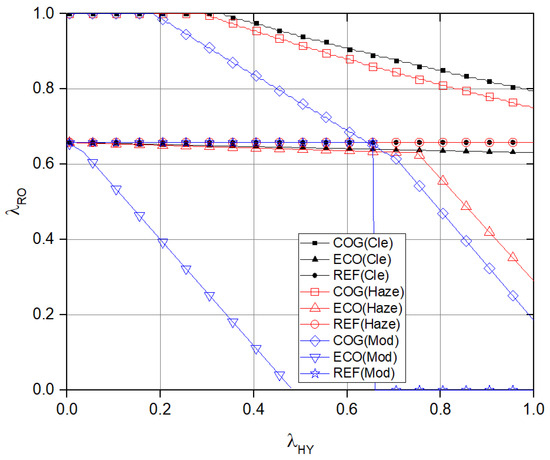
Figure 6. Comparison of the stable region for SMP with $z=z^I=3000$ m.

Figure 7 compares the stable regions for the SMP with $z=3000 \mathrm{m}$ and $z^I=2500 \mathrm{m}$. The value of ${\lambda }_{\mathtt{RO}}$ decreases as the interference signal increases when $z^I=3000 \mathrm{m}$. When $z^I=3000 \mathrm{m}$, the RF pair can remain stable with ${\lambda }_{\mathtt{RO}}\le 1$ in the following ranges of ${\lambda }_{\mathtt{HY}}$:

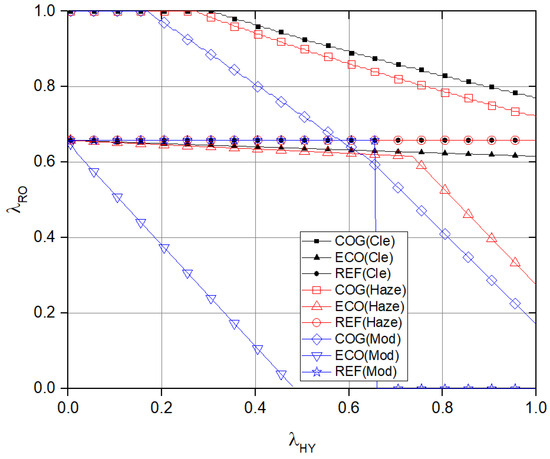
Figure 7. Comparison of stable regions for simultaneous multipacket transmission with $z=3000$ m, $z^I=2500$ m.

• For clear conditions: $0.354<{\lambda }_{\mathtt{HY}}$,
• For haze: $0.315<{\lambda }_{\mathtt{HY}}$, and
• For moderate rain: $0.205<{\lambda }_{\mathtt{HY}}$.

In contrast, when $z^I=2500 \mathrm{m}$, the RF pair can remain stable with ${\lambda }_{\mathtt{RO}}\le 1$ in these ranges:

• For clear conditions: $0.307<{\lambda }_{\mathtt{HY}}$,
• For haze: $0.273<{\lambda }_{\mathtt{HY}}$, and
• For moderate rain: $0.167<{\lambda }_{\mathtt{HY}}$

For the moderate rain scenario, when $z^I=3000 \mathrm{m}$, the cooperative case always shows a higher ${\lambda }_{\mathtt{RO}}$ than the REF case. However, when $z^I=2500 \mathrm{m}$, the REF case has a higher ${\lambda }_{\mathtt{RO}}$ in the interval $0.610<{\lambda }_{\mathtt{HY}}<0.652$. For this reason, the interval where ${\lambda }_{\mathtt{HY}}<0.775$ exhibits a higher ${\lambda }_{\mathtt{RO}}$ compared to the SMP.

In the cognitive FSO/RF system in this study, the interference occurs when the HY node transmits or receives RF signals to or from RF node, respectively. In the COG system, both $f_1$ and $f_2$ induce such interference, while in the ECO system, the interference only occurs on the $f_1$ channel. In Figure 4 and Figure 6, where the distance between HY and RO nodes is assumed to be 3000 m, the success probability $s_{f_1,j}^I$ becomes 0.2389 when the RF interference occurs, while it is 0.6581 without the interference. In Figure 5 and Figure 7, where the above distance is assumed to be 2500 m, the success probability $s_{f_1,j}^I$ is further reduced to 0.0141 due to the stronger RF interference. For the SAS system demonstrated in Figure 5, an achievable ${\lambda }_{RO}$ decreases up to 1.47%, maintaining the same ${\lambda }_{HY}$ due to interference. For the SMT system considered in Figure 7, achievable ${\lambda }_{HY}$ decreases from 13.27 to 18.53% when ${\lambda }_{RO}<1$.

Figure 8 illustrates the stability regions for the cooperative system with $z=z^I=3000$ m. The SAS-SMP represents the hybrid variation of the cooperative system discussed in (58). In the SAS-SMP configuration, the node $\mathtt{HY}$ operates under the SAS, while $\mathtt{RO}$ operates under the SMP. Consequently, in clear conditions ($s_{f_0\mathtt{HY}}=1$) and in haze conditions ($s_{f_0\mathtt{HY}}=0.731$), the likelihood of $\mathtt{HY}$ transmitting packets through FSO channels, rather than using wireless channels, increases. This, in turn, enhances the probability of successful packet transmission via wireless channels by $\mathtt{RO}$. However, since $\mathtt{HY}$ does not operate in SMP, the likelihood that $Q_{\mathtt{HY}}$ is empty decreases. This increase raises the probability of interference between $\mathtt{HY}$ and $\mathtt{RO}$ within the SMP scenario. Thus, the relationship between ${\lambda }_{\mathtt{RO}}$ can be summarized as follows: SAS < SAS-SMP < SMP. In a moderate rain scenario, the probability of packet transmission through the FSO link drops to zero. Additionally, the probability that $\mathtt{HY}$ in SAS-SMP generates an interference signal on channel $f_1$ is lower than that of $\mathtt{HY}$ in SMP. For this reason, the interval where ${\lambda }_{\mathtt{HY}}<0.775$ exhibits a higher ${\lambda }_{\mathtt{RO}}$ compared to SMP.

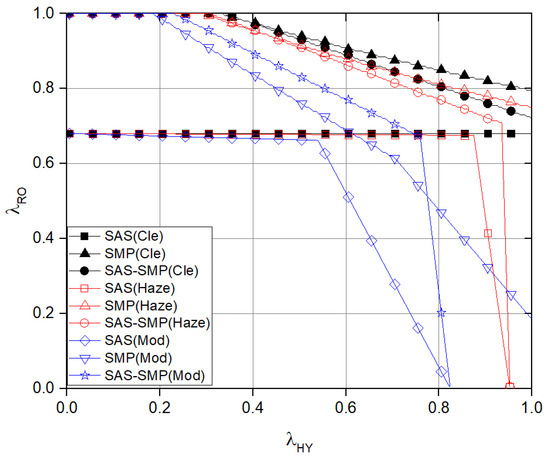
Figure 8. Comparison of stable regions for simultaneous multipacket transmission with $z=z^I=3000$ m.

Figure 9 illustrates the maximum values of ${\lambda }_{\mathtt{RO}}$, ${\lambda }_{\mathtt{HY}}$, and ${\lambda }_{\mathtt{sum}}={\lambda }_{\mathtt{RO}}+{\lambda }_{\mathtt{HY}}$ as a function of the detection probability for RF and hybrid FSO/RF pairs, assuming haze conditions. In the cooperative system with SAS, the maximum values of ${\lambda }_{\mathtt{RO}}$ and ${\lambda }_{\mathtt{HY}}$ decrease as the detection probability increases. In this cooperative system, both the RF and hybrid FSO/RF pairs compete to access each other’s frequency. A higher detection probability reduces the likelihood of missed detections, but it also increases the false alarm probability, thereby diminishing the chance of successfully accessing the other frequency pair.

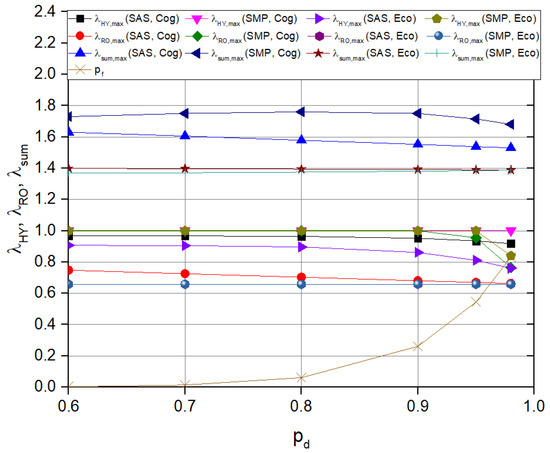
Figure 9. Stable regions as a function of the detection probability with $z=z^I=3000$ m.

A similar trend is observed for the maximum ${\lambda }_{\mathtt{RO}}$ in the cooperative system with SMP; however, ${\lambda }_{\mathtt{HY}}$ remains constant at 1. The maximum value of ${\lambda }_{\mathtt{sum}}$ in the cooperative system with SAS decreases as the detection probability increases. In contrast, the maximum ${\lambda }_{\mathtt{sum}}$ for the cooperative system with SMP initially increases and then decreases with a rising detection probability. Compared to SMP, SAS is less likely to interfere with other pairs. Consequently, the advantages of reducing interference from other pairs are outweighed by the disadvantages of decreasing transmission opportunities as detection probability increases. In the economic system, the maximum value of ${\lambda }_{\mathtt{RO}}$ remains unchanged as detection probability increases, since the RF pair cannot borrow the $f_2$ frequency. However, the maximum values of ${\lambda }_{\mathtt{HY}}$ and ${\lambda }_{\mathtt{sum}}$ decrease with increasing detection probability, as this reduces the chance for hybrid FSO/RF pairs to access the $f_1$ frequency.

7. Conclusions

In this study, we analyzed the performance of a cooperative communication system within a heterogeneous network that includes an FSO-RF link for enhanced reliability. To achieve this, we compared cooperative and economic models regarding the method of frequency resource sharing. We also evaluated the SAS method in conjunction with the SMT method. The low-cost economic model demonstrates performance levels that are comparable to the reference model when ${\lambda }_{\mathtt{HY}}$ is low; however, it exhibits the poorest performance as ${\lambda }_{\mathtt{HY}}$ increases. While the cooperative model generally outperforms the reference model, the reference model performs better in scenarios where ${\lambda }_{\mathtt{HY}}$ is quite high. Additionally, the simultaneous multipacket transmission method consistently outperforms the switch-and-stay method. The hybrid SAS-SMP method, which combines both approaches, performs better than the simultaneous multipacket transmission in moderately rainy environments where establishing the FSO link is challenging. However, this trend reverses as ${\lambda }_{\mathtt{HY}}$ increases.

Finally, the proposed cognitive RF/FSO systems are currently not being implemented and the performance should be evaluated with more real-world applications. When practically applying the proposed systems, each transmitter–receiver pair does not require a separate control device because it does not share information. In the cognitive mode, the hybrid transmitter can transmit up to three packets to one FSO channel and two FSO channels, and the RF-only transmitter is capable of transmitting up to two packets to RF channels, which may be a manageable requirement in implementation. In the stability analysis, the buffer size is usually assumed to be infinite, but in practical systems, certain packets could be lost if the buffer is full. This induces some limitation in applying stability analysis, which is left for future study.

Appendix A.1. Stay and Switch Mode

The transmission success rate varies depending on the state of $Q_{\mathtt{RO}}$ and $Q_{\mathtt{HY}}$. Let $v_{j,1,0}$ and $v_{j,1,1}$ be the success rates of packet transmission for $j\in \{\mathtt{RO},\mathtt{HY}\}$ with conditions $Q_{k|k\in \{\mathtt{RO},\mathtt{HY}\},k\ne j,}=0$ and $Q_k\ne 0$, then we have

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},1,0}& =& p_{f,\mathtt{HY}}(s_{f_0,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}})+(1-p_{f,\mathtt{HY}})(s_{f_0,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})s_{f_1,\mathtt{HY}}),\hfill \end{array}$$

(A1)

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},1,1}& =& s_{f_0,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}(1-(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}(1-s_{f_1,\mathtt{RO}}))\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}^I(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}(1-s_{f_1,\mathtt{RO}})+(1-p_{d,\mathtt{HY}})(1-s_{f_0,\mathtt{HY}})\hfill \\ & & \times [(s_{f_2,\mathtt{HY}}-s_{f_2,\mathtt{HY}}^I)s_{f_1,\mathtt{HY}}(1-s_{f_1,\mathtt{RO}})(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}+(1-s_{f_2,\mathtt{HY}})s_{f_1,\mathtt{HY}}^I{s}_{f_1,\mathtt{RO}}\hfill \\ & & +(1-s_{f_2,\mathtt{HY}})s_{f_1,\mathtt{HY}}(1-s_{f_1,\mathtt{RO}})(1-(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}})],\hfill \end{array}$$

(A2)

$$\begin{array}{ccc}\hfill v_{\mathtt{RO},1,0}& =& p_{f,\mathtt{RO}}{s}_{f_1,\mathtt{RO}}+(1-p_{f,\mathtt{RO}})(s_{f_1,\mathtt{RO}}+(1-s_{f_1,\mathtt{RO}})s_{f_2,\mathtt{RO}}),\hfill \end{array}$$

(A3)

$$\begin{array}{ccc}\hfill v_{\mathtt{RO},1,1}& =& s_{f_1,\mathtt{RO}}(1-(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})(1-s_{f_0,\mathtt{HY}}))\hfill \\ & & +s_{f_1,\mathtt{RO}}^I(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})(1-s_{f_0,\mathtt{HY}})+(1-p_{d,\mathtt{RO}})[(1-s_{f_1,\mathtt{RO}})s_{f_2,\mathtt{RO}}\hfill \\ & & \times [s_{f_0,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})(1-(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}})]\hfill \\ & & +(s_{f_1,\mathtt{RO}}-s_{f_1,\mathtt{RO}}^I)s_{f_2,\mathtt{RO}}(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}}\hfill \\ & & +(1-s_{f_1,\mathtt{RO}})(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{RO}}^I{s}_{f_2,\mathtt{HY}}].\hfill \end{array}$$

(A4)

Appendix A.2. Simultaneous Packet Transmission Mode

Let $v_{j,n,0}$ and $v_{j,n,1}$ be the success rate of n- packet transmission in a single time slot for $j\in \{\mathtt{RO},\mathtt{HY}\}$ with conditions $Q_{k|k\in \{\mathtt{RO},\mathtt{HY}\},k\ne j,}=0$ and $Q_k\ne 0$, then we have

$$\begin{array}{ccc}\hfill v_{\mathtt{RO},1,0}& =& (p_{f,\mathtt{RO}}{s}_{f_1,\mathtt{RO}}+(1-p_{f,\mathtt{RO}})(s_{f_1,\mathtt{RO}}(1-s_{f_2,\mathtt{RO}})+(1-s_{f_1,\mathtt{RO}})s_{f_2,\mathtt{RO}})),\hfill \end{array}$$

(A5)

$$\begin{array}{ccc}\hfill v_{\mathtt{RO},1,1}& =& p_{d,\mathtt{RO}}[s_{f_1,\mathtt{RO}}(1-(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}})+s_{f_1,\mathtt{RO}}^I{p}_{d,\mathtt{HY}}{s}_{f_1,\mathtt{HY}}]\hfill \\ & & +(1-p_{d,\mathtt{RO}})[\{s_{f_1,\mathtt{RO}}(1-s_{f_2,\mathtt{RO}})+(1-s_{f_1,\mathtt{RO}})s_{f_2,\mathtt{RO}}\}\hfill \\ & & \times (1-(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})\hfill \\ & & +\{s_{f_1,\mathtt{RO}}^I(1-s_{f_2,\mathtt{RO}})+(s_{f_1,\mathtt{RO}}-s_{f_1,\mathtt{RO}}^I)s_{f_2,\mathtt{RO}}\}(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})\hfill \\ & & +\{s_{f_1,\mathtt{RO}}(s_{f_2,\mathtt{RO}}-s_{f_2,\mathtt{RO}}^I)+(1-s_{f_1,\mathtt{RO}})s_{f_2,\mathtt{RO}}^I\}(1-(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}})s_{f_2,\mathtt{HY}}\hfill \\ & & +\{s_{f_1,\mathtt{RO}}^I(s_{f_2,\mathtt{RO}}-s_{f_2,\mathtt{RO}}^I)+(1-s_{f_1,\mathtt{RO}}^I)s_{f_2,\mathtt{RO}}^I\}(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}],\hfill \end{array}$$

(A6)

$$\begin{array}{ccc}\hfill v_{\mathtt{RO},2,0}& =& (1-p_{f,\mathtt{RO}})s_{f_1,\mathtt{RO}}{s}_{f_2,\mathtt{RO}},\hfill \end{array}$$

(A7)

$$\begin{array}{ccc}\hfill v_{\mathtt{RO},2,1}& =& (1-p_{d,\mathtt{RO}})(s_{f_1,\mathtt{RO}}{s}_{f_2,\mathtt{RO}}(1-(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})\hfill \\ & & +s_{f_1,\mathtt{RO}}^I{s}_{f_2,\mathtt{RO}}(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})+s_{f_1,\mathtt{RO}}{s}_{f_2,\mathtt{RO}}^I(1-(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}})s_{f_2,\mathtt{HY}}\hfill \\ & & +s_{f_1,\mathtt{RO}}^I{s}_{f_2,\mathtt{RO}}^I(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}).\hfill \end{array}$$

(A8)

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},1,0}& =& p_{f,\mathtt{HY}}[s_{f_0,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}]+(1-p_{f,\mathtt{HY}})[s_{f_0,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})(1-s_{f_1,\mathtt{HY}})\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}(1-s_{f_1,\mathtt{HY}})+(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})s_{f_1,\mathtt{HY}}],5:\hfill \end{array}$$

(A9)

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},1,1}& =& p_{d,\mathtt{HY}}[s_{f_0,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})(p_{d,\mathtt{RO}}+(1-p_{d,\mathtt{RO}})(1-s_{f_2,\mathtt{RO}}))\hfill \\ & & +s_{f_0,\mathtt{HY}}(s_{f_2,\mathtt{HY}}-s_{f_2,\mathtt{HY}}^I)(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}(p_{d,\mathtt{RO}}+(1-p_{d,\mathtt{RO}})(1-s_{f_2,\mathtt{RO}}))\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}^I(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}]+(1-p_{d,\mathtt{HY}})\left[\right\{s_{f_0,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})(1-s_{f_1,\mathtt{HY}})\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}(1-s_{f_1,\mathtt{HY}})+(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})s_{f_1,\mathtt{HY}}\}\hfill \\ & & \times [p_{d,\mathtt{RO}}+(1-p_{d,\mathtt{RO}})(1-s_{f_2,\mathtt{RO}})](1-s_{f_1,\mathtt{RO}})+[s_{f_0,\mathtt{HY}}(s_{f_2,\mathtt{HY}}-s_{f_2,\mathtt{HY}}^I)(1-s_{f_1,\mathtt{HY}})\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}^I(1-s_{f_1,\mathtt{HY}})+(1-s_{f_0,\mathtt{HY}})(s_{f_2,\mathtt{HY}}-s_{f_2,\mathtt{HY}}^I)s_{f_1,\mathtt{HY}}]\hfill \\ & & \times (1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}(1-s_{f_1,\mathtt{RO}})+[s_{f_0,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})(s_{f_1,\mathtt{HY}}-s_{f_1,\mathtt{HY}}^I)\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}(1-s_{f_1,\mathtt{HY}}^I)\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})s_{f_1,\mathtt{HY}}^I]\times [1-(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}]s_{f_1,\mathtt{RO}}\hfill \\ & & +[s_{f_0,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}}^I)(s_{f_1,\mathtt{HY}}-s_{f_1,\mathtt{HY}}^I)+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}^I(s_{f_1,\mathtt{HY}}-s_{f_1,\mathtt{HY}}^I)\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})(s_{f_2,\mathtt{HY}}-s_{f_2,\mathtt{HY}}^I)s_{f_1,\mathtt{HY}}^I\left]\left[(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}{s}_{f_1,\mathtt{RO}}\right]\right],\hfill \end{array}$$

(A10)

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},2,0}& =& p_{f,\mathtt{HY}}{s}_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}+(1-p_{f,\mathtt{HY}})[s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}(1-s_{f_1,\mathtt{HY}})\hfill \\ & & +s_{f_0,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})s_{f_1,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}{s}_{f_1,\mathtt{HY}}],\hfill \end{array}$$

(A11)

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},2,1}& =& p_{d,\mathtt{HY}}[s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}(1-(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}})+s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}^I(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}]\hfill \\ & & +(1-p_{d,\mathtt{HY}})\left[\right[s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}(1-s_{f_1,\mathtt{HY}})+s_{f_0,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})s_{f_1,\mathtt{HY}}\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}{s}_{f_1,\mathtt{HY}}][p_{d,\mathtt{RO}}+(1-p_{d,\mathtt{RO}})(1-s_{f_2,\mathtt{RO}})](1-s_{f_1,\mathtt{RO}})\hfill \\ & & +[s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}^I(1-s_{f_1,\mathtt{HY}})+s_{f_0,\mathtt{HY}}(s_{f_2,\mathtt{HY}}-s_{f_2,\mathtt{HY}}^I)s_{f_1,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}^I{s}_{f_1,\mathtt{HY}}]\hfill \\ & & \times (1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}(1-s_{f_1,\mathtt{RO}})\hfill \\ & & +[s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}(s_{f_1,\mathtt{HY}}-s_{f_1,\mathtt{HY}}^I)+s_{f_0,\mathtt{HY}}(1-s_{f_2,\mathtt{HY}})s_{f_1,\mathtt{HY}}^I+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}{s}_{f_1,\mathtt{HY}}^I]\hfill \\ & & \times [1-(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}]s_{f_1,\mathtt{RO}}+[s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}^I(s_{f_1,\mathtt{HY}}-s_{f_1,\mathtt{HY}}^I)\hfill \\ & & +s_{f_0,\mathtt{HY}}(s_{f_2,\mathtt{HY}}-s_{f_2,\mathtt{HY}}^I)s_{f_1,\mathtt{HY}}^I+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}^I{s}_{f_1,\mathtt{HY}}^I]\hfill \\ & & \times (1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}{s}_{f_1,\mathtt{RO}}],\hfill \end{array}$$

(A12)

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},3,0}& =& (1-p_{f,\mathtt{HY}})s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}{s}_{f_1,\mathtt{HY}},\hfill \end{array}$$

(A13)

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},3,1}& =& (1-p_{d,\mathtt{HY}})[s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}{s}_{f_1,\mathtt{HY}}[1-(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}](1-s_{f_1,\mathtt{RO}})\hfill \\ & & +s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}^I{s}_{f_1,\mathtt{HY}}\left[(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}(1-s_{f_1,\mathtt{RO}})\right]\hfill \\ & & +s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}{s}_{f_1,\mathtt{HY}}^I[1-(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}]s_{f_1,\mathtt{RO}}\hfill \\ & & +s_{f_0,\mathtt{HY}}{s}_{f_2,\mathtt{HY}}^I{s}_{f_1,\mathtt{HY}}^I(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}{s}_{f_1,\mathtt{RO}}]\hfill \end{array}$$

(A14)

Appendix A.3. A Hybrid SMT and SAS Transmission Mode

Let $v_{j,n,0}$ and $v_{j,n,1}$ be the respective success rate of n packets transmitted in a single time slot for $j\in \{\mathtt{RO},\mathtt{HY}\}$ with conditions $Q_{k|k\in \{\mathtt{RO},\mathtt{HY}\},k\ne j,}=0$ and $Q_k\ne 0$. Then, we have

$$\begin{array}{ccc}\hfill v_{\mathtt{RO},1,0}& =& p_{f,\mathtt{RO}}{s}_{f_1,\mathtt{RO}}+(1-p_{f,\mathtt{RO}})[s_{f_1,\mathtt{RO}}(1-s_{f_2,\mathtt{RO}})+(1-s_{f_1,\mathtt{RO}})s_{f_2,\mathtt{RO}}],\hfill \end{array}$$

(A15)

$$\begin{array}{ccc}\hfill v_{\mathtt{RO},1,1}& =& p_{d,\mathtt{RO}}[s_{f_1,\mathtt{RO}}\{1-(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}}\}\hfill \\ & & +s_{f_1,\mathtt{RO}}^I(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}}]\hfill \\ & & +p_{d,\mathtt{RO}}\left[(s_{f_1,\mathtt{RO}}(1-s_{f_2,\mathtt{RO}})+(1-s_{f_1,\mathtt{RO}})s_{f_2,\mathtt{RO}})\right\{s_{f_0,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})\hfill \\ & & \times (p_{d,\mathtt{HY}}+(1-p_{d,\mathtt{HY}})(1-s_{f_1,\mathtt{HY}}))\}+(s_{f_1,\mathtt{RO}}^I(1-s_{f_2,\mathtt{RO}})\hfill \\ & & +(s_{f_1,\mathtt{RO}}-s_{f_1,\mathtt{RO}}^I)s_{f_2,\mathtt{RO}})\times \left((1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}}\right)\hfill \\ & & +(s_{f_1,\mathtt{RO}}(s_{f_2,\mathtt{RO}}-s_{f_2,\mathtt{RO}}^I)+(1-s_{f_1,\mathtt{RO}})s_{f_2,\mathtt{RO}}^I)\left\{(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}\right\},]\hfill \end{array}$$

(A16)

$$\begin{array}{ccc}\hfill v_{\mathtt{RO},2,0}& =& (1-p_{f,\mathtt{RO}})s_{f_1,\mathtt{RO}}{s}_{f_2,\mathtt{RO}},\hfill \end{array}$$

(A17)

$$\begin{array}{ccc}\hfill v_{\mathtt{RO},2,1}& =& s_{f_1,\mathtt{RO}}{s}_{f_2,\mathtt{RO}}(1-p_{d,\mathtt{RO}})[s_{f_0,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})(p_{d,\mathtt{HY}}+(1-p_{d,\mathtt{HY}})(1-s_{f_1,\mathtt{HY}})]\hfill \\ & & +s_{f_1,\mathtt{RO}}^I{s}_{f_2,\mathtt{RO}}(1-p_{d,\mathtt{RO}})(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})(1-p_{d,\mathtt{HY}})s_{f_1,\mathtt{HY}}\hfill \\ & & +s_{f_1,\mathtt{RO}}{s}_{f_2,\mathtt{RO}}^I(1-p_{d,\mathtt{RO}})(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}},\hfill \end{array}$$

(A18)

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},1,0}& =& s_{f_0,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})(1-p_{f,\mathtt{HY}})s_{f_1,\mathtt{HY}},\hfill \end{array}$$

(A19)

$$\begin{array}{ccc}\hfill v_{\mathtt{HY},1,1}& =& s_{f_0,\mathtt{HY}}+(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}[p_{d,\mathtt{RO}}+(1-p_{d,\mathtt{RO}})(1-s_{f_2,\mathtt{RO}})]\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})s_{f_1,\mathtt{HY}}\hfill \\ & & \times [p_{d,\mathtt{RO}}(1-s_{f_1,\mathtt{RO}})+(1-p_{d,\mathtt{RO}})(1-s_{f_2,\mathtt{RO}})(1-s_{f_1,\mathtt{RO}})]\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})s_{f_2,\mathtt{HY}}^I\left[(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}\right]\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})(1-s_{f_2,\mathtt{HY}})s_{f_1,\mathtt{HY}}^I\left[(1-(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}})s_{f_1,\mathtt{RO}}\right]\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})(s_{f_2,\mathtt{HY}}-s_{f_2,\mathtt{HY}}^I)s_{f_1,\mathtt{HY}}\left[(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}(1-s_{f_1,\mathtt{RO}})\right]\hfill \\ & & +(1-s_{f_0,\mathtt{HY}})(s_{f_2,\mathtt{HY}}-s_{f_2,\mathtt{HY}}^I)s_{f_1,\mathtt{HY}}^I\left[(1-p_{d,\mathtt{RO}})s_{f_2,\mathtt{RO}}{s}_{f_1,\mathtt{RO}}\right].\hfill \end{array}$$

(A20)