Generalized NTRU Algorithms on Algebraic Rings

Abstract

The NTRU (Number Theory Research Unit) is a prominent post-quantum public key cryptography algorithm and a current focus of research. Although many NTRU variants have been proposed, a comprehensive generalization of these variants is still lacking. To address this issue, we propose the G-NTRU (Generalized NTRU), an algorithmic framework for NTRU variants on algebraic rings. This framework generalizes specific ring extensions to more general algebraic structures, allowing the unification of various NTRU variants. We then analyze the key properties of the G-NTRU, including correctness, lattice-based characteristics, and security. The semantic security of the G-NTRU is demonstrated through the introduction of the G-AGCD (Generalized Approximate Greatest Common Divisor). To validate the generality of the G-NTRU framework, we introduce the CNTRU (Complex Number NTRU), a variant of the NTRU over the ring of complex numbers. The CNTRU shares the same properties as the G-NTRU, further confirming the versatility of the G-NTRU in studying NTRU variants over algebraic rings.

1. Introduction

With the advancement of the Internet, while fostering closer connections between people, private information has also become increasingly vulnerable to exposure. Cryptographic algorithms remain the most effective, economical, and reliable method for securing network data. The evolution of public key cryptography has progressed through traditional algorithms, which are based on hard mathematical problems. Classical public key cryptography relies on challenges such as integer factorization and the discrete logarithm problem, exemplified by the RSA encryption algorithm [1], the DSA signature algorithm [2], the ElGamal encryption algorithm [3], and the Paillier encryption algorithm [4]. However, Shor demonstrated that quantum computers can efficiently solve integer factorization and discrete logarithm problems [5], reducing these once-hard problems to tractable P-problems. As a result, researchers have shifted toward developing cryptographic algorithms resistant to quantum computing, known as quantum-resistant or post-quantum cryptography.

In 2016, the National Institute of Standards and Technology (NIST) initiated the Post-Quantum Cryptography Standardization Process [6], aiming to standardize cryptographic algorithms resistant to quantum attacks. Lattice-based cryptography quickly emerged as one of the leading candidates due to its strong security foundations and versatility. By August 2024, NIST published three post-quantum cryptography (PQC) standards [6]: ML-KEM, ML-DSA, and SLH-DSA. Among these, ML-KEM (Modular Lattice Key Encapsulation Mechanism) and ML-DSA (Modular Lattice Digital Signature Algorithm) are both based on modular lattice structures, underscoring the significant role of lattice-based cryptography in the field.

A lattice is a mathematical structure consisting of discrete points generated by a set of vectors, forming a regular, structured grid. Lattice cryptosystems, a promising class of post-quantum public key cryptosystems, derive their security from the hardness of solving lattice problems. These problems, such as the Shortest Vector Problem (SVP) and the Closest Vector Problem (CVP), involve finding specific lattice points in a high-dimensional Euclidean space. The challenge lies in the rapid increase in complexity as the dimensionality rises, leading to an exponential growth in the computational effort required to solve these problems using classical algorithms. To date, no efficient algorithms have been discovered for solving these lattice problems on either classical or quantum computers, making them a strong candidate for secure post-quantum encryption schemes.

Lattice-based cryptographic schemes continue to dominate research in post-quantum cryptography, offering robust security against quantum computational threats, and are regarded as key to the future of secure communication in the quantum era. The extensive study of lattice structures for cryptographic purposes, such as NTRU and its variants, reflects the broader effort to develop practical, quantum-resistant encryption and signature algorithms.

In 1998, Hoffstein, Pipher, and Silverman proposed the NTRU (Number Theory Research Unit) public key encryption algorithm [7]. The NTRU algorithm features a simple structure and is algebraically based on polynomials, constructed over a polynomial quotient ring. It offers higher operational speed compared to traditional public key cryptographic algorithms, and its security can be reduced to the lattice problem, providing resistance against quantum computing attacks. Over time, the NTRU has been further developed, leading to the emergence of several NTRU variants. A brief chronological introduction to these variants is provided below, as illustrated in Table 1.

Table 1. NTRU variants.

	Time	Ring	Descriptions
CTRU [8]	2002	Binary finite fields	It has been found to be insecure, failing to improve performance or protect against linear algebra attacks.
MaTR [9]	2005	$k\times k$t matrix ring	It offers a speed improvement of $k$ times over the NTRU algorithm.
GNTRU [10]	2006	Ring of Gaussian integer matrices	It provides enhanced complexity and security compared to NTRU.
Matrix NTRU [11]	2008	Matrix ring	It is faster than NTRU.
GBNTRU [12]	2008	Ring of binary polynomials	Its computational speed is lower than that of NTRU.
NNRU [13]	2009	Polynomial $k\times k$ ring of matrices	It demonstrates complete security against lattice attacks and significantly outperforming NTRU in speed.
OTRU [14]	2010	Octonionic algebraic ring	It is simple in construction but slower than NTRU.
QTRU [15]	2011	Quaternions	It is a secure structure, resistant to LLL attacks.
DBTRU [16]	2015	Ring of binary truncated polynomials with positive integer coefficients	It offers enhanced security and efficiency compared to NTRU.
mini-NTRU [17]	2016	Binary parameters	It creates a smaller version of NTRU.
ITRU [18]	2017	Ring of integers modulo $n$	It operates with simpler and more convenient parameter choices.
D-NTRU [19]	2018	Integer polynomial ring	It provides smaller ciphertext extensions and greater efficiency than NTRU.
Flattening NTR [20]	2021	Ring of integer polynomials	It offers improved efficiency and speed over NTRU.

There are several other NTRU variants of the algorithm [21]. The primary distinction among the various NTRU variant algorithms lies in the different rings on which they are based. The characteristics of NTRU variants constructed over different rings differ, impacting their speed, security, and other properties. However, NTRU variant algorithms based on the same type of ring also exhibit commonalities and share similarities in their nature. In 2015, Yasuda et al. summarized and analyzed a class of NTRU variant algorithms, proposing a generalized NTRU cryptographic algorithm based on a group ring, referred to as GR-NTRU [22]. The ring associated with GR-NTRU is isomorphic to the ring of NTRU polynomial quotient rings, $Z\left[x\right]/(x^N-1)$. Additionally, there are many NTRU variant algorithms defined over other rings, such as the ring of integers, the ring of Gaussian integers, and the ring of matrices.

This paper focuses on generalizing NTRU variant algorithms by extending them over algebraic rings to propose the G-NTRU algorithms. It aims to facilitate the study of the properties of this kind of NTRU variant through the G-NTRU algorithm framework. To enable a thorough analysis of the semantic security of the G-NTRU, the AGCD problem is extended from the ring of integers to the generalized AGCD problem over rings, referred to as the G-AGCD problem. The framework for the semantic security proof of the G-NTRU is constructed under the assumption of the G-AGCD hard problem. The innovative contributions of this research are described below:

(1)

A generalized NTRU algorithm over algebraic rings, referred to as the G-NTRU algorithm, is proposed to extend existing NTRU algorithms within this context. The G-NTRU framework enables a more comprehensive understanding and exploitation of the properties and performance of the NTRU algorithm across different algebraic structures, thus opening up new possibilities for the advancement of post-quantum cryptography. A comparative analysis of the G-NTRU algorithm is conducted, and its variants over different algebraic rings are comprehensively compared with other NTRU variant algorithms. This analysis aims to better assess their performance and security, providing deeper insights and directions for future research on NTRU algorithms.

(2)

The generalized AGCD problem over an algebraic ring, referred to as the G-AGCD problem, is presented. This extension of the traditional AGCD problem from the ring of integers to generalized algebraic rings facilitates the analysis of the semantic security of the G-NTRU. The AGCD problem can also be adapted to different rings; for example, in the context of a matrix ring, it becomes the AMGCD problem. Assuming the G-AGCD problem is difficult, the IND-CPA security of the G-NTRU is demonstrated through the combination of residual hash primitives.

(3)

To verify the generality of the G-NTRU algorithmic framework, a variant of the NTRU algorithm over the complex ring, referred to as the complex NTRU algorithm (CNTRU), is proposed. The CNTRU algorithm is constructed based on the G-NTRU framework, facilitating a more convenient study of its properties through the lens of the G-NTRU. The CNTRU algorithm retains the same properties as those in the G-NTRU framework, thereby validating the generality of the G-NTRU in the context of NTRU variants over algebraic rings.

Section 2 of this paper introduces the relevant theoretical concepts. Section 3 describes the algorithmic structure of the G-NTRU. Section 4 outlines the properties and security of the G-NTRU, including a comparative analysis. Section 5 details the algorithmic structure of the CNTRU. Finally, Section 6 concludes this paper.

2. Theoretical Background

This section outlines the foundational concepts utilized in this paper.

2.1. Lattice

In cryptography, lattice is a mathematical structure with significant applications. Below are some definitions of lattice:

Definition 1

(lattice). Let $v_1,v_2...v_n\in R^m$ be a set of linearly independent row vectors. From this set of row vectors, we form a row-full rank matrix $\mathit{B}$. The set $\mathcal{L}=\left\{x\mathit{B}\right|x\in Z^n\}$ is then called the lattice generated by the vectors $\left\{v_i\right|i\in n\}$ over $Z$, denoted $\mathcal{L}\left(\mathit{B}\right)$.

Any set of linearly independent vectors generated by $\left\{v_i\right|i\in n\}$ can serve as a basis for the lattice. The number of vectors in the lattice basis is referred to as the dimension of the lattice.

Definition 2

(NTRU lattice). There exists a ring $R_q=Z_q\left[x\right]/x^n+1$, where the elements of  $R_q$  are polynomials of degree at most$n-1$  , with coefficients in the range  $(-{\displaystyle \frac{q}{2}},{\displaystyle \frac{q}{2}}]$. These polynomials take the form  $y=a_0+a_{1}x+a_2{x}^2+,\dots ,+a_{n-1}{x}^{n-1}$. In this ring, there exists a polynomial  $g$  and an invertible polynomial  $f$  , such that  $a=g/f modq$  . The NTRU lattice is determined by  $a$  and  $q$  and is defined as follows:

$${\Lambda }_{h,q}=\left\{\left(u,v\right)\in R^2\mid u+v^{\ast }h=0\left(modq\right)\right\}$$

(1)

2.2. Gaussian Heuristic

The Gaussian distribution can be applied to lattices for studying and analyzing their properties. It is also a crucial tool for the analysis and design of public key cryptographic schemes based on lattices.

Definition 3

(Gaussian function). Let $s>0$. For any $n$-dimensional vector $\overrightarrow{\mathit{x}},\overrightarrow{\mathit{c}}\in Z^n$, let ${\rho }_{s,c}(\overrightarrow{\mathit{x}})=e^{-\pi \parallel (\overrightarrow{\mathit{x}}-\overrightarrow{\mathit{c}})/s{\parallel }^2}$ be the Gaussian function with $c$ centred and $s$ factored as a Gaussian function. For any set $\mathit{A}\in Z^n$ of $n$ dimensional vectors, the Gaussian function is ${\rho }_{s,c}(A)=\sum _{\overrightarrow{\mathit{x}}\in A} {\rho }_{s,\overrightarrow{\mathit{c}}}\left(\overrightarrow{\mathit{x}}\right)$.

Definition 4

(discrete Gaussian distribution on lattice). Let real $s>0$. For any $n$ dimensional vector $\overrightarrow{\mathit{c}}\in Z^n$ and lattice $\Lambda$, define a discrete Gaussian distribution on lattice $\Lambda$ $D_{\Lambda ,s,e}(x)={\displaystyle \frac{{\rho }_{s,c}\left(x\right)}{{\rho }_{s,c}\left(\Lambda \right)}}$, where $\forall x\in \Lambda$.

The geometric significance of the discrete Gaussian distribution on the lattice $\Lambda$ lies in the fact that, under the Gaussian distribution $D_{\mathsf{\Lambda },s,e}\left(x\right)$, the distance from all points on the lattice $\Lambda$ to the center point ccc is approximately $s\sqrt{n/2\pi }$.

Definition 5

(Gaussian Heuristic). For the n-dimensional lattice $\mathcal{L}\left(\mathit{B}\right)$, the Gaussian expectation of the shortest length is as follows:

$$\sigma \left(\mathcal{L}\right)=\sqrt{{\displaystyle \frac{n}{2\pi e}}}{det\left(\mathit{B}\right)}^{{\displaystyle \frac{1}{n}}}$$

(2)

It is called the Gaussian Heuristic. Here,  $\mathrm{d}\mathrm{e}\mathrm{t}\left(\mathit{B}\right)$ represents the volume (or capacity) of the lattice  $\mathcal{L}\left(\mathit{B}\right)$ , which is also the determinant of the lattice basis matrix  $\mathit{B}$ . In a randomly chosen lattice  $\mathcal{L}\left(\mathit{B}\right)$ , the length ( ${\left|\overrightarrow{v}\right|}_2$ ) of the shortest nonzero vector ( $v$ ) is satisfied:

$${\left|\overrightarrow{\mathrm{v}}\right|}_2\approx \mathsf{\sigma }\left(\mathcal{L}\right)$$

(3)

If  $\epsilon >0$  is a constant, then an  $n$ -dimensional randomly chosen lattice satisfies, for all sufficiently large  $n$ ,

$$\left(1-\epsilon \right)\sigma \left(L\right)⩽‖{\overrightarrow{\mathit{v}}}_{\mathit{m}\mathit{i}\mathit{n}}‖⩽\left(1+\epsilon \right)\sigma \left(L\right)$$

(4)

2.3. GCD Problem Variants

The Greatest Common Divisor problem is a challenging issue involving integers, centered on finding the Greatest Common Divisor among them. Several other difficult problems are extensions of the GCD problem.

Definition 6

(GCD problem). For a large prime $p$, given a set of products $\{b_i=a_{i}p|a_i\in Z_{+}{\}}_{i=0}^{\tau }$ of $p$, where $a_i$ is chosen randomly, solve for $p$.

Definition 7

(AGCD problem). For a large prime $p$, given a set of error products $\{b_i=a_{i}p+e_i|a_i\in Z_{+},e_i\in Z,\left|e_i\right|<2^{n-1}{\}}_{i=0}^{\tau }$ of p, where $e_i$ is the small-integer error, and $a_i$ and $e_i$ are chosen randomly to solve $p$.

Definition 8

(DAGCD problem). For a large prime $p$, given a set of error products $b=ap+e$ of p and a random number $r$, distinguish between $b$ and the random number $r$.

Definition 9

(AMGCD problem). For an integer matrix $\mathit{A}$, given a set of error matrices $\left\{{\mathit{B}}_{\mathit{i}}=\mathit{A}{\mathit{R}}_{\mathit{i}}+{\mathit{E}}_{\mathit{i}}\in Z_p^{n\times n}|{\mathit{R}}_{\mathit{i}},{\mathit{E}}_{\mathit{i}}\in Z^{n\times n},det\left(\mathit{A}\right)=p\right\}$, det(A) = p}, find $\mathit{A}$ such that $\parallel p\cdot {\mathit{A}}^{-1}{\mathit{E}}_{\mathit{i}}\parallel <p/2$.

2.4. Ring

In mathematics, the term “ring” refers to an algebraic structure that includes the operations of “$+$” and “$\times$”, satisfying specific axioms, such as the associative and distributive laws. The following is a precise definition of a ring:

Definition 10

(ring). A nonempty set $R$ defining two algebraic operations, also denoted  $\{R,+,\times \}$, is called a ring if the following is true:

• Addition “+”:

• $R$  is closed for the “+” operation, which means that for any  $a,b\in R$, there is  $a+b\in R$;
• There exists a unit element “0” in R, which means that for  $a\in R$, there exists  $0\in R$  satisfying  $a+0=a$;
• All elements in  $R$  satisfy the associative law, which means that for any  $a,b,c\in R$, there is  $(a+b)+c=a+(b+c)$;
• All elements in  $R$  satisfy the commutative law, which means that for any  $a,b\in R$, there is  $a+b=b+a$;
• All elements in $R$ have inverse elements corresponding to them, which means that for any $a\in R$, there exists $b=-a\in R$ satisfying $a+b=0$.

2.

Multiplication “$\times$”:

• $R$  is closed for the “$\times$” operation, which means that for  $a,b\in R$, there is  $a\times b\in R$;
• All elements in  $R$  satisfy the associative law, which means that for any  $a,b,c\in R$, there is  $(a\times b)\times c=a\times (b\times c)$;
• All elements in $R$ satisfy the distributive law, which means that for any $a,b,c\in R$, there are $a\left(b+c\right)=ab+ac, (b+c)a=ba+ca$.

Definition 11

(division ring): Ring R is called a division ring if the following is true:

• There exists at least one element not equal to zero in R, and the zero element 0 satisfies  $0\times a=a\times 0=0$;
• There exists a unit element “1” in  $R$, which means that for  $a\in R$, there exists  $1\in R$  satisfying  $a\times 1=a$  and  $1\times a=a$;
• Every nonzero element has an inverse element in $R$, which means that for any $a\in R$, there exists $b=a^{-1}\in R$ satisfying $a\times b=b\times a=1$.

2.5. Verifiable Security

Semantic security refers to a property of encryption schemes that ensures the ciphertext does not reveal any meaningful information about the plaintext, even if an adversary has access to auxiliary information. In other words, the encryption should be indistinguishable from random data, making it computationally infeasible for an attacker to deduce any information about the original message.

The IND-CPA (Indistinguishability under Chosen Plaintext Attack) game is a framework used to demonstrate the security of a cryptographic algorithm against chosen plaintext attacks. In this game, an adversary is given the ability to choose plaintexts and receive corresponding ciphertexts, ultimately attempting to distinguish between two different messages encrypted under the same key.

Definition 12

(IND-CPA game). IND-CPA security is demonstrated through a game between an adversary and a challenger, divided into the following sessions:

(1) Initialization: The challenger generates a public key from the key generation algorithm of the cryptographic regime and then gives that public key to the adversary.

(2) Access to Oracle: An adversary can select a plaintext message multiple times and then access the Oracle to obtain the ciphertext encrypted by the system.

(3) Challenge: The adversary outputs plaintext messages  $m0$  and  $m1$. After receiving the two plaintext messages, the challenger randomly chooses  $b\in \{0,1\}$ and generates the target ciphertext  $c=Enc(pk,mb)$  to send to the adversary.

(4) Conjectures: The adversary guesses and outputs  $b_1$. If  $b_1=b$, the adversary wins.

The adversary’s advantage in winning the game is defined as $Avd\left(A\right)=\left|p\left[b_1=b\right]-{\displaystyle \frac{1}{2}}\right|$. An encryption algorithm is considered indistinguishable under a chosen plaintext attack, or IND-CPA-secure, if for any polynomial-time adversary, there exists a negligible function $negl\left(k\right)$ such that $Avd\left(A\right)\le negl\left(k\right)$.

3. G-NTRU Algorithm

The G-NTRU algorithm is not a single algorithm but a framework for generalized NTRU variants over algebraic rings. It is not designed for a specific ring but rather for a generalized algebraic ring, denoted as $G$. First, we introduce the structure of the ring $G$, followed by a detailed description of the algorithmic steps.

Given a division ring $⟨G\left[Z\right],+,\times ⟩$, where each coefficient of $f\in G\left[Z\right]$ is an integer, for example, $G$ can represent a ring of integer polynomials, where each coefficient of the polynomials $f$ is integer, or $G$ can represent a ring of integer matrices, where each element of the matrix $f$ is an integer.

For $f,f_q^{-1}\in G\left[Z\right]$ and $q\in Z$, define $f mod q$ as the operation where each integer coefficient of $f$ is taken by modulo $q$, $f\times q$ as the operation where each integer coefficient of $f$ is multiplied by $q$, and $f+q$ as the operation where each integer coefficient of $f$ is incremented by $q$. Clearly, after performing these operations, the resulting element remains in the ring $G$. The element $f_q^{-1}$ is called the inverse of $f$ modulo $q$ if it satisfies $f\times f_q^{-1}(mod q)=1$.

The following defines the NTRU algorithm over the algebraic ring $G$, referred to as the G-NTRU algorithm.

• $\mathit{K}\mathit{e}\mathit{y}\mathit{G}\mathit{e}\mathit{n}\left(f,g\right)$:

 1.

Inputs:

Let $f,g\in G\left[Z\right]$ be the elements in the generalized ring $G\left[Z\right]$, where $f$ has an inverse $f_q^{-1}$ modulo $q$($f\times f_q^{-1}(mod q)=1$). The $Z$ is generally $\{-\mathrm{1,0},1\}$.

Here, $q$ is chosen as a large prime number, while $p$ is an integer that is homogeneous with $q$($gcd(q,p)=1$), with the condition that $q$ is much larger than $p$.

 2.

Calculate the inverse:

Compute the inverse of $f$ modulo $q$, denoted as $f_q^{-1}$, and the inverse of $f$ modulo $p$, denoted as $f_p^{-1}$. This operation ensures that

$$f_q^{-1}\times f\equiv 1\left(mod q\right), f_p^{-1}\times f\equiv 1\left(mod p\right)$$

(5)

Store this inverse:

$$f_q^{-1},f_p^{-1}$$

(6)

 3.

Calculate h:

Multiply $f_q^{-1}$ with $g$, and then reduce the result modulo $q$ to obtain

$$h\equiv f_q^{-1}\times g\left(mod q\right)$$

(7)

Ensure that all the coefficients of $h$ lie in the interval $\left[-{\displaystyle \frac{q}{2}},{\displaystyle \frac{q}{2}}\right]$.

If any coefficient $h_i>{\displaystyle \frac{q}{2}}$, set $h_i=h_i-q$.

If any coefficient $h_i<-{\displaystyle \frac{q}{2}}$, set $h_i=h_i+q$.

 4.

Output keys:

The public key is

$$pk=h$$

(8)

The private key is

$$sk=\left(f,f_p^{-1}\right)$$

(9)

• $\mathit{E}\mathit{n}\mathit{c}\mathit{r}\mathit{y}\mathit{p}\mathit{t}\left(pk,m\right)$:

 1.

Choose the plaintext:

Select a plaintext element $m\in G\left[Z\right]$ with coefficients in the range $\left[-{\displaystyle \frac{p}{2}},{\displaystyle \frac{p}{2}}\right]$.

 2.

Randomly select element:

Randomly select an element $\varphi \in G\left[Z\right]$. The coefficients of $\varphi$ can also be within $\left[-{\displaystyle \frac{p}{2}},{\displaystyle \frac{p}{2}}\right]$.

 3.

Calculate c:

Compute the product $p\times h\times \varphi +m\left(mod p\right)$, where $h$ is the public key obtained from the previous steps.

$$c\equiv p\times h\times \varphi +m\left(mod p\right)$$

(10)

Ensure that the coefficients of the ciphertext $c$ are within the appropriate range $\left[-{\displaystyle \frac{p}{2}},{\displaystyle \frac{p}{2}}\right]$.

 4.

Output c:

The ciphertext $c$ is then returned as the output.

• $\mathit{D}\mathit{e}\mathit{c}\mathit{r}\mathit{y}\mathit{p}\mathit{t}\left(sk,c\right)$:

 1.

Inputs:

$f\in G\left[Z\right]$, $f_p^{-1}\in G_p$: the private key.

$c\in G_q$: the ciphertext.

$q$: a large modulus.

$p$: a small modulus.

 2.

Calculate a:

Multiply the private key $f$ with the ciphertext $c$, and then reduce the result modulo $q$ to obtain

$$a\equiv f\times c\left(mod q\right)$$

(11)

After computing $a\in G_q$, ensure that all its coefficients are within the range $\left[-{\displaystyle \frac{p}{2}},{\displaystyle \frac{p}{2}}\right]$.

 3.

Calculate b:

Multiply the private key $f_p^{-1}$ with $a$, and then reduce the result modulo $q$ to obtain

$$b\equiv f_p^{-1}\times a\left(mod p\right)$$

(12)

Reduce the result $b\in G_p$; ensure that all its coefficients lie within the range $\left[-{\displaystyle \frac{p}{2}},{\displaystyle \frac{p}{2}}\right]$.

 4.

Output b:

The value $b$ is the decrypted plaintext $m$.

 5.

Encryption and decryption correctness:

By analyzing the decryption algorithm, we can evaluate the correctness of both the encryption and decryption processes.

$$\begin{array}{l}a\equiv f\times c\left(modq\right)\\ \equiv p\times g\times \varphi +f\times m\left(modq\right)\\ b\equiv f_p^{-1}\times a\left(modp\right)\\ \equiv f_p^{-1}\times \left(p\times g\times \varphi +f\times m\right)\left(modp\right)\\ \equiv p\times g_p^{-1}\times g\times \varphi +m\left(modp\right)\\ \equiv m\end{array}$$

(13)

The decryption is successful.

4. Algorithm Analysis

Section 4 primarily discusses the security of the G-NTRU algorithm and provides a comparative analysis with other algorithms. The AGCD problem and its extended versions are introduced. The generalized GCD problem over different algebraic rings, termed the G-AGCD problem, is formulated inductively. For example, over the ring of integers, G-AGCD reduces to AGCD, and over the ring of matrices, G-AGCD reduces to AMGCD. Finally, the security of G-AGCD is analyzed in the context of the G-AGCD problem.

4.1. Security Analysis

4.1.1. Lattice Attack

The lattices underlying different NTRU variant algorithms differ, but they share common characteristics. Here, we summarize the lattice structure on which these NTRU variants are based in a generalized form, referred to as the G-NTRU lattice.

Definition 13

(G-NTRU lattice). The generalized NTRU lattice $\mathcal{L}\left(\mathit{B}\right)$ is generated from the  $2N\times 2N$  dimensional lattice basis matrix  $\mathit{B}$, which is constructed using the public key  $h$  from the generalized NTRU algorithm.

$$\mathit{B}={\left[\begin{array}{cc}\begin{array}{cccc}\alpha & 0& \cdots & 0\\ 0& \alpha & \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & \alpha \end{array}& {\mathit{H}}_{N\times N}\\ \begin{array}{cccc}0& 0& \cdots & 0\\ 0& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 0\end{array}& \begin{array}{cccc}q& 0& \cdots & 0\\ 0& q& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & q\end{array}\end{array}\right]}_{2N\times 2N}={\left[\begin{array}{cc}\alpha {\mathit{E}}_{N\times N}& {\mathit{H}}_{N\times N}\\ 0_{N\times N}& q{\mathit{E}}_{N\times N}\end{array}\right]}_{2N\times 2N}$$

(14)

where  ${\mathit{H}}_{N\times N}$  is the matrix generated by the public key  $h$, and  $\alpha$  is a parameter to be determined, typically set to 1, as discussed below.

The NTRU lattice structure varies depending on the algebraic ring it is constructed on, with differences primarily in the formation of the ${\mathit{H}}_{N\times N}$ matrix. For example, on polynomial rings, the NTRU lattice is defined by a cyclic matrix $\mathit{H}$ generated from the public key coefficients $\{h_0,h_1...h_{N-1}\}$, represented as follows:

$$\mathit{H}=\left[\begin{array}{ccc}{h}_0& h_1& \begin{array}{cc}\cdots & h_{N-1}\end{array}\\ h_{N-1}& h_0& \begin{array}{cc}\cdots & h_{N-2}\end{array}\\ \begin{array}{c}⋮\\ h_1\end{array}& \begin{array}{c}⋮\\ h_2\end{array}& \begin{array}{cc}\begin{array}{c}\ddots \\ \cdots \end{array}& \begin{array}{c}⋮\\ h_0\end{array}\end{array}\end{array}\right]$$

(15)

In the case of matrix rings, the Matrix NTRU lattice H is generated from the matrix public key coefficients ${\{h}_{ij}|i,j\in [1,N]\cap Z\}$, represented as follows:

$$\mathit{H}=\left[\begin{array}{ccc}{h}_{11}& h_{12}& \begin{array}{cc}\cdots & h_{1N}\end{array}\\ h_{21}& h_{22}& \begin{array}{cc}\cdots & h_{2N}\end{array}\\ \begin{array}{c}⋮\\ h_{N1}\end{array}& \begin{array}{c}⋮\\ h_{N2}\end{array}& \begin{array}{cc}\begin{array}{c}\ddots \\ \cdots \end{array}& \begin{array}{c}⋮\\ h_{NN}\end{array}\end{array}\end{array}\right]$$

(16)

For integer rings, the lattice structure $\mathit{H}$ is simply the one-dimensional case of the Matrix NTRU lattice, reflecting the algebraic equivalence between congruence cryptographic algorithms and the Matrix NTRU algorithm in one dimension.

Theorem 1.

The $(\alpha f,g)$, formed by multiplying the private key $f$ by $\alpha$ and concatenating it with $g$, lies on the lattice $\mathcal{L}\left(\mathit{B}\right)$.

Proof of Theorem 1.

Given

$$h\equiv f_q^{-1}\times g\left(modq\right)$$

(17)

there exists $u\in G$ such that

$$f\times h=g+qu$$

(18)

Now, consider the $\left(f,-u\right)$ and multiply it by the lattice basis matrix $\mathit{B}$:

$$\left(f,-u\right)·\mathit{B}=\left(f,-u\right)·\left[\begin{array}{cc}\alpha {\mathit{E}}_{N\times N}& {\mathit{H}}_{N\times N}\\ {\mathbf{0}}_{N\times N}& q{\mathit{E}}_{N\times N}\end{array}\right]$$

(19)

Expanding this product yields the following:

$$\left(f,-u\right)·\left[\begin{array}{cc}\alpha {\mathit{E}}_{N\times N}& {\mathit{H}}_{N\times N}\\ {\mathbf{0}}_{N\times N}& q{\mathit{E}}_{N\times N}\end{array}\right]=\left(\alpha f-u\mathbf{0},f\mathit{H}-uq\mathit{E}\right)=\left(\alpha f,g\right)$$

(20)

Thus, $(\alpha f,g)$ can be expressed in terms of the lattice basis $\mathit{B}$, implying that $(\alpha f,g)$ lies on the lattice $\mathcal{L}\left(\mathit{B}\right)$.

This completes the proof. □

$(\alpha f,g)$ may represent either a vector or a matrix; however, it will be discussed below in the context of $(\alpha f,g)$ as a vector. Assuming that $(\alpha f,g)$ is a matrix, if any of its row vectors is close to the shortest vector in the lattice, then it can be generalized that solving the matrix $(\alpha f,g)$ is equivalent to solving the Shortest Vector Problem (SVP).

According to the Gaussian Heuristic, the expected length of the shortest vector $\overrightarrow{v}$ in the lattice $\mathcal{L}\left(\mathit{B}\right)$ can be expressed as follows:

$${\left|\overrightarrow{v}\right|}_{\mathbf{2}}=\sigma \left(\mathcal{L}\right)=\sqrt{{\displaystyle \frac{n}{2\pi e}}}{det\left(\mathit{D}\right)}^{{\displaystyle \frac{1}{n}}}=\sqrt{{\displaystyle \frac{N\alpha q}{\pi e}}}$$

(21)

Furthermore, the length of the target vector $(\alpha f,g)$ is given by the following:

$${\left|\left(\alpha f,g\right)\right|}_{\mathbf{2}}=\sqrt{{\alpha }^2{{\left|f\right|}_2}^2+{{\left|g\right|}_2}^2}$$

(22)

Here, a good choice of the parameter $\alpha$ can facilitate the attacker’s ability to find the vector $(\alpha f,g)$ or vectors of length close to $(\alpha f,g)$. As the ratio ${\displaystyle \frac{{\left|v\right|}_{\mathbf{2}}}{{\left|(\alpha f,g)\right|}_{\mathbf{2}}}}$ increases, it becomes easier to locate the target vector. If this ratio gradually approaches 1, the difficulty of finding the target vector becomes more akin to solving the Shortest Vector Problem (SVP) on the lattice.

The ratio can be expressed as follows:

$${\displaystyle \frac{{\left|v\right|}_{\mathbf{2}}}{{\left|\left(\alpha f,g\right)\right|}_{\mathbf{2}}}}=\sqrt{{\displaystyle \frac{Nq}{\pi e}}·{\displaystyle \frac{\alpha }{{\alpha }^2{{\left|f\right|}_2}^2+{{\left|g\right|}_2}^2}}}=\sqrt{{\displaystyle \frac{Nq}{\pi e}}}·\sqrt{{\displaystyle \frac{1}{\alpha {{\left|f\right|}_2}^2+{{\alpha }^{-1}{\left|g\right|}_2}^2}}}$$

(23)

It is easy to see that this ratio reaches its maximum value of $\sqrt{{\displaystyle \frac{Nq}{{2\pi e\left|f\right|}_2{\left|g\right|}_2}}}$ when $\alpha {{\left|f\right|}_2}^2={{\alpha }^{-1}{\left|g\right|}_2}^2$, which simplifies to $\alpha ={\displaystyle \frac{{\left|f\right|}_2}{{\left|g\right|}_2}}$. Given that the elements $f,g\in G\left[Z\right]$ are chosen uniformly and approximately equal in norm, ${\left|f\right|}_2\approx {\left|g\right|}_2$, the common parameter $\alpha$ is generally taken to be 1.

Since the elements in $f,g\in G\left[Z\right]$ are uniformly chosen, with $Z=\{-\mathrm{1,0},1\}$, we have $max\left({\left|f\right|}_2\right)=max\left({\left|g\right|}_2\right)=\sqrt{N}$. When ${\left|f\right|}_2$ and ${\left|g\right|}_2$ take their maximum values, we have the following:

$${\left|\left(\alpha f,g\right)\right|}_{\mathbf{2}}=\sqrt{2N}$$

(24)

$${\left|\overrightarrow{v}\right|}_{\mathbf{2}}=\sqrt{2N}·\sqrt{{\displaystyle \frac{q}{2\pi e}}}$$

(25)

In the generalized NTRU algorithm, since $q$ is a large prime and $\sqrt{{\displaystyle \frac{q}{2\pi e}}}>1$, the length ${\left|(\alpha f,g)\right|}_{\mathbf{2}}$ of the target vector $(\alpha f,g)$ is much smaller than the Gaussian expectation of the lattice $\mathcal{L}\left(\mathit{B}\right)$. This leads to a high probability that the shortest vector of the lattice $\mathcal{L}\left(\mathit{B}\right)$ is either the target vector $(\alpha f,g)$ or its cyclic form.

Thus, breaking the G-NTRU cipher algorithm is somewhat equivalent to solving the Shortest Vector Problem (SVP) in the G-NTRU lattice. For instance, in the case of the NTRU, one of the shortest vectors of the lattice $\mathcal{L}\left(\mathit{B}\right)$ consists of the coefficients of the private key polynomials $f$ and $g$. In the Matrix NTRU variant, the matrix formed by the shortest vectors of the lattice $\mathcal{L}\left(\mathit{B}\right)$ represents the private key $F$ and $G$. However, the security of the lattice is also influenced by the number of dimensions in the lattice basis. For example, congruent cryptosystems based on the ring of integers have lattice basis matrices of only two dimensions, which makes solving the SVP problem considerably easier.

4.1.2. Generalized AGCD Problem

There are many cryptographic algorithms whose security is built on the AGCD problem. For instance, the DGHV10 algorithm [23] relies on the AGCD problem defined over the ring of integers. In this context, the AGCD problem is then extended from the ring of integers to other algebraic rings.

Definition 14

(Generalized Approximate Greatest Common Divisor, G-AGCD, problem). For an element $p$ on an algebraic ring  $\left(R\left[Z\right],+,\times \right)$, given a list of multiples of  $p$  with errors over the ring  $R$,$b_i=a_i\times p+e_i$, where  $a_i,e_i\in R$,$\left|e_i\right|<\beta$, find p such that  $p$  satisfies certain conditions.

The element $p$ solved by $b_i=a_i\times p+e_i$ is not necessarily unique. For example, the subproblems of G-AGCD, such as AGCD over a matrix ring and the AMGCD problem, require finding the original $\mathit{A}$ while satisfying specific restrictions. Therefore, when specifying G-AGCD on a particular ring, it is necessary to stipulate specific restrictions.

Definition 15

(Generalized Decisional Approximate Greatest Common Divisor, G-DAGCD, problem). On the algebraic ring  $\left(R\left[Z\right],+,\times \right)$, given multiples of $p$ with errors by G-AGCD, b = a × p + e and a randomly chosen element v ∈ R, distinguish between $b$ and a random element $v$.

Definition 16

(Learning With Error, LWE). Know the matrix $\mathit{A}\in Z_q^{m\times n}$. Given multiples of the matrix $\mathit{A}$ and the column vector $\overrightarrow{s}\in Z_q^n$ with errors, where $\overrightarrow{e}\in Z_q^n$, find the vector $\overrightarrow{s}$.

The Learning With Error (LWE) problem can be reduced to the lattice difficulty problem, specifically the Shortest Vector Problem (SVP). There are many variants of the LWE problem, such as the Ring LWE (RLWE) problem and the polynomial LWE problem. The LWE problem and its variants significantly facilitate the construction of lattice-based cryptosystems. The security of the NTRU is grounded in the RLWE problem.

By expanding the vector $s$ and vector $e$ in the LWE problem into matrices, the LWE problem becomes analogous to the Augmented Matrix GCD (AMGCD) problem. In fact, the AMGCD problem can also be generalized to the LWE problem. Additionally, AMGCD reduces to the Approximate GCD (AGCD) problem when $n=1$. As G-AGCD subproblems, AGCD and AMGCD are likely to be difficult, suggesting that G-AGCD also presents a high level of difficulty.

Assumption 1

(G-AGCD). There is no polynomial-time algorithm that finds $p$ satisfying certain conditions from a list of multiples of  $p$  with errors over the ring  $\left(G\left[Z\right],+,\times \right)$,  $b_i=a_i\times p+e_i$, where  $p,a_i,e_i\in G$,$\left|e_i\right|<\gamma$, and  $p$  satisfies certain conditions.

Theorem 2.

There exists a polynomial-time algorithm which reduces G-AGCD to MGCD in Assumption 1.

Proof of Theorem 2.

Denote any integer part of $b\in G\left[Z\right]$ as $b_z$, such as the matrix $\mathit{B}$ with $b_z=b_{ij}$. The multiplication of two elements in $G\left[Z\right]$, $c=a\times b$, results in $c_z$ being of the form $\alpha a_z\times b_z+\beta$. For one integer part of $b=a\times p+e$, we have $b_z=\alpha a_z\times p_z+\beta +e_z=a_{z1}\times p_z+e_{z1}$. From the AGCD problem, it is difficult to find $p_z$ given a list of $b_z$. By the same reasoning, solving for the other integer parts of $p$ is also difficult, implying that finding $p$ is difficult. □

Clearly, the G-AGCD problem is reduced to the AGCD problem when there exists only one integer part of the elements in the ring $G\left[Z\right]$.

Due to three steps, our G-NTRU scheme is semantically secure under the AGCD assumption:

Step 1: AGCD $⟶$ G-AGCD;

Step 2: G-AGCD $⟶$ G-DAGCD;

Step 3: G-DAGCD $⟶$ G-NTRU.

4.1.3. IND-CPA Security

The security of the G-NTRU algorithm presented in this paper relies on the hardness of the G-AGCD problem. In the following sections, the security of the proposed scheme will be demonstrated under the assumption that the G-AGCD problem is computationally difficult.

Lemma 1

(Leftover Hash Lemma, [24]). Let $X\subset \{\mathrm{0,1}{\}}^n$, $\left|X\right|\ge 2^l$. Let $e>0$, and let $H$ be an almost universal family of hash functions mapping the value domain $X$ to the value domain $Y$.The $(h,h(x\left)\right)$ is quasi-random within ${\displaystyle \frac{1}{2}}\sqrt{\left|Y\right|/\left|X\right|}$(on the set $H\times Y$), where $h$ is chosen uniformly at random from $H$ and $x$ uniformly from $X$.

Theorem 3.

The G-NTRU proposed in Section 3 of this paper is IND-CPA-secure.

Proof of Theorem 3.

This theorem is proved below using the game sequence method.

(1)

Game 0. The game is designed as an IND-CPA game between a challenger and an adversary of the G-NTRU encryption scheme.

(2)

Game 1. Compared to Game 0, in Game 1, the public key generation method no longer generates $h\equiv f_q^{-1}\times g\left(mod q\right)$ by the key generation algorithm but randomly and uniformly selects $h\leftarrow R_q\left[Z\right]$. Since $f,g\leftarrow \{-\mathrm{1,0},1\}$ are chosen randomly and uniformly, and since the mapping from $f$ to $f_q^{-1}$ is one-to-one, Game 0 and Game 1 are statistically indistinguishable from the adversary’s perspective.

(3)

Game 2. Compared to Game 1, in Game 2, only the target ciphertext $C$ is modified. Instead of generating the ciphertext through the encryption algorithm, the challenger chooses $C_1$ randomly and uniformly over $G_q$. From Definition 15, it is difficult to distinguish between $C$ and $C1$. From the adversary’s perspective, Game 1 and Game 2 are indistinguishable.

In Game 2, the public key and ciphertext provided by the challenger are chosen randomly and uniformly, resulting in a negligible advantage for the adversary in Game 2. Consequently, the advantage of an adversary attempting to attack the G-NTRU scheme in Game 0 is negligible, indicating that the G-NTRU encryption scheme is IND-CPA-secure. □

4.2. Comparison of Algorithms

The ring underlying the NTRU variants of GR-NTRU is isomorphic to the polynomial ring over the NTRU. In contrast to GR-NTRU, the G-NTRU proposed in this paper generalizes the ring across various basic algebraic NTRU variants. Table 2 presents a comparative overview between GR-NTRU and G-NTRU.

Table 2. Two types of NTRU variants.

NTRU Variant	G-NTRU	GR-NTRU
Algorithmic structure	Generalized NTRU algorithms based on algebraic rings offer the ability to operate in a variety of algebraic structures, such as integers, polynomials, matrices, Gaussian integers, and more. They have a high degree of flexibility.	GR-NTRU is an extension of the NTRU algorithm to a group ring structure. In this variant, both addition and multiplication are defined within the group ring, enabling GR-NTRU to maintain the simplicity of key generation and encryption operations, much like the original NTRU algorithm.
Ring	$\mathrm{G}\left[\mathrm{Z}\right]$.	$\mathrm{Z}\left[\mathrm{x}\right]/({\mathrm{x}}^{\mathrm{N}}-1)$.
Security assumption	The security of the G-NTRU algorithm relies on the problem of approximate estimation of the Greatest Common Divisor (G-AGCD), and its IND-CPA security is proven under this assumption.	By embedding Z[G] into a matrix ring, GR-NTRU is analyzed using attack methods designed for NTRU variants on matrix rings.
Versatility	G-NTRU demonstrates high generality across different algebraic structures, with its performance varying depending on the underlying rings.	GR-NTRU, built on a group ring, is constrained by the group structure and the embedding mapping parameters. The security of the algorithm can be adjusted by selecting different group structures, such as cyclic groups or dihedral groups.
Performance	The performance of the G-NTRU algorithm can vary depending on the underlying ring. For small-scale applications, G-NTRU can select rings with lower dimensions to enhance efficiency.	The performance of GR-NTRU is closely tied to the specific structure of the group ring. In certain complex group structures, such as non-commutative groups, performance degradation may occur.
Example	Matrix NTRU.	QTRU.

Overall, G-NTRU offers greater flexibility by generalizing algebraic rings, enabling applications across different architectures. In contrast, GR-NTRU leverages the structure of group rings to facilitate diverse security analyses and performance optimizations tailored to specific group ring structures.

Common algebraic structures include integers, matrices, and polynomials, among others, and various NTRU variants can be constructed based on different algebraic rings. This paper compares G-NTRU algorithms over several common algebraic rings, examining their properties across these different structures. The results are summarized in Table 3.

Table 3. G-NTRU on different rings.

NTRU Variant	Ring	PK	Dimensionality of the Lattice
Congruent cipher	$Z$	$h\equiv f_q^{-1}\times g\left(\mathit{mod}q\right)$	$2$
Matrix NTRU	$R\left[Z\right]$	$H=p·{\mathit{X}}_q·\mathit{Y}(mod q)$	$2n$
NTRU	$Z\left[x\right]/(x^N-1)$	$h=F_q\ast g(mod q)$	$2N$

5. The NTRU Variant Algorithm on Complex Rings

The NTRU variant algorithm on complex rings, referred to as the CNTRU, is derived from the G-NTRU algorithmic framework. The CNTRU is constructed over the ring of complex numbers, shifting the algebraic structure from polynomials used in the traditional NTRU algorithm to pure imaginary numbers. Throughout the operation of the CNTRU algorithm, complex numbers with nonzero real parts are intentionally not produced. The fundamental properties of the CNTRU remain consistent with the findings and studies related to the G-NTRU.

5.1. CNTRU Algorithm

The most significant feature of the NTRU algorithm is its double-mode operation. However, the NTRU variant algorithm defined over the ring of complex numbers lacks modulo operations when $a\ne 0$ due to the structure of complex numbers represented as $f=a+bi$. When $a=0$, the complex numbers become purely imaginary, allowing for the modulo operations to be satisfied.

In the context of a complex ring $⟨R_q\left[Z\right],+,\times ⟩$, let $f\in R_q\left[Z\right]$, where $f$ takes the form $f=\left\{ai|a\in Z\cap \left(\left.-{\displaystyle \frac{q}{2}},{\displaystyle \frac{q}{2}}\right]\right.\right\}$. The algebraic structure over the ring $R$ determines the parameters used in the CNTRU algorithm.

Given two purely imaginary numbers $f=ai$ and $g=bi$ (with $a,b\in Z$), the operations are defined as follows:

For purely imaginary addition:

$$f+g=\left(a+b\right)i$$

(26)

For purely imaginary multiplication:

$$f\times g=-ab$$

(27)

For multiplying integers with purely imaginary numbers:

$$f\times b=abi$$

(28)

For the modulo operation with purely imaginary numbers:

$$f\left(mod q\right)=a\left(mod q\right)i$$

(29)

In this algorithm, the mod $q$ ranges over the interval $\left(\left.-{\displaystyle \frac{q}{2}},{\displaystyle \frac{q}{2}}\right]\right.$. When $a \left(mod q\right)=b$, it holds that $b\in \left(\left.-{\displaystyle \frac{q}{2}},{\displaystyle \frac{q}{2}}\right]\right.$. The element $f_q^{-1}$ is defined as the inverse of $f$ modulo $q$ if it satisfies the following condition:

$$f\times f_q^{-1} \left(mod q\right)=1$$

(30)

The following section defines the NTRU algorithm on the ring $R$, specifically focusing on the CNTRU algorithm.

• $\mathit{K}\mathit{e}\mathit{y}\mathit{G}\mathit{e}\mathit{n}\left(f,g\right)$:

 1.

Inputs:

The coefficients of the imaginary part of $a\in R\left[Z\right]$ are then uniformly chosen on $Z$ as

$$a\leftarrow Z$$

(31)

Choose the parameters $q$ and $p$ such that $p,q\in Z$, $p$ and $q$ are coprime (mutually prime), and $q$ is much larger than $p$.

Let $f,g\in R$ be the elements in the generalized ring $R$, where $f$ has an inverse $f_q^{-1}$ modulo $q$($f_p^{-1}$ modulo $p$).

Choose the parameter space as follows:

$$p\leftarrow Z_1$$

(32)

$$f\leftarrow Z_2$$

(33)

$$g\leftarrow Z_3$$

(34)

 2.

Calculate the inverse:

Compute the inverse of $f$ modulo $q$, denoted as $f_q^{-1}$, and the inverse of $f$ modulo $p$, denoted as $f_p^{-1}$. This operation ensures that

$$f_q^{-1}\times f\equiv 1\left(mod q\right), f_p^{-1}\times f\equiv 1\left(mod p\right)$$

(35)

Store this inverse:

$$f_q^{-1},f_p^{-1}$$

(36)

 3.

Calculate h:

Multiply $f_q^{-1}$ with $g$, and then reduce the result modulo $q$ to obtain

$$h\equiv f_q^{-1}\times g\left(mod q\right)$$

(37)

Ensure that all the coefficients of $h$ lie in the interval $\left[-{\displaystyle \frac{q}{2}},{\displaystyle \frac{q}{2}}\right]$.

If any coefficient $h_i>{\displaystyle \frac{q}{2}}$, set $h_i=h_i-q$.

If any coefficient $h_i<-{\displaystyle \frac{q}{2}}$, set $h_i=h_i+q$.

 4.

Output keys:

The public key is

$$pk=h$$

(38)

The private key is

$$sk=\left(f,f_p^{-1}\right)$$

(39)

• $\mathit{E}\mathit{n}\mathit{c}\mathit{r}\mathit{y}\mathit{p}\mathit{t}\left(pk,m\right)$:

 1.

Input:

Public key $pk=h$.

Purely imaginary plaintext $m\in R$ (where “mmm” is selected such that $m\leftarrow Z_3$).

Random element $r\in R$ (where $m$ is selected such that $r\leftarrow Z_3$).

Parameter $p$.

 2.

Calculate c:

Compute the product $p\times h\times \varphi +m\left(mod p\right)$, where $h$ is the public key obtained from the previous steps.

$$c\equiv p\times h\times \varphi +m\left(mod p\right)$$

(40)

Ensure that the coefficients of the ciphertext $c$ are within the appropriate range $\left[-{\displaystyle \frac{p}{2}},{\displaystyle \frac{p}{2}}\right]$.

 3.

Output c:

Output the ciphertext $c$:

$$c\in R_q$$

(41)

The first step is to compute the following:

$$a\equiv f\times c \left(mod q\right)$$

where $a\in R_q\left[Z\right]$ and its coefficients are kept between $\left(\left.-{\displaystyle \frac{q}{2}},{\displaystyle \frac{q}{2}}\right]\right.$.

The second step is to compute the following:

$$b\equiv f_p^{-1}\times a \left(mod p\right)$$

where $b\in R_q\left[Z\right]$, and $b$ is the decrypted plaintext $m$.

• $\mathit{D}\mathit{e}\mathit{c}\mathit{r}\mathit{y}\mathit{p}\mathit{t}\left(sk,c\right)$:

 1.

Inputs:

The private key $f\in R$, $f_p^{-1}\in R_p$.

The ciphertext $c\in R_q$.

A large modulus $q$.

A small modulus $p$.

 2.

Calculate a:

Multiply the private key $f$ with the ciphertext $c$, and then reduce the result modulo $q$ to obtain

$$a\equiv f\times c\left(mod q\right)$$

(42)

After computing $a\in R_q$, ensure that all its coefficients are within the range $\left[-{\displaystyle \frac{p}{2}},{\displaystyle \frac{p}{2}}\right]$.

 3.

Calculate b:

Multiply the private key $f_p^{-1}$ with $a$, and then reduce the result modulo $q$ to obtain

$$b\equiv f_p^{-1}\times a\left(mod p\right)$$

(43)

Reduce the result $b\in R_p$; ensure that all its coefficients lie within the range $\left[-{\displaystyle \frac{p}{2}},{\displaystyle \frac{p}{2}}\right]$.

 4.

Output b:

Output the ciphertext $m$:

$$b=m$$

(44)

5.2. Parameter Space

NTRU variant algorithms, like the original NTRU algorithm, commonly encounter the issue of decryption failure. This failure typically arises due to the double-modulus operation in the decryption process. Specifically, during the first step of the operation, if $a>q$, modulus crossing occurs in the second modulus $p$, leading to the inability of the second step of the operation to correctly recover the plaintext m.

In this paper, the decryption failure problem is addressed by carefully adjusting the parameter selection space [25]. By refining the choice of parameters, the likelihood of modulus crossing can be reduced, thus mitigating the occurrence of decryption failures and enhancing the overall reliability of the algorithm.

Specifically, we choose a large prime $q\in Z$ and define the following sets:

$$Z_1=\left\{a|a\in Z,\sqrt[4]{{\displaystyle \frac{\mathrm{q}}{4}}}<a<\sqrt{{\displaystyle \frac{q}{4}}}\right\}$$

(45)

$$Z_2=\left\{a|a\in Z,-\sqrt{{\displaystyle \frac{q}{9}}}\le a\le \sqrt{{\displaystyle \frac{q}{9}}}\right\}$$

(46)

$$Z_3=\left\{a|a\in Z,-\sqrt[4]{{\displaystyle \frac{\mathrm{q}}{4}}}\le a\le \sqrt[4]{{\displaystyle \frac{\mathrm{q}}{4}}}\right\}$$

(47)

Then, the parameters $p\leftarrow Z_1$, $f\leftarrow Z_2$, $g\leftarrow Z_3$, $r\leftarrow Z_3$, and $m\in Z_3$ are chosen accordingly. Table 4 presents the specific details:

Table 4. Correspondence table of parameter sets.

Set	Coefficients of Parameters
$Z_1=\left\{a|a\in Z,\sqrt[4]{{\displaystyle \frac{\mathrm{q}}{4}}}<a<\sqrt{{\displaystyle \frac{q}{4}}}\right\}$	$p$
$Z_2=\left\{a|a\in Z,-\sqrt{{\displaystyle \frac{q}{9}}}\le a\le \sqrt{{\displaystyle \frac{q}{9}}}\right\}$	$f$
$Z_3=\left\{a|a\in Z,-\sqrt[4]{{\displaystyle \frac{\mathrm{q}}{4}}}\le a\le \sqrt[4]{{\displaystyle \frac{\mathrm{q}}{4}}}\right\}$	$g,r,m$

The CNTRU algorithm, in comparison to both the G-NTRU and the original NTRU algorithms, first extends the parameter space from the limited set $\{-\mathrm{1,0},1\}$ to the integers $R\left[Z\right]$. It then compresses the parameter range to the specific sets $p\leftarrow Z_1$, $f\leftarrow Z_2$, $g\leftarrow Z_3$, $r\leftarrow Z_3$, and $m\in Z_3$, ensuring a refined and controlled selection of parameters.

5.3. Accuracy Analysis

The following is the explanation of the given parameter assumptions and the correctness of the encryption and decryption processes within the framework:

Parameters and assumptions:

$$f=a_{1}i, f_q^{-1}=a_{2}i, f_p^{-1}=a_{3}i, g=a_{4}i, r=a_{5}i, m=a_{6}i.$$

From the relationship $f\times f_q^{-1}(mod q)\equiv 1$, we derive $a_1{a}_2\left(mod q\right)=-1$.

Similarly, from $f\times f_p^{-1}(mod q)\equiv 1$, we derive $a_1{a}_3\left(mod p\right)=-1$.

For the public key $h$, we have the following:

$$\begin{array}{c}h\equiv f_q^{-1}\times g \left(mod q\right)\\ \equiv -a_2{a}_4 \left(mod p\right)\end{array}$$

(48)

Expanding the ciphertext $c$, we obtain the following:

$$\begin{array}{l}c\equiv p\times h\times r+m \left(mod q\right)\\ \equiv p\times \left(-a_2{a}_4\right)\times a_{5}i+a_{6}i \left(mod q\right)\\ \equiv \left(a_6-p{a}_2{a}_4{a}_5\right)i \left(mod q\right)\end{array}$$

(49)

For decryption algorithms, there are the following:

Step one:

$$\begin{array}{l}a\equiv f\times c \left(mod q\right)\\ \equiv a_{1}i\times \left(a_6-p{a}_2{a}_4{a}_5\right)i \left(mod q\right)\\ \equiv -p{a}_4{a}_5-a_1{a}_6 \left(mod q\right)\end{array}$$

(50)

Step two:

$$\begin{array}{l}b\equiv f_p^{-1}\times a \left(mod p\right)\\ \equiv a_{3}i\times \left(-p{a}_4{a}_5-a_1{a}_6\right) \left(mod p\right)\\ \equiv \left(-p{a}_3{a}_4{a}_5+a_6\right) \left(mod p\right)\\ \equiv a_{6}i \left(mod p\right)\end{array}$$

(51)

Since $a_6\left(mod p\right)$ is less than $p$ and m is less than $p$, the final decrypted result is the same as the plaintext $m$, and the decryption is successful.

For the case of CNTRU decryption failure, the decryption can be satisfied with correct decryption by controlling the parameter space in Section 5.2, as shown by (50):

$$a\equiv -p{a}_4{a}_5-a_1{a}_6 \left(mod q\right)$$

(52)

Then, for the maximum value of $a$, there is the following:

$$\begin{array}{l}\left|a\right|\le \sqrt{{\displaystyle \frac{q}{4}}}\times \sqrt[4]{{\displaystyle \frac{\mathrm{q}}{4}}}\times \sqrt[4]{{\displaystyle \frac{\mathrm{q}}{4}}}+\sqrt{{\displaystyle \frac{q}{9}}}\times \sqrt[4]{{\displaystyle \frac{\mathrm{q}}{4}}}\\ \le {\displaystyle \frac{\mathrm{q}}{4}}+\sqrt{{\displaystyle \frac{q}{9}}}\times \sqrt[4]{{\displaystyle \frac{\mathrm{q}}{4}}}\\ <{\displaystyle \frac{\mathrm{q}}{2}}\end{array}$$

(53)

Since the maximum value of $a$ is not greater than $q/2$, the correctness of the subsequent module $p$ is guaranteed.

Specific examples will be provided below for smaller values of $q$ to facilitate better understanding of the algorithm and its validation, as follows: Given $q=541$, we compute $\sqrt{{\displaystyle \frac{q}{4}}}\approx 11.6,\sqrt{{\displaystyle \frac{q}{9}}}\approx 7.8,\sqrt[4]{{\displaystyle \frac{\mathrm{q}}{4}}}\approx 3.4$, rounding each result to one decimal place.

By the definition in Table 3, we find the following:

$$Z_1=\left\{a|a\in Z,3.4<a<11.6\right\}$$

(54)

$$Z_2=\left\{a|a\in Z,-7.8\le a\le 7.8\right\}$$

(55)

$$Z_3=\left\{a|a\in Z,-3.4\le a\le 3.4\right\}$$

(56)

Thus, we have $p\leftarrow Z_1$,$f\leftarrow Z_2$,$g\leftarrow Z_3$,$r\leftarrow Z_3$,$m\leftarrow Z_3$.

(1) $\mathit{K}\mathit{e}\mathit{y}\mathit{G}\mathit{e}\mathit{n}\left(f,g\right)$:

For the large prime $q=541$, the parameter space is chosen such that $p\leftarrow Z_1$,$f\leftarrow Z_2$,$g\leftarrow Z_3$. In this case, we generate $p=5$, $f=6i$, and $g=-i$.

The inverse of $f$ modulo $q$ and modulo $p$ is calculated as follows:

$$f_q^{-1}=90i, f_p^{-1}=4i$$

(57)

This is achieved by using the conjugate property and the Euclidean algorithm.

Next, we compute the public key $h$ as follows:

$$h\equiv f_q^{-1}\times g \left(mod q\right)$$

(58)

Calculating this step by step as follows:

$$h\equiv 90i\times -i \left(mod 541\right)\equiv 90 \left(mod 541\right)$$

(59)

Output public key $pk=90$ and private key $sk=(6i,90i)$.

(2) $\mathit{E}\mathit{n}\mathit{c}\mathit{r}\mathit{y}\mathit{p}\mathit{t}\left(pk,m,p,r\right)$:

We select the pure dummy plaintext $m=3i$ from $Z_3$ and randomly generate $r=2i$ from $Z_3$. We then compute the ciphertext $c$ as described in Formula (40):

Substituting in the values:

$$\begin{array}{l}c\equiv p\times h\times r+m \left(mod q\right)\\ \equiv 5\times 90\times 2i+3i \left(mod 541\right)\\ \equiv 903i \left(mod 541\right)\\ \equiv -179i \left(mod 541\right)\end{array}$$

(60)

Output the ciphertext $c=-179i$.

(3)$\mathit{D}\mathit{e}\mathit{c}\mathit{r}\mathit{y}\mathit{p}\mathit{t}\left(sk,c\right)$:

The first step is to compute the following:

$$\begin{array}{l}a\equiv f\times c \left(mod q\right)\\ \equiv 6i\times \left(-179i\right) \left(mod 541\right)\\ \equiv -1074 \left(mod 541\right)\\ \equiv -8 \left(mod 541\right)\end{array}$$

(61)

Output $a=-8$.

The second step is to compute the following:

$$\begin{array}{l}b\equiv f_p^{-1}\times a \left(mod p\right)\\ \equiv 4i\times \left(-8\right) \left(mod 5\right)\\ \equiv -32i \left(mod 5\right)\\ \equiv 3i \left(mod 5\right)\end{array}$$

(62)

Since the plaintext $m=3i$, we find that $b=m$. Therefore, the decryption is successful.

5.4. Security Analysis

This subsection analyzes the security of the CNTRUs from two main aspects, namely security on the lattice and the semantic security of the CNTRU.

5.4.1. Lattice Analysis

From Section 4.1.1 of this paper, it is evident that the lattice basis matrices for the algorithms of NTRU variants on different algebraic rings differ primarily in the choice of the $\mathit{H}$-matrix. Below is the definition of the CNTRU lattice:

Definition 17

(CNTRU lattice). The CNTRU lattice L(B) is generated by the 2N × 2N dimensional lattice basis matrix B constructed from the public key h of the CNTRU algorithm.

$$\mathit{B}={\left[\begin{array}{cc}\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}& {\mathit{H}}_{N\times N}\\ \begin{array}{cccc}0& 0& \cdots & 0\\ 0& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 0\end{array}& \begin{array}{cccc}q& 0& \cdots & 0\\ 0& q& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & q\end{array}\end{array}\right]}_{2N\times 2N}={\left[\begin{array}{cc}{\mathit{E}}_{N\times N}& {\mathit{H}}_{N\times N}\\ 0_{N\times N}& q{\mathit{E}}_{N\times N}\end{array}\right]}_{2N\times 2N}$$

(63)

where ${\mathit{H}}_{N\times N}$ is the matrix generated by the public key $h$ in the form $\mathit{H}={\left[a_h\right]}_{1\times 1}$, $a_h$ is the integer part of the public key $h$, and $N=1$.

Theorem 4.

The $(\alpha f,g)$, formed by multiplying the private key $f$ by $\alpha$ and concatenating it with $g$, lies on the lattice $\mathcal{L}\left(\mathit{B}\right)$.

Proof of Theorem 4.

The equation $h\equiv f_q^{-1}\times g\left(mod q\right)$ implies that there exists some integer vector u such that $a_f\times a_h=a_g+qu$. Here, $a_f$ is the imaginary part of the private key $f$, and $a_g$ is the imaginary part of $g$. Consider the vector $\left(a_f,-u\right)$. When multiplied by the lattice basis matrix $B$, it yields the following:

$$\begin{array}{l}\left(a_f,-u\right)·\mathit{B}=\left(a_f,-u\right)·\left[\begin{array}{cc}1& a_h\\ 0& q\end{array}\right]\\ =\left(a_f-u0,a_f\times a_h-uq\right)\\ =\left(\alpha ,g\right)\end{array}$$

(64)

Since $(a_f,a_g)$ can be written as a linear combination of the lattice basis matrix $B$ with integer coefficients, it is a vector on the lattice $\mathcal{L}\left(\mathit{B}\right)$. This proves that $(a_f,a_g)$ indeed lies on the lattice $\mathcal{L}\left(\mathit{B}\right)$.

From the Gaussian Heuristic, the expected length of the shortest vector $\overrightarrow{v}$ in the lattice $\mathcal{L}\left(\mathit{B}\right)$ is given by the following:

$${\left|\overrightarrow{v}\right|}_2=\sigma \left(\mathcal{L}\right)=\sqrt{{\displaystyle \frac{n}{2\pi e}}}{det\left(\mathit{B}\right)}^{{\displaystyle \frac{1}{n}}}=\sqrt{{\displaystyle \frac{q}{\pi e}}}$$

(65)

The length of the target vector $(a_f,a_g)$ is given by the following:

$${\left|\left(a_f,a_g\right)\right|}_2=\sqrt{{a_f}^2+{a_g}^2}\le \sqrt{{\displaystyle \frac{q}{9}}+\sqrt{{\displaystyle \frac{q}{4}}}}$$

(66)

The function $f\left(q\right)$) compares the length of the target vector with the Gaussian expectation of the shortest vector:

$$f\left(q\right)={{\left|\left(a_f,a_g\right)\right|}_2}_{\mathit{m}\mathit{a}\mathit{x}}-{\left|\overrightarrow{v}\right|}_2=\sqrt{{\displaystyle \frac{q}{9}}+\sqrt{{\displaystyle \frac{q}{4}}}}-\sqrt{{\displaystyle \frac{q}{\pi e}}}$$

(67)

From the Gaussian Heuristic, the Gaussian expectation of the length of the shortest vector $\overrightarrow{v}$ on the lattice $\mathcal{L}\left(\mathit{B}\right)$ can be obtained as follows:

$${\left|\overrightarrow{v}\right|}_2=\sigma \left(\mathcal{L}\right)=\sqrt{{\displaystyle \frac{n}{2\pi e}}}{det\left(\mathit{B}\right)}^{{\displaystyle \frac{1}{n}}}=\sqrt{{\displaystyle \frac{q}{\pi e}}}$$

(68)

And the length of the target vector $(a_f,a_g)$ is as follows:

$${\left|\left(a_f,a_g\right)\right|}_2=\sqrt{{a_f}^2+{a_g}^2}\le \sqrt{{\displaystyle \frac{q}{9}}+\sqrt{{\displaystyle \frac{q}{4}}}}$$

(69)

The constructor $f\left(q\right)$ is as follows:

$$f\left(q\right)={{\left|\left(a_f,a_g\right)\right|}_2}_{\mathit{m}\mathit{a}\mathit{x}}-{\left|\overrightarrow{v}\right|}_2=\sqrt{{\displaystyle \frac{q}{9}}+\sqrt{{\displaystyle \frac{q}{4}}}}-\sqrt{{\displaystyle \frac{q}{\pi e}}}$$

(70)

The function $f\left(q\right)$ is shown in Figure 1, where $q\in \left[\left.0,+\infty \right)\right.$. It is a convex function with extrema at $(a,b)$ and zeros at $(0,0)$ and $(c,0)$. Here, $a\approx 59.28,b\approx 0.60,c\approx 6971.02$, with values of $a$, $b$, and $c$ retained to two significant decimal places.

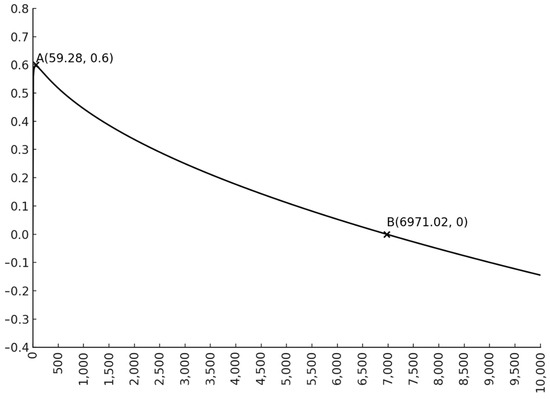
Figure 1. Plot of $f\left(q\right)$ function.

The CNTRU lattice is a discrete integer lattice, and $q$ is a large integer. When $q\in \left(\mathrm{0,6971}\right]$, the target vector length is greater than the Gaussian expectation of the CNTRU lattice, with the difference being approximately 0.596, which makes the target vector length close to the Gaussian expectation of the CNTRU lattice. However, when $q\in (6971,+\mathrm{\infty })$, the target vector length is less than the Gaussian expectation of the CNTRU lattice. Thus, with a high probability, the shortest vector on the CNTRU lattice is the target vector $\left(a_f,a_g\right)$. □

Therefore, breaking the private key of the CNTRU cryptographic algorithm is somewhat equivalent to solving the Shortest Vector Problem (SVP) in the CNTRU lattice. Compared to the CNTRU lattice, which is two-dimensional, the NTRU lattice and matrix NTRU lattice are high-dimensional lattices, providing higher security on the lattice.

5.4.2. Semantic Security Analysis

The security of the CNTRU scheme proposed in this paper relies on the difficulty of the DAGCD problem. The security of the scheme is demonstrated under the assumption that DAGCD is hard.

Theorem 5.

The CNTRU encryption scheme proposed in Section 5.1 of this paper is IND-CPA-secure.

Proof of Theorem 5.

The following proves this theorem by using the game sequence method.

(1)

Game 0. The game is designed as an IND-CPA game between a challenger and an adversary of the CNTRU encryption scheme.

(2)

Game 1. Compared to Game 0, in Game 1, the public key $PK$ generation method no longer generates $h\equiv f_q^{-1}\times g\left(modq\right)$ by the key generation algorithm but randomly and uniformly selects $h\leftarrow R_q\left[Z\right]$. Since $f,g\leftarrow \{-\mathrm{1,0},1\}$ is randomly and uniformly chosen and $f$ to $f_q^{-1}$ is a one-to-one mapping, Game 0 and Game 1 are statistically indistinguishable to the adversary.

(3)

Game 2. Compared to Game 1, in Game 2, only the target ciphertext $C$ is modified. Instead of generating the ciphertext by the encryption algorithm, the challenger chooses $C_1$ randomly and uniformly over $R_q$. From DAGCD, it is difficult to distinguish between $C$ and $C1$. Therefore, Game 1 and Game 2 are indistinguishable to the adversary.

Since the public key and ciphertext provided by the challenger in Game 2 are randomly and uniformly chosen, the adversary has a negligible advantage in Game 2. Consequently, the advantage of an adversary attacking the generalized NTRU scheme in Game 0 is negligible, proving that the CNTRU encryption scheme is IND-CPA-secure. □

5.5. Efficiency Analysis

The algebraic structure of the parameters in the CNTRU algorithm is purely imaginary, ensuring that no complex numbers with nonzero real parts are generated during the algorithm’s operations. The operations in the CNTRU algorithm are as efficient as integer modulo operations, and the computational overhead is measured in terms of bit operations.

The modulo addition operation $a+b(mod q)$ for integers has a time complexity of $2lo{g}_{2}q$, while the modulo multiplication operation $a\times b(mod q)$ has a time complexity of $2lo{g}_2^{2}q$. Inverses of complex numbers can be computed efficiently by conjugation, whereas inverses of purely imaginary numbers are computed similarly to integer inverses, with a time complexity of $lo{g}_{2}q$, by using the Euclidean algorithm. Table 5 summarizes the inverse time complexity for the three algebraic structures.

Table 5. Inverse time complexity.

Operation Type	Time Complexity Level
Inverse of pure imaginary numbers	$lo{g}_{2}q$
Matrix inverse	$O\left(n^{2.373}\right)$
Polynomial inverse	$O\left(N{\mathit{log}}_{2}N\right)$

Regarding the time complexity of the CNTRU encryption algorithm, in the CNTRU algorithm, the encryption operation is defined as $c\equiv p\times r\times \mathrm{h}+m(mod p)$. Ignoring the overhead of randomly selecting $r$, the time complexity of the CNTRU encryption algorithm is determined by the modular multiplication of $p$ with $r$, the modular multiplication with $h$, and the modular addition with the polynomial mmm, which is $2lo{g}_2^{2}q+2lo{g}_2^{2}q+2lo{g}_{2}q$. Therefore, the overall time complexity of the encryption process is $O\left(2lo{g}_2^{2}q\right)$.

Similarly, the time complexity of the CNTRU decryption algorithm is based on the decryption operations $\equiv f\times c(mod q)$ and $b\equiv f_p^{-1}\times a(mod p)$. The time spent on decryption is dominated by the modular multiplications, each with a complexity of $2lo{g}_2^{2}q+2lo{g}_2^{2}q$, leading to an overall decryption time complexity of $O\left(2lo{g}_2^{2}q\right)$.

Given that the length of the encrypted plaintext is ${\log }_{2}p$, encrypting and decrypting 1 bit of plaintext and ciphertext both involve a feature of constant time complexity, making these operations very fast compared to the NTRU and Matrix NTRU algorithms, as illustrated in Table 6.

Table 6. Comparison of encryption and decryption time complexity levels.

Arithmetic	Time Complexity Levels
NTRU	$O\left(n^k\right)$
Matrix NTRU	$O\left(n^k\right)$
CNTRU	$O\left(n\right)$

The CNTRU algorithm offers the significant advantage of a fast key generation process, resulting in higher algorithmic efficiency. When constructing the scheme, the same parameter space control method is employed to avoid decryption failures, similar to those observed in the traditional NTRU algorithm. However, due to the CNTRU lattice being two-dimensional—a low-dimensional lattice—it is less secure compared to other NTRU algorithm variants.

Notably, in the context of the complex ring, if the imaginary parts of all complex numbers are zero, the algorithm behaves identically to an NTRU variant built on an integer ring, making it equivalent to a congruent cipher algorithm. Conversely, if the real parts of the complex numbers are all zero, the algorithm becomes identical to the CNTRU algorithm.

Constructing NTRU variant algorithms on complex rings not only enriches the system of NTRU variant algorithms but also provides lateral verification of the generality of the G-NTRU algorithm.

6. Conclusions

In this paper, we summarize different NTRU algorithms over algebraic rings, integrate NTRU lattices over these rings, and analyze attacks on these lattices. Extending related hard problems facilitates the study of the security of the extended NTRU algorithm. The integer ring AGCD problem is extended to the G-AGCD problem over generalized rings, and the extended G-NTRU algorithm is proved to be semantically secure under the assumption of the hardness of the G-AGCD problem. However, the complexity of the G-AGCD problem requires further study. Additionally, the CNTRU is proposed based on the G-NTRU algorithmic framework, and the generality of the G-NTRU framework is verified.

The NTRU algorithm holds significant practical importance as a generalized post-quantum cryptographic framework. The algebraic ring generalization of the G-NTRU enables it to operate on a wide range of structures, such as rings of integers, rings of complex numbers, and rings of matrices. This flexibility enhances its applicability to diverse security needs and performance requirements. However, a limitation of the G-NTRU is that its complexity varies depending on the chosen algebraic structures and rings, with implementations based on complex structures potentially leading to decreased computational efficiency. Furthermore, the G-NTRU algorithm operating on low-dimensional rings is less secure than its counterparts on high-dimensional rings.

For future research, several directions can be pursued. First, the parameter selection for the G-NTRU can be further optimized to reduce computational complexity and communication overhead, making it more suitable for application scenarios that require high real-time performance. Second, the theoretical analysis of the anti-quantum security of the G-NTRU can be enhanced by investigating the intractability of the G-AGCD problem within various algebraic structures, providing more rigorous complexity proofs. Finally, exploring the applicability of other algebraic rings could generalize the G-NTRU to incorporate novel mathematical structures, leading to more efficient and secure algorithmic implementations.

This paper enriches the research direction of post-quantum cryptography related to the NTRU by proposing the G-NTRU framework, which extends the applicability and security analysis dimensions of NTRU algorithms. The G-NTRU provides a new perspective for developing anti-quantum encryption algorithms and establishes a solid theoretical foundation for academic research on NTRU variants. In the future, the application and further exploration of the G-NTRU will contribute to the realization of secure, reliable, and efficient communication systems in the quantum era.