Abstract
Ensuring stable power system performance is crucial for reliable grid operation. This study assesses various Load Frequency Control (LFC) strategies, including conventional PID, pole placement, Genetic Algorithm (GA)-optimized PID, Particle Swarm Optimization (PSO)-optimized PID, and an Artificial Neural Network (ANN)-based controller, in single and interconnected power grids. The results reveal that GA- and PSO-optimized PID outperform conventional methods, offering minimal overshoot and fast settling times. Pole placement strikes a balance between response time and stability, while the ANN controller demonstrates adaptability and quick rise times but exhibits higher overshoot and longer settling times compared to the optimization techniques. Tie-line bias control aids in frequency stabilization but presents challenges with overshoot and prolonged settling times. Notably, PSO-optimized PID emerges as a promising solution, effectively mitigating overshoot and achieving rapid frequency recovery. This study underscores the importance of tailored control strategies for optimal LFC, which are essential for enhancing power system stability and efficiency. Future research should explore the potential of advanced techniques, such as deep learning and reinforcement learning, to further improve control performance.
1. Introduction
Modern power systems encounter issues owing to changes in energy generation, distribution, and consumption patterns. Renewable energy sources increase variability, necessitating complex load balancing and frequency management. LFC is a critical component of a power system that directly represents the balance between actual power output and demand [1]. The reliability of energy networks depends on the stability and performance of power systems [2]. LFC is a significant issue in electric power system design and operation [3]. In linked power systems, tackling the issues posed by dynamic load changes is critical [4,5]. Stable power system operation requires careful balancing of power generation and demand. However, maintaining this equilibrium is inherently challenging, particularly in the event of sudden and drastic fluctuations in load [6]. Using matrix techniques from multipole system feedback control theory, ref. [7] proposed a thorough approach for designing frequency and tie-line power regulators, as well as performing transient analysis of linked electric power systems. According to recommendations made by the North American Power Systems Interconnection Committee [8], each control area should adjust its frequency bias to match the so-called area frequency response characteristic (AFRC). A number of factors related to the control of generation and power flow on interconnected systems have been analyzed [9]. The turbine’s gate or valve position is automatically modified to lessen the imbalance between the amount of energy generated and consumed. This is achieved through the use of an AGC system [10]. The water or steam input to the turbine is changed to meet current power needs. This approach is known as automatic LFC or AGC [11]. Prime mover control systems are critical for ensuring frequency stability and power regulation within a power system. Under nominal conditions, the complex task of precisely matching produced power to load becomes much more difficult. When human control is no longer possible, the complexity increases, particularly in managing tie-line power and frequency in linked power grids [10,12,13]. These control systems are designed to continually modify the input to prime movers, such as turbines or engines, so that the generated power closely matches the varying power demand. This dynamic process, known as AGC and automatic LFC, is increasingly important in large-scale power grids where stability is critical. In modern power systems, LFC is critical for ensuring the electrical grid’s stability and reliability. LFC employs complex control techniques to dynamically adjust the generating output, guaranteeing synchronization with changing loads while keeping the system frequency within acceptable limits. For this level of precise control, complex controllers such as proportional–integral–derivative (PID) controllers are utilized [14,15,16], in addition to more complex strategies like Model Predictive Control (MPC) [17,18,19] and adaptive control methods. By receiving real-time data on tie-line power variations and system frequency, these controllers enable operators to quickly and precisely alter the generator setpoints.
Recent works on LFC schemes have been reported by many authors [3,20,21]. The method proposed in [22] combines enhanced LFC with controlled energy storage technologies, namely redox flow batteries, to reduce uncertainties associated with renewable energy integration in power grids, thereby ensuring grid stability and reducing interruptions. The authors of [23] proposed a method to increase frequency stability during the high penetration of renewable energy sources by utilizing energy storage devices, such as PEVs, with load frequency regulation. The novel cascaded controller is verified for efficiency using an IEEE 39-bus system and employs fractional-order proportional–integral and fractional-order proportional–derivative terms. A new method for preserving frequency stability in a diverse-source power system was introduced in [24]. It employs a multi-degree-of-freedom FOTID controller and optimized fuel cells, and its performance was compared to that of traditional controllers and grid nonlinearities. In [25], the authors described a frequency management technique that uses virtual inertia control and superconducting magnetic energy storage to increase system stability and inertia in renewable energy sources. A PID controller combined with a Linear Quadratic Gaussian approach was utilized in [26]. The authors of [27] proposed a new method for regulating load frequency by combining wind turbines, high-voltage direct current (HVDC), battery energy storage devices, and conventional synchronous generators (SGs). Their technique increases frequency responsiveness, decreases system inertia, and maintains frequency stability in disturbance-prone environments. In order to investigate resilient load frequency management in multi-area power systems with parameter uncertainties, ref. [28] presented a distributed adaptive protocol for efficiency testing, as well as a distributed RLFC method. The authors of [29] presented an optimized fuzzy adaptive virtual inertia control strategy for small-inertia microgrids using golden jackal optimization. They evaluated its effectiveness and tuned proportional–integral–derivative controllers under irregular load changes and varying RES amalgamation rates. Artificial intelligence (AI) and machine learning (ML) are intelligent technologies that have had a considerable impact on current LFC systems [30,31,32]. The addition of AI and ML to these control systems improves their predictive capabilities, flexibility across a wide range of operating conditions, and control scheme optimization. This integration significantly improves the performance of complex and linked power networks. By utilizing AI and ML algorithms, these systems acquire the ability to forecast and adapt to shifting load patterns and unforeseen events, thereby increasing resilience and responsiveness. The optimization of control systems entails fine-tuning parameters and techniques in real time to ensure efficient and effective power generation and delivery. The evolution of load frequency management exemplifies the continuous advancements in control theory and technology. As a vital aspect, it allows for the smooth integration of renewable energy sources into the power grid while effectively addressing the complex nature of current power networks. The dynamic nature of renewable energy generation needs complex control mechanisms, and the use of AI and ML technologies allows these systems to better manage the instability and unpredictability associated with renewable sources [33,34].
Research Gaps
Previous studies have overlooked the integration of intelligent techniques, such as GAs and PSO, in LFC. Typically, these studies focus solely on isolated power systems and apply a single intelligent technique without extending the analysis to interconnected two-area systems. This research aims to address these gaps by first analyzing the optimal technique for a single-area system and then extending it to a two-area interconnected system. In many cases, conventional control methods are employed without considering the potential benefits of using GAs and PSO for LFC in interconnected grids. By examining the effectiveness of these intelligent optimization techniques in both single and interconnected power systems, this study seeks to enhance the understanding of their applicability and performance in real-world scenarios. The research methodology involves conducting a comprehensive analysis of various LFC strategies, including conventional methods and those optimized using GAs and PSO. This analysis will initially focus on a single-area power system to identify the most effective technique. Subsequently, the identified optimal technique will be extended and evaluated in the context of a two-area interconnected system. By systematically comparing the performance of different control strategies and assessing their suitability for interconnected grids, this study aims to provide valuable insights into the potential advantages of employing intelligent techniques like GAs and PSO in LFC. Ultimately, the findings from this research will contribute to advancing the understanding and application of intelligent control techniques in power system optimization and stability. The present study offers several contributions to the domain of power system optimization and control, particularly focusing on LFC strategies in interconnected grids. The key novelties and contributions of this research can be summarized as follows:
- Integration of Intelligent Techniques: A proactive method is employed to use sophisticated optimization techniques, such as GAs, PSO, and ANNs, to determine the optimal control strategy for single-area power systems. This study goes beyond standard methodologies to investigate the effectiveness of intelligent algorithms in power system optimization.
- Extension to Interconnected Systems: Building on the findings from the optimization of single-area systems, this research expands its investigation to interconnected power grids. By applying the previously determined optimal control approaches to two-area linked systems, this study evaluates their usefulness in preserving grid stability and frequency regulation across interconnected regions.
- Comparative Evaluation of Control Strategies: Through a systematic comparison of multiple control strategies, including conventional PID, pole placement, GA-optimized PID, PSO-optimized PID, and ANN-based control, this study provides valuable insights into their relative performance and suitability for different grid configurations. The comparative evaluation facilitates a thorough understanding of the strengths and limitations of each approach, aiding in the selection of appropriate LFC strategies based on specific system requirements.
- Dynamic System Modeling and Analysis: Rigorous system modeling and dynamic analysis are conducted to elucidate the complex interactions between control parameters, system dynamics, and performance metrics. Utilizing simulation toolboxes of Simulink-MATLAB Release 2022b; this research accurately captures the transient response characteristics of interconnected power grids under varying operating conditions, enabling a detailed examination of control strategy efficacy.
- Optimization-Based Control Design: The application of optimization algorithms, particularly GAs and PSO, for tuning PID parameters represents a departure from traditional heuristic methods and manual tuning approaches. By harnessing the computational power of evolutionary algorithms, this study demonstrates the potential for achieving near-optimal control performance while minimizing manual intervention and tuning expertise requirements.
- Implementation of an ANN for Control Enhancement: The incorporation of an ANN-based controller showcases the potential of machine learning techniques in improving LFC performance. The ANN provides adaptability to changing system dynamics and enhances control accuracy, demonstrating the effectiveness of integrating modern AI methods into traditional control strategies. This contribution highlights the relevance of ANNs in achieving robust and responsive control in complex power systems.
2. Load Frequency Control (LFC)
LFC is an important mechanism in an electrical system that changes tie-line power and frequency in response to changing loads. The fundamental goal is to maintain a balance between generation and demand, providing steady and dependable operation. Because of their efficacy and ease of use, traditional approaches such as proportional–integral (PI) and proportional–integral–derivative (PID) controllers have been frequently used in LFC.
2.1. Proportional–Integral–Derivative (PID) Control
PID control is a well-known and commonly used approach for maintaining power system stability. It offers a simple yet effective method for altering derivative, integral, and proportional terms to regulate system characteristics. The literature on power system stability covers a wide range of approaches used to ensure the stable and dependable functioning of energy networks. Because of their simplicity and effectiveness in directing system behavior, PID control methods have been widely adopted. The expression for a standard PID controller can be represented as follows:
where is the control signal, is the error signal, and , , and are the proportional, integral, and derivative gains, respectively.
2.2. Genetic Algorithm (GA)
The optimization of power system controller parameters using the GA is inspired by the principles of natural selection. One possible solution may be a chromosome C with genes that encode specific characteristics. Initializing a population P, assessing fitness , and choosing parents for crossover are the first steps in the procedure. Recombining the genes of the parents results in offspring, which introduces mutations for diversity. The next generation is chosen from survivors based on their fitness levels, and this process is repeated until the termination criteria are satisfied. This methodically adjusts settings for optimal power system performance.
2.3. Pole Placement Technique
A classical control approach called pole placement involves locating the closed-loop system poles in order to attain the desired performance and stability characteristics. Control in the pole placement scheme is accomplished by using feedback from the state variables via a constant gain regulator. Consider a control system represented in state-variable form:
Here, K is a vector representing the constant feedback gains. The compensated system’s state-variable representation is given by
The characteristic equation of the compensated system is expressed as
where s is the complex variable, I is the identity matrix, A is the system matrix, B is the input matrix, and K is the feedback gain matrix. This equation is pivotal for determining the closed-loop poles of the system. The matrix K is strategically designed to influence the locations of these poles, thereby shaping the stability and dynamic behavior of the system.
2.4. Interconnected Power Grid Frequency Stabilization
To maintain grid frequency, connected power grid frequency stabilization involves balancing generation and load across several linked areas. In contemporary electrical power systems, this balance is essential for reliability and system stability. Systems that effectively stabilize frequencies decrease deviations caused by oscillations, fluctuations, or sudden changes in the system’s conditions. Interconnected grid frequency control employs a variety of control strategies and methodologies, including Automatic Generation Control (AGC) [35,36], LFC [37,38], and tie-line bias control [39,40,41]. These control techniques aim to continuously adjust the generating outputs of power plants in response to variations in load demand, generation capacity, and disturbances to maintain the system frequency near its nominal value. Tie-line bias control is a method for minimizing tie-line power imbalances and improving load sharing in power systems. However, it faces several challenges, including sensitivity to parameter tuning, lack of adaptability, potential for overcorrection, limited robustness to uncertainties, and complexity of implementation. Improper tuning can lead to oscillations, instability, and suboptimal control performance. Fixed bias signals may not always provide optimal control under varying conditions or disturbances. Researchers and engineers are exploring advanced control techniques to address these challenges and enhance the performance of tie-line bias control methods. PSO is a flexible and powerful approach to tie-line bias control in interconnected power systems. It is adaptive, self-tuning, and can adapt to changes in system dynamics and load demand. PSO operates by iteratively searching the solution space to find the optimal solution, avoiding local optima and providing robustness to uncertainties. Its distributed nature makes it suitable for decentralized control in large-scale systems. PSO can be implemented in real time, ensuring optimal control performance. It can be integrated with advanced control strategies to enhance performance. Overall, PSO offers a promising solution for optimizing complex and dynamic power systems.
2.5. Particle Swarm Optimization (PSO)
A metaheuristic optimization technique called PSO is motivated by natural swarming patterns. It is renowned for being flexible, effective, and simple to use for tackling challenging issues [42,43]. PSO entails particles moving through a multi-dimensional search space, changing their positions according to both personal and group experiences. Applications in machine learning, engineering, and finance demonstrate its versatility and efficiency in optimizing intricate systems.
The PSO optimization method, as outlined in [44], is described as follows:
- 1.
- Particle Position Update: The position of each particle is updated based on its current position, velocity, personal best position, and the global best position
- 2.
- Velocity Update: The velocity of each particle is updated based on its current velocity, personal best position, and the global best position is given below:
- 3.
- Objective Function Evaluation: The objective function value for each particle is evaluated using the current position of swarm as follows:
- 4.
- Personal Best Update: If the objective function value at the current position is better than the personal best, the personal best position and value are updated as given below:
- 5.
- Global Best Update: If the personal best of a particle is better than the global best, the global best position and value are updated:
- 6.
- Inertia Weight Update: The inertia weight w is often updated during the optimization process. A common approach is to linearly decrease the inertia weight over iterations:
2.6. Artificial Neural Networks (ANNs) in Control Systems
ANNs are ML-based controllers that offer adaptability, generalization, and real-time control capabilities [30,31,32]. They can learn from input-output pairs and generalize their knowledge to unseen data, making them suitable for applications like LFC. ANNs can perform real-time control with low latency, allowing for fast and responsive control actions. However, challenges include the need for large amounts of training data, the potential for overfitting, a lack of interpretability of learned control policies, and computational complexity. Integrating ANNs into LFC systems requires careful consideration of the ANN’s architecture, training algorithm, and validation procedures. The trained ANN is integrated into the system, continuously monitoring and adjusting control actions to maintain desired performance. Regular monitoring and optimization ensure optimal performance over time.
3. Methodology
The methodology begins by selecting an isolated power system, which is modeled using Simulink. In the initial phase, a simple power system is utilized, introducing a sudden load to observe the ensuing frequency deviation. Subsequently, the conventional PID controller is implemented to assess its performance in mitigating frequency deviations. The Integral of Time-weighted Absolute Error (ITAE) is employed as a fitness function for PID, and the obtained data are sent to the Workspace. The optimization of PID parameters is then conducted using the GA through the optimtool in MATLAB.
For further optimization exploration, the methodology is extended to include PSO. Similar to the GA approach, the PSO algorithm adjusts PID parameters to minimize the ITAE. The optimization process is executed within the MATLAB/Simulink environment, and the results are compared with those of the GA-optimized PID and conventional PID controllers.
Additionally, for a comprehensive comparative analysis, a pole placement design is also examined. This holistic approach enables the systematic evaluation of the considered control strategies in addressing frequency deviations and enhancing power system stability.
After identifying the optimal intelligent technique for a single-area system, the model is extended to a two-area system with interconnected power grid frequency stabilization. While the frequency deviations and tie-line power changes have different units (Hz and pu MW, respectively), their combined effect on the ITAE index has been widely used in similar studies to evaluate the dynamic performance of control strategies. The relative magnitudes of these deviations are small, and the practical impact of summing them without normalization is minimal. Thus, in this study, the original ITAE formulation is employed to assess control strategy performance, as the unit differences do not significantly affect the overall system comparison.
3.1. System Modeling
To understand the dynamic behavior of power systems and create efficient control strategies, accurate modeling of the system is essential. We provide a thorough summary of the parameters related to the isolated power plant examined in this section.
The parameters for the isolated power station utilized in this study were sourced from Haadi Sadaat’s work [45]. The specific parameters include the turbine time constant (), governor time constant (), generator inertia constant (H), and governor speed regulation (R), among others.
The collected data serve as the foundation for our simulation and analysis. The parameters of the isolated power station are summarized in Table 1 and the parameters of interconnected two-area power system is presented in Table 2.

Table 1.
Isolated power station parameters.

Table 2.
Parameters for interconnected two-area power system.
The dynamic behavior of the isolated power station is a key aspect of our study. The turbine time constant (), governor time constant (), and generator inertia constant (H) play crucial roles in determining the response of the power system to sudden load changes.
The complete open-loop and closed-loop transfer functions are derived by combining the transfer functions of the generator, load, prime mover, and governor:
The study of these transfer functions provides valuable insights into the dynamic characteristics of power systems, aiding in the analysis and design of control strategies.
3.2. Power System Description
In this study, two distinct types of power systems were considered: a single-area hydropower system and a single-area thermal power system, as well as their interconnected configuration. and their description are as follow:
- Single-Area Hydropower System: This system consists of a hydroelectric generator that produces electricity using water flow. It features a governor control mechanism that regulates the generator’s output to maintain frequency stability. The dynamics of the hydropower system are influenced by factors such as water reservoir levels, flow rates, and turbine characteristics.
- Single-Area Thermal Power System: This system is based on a thermal generator that converts thermal energy from burning fossil fuels into electricity. It includes a steam turbine, boiler, and control mechanisms to regulate output power and ensure frequency stability. The thermal system’s dynamics are affected by fuel supply, thermal inertia, and heat exchange processes.
- Interconnected Two-Area System: The interconnected system combines the hydropower and thermal power systems, allowing for power exchange between them. This configuration enhances overall system stability and reliability by leveraging the strengths of both generation types. Coordinating the hydropower and thermal power systems is crucial for maintaining frequency regulation and stability across the interconnected grid. These descriptions provide a comprehensive understanding of the structures and dynamics of the power systems utilized in this study.
3.3. Formulation of the State Equations
A collection of state equations serves as a mathematical representation of the power system’s dynamic behavior. These equations express the relationship between the system’s inputs and state variables. In our case, the state variables include the changes in generator power (), mechanical power (), and system frequency ().
Transforming into the time domain and expressing in matrix form, the state equations become:
These equations describe the relationship between changes in generator power, mechanical power, and system frequency in response to load changes and reference power adjustments.
3.4. Case 1: Without Any Controller
In this scenario, the isolated power system is subjected to sudden load changes without any controlling mechanism. Simulink model as shown in Figure 1 is employed to model the power system, and the ensuing frequency deviations are observed.
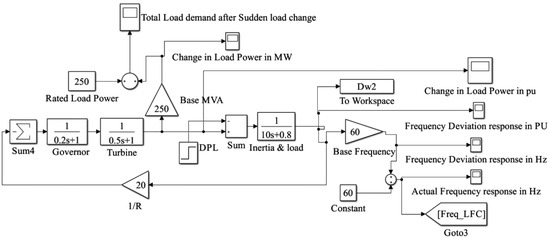
Figure 1.
Simulink- model: LFC system illustration without PID controller.
3.5. Case 2: With Conventional PID Controller
A conventional PID controller is introduced to the power system to assess its performance in mitigating frequency deviations. Simulink is again utilized to model the controlled system as depicted in Figure 2, and the impact on the frequency response is analyzed.
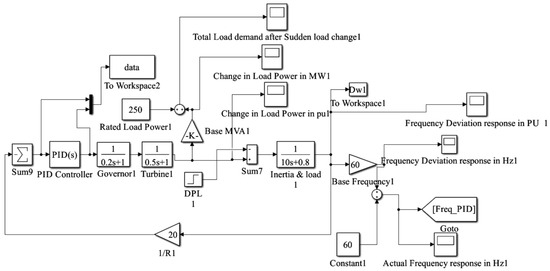
Figure 2.
Simulink-model: LFC system with conventional PID controller.
3.6. Case 3: GA-Optimized PID
The power system is simulated in Simulink, and a GA optimizes PID parameters using the Integral of Time-weighted Absolute Error (ITAE) as the fitness function. The flowchart is presented in Figure 3, outlines the systematic implementation of LFC using the GA-optimized PID controller. The GA refines PID parameters through iterative generations, optimizing , , and to minimize the cost function J. The effectiveness of the GA-optimized PID controller in enhancing power system stability is evaluated through simulations, comparing its performance with that of the conventional PID and pole placement strategies. Its implementation in Simulink is shown in Figure 4.
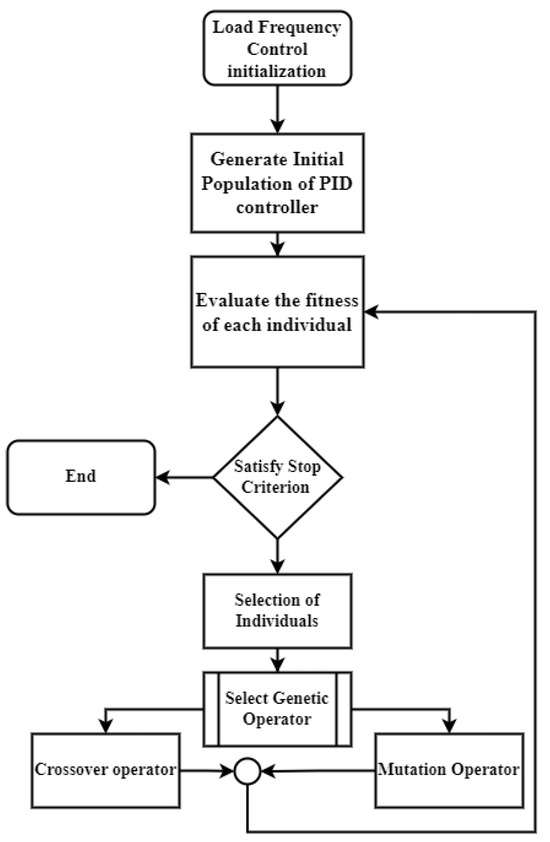
Figure 3.
Flowchart depicting the GA optimization process. The diagram illustrates the systematic implementation of the GA in tuning PID parameters for LFC in power systems.
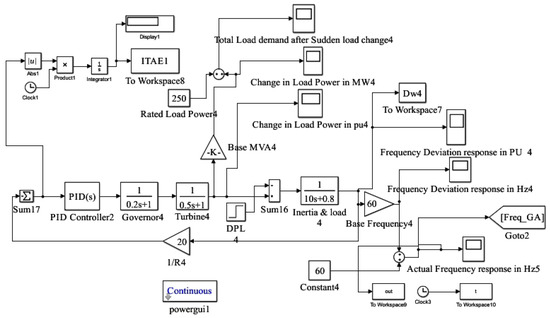
Figure 4.
Simulink-model: LFC system featuring GA-optimized PID controller.
3.7. Case 4: With Pole Placement Design
For comparative analysis, a pole placement design is implemented in the power system. Simulink is used to model the system as shown in Figure 5, and the effects of pole placement on the frequency response are studied. We demonstrate the use of the pole placement design by applying it to the LFC of an isolated power system, which was previously considered with conventional PID and GA-optimized PID controllers.
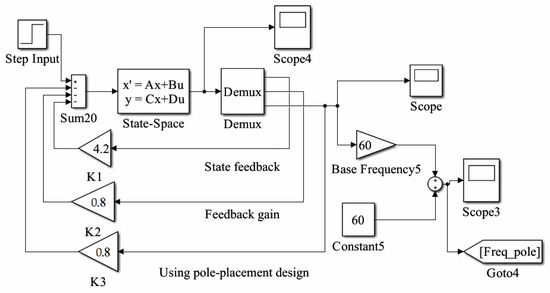
Figure 5.
Simulink-model: LFC system employing pole placement technique.
Algorithm 1 designs a state feedback controller using pole placement and Ackermann’s formula for the system matrices A, B, and C, and desired poles P. It checks controllability, computes the state feedback gain vector K, and derives the closed-loop system matrix . The systematic procedure achieves the desired closed-loop poles, influencing transient response and stability. The impact on power system stability is evaluated through simulations, comparing its performance with that of other control strategies.
| Algorithm 1: Pole placement using Ackermann’s formula |
 |
3.8. Case 5: PSO-Optimized PID
For PSO, the Simulink model is designed to optimize PID parameters similarly to the GA case. The PSO algorithm is tabulated in Algorithm 2 is employed to iteratively adjust , , and to minimize the ITAE. The PSO flowchart in Figure 6 illustrates the systematic approach. The algorithm initializes a swarm of particles, and their positions are updated iteratively based on their individual and global best positions. The PSO algorithm converges toward the optimal PID parameters, enabling precise control and improved power system stability. The comparative analysis includes the GA- and PSO-optimized PID controllers, providing insights into the efficacy of evolutionary algorithms for LFC.
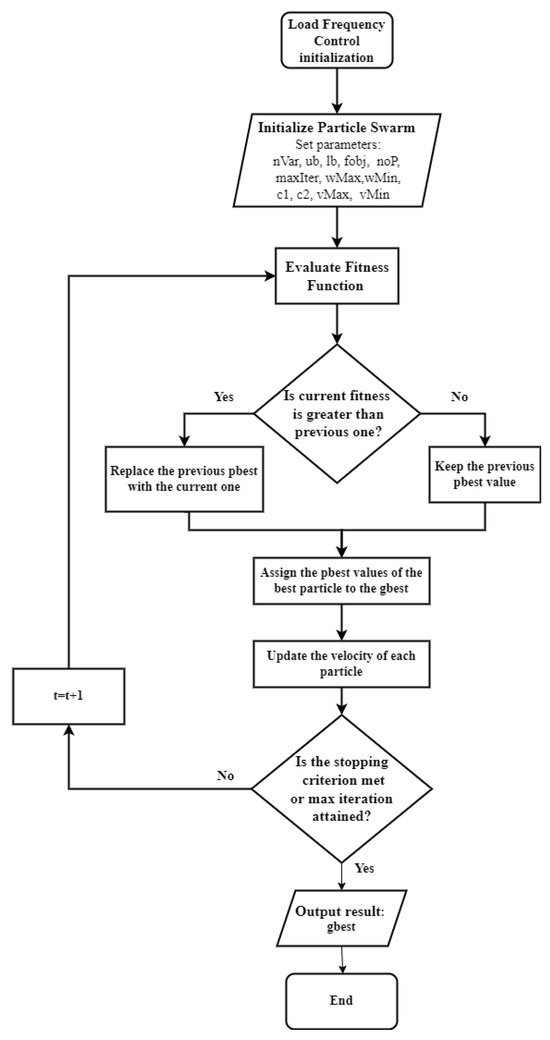
Figure 6.
Flowchart illustrating the PSO algorithm. The diagram depicts the systematic implementation of PSO in optimizing PID parameters for LFC in power systems.
| Algorithm 2: Particle Swarm Optimization (PSO) | |
| 1: | Initialize parameters and particles |
| 2: | for t = 1 to maxIter do |
| 3: | for k = 1 to noP do |
| 4: | Evaluate Swarm.Particles(k).O = fobj(Swarm.Particles(k).X) |
| 5: | if Swarm.Particles(k).O < Swarm.Particles(k).PBEST.O then |
| 6: | Update personal best |
| 7: | end if |
| 8: | if Swarm.Particles(k).O < Swarm.GBEST.O then |
| 9: | Update global best |
| 10: | end if |
| 11: | end for |
| 12: | for k = 1 to noP do |
| 13: | Update velocities and positions using PSO equations |
| 14: | end for |
| 15: | Display ‘Iteration# t Swarm.GBEST.O = Swarm.GBEST.O’ |
| 16: | Store cgCurve(t) = Swarm.GBEST.O |
| 17: | end for |
3.9. Algorithm Parameters
The parameters for each algorithm such as GA and PSO were selected based on preliminary tests as tabulated in Table 3 and established practices in the literature to ensure optimal performance.

Table 3.
Parameters for GA and PSO.
These parameters were optimized to enhance the performance of the control strategies implemented in the LFC system, facilitating effective and efficient optimization.
3.10. Case 6: Artificial Neural Network (ANN) Implementation
The methodology for implementing ANN-based control in an LFC system involves several key steps, as depicted in Algorithm 3.
| Algorithm 3: Transition from PID control to Artificial Neural Network control |
 |
Algorithm 3 outlines a systematic approach to transitioning from a proportional–integral (PID) controller to an ANN controller in an LFC system. The ANN-based control for the LFC system was implemented following these steps:
3.10.1. Data Acquisition
Input and output data were collected from closed-loop PID controller simulations in MATLAB Simulink. The dataset was split into 70% for training and 30% for validation.
3.10.2. Network Architecture
The ANN featured two hidden layers with 3 and 50 neurons, respectively. The transfer functions used were logsig, tansig, and purelin, with the Levenberg–Marquardt algorithm for training.
3.10.3. Training Configuration
The network was configured with the acquired data, trained for up to 10,000 epochs, and aimed for a mean squared error (MSE) of .
3.10.4. Evaluation
Post-training, the ANN’s performance was assessed by predicting outputs and calculating the MSE and root mean square error (RMSE). The ANN demonstrated robust performance with low MSE and RMSE values, highlighting its effectiveness in enhancing the buck converter’s control performance.
3.11. Interconnected Power Grid Frequency Stabilization
The Simulink model of a single-area power system is extended to a two-area power system to validate the optimal technique identified in the single-area system. Table 2 shows the parameters for two-area systems taken from [45]. A two-area system is connected by a tie line with a 1000 MVA common base, as shown in Figure 7. The parallel operation of the two power plants occurs at the nominal frequency of 60 Hz. Suddenly, there is an 187.5 MW load increase in Area 1, as a result of which the system frequency will fluctuate, and power plants must boost their capacity to keep up with the growing demand. The new steady-state frequency and the changing tie-line flow must be ascertained in this case.
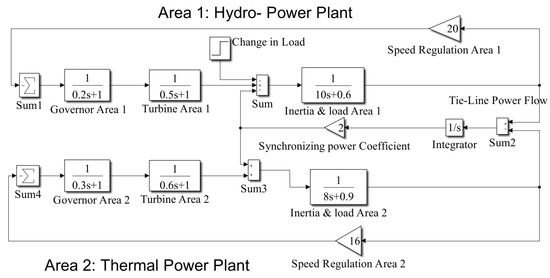
Figure 7.
Simulink-model of a conventional two-area power system.
Tie-Line Bias Control Heading
Tie-line bias control aims to reduce the area control error (ACE) to zero, where the ACE is given by
The simulink-model of ie-Line Bias Control heading is depicted in Figure 8.
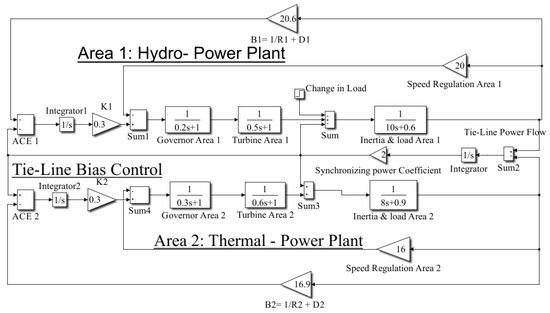
Figure 8.
Simulink-model of a two-area power system with tie-line bias control.
The area bias determines the amount of interaction during a disturbance in the neighboring areas. Overall satisfactory performance is achieved when is selected equal to the frequency bias factor of that area, given by
3.12. Computational Complexity Analysis
The computational complexity of the optimization algorithms used in this study—GA and PSO—was analyzed based on the population size, number of iterations (or generations), and the computational cost of the fitness function evaluation.
For the GA, the overall computational complexity is given by [46]
where G is the number of generations, P is the population size, and is the complexity of evaluating the fitness function.
In our simulations, we used a population size of and ran the algorithm for generations. The fitness function involved computing the system’s frequency deviation and tie-line power response, which required solving the system model with a complexity of , where n represents the number of state variables. With a fitness evaluation complexity of , the overall computational complexity for the GA in our simulations was
For PSO, the computational complexity is given by
where I is the number of iterations, P is the number of particles, and is the fitness evaluation complexity.
In the PSO simulations, we used particles and ran the algorithm for iterations. The fitness evaluation involved the same model complexity , leading to an overall computational complexity for PSO of
Execution Time and Practical Considerations
In terms of execution time, the GA took more than 5 h to complete 100 generations with a population size of 50, while PSO completed the optimization in 4 h with 150 iterations and 40 particles. Both algorithms were executed in MATLAB/Simulink on a system with an Intel Core i7 processor and 16 GB of RAM. The time-consuming nature of the fitness function evaluations (which involved solving the power system model) significantly contributed to the overall execution time.
Despite the slightly higher computational complexity of PSO, it demonstrated faster optimization performance compared to the GA in terms of overall execution time. Both algorithms remain feasible for optimization tasks in power systems, although PSO provides a computational advantage in this particular application.
4. Results and Discussion
The frequency response of the system without any controller, as shown in Figure 9, exhibited a moderate response but had a longer settling time of 6.92 s. The overshoot of 0.9709% indicates a slight oscillation or overcompensation before reaching the final value. The rise time of 0.4143 s suggests a moderate speed of response.
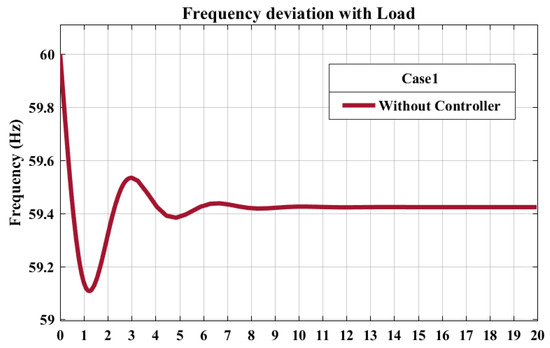
Figure 9.
Frequency response of the power system without a controller. The plot illustrates the system’s behavior in response to sudden load changes, highlighting the impact of the absence of a controller on frequency deviations.
The response of the conventional PID controller, as shown in Figure 10, demonstrated an incredibly fast rise time of s, indicating a rapid response to changes. The settling time of 4.6951 s was relatively fast, showcasing the effectiveness of the PID control strategy. The minimal overshoot of 0.0016% suggests excellent control with almost no oscillation.
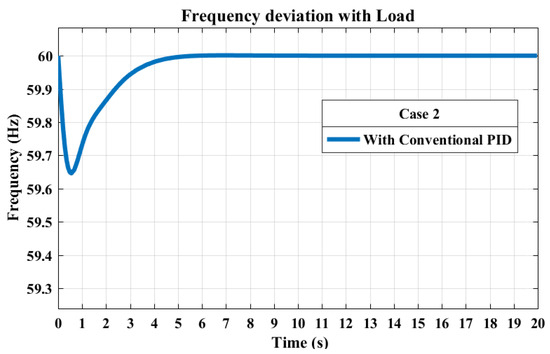
Figure 10.
Frequency response with conventional PID controller, showcasing effective mitigation of frequency deviations in response to sudden load changes.
The frequency response of the system with pole placement, as shown in Figure 11, exhibited a moderate rise time of 0.0725 s, indicating a reasonably fast response. The settling time of 2.1093 s was faster than the system without any controller but slower than the conventional PID case. The overshoot of 0.1669% suggests a controlled oscillation before reaching the final value.
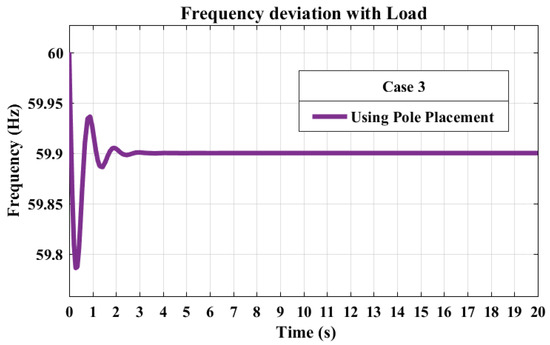
Figure 11.
Frequency response with pole placement.
The GA-optimized PID controller, as shown in Figure 12, demonstrated an exceptionally fast rise time of s, indicating an almost instantaneous response to changes. The settling time of 1.3561 s was very fast, showcasing the efficiency of the optimization process. The extremely low overshoot of % indicates highly precise control with almost no oscillation.
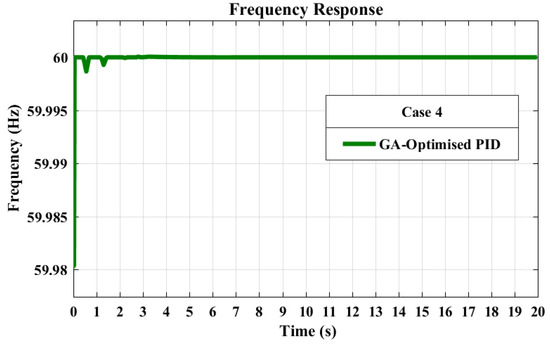
Figure 12.
Frequency response with GA-optimized PID controller. The plot illustrates the system’s behavior in response to sudden load changes, showcasing the effectiveness of GA optimization in minimizing frequency deviations.
The PSO-optimized PID controller, as depicted in Figure 13, exhibited commendable performance characteristics. The rise time of s suggests a rapid response to changes, showcasing the effectiveness of the PSO algorithm in refining PID parameters. The settling time of 1.5093 s was relatively fast, indicating efficient control. With a minimal overshoot of %, the PSO-optimized PID controller demonstrated precise control with negligible oscillation. This analysis underscores the efficacy of the PSO optimization approach in achieving stability and precision in LFC systems.
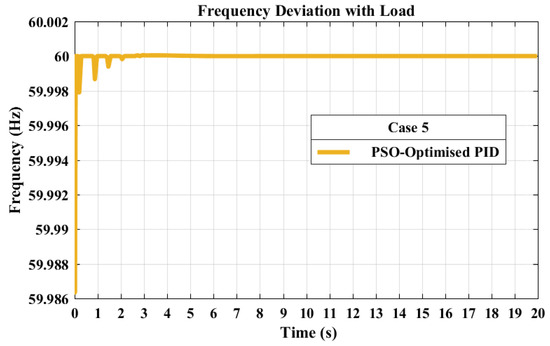
Figure 13.
Frequency response with PSO-optimized PID controller. The plot illustrates the system’s response to sudden load changes, demonstrating the efficacy of PSO optimization in minimizing frequency deviations.
Figure 14 shows the ANN-based controller’s response to disturbances in the LFC system. Its rapid rise time and longer settling time indicate stability, but its higher overshoot suggests potential for improvement. Despite this, the ANN controller maintained a steady response, demonstrating its potential for improvement.
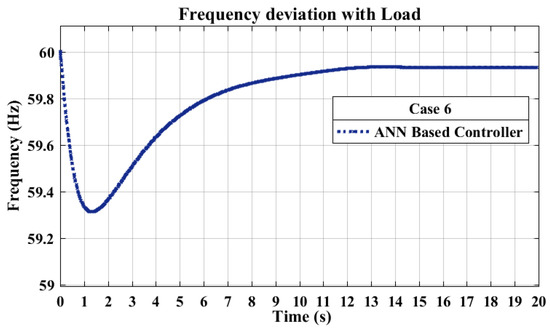
Figure 14.
Frequency response with ANN controller.
Figure 15 presents a comprehensive comparison of the actual frequency responses for all considered cases. The GA-optimized PID controller, as shown in Figure 12, stands out with an exceptionally fast rise time of s, a rapid settling time of 1.3561 s, and an extremely low overshoot of %. This indicates highly precise control with almost no oscillation, making it a robust choice for LFC. Similarly, the PSO-optimized PID controller, as depicted in Figure 11, exhibits commendable performance with a rapid rise time of s, a fast settling time of 1.5093 s, and a minimal overshoot of %. Overall, both optimization techniques showcase their effectiveness in enhancing stability and performance in the considered system, with the choice between them depending on the specific application requirements.
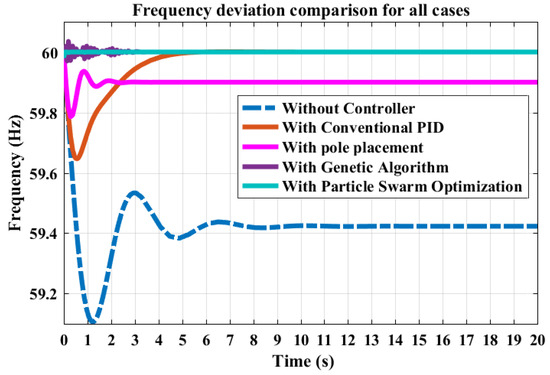
Figure 15.
Comparison of actual frequency deviations across all cases. The plot provides an overview of frequency deviations in different control scenarios, highlighting performance variations among systems with different control strategies.
Overall, Case 1, operating without a controller, achieved moderate performance with a moderate response time. Case 2, employing a conventional PID controller, stood out with an extremely fast response time and a minimal overshoot, making it suitable for applications that require rapid and precise control. Case 3, utilizing pole placement, achieved balanced performance with a moderate response time, settling time, and controlled oscillations, making it ideal for scenarios that require a compromise between speed and stability. In Case 4, the GA-optimized PID controller demonstrated exceptional characteristics, making it suitable for applications that demand both precision and speed. Additionally, Case 5, with the PSO-optimized PID controller, showcased competitive performance with a swift response time, a tight settling time, and precise frequency control.
Case 6, incorporating the ANN-based controller, offered a fast rise time and adaptability, making it suitable for dynamic environments. However, it exhibited a longer settling time and higher overshoot compared to the GA- and PSO-optimized PID controllers, indicating that while the ANN adapts well to system changes, there are trade-offs in terms of precision and stabilization speed. The ANN controller shows potential for further optimization in more complex or real-time control scenarios, where its ability to learn and adjust to system disturbances provides an advantage. The optimal choice among these control strategies depends on the specific application requirements and system characteristics, with the GA and PSO excelling in precision and speed, while the ANN-based controller offers adaptability and robustness in dynamic environments. Table 4 shows that conventional PID, pole placement, GA-optimized PID, PSO-optimized PID, and the ANN-based controller are all optimization techniques with strengths and weaknesses. Conventional PID has a fast response time and minimal overshoot, while pole placement balances rise and settling times. The GA optimizes PID with an exceptional response time, negligible overshoot, and a settling time of 1.3561 s. PSO optimizes PID with a fast response time, precise control, and a settling time of 1.5093 s.

Table 4.
Response time parameters for LFC cases.
4.1. Interconnected Power Grid Frequency Stabilization Results
When the sudden load was increased in Area 1, a frequency deviation of −0.3 Hz occurred in Area 1 as shown in Figure 16a and a similar deviation occurred in Area 2 as shown in Figure 16b. The resulting frequencies in both areas after the sudden load are shown in Figure 16c for Area 1 and, Figure 16d for Area 2. It can be seen that the frequencies in both areas were reduced to 59.7 Hz.
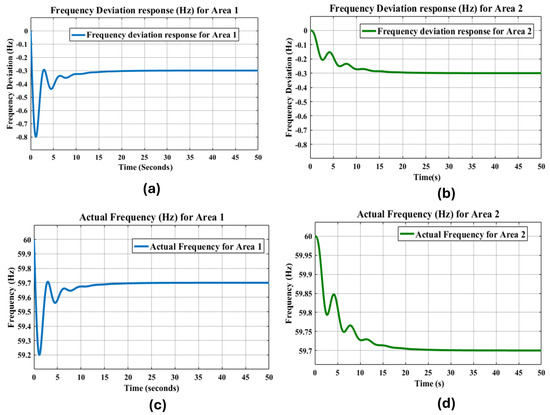
Figure 16.
Frequency-deviation and resulting frequencies after sudden load increase in Area 1 and Area 2, causing a frequency deviation of −0.3 Hz and a resulting frequency of 59.7 Hz in both areas.
For the 187.5 MW increase in load in Area 1, the power plant in Area 1 should enhance its generation to meet the increased demand. Figure 17a shows that 100 MW of power was increased in Area 1 to meet the increased load demand. Figure 17b shows that 80 MW of power was also increased in Area 2 to meet the increased load demand.
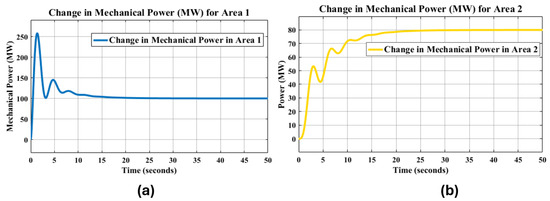
Figure 17.
Power generation adjustment in Area 1 and Area 2 to meet increased load demand.
Figure 18 shows that for the increased load in Area 1, 84.5 MW of power from Area 2 to Area 1 flowed through the tie line. A crucial point to note is that, although the load in Area 1 increased, the power in both generators increased to accommodate the higher load demand. This is not true in practice. Any location that experiences a sudden shift in demand must either adapt on its own or rely solely on its generator to supply power. This implies that, in the event of a load shift of 187.5 MW in Area 1, the mechanical power change in Area 1 should be raised to 187.5 MW, while the mechanical power change in Area 2 must stay at zero. Moreover, there should be no change in the tie-line power flow. Also, the system frequency reached 59.7 Hz and did not return to 60 Hz. Because of this, only 180 MW of demand was delivered by both generators despite the 187.5 MW increase in load, and it was still short of 7.5 MW. Both generators will be able to deliver the entire 187.5 MW once the frequency recovers to 60 Hz.
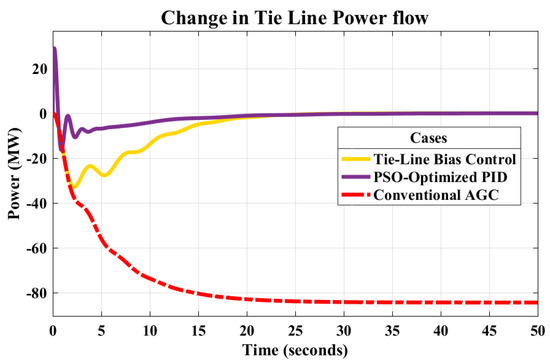
Figure 18.
Change in tie−line power flow from Area 1 to Area 2 when sudden load is added to the system.
To resolve these problems, tie-line bias control was utilized, where each area aimed to reduce the area control error (ACE) to zero. Table 2 presents the values of B1 and B2. The values of K1 and K2 were chosen using the hit-and-trial method. For this purpose, we needed to change the values again and again until we obtained a satisfactory response.
The simulation results for tie-line bias control show that we successfully achieved a frequency deviation of 0 Hz in both Area 1 and Area 2, as shown in Figure 19a,b. Also, the actual frequency was recovered from 59.7 Hz to 60 Hz in Area 1 and Area 2, as shown in Figure 20a,b.
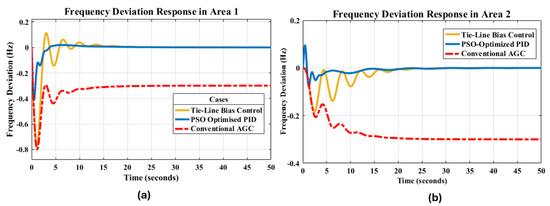
Figure 19.
Comparison of frequency deviation responses for Area 1 and Area 2 across all cases.
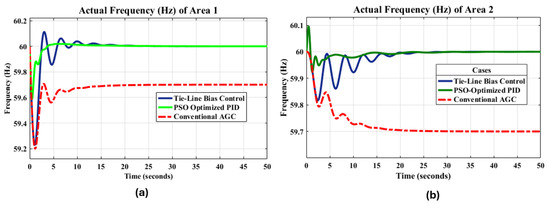
Figure 20.
Comparison of actual frequency responses for Area 1 and Area 2 across all cases.
When the frequency was recovered to 60 Hz, it meant that the generation was equal to the load demand; therefore, the change in the tie-line power flow also became zero, as shown in Figure 18. Additionally, Area 1 supplied the entire demand of 187.5 MW itself, as depicted in Figure 21a. Consequently, the power supplied from Area 2 should be zero, as evident in Figure 21b.
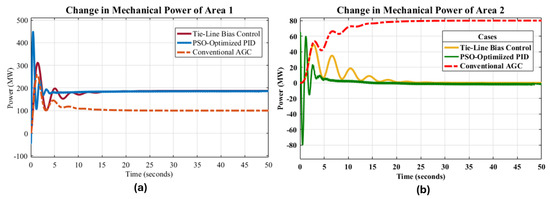
Figure 21.
Comparison of changes in mechanical power of Area 1 to Area 2 across all cases.
However, despite achieving the desired frequency of 60 Hz for both areas and controlling generation, the system still exhibited significant overshoot, undershoot, and a long settling time. To address these issues, PSO-optimized PID control was employed in this model. The PSO-optimized PID control aimed to reduce overshoot, undershoot, and settling time, thereby facilitating rapid frequency recovery. The comparative analyses in Figure 18 and Figure 21 demonstrate that PSO-optimized PID exhibited superior performance compared to tie-line bias control.
4.2. Comparison of Optimization Performance
In this study, both the Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) were employed to optimize the Load Frequency Control (LFC) system. While both algorithms achieved satisfactory control performance, a notable difference was observed in their computational performance, particularly in terms of execution time and optimization speed, as tabulated in Table 5.

Table 5.
Comparison of execution times for GA and PSO.
4.2.1. Execution Time and Convergence
The GA took more than 5 h to complete the optimization process, running for 100 generations with a population size of 50. In contrast, the PSO completed its optimization in 4 h, with 150 iterations and a particle swarm size of 40. These differences can be attributed to the computational efficiency of PSO, which converged more quickly despite having slightly higher computational complexity.
4.2.2. Impact on Optimization and Control Performance
Both algorithms demonstrated effective optimization of the LFC system, with improvements in system frequency deviation and tie-line power control. However, the faster execution time of PSO provides a practical advantage, particularly in real-time or large-scale power systems, where timely optimization is crucial. The trade-off between convergence speed and computational complexity was evident, with PSO offering a more efficient solution for this application.
Despite the slightly higher computational complexity (as discussed in the methodology), PSO’s ability to converge more rapidly without compromising control performance made it a more computationally efficient algorithm for this specific LFC task.
5. Stability Analysis Using Bode Plots
The stability of the control strategies—conventional PID, GA-optimized PID, and PSO-optimized PID—was evaluated using Bode plots. The key stability metrics, including gain margin, phase margin, and crossover frequency, are summarized in Table 6.

Table 6.
Comparison of stability metrics.
Figure 22 presents the Bode plots for each control strategy, illustrating their frequency responses and confirming their stability. The differences in crossover frequencies highlight the varying response times of the controllers.
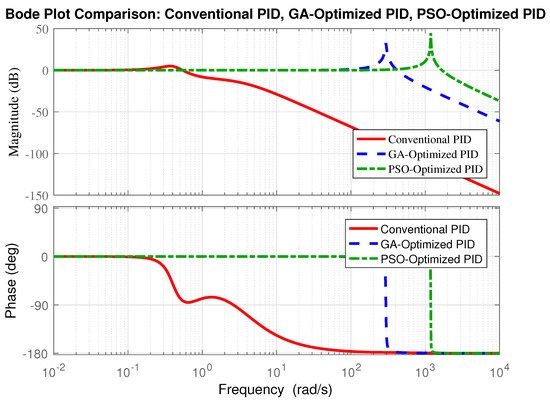
Figure 22.
Bode-plots of the conventional PID, GA-optimized PID, and PSO-optimized PID controllers, illustrating their magnitude and phase responses along with their stability characteristics.
All controllers exhibited positive phase margins, indicating that they are stable systems. The higher crossover frequencies of the GA-optimized (417.76 rad/s) and PSO-optimized PID (1678.59 rad/s) controllers suggest that they can respond more rapidly to disturbances compared to the conventional PID controller (0.54 rad/s). In conclusion, the stability analysis confirms that all control strategies are effective for LFC systems.
6. Conclusions
This study has explored LFC systems, which are essential for maintaining stable and optimal performance in interconnected power grids. Through extensive simulations and analyses, five distinct control strategies were evaluated: conventional PID, pole placement, GA-optimized PID, PSO-optimized PID, and an ANN-based controller. Each control strategy was rigorously assessed based on key metrics, including response time, settling time, overshoot, and precision in frequency control. The findings indicate that while conventional PID provides a rapid response with minimal overshoot, it lacks the adaptability needed for dynamic system changes. GA-optimized PID and PSO-optimized PID demonstrated exceptional performance with negligible overshoot and fast settling times, making them ideal for applications that require both precision and stability. Pole placement offered a balanced solution, maintaining a compromise between speed and stability, suitable for scenarios where such a trade-off is desired. The introduction of the ANN-based controller in this study highlighted its ability to provide a fast response and adapt to varying system conditions, which is advantageous in dynamic environments. However, the ANN controller exhibited a higher overshoot and longer settling time compared to the GA- and PSO-optimized controllers, indicating that while it is adept at handling system nonlinearities, it requires further refinement to improve its precision and stabilization performance. Despite these limitations, the ANN controller’s adaptability suggests it holds promise for real-time control applications where system conditions are unpredictable. Additionally, tie-line bias control was explored for frequency stabilization in interconnected grids, successfully demonstrating frequency recovery, although some issues with overshoot and prolonged settling times persisted. This study makes significant contributions to the field of power system control and optimization, highlighting the importance of selecting tailored control solutions and optimization techniques to address the specific challenges posed by LFC systems. Ultimately, the findings provide valuable guidance for choosing optimal control strategies to enhance the stability and efficiency of power systems. Future studies could focus on examining the robustness of these control strategies under various disturbance scenarios and system uncertainties to improve their applicability in more dynamic environments. Additionally, further research will explore advanced methods such as deep learning and reinforcement learning, which offer the potential for real-time learning and adaptive control in power systems. These techniques are expected to improve system resilience, optimize performance in complex scenarios, and address the limitations observed in the ANN-based controller by enabling better decision making and adaptability under uncertain conditions.
Author Contributions
Conceptualization, F.B., M.A. and D.-e.-Z.B.; methodology, M.A.; software, M.A.; validation, M.A., D.-e.-Z.B. and S.M.H.R.; formal analysis, M.A.; investigation, M.A.; resources, F.B.; data curation, M.A.; writing—original draft preparation, M.A.; writing—review and editing, M.A. and D.-e.-Z.B.; visualization, M.A.; supervision, F.B. and D.-e.-Z.B.; project administration, D.-e.-Z.B. and S.M.H.R.; funding acquisition, F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant no. G-600-144-1441.
Data Availability Statement
Data are available on request.
Acknowledgments
The authors wish to express their gratitude for the technical support received from the Ghulam Ishaq Khan Institute of Engineering and Technology, Pakistan and are thankful for the financial backing provided by the Deanship at King Abdulaziz University, Jeddah, Saudia Arabia.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LFC | Load Frequency Control |
| AGC | Automatic Generation Control |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| PID | proportional–integral–derivative |
| MPC | Model Predictive Control |
| AI | Artificial intelligence |
| ML | machine learning |
| ITAE | Integral of Time-weighted Absolute Error |
| ANN | Artificial Neural Network |
References
- Sanajaoba Singh, S. Load frequency control of a three-area system with multiple-energy sources using exchange market algorithm optimized cascade IDD-PID controllers. Electr. Power Compon. Syst. 2022, 50, 27–37. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Mohamed, E.A.; Selim, A.; Aly, M.; Alsadi, A.; Alhosaini, W.; Alnuman, H.; Ramadan, H.A. Improving load frequency control performance in interconnected power systems with a new optimal high degree of freedom cascaded FOTPID-TIDF controller. Ain Shams Eng. J. 2023, 14, 102207. [Google Scholar] [CrossRef]
- Hassan, M.; Abouelsoud, A.; Soliman, H. Constrained load-frequency control. Electr. Power Compon. Syst. 2008, 36, 266–279. [Google Scholar] [CrossRef]
- Ram Babu, N.; Bhagat, S.K.; Saikia, L.C.; Chiranjeevi, T.; Devarapalli, R.; García Márquez, F.P. A comprehensive review of recent strategies on automatic generation control/load frequency control in power systems. Arch. Comput. Methods Eng. 2023, 30, 543–572. [Google Scholar] [CrossRef]
- Shakerighadi, B.; Johansson, N.; Eriksson, R.; Mitra, P.; Bolzoni, A.; Clark, A.; Nee, H.P. An overview of stability challenges for power-electronic-dominated power systems: The grid-forming approach. IET Gener. Transm. Distrib. 2023, 17, 284–306. [Google Scholar] [CrossRef]
- Cohn, N. Some aspects of tie-line bias control on interconnected power systems [includes discussion]. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1956, 75, 1415–1436. [Google Scholar] [CrossRef]
- Quazza, G. Noninteracting controls of interconnected electric power systems. IEEE Trans. Power Appar. Syst. 1966, PAS-85, 727–741. [Google Scholar] [CrossRef]
- Elgerd, O.I.; Fosha, C.E. Optimum megawatt-frequency control of multiarea electric energy systems. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 556–563. [Google Scholar] [CrossRef]
- Cohn, N. Considerations in the regulation of interconnected areas. IEEE Trans. Power Appar. Syst. 1967, PAS-86, 1527–1538. [Google Scholar] [CrossRef]
- Elgerd, O.I. Electric Energy Systems Theory: An Introduction; Tata McGraw-Hill Publishing Company Limited: New York, NY, USA, 1983. [Google Scholar]
- Arya, Y. Impact of ultra-capacitor on automatic generation control of electric energy systems using an optimal FFOID controller. Int. J. Energy Res. 2019, 43, 8765–8778. [Google Scholar] [CrossRef]
- Mohammadi, M.; Mohammadi, A. Empowering distributed solutions in renewable energy systems and grid optimization. arXiv 2023, arXiv:2310.15468. [Google Scholar]
- Kundur, P. Power system stability. In Power System Stability and Control; CRC Press: Boca Raton, FL, USA, 2007; Volume 10, ISBN 978-0-8493-9291-7. [Google Scholar]
- Feleke, S.; Satish, R.; Salkuti, S.R.; Abdelaziz, A.Y. Load Frequency Control in Two-Area Interconnected Systems Using DE-PID and PSO-PID. In Power Quality in Microgrids: Issues, Challenges and Mitigation Techniques; Lecture Notes in Electrical Engineering; Springer Singapore Nature: Singapore, 2023; Volume 1039, pp. 391–407. [Google Scholar] [CrossRef]
- Dong, M.; Liu, K.; He, J.; Li, X.; Qiao, L.; Zhao, X. Power grid load frequency control based on Fractional Order PID combined with pumped storage and battery energy storage. Energy Rep. 2023, 9, 1402–1411. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Davoodkhani, I.F.; Kamyab, H.; Ali, R.R. Load-frequency control in an islanded microgrid PV/WT/FC/ESS using an optimal self-tuning fractional-order fuzzy controller. Environ. Sci. Pollut. Res. 2023, 30, 71677–71688. [Google Scholar] [CrossRef] [PubMed]
- Gulzar, M.M.; Sibtain, D.; Khalid, M. Cascaded Fractional Model Predictive Controller for Load Frequency Control in Multiarea Hybrid Renewable Energy System with Uncertainties. Int. J. Energy Res. 2023, 2023, 5999997. [Google Scholar] [CrossRef]
- Kumar, V.; Sharma, V.; Naresh, R. HHO-based model predictive controller for combined voltage and frequency control problem including SMES. IETE J. Res. 2023, 69, 2926–2940. [Google Scholar] [CrossRef]
- Khamies, M.; Magdy, G.; Kamel, S.; Elsayed, S.K. Optimal Parameter Design of MPC for Performance Enhancement of a Two-Area Interconnected Power Grid. In Proceedings of the 2021 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Valparaíso, Chile, 6–9 December 2021; pp. 1–9. [Google Scholar] [CrossRef]
- Majumder, R.; Ghosh, A.; Ledwich, G.; Zare, F. Load frequency control for rural distributed generation. Electr. Power Compon. Syst. 2010, 38, 637–656. [Google Scholar] [CrossRef]
- Khokhar, B.; Dahiya, S.; Parmar, K.P.S. Load frequency control of a multi-microgrid system incorporating electric vehicles. Electr. Power Compon. Syst. 2021, 49, 867–883. [Google Scholar] [CrossRef]
- Elkasem, A.H.; Kamel, S.; Khamies, M.; Nasrat, L. Frequency regulation in a hybrid renewable power grid: An effective strategy utilizing load frequency control and redox flow batteries. Sci. Rep. 2024, 14, 9576. [Google Scholar] [CrossRef]
- Elkasem, A.H.; Khamies, M.; Hassan, M.H.; Nasrat, L.; Kamel, S. Utilizing controlled plug-in electric vehicles to improve hybrid power grid frequency regulation considering high renewable energy penetration. Int. J. Electr. Power Energy Syst. 2023, 152, 109251. [Google Scholar] [CrossRef]
- Ahmed, M.; Khamies, M.; Kamel, S. A robust control approach integrating with optimal fuel cells to strengthen the frequency stability of a diverse-sources power system including renewables. ISA Trans. 2023, 143, 420–439. [Google Scholar] [CrossRef]
- Khamies, M.; Kamel, S.; Hassan, M.H.; Elnaggar, M.F. A developed frequency control strategy for hybrid two-area power system with renewable energy sources based on an improved social network search algorithm. Mathematics 2022, 10, 1584. [Google Scholar] [CrossRef]
- Khamies, M.; Magdy, G.; Hussein, M.E.; Banakhr, F.A.; Kamel, S. An Efficient Control Strategy for Enhancing Frequency Stability of Multi-Area Power System Considering High Wind Energy Penetration. IEEE Access 2020, 8, 140062–140078. [Google Scholar] [CrossRef]
- Trinh, D.T.; Wu, Y.K.; Pham, M.H. A Novel Load Frequency Control Strategy for a Modern Power System by Considering State-Space Modeling and Stability Analysis. IEEE Access 2024, 12, 115085–115101. [Google Scholar] [CrossRef]
- Wang, B.; Xu, Z.; Guan, X. Robust Load Frequency Control for Uncertainties Multi-area Power Systems with Couplings of Systems Dynamics and Reconfigurable Communication Networks. IEEE Trans. Power Syst. 2024, 1–12. [Google Scholar] [CrossRef]
- Nanda Kumar, S.; Mohanty, N.K.; Dash, S.S. Frequency Regulation of Microgrid with Renewable Sources Using Intelligent Adaptive Virtual Inertia Control Approach. Electr. Power Compon. Syst. 2023, 1–16. [Google Scholar] [CrossRef]
- Ismail, M.M.; Hassan, M.M. Load frequency control adaptation using artificial intelligent techniques for one and two different areas power system. Int. J. Control Autom. Syst. 2012, 1, 12–23. [Google Scholar]
- Chang-Chien, L.R.; Wu, Y.S.; Cheng, J.S. Online estimation of system parameters for artificial intelligence applications to load frequency control. IET Gener. Transm. Distrib. 2011, 5, 895–902. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. A multi-agent deep reinforcement learning method for cooperative load frequency control of a multi-area power system. IEEE Trans. Power Syst. 2020, 35, 4599–4608. [Google Scholar] [CrossRef]
- Fan, Z.; Yan, Z.; Wen, S. Deep learning and artificial intelligence in sustainability: A review of SDGs, renewable energy, and environmental health. Sustainability 2023, 15, 13493. [Google Scholar] [CrossRef]
- Srinivasan, S.; Kumarasamy, S.; Andreadakis, Z.E.; Lind, P.G. Artificial intelligence and mathematical models of power grids driven by renewable energy sources: A survey. Energies 2023, 16, 5383. [Google Scholar] [CrossRef]
- Verma, R.; Gawre, S.K.; Patidar, N.; Nandanwar, S. A state of art review on the opportunities in automatic generation control of hybrid power system. Electr. Power Syst. Res. 2024, 226, 109945. [Google Scholar] [CrossRef]
- Kuang, M.; Tian, Y.; Liu, Q.; Zhao, M.; Wu, X. A review of control strategies for automatic generation control in power systems with renewable energy. Prog. Energy 2024, 6, 022001. [Google Scholar] [CrossRef]
- Wadi, M.; Shobole, A.; Elmasry, W.; Kucuk, I. Load frequency control in smart grids: A review of recent developments. Renew. Sustain. Energy Rev. 2024, 189, 114013. [Google Scholar] [CrossRef]
- Khalil, A.E.; Boghdady, T.A.; Alham, M.; Ibrahim, D.K. Enhancing the conventional controllers for load frequency control of isolated microgrids using proposed multi-objective formulation via artificial rabbits optimization algorithm. IEEE Access 2023, 11, 3472–3493. [Google Scholar] [CrossRef]
- Das, A.; Rayhan, M.A.; Hossain, N.; Shuvo, M.R.A.; Akbor, M.S.; Das, T. Analysis of the Controller’s Stability for Multi-Area Power Systems with a Variety of Energy Sources Using Automatic Generation Control (AGC). In Proceedings of the 2023 10th IEEE International Conference on Power Systems (ICPS), Cox’s Bazar, Bangladesh, 13–15 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Ranjan, M.; Shankar, R. A literature survey on load frequency control considering renewable energy integration in power system: Recent trends and future prospects. J. Energy Storage 2022, 45, 103717. [Google Scholar] [CrossRef]
- Peddakapu, K.; Mohamed, M.; Srinivasarao, P.; Arya, Y.; Leung, P.; Kishore, D. A state-of-the-art review on modern and future developments of AGC/LFC of conventional and renewable energy-based power systems. Renew. Energy Focus 2022, 43, 146–171. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Nayak, J.; Swapnarekha, H.; Naik, B.; Dhiman, G.; Vimal, S. 25 years of particle swarm optimization: Flourishing voyage of two decades. Arch. Comput. Methods Eng. 2023, 30, 1663–1725. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Saadat, H. Power System Analysis; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Goldreich, O. Computational complexity: A conceptual perspective. ACM Sigact News 2008, 39, 35–39. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).