Aggregators Used in Fuzzy Control—A Review

Abstract

An important group of decision-making problems is decision-making under uncertainty, including with incomplete or linguistically described data. Command and control systems, fitting into the multi-sensor paradigm of Industry 4.0/5.0, are becoming increasingly multifactorial. This trend will intensify, requiring uncertainty and incompleteness to be considered and mathematical description and data-processing systems better adapted to them. Aggregators are a group of tools used in solving the aforementioned decision problems, including within fuzzy systems. Aggregating functions are a useful tool mainly in those artificial intelligence systems with problems arising from incomplete data. The aim of this article is to review and describe existing aggregators used in fuzzy control in terms of their usefulness and limitations of their use. Particular attention is paid to the criteria for matching a suitable aggregator to a particular computational problem. This represents an important step towards the further use of this group of technologies in electronic devices and IT systems.

1. Introduction

Command and control systems are becoming increasingly multi-sensor, fitting into the multi-sensor paradigm of Industry 4.0/5.0. Many electronic devices use multiple signals from different sensors and effectors (also within the information feedback of cyber-physical systems). This trend will increase, requiring better-suited mathematical descriptions and information systems, including accounting for uncertainty and incompleteness within fuzzy systems. Extending the description of the above-mentioned phenomena will allow many factors to be better considered and translated into the operation of systems, including industrial systems (but also: transport or medical technology). These solutions are, therefore, useful in many electronic systems. Their development and evolution require the selection, application, and verification of specific aggregators from among their many groups. In addition, there may be aggregators that should be improved or even developed from scratch on the basis of current revised requirements. For the aforementioned reasons, multi-criteria evaluation should be developed in aggregator-based command and control systems.

Aggregation functions are fundamental mathematical tools widely used in various scientific and engineering disciplines. The above functions are key for data analysis, decision-making processes, machine learning, and numerous information-fusion applications. The aim of this review is to provide a comprehensive overview of the properties, progress, and applications of aggregation functions, highlighting their importance and versatility. In the context of imprecise data, the origins of the coherent concept of aggregation functions can be found already at the end of the last century (Klir and Folger [1]). Since then, this area of knowledge has expanded considerably and continues to evolve, subject to continuous development, analysis, and various applications.

One recent interesting area of application of aggregation functions is presented by Silva et al. [2]. They delve into the security and privacy aspects of data aggregation in cloud environments, proposing strategies for enhancing data confidentiality. This research highlights the crucial role of secure aggregation functions in maintaining the integrity and security of data stored in the cloud.

Recommendation systems have become indispensable tools in the digital age, supporting decision-making by providing personalised suggestions to users. Zheng and Wang’s article [3] introduces a novel framework for multi-criteria recommender systems, using Pareto ranking to improve recommendation quality. Their approach shows how aggregation functions can effectively integrate multiple user preferences to generate accurate and personalised recommendations.

In addition, aggregation functions find application in multi-objective optimisation, where they help to balance conflicting objectives to obtain optimal solutions. A study on generating collective opinions based on multi-objective optimization [4] provides an example of this application, showing how these functions can ensure fairness in decision-making processes.

Aggregation functions are also attracting attention in the computer-vision area. Edge detection is a critical task for various applications such as object recognition, medical imaging, and autonomous navigation. A systematic review by Amorim et al. [5] highlights advances in the use of aggregation functions for image edge detection, addressing the challenges of image uncertainty and variability. In their work, they reviewed various aggregation and pre-aggregation techniques, demonstrating their effectiveness in improving edge-detection accuracy.

Moreover, the role of aggregation functions in distributed computing systems is crucial to ensure robust and efficient data processing. A study by Sartori et al. [6] examines the impact of aggregation functions on distributed computing, highlighting their importance in optimising system performance and reliability.

New models for describing imprecise information are emerging in the processing of imprecise information. This also opens up an area for the use of aggregation operators, particularly in developing solutions specific to these new models. One such model is the ordered fuzzy number (OFN)summarized in [7]. It is a new concept that is an alternative to Zadeh fuzzy numbers, which combine imprecision and trend. In [8], innovative aggregation methods that consider directional preferences are presented, increasing the applicability of fuzzy logic in different decision-making scenarios. This study highlights the evolving nature of aggregation functions and their adaptability to complex real-world problems.

Additionally, Senapati et al. [9] discuss the development of intuitionistic fuzzy geometric aggregation operators using triangular Aczel–Alsina norms. These operators are applied to multi-attribute decision-making, demonstrating their effectiveness in practical scenarios such as supplier selection and medical waste disposal. This work extends the applications of aggregation functions in dealing with uncertainty and improving the quality of decision-making.

Seliga et al. [10] contribute to this field by characterising positively homogeneous and super/subadditive aggregation functions. They present a comprehensive survey of these functions, including methods for verifying non-decreasing in higher dimensions and their applications in areas such as risk management and economics. Their work highlights the importance of positive homogeneity in constructing efficient aggregation functions for various applications.

Finally, the use of generalised Choquet integrals in classification problems, as discussed in a study of quadrature-inspired Choquet integrals [11], illustrates the adaptability of aggregation functions in improving classification accuracy. This approach exploits the flexibility of Choquet integrals to model complex interactions between features, thereby improving the performance of classification algorithms.

In summary, this very brief introduction shows that aggregation functions are versatile and powerful tools with a wide range of applications in various fields. This review aims to provide an in-depth understanding of their properties, advances, and applications, highlighting their crucial role in contemporary scientific and engineering practices. Through this comprehensive review, we aim to highlight the importance of aggregation functions and inspire further research and innovation in this dynamic field.

The main aims of the study are:

• Provide an accurate and detailed summary of the current state of re-examination of aggregation functions;
• Cover theoretical advances, practical applications, and empirical research in one comprehensive document;
• Highlight the importance of this research and its results for a better understanding and application of aggregation functions;
• Synthesise findings from different studies to identify common themes, patterns, and trends;
• Integrate insights from different research areas to provide a broad perspective and holistic view of the field.

In addition to this introduction, this article is organised as follows.

• Section 2 (Preliminaries)—basic assumptions and definitions to remind and facilitate the concept of aggregation and others related to this paper;
• Section 3 (Materials and Methods)—an approach to article search and selection;
• Section 4 (Results)—a synthetic summary of the selected publications and their collation;
• Section 5 (Discussion)—analysis and review of the results;
• Section 6 (Conclusions)—presents conclusions and a summary of the scope of the selected articles.

2. Preliminaries

2.1. Basic Definitions

In general, aggregation is an operation used when there is a need to find a single value that represents a set of different numbers/data [12]. The mathematical functions that provide the mechanism to do this are called aggregation functions. This is usually denoted as:

f:[0,1]ⁿ→ [0, 1].

(1)

Example (Fuzzy logic—connectives). Object x has partial degrees of membership in n fuzzy sets, denoted by μ₁, μ₂, …, μ_n. The goal is to obtain the overall membership value in the combined fuzzy set μ = f (μ₁, μ₂, …, μ_n). A combination can be a union set operation, an intersection, or a more complex operation.

Example (Rules in fuzzy system).The rule-based system contains rules formulated as follows:

IF t₁ is A₁AND t₂ is A₂AND … t_n is A_nTHEN

(2)

x₁, x₂, …, x_n denote the degrees of satisfaction of the rule predicates t₁ is A₁, t₂ is A₂, etc. The goal is to calculate the overall degree of satisfaction of the combined predicate of the rule antecedent f (x₁, x₂, …, x_n).

Definition 1.

An aggregation function is a function of n > 1 arguments that maps the (n-dimensional) cube onto an interval I = [a, b], f: Iⁿ→ I, with the properties [12]:

• f(a, a, a, …, a) = a and f(b, b, b, …, b) = b;-*
• for x, y argument values x ≤ y implies f (x) ≤ f (y) for all x, y ∈ Iⁿ.

Definition 2.

An extended aggregation function:

$$\mathrm{F}:{\bigcup }_{\mathrm{n}\in \{\mathrm{1,2},\dots \}}{\mathrm{I}}^{\mathrm{n}}\to \mathrm{I}$$

(3)

such that restriction of this mapping to the domain Iⁿ for a fixed n is an n-ary aggregation function f, with the convention F(x) = x for x = 1 [12].

2.2. Classification and General Properties

2.2.1. Main Classes

There are four main classes of aggregation functions [12]:

• Averaging;
• Conjunctive;
• Disjunctive;
• Mixed.

Definition 3.

An aggregation function f has an averaging behaviour (or is averaging) if for every x ∈ Iⁿ it is bounded by:

min(x) ≤ f (x) ≤ max(x).

(4)

Definition 4.

An aggregation function f has a conjunctive behaviour (or is conjunctive) if for every x it is bounded by:

f (x) ≤ min(x) = min(x₁, x₂, …, x_n).

(5)

Definition 5.

An aggregation function f has a disjunctive behaviour (or is disjunctive) if for every x it is bounded by:

f (x) ≥ max(x) = max(x₁, x₂, …, x_n).

(6)

Definition 6.

An aggregation function f is mixed if it does not belong to any of the above classes, i.e., it exhibits different types of behavior on different parts of the domain.

2.2.2. Main Properties

Analyzing aggregations, specific properties, and characteristic features can be identified [12].

Definition 7.

An aggregation function f is called idempotent if for every input x = (t, t, …, t), t ∈ I the output is f (t, t, …, t) = t.

Definition 8.

Let f:Iⁿ→Ibe a function. The diagonal of f, d_f: I →I is the function d_f(t) = f (t, t, …, t). The inverse of the diagonal, if it exists, is the function d⁻¹_f:I→I, which satisfies d⁻¹_f(f(t, t, …, t)) = t.

Definition 9.

An aggregation function f is called symmetric, if its value does not depend on the permutation of the arguments, i.e.,

f (x₁, x₂, …,x_n) = f (x_P(1), x_P(2), …, x_P(n)),

(7)

for every x and every permutation P = (P(1), P(2), …, P(n)) of (1, 2, …, n).

Definition 10.

An aggregation function f is strictly monotonically increasing if

x ≤ y but x = y implies f (x) < f (y) for every x, y ∈ Iⁿ

(8)

Definition 11.

An aggregation function f has a neutral element e ∈ I, if for every t ∈ I in any position it holds:

f (e, …, e, t, e, …, e) = t.

(9)

2.2.3. Comparability

Various aggregation functions need to be explored and established among them. To compare aggregation functions, we can check every x ∈ Iⁿ.

Definition 12.

Particular aggregation function f is stronger than another aggregation function [12] of the same number of arguments g, if for all x ∈ Iⁿ:

g (x) ≤ f(x)

(10)

2.2.4. Continuity and Stability

Continuous aggregate functions are functions such that a small change in the input causes a small change in the output. The actual change in value caused by changes in the input is shown in:

Definition 13.

An aggregation function f is called Lipschitz continuous [12] if there is a positive number M, such that for any two vectors x,y in the domain of definition of f:

|f (x) − f (y)| ≤ Md(x,y),

(11)

where d(x,y) is a distance between x and y.

2.3. Main Families

2.3.1. Min and Max

The two aggregation functions most commonly used in fuzzy theory are minimum and maximum functions [12]. This is because these are the only two operations consistent with a number of set-theoretic properties

min(x) = min{x₁, x₂, …, x_n}

(12)

max(x) = max{x₁, x₂, …, x_n}

(13)

2.3.2. Means

Means are averaging aggregating functions [12]. Formally, mean is a function f with the property:

min(x) ≤ f (x) ≤ max(x)

(14)

2.3.3. Medians

Definition 14.

Median-denoted Med constitutes the function [12]

$$Med\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}}\left(x_{\left(k\right)}+x_{\left(k+1\right)}\right),& if n=2k is even\\ x_{\left(k\right)}, & if n=2k-1 is odd,\end{array}\right.$$

(15)

2.3.4. Choquet and Sugeno Integrals

In fuzzy theory, we can apply two classes of averaging functions that are used for fuzzy measures. They are useful for modeling interactions between variables x_i.

Definition 15.

Let N = {1, 2, …, n}. A discrete fuzzy measure constitutes a set function v: 2N → [0, 1], which is monotonic (i.e., v(S) ≤ v(T) whenever S ⊆ T) and satisfies v(∅) = 0, v(N) = 1 [12].

Definition 16.

The discrete Choquet integral, with respect to fuzzy measure v, is described as:

$$C_v\left(x\right)=\sum _{i=1}^n{x}_{\left(i\right)}\left[v\left(A_{\left(i\right)}\right)-v\left(A_{\left(i+1\right)}\right)\right]$$

(16)

where x = (x₍₁₎, x₍₂₎, …, x_(n)) is a non-decreasing permutation of the input x, and x_(n+1) = ∞ by convention [12].

Definition 17.

The Sugeno integral with respect to a fuzzy measure v is described as:

$$S_v\left(x\right)=\underset{i=1,\dots ,n}{\mathit{max}}\mathit{min}\left(x_{\left(i\right)},v\left(A_{\left(i\right)}\right)\right)$$

(17)

where x = (x₍₁₎, x₍₂₎, …, x_(n)) is a non-decreasing permutation of the input x, and Hi = {(i), …, (n)} [12].

2.4. Selection of Aggregation Function

The problem-solving approach to aggregators in fuzzy control seems to focus on solving a fundamental question: which aggregator to choose for the form of signal and type of fuzzy control we need to use.

There are an infinite number of aggregator functions. They are grouped into different families, such as averages, triangular norms and conorms, Choquet and Sugeno integrals, and many others. The question is how to choose the most appropriate aggregating function for a particular application [12]. To answer this question, we have to:

• Select an aggregation function that must match the semantics of the aggregation procedure;
• Choose the right member of the class/family that does what it is supposed to do—produce the right output for the input.

We are, therefore, faced with a data-matching problem. Data can come from a variety of sources: mental experiments, opinions of experts in the field, and experiments involving asking a group of experts about their input and output values. Data can also be collected in an automaticway by gathering the reactions of subjects to certain stimuli. When fitting aggregation functions to data, we distinguish between interpolation and approximation problems.

When choosing an aggregation function, other issues should also be considered: simplicity, ease of interpretation, numerical efficiency, and the specificity of the objects to be aggregated(as in the case of ordered fuzzy numbers) [13,14]. No general rules have been developed yet, so the choice of solution rests with the system creator. In the following, we will focus on two criteria: compliance with the semantically correct properties of the aggregation procedure and matching the desired data.

In the most typical case, the data come in pairs (x, y), where x ∈ [0,1] n is the input vector and y ∈ [0,1] is the desired output. There are several pairs, which will be denoted by a subscript k: (xk, yk), k = 1, …, K. However there are variations of the dataset: (a) some components of vectors xk may be missing, (b) vectors xk may have varying dimension by construction, and (c) the outputs yk could be specified as a range of values (i.e., the interval [yk, yk]).

Formalising the selection problem [12], we consider a series of mathematical properties P1, P2, … and the data:

$$\mathrm{D}=\{\left(x_k,y_k\right){\}}_{k=1}^K$$

(18)

where D denotes the dataset represented by pairs (x, y), where x is the input vector and y is the output vector. In addition, K is the number of such pairs.

For the aggregation function f, consistent with P1, P2, …, and satisfying f (x_k) ≈ y_k, k = 1, …, K, we have a satisfaction of approximate equalities f (x_k) ≈ y_k, which is usually shown as following the minimization problem:

minimize ||r||

subject of f satisfies P1,P2,

where ||r|| is the norm of the residuals, and r ∈ R^K is the vector of the differences between the predicted and observed values r_k = f (x_k) − y_k. We can choose the p-norms in the following way:

• the least-squares norm (p = 2)

$${\left|\left|\mathrm{r}\right|\right|}_2={\left(\sum _{k=1}^K{r}_k^2\right)}^{1/2}$$

(19)

• the latest absolute deviation norm (p = 1):

$$||\mathrm{r}|{|}_1=\sum _{\mathrm{k}=1}^{\mathrm{K}}\left| r_k \right|$$

(20)

• the Chebyshev norm (p = ∞):

$${\left|\left|\mathrm{r}\right|\right|}_{\mathrm{\infty }}=\underset{\mathrm{k}=1,\dots ,\mathrm{K}}{\max }|{\mathrm{r}}_{\mathrm{k}}|$$

(21)

• or their weighted analogues, like:

$$\left|\left|\mathrm{r}\right|\right|={\left(\sum _{k=1}^K{u}_k{r}_k^2\right)}^{1/2}$$

(22)

where the weight u_k ≥ 0 expresses the relative importance to fit the k-th value y_k.

The use of p-norms for p > 1 makes the fitting problem susceptible to large errors in the data (outliers) [12]. There are alternative fit criteria, such as the use of trimmed least squares, maximum-likelihood trimmed criteria, least-median residuals, or Huber-type functions [15,16,17,18].

In some studies [19,20,21,22], it has been suggested that in decision problems, the actual numerical value of the output f (x_k) was not as important as the ranking of the outputs. For instance, if y_k ≤ y_l, then it should be f (x_k) ≤ f (x_l). This confirms that subjects are good at evaluating alternatives but not very good at assigning consistent numerical ratings to their preferences. Thus, it is argued in [22] that the appropriate choice of aggregation function should be consistent with the ranking of outputs y_k rather than their numerical values.

3. Materials and Methods

3.1. Dataset and Devices

In developing bibliometric analysis methods for this review, we focused on exploring the research picture in the area of aggregator/aggregator-selection strategies for fuzzy control and possible innovations in this area of research. For this, we use bibliometric methods as analytical tools in scientific publishing. In order to better guide our review and selection of publications, we have formulated research questions that will help us uncover key aspects of the area under study, concerning: the evolution of research topics/issues over time, the geographical distribution of studies/publications, authors, scientific institutions and publications with the greatest impact, and topics that may shape future research agendas. In order to fulfil the above objectives, it is crucial to have the fullest understanding of the current state of research, industry practices, efforts, and future research directions in the pursuit of optimal aggregator selection in fuzzy control. Here, the analysis and interpretation of bibliometric data can make a key contribution to the ongoing discussion and build a more solid foundation for further analysis and research (Figure 1).

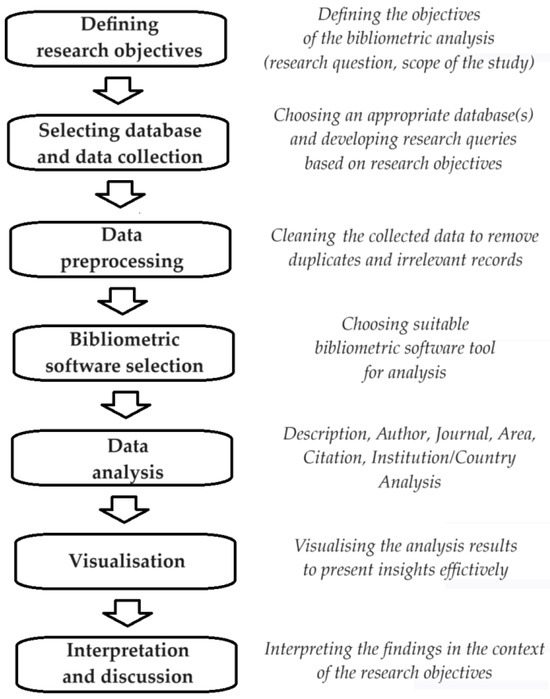
Figure 1. Bibliometric analysis procedure.

A certain criterion for the selection of papers is also that we wanted to use mostly open resources in order to select not only new but also easily accessible research for everyone and from different areas to show a broader perspective on the subject of aggregators.

3.2. Methods

In the review, we used both the tools built into the Web of Science (WoS) and Scopus databases and the Biblioshiny tool from the Bibliometrics Rv.4.1.3 package for bibliometric analysis. It is better suited to bibliometric and scientometric research, offering at times a more precise categorisation into conceptual/area/branch structures, authors, documents, and sources, and the various results are presented by means of graphs and information tables with a choice of analysis and visualisation.

4. Results

We searched research articles from two major databases: WoS and Scopus. This choice was dictated by the wide range of research results contained in them. In addition, both of the aforementioned databases contain detailed data on, for example, citation counts, which is particularly beneficial when conducting extensive bibliometric analyses and assessing the impact of research results.

When creating advanced queries tailored to our research objectives, we applied filters to select relevant literature. In doing so, we limited our search to articles in English. Later in the study, we manually reviewed the articles again, excluding some of them (including duplicate articles) to suit our research objectives, resulting in a final sample size (Figure 2). The WoS search was performed using “Topic” (search using the set: title, abstract, keyword plus and other keywords).The Scopus search was performed using the set: article title, abstract, keywords.

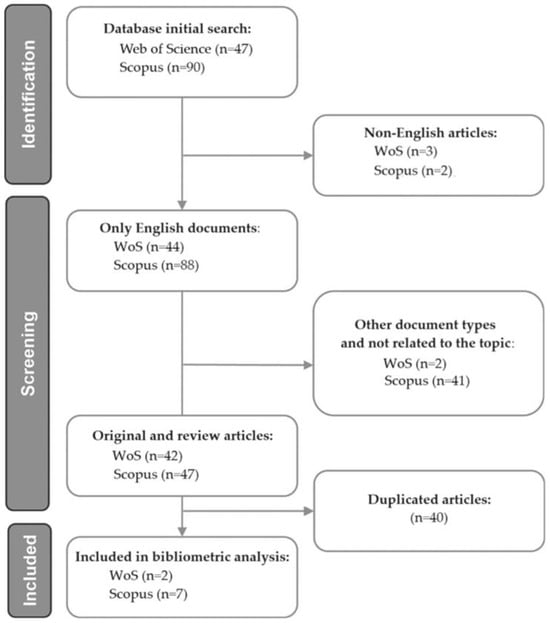
Figure 2. A flow chart of the review process using PRISMA.

A search in the WoS database using the keywords “aggregator” and “fuzzy control” yielded only two works. Therefore, the search was extended to include the keywords “aggregation” and “fuzzy logic”, which yielded 44 publications subjected to further selection. Similarly, a search in the WoS database using the keywords “aggregator” and “fuzzy control” yielded 11 works. Therefore, the search was extended to include the keywords “aggregation” and “fuzzy logic”, which yielded 88 publications subjected to further selection.

We began the bibliometric analysis with descriptive statistics to understand the characteristics of the dataset of a selected group of scientific publications, including leading authors, research institutions, topic areas, and emerging trends in the topic area under study. This allows you to identify evolving vocabulary and major research achievements. Examining changes in trends over time allows you to notice changes in the focus/mainstream of research over time and the type and dynamics of the area (Figure 3), including the categorization of publications into thematic clusters and an image of the connections of research topics. This will enable easier further identification of key themes and subdomains, including emerging research directions.

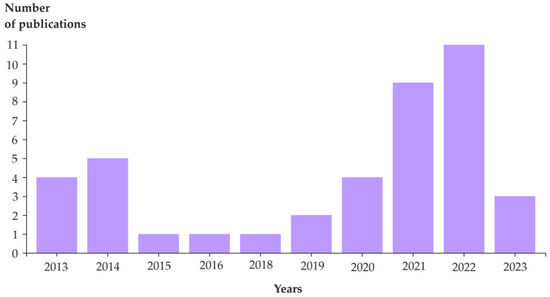
Figure 3. Annual publications trend (WoS).

The predominant article type was the original/research article (Figure 4).

Figure 4. Article types (WoS).

The two most popular application areas were electronics and computer science (Figure 5).

Figure 5. Categories of publications (WoS).

The largest number of studies have been conducted in India and the USA (Figure 6). Figure 7 and Figure 8 show the most active scientists and research centers in the study area.

Figure 6. Countries of research (WoS).

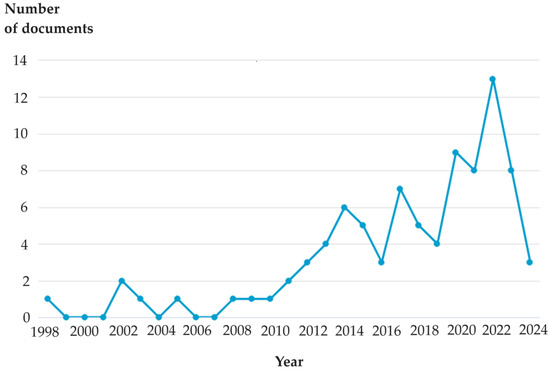
Figure 7. Annual publications trend (Scopus).

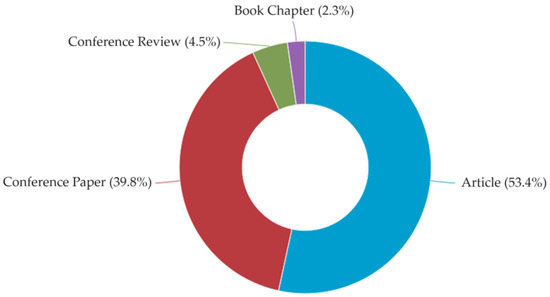
Figure 8. Publications by type (Scopus).

Most of the publications were original articles and conference papers; there are a low number of reviews (Figure 8).

The main research areas were computer science and engineering chemical engineering (Figure 9).

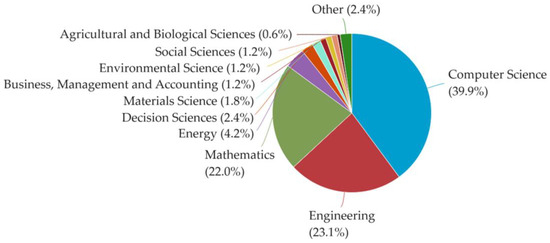
Figure 9. Publications by subject area (Scopus).

Most studies were conducted in Spain, India, and the USA (Figure 10). It is clear from the above that the source (despite the same keywords) is important for the results of the review. None of the authors or affiliations were prevailing (Figure 11 and Figure 12).

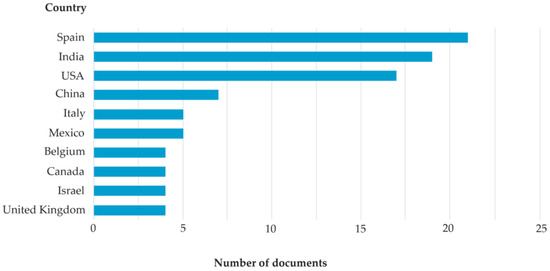
Figure 10. Publications by country (Scopus).

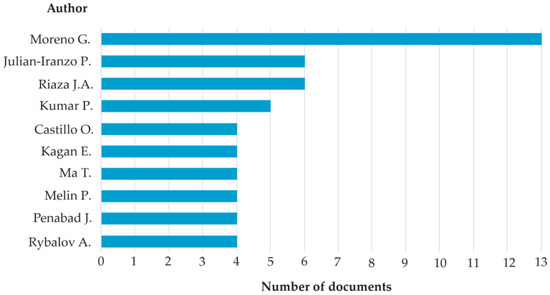
Figure 11. Publications by author (Scopus).

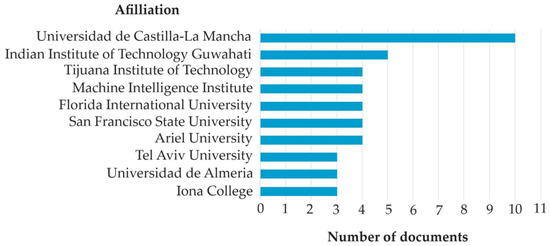
Figure 12. Publications by affiliation/research center (Scopus).

4.1. Scope of Topics in the Publications

Based on the above results of the literature review, it is possible to distinguish authors and centers who have made a significant contribution to this area of research. However, both the number and distribution of studies indicate that the researched area is only at the beginning of its development, leaders have not yet emerged, and many centers can become famous thanks to the results of their research. Therefore, this is an area of research that is a good area for debut, in which the fight for the palm and a place on the podium is still ongoing.

The conducted research shows a very wide range of applications of aggregators (aggregating functions) in connection with fuzzy sets, which have been addressed since the formulation/separation of the aggregation concept itself.

Various aggregation operators for better decision-making are available in the literature, including a generalisation of traditional aggregation functions defined on a set of real numbers. Each aggregation operator has a specific purpose in solving problems efficiently. In recent years, the power average (PA) operator has been used to reduce the influence of biased data provided by decision-makers. Similarly, the hedonic mean (HM) operator has the property of considering the interrelationships between the different criteria available in a decision problem.

4.2. Early Attempts

Already in 1998, a simplified model of an oil refinery was presented as a fuzzy nonlinear problem with four inconsistent performance criteria(objective functions or objectives) and 10constraints—material balance equations were defined. It was assumed that the total annual refinery profit and sensitivity of profit to changes in conditions in the refinery are imprecise goals. Separate linear and S-type membership functions were assumed for all fuzzy objectives. The complex Box method was used to solve the explicit equivalent of the fuzzy problem of programming nonlinear goals. The “min” operator was used as an aggregator, and the software was developed in C. This fuzzy control approach to the problem allows the decision-maker great flexibility in setting goals over time and considering any number of goals in any combination [23].

The Continuous Inference Network (CINET) included as part of the Prototype Intelligent Controller (PIC) preceptor module the CINET fuzzy classifier as a fuzzy cascade and a fuzzy aggregator. This included improving the functionality of the fuzzy aggregator by adding a measure of randomness (called the degree of ambiguity) [24].

In 2003, it was proposed to extend the then-fuzzy connectives to β-Precision aggregators. They consider the tolerance for noise and errors in measuring the values of aggregated criteria when there are a large number of them. This was implemented within Yager’s MAM, MOM, and MICA operators [25].

4.3. Late Attempts

In 2009 FAIR, a fuzzy control-based aggregation platform ensuring network resiliency for wireless sensor networks (WSNs) was presented. It considers the possibility of data manipulation by malicious aggregator nodes and ensures data integrity based on the trust level of the WSN response while tolerating link or node failures. In the general aggregation model, the trust level is visible to the asker [26].

In 2010, an aggregator for vehicle-to-grid (V2G) frequency regulation services was proposed. It uses distributed power of electric vehicles enabling the generation of the desired power on a grid scale. The constrained cost function is an optimization problem, but practical constraints include, among others: reducing battery-energy consumption. The dynamic programming algorithm is used in this solution to calculate the optimal charging for each vehicle, developing a charging control strategy with various parameters [27].

The 33 kV Guwahati city distribution system was modeled in the MATLAB Simulink environment, considering four types of active and reactive load profiles. To control the power flow of the charging station and the distribution node support point, fuzzy control strategies and an optimal aggregator were implemented. A probability distribution function was also used to find the scheduled arrival of electric vehicles at the charging point by comparing the voltage, power, and energy of the charging station and the distribution-node support point [28].

The two-step charging strategy to address the charging control issues of plug-in electric vehicles (PEV) is as follows:

• In the first stage, the optimal charging of each PEV is calculated using the Bee algorithm as the aggregator optimizer;
• In the second stage, the aggregated power is distributed among electric vehicles using a fuzzy controller.

The selected process considers the non-linear dynamics of batteries in practical scenarios and reduces the load peak, and it smoothes the load profile and unplanned disconnection of vehicles from the charging stations [29].

Improving system performance may require a fuzzy logic-based adaptive two-degree-of-freedom internal model control (LFC) method. It follows that controller parameters are tuned using designed fuzzy rules to obtain a better closed-loop response, which improves the dynamic response of the controller [30].

Optimization procedures to calculate the optimal value of the weighting factors included in objective functions improve the controller’s ability to deal with uncertainties [31]. These procedures systematically adjust the weighting factors to achieve the best possible performance. By fine-tuning these factors, the controller can adapt more effectively to changing conditions and unpredictable scenarios. This leads to improved stability and robustness of system response. The inclusion of optimisation algorithms allows for dynamic adjustment, ensuring that the controller remains efficient under a variety of operating conditions. These algorithms often include iterative methods that continuously refine weighting factors based on real-time feedback and performance metrics. As a result, the controller can anticipate and compensate for potential disturbances and uncertainties. Furthermore, the optimisation process helps to balance the simultaneous achievement of multiple objectives, such as minimising error, reducing energy consumption, and maximising system durability. By properly prioritising these objectives, the controller can maintain optimal functionality while meeting seemingly conflicting requirements. This multitasking optimisation ensures that the system does not overcompensate for performance in one area at the expense of another, even at the expense of convergence speed. Ultimately, this optimisation ensures that the controller operates reliably even in the presence of significant uncertainties. This reliability is critical to maintaining system integrity and achieving the desired results in a variety of applications.

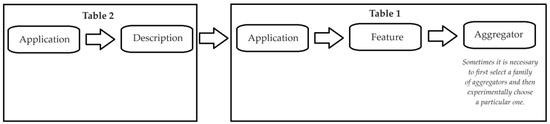
Choosing the right aggregation function is crucial to the accuracy and effectiveness of the fuzzy system in solving real-world problems. In fuzzy systems, aggregation is a key step that allows different conditions and rules to be combined to produce a final result. Aggregation functions in fuzzy systems can be divided into several categories depending on their properties and applications (Table 1).

Table 1. Definitions and general characteristics of the benefits of the various aggregators (own version based on [32]).

Family	Name	Feature	Application
Minimum (AND) and maximum (OR) functions	Minimum	Selects the smallest value from a set of membership degrees	The most commonly used conjunction (AND) function.
	Maximum	Selects the biggest value from a set of membership degrees	The most commonly used disjunction (OR) function.
Summation functions	Summation	Degrees of membership are added together, which can lead to values greater than 1.	Basic approach
	Probabilistic sum	Limits the result to the interval [0,1].	More sophisticated approach than basic summation
Algebraic functions	Algebraic product	Multiplies degrees of membership	Works well for simple models with a small number of inputs.
	Constrained sum	Ensures that the result does not exceed 1	System model with saturation or cut-off.
Weighted functions	Weighted average	Assigns different weights to different degrees of membership and then calculates their weighted average	When heavier weighted inputs have a greater impact on the average.
	Weighted sum	Similar to the sum method, but each value is multiplied by its weight before addition	When inputs have more weight they have a greater impact on their total.The weighted sum method is one of the best-known algorithms for multi-criteria analysis.
Specialised functions	T-norms (Triangular norms)	In addition to algebraic product and minimum, they also include other t-norms, such as the Lukasiewicz t-norm	Used to model conjunction in fuzzy systems
	S-norms (Triangular conorms)	In addition to the maximum and probabilistic sum, they also include other s-norms, such as the Lukasiewicz s-norm	Used to model alternatives in fuzzy systems

Aggregation functions in fuzzy systems have a wide range of applications in various fields, as they allow information from multiple sources or criteria to be combined, which is essential for decision-making and uncertainty modelling. The main areas where aggregation functions are used are shown in Table 2.

Table 2. Key areas of aggregation-function applications.

Area	Application	Description
Control systems	Industrial process control	Aggregation functions are used to combine different control variables to ensure stability and optimum performance of control systems, such as temperature, pressure, or flow control.
	Robot control	Aggregation functions combine data from different sensors, such as cameras or tactile sensors, to enable robots to make complex decisions in real time.
Expert systems and decision-making systems	Financial systems	Aggregation functions are used to analyse risk, combine different financial indicators, and predict market trends.
	Medical diagnosis	Aggregation functions combine different symptoms and test results to help diagnose diseases.
Recommendation systems	Product recommendations	Aggregation functions combine different product features and user preferences to generate personalised recommendations.
	Content recommendations	Aggregation functions combine data on viewed content, ratings, and user preferences to recommend e.g., new books, games, films, etc.
Intelligent transport systems, fleet management, and logistic chain management	Navigation and route planning	Aggregation functions combine data from different sources such as traffic, weather conditions, and user preferences to optimise routes and minimise travel time.
	Fleet management	Aggregation functions combine information on vehicle condition, routes, and schedules to optimise management and maintenance.
Resource and energy management	Energy management systems	Aggregation functions combine data on energy consumption, weather forecasts, and the availability of renewable energy sources to optimise energy management and distribution.
	Smart grids	Aggregation functions combine data from different metering points to manage energy flows and ensure grid stability.
Pattern recognition and classification systems	Image-recognitionsystems	Aggregation functions are used to combine the results of different image-processing algorithms to improve the accuracy of object recognition.
	Data-analysis systems	Aggregation functions combine different metrics and measures to classify and interpret large datasets.
Security and monitoring	Security systems	Aggregation functions combine data from various sensors such as cameras, motion sensors, and alarm systems to detect threats and unauthorised entry.
	Environmental monitoring	Aggregation functions combine data from air, water and soil quality sensors to monitor the state of the environment and detect pollution.
Agricultural decision support systems	Farm Management	Aggregation functions are used to combine weather, soil, plant, and resource-management data to help farmers make planting, irrigation, and fertilisation decisions.
	Plant-health monitoring	Aggregation functions combine data from sensors, satellite imagery, and drones to monitor plant health and detect potential problems.

For traditional Mamdani-type fuzzy systems, the selection of aggregators poses less difficulty for a small number of inputs. Otherwise, not only does the number of rules grow exponentially with the number of inputs, but it becomes increasingly difficult to assess their fit to the problem (i.e., researchers find it harder to understand the relationship between premises (inputs) and consequences (outputs/outputs)). This is due to the fact that no general transformation of expert knowledge into the above-mentioned inference rules has been formulated so far for fuzzy inference. Furthermore, no efficient (time, computationally) method for tuning the membership function in terms of minimising inference errors has yet been found. For the aforementioned reasons, the assignment of Table 1 to Table 2 is limited by the knowledge of the properties of the modelled system described in the Features and Applications column of Table 1 and the Application and Description columns of Table 2 (Figure 13).

Figure 13. Simplified aggregation-selection algorithm linking Table 1 and Table 2.

5. Discussion

There are some issues to consider when choosing an aggregation function, such as simplicity, numerical efficiency, ease of interpretation, etc. [14]. There are no general rules here, and the choice rests with the system creator. In what follows, we will focus on the first two criteria: compliance with the semantically important properties of the aggregation procedure and fit to the desired data.

5.1. Limitations of Current Approaches to Aggregators

Despite their wide application and effectiveness, current aggregator approaches in fuzzy control have several limitations:

• Selection of aggregator functions: its subjectivity and lack of standardization—there is no universally accepted standard for the selection of aggregation operators, which may lead to inconsistencies between different systems and applications;
• Computational complexity that limits performance and scalability, especially in real-time fuzzy control applications where fast response times are important, and as the number of input data increases, the computational burden of some aggregation methods may become too high;
• Potential loss of information: oversimplification, especially when using simple aggregation methods such as minimum or maximum operators, which may result in less accurate or less diverse resulting control;
• Nonlinearity and uncertainty: some aggregation methods may introduce nonlinearity into the system, making the behavior of a fuzzy control system more difficult to predict and analyze, as well as suboptimal performance in uncertain environments;
• Context dependence: lack of adaptability in dynamic environments where the relationships between inputs and outputs may change over time;
• Input interdependence: ignoring the interconnectedness of inputs can lead to incorrect control decisions;
• The complexity of designing and tuning aggregation operators can be high and time-consuming, especially when tuning for a specific application domain;
• Integration with other systems: aggregation methods in fuzzy control systems may not be easily integrated with other control or decision-making systems;
• Objectively assessing the performance of different aggregation operators can be difficult, placing high demands on comparison and selection of the most appropriate one for a particular application.

5.2. Directions of Further Studies on Aggregators

Several key promising research directions for aggregators in fuzzy control may allow for rapid progress in solving/avoiding existing limitations and increasing the efficiency and applicability of fuzzy control systems:

• Adaptive aggregation methods: developing aggregation operators that adapt to changing contexts or operating conditions in real time based on the current or predicted state of the system;
• Learning-based aggregation: implementing machine-learning techniques (neural networks, reinforcement learning) to learn optimal aggregation strategies from data to improve the adaptability and performance of fuzzy control systems;
• Complexity reduction: designing more computationally efficient aggregation algorithms that reduce the computational load, especially for real-time applications and systems with a large number of inputs, but also developing simplified aggregation models as a trade-off between computational efficiency and the accuracy of the aggregated result (sufficient aggregator instead of optimal aggregator);
• Creating aggregation operators resistant to uncertainty (e.g., based on the integration of concepts from the probabilistic and interval approaches);
• Development of nonlinear aggregation techniques that can better capture the complex relationships between inputs while maintaining computational feasibility;
• Correlation-aware aggregation: create multidimensional aggregation operators that consider common distributions of input data, providing a more accurate representation of their common behavior;
• Multi-criteria and multi-objective aggregation: development of multi-criteria decision-making (MCDM) techniques with fuzzy aggregation to handle scenarios with many conflicting goals or criteria—Pareto-optimal aggregation also applies here;
• Hybrid control systems: combining fuzzy aggregation methods with other control strategies;
• Development of aggregator performance metrics and benchmarking frameworks to objectively evaluate and compare different aggregation operators in terms of accuracy, robustness, computational efficiency, and adaptability in various practical applications.

The proposed approach can strengthen existing and future multi-criteria decision-making (MCDM) methods that currently produce questionable and unreliable results. It allows us to consider not only uncertainty but also the rank reversal paradox. Previous efforts in this direction, including modifications to the method of characteristic objects (COMET), may be insufficient [33,34]. In addition, the development and refinement of new aggregation methods should include their automatic or semi-automatic proper selection and tuning for a particular decision-making problem (i.e., a methodological and practical framework for selecting appropriate methods for a specific decision-making situation) since potential misapplication reduces the quality of recommendations and consistency of results. Such analysis, rules, and modeling of uncertainty in the description of the decision problem will allow for the building of a more accurate framework to support the selection of an aggregation method for the selected decision-making process. One possible solution for complex nonlinear systems is the interval Takagi–Sugeno Type 2 fuzzy set. It copes with uncertainties in the system but requires providing error detection through precise threshold design and increasing error sensitivity. This is especially true when operating in the presence of external interference and noise in the process channel and measurement channel. One possible solution involves testing the estimation of set members based on an admissible compact set of residuals. A fuzzy H-/L∞ unknown input observer based on zonotopic analysis is proposed to separate noise from residual dynamics. To analyze its stability and performance of H-/L∞ unknown input-observer detecting errors, the Lyapunov function of the fuzzy basis relation is used reducing the conservatism of the evaluation [35].

6. Conclusions

Analyzing current trends in science and technology, fuzzy control using aggregators will be increasingly necessary in electronics and computer science, and this need will grow with the increasing saturation of our environment with systems focused on human–computer interaction, e.g., within the Industry 5.0 paradigm, where man and the environment are at the very center of the activity of systems of all kinds. Aggregation functions in fuzzy systems enable information from different sources to be combined efficiently, which is key to making more precise and informed decisions in a variety of applications. Command and control systems based on multi-criteria analysis require advanced solutions that consider uncertainty and the aggregation of data from different sources. As technology develops, the need for such systems will increase as a result of the increasing complexity of computational problems and the number of factors needed to be considered. By pursuing the research directions discussed in this review, intensifying efforts in the field of fuzzy control can develop more advanced, efficient, and reliable aggregation methods, improving the performance and applicability of fuzzy control systems in a wide range of applications. The number of such applications will also increase with the development of the use of AI/ML and the 6G network and the associated increase in the amount of data of various types, with various uncertainties.