Computation Offloading Strategy for Detection Task in Railway IoT with Integrated Sensing, Storage, and Computing

Abstract

Online detection devices, powered by artificial intelligence technologies, enable the comprehensive and continuous detection of high-speed railways (HSRs). However, the computation-intensive and latency-sensitive nature of these detection tasks often exceeds local processing capabilities. Mobile Edge Computing (MEC) emerges as a key solution in the railway Internet of Things (IoT) scenario to address these challenges. Nevertheless, the rapidly varying channel conditions in HSR scenarios pose significant challenges for efficient resource allocation. In this paper, a computation offloading system model for detection tasks in the railway IoT scenario is proposed. This system includes direct and relay transmission models, incorporating Non-Orthogonal Multiple Access (NOMA) technology. This paper focuses on the offloading strategy for subcarrier assignment, mode selection, relay power allocation, and computing resource management within this system to minimize the average delay ratio (the ratio of delay to the maximum tolerable delay). However, this optimization problem is a complex Mixed-Integer Non-Linear Programming (MINLP) problem. To address this, we present a low-complexity subcarrier allocation algorithm to reduce the dimensionality of decision-making actions. Furthermore, we propose an improved Deep Deterministic Policy Gradient (DDPG) algorithm that represents discrete variables using selection probabilities to handle the hybrid action space problem. Our results indicate that the proposed system model adapts well to the offloading issues of detection tasks in HSR scenarios, and the improved DDPG algorithm efficiently identifies optimal computation offloading strategies.

1. Introduction

1.1. Background

With the rapid development of communication and artificial intelligence technologies, new horizons for development in the field of rail transit operation and maintenance have emerged. Particularly for high-speed railways (HSRs), due to the fast velocities of high-speed trains, the high safety standards required, the complexity of the operational environment, the substantial passenger load, and the prolonged duration of high-speed travel, there is a significant safety risk [1] associated with the detection of high-speed rail vehicles. The detection process for high-speed trains still relies heavily on manual efforts, with routine checks constituting the bulk of maintenance activities, leading to high safety risks, elevated maintenance costs, and low efficiency. The deployment of online detection devices, big data analytics [2], and machine vision-based non-contact non-destructive testing techniques [3] could allow for the synchronous and continuous detection of the condition of rail transit vehicles and the status of railway lines without stopping, without sacrificing accuracy and comprehensiveness. However, these detection tasks are typically computation-intensive and latency-sensitive. Equipping each detection device with extensive computing power is clearly a high-cost and wasteful approach.

A railway Internet of Things (IoT) [4] system with integrated sensing, storage, and computing, based on mobile edge computing (MEC) [5], can effectively address this issue. Such an integrated system embeds certain edge computing nodes that provide the necessary computing power and memory capacity for detection tasks. Thus, by utilizing MEC, these detection tasks can be offloaded to edge servers for processing. This approach can offer low-latency computational services and life-cycle-long management [6] for detection tasks.

Although some progress has been made in the research on the allocation of communication and computing resources in MEC based on optimization methods [7,8] within traditional IoT environments, the channel conditions in railway scenarios are rapidly time-varying, particularly for HSR. Moreover, given the massive number of detection devices along the entire railway, the computing power and memory capacity [9] of edge servers may not always be sufficient to immediately serve every task. In short, in dynamic and resource-constrained environments, system and environmental parameters are constantly changing. Thus, finding an optimal allocation strategy for communication, computing, and memory resources for detection tasks quickly and effectively is challenging.

1.2. Related Work and Contribution

Numerous noteworthy studies have concentrated on investigating the issues of computation offloading and resource management within the domain of MEC. Optimization-based methods are the primary solutions for addressing this problem. Zhao et al. [10] aimed to minimize the system’s maximum delay by optimizing user beamforming vectors, BS beamforming matrices, and MEC server resource allocation while adhering to communication and computing budget constraints. Xu et al. [8] proposed a novel approach to optimize network throughput in HSR scenarios by admitting as many tasks as possible under delay constraints and multicasting the maximum number of computation results, considering the high mobility of trains and frequent handovers. They introduced a multi-group-shared Group Steiner tree model and an efficient heuristic algorithm to address the multicast routing problem, enhancing the quality of data services for passengers during long journeys. Deep Reinforcement Learning (DRL) is being increasingly applied in resource allocation problems. Jiang et al. [11] investigated the optimization of task execution, focusing on offloading decisions and resource assignments in MEC environments to reduce task latency, and used Q-learning to solve the problem. Chen et al. [12] explored energy efficiency in AR task offloading and resource allocation in single and multiple MEC system environments and proposed a multiagent deep reinforcement learning model for dynamic communication environments. Ale et al. [13] tackled the challenge of task offloading in environments with multiple IoT devices and edge servers, formulating the problem as a Markov decision process (MDP) and introducing a DRL algorithm for hybrid action spaces that involve both task partitioning and computational power allocation. Deng et al. [14] developed an autonomous system for the partial offloading of delay-sensitive tasks in multiuser IIoT MEC systems, employing the Deep Deterministic Policy Gradient (DDPG) to facilitate continuous offloading decisions and optimize system performance.

While research has explored computation offloading and resource allocation in MEC from diverse optimization perspectives, the majority of these research studies focus on quasi-static system settings and do not take into account the requirements for multiple resources by dynamic systems with time-varying conditions in high-speed contexts. In the dynamic sector of MEC for railway IoT, Xu et al. [5] crafted a hybrid DRL approach that synergizes a Double Deep Q-Network (DDQN) and DDPG to minimize computational costs by fine-tuning subcarrier assignment, offloading ratios, and resource distributions. Addressing HSR, Li et al. [15] developed a joint resource allocation and computation offloading scheme based on millimeter waves and matched game theory to curtail latency and bolster user capacity. To maximize throughput, Xu et al. [8] addressed the issue of maximizing network throughput in HSR scenarios by proposing an efficient heuristic algorithm for multicasting computation results in an MEC network. The approach considered the dynamic nature of HSRs, optimizing multicast tree construction and task admission under delay constraints to enhance data services for passengers. Lastly, Tian et al. [16] introduced a blockchain-enhanced, multi-hop transmission framework for MEC in smart rail systems, applying DRL to refine offloading paths and strategies for improved system performance.

With the development of communication technology, many technologies have become increasingly mature and applied in practice, such as millimeter wave and multiple-input multiple-output technologies [17]. The introduction of these technologies has also brought more possibilities to MEC. In particular, the Non-Orthogonal Multiple Access (NOMA) technology has brought about significant performance enhancements. Xu et al. [18] tackled the complex joint task offloading and resource allocation in NOMA-based HetNets for MEC, proposing an iterative solution to the combinatorial problem. Du et al. [19] studied cost-effective offloading in NOMA-enabled vehicular networks, developing a Vehicle Edge Computing (VEC) network model to address the cost minimization challenge through heuristic algorithms and deriving closed-form solutions for cloud-based optimizations. Du et al. [20] introduced a NOMA-assisted ultra-dense edge computing model optimized by DDPG to enhance spectrum utilization and reduce task execution delay and energy consumption in healthcare IoT, outperforming local computation and traditional offloading methods.

Although some of the aforementioned papers have applied MEC to railway scenarios, the impact of high-speed movement on communication is often overlooked. Moreover, detection devices may be deployed on trains or alongside tracks, adding uncertainty and complexity to the computation offloading problem. However, summarizing these issues and considering the specific environment of high-speed railway IoT for train vehicle and track detection, we propose a computation offloading strategy for detection tasks in railway IoT with integrated sensing, storage, and computing. In this paper, we consider the interference caused by high-speed movement. Our system supports two communication modes, direct communication and relay communication, to accommodate the uncertainty in device deployment. Additionally, the differences in device and relay transmission power open up possibilities for the introduction of NOMA technology. We incorporate NOMA technology on top of Orthogonal Frequency Division Multiplexing (OFDM) to enhance channel utilization. By selecting appropriate edge servers, we also mitigate data congestion on each server. Building upon the aforementioned system model, we adopt an improved DDPG algorithm in conjunction with a low-complexity channel allocation algorithm to optimize the configuration of communication and computational resources. This study has threefold specific contributions, as follows:

• To better accommodate detection devices deployed in different locations and environments in various types of railways, we proposed two transmission models, namely the direct transmission model and the relay transmission model. Furthermore, in the OFDM system, we introduced NOMA technology to increase channel capacity.
• Taking into account the limitation of computing resources and memory capacity, we allocated computing resources through server selection, combined with the order of arrival, while also ensuring that the task queue pending for each server does not exceed its memory capacity.
• We proposed an improved DDPG algorithm combined with a low-complexity subcarrier allocation algorithm to solve the optimization problem of communication and computing resource allocation.

The organization of the rest of this paper is as follows. Section 2 describes the model of the MEC system in a railway IoT system for detection tasks and optimization problem formulation. Section 3 proposes the subcarrier allocation algorithm and the improved DDPG algorithm. Section 4 presents and analyzes the simulation results. Section 5 concludes this paper.

2. System Model and Problem Formulation

In this section, we initially outline the network framework of MEC for detection tasks in the railway IoT with integrated sensing, storage, and computing. We then present two transmission models, the NOMA-based transmission model and the limited computing resource and memory capacity allocation model. Finally, we formulate an optimization problem to minimize the average delay ratio.

2.1. System Model

As shown in Figure 1, we consider an MEC system beside HSR to provide task offloading services for multiple detection devices. Within a certain range along the track, a Base Station (BS) is deployed beside the railway, forming a cell. Meanwhile, a communication relay is installed on the train. Near the BS, there is an MEC server installed. The MEC servers along the entire railway are interconnected via fiber optic links to form an edge computing network. To achieve multi-directional intelligent safety detection in HSR, detection devices incorporate onboard detection sensors and ground detection sensors. The detection devices in this system are equipped with the necessary capabilities for detection and communication but lack computing capacity. Thus, the various detection tasks need to be offloaded to MEC servers for processing. The detection devices have two transmission modes. One is direct transmission, in which the detection devices transmit the detection tasks directly to the BS. The other is relay transmission, in which the detection devices first send the tasks to the communication relay on the train, which then forwards them to the BS.

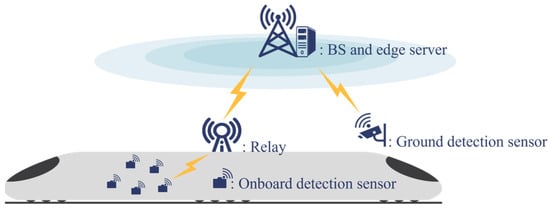
Figure 1. MEC system for detection task in railway IoT.

We assume that, in a time slot, there are $M$ onboard devices and $N$ ground devices that have requests for task offloading. Therefore, a total of $I$ tasks need to be offloaded to the MEC, denoted by $\mathcal{I}=\left\{1,2,\cdots ,I\right\}$, where $I=M+N$, $\left\{1,\cdots ,M\right\}$ represents the task from the onboard devices and $\left\{M+1,\cdots ,I\right\}$ represents the task from the ground devices. In a time slot, the $i\text{-}\mathrm{th}$ task, $i\in \mathcal{I}$, is represented by a quadruple $⟨l_i,{\mu }_i,T_i^{\max },L_i⟩$, where $l_i$ is the data size of the $i\text{-}\mathrm{th}$ task in bits, ${\mu }_i$ is the computation workload of the $i\text{-}\mathrm{th}$ task in cycles/bit, $T_i^{\max }$ is the maximum allowable delay for the $i\text{-}\mathrm{th}$ task, and $L_i$ is the loaded data size for the $i\text{-}\mathrm{th}$ task, including the data size of the neural network model to be loaded and the intermediate data generated during the calculation [21,22].

2.2. Direct Transmission Model

The detection devices directly transmit the tasks to the BS of the cell where the train is located, which is referred to as sensor-to-BS (S2B) data transmission. We assume that the transmission power of each detection device can be monitored before making decisions, and there will not be significant differences among the devices. This implies that the channel gain differences among different tasks during direct communication will not be too large. Thus, we adopt OFDM technology for the communication between ground devices and the BSs. Interference between subcarriers is negligible. At the same time, in the HSR environments, since the distance between trains exceeds 50 km, the interference between cells can be considered negligible.

However, for the detection tasks of onboard devices, namely $i\in \left\{1,\cdots ,M\right\}$, due to the high mobility of trains in the HSR environments, the transmitted signal will inevitably experience a Doppler shift, which leads to inter-channel interference (ICI) [23]. This interference can be considered a form of noise. Thus, the received Signal-to-Interference-plus-Noise Ratio (SINR) [24] of the detection $i\text{-}\mathrm{th}$ task created by the onboard device can be expressed as:

$${\mathrm{\Gamma }}_i^B={\displaystyle \frac{p_i{\left|h_i^B\right|}^2}{\varpi p_i{\left|h_i^B\right|}^2+{\sigma }^2}},$$

(1)

where ${\sigma }^2$ is the noise power, $p_i$ is the transmission power of the $i\text{-}\mathrm{th}$ device, ${\left|h_i^B\right|}^2$ is the channel gain between the $i\text{-}\mathrm{th}$ device and the BS, and $\varpi$ is the ICI factor due to the Doppler effect [24], which is given by:

$$\varpi =1-{\displaystyle {\int }_{-1}^1\left(1-\left|x\right|\right)J_0(2\pi f_c\frac{v}{c}{\tau }_{s}x)dx},$$

(2)

where $v$ and $c$ represent the velocity of the train and the speed of light, respectively. ${\tau }_s$ is the signal symbol duration. $J_0(·)$ is the zero-order Bessel function of the first kind.

However, for the ground detection devices, namely $i\in \left\{M+1,\cdots ,M+N\right\}$, which are fixed as is the BS, there is no other interference. The received SINR of the $i\text{-}\mathrm{th}$ task created by the ground device can be expressed as:

$${\mathrm{\Gamma }}_i^B={\displaystyle \frac{p_i{\left|h_i^B\right|}^2}{{\sigma }^2}}.$$

(3)

Assuming there are $C$ subcarriers in this OFDM system, ${\lambda }_{i,c}$ denotes the variable of subcarrier allocated, where ${\lambda }_{i,c}\in \left\{0,1\right\}$. When ${\lambda }_{i,c}$ is 1, the $i\text{-}\mathrm{th}$ task is offloaded to the BS via the $c\text{-}\mathrm{th}$ subcarrier. Otherwise, ${\lambda }_{i,c}$ is 0. Thus, the transmission rate for the $i\text{-}\mathrm{th}$ task can be expressed as:

$$R_i^B={\displaystyle \sum _{c=1}^C{\lambda }_{i,c}W {\log }_2\left(1+{\mathrm{\Gamma }}_i^B\right)},$$

(4)

where $W$ is the subcarrier bandwidth.

2.3. Relay Transmission Model

In addition to direct transmission, the detection devices can also choose the relay transmission model. This is divided into two phases. First, the device transmits the task to the relay located in the middle of the train, namely the sensor-to-relay (S2R) phase. Then, it is forwarded from the relay to the BS, which is the relay-to-BS (R2B) phase. To enhance spectrum utilization, we adopt Co-time Co-frequency Full Duplex (CCFD) [25]. This technology allows a relay to transmit and receive data simultaneously on the same channel. However, the received and transmitted signals on the same subcarrier will inevitably interfere with each other.

When the task is in the S2R phase, the onboard devices and the relay are relatively stationary, whereas the channel between the ground devices and the relay rapidly changes due to the Doppler effect. Thus, the S2R phase is the opposite of the direct communication model. The interference received by ground tasks needs to include ICI, while the onboard tasks do not require it. Furthermore, the signal received by the relay will be interfered with by the transmitted signal, and existing self-interference (SI) cancellation technologies can already eliminate the interference from the transmitted signal to a great extent.

Thus, during the S2R phase, the received SINR [26] of the $i\text{-}\mathrm{th}$ onboard device connected can be expressed as:

$${\mathrm{\Gamma }}_i^{S2R}={\displaystyle \frac{p_i{\left|h_i^{S2R}\right|}^2}{{\sigma }^2+\eta p_i^R}},$$

(5)

where ${\left|h_i^{S2R}\right|}^2$ is the channel gain between the $i\text{-}\mathrm{th}$ onboard device and the relay, $i\in \left\{1,\cdots ,M\right\}$, and $\eta$ denotes the SI cancelation level [26].

However, at this time, the received SINR of the $i\text{-}\mathrm{th}$ ground device connected can be expressed as:

$${\mathrm{\Gamma }}_i^{S2R}={\displaystyle \frac{p_i{\left|h_i^{S2R}\right|}^2}{\varpi p_i{\left|h_i^{S2R}\right|}^2+{\sigma }^2+\eta p_i}},$$

(6)

where $i\in \left\{M+1,\cdots ,M+N\right\}$.

Thus, during the S2R phase, the transmission rate of the $i\text{-}\mathrm{th}$ task can be expressed as:

$$R_i^{S2R}={\displaystyle \sum _{c=1}^C{\lambda }_{i,c}W {\log }_2\left(1+{\mathrm{\Gamma }}_i^{S2R}\right)}.$$

(7)

When the task is in the R2B phase, the relay moves at high speed relative to the BS, which can result in ICI caused by the Doppler effect. Thus, the SINR during the R2B phase can be expressed as:

$${\mathrm{\Gamma }}_i^{R2B}={\displaystyle \frac{p_i^R{\left|h^{R2B}\right|}^2}{\varpi p_i^R{\left|h^{R2B}\right|}^2+{\sigma }^2}},$$

(8)

where $p_i^R$ is the transmission power allocated to the $i\text{-}\mathrm{th}$ task and ${\left|h^{R2B}\right|}^2$ is the channel gain between the relay and the BS. During the R2B phase, the transmission rate of the $i\text{-}\mathrm{th}$ task can be expressed as:

$$R_i^{R2B}={\displaystyle \sum _{c=1}^C{\lambda }_{i,c}W {\log }_2\left(1+{\mathrm{\Gamma }}_i^{R2B}\right)}.$$

(9)

Since different subcarriers are allocated for the S2R and R2B transmission phases in the OFDM system, the relay can achieve full-duplex communication, which means it can receive and transmit at the same time. Thus, the transmission rate of the relay transmission model is determined by the slower phase and can be represented as:

$$R_i^R=\min \{R_i^{S2R},R_i^{R2B}\}.$$

(10)

2.4. NOMA-Based Transmission Model

When a task adopts the relay transmission model, the transmission power allocated by the relay often exceeds the transmission power of the device itself. Moreover, within a time slot, since the starting points of the tasks are all within the length range of the train and the transmission between the relay and the BS is often line-of-sight (LOS), the channel gain between the relay and the BS is always greater than that between the sensing device and the BS. As a result, the signal strength of the signal transmitted via the relay is higher than that of the signal from direct communication. Therefore, the NOMA-based transmission model [27] is viable. In this model, NOMA subcarriers can superimpose a group of signals with varying signal strengths. Signals in this group will interfere with one another. Successive Interference Cancellation (SIC) [28] technology can separate the signals in a group. SIC technology initially decodes the signal with the higher signal strength by treating the lower signal strength signal as interference. Then, it subtracts the decoded signal with high signal strength from the original signal. As a result, the remaining signal will be free of any additional interference.

After the relay transmission uses NOMA technology, the tasks uploaded in the R2B phase are considered signals with high signal strength. Thus, the interference they encounter needs to include the signal strength of the co-subcarrier signals. The transmission rate of the $i\text{-}\mathrm{th}$ task using NOMA can be expressed as:

$$R_i^{R2B\text{-}NOMA}={\displaystyle \sum _{c=1}^C{\lambda }_{i,c}^{NOMA}W {\log }_2\left(1+\frac{p_i^R{\left|h^{R2B}\right|}^2}{\varpi p_i^R{\left|h^{R2B}\right|}^2+{\sigma }^2+{\displaystyle \sum _{g=1}^A{\lambda }_{g,c}{p}_g{\left|h_g^B\right|}^2}}\right)},$$

(11)

where ${\displaystyle \sum _{g=1}^A{\lambda }_{g,c}{p}_g{\left|h_g^B\right|}^2}$ is the signal strength of the co-subcarrier signals. ${\lambda }_{i,c}^{NOMA}$ denotes the variable that indicates whether a subcarrier is allocated to the R2B-NOMA channel. It should be noted that the subcarriers allocated to the R2B-NOMA channel can overlap with any subcarriers allocated to direct transmission channels. However, these subcarriers must not overlap with those allocated to the relay transmission channel because their signal strengths are similar.

NOMA technology can increase the relay’s transmission rate on top of the existing OFDM system without altering the other two channels. Therefore, the total transmission rate when tasks choose the relay transmission model can be expressed as:

$$R_i^R=\min \{R_i^{S2R},R_i^{R2B}+R_i^{R2B\text{-}NOMA}\}.$$

(12)

2.5. Transmission Delay

For tasks using the direct transmission model, the transmission delay can be expressed as:

$$T_i^{uB}={\displaystyle \frac{l_i}{R_i^B}}.$$

(13)

For tasks using the relay transmission model, the transmission delay can be expressed as:

$$T_i^{uR}={\displaystyle \frac{l_i}{R_i^R}}.$$

(14)

For the $i\text{-}\mathrm{th}$ task, which can choose either of the two transmission models, the transmission delay can be expressed as:

$$T_i^u={\beta }_i{T}_i^{uB}+(1-{\beta }_i)T_i^{uR},$$

(15)

where ${\beta }_i$ is the model selection variable. When ${\beta }_i$ is 1, the task will use the direct transmission model. When ${\beta }_i$ is 0, the task will use the relay transmission model.

2.6. Computing Delay

We assume that the MEC servers communicate with each other via fiber optics, which allows us to neglect the delay. This means that a task can be processed by any server. However, considering the large volume of tasks generated by multiple trains within the entire railway range, deploying multiple servers near every base station along the entire railway is very expensive and wasteful. Thus, we consider the scenario where there is a limited number of MEC servers, meaning that not all tasks uploaded can be processed immediately. It is presumed that each server is limited to processing a single task concurrently. Additionally, the tasks within a time slot significantly outnumber the servers available to handle them.

In this system, there are $K$ MEC servers available in a time slot, denoted by $\mathcal{K}=\left\{1,2,\cdots ,K\right\}$. We use a tuple $⟨f_k,q_k^{\max }⟩$ to describe the performance of an MEC server, where $f_k$ denotes the computational capability of the $k\text{-}\mathrm{th}$ server and $q_k^{\max }$ denotes the memory capacity of the server. Let $z_{i,k}\in \left\{0,1\right\}$ denotes the variable of server allocation, where $k\in \mathcal{K}$. When $z_{i,k}$ is 1, the $i\text{-}\mathrm{th}$ task is processed on the $k\text{-}\mathrm{th}$ server. Otherwise, $z_{i,k}$ is 0. For the task processing order on the same server, we adopt the First-Come First-Served (FCFS) principle. The system can control the allocation of communication resources to allow tasks with the smaller maximum allowable delay to reach the server first, thereby prioritizing their processing. Let $o_{i,j}\in \left\{0,1\right\}$ denote the arrival order of the $i\text{-}\mathrm{th}$ task, where $j\in \mathcal{J}$, $\mathcal{J}=\left\{1,2,\cdots ,J\right\}$, $J=I$. $o_{i,j}=1$ indicates that the $i\text{-}\mathrm{th}$ task is the $j\text{-}\mathrm{th}$ to arrive. The matrix composed of $z_{i,k}$ is denoted as $Z_{I\ast K}$. The matrix composed of $o_{i,j}$ is denoted as $O_{I\ast J}$. Let matrix ${\mathrm{\Psi }}_{K\ast J}$ be the result of the cross product of matrices ${Z_{I\ast K}}^T$, ${\mathrm{\Phi }}_{I\ast I}$, $O_{I\ast J}$, denoted as ${\mathrm{\Psi }}_{K\ast J}={Z_{I\ast K}}^T\times {\mathrm{\Phi }}_{I\ast I}\times O_{I\ast J}$, where ${\mathrm{\Phi }}_{I\ast I}=diag\left(1,2,\cdots ,I\right)$, ${\psi }_{k,j}=i$ denote that on the $k\text{-}\mathrm{th}$ server, the $i\text{-}\mathrm{th}$ task is the $j\text{-}\mathrm{th}$ in the queue to be processed.

Thus, the total delay of the $i\text{-}\mathrm{th}$ task can be expressed as:

$$T_{{\psi }_{k,j}}=\{\begin{array}{c}{T}_{{\psi }_{k,j}}^u+T_{{\psi }_{k,j}}^c,j=1\\ \max \{T_{{\psi }_{k,j}}^u,T_{{\psi }_{k,j-1}}\}+T_{{\psi }_{k,j}}^c,j\ge 2\end{array},$$

(16)

where $T_{{\psi }_{k,j-1}}$ denotes the total delay from the start of a time slot to the completion of the task at the $j\text{-}\mathrm{th}$ position in the queue on the $k\text{-}\mathrm{th}$ server, $T_{{\psi }_{k,j}}^c$ denotes the computing delay that a server computing task ${\psi }_{k,j}$ costs, $T_{{\psi }_{k,j}}^c=l_{{\psi }_{k.j}}\cdot {\mu }_{{\psi }_{k,j}}/f_k$. Specifically, both $T_0^u$ and $T_0^c$ are equal to 0.

In addition, the maximum queue length of tasks being processed on the $k\text{-}\mathrm{th}$ server can be expressed as:

$$q_k=\underset{j\in }{{\displaystyle \max }}\left\{{\displaystyle \sum _{g=1}^j\left(l_{{\psi }_{k,g}}+L_{{\psi }_{k,g}}\right)}-{\displaystyle \sum _{g=1}^{j^{\prime }}\left(l_{{\psi }_{k,g}}+L_{{\psi }_{k,g}}\right)}\right\},$$

(17)

where ${\displaystyle \sum _{g=1}^j\left(l_{{\psi }_{k,g}}+L_{{\psi }_{k,g}}\right)}$ denotes the total length of tasks on the $k\text{-}\mathrm{th}$ server after the $j\text{-}\mathrm{th}$ task arrives and ${\displaystyle \sum _{g=1}^{j^{\prime }}\left(l_{{\psi }_{k,g}}+L_{{\psi }_{k,g}}\right)}$ denotes the length of tasks that have been processed so far.

2.7. Problem Formulation

We aim to minimize the average delay ratio through the joint optimization of communication and computational resources. The delay ratio refers to the proportion of the actual delay to the maximum allowable delay. Thus, we take the computation offloading strategy as the decision variable, with communication, computation, and memory resources as constraints, aiming to minimize the average delay ratio as the optimization objective. The problem formulation can be expressed as follows:

$$\begin{array}{l}\underset{p,\lambda ,\beta ,z}{{\displaystyle \min }}{\displaystyle \frac{1}{I}}{\displaystyle \sum _{i=1}^I\frac{T_i}{T_i^{\max }}}\\ s.t.\hspace{1em}\mathrm{C}1:{\displaystyle \sum _{i=1}^I\left(1-{\beta }_i\right)p_i^R}\le p_{\max }\\ \hspace{1em}\hspace{1em}\mathrm{C}2:{\displaystyle \sum _{i=1}^I{\lambda }_{i,c}}\le 1\\ \hspace{1em}\hspace{1em}\mathrm{C}3:{\displaystyle \sum _{c=1}^C\left({\lambda }_{i,c}^{NOMA}\cdot {\displaystyle \sum _{i=1}^I\left(1-{\beta }_i\right){\lambda }_{i,c}}\right)}=0\\ \hspace{1em}\hspace{1em}\mathrm{C}4:{\displaystyle \sum _{k=1}^K{z}_{i,k}}=1\\ \hspace{1em}\hspace{1em}\mathrm{C}5:T_i\le T_i^{\max }\\ \hspace{1em}\hspace{1em}\mathrm{C}6:q_k\le q_k^{\max }\end{array},$$

(18)

where constraint C1 denotes that the total sum of transmit power allocated to tasks using the relay transmission model cannot exceed the relay’s maximum transmission power. Constraint C2 denotes that tasks using OFDM cannot share a subcarrier. Constraint C3 denotes that subcarriers allocated to the NOMA system cannot overlap with those allocated to the R2B channel. Constraint C4 denotes that a task can only be allocated to one server and must be allocated to a server. Constraint C5 denotes that the total delay of a task cannot exceed the maximum tolerable delay. Constraint C6 denotes that the queue of tasks being processed and awaiting processing on the server cannot exceed the memory capacity of the server.

3. DDPG-Based Resource Allocation Algorithm

3.1. Subcarrier Allocation Algorithm

The performance of NOMA systems is affected by the difference in signal strengths between relayed and direct communications. A larger disparity in signal strength can yield better performance gains. Conversely, a minimal difference in signal strength can result in poor system performance and may even preclude the separation of the two signals. Therefore, we propose a low-complexity subcarrier matching strategy. This algorithm aims to reduce the likelihood of a small intensity gap between two signals, preventing the assignment of a relay communication signal with a lower intensity to a subcarrier of a direct communication signal with a higher intensity, which would make it impossible to decode and separate the two. While this algorithm may not be optimal, it allows NOMA technology to be stably compatible with the entire system. Employing this approach, the complex issue of allocating subcarriers in high dimensions can be simplified by distributing quantities of subcarriers. The step-by-step procedure for this method is outlined in the pseudocode as Algorithm 1.

Algorithm 1: Subcarrier Allocation Algorithm

Input: ${\delta }_i$$,{\delta }_i^{NOMA}$

Output: ${\lambda }_{a,c}$$,{\lambda }_{a,c}^{NOMA}$

1: Randomly allocate subcarriers to tasks based on the number of subcarriers ${\delta }_i$ assigned to the tasks, and obtain ${\lambda }_{a,c}$.

2: Sort the subcarriers for tasks that use the direct allocation model in descending order by signal strength.

3: Sort the tasks that use the relay communication model in descending order by the power allocated to the relay.

4: Based on the number of subcarriers ${\delta }_i^{NOMA}$ allocated to the R2B-NOMA channel, allocate subcarriers with higher signal strength to tasks with higher relay power, and obtain ${\lambda }_{a,c}^{NOMA}$.

5: Return ${\lambda }_{a,c}$ and ${\lambda }_{a,c}^{NOMA}$

Thus, the optimization problem of Equation (18) can be transformed into the following form:

$$\begin{array}{l}\underset{p,\lambda ,\beta ,z}{{\displaystyle \min }}{\displaystyle \frac{1}{I}}{\displaystyle \sum _{i=1}^I\frac{T_i}{T_i^{\max }}}\\ s.t.\hspace{1em}\mathrm{C}1:{\displaystyle \sum _{i=1}^I\left(1-{\beta }_i\right)p_i^R}\le p_{\max }\\ \hspace{1em}\hspace{1em}\mathrm{C}2:{\displaystyle \sum _{i=1}^I{\delta }_i}\le C\\ \hspace{1em}\hspace{1em}\mathrm{C}3:{\displaystyle \sum _{i=1}^I{\delta }_i^{NOMA}}\le {\displaystyle \sum _{i=1}^I\left(1-{\beta }_i\right){\delta }_i}\\ \hspace{1em}\hspace{1em}\mathrm{C}4\sim \mathrm{C}6\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\end{array},$$

(19)

where constraint C2 denotes that the aggregate sum of subcarriers assigned to all tasks must not surpass the total quantity of subcarriers at disposal, and constraint C3 denotes that the sum of subcarriers allocated to the R2B-NOMA channel cannot surpass the sum of subcarriers allocated to tasks using direct transmission models. All other constraints remain unchanged.

3.2. MDP Model

Since the problems of relay power allocation and server selection are non-convex, securing the optimal solution through conventional optimization techniques proves to be challenging. Thus, an MDP is introduced to effectively learn policies in complex environments. The aforementioned optimization problem can be formulated as an MDP, denoted as $\mathcal{M}=\left(\mathcal{S},\mathcal{A},\mathcal{P},r,\gamma \right)$, where components align with the state space, action space, state transition matrix, reward function, and discount factor of the problem, in that order.

Observation: in time slot $t$, the state space includes the basic information of the detection task and the data transmission rates between the sensors and BS, as well as between the sensors and the relay. In time slot $t$, the state space $S_t\in \mathcal{S}$ can be expressed as follows:

$$S_t=\left\{l_t,{\mu }_t,T_t^{\max },L_t,p_t,{\left|h_t^B\right|}^2,{\left|h_t^{S2R}\right|}^2\right\},$$

(20)

where $l_t$ is the data size in time slot $t$, ${\mu }_t$ is the computation workload in time slot $t$, $T_t^{\max }$ is the maximum allowable delay in time slot $t$, $L_t$ represents the data size of the neural network model to be loaded and the intermediate data generated in time slot $t$, $p_t$ is the power of the devices, ${\left|h_t^B\right|}^2$ is the data transmission rates between the sensors and BS, and ${\left|h_t^{S2R}\right|}^2$ is the data transmission rates between the sensors and the relay.

Action: in time slot $t$, the action space includes communication and computation resource allocation strategies. In time slot $t$, the action space $A_t\in \mathcal{A}$ can be expressed as follows:

$$A_t=\left\{{\beta }_t,{\delta }_t,{\delta }_t^{NOMA},p_t^R,z_t\right\},$$

(21)

where ${\beta }_t\in \left\{0,1\right\}$ is the selected model, ${\delta }_t$ is the number of subcarriers allocated to the tasks, ${\delta }_t^{NOMA}$ is the number of subcarriers allocated to the R2B-NOMA channel, $p_t^R$ is the power allocated to the task by the relay, and $z_t\in \left\{1,2,\cdots ,k\right\}$ is the server selection strategy.

Reward: the objective of the joint optimization problem of computation offloading and resource allocation is to minimize the average delay ratio. However, the aim of training with reinforcement learning is to optimize the total accumulated reward over time. Concurrently, tasks that surpass the threshold of the maximum allowable delay will trigger a predefined penalty. Thus, the reward for the $i\text{-}\mathrm{th}$ task in time slot $t$ can be expressed as follows:

$$r_{i,t}=\{\begin{array}{cc}-{\displaystyle \frac{T_i}{T_i^{\max }}},& T_i\le T_i^{\max }\hfill \\ \hspace{1em}-\epsilon ,& T_i>T_i^{\max } or Q_k>Q_k^{\max }\left(z_{i,k}=1\right)\hfill \end{array},$$

(22)

where $\epsilon$ is the absolute value of the penalty.

Thus, the total reward in time slot $t$ can be expressed as follows:

$$r_t={\displaystyle \frac{1}{I}}{\displaystyle \sum _{i=1}^I{r}_{i,t}}.$$

(23)

3.3. Improved Deep Deterministic Policy Gradient Algorithm

Given that the action space comprises both continuous and discrete variables, the DDPG algorithm demonstrates commendable performance in addressing continuous action control problems.

The DDPG algorithm merges the aspects of actor–critic algorithms with deep learning techniques to enable effective policy learning in high-dimensional, continuous action spaces. The core of DDPG lies in learning a deterministic policy, which specifies the action to be taken in each state, along with a Q-function that estimates the expected returns. The architecture of the DDPG algorithm is shown in Figure 2.

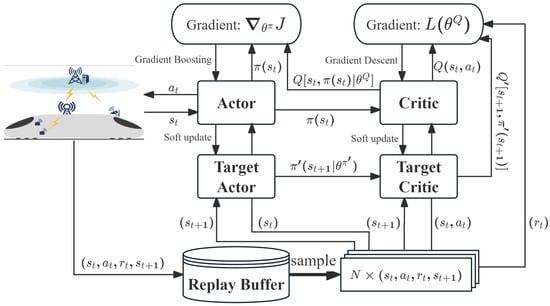
Figure 2. The architecture of the DDPG algorithm.

The Q-function, which estimates the expected reward of taking an action $A_t$ in state $S_t$, following a policy $\pi$, is defined as $Q\left(s_t,a_t|{\theta }^Q\right)$, where ${\theta }^Q$ are the parameters of the critic network. The expected return from the Q-function is computed as:

$$Q(s_t,a_t)=\mathbb{E}\left[R_t\left(s_t,a_t\right)\right],$$

(24)

where the return $R_t$ is the sum of the immediate reward $r$ and the discounted future rewards, and is given by:

$$R_t\left(s_t,a_t\right)=r\left(s_t,a_t\right)+\gamma Q\left[s_{t+1},\pi \left(s_{t+1}|{\theta }^{\pi }\right)\right],$$

(25)

where $\gamma$ is the discount factor that balances immediate and future rewards.

The objective of the critic network is to reduce the mean squared error, focusing on bringing the forecasted Q-values in line with the target Q-values as described by the following function:

$$L({\theta }^Q)={\displaystyle \frac{1}{N}}{\displaystyle \sum }_t{\left[y_t-Q\left(s_t,a_t|{\theta }^Q\right)\right]}^2,$$

(26)

where $y$ is the target value defined as:

$$y_t=r_t+\gamma Q^{\prime }\left[s_{t+1},{\pi }^{\prime }\left(s_{t+1}|{\theta }^{{\pi }^{\prime }}\right)|{\theta }^{Q^{\prime }}\right],$$

(27)

where $Q^{\prime }$ and ${\pi }^{\prime }$ represent the target critic and target actor networks, respectively.

The policy gradient for updating the actor network is derived from the critic network and is calculated using the sampled gradients of the Q-function with respect to the actions [14]:

$${\nabla }_{{\theta }^{\pi }}J\approx {\displaystyle \frac{1}{N}}{\displaystyle \sum _t{\nabla }_{\pi }Q\left[s_t,\pi \left(s_t\right)|{\theta }^Q\right]\cdot {\nabla }_{{\theta }^{\pi }}\pi \left(s_t|{\theta }^{\pi }\right)}.$$

(28)

Finally, the actor network is updated through gradient ascent using the policy gradient, adjusting the parameters ${\theta }^{\pi }$ in the direction that maximizes the Q-function:

$${\theta }^{\pi }\leftarrow {\theta }^{\pi }+\alpha {\nabla }_{{\theta }^{\pi }}J,$$

(29)

where $\alpha$ is the learning rate.

The pseudocode for the training process of the DDPG algorithm is presented in Algorithm 2.

Algorithm 2: The Training Process of DDPG Algorithm

1: Use random network weights ${\theta }^{\pi }$ and ${\theta }^Q$ initializing actor network and critic network, respectively

2: Copy the same weights ${\theta }^{{\pi }^{\prime }}\leftarrow {\theta }^{\pi }$ and ${\theta }^{Q^{\prime }}\leftarrow {\theta }^Q$ to initialize the target networks, respectively

3: Initialize replay buffer $\mathcal{B}$

4: for episode = 1 to M do

5:   Initialize a random process $\mathcal{N}$ for action exploration

6:   Obtain initial observation state $s_1$

7:   for time-step = 1 to T do

8:    Select action $a_t=\pi \left(s_t|{\theta }^{\pi }\right)+{\mathcal{N}}_t$ using the current policy affected by noise

9:    Perform action $a_t$ and observe reward $r_t$ and new state $s_{t+1}$

10:    Store transition $\left(s_t,a_t,r_t,s_{t+1}\right)$ in $\mathcal{B}$

11:    Sample a random minibatch of $N$ transitions $\left(s_t,a_t,r_t,s_{t+1}\right)$ from $\mathcal{B}$

12:    Set $y_t=r_t+\gamma Q^{\prime }\left[s_{t+1},{\pi }^{\prime }\left(s_{t+1}|{\theta }^{{\pi }^{\prime }}\right)|{\theta }^{Q^{\prime }}\right]$ for non-terminal states

13:    Update critic by minimizing the loss: $L({\theta }^Q)={\displaystyle \frac{1}{N}}{\displaystyle \sum _t}{\left[y_t-Q\left(s_t,a_t|{\theta }^Q\right)\right]}^2$

14:    Update the actor policy using the sampled policy gradient:

15:     ${\nabla }_{{\theta }^{\pi }}J\approx {\displaystyle \frac{1}{N}}{\displaystyle {\displaystyle \sum }_t{\nabla }_{\pi }Q\left[s_t,\pi \left(s_t\right)|{\theta }^Q\right]\cdot {\nabla }_{{\theta }^{\pi }}\pi \left(s_t|{\theta }^{\pi }\right)}$

16:    Update the target networks:

17:     ${\theta }^{{\pi }^{\prime }}\leftarrow \tau {\theta }^{\pi }+\left(1-\tau \right){\theta }^{{\pi }^{\prime }}$

18:     ${\theta }^{Q^{\prime }}\leftarrow \tau {\theta }^Q+\left(1-\tau \right){\theta }^{Q^{\prime }}$

19:   end for each time-step

20: end for each episode

However, the DDPG algorithm does not perform well with certain discrete variables, especially those that represent the selection of indices. Therefore, we modified the architecture of the actor network, as shown in Figure 3. Actions ${\beta }_t$ and $Z_t$ in the action space $A_t$ are exactly such discrete variables. Although for ${\beta }_t$, which is a binary variable, the tanh function can effectively solve the binary classification problem. As for the variable $Z_t$, if the number of servers is more than two, this becomes a multi-class variable, and common activation functions struggle to address this issue. We process $z_t$ as follows:

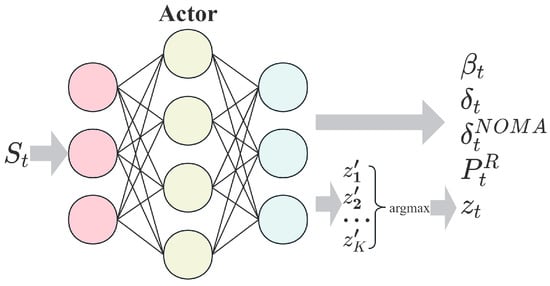
Figure 3. The architecture of actor network.

We replace $z_t$ in the action space with $Z_t^{\prime }$, where $Z_t^{\prime }$ is an $I\ast K$ matrix and $z_{i,k}^{\prime }$ represents the probability of choosing the $k\text{-}\mathrm{th}$ server for the $i\text{-}\mathrm{th}$ task. We select the server number $k$ with the highest probability as the choice strategy for the $i\text{-}\mathrm{th}$ task, which can be expressed as $z_i=\arg \underset{k\in \mathcal{K}}{\max }{z}_{i,k}^{\prime }$.

The optimization problem represented by Equation (17) can be effectively addressed by improving the DDPG algorithm through the aforementioned approach for discrete variables, in conjunction with the channel allocation algorithm presented in Section 4.1.

4. Simulation Results and Discussion

In this section, we use simulation experiments to evaluate the system model proposed in Section 3 and the algorithm presented in Section 4. The simulation results are obtained using Python 3.7 and Tensorflow 2.11 on a machine powered by an Intel Core i5-13400F CPU with an NVIDIA GeForce RTX 4060Ti GPU.

4.1. Simulation Setting

In real-world train detection scenarios, the generation of detection tasks is cyclical and patterned. To demonstrate the effectiveness of the system model and algorithms, we set the task generation locations to be random yet confined within the length range of the train. This is because ground detection equipment only generates tasks when the train passes by. Furthermore, the parameters describing the tasks are also random. Specifically, the task data length $l_i$ follows a uniform distribution of [1, 4] Mbits, the computation workload ${\mu }_i$ follows a uniform distribution of [800, 1000] cycles/bit, the maximum allowable delay $T_i^{\max }$ follows a uniform distribution of [1, 4] seconds, the loaded data size $L_i$ follows a uniform distribution of [15, 25] Mbits, and the power of the devices $p_i$ follows a uniform distribution of [0.1, 0.5] W [29]. For the entire railway system, the allocation of subcarrier numbers to each train, the number of available servers, and other parameter settings could be considered a queuing theory problem for optimization allocation. However, this is beyond the scope of this paper. Therefore, we assume that these parameters are pre-allocated and fixed. Specifically, the number of servers $k$ is set to 3, with computational capability $f_k$ of 7 GHz and maximum memory capacity $Q_k^{\max }$ of 128 Mbits. In addition, for the algorithm proposed in Section 4, the absolute value of the penalty $\epsilon$ is set to 5. Other determined parameters are provided in Table 1.

Table 1. Simulation parameters.

Parameter	Value
Number of subcarriers $\mathrm{\Lambda }$	256
Subcarrier bandwidth $W$	15 KHz
Carrier frequency $f_c$	3 GHz
Noise power ${\sigma }^2$	−130 dBm
Train speed $v$	300 km/h
Power of relay $p_{\max }$	20 W
signal symbol duration [30]: ${\tau }_s$	4 µs

We compare the proposed improved DDPG algorithms with standard DDPG as a benchmark algorithm, which was used in [31]. Then, we compare the system model proposed in Section 2 with three benchmark schemes as follows:

Full Direct Communication (FDC): As in the task offloading scheme for HSR described in [5], all detection tasks will be directly offloaded to the edge servers in this scheme.

Full Relay Communication (FRC): In this scheme, all detection tasks choose the relay communication model.

OFDM: In this scheme, no tasks will employ NOMA technology for transmission.

4.2. Result Analysis

In reinforcement learning algorithms, batch size is a critical hyperparameter. Smaller batch sizes can enhance generalization and facilitate the escape from local optima but may increase variance, affecting learning stability. Larger batch sizes provide more accurate gradient estimates, though they may lead to local optima and increased memory requirements. Figure 4 shows the influence of batch size on convergence. The calculation method of the reward is shown in Equation (23). The DDPG algorithm obtains rewards through interaction with the environment and learns to achieve higher rewards. Higher rewards also imply a lower average delay ratio. Despite the initial rapid increase and subsequent stabilization of the reward curves across four batch sizes, it indicates that our improved DDPG algorithm can learn a stable computation offloading policy. Notably, a batch size of 64 yields better rewards. Therefore, we set the batch size to 64 in subsequent simulations.

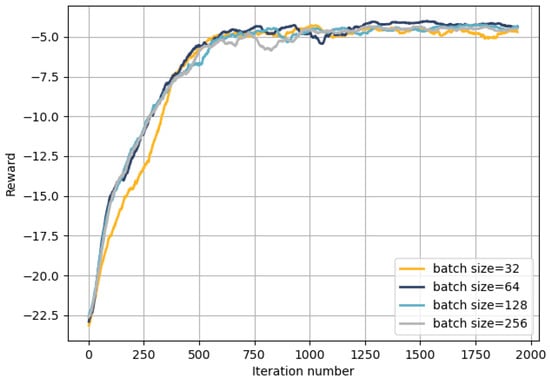
Figure 4. Influence of batch size on convergence.

Additionally, the learning rate is a crucial hyperparameter. Figure 5 shows the impact of different learning rates on training outcomes. It can be observed from the figure that the convergence of the improved DDPG algorithm is highly sensitive to the learning rate. When the learning rate is too low, the training process converges to a local optimum. This is also the reason for the reward curve’s pattern of the initial increase followed by a decline, ultimately making it challenging to achieve satisfactory training outcomes. Conversely, when the learning rate is too high, the parameters fluctuate too violently during training, making it difficult to converge to a desirable solution and resulting in significant volatility. However, it is evident that setting the learning rate to 0.00001 leads to stable convergence and superior performance. Therefore, in subsequent simulations, we will set the learning rate to 0.00001.

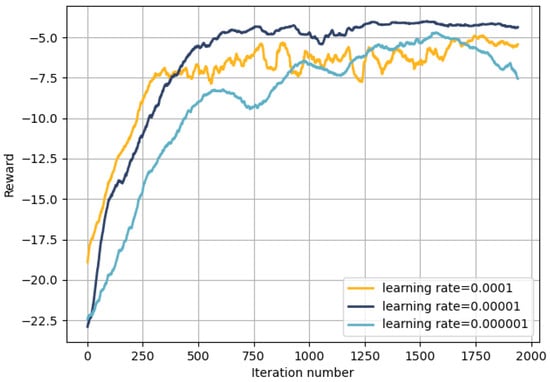
Figure 5. Influence of learning rate on convergence.

Figure 6 shows the average delay ratio and success rate under different absolute values of penalty $\epsilon$ when the number of devices is 20 (high load). In Figure 6a, the average delay ratio increases with the increase in $\epsilon$. However, when $\epsilon \ge 4$, the average delay ratio is not sensitive to changes in $\epsilon$. Within a 300% variation range of $\epsilon$, the average delay ratio only fluctuates by 2.27%. Due to the randomness of the simulation environment, these fluctuations are acceptable. In Figure 6b, the success rate also shows an increasing trend as $\epsilon$ increases. When $\epsilon \ge 4$, the success rate is also not sensitive to changes in $\epsilon$. Within a 300% variation range of $\epsilon$, the average delay ratio only fluctuates by 0.71%. By comparing these two figures, we can observe that when $\epsilon \le 3$, our proposed algorithm sacrifices the success rate to achieve a lower average delay ratio, as the penalty strength is not sufficient. Although a larger $\epsilon$ reduces algorithm errors and leads to a higher success rate, when $\epsilon \ge 4$, disregarding the bias in the training effect, we can consider the training effect of the algorithm to be stable and not sensitive to changes in $\epsilon$. However, when $\epsilon$ is too large, an increase in the number of tasks may cause the Q value to exceed the floating-point limit. Thus, setting $\epsilon$ as 5 is reasonable.

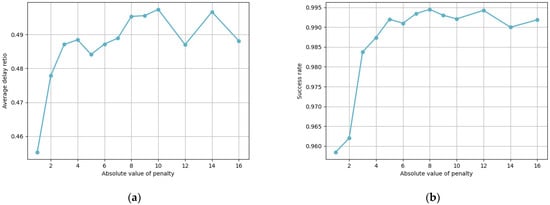
Figure 6. Simulation results of penalty. (a) Average delay ratio against absolute value of penalty; (b) success rate against absolute value of penalty.

In Figure 7, we demonstrate the performance comparison of our proposed improved DDPG algorithm against the standard DDPG algorithms mentioned in Section 4.1 under both low- and high-load conditions by varying the number of onboard and ground sensors. In Figure 7a, the numbers of both types of sensors are set to 5, whereas in Figure 7b, they are set to 10. It was observed that under low-load conditions, all algorithms show good performance, with the improved DDPG slightly outperforming the others. However, under high-load conditions, the differences between algorithms became more pronounced. Compared to the standard DDPG, our improved DDPG algorithm is able to find more optimal offloading strategies. This indicates its efficacy in handling hybrid action space problems and higher-dimensional action spaces.

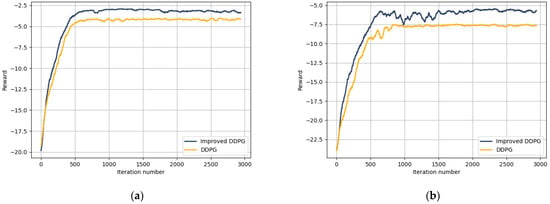
Figure 7. Simulation results of different algorithms. (a) Comparison of algorithm (number of devices is 10); (b) comparison of algorithm (number of devices is 20).

Figure 8 illustrates the average delay ratio and completion rate for different schemes. In the HSR scenario, a lower delay means anomalies can be detected more quickly, allowing for more time to respond; a higher success rate ensures that no details are missed, enhancing the completeness and meticulousness of the detection. Overall, these two metrics reflect the contribution of different schemes to safety.

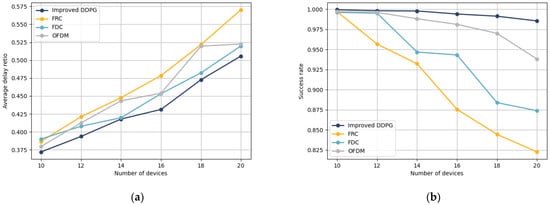
Figure 8. Simulation results of different schemes. (a) Average delay ratio against the number of devices; (b) the success rate against the number of devices.

Figure 8a demonstrates the trend of the average delay ratio obtained by different schemes as the number of devices varies. It should be noted that the quantity of the two types of devices is identical here. It is clear that the average delay ratio for each algorithm increases with the number of devices. When compared to the FDC, OFDM, and FRC schemes mentioned in Section 4.1, our scheme proposed in Section 2 consistently achieves lower delay ratios, reducing it by 4.69%, 6.56%, and 11.84%, respectively. This is attributed to the different channel conditions and interference that ground and onboard sensors experience under various transmission modes. Comparing the FDT and FDR schemes, we can demonstrate that our proposed approach better adapts to detection-oriented scenarios in railway IoT. The combination of these two transmission models allows for a more suitable transmission model for each detection task. Furthermore, the comparison with the OFDM scheme demonstrates that the introduction of NOMA technology indeed increases channel capacity, resulting in higher overall transmission rates and lower delay ratios. In summary, our proposed computation offloading model consistently delivers superior performance across different task quantities.

Figure 8b demonstrates the success rate trends of different schemes as the number of devices varies in the simulation. With an increase in device quantity, the success rate of each scheme generally decreases. Compared with the FDC, OFDM, and FRC schemes mentioned in Section 4.1, the scheme we proposed in Section 2 consistently achieves a higher completion rate. Specifically, in high-load environments, the failure rate is reduced by 89.6%, 64.9%, and 96.7%, respectively. This also indicates that our proposed scheme can better adapt to detection tasks in railway IoT. Furthermore, comparing the FDC and OFDM schemes in Figure 7, it is evident that FDC shows a lower delay ratio, while OFDM achieves higher completion rates. This observation reinforces the notion that a faster transmission rate is not always preferable. The server queue is closely linked to the task arrival time, influenced by the transmission rate. Excessive speed may result in server queue backlogs that exceed memory capacity. Thus, our enhanced DDPG algorithm effectively allocates communication and computational resources.

5. Conclusions

This study explores the dynamic resource management problem in the scenario of railway IoT systems with integrated sensing, storage, and computing, specifically focusing on the computation offloading for detection tasks. By optimizing subcarrier allocation, transmission mode selection, relay power allocation, and server selection, the objective is to minimize the average delay ratio, which is the ratio between the delay and the maximum tolerable delay. To address this problem, a low-complexity subcarrier allocation algorithm is proposed to reduce the action space dimension. Furthermore, an improved DDPG algorithm is proposed, which represents discrete variables using selection probabilities to handle the hybrid action space problem. Through simulation experiments, the performance of the improved DDPG algorithm is evaluated against existing benchmark schemes and algorithms, some of which referenced existing literature. The results indicate that the MEC system proposed in this paper can achieve a lower average delay ratio and a higher completion rate, demonstrating significant advantages over other schemes and algorithms, especially under high-load conditions. This also means that HSR will have a more secure guarantee. The findings also highlight the adaptability of the proposed MEC system model for detection tasks in HSR environments.

Through simulation, our proposed MEC system demonstrates lower average latency ratios and higher completion rates compared to other literature. In addition, due to its excellent adaptability, our proposed MEC system could be compatible with various types of rail transportation. However, the ultimate goal is to deploy it in a real HSR environment. However, the deployment of edge servers and online monitoring equipment is a significant undertaking. Future work will focus on the practical deployment of MEC, particularly in dealing with real-world network conditions. We will further collect data and conduct performance tests on the proposed MEC system to analyze its potential applications in various rail transit scenarios. Future work will also include research on potential issues such as energy consumption and security.