Current-Mode Active Filter Using EX-CCCII

Abstract

This paper presents a novel multiple-input and multiple-output current-mode universal analog filter with electronic tuning capability. The proposed circuit uses a single second-generation current-controlled current conveyor with extra-X terminals (EX-CCCII) and two grounded capacitors. The filter can offer five standard filtering functions, namely low-pass, high-pass, band-pass, band-stop, all-pass responses, in the same circuit without changing the internal configuration of the filter by selecting appropriate input and output signals. To obtain the five standard filtering functions, inverted input signal and input matching conditions are absent. The natural frequency of all filter responses can be electronically controlled. The proposed circuit was simulated by SPICE using 0.18 μm CMOS process from Taiwan Semiconductor Manufacturing Company (TSMC). The results of experiments using the integrated circuit operational amplifier AD844 confirm the functionality of the new filter.

1. Introduction

In many circuit designs, a second-generation current conveyor (CCII) is utilized to realize analog signal processing circuits, especially current-mode signal processing circuits. The circuits using CCII as an active element offer higher linearity, better signal bandwidth, and wider dynamic range compared to the operational amplifier (op-amp) based circuits [1,2]. Moreover, CCII is simpler to implement compared to the op-amp structure. There are many CCII structures available in literature [3,4,5,6,7,8,9,10,11,12,13,14,15]. In [3], a conventional CCII that has three terminals (the y-, x-, z-terminals) is proposed. This CCII provides the characteristics of V_y = V_x, I_x = I_z, a high resistance at the y- and z-terminals (ideally infinite), and a low resistance at the x-terminal (ideally zero). In practice, however, the resistance at the x-terminal is not equal to zero as it exhibits a parasitic resistance. In [4], a current-controlled CCII (CCCII) is introduced. Due to the CCCII, the parasitic resistance at the x-terminal (R_x) can be used as a parameter for filter application and this R_x can be electronically controlled. Moreover, the CCCII-based circuit does not contain a passive resistor. Note that the CCCII still has a single x-terminal, like the CCII.

Recently, the extra x-terminal CCII (EX-CCII) has been introduced [5]. This device is an enhancement of the conventional CCII, which increases the number of x- and z-terminals.

Figure 1 shows the electrical symbol of the conventional CCII and the EX-CCII. Compared with the conventional CCII in Figure 1a, the EX-CCII in Figure 1b has extra x-input terminals and z-output terminals. The characteristics of the EX-CCII can be given by V_y = V_x1 = V_x2, I_x1 = I_z1, and I_x2 = I_z2. In addition, the number of x-input terminals and z-output terminals of the EX-CCII can be increased to any number. Thus, the EX-CCII is a versatile and flexible active device. There are many applications of the EX-CCII available in literature, including precision rectifiers [6,7,8,9], fractional-order controllers [10,11,12], digital modulators [13], analog multipliers [14], wave signal generators [15], first-order filters [16,17], and universal filters [18]. It is worth noting that the EX-CCII based circuit does not provide electronic tuning capability.

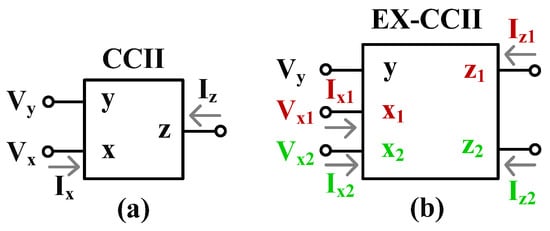
Figure 1. Electrical symbol of (a) a conventional CCII and (b) an EX-CCII.

If the parasitic resistance at the x-terminal of the EX-CCII is considered, then the circuit becomes EX-CCCII and its parasitic resistances at the x-terminals can be used as an adjustable parameter. This is advantageous for applications such active filters and oscillators. The EX-CCCII can be used for applications such as oscillators [19,20,21,22,23], instrumentation amplifiers [24,25], immittance simulators [26], precision rectifiers [27], first-order filters [28,29,30], and universal filters [31,32,33,34]. This work focuses on the EX-CCCII based universal filter. Considering the universal filters in [31,32,33,34], these filters suffer from some drawbacks. First, in order to obtain the five filtering functions (i.e., the low-pass filter (LPF), high-pass filter (HPF), band-pass filter (BPF), band-stop filter (BSF), and all-pass filter (APF)), the filters use inverted input signals and require input matching condition [31,32,33,34]. Second, the filters use passive component matching conditions [34]. The use of a single EX-CCCII based filter, made possible through the use of the current-mode technique, is advantageous in these universal filters [31,32,33,34]. Note that the realization of signal addition and subtraction in current-mode circuits is easier than for their voltage-mode counterparts.

This work proposes a single EX-CCCII-based current-mode universal filter. It is a multiple-input and multiple-output filter providing five standard filtering functions, namely low-pass, high-pass, band-pass, band-stop, and all-pass functions, that can be obtained by selecting appropriate input and output terminals. The proposed filter offers the following advantages: (i) it uses a single EX-CCCII; (ii) it does not require inverted input signals or the fulfilment of input matching conditions to realize the five standard filtering functions; (iii) it does not require matching of passive components; (iv) it offers electronic tuning capability of a natural frequency.

The rest of this paper is organized as follows: Section 2 provides a description of the proposed EX-CCCII and the proposed current-mode universal filter. Section 3 and Section 4 present the simulation and experimental results, respectively. Section 5 concludes the paper.

2. Circuit Description

This section contains four subsections, where the first subsection introduces the second generation current-controlled current conveyor with extra-x terminal that is used for realizing the proposed filter. The second subsection introduces the proposed current-mode universal filter, while the non-ideal gain analysis and non-ideal parasitic analysis are presented in the third and fourth subsections, respectively.

2.1. Second-Generation Current-Controlled Current Conveyor with Extra-X Terminal

Figure 2a shows the electrical symbol of the EX-CCCII and Figure 2b shows the equivalent circuit. The input voltage present at the y-terminal is conveyed to the x₁- and x₂-terminals. R_x1 and R_x2 are the parasitic resistances at the x₁- and x₂-terminals, respectively, that can be controlled by the DC biasing current.

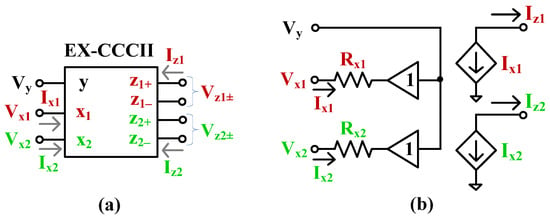
Figure 2. EX-CCCII (a) electrical symbol, (b) equivalent circuit.

The input current at the x₁- and x₂-terminals is conveyed to the z₁- and z₂-terminals, respectively. The minus-type output of the z₁- and z₂-terminals can easily be obtained using a cross-coupled current mirror topology. Thus, the port relationships of the ideal EX-CCCII shown in Figure 2a can be given by

$$\left(\begin{array}{c}{I}_y\\ V_{x1}\\ V_{x2}\\ I_{z1}\\ I_{z2}\end{array}\right)=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 1& R_{x1}& 0& 0& 0\\ 1& 0& R_{x2}& 0& 0\\ 0& \pm 1& 0& 0& 0\\ 0& 0& \pm 1& 0& 0\end{array}\right)\left(\begin{array}{c}{V}_y\\ I_{x1}\\ I_{x2}\\ V_{z1}\\ V_{z2}\end{array}\right)$$

(1)

The CMOS structure of the EX-CCCII in Figure 2a is shown in Figure 3. The circuit is based on complementary source followers, current mirrors, and cross coupled current mirrors. The complementary source follower is a dual translinear loop (M₁, M₂, M₄, M₅) and (M₁, M₃, M₄, M₆) where the gate-source voltages V_GS of the NMOS transistors (M₁, M₂ and M₃) and PMOS transistors (M₄, M₅ and M₆) are to match. In these loops, the input voltage $V_y$ is transferred to the outputs of the follower $V_{x1}$ and $V_{x2}$ precisely; if the drain currents of M₁, M₄ equal to the drain currents of M₂, M₅ and M₃, M₆ and vice versa, the drain current of M₁, M₄ is transferred precisely to M₂, M₅ and M₃, M₆ if the input and output voltages and the gate-source voltages of the respective transistors and their size are equal. The current mirrors (M₉, M₁₀, M₁₄, M₁₅, M₂₁, M₂₂, M₂₆, M₂₇) are used to transfer the x terminals current to their respective z+ terminals. The cross coupled current mirrors (M₁₁–M₁₃, M₁₆–M₁₈, M₂₃–M₂₅, M₂₈–M₃₀) are used to transfer the x+ terminals current to their respective negative z- terminals. The biasing circuit realized by the transistors M_b, M₇, M₈, M₁₉, M₂₀ and the biasing current source I_set provides all reference currents in the circuit.

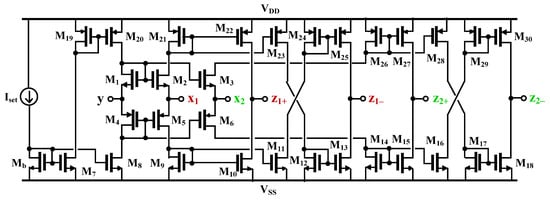
Figure 3. CMOS structure of EX-CCCII.

Considering a dual translinear loop, the parasitic resistances R_x1 and R_x2 at the x₁- and x₂-terminals, respectively, can be expressed [32] by

$$R_{x1}=R_{x2}=\frac{1}{\sqrt{2I_{set}{C}_{ox}}\left(\sqrt{{\mu }_p{\left(\frac{W}{L}\right)}_p}+\sqrt{{\mu }_n{\left(\frac{W}{L}\right)}_n}\right)}$$

(2)

where I_set is the biasing current, C_ox is the oxide capacitance per unit area, ${\mu }_p$ and ${\mu }_n$ are the mobility of the holes and electrons, respectively, (W/L)_p is the ratio of width to length of the channels of M₅–M₆, and (W/L)_n is the ratio of width to length of the channels of M₂–M₃. From (2), the parasitic resistances R_x1 and R_x2 can be controlled by the biasing current I_set. These resistors have the same resistance values.

The input current at the x₁-terminal is conveyed to the z₁₊-terminal by the current mirrors M₇–M₈, M₁₉–M₂₀, and the input current at x₂ is conveyed to z₂₊ by the current mirrors M₁₂–M₁₃, M₂₄–M₂₄. The minus-type outputs z₁₋ and z₂₋ can be implemented using the cross-coupled current mirror topology. Additional copies of these z_+,− outputs can be obtained using the cascade structure for these terminals.

2.2. Current-Mode Universal Filter Using EX-CCCII

Figure 4a shows the proposed current-mode universal filter, and the block diagram that corresponds to Figure 4a is shown in Figure 4b. It is based on one lossless integrator and one lossy integrator loop. It employs one EX-CCCII and two grounded capacitors. Thanks to the extra x-terminal and multiple-outputs of the EX-CCCII, the filter is realized with only one active block. The circuit has four input currents (I₁, I₂, I₃, I₄) and three output currents (I_o1, I_o2, I_o3). Using (1) and nodal analysis, the outputs of the circuit in Figure 4a is given by

$$I_{o1}=\frac{{D\left(s\right)I}_3+I_2-\left(s{C}_2{R}_{x2}+1\right)I_1}{D\left(s\right)}$$

(3)

$$I_{o2}=\frac{{D\left(s\right)I}_4-s{C}_1{R}_{x1}{I}_2+I_1}{D\left(s\right)}$$

(4)

$$I_{o3}=\frac{-s{C}_1{R}_{x1}{I}_2+I_1}{D\left(s\right)}$$

(5)

where $D\left(s\right)=s^2{C}_1{C}_2{R}_{x1}{R}_{x2}+s{C}_1{R}_{x1}+1$.

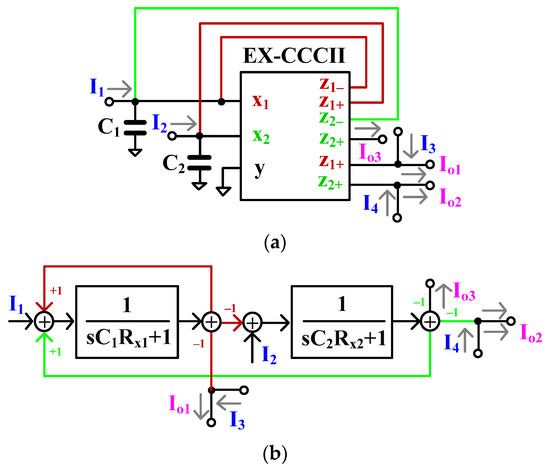
Figure 4. (a) Proposed current-mode universal filter using EX-CCCII, (b) its block diagram.

From (3)–(5), the variant filtering functions of the low-pass filter (LPF), high-pass filter (HPF), band-pass filter (BPF), band-stop filter (BSF), and all-pass filter (APF) can be obtained, as shown in Table 1. For Table 1, it should be noted that the input terminal that is not selected to supply input signals can be floating, while the output terminal that is not selected to supply output signals should be grounded.

Table 1. Variant filtering functions.

Filtering Function		Input	Output
LPF	Non-inverting	$I_2$	$I_{o1}$
	Non-inverting	$I_1$	$I_{o2}$$\mathrm{or}{I}_{o3}$
BPF	Inverting	$I_2$	$I_{o2}$$\mathrm{or}{I}_{o3}$
HPF	Non-inverting	$I_1=I_3$	$I_{o1}$
BSP	Non-inverting	$I_2=I_4$	$I_{o2}$
	Non-inverting	$I_1=I_3$	$I_{o1}+I_{o2}$
APF	Non-inverting	$I_2=I_4$	$I_{o2}+I_{o3}$

The natural frequency (${\omega }_o$) and the quality factor ($Q$) of all filter responses are given by

$${\omega }_o=\frac{1}{\sqrt{C_1{C}_2{R}_{x1}{R}_{x2}}}$$

(6)

$$Q=\sqrt{\frac{C_1{R}_{x1}}{C_2{R}_{x2}}}$$

(7)

From Table 1, it is evident that the circuit does not need an inverted input signal, i.e., $-$I_in, and double input signal, i.e., 2I_in, to realize all filtering functions.

From (6), we can see that the natural frequency can be controlled electronically by $R_{x1}$ and $R_{x2}$ through the biasing current I_set. The quality factor, as shown in (7), is given by $C_1/C_2$ while maintaining $R_{x1}$ = $R_{x2}$.

2.3. Non-Ideal Gain Analysis

Taking the errors of the EX-CCCII into account, the relationship of the terminal voltages and currents can be written by

$$\left.\begin{array}{c}{V}_{xj}={\alpha }_j{V}_y\\ I_{zj}={\beta }_j{I}_{xj}\end{array}\right\}$$

(8)

where ${\alpha }_j$ is the voltage gain from y-terminal to $x_j$-terminal, and ${\beta }_{j\pm }$ is the current gain from $x_{j\pm }$-terminals to $z_{j\pm }$-terminals ($j$ = 1, 2). Ideally, ${\alpha }_j$ and ${\beta }_{j\pm }$ should be equal to 1. However, in practice, these unity gains will be affected by the voltage and current tracking errors. These can be expressed by ${\beta }_{j\pm }=\left(1-{\epsilon }_{jv\pm }\right)$ and ${\alpha }_{j\pm }=\left(1-{\epsilon }_{ji\pm }\right)$, where ${\epsilon }_{jv\pm }$ is the voltage tracking error and ${\epsilon }_{ji\pm }$ is the current tracking error.

Taking into account the nonidealities of the EX-CCCII, the denominator of the non-ideal current-mode universal filter’s transfer functions can expressed by

$$\begin{gathered} D\left(s\right)=s^2{C}_1{C}_2{R}_{x1}{R}_{x2}+s\left(C_1{R}_{x1}+C_2{R}_{x2}\left(1-{\beta }_{1-}{\beta }_{1+}\right)\right) \\ +\left({\beta }_{1-}{\beta }_{1+}{\beta }_{2+}+\left(1-{\beta }_{1-}{\beta }_{1+}\right)\right) \end{gathered}$$

(9)

The parameters ${\omega }_o$ and $Q$ of the non-ideal filter are given by

$${\omega }_o=\sqrt{\frac{{\beta }_{1-}{\beta }_{1+}{\beta }_{2+}+\left(1-{\beta }_{1-}{\beta }_{1+}\right)}{C_1{C}_2{R}_{x1}{R}_{x2}}}$$

(10)

$$Q=\frac{\sqrt{\left({\beta }_{1-}{\beta }_{1+}{\beta }_{2+}+\left(1-{\beta }_{1-}{\beta }_{1+}\right)\right)C_1{C}_2{R}_{x1}{R}_{x2}}}{C_1{R}_{x1}+C_2{R}_{x2}\left(1-{\beta }_{1-}{\beta }_{1+}\right)}$$

(11)

The non-ideal gains of the EX-CCCII will slightly change the values of ${\omega }_o$ and $Q$.

2.4. Non-Ideal Parasitic Analysis

The non-ideal model of the EX-CCCII is shown in Figure 4. The terminals x₁ and x₂ have low resistances R_x2 and R_x2, respectively. The parasitic inductances in series with them are ignored. The terminals y, z_1±, and z_2± are shunted by parallel connections of parasitic resistances and capacitances, R_y//C_y, R_z1±//C_z1±, R_z2±//C_z2±.

Considering the EX-CCCII parasitics, the denominator of the transfer functions can be expressed by

$$\begin{gathered} D\left(s\right)=s^2{C}_1^{\prime }{C}_2^{\prime }{R}_{x1}{R}_{x2}+s{C}_1^{\prime }{R}_{x1}\left(1+\frac{C_2^{\prime }{R}_{x1}{R}_{x2}{G}_a+C_1^{\prime }{R}_{x1}{R}_{x2}{G}_b}{C_1^{\prime }{R}_{x1}}\right) \\ +\left(R_{x1}{R}_{x2}{G}_a{G}_b+R_{x1}{G}_a\right)+1 \end{gathered}$$

(12)

where $C_1^{\prime }=C_1+C_{z1-}+C_{z2-}$, $C_2^{\prime }=C_2+C_{z1+}$, $G_a=1/\left(R_{z1-}∕∕R_{z2-}\right)$, $G_b=1/R_{z1+}$.

Letting

$$\left.\begin{array}{r}\frac{C_2^{\prime }{R}_{x1}{R}_{x2}{G}_a+C_1^{\prime }{R}_{x1}{R}_{x2}{G}_b}{C_1^{\prime }{R}_{x1}}=0\\ R_{x2}{G}_a{G}_b+R_{x1}{G}_a=0\end{array}\right\}$$

(13)

which is possible if $R_{z1-}$, $R_{z2-}$, $R_{z1+}$ are very high resistances compared with $R_{x1}$, $R_{x2}$, the parameters ${\omega }_o$ and $Q$ of the non-ideal current-mode universal filter can be expressed by

$${\omega }_o=\frac{1}{\sqrt{C_1^{\prime }{C}_2^{\prime }{R}_{x1}{R}_{x2}}}$$

(14)

$$Q=\sqrt{\frac{C_1^{\prime }{R}_{x1}}{C_2^{\prime }{R}_{x2}}}$$

(15)

The parasitic capacitances will affect the parameters ${\omega }_o$ and $Q$ of the filter and their impact can be minimized by choosing $C_1\gg C_{z1-}+C_{z2-}$, $C_2\gg C_{z1+}$.

3. Simulation Results

The proposed current-mode analog filter was designed and simulated in SPICE using TSMC 0.18 μm CMOS technology (Taiwan Semiconductor Manufacturing Company (TSMC), Hsinchu, Taiwan). The aspect ratios of the transistors are shown in Table 2. The supply voltage was ±0.5 V. The summarized performance of the designed EX-CCCII is shown in Table 3 [32].

Table 2. Aspect ratios for the transistors in the EX-CCCII.

Transistor	W/L (µm/µm)
M1, M2, M3	5/0.36
M4, M5, M6	10/0.36
Mb, M7–M18	3/0.36
M19–M30	6/0.36

Table 3. Parameters of the designed EX-CCCII.

Parameters	Value
Supply voltage	±0.5 V
Technology	0.18 μm
DC voltage range	−100 mV to 100 mV
Voltage gain	0.953
Current gain
Iz+/Ix	1.01
Iz−/Ix	1.04
−3 dB bandwidth VF	0.502 GHz
−3 dB bandwidth CF
Iz+/Ix	141.9 MHz
Iz−/Ix	121.4 MHz
Rx (Iset = 2–60 μA)	20.3 kΩ–2.29 kΩ
Ry//Cy	100 kΩ//0.251 pF
Rz//Cz	462 kΩ//0.051 pF

Figure 5 shows the simulated parasitic resistance at the x-terminal (R_x) when the biasing current I_set was varied from 2 to 50 µA. When the biasing current was increased from 2 to 50 µA, the observed parasitic resistance R_x decreased from 20.32 to 2.29 kΩ.

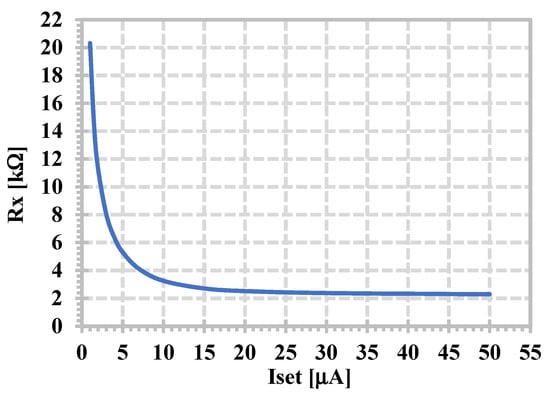
Figure 5. Simulated parasitic resistance R_x with different I_set.

Figure 6 shows the simulated magnitude and phase frequency responses of the LPF, HPF, BPF, and BSF with C₁ = C₂ = 20 pF and I_set = 20 µA. Figure 7 shows the simulated magnitude and phase frequency responses of the APF. The filters offer a 3.23 MHz of the natural frequency. Thus, it is evident from Figure 6 and Figure 7 that the proposed current-mode filter can realize the five standard filtering functions in the same circuit without inverted input signal requirements.

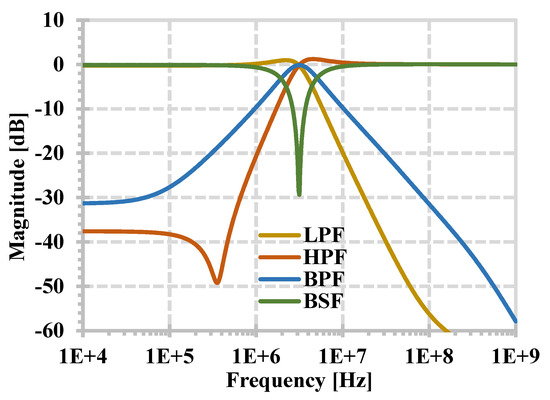
Figure 6. Simulated magnitude and phase frequency responses of the LPF, HPF, BPF, and BSF.

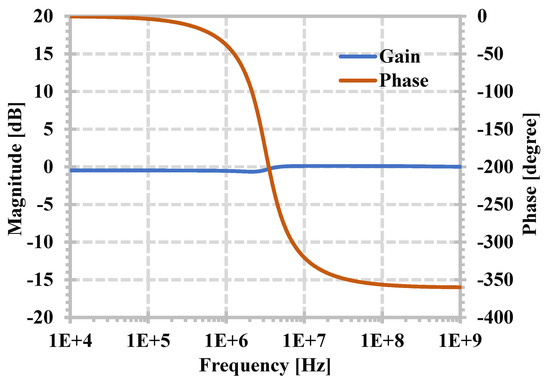
Figure 7. Simulated magnitude and phase frequency responses of the APF.

The tuning capability of the proposed current-mode filter was tested by varying the bias current I_set. The simulated magnitude frequency response is shown in Figure 8. The natural frequency was (0.724, 1.51, 3.47) MHz when the bias current I_set was (2, 5, 40) µA, respectively.

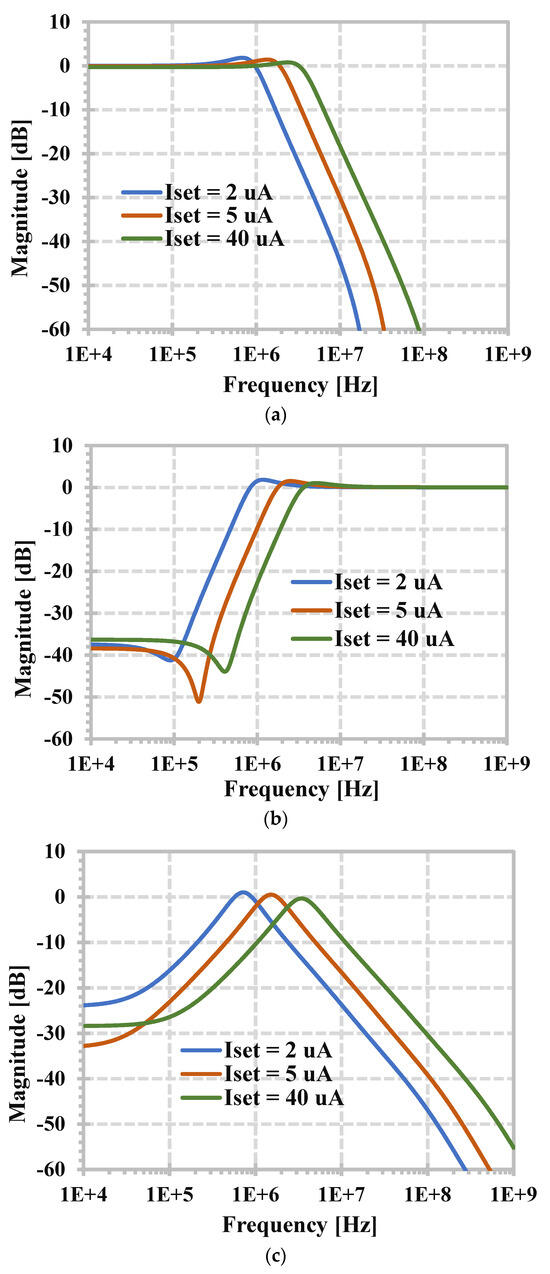
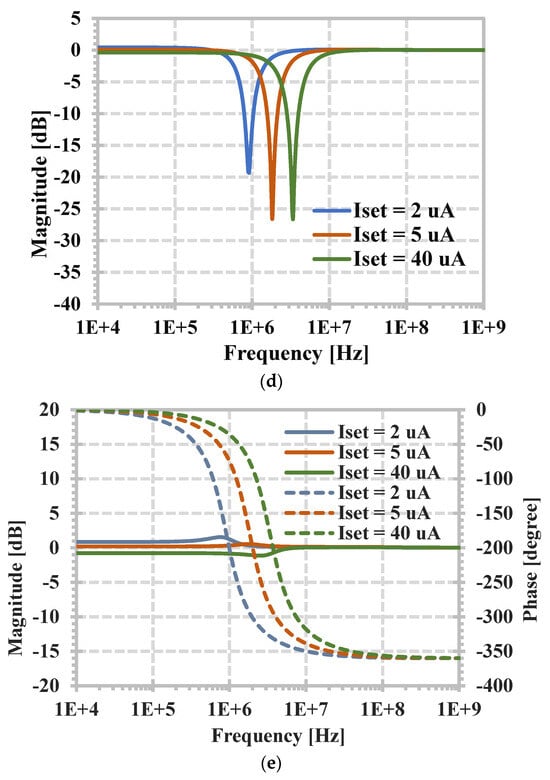
Figure 8. Simulated magnitude frequency responses with I_set = 2, 5, 40 µA, (a) LPF, (b) HPF, (c) BPF, (d) BSF, and (e) APF.

The LPF was used to test the linearity of the proposed current-mode filter. The input signal has an in-band frequency of 10 kHz and the amplitude was varied. Figure 9 shows the simulated total harmonic distortion (THD) of the current-mode filter when the input amplitude was varied. The THD was 1.038% when the amplitude was 70 µA (140 µA_p–p). Figure 10 shows the equivalent output current noise of the LPF. The integrated current noise over the bandwidth of 3.23 MHz was calculated to be 17.13 nA, giving a dynamic range of 69.2 dB.

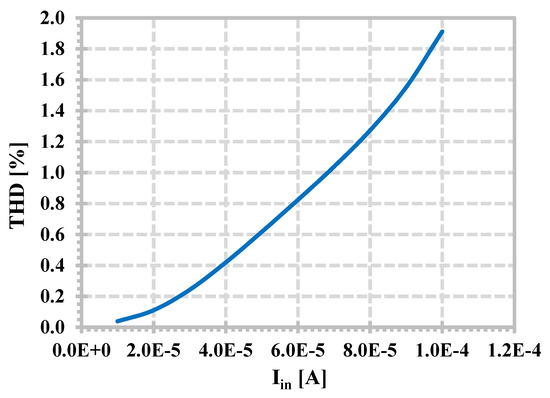
Figure 9. Simulated THD of the LPF with different amplitudes of I_in.

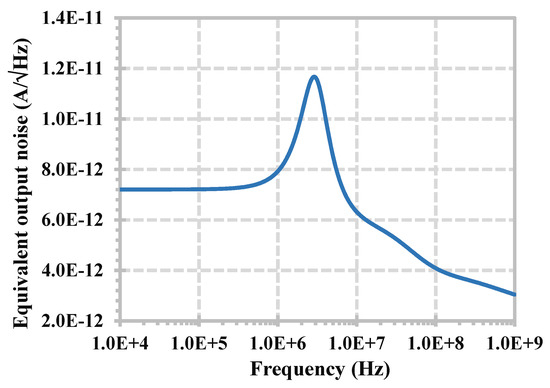
Figure 10. The equivalent output current noise of the LPF.

Figure 11 shows the simulated frequency responses of the LPF, HPF, BPF, BSP, and APF when the temperature was set to −30, 27, and 85 °C. Figure 12 shows the simulated frequency responses of the filter when the voltage supply was set to 0.975 V, 1 V, and 1.25 V (1 V ± 5%). In both cases the curves overlapped or closed each other.

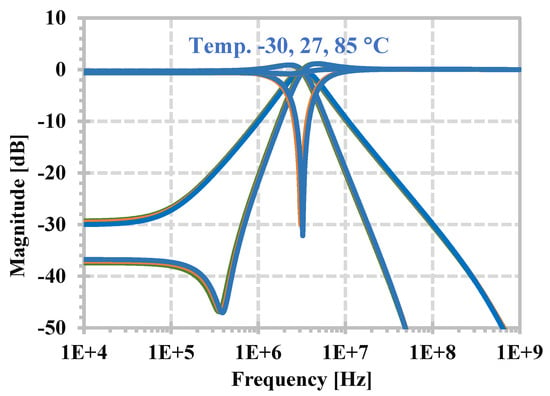
Figure 11. The frequency response of the LPF, HPF, BPF, BSF, and APF with temperature corners.

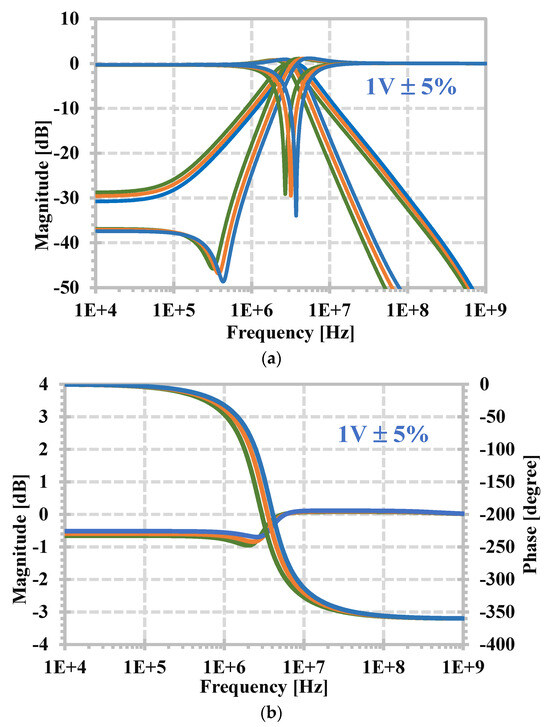
Figure 12. The frequency response of, (a) LPF, HPF, BPF, BSF, and (b) APF, with voltage supply corners.

Figure 13 shows the simulated magnitude frequency responses of the proposed filter when the threshold voltage in CMOS process was varied by 10% (LOT tolerance), which represents a process variation. As can be seen, the curves are closed to each other.

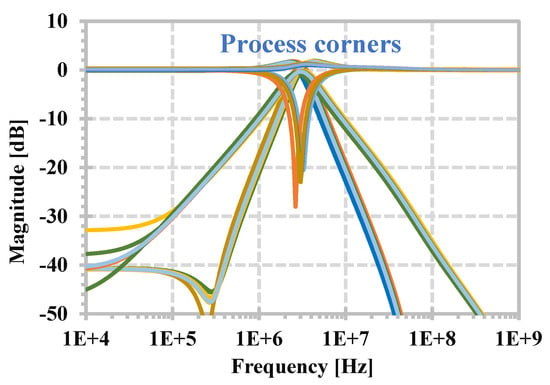
Figure 13. Simulated magnitude responses of the proposed filter for process corners.

The proposed current-mode filter was compared with previous works, as shown in Table 4. The current-mode filters that use similar active devices, such as VD-EXCCCII [18], EX-CCCII in [31,32], and DV-EXCCCII in [33,34], were used for comparison. Compared with [31,32,33,34], the proposed current-mode filter can realize LPF, HPF, BPF, BSF, and APF without inverted and double input signal conditions. Compared with [18], the proposed current-mode filter uses an EX-CCCII of a lower complexity than the VD-EXCCII. However, the VD-EXCCII based filter in [18] can offer mixed-mode operation (i.e., VM, CM, TAM, TIM), but two resistors are required. Moreover, for the filter in [18], it is difficult to tune the natural frequency because the equation of natural frequency includes both parameters of the transconductance g_m and resistance R. Thus, to tune the natural frequency without changing the quality factor, the condition g_m = 1/R should be met.

Table 4. Comparison of this work with selected analog filters.

Factor	Proposed	[18]	[31]	[32]	[33]	[34]
Number of active devices	1-EX-CCCII	1-VD-EXCCII (Figure 4)	1-EX-CCCII (Figure 3)	1-EX-CCCII	1-DV-EXCCCII	1-DV-EXCCCII
Realization	CMOS structure and commercial IC	CMOS structure	CMOS structure	CMOS structure and commercial IC	CMOS structure and commercial IC	CMOS structure
Number of passive elements	2-C	2-C, 2-R	2-C	2-C	2-C	2-C, 1-R
Type of filter	MIMO	SIMO	MISO	MIMO	MISO	MISO
Operation mode	CM	CM	CM	MM	CM	CM
Number of offered responses	7	5	5	5 (CM)	5	5
All grounded capacitors	Yes	Yes	Yes	Yes (CM)	Yes	Yes
Without inverted/double input conditions	Yes	Yes	No	No	No	No
High output impedances	Yes	Yes	Yes	Yes	Yes	Yes
Electronic control of ${\omega }_o$	Yes	Yes	Yes	Yes	Yes	Yes
Voltage supply (V)	±0.5	±1.25	±1.25	±0.5	±0.9	±0.9
Natural frequency (MHz)	3.31	8.04	3.93	23	3.9	~3.5–4.2
Power dissipation (mW)	0.465	5.76	3.18	1.35	205	2.2
Total harmonic distortion (%)	1.038@140 µApp	2.5%@360 µApp	1.122%@100 µApp (BP)	0.2%@200 µApp	<6%@200 µApp	5%@120 µApp (BP)
Verification	Sim/Exp	Sim/Exp	Sim	Sim/Exp	Sim/Exp	Sim

4. Experimental Results

The EX-CCCII implementation used in this section to implement the current-mode universal filter is shown in Figure 14. The circuit is based on AD844 ICs and resistors. The resistors in the circuit are set as R₁ = R₂ = R₃ = R₄ to obtain I_x1 = I_z1+ = −I_z1− and R_1c = R_2c = R_3c = R_4c to obtain I_x2 = I_z2+ = −I_z2−. In this test, the resistors R₁, R₂, R₃, R₄, R_1c, R_2c, R_3c, and R_4c were 1 kΩ. The resistors R_x1 and R_x2 work as parasitic resistors of the EX-CCCII. The voltage-to-current (V/I) converter using AD844 and a resistor is used to convert the input voltage from a function generator to current inputs I_in (i.e., I₁, I₂, I₃, and I₄) (I_in = V_in/R_in), the example case for converting the voltage V_in to the input I₁ (I_in) was shown in Figure 14. To measure the output currents, i.e., I_o1, I_o2, I_o3, the current-to-voltage (I/V) converters are used (V_out = I_outR_out), Figure 14 shows the example case for converting the current I_o3 (I_out) to the output V_out. In this test, the resistors R_in and R_out were 10 kΩ. Thus, a unity voltage gain was obtained. Figure 15 shows a photo of the experimental setup. The circuits were supplied from ±5 V and 22-nF capacitances C₁ and C₂ were used. The measurement was performed using a Keysight DSOX1204G oscilloscope with a built-in signal generator.

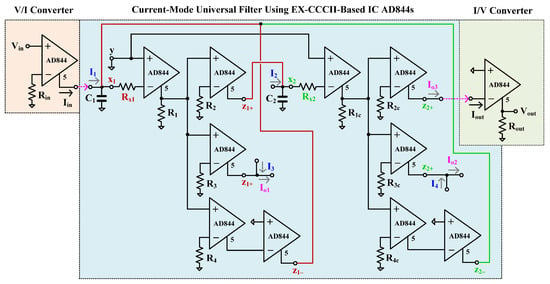
Figure 14. Implementation of the EX-CCCII using AD844s to realize the current-mode universal filter.

Figure 15. (a) Experimental setup, (b) close-up of the EX-CCCII and V/I converter.

Figure 16a,b show the measured magnitude responses of the LPF, HPF, BPF, BSP, and APF with setting resistances R_x1 = R_x2 = 5 kΩ. The measured natural frequency was 1.343 kHz while the filter was designed for a natural frequency of 1.446 kHz, giving an error of 7.12%. This result confirms the workability of the proposed current-mode filter.

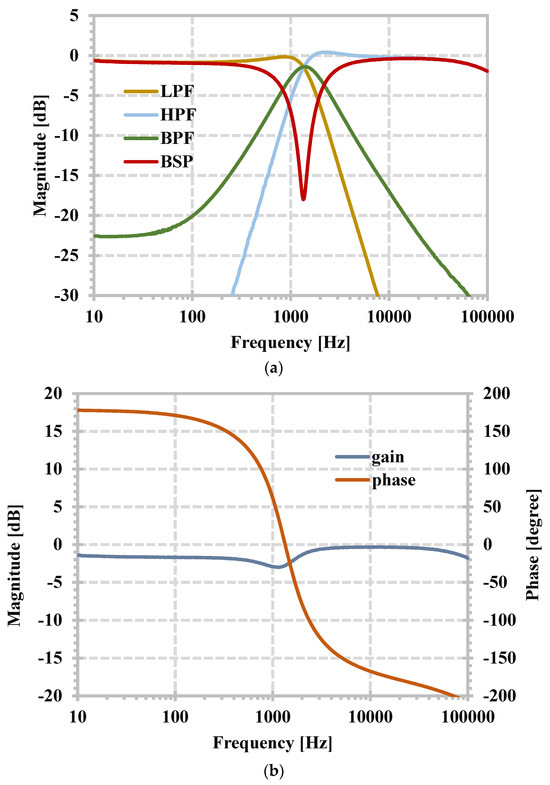
Figure 16. Magnitude responses with setting resistances R_x1 = R_x2 = 5 kΩ for (a) LPF, HPF, BPF, BSF, and (b) APF.

Figure 17 shows the measured magnitude responses of the BPF when the resistances R_x1 and R_x2 (R_x1 = R_x2) are set to 15 kΩ (a), 10 kΩ (b), 5 kΩ (c), and 1 kΩ (d). From (6) and (7), the natural frequency can be determined using R_x1 = R_x2 while the quality factor (Q) can be selected using C₁/C₂. The capacitor values were fixed as C₁ = C₂ = 22 nF and the resistors R_x1 = R_x2 are given, resulting in Q = 1. By setting the resistor’s values from 15 kΩ, 10 kΩ, 5 kΩ, and 1 kΩ, the measured natural frequencies were found to be 0.469 kHz, 0.704 kHz, 1.343 kHz, and 6.668 kHz, respectively. The filter is designed for natural frequencies of 0.482 kHz, 0.723 kHz, 1.446 kHz, and 7.234 kHz, respectively. Thus, the errors were 2.69%, 2.62%, 7.12%, and 7.82%, respectively. This experimentation serves to confirm the tuning capability of the current-mode filter expressed in (6).

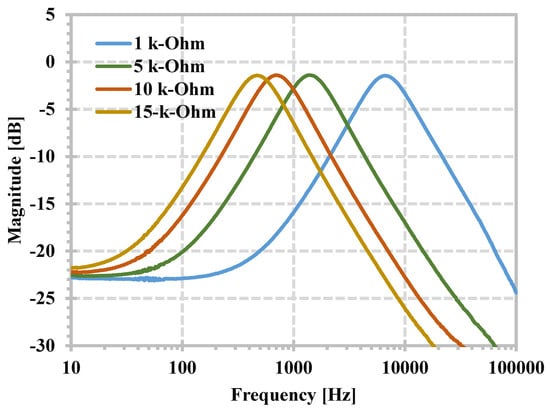
Figure 17. Measured magnitude frequency responses of the BPF with setting resistances R_x1 = R_x2 for (1, 5, 10, 15) kΩ.

5. Conclusions

In this study, a new electronically tunable current-mode universal analog filter with multiple inputs and multiple outputs is proposed. The filter employs only one EX-CCCII and two grounded capacitors. The topology can realize five standard filtering functions of low-pass, high-pass, band-pass, band-stop, and all-pass responses without changing the internal configuration of the filter by selecting the appropriate input and output signals. The inverted input signal and input matching conditions are absent for obtaining these filtering functions. The natural frequency of all filter responses can be electronically controlled. The proposed filter was simulated by SPICE and confirmed through experimental testing using IC AD844s.