Property Preservation of Object-Oriented Petri Reduction Net Based Representation for Embedded Systems

Abstract

Embedded systems are widely used in automotive electronics, smart home, smart medical, aerospace and other fields. Aiming at the problem of formal modeling and verification analysis of embedded systems, a solution is proposed using extended Petri net reduction operations. Petri net based representation for embedded system (PRES+) and the object-oriented technology are combined to obtain the object-oriented PRES+ (OOPRES+). Two kinds of subnet reduction rules of OOPRES+ are presented. The preservation of boundedness and liveness of the reduction net system has been investigated to alleviate the problem of state space explosion of OOPRES+. The modeling and analysis of the embedded control system of a smart restaurant is used as an example to verify the effectiveness of the subnet reduction rules. Results obtained can provide an effective way to examine the reduction property of Petri net systems, and present a powerful means to model and verify the large-scale complex embedded systems.

1. Introduction

With the rapid development of modern information technology, embedded system is undoubtedly one of the most popular technologies at present, and has been widely used in automotive electronics, smart home, smart medical, aerospace and other fields. In order to improve the design efficiency and reliability of embedded systems, it is necessary to conduct formal modeling and analysis of embedded systems.

In terms of embedded system modeling methods, traditional modeling methods mostly use informal modeling methods, which can basically describe the functional properties of the system, but it is not easy to strictly verify by mathematical methods. The formal method describes the properties of the system with symbols and mathematical language, and can describe and verify the system in a systematic way [1]. The formal modeling methods widely used mainly include: extended finite state machine method [2], data flow diagram method [3], Petri net method [4], entity-relationship diagram method, etc. These formal modeling methods describe the characteristics of embedded systems from different aspects, but do not form a unified standard.

Aiming at the problem of formal modeling and verification analysis of embedded systems, a solution is proposed using the object-oriented PRES+ (OOPRES+) reduction operations in this paper. The preservation of liveness and boundedness of the reduction net system has been investigated to alleviate the problem of state space explosion of OOPRES+. Results obtained can provide a powerful means to model and verify the large-scale complex embedded systems.

2. Related Works

Embedded systems are widely used in many fields. The research and application of embedded systems have become increasingly important. Most of aircrafts have systems for collision avoidance systems, navigation, flight data recorder, automatic flight control, monitoring systems as well as weather radar system. Embedded computer systems with increasing memory requirements are used in all of above systems. To reduce the electricity consumed by these systems, Weisberg et al. [5] suggested detecting the portion of the actually used computer memory. The other portion can be temporarily turned off and turned on again when needed. Lenhardt et al. [6] present algorithms for calculating a power-efficient distribution of a divisible workload, heterogeneous physical servers. The calculated algorithms can minimize the power consumption.

To improve the design efficiency of embedded systems, it is necessary to model and verify embedded systems. Petri net has a clear mathematical definition and strict specification of derivation rules, which is a relatively sound formal modeling method. Classical Petri nets can model systems with concurrency, conflict and uncertainty, but there are the following shortcomings in embedded system modeling: no hierarchy, no consideration of time factors and limited ability to describe data flow. In order to overcome these shortcomings, domestic and foreign scholars have investigated and proposed a variety of extended forms of Petri nets for embedded system modeling and analysis, such as colored nets [7], PRUE (Petri net based on unified representation), time Petri nets [8], fuzzy Petri nets [9], timed double-flow Petri nets, etc. These extended forms of Petri nets improve the ability to model and analyze embedded systems based on different application requirements, but there are still some problems. For example, although the token of colored net has information and hierarchical description ability, there is no clear time characteristic. Although time can be attached to the token, there is semantic inconsistency. Time Petri nets have time characteristics, but the tokens do not have information.

PRES+ (Petri net based representation for embedded systems) [10] has a hierarchical structure and the ability to analyze data flow. Real-time characteristics can be captured by the time delay attached to the transition and the timestamp in the token, but it is not convenient for modular modeling of large-scale complex embedded systems.

Object-oriented technology can effectively divide large-scale complex systems into multiple simple subsystems and model them accordingly. In order to facilitate the modular modeling of large-scale complex embedded systems, an Object-Oriented Petri net based Representation for Embedded System (OOPRES+) is obtained by integrating object-oriented technology and PRES+.

OOPRES+ can be used for formal modeling and analysis of embedded systems. However, with the increase of system scale and complexity, the state space increases exponentially, and the problem of “state space explosion” will be encountered, which seriously affects the application of OOPRES+ in the modeling and analysis of large-scale complex embedded systems. The problem of state space explosion is NP-hard and cannot be completely solved, but it can be alleviated by using some property preserving transformations.

Synthesis [11,12,13,14,15], reduction [16,17,18,19,20,21,22,23,24], and refinement [25,26,27,28,29] are three commonly used Petri net transformation methods. Reduction is an important transformation method. There have been many researches on Petri net reduction. Berthomieu et al. [16,17] proposed a method to count the number of reachable markings of a Petri net, and reduce the number of transitions and places in a system. Ceška et al. [18] focused on how to use an object-oriented Petri nets partial-order reduction approach to alleviate the state space explosion problem. Shah et al. [19] focused on reduction of the colored Petri net (CPN) model of a flexible manufacturing system to reduce the total number of elementary circuits. Chiachío et al. [20] introduced a method based on Approximate Bayesian Computation to infer the plausible values of the model parameters of the simplified model in a rigorous probabilistic way. Bønneland et al. [21] described the structure reduction techniques used in reachability queries on weighted Petri net with inhibitor arcs. Xia [22] proposed a set of reduction rules for the PRES+ model to preserve total equivalence. Xia et al. [23] proposed several reduction rules for Petri net with inhibitor arcs based representation for embedded systems (PIRES+). Li et al. [24] proposed several reduction rules for the bounded labeled Petri nets (LPNs). Under certain conditions, these reduction rules can preserve the diagnosability of the LPN system.

The above research works have played certain roles in the property analysis and system modeling of Petri nets, but OOPRES+ is a newly proposed extended Petri net, and its reduction operation has not been systematically studied. The property preservation reduction operation can alleviate the state space explosion problem of OOPRES+, and realize the formal modeling and analysis of large-scale complex embedded systems. Therefore, it is necessary to conduct in-depth research on it.

In this paper, two reduction rules of OOPRES+ are proposed, and the necessary and sufficient conditions for the reduction operation to preserve the boundedness and liveness of the original net system are presented. The reduced net system is obtained by reducing the original OOPRES+ net system according to the given reduction rules. The reduction rules can make the reduced net system have the same boundedness and liveness as the original net system, so that the relevant properties of the large system can be investigated with the small systems without the analysis of the reachable space, so as to alleviate the explosion of the state space of the OOPRES+.

3. Basic Concepts

In this section, we propose some related concepts of OOPRES+.

Definition 1.

A PRES+ model is $N=\left(P,T,I,O,M\right)$, where $P=\left\{p_1,p_2,\cdots ,p_m\right\}$ is a non-empty finite set of places, $T=\left\{t_1,t_2,\cdots t_n\right\}$ is a non-empty finite set of transitions, $I\subseteq P\times T$ is a non-empty finite set of input arcs, $O\subseteq T\times P$ is a non-empty finite set of output arcs. $M$ is a marking, which indicates the distribution of tokens in the place. $k=⟨v,r⟩$ is a token, where $v$ is the token value, and $r$ is the token time.

Figure 1 shows an example of the PRES+ model. For the example, in Figure 1, $P=\left\{p_1,p_2,p_3,p_4,p_5\right\}$, $T=\left\{t_1,t_2,t_3,t_4,t_5\right\}$, $\mathrm{I}=\left\{\left(p_1,t_1\right),\left(p_1,t_2\right),\left(p_2,t_3\right),\left(p_3,t_3\right),\left(p_4,t_4\right),\left(p_5,t_5\right)\right\}$, $O=\left\{\left(t_1,p_2\right),\left(t_2,p_3\right),\left(t_3,p_4\right),\left(t_3,p_5\right),\left(t_4,p_1\right),\left(t_5,p_1\right)\right\}$, $M_0$ is the initial marking, $M_0\left(p_1\right)=\left\{⟨2,0⟩\right\}$, $M_0\left(p_2\right)=M_0\left(p_3\right)=M_0\left(p_4\right)=M_0\left(p_5\right)=\varnothing$.

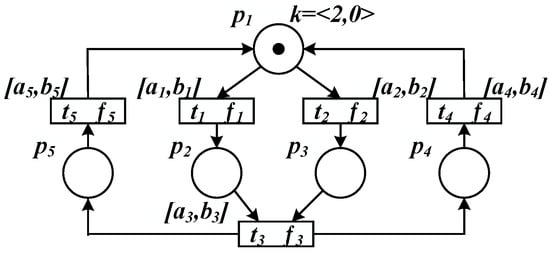
Figure 1. An example of PRES+ model.

Definition 2.

For every transition $t\in T$, there exists a transition function $f$, i.e., $\exists f:\tau \left(p_1\right)\times \tau \left(p_2\right)\times \cdots \times \tau \left(p_a\right)\to \tau \left(q\right)$, where $\tau$ is a type function that associates with every place, where $·t=\left\{p_1,p_2,\dots ,p_a\right\}$, $q\in t$.

Definition 3.

For every transition $t\in T$, there exists a minimum transition delay $a$ and a maximum transition delay $b$, both of which are non-negative real numbers and $a\le b$, where $a$ and $b$ represent the lower and upper bounds on the execution time of the transition function associated with the transition $t$.

In Figure 1, the transition functions associated with the transitions $t_1,t_2,t_3,t_4,t_5$ are $f_1,f_2,f_3,f_4,f_5$, and the transition delays are $\left[a_1,b_1\left],\right[a_2,b_2\left],\right[a_3,b_3\left],\right[a_4,b_4\left],\right[a_5,b_5\right]$, respectively.

Definition 4.

An OOPRES+ subnet is a six-tuple $SN=\left\{P,T,I,O,W,Q\right\}$, where $P=\left\{p_1,p_2,\dots \dots ,p_m\right\}$ is a non-empty finite set of places, denoted by $SN\left(P\right)$; $T=\left\{t_1,t_2,\dots \dots ,t_n\right\}$ is a non-empty finite set of transitions, denoted by $SN\left(T\right)$, and for each transition $t$, there exists a transition function and transition time delay corresponding to it; $I\subseteq \left(\left(P\times T\right)\cup \left(Q\times T\right)\right)$ is the input arc set; $O\subseteq \left(\left(T\times P\right)\cup \left(T\times Q\right)\right)$ is the output arc set; $W$ is the weight function, which defines the weight size on the flow relationship, and the default value is 1; $Q=\left\{q_1,q_2,\dots \dots ,q_s\right\}$ is the set of message places, denoted by $SN\left(Q\right)$.

The message place that receives messages from the subnet and transmits them to the gateway is called the output place (denoted by $Q_O$), and the message place that receives the messages from the gateway and transmits them to the subnet is called the input place (denoted by $Q_I$).

Figure 2 shows an example of the OOPRES+ subnet, where $P=\left\{p_1,p_2\right\}$,$T=\left\{t_1,t_2,t_3,t_4,t_5\right\},I=\left\{\left(q_1,t_1\right),\left(q_1,t_2\right),\left(p_1,t_3\right),\left(p_1,t_4\right),\left(p_2,t_5\right)\right\}, O=\{\left(t_1,p_1\right),\left(t_2,p_1\right),\left(t_3,p_2\right),$ $\left(t_4,p_2\right),\left(t_5,q_2\right)\}$, $M_0$ is the initial marking, $M_0\left(p_1\right)\ne \varnothing$, $M_0\left(p_2\right)=M_0\left(q_1\right)=M_0\left(q_2\right)=\varnothing ,Q=\left\{q_1,q_2\right\}$, where $q_1$ is the input message place and $q_2$ is the output message place.

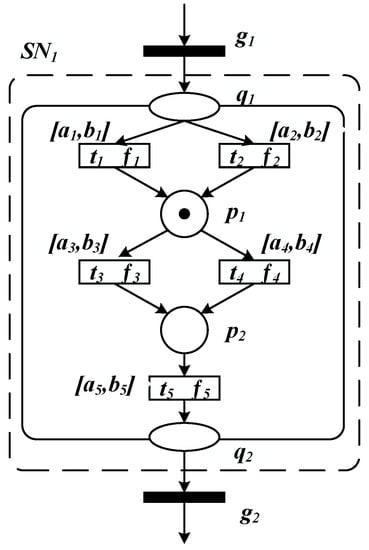
Figure 2. An example of OOPRES+ subnet.

Definition 5.

An OOPRES+ net is a four-tuple $\Sigma =\left\{N,F,G,M\right\}$, where $N=\left\{S{N}_1,S{N}_2,\dots \dots ,S{N}_m\right\}$ is the subnet set of OOPRES+ (where the place set, the transition set, and the messages place set are denoted by $N\left(P\right)$, $N\left(T\right)$, and $N\left(Q\right)$, respectively.); $F$ is the flow relation between subnets and gateways, including two parts $F_I$ and $F_O$, where $F_I\subseteq Q\times G$, $F_O\subseteq G\times Q$; $G=\left\{g_1,g_2,\dots \dots ,g_S\right\}$ is a set of gateways; $M$ is the system making, and the initial marking is $M_0$.

Definition 6.

Let $\Sigma =\left\{N,F,G,M\right\}$ be an OOPRES+ net system with $M\in R\left(M_0\right)$, and $M_0$ is the initial marking.

(i)

For transition$t\in T$, if  $·t\cap Q\ne \varnothing$, then  $t$ is said to be enabled under $M,$ if and only if

$$\forall p\in P:M\left(p\right)\ge W\left(p,t\right)$$

(1)

$$\forall q\in Q:M\left(q\right)\ge W\left(q,t\right)$$

(2)

(ii)

For  $t\in T$, if  $·t\cap Q=\varnothing$, then  $t$ is said to be enabled under  $M$, if and only if it satisfies formula (2).

(iii)

The system marking changes after the firing of transition  $t$:  $M\to M^{\prime }$, where

$$\begin{gathered} M^{\prime }\left(p\right)=\left\{\begin{array}{c}M\left(p\right)-W\left(p,t\right) pϵ·t-t· \\ M\left(p\right)+W\left(t,p\right) pϵt·-·t \\ M\left(p\right)-W\left(p,t\right)+W\left(t,p\right) pϵ·t \cap t·\\ M\left(p\right) else \end{array}\right. \\ {M}^{\prime }\left(q\right)=\left\{\begin{array}{c}M\left(q\right)-W\left(q,t\right) qϵ·t \\ M\left(q\right)+W\left(t,q\right) qϵt· \\ M\left(q\right) else \end{array}\right. \end{gathered}$$

Definition 7.

Let an OOPRES+ net system be $\Sigma =\left\{N,F,G,M_0\right\}$, with $M_0$  as the initial marking and $t\in N\left(t\right)$, then

(i)

A transition  $t$ is said to be live if for every  $M\in R\left(M_0\right)$, there exists  $M\prime \in R\left(M\right)$, such that  $M^{\prime }[t>$.

(ii)

An OOPRES+ net system  $\Sigma$ is said to be live if, for system  $\Sigma$,  $\forall t\in N\left(T\right)$,  $t$ is live.

Definition 8.

Let an OOPRES+ net system be $\Sigma =\left\{N,F,G,M_0\right\}$, and $M_0$ the initial marking, $p\in N\left(P\right)$, $q\in N\left(Q\right)$, then

(i)

A place $p$ is said to be bounded if there exists a positive integer $K$ such that $\forall M\in R\left(M_0\right),M\left(p\right)\le K$. A message place $q$ is said to be bounded if there exists a positive integer $B$ such that $\forall M\in R\left(M_0\right),M\left(q\right)\le B$.

(ii)

An OOPRES+ net system $\Sigma$ is said to be bounded if, for a system $\Sigma$, $\forall p\in N\left(P\right)$ and $\forall q\in N\left(Q\right)$, $p$ and $q$ are bounded.

4. Subnet Reduction Rules and Property Analysis of OOPRES+

In this section, we present two internal subnet reduction rules of the OOPRES+ net system, and propose the necessary and sufficient conditions for the reduced OOPRES+ net systems to preserve liveness and boundedness.

4.1. Q-Type Internal Subnet Reduction

In this section, we will introduce the Q-type internal subnet reduction rule of the OOPRES+. Figure 3 is an example of this reduction rule.

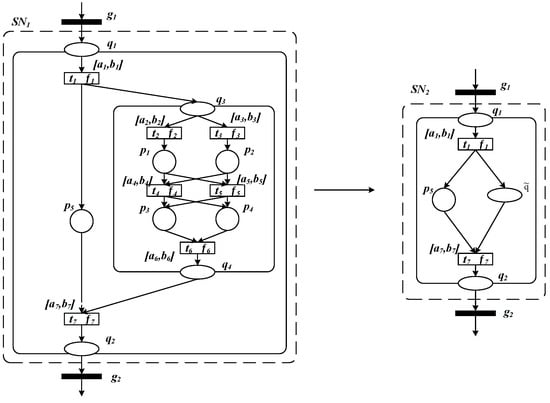
Figure 3. An example of Q-type internal subnet reduction rule.

Definition 9.

Let $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ be a subnet of OOPRES+ net system $\Sigma =\left\{N,F,G,M\right\}$. $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ is called a Q-type internal subnet of $S{N}_1$, if and only if the following conditions are satisfied.

(i)

$P_1^{\prime }\subseteq P_1,T_1^{\prime }\subseteq T_1,Q_1^{\prime }\subseteq Q_1, and P_1^{\prime }\ne \varnothing ,T_1^{\prime }\ne \varnothing ,Q_1^{\prime }\ne \varnothing$;

(ii)

$I_1^{\prime }=I_1\cap \left\{\left(P_1^{\prime }\times T_1^{\prime }\right)\cup \left(Q_1^{\prime }\times T_1^{\prime }\right)\right\},and O_1^{\prime }=O_1\cap \left\{\left(T_1^{\prime }\times P_1^{\prime }\right)\cup \left(T_1^{\prime }\times Q_1^{\prime }\right)\right\}$;

(iii)

$\left(·T_1^{\prime }\cup T_1^{\prime }·\right)\subseteq \left(P_1^{\prime }\cup Q_1^{\prime }\right)$;

(iv)

{$q_{in},q_{out}$} $\subseteq Q_1^{\prime }$, where $q_{in}$ is the only input message place of $S_1^{\prime }$ and $q_{out}$ is the only output message place of $S_1^{\prime }$.

For the transition set$N\left(T_1^{\prime }\right)$ of Q-type internal subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$, there exists the transition function $f_{T_1^{\prime }}$. Take Figure 3 as an example. Transitions $t_2$, $t_4$, and $t_6$ are sequence relations. Transitions $t_3$, $t_5$, and $t_6$ are sequence relations. Transition sets $\left\{t_2,t_4\right\}$ and $\left\{t_3,t_5\right\}$ are parallel relations. So, $f_{T_1^{\prime }}=\left(f_2\odot f_4\right)\left|\right|(f_3\odot f_5)\odot f_6$ (where the symbol $\odot$ represents compound operation, and $\left|\right|$ represents parallel operation).

For the transition set $N\left(T_1^{\prime }\right)$ of Q-type internal subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$, there exists a minimum transition time delay $a_{T_1^{\prime }}$ and a maximum transition time delay $b_{T_1^{\prime }}$, both of which are non-negative real numbers and satisfy $a_{T_1^{\prime }}\le b_{T_1^{\prime }}$. Take Figure 3 as an example. Transitions $t_2$, $t_4$, and $t_6$ are sequence relations. Transitions $t_3$, $t_5$, and $t_6$ are sequence relations. Transition sets $\left\{t_2,t_4\right\}$ and $\left\{t_3,t_5\right\}$ are parallel relations. So, $a_{T_1^{\prime }}=\max (a_2+a_4,a_3+a_5)+a_6$, $b_{T_1^{\prime }}=\max (b_2+b_4,b_3+b_5)+b_6$.

Based on the transition function of the transition set $N\left(T_1^{\prime }\right)$, the transition time delay, and the token information in the input place $q_{in}$, the token information in the output place $q_{out}$ can be calculated.

Definition 10.

(Q-type internal subnet reduction rule) Suppose $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ is a subnet of OOPRES+ net system $\Sigma =\left\{N,F,G,M\right\}$. Let the reduced subnet $S{N}_2=\left\{P_2,T_2,I_2,O_2,W_2,Q_2\right\}$ be obtained from using message place $\tilde{q}$ to replace the internal subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ of $S{N}_1$ where,

(i)

$P_2=P_1-P_1^{\prime }$;

(ii)

$T_2=T_1-T_1^{\prime }$;

(iii)

$Q_2=Q_1-Q_1^{\prime }+\left\{\tilde{q}\right\}$;

(iv)

$I_2=\left(I_1\cap \left\{\left(P_2\times T_2\right)\cup \left(Q_2\times T_2\right)\right\}\right)\cup \left(\tilde{q}\times q_{out}·\right)$;

(v)

$O_2=\left(O_1\cap \left\{\left(T_2\times P_2\right)\cup \left(T_2\times Q_2\right)\right\}\right)\cup \left(·q_{in}\times \tilde{q}\right)$;

(vi)

The token information in $\tilde{q}$ is the same as the token information in $q_{out}$.

Supposition 1.

In the OOPRES+ net system $\Sigma =\left\{N,F,G,M\right\}$, suppose that each transition of the Q-type internal subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ is live and each place of $S_1^{\prime }$ is bounded.

Theorem 1.

Let OOPRES+ net system ${\Sigma }^{\prime }=\left\{N\prime ,F\prime ,G\prime ,M\prime \right\}$ be obtained from $\Sigma =\left\{N,F,G,M\right\}$ by reducing the Q-type internal-subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ of the subnet $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ of $\Sigma$. Then ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is bounded if and only if $\Sigma =\left\{N,F,G,M\right\}$ is bounded.

Proof. 

(If) since $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ is bounded, then $\forall p\in N\left(P\right)$, there exists a positive integer $K_0$ such that $\forall \mathrm{M}\in \mathrm{R}\left(M_0\right),M\left(p\right)\le K_0$, and $\forall q\in N\left(Q\right)$, there exists a positive integer $B_0$ such that $\forall \mathrm{M}\in \mathrm{R}\left(M_0\right),M\left(q\right)\le B_0$. Obviously, there exist positive integers $K_1$ and $B_1$, such that $\forall p\in \left(N\left(P\right)-S{N}_1\left(P_1^{\prime }\right)\right), M_{\left(N\left(P\right)-S{N}_1\left(P_1^{\prime }\right)\right)}\left(p\right)\le K_1,\forall q\in \left(N\left(Q\right)-S{N}_1\left(Q_1^{\prime }\right)\right),M_{\left(N\left(Q\right)-S{N}_1\left(Q_1^{\prime }\right)\right)}\left(q\right)\le B_1$ (where $M_{\left(N\left(P\right)-S{N}_1\left(P_1^{\prime }\right)\right)}$ is the vector after removing the relevant component of $P_1^{\prime }$ of $M$, and $M_{\left(N\left(Q\right)-S{N}_1\left(Q_1^{\prime }\right)\right)}$) is the vector after removing the relevant component of $Q_1^{\prime }$ of $M$). Similarly, there exist positive integers $K_2$ and $B_2$, such that $\forall p\in S{N}_1\left(P_1^{\prime }\right),M_{\left(S{N}_1\left(P_1^{\prime }\right)\right)}\left(p\right)\le K_2,\forall q\in S{N}_1\left(Q_1^{\prime }\right), M_{\left(S{N}_1\left(Q_1^{\prime }\right)\right)}\left(q\right)\le B_2$. By Definition 10, $\forall p\in S{N}_2\left(P_2\right),M_{\left(S{N}_2\left(P_2\right)\right)}^{\prime }\left(p\right)\le K_2,\forall q\in S{N}_2\left(Q\right),M_{\left(S{N}_2\left(Q_2\right)\right)}^{\prime }\left(q\right)\le B_2$. Let $K=\max \left\{K_1,K_2\right\},B=\max \left\{B_1,B_2\right\}$, then $\forall p\in N^{\prime }\left(P\right)$ such that $\forall {\mathrm{M}}^{\prime }\in \mathrm{R}\left(M_0^{\prime }\right):M^{\prime }\left(p\right)\le K$; $\forall q\in N^{\prime }\left(Q\right)$ such that $\forall {\mathrm{M}}^{\prime }\in \mathrm{R}\left(M_0^{\prime }\right):M^{\prime }\left(q\right)\le B$.

(Only-if) Since ${\mathsf{\Sigma }}^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is bounded, according to Definition 10, the remaining places of the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ are bounded by removing the Q-type internal subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$. By Supposition 1, the Q-type internal subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ is bounded. So, the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ is bounded.  □

Theorem 2.

Let OOPRES+ net system ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ be obtained from $\Sigma =\left\{N,F,G,M\right\}$ by reducing the Q-type internal-subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ of the subnet $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ of $\Sigma$. Then ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is live if and only if $\Sigma =\left\{N,F,G,M\right\}$ is live.

Proof. 

(If) since $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ is live, then $\forall t\in N\left(T\right)$, $t$ is live. Since $\left(N\left(T\right)-S_1^{\prime }\left(T_1^{\prime }\right)\right)\subseteq N\left(T\right)$, $\forall t\in \left(N\left(T\right)-S_1^{\prime }\left(T_1^{\prime }\right)\right)$, then $t$ is live. It can be seen that after removing the internal subnet $S_1^{\prime }$ from $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$, the system is still live. According to Definition 10, $\forall t\in S{N}_2\left(T_2\right)$, $t$ is live. Thus, the net system ${\mathsf{\Sigma }}^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is live.

(Only-if) Since the net system ${\mathsf{\Sigma }}^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is live, according to Definition 10, the token information in $\tilde{q}$ is the same as that in $q_{out}$. By Supposition 1, each transition of the Q-type internal subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ is live, therefore, the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ is live.  □

Note that in the subnet $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ of the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$, if there are multiple Q-type internal subnets, as long as these internal subnets do not have the same pre-set and post-set, the above Q-type internal subnet reduction rule can still be used to reduce the net system and preserve the boundedness and liveness of the original net system.

Corollary 1.

Suppose $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ is a subnet of the net system $\Sigma =\left\{N,F,G,M\right\}$. In $S{N}_1$, there exists a Q-type internal subnet set $\left\{S_{11}^{\prime },S_{12}^{\prime },\dots ,S_{1k}^{\prime }\right\}$, where $·S_{1i}^{\prime }\cap ·S_{1j}^{\prime }=\varnothing$, $S_{1i}^{\prime }·\cap S_{1j}^{\prime }·=\varnothing$ (where $i,j=1,2,\dots ,k, i\ne j$). Let ${\Sigma }^{\prime }=\left\{N\prime ,F\prime ,G\prime ,M\prime \right\}$ be obtained from $\Sigma =\left\{N,F,G,M\right\}$ using Q-type internal subnet reduction rule to reduce the Q-type internal subnet set $\left\{S_{11}^{\prime },S_{12}^{\prime },\dots ,S_{1k}^{\prime }\right\}$ of $S{N}_1$, then ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is bounded and live if and only if $\Sigma =\left\{N,F,G,M\right\}$ is bounded and live.

For the subnet set $\left\{S{N}_1,S{N}_2,\dots \dots ,S{N}_m\right\}$ of the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$, if these subnets do not have the same pre-set and post-set between them, and there are multiple disjoint Q-type internal subnets in each subnet, the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ can be reduced using the Q-type internal subnet simplification rule, and the boundedness and liveness of the original net system can still be preserved.

Corollary 2.

Suppose $\left\{S{N}_1,S{N}_2,\dots \dots ,S{N}_m\right\}$ is a subnet set of the OOPRES+ net system $\Sigma =\left\{N,F,G,M\right\}$, where $·S{N}_i\cap ·S{N}_j=\varnothing$, $S{N}_i·\cap S{N}_j·=\varnothing$ (where $i,j=1,2,\dots ,m, i\ne j$). There exists a Q-type internal subnet set $\left\{S_{i1}^{\prime },S_{i2}^{\prime },\dots ,S_{il}^{\prime }\right\}$ of $S{N}_i \left(i=1,2,\dots ,m\right)$, where $·S_{iu}^{\prime }\cap ·S_{iv}^{\prime }=\varnothing , S_{iu}^{\prime }·\cap S_{iv}^{\prime }·=\varnothing$ (where $u,v=1,2,\dots ,l, u\ne v$). Let ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ be obtained from $\Sigma =\left\{N,F,G,M\right\}$ using Q-type internal subnet reduction rule to reduce the Q-type internal subnet set of $\left\{S{N}_1,S{N}_2,\dots \dots ,S{N}_m\right\}$, then ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is bounded and live if and only if $\Sigma =\left\{N,F,G,M\right\}$ is bounded and live.

4.2. TQ-Type Internal Subnet Reduction

In this section, we will introduce the TQ-type subnet reduction rule of the OOPRES+. Figure 4 is an example of this reduction rule.

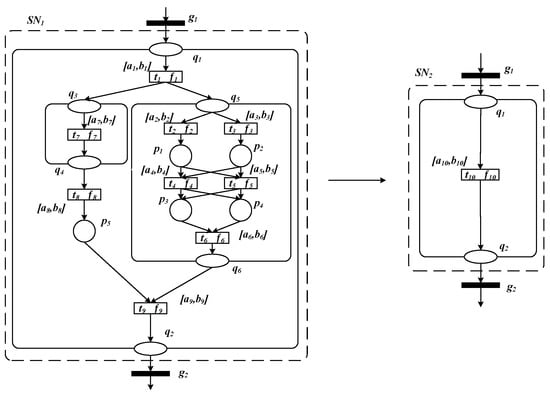
Figure 4. An example of TQ- type internal subnet reduction rule.

Definition 11.

Let $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ be a subnet of OOPRES+ net system $\Sigma =\left\{N,F,G,M\right\}$. $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ is called a TQ-type internal subnet of $S{N}_1$, if and only if the following conditions are satisfied.

• $P_1^{\prime }\subseteq P_1,T_1^{\prime }\subseteq T_1,Q_1^{\prime }\subseteq Q_1,and P_1^{\prime }\ne \varnothing ,T_1^{\prime }\ne \varnothing ,Q_1^{\prime }\ne \varnothing$;
• $I_1^{\prime }=I_1\cap \left\{\left(P_1^{\prime }\times T_1^{\prime }\right)\cup \left(Q_1^{\prime }\times T_1^{\prime }\right)\right\}$;
• $O_1^{\prime }=O_1\cap \left\{\left(T_1^{\prime }\times P_1^{\prime }\right)\cup \left(T_1^{\prime }\times Q_1^{\prime }\right)\right\}$;
• $\left(·P_1^{\prime }\cup P_1^{\prime }·\right)\cup \left(·Q_1^{\prime }\cup Q_1^{\prime }·\right)\subseteq T_1^{\prime }$;
• { $t_{in},t_{out}$} $\subseteq T_1^{\prime }$, where $t_{in}$ is the only input transition and $t_{out}$ is the only output transition.

For the transition set $T_1^{\prime }$ of TQ-type internal subnet ${\mathrm{S}}_1^{\prime }=\left\{{\mathrm{P}}_1^{\prime },{\mathrm{T}}_1^{\prime },{\mathrm{I}}_1^{\prime },{\mathrm{O}}_1^{\prime },{\mathrm{W}}_1^{\prime },{\mathrm{Q}}_1^{\prime }\right\}$, there exists the transition function ${\mathrm{f}}_{{\mathrm{T}}_1^{\prime }}$. Take Figure 4 as an example. Transitions $t_2$ and $t_4$ are parallel relations. Transitions $t_3$ and $t_5$ are parallel relations. Transition sets $\left\{t_1,t_3,t_5,t_6,t_9\right\}$ and $\left\{t_1,t_3,t_5,t_6,t_9\right\}$ are sequence relations. So, $f_{T_1^{\prime }}=f_1\odot \{\left(f_2\odot f_4\right)||\left(f_3\odot f_5\right)\odot f_6\}||\left(f_7\odot f_8\right)\odot f_9$.

For the transition set $T_1^{\prime }$ of TQ-type internal subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$, there exists a minimum transition time delay $a_{T_1^{\prime }}$ and a maximum transition time delay $b_{T_1^{\prime }}$, both of which are non-negative real numbers and satisfy $a_{T_1^{\prime }}\le b_{T_1^{\prime }}$. Take Figure 4 as an example. Transitions $t_2$ and $t_4$ are parallel relations. Transitions $t_3$ and $t_5$ are parallel relations. Transition sets $\left\{t_1,t_3,t_5,t_6,t_9\right\}$ and $\left\{t_1,t_3,t_5,t_6,t_9\right\}$ are sequence relations. So, $a_{T_1^{\prime }}=a_1+\max (a_7+a_8, \max \left(a_2+a_4,a_3+a_5\right)+a_6)+a_9$,$b_{T_1^{\prime }}=b_1+\max (b_7+b_8+\max$($b_2+b_4,b_3+b_5)+b_6)+b_9$.

Definition 12.

(TQ-type internal subnet reduction rule) Suppose $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ is a subnet of OOPRES+ net system $\Sigma =\left\{N,F,G,M\right\}$. Let the reduced subnet $S{N}_2=\left\{P_2,T_2,I_2,O_2,W_2,Q_2\right\}$ be obtained from $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ using transition $\tilde{t}$ to replace the TQ-type internal subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ of $S{N}_1$ where,

(i)

$P_2=P_1-P_1^{\prime }$;

(ii)

$T_2=T_1-T_1^{\prime }+\tilde{t}$;

(iii)

$Q_2=Q_1-Q_1^{\prime }$;

(iv)

$I_2=(I_1\cap \{$($P_2\times T_2)\cup \left(Q_2\times T_2\right)\}$)$\cup \left(·t_{in}\times \tilde{t}\right)$;

(v)

$O_2=(O_1\cap \{$($T_2\times P_2$)  $\cup \left(T_2\times Q_2\right)$})  $\cup \left(\tilde{t}\times t_{out}·\right)$;

(vi)

$f_{\tilde{t}}=f_{T_1^{\prime }}$;

(vii)

$a_{\tilde{t}}=a_{T_1^{\prime }}$,  $b_{\tilde{t}}=b_{T_1^{\prime }}$.

Supposition 2.

In the OOPRES+ net system $\Sigma =\left\{N,F,G,M\right\}$, suppose that each transition of the TQ-type internal subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ is live and each place of $S_1^{\prime }$ is bounded.

Theorem 3.

Let OOPRES+ net system ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ be obtained from $\Sigma =\left\{N,F,G,M\right\}$ by reducing the TQ-type internal-subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ of the subnet $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ of $\Sigma$. Then ${\Sigma }^{\prime }=\left\{N\prime ,F\prime ,G\prime ,M\prime \right\}$ is bounded if and only if $\Sigma =\left\{N,F,G,M\right\}$ is bounded.

Proof. 

(If) since $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ is bounded, then $\forall p\in N\left(P\right)$, there exists a positive integer $K_0$ such that $\forall \mathrm{M}\in \mathrm{R}\left(M_0\right),M\left(p\right)\le K_0$, and $\forall q\in N\left(Q\right)$, there exists a positive integer $B_0$ such that $\forall \mathrm{M}\in \mathrm{R}\left(M_0\right),M\left(q\right)\le B_0$. Obviously, there exist positive integers $K_1, B_1$, such that $\forall p\in \left(N\left(P\right)-S{N}_1\left(P_1^{\prime }\right)\right),M_{\left(N\left(P\right)-S{N}_1\left(P_1^{\prime }\right)\right)}\left(p\right)\le K_1, \forall q\in \left(N\left(Q\right)-S{N}_1\left(Q_1^{\prime }\right)\right),M_{\left(N\left(Q\right)-S{N}_1\left(Q_1^{\prime }\right)\right)}\left(q\right)\le B_1$ ($M_{\left(N\left(P\right)-S{N}_1\left(P_1^{\prime }\right)\right)}$ is the vector after removing the relevant component of $P_1^{\prime }$ of $M$, and $M_{\left(N\left(Q\right)-S{N}_1\left(Q_1^{\prime }\right)\right)}$ is the vector after removing the relevant component of $Q_1^{\prime }$ of $M$). According to Definition 12, ${\mathrm{N}}^{\prime }\left({\mathrm{P}}^{\prime }\right)=\mathrm{N}\left(\mathrm{P}\right)-{\mathrm{SN}}_1\left({\mathrm{P}}_1^{\prime }\right)$ and ${\mathrm{N}}^{\prime }\left({\mathrm{Q}}^{\prime }\right)=\mathrm{N}\left(\mathrm{Q}\right)-{\mathrm{SN}}_1\left({\mathrm{Q}}_1^{\prime }\right)$. Thus, $\forall \mathrm{p}\in {\mathrm{N}}^{\prime }\left({\mathrm{P}}^{\prime }\right)$, ${\mathrm{M}}_{\left({\mathrm{N}}^{\prime }\left({\mathrm{P}}^{\prime }\right)\right)}\left(\mathrm{p}\right)\le {\mathrm{K}}_1$, $\forall \mathrm{q}\in {\mathrm{N}}^{\prime }\left({\mathrm{Q}}^{\prime }\right)$, ${\mathrm{M}}_{\left({\mathrm{N}}^{\prime }\left({\mathrm{Q}}^{\prime }\right)\right)}\left(\mathrm{q}\right)\le {\mathrm{B}}_1$.

(Only-if) Since ${\mathsf{\Sigma }}^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is obtained from $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ using the TQ- type internal subnet rule to reduce the TQ-type internal subnet of $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$, according to Definition 12, $N\left(P\right)=N^{\prime }\left(P^{\prime }\right)\cup S{N}_1^{\prime }\left(P_1^{\prime }\right)$ and $N\left(Q\right)=N^{\prime }\left(Q^{\prime }\right)\cup S{N}_1^{\prime }\left(Q_1^{\prime }\right)$. By Supposition 2, $S{N}_1^{\prime }\left(P_1^{\prime }\right)$ and $S{N}_1^{\prime }\left(Q_1^{\prime }\right)$ are bounded. Since ${\mathsf{\Sigma }}^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is bounded, then both $N^{\prime }\left(P^{\prime }\right)$ and $N^{\prime }\left(Q^{\prime }\right)$ are bounded. Therefore, both $N\left(P\right)$ and $N\left(Q\right)$ are bounded. In summary, the OOPRES+ net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ is bounded.  □

Theorem 4.

Let OOPRES+ net system ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ be obtained from $\Sigma =\left\{N,F,G,M\right\}$ by reducing the TQ-type internal-subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ of the subnet $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ of $\Sigma$. Then ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is live if and only if $\Sigma =\left\{N,F,G,M\right\}$ is live.

Proof 

(If) Since$\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ is live, then $\forall t\in N\left(T\right)$, $t$ is live. Since $\left(N\left(T\right)-S_1^{\prime \left(T_1\prime \right)}\right)\subseteq N\left(T\right)$, then $\forall t\in \left(N\left(T\right)-S_1^{\prime \left(T_1\prime \right)}\right)$, $t$ is live. According to Supposition 2, in the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$, each transition of the TQ-type sub-internet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ is live. By Definition 12, $f_{\tilde{t}}=f_{T_1^{\prime }}$, $a_{\tilde{t}}=a_{T_1^{\prime }}$, and $b_{\tilde{t}}=b_{T_1^{\prime }}$, therefore, $\tilde{t}$ is live. Since $N^{\prime }\left(T^{\prime }\right)=\left(N\left(T\right)-S_1^{\prime }\left(T_1^{\prime }\right)\right)\cup \left\{\tilde{t}\right\}$, then $\forall t\in N^{\prime }\left(T^{\prime }\right)$, $t$ is live, i.e., the net system ${\mathsf{\Sigma }}^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is live.

(Only-if) Since ${\mathsf{\Sigma }}^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is live, then $\tilde{t}$ is live. According to Definition 12, $f_{\tilde{t}}=f_{T_1^{\prime }}$, $a_{\tilde{t}}=a_{T_1^{\prime }}$, $b_{\tilde{t}}=b_{T_1^{\prime }}$. By Supposition 2, it follows that in $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$, each transition of $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$ is live. Since the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ is obtained from ${\mathsf{\Sigma }}^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ using the TQ- type internal subnet reduction rule to replace the transition $\tilde{t}$ with the internal subnet $S_1^{\prime }=\left\{P_1^{\prime },T_1^{\prime },I_1^{\prime },O_1^{\prime },W_1^{\prime },Q_1^{\prime }\right\}$, then the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ is live.  □

Note that in the subnet $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ of the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$, if there are multiple TQ-type internal subnets, as long as these internal subnets do not have the same pre-set and post-set, the above TQ-type internal subnet reduction rule can still be used to reduce the net system and preserve the boundedness and liveness of the original net system.

Corollary 3.

Suppose $S{N}_1=\left\{P_1,T_1,I_1,O_1,W_1,Q_1\right\}$ is a subnet of the net system $\Sigma =\left\{N,F,G,M\right\}$. In $S{N}_1$ there exists a TQ-type internal subnet set $\left\{S_{11}^{\prime },S_{12}^{\prime },\dots ,S_{1k}^{\prime }\right\}$, where $·S_{1i}^{\prime }\cap ·S_{1j}^{\prime }=\varnothing$, $S_{1i}^{\prime }·\cap S_{1j}^{\prime }·=\varnothing$ (where $i,j=1,2,\dots ,k, i\ne j$). Let ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ be obtained from $\Sigma =\left\{N,F,G,M\right\}$ using TQ-type internal subnet reduction rule to reduce the TQ-type internal subnet set $\left\{S_{11}^{\prime },S_{12}^{\prime },\dots ,S_{1k}^{\prime }\right\}$ of $S{N}_1$, then ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is bounded and live if and only if $\Sigma =\left\{N,F,G,M\right\}$ is bounded and live.

Further, for the subnet set $\left\{S{N}_1,S{N}_2,\dots \dots ,S{N}_m\right\}$ of the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$, if these subnets do not have the same pre-set and post-set between them, and there are multiple disjoint TQ-type internal subnets in each subnet, the net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ can be reduced using the TQ-type internal subnet reduction rule, and the boundedness and liveness of the original net system can still be preserved.

Corollary 4.

Suppose $\left\{S{N}_1,S{N}_2,\dots \dots ,S{N}_m\right\}$ is a subnet set of the OOPRES+ net system $\Sigma =\left\{N,F,G,M\right\}$, where $·S{N}_i\cap ·S{N}_j=\varnothing$, $S{N}_i·\cap S{N}_j·=\varnothing$ (where $i,j=1,2,\dots ,m, i\ne j$). There exists a TQ-type internal subnet set $\left\{S_{i1}^{\prime },S_{i2}^{\prime },\dots ,S_{il}^{\prime }\right\}$ of $S{N}_i \left(i=1,2,\dots ,m\right)$, where $·S_{iu}^{\prime }\cap ·S_{iv}^{\prime }=\varnothing , S_{iu}^{\prime }·\cap S_{iv}^{\prime }·=\varnothing$ (where $u,v=1,2,\dots ,l, u\ne v$). Let ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ be obtained from $\Sigma =\left\{N,F,G,M\right\}$ using Q-type internal subnet reduction rule to reduce the TQ-type internal subnet set of $\left\{S{N}_1,S{N}_2,\dots \dots ,S{N}_m\right\}$, then ${\Sigma }^{\prime }=\left\{N^{\prime },F^{\prime },G^{\prime },M^{\prime }\right\}$ is bounded and live if and only if $\Sigma =\left\{N,F,G,M\right\}$ is bounded and live.

5. Application

This section applies the proposed OOPRES+ reduction rules to the modeling and analysis of the embedded control system of a smart restaurant, and verifies the reliability and effectiveness of the proposed reduction rules.

In the following, an OOPRES+ is applied to model and analyze a smart restaurant embedded control system. Figure 5 shows the net system OOPRES+ model $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ of this embedded control system. The four control modules of reservation, meal dispensing, purchasing and decision making are modeled as object subnet systems $S{N}_{1 },S{N}_2,S{N}_3,S{N}_4$, respectively.

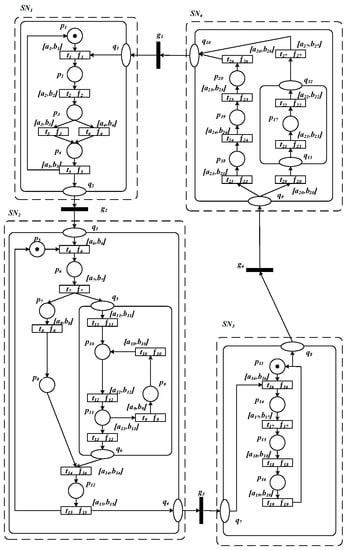
Figure 5. Embedded control system model of a smart restaurant $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$.

In Figure 5, $t_1$: request restaurant data; $t_2$: obtain display data; $t_3$: submit meal data; $t_4$: submit evaluation data; $t_5$: complete data upload; $t_6$: submit meal preparation data; $t_7$: complete data upload;$t_8$: make production plans; $t_9$: request inventory data; $t_{10}$: obtain inventory data; $t_{11}$: submit raw material data; $t_{12}$: submit inventory transfer data;$t_{13}$: complete data upload; $t_{14}$: submit recipe data; $t_{15}$: complete data upload; $t_{16}$: request to obtain purchase data; $t_{17}$: obtain purchase data; $t_{18}$: submit order data;$t_{19}$: complete data upload;$t_{20}$: request purchase data; $t_{21}$: obtain procurement data; $t_{22}$: upload costing data; $t_{23}$: request access to evaluation data; $t_{42}$: obtain evaluation data; $t_{25}$: submit feedback data; $t_{26}$: complete evaluation data upload; $t_{27}$: complete procurement data upload. $g_i$: gateway; $f_i$: the transition function of the corresponding transition; $\left[a_i,b_i\right]$: the transition time delay of the corresponding transition. By Definitions 7 and 8, the net system $\mathsf{\Sigma }=\left\{\mathrm{N},\mathrm{F},\mathrm{G},\mathrm{M}\right\}$ is bounded and live.

As shown in Figure 6, the Q-type internal subnet (generated by {$p_{17},t_{21},t_{22},q_{11},q_{12}$}) of $S{N}_1$ of the OOPRES+ net system model $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ is reduced to the message place $\tilde{q}$, and then the reduced net system ${\mathsf{\Sigma }}_1=\left\{N_1,F_1,G_1,M_1\right\}$ is obtained. It is easy to see that each place of this Q-type internal subnet is bounded and each transition is live. By Theorems 1 and 2, the net system ${\mathsf{\Sigma }}_1=\left\{N_1,F_1,G_1,M_1\right\}$ is bounded and live if and only if $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ is bounded and live.

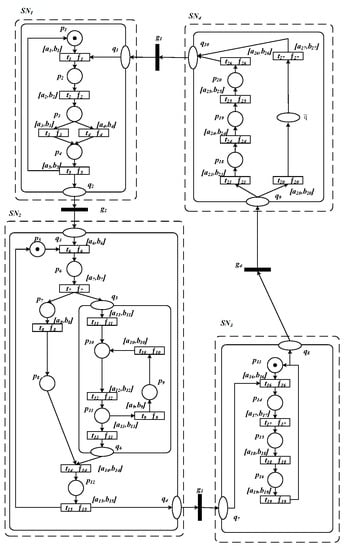
Figure 6. ${\mathsf{\Sigma }}_1=\left\{N_1,F_1,G_1,M_1\right\}$ obtained using the Q-type internal subnet reduction rule.

As shown in Figure 7, the TQ-type internal-subnet (generated by {$p_2,p_3,p_4,t_1,t_2,t_3,t_4,t_5\}$ of $S{N}_1$, the TQ-type internal subnet (generated by {$p_6,p_7,p_8,p_9,p_{10},p_{11},p_{12},t_6,t_7,t_8,t_9,t_{10},t_{11},t_{12},t_{13},t_{14},t_{15},q_5,q_6$}) of $S{N}_2$, the TQ-type internal subnet (generated by $\{p_{14},p_{15},$ $p_{16},t_{16},t_{17},t_{18},t_{19}$}) of $S{N}_3$, and the TQ-type internal subnet (generated by $\{p_{18},p_{19},p_{20},t_{23},$ $t_{24},t_{25},t_{26}$}) of $S{N}_4$ of the OOPRES+ net system model ${\mathsf{\Sigma }}_1=\left\{N_1,F_1,G_1,M_1\right\}$ are reduced to the transitions $t_{28}$, $t_{29}$, $t_{30}$, and $t_{31}$, respectively, and then the reduced net system ${\mathsf{\Sigma }}_2=\left\{N_2,F_2,G_2,M_2\right\}$ is obtained. It is easy to know that each place of the above four the TQ-type internal subnets is bounded and each transition is live. Since the above the TQ-type internal subnet reductions satisfy the conditions of Theorems 3 and 4, it is easy to see that the net system ${\mathsf{\Sigma }}_2=\left\{N_2,F_2,G_2,M_2\right\}$ is bounded and live if and only if ${\mathsf{\Sigma }}_1=\left\{N_1,F_1,G_1,M_1\right\}$ is bounded and live.

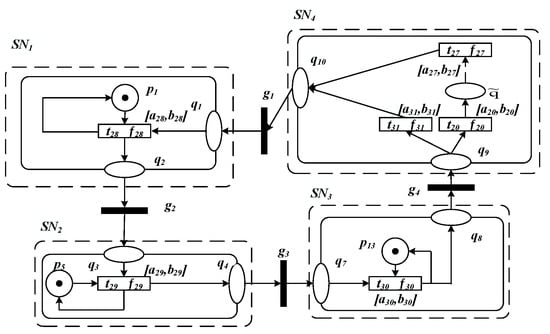
Figure 7. ${\mathsf{\Sigma }}_2=\left\{N_2,F_2,G_2,M_2\right\}$ obtained using the TQ-type internal subnet reduction rule.

Note that, the boundedness and liveness of the OOPRES net system $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$, ${\mathsf{\Sigma }}_1=\left\{N_1,F_1,G_1,M_1\right\}$ and ${\mathsf{\Sigma }}_2=\left\{N_2,F_2,G_2,M_2\right\}$ in Figure 5, Figure 6 and Figure 7 can also be verified by the modeling tool software Tina 3.7.0. (Tina 3.7.0 is a simulation tool used only for simulation analysis and viewing property analysis results.) The verification of boundedness and liveness of the original OOPRES+ net system and the reduced OOPRES+ net system can be seen from Figure 8, Figure 9, Figure 10 and Figure 11.

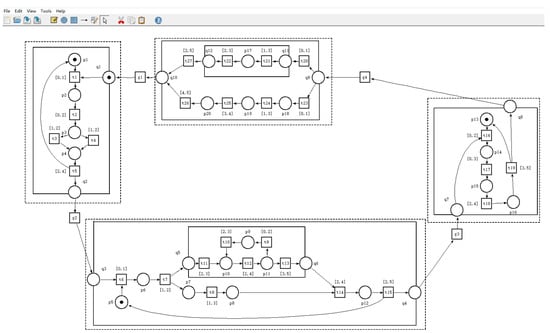
Figure 8. The original smart restaurant model $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$ in Tina.

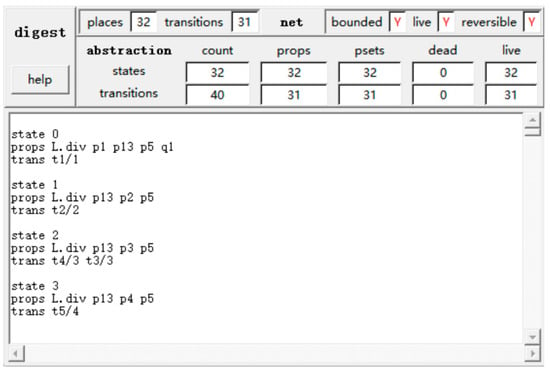
Figure 9. Verification result of the boundedness and liveness of $\mathsf{\Sigma }=\left\{N,F,G,M\right\}$.

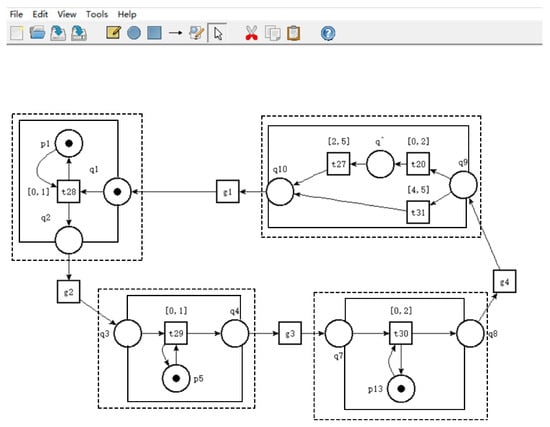
Figure 10. The reduced smart restaurant model ${\mathsf{\Sigma }}_2=\left\{N_2,F_2,G_2,M_2\right\}$ in Tina.

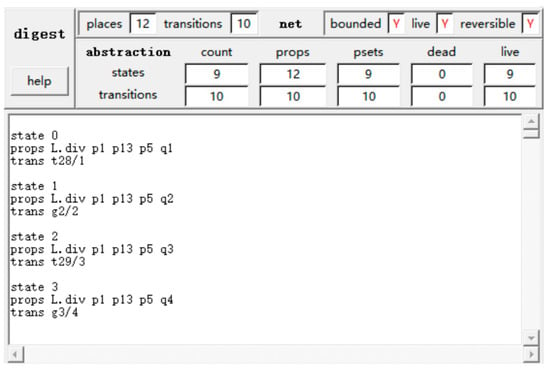
Figure 11. Verification result of the boundedness and liveness of ${\mathsf{\Sigma }}_2=\left\{N_2,F_2,G_2,M_2\right\}$.

It can be seen from Figure 9 and Figure 11 that the original smart restaurant OOPRES+ model and the reduced OOPRES+ model are all bounded and live.

In summary, the original OOPRES+ net system is reduced by using the Q-type internal subnet reduction rule and the TQ-type internal subnet reduction rule. Some sufficient and necessary conditions for the reduction rules given in this paper can make the target network system keep the boundedness and liveness of the original network system unchanged, so that the boundedness and liveness of the original network system can be studied with the reduced net system, and the purpose of studying the large system with the small system can be achieved, so as to alleviate the “state space explosion” problem of the OOPRES+ net system.

6. Conclusions

Aiming at the problem of formal modeling and verification analysis of embedded systems, this paper presents two internal-subnet reduction rules of an object-oriented PRES+ (OOPRES+), and investigates the problem of preserving the liveness and boundedness of the reduction operation. This paper proposes certain necessary and sufficient conditions for the reduction operation to preserve the boundedness and liveness of the original net system, and applies these reduction rules to the modeling and analysis of the intelligent restaurant embedded control system. The research results of this paper will provide a new way for the analysis of large-scale complex embedded system model.

The next research work is to give broader conditions and investigate the preservation of other important properties (such as timing, reachability, and functionality) of the reduction operations of OOPRES+.