Parallel Stochastic Computing Architecture for Computationally Intensive Applications

Abstract

Stochastic computing requires random number generators to generate stochastic sequences that represent probability values. In the case of an 8-bit operation, a 256-bit length of a stochastic sequence is required, which results in latency issues. In this paper, a stochastic computing architecture is proposed to address the latency issue by employing parallel linear feedback shift registers (LFSRs). The proposed architecture reduces the latency in the stochastic sequence generation process without losing accuracy. In addition, the proposed architecture achieves area efficiency by reducing 69% of flip-flops and 70.4% of LUTs compared to architecture employing shared LFSRs, and 74% of flip-flops and 58% of LUTs compared to the architecture applying multiple LFSRs with the same computational time.

1. Introduction

Stochastic Computing (SC) adopts the concept of probability and approximates the binary number to the probability value between 0 and 1. SC utilizes a bit stream of ‘0’ s and ‘1’ s called stochastic sequences for computation instead of binary numbers. The stochastic sequence is obtained by comparing the random number and the binary number. The comparator outputs ‘1’ when the size of the binary number is larger than the random number and ‘0’ in the opposite case. In this way, the output bits from the comparator become a stochastic sequence, and the stochastic sequence is encoded as a probability value, approximated as a ratio of 1s out of the total number of bits in the sequence. Figure 1 shows the basic method of encoding a sequence to a probability value P. When the number of 1 is defined as N, and the length of the entire sequence is L, the sequence represents a probability value ‘N/L’ [1].

Figure 1. Concept of stochastic encoding. The number 1 is defined as N, and the length of the entire sequence is L.

Outputs from traditional binary arithmetic operations are accurate, but the outputs are vulnerable to errors. However, SC inherently loses accuracy but offers fault tolerance and the advantage of area efficiency with lightweight computational circuits [2]. Therefore, recent works apply SC to computationally intensive applications such as image processing [3], cloud systems [4], artificial intelligence [5,6], and filter operations [7], reducing circuit area and improving accuracy. For example, ref. [3] replaced the existing scaled adder with an adder that does not require scaling and implemented efficient image sharpening. Further, reference work [6] implemented SC for artificial intelligence neural networks by applying extended SC logic to achieve high accuracy.

However, SC requires a stochastic sequence including a large number of ‘0’ s and ‘1’ s [8], and generating the long stochastic sequence results in latency issues [9,10]. For instance, in 8-bit computation, the SC requires a 256-bit-long stochastic sequence [8]. Traditionally, the SC employs a linear feedback shift register (LFSR) to obtain random numbers and stochastic sequences. Since one LFSR with one feedback loop generates only one pseudo-random number in each clock cycle, 256 clock cycles are required to obtain 256 bits of a stochastic sequence. Therefore, to address the latency issue and apply parallel architecture, ref. [11] replaced an LFSR with analog circuits by applying a memristor. Additionally, ref. [12] applied the Sobol sequence, a quasi-random sequence, significantly reducing computational time.

In this paper, a stochastic computing architecture employing parallel LFSRs is proposed to address the latency issue. Moreover, the proposed parallel architecture demonstrates the following benefits of applying a parallel LFSR in stochastic computing; computation time, area efficiency, and accuracy. The proposed architecture achieves high area efficiency compared to an architecture employing shared LFSRs, reducing the computational time by sharing LFSRs, and architecture based on multiple LFSRs. The proposed parallel architecture achieves area efficiency by reducing 69% of flip-flops and 70.4% of LUTs compared to an architecture employing shared LFSRs. Furthermore, the proposed architecture obtains the stochastic sequence in one clock cycle without losing accuracy. The contributions of this work are as follows:

• The proposed architecture demonstrates the advantages of applying a parallel LFSR to stochastic computing through hardware implementation
• The proposed parallel stochastic computing architecture reduces the latency and obtains the stochastic sequence in one clock cycle without losing accuracy
• Three different types of parallel LFSRs are implemented, and the proposed architecture achieves the area efficiency and the lowest error rate

2. Backgrounds

2.1. Concept of Stochastic Computing

As shown in Figure 2, three steps are required to implement SC; stochastic number generation, stochastic computing, and binary converting. The first step is to convert binary numbers into a stochastic sequence with an LFSR and a comparator. The next step is to compute operations with the stochastic sequence and convert the sequence back into binary numbers.

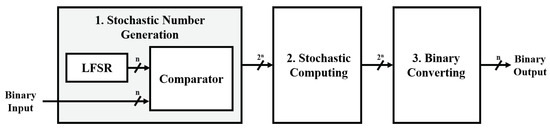
Figure 2. Flow of a stochastic computing.

2.1.1. Stochastic Number Generation

Stochastic number generators are responsible for converting binary numbers into stochastic sequences, consisting of an LFSR, random number generator, and comparator, as shown in Figure 2. The two inputs of the comparator are connected to the outputs of the LFSR and binary input, respectively. The comparator compares the size of the random number from the LFSR and the binary input for each clock cycle and outputs ‘0’ or ‘1’, and the output bits become a stochastic sequence.

The circuit shown in Figure 3a is a 4-bit Fibonacci LFSR, and the circuit shown in Figure 3b is the 4-bit Galois LFSR circuit. The Fibonacci LFSR is converted to the Galois circuit one-on-one through reversing output. The LFSR includes a feedback loop consisting of a shift register and an XOR gate. The LFSR cannot have an initial seed value of zero because the output is always zero, even if a bit shift occurs. Starting with the seed value containing 1, the bit is shifted in every clock cycle, and the next output is determined by the output of the XOR gate.

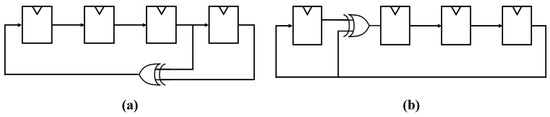
Figure 3. Circuit of Fibonacci LFSR and Galois LFSR to obtain random numbers (a) Fibonacci LFSR (b) Galois LFSR.

2.1.2. Stochastic Computing

Since the stochastic sequence refers to the probability value, the independent stochastic sequence represents the independent probability value. The characteristics of binary computing and stochastic computing are distinguished in stochastic computing circuits due to the SC replacing the general binary operator with a specific operator through stochastic interpretation. For example, arithmetic operations such as multiplication, addition, and subtraction are implemented through logic gates, as shown in Figure 4. Further, complex operations such as division, absolute value operations, hyperbolic tangent operations, and exponential functions are implemented through sequential circuits [13,14].

Figure 4. Stochastic computing circuits; (a) Stochastic uni-polar multiplier (b) Stochastic bipolar multiplier (c) Stochastic adder (d) Stochastic subtractor.

AND gates for uni-polar and XNOR gates for bipolar replace arithmetic operators based on the Monte Carlo method [1]. This point enables reducing the circuit area when applying SC to computationally intensive applications that repeat a multiplication. Further, MUX implements addition and subtraction and requires three stochastic sequences at the same time. In the case of absolute value operation, hyperbolic tangent function, and exponential operation, the SC circuit is implemented in a Markov Chain method based on a finite state machine (FSM) [15,16].

2.1.3. Binary Converting

SC utilizes stochastic sequences, and the output of the operation is also the stochastic sequences, not binary. Therefore, a process of converting the sequence back into binary numbers is required. Since the N, the number of ‘1’ s, is approximated to binary number X in the probability value P = N/L, as shown in Figure 5, the number of 1 s in the stochastic sequence is converted to binary number X.

Figure 5. Flow of binary converting.

2.2. Area Efficiency

SC replaces arithmetic operators with simple logic gates. For example, a multiplier is replaced by an AND gate, and an adder is replaced by MUX. This is because the probability that two independent events occur at the same time is mathematically the multiplication of the probabilities. If two independent stochastic sequences, i.e., probability values, are the inputs of an AND gate, then the output of an AND gate is equal to the product of the probabilities. For example, if two sequences represent independent probability values 4/8 and 6/8 each, the result of the multiplication, 3/8, is obtained as the output, as shown in Figure 6. Therefore, if SC is applied to repeated operations, the multipliers are replaced with AND gates effectively.

Figure 6. Example of stochastic multiplication.

Similarly, the probability of two independent events, A and B, occurring is the sum of their respective probability values. If the probability of the selection signal for the MUX being 1 is P(S), and the probabilities of events A and B being 1 are P(A) and P(B), respectively, the output of the MUX is P(A) × P(S) if the selection signal is 1, and P(B) × (1 − P(S)) if the selection signal is 0. Therefore, the final output of MUX is as follows:

$$P=\left(P\right(A\left)P\right(S\left)\right)+\left(P\right(B\left)\right(1-P\left(S\right)\left)\right)$$

(1)

If the probability of the selection signal for the MUX being 1 is 1/2, then the output of the MUX is equal to the sum of the probabilities scaled to 1/2, as shown in Figure 7a. In addition, as shown in Figure 7b, the subtractor is implemented by adding a NOT gate.

Figure 7. Example of stochastic addition and subtraction: (a) Stochastic addition, (b) Stochastic subtraction.

By utilizing the scaled values obtained from the MUX, SC implements the tri-linear interpolation expression for finding the middle coordinate of a cuboid using only seven MUXs [17]. This approach offers area efficiency by reducing hardware complexity and computational requirements.

2.3. Fault-Tolerance

The stochastic sequence is generated using a random number generator and a comparator. Therefore, as shown in Figure 8, when some bits are flipped, the final output is not significantly affected compared to the situation where a bit error occurs in a binary number. For example, in the case of Figure 8, even if a bit flip occurs in the stochastic sequence, the ideal output is 3/8. In a faulty case, the output is 2/8, resulting in a difference of 1/8 compared to the ideal output.

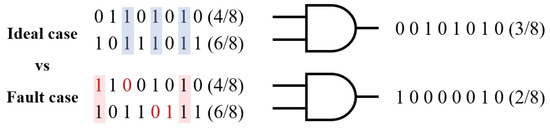
Figure 8. Comparison between ideal case and fault case.

In addition, unlike binary numbers, where each digit has a different weight, each of the 256 bits in a stochastic sequence representing an 8-bit binary number has the same weight. If an error occurs in one of the 256 bits, it has a relatively small influence since the weight of each bit is 1/256. Therefore, even if an error occurs in any of the bits, the impact on the final output is relatively small compared to a binary number, where errors in higher-weighted bits have a larger impact on the overall value.

3. Related Works

This chapter provides an overview of related research that has focused on reducing computational time and increasing hardware efficiency. In particular, the chapter examines several works that have explored the use of stochastic computing (SC) to achieve these goals. Additionally, the chapter highlights the broad range of applications where SC has been successfully applied, from image processing to neural networks.

3.1. Parallel Architectures for LFSRs

Research is being conducted to parallelize LFSRs and further improve path delay or reduce complexity. First, in [18], the complexity of the parallel LFSR feedback loop was reduced, and pipelining was applied. The feedback loop connected in parallel was shorter and simpler than the feedback loop in the traditional LFSR. This technique was applied to the IIR filter design to reduce the critical path.

Moreover, ref. [19] also proposed a parallel architecture and reduced path delay and hardware complexity. The proposed architecture eliminates unnecessary registers and XOR gates and calculates the output by using only the past feedback values.

Unlike those studies that focused on improving the parallel LFSR, this work aimed to utilize the characteristic of the parallel LFSR’s output, which cycles to obtain multiple non-overlapping random numbers simultaneously, in stochastic computing. Specifically, this work analyzed the advantages of using these random numbers in stochastic computing.

3.2. Parallel Stochastic Number Generators

3.2.1. SC Utilizing Shared Random Number Source

Stochastic number generators account for converting binary numbers into probability values in stochastic computing, but their implementation occupies a large portion of the circuit area and increases latency. Thus, refs. [20,21] have proposed techniques for sharing random number generators to reduce both circuit area and latency. However, sharing LFSRs introduces accuracy loss due to the correlation between probability values [22,23]. To mitigate the correlation, ref. [21] has proposed cyclically shifting the output of the random number generator, and this technique was used in a designed SC circuit for image processing, resulting in a reduction in circuit area [21].

In [20,21], the proposed technique for sharing random number generators was implemented using a circular shifter to reduce the correlation between probability values. However, this work explored an alternative approach using a combinational circuit. To compare the effectiveness of sharing LFSRs, this work examined the advantages and disadvantages in relation to a proposed parallel architecture.

3.2.2. SC with Increased Energy Efficiency Using Sobol Sequence

To address latency issues in SC, ref. [12] explored the use of a Sobol sequence with a quasi-random number instead of LFSRs. The Sobol sequence has a shorter length than LFSRs and improves the accuracy of stochastic computations. Moreover, the proposed architecture in [12] offers a parallel implementation of the random number generator utilizing the Sobol sequence, which results in improved hardware efficiency.

Ref. [12] demonstrated improved efficiency by utilizing a Sobol sequence. However, this work proposes an architecture that increases efficiency by employing LFSR.

3.3. Application of SC

3.3.1. Image Processing

Image processing on a pixel basis is relatively simple, but the overall computation of image processing is very large because of the large number of pixels. The SC enables repetitive image computation circuits at a low cost through the simplification of the circuits [24]. Image processing with SC is implemented through various algorithms such as edge detection [15] and Gamma Correction [25] and applied to complex systems such as autonomous driving [26].

Since the central difference algorithm includes only absolute value operations and scaled addition and subtraction operations, SC requires lightweight logic to implement the algorithm [15]. The central difference algorithm is implemented only with MUX and NOT gates, which are SC addition and subtraction calculators and SC absolute value calculators [15]. Experimental results from [15] show that there is no significant difference between the edge detection image implemented through SC and the edge detection image implemented through the deterministic operation.

Gamma Correction, which non-linearly transforms the intensity signal of light, includes an exponential function. The corresponding operation is approximated by the Bernstein Polynomial operation and implemented through SC [25]. Reference work [25] changed the length of stochastic sequences and analyzed error changes and hardware costs with the length of the sequence. Moreover, ref. [25] demonstrated the strength in terms of cost by comparing and analyzing Gamma Correction implemented through the SC module proposed in [25] with the traditional method.

3.3.2. Neural Networks

Ref. [6] demonstrated efficiency in terms of area and power consumption by applying SC to solve the power issue of ANN hardware arising from high-density neuron computing [6]. Ref. [6] proposed extended stochastic logic (ESL) to support a wider range of input coding and to use ESL-based ReLU functions as related active functions. By applying the ESL method, the accuracy is improved by 48%; the area cost is reduced by 84%, and the power consumption by 60% compared to modules to which SC is not applied.

Ref. [27] proposed a deep-learning parameter optimization method. For deep-learning parameter optimization, probabilistic conductive bridging RAM (CBRAM) was applied to efficiently generate stochastic sequences. Furthermore, the proposed method was applied to the convolutional neural network (CNN) and obtained 167 uW of power consumption.

Refs. [28,29] implemented an artificial neural network (ANN) with SC to reduce area overhead and power consumption due to large numbers of parameters and complex connections between neurons. Ref. [29] achieved 95.3% area reduction and 90% power reduction compared to an ANN without applying SC.

4. Parallel Stochastic Computing Architecture

In this paper, parallel SC architecture is proposed to address the latency issue. The proposed architecture obtains multiple random numbers simultaneously, which reduces the latency in the stochastic number generation process. Figure 9a shows the concept of a basic stochastic number generator, which consists of an LFSR and a comparator.

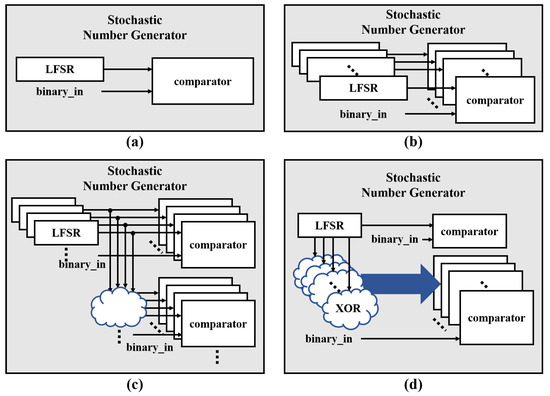
Figure 9. Three different types of parallel LFSRs: (a) Basic LFSRs (b) Multiple LFSRs (c) Shared LFSRs (d) Parallel LFSRs.

To address the latency issue, this work compares three methods. The first method, shown in Figure 9b, is to increase the number of LFSRs. However, this approach is inefficient in terms of circuit area because the number of registers increases with the number of random numbers generated simultaneously. The second method is to share LFSRs, shown in Figure 9c, where a single LFSR output is converted into multiple random numbers using additional combinational circuits. However, shared LFSRs have limitations in generating a large number of random numbers simultaneously due to correlations between the random numbers [30,31,32].

Finally, the proposed architecture employs a parallel LFSR [33] as shown in Figure 9d to generate multiple random numbers simultaneously without significantly increasing the circuit area or compromising the error rate. This results in reduced latency, as multiple random numbers are obtained at the same time. The proposed architecture achieves reduced latency by adding only XOR gates without additional registers.

4.1. Stochastic Computing Employing Multiple LFSRs

As illustrated in Figure 10, employing multiple LFSRs reduces the time for obtaining multiple random numbers. However, when applying multiple LFSRs, the initial seed values of the LFSRs affect the error rate due to the correlation between random numbers. However, since the output random numbers are directly connected to the registers, multiple LFSRs offer the advantage of being able to operate at a high clock frequency.

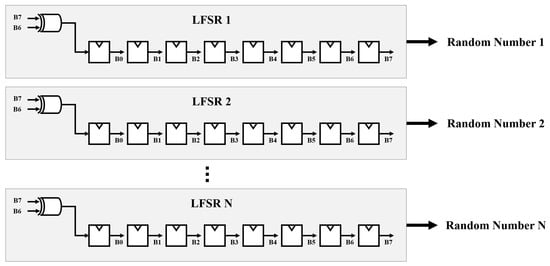
Figure 10. Employing multiple LFSRs to obtain multiple random numbers at the same time.

For example, in an 8-bit operation, 256 LFSRs are required, and 256 random initial seed values are also required for the LFSRs. As shown in Figure 11, the stochastic computing unit includes three stochastic number generators to compute addition and subtraction in one clock cycle.

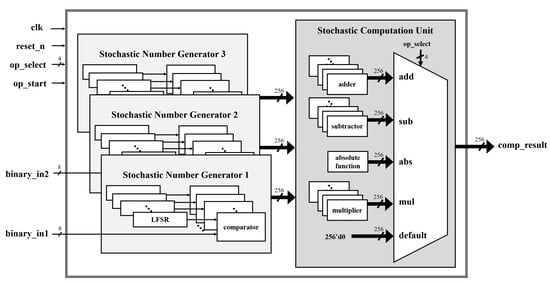
Figure 11. Architecture applying multiple LFSR.

4.2. Stochastic Computing Employing Shared LFSRs

Shared LFSRs allow for area efficiency without increasing the number of LFSRs, as they enable multiple random numbers to be obtained from a single LFSR at the same time through the use of additional combinational circuits, as shown in Figure 12. The architecture employing shared LFSRs is depicted in Figure 13.

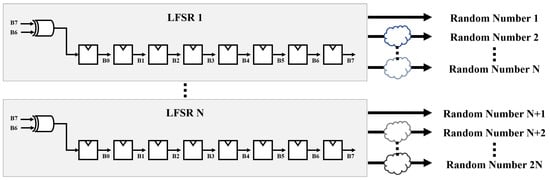
Figure 12. Employing shared LFSRs to obtain multiple random numbers at the same time.

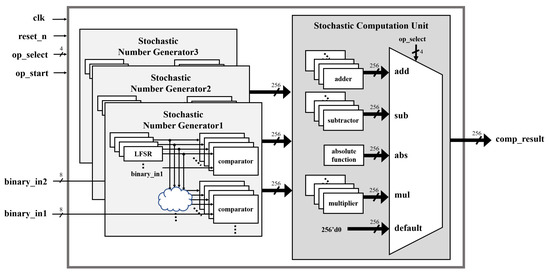
Figure 13. Architecture applying shared LFSR.

By utilizing additional combinational circuits, different random numbers are obtained from a single LFSR, which offers area efficiency compared to using multiple LFSRs. However, this method is sensitive to error rates due to the correlation between the generated random numbers.

4.3. Stochastic Computing Employing Parallel LFSR

A parallel LFSR circuit is implemented to generate stochastic sequences with reduced latency and higher area efficiency. The parallel LFSR circuit shown in Figure 14 uses the first output value of the LFSR as the input of the next output, and the second output becomes the next value of the first output [33]. Unlike the shared-LFSR and multiple-LFSR methods, the circuit utilizes only one LFSR, eliminating the risk of error rate loss due to correlation. By utilizing only XOR gates, the circuit achieves area efficiency without additional registers. Since multiple XOR gates are required, the time delay caused by XOR gates should be considered when implementing the circuit in high-speed frequency systems.

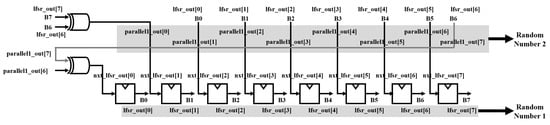
Figure 14. Circuit of 2-stage parallel LFSR.

Figure 15 shows the circuit for implementing a 4-stage parallel LFSR. The eight bits lfsr_out[0], lfsr_out[1], lfsr_out[2], lfsr_out[3], lfsr_out[4], lfsr_out[5],lfsr_out[6], and lfsr_out[7] are one 8-bit random number, and bits parallel1[0], parallel1[1], parallel1[2], parallel1[3], parallel1[4], parallel1[5], parallel1[7] are the next eight bits to be output. In the same way, a random number generation circuit was implemented by employing parallel LFSR, as shown in Figure 16.

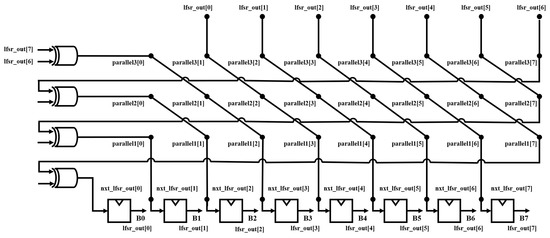
Figure 15. Circuit of 4-stage parallel LFSR.

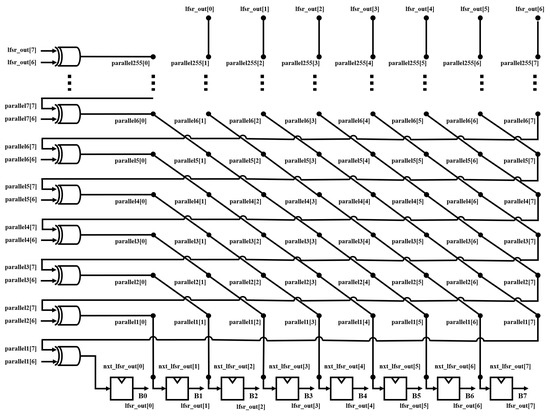
Figure 16. Circuit of multi-stage parallel LFSR.

A general LFSR outputs an arbitrary random number per clock. Therefore, 256 clocks are required to obtain 256 random numbers through an 8-bit LFSR. In the proposed architecture employing the parallel LFSR, as shown in Figure 17, the stochastic sequence is obtained in one clock cycle. The proposed architecture includes three stochastic number generators to compute addition and subtraction in one cycle.

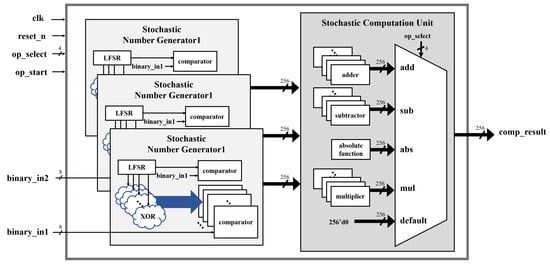
Figure 17. The proposed architecture applying parallel LFSRs.

5. Discussion

This section demonstrates the benefits of the proposed architecture, applying parallel LFSRs in stochastic computing. First, computation time is reduced when applying parallel LFSR. In the case of an 8-bit operation, the parallel LFSR requires only one clock cycle to obtain 256 random numbers, and the 256-bit length of a stochastic sequence is generated in one clock cycle. Thus, applying stochastic computing with parallel LFSR results in significant gains in computation time.

Second, the stochastic computing architecture with parallel LFSR offers circuit area efficiency. We compared the area of three types of architecture employing circuits that generate stochastic sequences in the same amount of time through hardware implementation. The architecture applying a parallel LFSR had the smallest area to perform the same computation.

Lastly, when applying a stochastic sequence generated by comparing the size of a uniform random number between 1 and 255 for 8-bit computation, the probability of obtaining accurate results is higher. Applying 256 parallel LFSRs for 8-bit computation allows for obtaining 256 non-overlapping random numbers simultaneously. However, employing multiple LFSRs or a shared LFSR results in a correlation between each bit of the stochastic sequence, decreasing the accuracy of the stochastic computation.

We evaluated the 8-bit stochastic computing operator using 8-bit LFSRs on an Altera MAX10, 10M50SCE144C8G FPGA and analyzed hardware efficiency and an error rate of add operation as follows.

5.1. Hardware Efficiency

The hardware resource usage of multiple-LFSR-based, shared-LFSR-based, and parallel-LFSR-based stochastic computing architectures implemented on an FPGA, are compared as shown in Table 1 and Figure 18a. The architecture based on multiple LFSRs uses the greatest number of flip-flops. Although a shared-LFSR-based architecture is set to utilize 1/32 flip-flops over a multiple-LFSR-based architecture, it is difficult to obtain a large reduction in hardware resource usage while maintaining the error rate. In addition, the LUT usage in the stochastic number generators increases while applying additional combinational logic compared to the multiple-LFSR-based architecture. Finally, an architecture based on parallel LFSR reduces 58% of LUTs and 74% of flip-flops compared to the hardware usage of a multiple-LFSR-based architecture. Compared to the architecture employing shared LFSRs, the hardware resource usage is reduced to 70% of LUTs and 69% of flip-flops.

Table 1. Hardware efficiency evaluation.

	Multiple		Shared		Parallel
	LUT	FF	LUT	FF	LUT	FF
Stochastic Number Generator × 3	3277	6529	5281	5407	1141	1183
Stochastic Computation	630	680	697	558	188	223
Binary Converter	787	809	746	768	655	677
Sum	4694	8018	6724	6733	1984	2083

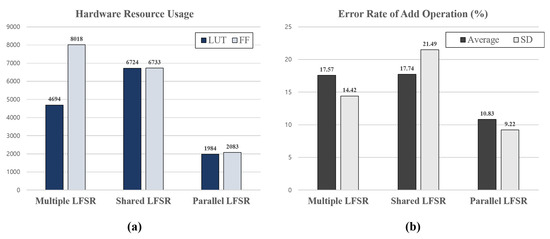
Figure 18. (a) Hardware resource usage applying three different LFSRs in SC (b) Error rate in addition applying three different LFSRs.

5.2. Error Rate

When a parallel LFSR is applied in 8-bit operations, 256 random numbers are obtained in one clock cycle, and these random numbers are identical to the outputs generated by the LFSR with one feedback loop in 256 clock cycles. Therefore, the stochastic sequence obtained through a parallel LFSR is generated by comparing it with an input binary number and non-overlapping random numbers 256 times. If the distribution of random numbers is skewed or has a correlation, it affects the accuracy of the computation. On the other hand, the random numbers obtained through a shared LFSR are inevitably correlated. Since the random numbers are manipulated and obtained from the same seed value, there is a correlation of the stochastic sequence, which affects the accuracy of the operation. While a shared LFSR offers multiple random numbers from one seed value, the additional logic has to be carefully considered to manipulate the random output. In addition, a shared LFSR requires more than one seed value, and the selection of the seed value affects the computational accuracy [34].

The error rates were compared as shown in Table 2 and Figure 18b by implementing multiple LFSR-based, shared LFSR-based, and parallel LFSR-based architectures. The multiple-LFSR-based architecture obtains an average error rate of 17.57% compared to the exact addition operation. In the case of the architecture based on shared LFSRs, the average error rate is 0.17% higher than that of a multiple-LFSR-based architecture because of the correlation between random numbers. In the case of the proposed parallel SC architecture, the error rate is 6.74%, 6.91% lower than an architecture applying shared LFSRs.

Table 2. Error rate of add operation.

%	Multiple	Shared	Parallel
Average	17.57	17.74	10.83
Standard Deviation	14.42	21.49	9.22

6. Conclusions

This work demonstrated the advantages of employing a parallel LFSR in stochastic computing. Since the process of generating the stochastic sequence involves a long delay, this work addressed the latency issue by applying parallel LFSRs. For 8-bit operations, a typical SC requires 256 clock cycles to generate the stochastic sequence, while the computation time was reduced to 1 cycle without loss of accuracy. In addition, among the three architectures, multi-LFSR-based, shared-LFSR-based, and parallel-LFSR-based architectures, the proposed stochastic computing architecture employing parallel LFSR reduced combinational circuits by up to 70% and sequential circuits by up to 74% compared to a multi-LFSR-based and shared- LFSR-based architecture. The average error rate of the addition operation was 10.83%, which was 6.91% lower than the shared-LFSR-based architecture.

The proposed parallel SC architecture was designed in the Verilog HDL and validated through RTL simulation and FPGA implementation. Since the computation time was reduced without loss of accuracy or area efficiency, the proposed parallel architecture highlights the potential of stochastic computing for computationally intensive applications such as image processing or convolutional neural networks.