A Novel Channel Pruning Compression Algorithm Combined with an Attention Mechanism

Abstract

To solve the problem of complex network models with a large number of redundant parameters, a pruning algorithm combined with an attention mechanism is proposed. Firstly, the basic training is performed once, and the network model is then re-trained with the attention mechanism for the baseline. The obtained model is pruned based on channel correlation, and finally a simplified model is obtained via continuous cyclic iteration while the accuracy rate is kept as close as possible to that of the baseline model. The algorithm was experimentally validated on ResNet based on different datasets, and the results showed that the algorithm provided strong adaptability to different datasets and different network structures. For the CIFAR-100 dataset, ResNet50 was pruned to reduce the amount of model parameters by 80.3% and the amount of computation by 69.4%, while maintaining accuracy. For the ImageNet dataset, the ResNet50 parameter volume was compressed by 2.49 times and the computational volume was compressed by 3.01 times. The ResNet101 parameter volume was reduced by 61.2%, and the computational volume was reduced by 68.5%. Compared with the traditional fixed threshold, the model achieves better results in terms of detection accuracy, compression effect, and inference speed.

1. Introduction

Deep learning has been widely used in many fields, such as image classification, target detection, and semantic segmentation. In order to achieve excellent performance, researchers have proposed VggNet [1], GoogleNet [2], ResNet [3], DenseNet [4], and other backbone architecture networks. More recently, attention mechanism have been introduced to further improve network accuracy. Jiang et al. [5] introduced a convolutional attention mechanism in a residual network to reduce the redundant mapping of remote sensing scene features at a reasonable extra time cost. Zheng et al. [6] added channel and spatial modules based on the self-attention mechanism to the backbone network and the enhanced feature extraction network of pyramid scene parsing, respectively, to extract more important feature detail information from images. However, the large computational resource requirements and high power consumption of deep learning networks limit their potential applications. In order to reduce memory consumption and speed up inference time, researchers have proposed many compression strategies, and these can be divided into weight quantization [7], knowledge distillation [8], low-rank decomposition [9], and network pruning [10]. Pruning as a method to accelerate larger pre-trained models is a common way to compress networks. Wang et al. [11], in their work on network structure, found that pruning the least important filters in the layers with the most structural redundancy enabled them to identify the structural redundancy of the CNN and prune the filters in the selected layers with the most redundancy. Shao et al. [12] proposed a novel filter pruning method that combines convolutional filters and feature map information for convolutional neural network compression, i.e., network pruning using clustered similarity and large eigenvalues. Kim [13] proposed a new technique to shrink the previously used style transfer network to eliminate redundancy in terms of memory consumption and computational cost.

The aforementioned methods have resulted in some progress for neural network model streamlining and other related applications, but the degree of model compression and the degree of accelerated computation are not sufficient and are not necessarily suitable for deployment in mobile terminal devices. Because of this, a cyclic pruning compression algorithm combined with an attention mechanism is proposed.

The remainder of this paper is organized as follows. A basic introduction to the attention mechanism and pruning algorithm is presented in Section 2. A detailed description of the steps and details of the algorithms are then presented in Section 3. Section 4 gives the experimental results and analyzes them. Lastly, the paper is summarized in Section 5.

2. Related Work

2.1. Attention Mechanism

The proposed attention mechanism is a structure based on the human observation pattern. When the human eye observes a picture, it will first quickly scan the whole picture and then focus on certain key regions of the picture so that the brain can focus more on that region and give it particular attention to obtain more effective information, and then integrate this information to draw conclusions. The attention mechanism allows the neural network to analyze and learn the relationships between global and local information to obtain important target regions in the same way the human eye acquires images, and then put more weight on these regions to obtain important image features while ignoring irrelevant image features and using limited resources to select the more critical information for processing the current task, greatly improving the processing efficiency and accuracy. In the field of computer vision, research has been carried out on attention mechanisms such as channel attention mechanisms, spatial attention mechanisms, and hybrid attention mechanisms. Figure 1 is a diagram of the generic structure of an attention mechanism. Different heights in the figure represent different importance. The different colors are used for easy differentiation and have no special meaning.

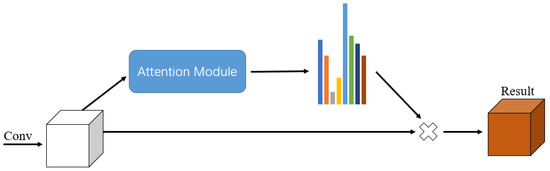
Figure 1. Generalized structure of an attention mechanism.

The improvement of deep neural network (DNN) classification performance is effectively achieved through the utilization of an attention mechanism by enhancing feature map representations with crucial information while suppressing irrelevant interference [14,15,16]. Attention mechanisms have found widespread use in several modern applications, including (but not limited to) neural machine translation [17], image captioning [18], object detection [19], and generative modeling [20]. SENet [21] introduced a lightweight gating mechanism to exploit channel relationships for improved image classification performance. This mechanism dynamically re-weights the channels in feature maps to better capture discriminative features for classification. Compared with traditional convolutional neural networks, SENet’s gating mechanism is more adaptable to datasets and achieves higher classification accuracy. This approach has been widely used in various computer vision tasks, including image classification, object detection, and semantic segmentation. It is an attention mechanism that operates along the channel dimension, but it overlooks the significance of the spatial dimension. The SGE module [22] is designed to improve the semantic expression capability of each feature group while suppressing noise and interference. The described module essentially contains spatial attention, but it unfortunately lacks full integration of this particular attention type. Convolutional block attention modules (CBAMs) [23] and bottleneck attention modules (BAMs) [24] take advantage of both spatial and channel attention in their design, providing empirical evidence that combining these two forms of attention yields better results than can be achieved using only one type. Zhang [25] proposed a sparse layer activation-based greedy strategy.

2.2. Structured Pruning

Pruning methods can generally be classified into two categories, namely unstructured pruning and structured pruning. Unstructured pruning refers to the zeroing of some parameters in the convolutional kernel according to a threshold and thereby obtaining a sparse convolutional kernel. Prior research [26,27,28,29] has focused primarily on weight pruning, which leads to unstructured sparsity in the pruned model. Such methods can obtain theoretically high compression ratios, but such theoretical compression ratios are difficult to achieve in practical compression. Due to irregular memory access [30], runtime acceleration is difficult to achieve unless specialized hardware and libraries are used.

The initial breakthroughs in structured pruning, introduced by [30,31], addressed this issue by removing entire filters or channels and thereby producing a non-sparse compressed model [28,30,32]. It should be noted that there is a correlation between channel pruning and filter pruning, as the removal of a channel from the current layer would result in the corresponding filter being eliminated from the upper layer [31]. The primary focus of this paper is channel pruning, a technique aimed at model compression. It achieves this by eliminating a specific number of channels and their associated filters. The approach proposed in [33] utilizes the ${\ell }_1$-norm as a pruning criterion whereby the filters’ ${\ell }_1$-norm is utilized in the pruning process. In network thinning [34], a batch normalization (BN) layer is incorporated to rescale different channels. The unimportant channels are then identified for pruning based on their relatively small scaling factors. Certain studies recommend pruning channels with minimal impact on feature reconstruction error between the original and pruned models. In [35], a greedy search-based method is proposed to minimize reconstruction error, while [31] preserves representative channels by solving a lasso regression problem related to reconstruction error. Both approaches only consider the local statistics of two adjacent layers, meaning that they prune one layer to minimize reconstruction error in the next layer. To account for error propagation throughout the network, NISP [36] proposes utilizing the global importance score propagated from the second-to-last layer to minimize reconstruction error prior to classification. It should be emphasized that a reliable channel pruning metric must take into account not only the global significance of channels, but also the correlation amongst different channels [21,36].

2.3. Attention-Based Pruning

Attention mechanisms have been introduced in recent years to enhance the performance of model pruning. As an example, [37] proposes utilizing the SENet model to assess channel importance, identifying and removing redundant channels with minimal significance. Nonetheless, the inherent limitations of SENet produce scalar values that incompletely represent channel significance and are inadequate for improving pruning performance. PCAS [38] devised a novel attention model to evaluate channel importance based on attention statistics. The module in PCAS is essentially a channel attention module that comprises two fully connected layers. However, this structure imposes extra complexity and overhead. Furthermore, the prediction of channel attention can be affected by the side effects that arise from dimensionality reduction operations [39,40]. To address these issues, a combination of spatial and channel attention modules is employed. Through an efficient structural design, this approach showcases superior performance during the pruning process.

3. Algorithm

Within this section, we will first provide an overview of the channel correlation pruning based on the channel–spatial attention mechanism (CCPCSA). Subsequently, we will present the structural components of the BAM attention module. Lastly, we will propose a CCPCSA algorithm that accomplishes network model pruning in the context of BAM.

An overview of our CCPCSA approach is illustrated in Figure 2. The BAM module, which captures channel importance, is integrated into the original network, and the resultant network is then trained. Subsequently, based on the relevance of the channels, the final network model is obtained by performing channel pruning on top of this trained network.

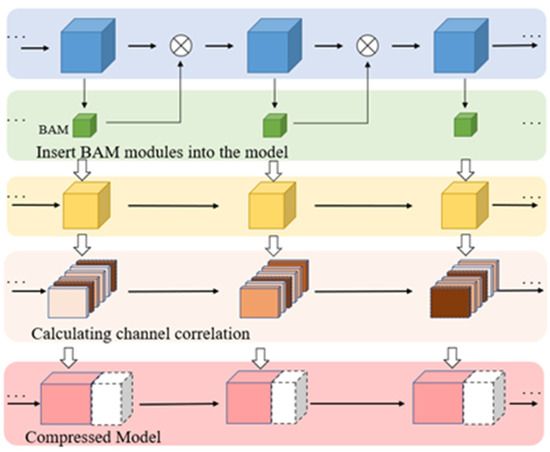
Figure 2. Overview of CCPCSA method.

3.1. Attention Mechanism

In accordance with the details put forward in reference [24], Figure 3 depicts the complete and comprehensive structural arrangement of our BAM (spatial and channel attention) module. The figure provides insights into the architecture of the module which could prove useful in understanding its functioning and benefits. Indeed, if we solely employ spatial attention, the channel dimension information will be disregarded because it treats features in distinct channels equally. Similarly, if we solely utilize channel attention, the information within the channel will also be overlooked. Hence, we believe that better performance can be achieved by integrating the spatial and channel attention modules into a unified module.

Figure 3. Schematic diagram of clustering.

For a given input feature map $F\in {ℝ}^{C\times H\times W}$ BAM infers a three-dimensional attention map $M\left(F\right)\in {ℝ}^{C\times H\times W}$. C represents the number of channels in the feature graph, H is the height of the feature graph, and W is the width of the feature graph. The 3D attention map $M\left(F\right)$ is multiplied element by element with the input feature map $F$ and then added to the original input feature map to obtain the final feature map $F^{\prime }$. The extracted feature map $F^{\prime }$ is calculated using Equation (1):

$$F^{\prime }=F+F\otimes M\left(F\right)$$

(1)

where ⊗ denotes element-by-element multiplication. To calculate the channel attention $M_C\left(F\right)\in {ℝ}^C$ and the spatial attention $M_S\left(F\right)\in {ℝ}^{H\times W}$ in two separate branches, the attention map $M\left(F\right)$ is calculated using Equation (2):

$$M\left(F\right)=\sigma \left(M_C\left(F\right)+M_S\left(F\right)\right)$$

(2)

where $\sigma$ is the Sigmoid activation function, and attention is mapped to ${ℝ}^{C\times H\times W}$ before the output of both channels.

Each channel of the feature map is aggregated in the channel branch using inter-channel relationships, global average pooling is performed on the feature map $F$, and a channel vector is generated at $F_C\in {ℝ}^{C\times 1\times 1}$. This vector encodes global information in each channel. To estimate the cross-channel attention from the channel vector, a multilayer perceptron MLP is used. To save parameter overhead, the hidden activation size is set to ${ℝ}^{\raisebox{1ex}{$C$}\!\left/ \!\raisebox{-1ex}{$r$}\right.\times 1\times 1}$, where r is the compression ratio. For the sake of description, instead of using the compressed result directly, we use the compression ratio. After the MLP, a batch normalization (BN) layer is used to scale the spatial branching output. The channel attention is calculated using Equation (3):

$$M_C\left(F\right)={\Phi }_{BN}\left(MLP\left(AvgPool\left(F\right)\right)\right)={\Phi }_{BN}\left(W_1\left(W_{0}AvgPool\left(F\right)+b_0\right)+b_1\right)$$

(3)

where ${\Phi }_{BN}$ denotes batch regularized, and $W_0\in {ℝ}^{\raisebox{1ex}{$C$}\!\left/ \!\raisebox{-1ex}{$r$}\right.\times C}$, $b_0\in {ℝ}^{\raisebox{1ex}{$C$}\!\left/ \!\raisebox{-1ex}{$r$}\right.}$, $W_1\in {ℝ}^{C\times \raisebox{1ex}{$C$}\!\left/ \!\raisebox{-1ex}{$r$}\right.}$, $b_1\in {ℝ}^C$, and $F$ denote input features.

Spatial branching produces spatial attention maps $M_S\left(F\right)\in {ℝ}^{H\times W}$ to emphasize or suppress features in different spatial locations. We use inflated convolution to expand the receptive field to make effective use of global information. Inflated convolution helps to construct a more efficient spatial feature map than standard convolution. The features $F\in {ℝ}^{C\times H\times W}$ are projected into the reduced dimension ${ℝ}^{\raisebox{1ex}{$C$}\!\left/ \!\raisebox{-1ex}{$r$}\right.\times H\times W}$, and the feature map is integrated and compressed across channel dimensions using $1\times 1$ convolution. The same reduction rate used for the channel attention is used ($r$). After normalization, convolution with two $3\times 3$ expansions is used to efficiently utilize contextual information. Finally, the feature map is reduced again to the spatial attention map ${ℝ}^{1\times H\times W}$ using $1\times 1$ convolution. Batch normalization is performed at the end of the spatial channel using BN. The spatial attention is calculated using Equation (4):

$$M_S\left(F\right)=BN\left(f_3^{1\times 1}\left(f_2^{3\times 3}\left(f_1^{3\times 3}\left(f_0^{1\times 1}\left(F\right)\right)\right)\right)\right)$$

(4)

where $f$ denotes convolution, BN denotes batch normalization, and the superscript denotes the size of the convolution kernel. Two $1\times 1$ convolutions are used to narrow the channels and two $3\times 3$ convolutions are used to aggregate contextual information with larger sensory fields. The main purpose of introducing this attention mechanism into the network is to reweight the different features to eliminate the influence of background, as well as other factors, as much as possible and to focus more on the extraction of effective features.

3.2. Pruning Algorithm Based on Channel Correlation

Filter pruning is primarily a data-driven technique. When the importance of a filter is solely determined by the feature mappings it produces, it can render the importance scale unstable and vulnerable to minor perturbations in the input data. Conversely, when importance is evaluated based on the information present in multiple feature maps, it has the potential to minimize interference from input data variations, leading to more dependable and robust importance rankings, provided that it is implemented accurately. Cross-channel strategies have an inherent advantage in terms of facilitating improved modeling and the capture of correlations between different channels. This is due to the fact that such strategies enable more precise modeling, and thereby enable the more accurate identification of inter-channel correlations. In the context of compressing models, correlations identified through cross-channel strategies are viewed as redundancies at the architectural level and serve as the target of filter pruning techniques. This approach aims to eliminate unnecessary filters while ensuring that the model remains effective and accurate. Therefore, by adopting a channel-to-channel strategy, it becomes possible to implement more aggressive pruning techniques while still achieving high levels of accuracy. Building on this insight, we propose to investigate the significance of filters from an inter-channel perspective [41]. Our primary concept is to leverage channel correlations as a means of determining the importance of each feature map (and its corresponding filter). A particular feature map exhibits substantial linear interdependence with feature maps from different channels, and this implies that the content it carries is already extensively encoded in those other feature maps. Thus, despite removing the correlated filter, valuable information and knowledge regarding the representation of highly correlated feature maps can still be preserved and effectively reconstructed by other filters through approximation during the fine-tuning process. This suggests that filters producing highly correlated feature maps may have greater “interchangeability” and lower importance. Consequently, it is reasonable to remove filters associated with high correlation feature map channels while maintaining model capacity.

To extract the linear dependence information of each feature map within the 3D tensor feature atlas generated from a single layer, a methodology based on linear algebra is proposed. This approach addresses the challenge of analyzing the large and complex datasets often encountered in deep learning applications. Specifically, assuming that the output feature atlas of the $l$ layer is ${\mathscr{H}}^l$, we first transform the matrix ${\mathscr{H}}^l$ into $H^l-{\left[{\alpha }_1^l{}^T,{\alpha }_2^l{}^T,\dots ,{\alpha }_{c^l}^l{}^T\right]}^T$, where the row vector ${\alpha }_i^l\in {ℝ}^{h\times w}$ is vectorized $H_i^l$. The h and w are the dimensions of the feature map. In this case, the linear correlation of each vectorized feature map ${\alpha }_i^l$ can be measured by existing matrix analysis tools as a row in the matrixed whole set of feature maps $H_i^l$. The most straightforward solution is to use the rank to determine the correlation of ${\alpha }_i^l$, since the rank mathematically represents the maximum number of linearly independent rows/columns in the matrix. For example, one can remove a row from a matrix and calculate its rank change, and then determine the impact and importance of the removed row—the smaller the rank change, the higher the relevance of the matrix of the removed row.

However, within the background of filter pruning, we believe that the change in the nuclear norm of the whole set of feature maps is a better indicator for quantifying the relevance of each feature map. This is because the nuclear norm, i.e., the ${\ell }_1$-norm of the matrix singular values, can reveal more about the effect of deleting rows on the matrix, whereas the rank, i.e., the ${\ell }_0$-norm of the singular values, cannot reflect these changes.

For layer $i$ of the output feature map ${\mathscr{H}}^l=\left\{H_1^l,H_2^l,\dots ,H_{c^l}^l\right\}\in {ℝ}^{c^l\times h\times w}$, the channel correlation ($\mathcal{C}$) of one of the $i$ channels of the feature map $H_i^l\in {ℝ}^{h\times w}$ is defined and calculated using Equation (5):

$$\mathcal{C}\left(H_i^l\right)\triangleq {\left|\left|H^l\right|\right|}_{*}-{\left|\left|M_i^l\odot H^l\right|\right|}_{*}$$

(5)

where $H^l\in {ℝ}^{c^l\times h\times w}$ is the matrixed ${\mathscr{H}}^l$, ${\left|| |\right|}_{*}$ is the nuclear norm, $\odot$ is the Hadamard product, and $M_i^l\in {ℝ}^{c^l\times h\times w}$ is the row mask matrix whose entries in the $i$ row are zero and whose other entries are one.

Equation (5) defines the channel correlation measurement for a single feature map. However, practical filter pruning targets the removal of multiple filters, requiring the computation of correlations across combinations of feature maps. For filter pruning, this entails evaluating the change in the nuclear norm of $F^l$ in the original $c^l$ rows following the removal of the m rows $\left({\alpha }_i^l\right)$. One solution is to calculate the variation in $C_m^{c^l}$, the number of kernel parameters, for all possible m row removal options and select the option with the smallest variation. However, this approach may be computationally expensive and challenging to manage for large $c^l$ values.

To effectively address this computational challenge, our proposal entails leveraging the inter-feature map correlation as an approximation for the correlation exhibited by its amalgamation. This strategy seeks to mitigate the computation burden associated with analyzing the combined set of features. To identify the $m$ smallest linearly independent rows in the matrix $H^l$, we adopt an iterative approach that involves removing a single row (${\alpha }_i^l$) from $H^l$ and calculating the resulting change in the nuclear norm between the reduced matrix ($c^l-1$) and the original $c^l$ row matrix ($H^l$). This process is repeated until $m$ independent rows have been determined. Among the set of computed changes in $c^l$, we select the smallest change and subsequently remove the $m$ rows (${\alpha }_i^l$) from $H^l$ that contributed most significantly to this change. The chosen set of $m$ vectorized feature maps (${\alpha }_i^l$) were deemed to possess higher correlations with other feature maps. Consequently, the corresponding filters (${ℱ}_i^l$) were identified as being less important and subjected to pruning. Overall, the utilization of individual correlation-based measures can often yield a highly accurate approximation of the combined correlation arising from multiple feature maps.

This approximation method requires less computational complexity while still achieving excellent filter pruning performance.

For layer $i$ of the output feature map ${\mathscr{H}}^l\in {ℝ}^{c^l\times h\times w}$, the channel correlation of the combined $m$ feature map ${\left\{H_{b_i}^l\right\}}_{i=1}^m$, where $H_{b_i}^l\in {ℝ}^{h\times w}$ is in the first $b_i$ channel, is defined and approximated using in Equation (6):

$$\mathcal{C}\left({\left\{H_{b_i}^l\right\}}_{i=1}^m\right)\triangleq {\left|\left|H^l\right|\right|}_{*}-{\left|\left|M_{b_1,\dots ,b_m}^l\odot H^l\right|\right|}_{*}\approx {\displaystyle \sum }_{i=1}^m\mathcal{C}\left(H_{b_i}^l\right)$$

(6)

where $M_{b_1,\dots ,b_m}^1$ is a multi-row mask matrix in which the $b_1,\dots ,b_m$ row is zero and all the other rows are one.

Given that our proposed filter pruning method based on channel correlation property is a data-driven approach, it should be carefully ensured and checked for its reliability using different input data distributions. To accomplish this, we conducted an empirical assessment of the channel correlation across multiple input images, and consistently observed a high degree of stability in the average channel correlation for each feature map within each batch of samples that we processed. Consequently, we computed the average channel correlation for small batches of image samples and employed this value to estimate the channel correlation of all input data.

3.3. Overall Flow of the Algorithm

The attention mechanism can explicitly describe the importance of relationships between channels in the same layer and continuously adjust the parameters of the fully connected layer during back propagation [23,42]. By inserting the attention module, the network can show a tendency to gradually enhance or suppress some channels. Then, based on channel similarity, channels with high similarity are continuously filtered out while maintaining high accuracy, and these deleted channels are removed for restorative training. The Figure 4 shows the pruning flow chart.

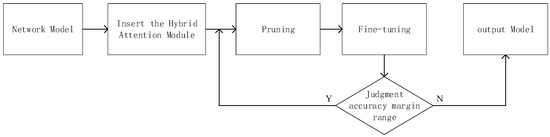
Figure 4. Flow chart of the pruning process guided by the hybrid attention mechanism.

The Algorithm 1 flow is shown below.

Algorithm 1. CCPCSA Algorithm
Input:
M:	The initial network model
D:	The training dataset
L:	The number of the layers in M
m:	The number of channel groups removed per epoch
Output:
M′:	The pruned network model
Steps:
1:	Obtain ACC by training the model M
2:	Obtain a model named M’ by training model M within BAM modules
3:	For each batch $d\in D$
4:	Train M’ with d
5:	For each layer $l\in \left\{1,\dots ,L\right\}$
6:	For each channel $i\in \left\{1,\dots ,{\mathcal{C}}_l\right\}$
7:	Calculate the $\mathcal{C}\left(H_i^l\right)$
8:	Sort all the $\mathcal{C}\left(H_i^l\right)$ and prune the smaller $m$ rows of channels
9:	Fine-tune M’ and obtain the Acc’
10:	If Acc-Acc’ < 0.5%, then go back to Step 3
11:	Return M’

4. Experiment

To validate the efficacy of our model pruning algorithm, we conducted experiments on the ResNet model utilizing the PyTorch framework. The experimental setup was based on a Windows 10 system equipped with an Intel(R) Core(TM) i5-10300H CPU @ 2.50 GHz and a NVIDIA GeForce GTX 1650 graphics card, and it was run in a virtual environment using PyCharm 2020.1.2 (Professional Edition) with PyTorch version 1.8.0, TorchVision version 0.9.0, and CUDA version 10.2.89.

We conducted image classification experiments to evaluate the feasibility of the method. In the ResNet network, the attention module was placed on the convolutional output of the ResBlock. Experiments were performed on CIFAR-100 and ImageNet datasets and compared with other representative pruning schemes.

FLOPs stands for floating point operations. The mathematical unit of FLOPs(M) is million and the mathematical unit of GFLOPs is billion. The “↑” represents an increase or raise relative to the original model, while the “↓” represents a decrease or lower. OTO* indicates the best performing result in the cited paper, which is identified by *. Based on these results, it can be concluded that CCPCSA shows excellent performance with very little loss of inference accuracy. Based on the results presented in Table 1 and Table 2, it can be concluded that the CCPCSA method outperformed the other advanced pruning methods comprehensively on both datasets, indicating its effectiveness. The CCPCSA method is capable of achieving high accuracy, particularly when the pruning ratio is low. This finding demonstrates the effectiveness of the proposed channel pruning approach in enhancing model accuracy while reducing model complexity. The results obtained by compressing the model as much as possible are shown in Table 1 and Table 2. The results show that a larger network pruning ratio leads to a partial loss of accuracy. On both the CIFAR-100 and ImageNet datasets, the accuracy of the CCPCSA algorithm was almost the same as the original accuracy, and the compression effect results were much better than those of other methods. In particular, the proposed CCPCSA pruning algorithm can significantly speed up the inference computation because of the reduced parameters and computational effort. All these observations clearly show that pruning channels under the guidance of the attention module is beneficial.

Table 1. Comparison of different pruning algorithms for ResNet50 on CIFAR-100.

Method	Acc (%)		Para (M)		FLOPs (M)
Baseline [3]	78.51	-	23.71	-	1224	-
PCAS-60 [38]	77.89	↓0.62	5.57	↓76.5%	412	↓66.3%
Pruned-B [43]	74.85	↓3.66	13.64	↓42.47%	610	↓50.16%
16% Pruned [44]	78.32	↓0.19	8.5356	↓64.0%	670	↓45.3%
Proposed	77.78	↓0.73	4.67	↓80.3%	375	↓69.4%

Table 2. Comparison of different pruning algorithms for different ResNet backbones on ImageNet.

Model	Method	Acc (%)		Para (M)		GFLOPs
ResNet50	Baseline [3]	75.44	-	25.56	-	3.86	-
	PCAS-50 [38]	75.40	↓0.04	12.47	↓51.2%	1.56	↓56.7%
	BWCP [45]	74.96	↓0.48	-	-	1.87	↓51.8%
	Wang [46]	75.23	↓0.21	19.86	↓22.3%	1.65	↓57.3%
	Afalo [47]	75.71	↑0.27	-	-	2.29	↓40.6%
	OTO* [48]	74.52	↓0.92	9.07	↓64.5%	1.33	↓65.5%
	Proposed-low rate	75.75	↑0.31	14.36	↓43.8%	1.94	↓49.7%
	Proposed	75.38	↓0.06	10.28	↓59.8%	1.28	↓66.8%
ResNet101	Baseline [3]	76.62	-	44.55	-	7.57	-
	Afalo [47]	75.37	↓1.25	-	-	2.33	↓69.21%
	TFB-55% [49]	75.95	↓0.67	20.7	↓53.5%	2.85	↓62.35%
	Proposed	75.76	↓0.86	17.28	↓61.2%	2.38	↓68.5%

5. Conclusions

The proposed method, called CCPCSA, is a new channel pruning approach that utilizes a channel–spatial attention mechanism to compress network models for use in edge computing. The core idea of CCPCSA is to use the attention statistics provided by a new attention module called BAM and prune the network based on channel correlation information to achieve model efficiency and compression. The BAM module combines spatial attention and channel attention as a whole, which not only enhances the representation capability of the network model, but also reveals the impact of the presence of channels on the inference performance. The pruning operation is then completed by removing channels with high similarity based on inter-channel correlation. The comprehensive experiments we conducted on two benchmark datasets validated the superior effectiveness of the CCPCSA approach compared with other state-of-the-art solutions. In future work, we plan to combine this approach with other model compression strategies (e.g., quantization) and other edge intelligence techniques (e.g., edge cloud collaboration) to further reduce model size and inference costs.