Toward Privacy-Preserving Directly Contactable Symptom-Matching Scheme for IoT Devices

Abstract

The development of IoT devices has driven technological advancements across industries, especially in healthcare. IoT devices have brought many conveniences to patients, such as symptom matching, the real-time acquisition of health data, and online diagnosis. However, the development of the Internet of Things also brings security and privacy challenges, which have attracted the attention of many scholars. In symptom matching, patients can communicate with patients similar to themselves through symptom matching, exchange treatment experiences, and encourage each other. However, matching in plaintext will pose a huge threat to user privacy, such as discrimination, which in turn affects job hunting, etc. Therefore, this paper proposes a symptom-matching scheme for IoT devices based on the Diffie–Hellman key agreement. Specifically, we construct and formally define the Switching Threshold Label Private Set Intersection (STLPSI) protocol based on the Diffie–Hellman key agreement and apply it for medical symptom matching. Our protocol can not only set the threshold of the same symptoms, but also patients who meet the threshold can obtain one another’s contact information. Furthermore, our scheme does not rely on any trusted third parties. Through security analysis and experiments, our scheme is shown to be effective in preserving privacy during symptom matching.

1. Introduction

The increasing prevalence of Internet of Things (IoT) devices has prompted extensive research into mobile medical health [1,2,3]. IoT devices empower patients to monitor their own health status [4], while medical centers can leverage the devices to analyze and diagnose diseases and then relay the results back to the devices. As a result, IoT devices serve as a vital link between medical centers and patients, facilitating patient-to-patient communication based on symptom similarity, thereby providing mutual encouragement and the opportunity to share treatment experiences. Symptom similarity between different patients is typically determined by the number of identical symptoms in the symptom set. Effective communication between patients who share a certain number of symptoms is pivotal for successful disease treatment.

However, security and privacy issues have become obstacles to matching patients’ symptoms and enabling their communication with each other. The patient’s symptom information is private data, and if it is leaked or used maliciously, it will cause heavy losses to the patient, such as discrimination, property damage, etc. In order to cope with this challenge, Shunrong Jiang et al. [5] designed two blind signature-based symptom-matching schemes in SDN-based MHSNs, which can achieve coarse-grained symptom matching and fine-grained symptom matching, respectively. Ming Li et al. [6] proposed a set of privacy-preserving profile-matching schemes for proximity-based mobile social networks. Chengzhe Lai et al. [7] designed a trust-based privacy-preserving friend-matching scheme in the social Internet of Vehicles. It can prevent the leakage of sensitive information caused by the matching of user attributes, and make the interaction between vehicles faster and more convenient. Hui Xing et al. [8] proposed a secure and privacy-preserving symptom-matching scheme based on homomorphic encryption, which not only preserves the privacy of personal health information (PHI) but also prevents inflation attacks and other active attacks. However, these schemes either distribute keys through a trusted third party or use cryptographic tools. They not only have a large overhead but, more importantly, there is no direct communication between two patients between these schemes.

Among the existing privacy protection technologies, Private Set Intersection is an emerging privacy protection technology that effectively satisfies the need to return to the intersection, while preserving the privacy of all parties involved. At the same time, the extended PSI protocol (Set Threshold Label Private Set Intersection) also provides solutions for threshold and label requirement scenarios. However, the current STLPSI protocol only satisfies the receiver to receive the sender’s label, and the sender knows nothing about the receiver’s data. For direct-contact symptom matching, both the receiver and sender are required to obtain each other’s tags. We do not seem to have found the relevant technology for this. Therefore, in this context, we need to study new solutions to meet this condition.

In this work, we propose a privacy-preserving direct-contact symptom-matching scheme that guarantees privacy. The core technology of our scheme is the Switching Threshold Label Private Set Intersection (STLPSI) protocol, which is based on the Diffie–Hellman key agreement. Unlike previous threshold-based approaches that only allow the receiver to reconstruct labels, our protocol allows both the receiver and sender to reconstruct labels. By leveraging our protocol for symptom matching, our scheme facilitates direct contact between patients $p_1$ and $p_2$ only when a certain threshold of symptom matching is reached, thereby safeguarding the privacy of patient symptom information. Furthermore, the protocol employs a hash function to reduce communication and enhance the matching efficiency. We also conduct a rigorous analysis of the correctness and security of the protocol. Our contributions are summarized as follows.

• In the absence of a trusted third party, we propose the Switching Threshold Label Private Set Intersection (STLPSI) protocol, which is based on the Diffie–Hellman key agreement, and we provide a formal definition of it. Our protocol improves upon previous work by allowing both the receiver and the sender to reconstruct labels. We achieve this by using hashed Diffie–Hellman key agreement and hash functions, which also enhance the overall efficiency of the protocol.
• We apply the proposed protocol to the symptom matching of IoT devices to achieve patient symptom matching and contact information exchange. We demonstrate our system using a concrete numerical example.
• We provide a correctness and security analysis, showing that our scheme is correct and protects privacy. Additionally, we compare our work theoretically and experimentally with previous work, and the results show that our protocol is feasible.

2. Related Works

2.1. Symptom Matching

Symptom matching plays an important role in patient interaction and psychological support. Recently, many scholars have put forward matching schemes to solve the privacy problem. Shengnan Wang et al. [9] proposed a privacy-preserving target pattern matching scheme (PP-TPMS). The scheme uses a bloom filter and secret sharing technology to realize the security pattern matching between a given query request and massive medical information. The auxiliary diagnosis result is returned to the user. Shunrong Jiang et al. [5] designed two blind signature-based symptom-matching schemes in SDN-based MHSNs, which can achieve coarse-grained symptom matching and fine-grained symptom matching, respectively. Moreover, these schemes do not rely on any trusted third party. In addition to the schemes directly designed for symptom matching, other matching schemes can also be used for reference. Ming Li et al. [6,10] proposed privacy-preserving personal profile-matching schemes for mobile social networks. They leveraged secure multi-party computation (SMC) based on polynomial secret sharing and proposed several key enhancements to improve the computation and communication efficiency. Hui Xing et al. [8] proposed a privacy-preserving symptom-matching scheme, called SymMatch, which is based on homomorphic encryption to thwart the inflation attack and other active attacks. Wenjuan Tang et al. [11] proposed a personalized and trusted healthcare service approach to enable trusted and privacy-preserving healthcare services in social media health networks, which can improve the trust between patients and caregivers through authentic ratings toward caregivers and guarantee the patients’ privacy. Chengzhe Lai et al. [7] designed a trust-based privacy-preserving friend-matching scheme in the social Internet of Vehicles, which can prevent the leakage of sensitive information caused by the matching of user attributes, and make the interaction between vehicles faster and more convenient.

2.2. Private Set Intersection

PSI has attracted much attention since it was proposed [12,13], and it is still being studied [14,15,16,17] by many people both in terms of application and technology. In order to improve the efficiency and realize extended functions [18], the OT-based PSI protocol, multi-party PSI protocol, fuzzy labeled PSI protocol, and Threshold PSI protocol have been proposed successively.

Erkam Uzun et al. [19] proposed fuzzy labeled private set intersection with applications to the private real-time Biometric Search. The communication of this protocol is sublinear in database size and is concretely efficient. This scheme combines secret sharing and homomorphic encryption to achieve biometric identification in two parties. This scheme is efficient, but unfortunately cannot be directly applied to our scenario. The solution is to make a judgment on the set and return the result, and the labels cannot be exchanged. Kelong Cong et al. [20] proposed labeled PSI from homomorphic encryption with reduced computation and communication. Hao Chen et al. [21] proposed labeled PSI from fully homomorphic encryption with malicious security based on [22]’s proposed protocol. However, Kelong Cong et al. and Hao Chen et al.’s work is more focused on unbalanced PSI. Saikrishna Badrinarayanan et al. [23] proposed a multi-party threshold private set intersection with sublinear communication. At the same time, it also realized the two-party threshold PSI. Gayathri Garimella et al. [24] considered the general notion of an oblivious key–value store (OKVS) to encode input sets and constructed a new private set intersection protocol. They have good performance, but the labels cannot be exchanged.

3. Preliminaries

3.1. Notations

In this paper, we denote the sender’s data set, which has a size of n, as $\{x_1,\dots ,x_n,L_s\}$. Here, $x_i$ represents the sender’s symptoms, and $L_s$ represents the sender’s personal contact information. $L{s}_i$ is the secret share of the label $L_s$. $L_s^{\prime }$ denotes the construction of $L_s$. Similarly, we represent the receiver’s data set as $\{y_1,\dots ,y_m,L_r\}$, where m is the size, $y_i$ indicates the receiver’s symptoms, and $L_r$ indicates the receiver’s personal contact information. $L{r}_i$ is the secret share of the label $L_r$, and $L_r^{\prime }$ is the construction result of $L_r$. Note that the size of the two parties’ sets in our protocol may differ. At the same time, the threshold t is smaller than the minimum value of m and n.

In the protocol, $m_{ij}$ denotes the intersection set of X and Y. The number of $m_{ij}$ elements contained is denoted as $|m_{ij}|$. $sk$ denotes the negotiated key. We use $\lambda$ to denote the number of hash functions. The size of the elliptic curve group elements is 256. Other special symbols will be introduced when using them.

3.2. Threshold Label Private Set Intersection Functionality

In Figure 1, we formally describe the threshold label private set intersection functionality. The threshold label private set intersection protocol is a special type of PSI. In this scenario, each element in the Sender’s set has associated data (a label), and the receiver hopes to learn the labels of the elements in the intersection if he/she satisfies the intersection threshold, while the sender obtains no information.

Figure 1. The functionality of set threshold label private set intersection.

3.3. Shamir’s Secret Sharing

Secret sharing [25] is an important cryptographic tool. It can be used to build secure multi-party computing, which is used in many multi-party secure computing protocols, such as threshold PSI, secure multi-party computation, and so on. In this work, we use Shamir’s secret sharing. We explain the scheme at a high level. Given integers n, t (n≤t) and the finite field F, Shamir’s secret-sharing scheme contains two steps.

Sharing step:

• Choose a random polynomial $f\left(x\right)$ of degree t that satisfies f(0) = s and distinct points $x_1,\dots ,x_n$.
• Compute $f\left(x_i\right),i\in \{1,\dots ,n\}$. The set S = $\{f\left(x_1\right)=s_1,\dots ,f\left(x_n\right)=s_n\}$. Note that $x_i$ is the secret shared value.

Reconstruction step:

• Input set $R\in S$ of size $t+1$.
• Use Lagrangian interpolation to compute the polynomial $f^{\prime }\left(x\right)$, which satisfies $f^{\prime }\left(x_i\right)=s_i^{\prime }$, where $s_i^{\prime }\in R$ and output $f^{\prime }\left(0\right)$.

The privacy requirement of Shamir’s secret sharing is that any subset $R^{\prime }$ of size smaller than the threshold cannot know any information about s, i.e., its probability distribution is independent of s. In our protocol, the sender and receiver each generate t-out-of-T secret shares for the label $L_p$($p\in \{s,r\}$).

3.4. Diffie–Hellman Key Agreement

The classic Diffie–Hellman key agreement protocol is a one-round KA protocol, which means that two messages can be sent simultaneously. Given a cyclic group $G=⟨g⟩$ of order q, the agreement follows:

• Sender chooses a random message a, computes $m_s=g^a$, and sends $m_s$ to receiver;
• Receiver chooses a random message b, computes $m_r=g^b$, and sends $m_r$ to sender;
• Sender computer $Key={\left(m_r\right)}^a$;
• Receiver computer $Key={\left(m_s\right)}^b$.

In this work, we use “hashed” Diffie–Hellman key exchange and use elliptic curves for the underlying cyclic group, which means that the negotiated keys are processed by the same hash function. The hashed Diffie–Hellman key exchange algorithm uses the public and private keys to encrypt and decrypt when exchanging public keys—that is, $m_s=enc\left(g^a\right)$ and $m_r=enc\left(g^b\right)$. After receiving the public key, the sender and receiver calculate the negotiation key $sk={\left(dec\left(s{k}_b\right)\right)}^a={\left(dec\left(s{k}_a\right)\right)}^b$. The security of the protocol is based on the oracle Diffie–Hellman (ODH) assumption. In brief, the oracle Diffie–Hellman (ODH) assumption is that $g^a$, $g^b$, $H\left(g^{ab}\right)$ is indistinguishable from random in the presence of an oracle for $H\left(x^a\right)$, as long as the distinguisher does not know the value of $g^b$. The detailed proof is given in [26].

3.5. Cuckoo Hashing

Cuckoo hashing is a hash table data structure that provides constant time $O\left(1\right)$ average case lookup, insertion, and deletion operations, which was introduced by Pagh and Rodler in [27]. It uses two hash functions and two separate arrays, called tables, to store the key-value pairs. The cuckoo hashing works as follows.

Let H be a hash table of size m, and let $h_1$ and $h_2$ be two independent hash functions that map keys to the integers 0 to $m-1$. The hash table H consists of two arrays, $T_1$ and $T_2$, each of size m.

The insertion algorithm works as follows: when a key–value pair $(k,v)$ is inserted into the hash table, first the hash functions $h_1$ and $h_2$ are used to calculate two possible index positions $i_1$ and $i_2$, respectively, in the two arrays. If either $T_1\left[i_1\right]$ or $T_2\left[i_2\right]$ is empty, the pair is stored at the corresponding position. Otherwise, one of the pairs currently stored at $T_1\left[i_1\right]$ or $T_2\left[i_2\right]$ must be moved to its other position in the other table. This displacement process continues recursively until an empty position is found or a cycle is detected. In the latter case, the table is rehashed with new hash functions.

The lookup operation works similarly. Given a key k, the two hash functions $h_1$ and $h_2$ are used to calculate the two possible index positions $i_1$ and $i_2$ in the two arrays. If either $T_1\left[i_1\right]$ or $T_2\left[i_2\right]$ contains the key k, the corresponding value can be returned.

4. Problem Formulation

In this section, we define our system model and security model, and identify the design goals.

4.1. System Model

As illustrated in Figure 2, this paper considers the direct interaction between two parties via IoT devices (mobile phones, smart watches, etc.) without a trusted third party. The system model mainly has two entities involved, the sender and the receiver.

Figure 2. System model.

• Sender: Patients who want to find patients with similar symptoms are considered the senders. The sender has his own contact information and symptom information. When running the protocol, he encrypts his information and preprocesses it according to the protocol, and sends it to the receiver. Through two rounds of interaction, the sender can obtain the contact information of the other party (meeting the set threshold) or a random value.
• Receiver: The receiver is identical to the sender, with its own contact and symptom information. The receiver will comply with the protocol and preprocess its own data and send them to the sender according to the sender’s threshold. In our system, the sender and receiver can obtain each other’s contact information if their symptoms reach a threshold. Obviously, in our system, the only difference between the receiver and sender is the threshold setting, and the other settings are identical. In the following, we define the threshold to be determined by the sender.

4.2. Security Model

We consider the problem of symptom matching under the semi-honest adversary model. Specifically, we assume that the parties are semi-honest and correctly follow the protocol specification but attempt to learn additional information by analyzing the transcripts of messages received during the execution. For example, the sender honestly encrypts data according to the protocol and sends the threshold to the receiver. However, the sender is interested in the data information sent by the receiver and may attempt to decrypt it. Additionally, our work assumes that the sender and receiver do not collude.

4.3. Design Goal

Under the foregoing system model and security model, our design goal is to design a privacy-preserving directly contactable symptom-matching scheme. In particular, we should achieve the following goal.

Sender and receiver symptom privacy: Privacy protection is a fundamental requirement of this scheme. If the number of identical symptoms for both parties is less than a threshold, the sender and receiver cannot disclose any information about their own symptoms to the other party. Participants will only receive each other’s contact details if their symptoms match. They may also obtain information on the same symptom provided that the symptom-matching threshold is met.

5. Our Proposed Protocol

In this section, we propose a detailed protocol called Switching Threshold Label Private Set Intersection (STLPSI) for privacy-preserving directly contactable symptom matching. First, we formally define the general syntax and correctness of our protocol. Next, we present the protocol design in Figure 3. To help readers to better understand our innovation, we also provide specific examples from the symptom-matching system.

Figure 3. The protocol of Switching Threshold Label Private Set Intersection (STLPSI).

5.1. Formal Definition of STLPSI

Definition 1. 

Switching Threshold Label Private Set Intersection (STLPSI). The protocol definition has several parameters:

• ζ is the input space of the two parties;
• ψ is the label space of the two parties;
• t is a threshold value, which $t\in N$;
• Finite field F.

In addition, four algorithms are included in the definition: $SSGen\left(s\right)\to S$, $SKGen(a,b)\to sk$, $F(X,Y)\to R$, $ReCons\left(R\right)\to s$ OR ⊥.

Given two sets $X=\{x_1,\dots ,x_n,Ls\}\in \zeta$ and $Y=\{y_1,\dots ,y_n,Lr\}\in \zeta$, $SSGen\left(s\right)\to S$ generates secret sharing $\{L{s}_1,\dots L{s}_n\}$ and $\{L{r}_1,\dots ,L{r}_m\}$ for $Lr$ and $Ls$. Then, the F algorithm inputs the set M and N, which is the encrypted set by the key $sk$ generated by the $SKGen(a,b)\to sk$ algorithm, and outputs the sets R and S. Finally, R and S are input into the $ReCons\left(R\right)\to s$ algorithm, and the output is $Lr,Ls$ OR ⊥. The details of the four algorithms are as follows.

• $SSGen(s,n)\to \{s{s}_1,\dots ,s{s}_n\}$. Given a secret value $s\in \zeta$ and an integer n, generate a sharing set $S=\{s{s}_1,\dots ,s{s}_n\}$, where each $s{s}_i\in \zeta$ is a share of s.
• $SKGen(a,b)\to sk$. Generate a secret key $sk$ using the input parameters a and b.
• $F(M,N)\to (R,S)$. Input two sets $X\in \zeta$ and $Y\in \zeta$, and the function outputs two sets, $R=\{r{r}_1,\dots ,r{r}_k\}$($r{r}_i\in \psi$) and $S=\{s{s}_1,\dots ,s{s}_k\}$($s{s}_i\in \psi$) through interaction between two parties.
• $ReCons\left(R\right)\to s$ or ⊥. The algorithm inputs a set R and returns s if $k\ge t$, or ⊥ if $k<t$.

Correctness and privacy. For correctness, we require that for any s and $R\in \zeta$, it holds that $ReCons\left(R\right)=s$ with probability 1 if the size of R is greater than t. For privacy, we require that any information of X and Y cannot be revealed if the size of R is lower than t. Otherwise, elements other than the same elements in the X and Y sets cannot be disclosed even if the threshold is met.

5.2. STLPSI Protocol Design

Protocol overview: At a high level, after giving the threshold t, our protocol is executed by a sender and a receiver. First, the sender and receiver share their own labels secretly, where the sender generates $(p{s}_i,L{s}_i)$ and the receiver generates $(p{r}_i,L{r}_i)$. In order to preserve the corresponding relationship between the sender and the receiver $p{s}_i$ and $L{s}_i$, $p{r}_i$ and $L{r}_i$, we use cuckoo hashing to generate the hash tables $T_s$ and $T_r$ for the corresponding relationship. Then, they agree on a key $SK$ using the Diffie–Hellman algorithm and encrypt their hashed elements as $enc\left(H\left(x_i\right)\right)$ and $enc\left(H\left(y_i\right)\right)$. Next, the two parties exchange labels through interaction. More specifically, the sender computes the set $S=\{s_1,\dots ,s_n\}$. Among them, $s_i=enc\left(H\left(x_i\right)\right)-L{s}_i$. Finally, the sender sends the hash table $T_s$ and set S to the receiver. The receiver calculates the set $R=\{r_1,\dots ,r_m\}$, where $r_i=enc\left(H\left(y_i\right)\right)-L{r}_i$. Then, the receiver sends the set R and $T_r$ to the sender. It is obvious that the label-sharing values $L{s}_i$ and $L{r}_i$ will be observed if $H\left(x_i\right)\equiv H\left(y_j\right)$. Furthermore, the sender and receiver will obtain $\ge t$ label sharing and rebuild the label if the two sets have $\ge t$ elements that are the same. Otherwise, the protocol is terminated and both parties will obtain nothing.

To better illustrate our protocol, our protocol uses the four algorithms defined above and is divided into three stages: (1) the preprocessing stage, (2) the interactive stage, and (3) the result recovery stage. During this process, the private data of the two parties will not be disclosed. In addition, we assume that the two parties have negotiated hash functions, security parameters, and other information before the protocol starts. The detailed description of our Switching Threshold Label Private Set Intersection is shown in Figure 3.

5.3. Symptom-Matching System

In this section, we apply the Switching Threshold Label Private Set Intersection (STLPSI) protocol to the symptom-matching system. Similar to the protocol, our system consists of three stages: the preprocessing stage, the interaction stage, and the result recovery stage. We demonstrate the operation of each stage of the system using specific numerical values.

5.3.1. The Preprocessing Stage

The preprocessing phase is an offline phase, and two patients who want to exchange contact information will prepare for the next phase by performing this phase. We assume that the two patients are the receiver and the sender, and symptom information and contact information are mapped to the integer field of 256. We use the example of the symptom-matching system, where the set $X=\{45,87,39,42,53,78,12,48,124\}$ represents the sender and the set $Y=\{14,74,12,45,42,53,94,78,21\}$ represents the receiver. The last element in the set represents the contact information of the two patients. We set the threshold to 4, which means that only when the number of identical elements in both sets X and Y is greater than or equal to 4, the sender and receiver can reconstruct contact information.

At this stage, the sender and receiver first randomly select polynomial interpolation functions based on a threshold of 4. To demonstrate the system, we assume that the sender randomly selects the polynomial $P_s=3x^3+2x^2+4x+124\mathrm{mod}256$ and the receiver selects the polynomial $P_r=2y^3+6y^2+4y+21\mathrm{mod}256$. We evaluate eight points as the secret shared values of the label using the two polynomials, obtaining the sets $(ps,Ls)=\left\{\right(45,145),(87,87),(39,167),(42,68),(53,93),(78,188),(48,76),(124,44\left)\right\}$ and $(pr,Lr)=\left\{\right(14,29),(74,15),(12,253),(45,201),(42,57),(53,121),(94,109),(78,57\left)\right\}$. Then, we map the items of $ps$ and $pr$ into b bins. To be more specific, item $p{r}_i$ will be added into $Tr\left[h_1\left(L{s}_i\right)\right],Tr\left[h_2\left(L{s}_i\right)\right],\cdots ,Tr\left[h_{\lambda }\left(L{s}_i\right)\right]$, regardless of whether these bins are empty. Correspondingly, $p{s}_i$ is also added into $Ts\left[h_1\left(L{r}_i\right)\right],Ts\left[h_2\left(L{r}_i\right)\right],\cdots ,Ts\left[h_{\lambda }\left(L{r}_i\right)\right]$.

5.3.2. The Interactive Stage

During the interaction phase, the sender and receiver first obtain a shared secret key $sk$ through the DH key negotiation protocol. Here, we assume that the negotiated key is $sk=32$ and XOR is used as the encryption method. During this process, the sender and receiver first encrypt sets X and Y into sets $X^{\prime }=\{13,119,7,10,21,110,44,16\}$ and $Y^{\prime }=\{46,106,44,13,10,21,126,110\}$, respectively. Then, for each element $X_i^{\prime }$ and $Y_i^{\prime }$ in $X^{\prime }$ and $Y^{\prime }$, the sender and receiver, respectively, compute $S_i=X_i^{\prime }-L{s}_i$ and $R_i=Y_i^{\prime }-L{r}_i$. This yields sets $S=\{124,32,96,198,184,178,228\}$ and $R=\{17,91,47,68,209,156,17\}$. Finally, the sender sends the set S and $Ts$ to the receiver, and correspondingly the receiver sends the set R and $Tr$ to the sender.

5.3.3. The Result Recovery Stage

The result recovery stage is also for offline operation. In this phase, after the receiver receives the set R from the sender, the receiver calculates the set $m=\{252,\dots ,178,60,\dots ,219\}$ based on its own encrypted data. Each element in the set is expressed as $m_{i,j}=E_{sk}\left(H\left(x_j\right)\right)-r_i(j\in 1,\dots ,n)$. Similarly, after the sender receives the set R from the receiver, the sender calculates the set $n=\{252,\dots ,60,\dots ,219\}$. Each element in the set is expressed as $n_{i,j}=E_{sk}\left(H\left(y_j\right)\right)-s_i(j\in 1,\dots ,m)$. In the demonstration system, both the m and n sets contain eight elements. Finally, the receiver and the sender select the t value from their respective sets and look up the corresponding point value in the hash table for reconstruction according to Equations (1) and (2). We use points (16,252), (45,178), (14,23), and (41,32) to reconstruct the polynomial on the field of 256 as a presentation.

$$P\left(x\right)=y_1·L_1\left(x\right)+y_2·L_2\left(x\right)+\dots +y_n·L_n\left(x\right),$$

(1)

with $L_i\left(x\right)$ satisfying Equation (2).

$$L_i\left(x\right)=\frac{(x-x_1)}{(x_i-x_1)}·\frac{(x-x_2)}{(x_i-x_2)},\dots ,\frac{(x-x_n)}{(x_i-x_n)},wherei=1,2,\dots ,n.$$

(2)

Substituting the given points, we obtain Equation (3),

$$\begin{array}{c}\hfill P\left(x\right)=252·\frac{\left[\right(x-45\left)\right(x-14\left)\right(x-41\left)\right]}{\left[\right(16-45\left)\right(16-14\left)\right(16-41\left)\right]}+178·\frac{\left[\right(x-16\left)\right(x-14\left)\right(x-41\left)\right]}{\left[\right(45-16\left)\right(45-14\left)\right(45-41\left)\right]}\\ \hfill +23·\frac{\left[\right(x-16\left)\right(x-45\left)\right(x-41\left)\right]}{\left[\right(14-16\left)\right(14-45\left)\right(14-41\left)\right]}+32·\frac{\left[\right(x-16\left)\right(x-45\left)\right(x-14\left)\right]}{\left[\right(41-16\left)\right(41-45\left)\right(41-14\left)\right]}.\end{array}$$

(3)

Simplifying, we obtain $f\left(x\right)=155+218x+44x^2+39x^3$. The label information is the value of $f\left(0\right)=155$. Using this method, the sender and receiver can obtain the contact information of one another.

6. Correctness

In this section, we analyze the correctness of the Switching Threshold Label Private Set Intersection (STLPSI) protocol. We justify each step of the Switching Threshold Label Private Set Intersection (STLPSI) protocol as described in Figure 3.

In the preprocessing stage, the sender and receiver use polynomial interpolation to ensure that their respective polynomials $P_s$ and $P_r$ pass through the designated points $(x_i,L{s}_i)$ and $(y_i,L{r}_i)$, respectively, in step 1 and 2. Since both $P_s$ and $P_r$ have degree $(t-1)$, they can interpolate up to t points uniquely.

In step 3, the sender and receiver then hash their sets X and Y using the collision-resistant hash function H, respectively. It guarantees that each element of the X and Y is mapped to a unique hash value. If two elements in different sets have the same hash value, they are assumed to be the same element. In step 4, the sender and receiver generate hash tables, and the correctness is based on the failure probability. According to the empirical analysis in [28], we can adjust the values of $\lambda$ and $\eta$ to reduce the stash size to 0 while achieving a hashing failure probability of $2^{40}$, which can be negligible.

In the interactive stage, the sender and receiver use the hashed Diffie–Hellman key exchange to generate a shared agreement key $sk$ in step 1 to 4. To prove the correctness of the hashed Diffie–Hellman key exchange protocol, we need to show that the two parties can derive the same shared secret key from the public values exchanged during the protocol. In steps 1 and 2 of the interactive stage, the sender and receiver calculate $s{k}_a=enc\left(g^a\right)$ and $s{k}_b=enc\left(g^b\right)$, respectively, and send them to each other. In step 3, the sender computes the shared secret key as $sk=dec{\left(s{k}_b\right)}^a$. In step 4, the receiver computes the shared secret key as $sk=dec{\left(s{k}_a\right)}^b$. Now, we should prove that the sender and receiver can derive the same shared secret key. From step 2, we have $H\left(dec{\left(s{k}_b\right)}^a\right)=H\left({\left(g^b\right)}^a\right)$. From step 1, we have $H\left(dec{\left(s{k}_a\right)}^b\right)=H\left({\left(g^a\right)}^b\right)$. Because ${\left(g^a\right)}^b=g^{ab}$ and ${\left(g^b\right)}^{a}modp=g^{ba}$, we can see that $H\left(dec{\left(s{k}_b\right)}^a\right)=H\left(dec{\left(s{k}_a\right)}^b\right)$. This shows that the sender and receiver can derive the same shared secret key from the Diffie–Hellman key exchange during the protocol.

At the result recovery stage, the sender computes $m_{i,j}=E_{sk}\left(H\left(x_j\right)\right)-r_i$ for each $r_i$ sent by the receiver, and the receiver computes $n_{i,j}=E_{sk}\left(H\left(y_j\right)\right)-s_i$ for each $s_i$ sent by the sender. We divide the correctness of this phase into two cases.

Case one: $x_i\in X=y_j\in Y$—that is, the elements in the intersection of sets X and Y. Then, according to the construction of Figure 3, we have $E_{sk}\left(H\left(x_i\right)\right)=E_{sk}\left(H\left(y_j\right)\right)$. In the interaction phase, the sender obtains the value $r_i=E_{sk}\left(H\left(y_i\right)\right)-L{r}_i$. Then, the sender computes $m_{i,j}=E_{sk}\left(H\left(x_j\right)\right)-r_i=E_{sk}\left(H\left(x_j\right)\right)-(E_{sk}\left(H\left(y_i\right)\right)-L{r}_i)$. Due to $E_{sk}\left(H\left(x_i\right)\right)=E_{sk}\left(H\left(y_j\right)\right)$, the value of $m_{i,j}$ is equal to $L{r}_i$. According to this, if there are k (k greater than t) elements in the intersection set, then the sender will obtain k secret shared values of $Lr$, i.e., $\{L{r}_1,\dots ,L{r}_k\}$. Note that we here only represent any k of the n secret shared values. The receiver is the same as the sender, and the receiver will obtain k secret shared values of $Ls$. In the reconstruction phase, we share labels using the Shamir secret sharing method. Therefore, when recovering labels, the sender and receiver will construct a Lagrangian interpolation function to reconstruct the labels. The correctness is proven below, which follows the proof of Shamir [25]. To prove the correctness of Shamir’s secret reconstruction, we need to show that the polynomials $P_s$ and $P_r$ can be reconstructed from any $k(k>t)$ shares, and the secret can be recovered by evaluating the reconstructed polynomial at $x=0$.

First, let us consider the interpolation problem. Given k points ($x_1,y_1$), ($x_2,y_2$), …, ($x_k,y_k$), where the $x_i$ are distinct, we want to find a polynomial $p\left(x\right)$ of degree $k-1$ such that $p\left(x_i\right)=y_i$ for $i=1,2,\dots ,t$. It can be found using Lagrange interpolation, whose equation is Equation (5). Using this equation, we can reconstruct the polynomial from any k shares, since each share corresponds to a distinct point ($x_i,y_i$). The correctness of the polynomial interpolation can be ensured by Lagrange’s interpolation theorem, which states that given a set of t points $(x_i,y_i)$, where $x_i\ne x_j$ if $i\ne j$, there exists a unique polynomial P of degree at most $(t-1)$ such that $P\left(x_i\right)=y_i$ for all $i\in 1,2,\dots ,t$. The proof process is as follows.

Let ($x_1$, $y_1$), ($x_2$, $y_2$), …, ($x_n$, $y_n$) be n distinct data points. We want to find a polynomial $P\left(x\right)$ of degree at most $n-1$ that passes through all these points. We start by defining the Lagrange basis polynomials as Equation (4).

$$L_i\left(x\right)=\frac{(x-x_1)}{(x_i-x_1)}·\frac{(x-x_2)}{(x_i-x_2)},\dots ,\frac{(x-x_n)}{(x_i-x_n)},wherei=1,2,\dots ,n.$$

(4)

Note that each $L_i\left(x\right)$ is a polynomial of degree $n-1$ and has the property that $L_i\left(x_i^{\prime }\right)=0$ for $i^{\prime }\ne i$ and $L_i\left(x_i\right)=1$. Using these basis polynomials, we can construct the interpolating polynomial as Equation (5).

$$P\left(x\right)=y_1·L_1\left(x\right)+y_2·L_2\left(x\right)+\dots +y_n·L_n\left(x\right),$$

(5)

where $y_i$ is the value of the function at the point $x_i$. To show that $P\left(x\right)$ passes through all the given data points, we substitute each $x_i$ into $P\left(x\right)$ and show that $P\left(x_i\right)=y_i$ for all i. For any $i\in \{1,\dots ,n\}$, we have an equation as a description, i.e., Equation (6),

$$\begin{array}{cc}\hfill P\left(x_i\right)& =y_1·L_1\left(x_i\right)+y_2·L_2\left(x_i\right)+\dots +y_n·L_n\left(x_i\right)\hfill \\ \hfill & =y_i·L_i\left(x_i\right)\hfill \\ \hfill & =y_i·\frac{(x-x_1)}{(x_i-x_1)}·\frac{(x-x_2)}{(x_i-x_2)},\dots ,\frac{(x-x_n)}{(x_i-x_n)}\hfill \\ \hfill & =y_i.\hfill \end{array}$$

(6)

Therefore, $P\left(x_i\right)=y_i$ for all $i\in \{1,\dots ,n\}$, which means that $P\left(x\right)$ passes through all the given data points. Since $P\left(x\right)$ is a polynomial of degree at most $n-1$ and it passes through n distinct points, it must be unique. Based on this, we can claim that $P_s$ and $P_r$ are unique polynomials that satisfy the given conditions in our construction.

Secondly, let us consider the secret recovery problem. Given the reconstructed polynomial $p\left(x\right)$, we want to recover the secret s, which is the constant term of the polynomial. We can do this by evaluating the polynomial at $x=0$ since $p\left(0\right)=l_r$. Therefore, Shamir’s secret reconstruction is correct.

Case two: $x_i\in X\ne y_j\in Y$. In this case, $x_i$ and $y_i$ are not in the intersection of X and Y. Since we encrypt the elements with an AES symmetric key, we obtain $E_{sk}\left(H\left(x_i\right)\right)\ne E_{sk}\left(H\left(y_j\right)\right)$. For different $x_i$ and $y_i$, the value of $E_{sk}\left(H\left(x_i\right)\right)$ and $E_{sk}\left(H\left(y_j\right)\right)$ is pseudorandom. In the following stages, values calculated from this are random and meaningless. This suffices to confirm our protocol’s correctness.

7. Security Proof

In this section, we prove the security of the STLPSI protocol under the semi-honest model [29]. The definition is as follows.

Definition 2. 

For a two-party protocol Π to compute $F(\alpha ,\beta )$, $P_1$ and $P_2$, respectively, calculate the functions $F_{P_1}(\alpha ,\beta )$, $F_{P_2}(\alpha ,\beta )$. α and β are the inputs of $P_1$ and $P_2$, $F=(F_{P_1},F_{P_2})$. We denote the view generated by $P_b(b\in \{0,1\})$ during the execution of the protocol as $Vie{w}_{P_b}(\alpha ,\beta )$. The output is denoted as $O_{P_b}(\alpha ,\beta )$. We say that Π is secure against semi-honest adversaries if there exist probabilistic polynomial time (PPT) simulators $P_1$ and $P_2$ such as Equations (7) and (8):

$$(P_1(\alpha ,F_{P_1}(\alpha ,\beta ),F(\alpha ,\beta ))\stackrel{C}{\equiv }(Vie{w}_{P_1}(\alpha ,\beta ),O(\alpha ,\beta ))$$

(7)

$$(P_1(\beta ,F_{P_2}(\alpha ,\beta ),F(\alpha ,\beta ))\stackrel{C}{\equiv }(Vie{w}_{P_2}(\alpha ,\beta ),O(\alpha ,\beta ))$$

(8)

where $\stackrel{C}{\equiv }$ denotes computational indistinguishability.

In other words, it means that a real-world protocol $\mathsf{\Pi }$ is secure if for the ideal-world function F, which is possessed by a simulator $Sim$, the output of F should be indistinguishable from the output of the real protocol. Therefore, we construct ideal-world simulators $Si{m}_S$ and $Si{m}_R$ to emulate the views $VIE{W}_S$ and $VIE{W}_R$ of the sender and receiver in the real execution.

Theorem 1. 

The protocol of Switching Threshold Label Private Set Intersection (STLPSI) shown in Figure 3 is secure (in the semi-honest model) if the hashed Diffie–Hellman key agreement (DHKA) protocol and Shamir’s secret sharing scheme are secure.

Proof. 

To enhance the clarity, we assume that the simulator possesses fixed and public parameters utilized in our protocol for illustrative purposes. Subsequently, we introduce the view that necessitates simulation and then proceed to delineate the views of the simulators $Si{m}_S$ and $Si{m}_R$, respectively. □

Simulating the sender. To construct $Si{m}_S$, we first describe the real view that needs to be simulated. Recall that, in the preprocessing stage, the sender receives nothing from the receiver; thus, $Si{m}_S$ is not necessary to simulate the view. In the interactive stage, the sender obtains $s{k}_b$, $T_r$, and R from the receiver, which should be simulated. The result recovery phase is offline, and the sender computes the label or random result locally. We note the final result as v. Therefore, the real view of the sender can be denoted as Equation (9).

$$Vie{w}_S^{\mathsf{\Pi }}(sender,receiver,F)=(X;s{k}_b,R,T_r;v).$$

(9)

For $Si{m}_S$, it works as follows:

• $Si{m}_S$ obtains the sender’s input X and output v from an adversary A.
• $Si{m}_S$ generates random value $\rho$ and then computes the value of $w=g^{\rho }$ for the simulation of the $s{k}_b$ received by the receiver.
• $Si{m}_S$ randomly generates $R^{\prime }=\{r_1^{\prime },\dots ,r_m^{\prime }\}$ to simulate the received set R from the receiver, where each element $r_i=E_{sk}((H\left(y_i\right)-L{r}_i)$.
• $Si{m}_S$ generates hash label $T_r^{\prime }$ for the simulation of the $s{k}_b$ received by the receiver.
• $Si{m}_S$. According to the above analysis, the view of $Si{m}_S$ is denoted by Equation (10).

  $$Si{m}_S(X,v)=(X;w,R^{\prime },T_r^{\prime };v).$$

  (10)

Now, we prove that the simulator’s view and the rear view are indistinguishable. Based on the security of hashed Diffie–Hellman key agreement (DHKA) proposed by Abdalla, Bellare, and Rogaway [26], we know that $g^b$, $H\left(g^{ab}\right)$ are indistinguishable from a random value. The value w is computed by $Si{m}_S$’s chosen random value $\rho$. It is indistinguishable from $g^b$. For each element of set R, $r_i=E_{sk}((H\left(y_i\right)-L{r}_i)$, Shamir’s secret sharing scheme guarantees the indistinguishability of each individual share from a random item in the shared domain F. $y_i$ is secret for $Si{m}_S$. At the same time, we use AES as the encryption algorithm. Thus, it is obvious that $r_i$ is random for $Si{m}_S$ and is indistinguishable from $r^{\prime }$. From this, we can claim that the simulator’s view and the real view are indistinguishable, as shown by Equation (11).

$$(X;s{k}_b,R,T_r;v)\stackrel{C}{\equiv }(X;w,R^{\prime },T_r^{\prime };v).$$

(11)

Simulating the receiver. In the same way as for the sender, we first provide the real view, and then we construct the view of the receiver.

When the entire protocol is running, there are only two rounds of interaction—that is, the receiver receives the sender’s $s{k}_a$, S, and $T_s$. We note the result of the receiver computed locally as e. Therefore, the receiver’s view can be represented as Equation (12).

$$Vie{w}_R^{\mathsf{\Pi }}(sender,receiver,F)=(Y;s{k}_a,S,T_s;e).$$

(12)

For $Si{m}_R$, it works as follows:

• $Si{m}_R$ obtains the receiver’s inputs Y and outputs e from an adversary A.
• $Si{m}_R$ generates random value $\sigma$ and then computes the value of $u=g^{\sigma }$ for the simulation of the $s{k}_a$ received by the sender.
• $Si{m}_S$ randomly generates $S^{\prime }=\{s_1^{\prime },\dots ,s_m^{\prime }\}$ to simulate the received set S from the sender.
• $Si{m}_S$ randomly generates $T_s^{\prime }$ to simulate the received set S from the sender.
• $Si{m}_S$. According to the above analysis, the view of $Si{m}_S$ is denoted by Equation (13).

  $$Si{m}_R(Y,e)=(Y;u,S^{\prime }{T}_s^{\prime };e).$$

  (13)
  What we should prove is that the receiver’s real views and $Si{m}_R$’s views are indistinguishable. First, $s{k}_b$ is random for $Si{m}_R$ based on the security of hashed Diffie–Hellman key agreement (DHKA). The value of u is indistinguishable from $s{k}_a$. Secondly, for each element $s_i=E_{sk}((H\left(x_i\right)-L{s}_i)$ of set S, $L{s}_i$ is indistinguishable from the value of domain F. Then, $s_i$ is also random. Therefore, the value of $s_i$ is random. A semi-honest receiver cannot distinguish between the values of $s_i$ and $s_1^{\prime }$. Based on the above, we can obtain that the $Si{m}_R$’s view is indistinguishable from the receiver’s view, as shown by Equation (14).

  $$(Y;s{k}_a,S,T_s;e)\stackrel{C}{\equiv }(Y;u,S^{\prime }{T}_s^{\prime };e).$$

  (14)

According to the above analysis, we can claim that the Switching Threshold Label Private Set Intersection (STLPSI) is secure under the semi-honest adversaries model.

8. Complexity Analysis of STLPSI

In this section, we first show the complexity of our scheme, including the communication complexity and computational complexity. Then, we compare the symptom-matching scheme with [5] and Zhu [30] as shown in Table 1. Additionally, we compare the number of communication rounds with [5] and Zhu [30] as shown in Table 2.

Table 1. Comparison of matching schemes.

Protocol	Offine		Online		Comm. (bits)
	Sender	Receiver	Sender	Receiver	Sender	Receiver
Ours	(n+1+$C{}_m^t$) $·mu{l}_3$+ $(C_m^t+n)·ex{p}_3$	$(m+1+C_n^t)$ $·mu{l}_3+$ $(C_n^t+m)$ $4·ex{p}_3$	n · $Enc$	m · $Enc$	$256(n+\eta ·n+1)$	$256(m+\eta ·m+1)$
Coarse- grained [7]	-	m· hash+ m· $ex{p}_2$+ $k·$m· hash	k· m· hash +4m($2mu{l}_2$+ hash)	m · $ex{p}_2$	1024m	1024m+$L_{F{B}_A}$
Fine- grained [7]	-	2m· hash+ +m· $mu{l}_2$ +m· $ex{p}_2$	m· hash +2$mu{l}_2$	m($mu{l}_2$ +$ex{p}_2$)+ n· hash	1024m + $512n_c$	2560· m
$Zhu$ [27]	-	m· hash + m · $mu{l}_1$+ km· hash	km· hash +$2mu{l}_2$	m· $mu{l}_1$	256m	256m+$L_{F{B}_A}$

Table 2. Comparison of communication rounds.

Protocol	Ours	Corase-Grained [7]	Fine-Grained [7]	Zhu [28]
rounds	2	2	2	2

In order to compare under the same standard, we continue the method in [5], which takes the bits transmitted by the receiver and the sender as the communication overhead. The number of instances of modular multiplication and modular exponentiation is taken as the computation overhead. We compare them in two rows in Table 1 since Jiang et al. [5] proposed coarse-grained and fine-grained symptom-matching schemes. We denote $mul1$, $mul2$, and $mul3$ as 160-bit, 1024-bit, and 256-bit modular multiplication. Moreover, we denote $exp1$, $exp2$, $exp3$ as 160-bit, 1024-bit, and 256-bit modular exponentiation. $Enc$ represents an encryption operation. $hash$ represents the hash function, such as SHA-256. $L_{F{B}_A}$ is the length of the bloom filter used in Zhu’s system, see [30] and [5]. Note that we neglect the overhead of the Diffie–Hellman key generation operation.

Communication complexity. In our scheme, there are two interactions in the protocol. The sender must send KA information and calculate the set S to the receiver. The receiver responds to a KA message and sets R and hash table $T_r$ to the sender. Therefore, the total communication overhead consists of three parts. (1) Two rounds of KA messages from the sender and receiver. Each size has 256 bits. (2) The set S, which is from the sender and contains n elements, and set R contains m elements from the receiver. Each element is 256 bits. (3) The size of the hash table. For the sender, according to the parameters of our hash table, the size of our table is $256·\eta ·n$. The size of the receiver’s hash table is $256·\eta ·m$. In summary, the total communication cost of the sender is $256·(n+1+\eta ·n)$ bits. The total communication cost of the receiver is $256·(m+1+\eta ·m)$ bits.

Computation complexity. Given a threshold t, in the preprocessing stage, the sender and receiver generate random polynomials $P_s$ and $P_r$ of order $t-1$, respectively. The process of generating a random polynomial involves $t-1$ modular multiplications. Then, the sender and the receiver select n and m points on the polynomial and calculate the corresponding $P_s(·)$ and $P_r(·)$. This process involves $m·t$ times modular exponentiation and $m·t$ times modular multiplication for the receiver and $m·t$ times modular exponentiation and $m·t$ times modular multiplication for the sender. In the result recovery stage, the sender and the receiver select t points from m and n numbers, respectively, to reconstruct the result by using the Lagrange interpolation method. The reconstruction in turn secretly involves t modular exponentiations and t modular multiplications. Therefore, the complexity of the sender and receiver at this stage is $C_m^{t}t(mu{l}_3+ex{p}_3)$ and $C_n^{t}t(mu{l}_3+ex{p}_3)$, respectively. Both the preprocessing phase and the result recovery phase are completed offline, so we can obtain the complexity of the offline phase of the sender and receiver as $(m+1+C_n^t)mu{l}_3+(C_n^t+m)·ex{p}_3$ and $(n+1+C_m^t)mu{l}_3+(C_m^t+n)·ex{p}_3$.

Comparison. As shown in Table 1, the computational complexity of our protocol in the offline stage is not dominant compared to Jiang’s system; see [5] and [30]. In their work, the sender does not need any computation in the offline phase, while our protocol needs to have the same computation as the receiver. This is because our protocol can permit both the sender and the receiver to recover the result, compared to their work, which can only allow the receiver to obtain the result. Therefore, it is reasonable to have computations on the sender’s side during the offline phase. In addition, we can see from the table that the communication and computation in our online stage are lower than in their work. This is even more advantageous in IoT devices.

As shown in Table 2, we compare the number of communication rounds between our protocol and other protocols. It is obvious that our work and theirs both require two rounds of communication, with no significant difference. Therefore, the number of communication rounds in our protocol is reasonable. However, according to the result of Table 3 the comparison of communication bits in Table 4, our protocol has certain advantages compared to other protocols. Therefore, although our protocol is not optimized in terms of communication rounds, the communication cost of our protocol is lower than in other works.

Table 3. The communication and time cost of STLPSI protocol with the same set size.

Set Size			Offine	Online
Sender’s Sizes	Receiver’s Sizes	t	Preprocess (ms)	Time (ms)	Comm. (mb)
20	20	12	0.215	0.78	1.32
40	40	24	0.813	0.812	2.61
60	60	36	2.091	0.837	3.78
80	80	36	3.944	0.853	5.23
100	100	36	6.156	0.884	6.34

Table 4. Communication overhead for different schemes with different numbers of symptoms.

Symptoms	Ours	Corase-Grained [7]	Zhu [30]
	Comm. (mb)	Comm. (mb)	Comm. (mb)
20	1.32	6.53	6.42
40	2.61	11.98	11.84
60	3.78	17.44	17.32
80	5.23	22.89	22.75
100	6.34	28.33	28.8

9. Implementation

In this section, we present the experimental results of our proposed protocol. For different set sizes, we show the time overhead of preprocessing in the offline phase. Of course, we benchmark the time and communication costs of the online phase of the protocol under different data volumes, which is generally more important. Moreover, to show that the communication cost of our protocol is much lower than in other works, we compare the communication cost of our scheme with Jiang et al. [5] and Zhu et al. [30].

9.1. Experimental Setting

We implement our protocol in JAVA and conduct experiments on a machine with an AMD Ryzen 7 4800H CPU with Radeon Graphics 2.90 GHz, 16 GB RAM, and a Windows 10 operating system. For the convenience of the experiment, we assume that all symptoms have been mapped to domain 256. Labels are also mapped. The security parameter $\lambda =128$. We take SHA-256 as the hash function. In terms of encryption algorithm selection, theoretically, all symmetric encryption can be used. In this paper, we use the AES-256 algorithm. For key agreement protocols, we instantiate hashed Diffie–Hellman key agreement (hashed DHKA) using elliptic curve groups and choose the Curve25519 Montgomery curve [31]. The Curve25519 is defined over $GF(q=2^{55}-19)$. We implement the protocol based on the open source library https://www.bouncycastle.org/ (accessed on 23 January 2023). For Jiang et al.’s [5] scheme, we implement their scheme in the same environment. We take SHA-256 as the hash function. Moreover, the fixed false positive probability is $p={10}^{-4}$ for the bloom filter.

In order to be more realistic, we set the amount of data between 10 and 100. At the same time, to reflect the flexibility of the agreement, we divide the experiment into two parts. In the first part, we set the data size of the sender and receiver to be the same. The second part sets the data size of the receiver and the sender to be different. In Jiang et al. [5] and Zhu et al’s. [30] work, the data set sizes used are equal, so, in this part, we compare the communication cost of our scheme with their work. Moreover, the threshold t is set at $60\%$ of the set size of the smaller set. For example, if the sender set size is 50 and the receiver set size is 40, then the threshold t is 24.

9.2. Computation Overhead and Communication Overhead

The size of the collection is the most obvious factor affecting the cost. First of all, we evaluate the time and communication required for the protocol under the condition that the collection size is different, but the sender and receiver elements are the same. The evaluation results are shown in Table 3. Time and communication costs increase gradually with the increase in set elements. Take the communication cost as an example. When the elements of the sender and receiver are both 20, the communication cost is only 1.32 MB. However, when the set element number is 100, the communication cost is 6.34 MB. Note that because the interaction of the online phase does not involve threshold calculation, the difference in the threshold will not affect the time and communication of the online phase.

Table 4 and Figure 4 compare our protocol with Jiang et al. [5] and Zhu et al.’s [30] work. From Table 4 and Figure 4, we can find that with the increase in the number of symptoms, the communication cost is also increasing. This is the same in all three scenarios. However, specifically, for different numbers of symptoms, our scheme has a much lower communication cost than the other two works. For example, when the number of symptoms is 60, the traffic of our scheme is 3.78 MB, while the other two works have values of 17.44 MB and 17.32 MB, respectively. Our protocol communication cost has almost been reduced by half, which is particularly applicable to IoT devices.

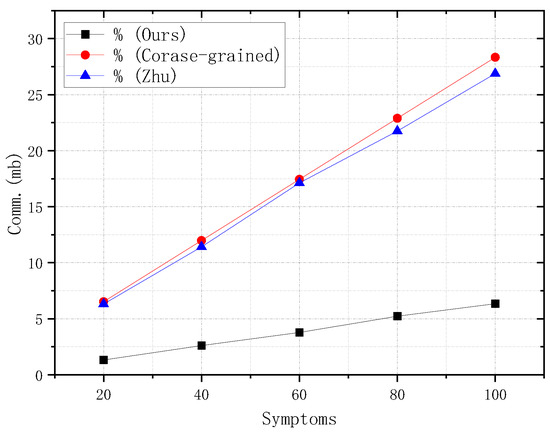
Figure 4. Communication overhead for different schemes with different numbers of symptoms.

For different data sizes of the receiver and sender, Table 5 illustrates the time and communication costs, respectively. From Table 5, we can see that the computational and communication cost of the STLPSI protocol online phase increases with the set size. However, compared with the change in communication cost in the online phase, the time cost has little change. For example, when the set size is 30 (the sum of the number of sender sets and receiver sets), the online communication overhead is 1.41 MB, and when the set size is 100, the communication overhead is 4.72 MB, an increase of $\times 3.347$. The time cost only increases from 0.78 ms to 0.812 ms, which is only a $\times 1.041$ increase.

Table 5. The communication and time cost of STLPSI protocol with different set sizes.

Set Size			Offine	Online
Sender’s Sizes	Receiver’s Sizes	t	Preprocess (ms)	Time (ms)	Comm. (mb)
20	10	6	0.12	0.78	0.94
40	20	12	0.28	0.79	1.94
60	40	24	1.02	0.812	3.21
80	60	36	2.36	0.84	4.38

We evaluated the cost of different collection sizes (the size of the elements in the collection is equal to the sender’s data plus the receiver’s collection elements), as shown in Figure 5 and Figure 6. We found that the protocol overhead increases with the increase in collection elements, as shown in Figure 5 and Figure 6. This is consistent with the previous discussion, indicating that our protocol is applicable to balanced or unbalanced sets and has strong flexibility.

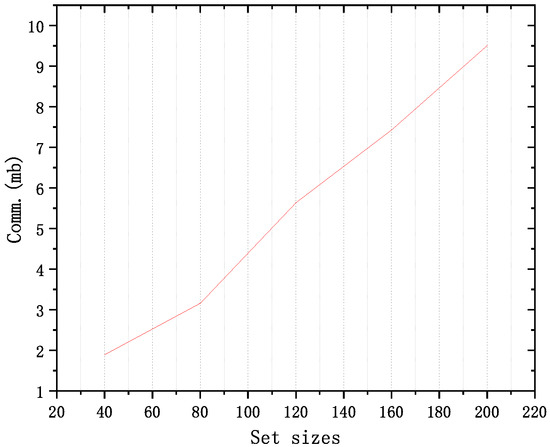
Figure 5. The communication cost of the STLPSI protocol under different set sizes.

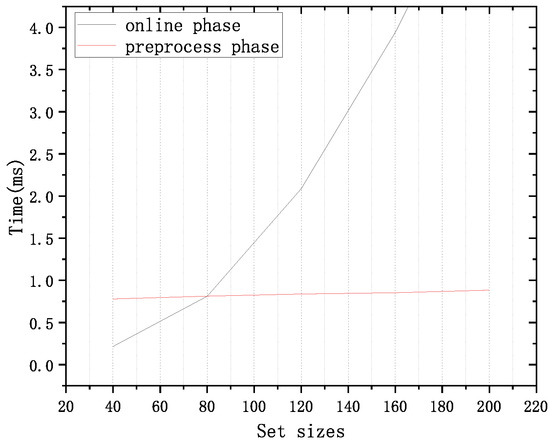
Figure 6. The time of the STLPSI protocol under different set sizes.

10. Conclusions

In this work, we introduce the Switching Threshold Label Private Set Intersection (STLPSI) protocol and present a comprehensive framework for its application in symptom matching. Our approach preserves patients’ privacy while allowing those who meet a particular symptom threshold to share their contact information directly, without involving any third-party intermediaries. Our experiments demonstrate that the protocol has a low communication overhead, making it suitable for Internet of Things (IoT) devices. Moreover, we thoroughly analyze the correctness and security of our protocol. Finally, we perform extensive performance evaluations, and the results demonstrate that our proposed scheme is highly efficient and performs exceptionally well.