Efficient Decision-Making Scheme Using Secure Multiparty Computation with Correctness Validation

Abstract

In the era of big data, it is essential to securely and efficiently combine the large amounts of private data owned by different companies or organizations to make correct decisions. Secure Multiparty Computation (SMPC) works as a general cryptographic primitive, which enables distributed parties to collaboratively compute an arbitrary functionality without revealing their own private inputs. While SMPC may potentially address this task, several issues, such as computation efficiency and correctness validation, have to be overcome for practical realizations. To tackle these issues, we designed a secure and efficient decision-making scheme to enable clients to outsource data and computations to cloud servers while ensuring the integrity and confidentiality of the input and output, in addition to the correctness of the results. Moreover, we implemented our scheme based on an SMPC computation framework named MP-SPDZ. The experimental evaluation results showed that our proposed scheme is feasible and efficient for practical realizations.

1. Introduction

With the flourishing development of the big data era, data are growing at an exponential rate every year, especially private data in business environments. Most companies and organizations that possess private data, such as healthcare centers, electronic commerce companies, online banks, and insurance companies, are unwilling to trade data in plaintext form. In today’s distributed network environment, which uses vulnerable and diverse communication channels, performing various computations on data in plaintext form inevitably comes with the issues of private data or confidential information leakage caused by network deception attacks or eavesdropping [1]. Therefore, a solution to combine data owned by different companies or organizations to make correct decisions while also protecting data privacy is urgently needed and will greatly increase the value of the data.

In general, traditional privacy-preserving techniques used in industry mainly include data anonymization [2], anonymity algorithms [3], differential privacy [4], and data encryption. These different privacy-preserving techniques protect privacy by changing sensitive data to conceal or erase the original sensitive information. Our goal was to find a solution that can combine large amounts of sensitive data from different companies or organizations while ensuring the confidentiality of the data. Unfortunately, data anonymization and anonymity algorithms may lose their effectiveness in protecting data privacy under the powerful data analysis capabilities of big data. For example, by conducting correlation analyses and carrying out deep mining on multi-source data, users’ privacy information can be easily restored. Differential privacy achieves privacy preservation by transforming the original data or adding noise to the statistical results, but for some complex queries, the addition of noise may lead to excessive errors. Data encryption utilizes cryptographic techniques to transform sensitive data into ciphertext, attempting to not reveal any information about the original data unless it can be inferred from the task output. Secure Multiparty Computation (SMPC) is a typical cryptography-based method. In recent years, SMPC has been widely applied in real-world applications to achieve privacy protection, such as disease diagnosis [5], bank customer risk prediction [6], etc., because it is more effective and efficient than other methods. SMPC enables distributed parties to collaboratively compute any function without revealing their own private inputs and outputs. For large-scale data in real-world scenarios, it can also support efficient fixed-point and floating-point operations [7], and arithmetic operations can be achieved with controlled linear complexity [8]. Due to these advantages, researchers have shifted their focus from purely theoretical research to real-world applications. However, there are still some problems, such as efficiency, computational overhead, and validation, that need to be addressed in practical applications.

Traditional SMPC is often unable to address the issues of low efficiency and unverifiable results when it comes to solving privacy-preserving computations across institutions. In this paper, we considered a novel real-world scenario, i.e., health insurance, to bridge the medical field with the financial sector’s data to achieve secure and efficient privacy-preserving health insurance decision-making. To support these requirements, we utilized the SPDZ protocol [9,10] hypothetically under a malicious security model. Meanwhile, in a realistic situation, insurance companies typically need a third-party institution for notarization or verification when making health insurance decisions. Towards this end, we extended the SPDZ protocol by adding an Honest Validator (HV) as a third party to verify the results. Doing so increases the computation and communication costs of SMPC nodes, but a slight loss of efficiency is deemed tolerable for the real application. We implemented the proposed protocol using the open-source MP-SPDZ framework [11] and safely calculated the decision-making results with it. To further accommodate potential real-world applications, we designed programs that can support parallel computing to improve the efficiency. In summary, our goal in this work was to design a scheme that combines data owned by various companies or organizations to make correct decisions while also safeguarding data privacy.

The primary contributions of this paper are as follows:

• For the health insurance scenario, based on data vectorization, Pedersen commitments, and non-interactive zero-knowledge proofs, we designed and implemented an efficient scheme to ensure the security of private data. To the best of our knowledge, this is the first work that applies Secure Multiparty Computation to the health insurance scenario.
• We propose a specific Secure Multiparty Computation protocol based on our scheme. In detail, we extended the SPDZ protocol by adding a third party, i.e., an Honest Validator (HV), to verify the correctness of the result.
• We implemented the proposed scheme on the open-source MP-SPDZ framework and carried out experiments with a large amount of real-world data. The key performance metrics, transmission data size, bytecode size, and execution time, demonstrated the feasibility and effectiveness of our model for health insurance decision-making scenarios. Furthermore, compared to traditional approaches, where any computing party can act as a validator, our scheme demonstrated approximately 10% improved efficiency.

The rest of this paper is organized as follows. In Section 2, we briefly introduce related works on SMPC and its applications in the medical field and the financial sector. Then, in Section 3 and Section 4, we introduce our system framework, threat model, and some fundamental knowledge of our scheme. The proposed scheme for the health insurance scenario is discussed in Section 5. In Section 6, we present the experimental results of our scheme to show its effectiveness. Finally, we summarize this work and discuss our future work.

2. Related Work

Collecting data from multiple parties to make correct decisions is an important task. Secure Multiparty Computation works as a general cryptographic primitive, which enables joint computing in a privacy-preserving manner. Yao [12] first proposed the problem of secure two-party computation and its solution in 1982. Then, researchers extended secure two-party computation to the case of multiple parties [13,14] and developed many high-performance multiparty protocols with the help of techniques such as oblivious transfer, secret sharing, zero-knowledge proofs, garbled circuits, and homomorphic encryption. The SPDZ (pronounced “speedz”) protocol [10] was one of them. It emerged as one of the most-effective and practical because it shifted the vast majority of computation to an offline phase (also known as preprocessing phase), which can be performed locally in advance. In the following decade, researchers have proposed several variants of the protocols [15,16,17] based on the SPDZ protocol further to improve its computation and communication efficiency, while also paying attention to specific applications.

There have been many works to investigate the application of SMPC in the medical field or financial sector. The study in [18] demonstrated that Secure Multiparty Computation using garbled circuits is a viable technology for addressing clinical use cases that require cross-institutional data exchange and collaboration. Li et al. [5] proposed a secure and efficient assisted multiparty decision-making scheme appropriate for Internet of Medical Things applications. Garofalakis [19] leveraged SMPC to provide an end-to-end infrastructure for computing privacy-preserving analytics on confidential healthcare data. The authors in [6,20] analyzed private data in the financial sector such as banks, insurance, and securities using SMPC. However, we noticed that most of the work using SMPC applications has not yet addressed the implementation in cross-institutional scenarios. In this paper, we overcame the obstacles and united different fields soundly to perform secure computation.

Concerning the validability of the results, to the best of our knowledge, this was first employed in electronic voting systems [21] and was termed public verifiability. Later, widely known publicly auditable voting protocols such as [22,23] were proposed. Among these voting systems, most use commitment mechanisms and zero-knowledge proofs to enforce verifiability. Baum et al. [24] first integrated Pedersen commitments [25] with an efficient information-theoretic SPDZ protocol [10] and proposed a protocol for which any party could function as an auditor, with approximately twice the efficiency of the original SPDZ protocol. Then, the work in [26,27,28,29] built on this foundation and proposed protocols with higher security requirements or efficiency. Our work utilized a single-party HV as the validator, which has the merit that the validation phase can be executed simultaneously with the computational protocol.

3. System Model

In this section, we introduce a detailed model of the health insurance scenario system, including the roles of all participants and their functions.

3.1. System Model

The scheme has four distinct types of participants, as shown in Figure 1.

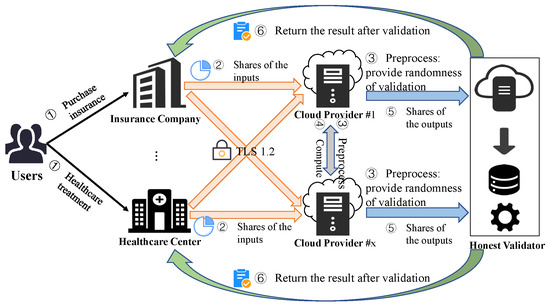
Figure 1. System scheme with Secure Multiparty Computation.

Users: When purchasing health insurance, visiting a hospital when sick, and the reimbursement of the costs occurs, the user’s personal information, including sensitive data such as occupation and annual income, as well as the records of the medical visits, are stored in the relevant institutions.

Healthcare institutions: These include healthcare centers and insurance companies. They each own a large amount of information about users and desire to leverage both parties’ resources to make health insurance decision-making for financial benefit. Before that, they need to perform unified preprocessing of their respective data according to trusted third parties’ standards.

Cloud providers: They are also referred to as SMPC nodes. They receive the data from healthcare institutions and perform secure calculations using SMPC while transmitting the parameters required for subsequent verification to the validator.

Honest validator: This is also a cloud provider, unless it validates the result from the SMPC nodes, thus guaranteeing the computation’s correctness.

3.2. Threat Model

As depicted in Figure 1, the scheme consists of four participants, including one honest validator, which can be relied upon for its credibility. The remaining three participants, however, may not be trustworthy. In this scenario, we assumed the presence of an adversary, denoted as $\mathcal{A}$, who may gain access to data outside of the honest validator.

$\mathcal{A}$ may launch an attack on the cloud to obtain encrypted data stored by users there. Similarly, $\mathcal{A}$ can obtain encrypted data from all parties by eavesdropping the network communication link. The worst-case scenario is that $\mathcal{A}$ may be able to collaborate with other participants to deduce users’ private information from the ciphertext. Security and efficiency will be realized through the proposed protocol to address these concerns in this system.

4. Preliminaries

In this section, we introduce some crucial notations, define the secret-sharing primitive, and give a basic overview of the SPDZ protocol, the Pedersen commitment, and non-interactive zero-knowledge proofs.

Notions: The protocol we present for the health insurance scenario in this paper considers arithmetic circuits over p-order fields, where p is a large Sophie Germain prime, that is $q=2p+1$ is also a prime. ${\mathbb{Z}}_p$ refers to the field $\{0,\dots ,p-1\}$; ${\mathbb{Z}}_p^{*}$ refers to ${\mathbb{Z}}_p\backslash \left\{0\right\}=\{1,\dots ,p-1\}$. We claim that an element g of a cyclic group G is a generator of this group only if $\forall x\in G$, $\exists a$ satisfies $g^a=x$. We write ${⟨x⟩}_i$ to denote the share of value x in the original SPDZ protocols and use ${\left[x\right]}_i$ to denote the share of the validation phase x.

We use ${\mathcal{P}}_i\in \mathcal{P}=\left\{{\mathcal{P}}_1,\dots ,{\mathcal{P}}_n\right\}$ to identify a compute party (i.e., a server in the client–server model) and use ${\mathcal{P}}_i^I\in {\mathcal{P}}^I=\left\{{\mathcal{P}}_1^I,\dots ,{\mathcal{P}}_m^I\right\}$ to identify an input party (i.e., a client). We use $\mathcal{C}\subseteq \mathcal{P}$ for the set of statically corrupted parties and $\mathcal{H}=\mathcal{P}\backslash \mathcal{C}$ for the setting of honest parties. The input side ${\mathcal{P}}_i^I$ can also be statically corrupted, but all our results are independent of the exact set of corrupted input sides $\mathcal{C}$.

4.1. The SPDZ Protocol

SDPZ is a state-of-the-art SMPC protocol, which operates on secret-sharing principles, enabling joint computation of arithmetic circuits. It allows shareholders to compute linear functions of secret inputs while ensuring that they learn nothing beyond the final output of those functions. Moreover, SPDZ secret sharing exhibits homomorphic properties, which means that addition operations can be performed on the shares without revealing the underlying values. To illustrate this, suppose X and Y are shared as $x_1$, $x_2$ and $y_1$, $y_2$, respectively, where $X={\sum }_i{x}_i$ mod p and $Y={\sum }_i{y}_i$ mod p for some prime p. In that case, $(x_1+x_2)$ and $(y_1+y_2)$ will also be shares of $(X+Y)$. The SPDZ protocol operates in two phases: an offline preprocessing phase, which generates the necessary raw materials, and an online evaluation phase, which executes the circuit.

Offline phase: This utilizes the Somewhat Homomorphic Encryption (SHE) [30] scheme to generate an ample supply of triples that can be used in multiplication operations based on Beaver’s method [31]. For instance, to compute $⟨xy⟩$, given some $⟨x⟩$ and $⟨y⟩$, it is necessary to possess three secret-sharing values called a triple: $⟨a⟩$, $⟨b⟩$, and $⟨c⟩$, where $c=ab$. It is worth noting that this phase can generate as many triples as required in advance, independent of the input data and function to be computed.

Besides, in the primitive SPDZ protocol, a global private key denoted by $\alpha$ is generated during the offline phase. This key serves as a Message Authentication Code (MAC) and is utilized by the participating nodes to verify the “correctness” of the computation results. Notably, $\alpha$ is distributed secretly among the nodes, such that $\alpha ={\sum }_i{\alpha }_i$ and each node possesses ${\alpha }_i$. Unfortunately, despite its efficacy in guaranteeing the integrity and authenticity of transmitted messages, MACs alone cannot verify the results’ correctness.

Online phase: The online phase evaluates the function. Some operations on shares, like addition or multiplication by a constant, can be performed without communication among computation nodes. Then, we define a share of x as

$$⟨x⟩=\left\{\left(x_1,\dots ,x_n\right),\left(\delta {\left(x\right)}_1,\dots ,\delta {\left(x\right)}_n\right)\right\}$$

where $x={\sum }_{i=1}^n{x}_i$ and $\alpha ·x={\sum }_{i=1}^n\delta {\left(x\right)}_i$. Moreover, we define

$$\begin{array}{c}⟨x⟩+⟨y⟩=\left\{\left(x_1+y_1,\dots ,x_n+y_n\right),\left(\delta {\left(x\right)}_1+\delta {\left(y\right)}_1,\dots ,\delta {\left(x\right)}_n+\delta {\left(y\right)}_n\right)\right\}\\ ⟨x⟩·s=\left\{\left(x_1·s,\dots ,x_n·s\right),\left(\delta {\left(x\right)}_1·s,\dots ,\delta {\left(x\right)}_n·s\right)\right\}\\ ⟨x⟩+s=\left\{\left(x_1+s,x_2,\dots ,x_n\right),\left(\delta {\left(x\right)}_1+{\alpha }_1·s,\dots ,\delta {\left(x\right)}_n+{\alpha }_n·s\right)\right\}\end{array}$$

where $y={\sum }_{i=1}^n{y}_i$ and s is a constant. When opening a shared value $⟨x⟩$, parties first broadcast their shares $x_i$ and compute x. To ensure that x is correct, they then check the MACs by committing to and opening $\delta {\left(x\right)}_i-x·{\alpha }_i$ and checking that these shares sum up to zero.

4.2. The Pedersen Commitment

Considering the linear nature of the existing SPDZ framework, our proposal entails leveraging a Pedersen commitment [25] scheme as a means of validating the correctness of the computation results. Let g and h be elements of G such that nobody knows ${log}_{g}h$. When the protocol is initialized, these elements should be chosen in the offline phase. When the committer commits himself/herself to an $x\in {\mathbb{Z}}_p$, the commitment function chooses $r\in {\mathbb{Z}}_p$ at random and computes

$$\mathcal{W}(x,r)=g^x{h}^r\in G.$$

Such a commitment can be later revealed by x and r. It is straightforward to prove that $\mathcal{W}(x,r)$ indicates no information about x and that the committer opens a commitment to x as $x^{\prime }\ne x$ unless he/she can find ${log}_{g}h$. Thus, we can say the Pedersen commitment scheme is hiding and binding.

4.3. Non-Interactive Zero-Knowledge Proofs

To achieve the audibility property in the offline phase of our proposed protocol, we utilized efficient Non-Interactive Zero-Knowledge Proofs (NIZKPs) [32]. This is a two-party protocol between a prover and a verifier, where the prover convinces the verifier that a statement is accurate and the verifier learns nothing beyond the claim statement. It can be expressed as follows:

(1)

The prover chooses $t_1,t_2\in {\mathbb{Z}}_n$, then computes $T=g^{t_1}{h}^{t_2}$ and sends T to the verifier.

(2)

The verifier chooses $c\in {\mathbb{Z}}_n$ and sends c to the prover.

(3)

After receiving c, the prover calculates $s_1=t_1+cx$ mod $\varphi \left(n\right)$ and $s_2=t_2+cr$ mod $\varphi \left(n\right)$ and sends $s_1,s_2$ to the verifier.

(4)

Finally, the verifier checks $T{c}^c=g^{s_1}{h}^{s_2}$ mod $\varphi \left(n\right)$.

The prover proves knowledge of an element x and decommitment value r such that $Com=g^x{h}^r$ mod n.

5. Our Scheme

In this section, we will provide a detailed description of our scheme.

5.1. Overview

As shown in Figure 1, we designed a novel and efficient scheme to combine private information about users in healthcare centers and insurance companies to make valuable decisions while validating the correctness of decision-making results. The scheme is based on the SPDZ protocol and Pedersen commitments and is divided into offline and online phases. The offline phase primarily provides the necessary preprocessing and information exchange for the subsequent online computation phase and generates the required parameters for validation. The online phase enables the participants to securely compute the decision results together, without revealing their respective private inputs and ultimately returns the results to HV for correctness validation. The decision-making algorithm used in the online computation phase is derived from real-world applications, which will be described in detail in the last subsection of this section.

Online phase: In this phase, SMPC nodes carry out the computational steps and obtain the required decision-making results while protecting privacy. However, to validate the results, modifying the shared values in the original SPDZ protocol with Pedersen commitments is essential. On the other hand, we assumed that there is a transcript $ϵ$ on the HV to store the communication data sent by the computational nodes, and we used Algorithm 1 to keep an eye on all values needed for validation.

Algorithm 1: Store_Load—algorithm for storing and loading message on the transcript $ϵ$.

Offline phase: As the name suggests, this phase can be completed in advance, allowing it to generate the necessary randomness for the online computation phase. For example, it can createsecret keys for message authentication codes, ample multiplication triples, commitment parameters required for result validation, etc. These preprocessing and generation of necessary parameters in the offline phase significantly enhance the efficiency of online computation. The SMPC nodes run the offline phase of the protocol, preparing all correlated randomness for the online phase, including some parameters necessary for the validator.

5.2. Online Phase

To enforce the validation of the output, it is essential to modify the shared values in the original SPDZ protocol. Specifically, we propose altering the inputs, opened values, and outputs of the computational nodes at the point of their commitment. These modified values are then transmitted to the transcript $\epsilon$ on the HV, where the correctness of all intermediate steps can be verified. The Pedersen commitment scheme is information-theoretically hiding during the whole computation process. When we open a Pedersen commitment $\mathcal{W}(x,x_r)$, we reconstruct both x and $x_r$, and the HV can check that it is correct.

Let $x,x_r\in \mathbb{F}$, $g,h\in G$, and then, we define the new way to represent shared value x with a Pedersen commitment as

$$\left[x\right]=\left\{⟨x⟩,⟨x_r⟩,\mathcal{W}(x,x_r)\right\},$$

where $⟨x⟩$ is a representation of x as introduced in Section 4.1. Similarly, with this new linear representation, we can perform the same operations linearly as in Section 4.1. We can still employ Beaver’s circuit randomization technique for the multiplication of $\left[x\right]$ and $\left[y\right]$ since the representation is linear.

Given that operations in the online phase depend on multiplication triples and the randomness required for the validation phase, we define the functionality ${\mathcal{F}}_{offline}$ that describes the behavior and output of the preprocessing. In general, ${\mathcal{F}}_{offline}$ must perform the following: (1) establish an additively secret-sharing MAC key $\alpha$; (2) generate random $\left[x_r\right]$ shared values to be used during Input; (3) generate $[a,b,c]$ shared Beaver triples for every multiplication to be performed in the online phase.

In Figure 2, we present the protocol of the online phase. It uses ${\mathcal{F}}_{offline}$ for the offline phase and the transcript $ϵ$ for all communication.

Figure 2. Protocol ${\mathsf{\Pi }}_{Online}$.

At the beginning step Prepare, the parties $\mathcal{P}$ generate the parameters $g,h$ of the Pedersen commitment via a Common Reference String (CRS), establish the secret shared MAC key $\alpha$, as well as produce views for random triples $a,b,c$, where $c=a·b$. Once the offline phase is called to obtain the initial randomness, a new input-independent view ${\left[r\right]}_i$ can be utilized to generate the values for the Input step. Each party ${\mathcal{P}}_i^I\in {\mathcal{P}}^I$ submits a value $x_i\in \mathbb{F}$ to the computation, where each ${\mathcal{P}}_i^I$ uses the new ${\left[r\right]}_i$ to secretly open it. Then, each can check the correctness of the commitment on it and use $m_i=x_i-r_i$ to mask his/her input.

Similarly, in Compute, the provided triples ($\left[a\right],\left[b\right],\left[c\right]$) will be used in the computation. They are used to multiply with linear operations as follows:

$$\left[x·y\right]=\left[c\right]+\sigma ·\left[b\right]+\tau ·\left[a\right]+\sigma ·\tau .$$

$\left[\sigma \right]=\left[x\right]-\left[a\right]$ and $\left[\tau \right]=\left[y\right]-\left[b\right]$ are opened values. Other linear operations (addition, subtraction, or with publicly known constants) can be performed locally. The last operation left for the step is outputting the results. Here, we ran the MAC check to verify the result y and its correlated $\overline{y}$; thus, the parties can open the output and send the result to transcript $\epsilon$ pending further validation.

In the final step Validate, the validator HV will execute the calculation process gate by gate as was performed by ${\mathcal{P}}_i$. For the records on the transcript $\epsilon$, the HV checks every opened value. When this is performed, the result of the computation and the commitment of [y] will finally be checked for correctness against the views on $\epsilon$.

5.3. Offline Phase

As described above, the offline phase has to produce views of secure MAC key $\alpha$, views of Beaver triples, and a masked input m.

We reused a homomorphic encryption scheme like Damgård et al. in [10] to achieve these goals. Let $\mathcal{S}=(KeyGen,Enc,Dec)$ be such a scheme. It must support the evaluation of circuits with polynomially many additions and one homomorphic multiplication. It should also facilitate distributed vital generation. Each participant obtains a share of the secret decryption key in this process, while all parties possess the public encryption key. Then, the secret-sharing decryption key will be utilized for distributed decryption, which involves processing a ciphertext and distributing the resulting plaintext to each party involved. Here, each participant can employ NIZKPs to guarantee the correctness and security of scheme $\mathcal{S}$.

The first step is to generate a secret-sharing MAC key $\alpha$, which is used to calculate the product with the input shared value and, then, Reshare the result. As shown in Algorithm 2, it is a functionality for distributed MAC key generation. Its result is a ciphertext, and we can learn the value by using distributed decryption in $\mathcal{S}$. However, we really need a $\left[x\right]$-shared value. A sub-protocol ${\mathsf{\Pi }}_{Reshare}$ (shown in Algorithm 3) can produce a ciphertext as a plain $\left[x\right]$-shared value.

Algorithm 2: MacKeyGen—algorithm for generating a secret-sharing MAC key.

With the algorithm $Reshare$, similarly, we can easily generate a $\left[x\right]$-shared random value. Now, the rest of the preprocessing phase is how to generate Beaver triples. Like the above functionality, we assumed that each party ${\mathcal{P}}_i\in \mathcal{P}$ already knows the public encryption key $pk$ and has an additive secret sharing of the decryption key $sk$. Simultaneously, parameters $(g,h)$ for the Pedersen commitments are known. The parties are assumed to have run the algorithm $MacKeyGen$. Thus, each party has an additive secret sharing of the MAC key $\alpha$ and an encryption $e_{\alpha }$. Now, we briefly describe the functionality $GenTriples$:

(1)

Using the same method in the algorithm $Reshare$, each party ${\mathcal{P}}_i$ can hold two random $\left[x\right]$-shared values $\left[a\right]$ and $\left[b\right]$. Each party calculates ciphertexts $e_{a_i}=Enc(pk,{⟨a⟩}_i)$ and $e_{b_i}=Enc(pk,{⟨b⟩}_i)$ together with the NIZKPs of both. Then, they broadcast $e_{a_i}$, $e_{b_i}$, and the NIZKPs to all other parties and $ϵ$. When each receives the ciphertexts and the corresponding NIZKPs from all parties, check all the NIZKPs. If cheaters exist, abort.

(2)

Utilizing the additive and multiplicative homomorphic properties of the scheme $\mathcal{S}$, all parties compute: (1) a ciphertext $e_a$ such that $a={\sum }_{i=1}^n{a}_i$; (2) a ciphertext $e_b$ such that $b={\sum }_{i=1}^n{b}_i$; (3) an encryption $e_{a·b}$ of the product of a and b.

(3)

The parties run the algorithm $Reshare$ on $e_{a·b}$, resulting in a secret sharing $\left[c\right]$, where $c=a·b$.

Finally, we can assemble these components to obtain the offline protocol ${\mathsf{\Pi }}_{Offline}$ (shown in Figure 3). Steps 1–4 utilize the algorithms described above to generate the needed randomness for the online computation. Likewise, these generated random values need to be validated. Benefiting from the fact that the corresponding commitments and NIZKPs were generated at each phase and sent to $ϵ$, the HV can validate their correctness in Validate.

Algorithm 3: Reshare—algorithm for producing a plain $\left[x\right]$-shared value.

Figure 3. Protocol ${\mathsf{\Pi }}_{Offline}$.

5.4. Decision-Making Algorithm

Based on the protocol above, Algorithm 4 is proposed to describe the decision-making algorithm, which is a case in the health insurance scenario. We used it as the basis of the experimental phase.

Algorithm 4: Dec_Make—algorithm for making a health insurance decision using SMPC.

This algorithm’s inputs are two two-dimensional matrices from the medical records and insurance information, and the output is a matrix with size $n\times 9$ since there are nine different decision outcomes. Firstly, the algorithm verifies if specific diseases exist in the input matrices. Then, it applies other decision rules to modify the corresponding values in the output matrix. It is important to note that not all rules are explicitly listed in the algorithm. Lastly, multiple modifications can occur in the result matrix during numerous judgments, so the algorithm identifies the first changed value in each row. Based on this information, the algorithm generates a new result matrix, yielding the correct decision outcome.

6. Analysis and Evaluation

In this section, we first provide a brief security analysis of our scheme. Then, we carry out a set of experiments to evaluate our decision-making scheme.

6.1. Security Analysis

Theorem 1. 

Assuming that the Discrete Logarithm Problem (DLP) is hard in the Pedersen commitment group G and non-interactive zero-knowledge proofs, our proposed protocol is secure against up to $n-1$ parties’ collusion attack and guarantees the correctness validation.

Proof. 

During the execution of the online phase protocol, we assumed there exists $\mathcal{A}$ controlling the participants. For the Prepare, Input, and Compute steps, since at most $n-1$ shares of the set for each value are uniformly random and do not reveal any information about the secret shares, it is impossible that $\mathcal{A}$ could tamper with the real transcript $ϵ$. During the output of Result, due to the information-theoretic hiding of our scheme, any of the values opened by the dishonest parties will be identified if the MAC checking fails. But, this happens with the possibility at most $2/p$ as proven in [9]. In the Validate step, assume that $\mathcal{A}$ changed the output y with another value that must open the commitment $co{m}_y$ correctly. But, in fact, we already obtained the correct commitment $\mathcal{W}(y,\overline{y})$ for y, and $\mathcal{A}$ can only calculate ${log}_{g}h$. It is impossible to break based on the DLP.

Concerning the offline phase, the security of the Prepare, GenMacKey, Input, and Triples steps were proven exhaustively in [9]. Regarding the Validate step, it is also impossible for adversary $\mathcal{A}$ to break the commitments and NIZKPs since they are based on the difficulty of the DLP. Therefore, our protocol can be secure against collusion attacks by up to $n-1$ parties and guarantees correctness validation. □

6.2. Setup and Experimental Datasets

We ran our experiments on a laptop with an Intel(R) Core(TM) i5-12500H 2.50 GHz CPU, 16.0 GB RAM, and WSL 2 with the Ubuntu-22.04.2 LTS system in the LAN setting. The programming tools were Clion and Pycharm with C++ 17 and Python 3.10. We used a 128 bit prime as the computational modulus because this is a common choice, and the (statistical) security parameter was set to 40.

We collected two real-world datasets to conduct our experiments: patient medical records and insured person information. Table 1 and Table 2 describe the variable names, types, and corresponding examples for these two datasets, respectively.

Table 1. The description of the medical center dataset.

Variable Name	Variable Type	Example
personnel ID	numerical	90209673
disease code	categorical	I10.X02
disease name	categorical	hypertension
total fees	numerical	7950.88
reimbursement amount	numerical	7189.04
settlement date	numerical	16 March 2022 10:06

Table 2. The description of the insurance company dataset.

Variable Name	Variable Type	Example
personnel ID	numerical	90209673
age	numerical	55
job hazard category	categorical	high
overweight condition	categorical	moderate
annual income	numerical	100,000
insurance premium	numerical	5000
insurance coverage	numerical	100,000
insurance type	categorical	hospitalization

6.3. Performance Evaluation

We compared the concrete performance of this paper’s decision-making scheme with a normal one, i.e., choosing an arbitrary SMPC node as the validator without the HV (denoted as without-HV). To obtain the runtime of our solution, we implemented a benchmark that emulates both the online and offline phases. Notably, although the number of SMPC nodes had been set to 2 in the previous framework diagram, for this benchmark, we shall compare the performance under different computational nodes, and their size in the range of 2–6 was set. For the experimental data to be statistically meaningful, we conducted the same experiment several times and took the mean values.

For the online phase, as illustrated in Figure 4, the runtime increased at a linear rate as the number of SMPC nodes grew, with the scheme without-HV or our scheme. When calculating in two nodes, it took approximately 19 ms to run the decision-making algorithm once using our proposed online protocol, and for without-HV, it took about 22 ms. It can be seen that, with an external validator to perform the verification work, the efficiency was roughly 1.14-times higher than the scheme without-HV. The follow-up multiparty scheme also remained at 1.1–1.2.

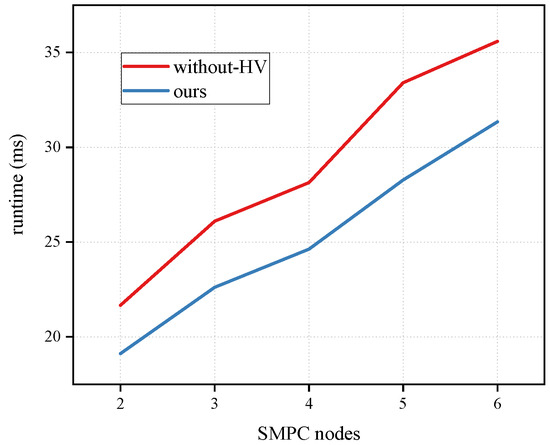
Figure 4. Time consumption for one-time online computation compared to the normal one without the HV (denoted as “without-HV”). The size of the computational nodes were set in the range of 2–6, and the runtime was measured in milliseconds.

Our primary concern in the preprocessing phase was the speed of triples’ generation and ignoring the simultaneous generation of other examples such as squares $(a,a^2)$, inverses $(a,a^{-1})$, and random bits. As shown in Figure 5, once the generated number was set to 4096, the execution time of the program tended to grow as the number of participants increased. For two parties, our proposed offline protocol took about 1.98 s. At the same time, the scheme without-HV was close to 2.49 s, almost 1.3-times more, attributed to the cumbersome verification and communication consumption.

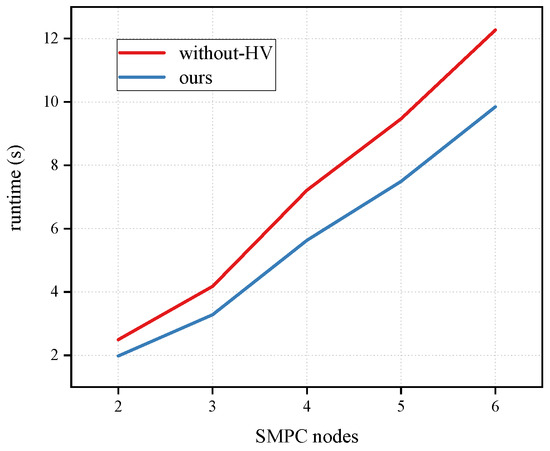
Figure 5. Time consumption for generating 4096 triples in the offline phase. Similarly, comparisons were made with the “without-HV” scheme, where the number of computational nodes ranged from 2 to 6, and the time was measured in seconds.

We also considered that, in real-world applications, if several users’ decision-making requests need to be processed simultaneously, then there should be support for batch processing as well. Therefore, we prepared programs in an open-source platform to enable parallel computation. As depicted in Figure 6, we can see that the time consumption of the calculation did not grow in a rather regular linear manner as the number of inputs increased due to the parallelization, which somewhat improved the efficiency. Our experiments found that the hardware used in this experiment can support simultaneous computation of up to approximately 20,000 inputs at a time.

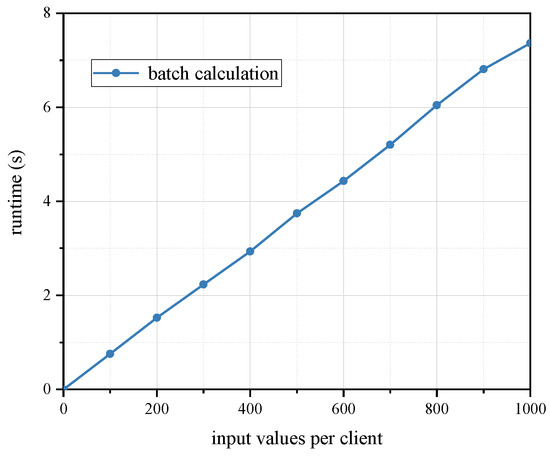
Figure 6. Execution time for parallel computation with different numbers of inputs in a two-SMPC-node setting.

Finally, as shown in Table 3, we gathered a set of meaningful metrics to display the overall performance of our scheme compared with without-HV in a two-node setting. We evaluated the disk consumption by the size of the compiled bytecode, transmission data, and preprocessing data volume. These metrics demonstrated that our scheme was acceptable for the disk consumption. In addition, the computation time of the two diverse schemes was 19.121 ms and 21.667 ms, respectively. This shows that our solution is efficient in terms of time consumption.

Table 3. Overall performance metrics of one-time online computation.

Type	Performance Metrics	Performance Data
	complied bytecode	369 KB
	communication round	80
our scheme	transmission data	0.050504 MB
	preprocessing data view	1562 triples + 3444 bit
	computational time	19.2127 ms
	complied bytecode	375 KB
	communication round	94
without-HV	transmission data	0.058192 MB
	preprocessing data view	2124 triples + 4688 bit
	computational time	21.667 ms

7. Conclusions and Future Work

In this paper, we first implemented an efficient decision-making scheme in the health insurance scenario using Secure Multiparty Computation. We introduced a novel framework diagram of our scheme by adding an external party (honest validator) to verify the correctness of the results. We extended the original SPDZ protocol and involved the Pedersen commitments to ensure correctness. Eventually, we implemented our scheme in the open-source framework MP-SPDZ, and in terms of the experimental results, our scheme was slightly more efficient than the ordinary one. In other words, it is feasible and practical. In addition, our scheme applies to general cross-institutional financial scenarios.

Although the offline phase can be accomplished before the evaluation, it is indisputable that the preprocessing of our solution was far worse than the original protocol. Especially in scenarios involving fewer participants, the triple generation speed was relatively slower than traditional approaches. Moreover, the time consumption of the online computation also increased exponentially as the number of inputs grew in parallel. So, how to tackle the efficiency issue is what we need to solve desperately, and this is the direction of our future work.

Firstly, since the SPDZ protocol utilizes a linear secret-sharing scheme, we could contemplate employing a more-efficient one, such as the lattice-based commitment scheme BDLOP mentioned in [33]. It outperforms the Pedersen commitment scheme due to its linear homomorphic property, efficient ZKPs, and support for larger message space. Secondly, another more-straightforward approach involves leveraging high-performance GPUs [34] to enhance efficiency at the hardware level. Segregating computationally parallelizable portions into different grids for simultaneous computation—for instance, generating triples in the offline phase concurrently—might significantly augment the overall operational efficiency of the entire protocol.