Frame Duplication Forgery Detection in Surveillance Video Sequences Using Textural Features

Abstract

Frame duplication forgery is the most common inter-frame video forgery type to alter the contents of digital video sequences. It can be used for removing or duplicating some events within the same video sequences. Most of the existing frame duplication forgery detection methods fail to detect highly similar frames in the surveillance videos. In this paper, we propose a frame duplication forgery detection method based on textural feature analysis of video frames for digital video sequences. Firstly, we compute the single-level 2-D wavelet decomposition for each frame in the forged video sequences. Secondly, textural features of each frame are extracted using the Gray Level of the Co-Occurrence Matrix (GLCM). Four second-order statistical descriptors, Contrast, Correlation, Energy, and Homogeneity, are computed for the extracted textural features of GLCM. Furthermore, we calculate four statistical features from each frame (standard deviation, entropy, Root-Mean-Square RMS, and variance). Finally, the combination of GLCM’s parameters and the other statistical features are then used to detect and localize the duplicated frames in the video sequences using the correlation between features. Experimental results demonstrate that the proposed approach outperforms other state-of-the-art (SOTA) methods in terms of $Precision$, $Recall$, and $F1Score$ rates. Furthermore, the use of statistical features combined with GLCM features improves the performance of frame duplication forgery detection.

1. Introduction

Nowadays, digital cameras have become more powerful due to the rapid developments in technology. In the last decade, smartphone camera and surveillance cameras are widely used for recording digital videos in our daily life and produce high-quality videos which can be taken as credible news. The authentic videos provide stronger evidence than an authentic image. Moreover, these videos can be used as evidence of conviction or acquittal in the courts of law. However, digital video contents can be easily modified or forged by using digital video editing tools (e.g., Filmora, Adobe Premiere Pro, Windows Movie Maker, etc.). Recently, there are many types of attacks that can be applied on video surveillance systems [1]. Therefore, there is a big need to protect the authenticity of such videos. Consequently, digital video forensics attract many researchers’ attention [2]. In the literature, digital video forgery detection is a common research area for digital video forensics [3,4,5]. It can be classified into two main categories: video inter-frame forgery and video intra-frame forgery.

Inter-frame forgery is the most common forgery type for digital videos. This kind of forgery is usually performed in the temporal domain (between frames), such as frame duplication, frame deletion, frame shuffling, and frame insertion. Usually, it occurs in surveillance video sequences because the scene under the camera and camera position itself are stable. In this case, the forgery operation is easy to be performed and extremely imperceptible. On the other side, the intra-frame forgery occurs in the spatial domain (inside frame) or the spatio-temporal domain, such as region duplication (copy-move) inside frames, frame splicing, or region splicing [3,6]. In this paper, we consider only inter-frame duplication forgery. Inter-frame duplication forgery is the most common forgery type in digital video sequences, which can be in the temporal domain. It is performed by just copying one or more frames from the video sequence and then pasting it into another location within the same video sequence, to hide or duplicate some details inside the video, as shown in Figure 1, during which frames from 790 to 860 are copied and then pasted instead of frames from 865 to 1035, to hide the existence of the moving blue car from the video without producing any observable traces for the forgeries. The original video sequence of Figure 1 is taken from the SULFA dataset [7] using a stationary camera. Compared with image copy-move forgery detection (CMFD) approaches [8,9], video inter-frame duplication forgery detection is challenging due to their temporal dimension. Furthermore, processing videos frame-by-frame with CMFD methods will result in temporal inconsistency due to the complex motion of the objects and cameras.

Figure 1. Inter-frame duplication forgery example. We select only 15 frames from the total 70 forged frames to highlight the removal of the moving blue car from the recorded video sequences. The original video sequence is taken from SULFA dataset [7].

Although many video inter-frame duplication forgery detection algorithms have been proposed [3,4], these algorithms still have some problems, such as a poor forgery detection rate in stable scenes taken by stationary surveillance cameras, the inability to find the exact location of the duplicated frame pairs, and high computational complexity.

This paper proposes a frame duplication forgery detection method for digital video sequences based on the combination of Gray Level Co-occurrence Matrix parameters (GLCM) and some statistical features of each frame in the forged video sequences. The proposed method consists of three main steps: frame wavelet decomposition, frame textural features extraction and frame feature matching. The proposed method combines the advantages of the GLCM parameters and the discrete wavelet transform (DWT) coefficients. First, each frame in the forged video sequence is decomposed using DWT to provide sub-band images. Second, GLCM is applied to sub-band images to extract the texture features. Furthermore, the second-order statistical descriptors such as Contrast, Correlation, Energy, and Homogeneity are computed for GLCM. Third, some statistical features from each frame, such as standard deviation, entropy, RMS, and variance, are also computed. Finally, we combine GLCM’s parameters with the other statistical features for frame duplication forgery detection. The main contributions of this paper are summarized as follows:

• We introduce a robust and efficient inter-frame duplication forgery detection method for digital video sequences.
• We apply single-level 2-D discrete wavelet transform (2DWT) decomposition for each frame in the forged video sequences.
• We employ GLCM for the DWT coefficients to extract textural features from each frame. Then, we combine it with other statistical features for the features’ representation.
• We evaluate the proposed method performance compared with other SOTA methods on two established datasets. The experimental results show the efficacy of the proposed method for detecting frame duplication forgery from the surveillance videos.

The remainder of this paper is organized as follows: Section 2 introduces the related works. Section 3 presents an analysis of the proposed frame duplication forgery detection approach. The experimental results and comparisons of the performance evaluation with the SOTA methods are presented in Section 4. Finally, Section 5 concludes this paper.

2. Related Work

Most of the existing video inter-frame duplication forgery detection algorithms share the same pipeline. Firstly, the input is pre-processed, which tampers with the video sequence. Secondly, the video sequences are divided into small overlapping sub-sequences. Thirdly, features are extracted from each small sub-sequence. Finally, the extracted features are then matched to find the most similar frames.

Wang W. and Farid H. [10] introduced the first forgery detection algorithm for inter-frame duplication forgery in digital videos based on spatial and temporal correlation coefficients between frames. However, this method failed to find inter-frame duplication forgeries when highly similar frames were used for frame duplication and also when post-processing attacks (e.g., noise addition) were applied on the duplicated frames. Lin et al. [11] developed a coarse-to-fine approach to detect inter-frame duplication forgery based on candidate selection, a calculation of the spatial correlation, and then the classification of frame duplication. They computed the temporal and spatial correlations by calculating the histogram difference. Their approach also failed to detect the inter-frame duplication forgery in static scenes with stationary cameras. Li and Huang [12] presented a frame duplication forgery detection algorithm based on the structural similarities between video frames. They first divided the input-tampered video sequence into small overlapping sub-sequences. Then, they used the structural similarity to compute the similarities between the frames. Finally, they calculated similarities between subsequences in the temporal domain and then combined the matched sub-sequences to localize the duplication forgery. Their algorithm is robust, but it fails to detect the forgery from the static scenes and it also has a high computation time. Singh et al. [13] partitioned the input video into four subblocks and extracted nine features from each frame. Furthermore, the nine features were lexicographically sorted to find out the similar frames. Then, they calculated the similarity between the features of an adjacent pair of frames via the Root-Mean-Square-Error to identify the suspicious frames. Finally, the correlation between the suspicious frames was performed to detect the inter-frame duplication forgery. Their algorithm was also unable to detect frame duplication in videos taken by a stationary fixed camera and also when the duplication forgery occurred in a different order [14]. Yang et al. [15] improved the forgery detection method in [10] by proposing a two-stage similarity analysis approach. First, the features from each frame in the tampered video were extracted via singular value decomposition and the distance similarity measure was computed between the extracted features by using Euclidean distance. Second, the candidates were matched for possible duplication by using random block matching. However, their approach was unable to detect forgeries when they occurred in a different order too [14]. Fadl et al. [16] introduced an inter-frame duplication forgery detection algorithm for video sequences using residual frames instead of original frames. Then, they calculated the entropy of the discrete cosine transform coefficients for each residual frame. After that, they detected frame duplication based on sub-sequence feature analysis. An inter-frame forgery detection approach based on the Polar Cosine Transform (PCT) and a neighbor binary angular pattern was developed by Shelke and Kasana [17] to detect multiple forgeries such as frame duplication, insertion, and deletion from the video sequences. However, their approach failed to detect the exact location of the duplicated frames, especially in static scenes with highly similar frames, and it is also not useful for the real-time screening of videos [17]. Bozkurt and Ulutaş [18] divided video frames into small blocks during features extraction using DCT. A template of the tampered frame group was obtained by processing the binary image and then applying a search using this template. Their method brought outstanding results for uncompressed and compressed video sequences and a good robustness against blurring attacks. However, their method was unable to determine the exact location of the forgery rather than their high complexity.

Generally, surveillance video sequences contain static scenes with highly similar frames. Usually, these similar frames are used to tamper video contents by removing or duplicating video shots within the video sequence, without leaving any obvious signs of fraud. The aforementioned approaches divide forged video sequences into overlapping subsequences, and then the similarities between these subsequences are computed to find the duplicated frames. Furthermore, these approaches usually depend on global thresholds with predefined values during the frame duplication detection process. These thresholds can potentially be appropriate for one scenario and ineffective for another. Furthermore, many duplicated frame pairs are misdetected by these approaches and so many false positive frames exist. Additionally, it limits the generality of these approaches.

Overall, the existing approaches may have some problems, e.g., low forgery detection rate in stable scenes, inability to find the exact location of the duplicated frames, and high computational complexity. So, it may not be suitable for detecting and localizing inter-frame duplication forgeries in real-time applications because these methods are based on dividing video sequences into small sub-sequences, which require more time. Furthermore, these methods require high hardware specifications and much data. Therefore, there is still a need for improvements, especially in the speed and accuracy of the proposed methods. In this paper, we proposed a robust frame duplication forgery detection method. Extensive experiments and comparisons on two different datasets are carried out to evaluate the performance of the proposed approach. The experimental results show that the proposed approach outperforms other SOTA methods, and the proposed approach is presented in detail in the following Section 3.

3. Proposed Method

Generally, surveillance videos consist of static scenes (similar frames), which can be used as a useful tool for removing or duplicating events within the video sequence to produce new tampered videos with duplicated frames without leaving any visual traces of forgery. However, video frames in static scenes are not exactly the same based on their intensity values due to the existence of noise disturbance during the video acquisition step. The GLCM textural features’ operators for video frames can be used for detecting duplicated frames efficiently without dividing video frames into overlapping sub-sequences as in the literature. Figure 2 shows the GLCM textural features (Contrast, Correlation, Energy, and Homogeneity) of original and tampered video sequences, where the original frames (from 1:20) and tampered frames (from 301:320) have the same GLCM values in the tampered video sequence, which indicates the existence of frame duplication forgery, as indicated in the red box.

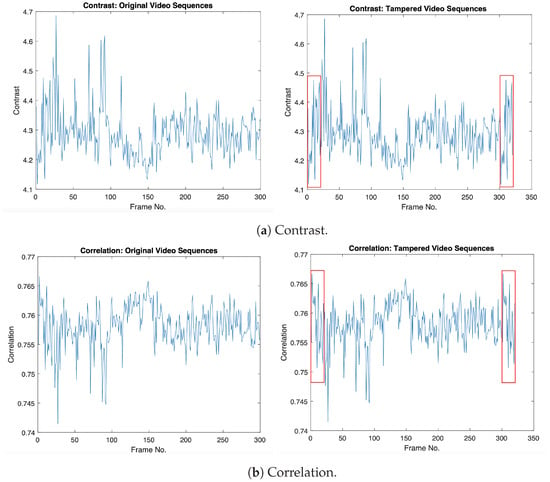
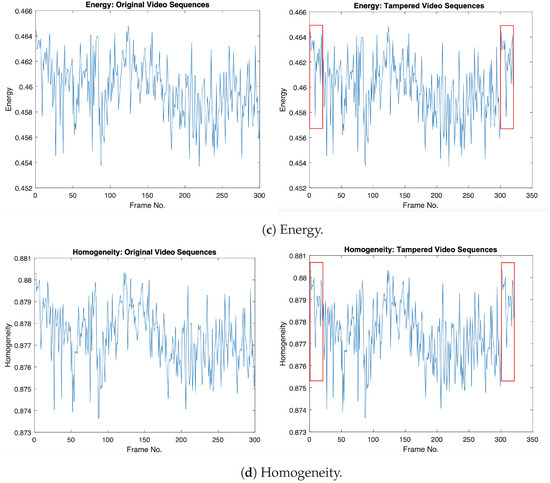
Figure 2. Illustrations of the GLCM textural features for the original and forged videos: (1st column) GLCM textural features for the original video; (2nd column) GLCM textural features for the forged video with frame duplication. Original video sequence (akio video) comes from Video Trace Library dataset [19] (where frames from 1 to 20 are copied and then pasted into the frame location from 301 to 320, as indicated in the red box).

Furthermore, we extract other statistical features from the video sequences and then combine them with the GLCM textural features to represent the final feature vector for each tampered video sequence. The statistical features used are Entropy, the Root-Mean-Square level, Standard deviation, and Variance. Figure 3 shows the statistical features that are combined with GLCM features, where the original frames (from 1:20) and tampered frames (from 301:320) have the same statistical values in the tampered video sequence, as indicated in the red box.

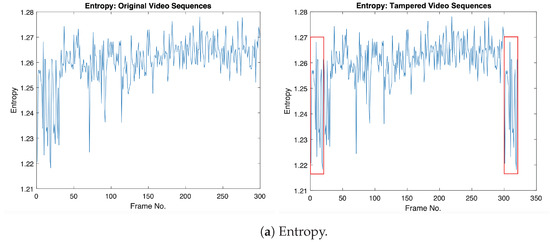
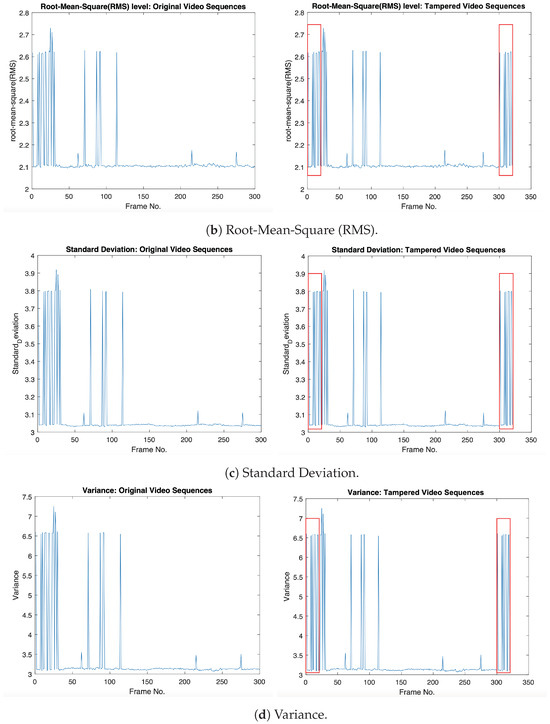
Figure 3. Illustrations of the selected statistical features for the original and forged videos: (1st column) statistical features for the original video; (2nd column) statistical features for the forged video with frame duplication. Original video sequence (akio video) comes from Video Trace Library dataset [19] (where frames from 1 to 20 are copied and then pasted into the frame location from 301 to 320).

The main steps of the proposed method can be seen in Figure 4.

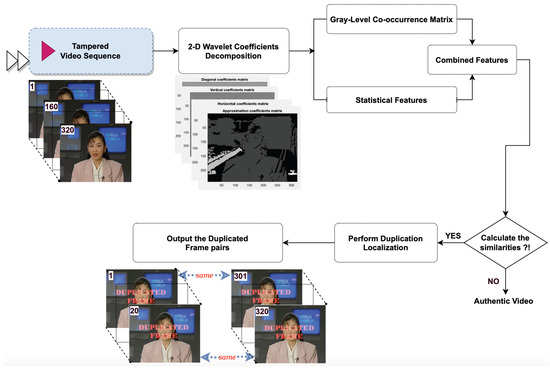
Figure 4. General framework of the proposed method.

3.1. 2-D Wavelet Decomposition

The tensor product of the one-dimensional wavelet and scaling function is usually used to obtain 2-D wavelet decomposition and its scaling function. In 2-D wavelet decomposition, the approximation coefficient matrix at level j is decomposed into four parts: the detail coefficients in three directions (horizontal, vertical, and diagonal), and the approximation coefficient at level j + 1 [20]. Four sub-bands are created at each transformation level in an image that is subjected to the Haar wavelet transformation. The first sub-band represents the input image that has been compressed to half and filtered using a low pass filter (LPF). This sub-band is also called “approximation coefficients matrix cA”. The high pass filter (HPF) is applied on the remaining three sub-bands, which are called “details coefficients matrices” (horizontal “cH”, vertical “cV”, and diagonal “cD”). The size of each sub-band is reduced by half. The LPF is an averaging operator, which contains the useless information, whereas HPF is a differential operator, which contains the detailed information. As shown in Figure 5, the upper left side of the figure contains the approximation coefficients, while the down and right side contain the details coefficients.

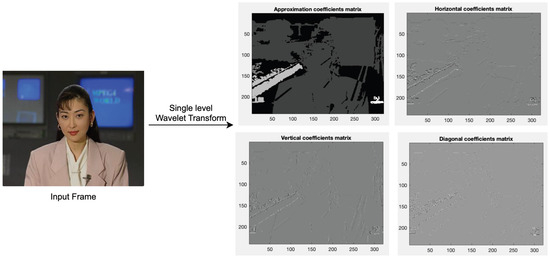
Figure 5. The 2-D wavelet decomposition of an input image into approximation and details sub-bands using single level 2-D DWT.

In the proposed method, we select Haar wavelet transform to apply single-level 2-D discrete wavelet transformation (DWT). Furthermore, DWT offers a distinct and selective representation that effectively quantifies frame texture with a small number of wavelet coefficients and high resolution. The structural differences in frames are well highlighted by the wavelet coefficients. Haar wavelet transform is selected due to the high correlation between the output wavelet bands and the orientation elements in GLCM. Additionally, total pixel entries are usually minimum in the Haar wavelet transformation. Therefore, GLCM computations can be reduced [20,21].

Each frame $F_N$ (N is the total number of frames) in the forged video V is divided into four sub-bands at the single transformation level, as shown in Figure 5. In this paper, we select the approximation coefficient matrix “cA” (low-frequency components) and reject the other detail coefficient matrices “cH”, “cV”, and “cD”. Overall, the Haar wavelet transform is so simple and fast because it is constructed from a square wave [21,22]. The Haar wavelet transform function $\psi \left(t\right)$ and its scaling function $\phi \left(t\right)$ can be expressed using Equations (1) and (2), respectively, as follows:

$$\psi \left(t\right)=\left\{\begin{array}{cc}1,\hfill & 0\le t<\frac{1}{2}\hfill \\ -1,\hfill & \frac{1}{2}\le t<1\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

$$\phi \left(t\right)=\left\{\begin{array}{cc}1,\hfill & 0\le t<1\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(2)

where t is the time variable of the wavelet function.

Furthermore, the Haar wavelet computation contains only the coefficients that do not require a temporary matrix for the multi-level transformations [23]. Consequently, each pixel in each frame can be utilized only one time and there is no overlapping of the pixels during Haar wavelet computations. Generally, these characteristics can be used to minimize the computations of the GLCM in the following step.

3.2. Frame Textural Feature Extraction

The textural features from DWT of each frame ($F_{dwt}\left(N\right)$) in forged video sequences $V_i$ are extracted from two main steps: The Gray-Level Co-occurrence Matrix features step $\left(GLC{M}_{feat}\left(V_i\right)\right)$ and statistical features step $\left(Sta{t}_{feat}\left(V_i\right)\right)$. Then, the extracted features from the two steps are combined together in a matrix $M_{feat}\left(V_i\right)$ to form a feature matrix for each video, as indicated in Equation (3). The combined features in $M_{feat}\left(V_i\right)$ are then sorted for further matching in the next step.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & M_{feat}\left(V_i\right)=GLC{M}_{feat}\left(V_i\right)|Sta{t}_{feat}\left(V_i\right),\hfill \\ \hfill & GLC{M}_{feat}=[Contrast,Correlation,Energy,Homogeneity],\hfill \\ \hfill & Sta{t}_{feat}=[Entropy,RMS,StandardDeviation,Variance]\hfill \end{array}\end{array}$$

(3)

where | denotes the concatenation operation.

The Gray level co-occurrence matrix (GLCM) is a powerful tool for textural analysis [24]. The GLCM matrix is created by computing how a pixel with a gray-level intensity m horizontally exists adjacent to another pixel with an intensity n using the ’Offsets’ parameter, which can be used to specify other pixel spatial relationships (vertically and diagonally). Therefore, each element $(m,n)$ in the GLCM matrix represents the number of times that the pixel with value m occurred horizontally adjacent to a pixel with value n. GLCM has been widely used in a wide range of applications such as pattern recognition and image classification [25,26]. Textural features represent the spatial contextual details of the pixel values in the textured image. Furthermore, GLCM features of similar textures have the same values. Therefore, using GLCM for textural feature analysis will lead to an outstanding performance due to its excellent description and distinction among image textures.

In this paper, four GLCM indicators are selected: textural GLCM-Contrast (CON), GLCM-Correlation (COR), GLCM-Energy (ENG), and GLCM-Homogeneity (HOM).

The textural contrast (gray-level local variations) and correlation (gray-level linear dependency) can be computed using the values of the probability (P) for the changes among gray-levels m and n, as shown in Equations (4) and (5), respectively:

$$CON=\sum _m\sum _n{(m-n)}^k{P}_d{[m,n]}^i$$

(4)

$$COR=\frac{{\sum }_m{\sum }_n\left(mn\right)P(m,n)-{\mu }_x{\mu }_y}{{\sigma }_x{\sigma }_y}$$

(5)

where m and n represent the gray values/coordinates in the co-occurrence matrix. ${\mu }_x$, ${\mu }_y$, ${\sigma }_x$, and ${\sigma }_y$ represent the mean and the standard deviations of x and y, respectively.

Furthermore, we also quantified the textural energy and homogeneity as additional features which supplement the textural contrast and correlation, as expressed in Equations (6) and (7), respectively. The energy (ENG) provides the texture uniformity by calculating the summation of the squared elements in the co-occurrence matrix, which is also known as the angular second moment, and the textural homogeneity (HOM) measures the distribution closeness as follows.

$$ENG=\sum _m\sum _n{\left\{P\right(m,n\left)\right\}}^2$$

(6)

$$HOM=\sum _m\sum _n\frac{1}{1+{(m-n)}^2}P(m,n)$$

(7)

Additionally, Entropy (textural disorder), the Root-Mean-Square level (RMS), Standard deviation, and Variance (heterogeneity) are selected as additional features from each frame $F_{dwt}\left(N\right)$, as expressed in Equations (8)–(11).

$$Entropy=\sum _{i=1}^R\sum _{j=1}^{C}P(i,j)log\left(P\right(i,j\left)\right)$$

(8)

$$RMS=\sqrt{\frac{1}{R\ast C}\sum _{i=1}^R\sum _{j=1}^C{P(i,j)}^2}$$

(9)

$$StandardDeviation=\sqrt{\frac{1}{R\ast C}\sum _{i=1}^R\sum _{j=1}^C{\left|P\right(i,j)-\mu |}^2}$$

(10)

$$Variance=\sum _{i=1}^R\sum _{j=1}^C{(i-\mu )}^{2}P(i,j)$$

(11)

where R, C are the frame dimensions, $\mu$ is the mean of the corresponding frame, and N is the frame number in the forged video sequences.

3.3. Frame Feature Matching

We constructed the combined feature matrix $M_{feat}\left(V_i\right)$ for each video sequence, where each row represents the feature vector of each frame, of which a single frame contains eight features. The matching process between frame features of each video can be performed by calculating the 2-D correlation coefficient between all possible pairs of feature vectors, as expressed in Equation (12).

$$Corr2=\frac{{\sum }_{i=1}^{N-1}{\sum }_{j=i+1}^N(M_{feat}\left(i\right)-{\mu }_i)(M_{feat}\left(j\right)-{\mu }_j)}{\sqrt{\left({\sum }_{i=1}^{N-1}{\sum }_{j=i+1}^N{(M_{feat}\left(i\right)-{\mu }_i)}^2\right)\left({\sum }_{i=1}^{N-1}{\sum }_{j=i+1}^N{(M_{feat}\left(j\right)-{\mu }_j)}^2\right)}}$$

(12)

where $M_{feat}\left(i\right)$ and $M_{feat}\left(j\right)$ are two feature vectors of frames i and j; respectively. ${\mu }_i$ and ${\mu }_j$ are the mean of the feature vectors $M_{feat}\left(i\right)$ and $M_{feat}\left(j\right)$, respectively. N is the total number of frames in the forged video. In the experiments, we set the correlation coefficient threshold to 1.

4. Experimental Results and Analysis

This section discusses the obtained experimental results via the evaluation of the proposed frame duplication forgery detection method for tampered video sequences.

4.1. Dataset Preparation

This subsection describes the two datasets used in the experiments. The main issue with the current video frame duplication forgery detection methods is the lack of digital video forgery datasets. Consequently, we used some existing video sequences datasets which are available online and created our own video sequence forgery datasets. We established two video sequence forgery datasests for frame duplication forgery detection. The first dataset is constructed using the Video Trace Library (ASU) dataset [19] or YUV Video Sequences (http://trace.eas.asu.edu/yuv/index.html accessed on 24 July 2023). This database consists of 24 video sequences of commonly used video sequences in the format 4:2:0 YUV. The resolution of the tampered videos is 352 × 288 pixels and the frame rate is 30 frames per second (fps). The second dataset was selected from the Surrey University Library for the Forensic Analysis (SULFA) dataset [7]. The SULFA dataset contains the original and tampered video sequences and it has about 150 videos captured using three cameras (Canon SX220 from Canon company: Address: 30-2 Shimomaruko 3-chome, Ota-ku, Tokyo 146-8501, Japan; Nikon S3000m from Nikon company: Address: Shinagawa Intercity Tower C, 2-15-3, Konan, Minato-ku, Tokyo 108-6290, Japan; and Fujifilm S2800HD from Fujifilm company: Address: 2274, Hongou, Ebina-shi, Kanagawa 243-0497, Japan), ranging between stationary and moving cameras. The average duration of each video is 10 s. The tampered videos have a resolution of 320 × 240 pixels and a frame rate of 30 fps.

4.2. Implementation Details

All experiments are conducted on Intel Core i7-9700 CPU, 3.0 GHz with RAM 16 GB DDR4 running on a 64-bit Windows operating system. The proposed and comparative methods were implemented using MATLAB R2021a. In the experiments, we set the ‘Offsets’ parameter during GLCM calculations to 0${}^{\circ }$ = $\left[01\right]$.

4.3. Evaluation Metrics

To evaluate the detection performance of the proposed method, we select the measures of $Precision$, $Recall$, and $F1Score$, as expressed in the following formulas:

$$Precision=\frac{TP}{TP+FP}\ast 100\%$$

(13)

$$Recall=\frac{TP}{TP+FN}\ast 100\%$$

(14)

$$F1Score=2\ast \frac{Precision\ast Recall}{Precision+Recall}\ast 100\%$$

(15)

where, TP is the True Positive frame pairs (number of forged frames which are correctly detected as frame duplication). FP is the False Positive frame pairs (number of original frames which are falsely detected as frame duplication). FN is the False Negative frame pairs (number of forged frame pairs which are detected as original frames).

4.4. Visualization Results

Figure 6 and Figure 7 show two examples of the visualization results to better visualize the performance of the proposed method on the two established datasets from the Video Trace Library [19] and SULFA [7] datasets, respectively.

Figure 6. Visualization example for the performance of the proposed approach. Original video sequence ‘$akiyo.avi$’ is taken from Video Trace Library dataset [19], where frames from 1 to 5 are duplicated into frames from 11 to 15.

Figure 7. Visualization example for the performance of the proposed approach. Original video sequence ‘$Video22.avi$’ is taken from SULFA [7], where frames from 1 to 5 are duplicated into frames from 11 to 15.

The proposed approach efficiently detects the duplicated frame pairs in the video sequences as shown in Figure 6 and Figure 7, where frames from 1 to 5 are copied and pasted into the location from 11 to 15 in the same video sequence.

Furthermore, the proposed method can also accurately localize the location of the duplicated frames, as listed in Table 1, for some test video sequences from the Video Trace Library dataset. We notice that the proposed method is capable of accurately localizing the duplicated frame pairs within the tampered video sequences in addition to its high performance detection capabilities.

Table 1. Detection and Localization results for some tampered video sequences from Video Trace Library dataset [19].

		Frame Localization Results
Test Video *	Forgery Location	Wang et al. [10]	Li et al. [12]	Bozkurt et al. [18]	Ours
akiyo.avi	frames 1–20 are copied to 301–320	Authentic video	Original frames 1–20, Duplication 301–320 with 192 false-matched pairs	Original frames 1–20. Duplication 301–320	Original frames 1–20. Duplication 301–320
coastguard.avi	frames 1–20 are copied to 301–320	Authentic video, with 6 false-matched frame pairs	Original frames 1–20, Duplication 301–320	Original frames 1–20. Duplication 301–320	Original frames 1–20, Duplication 301–320
container.avi	frames 1–20 are copied to 301–320	Authentic video	Original frames 1–20, Duplication 301-320 with 39 false-matched frames	Original frames 1–20, Duplication 301–320, with 7 false-matched frame pairs	Original frames 1–20, Duplication 301–320
flower.avi	frames 1–20 are copied to 251–270	Original frames 1–20, Duplication 251–270, with 61 false-matched frame pairs	Original frames 1–20, Duplication 251–270	Original frames 1–20, Duplication 251–270	Original frames 1–20, Duplication 251–270
foreman.avi	frames 1–20 are copied to 301–320	Original frames 1–20, Duplication 301–320, with 17 false-matched frame pairs	Original frames 1–20, Duplication 301–320	Original frames 1–20, Duplication 301–320, with 11 false-matched frame pairs	Original frames 1–20, Duplication 301–320
hall.avi	frames 1–20 are copied to 301–320	Authentic video	Original frames 1–20, Duplication 301–320	Original frames 1–20, Duplication 301–320, with 21 false-matched frame pairs	Original frames 1–20, Duplication 301–320
mobile.avi	frames 1–20 are copied to 301–320	Original frames 1–20, Duplication 301–320, with 407 false-matched frame pairs	Original frames 1–20, Duplication 301–320	Original frames 1–20, Duplication 301–320	Original frames 1–20, Duplication 301–320
mother daughter.avi	frames 1–20 are copied to 301–320	Authentic video	Original frames 1–20, Duplication 301–320, with 57 false-matched frame pairs	Original frames 1–20, Duplication 301–320, with 102 false-matched frame pairs	Original frames 1–20, Duplication 301–320
silent.avi	frames 1–20 are copied to 301–320	Original frames 11–18, Duplication 311–318	Original frames 1–20, Duplication 301–320, with 24 false-matched frame pairs	Original frames 1–16, Duplication 301–316	Original frames 1–20, Duplication 301–320
waterfall.avi	frames 1–20 are copied to 261–280	Original frames 186–190, Duplication 193–197	Original frames 1–20, Duplication 261–280	Original frames 1–12, Duplication 261–272	Original frames 1–20, Duplication 261–280

* The original tested video sequences are taken from Video Trace Library dataset [19].

4.5. Performance Evaluation and Analysis

To evaluate the performance of the proposed approach, we compare the results of the proposed approach with the results of Wang and Farid [10], Lin et al. [11], Li and Huang [12], Singh et al. [13], Yang et al. [15], Fadl et al. [16], Shelke and Kasana [17], and Bozkurt et al. [18]. The measures of Precision, Recall, and F1 score rates are computed for all the tampered videos in the two established datasets, for the proposed method, and for comparing the other SOTA techniques. Table 2 lists the detection capabilities of the proposed approach and other SOTA techniques in terms of Precision, Recall, and F1 score on the Video Trace Library [19] dataset (Dataset 1) and the SULFA [7] dataset (Dataset 2), respectively.

Table 2. The performance evaluation results.

Dataset	Method	Precision (%)	Recall (%)	F1 Score (%)
Dataset 1 *	Wang and Farid [10]	88.90	87.67	88.28
	Lin et al. [11]	92.13	65.42	76.51
	Li and Huang [12]	80.59	96.32	87.80
	Singh et al. [13]	95.64	79.74	86.97
	Yang et al. [15]	96.51	87.30	91.67
	Fadl et al. [16]	97.59	96.93	97.25
	Shelke and Kasana [17]	97.58	94.56	96.05
	Bozkurt et al. [18]	97.33	96.64	96.98
	Ours	99.60	100	99.80
Dataset 2 **	Wang and Farid [10]	50.01	35.87	41.78
	Lin et al. [11]	72.39	39.76	51.33
	Li and Huang [12]	76.18	89.34	82.24
	Singh et al. [13]	82.94	40.00	53.97
	Yang et al. [15]	92.83	53.26	67.69
	Fadl et al. [16]	96.54	95.83	96.18
	Shelke and Kasana [17]	96.82	94.40	95.59
	Bozkurt et al. [18]	95.00	92.94	93.96
	Ours	98.42	96.17	97.28

* Dataset 1 is the established dataset from Video Trace Library dataset [19]. ** Dataset 2 is the established dataset from SULFA dataset [7].

The performance of the proposed approach with eight related methods is compared in Table 2. All of the eight related methods were implemented and tested on our established datasets.

The proposed approach outperforms the SOTA techniques in terms of the robustness against frame duplication forgery. Furthermore, our proposed method exhibits good robustness in terms of the Precision, Recall, and F1 Score rates for the two established datasets.

Overall, we can conclude that the proposed approach is more robust to frame duplication forgery than other comparing methods. Furthermore, the proposed approach is perfect in detecting and localizing frame duplication forgery from digital video sequences.

5. Conclusions and Future Work

This paper presents a frame duplication forgery detection approach for digital video sequences. The first step involves computing the single-level 2-D wavelet decomposition for each frame of the forged video sequences. Then, the textured features are extracted by using the Gray-Level Co-occurrence Matrix (GLCM) and then combined with other statistical features to better represent the features of each frame. The combined features are then matched to filter out the highly similar frames. The combination of GLCM parameters and the other statistical features have proven to display a better performance than only considering the statistical features alone. A comparative analysis with seven existing SOTA frame duplication forgery detection methods is also presentesd. Experimental results demonstrate an overall F1 Score of 99.8% on the Video Trace Library tampered-videos dataset that can efficiently detect frame duplication forgeries for video sequences. Additionally, the proposed approach detects frame duplication forgery operations and fails to detect inter-frame insertion and inter-frame deletion operations. In the future work, we will improve the proposed approach to detect different inter-frame forgery operations such as frame insertion and frame deletion.