A Multi-Faceted Exploration Incorporating Question Difficulty in Knowledge Tracing for English Proficiency Assessment

Abstract

Knowledge tracing (KT) aims to trace a learner’s understanding or achievement of knowledge based on learning history. The surge in online learning systems has intensified the necessity for automated measurement of students’ knowledge states. In particular, in the case of learning in the English proficiency assessment field, such as TOEIC, it is required to model the knowledge states by reflecting on the difficulty of questions. However, previous KT approaches often overly complexify their model structures solely to accommodate difficulty or consider it only for a secondary purpose such as data augmentation, hindering the adaptability of potent and general-purpose models such as Transformers to other cognitive components. Addressing this, we investigate the integration of question difficulty within KT with a potent general-purpose model for application in English proficiency assessment. We conducted empirical studies with three approaches to embed difficulty effectively: (i) reconstructing input features by incorporating difficulty, (ii) predicting difficulty with a multi-task learning objective, and (iii) enhancing the model’s output representations from (i) and (ii). Experiments validate that direct inclusion of difficulty in input features, paired with enriched output representations, consistently amplifies KT performance, underscoring the significance of holistic consideration of difficulty in the KT domain.

1. Introduction

Over recent years, the integration of artificial intelligence (AI) methodologies into educational frameworks has witnessed a substantial increase. The unforeseen educational disruptions caused by the COVID-19 pandemic have further hastened this trend. In this context, intelligent tutoring systems (ITS) have emerged as a focal point in AI-driven educational endeavors. The crux of ITS’s success lies in their capacity to ascertain the present knowledge levels of individual students and subsequently present pertinent questions, leveraging the vast datasets acquired from online learning environments.

The knowledge tracing (KT) task aims to predict future achievement by tracing learners’ current understanding of knowledge based on their past learning history. According to past correct/incorrect answers for each knowledge concept, it is determined to what extent the learner has acquired the knowledge [1]. KT approaches are crucial in contemporary online learning platforms, where they play a vital role in automatically gauging the knowledge levels of numerous students [2]. These platforms strive to enhance learning outcomes significantly by offering personalized feedback and recommendations tailored to each individual [3]. Tracing the user’s knowledge state from the learning perspective is complex enough that numerous factors, such as the question’s difficulty, the order of problem-solving, and the process of forgetting, must be considered [4].

Capturing cognitive relations among the learning materials, such as prerequisite relations, by leveraging a knowledge structure inspired by the existing pedagogical literature [5] can be an alternative to the complexity. For example, the knowledge structure can be regarded as a chain-type directed acyclic graph based on the question difficulty for simplicity. In particular, it is essential to consider the difficulty of questions to track the user’s current knowledge state accurately. Without considering the difficulty of the question, if the user’s knowledge state is estimated only from the distribution of questions answered correctly versus questions responded to, an overestimation problem occurs in the case of difficulty imbalance [6]. Furthermore, difficulty consideration is even more crucial in the field of foreign language learning, such as English proficiency assessment, because subtle differences in difficulty play a significant role in learners acquiring a foreign language.

Figure 1 shows test examples of the Test of English for International Communication (TOEIC). According to the examples, (a) is a question that can be solved within a short time if one knows that the gerund comes after ’after’, whereas (b) is a question that needs to capture subtle meaning differences in context while distinguishing intransitive/transitive verbs. Previous studies for the KT task that utilize the difficulty factor exist. However, they use the difficulty only for secondary purposes for augmenting data or adopt complicated model structures only for the difficulty, reducing versatility [6,7].

Figure 1. Examples of the TOEIC test. Both questions on both sides are 4-choice, but the difficulty level experienced by foreign language learners is actually different. (a) represents a question with a straightforward solution, easily solvable in a brief moment if one is aware of the gerund following ’after.’ Conversely, (b) portrays a question requiring the nuanced interpretation of context, necessitating the differentiation between intransitive and transitive verbs.

Therefore, we explore how to effectively reflect question difficulty in a general-purpose self-attentive KT model by applying various experimental methods, in order to serve as a reference indicator for the experimental aspect of future research. In particular, our methods are verified with a focus on tracing the learner’s knowledge state in the field of English proficiency assessment, which is designed by adequately arranging the difficulty level. The three experimental methods to ensure the model leverages the difficulty effectively are as follows; (i) input feature diversification: feeding difficulty information into the model as variants of input features; (ii) difficulty prediction: having the model predict the question difficulty to enhance understanding of the difficulty of the problem by employing the multi-task learning (MTL) manner; and (iii) representation enrichment: enriching the output representation in the latent vector dimension. In detail, the question sequence is organized in a specific order based on the probability of the correct answer computed from the training data. More complex structures can be readily adopted for the knowledge structure. Moreover, we provide additional analysis regarding the training time and dimensions of the model. The experimental results show that providing difficulty as a training feature and enriching the representation is consistent with performance improvement. In addition, as the learning time and model dimension increase, the gap in the positive effect on performance widens.

2. Related Works

2.1. E-learning and Cybernetic Pedagogy

E-learning, also referred to as electronic learning, is a structured educational system that utilizes electronic resources [8]. Due to information technology (IT) advancements, e-learning has gained widespread acceptance within the education sector, particularly in higher education. Nearly 99% of institutions have implemented learning management systems (LMSs), with approximately 85% actively utilizing them [9]. The recent challenges posed by the COVID-19 pandemic have prompted the expansion of online learning, encompassing diverse modalities such as intelligent tutoring systems and massive open online courses, all of which have become crucial in mitigating disruptions to the field of education [10,11].

In order to improve understanding of e-learning systems, it is necessary to describe existing research in the field of cybernetic pedagogy, a fundamental theory that explains the human learning process. The authors in [12] developed a cybernetic pedagogy that was based on natural sciences, and [13] set the cybernetic foundations for learning and teaching. Cybernetic pedagogy, which is a scientific discipline of how a learning process can be influenced, leads to significant updates and is a useful basis for modern intelligent learning environments.

In the realm of cybernetic pedagogy, the foundational premises encompass:

• The delineation and examination of instructional and learning trajectories manifest in subsidiary systems, and their role in rendering the educational procedure objective. This entails the transition of all undertakings from human-operated domains to technological infrastructures or software applications.
• Scrutiny of the interconnections and consequential impacts between objective (technological) and subjective (human) components of the educational mechanism, such as appraising the interplay between a human educator and digital instructional resources with an aim to fulfill established pedagogical objectives.
• Elucidation of the ties amongst varying forms of subsidiary systems within a specified educational framework.

Within the academic sphere of online intelligent education, a learning process can be technologically manifested as an intelligent tutoring system. In this context, it necessitates the incorporation of a pedagogic algorithm, explicitly articulated through symbolic representations grounded in mathematical logic. This algorithm takes into consideration five conditional variables: L (learning material), M (media), P (psychological structure), S (social structure), and Z (setting learning goals). In other words, the learning process can be systematically represented as an integrative educational model, amalgamating all the previously mentioned components into a cohesive entity [12,14].

From an e-learning perspective, the teacher, students, learning process, and the organization of lessons collectively constitute a distinct subsystem within an educational system [15]. Considering that an e-learning system is an information system that combines human elements (such as learners and instructors) with non-human components (such as learning management systems), it is essential to explore various aspects of success concerning both of these components [16]. Since the spread of e-learning, research has been conducted on various aspects. Traditionally, earlier studies placed greater emphasis on the technology itself. However, with the growing reliability and accessibility of technology, contemporary research has increasingly centered on understanding the attitudes and interactions of both students and instructors, recognizing their pivotal roles in e-learning’s success [17,18].

2.2. Various Branches in Knowledge Tracing

The knowledge tracing (KT) task, which models the human cognitive process, encompasses concepts such as the knowledge concept, knowledge state, and interaction. A knowledge concept refers to a specific concept to which a question belongs, akin to a skill class. For instance, in the English education domain, knowledge concepts can consist of grammar, reading comprehension, and vocabulary. Knowledge state is an evaluative measure of a learner’s grasp and acquisition of knowledge concepts based on prior learning records. In addition, interaction in the KT task refers to a set of questions a user solves during a specific period, along with the outcomes for the questions.

A KT task is a long-standing task that has been studied since before the era when deep learning was prevalent, and the approach has branched into various streams based on perspectives on how to model human cognition. Before the advent of deep learning, the most conventional methodology was Bayesian knowledge tracing (BKT), which draws inspiration from mastery learning in educational psychology, representing a learner’s KS as binary latent variables [1]. Building upon the methodology of BKT, subsequent research has expanded the tracing techniques by introducing features such as difficulty, cognitive factors, and multiple knowledge concepts into KT models [19,20,21]. The initial deep learning-based methodology is deep knowledge tracing (DKT), which departs from analyzing users and extracting static features, instead utilizing problem-solving response records (correct/incorrect responses to questions) as sequential data within a recurrent neural network framework to predict the probability of correct answers for unseen questions [22]. However, there is a problem in that the learning state is stored as a single hidden state without distinction for a specific concept, and the interpretability for individual students needs to be improved.

Inspired by the DKT model, various deep learning-based studies have emerged, such as attentive KT models and memory-augmented KT models [4]. Zhang et al. [20] introduced the dynamic key-value memory networks for KT, which model the knowledge state for individual students using key matrix-value matrix pairs with the concept of human memory. In addition, research to improve the tracing ability by advancing the model structure has emerged, including self-attention-based KT studies. Pandey and Karypis [23] applied the self-attention mechanism for the first time in a KT task. This approach benefits the generalization to sparse data where only a few students interact with a given knowledge concept by assigning attention weights to the concept that are related to previously answered questions. In order to capture the relation between questions and answers even when prior learning records are limited, Somepalli et al. [24] constructed the embedding of questions as input for the encoder and the embedding of responses (interactions) as input for the decoder. By extending this approach, Shin et al. [25] further expanded the type of considered factors, including the temporal information, such as the time taken to solve the problem, resulting in enhanced model performance.

2.3. Question Difficulty in Knowledge Tracing

The question difficulty that we focus on is an essential factor to model the human learning process, not only within KT tasks but also to the extent that other downstream tasks that solely predict the question difficulty exist [26,27,28]. Utilizing the difficulty levels associated with given questions and knowledge concepts plays a crucial role in tracking students’ knowledge states. This is because questions in the assessment cannot be of the same difficulty level, and the proper question distribution based on the question difficulty is important during test design [29,30]. Furthermore, without consideration of difficulty during the learning process, KT-based application tasks may prove challenging. For instance, in the student learning curricula, receiving only excessively challenging problems relative to students’ level can diminish the desire to achieve, whereas consistently encountering overly simple problems might lead to reduced interest [31,32].

Among KT studies, there have been attempts to modify the model with the difficulty factor or deliberately exploit it as a training feature. For example, [6] designed a model structure for computing user knowledge acquisition, including the difficulty. In detail, the subjective difficulty that students perceive in the question is measured before the actual evaluation and used for initialization. After the evaluation, the student’s knowledge states are updated based on the newly obtained difficulty level. Lee et al. [7] adopted a question replacement strategy according to the difficulty in terms of data augmentation. It is assumed that if a learner cannot solve a particular question, he or she will not be able to solve a more difficult question, and conversely, if they can solve it, they will be able to solve a more manageable problem.

However, the existing studies either build a complex model structure only for considering the difficulty factor or use difficulty only as a secondary factor, which hinders application to pre-trained language models (PLMs) with general-purpose yet powerful performance. It is necessary to explore how to dissolve desired features properly, i.e., difficulty factors based on a general-purpose model such as the already existing Transformers structure. Therefore, this study focuses on exploring methods enabling self-attention-based models to leverage the difficulty factor effectively.

3. Materials and Methods

We introduce the following three approaches to allow the model to effectively leverage the difficulty factor: (i) feeding the variants of input features with difficulty to the model; (ii) learning the model using the MTL method, while adding an objective to predict the difficulty; and (iii) enriching the representation including the difficulty information output in the latent vector dimension through phases (i) and (ii). Figure 2 illustrates the overall structure of the model to which our exploration methods are applied, and the Transformers model with an encoder–decoder structure that shows good performance in the KT task is used as the base model, following Shin et al. [25]. In the original SAINT+ model, question and part information is fed into the encoder module, and correctness and temporal information (i.e., elapsed time, lag time) are fed into the decoder module. However, unlike the original SAINT+ model’s input structure, which is the baseline, we modify the input structure to account for the difficulty factor.

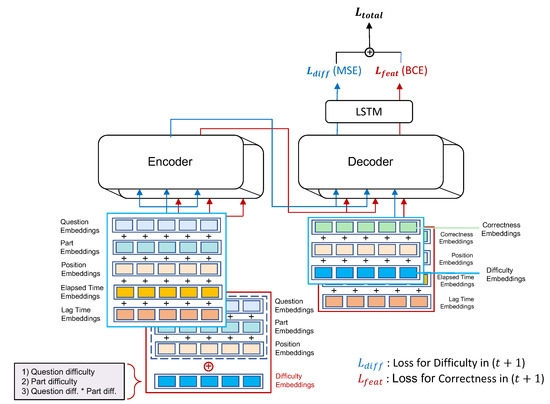
Figure 2. Overview of our methods for knowledge tracing with a difficulty factor. diff.indicates difficulty (e.g., question diff., etc.).

3.1. Notations and KT Task Statement

Let us first elaborate on the basic denotations for the KT task. We denote the user set as $\mathrm{U}=\{u_1,u_2,\dots ,u_{\left|\mathrm{U}\right|}\}$ with $\left|\mathrm{U}\right|$ different users, and the question set as $Q=\{q_1,q_2,\dots ,q_{\left|Q\right|}\}$ with $\left|Q\right|$ unique questions. A user’s learning interactions (i.e., previous learning history) are denoted as $X=\{(q_1,r_1),(q_2,r_2),\dots ,(q_{\left|X\right|},r_{\left|X\right|})\}$, where each interaction $x_t$ consists of ($q_t$, $r_t$), a tuple of question and response correctness at time t. $q_t$ is the question answered at time step t and $r_t$ is the corresponding response correctness label. In other words, $r_t$ is 1 when the response is correct and 0 otherwise.

The KT task is formulated for predicting the probability of a student’s answer to a particular question being correct given their previous interaction histories. Therefore, the KT task aims to estimate the probability,

$$\mathrm{P}[r_t=1|x_1,x_2,\dots ,x_{t-1},q_t].$$

(1)

3.2. Input Features Diversification

First, to diversify the input features through difficulty information, the difficulty is computed based on learners’ response accuracy and provided together as input. Each input of the encoder and decoder is reconstructed, including configured difficulty embedding. Difficulty information is composed of question difficulty, part difficulty, or question difficulty weighted by a relevant part weight. The red boxes and lines in the bottom left of Figure 2 indicate the input features fed into the model. In particular, followed by Shin et al. [25]’s input structure, part information is included along with the question in the encoder part, and the obtained difficulty vector is concatenated together and provided as input.

3.2.1. Question Difficulty

The question difficulty level is computed through distributional knowledge estimated based on response correctness information for a specific question. In other words, when constructing the difficulty vector, the individual difficulty D calculated based on $r_t$, which is the correct answer to question $q_t$, is used and can be formalized as follows:

$$D=\sum _i^{|{\mathrm{U}}_i|}\frac{\{r_{ij}==1\}}{|{\mathrm{U}}_i|}·p_k,$$

(2)

where ${\mathrm{U}}_i$ is a set of users who answer the question $q_j$, and $r_{ij}$ is the i-th user’s response correctness corresponding to the j-th question. In addition, $p_k$ is a k-th component from P, a set of weights for each part relevant to a specific problem q, and fixed to 1 if not used as a weight. When $p_k$ is used as a weight, P is a set of heuristically defined weights or part difficulties, and the method for obtaining it is described below.

3.2.2. Part Difficulty

Part difficulty p is calculated through distributional knowledge for each part instead of estimating the distribution for individual questions. In other words, the difficulty is obtained based on the corresponding part for each question, and the formula is calculated based on the response correctness r, in the same way as the question difficulty.

3.2.3. Question Difficulty Weighted by Part

A weighted question difficulty set is obtained by multiplying the weight for each part by the already calculated question difficulty. The type of weight set is divided into two cases. The first is ‘Heuristic’, which consists in setting the ratio fixedly according to the part. In particular, the English proficiency evaluation is divided into several parts, and although it may differ depending on the question, there is actually a more difficult part. In the case of TOEIC, in reading comprehension, part 7, which infers problems through reading long sentences, is more complicated than part 5, which consists of vocabulary and grammar problems such as idioms that can be solved quickly through memorization. In listening comprehension, part 4, where the questions should be answered by listening to a long monologue such as a phone recording, is more difficult than part 1, which one must match sentences describing the situation by looking at pictures. Part 3 is usually the most difficult of the parts, as the conversation between multiple speakers should be understood, and the details grasped. Therefore, based on this difficulty tendency for parts, pre-defined weights are multiplied according to the part to which the question belongs. The second case is ‘Distribution’, where the difficulty is calculated through the aggregation of the question difficulty and the part difficulty. As described above, the part difficulty set is calculated through distribution according to the correct answer rate for each part.

For the training objective, since the goal is to predict response correctness $r_{t+1}\in \{0,1\}$ for $q_{t+1}$, binary cross-entropy (BCE) loss is employed. The objective is formulated as follows:

$${\mathcal{L}}_{feat}=-\frac{1}{\left|Q\right|}\sum _1^{\left|Q\right|}{r}_j\ast log\left({\widehat{r}}_j\right)+(1-r_j)\ast log(1-{\widehat{r}}_j),$$

(3)

where ${\widehat{r}}_j$ is the correctness predicted by the model for the j-th question $q_j$.

3.3. Difficulty Prediction

We introduce a training objective that allows the model to predict the difficulty level of question $q_{t+1}$ at time $t+1$, where response correctness must be predicted, verifying its effectiveness. In other words, by training the model in an MTL manner, we allow the model to learn information related to difficulty directly. The blue boxes and lines in Figure 2 indicate input features employed for MTL. For the model to effectively predict the difficulty, the question, part, and temporal data are input into the encoder part, and the correct answer and difficulty data are used as input features of the decoder.

The difficulty feature is a vector composed of float-type labels, i.e., continuous distribution knowledge. Therefore, we compute the average of the squared differences between actual difficulty values and predicted difficulty values by adopting the mean squared error (MSE) loss. It is trained by utilizing the objective as follows:

$${\mathcal{L}}_{diff}=-\frac{1}{\left|Q\right|}\sum _1^{\left|Q\right|}{({\widehat{D}}_j-D_j)}^2,$$

(4)

where $D_j$ and ${\widehat{D}}_j$ are the actual difficulty and the difficulty value predicted by the model, respectively. The entire MTL model is trained as a joint loss between the loss ${\mathcal{L}}_{feat}$ (Section 3.2) of the model having the input structure including the difficulty feature and the loss ${\mathcal{L}}_{diff}$ of the model predicting the difficulty as follows: ${\mathcal{L}}_{total}={\lambda }_1·{\mathcal{L}}_{feat}+{\lambda }_2·{\mathcal{L}}_{diff}$.

3.4. Representation Enrichment

This section explores how to enhance the quality of representations that reflect the difficulty factor output through Section 3.2 and Section 3.3. Since the user’s learning history information has a sequential data structure, we enrich the pooler output from the decoder of the backbone model by using an additional layer that can deal with these characteristics well. In detail, the output representation is improved by passing the vector from the Transformer model into the LSTM [33] before being fed to the linear layer for label classification.

4. Experiments

4.1. Experimental Setup

The hyperparameters for the experiments are detailed in Appendix A.

4.1.1. Dataset

As a dataset for our experiments, we experimented with actual user learning assessment data from TOEIC, a representative English language education assessment. The EdNet dataset is a comprehensive resource that captures various aspects of student actions in an intelligent tutoring system (ITS) [34]. It encompasses a vast scale, with over 131 million interactions from more than 780,000 students since 2017. This dataset provides a diverse range of interactions, including learning materials consumption, responses, and time spent on tasks. It also offers a hierarchical structure, categorizing data points into four levels based on the complexity of actions. The EdNet dataset has multiple versions, and the EdNet-KT1 version is used in this experiment. Statistical information about EdNet-KT1 data is shown in Table 1. We divided the data into train, validation, and test sets in a ratio of 8 to 1 to 1 and used them in the experiment.

Table 1. Statistics of EdNet-KT1 dataset.

	EdNet KT1
# of students	784,309
# of interactions	224,461,772
# of KCs	188
# of unique questions	12,284
# of correct answers	152,561,335
# of wrong answers	71,900,437

4.1.2. Metrics

We utilized the accuracy (ACC) score as the evaluation metric. ACC, widely employed in classification tasks as an evaluation metric, can be defined as the ratio of correctly classified data instances to the total number of observations. In addition, we calculated the area under the receiver operating characteristic curve (AUC), which is frequently adopted for binary classification for discriminating between positive and negative target classes. AUC represents the degree or measure of separability, telling us to what extent is the model capable of distinguishing between classes [35]. Our experimental performance measurement recorded the average value of performance calculated from five random seeds.

4.2. Experimental Results

Table 2 shows the experimental results of the model with the diversified input by considering the difficulty factor as a feature, the model trained in an MTL manner by adding the difficulty prediction objective, and the model with representation enrichment.

Table 2. Main results for EdNet-KT1 dataset. * indicates our re-implementation version. The highest performance is bolded.

Method	AUC	ACC
SAINT+ * [25]	79.23	73.78
+ Part Diff.	79.28 (+0.05)	73.81 (+0.03)
+ Question Diff. (dist.)	79.33 (+0.10)	73.84 (+0.07)
+ Question Diff. * Part Wgt. (dist.)	79.29 (+0.06)	73.83 (+0.05)
+ Question Diff. * Part Wgt. (heuristic)	79.34 (+0.11)	73.85 (+0.07)
+ Diff. Prediction (0.5)	79.30 (+0.07)	73.84 (+0.06)
+ Diff. Prediction (0.3)	79.34 (+0.11)	73.86 (+0.08)
+ Diff. Prediction (0.3) —  CE	79.15 (−0.08)	73.72 (−0.06)
+ Question Diff. (dist.) + LSTM	79.43 (+0.20)	73.89 (+0.11)
+ Diff. Prediction (0.5) + LSTM	79.19 (−0.04)	73.71 (−0.07)
+ Diff. Prediction (0.3) + LSTM	79.36 (+0.13)	73.85 (+0.07)

In the feature diversification part, providing difficulty in the question unit tends to yield better overall performance than providing part difficulty. It was observed that the additional consideration of the weight for each part also affected the performance, but this was marginal. The model trained with the MTL method performed slightly better when ${\mathcal{L}}_{diff}$ was 0.3 than when it was 0.5, achieving an improvement of 0.11%p in AUC and 0.08%p in ACC compared to the baseline. In addition, when replacing the type of loss for the learning objective that predicts difficulty with cross-entropy (CE) loss rather than the MSE loss presented earlier, we observed that performance actually decreased. In the representation enrichment part, the model with the question difficulty feature and the representation enhancement improved by 0.2%p in AUC and 0.11%p in ACC, indicating that enriching the representation by considering the sequential characteristic of the users’ learning history data leads to performance improvement.

In previous KT studies, the SAKT model [23], which introduced self-attention into the KT task, achieved a 0.25%p improvement in AUC from 76.38 to 76.63 and a 0.13%p improvement in ACC from 70.60 to 70.73, compared to the initial deep learning-based KT model [22]. Therefore, this study can interpret the AUC score improvement in the main results by integrating the difficulty factor in the same self-attentive model structure as significant.

5. Discussion

5.1. Efficacy based on Training Time and Model Dimension

In this section, we verify whether training a self-attentive model considering the difficulty factor ensures consistent performance improvement, regardless of the increase in training time and model dimensions, and Figure 3 illustrates the performance comparison (the table with detailed experimental results is provided in Appendix A). In detail, we experimented by varying the number of epochs from 10 to 20 and the model dimension from 128 to 256. The baseline, SAINT+ [25] with a model dimension of 128, was trained for ten epochs. Both increasing the model dimension and the number of epochs contributed to performance improvement, but the increase in epochs had a more significant impact. In other words, it was observed that performance improved as the training time for students’ interaction records lengthened, and also, the performance continuously increased in each epoch until the 20th epoch.

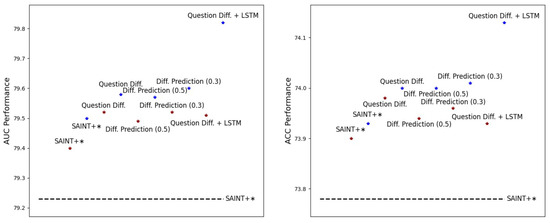
Figure 3. Performance comparison according to the number of training epochs and the model dimension for the EdNet-KT1 dataset. * indicates our re-implementation version. 🟉 models set with the model dimension as 256 and the number of epochs as 10. 🟉 models set with the model dimension as 128 and the number of epochs as 20.

In particular, the model with the Question Diff. + LSTM methods, which showed the most substantial improvement in the main results (Table 2) by 0.2%p of AUC, showed an improvement of 0.32%p of AUC compared to the SAINT+ model, which was trained for 20 epochs, showing a more significant increase than in the main experiment. Thus, this larger performance gap indicates that providing a difficulty factor positively impacts KT task, regardless of training hyperparameters such as training time.

5.2. Comparative Results on the Composition of Difficulty Values

Since the main focus of this study is the appropriate integration of difficulty into deep learning models, how to finely adjust the value of the initially estimated difficulty factor is a significant issue. Therefore, this section analyzes the results of experiments, providing variants for these values.

Variations on constructing the question difficulty vector as distributional information or rank information were provided to the model. Rank information is provided after being converted in a sorted order according to the size of the estimated distribution value. Distribution information estimated based on response correctness (Equation (2) in Section 3.2) consists of two cases. One is to express the difficulty level with a higher number as it is more difficult in the real world, and the other is to indicate that the higher the number, the easier it is (i.e., inverse).

According to the results in Table 3, when the difficulty information was given similarly to reality, where the value is larger when a specific question is harder (dist. inverse), the performance of 0.11%p of AUC and 0.07%p of ACC improved. Additionally, in the case of the dist. round method, which consists of rounding the computed difficulty level to the first decimal place, the score slightly decreased. In particular, we observed that when we gave the difficulty vector for questions as a rank, the performance dropped by a large margin, implying that how one adjusts the value of the difficulty factor is also significant.

Table 3. Performance comparison according to the difficulty value types. * indicates our re-implementation version.

Difficulty Type	AUC	ACC
SAINT+ * [25]	79.23	73.78
+ Question Diff. (dist.)	79.33 (+0.10)	73.84 (+0.07)
+ Question Diff. (dist. inverse)	79.34 (+0.11)	73.85 (+0.08)
+ Question Diff. (dist. round)	79.16 (−0.07)	73.74 (−0.04)
+ Question Diff. (rank)	75.87 (−3.36)	71.41 (−2.37)

6. Conclusions

In English language learning assessment, accounting for difficulty is pivotal to understanding human learning trajectories. However, prior work in the KT task domain has often incorporated difficulty factors through intricate model architectures without delving into broader applications. Such methods sometimes grapple with integrating new information effectively while preserving an already successful general-purpose model architecture.

In this paper, we foreground a nuanced approach to incorporate difficulty metrics derived from users’ historical interactions. We systematically investigate three strategies: (i) input feature diversification, wherein difficulty is treated as a variant of input features, (ii) difficulty prediction, which tasks the model with predicting item difficulty via a multi-task learning (MTL) framework, and (iii) representation enrichment, aiming to augment the latent space.

Our empirical findings indicate that embedding difficulty as a training feature offers tangible performance gains. While the MTL strategy’s impact remains subtle, the strategy involving representation enrichment using an additional LSTM layer emerges as the most effective. Our supplemental analyses concerning training duration and model dimensions further corroborate these findings. Notably, as training time and model dimensions increase, the performance benefits of integrating the difficulty factor become more pronounced, suggesting its positive influence on model training dynamics. In addition, according to the analysis of KT performance changes depending on the difficulty factor’s value, a positive performance difference can be observed when selecting an appropriate value type, such as providing reverse order distribution knowledge.

Limitations and Future Works

The question difficulty is calculated based on the users’ past interactions, so there are still challenges regarding the natural language information of questions. In real-world learning and assessment procedures, humans utilize textual information, namely natural language information, within problem statements, to gauge the difficulty of questions. However, in the KT field, there have yet to be publicly available datasets containing natural language information as a form of textual data, which is a significant obstacle to the higher quality of difficulty estimation. Some studies with exercise-aware methods utilize natural language information from questions [36]. However, these are conducted using proprietary corporate data and remain publicly inaccessible.

In the computer education domain, based on code examples written by users, there has recently been a study that generated codes that can be implemented according to the user’s knowledge level [37]. Nonetheless, within the realm of education, the uniqueness of each learning domain—spanning subjects such as English, computer science, mathematics, and even secondary languages like Spanish—requires sufficient domain-specific data.

In particular, in English language assessment, only a few companies possessing commercial assessment systems hold valuable data, and natural language information is still not easily used by individual researchers. Therefore, we plan to adopt the natural language information released as a form of non-textual data of accessible benchmarks. For example, among the available KT datasets, the EEDI dataset [38] provides some samples of learning questions in the form of images. We may exploit the natural language information in the images through optical character recognition techniques in order to improve the difficulty representation capability.

Appendix A.1. Hyperparameters

We defaulted the hyperparameters to the same as the SAINT+ model [25]. The learning rate was 0.001, batch size was 512, dropout was 0.1, the number of epochs was 10, sequence length was 100, and the Noam scheduler [39] and Adam optimizer [40] were employed. The ratios for joint loss with multitask learning were ${\lambda }_1$ and ${\lambda }_2$, respectively, and the ${\lambda }_2$ for the difficulty prediction task ${\mathcal{L}}_{diff}$ was set as 0.3 or 0.5.

Appendix A.2. Detailed Results

Table A1. Performance comparison according to the number of training epochs and the model dimension for EdNet-KT1 dataset. * indicates our re-implementation version. The highest performance is bolded.

Method	Model dim.	Epoch	AUC	ACC
SAINT+ *	128	10	79.23	73.78
SAINT+ *	256	10	79.40	73.90
	128	20	79.50	73.93
+ Question Diff.	256	10	79.52	73.98
	128	20	79.58	74.00
+ Diff. Prediction (0.5)	256	10	79.49	73.94
	128	20	79.57	74.00
+ Diff. Prediction (0.3)	256	10	79.52	73.96
	128	20	79.60	74.01
+ Question Diff. + LSTM	256	10	79.51	73.93
	128	20	79.82	74.13

Table A1. Performance comparison according to the number of training epochs and the model dimension for EdNet-KT1 dataset. * indicates our re-implementation version. The highest performance is bolded.

Method	Model dim.	Epoch	AUC	ACC
SAINT+ *	128	10	79.23	73.78
SAINT+ *	256	10	79.40	73.90
	128	20	79.50	73.93
+ Question Diff.	256	10	79.52	73.98
	128	20	79.58	74.00
+ Diff. Prediction (0.5)	256	10	79.49	73.94
	128	20	79.57	74.00
+ Diff. Prediction (0.3)	256	10	79.52	73.96
	128	20	79.60	74.01
+ Question Diff. + LSTM	256	10	79.51	73.93
	128	20	79.82	74.13