Robust Blind Image Watermarking Using Coefficient Differences of Medium Frequency between Inter-Blocks

Abstract

The existing discrete cosine transform (DCT) differential quantization robust watermarking has poor robustness against JPEG compression, cropping, and combined attacks. To improve such issues, a pair of adjacent block coefficients are selected to reduce the offset and improve the robustness of the watermarking. Firstly, at adjacent positions of neighboring blocks, the differences of medium frequency coefficients are calculated, and then the differences are used to divide regions. Experimental results show that this method is more robust to various attacks than the existing DCT differential quantization robust watermarking. The accuracy of watermark extraction under a JPEG compression attack increased by 2%, while the error rates of watermark extraction under a cropping attack and a combination attack decreased by 4.4% and 9%.

1. Introduction

The promotion of digitization spreads multimedia widely, which inevitably leads to the problem of copyright infringement. Compared with other copyright protection objects, digital images spread rapidly in the network and are more vulnerable to attacks. The types of attacks can be divided into malicious attacks, such as cropping and rotation, and inevitably non-malicious attacks, such as noise and compression. Effective technologies are needed to resist these attacks. Therefore, digital watermarking has been invented to effectively protect the security of digital images, accurately locate the area of malicious tampering, and resist attacks.

The quality of watermarking mainly depends on its robustness, vulnerability, capacity, and imperceptibility [1,2]. Digital watermarking can be divided into two main categories according to embedding methods: spatial domain watermarking [3,4,5,6,7] and frequency domain watermarking [8,9,10,11,12,13,14,15,16,17,18]. The former is to embed a watermark directly into the host image pixels, and the most classic algorithm is the LSB (least significant bit) method [19,20,21,22,23,24]. Although this technique has lower computational complexity and higher image quality, it has poor robustness and it is vulnerable to attacks. Frequency domain watermarking is mainly designed to improve the robustness of watermarking, where modifying a single coefficient in the spatial domain brings about changes in all pixels corresponding to an image block [25,26,27,28,29,30,31,32,33,34,35,36,37]. The host image is transformed through the use of SVD (Singular Value Decomposition), IWT (Integer Wavelet Transform), DCT, etc. [10,11,12,13,14,15,16,17].

SVD is divided into quantization index modulation (QIM) and relative modulation (RM), but it cannot fully extract the embedding watermark, for there is information loss after the transform. Hu et al. [10] proposed a hybrid modulation, integrating QIM and RM, to completely extract the watermark without attacks. The advantage is that the watermark can be recovered well when the JPEG and cropping attacks are less than 25%. The disadvantages are that the embedding process is complicated, and the time complexity is high. The image quality evaluated using the peak signal-to-noise ratio (PSNR) is 38.5 dB, which is lower than the acceptable value of 40 dB [2].

IWT divides a signal into four frequency subbands. Low-frequency subbands contain abundant information, where the information embedding will reduce the image quality. High-frequency subbands contain less information, but information embedding will lead to poor robustness. Therefore, researchers have put forward a series of hybrid transform-based methods [11,12,13]. Salehnia et al. [11] combined LWT and SVD to improve the incomplete watermark extraction of SVD and the poor robustness of WT (wavelet transforms). They embedded the watermark into three subbands of the first-level LWT. This method reduces the extraction error rate and improves the robustness under the attacks of JPEG, noise, and cropping. To further improve the robustness, Sinhal et al. [12] performed DCT on the low-frequency subbands after a wavelet transform, embedded information into DCT coefficients, and applied a neural network to accelerate the embedding speed. It has higher robustness under JPEG and noise attacks, but the PSNR is less than 40 dB. The methods based on DCT inter-block coefficient difference [14,15,16,17] effectively guarantee a PSNR greater than 40 dB and improve robustness under compression and hybrid attacks. Both SVD-based and WT-based methods have their own disadvantages: (1) An SVD-based method cannot extract a watermark accurately without attacks; (2) WT-based methods divide the subbands into low, medium, and high frequencies. When the watermark is embedded in low frequency, PSNR is not ideal, and the robustness is weak in medium and high frequency.

DCT-based watermarking is superior to other methods in terms of accuracy, imperceptibility, and robustness. The method, based on the DCT inter-block coefficient difference, can effectively ensure imperceptibility and increase robustness against compression and hybrid attacks. The literature [14,15,16,17] uses the method of quantizing DCT inter-block coefficient difference to embed watermarks, but the selected coefficients and quantized regions can be further optimized and improve the robustness.

The rest of the paper is organized as follows. Section 2 describes the state of the art of the existing schemes and the improvement idea of our scheme. Section 3 illustrates our method in detail. Section 4 gives the experimental results and comparisons to prove the effectiveness and superiority of our scheme. Section 5 concludes this paper.

2. Related Work

DCT can be performed on the entire image or used on selected blocks. The matrix after DCT is shown in Figure 1, the first coefficient in the upper left corner of the matrix is a DC coefficient, and the others are AC coefficients. The matrix is divided into three parts in zig-zag order: low, medium, and high frequency. The low frequency contains the main information of the image and has the greatest impact on the image, while the high frequency contains a small amount of image information and has little impact on the image. Therefore, considering the balance of robustness and imperceptibility, the watermark is generally embedded into the medium frequency coefficients.

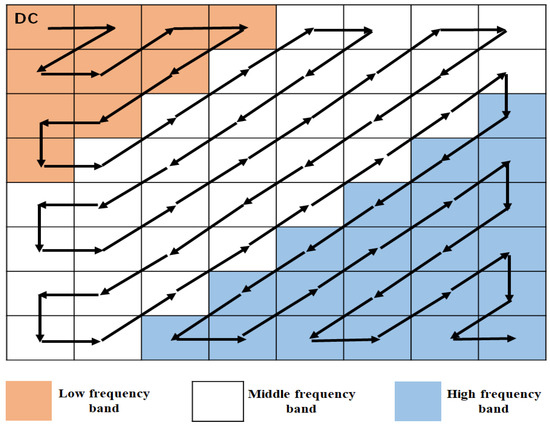
Figure 1. Zig-zag ordering for DCT coefficients.

Das et al. [14] proposed a watermarking scheme based on the correlation of coefficients between DCT blocks. According to a predefined threshold, they changed only one coefficient in each block. The scheme is robust in terms of JPEG compression and common image attacks. For a 512 × 512 cover image, the watermark is limited to 64 × 63 because some blocks on the boundary cannot be used for embedding. To solve the limitation of the watermark size, Parah et al. [15] proposed embedding the watermark by using the DCT coefficient difference of adjacent blocks. The method is to select and use the intermediate frequency coefficients of two adjacent rows to divide the difference into five regions. However, this scheme only considers the left-to-right (LR) relationship of adjacent blocks and ignores the normal adjacent relationship and up-to-down (UD) relationship. Although it improves robustness under mixed attacks, it performs poorly in single attacks and PSNR. The method proposed by Hjk et al. [16] considered the left–right–up–down relationship of the image, and improved the inter-block relationship of the scheme [15]. The PSNR is increased to 41.3 dB, and it better resists rotation and cropping attacks. However, there are still problems in the selection and quantitative segmentation of DCT inter-block coefficients, and the robustness and PSNR are not optimal due to the inappropriate setting of region partition and threshold offset. The robust watermark proposed by Kamili et al. [17] also adopt the method based on DCT inter-block coefficients. While comprehensively taking into account the LR and UD adjacencies, they improved the rationality of DCT coefficient division and raised PSNR to 42 dB. The NC value is still higher than 0.76 under a 75% cropping attack, and it is basically 1 under JPEG compression. Nevertheless, the DCT coefficient partitioning in [17] has not been further optimized, and no experiments related to the combined attacks have been carried out.

Generally speaking, the current scheme based on the DCT inter-block coefficient has the following limitations.

(1)

Iteratively modifying a coefficient will increase the error rate and affect the accuracy of watermark extraction under JPEG compression,

(2)

In the case of combined attacks, the error rate of extracted watermarks is too high,

(3)

The partitioning and offset selection is inappropriate and does not balance robustness and imperceptibility.

To push the limit of existing methods, aiming at problems (1) and (2), in this paper, two adjacent medium-frequency coefficients are iteratively modified to eliminate the interaction between the parameters, thus improving robustness under JPEG compression and hybrid attacks. Aiming at problems (2) and (3), the partition and offset are selected appropriately to better balance the robustness and image quality and thus improve the error rate after joint attack. In the third chapter of the proposed methods, a detailed description will be given of the intermediate-frequency coefficients, offset intervals, and iteration process selected for this experiment.

3. Proposed Method

The proposed embedding method is based on the DCT coefficient differences. The watermark is embedded according to the predefined rules and the difference offsets. The watermark is extracted according to the region where the differences are located.

This paper compares the deficiencies of previous methods and puts forward some selection rules in terms of inter-block adjacency, difference regions, and offset coefficients.

Selection of inter-block adjacency: The adjacency used in [14] is UD, where each DCT block is the block in the next row. The selected adjacency in [15] is LR and RL (right to left), and the selection of a UD block is used for the connecting part of two rows; please refer to the location indicated by RD and LD in Figure 2. The selected adjacencies in [16] are LR, UD, RL, and DU (down to up), as shown in Figure 3. A 16 × 16 block is divided into four 8×8 sub-blocks to fully consider the correlation between image blocks. The rules of adjacency selection used in this paper also follow the rules in [16].

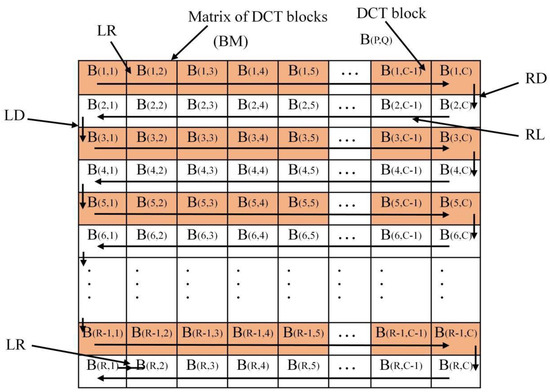
Figure 2. Arrangement of DCT blocks 1.

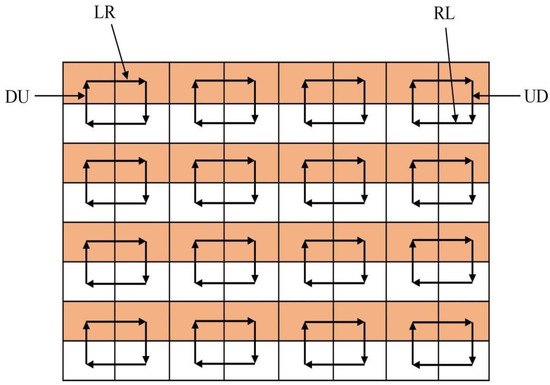
Figure 3. Arrangement of DCT blocks2.

Selection of difference regions: The difference partition in [15,16] is set to five regions; watermark bits are embedded in different regions. It can be concluded that Region 3 is not used for embedding. The difference between the coefficients of the same position of adjacent blocks is very small. Thus, most of the difference is within Region 3. This means that all differences need to be modified, and increasing the number and amount of difference offsets will reduce the robustness of the watermark. As a result, the proposed method reduces the difference regions to four, and embeds watermark bits into Region 1, 3 and Region 2, 4, which can reduce the number and the value of offsets and improve the robustness of the watermarking. The rule of partitioning is shown in Figure 4.

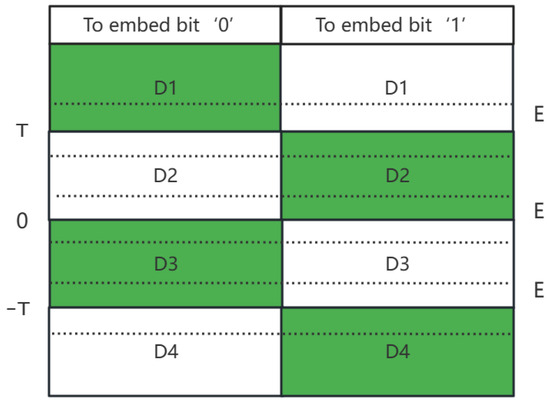
Figure 4. Modification of coefficient for embedding a watermark bit.

Selection of offset coefficients: Adjacent blocks in [15,16] are selected as separate medium-frequency coefficients, which will inevitably cause the iterative influence of coefficient offset in watermark embedding, increase the reference coefficient offset and offset amplitude, and also affect the robustness and imperceptibility of the watermarking scheme. In this paper, two adjacent coefficients in the same block are selected as the correction and the reference coefficients, respectively, so as to eliminate the influence caused by iterative offset coefficients and improve the robustness.

3.1. Embedding Process

Step1: subtract the original image pixel value by 128, and limit the pixel size to the range of $[-128,128]$.

Step2: Divide the image size of H × W into 8 × 8 non-overlapping blocks.

Step3: Perform DCT on each 8 × 8 block, and denote the block matrix as ${\mathrm{B}}_{\mathrm{P},\mathrm{Q}}$, where P, Q represents the position of the block in the image.

Step4: Find the four relationships from LR, RD (rightmost to down), RL, DU according to the selection rule of inter-block adjacency, $\mathrm{C}$ is the next block of ${\mathrm{B}}_{\mathrm{P},\mathrm{Q}}$.

LR:$\mathrm{C}=$ RD:$\mathrm{C}=$ RL:$\mathrm{C}={\mathrm{B}}_{\mathrm{P},\mathrm{Q}-1}$ DU:$\mathrm{C}={\mathrm{B}}_{\mathrm{P}-1,\mathrm{Q}}$

Step5: Calculate the difference between adjacent blocks by Equation (1).

$$\mathrm{Diff}={\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)-\mathrm{C}\left({\mathrm{x}}_2,{\mathrm{y}}_2\right)$$

(1)

Step6: Calculate the difference by ${\mathrm{B}}_{\mathrm{P},\mathrm{Q}}$. The DC, $\mathrm{M}\mathrm{e}\mathrm{d}\left({\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\right)$ is the median value of the first nine low-frequency zig-zag-ordered AC coefficients. The scale factor to calculate the difference each time of the offset M(${\mathrm{B}}_{\mathrm{P},\mathrm{Q}}$) is found by using Equation (2).

$$\mathrm{M}\left({\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\right)=\mathrm{abs}\left(\mathrm{Z}\times \frac{\mathrm{DC}\left({\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\right)-\mathrm{Med}\left({\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\right)}{\mathrm{DC}\left({\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\right)}\right)$$

(2)

Step7: Embed the binary watermark map into the difference according to the corresponding position, and iterate the offset by the offset. After each offset, the diff is recalculated by using Equations (3) and (4).

Embedding bit.

$$0\left\{\begin{array}{c}{\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)+\mathrm{M}\left({\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\right)\hspace{1em}\hspace{1em}\frac{\mathrm{T}}{2}\le \mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\le \mathrm{T}+\mathrm{E}\hfill \\ {\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)-\mathrm{M}\left({\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\right)\hspace{1em}\hspace{1em}-\mathrm{E}\le \mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\le \frac{\mathrm{T}}{2}\hfill \\ {\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)+\mathrm{M}\left({\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\right)\hspace{1em}\hspace{1em}\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\le -\mathrm{T}+\mathrm{E}\hfill \end{array}\right.$$

(3)

Embedding bit.

$$1\left\{\begin{array}{c}{\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)-\mathrm{M}\left({\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\right)\hspace{1em}\hspace{1em}\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\le \mathrm{T}-\mathrm{E}\hfill \\ {\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)+\mathrm{M}\left({\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\right)\hspace{1em}\hspace{1em}-\mathrm{T}/2\le \mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\le \mathrm{E}\hfill \\ {\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\left({\mathrm{x}}_1,{\mathrm{y}}_1\right)-\mathrm{M}\left({\mathrm{B}}_{\mathrm{P},\mathrm{Q}}\right)\hspace{1em}\hspace{1em}\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\le -\mathrm{T}/2\hfill \end{array}\right.$$

(4)

Step8: Generate all the image blocks by using step4 to step7.

Step9: Perform inverse DCT operation on all blocks; all pixels are added by 128 to generate a watermark image.

For the overall embedding framework of the watermark, the overall steps are shown in the following Figure 5: I represents the original image, W represents the binary watermark image, and I’ represents the embedded watermark image. The quantization and encryption methods used for embedding have been discussed in the previous text.

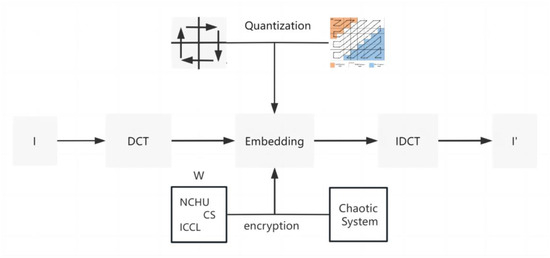
Figure 5. Watermark embedding flowchart.

3.2. Extraction Process

Step1: Subtract the original image pixel value by 128, and the pixel size is limited to the range of −128 to 128.

Step2: Divide the H × W size image into 8 × 8 non-overlapping blocks.

Step3: Perform DCT on each 8 × 8 block, denote the block matrix as ${\mathrm{B}}_{\mathrm{P},\mathrm{Q}}$, where P, Q represents the position of the block in the image.

Step4: According to the selection rule of inter-block adjacency, find the four relationships from LR, RD, RL, DU. $\mathrm{C}$ is the next block of ${\mathrm{B}}_{\mathrm{P},\mathrm{Q}}$.

Step5: Calculate the difference between adjacent blocks, extract the watermark according to the partition threshold T, difference region 1, 3 extract watermark bits0, difference region 2, 4 extract watermark bits1.

3.3. Embedding and Extraction of Color Image Watermark

In this experiment, the RGB color channels are divided into three planes, namely R, G, and B. Each plane is regarded as a separate gray scale image, and the watermark is embedded into each plane separately. In the RGB channels, we use the same key and binary watermark.

4. Experimental Results

This experiment tests the robustness and imperceptibility of watermarking by various attacks. Figure 5 shows the original images and the watermarked images, which are labelled as the Lena, Airplane, and Peppers images. The size of each original image is 512 × 512 and the binary watermark is 64 × 64.

Mean square error (MSE) is used to calculate the difference between the original image and the watermark image. PSNR is used to evaluate the quality of the watermark image. Normalized correlation (NC) and bit error rate (BER) are used as the measures of accuracy for the binary watermark extracted from the watermarked image. The definitions of PSNR, NC, and BER are as follows:

PSNR: This is the most important and commonly used image quality assessment. If $\mathrm{I}$ denotes the original image and ${\mathrm{I}}_{\mathrm{w}}$ denotes the watermarked image, the PSNR is defined by Equation (5).

$$\mathrm{PSNR}=10{\log }_{10}\frac{{255}^2}{\mathrm{MSE}}$$

(5)

MSE is defined in Equation (6).

$$\mathrm{MSE}=\sum _{\mathrm{i}=1}^{\mathrm{W}}\sum _{\mathrm{j}=1}^{\mathrm{H}}\left[{\left(\mathrm{I}(\mathrm{i},\mathrm{j})-{\mathrm{I}}_{\mathrm{w}}(\mathrm{i},\mathrm{j})\right)}^2\right]$$

(6)

where $\mathrm{W}$ and $\mathrm{H}$ are the width and height of the image, respectively, $\mathrm{I}(\mathrm{i},\mathrm{j})$ are the original pixel values, and ${\mathrm{I}}_{\mathrm{w}}\left(\mathrm{i},\mathrm{j}\right)$ are the original pixel values. MSE indicates the difference between the original image and the watermarked image, and the PSNR value evaluates the imperceptibility of the watermarked image, so MSE is as small as possible and PSNR is as large as possible.

NC: This is used to evaluate the watermark. NC is defined in Equation (7).

$$\mathrm{NC}=\frac{{\sum }_{\mathrm{i}}{\sum }_{\mathrm{j}}\left(\mathrm{W}{\left(\mathrm{i},\mathrm{j}\right)\times \mathrm{W}}_{\mathrm{x}}\left(\mathrm{i},\mathrm{j}\right)\right)}{{\sum }_{\mathrm{i}}{\sum }_{\mathrm{j}}\left({\mathrm{W}(\mathrm{i},\mathrm{j})}^2\right)}$$

(7)

where $\mathrm{W}$ is the watermarked image, ${\mathrm{W}}_{\mathrm{x}}$ is the image that the watermark is extracted from, and (i,j) is the position of the watermark pixels in the image. Larger NC values indicate that the extracted watermark is more similar to the original watermark, which means the robustness is higher.

BER: This is defined as the ratio of the number of erroneous watermark bits to the total number of embedded bits. The lower the BER, the more robust the watermark is to attacks. The BER is defined in Equation (8).

$$\mathrm{BER}=\left[\sum _{\mathrm{j}=1}^{\mathrm{n}}\mathrm{B}\left(\mathrm{j}\right)\oplus {\mathrm{B}}_{\mathrm{x}}\left(\mathrm{j}\right)\right]\times 100$$

(8)

where n is the total number of embedded watermarked bits, $\mathrm{B}\left(\mathrm{j}\right)$ is the original watermarked bits, and ${\mathrm{B}}_{\mathrm{x}}\left(\mathrm{j}\right)$ is the extracted watermark bits.

In this experiment, the tests of payload, imperceptibility, and robustness are performed on different gray and color images. The scheme is compared with existing DCT inter-block difference watermarking, and the results show that the scheme outperforms existing watermarking techniques in terms of imperceptibility and robustness. In addition, it is able to provide high-quality watermarked images.

4.1. Non-Attack Watermark Extraction

Different offsets E have various effects on the imperceptibility and robustness of the image. Figure 6a shows the effect of the offset from E = 5 to E = 20 on the PSNR.

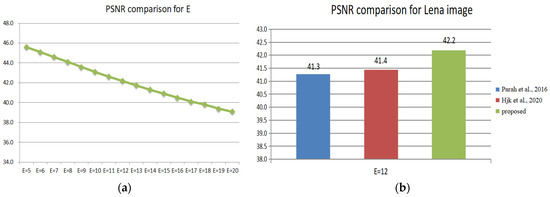
Figure 6. PSNR comparison of Lena watermark images under different values of E. (a) PSNR under different values of E using proposed method; (b) PSNR under different methods using the same values of E [15,16].

Figure 6b is used to compare the imperceptibility of the present experimental method with the two current methods based on the difference between DCT blocks, and it can be clearly seen that the proposed method and the methods of [15,16] are accurate when extracting the watermark without attacks. The imperceptibility of the proposed method is higher than that in [15,16] when the offset E = 12. For this, two coefficients are chosen to eliminate the effect of iteration to improve the image quality and increase the robustness. However, in the following experiments, to achieve the best balance between imperceptibility and robustness, E = 14 is used in single and hybrid attacks. In order to compare with the methods of [15,16] under as similar conditions as possible, the E value of JPEG compression attack is changed to 20.

The I, I′, and W′ in Figure 7 represent the original image, watermark image, extracted binary watermark, and corresponding PSNR, NC, and BER, respectively. It indicates that the watermark can be extracted losslessly without attack.

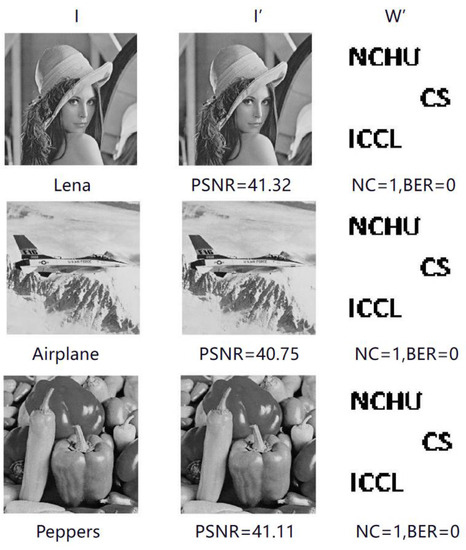
Figure 7. PSNR experimental results.

4.2. Robustness Analysis after a Single Attack

In this section, single attacks such as cropping, JPEG, noise, histogram equalization, and sharpening are performed on the watermarked image to test the robustness and whether the watermark can be extracted under the attacks.

4.2.1. Watermark Extraction after Crop Attack

Figure 8 shows an image with a 10% crop in the center; the BER of the extracted watermark is 1.03%. Figure 8 shows the Lena image with 25% cropping of the image (in different regions: top left, top right, bottom left, bottom right) with an average BER of 2.40%. It also shows the Lena image with 50% bottom crop and a BER of 4.71% for the extracted watermark. The results of the cropping attack experiments show that the method can extract the watermark under a cropping attack, and the robustness of the proposed method is compared with robustness under a cropping attack (Lena image) proposed in schemes [15,16] and shown in Figure 9; the proposed method has a lower BER of about 36% compared to scheme [15] and about 4.4% compared to scheme [16].

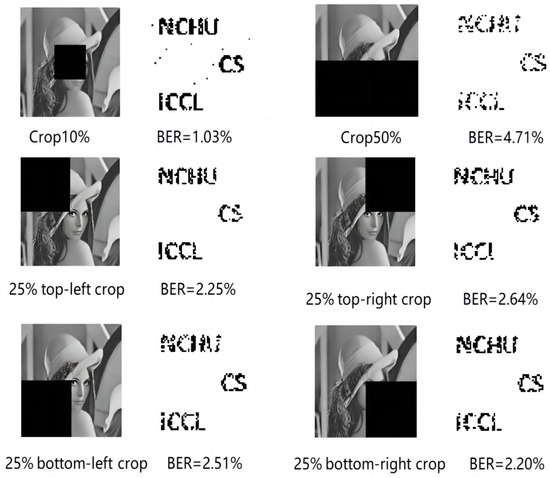
Figure 8. Cropped Lena images in six different regions.

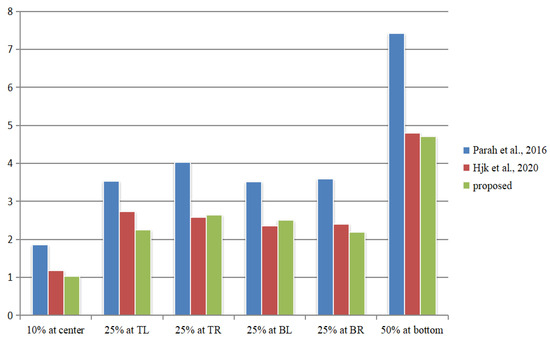
Figure 9. BER comparison of different cropping methods [15,16].

4.2.2. Watermark Extraction after JPEG Attack

JPEG is a standard compression technique used to minimize image storage requirements and to reduce the bandwidth required for transmission. In our work, we use JPEG compression for the watermarked Lena image with different quality factors (Q = 90 to 40). In methods [15,16], they have changed the offset threshold E = 12 to E = 20 in the process of embedding in order to increase the robustness under JPEG attack and reduce the invisibility of the watermarked image. Our experiment also performs a JPEG attack with E = 20 and outperforms the previous schemes in terms of PSNR, NC, and BER. As Figure 10 shows, when the JPEG compression quality factor Q is at 90 to 60, the proposed scheme can extract binary watermarking without loss with NC = 1 and BER = 0. As shown in Figure 11, our method can still extract watermarks when the Q values are 50 and 40.

Figure 10. After JPEG compression (Q = 90 − 60) and extracted watermarks.

Figure 11. After JPEG compression (Q = 50 − 40) and extracted watermarks.

Table 1 shows that the proposed scheme can extract the watermark accurately when the quality factor Q is from 60 to 90, while [15,16] cannot extract it with a minor JPEG compression of Q = 90 and Q = 70. In addition, ref. [17] extracts the watermark accurately with Q from 90 to 70, but the NC values are lower than the proposed scheme with Q = 60 to 40.

Table 1. NC Comparisons under JPEG compression with various QF.

QF	[15]	[16]	[17]	This Program
90	0.9770	0.9845	1	1
80	NA	NA	1	1
70	0.9767	0.9819	1	1
60	NA	NA	0.9998	1
50	NA	NA	0.9914	0.9995
40	NA	NA	0.9098	0.9789

4.2.3. Watermark Extraction after Noise and Other Attacks

The proposed method was tested via noise addition, sharpening, histogram equalization, and median filtering. The detailed results for the various attacks are listed as shown in Figure 12.

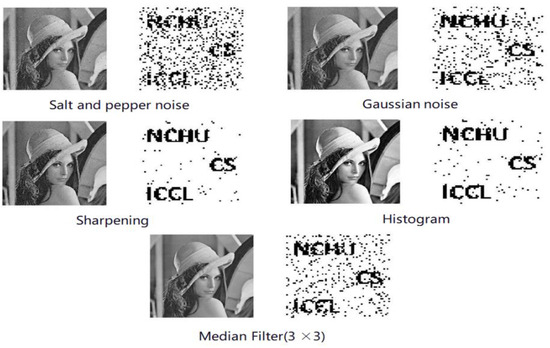
Figure 12. Comparisons for a variety of attacks.

Salt and Pepper noise: The watermarked image is affected by salt and pepper noise with noise density = 0.01.

Gaussian noise: After adding Gaussian noise 0.001 with zero mean and variance.

Sharpening: The watermarked Lena image after sharpening.

Histogram equalization: The watermarked Lena image after histogram equalization.

Median filtering: The Lena image with the extracted watermark is filtered using a median filter of size 3 × 3.

The comparison of the experimental results is shown in Figure 13 and Table 2, which indicates that the proposed method is generally better than those in the literature [15,16]. The comprehensive watermarking performance of this experimental method after a single attack is higher than that of [15,16], with a 3.9% improvement in BER and 16% improvement in PSNR compared to scheme [15] after a single attack, and a slight improvement in BER and PSNR compared to scheme [16] after a single attack.

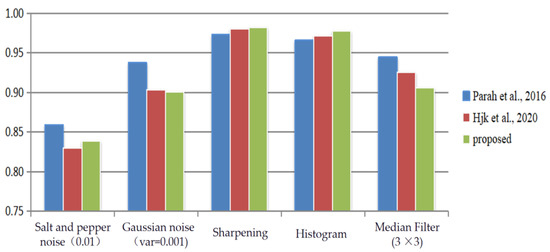
Figure 13. NC comparisons for a variety of attacks [15,16].

Table 2. Comparisons after noise and other attacks.

Schemes		[15]			[16]		Proposed
Attack	NC	PSNR	BER	NC	PSNR	BER	NC	PSNR	BER
Salt and pepper noise (0.01)	0.8589	24.9	15.6	0.8299	25.36	17.06	0.8390	25.24	16.48
Gaussian noise (var = 0.001)	0.9375	20.69	8.66	0.9035	20.69	9.98	0.9006	29.67	9.74
Median Filter (3 × 3)	0.9445	33.52	9.95	0.9258	37.18	7.64	0.9060	35.08	9.30
Sharpening	0.9731	25.69	2.98	0.9807	30.03	1.92	0.9822	25.34	1.76
Histogram	0.9665	11	3.87	0.9716	18.8	2.97	0.9779	19.11	2.17

4.3. Robustness Analysis after Combined Attacks

This proposed method is robust not only against a single attack but also against 2–3 hybrid attacks. The experimental results under six mixed attacks are shown in Figure 14 and Figure 15. It can be seen that BER is greatly improved compared to scheme [15], with a combined improvement of 9%.

Figure 14. BER comparison with various combined attacks. (a): salt and pepper noise and median filter; (b) histogram equalization, sharpening and scaling; (c) histogram equalization and scaling; (d) degree rotation and crop by 25% on the left; (e) 5-degree rotation, 25% crop on the upper left, and histogram equalization; (f) 5-degree rotation, upper left 25% crop, and sharpening.

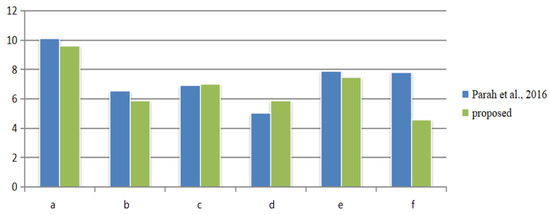
Figure 15. BER comparison with various combined attacks. (a): salt and pepper noise and median filter; (b) histogram equalization, sharpening and scaling; (c) histogram equalization and scaling; (d) degree rotation and crop by 25% on the left; (e) 5-degree rotation, 25% crop on the upper left, and histogram equalization; (f) 5-degree rotation, upper left 25% crop, and sharpening [15].

5. Conclusions

A robust watermarking method based on DCT inter-block coefficient difference is proposed in this paper. A pair of coefficients in an 8 × 8 DCT block is selected, and the coefficients are slightly changed and offset to a prescribed interval by the adjacent inter-block relations. The proposed method improves the accuracy and robustness of watermarking, which is mainly reflected in the following four aspects. Under the crop attack, BER is about 36% better than [15] and about 4.4% better than [16]. Under JPEG compression above QF = 60, the scheme extracts the watermark accurately and BER = 0. Under the hybrid attack, the average BER is about 9% better than [15]. Under the attacks of noise, histogram equalization, sharpening, and median filter, BER, in comparison with the literature [15], is increased by 3.9%, and the PSNR is increased by 16%, which is also slightly higher than [16]. From the above experimental data, it can be concluded that our scheme has better robustness compared with the existing DCT differential quantization robust watermarking schemes. The existing scheme only targets traditional robust attacks, and the subsequent research on the method’s resistance to adversarial attacks will be based on [38,39].