Abstract
For the fully resonant wireless power transfer (WPT) system, the high coupling of the converter and the resonant network introduced many problems, such as frequency splitting, the power curve peak limit, and the strict switch strategy. To solve these problems, this paper proposed a new six-switch topology based on the full–-bridge converter. With the unique structures containing two capacitor-isolated switches and a source-isolated diode, the system decouples the converter and the resonant network, and its modes have been decoupled, called the independent power injection and free resonance WPT (IPIFR–WPT) system. The capacitor-isolated switches and the source-isolated diode make the converter operate only when the voltage on the primary capacitor is equal to the source voltage, and the source will be isolated by the diode when the capacitor voltage is great than the source, which provides a wide time margin for the switches of the converter to turn on in advance. In this margin, the operation point is self-determined the same whenever the switches turn on so that the system’s performance is consistent. Based on this characteristic, the system can self-adapt a dynamic change in system parameters, with at least 15% tolerance for the coupling coefficient and 14% for the load resistance.
1. Introduction
Wireless power transfer (WPT) technology uses electromagnetic fields for contactless power transfer [1]. Because there is no direct physical connection, it has higher security and better flexibility than traditional wired power transfer [2]. Therefore, WPT technology has developed very fast in recent years, especially on movable and rotatable devices, such as robots, electric vehicles, underwater devices, portable applications and implantable medical equipment [3,4,5,6,7].
The fully resonant wireless power transfer (FR–WPT) system has attracted the widest research in recent decades [8]. Due to the high coupling of the converter and the compensation network, FR–WPT systems really require the converter’s switching frequency to be equal to the fixed frequency of the resonant network to achieve stable and efficient operation. Since the converter is fully coupled with the resonant network, the FR–WPT system has faced some issues, such as the power peak limit, the parameter change sensitivity, frequency splitting, and so on [9,10,11]. To solve these issues, some closed-loop strategies including impedance matching and frequency tracking are proposed to improve the dynamic performance and ensure the system’s stable operation [12,13,14,15]. However, due to the limitation of the system’s structure, the closed-loop strategy is limited by the power peak limit. Furthermore, because of the frequency splitting phenomenon, it is easy to fall into local solutions and even make the system unstable, causing irreversible damage to the device [16].
The independent power injection and free resonance wireless power transfer (IPIFR–WPT) system uses a novel and unique topology structure that separates the switching converters from the resonant tanks [17,18]. The characteristic of this circuit structure is that the power injection process and the free resonance process are independent so that the converter and the resonance network are completely decoupled. In the IPIFR–WPT system, the power injection process is completely controlled independently, and the free resonance is also completely independent. This control strategy’s advantage is isolating the converter from the system and making the resonant network conduct passive-free resonance. Therefore, the frequencies of the converter and the resonant network are different, decoupling the resonant network and the converter, and simplifying the power control strategy [19]. At the same time, the operating frequency of the resonant network is also free to adapt to the influence of the change in the working parameters because it does not have to be affected by the operation of the converter, which solves the issues of frequency splitting and frequency tracking in the system.
Article [20] proposes a pulsed power injection IPIFR–WPT system. The principle is mainly to control the power injected into the coil inductance by controlling the turn-on time of the switch S1. However, the system requires precise control for switch S2, and its switching times must be strictly aligned with the zero crossing point of the resonant current. Otherwise, the soft switching condition will not be satisfied. This shortcoming causes strong adhesion between the converter and the resonance network, fails to achieve complete decoupling, has high requirements for the accuracy of the control system, is sensitive to parameter changes, and needs better dynamic performance. Article [21] proposes a full-bridge IPIFR–WPT system with six switches. The switches are used to periodically connect or isolate the resonant capacitor and the DC power supply into or out of the system to achieve power injection and free resonant mode switching. The single-switch IPIFR–WPT system uses only one switch to control mode switching, greatly reducing system switching losses and improving system efficiency [22,23]. The energy of the injection system can be adjusted by controlling the turn-on time of the switch to achieve the regulation of power, but the injection time cannot be too large. Furthermore, it is necessary to ensure that the current flowing through the primary inductor can be less than zero during the resonance process. Therefore, there is a theoretical power peak for the single-switch IPIFR–WPT system, which means the system cannot achieve wide-range power regulation.
Furthermore, a comparison of the technologies to improve the dynamic performance of the WPT system is summarized in Table 1. Normally, for the impedance matching method, a lot of components are used to adjust the equivalent input impedance [14]. Hence, the impedance matching method leads to the higher cost and larger size of the system. Moreover, the actual dynamic performance is discrete and approximate. Articles [15,16] use different frequency tracking methods to improve dynamic performance and eliminate frequency splitting. However, the high sensibility to the parameters needs precise design. Article [20] changes the structure of the converters to achieve the decoupling between the converter and the compensation network. However, the decoupling is incomplete, and the system is sensitive to the parameters.

Table 1.
Comparison of the technologies to improve dynamic performance.
In this paper, based on the traditional bridge circuit, a six-switch IPIFR–WPT system is proposed. Its unique capacitor-isolated switches and power-source-isolated diode mean the power supply and parallel resonant capacitor can be periodically connected or isolated from the system. When the power supply is connected to the system and the resonant capacitor is isolated, it is in the power injection mode. The longer the power injection mode duration, the more power is injected into the system. When the resonant capacitor is connected to the system and the power supply is isolated, the resonant network will use the energy stored in the inductance and capacitor to conduct free resonance. The resonant frequency is the fixed frequency of the resonant network and does not need to be controlled by the switches. Therefore, the six-switch IPIFR–WPT system realizes the mode decoupling of power injection and free resonance and the decoupling of the converter and resonant network. In addition, due to the source-isolated diode, the power supply can only inject energy into the system in one direction. Thus, the switches have been turned on in advance to ensure that the power supply will not be connected to the system in advance, only when the voltage on the primary resonant capacitor drops to equal the power supply voltage, and the leading time range is relatively wide, which is called the soft switching margin. At the same time, the parasitic diode on the switch can ensure the zero voltage switching (ZVS) condition.
2. Circuit Structure and Mode Analysis
2.1. Circuit Structure and Mode Analysis
The prototype of the six-switch IPIFR–WPT system is shown in Figure 1. In Figure 1, a unidirectional power supply comprises an isolation diode D0 and a DC power supply Edc. The purpose of a one-way power supply is to ensure that energy entering the system does not return to the power supply. Switches S1–S4 form a full-bridge converter to connect power Edc to the system and inject energy into the system. Switches S5 and S6 let the primary compensation capacitor Cp be isolated from or connected to the system. Diodes D1–D6 are the bypass diodes of switches S1–S6, wherein bypass diodes D1–D4 do not function during the entire working process due to their different directions from isolation diode D0; the bypass diodes D5 and D6 are used for continuous current conduction during the resonance process and can isolate Cp from the system. The self-inductances of the primary and secondary coils are Lp and Ls, while M is the mutual inductance of the coils. Rp and Rs are the parasitic resistance of the primary and secondary coils, respectively. The load R0 consumes the energy received by the secondary circuit after being rectified by the back-end rectifying circuit of the secondary circuit. Supposing the inductive characteristics and the voltage drop of the back-end rectifier circuit are ignored, in that case, the equivalent load RL can be used to convert the load resistance R0 to the input terminal of the rectifier circuit, and the conversion relationship is as follows:
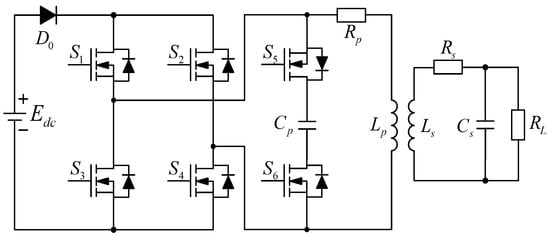
Figure 1.
The topology of the six-switch IPIFR system.
Figure 2 is the schematic diagrams of the operation modes of the six-switch IPIFR–WPT system. When the system operates, there are eight operating modes. Mode 1 connects the power supply Edc to the system in a forward direction, a forward power injection mode. Modes 2–4 are resonant modes, also called free resonance processes, due to the isolation of the power supply Edc from the system. Note that Modes 2 and 4 are transitional modes, both of which are unidirectional resonance processes. According to the symmetry of the full-bridge converter operation, Mode 5 reversely connects the power supply Edc to the system as a reverse power injection mode. Furthermore, Modes 6–8 are resonant processes opposite to the working processes of Modes 2–4.
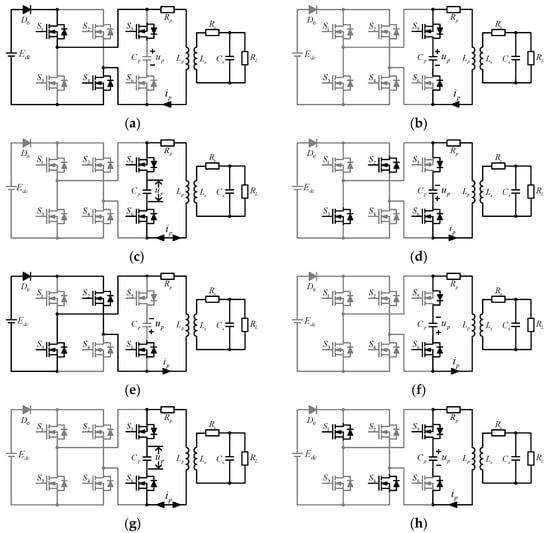
Figure 2.
The operation mode diagram of the six-switch IPIFR–WPT system: (a) Mode 1, (b) Mode 2, (c) Mode 3, (d) Mode 4, (e) Mode 5, (f) Mode 6, (g) Mode 7, and (h) Mode 8.
Figure 3 shows the waveform diagram of the source current i1, the primary capacitor voltage up, and the primary inductor current ip of the six-switch IPIFR–WPT system under steady-state operation. According to Figure 2 and Figure 3, the operation modes of the six-switch IPIFR–WPT system can be analyzed as follows:
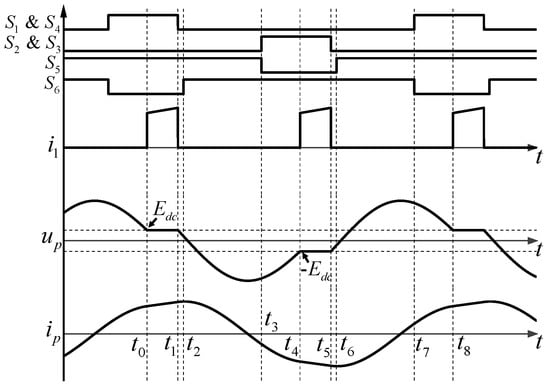
Figure 3.
The steady-state operation waves of the six-switch IPIFR–WPT system.
Mode 1 [t0, t1]: This is a forward power injection mode with a duration of ξ1 = t1–t0. Before the time t0, the switches S1 and S4 have been turned on in advance, and the switches S2 and S3 remain turned off. At this time, the primary capacitor voltage up is greater than Edc, forcing D0 to be turned off, isolating the power supply Edc from the system, thereby preventing the energy from being injected into the system. Until the time t0, the voltage up drops to equal to Edc, causing diode D0 to turn on, and the current ip flows from the branch D6–Cp–S5 to the switches S1 and S4 that have been turned on in advance. During the period [t0, t1], while the primary capacitor Cp is isolated from the system, the DC power supply Edc directly injects energy into the primary inductor Lp.
Mode 2 [t1, t2]: This is a transitional mode of the first free resonance process. At the moment t1, the switches S1 and S4 turn off, and at the same time, the current ip will continuously conduct through the bypass diode D6. At this time, the turning off of switches S1 and S4 meets the ZVS condition. In Mode 2, the primary inductor Lp and the primary compensation capacitor Cp form a resonant cavity and begin passive free resonance. The duration of Mode 2 is very short and can generally be taken as 1–2 μs, even a few hundred nanoseconds.
Mode 3 [t2, t3]: This is a bidirectional free resonant mode. Since the switch S6 turns on at t2, the primary current ip can achieve bidirectional free resonance in the resonant network Lp–Cp. During Mode 3, after the value of the current ip resonates to less than zero, the flow direction of ip in the branch is S5–Cp–S6. After that, at time t3, the switch S5 turns off, and the current ip can still continuously conduct through the bypass diode D5. The switch S5 turns off to meet the ZVS condition. At the same time, at t3, the switches S2 and S3 turn on. Due to the capacitance voltage up being less than −Edc at this time, the isolation diode cannot be turned on, and the current cannot be exchanged from the branch D5–Cp–S6 to the switches S2 and S3. That is, before and after the turn-on of S2 and S3, the current flowing through them is zero, satisfying the zero current switching (ZCS) condition.
Mode 4 [t3, t4]: In this mode, the system remains in a state of free resonance. In addition, the current ip continuously conducts through the branch D5–Cp–S6 during the time span until the time of t4, when the value of up rises to equal to −Edc through resonance. At time t4, because the switches S2 and S3 have turned on in advance at t3, the current ip can be naturally switched from the branch D5–Cp–S6 to the switches S2 and S3, thereby switching to Mode 5.
Mode 5 [t4, t5]: This is a reverse power injection mode, which is reversed with Mode 1. Due to the natural commutation of the current ip from the branch D5–Cp–S6 to the switches S2 and S3 that have turned on before t4, the power supply Edc is reversely connected to the system and injects energy into the primary inductor Lp.
Mode 6 [t5, t6]: This is a transitional mode of the second free resonance process, which is symmetric to Mode 2 and has a short duration. At time t5, the switches S2 and S3 turn off. Since the current ip will be continuously conducted through the bypass diode D5, turning off switches S2 and S3 meets the ZVS condition. In Mode 6, the primary inductor Lp and the primary compensation capacitor Cp form a resonant network and begin free resonance.
Mode 7 [t6, t7]: This is a bidirectional free resonant mode symmetric to Mode 3. At t6, the switch S5 turns on. Due to the capacitance voltage up greater than Edc, the current ip continuously conduct through the bypass diode D5 without commutation to S1 and S4. Therefore, the turn-on of switch S5 satisfies the ZVS condition. Then the primary current ip can achieve bidirectional free resonance in the resonant network Lp–Cp during [t6, t7].
Mode 8 [t7, t8]: This is a transitional mode symmetric to Mode 4. At t7, switch S6 turns off while turning on switches S1 and S4. Because of the voltage up being greater than Edc, D0 is turned off, and the current ip continuously conducts through D6 without commutation to S1 and S4. Therefore, S6 meets the ZVS condition, while the opening of S1 and S4 satisfies the ZCS condition. The resonant network maintains resonance during [t7, t8]. Until t8, the voltage up is equal to Edc, and the current ip naturally commutates from the resonant network to S1 and S4. Meanwhile, the system operates into Mode 1.
2.2. Calculation of System Soft Switching Operating Point
Based on the mode analysis of the six-switch IPIFR–WPT system in the previous section, the switching conditions for its eight operation modes are shown in Figure 4. The eight operation modes of a six-switch IPIFR–WPT circuit can be classified as four cyclic operating processes, namely, the forward power injection process, the first free resonance process, the reverse power injection process, and the second free resonance process. Among them, Mode 1 and Mode 5 are forward and reverse power injection processes, respectively. Modes 2, 3, and 4 jointly constitute the first free resonance process, and Modes 6, 7, and 8 jointly constitute the second free resonance process.
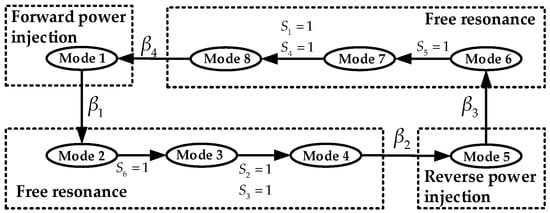
Figure 4.
The diagram of mode switching boundaries.
Figure 4 shows no switch operates when the free resonance process switches to the power injection process. The switching condition is to rely on the voltage up to form a voltage clamp with the power supply voltage Edc through the diode D0. In Mode 8, the switch groups S1 and S4 have turned on, but at this time, the voltage up is greater than Edc, and the system remains in the free resonance process. Meanwhile, ip > 0, that is, up will continue to decrease until up drops to equal to Edc, and the diode D0 reaches the critical conduction condition. At the same time, the current is commutated from branch S6–Cp–S5 to branch S4–Edc–D0–S1. The system switches from a free resonance process to a forward power injection process, and the voltage up on the primary capacitor Cp will maintain the voltage clamp at Edc. Similarly, when switching from Mode 4 to Mode 5, it is necessary to clamp the voltage up on the primary capacitor Cp to −Edc, and the free resonance process completes the switching to the reverse power injection process.
For convenience, the switching conditions β1, β2, β3, and β4 between the four operation processes are shown in Figure 4 and written in parallel:
- β1: S1 = 0 and S4 = 0;
- β2: up = −Edc and ip < 0;
- β3: S2 = 0 and S3 = 0;
- β4: up = Edc and ip > 0.
Figure 5 shows the equivalent circuit diagram of the main operation process of the six-switch IPIFR–WPT system. Since the state space model of the system during the forward power injection process and the reverse power injection process are entirely consistent, the equivalent circuit model is shown in Figure 5a. However, the bus voltages during the forward power injection and reverse power injection processes are different due to the conduction switch sets of the full-bridge converters, and their input voltages are Edc and −Edc, respectively. At the same time, the system models for the first and second free resonance processes are also entirely consistent, with their equivalent circuit models shown in Figure 5b, and there is no power input in the free resonance process.

Figure 5.
The equivalent circuits of the operation processes of the six-switch IPIFR–WPT system: (a) power injection process and (b) self–resonance process.
During the power injection process in Figure 5a, the primary compensation capacitor Cp is isolated from the system by the switches S5 and S6 being turned off. The DC power supply directly charges the primary inductance Lp through full-bridge forward conduction (switches S1 and S4) or reverse conduction (switches S2 and S3), with input voltages of Edc or −Edc, respectively. At the same time, due to the isolation diode D0, the current i1 only flows in one direction, i1 > 0, and energy can only be injected into the system from the power source and cannot be returned to the power source. In the free resonance process shown in Figure 5b, the DC power source is isolated from the system, while the inductance Lp and capacitance Cp in the primary circuit are directly connected to form a resonance circuit. Hence, through mutual inductance coupling, electrical power is transferred from the primary circuit to the secondary circuit.
According to Figure 5, set the state variable as the voltage up on the primary capacitor Cp, the current ip on the primary coil inductance Lp, the current is on the secondary coil inductance Ls, and the voltage uo on the secondary capacitor Cs, that is, x = [up, ip, is, uo]T. Because the secondary capacitance Cs and the equivalent load resistance RL are in parallel, the voltage uo can also be considered as the equivalent output voltage. Assuming the system input is u = [Edc], differential equations can be listed as follows for each state variable according to Kirchhoff’s voltage law and current law:
Forward power injection process:
First free resonance process:
Reverse power injection process:
Second free resonance process:
where
For a linear time-invariant system Σ: (A, B, C, D), if the system matrix A is invertible, and when the initial time is t0, the corresponding time domain solution can be expressed as follows [24]:
where Φ(t) = exp{At}, I is the identity matrix, xzi(t) is the zero input response, xzt(t) is the zero state response, and x0 is the initial state of the system at the initial time t0.
Since the system matrices A1 and A3 of the power injection process are irreversible, it is impossible to bring them into Equation (11) directly. Furthermore, the voltage up on the primary capacitor Cp is clamped at Edc during the power injection process. Hence, the differential equation of up can be rewritten as follows:
Note that Equations (2) and (3) only hold during the power injection process. The system matrices A1, A3 and input matrices B1, B3 of the power injection process will be rewritten to be reversible as follows:
According to Equation (11), if the initial state of the four linear time-invariant systems at their respective initial time t0 is x0, the time domain solutions of the subsystems can be expressed as follows:
Forward power injection process:
First free resonance process:
Reverse power injection process:
Second free resonance process:
Due to the symmetry of the two energy resonance processes and the two free resonance processes, the time interval experienced by their subsystems is the same, so the time interval between the two power injection processes is assumed to be ξ1. Set the time interval between two power injection processes as ξ2. Let the initial value of the system in the nth cycle be xn, and the terminal values of the four subsystems be xn1, xn2, xn3, and xn+1, respectively, where xn+1 is the terminal value of the system in the nth cycle and also the initial value of the system in the (n + 1) cycle. The expressions for the terminal values xn1, xn2, xn3, and xn+1 of each subsystem are as follows:
According to the modal analysis and the symmetry of the full-bridge system, when the system’s operating state reaches a steady state, there is xn = −xn2 = xn+1. Generally, xn = xn+1 is called a fixed point, and the mapping relationship between xn and xn+1 becomes a fixed point mapping. To simplify the iterative process, take xn = −xn2 for fixed point mapping calculations, and the following equation can be obtained:
After transforming and bringing ξ2 = 1/2T − ξ1 for Equation (23), we can obtain the following equation:
According to the modal analysis and subsystem switching conditions, the initial value of the system needs to meet the boundary β4:up = Edc and ip > 0. Namely, the element up in the fixed point xn is constant, and the following equation can be expressed:
Therefore, the soft switching operation point of the six-switch IPIFR–WPT system is the solution of Equation (25), and we can construct the following function g(ξ1) to solve Equation (25):
The parameters of the six-switch IPIFR–WPT system are shown in Table 2. The curve of the function g(ξ1) with T = 110 μs is shown in Figure 6. There are two results of g(ξ1) = 0, that is, ξ1a = 11.11 μs and ξ1b = 36.02 μs. Then, we bring ξ1a and ξ1b into (20) to solve the corresponding fixed point xn, listed in Table 3.

Table 2.
The main parameters of the six-switch IPIFR–WPT system.
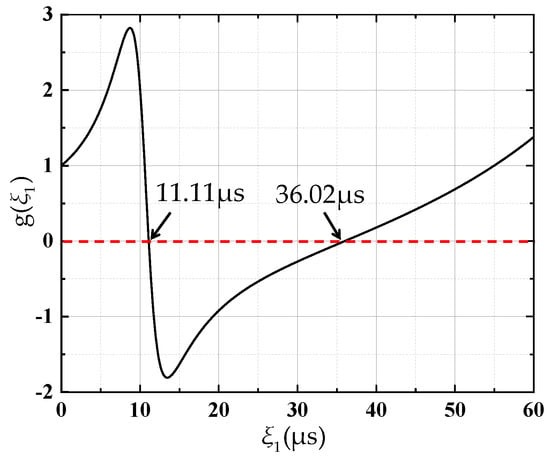
Figure 6.
The curve of the function g(ξ1) with respect to ξ1.

Table 3.
The calculated result of the fixed point xn and the intermediate variable xn1.
The fixed point xn is both the initial and final values of the steady-state period. Moreover, the fixed point xn must satisfy the boundary condition β4 (up = Edc and ip > 0). In Table 3, when taking ξ1a = 11.11 μs, the value of fixed point xn satisfies the boundary condition β4., and when taking ξ1b = 36.02 μs, ip = −3.272 A < 0 does not meet the boundary condition β4. Therefore, the root ξ1b = 36.02 μs could be abandoned (xn = −xn2 = xn+1).
After calculating the fixed point xn and the transition state quantity xn1 of the six-switch IPIFR–WPT system, according to the proposed symmetry of the full-bridge converter, there are xn = −xn2 = xn+1, xn1 = −xn3. Then, in order to more intuitively represent the trade-off between the two results mentioned above, by substituting xn and xn1 obtained in Table 3 into Equations (19)–(22), the curves of state variables in the complete steady-state cycle can be obtained, and the curves of current ip and voltage up in them can be plotted in Figure 7.
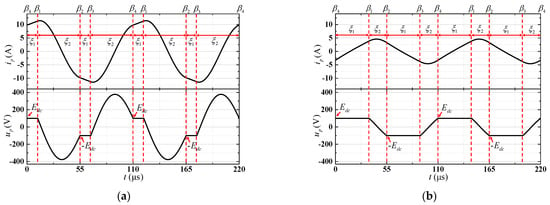
Figure 7.
The waves of system state variables under the calculated steady-state operation points: (a) ξ1 = 11.11 μs and (b) ξ1 = 36.02 μs.
As can be seen from Figure 7, taking ξ1a = 11.11 μs, the simulation waveform is consistent with the mode analysis, and all boundary conditions can be satisfied within a steady-state cycle. However, taking ξ1b = 36.02 μs, the calculated operating waveform is inconsistent with the expected, and the boundary conditions β2 (up = −Edc and ip < 0) and β4 (up = Edc and ip > 0) cannot be satisfied, so that ξ1b can be abandoned.
3. System Characteristics and Experimental Results
3.1. Experimental Devices
In order to verify the characteristics of the six-switch IPIFR–WPT system, an experimental platform was built, as shown in Figure 8. As shown in Figure 8a, the DC power supply used in the system consists of three parts: an AC voltage regulator TDGC2–3kVA (Delixi, China), a single-phase rectifier module MDQ100A1600V, and a filter capacitor. The oscilloscope is RTB2004, produced by Rohde & Schwarz Company. The power analyzer is the WT500, produced by Yokogawa Company. The resonance capacitors Cs and Cp are MKPH–R 0.4 μF. In Figure 8b, the isolation diode D0 used in the system is FR607 (1000 V, 6 A) and the switches S1–S6 are IXFN56N90P (900 V, 56 A).

Figure 8.
Experimental devices of the six-switch IPIFR–WPT system: (a) the whole system and (b) the converter.
The square coupling coils used in this system use litz wires while using a radial layout of ferrite to increase their self-inductances and mutual inductance. The size of the square coils is 32 cm times 40 cm. The self-inductances Lp and Ls of the primary and secondary coils are 660 μH and 585 μH, respectively. The internal resistances Rp and Rs are both 0.2 Ω. The relationship between the coupling coefficient k and the coil distance d is shown in Figure 9.
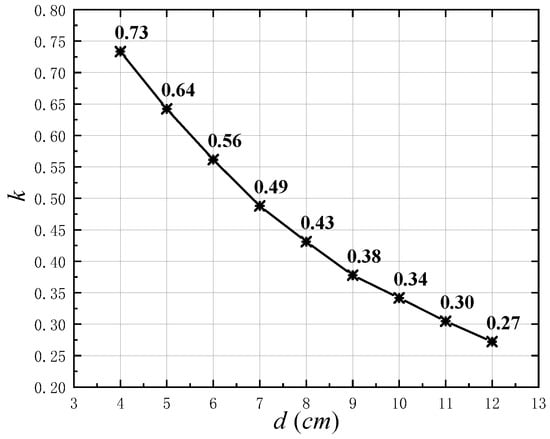
Figure 9.
The relationship between the coupling coefficient k and coil distance d of the flat coils.
3.2. Soft Switching Margin Characteristic
The six-switch IPIFR–WPT system has a unique wide soft switching margin characteristic due to its particular structure. In Mode 4 and Mode 8, the last modes of the free resonance process, the full-bridge converter has been turned on in advance, but the voltage up is greater than Edc so that the diode D0 is turned off and the power supply is isolated from the system. Since the free resonance process will maintain until the voltage up is equal to Edc, the switches of the full-bridge converter could turn on before in a very time margin when the voltage up is greater than Edc. Hence, in this time margin, the system itself will achieve the soft switching condition and determine the operation point without any switching action. The time margin is called the soft switching margin.
Figure 10 is a schematic diagram of the wide soft switching margin of a six-switch WPT system. In Figure 10, the black curve is the voltage input of the full-bridge converter, and the orange and red curves represent the values of the primary capacitor voltage up and the primary inductor current ip, respectively.
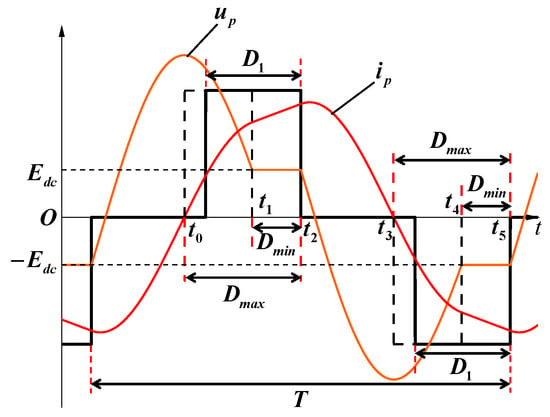
Figure 10.
The diagram of the wide soft switching margin of the six-switch IPIFR–WPT system.
According to the modal analysis above, boundary conditions must be met when switching from the second free resonance process to the forward power injection process β4 (up = Edc and ip > 0), and switches S1 and S4 have been turned on in advance. It can be known from the waveforms of voltage up and current ip in Figure 10 that the timing of turn-on of S1 and S4 must meet the following conditions: up > Edc and ip > 0. Therefore, the margin that satisfies the soft switching condition is [t0, t1]. Namely, the maximum pulse width for S1 and S4 is Dmax = t2 − t0, and the minimum opening pulse width is Dmin = t2 − t1. Based on the symmetry of the full-bridge converter, there are Dmax = t5 − t3 = t2 − t0 and Dmin = t5 − t4 = t2 − t1. The pulse widths of switch groups (S1, S4) and (S2, S3) can meet the conditions by taking any value of [Dmin, Dmax]. Therefore, the time range [Dmin, Dmax] can be called the wide soft switching margin of a six-switch IPIRF–WPT system, and MZVS is defined as the wide soft switching margin of the system, and its calculation formula is as follows:
In Figure 11a–c, let the fixed coil spacing be d = 6 cm (k ≈ 0.5), the equivalent load resistance be RL = 10 Ω, and the period be T = 110 μs. Then, taking the positive pulse widths of the switching strategy as (a) D = 15 μs, (b) D = 20 μs, and (c) D = 26 μs, the system can self-determine the same operating point, ξ1 = 10.52 μs, very close to the theoretical value, ξ1 = 11.11 μs. Meanwhile, the waveform shape and amplitude of the capacitor voltage up and the inductor current ip are consistent. According to the measurement results in Figure 11, the soft switching margin under the above static parameters is Dmin = 10.52 μs to Dmax = 29.95 μs. In Figure 11, the three positive pulse widths of (a), (b), and (c) are all within the range of [Dmin, Dmax] and can enable the system to operate at the same operating point and meet soft switching conditions. Therefore, it can be proven that the unique topology of the six-switch IPIFR–WPT system enables it to have a wide soft switching margin, which provides a wide tolerance for the control system, improves system stability, and reduces control difficulty.
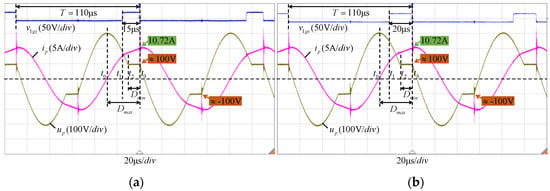
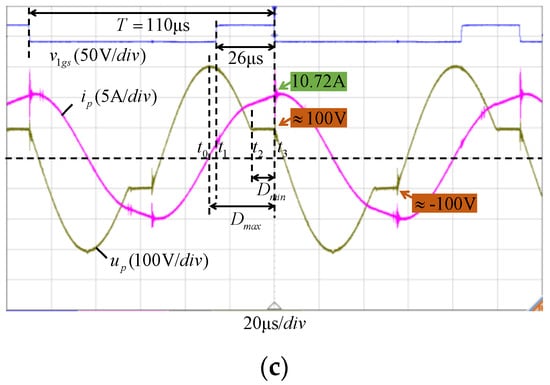
Figure 11.
The verification waveforms of the wide soft switching margin: (a) D = 15 μs, (b) D = 20 μs, and (c) D = 26 μs.
3.3. Dynamic Parameter Adaptation Characteristic
The resistance to dynamic parameter changes is a significant dynamic characteristic of WPT systems. Due to no fixed physical connection for wireless coils, environmental disturbances will affect the relative position of the wireless coils to a certain extent, resulting in dynamic changes in the coil coupling coefficient k. On the other hand, a WPT system’s equivalent resistance RL will change as the charging process progresses. Therefore, the coil coupling coefficient k and the equivalent resistance RL are the main dynamic parameters for research. When the power injection process switches to the free resonance process, the boundary condition depends on the values of the system state variables instead of the switches. The wide soft switching margin characteristic analyzed above, that is, any switching duty D1 ∈ [Dmin, Dmax] allows the system to operate at ξ1 = Dmin, the soft switching operating point. When parameters change dynamically, its soft switching margin has a certain degree of overlap, which can ensure that the system has the characteristics of resisting changes in dynamic parameters, called dynamic parameter adaptive characteristics.
In Figure 12, under the same switching strategy, T = 110 μs and D = 110 μs, there are the curves of MZVS, Dmin, and Dmax concerning the coupling coefficient k. The system parameters are taken according to Table 2, and Dmin and Dmax are measured under different k. As seen from Figure 12, in the process of gradually increasing the coupling coefficient k from 0.30 to 0.60, although the soft switching margin has decreased, it has maintained more than 15%.
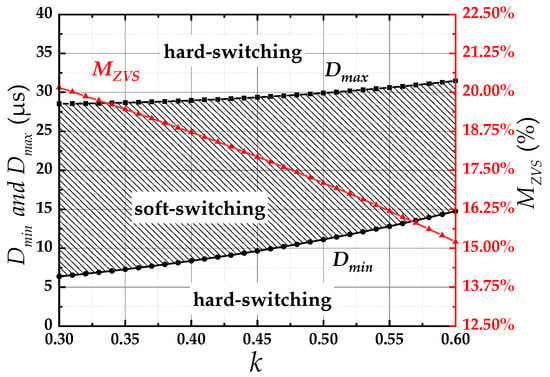
Figure 12.
The curves of wide soft switching margin concerning the coupling coefficients k.
Due to the unique hardware structure, the six-switch IPIFR–WPT system can have the ability to dynamically change the coupling coefficient and equivalent load resistance without changing the switching control strategy in the whole process, that is, in the open-loop state.
In the experimental waveforms shown in Figure 13, the switching control strategy of the system is fixed: T = 110 μs and D = 25 μs. Increasing the coil spacing d (a) 6 cm, (b) 7 cm, (c) 8 cm, and (d) 9 cm, the corresponding coupling coefficients k are (a) 0.56, (b) 0.49, (c) 0.43, and (d) 0.38. From the waveforms of the current i1, during the process of changing the coupling coefficient k, the system can determine its own soft switching operating point, and its power injection times ξ1 are self-determined as (a) 12.26 μs, (b) 10.52 μs, (c) 9.26 μs, and (d) 7.86 μs. The waveform trends of the capacitor voltage up and the inductor current ip are always consistent, and the soft switching boundary conditions are satisfied at the boundaries of the free resonance process and the power injection process. In particular, the capacitor voltage up can clamp at Edc and −Edc during the power injection process at different coupling coefficients k, which indicates the soft switching conditions have been met. Therefore, this experiment proves that the six-switch IPIFR–WPT system can adapt to the dynamic change of the coupling coefficient k in a great range.
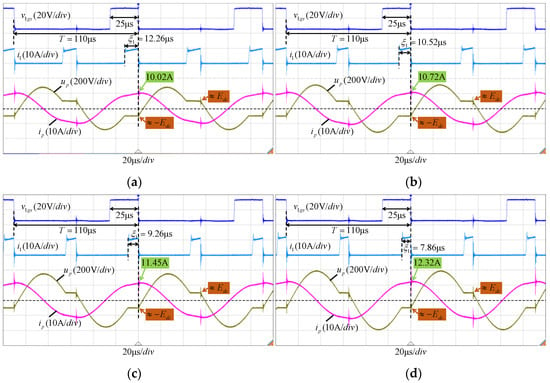
Figure 13.
The waveforms of i1, ip, and up when coil distance d changes in the open-loop state: (a) d = 6 cm, (b) d = 7 cm, (c) d = 8 cm, and (d) d = 9 cm.
Similarly, when the equivalent load resistance RL changes dynamically, the six-switch IPIFR–WPT system can maintain its adaptive characteristics. As shown in Figure 14, there are curves of the soft switching margin Dmin and Dmax concerning the equivalent resistance RL. In Figure 14, when the equivalent load resistance RL increases from 5 Ω to 20 Ω, although the soft switching margin can maintain more than 14%, and when the equivalent load resistance RL changes in the range of 5 Ω to 20 Ω, there is a significant overlap range, which allows the system to resist changes in load resistance over a large range.
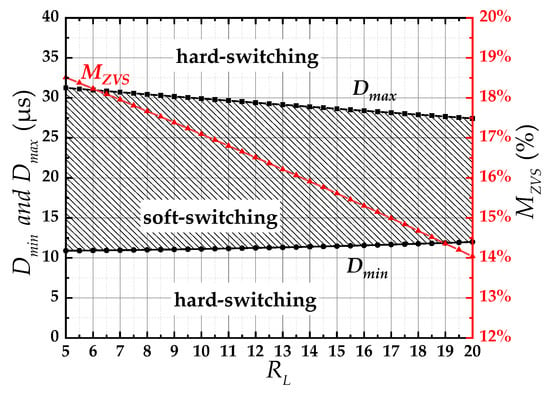
Figure 14.
The curves of the wide soft switching margin concerning the equivalent load resistance RL.
As shown in Figure 15, the switching control strategy of the system is fixed to T = 110 μs and D = 20 μs. When the equivalent load resistances RL changes, (a) 10 Ω, (b) 15 Ω, and (c) 20 Ω, the waveforms of the current i1 indicate that the system can determine its own soft switching operating point and power injection times ξ1 are self-determined as (a) 10.52 μs, (b) 11.29 μs, and (c) 11.94 μs. The waveform trends of the capacitive voltage up and the inductive current ip are consistent. The larger the equivalent load resistance RL, the smaller the amplitude of up and ip, indicating that the larger the load resistance, the less energy the system inputs. At the same time, the boundary conditions for switching between the free resonance process and the power injection process can be satisfied. Significantly, the capacitor voltage up can be clamped at Edc and −Edc during the power injection process under different equivalent load resistances RL, which means the soft switching conditions have been satisfied. Therefore, this experiment proves that the six-switch IPIFR–WPT system can adapt to the dynamic changes in the equivalent load resistance RL over a large range.
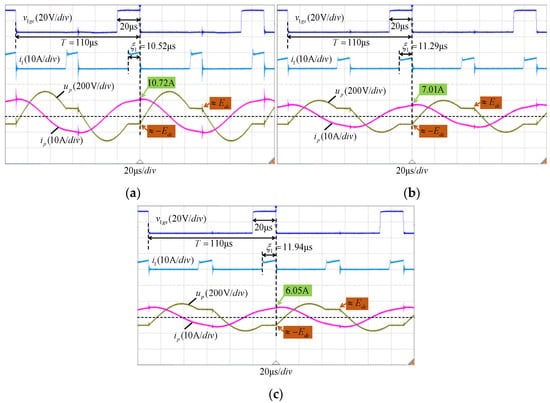
Figure 15.
The waveforms of i1, ip, and up when load resistance RL changes in the open–loop state: (a) RL = 10 Ω, (b) RL = 15 Ω, and (c) RL = 20 Ω.
In summary, even in open-loop states, the six-switch IPIFR–WPT system has good adaptability to dynamic changes in parameters such as coupling coefficient k and equivalent load resistance RL.
3.4. Decoupling Characteristic of Power Injection and Free Resonance
With the changes in T, the curves of the self-determined operating points (ξ1, ξ2) are shown in Figure 16. In Figure 16, as the period T increases, the injection time ξ1 rises significantly, and ξ2 remains unchanged, increasing the power injected into the system. Furthermore, due to ξ2 remaining unchanged, the power injection and free resonance processes exhibit significant decoupling characteristics, which makes the power regulation strategy of the six-switch IPIRF–WPT system extremely simple, that is, directly adjusting the length of the period T.
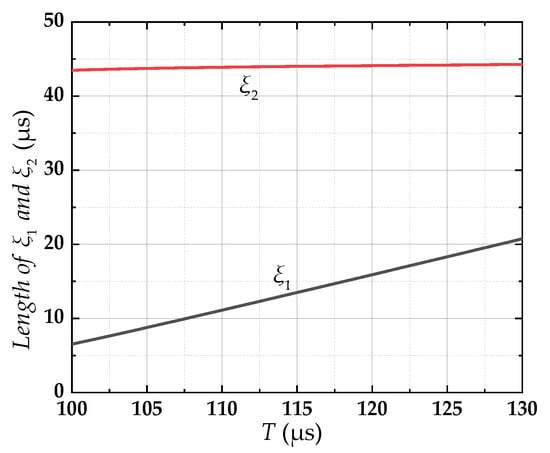
Figure 16.
The curves of the self-determining soft switching operation points concerning the period T.
Under static parameters, adjusting the input and output power of the system by changing the length of the period T is actually achieved by changing the power injection time ξ1. As shown in Figure 17, when the periods T of the system are (a) 100 μs, (b) 110 μs, (c) 120 μs, and (d) 130 μs, respectively, the determined power injection times ξ1 are (a) 5.94 μs, (b) 10.52 μs, (c) 13.10 μs, and (d) 20.07 μs. Therefore, as the period T grows, the duration of the power injection time ξ1 also increases. Meanwhile, the amplitudes of up and ip both increase significantly with the rise of T, meaning the input power increases synchronously.
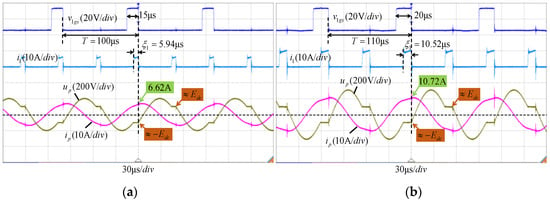
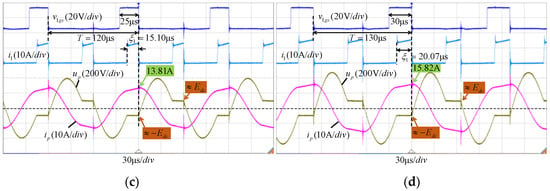
Figure 17.
The waveforms of i1, ip, and up when T changes in the open-loop state: (a) T = 100 μs, (b) T = 110 μs, (c) T = 120 μs, and (d) T = 130 μs.
The calculation methods of the input power Pin, the output power Pout, and the efficiency η are expressed as follows:
where I1 is the average value of i1, and Uo,rms is the root mean square (RMS) value of uo.
The curves of the output power Pout and the operation efficiency of the six-switch IPIFR–WPT system varying with the period T are shown in Figure 18. It can be seen from Figure 18 that the output power monotonically increases as the period T increases.
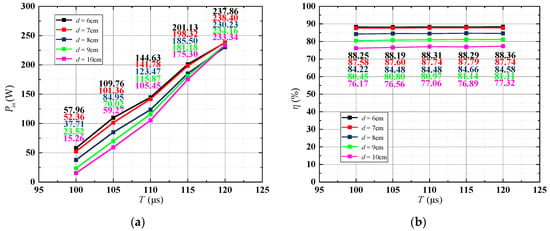
Figure 18.
The experimental curves of the output power and efficiency concerning the period T: (a) output power and (b) efficiency.
In Figure 18b, under the same coil spacing d, the operation efficiency of the system remains stable, while with the decrease in coil spacing d, the operation efficiency of the system increases relatively.
In summary, the converter and the resonant network have been decoupled by the unique hardware structures of the six-switch IPIFR–WPT system so that the power injection and the free resonance processes are also decoupled in mode. Under static parameters, the power injected into the system is only determined by the power injection time ξ1, and increasing T can make ξ1 grow, which results in a monotonic relationship between the output power and the period T. Therefore, compared to the fully resonant WPT system, the six-switch IPIFR–WPT system eliminates the peak power point, significantly simplifying power regulation strategies, eliminating system detuning caused by frequency splitting, and improving system stability.
4. Conclusions
This paper completes the theoretical analysis and experimental verification of the dynamic parameter adaptive characteristics and the decoupling of power injection and free resonance in the six-switch IPIFR–WPT system. Firstly, the state space modal is established based on the modal analysis of the six-switch IPIFR–WPT system. Secondly, using the stroboscopic mapping method and boundary conditions, a method is proposed to calculate all possible operating points of the system. Finally, the system characteristics are verified and explained based on simulations and experiments. Unlike traditional FR–WPT systems, the unique topology enables the six-switch IPIFR–WPT system to have adaptive characteristics of dynamic parameters and accomplish decoupling of the power injection and free resonance in modes. The experimental results were consistent with theoretical analysis.
In summary, under open-loop operation states, the unique topology makes the six-switch IPIFR–WPT system have at least 15% and 14% tolerance to the dynamic changes in the coil coupling coefficient k and the equivalent resistance RL, respectively. Furthermore, the power injection and the free resonance processes are decoupled. Namely, the converter and the resonant network are decoupled. Hence, the power injected into the system is completely controlled, and the curve of output power is monotonic with the injection time ξ1 or the period T. Moreover, according to the experiments, the power loss is greatest on the coils instead of the diode D0. However, in this paper, without precise parameter design, the system efficiency could still achieve 88%.
Furthermore, a suitable parameter design can decrease the internal resistance of coils to improve the system efficiency and reduce the voltage stress to promote the output power.
Author Contributions
Software, W.W.; Formal analysis, W.W.; Resources, W.W.; Data curation, Z.T.; Writing—original draft, W.W.; Writing—review & editing, D.L.; Project administration, D.L.; Funding acquisition, J.H. and W.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Natural Science Foundation of China, Grant 52177222, in part by the Natural Science Foundation of Fujian Province, Grant 2021J05262, and in part by the Education Project for Young and Middle aged Teachers of Fujian Provincial Department of Education, Grant JAT200462.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhong, W.; Lee, C.K.; Hui, S.Y.R. General Analysis on the Use of Tesla’s Resonators in Domino Forms for Wireless Power Transfer. IEEE Trans. Ind. Electron. 2013, 60, 261–270. [Google Scholar] [CrossRef]
- He, L.; Guo, D. A Clamped and Harmonic Injected Class-E Converter with ZVS and Reduced Voltage Stress over Wide Range of Distance in WPT System. IEEE Trans. Power Electron. 2021, 36, 6339–6350. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, B. Omnidirectional and Efficient Wireless Power Transfer System for Logistic Robots. IEEE Access 2020, 8, 13683–13693. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, L.; Guo, Y.; Liao, C.; Li, F. Applying LCC Compensation Network to Dynamic Wireless EV Charging System. IEEE Trans. Ind. Electron. 2016, 63, 6557–6567. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, Y.; Liao, C.; Guo, Y.; Wang, L.; Li, F. Experimental Study on Asymmetric Wireless Power Transfer System for Electric Vehicle Considering Ferrous Chassis. IEEE Trans. Transp. Electrif. 2017, 3, 427–433. [Google Scholar] [CrossRef]
- Feezor, M.; Sorrell, F.Y.; Blankinship, P.R. An interface system for autonomous undersea vehicles. IEEE J. Ocean. Eng. 2001, 26, 522–525. [Google Scholar] [CrossRef]
- Lu, Y.; Ma, D.B. Wireless Power Transfer System Architectures for Portable or Implantable Applications. Energies 2016, 9, 1087. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, Y.; Liu, X.; Lin, F.; Xu, D. A Novel Parameter Tuning Method for a Double-Sided LCL Compensated WPT System with Better Comprehensive Performance. IEEE Trans. Power Electron. 2018, 33, 8525–8536. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, B.; Qiu, D.; Zhang, Y. Frequency Splitting Phenomena of Magnetic Resonant Coupling Wireless Power Transfer. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, B. Frequency, Impedance Characteristics and HF Converters of Two-Coil and Four-Coil Wireless Power Transfer. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 177–183. [Google Scholar] [CrossRef]
- Liao, Z.-J.; Ma, S.; Feng, Q.-K.; Xia, C.; Yu, D. Frequency Splitting Elimination and Utilization in Magnetic Coupling Wireless Power Transfer Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 929–939. [Google Scholar] [CrossRef]
- Lim, Y.; Tang, H.; Lim, S.; Park, J. An Adaptive Impedance-Matching Network Based on a Novel Capacitor Matrix for Wireless Power Transfer. IEEE Trans. Power Electron. 2014, 29, 4403–4413. [Google Scholar] [CrossRef]
- Ann, S.; Lee, B.K. Analysis of Impedance Tuning Control and Synchronous Switching Technique for a Semi-bridgeless Active Rectifier in Inductive Power Transfer Systems for Electric Vehicles. IEEE Trans. Power Electron. 2021, 36, 8786–8798. [Google Scholar] [CrossRef]
- Wu, M.; Yang, X.; Chen, W.; Wang, L.; Jiang, Y.; Zhao, C.; Yan, Z. A Dual-Sided Control Strategy Based on Mode Switching for Efficiency Optimization in Wireless Power Transfer System. IEEE Trans. Power Electron. 2021, 36, 8835–8848. [Google Scholar] [CrossRef]
- Namadmalan, A. Self-Oscillating Tuning Loops for Series Resonant Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2016, 31, 7320–7327. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, J.; Fang, Z.; Hu, M.; Cai, C.; Zhang, J. Accurate Maximum Power Tracking of Wireless Power Transfer System Based on Simulated Annealing Algorithm. IEEE Access 2018, 6, 60881–60890. [Google Scholar] [CrossRef]
- Luo, D.; Hong, J.; Chen, W. Discrete-Time Modelling to Determine the Possible Operation Points of Incomplete-Resonance Wireless Power Transfer System. J. Phys. Conf. Ser. 2022, 2179, 012011. [Google Scholar] [CrossRef]
- Chen, L.; Hong, J.; Guan, M.; Lin, Z.; Chen, W. A Converter Based on Independently Inductive Energy Injection and Free Res-onance for Wireless Energy Transfer. Energies 2019, 12, 3467. [Google Scholar] [CrossRef]
- Chen, L.; Hong, J.; Lin, Z.; Luo, D.; Guan, M.; Chen, W. A Converter with Automatic Stage Transition Control for Inductive Power Transfer. Energies 2020, 13, 5268. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, L.; Liao, X.; Ju, X.; Su, S.W.; Ma, H. A Pulse Energy Injection Inverter for the Switch-Mode Inductive Power Transfer System. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 2330–2340. [Google Scholar] [CrossRef]
- Chen, L.; Hong, J.; Guan, M.; Wu, W.; Chen, W. A Power Converter Decoupled from the Resonant Network for Wireless Inductive Coupling Power Transfer. Energies 2019, 12, 1192. [Google Scholar] [CrossRef]
- Yue, R.; Wang, C.; Li, H.; Liu, Y. Constant-Voltage and Constant-Current Output Using P-CLCL Compensation Circuit for Single-Switch Inductive Power Transfer. IEEE Trans. Power Electron. 2021, 36, 5181–5190. [Google Scholar] [CrossRef]
- Wang, C.; Yue, R.; Li, H.; Li, D. Research on Constant-Current and Constant-Voltage Wireless Charging System Based on Sin-gle-Switch Circuit. Trans. China Electrotech. Soc. 2021, 36, 4638–4647+4657. [Google Scholar]
- Tang, C.S.; Sun, Y.; Su, Y.G.; Nguang, S.K.; Hu, A.P. Determining Multiple Steady-State ZCS Operating Points of a Switch-Mode Contactless Power Transfer System. IEEE Trans. Power Electron. 2009, 24, 416–425. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).