Video Super-Resolution Using Multi-Scale and Non-Local Feature Fusion

Abstract

Video super-resolution can generate corresponding to high-resolution video frames from a plurality of low-resolution video frames which have rich details and temporally consistency. Most current methods use two-level structure to reconstruct video frames by combining optical flow network and super-resolution network, but this process does not deeply mine the effective information contained in video frames. Therefore, we propose a video super-resolution method that combines non-local features and multi-scale features to extract more in-depth effective information contained in video frames. Our method obtains long-distance effective information by calculating the similarity between any two pixels in the video frame through the non-local module, extracts the local information covered by different scale convolution cores through the multi-scale feature fusion module, and fully fuses feature information using different connection modes of convolution cores. Experiments on different data sets show that the proposed method is superior to the existing methods in quality and quantity.

1. Introduction

Video super-resolution is also called multi-frame image super-resolution. Compared with single-image super-resolution, video super-resolution can use time series information to reconstruct the results, so it can achieve better reconstruction results.

Before the popularization of deep learning methods, sparse coding and manual feature extraction were mainly used to deal with video super-resolution [1,2]. In reference [3], convolutional neural network is first proposed to deal with video super-resolution. The methods of [4,5,6,7] did not align the adjacent video frames, and used 2D or 3D convolution for feature extraction to realize video super-resolution. The recurrent neural network [8,9] is also used to solve the super-resolution reconstruction of video frame sequence. The existing video super-resolution methods [10,11,12,13,14,15] predict the motion trajectory by calculating the optical flow relationship between adjacent frames, and then the input video frames are warped to align the adjacent video frames. The problem with this method is that the accuracy of the video frame alignment directly affects the subsequent super-resolution work. Time correlation has also been proved to be very important for super-resolution of video frames [16,17,18,19], the use of temporal correlation can effectively improve the accuracy of video super-resolution.

Video super-resolution methods [20,21,22,23] based on deep learning adopt different deep learning strategies in the super-resolution part to reconstruct the video frame, though the performance of these methods is still limited by the accuracy of low-resolution optical flow. In the SOF-VSR [24] method, in order to solve the problem of limited accuracy of low-resolution optical flow, high-resolution optical flow is generated to provide the corresponding relationship between video frames, thereby improving the super-resolution performance. The above methods have proposed targeted solutions to the existing problems of video super-resolution, but these methods do not fully mine the effective information contained in the video frame itself in the process of super-resolution, and the extraction of feature information only stays at a single scale. In order to solve these problems, we propose the method in this paper.

To generate high-resolution video frames, we propose an end-to-end network. Firstly, a non-local module, using the information of all points in the video frame to calculate the corresponding output of a certain point, is introduced into the network structure. Then, the effective information is further excavated by calculating the similarity between long-distance pixels in the video frame. Secondly, the high-resolution optical flow is calculated through the optical flow reconstruction network (OFRnet) connected in parallel.

The proposed OFRnet is a pyramid structure with a three-layer network. Video frames are first downsampled in the OFRnet, and then amplified step-by-step through different network layers to obtain the required high-resolution optical flow. Compared with SOF-VSR method, the similar optical flow network structure is adopted, but in our OFRnet, multi-scale feature fusion block (MSFFB) is used to extract more feature information in the process of generating high-resolution optical flow.

In the super-resolution networks, we propose MSFFB, which contains convolution kernels with different sizes and different convolution kernel connection methods. Compared with the existing video super-resolution methods, our method obtains better PSNR and SSIM values on different test datasets. As shown in Figure 1, we shows some results of different reconstruction methods by ×4 scale on calendar video sequence.

Figure 1. Results of different reconstruction methods by ×4 scale on calendar video sequence.

Our algorithm has two main contributions:

• The non-local module overcomes the limitation of convolution operation in the feature-extraction process, fully excavates the global information of the video frames, expands the receptive field, and improves the utilization of effective information.
• Multi-scale feature fusion blocks are connected by different convolution kernels with different sizes, which makes the feature information extracted by different convolutions be fused efficiently, so the reconstruction results contain more details.

The rest of the paper is arranged as follows. In the second section, the development of video super-resolution based on convolutional neural network is introduced. In the third section, the network structure and the specific functions of each module proposed in this paper are elaborated in detail. In the fourth section, the ablation experiment is carried out to show the specific functions of different network modules. Finally, the fifth section summarizes the paper.

2. Related Work

In this section, we briefly introduce single-image super-resolution methods and different methods of video super-resolution.

2.1. Single-Image Super-Resolution

With the development of deep learning, many very effective single-image super-resolution methods have been proposed. Compared with traditional methods, deep learning methods have achieved more effective super-resolution results. Dong et al. [25] first applied the deep learning method to the super-resolution of a single image, and used a three-layer convolutional neural network to learn the mapping relationship between low-resolution images and high-resolution images. Shi et al. [26] proposed a sub-pixel convolution method, which effectively reduces the computational complexity of the network. In addition to being used in single-image super-resolution, this method can also reconstruct video sequences in real-time. Kim et al. [27] proposed a very deep convolution neural network. The network model has 20 layers, which improves the accuracy of image reconstruction. Lai et al. [28] proposed a Laplace pyramid network. This method does not use bicubic interpolation preprocessing, which reduces the computational complexity. On the basis of ResNet [29], Ledig et al. [30] proposed SRResNet method to remove the ReLU layer in the residual block and improve the reconstruction effect. EDSR [31] is based on SRResNet except for the batch-normalization layer, which makes the residual learning method more suitable for low-level super-resolution problems. Hu et al. [32] proposed a channel and spatial modulation network to enhance the valuable information in the network and suppress the redundant information. Kim et al. [33] proposed the method of deep recursive convolution network to reconstruct the image, which can improve the network performance without introducing additional parameters. Ahn et al. [34] proposed cascade method for super-resolution, which makes this method closer to practical application. Zhang et al. [35] proposed residual dense network to make full use of the hierarchical characteristics of all convolution layers. Zhang et al. [36] proposed a very deep residual channel attention network to solve the problem that low-frequency information is treated equally in the network. The above methods have certain reference significance for the proposal of video super-resolution methods.

2.2. Video Super-Resolution

2.2.1. Methods with Video Frames Alignment

On the basis of SRCNN [25] processing a single image, Kappeler et al. [3] completed the super-resolution reconstruction of multi frame images in spatial information and temporal information, which is generally considered to be the first application of deep learning method in the field of video super-resolution. Liao et al. [11] generated an ensemble SR-drafts through two classical optical flow methods with different parameters, and then predicted the final HR frame by a deep convolutional neural network. Caballero et al. [10] first proposed the end-to-end video super-resolution network named VESPCN, which contains two main parts: sub-pixel convolutional super-resolution and spatio-temporal network. Since then, end-to-end network structures have been widely used in video super-resolution. Tao et al. [12] used a sub-pixel motion compensation (SPMC) layer to effectively deal with motion compensation and feature map scaling, and used an LSTM-based framework to deal with multi-frame input. Chu et al. [18] proposed a spatio-temporal discriminator called TecoGAN to obtain realistic and coherent video super-resolution. Sajjadi et al. [14] input the HR image generated previously into the network when generating the next frame image, and the method can not only produce time-continuous results but also reduce the computational complexity. Haris et al. [37] proposed recursive back-projection network that integrated spatial and temporal relations to generate target frames. Bao et al. [38] proposed an adaptive warping layer to complete the frame interpolation of sequence images. In order to make full use of the shared redundancy between consecutive frames, Kalarot et al. [39] took the output of the first stage as the input of the second stage, and gradually improved the quality of the reconstructed image. Chen et al. [40] improved the accuracy of low-resolution face recognition by constructing the nearest-neighbor network. Haris et al. [41] proposed an end-to-end network model, which can perform video frame insertion at the same time of video super-resolution. Most of these methods use motion estimation for motion compensation, so as to achieve the purpose of video frame alignment and improve the quality of reconstruction results.

Other methods realize the alignment of adjacent video frames through implicit motion compensation. Dai et al. [42] first proposed the application of deformable convolution in high-level visual tasks, and then continuously improved it in low-level visual tasks. Currently, there are also methods to achieve video frame alignment through deformation convolution. Wang et al. [43] proposed a video frame with enhanced deformable convolution to effectively fuse different video frames with different motion and blur. Tian et al. [17] proposed an adaptive alignment reference frame of feature layer without calculating optical flow to achieve the purpose of video frame prediction. Ying et al. [44] proposed three-dimensional deformable convolution to realize motion compensation and spatial information acquisition. Isobe et al. [45] input the previous frame and the current frame into the network as hidden states, and saved the texture details through the middle layer of the network.

2.2.2. Methods without Video Frames Alignment

Such methods do not align video frames, and super-resolution of video frames is achieved by extracting spatial information and time series information. Lucas et al. [4] used adaptation and perceptual losses to improve the ability of network to recover image details in super-resolution tasks. By reusing previous frames and feature information, Yan et al. [46] not only maintained real-time speed, but also produced high-quality results. Jo et al. [5] proposed a method to reconstruct a high-resolution image from the input image with a dynamic up sampling filter, and add details through calculation, which also improved the reconstruction quality. Huang et al. [47] proposed a bidirectional recursive convolution network for time series modeling to complete the reconstruction of video frames. This method does not calculate optical flow, but simulates time series through recursive neural network, which reduces the computational complexity. Yi et al. [48] avoided motion estimation and motion compensation through improved non-local operation, achieved good performance and greatly improved operation speed. Li et al. [49] proposed a time multi-correspondence aggregation strategy, which can extract the self-similarity of video frames by using the similarity of patches between video frames and a cross-scale non-local module.

Song et al. [50] used gradient mapping between high-resolution frames and low-resolution frames to regularize multi-frame fusion to achieve video super-resolution. Wang et al. [51] used edge enhancement method on the basis of generative adversarial network, which further improves the visual experience of video super-resolution. Liu et al. [52] proposed a real-time video super-resolution model based on neural structure search, and applied this method to mobile devices.

However, most of the mentioned networks use convolution kernel with single scale and fixed size, which has certain limitations on feature extraction. Moreover, the current extraction method of effective information only considers the coverage area of convolution kernel, which cannot establish the relationship between long-distance similar pixels. Some works consider the relationship between long-distance pixels, but they only solve the case in which low-resolution video frames are obtained by interpolation downsampling, and do not involve the case in which low-resolution video frames are blurred. Therefore, we deeply mine the effective information of video frames through nonlocal features and multi-scale information fusion. Furthermore, we discuss the effect of the proposed method on the reconstruction of low-resolution video frames with fuzzy factors.

3. Proposed Method

In this section, the improved network structure will be explained in detail. Our network structure consists of three parts, which are non-local module, optical flow reconstruction and super-resolution reconstruction, as shown in Figure 2. In our model architectures, the introduced non-local module can make full use of the global information of the video frame, because it considers the information of all feature points to calculate the corresponding output of a feature point in the feature map. Parallel to it is OFRnet, which uses multi-scale feature fusion blocks, the main function of this module is to align different video frames. Finally, the results of the non-local module and OFRnet are connected and sent to the SRnet. SRnet is composed of multi-scale feature fusion blocks in series to perform the final super-resolution. Among them, the multi-scale feature fusion block is a feature extraction module we proposed. The module has convolution kernels of different sizes and is connected in different ways to fully fuse feature information of different scales.

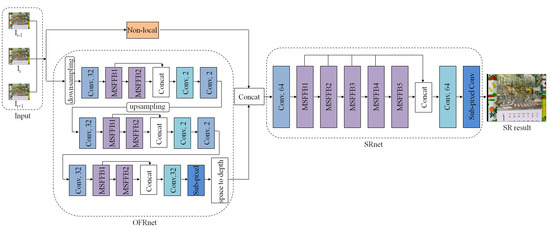
Figure 2. The framework of the proposed video super-resolution network.

3.1. Network Architecture

Recently, optical flow reconstruction networks (OFRnet) are widely used in video super-resolution methods [24,53,54], many of them utilize adjacent frames of video to estimate the optical flow. Our OFRnet is a three-layer pyramid structure. After low-resolution video frames are sent to the optical flow reconstruction network, they are downsampled first, and then amplified step-by-step through different network layers. In different network layers of our OFRnet, we uses multi-scale feature fusion block (MSFFB) to extract and fuse the feature information extracted by different scale convolution kernels. Through the layer-by-layer amplification in OFRnet, the high-resolution optical flow containing more detailed information is finally obtained.

The non-local module captures the information of all the feature points when calculating the corresponding output of a certain point in the feature map. The feature points with relatively large relevance are given more weight, and their output contribution to the current point is also greater than others during calculation. This module is conducive to fully mine the global information contained in the entire feature map, which effectively overcomes the limitation that the convolution operation only involves the feature points in its neighborhood while ignores other feature points. As a result, the utilization of effective information is improved, the range of perception is expanded, the ability to perceive the network is enhanced as well.

As illustrated in Figure 2, SRnet, which reconstructs low-resolution frames into high-resolution frames, is the last part of the network structure. The features extracted by feature-extraction layer are sent to the multi-scale feature fusion blocks, and the feature maps corresponding to different convolution kernels are fully mined and extracted. Then, the network uses the feature fusion layer to extract all the features. Finally, a high-resolution frame is generated through the sub-pixel layer.

3.2. Non-Local Module

The authors of [4,5,46] use 2D convolution to extract the feature information contained in the video frames. This method can only extract limited information because the convolution kernel can only slide in the width and height directions of the image. It only considers the correlation between adjacent pixels or feature points in the convolution kernel, and cannot use global information. It is a local operation. Therefore, as shown in Figure 2, video frames are input to OFRnet and non-local modules in parallel, and we expect to capture global information through non-local modules.

In the video classification task, Wang et al. [55] tried the non-local method for the first time and achieved better results. Here, we introduce non-local modules into the video super-resolution task. The module uses all the corresponding points information to calculate the output of the corresponding point in the feature map. The non-local module has a larger search range. It directly captures the long-distance effective information by calculating the similarity between any two positions in the feature map, and weights them. This is not limited to the calculation between adjacent points, but equivalent to constructing a convolution kernel as large as the size of the feature map to calculate the global information, so that more information can be maintained.

As mentioned above, the specific formula of non-local module in neural network is as follows:

$$y_i=\frac{1}{C\left(x\right)}\sum _{{\forall }_j}f(x_i,x_j)g\left(x_j\right)$$

(1)

where, x and y are the input signal and output signal, respectively, with the same size. $f(x_i,x_j)$ represents the Gaussian function $f(x_i,x_j)=e^{x_i^T{x}_j}$ we chose, it can compute the similar relationship between i and all possible associated positions j in the feature map. $g\left(x_j\right)$ is $1\times 1$ convolution, it stands for the characteristic value of the input signal at position j, and $C\left(x\right)={\sum }_{\forall j}f(x_i,x_j)$ is the normalized parameter.

As illustrated in Figure 3, when the non-local module calculates the output matrix Y of the feature map X, the size of the input and output feature map are consistent, and the output of each point is associated with all other points. Take a $3\times 3$ feature map as an example, when calculating the output of the $x_1$ point corresponding to the $y_1$ point, according to the similarity calculation function f in formula (1), the correlation between this point and all other points in the feature map is firstly calculated, and the correlation matrix F is obtained. Secondly, through the mapping function g, each point in the feature map is transformed to obtain the mapping matrix G. Finally, multiply the corresponding points in the two feature matrices and sum them to obtain the output $y_1$ of this point.

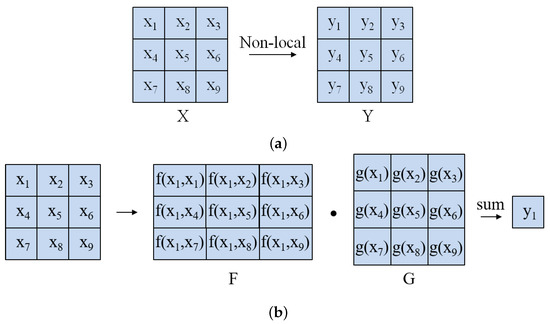
Figure 3. Non-local calculation in module. (a) The output matrix of feature map X through non-local module; (b) The calculation process of non-local module.

3.3. Multi-Scale Feature Fusion Block

In order to fully extract the feature information of video frame sequence and improve the utilization of network parameters, we propose a multi-scale feature fusion block, which is applied to the OFRnet and SRnet parts of the network respectively.

The specific structure of multi-scale feature fusion block is shown in Figure 4. The first part, the convolution kernel of $3\times 3$ and $5\times 5$ are arranged in parallel, which mainly extract the feature information of different scales and splice the convolution results, so that the spliced results contain the feature information of different scales. Here, $3\times 3$, $5\times 5$ and the aforementioned $1\times 1$ represent the size of the convolution kernels, respectively. The second part, convolution kernels of size $3\times 3$ and size $5\times 5$ are connected by superposition, so as to better extract non-linear features through stacking, and fuse feature information of different scales at the same time. Different connection methods effectively fuse and use the feature information extracted by the convolution of different scales, so that the reconstruction results contain richer high-frequency information.

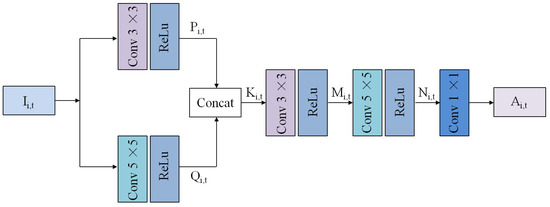
Figure 4. The structure of the proposed MSFFB.

The feature map $I_{i,j}$ in Figure 4 is processed by parallel $3\times 3$ convolution kernel and $5\times 5$ convolution kernel, and the nonlinear transformation of the obtained features is carried out through the ReLU function to obtain feature matrices P and Q. The calculation method is as follows:

$$P_{i,t}=L(w_{3\times 3}^{\left(1\right)}\ast I_{i,t}+b_1)$$

(2)

$$Q_{i,t}=L(w_{5\times 5}^{\left(1\right)}\ast I_{i,t}+b_2)$$

(3)

where, L is the ReLU activation function, the subscripts i and t respectively represent the t-th frame of the i-th video sequence, and the parameters $w_{3\times 3}^{\left(1\right)}$, $w_{5\times 5}^{\left(1\right)}$, $b_1$ and $b_2$ are obtained by network training. The symbol ∗ represents the convolution operations.

Next, the obtained feature matrices P and Q are spliced according to the channel to obtain the feature matrix K. The feature matrices M and N are obtained by successively passing through the $3\times 3$ convolution kernel and the $5\times 5$ convolution kernel in series. Where M and N are calculated as follows:

$$M_{i,t}=L(w_{3\times 3}^{\left(2\right)}\ast K_{i,t}+b_3)$$

(4)

$$N_{i,t}=L(w_{5\times 5}^{\left(2\right)}\ast M_{i,t}+b_4)$$

(5)

where, L is the ReLU activation function, the subscripts i and t respectively represent the t-th frame of the i-th video sequence, and the parameters $w_{3\times 3}^{\left(2\right)}$, $w_{5\times 5}^{\left(2\right)}$, $b_3$ and $b_4$ are obtained by network training.

Finally, the $1\times 1$ convolution kernel is used to reduce the dimension of the feature matrix $N_{i,t}$, so that the number of channels becomes half of the original, and the output feature $A_{i,t}$ of the module is obtained.

4. Experiments

We selected 145 video clips with 1080P HD from the CDVL database as training data, which include different natural and urban scenes, as well as rich textures. We selected four video clips including foreman, garden, husky and coastguard from the Derf’s collection as the validation set. In order to compare with other video super-resolution methods fairly, we tested our method on the benchmark dataset Vid4 [56], which contains four different scenarios. We selected 10 scenarios from the DAVIS dataset to further compare our methods, and named the selected data as DAVIS-10, which is consistent with the practice of reference [57]. Each test dataset contained 31 consecutive frames in the video clip.

We downsampled the original video clips of CDVL dataset to a size of $540\times 960$ through bicubic interpolation as HR groundtruth. These high-resolution video clips are further downsampled to generate low-resolution video clips with different upscaling factors. During training, we randomly extracted three consecutive frames from low-resolution video clips, and then randomly crop a $32\times 32$ patch as input. The position of the high-resolution video clips corresponding to the patch is also cropped out as the groundtruth. In order to increase the generalization ability of the network, we used random rotation and reflection to enhance the data.

We used peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) to evaluate the quality of the generated video sequences. PSNR can measure the objective quality of video frames, and SSIM can assess the similarity of video frames. All evaluation indicators were carried out on luminance channel in YCbCr color space of the video frames.

We trained our model with ADAM optimizer by setting ${\beta }_1=0.9$, ${\beta }_2=0.999$, and we set minibatch size as 16 in PyTorch. The initial learning rate is set to $2\times {10}^{-4}$, and it reduced by half every 50K iterations. We have trained a total of 400K iterations from the beginning on NIVIDIA GTX 1080Ti GPU.

4.1. Ablation Experiments

In this section, we performed ablation experiments on the DAVIS-10 dataset. By removing different modules of the proposed method, the effects of the different parts of the proposed method are shown by comparing with SOF-VSR method. The bicubic interpolation (BI) degradation model based on bicubic interpolation was also used here.

The main comparison method in this section is SOF-VSR [24]. Firstly, we used residual dense block (RDB) to reconstruct the video frames in our network in super-resolution. Secondly, we removed the non-local module in our network to super-resolution reconstruct the video frames. Finally, we used our complete method to super-resolution reconstruct the video frames. As shown in Table 1, we use PSNR/SSIM values to evaluate the performance of the proposed method.

Table 1. PSNR and SSIM of the reconstruction results by ×4 scale of the proposed method and the variant method on the DAVIS-10 dataset. The result of the SOF-VSR* method is the result reproduced under the same operating environment of the proposed method, and the best results are shown in boldface.

Method	PSNR	SSIM
SOF-VSR*	34.19	0.923
Proposed without MSFFB	34.26	0.924
Proposed without Non-local	34.29	0.927
Proposed	34.52	0.930

It can be seen from Table 1 that, compared with SOF-VSR method, the reconstruction result of the video frame is improved in the method of removing MSFFB. Due to the existence of the non-local module, the connection between remote pixels of the video frame is established. When using MSFFB with the non-local module removed, compared with the method of only introducing the non-local module, this method has richer texture and better PSNR/SSIM values since MSFFB can extract the feature information of video frames at different scales. Finally, the proposed method achieves the best results because it combines the advantages of non-local module and MSFFB.

Figure 5 shows the histogram of PSNR comparison the reconstruction results of the SOF-VSR method and different modules removed by the proposed method in the ablation experiment. From the figure, we can see the impact of removing different modules on the super-resolution results of different video sequences. The proposed method combines the advantages of each module and achieves the highest PSNR value in the super-resolution reconstruction results of different video sequences.

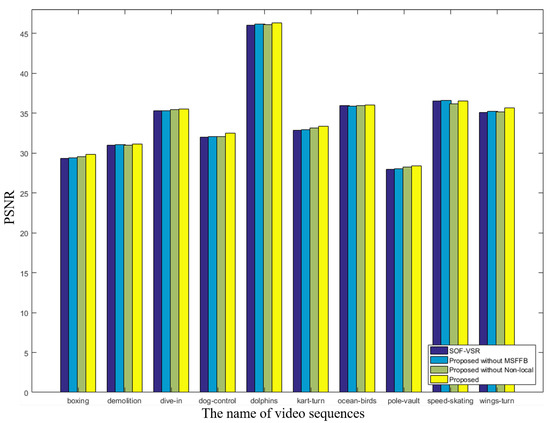
Figure 5. Reconstruction of different video sequences on DAVIS-10 dataset with ×4 scale, the reconstruction results of different methods are compared. The vertical axis represents the PSNR value and the horizontal axis represents the video frame sequence.

In order to further verify the restoration effect of the algorithm on the texture details in the video frames, we used the Sobel operator to extract the details of the video frames, constructed a mask with algorithms with small restoration deviations, and observed the restoration effects of different algorithms on different intensities of details. Table 2 compares the percentage of the dominant points in the Sobel texture region of the label image between the SOF-VSR method and the proposed method. The HR column represents the percentage of the Sobel texture of the label image in the whole image, while the S/HR column and P/HR column represent the percentage of the dominant point of the Sobel texture area of reconstruction results of the SOF-VSR method and proposed method, respectively, to the Sobel texture area of the label image.

Table 2. The percentage of reconstruction results of different methods with ×4 scale in Sobel texture region of label image on city video sequence of Vid4 dataset.

Threshold Value	HR	S/HR	P/HR	(P+S)/HR	(P-S)/HR
<150	2.74	36.95	42.84	79.79	5.89
<100	6.84	38.73	44.42	83.15	5.69
<50	16.70	38.80	45.56	84.36	6.76
=0	31.23	36.63	43.36	79.99	6.73
>20	4.91	30.33	36.69	67.02	6.36
>50	14.82	34.10	40.93	75.07	6.83
>100	24.50	36.06	43.06	79.12	7.00
>150	28.54	36.59	43.42	80.01	6.83

The (P+S)/HR column represents the percentage of the sum of the dominant points of the proposed method reconstruction result and the dominant points of the SOF-VSR method reconstruction result to the Sobel texture of the label image. The (P-S)/HR column represents the percentage of the difference between the dominant points of the proposed method reconstruction result and the dominant points of the SOF-VSR method reconstruction result to the Sobel texture of the label image. It can be seen from this column that the texture reconstruction details of the proposed method in different pixel intervals are better than SOF-VSR method.

In the first column of Table 2, <150 means that the Sobel texture area sets all points with a pixel value less than 150 to 0, that is, only the strongest fine nodes are considered. Similarly, <100 means that more strong texture details are counted, =0 means that no action has been taken on each method to reconstruct the results, while >20 means to set all points greater than 20 to 0, that is, the weakest texture point is obtained. Similarly, >150 means to count more weak texture details. The purpose is to view the reconstruction results of different methods in the strong texture pixel interval and weak texture pixel interval of the image, so as to compare which interval is more suitable for different methods of super-resolution reconstruction. It can be seen from Table 2 that in each different pixel interval, our method is better than the SOF-VSR method.

Figure 6 is a comparison between the reconstruction results of the proposed method in the ablation experiment and the reconstruction results of the SOF-VSR method in the texture area of the video frame. This figure intuitively shows the difference between the reconstruction results of the proposed method and the SOF-VSR method in the contour and texture of the object in the video frame. Figure 6c shows the distribution of the pixel points in the image texture with the advantage of the SOF-VSR method in the result comparison, and Figure 6d shows the distribution of the points in the image texture with the advantage of the proposed method in the result comparison. For more intuitive comparison, Figure 6(e1,f1,g1) enlarges the texture area of the label image, Figure 6(e2,f2,g2) enlarges the texture area of the reconstruction result of SOF-VSR method and Figure 6(e3,f3,g3) enlarges the texture area of the reconstruction result of proposed method. From the comparison, it can be seen that the reconstruction result of proposed method has richer texture.

Figure 6. Texture of reconstruction results between proposed method and SOF-VSR method on city video sequence of Vid4 dataset. Figure (a) is the label image, and Figure (b) is the texture image processed by the Sobel operator of the label image; Figure (c) shows the dominant pixel distribution of the reconstruction result of SOF-VSR method in the texture region, and Figure (d) shows the dominant pixel distribution of the reconstruction result of proposed method in the texture region; Figures (e1,f1,g1) show the enlargement of the local texture area of the label image, Figures (e2,f2,g2) show the enlargement of the result local area of the SOF-VSR method, and Figures (e3,f3,g3) show the enlargement of the result local area of the proposed method.

Under different downsampling methods, the performance of different methods is also different. Here, we use ×4 scale of average downsampling and bilinear downsampling for Vid4 dataset to obtain different low-resolution video sequences. Different methods are used for super-resolution, and the reconstruction results are compared, as shown in Table 3. The PSNR of the average downsampling reconstruction results of the proposed method is slightly lower than that of the SOF-VSR method, but the proposed method has higher SSIM reconstruction results for different downsampling methods than the SOF-VSR method, which shows that the proposed method has good generalization ability for maintaining the detailed structure of video frames.

Table 3. The reconstruction results of ×4 scale of mean downsampling and bilinear downsampling with different methods of super-resolution. The best results are shown in boldface.

Model	Method	PSNR	SSIM
Average	SOF-VSR	24.90	0.752
	Proposed	24.82	0.756
Bilinear	SOF-VSR	25.49	0.742
	Proposed	25.68	0.752

4.2. Comparative Experiment

We test our method on the Vid4 dataset and DAVIS-10 dataset, we use two degradation methods to obtain different low-resolution video frames. The BI degradation method is based on bicubic interpolation downsampling and the BD degradation method is formed by Gaussian kernel blur and downsampling.

In the BI degradation model, we reconstruct the Vid4 dataset by ×2, ×3, ×4 upsampling factors. As shown in Table 4, our method significantly improves the PSNR and SSIM values compared with other video super-resolution methods. At the same time, we also show the results of only adding non-local module in the proposed method, which also improves the PSNR and SSIM values to a certain extent.

Table 4. The reconstruction results of the Vid4 dataset at different reconstruction scales. The method marked with * only used the non-local module, and the best results are indicated in boldface.

Model	Scale	Method	PSNR	SSIM
BI	×2	Bicubic	28.42	0.866
		DRCN [33]	31.57	0.924
		LapSRN [28]	31.41	0.923
		CARN [34]	31.96	0.931
		VSRnet [3]	31.29	0.927
		SOF-VSR [24]	33.17	0.947
		Proposed*	33.29	0.948
		Proposed	33.63	0.951
	×3	Bicubic	25.26	0.730
		DRCN [33]	26.82	0.805
		CARN [34]	27.16	0.818
		VSRnet [3]	26.75	0.807
		VESPCN [10]	27.25	0.845
		SOF-VSR [24]	28.09	0.861
		Proposed*	28.26	0.864
		Proposed	28.46	0.871
	×4	Bicubic	23.75	0.630
		DRCN [33]	24.94	0.707
		LapSRN [28]	24.98	0.711
		CARN [34]	25.27	0.725
		VSRnet [3]	24.81	0.702
		VESPCN [10]	25.35	0.756
		SOF-VSR [24]	26.01	0.771
		Proposed*	26.05	0.773
		Proposed	26.21	0.782
BD	×4	SPMC [12]	25.99	0.773
		SOF-VSR [24]	26.19	0.785
		Proposed*	26.29	0.791
		Proposed	26.43	0.797

In the BD degradation model, as shown in Table 4, we only compare the reconstruction ×4 upsampling factor. The PSNR and SSIM values of our two methods are higher than those of other methods, which objectively proves the effectiveness of our method.

We select calendar and city video sequences from Vid4 dataset to intuitively display the super-resolution results of different methods. As shown in Figure 7, this is the results of reconstructing ×4 upsampling factor under the BI degradation model. On calendar video frames, our two methods have clear handwriting and object contour, while other methods have problems such as blurred handwriting and object edge. On the city video frames, our method can clearly distinguish the windows of buildings, while in the magnification results of other methods, the windows of buildings are blurred.

Figure 7. Visual comparisons of reconstruction results of ×4 scale on calendar and city video frames. The left side of the dashed line is the reconstruction result of the BI degradation model. The magnified area is the HR in sequence, and the reconstruction results of methods Bicubic, CARN, SOF-VSR, Proposed*, Proposed. The right side of the dashed line is the reconstruction result of the BD degradation model, and the zoomed-in area is HR, the reconstruction results of methods SOF-VSR, Proposed* and Proposed based on BD degradation model. The method marked with * only used non-local module.

The reconstruction results of the ×4 upsampling factor in the BD degradation model are also shown. It can be seen from Figure 7 that our method clearly reconstructs the contour of the object.

In the DAVIS-10 dataset, we also show the reconstruction results of different methods under BI degradation model and BD degradation model. As shown in Table 5, the PSNR and SSIM values of our method are higher than other methods in the reconstruction results of ×2, ×3 and ×4 upsampling factors.

Table 5. The reconstruction results of the DAVIS-10 dataset at different reconstruction scales. The method marked with * only used non-local module, and the best results are indicated in boldface.

Model	Scale	Method	PSNR	SSIM
BI	×2	Bicubic	36.43	0.958
		DRCN [33]	40.62	0.979
		LapSRN [28]	40.30	0.978
		CARN [34]	40.99	0.981
		VSRnet [3]	39.00	0.972
		SOF-VSR [24]	41.38	0.983
		Proposed*	41.00	0.982
		Proposed	41.35	0.984
	×3	Bicubic	32.94	0.912
		DRCN [33]	36.08	0.947
		CARN [34]	36.70	0.952
		VSRnet [3]	34.94	0.936
		SOF-VSR [24]	36.80	0.955
		Proposed*	36.63	0.953
		Proposed	37.02	0.958
	×4	Bicubic	30.97	0.870
		DRCN [33]	33.49	0.911
		LapSRN [28]	33.54	0.911
		CARN [34]	34.12	0.921
		VSRnet [3]	32.63	0.897
		SOF-VSR [24]	34.32	0.925
		Proposed*	34.26	0.924
		Proposed	34.52	0.930
BD	×4	SPMC [12]	33.02	0.911
		SOF-VSR [24]	34.28	0.927
		Proposed*	34.43	0.930
		Proposed	34.69	0.933

We select two different video frames to visually display the ×4 upsampling factor reconstruction results of different methods in BI degradation model in Figure 8. Analyzing the reconstruction of the boxing video sequence, it is not difficult to see that the letters behind athletes appear blur or adhere after using other reconstruction methods, while the reconstruction results of our method are clear and accurate. On the demolition video sequence, compared with other methods, the result of the proposed method can achieve a clear character outline on the building.

Figure 8. Visual comparisons of reconstruction results of ×4 scale on boxing and demolition video frames. The left side of the dashed line is the reconstruction result of the BI degradation model. The magnified area is the HR in sequence, and the reconstruction results of methods Bicubic, CARN, SOF-VSR, Proposed*, Proposed. The right side of the dashed line is the reconstruction result of the BD degradation model, and the zoomed-in area is HR, the reconstruction results of methods SOF-VSR, Proposed* and Proposed based on BD degradation model. The method marked with * only used non-local module.

On displaying the reconstructed boxing and demolition video sequences of the BD degradation model with an upsampling factor of ×4, we can see that the contours of the letters in our reconstruction result are clear, while the letters reconstructed by other methods are blurred.

5. Conclusions

In this work, from the perspective of feature space, we use the non-local module to process the feature points that are far away from each other in the feature map, which overcomes the limitation of convolution operation, amplifies the receptive field of the network and improves the quality of the network reconstruction results. Furthermore, we propose a multi-scale feature-fusion block to extract different video frame features by convolution kernel of different scales. Compared with the existing video super-resolution methods, our method achieves the better reconstruction results on test datasets Vid4 and DAVIS-10.