Reconfigurable Low-Density Parity-Check (LDPC) Decoder for Multi-Standard 60 GHz Wireless Local Area Networks

Abstract

In this study, a reconfigurable low-density parity-check (LDPC) decoder is designed with good hardware sharing for IEEE 802.15.3c, 802.11ad, and 802.11ay standards. This architecture flexibly supports 12 types of parity-check matrix. The switching network adopts an architecture that can flexibly switch between different inputs and achieves a low hardware complexity. The check node unit adopts a switchable 8/16/32 reconfigurable structure to match different row weights at different code rates and uses the normalised probability min-sum algorithm to simplify the structure of searching for the minimum value. Finally, the chip is implemented using the TSMC 40 nm CMOS process, based on the IEEE 802.11ad standard decoder, extended to support the IEEE 802.15.3c standard, and upwardly compatible with the next-generation advanced standard IEEE 802.11ay. The chip core size was 1.312 mm × 1.312 mm, the operating frequency was 117 MHz when the maximum number of iterations was five with the power consumption of 57.1 mW, and the throughput of 5.24 Gbps and 3.90 Gbsp was in the IEEE 802.11ad and 802.5.3c standards, respectively.

1. Introduction

With the rapid development of multimedia equipment and the advancement of technology, ultra-high-quality equipment with a resolution of 3840 × 2160 (4K2K) pixels, such as ultra-high-definition television (UHDTV) projectors, has been developed. Most products use high-definition multimedia interface (HDMI) lines as transmission media, which is expensive and has length limitations; therefore, wireless transmission is an ideal solution. Equipment for augmented reality (AR) or virtual reality (VR), mirroring mobile devices, etc., also tend to use wireless transmission. Thus, 60 GHz wireless transmission plays an important role in the fifth-generation (5G) era, where a high transmission rate, large data volume, and low latency are emphasised.

In communication systems, forward error correction (FEC) is used to protect data from errors caused by noise interference during transmission. After the data are encoded by the error correction code, even if noise interference occurs in the transmission channel during transmission, the error message can be recovered at the receiving end through the decoding process. In 1962, Gallager invented a low-density parity-check (LDPC) [1] code, and after MacKay added the concept of iterative processing in 1999 [2], the decoding performance was very close to the Shannon limit. Because LDPC codes have excellent error correction performance, they are widely used in wireless communication systems, including the IEEE 802.11ad/ay standard adopted by Wireless Gigabit (WiGig), the IEEE 802.15.3c standard adopted by Wireless HD (WiHD), and the IEEE 802.11ax standard adopted by Wi-Fi. Furthermore, LDPC codes can be considered to improve the quality of transmission of critical applications using the 2.4 GHz-based Zigbee/Bluetooth communications [3,4] and artificial-intelligence-assistant wireless sensor networks [5,6,7] because of their excellent error correction performance and efficient hardware acceleration. Additionally, the LDPC code was proposed in the 15th edition of the 5G new-radio (NR) specification published in 2018. Recently, several studies proposed hardware-efficient LDPC encoders [8,9] and decoders [10,11] for high-throughput 5G NR communication systems.

In recent years, many communication standards that adopted the LDPC code have been introduced in HD video wireless transmission, as shown in Table 1. It can be seen that, compared with the crowded 2.4 GHz band, the standard applied on the 60 GHz frequency band has the advantage of a high transmission rate. While WiHD uses the IEEE 802.15.3c communication standard and WiGig uses IEEE 802.11ad and its upgrade standard IEEE 802.11ay, the communication specifications of the three standards are different. If hardware sets are designed independently for each communication standard, the associated costs are extremely high. Thus, the previous study in [12] has been proposed a key reconfiguarable processing unit of LDPC decoding for the IEEE 802.15.3c and IEEE 802.11ad standards.

Table 1. Current wireless transmission technology for 60GHz wireless local area networks.

Application	WiHD	WiGig
Transmission standard	IEEE 802.15.3c	IEEE 802.11ad	IEEE 802.11ay
Working frequency	60 GHz	60 GHz	60 GHz
FEC code	LDPC codes (Code rate: 1/2–7/8)	LDPC codes (Rate 1/2–13/16)	LDPC codes (Rate 1/2–13/16)
Theoretical transmission rate	10~28 Gbps	7~28 Gbps	20~100 Gbps

In this study, we have further designed and implemented a complete LDPC decoder based on the IEEE 802.11ad standard, extended to support the IEEE 802.15.3c standard and upwardly compatible with the IEEE 802.11ay standard, with low hardware cost, low power consumption, and high throughput. To our best knowledge, this study presents the first reconfigurable multimode LDPC decoder architecture that flexibly supports 12 LDPC matrices of the IEEE 802.15.3c, IEEE 802.11ad, and IEEE 802.11ay standards for HD video wireless transmission and provides sufficient details through detailed architecture design and the prototyping chip implementation. To support different standards, block-layer divisions of the matrices in the different standards are initially proposed to achieve reconfigurability and good hardware sharing for the reconfigurable LDPC decoding. In order to match the different row weights of different LDPC matrices, a switchable 8/16/32 hardware-shared structure is subsequently proposed for the key computational units, memories, and switching network and employed in the reconfigurable LDPC decoder architecture. The designed switching network flexibly switches between different inputs and achieves low hardware complexity. Compared with the traditional switching network, the designed switching network only requires 0.08% look-up-table bits to reconfigure the switches and support the multiple standards. The reconfigurable multimode LDPC decoder has been implemented using the TSMC 40 nm CMOS process in a core size of 1.72 mm² with the power consumption of 57.1 mW and throughput of 5.24 Gbps at the maximum operating frequency of 117 MHz in the IEEE 802.11ad standard. Additionally, the throughput of 3.9 Gbps and power consumption of 57.1 mW are achieved at the same operating frequency in the IEEE 802.15.3c standard. Compared with the LPDC decoders that support the individual standard, the reconfigurable multimode LDPC decoder implementation achieves approaching area efficiency and energy efficiency to alternatively support the IEEE 802.15.3c, IEEE 802.11ad, and IEEE 802.11ay standards.

The rest of this study is organised as follows. In Section 2, the characteristics and decoding of LDPC code are introduced. In Section 3, LDPC decoding is evaluated using the matrices of three standards for the 60 GHz wireless local area networks. In addition, for reconfigurability, the matrixes are divided into block layers. Section 4 describes the proposed decoder architecture in detail, including the computational units, switching network, and memory. Section 5 presents the VLSI implementation results of the proposed LDPC decoder and compares them with other related works. Finally, Section 6 concludes the study.

2. Fundamentals of LDPC Code and Decoding

The LDPC code is a type of linear block code composed of a sparse matrix. The sparse matrix is a parity-check matrix H composed of mostly 0′s and a lesser number of 1′s. There are N columns and M rows in the H matrix, and the code rate is defined as $R=\left(N-M\right)/N$. In the H matrix, each row represents a check node (CN), and the number of 1′s in each row is called the row weight ($w_r$); each column represents a variable node (VN), and the number of 1′s in each column is called the column weight ($w_c$). The 1 in the H matrix also represents the exchange of data between the CN and VN, as shown in Figure 1.

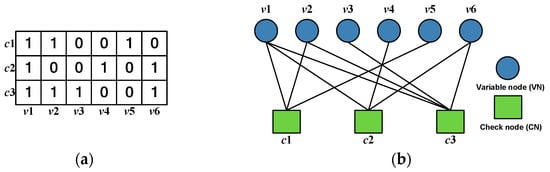
Figure 1. Example of (a) H matrix mapping to the (b) Tanner graph.

The quasi-cyclic (QC) LDPC code [13] is a common method for hardware implementation of LDPC decoding because it achieves different parallelisms in decoding with greater ease and enables easier memory access owing to its regularity. Figure 2 shows the QC-LDPC H matrix with R = 13/16 in the IEEE 802.11ad standard. Each block is a submatrix with an expending factor $z$. The blank block is a $z\times z$ zero matrix. The number represents the number of shifts in the $z\times z$ identity matrix to the right. The entire matrix can be expressed as $m\times n$ where $m=M\times z$ and $n=N\times z$.

Figure 2. Example of QC-LDPC matrix.

The recent soft and hard decoding algorithms of LDPC codes have been significantly reviewed and summarized in [14]. The original soft decoding algorithm is the sum-product algorithm (SPA) [2], which has excellent error correction performance; however, the hardware implementation complexity is high. The normalised min-sum algorithm (NMSA) [15] instead of the SPA was widely used in chip implementations because of its low hardware complexity and good error-correction capabilities [16]. In terms of decoding, the iterative layer decoding schedule [17] was utilised, which includes two operations, CN and VN, and the decoding process, as shown in Figure 3. After receiving the channel information, the decoder starts iterative decoding. In the NMSA, we initially define $y_j$ as the received channel information, $L_{init, j}$ as initial log-likelihood ratio (LLR) message, $Q_{i,j}^k$ as prior message, $R_{i,j}^k$ as extrinsic message, and L_j as posterior message, where i is the index of the row of H, j is the index of the column of H, and k is the index of the decoding iteration. The NMSA includes four steps, and the equations are described as follows.

Figure 3. Flowchart of iterative LDPC decoding.

• Initialization:
  The decoder receives each jth channel message y_j to initialise $L_{init, j}$.

  $$L_{init, j}=log\left( \frac{P(x_j=0|y_j)}{P(x_j=1|y_j)}\right).$$

  (1)
• Prior message updates:
  If k = 1, $L_j$ is updated as $L_{init, j}$ and $R_{i,j}^0$ is set to zero.

  $$Q_{i,j}^k=L_j-R_{i,j}^{k-1}.$$

  (2)
• CN (extrinsic message) updates:

  $$R_{i,j}^k=\alpha ·\left({\displaystyle \prod }_{j^{\prime }\in N\left(c\right)\backslash j}sign\left(Q_{i,j^{\prime }}^k\right)\right)\left(\underset{j^{\prime }\in N\left(c\right)\backslash j}{\min }\left|Q_{i,j^{\prime }}^k\right|\right),$$

  (3)

  where $\alpha$ is a normalisation factor.
• VN (posterior message) updates:

  $$L_j=Q_{i,j}^{k-1}+{\displaystyle \sum }_{i\in M\left(v\right)}{R}_{i,j}^k.$$

  (4)

The steps 2–4 iteratively continues until the maximum number of iterations is reached. When the iteration terminates, a hard decision is made by

$$h_j=\{\begin{array}{c}0, \mathrm{if} L_j\ge 0\\ 1, \mathrm{if} L_j<0\end{array}.$$

(5)

For reference, the study in [18] extends single-decoder decoding to parallel decoding with multiple sub-decoders and improves decoding performance of an LDPC code.

To reduce the hardware complexity of independently designing a set of decoders for different standards, this study proposes that it can be used in IEEE 802.11ad, IEEE 802.15.3c, and IEEE 802.11ay multimode LDPC decoders. Instead of using the NMSA, this study used the normalised probability min-sum algorithm (NPMSA) [19], which has low hardware complexity. In general, Equation (3) is the critical step with the highest computational complexity. To further simplify the computational complexity, the NPNSA was used to simplify the comparator in the sorter. The original comparator compares the two input data (IN_1 and IN_2) and outputs the minimum value (Min) and the second minimum value (2nd Min), as shown in Figure 4a. However, the simplified comparator discards the information of the second minimum value and outputs only that of the first minimum value, as shown in Figure 4b. According to this method, the second minimum value obtained was probably correct (Prob. Min), as shown in Figure 5. Dividing the input of the sorter into G groups and using G to 2 comparators in the last stage of the comparators slightly reduces the performance, but it can significantly reduce the hardware complexity of the operation. For reference, several alternative methods [11,20,21] were proposed to reduce the gap between the accurate second minimum and probabilistic second minimum and recover the decoding capability.

Figure 4. (a) 2-to-2 comparator and (b) 2-to-1 comparator.

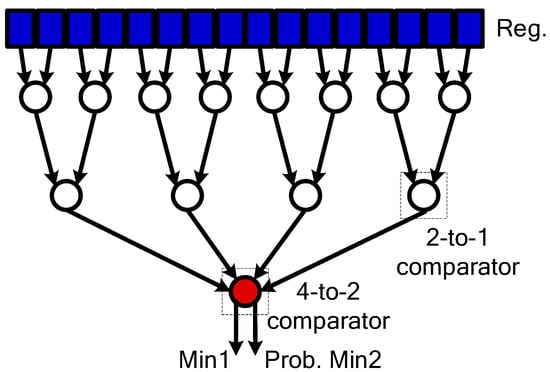
Figure 5. The architecture of the NPMSA minimum sorter.

3. Proposed LDPC Decoding for the Multi-Standard 60 GHz Wireless Local Area Networks

To design a set of hardware-sharing decoders, it is necessary to understand the matrix parameters in all standards and to identify the parts that can be shared in different standards.

3.1. Standard Parameters and Matrix Configuration

The QC-LDPC matrix used by IEEE 802.11ad has R = 1/2, 5/8, 3/4, and 13/16, as shown in Figure 6a,b. M changes according to distinct R, that is, 8, 6, 4, and 3. N is fixed at 16 and z is 42. Therefore, n is 16 × 42 = 672. The QC-LDPC matrix used in the IEEE 802.15.3c standard also has R = 1/2, 5/8, 3/4, and 7/8, as shown in Figure 7a,b. N is fixed at 32, and z is 21. It can be observed that n is 32 × 21 = 672, as for IEEE 802.11ad.

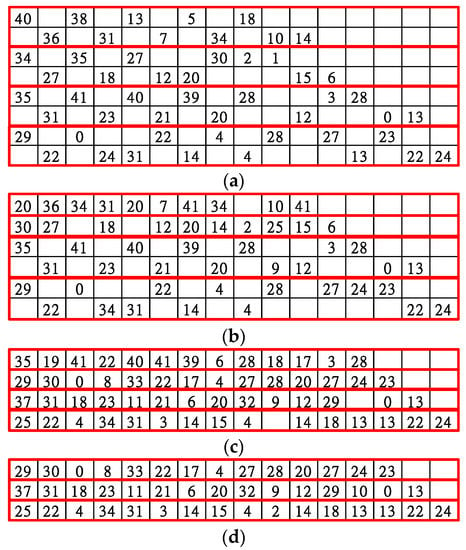
Figure 6. IEEE 802.11ad parity check matrix with R = (a) 1/2, (b) 5/8, (c) 3/4, and (d) 13/16.

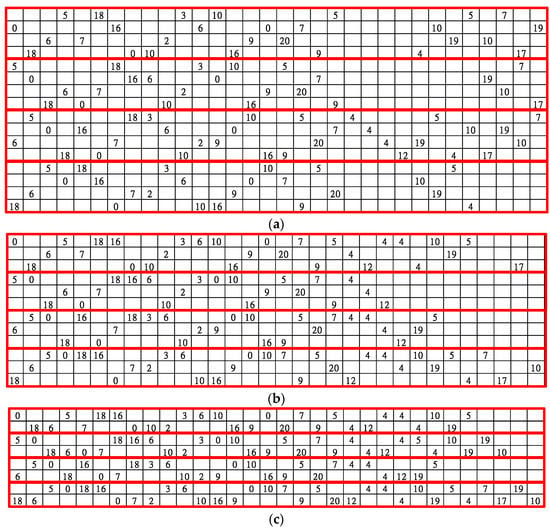
Figure 7. IEEE 802.15.3c parity check matrix with R = (a) 1/2, (b) 5/8, (c) 3/4, and (d) 7/8.

IEEE 802.11ay is the upgraded standard of IEEE 802.11ad, and its QC-LDPC matrix is made up of the IEEE 802.11ad matrix in-place 2nd lifting, as shown in Figure 8. Taking R = 13/16 as an example, the first submatrix with a value of 29 is expanded into four submatrices after the 2nd lifting operation. The 2nd lifting matrix only has two values: 0 and 1. Zero indicates that the value of the original matrix is expanded in the format of the identity matrix, and 1 indicates that the value of the original matrix is expanded in the format of the identity matrix and shifted by one unit to the right. The IEEE 802.11ay matrix and the 2nd lifting matrix are shown in Figure 9 and Figure 10. Finally, we unified the three standard parameters in Table 2.

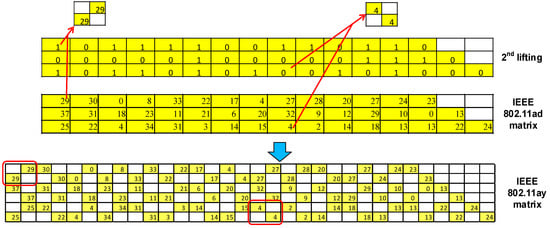
Figure 8. Generation of parity check matrix at IEEE 802.11ay R = 13/16.

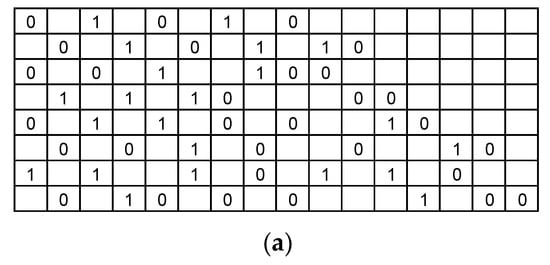
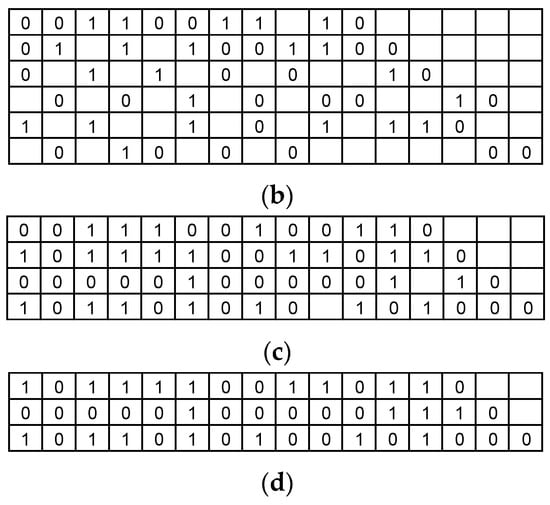
Figure 9. IEEE 802.11ay 2nd lifting matrix with R = (a) 1/2, (b) 5/8, (c) 3/4, and (d) 13/16.

Figure 10. IEEE 802.11ay parity check matrix with R = (a) 1/2, (b) 5/8, (c) 3/4, and (d) 13/16.

Table 2. Parameters of three standards for 60 GHz wireless local area networks.

Standards	IEEE 802.11ay				IEEE 802.11ad				IEEE 802.15.3c
Rate	1/2	5/8	3/4	13/16	1/2	5/8	3/4	13/16	1/2	5/8	3/4	7/8
Row	16	12	8	6	8	6	4	3	16	12	8	4
Column	32	32	32	32	16	16	16	16	32	32	32	32
Expansion factor	42	42	42	42	42	42	42	42	21	21	21	21
Code length	1344	1344	1344	1344	672	672	672	672	672	672	672	672
Row weight	8	10	15	16	8	10	15	16	8	15	16	32

3.2. Proposed Block Layer Decoding for the IEEE 802.11ad, IEEE 802.11ay, and IEEE 802.15.3c Standards

Before deciding on the hardware architecture, we must consider the characteristics of the matrix to determine the hardware parallelism and the amount of computation required. The transmission of decoding information in layer decoding is closely related to the row weights. As an example, the IEEE 802.11ad R = 1/2 matrix is illustrated in Figure 11a. We observe that the row weights are staggered between layers 1 and 2, which implies that the data are not transferred between the two layers for calculation. Therefore, to improve the decoding efficiency, we can decode the two layers without data dependency together, and we refer to this as a block layer, as shown in Figure 11b.

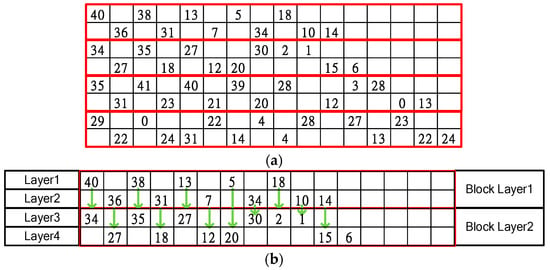
Figure 11. IEEE 802.11ad R = 1/2 block layer: (a) divided block layer and (b) block layer decoded data update transmission.

In the IEEE 802.11ad R = 5/8 matrix shown in Figure 6b, the row weights of layers 1 and 2 are larger and overlap compared with the R = 1/2 matrix. Therefore, layers 1 and 2 in the R = 5/8 matrix are separately regarded as a block layer. However, layers 3–4 and layers 5–6 in the R = 5/8 matrix are the same as those of the R = 1/2 matrix; therefore, the two layers can be regarded as one block layer. R = 3/4 and 13/16 have a high row weight distribution density; therefore, they can be decoded according to the original layer. All the matrix layouts marked in the red blocks are shown in Figure 6.

On the other hand, the IEEE 802.15.3c standard can also use the block layer for decoding operations. It is worth noting that the four matrices of the four code rates of the IEEE 802.15.3c standard can be divided into four block layers, which are the same as those of the IEEE 802.11ad standard as shown in Figure 7.

Finally, the IEEE 802.11ay standard can merge more layers into one block layer for operation. Considering the subsequent hardware parallelism planning, only two layers were merged into one block layer, making the matrix operation similar to the IEEE 802.11ad standard, as shown in Figure 10.

3.3. Finite Word-Lengths of Reconfigurable Multimode LDPC Decoder

Before introducing the proposed architecture of reconfigurable multimode LDPC decoder, it is very important to initially decide the finite word-lengths of the decoder using the fixed-point simulations. First, the floating-point simulations must be performed for evaluating the NPMSA compared with the original NMSA. The simulated channel was AWGN, the normalisation factor was 0.75, and the maximum number of iterations was 5. We simulated IEEE 802.11ad, IEEE 802.15.3c, and IEEE 802.11ay, respectively, as shown in Figure 12, Figure 13 and Figure 14. In the two standards IEEE 802.11ad and IEEE 802.15.3c with a code length of 672, it can be seen that the use of NPMSA will cause some performance loss, but there will be the advantage of reduced hardware complexity. However, in the higher code length IEEE 802.11ay standard, it can be seen that the loss of performance is very small. It can be seen that the longer the code length of the LDPC, the better the decoding performance.

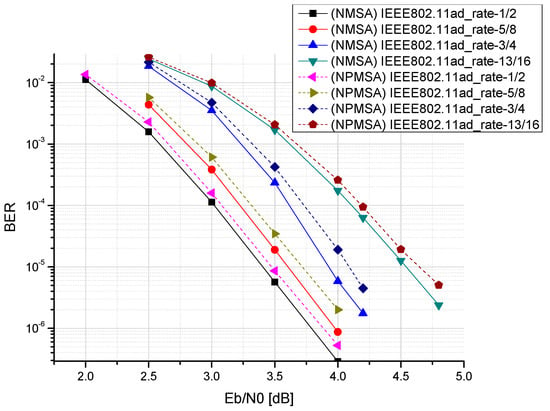
Figure 12. Comparison of decoding performance of different algorithms in IEEE 802.11ad.

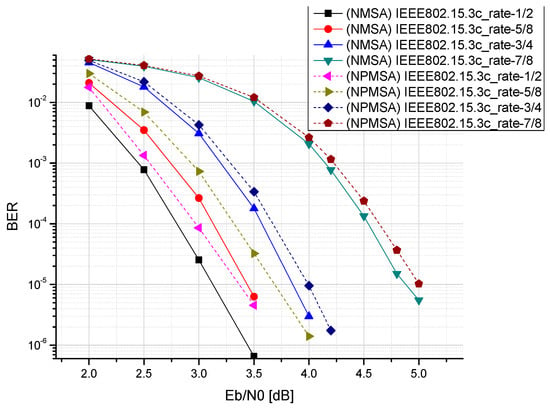
Figure 13. Comparison of decoding performance of different algorithms in IEEE 802.15.3c.

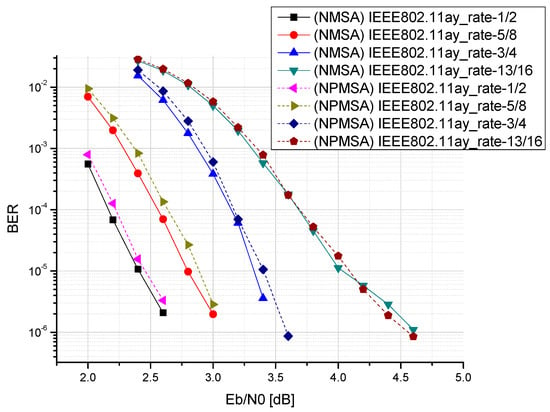
Figure 14. Comparison of decoding performance of different algorithms in IEEE 802.11ay.

After confirming the performance of the algorithm through a floating-point simulation, the fixed-point simulations are used to determine the finite word-lengths required for the quantised multimode LDPC decoding on the hardware. The integer digits are fixed and the fractional bits are increased upwards, as shown in Figure 15, Figure 16 and Figure 17. The bit is represented as (integer bit, fractional bit), and the integer bit does not include a sign bit. Finally, we set the integer bits to five, with one fractional bit. The total number of bits, including the sign bit, is seven. The simulated performance was close to the result of the floating-point simulation.

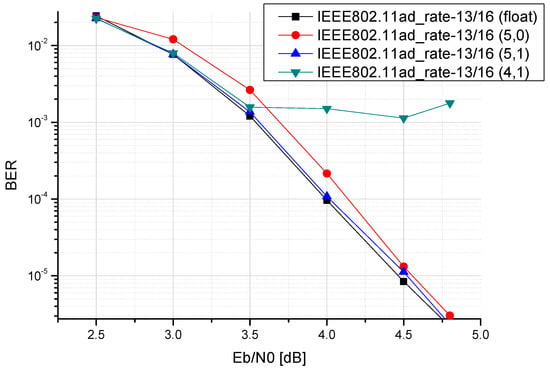
Figure 15. Fixed-point simulation in IEEE 802.11ad R = 13/16.

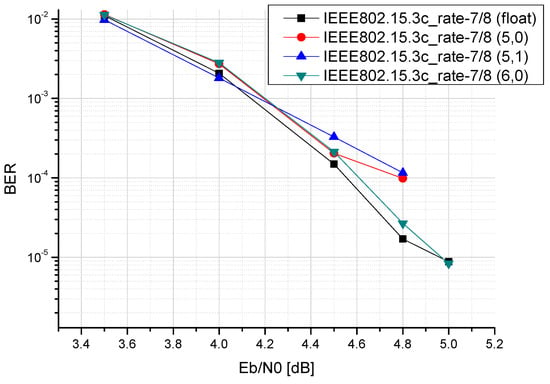
Figure 16. Fixed-point simulation in IEEE 802.15.3c R = 7/8.

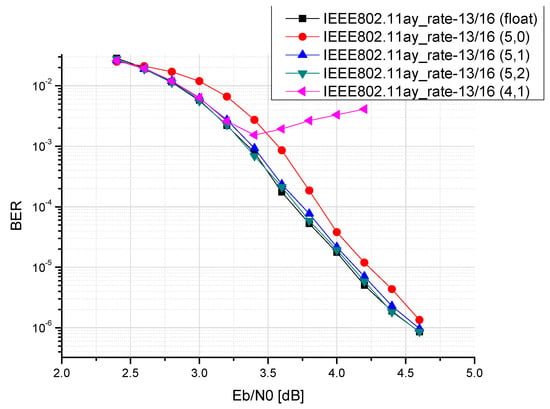
Figure 17. Fixed-point simulation in IEEE 802.11ay R = 13/16.

4. Architecture Design of Proposed Reconfigurable Multimode LDPC Decoder

This section introduces the architecture of a multi-mode LDPC decoder that supports the IEEE 802.11 ad, IEEE 802.15.3 c, and IEEE 802.11 ay standards. This can be divided into three parts. The first part consists of the memory for the calculation result, which includes posterior memory and extrinsic memory. The second part comprises an information switch network with different matrices for different standards. The third part is the computing kernel that contains the prior message processing unit (PMU) for calculating the prior messages, the CN processing unit (CNU) for calculating the extrinsic messages, and the VN processing unit (VNU) for calculating the posterior messages. The architecture is shown in Figure 18. The entire decoder hardware uses seven quantised bits for data transmission, and the arithmetic unit is performed at 21 parallelisms. For more details of the entire LDPC decoder, readers can refer to [22,23].

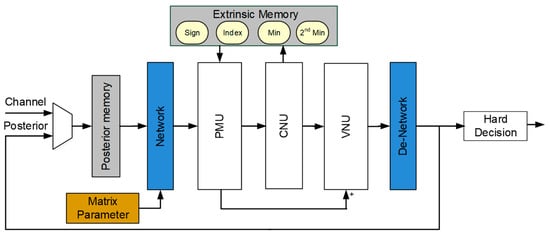
Figure 18. Reconfigurable multi-standard decoder architecture.

4.1. PMU

The PMU receives the prior messages and extrinsic messages of the previous iteration and updates the prior messages. For the first iteration, as there is no information from a previous iteration, the extrinsic messages are initialised to zero, and the information is passed to the CNU for the calculation. In subsequent iterations, the input of the extrinsic messages selects different split blocks according to different matrices. The PMU architecture is illustrated in Figure 19.

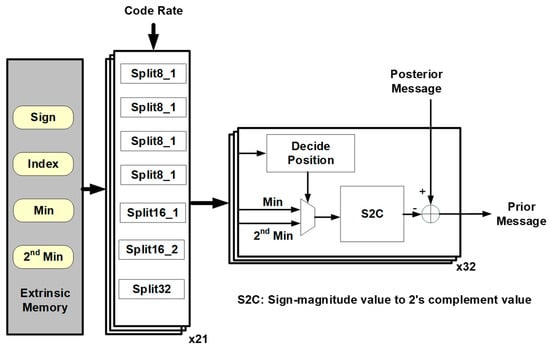
Figure 19. The architecture of the PMU.

4.2. CNU

Figure 20 shows the architecture of the CNU. After receiving the prior message, the sign and magnitude of the message were separated. Because the value of the minimum searcher in CNU must be an absolute value, in terms of signs, exclusive OR logic operations are performed on all signs.

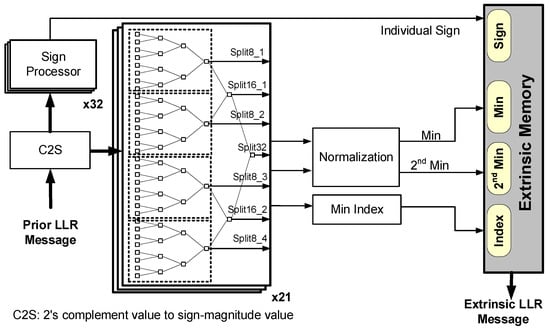
Figure 20. Reconfigurable CNU architecture.

In the sorter, the number of inputs is mainly determined according to the row weight in layered decoding, and a set of sorters can perform a row operation. Thus, the expansion factor $z$ represents the maximum parallelism of the hardware. However, in a multimode decoder, we can regard the defined block layer as a layer operation, and a block layer operation requires 21 sets of the 32-input sorter to be realised. We refer to the reconfigurable architecture of [24], as shown in Figure 21, and apply it to our multimode decoder. This reconfigurable sorter was originally used in the IEEE 802.15.3c standard; however, we extended it to the IEEE 802.11ad and IEEE 802.11ay standards. Specific arrangements are made such that the block layer under different standards and code rates cannot have redundant idle hardware during the calculation process.

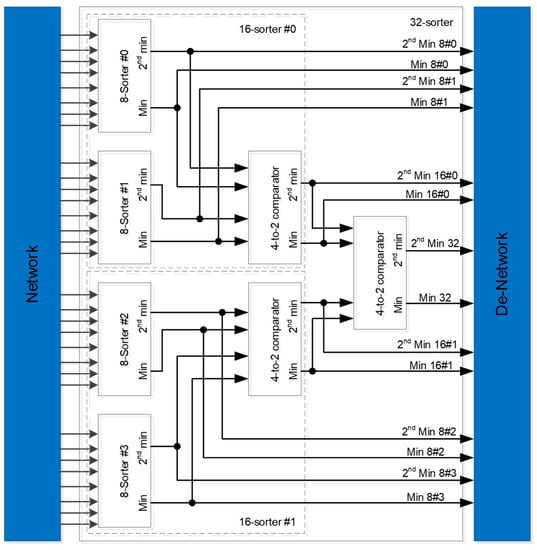
Figure 21. Reconfigurable 8/16/32 input sorter architecture.

Figure 22 shows the IEEE 802.11ad R = 1/2 arrangement. Each sorter-8 represents a minimum value finder (MVF) with eight inputs, and we use 21 sets of parallel hardware for simultaneous operation. We know that the maximum row weight of the IEEE 802.11ad R = 1/2 is 8; therefore, each sorter-8 can calculate one row, and 21 parallelisms can calculate rows 1 to 21. Therefore, sorter-8#1 and sorter-8#2 can only calculate a layer with an expansion factor of 42, and sorter-8#1 to sorter-8#4 can only perform block-layer calculations.

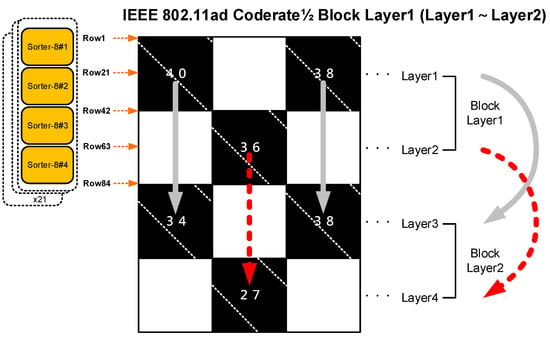
Figure 22. Reconfigurable sorter configuration in IEEE 802.11ad R = 1/2.

The expansion factor of IEEE 802.15.3c is 21, which is half that of IEEE 802.11ad, but the number of layers contained in one block layer is twice that of IEEE 802.11ad; therefore, the same hardware can be used for calculation. Taking the IEEE 802.15.3c R = 1/2 as an example, as shown in Figure 23, R = 1/2 uses four sets of sorter-8 for calculation. In the case of a parallelism of 21, sorter-8#1 can handle operations from rows 1 to 21 in one layer, whereas sorter-8#1 to sorter-8#4 can only operate on one block layer.

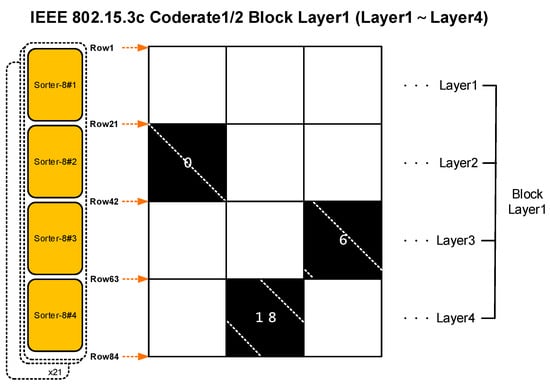
Figure 23. Reconfigurable sorter configuration in IEEE 802.15.3c R = 1/2.

Because IEEE 802.11ay is an extension of IEEE 802.11ad, the arrangement of the IEEE 802.11ay sorter is the same as that of IEEE 802.11ad. The difference is that each block layer is doubled, so the number of calculations required is doubled. Regardless of the standard, the reconfigurable 32-input sorter can support block-level operation. There are a total of 4 schemes that will be used, as shown in Figure 24.

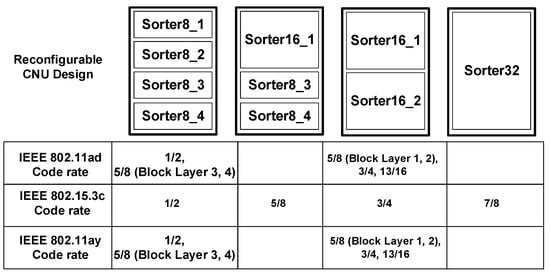
Figure 24. The configuration of the sorter under different code rates for each standard.

4.3. VNU

The VNU is similar to the PMU. It contains 32 sets of parallel-computing processors. The difference is that the prior messages are obtained from the PMU and the extrinsic messages are obtained from the CNU for calculation. The final calculated posterior message is stored in the posterior memory for the next iteration operation, as shown in Figure 25.

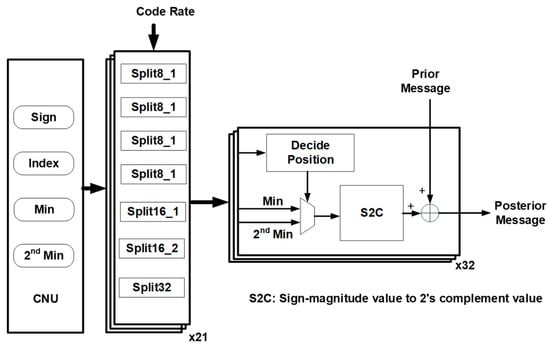
Figure 25. The architecture of the VNU.

4.4. Switching Network

The design of the switching network in the reconfigurable multimode decoder architecture is also a topic that is often discussed. A multimode switching network requires different input and output sizes in different standards between the memory and processing units, and the control signal in the reconfigurable design will also be very complicated. Therefore, the designed switching network architecture is based on the architecture in [25]. Compared to the traditional Benes network [26], this architecture has the following advantages:

• The number of inputs may not be a power of 2.
• The number of bits required for the look-up table is very small.
• The hardware usage rate of the proposed multi-mode architecture is extremely high.

This switching network is based on the expansion of 2 × 2, 3 × 3, or 5 × 5 switching networks, so the maximum input size $P_M$ may not be a power of 2, where $P_M=\beta 2^i, \beta \in \left\{2, 3, 5\right\}, \mathrm{and} i\in \left\{1, 2, 3,\dots \right\}$. When the number of inputs required is 42, a traditional Benes network will need to use a network with $2^6=64$ inputs, and the set of hardware will use $S_M/2\times \left(2{\log }_2{S}_M-1\right)=352$, 2 × 2 switches, where $S_M$ is the Benes network input size. However, using the network architecture proposed in [25] requires the use of a $3\times 2^4=48$ input network; the set of hardware will use $3\times 2^i+3\times 2^i{\log }_2{2}^i=240$, 2×2 switches, and the number of 2 × 2 switches used will be reduced by 112.

In this study, we employ the similar notations and illustration revealed in [25] to demonstrate the reconfigurable switching network. Figure 26a illustrates the example of six-input switching network architecture for (p, c, $P_M$) = (5, 3, 6) used in the reconfigurable decoder architecture, where $p$ is the size of the submatrix and $c$ is the shifting value. There are three stages, F1, FL, and L1. F1 stage has three switches with the control signal f_1,j. L1 stage also has three switches with the control signal l_1,j. FL stage has six switches with the control signal fl_j. Figure 26b shows the values of control signals for this six-input switching network. When the status of the switch is “CROSS”, the value of control signal is “1”. When the status of the switch is “BAR”, the value of control signal is “0”. It is noteworthy that the large switching network architecture can be split into two small switching network architectures. As shown in Figure 26, (5, 3, 6), switching network is split into (2, 1, 3) and (3, 2, 3) switching network architectures.

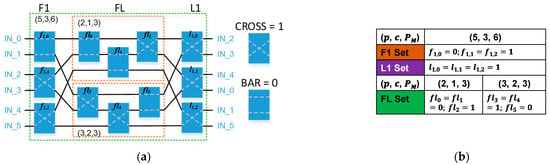
Figure 26. (a) Six-input switching network architecture and (b) its control signal table for (p, c, $P_M$) = (5, 3, 6).

As $P_M$ increases, the switching network architecture becomes complicated. Practically, the control signal in the switching network can be realised using a lookup table. The method for determining the control signal is shown in Figure 27. Block (A) is used to determine the control signal of switches in the F stages, and Block (B) is used to determine the control signal of switches in the L stages. Finally, the control signal of switches in the FL layers is determined in Block (C). When $P_M$ is large, the control signal of each switch can be feasibly determined using the above process illustrated in Figure 27. For the more details of the control signal generation of the switch, readers can refer to [25]. Taking the 24 × 24 shifting network as an example, the control signal generated by a shifting value of 14 is shown in Figure 28. In F1–F3 and L1–L3 stages, each stage has twelve switches. FL stage has 24 switches. The control signal of each switch (i.e., f_i,j, l_i,j, and fl_j) was determined by the method shown Figure 27.

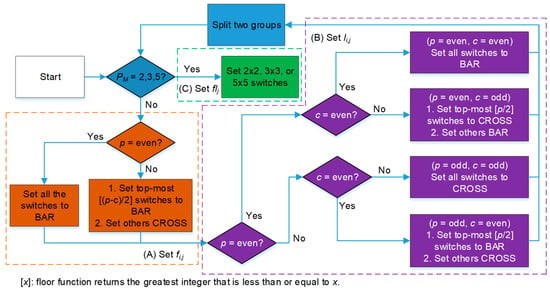
Figure 27. Flow chart of control signal generation of the switch in the switching network in the reconfigurable multimode LDPC decoder architecture.

Figure 28. Control signal table for (p, c, $P_M$) = (21, 14, 24).

Figure 29 illustrates the top 48 × 48 shifting network used in the reconfigurable LDPC decoder architecture, and the control signals of switches are determined for (p, c, $P_M$) = (42, 29, 48). It is too complicated and trivial to illustrate the control signal table in this study. We believe readers can achieve it based on the examples demonstrated in Figure 26, Figure 27 and Figure 28. Compared with the traditional Benes network [26], the control signals that we need is simplified and requires only 588 bits, as shown in Table 3. Applying the architecture in [25] to the designed architecture successfully reduced the hardware complexity significantly. Compared with the Benes network, the designed architecture reduces 1792 2 × 2 switches. Finally, we used 16 sets of parallel 48 × 48 shifting networks that can meet the parallel computing requirements of the IEEE 802.11ad and IEEE 802.11ay standards with an input requirement of 42 and a maximum row weight of 16. In the IEEE 802.15.3c standard, the required number of inputs is 21 and the maximum row weight is 32, which means that 32 sets of parallel hardware are required, and the number of inputs of each set must satisfy the requirement of 21 inputs. However, we observed that a 48 × 48 shifting network transforms into two 24 × 24 shifting networks after being split into two groups for the first time. According to this, 16 sets of 48 × 48 shifting networks can meet the requirement of 32 sets of 24 × 24 shifting networks for IEEE 802.15.3c standard. This only requires the additional multiplexers between the F4 to F3 and L3 to L4 transmission networks, as illustrated in Figure 29. Only adding multiplexers can complete the switching between different modes, so that hardware sharing is high.

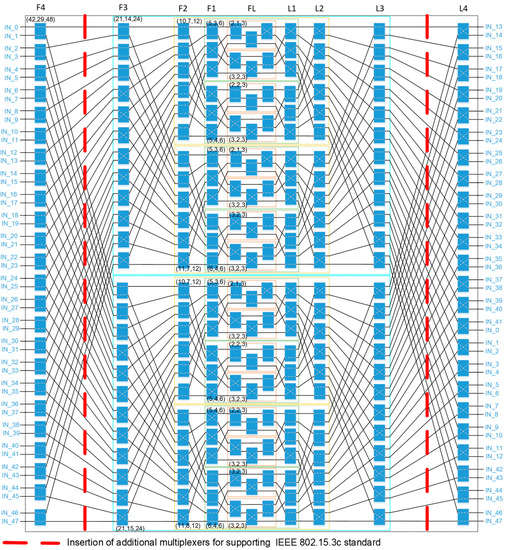
Figure 29. Forty-eight-input switching network architecture for (p, c, $P_M$) = (42, 29, 48).

Table 3. Comparison of distinct switching networks.

Network	Benes Network [26]	This Work
Network size	$64\times 64$	$48\times 48$
Look-up table (bits)	709,984 (100%)	588 (0.08%)

4.5. Memory Organization

Memory is divided into two parts: posterior memory and extrinsic memory, both of which are used to save the posterior messages and extrinsic messages required for the next iteration after the current iteration update. Considering the auto place and route (APR) congestion problem, the memory design adopts a register-based design that can be placed more flexibly. The posterior memory part adopts a single-port design, and the extrinsic memory adopts a two-port design. The posterior memory must save the post-probability value of the code length. In the IEEE 802.11ad and IEEE 802.15.3c standards, the code length is 672, but the code length of the IEEE 802.11ay standard is 1344; therefore, we must follow the maximum demand IEEE 802.11ay standard 1344 code length multiplied by our quantisation bits 7. Thus, the required memory size is 9408 bits (=1344 × 7).

Four pieces of information need to be saved in the extrinsic memory: address information of the minimum value, sign, minimum value, and second minimum value. However, the amount of information that must be stored in different standards and code rates is also different. Different data-storage arrangements must be made according to the calculation results of each block layer. The storage requirements of each code rate under different standards are listed in Figure 30 and Figure 31. Figure 30 shows the extrinsic memory capacity required by IEEE 802.11ad, and it is worth noting that the IEEE 802.11ay matrix is extended by the IEEE 802.11ad matrix, so the required extrinsic memory capacity is the same.

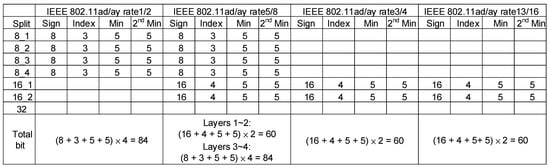
Figure 30. The number of bits required by the extrinsic memory in the IEEE 802.11ad/ay standard with different code rates.

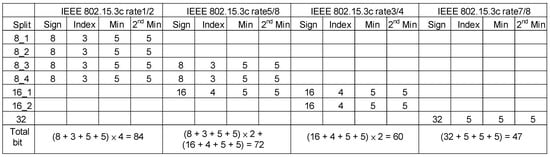
Figure 31. The number of bits required by the extrinsic memory in the IEEE 802.15.3c standard with different code rates.

Finally, the extrinsic memory structure, as shown in Figure 32, was divided into two parts: Memory_1 and Memory_2. Memory_2 is used only in IEEE 802.11ay. Each memory is divided into 21 memory banks to store 21 pieces of parallel hardware information, and each memory bank has four memory cells to store four block-level information. The memory cell size is 84 bits, and the data will be stored in a total of four cases of different sizes. The total extrinsic memory size is 14,112 bits (=2 × 21 × 4 × 84).

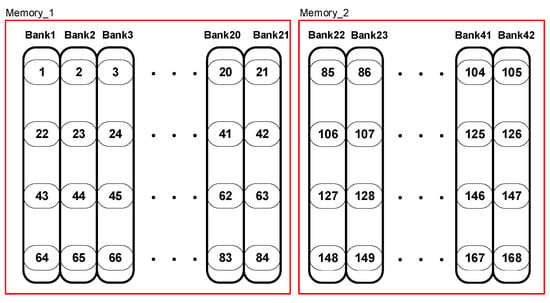
Figure 32. Extrinsic memory in reconfigurable multi-standard decoder.

5. VLSI Implementation of Proposed Reconfigurable Multimode LDPC Decoder

Figure 33 reveals the block-level chip implementation results of the proposed reconfigurable LDPC decoder. The chip was implemented using a TSMC 40 nm CMOS process with an operating voltage of 0.9 V; operating frequency of 117 MHz; and core area $1.312 \mathrm{mm}\times 1.312 \mathrm{mm}$, that is, 1.72 mm². The throughput is described as follows:

$$Throughput \left(Tp\right)=\frac{Codeword\times Frequency}{\left[\frac{z}{parallelism\times S_p}\times Block layer\right]\times Iteration},$$

(6)

where $z$ is the expending factor and $S_p$ is the standard parameter (=1 for IEEE 802.15.3c; =2 for IEEE 802.11ad/ay).

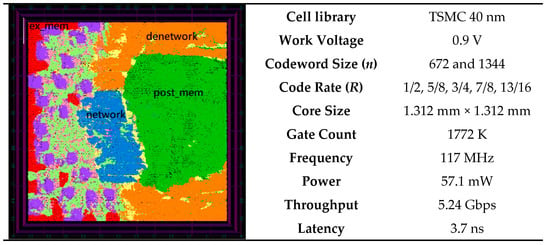
Figure 33. Chip summary and layout of the proposed reconfigurable multi-standard LDPC decoder.

Currently, there are no other studies discussing the integration of LDPC decoders for 60 GHZ wireless transmission, and there are no related studies on the implementation of the IEEE 802.11ay standard on the chip. Therefore, the results can only be compared with the single standard studies of IEEE 802.11ad or IEEE 802.15.3c. For a fair systematic comparison with other studies, normalised metrics [11,27] are utilised and listed as follows:

$$Normalized Area Efficiency \left(NAE\right)=\frac{Tp\times Normalized Area factor\left(={\left(S/40\right)}^2\right)}{Area\times Frequency},$$

(7)

$$Normalized Energy Efficiency \left(NEE\right)=\frac{Power\times Normalized energy factor\left(=\left(40/S\right)\times {\left(0.9/U\right)}^2\right)}{Tp\times Iteration},$$

(8)

where $S$ is the scaled technology and $U$ is the scaled supply voltage. Table 4 shows a comparison with other IEEE 802.11ad studies. In terms of the NEE, the hardware architecture we proposed is superior to that of other studies. In the NAE, the performance is particularly outstanding because [28] only operates at one rate. Table 5 shows a comparison with other IEEE 802.15.3c-related studies. In comparison with IEEE 802.15.3c, the proposed hardware architectures are slightly inferior. This is because a large part of the proposed hardware architecture complies with the hardware added by IEEE 802.11ad and IEEE 802.11ay; therefore, the values cannot be compared with a single standard.

Table 4. Chip comparisons among different LDPC decoders for IEEE 802.11ad standard.

Decoders	This Study	[28]	[29]	[30]	[31]
Implementation	Post-layout	Measurement	Measurement	Measurement	Measurement
Technology	40 nm	40 nm	40 nm	28 nm	28 nm
Voltage	0.9 V	0.9 V	1.1 V	0.9 V	0.9 V
Standard	IEEE 802.11ad/ay IEEE 802.15.3c	IEEE 802.11ad	IEEE 802.11ad	IEEE 802.11ad	IEEE 802.11ad
Code rate (R)	1/2, 5/8, 3/4 7/8, 13/16	13/16	1/2, 5/8, 3/4, 13/16	1/2, 5/8, 3/4, 13/16	1/2, 5/8, 3/4, 13/16
Algorithm	NPMSA	MSA	MSA	MSA	MSA
Quantization (bits)	7	5	5	5	4
Iteration	5	5	7	10	4
Parallelism	21	42	16	168	42
Frequency (MHz)	117	500	220	202	470
Tp (Gbps)	5.24	5.6	6.16	6.78	18.4
Area (mm2)	1.72	0.16	0.8	1.99	0.78
Power (mW)	57.1	99	203	104	166
NAE (bits/mm2)	0.026	0.07	0.035	0.0082	0.024
NEE (pJ/bit)	2.179	3.53	3.15	2.19	3.22

Table 5. Chip comparisons among different LDPC decoders for IEEE 802.15.3c standard.

Decoders	This Study	[32]	[33]	[34]	[24]
Implementation	Post-layout	Measurement	Measurement	Measurement	Measurement
Technology	40 nm	90 nm	65 nm	90 nm	65 nm
Voltage	0.9 V	1.2 V	1.2 V	1.05 V	1.0 V
Standard	IEEE 802.11ad/ay IEEE 802.15.3c	IEEE 802.15.3c	IEEE 802.15.3c	IEEE 802.15.3c	IEEE 802.15.3c
Code rate	1/2, 5/8, 3/4 7/8, 13/16	1/2, 5/8, 3/4, 7/8,	1/2, 5/8, 3/4, 7/8,	1/2, 5/8, 3/4, 7/8,	1/2, 5/8, 3/4, 7/8,
Algorithm	NPMSA	NMSA	NMSA	NMSA	NMSA
Quantization (bits)	7	10	6	6	6
Iteration	5	10	10	5	5
Parallelism	21	21	21	21	21
Frequency (MHz)	117	768	400	157	197
Tp (Gbps)	3.90	7.92	6.72	5.28	5.79
Area (mm2)	1.72	2.67	1.3	2.25	1.56
Power (mW)	57.1	437.2	537.6	182	361
NAE (bits/mm2)	0.019	0.019	0.034	0.075	0.049
NEE (pJ/bits)	2.92	1.98	2.76	2.25	6.21

6. Conclusions

In this study, a reconfigurable LDPC decoder was proposed to support the application of three standards of 60 GHz wireless transmission: IEEE 802.11ad, IEEE 802.15.3c, and IEEE 802.11ay. To support different standards, we divide the matrix in different standards into block layers for decoding to ensure good hardware sharing and use reconfigurable hardware architecture in the CNU and switch network to save a lot of hardware consumption. Finally, the multi-mode reconfigurable LDPC decoder applied to 60 GHz wireless transmission is realised using the TSMC 40 nm CMOS process, using 21 parallelisms, two pipeline stages, an operating frequency of 117 MHz, and a core area of $1.312 \mathrm{mm}\times 1.312 \mathrm{mm}$; the power consumption is only 57.1 mW. The throughput is up to 5.24 Gbps in the IEEE 802.11ad and IEEE 802.11ay modes, and the throughput is 3.9 Gbps in the IEEE 802.15.3c mode.