Coverage Probability Analysis for Device-to-Device Communication Underlaying Cellular Networks

Abstract

As one of the most promising techniques in wireless communication systems, device-to-device (D2D) has drawn much attention due to its superior performance. Meanwhile, the interference between cellular users and D2D users is still a challenging problem and needs to be mitigated effectively. A large number of simulation experiments for D2D communications have been studied to reduce the impact of the interference in the existing literature. However, theoretical research is still lacking. Thus, in this paper, we use stochastic geometry to evaluate the uplink performance of users by considering the impact of the previous moment on the next moment, which captures the effect of temporal and the spatial correlation of the interference in D2D communication underlaying cellular networks. Using a Poisson point process to model locations of D2D users, we derive an analytic expression for conditional probability and unconditional probability of link success, and prove that the probability of link success is temporally correlated. Moreover, we provide a theoretical framework for interference mitigation in D2D underlaying cellular networks.

1. Introduction

In order to provide higher speed and lower power consumption service in communication networks, lots of wireless transmission technologies are investigated [1,2,3]. Among them, D2D (device-to-device) communication underlaying cellular networks, which is considered as a promising technique, has received widespread attention due to high spectrum efficiency and low power consumption characteristics. According to current investigations for D2D underlaying cellular networks, the spectrum of cellular users (CUE) can be reused by D2D users. However, the sharing of spectrum causes serious co-channel interference between CUE and D2D users. Correspondingly, this will lead to a performance loss of CUE and D2D users [4,5,6,7]. To solve this problem, effective resource allocation schemes based on tractable analytical framework for user performance is critical.

According to recent investigations, stochastic analysis is applied to cellular networks for interference analysis. The users and BSs are considered as the realization of stochastic point processes which is assumed to be independent and Poisson. Because of the convenient mathematical properties of the Poisson point process, it is frequently used to analyze the asymptotic statistical characteristics of signal-to-interference ratio (SIR) to further enhance system performance [8,9,10].

So far, based on Poisson point process theory, some works have been investigated about performance analysis of D2D communication. In [11,12], the authors give the expression for capacity and coverage probability of CUE and D2D users. The work of [13] models D2D user locations as a marked Poisson point process (MPPP) and derives an expression for the coverage gain of CUE and the corresponding D2D user density. Nonetheless, all of the above works ignore the temporal correlation of interference. Recently, researchers [14,15,16,17] have shown that the interference is temporally correlated. The athors in [14] derive an outage probability expression by analyzing the temporal correlation of the interference for Poisson line networks. The athors in [15] derive an expression for the coverage probability when the reference user is able to perform MRC of the received signals in two transmissions in heterogeneous networks. The athors in [16] quantify the correlation of the interference for Ad Hoc Networks which can be used to design re-transmission strategy. However, none of them mentions the coverage probability in the case that new interference joins in the network with a given probability. Furthermore, how to design the resource allocation schemes for systems by considering the time correlation of probability is still of concern. Thus, we focus on theoretical analysis of user’s state transition probability in this paper. To the best of our knowledge, there is no published research that analyzes performance by considering the effect of temporal correlation of the interference in D2D communication underlaying cellular networks.

We present the following contributions in this paper. First, we introduce the stochastic geometry modeling to the D2D underlaying cellular communication networks. Second, we consider the impact of interference of the previous moment on the next moment and derive the coverage probability by considering the user’s performance of previous moment. Third, we show that resource allocation schemes should be treated differently based on previous information. Finally, simulation results validate the conclusions of our theorems.

The remaining of the paper is organized as follows. Section 2 presents stochastic geometry modeling and system model of D2D underlaying cellular networks. Different from the existing literature, we establish a framework to analyze the coverage probability by considering time correlation, where we split the set of interference at time slot $l+1$ into two orthogonal subsets. One is a subset of those transmitting at time slot l and sharing frequency with the reference CUE. The other is a set of new D2D users who are allowed to transmit signals at time slot $l+1$ and share the same frequency with the reference CUE. Based on this, we explore the coverage probability (namely the probability of link success) over two time slots in D2D communication underlaying cellular networks where the interferer forms a Poisson point process (PPP). In Section 3, we analyze the temporary correlation of coverage probability based on interference modeling and stochastic theory. In Section 4, we evaluate the performance of CUE by simulations. In Section 5, we conclude this work.

2. Stochastic Geometry Modeling and System Model

We consider the uplink transmission in a D2D communication underlaying cellular network, shown in Figure 1. The system model consists of one cellular base station (CBS), one CUE and potential D2D users arranged according to a homogeneous PPP $\mathsf{\Psi }$ of intensity $\lambda$. The locations of D2D users who share the uplink frequency band with the CUE are modeled as a PPP ${\mathsf{\Psi }}_1$ of intensity ${\lambda }_1$ at time slot l. In terms of user modeling, we divide D2D users into two categories: D2D transmitter and D2D receiver who is omitted for simplicity in Figure 1. In the rest of this paper, a D2D user mainly refers to a D2D transmitter. The location of CUE is modeled as a uniform distribution. The distance between the CUE and the CBS is r. r follows uniform probability distribution function (p.d.f.) [13]:

$$\begin{array}{c}\hfill f\left(r\right)=\frac{2r}{R^2}\end{array}$$

(1)

where $0<r\le R$. R is the cellular radius.

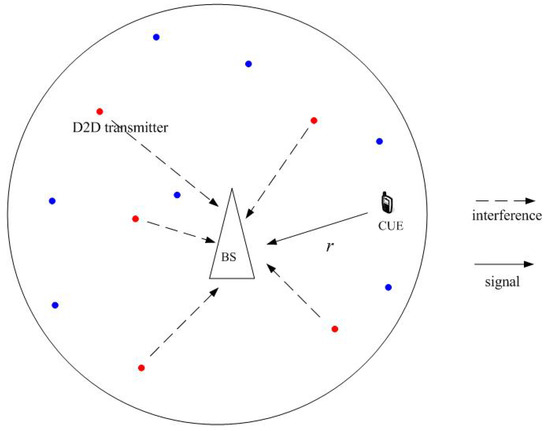
Figure 1. System model (Red dots denote D2D transmitters who share the frequency band with the CUE at time slot l. Blue dots denote members of $\mathsf{\Psi }\setminus {\mathsf{\Psi }}_1$. D2D receivers are omitted in the figure).

We assume that only some of the D2D users transmitting at time slot l also transmit at time slot $l+1$; this occurs with probability ${\rho }_1$; hence the transmitting D2D users at time slot $l+1$ are a subset of those at time slot l. At the same time, we allow that new D2D users who are members of the set $\mathsf{\Psi }\setminus {\mathsf{\Psi }}_1$ at time slot l transmitting at time slot $l+1$ with probability ${\rho }_2$, where $\mathsf{\Psi }\setminus {\mathsf{\Psi }}_1$ is denoted as the set difference of $\mathsf{\Psi }$ and ${\mathsf{\Psi }}_1$.

Now, we consider the coverage probability of CUE at time slot $l+1$ which depends on two SIR values: $SI{R}_1$ at time slot l and $SI{R}_2$ at the next time slot. Here, $SI{R}_1$ is the first SIR of CUE, where the interfering D2D users set is ${\mathsf{\Psi }}_1$ of intensity ${\lambda }_1$. $SI{R}_2$ is the actual SIR at time slot $l+1$ with a new set of interfering D2D users denoted $\mathsf{\Phi }$. Hence, $SI{R}_1$ can be described as [7]:

$$\begin{array}{c}\hfill SI{R}_1=\frac{ph{r}^{-\alpha }}{{\displaystyle \sum _{i\in {\mathsf{\Psi }}_1}}q{f}_i{d}_i^{-\alpha }}\doteq \frac{ph{r}^{-\alpha }}{I}\end{array}$$

(2)

where p and q are the transmit power of CUE and D2D users, respectively; h and $f_i$ are respective small scale fading obeying the pdf of $exp\left(\mu \right)$. The corresponding distance dependent path losses are $r^{-\alpha }$ and $d_i^{-\alpha }$. $\alpha$ is the path loss exponent. Hence, $ph{r}^{-\alpha }$ can be regarded as the received signal power. $I={\displaystyle \sum _{i\in {\mathsf{\Psi }}_1}}q{f}_i{d}_i^{-\alpha }$ is the interference from the set ${\mathsf{\Psi }}_1$ at time slot l. T is the SIR threshold. The probability of $SIR>T$ is also called as probability of link success.

Assume that the location of CUE has not changed from time slot l to $l+1$, and thus the dominant path loss remains the same. Therefore, $SI{R}_2$ can be written as

$$\begin{array}{c}\hfill \begin{array}{c}SI{R}_2=\frac{p\widehat{h}{r}^{-\alpha }}{{\displaystyle \sum _{i\in \mathsf{\Phi }}}q\widehat{f_i}{d}_i^{-\alpha }\mathbf{1}(i\in {\mathsf{\Psi }}_1)+{\displaystyle \sum _{i\in \mathsf{\Phi }}}q\widehat{f_i}{d}_i^{-\alpha }\mathbf{1}(i\in \mathsf{\Psi }\setminus {\mathsf{\Psi }}_1)}\doteq \frac{p\widehat{h}{r}^{-\alpha }}{I_1+I_2}\hfill \end{array}\end{array}$$

(3)

where $\widehat{h}$ and $\widehat{f_i}$ are the new fading values that CUE and D2D users experience, respectively; $\widehat{h}\sim exp\left(\mu \right)$ and $\widehat{f}\sim exp\left(\mu \right)$. $\mathbf{1}(i\in {\mathsf{\Psi }}_1)$ is an indicator function. $\mathsf{\Phi }$ is the interference set at time slot $l+1$. Correspondingly, $I_1={\displaystyle \sum _{i\in \mathsf{\Phi }}}q\widehat{f_i}{d}_i^{-\alpha }\mathbf{1}(i\in {\mathsf{\Psi }}_1)$ is the interference, which results from D2D users who are members of ${\mathsf{\Psi }}_1$ at time slot l remaining their communications at time slot $l+1$. $I_2={\displaystyle \sum _{i\in \mathsf{\Phi }}}q\widehat{f_i}{d}_i^{-\alpha }\mathbf{1}(i\in \mathsf{\Psi }\setminus {\mathsf{\Psi }}_1)$ is the interference, which comes from new D2D users who belong to $\mathsf{\Psi }\setminus {\mathsf{\Psi }}_1$ at time slot l and work at time slot $l+1$. In the paper, the network is assumed to be interference-limited and the noise is neglected.

3. The Temporal Correlation of Coverage Probability

In this section, we focus on evaluation of the coverage probability for the CUE in the uplink of going from time slot l to time slot $l+1$.

Theorem 1.

We consider D2D underlay cellular networks, where intensity of D2D users is λ and intensity of D2D users who share the frequency of CUE at time slot l is ${\lambda }_1$. Then, the conditional probability of $SI{R}_2>T$ at time slot $l+1$, under the condition that $SI{R}_1>T$ at time slot l holds, can be expressed as

$$\begin{array}{c}\hfill \begin{array}{c}P(SI{R}_2>T|SI{R}_1>T)\hfill \\ =\frac{P(SI{R}_2>T,SI{R}_1>T)}{P(SI{R}_1>T)}\hfill \\ =\frac{a_1}{a}·\frac{1-exp(-\pi a{R}^2)}{1-exp(-\pi a_1{R}^2)}\hfill \end{array}\end{array}$$

(4)

where p and q are the transmit power of CUE and D2D users, respectively; The D2D user works at both time slots with probability ${\rho }_1$; $a={\lambda }_1\phi (T,{\rho }_1,p,q)+{\rho }_2(\lambda -{\lambda }_1)\phi (T,0,p,q)$; $a_1={\lambda }_1\phi (T,0,p,q)$ and

$$\begin{array}{c}\hfill \begin{array}{c}\phi (T,{\rho }_1,p,q)={\int }_0^{\infty }\left(1-\frac{1+(1-{\rho }_1)T{p}^{-1}q{t}^{-\alpha /2}}{{(1+T{p}^{-1}q{t}^{-\alpha /2})}^2}\right)dt\hfill \end{array}\end{array}$$

(5)

Proof of Theorem 1.

The joint probability of the success is

$$\begin{array}{c}\hfill \begin{array}{c}P(SI{R}_2>T,SI{R}_1>T)\hfill \\ =P\left(\frac{p\widehat{h}{r}^{-\alpha }}{I_1+I_2}>T,\frac{ph{r}^{-\alpha }}{I}>T\right)\hfill \\ ={\mathbf{E}}_r{P}_r\left(\widehat{h}>T(I_1+I_2)r^{\alpha }{p}^{-1},h>TI{r}^{\alpha }{p}^{-1}\right)\hfill \\ \stackrel{\left(a\right)}{=}{\mathbf{E}}_r\mathbf{E}\left(exp(-\mu T(I_1+I_2)r^{\alpha }{p}^{-1})exp(-\mu TI{r}^{\alpha }{p}^{-1})\right)\hfill \\ \stackrel{\left(b\right)}{=}{\mathbf{E}}_r\mathbf{E}exp(-s(I+I_1+I_2))\hfill \end{array}\end{array}$$

(6)

where ${\mathbf{E}}_r$ is the expectation of random variable r; $P_r$ is the probability when r is given. $\left(a\right)$ results from the independence of the small-scale fading powers [11]. $\left(b\right)$ follows from a change of variables $s=\mu T{r}^{\alpha }{p}^{-1}$.

Here, we have

$$\begin{array}{c}\hfill \begin{array}{c}exp(-s(I+I_1))\hfill \\ ={\displaystyle \prod _{i\in \mathsf{\Phi }}}exp\left(-sq\widehat{f_i}{d}_i^{-\alpha }\mathbf{1}(i\in {\mathsf{\Psi }}_1)\right){\displaystyle \prod _{i\in {\mathsf{\Psi }}_1}}exp(-sq{f}_i{d}_i^{-\alpha })\hfill \\ ={\displaystyle \prod _{i\in {\mathsf{\Psi }}_1}}exp\left(-sq\widehat{f_i}{d}_i^{-\alpha }\mathbf{1}(i\in \mathsf{\Phi }\cap {\mathsf{\Psi }}_1)\right)exp(-sq{f}_i{d}_i^{-\alpha })\hfill \end{array}\end{array}$$

(7)

A simple calculation shows that

$$\begin{array}{c}\hfill \begin{array}{c}exp\left(-sq\widehat{f_i}{d}_i^{-\alpha }\mathbf{1}(i\in \mathsf{\Phi }\cap {\mathsf{\Psi }}_1)\right)\hfill \\ =1-\mathbf{1}(i\in \mathsf{\Phi }\cap {\mathsf{\Psi }}_1)\left(1-exp(-sq\widehat{f_i}{d}_i^{-\alpha })\right)\hfill \end{array}\end{array}$$

(8)

and

$$\begin{array}{c}\hfill \begin{array}{c}\mathbf{E}\mathbf{1}(i\in \mathsf{\Phi }\cap {\mathsf{\Psi }}_1)={\rho }_1\hfill \end{array}\end{array}$$

(9)

Substituting (8) into (7), and calculating the expected value of $exp(-s(I+I_1))$, we have

$$\begin{array}{c}\hfill \begin{array}{c}\mathbf{E}exp(-s(I+I_1))\hfill \\ \begin{array}{cc}\hfill =\mathbf{E}[& {\displaystyle \prod _{i\in {\mathsf{\Psi }}_1}}\left(1-\mathbf{1}(i\in \mathsf{\Phi }\cap {\mathsf{\Psi }}_1)(1-exp(-sq\widehat{f_i}{d}_i^{-\alpha }))\right)\hfill \\ & ·exp(-sq{f}_i{d}_i^{-\alpha })]\hfill \end{array}\hfill \\ \begin{array}{cc}\hfill \stackrel{\left(c\right)}{=}\mathbf{E}[& {\displaystyle \prod _{i\in {\mathsf{\Psi }}_1}}\left(1-{\rho }_1(1-\mathbf{E}exp(-sq\widehat{f_i}{d}_i^{-\alpha }))\right)\hfill \\ & ·\mathbf{E}exp(-sq{f}_i{d}_i^{-\alpha })]\hfill \end{array}\hfill \\ \stackrel{\left(d\right)}{=}\mathbf{E}\left[{\displaystyle \prod _{i\in {\mathsf{\Psi }}_1}}\left(1-{\rho }_1(1-\frac{\mu }{\mu +sq{d}_i^{-\alpha }})\right)\frac{\mu }{\mu +sq{d}_i^{-\alpha }}\right]\hfill \\ \stackrel{\left(e\right)}{=}exp\left(-2\pi {\lambda }_1{\int }_0^{\infty }\left(1-\frac{\mu (\mu +(1-{\rho }_1)sq{x}^{-\alpha })}{{(\mu +sq{x}^{-\alpha })}^2}\right)xdx\right)\hfill \\ \stackrel{\left(f\right)}{=}exp\left(-\pi {\lambda }_1{r}^2{\int }_0^{\infty }\left(1-\frac{1+(1-{\rho }_1)T{p}^{-1}q{t}^{-\alpha /2}}{{(1+T{p}^{-1}q{t}^{-\alpha /2})}^2}\right)dt\right)\hfill \\ \doteq exp\left(-\pi {\lambda }_1{r}^2\phi (T,{\rho }_1,p,q)\right)\hfill \end{array}\end{array}$$

(10)

where $\left(c\right)$ results from the i.i.d. distribution of $f_i$ and $\widehat{f_i}$. $\left(d\right)$ results from the assumptions that $f_i\sim exp\left(\mu \right)$ and $\widehat{f_i}\sim exp\left(\mu \right)$. $\left(e\right)$ results from the probability generating functional [8]. $\left(f\right)$ follows from a change of variables $t={(x/r)}^2$. In the last step of (10), we denote that

$$\begin{array}{c}\hfill \begin{array}{c}\phi (T,{\rho }_1,p,q)={\int }_0^{\infty }\left(1-\frac{1+(1-{\rho }_1)T{p}^{-1}q{t}^{-\alpha /2}}{{(1+T{p}^{-1}q{t}^{-\alpha /2})}^2}\right)dt\hfill \end{array}\end{array}$$

(11)

In a similar way, the expected value of $exp(-s{I}_2)$ can be computed as

$$\begin{array}{c}\hfill \begin{array}{c}\mathbf{E}exp(-s{I}_2)\hfill \\ =\mathbf{E}\left({\displaystyle \prod _{i\in \mathsf{\Phi }}}exp\left(-sq\widehat{f_i}{d}_i^{-\alpha }\mathbf{1}(i\in \mathsf{\Psi }\setminus {\mathsf{\Psi }}_1)\right)\right)\hfill \\ =\mathbf{E}\left({\displaystyle \prod _{i\in \mathsf{\Psi }\setminus {\mathsf{\Psi }}_1}}exp\left(-sq\widehat{f_i}{d}_i^{-\alpha }\mathbf{1}(i\in \mathsf{\Phi })\right)\right)\hfill \\ \stackrel{\left(g\right)}{=}exp\left(-2\pi {\rho }_2(\lambda -{\lambda }_1){\int }_0^{\infty }\left(1-\frac{\mu }{\mu +sq{x}^{-\alpha }}\right)xdx\right)\hfill \\ \stackrel{\left(h\right)}{=}exp\left(-\pi {\rho }_2(\lambda -{\lambda }_1)r^2\phi (T,0,p,q)\right)\hfill \end{array}\end{array}$$

(12)

where $\left(g\right)$ follows by taking the average with respect to $\widehat{f_i}$ and follows from the probability generating functional of the PPP. $\left(h\right)$ follows from a change of variables $t={(x/r)}^2$ and Equation (11).

De-conditioning on r, we have

$$\begin{array}{c}\hfill \begin{array}{c}P(SI{R}_2>T,SI{R}_1>T)\hfill \\ ={\mathbf{E}}_r\mathbf{E}\left(exp(-s(I+I_1+I_2))\right)\hfill \\ ={\int }_0^R\mathbf{E}exp(-s(I+I_1+I_2))\frac{2r}{R^2}dr\hfill \\ ={\int }_0^{R}exp(-\pi a{r}^2)\frac{2r}{R^2}dr\hfill \\ =\frac{1}{\pi a{R}^2}\left(1-exp(-\pi a{R}^2)\right)\hfill \end{array}\end{array}$$

(13)

where $a={\lambda }_1\phi (T,{\rho }_1,p,q)+{\rho }_2(\lambda -{\lambda }_1)\phi (T,0,p,q)$.

Similarly, we have

$$\begin{array}{c}\hfill \begin{array}{c}P(SI{R}_1>T)\hfill \\ ={\int }_0^{R}exp\left(-\pi {\lambda }_1{r}^2\phi (T,0,p,q)\right)\frac{2r}{R^2}dr\hfill \\ =\frac{1}{\pi a_1{R}^2}\left(1-exp(-\pi a_1{R}^2)\right)\hfill \end{array}\end{array}$$

(14)

where $a_1={\lambda }_1\phi (T,0,p,q)$.

Combining (13) and (14), we calculate the conditional probability as:

$$\begin{array}{c}\hfill \begin{array}{c}P(SI{R}_2>T|SI{R}_1>T)\hfill \\ =\frac{P(SI{R}_2>T,SI{R}_1>T)}{P(SI{R}_1>T)}\hfill \\ =\frac{a_1}{a}·\frac{1-exp(-\pi a{R}^2)}{1-exp(-\pi a_1{R}^2)}\hfill \end{array}\end{array}$$

(15)

□

Theorem 2.

If a transmission succeeds at a time slot l, it is more likely to hold at next time slot.

Proof of Theorem 2.

The unconditional probability can be calculated as

$$\begin{array}{c}P(SI{R}_2>T)\hfill \\ ={\mathbf{E}}_r\mathbf{E}\left(exp(-s(I_1+I_2))\right)\hfill \\ ={\mathbf{E}}_r\mathbf{E}\left(exp(-s{I}_1)\right)+{\mathbf{E}}_r\mathbf{E}\left(exp(-s{I}_2)\right)\hfill \end{array}$$

(16)

Similar with (12), we have

$$\begin{array}{c}\hfill \begin{array}{c}\mathbf{E}exp(-s{I}_1)\hfill \\ =\mathbf{E}{\displaystyle \prod _{i\in {\mathsf{\Psi }}_1}}\left(1-\mathbf{1}(i\in \mathsf{\Phi }\cap {\mathsf{\Psi }}_1)(1-exp(-sq\widehat{f_i}{d}_i^{-\alpha }))\right)\hfill \\ =\mathbf{E}{\displaystyle \prod _{i\in {\mathsf{\Psi }}_1}}\left(1-{\rho }_1(1-\mathbf{E}exp(-sq\widehat{f_i}{d}_i^{-\alpha }))\right)\hfill \\ =\mathbf{E}{\displaystyle \prod _{i\in {\mathsf{\Psi }}_1}}\left(1-{\rho }_1(1-\frac{\mu }{\mu +sq{d}_i^{-\alpha }})\right)\hfill \\ =exp\left(-2\pi {\lambda }_1{\rho }_1{\int }_0^{\infty }\left(1-\frac{\mu }{(\mu +sq{x}^{-\alpha })}\right)xdx\right)\hfill \\ =exp\left(-\pi {\lambda }_1{\rho }_1{r}^2\phi (T,0,p,q)\right)\hfill \end{array}\end{array}$$

(17)

Inserting (12) and (17) into (16), this leads to

$$\begin{array}{c}\hfill \begin{array}{c}P(SI{R}_2>T)\hfill \\ ={\mathbf{E}}_r\mathbf{E}\left(exp(-s(I_1+I_2))\right)\hfill \\ ={\mathbf{E}}_{r}exp\left(-\pi ({\lambda }_1{\rho }_1+{\rho }_2(\lambda -{\lambda }_1))r^2\phi (T,0,p,q)\right)\hfill \\ ={\int }_0^{R}exp\left(-\pi ({\rho }_1{\lambda }_1+{\rho }_2(\lambda -{\lambda }_1))r^2\phi (T,0,p,q)\right)\frac{2r}{R^2}dr\hfill \\ =\frac{1}{\pi a_2{R}^2}\left(1-exp(-\pi a_2{R}^2)\right)\hfill \end{array}\end{array}$$

(18)

where $a_2=({\rho }_1{\lambda }_1+{\rho }_2(\lambda -{\lambda }_1))\phi (T,0,p,q)$.

Therefore, the ratio of conditional and the unconditional probability is given by

$$\begin{array}{c}\hfill \begin{array}{c}\frac{P(SI{R}_2>T|SI{R}_1>T)}{P(SI{R}_2>T)}\hfill \\ =\frac{\pi a_1{a}_2{R}^2}{a}·\frac{1-exp(-\pi a{R}^2)}{\left(1-exp(-\pi a_1{R}^2)\right)\left(1-exp(-\pi a_2{R}^2)\right)}\hfill \end{array}\end{array}$$

(19)

Notice that, for a given r, the ratio of conditional and unconditional probability is calculated as

$$\begin{array}{c}\hfill \begin{array}{c}\frac{P_r(SI{R}_2>T|SI{R}_1>T)}{P_r(SI{R}_2>T)}\hfill \\ =\frac{exp(-\pi a{r}^2)}{exp(-\pi a_1{r}^2)exp(-\pi a_2{r}^2)}\hfill \\ =exp\left(\pi r^2{\rho }_1{\lambda }_1{\int }_0^{\infty }\frac{1}{{(T^{-1}p{q}^{-1}{t}^{\alpha /2}+1)}^2}dt\right)\hfill \\ \doteq \vartheta \left(r\right)\hfill \\ >1\hfill \end{array}\end{array}$$

(20)

It is observed that the ratio in (20) increases with the increasing of r. Therefore, the correlation of interference can cause a more significant effect on performance of cell-edge CUE who is far away from CBS than cell-center CUE who is close to CBS.

From (20), we have

$$\begin{array}{c}\hfill \begin{array}{c}\frac{P(SI{R}_2>T|SI{R}_1>T)}{P(SI{R}_2>T)}>1\hfill \end{array}\end{array}$$

(21)

From (20) and (21), we observe that conditional probability is always larger than unconditional probability. That is to say, if a transmission succeeds at a time slot l, it will succeed at a time slot $l+1$ with a higher probability. This fact should be taken into account when designing resource allocating or re-transmission strategies. □

Theorem 3.

The conditional probability of $SI{R}_2>T$ at time slot $l+1$ under the condition that $SI{R}_1<T$ at time slot l holds can be expressed as

$$\begin{array}{c}\hfill \begin{array}{c}P(SI{R}_2>T|SI{R}_1<T)\hfill \\ =\frac{\frac{1}{a_2}\left(1-exp(-\pi a_2{R}^2)\right)-\frac{1}{a}\left(1-exp(-\pi a{R}^2)\right)}{\pi R^2-\frac{1}{a_1}\left(1-exp(-\pi a_1{R}^2)\right)}\hfill \end{array}\end{array}$$

(22)

Proof of Theorem 3.

We rewrite the conditional probability of $P(SI{R}_2>T|SI{R}_1<T)$ as follows

$$\begin{array}{c}\hfill \begin{array}{c}P(SI{R}_2>T|SI{R}_1<T)\hfill \\ =P\left(\frac{p\widehat{h}{r}^{-\alpha }}{I_1+I_2}>T|\frac{ph{r}^{-\alpha }}{I}<T\right)\hfill \\ \stackrel{\left(i\right)}{=}\frac{P\left(\widehat{h}>T\left(I_1+I_2\right)p^{-1}{r}^{\alpha },h<TI{p}^{-1}{r}^{\alpha }\right)}{P\left(h<TI{p}^{-1}{r}^{\alpha }\right)}\hfill \\ \stackrel{\left(j\right)}{=}\frac{\mathbf{E}\left(exp(-\mu T\left(I_1+I_2\right)r^{\alpha }{p}^{-1})\left(1-exp(-\mu T_{0}I{r}^{\alpha }{p}^{-1})\right)\right)}{\mathbf{E}\left(1-exp(-\mu TI{r}^{\alpha }{p}^{-1})\right)}\hfill \\ =\frac{\mathbf{E}(exp(-s\left(I_1+I_2\right))-\mathbf{E}(exp(-s\left(I_1+I_2+I\right))}{1-\mathbf{E}\left(exp\right(-sI)}\hfill \end{array}\end{array}$$

(23)

where $\left(i\right)$ follows from the Bayes theorem. $\left(j\right)$ results from the independence of the small-scale fading powers.

Inserting (13), (14) and (18) into (24), we prove Theorem 3. □

4. Simulation Results

In this section, we will present some simulation results to evaluate the conditional performance and the unconditional performance of CUE. In the simulation, D2D transmitter power is taken as 100 mW [7] and the power of the CUE is taken as 200 mW; $\alpha =4$; $\mu =1$; $\lambda =50/$km${}^2$; $R=0.5$ km.

In Figure 2, we give comparison between conditional probability in (4) and unconditional probability in (16) for different ${\rho }_2$ as a function of ${\rho }_1$. We compare the following cases in the figure: conditional probability with ${\rho }_2=0$, unconditional probability with ${\rho }_2=0$, conditional probability with ${\rho }_2=0.3$, and unconditional probability with ${\rho }_2=0.3$. In this figure, we fix T as 0 dB. As expected, the coverage probability of CUE decreases with the increase of ${\rho }_1$. That is to say, the coverage probability of CUE would be improved significantly when D2D users with lower ${\rho }_1$ are employed to share the frequency band with the CUE.

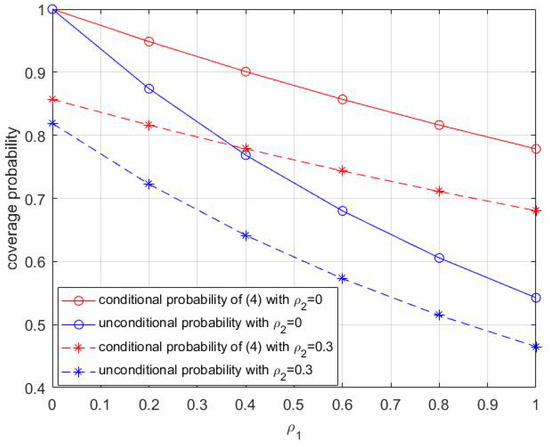
Figure 2. The coverage probability comparison between conditional and unconditional probability for different ${\rho }_1$ with ${\lambda }_1=25$/km${}^2$.

Figure 2 also shows that the gap between the conditional value and unconditional value increases with the increasing of ${\rho }_1$. This is because that the number of D2D users who transmit signals both at time slot l and at time slot $l+1$ rises, thereby causing fast dropping of unconditional probability.

Figure 3 illustrates the coverage probability comparison of CUE among 3 cases as a function of ${\rho }_2$ with $T=0\mathrm{dB}$. Case 1: the conditional probability in (4) with previous $SIR>T$; Case 2: the conditional probability in (22) with previous $SIR<T$; Case 3: unconditional probability in (16) without previous information about CUE. In this figure, we fix ${\rho }_1$ as 0.5 which means that about half of D2D users sharing frequency with CUE at time l still work in the next moment. As expected, the coverage probability of CUE decreases with the increasing of ${\rho }_2$. The increase in ${\rho }_2$ is because that more D2D interference is introduced in the network. As observed, there are three intersections of the curves and black horizontal line. This indicates that the number of new D2D users who are allowed to reuse the frequency with the reference CUE in case 1 is larger than that of case 3 in which the previous SIR is unknown. It is also larger than that of case 2 with CUE’s previous $SIR<T$. Specifically, the coverage probability of CUE will keep larger than 0.6 if 50 percent, 40 percent and only 7 percent of new D2D users are allowed to reuse frequency in case 1, case 2 and case 3, respectively. Therefore, an accurate information of CUE in the previous moment is a great help to the resource allocation.

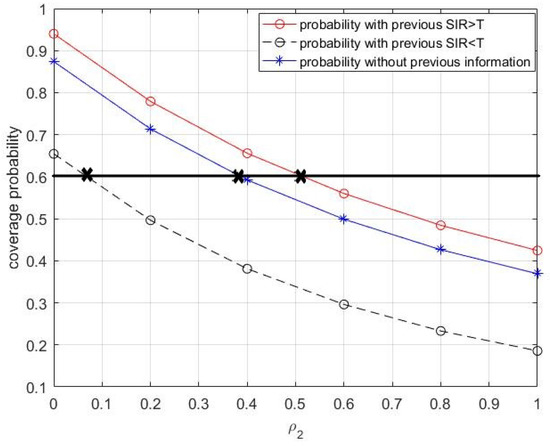
Figure 3. The coverage probability comparison of CUE v.s. ${\rho }_2$ with ${\rho }_1$ = 0.5 and ${\lambda }_1=10$/km${}^2$.

The ratio of conditional probability in Theorem 1 and unconditional probability is shown in Figure 4. We compare the following cases in the figure: ${\lambda }_1=10$/km${}^2$, ${\lambda }_1=20$/km${}^2$, and ${\lambda }_1=30$/km${}^2$. As observed, the ratio is always larger than 1 which validates the result in Theorem 2 and increases with T and ${\lambda }_1$. Hence, the correlation of coverage probability has a great impact on system performances, especially for systems with large T and ${\lambda }_1$.

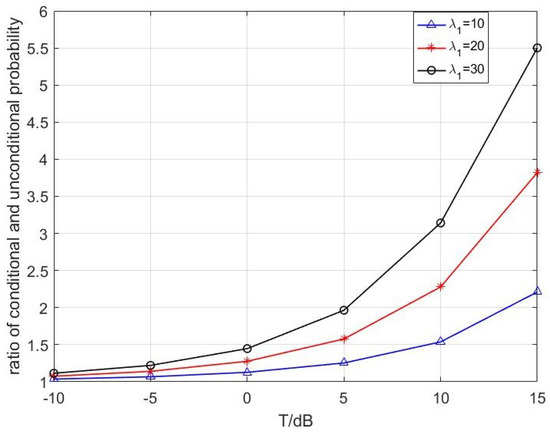
Figure 4. The ratio of conditional probability of Theorem 1 and unconditional probability v.s. $T\left(dB\right)$ with ${\rho }_1$ = 0.8 and ${\rho }_2$ = 0.1.

Figure 5 describes the comparison of $P(SI{R}_2>T|SI{R}_1>T)$ and $P(SI{R}_2>T|SI{R}_1<T)$ which is derived in Theorem 1 and Theorem 3, respectively. As observed, the coverage probability of a user with $SIR>T$ is much larger than the probability of the one with $SIR<T$ at time slot l. The coverage probability decreases with the increasing of ${\rho }_2$. Because a larger value of ${\rho }_2$ introduces more interference.

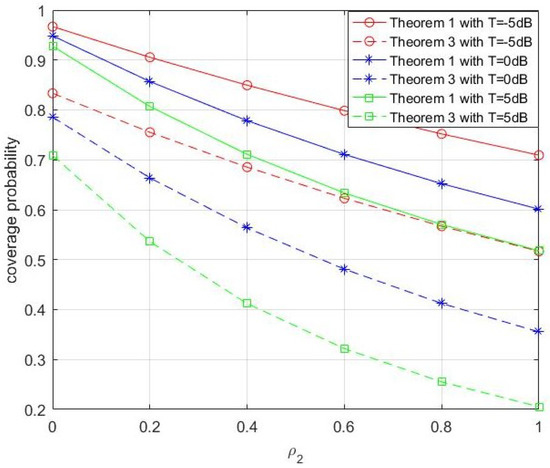
Figure 5. Conditional coverage probability in Theorems 1 and 3 v.s. ${\rho }_2$.

In Figure 5, the coverage probability is 0.9 for ${\rho }_2=0.2$, which means 20% of new users will be arranged to share the frequency of the reference CUE, in case of Theorem 1 with T = 5 dB. But in case of Theorem 3 with T = 5 dB, the coverage probability reduces to about 0.53. Hence, more new D2D users are allowed to share the frequency of the CUE if the CUE has a higher SIR in previous moment. This plays an important role in designing frequency sharing scheme.

In Figure 6, we compare analytical coverage probabilities derived in the paper using the Poisson model versus Monte-Carlo simulations. Theorems 1 and 3 in Figure 6 means the probability (4) and (22) derived in Theorems 1 and 3, respectively. Figure 6 shows that the analytical curves match very well with the Monte-Carlo simulation results. Because the simulation number of times is not large enough, there exits a small difference between these two kinds of curves, but it goes to 0 with the increase of simulation number of times. The coverage probability of users who has higher SIR in previous moment will be larger than the coverage probability of the one with lower SIR in previous moment. Figure 6 also indicates that if D2D users keep sharing the frequency of CUE with a large probability ${\rho }_1$, the coverage probability of CUE at time slot $l+1$ will decrease. This is in accordance with our experience.

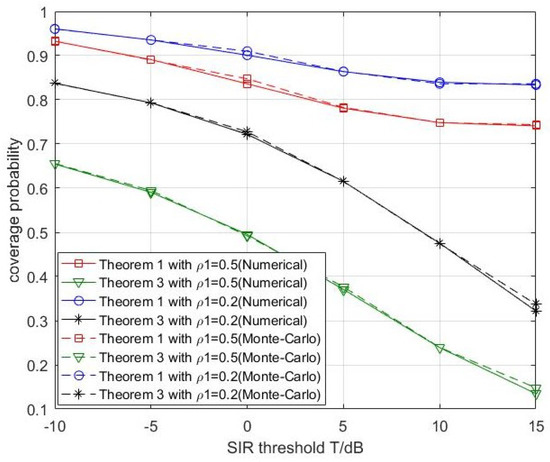
Figure 6. Comparison of analytical coverage probability expressions using the Poisson model versus Monte-Carlo simulations with ${\rho }_2$ = 0.1.

5. Conclusions

In this paper, a general model is developed to analyze the performance over two time slots by considering temporal and spatial correlation of interference. We divided the interference at time slot $l+1$ into two orthogonal subsets. One is a subset of those transmitting at time slot l. The other is a set of new D2D users who are allowed to transmit at time slot $l+1$. Then, we derive the conditional and unconditional probability of link success by modeling D2D user locations as a homogeneous PPP, and prove that the probabilities are correlated in space and in time, so does the interference character. Finally, simulation results verify the proposed conclusions.