The Transition Phenomenon of (1,0)-d-Regular (k, s)-SAT

Abstract

For a d-regular $(k,s)$-CNF formula, a problem is to determine whether it has a (1,0)-super solution. If so, it is called (1,0)-d-regular ($k,s$)-SAT. A (1,0)-super solution is an assignment that satisfies at least two literals of each clause. When the value of any one of the variables is flipped, the (1,0)-super solution is still a solution. Super solutions have gained significant attention for their robustness. Here, a d-regular $(k,s)$-CNF formula is a special CNF formula with clauses of size exactly k, in which each variable appears exactly s-times, and the absolute frequency difference between positive and negative occurrences of each variable is at most a nonnegative integer d. Obviously, the structure of a d-regular ($k,s$)-CNF formula is much more regular than other formulas. In this paper, we certify that, for $k\ge 5$, there is a critical function $\phi (k,d)$ such that, if $s\le \phi (k,d)$, all d-regular $(k,s)$-CNF formulas have a (1,0)-super solution; otherwise (1,0)-d-regular ($k,s$)-SAT is NP-complete. By the Lopsided Local Lemma, we get an existence condition of (1,0)-super solutions and propose an algorithm to find the lower bound of $\phi (k,d)$.

1. Introduction

In recent years, a great deal has been done to improve the efficiency of SAT solvers. Most techniques assume that all constraints in the SAT problem are fixed and inflexible. In many real world problems, conditions are partially known, imprecise and dynamic. For example, renewable energy modeling and prediction are often disturbed by many natural factors, and so are wireless sensor networks. The stability of prediction schemes has received attention in [1,2,3]. In the process of problem solving, not only may some activities not achieve expected results, but also some unexpected circumstances may disrupt the execution of the solution. For instance, it is important to guarantee robustness in the face of changing operating conditions for context-aware and smart systems. Therefore, Powell pointed out that dealing with uncertainty in optimization is increasingly recognized as a key necessity for tackling real-world problems in [4]. In a dynamic, uncertain or interactive environment, once some constraints are changed or the implementation of the solution encounters unexpected difficulties, the solution no longer works. Accordingly, it is worth sacrificing some optimality for a robust solution that is resilient to change. The robust solution is much less sensitive to small changes in uncertain and dynamic environments, and guarantees that some small fixes can meet the challenge of the future changes. In order to quantify the robustness of a solution, the concept of the ($a,b$)-super solution was introduced in [5]. For given a solution, if the values of any a variables are no longer available, flipping values of the a variables and no more than b other variables can tackle the problem. The solution is called an ($a,b$)-super solution. A (1,0)-super solution is a special case of an ($a,b$)-super solution. If the value of any one of the variables is flipped, a (1,0)-super solution is still a solution. That is, for all clauses, at least two literals can be satisfied by a (1,0)-super solution. When a CNF formula has a (1,0)-super solution, we denote that the CNF formula is (1,0)-satisfiable; otherwise it is considered (1,0)-unsatisfiable.

We observed a growing need to extend SAT to deal with more sophisticated problems in the real world. For example, the Super SAT problem is a gap version of SAT in which each assignment is attached integer weights, and was introduced in [6,7,8] to prove the hardness of approximation of some popular lattice problems. The promise SAT problem is a promise version of SAT, such as Unique SAT with a promise of a unique satisfying assignment in [9], ($a,g,k$)-SAT with a promise of g-satisfying assignment in [10,11], etc. In [10], it was shown that a simple random walk algorithm can solve a g-satisfiable k-CNF formula in expected polynomial time for $g\ge k/2$. A g-satisfiable k-CNF formula implies there is an assignment that satisfies at least g literals of every clause of the formula. It is observed that these formulas with special solutions must have their own characteristics.

Analysing regular structures of CNF formulas is often cited as the starting point of studying SAT problems. For a ($k,s$)-CNF formula, each clause is the disjunction of k distinct literals and each variable appears in at most s clauses. For a regular ($k,s$)-CNF formula, it is modified so that each variable appears in exactly s clauses. In [12,13,14], we introduced the d-regular ($k,s$)-CNF formula. For a d-regular ($k,s$)-CNF formula, it is further restricted that the absolute difference between positive and negative occurrences of each variable is no more than a nonnegative integer d. Obviously, for regular ($k,s$)-CNF formulas and d-regular ($k,s$)-CNF formulas, their constrained density $\alpha$ (the clause-to-variable ratio) is fixed. This renders some methods based on the constrained density no longer effective. The structure of a d-regular ($k,s$)-CNF formula is much more regular than ($k,s$)-CNF formula. In [12], we proved that a d-regular ($k,s$)-SAT problem has the Transition Phenomenon from triviality (output the affirmative answer without computation) to NP-completeness. In [14], it was shown that the random d-regular (3,s)-SAT problem has an SAT-UNSAT (satisfiable-unsatisfiable) phase transition. In [15], the structural information of formulas was used to solve the SAT problem. These more regular structures contribute to analyzing SAT problems.

We focus on (1,0)-d-regular ($k,s$)-SAT. It is to determine if a given d-regular ($k,s$)-CNF formula is (1,0)-satisfiable. For the special SAT problems, their NP-completeness deserves further research.

In this paper, our main contributions are described below.

(i)

We analyze the structure of the d-regular ($k,s$)-CNF formula, investigate the NP-completeness of (1,0)-d-regular $(k,s)$-SAT and give some conditions for retaining the NP-completeness.

(ii)

We propose some reduction methods, and prove that (1,0)-d-regular $(k,s)$-SAT has the Transition Phenomenon under the certain conditions.

(iii)

By the Lopsided Local Lemma, we get an existence condition for a (1,0)-super solution and propose an algorithm to obtain a better lower bound of $\phi (k,d)$.

This paper is structured as follows: related works are described in Section 2. All necessary preliminary definitions and lemmas appear in Section 3. The NP-completeness of (1,0)-d-regular $(k,s)$-SAT is discussed in Section 4. The Transition Phenomenon of (1,0)-d-regular $(k,s)$-SAT is in Section 5.

2. Related Works

In order to deal with uncertainty of constraints, various approaches have been proposed by researchers. Fault tolerant solutions were introduced in [16] by R. Weigel and C. Bliek for constraint programming (CP), and Wallace and Freuder in [17] introduced the concept of stable solutions for the dynamic constraint satisfaction problem. For the propositional satisfiability problem, Ginsberg, Parkes and Roy in [18] came up with Supermodels to measure solution robustness. An (a,b)-super solution was introduced in [5] to SAT problems. It is a generalization of Supermodels. In order to find super solutions, some algorithms were presented in [19,20,21], including some local search algorithms.

The robustness is a valuable property of solutions, particularly for decision problems and combinatorial optimization problems. However, robustness and reliability all have a cost. We expect slight reconfiguration is enough to cope with changes in the environment. A (1,0)-super solution just meets the requirement. Even if the value of any one variable on a (1,0)-super solution is inverted, it still is a satisfying assignment. A (1,0)-super solution can be able to cope with assignment breach of only one variable. The problem to determine if a CNF formula is (1,0)-satisfiable is represented as (1,0)-SAT, and this corresponds to a k-CNF formula. It was shown in [22] that, for $k\le 3$, (1,0)-k-SAT is in P; otherwise it is in NP-complete. They also proved that, for Constrained Density (which is the clause-to-variable ratio) $\alpha <1/3$, a random 3-CNF formula is (1,0)-satisfiable with high probability, and not (1,0)-satisfiable with high probability for $\alpha >1/3$. Moreover, the cutoff point is called the phase transition point. For $k=3$, the phase transition point is equal to $1/3$. For $k\ge 4$, its upper bound is $2kln2/(k+1)$. A better lower bound of it was obtained in [23] by utilizing an enhanced weighting scheme.

Kratochvíl, Savický and Tusa in [24] studied the transition phenomenon of ($k,s$)-SAT. They indicated that, for $k\ge 3$, a critical function $f\left(k\right)$ can be found such that

(i)

any one of the ($k,s$)-CNF formulas is satisfiable for $s\le f\left(k\right)$;

(ii)

The ($k,s$)-SAT problem is NP-complete for $s\ge f\left(k\right)+1$.

The critical function $f\left(k\right)$ equals just the maximum of s that can be set to ensure that any one of the $(k,s)$-CNF formulas has a solution. They showed that $f\left(k\right)\ge \lfloor 2^k/ek\rfloor$ by using the Lovász Local Lemma in [24]. Berman, Karpinski and Scott in [25] obtained a better lower bound of $f\left(k\right)$ by using the Lopsided Local Lemma. In [26], it was shown that $f\left(k\right)\ge \lfloor 2^{(k+1)}/e(k+1)\rfloor$. In [12], we proved that d-regular ($k,s$)-SAT also has the Transition Phenomenon from triviality (output the affirmative answer without computation) to NP-completeness, and gave some favorable properties of the critical function $f(k,d)$. In [27], we gave some existence conditions of a (1,0)-super solution, and pointed out that if there is an unsatisfiable (1,0)-($k,s$)-SAT instance, then (1,0)-($k,s$)-SAT problem is NP-complete for $k>3$. That paper shows that the (1,0)-($k,s$)-SAT problem also exhibits the Transition Phenomenon. The corresponding critical function is marked as $\phi \left(k\right)$.

The Lovász Local Lemma proposed in [28] is regarded as a classical tool in probabilistic combinatorics. It provides a sufficient condition to avoid all events deemed to be ‘bad’ in a probability space. In [29], an algorithm based on the variable framework of the Lovász Local Lemma was discovered to sample satisfying assignments of k-CNF formulas with bounded variable occurrences. In [30], by utilizing the Lovász local lemma, some algorithms based on Markov chains were presented to sample and approximately count satisfying assignments of $(k,s)$-CNF formulas. The Lopsided Local Lemma was proposed in [31] based on a lopsidependency graph.

For the study, we put forward a new reduction method to transform from k-SAT to (1,0)-d-regular ($k+1,s$)-SAT if $k\ge 4$ and an unsatisfiable (1,0)-d-regular $(k+1,s)$-SAT instance is given. It shows that, for $k\ge 5$, a critical function $\phi (k,d)$ can be found such that for $s\le \phi (k,d)$ all d-regular $(k,s)$-CNF formulas are (1,0)-satisfiable, and for $s>\phi (k,d)$ (1,0)-d-regular ($k,s$)-SAT is NP-complete. It is observed that, for $k\ge 5$, (1,0)-d-regular ($k+1,s$)-SAT also has the Transition Phenomenon from triviality to NP-completeness. Furthermore, we give some characteristics of the critical function $\phi (k,d)$ and show a better lower bound of $\phi (k,d)$ by Lopsided Local Lemma.

3. Notations

Given a propositional variable x, the variable has two corresponding literals: positive literal (the variable itself x) and negative literal (negation of the variable is $\neg x$). A clause $C=L_1\vee L_2\vee \dots \vee L_k$ is an elementary disjunction of these literals, and is also simply written as $C=L_1,L_2,\dots ,L_k$. A CNF formula $\mathsf{\Psi }=C_1\wedge C_2\wedge \dots \wedge C_m$ is the conjunction of a set of clauses, and is also simply written as $\mathsf{\Psi }=[C_1,C_2,\dots ,C_m]$. For a formula $\mathsf{\Psi }$, $var\left(\mathsf{\Psi }\right)$ denotes the set of variables occurring in F, the number of these variables is $\#var\left(\mathsf{\Psi }\right)$, and the number of clauses is $\#cl\left(\mathsf{\Psi }\right)$. For a formula $\mathsf{\Psi }$ and a variable x, $Occ(\mathsf{\Psi },x)$ is the number of occurrences of x in the formula $\mathsf{\Psi }$, $Pos(\mathsf{\Psi },x)$ is the number of positive occurrences of x in the formula $\mathsf{\Psi }$, and $Neg(\mathsf{\Psi },x)$ corresponds to negative occurrences. That is, $Pos(\mathsf{\Psi },x)=Neg(\mathsf{\Psi },x)+Pos(\mathsf{\Psi },x)$.

If two formulas $\mathsf{\Phi }$ and $\mathsf{\Psi }$ are SAT-$equivalents$, then the two formulas are either simultaneously satisfiable or simultaneously unsatisfiable. Given a CNF formula $\mathsf{\Psi }$, if ${\mathsf{\Psi }}^{\prime }$ is a copy of $\mathsf{\Psi }$ but does not have the same variable with $\mathsf{\Psi }$, then ${\mathsf{\Psi }}^{\prime }$ is regarded as the disjoint copy of $\mathsf{\Psi }$. Variables can be divided into two categories: forced variables and unforced variables. Given a formula, if all satisfying assignments force a variable to be a same value, then the variable is termed a forced variable.

Definition 1.

A regular $(k,s)$-CNF is a CNF formula such that the length of each clause is exactly k and each variable appears exactly s-times. If the absolute difference between positive and negative occurrences of every variable is no more than $d\ge 0$, such a regular (k, s)-CNF formula is called a d-regular (k, s)-CNF formula.

Definition 2.

A minimal (1,0)-unsatisfiable formula is a CNF formula such that it is not (1,0)-satisfiable but is (1,0)-satisfiable as soon as any of its clauses is removed.

Definition 3.

For $k\ge 3$, the critical function of $(k,s)$-SAT, denoted by $f\left(k\right)$, is the maximum of s such that any one of $(k,s)$-CNF formulas has a solution. The critical function of d-regular $(k,s)$-SAT is denoted $f(k,d)$. The critical function of $(1,0)$-$(k,s)$-SAT, denoted by $\phi \left(k\right)$, is the maximum of s such that any one of $(k,s)$-CNF formulas must be (1,0)-satisfiable.

Definition 4.

A ($k,s$)-CNF formula Φ is called a forced-d-regular $(k,s)$-CNF formula if

(i)

there are two variables x and y such that $Occ\left(\mathsf{\Phi },x\right)=1$, $Occ\left(\mathsf{\Phi },y\right)=s-1$ and

$$\left|Pos\right(\mathsf{\Phi },y)-Neg(\mathsf{\Phi },y)-1|\le d;$$

(ii)

except for $x,y$, each variable exactly occurs s-times, and the absolute difference between positive and negative occurrences of every variable is at most $d\ge 0$;

(iii)

Φ must be (1,0)-satisfiable and for any one (1,0)-super solution τ, it is tenable that $\tau \left(x\right)=\tau \left(y\right)=true$.

Definition 5

([31]). Given an undirected graph $G=(X,E)$ and its vertex set X. A collection of events in a probability space is denoted as $A={\left\{A_x\right\}}_{x\in X}$. G is called a lopsidependency graph for the events A if

$$Pr\left[A_x|\bigcap _{y\in Y\left(x\right)}\stackrel{-}{A_y}\right]\le Pr\left[A_x\right].$$

Here $Y\left(x\right)=X/N^{+}\left(x\right)$, $N^{+}\left(x\right)=\{N\left(x\right)/x\}$ and $N\left(x\right)$ is the set of neighbours of x.

Lemma 1

([31]). (The Lopsided Local Lemma) Suppose a graph $G=(X,E)$ is the lopsidependency graph for a collection of events $A={\left\{A_x\right\}}_{x\in X}$. If there are real numbers ${\left\{p_x\right\}}_{(x\in X)}$ such that, for each $x\in X$

$$Pr\left[A_x\right]\le p_x\prod _{y\in N\left(x\right)}\left(1-p_y\right),$$

then $Pr\left[\bigcap _{x\in X}\stackrel{-}{A_x}\right]>0$.

Lemma 2

([12]). For given $k\ge 3$ and $s>0$, if an unsatisfiable d-regular ($k,s$)-CNF formula can be found, then the d-regular ($k,s$)-SAT problem is NP-complete.

Lemma 3

([12]). $f(k,d)\le f(k+1,d).$

Lemma 4.

Given a formula F, if its representation matrix is

$$\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ ⋮\\ x_{n-1}\\ x_n\end{array}\left(\begin{array}{ccccc}+& & & & -\\ -& +& & & \\ & -& & & \\ & & \ddots & & \\ & & & +& \\ & & & -& +\end{array}\right),$$

then F is satisfiable and any one of variables is forced to be a same value by all satisfying assignments.

In the representation matrix of a CNF formula, each row corresponds to a variable and each column corresponds to a clause. If an element $a_{ij}$ is + (i is row number and j is column number), this implies the ith variable appears as positive literal in the jth clause. If $a_{ij}=-$, then the ith variable appears as negative literal in the jth clause. Otherwise, $a_{ij}=0$. Evidently, F implies that

$$x_1\to x_2\to \dots \to x_{n-1}\to x_n\to x_1.$$

4. The NP-Completeness of (1,0)-$\mathit{d}$-Regular $(\mathit{k},\mathit{s})$-SAT

In the field of complexity theory, the NP-completeness of a hard problem is an important attribute. In this section, we will determine some requirements such that (1,0)-d-regular $(k,s)$-SAT problem is a NP-complete problem.

Theorem 1.

Given $k>3$ and $s>d\ge 0$, (1,0)-d-regular $(k+1,s)$-SAT is an NP-complete problem if d-regular $(k,s)$-SAT is an NP-complete problem.

Proof. 

Because d-regular $(k,s)$-SAT is an NP-complete problem, we only need to construct a reduction method to transform a d-regular ($k,s$)-SAT problem to a (1,0)-d-regular $(k+1,s)$-SAT problem.

Assume we have a d-regular ($k,s$)-CNF formula $\mathsf{\Psi }$ which has $nk>0$ variables and $ns$ clauses, $n\ge 1$. There are four steps to our reduction method, as described below.

Step 1. Introduce a fresh set of variables $X=\{x_i:1\le i\le t\}$. Here, $t>max\{ns,{\displaystyle \frac{2n(sk-s)}{sk-3s}}\}$, and $ts-ns$ is a multiple of $k+1$.

Step 2. Let ${\mathsf{\Psi }}_1={\wedge }_{C_i\in \mathsf{\Psi }}(C_i\vee x_i)$.

Step 3. Build a new k-CNF formula ${\mathsf{\Psi }}_2$ consisting of X, and satisfying the following requirements.

(i)

For $1\le i\le ns$ and each variable $x_i\in X$, $Pos({\mathsf{\Psi }}_2,x_i)=\lceil s/2\rceil -1$ and $Occ({\mathsf{\Psi }}_2,x_i)=s-1$;

(ii)

For $ns+1\le i\le t$ and each variable $x_i\in X$, $Occ({\mathsf{\Psi }}_2,x_i)=s$ and $Pos({\mathsf{\Psi }}_2,x_i)=\lceil s/2\rceil$;

(iii)

Any one of clauses of ${\mathsf{\Psi }}_2$ includes no less than two positive literals from X.

Step 4. Construct a new CNF formula $\mathsf{\Phi }={\mathsf{\Psi }}_1\wedge {\mathsf{\Psi }}_2$.

Obviously, $\mathsf{\Phi }$ is just a d-regular $(k+1,s)$-CNF formula. Next, the top concern is the feasibility of constructing $\mathsf{\Phi }$. Because $ts-ns$ is a multiple of $k+1$, we only focus on whether the condition (iii) is going to be met.

In the subformula ${\mathsf{\Psi }}_2$ constructed in Step 3, the number of clauses is

$$\#cl\left({\mathsf{\Psi }}_2\right)=\frac{ts-ns}{k+1},$$

and the number of non-negative occurrences of X is

$$Pos({\mathsf{\Psi }}_2,X)=t\lceil s/2\rceil -ns.$$

For $k>3$, we get $sk-3s>0$. For $t>max\{ns,\frac{2n(sk-s)}{sk-3s}\}$, we get

$$\begin{array}{cc}\hfill t(sk-3s)& >2n(sk-s),\hfill \\ \hfill tsk-2nsk+st-2ns& >4st-4ns,\hfill \\ \hfill ts-2ns& >\frac{4ts-4ns}{k+1},\hfill \\ \hfill ts/2-ns& >2\frac{ts-ns}{k+1},\hfill \\ \hfill Pos({\mathsf{\Psi }}_2,X)& >2\#cl\left({\mathsf{\Psi }}_2\right).\hfill \end{array}$$

From this, there are more than twice as many non-negative literals from X in ${\mathsf{\Psi }}_2$ as clauses. That is, the formula ${\mathsf{\Psi }}_2$ can be constructed in polynomial time by simple placement. Hence, constructing $\mathsf{\Phi }$ is practicable.

Finally, we will show that $\mathsf{\Psi }$ is satisfiable iff $\mathsf{\Phi }$ is (1,0)-satisfiable.

First, we presume that an assignment $\tau$ satisfies $\mathsf{\Psi }$. Define a new truth assignment ${\tau }^{\prime }\left(x\right)$ as

$${\tau }^{\prime }\left(x\right):=\left\{\begin{array}{cc}\tau \left(x\right),& ifx\in var\left(\mathsf{\Psi }\right)\\ true,& ifx\in X\end{array}\right.$$

Obviously, at least two literals of every clause of $\mathsf{\Phi }$ can be satisfied by the truth assignment ${\tau }^{\prime }\left(x\right)$. This would mean that ${\tau }^{\prime }\left(x\right)$ is a (1,0)-super solution of $\mathsf{\Phi }$.

Next, let us suppose $\mathsf{\Phi }$ has a (1,0)-super solution $\tau$. What that means is that no less than two literals of every clause of ${\mathsf{\Psi }}_1$ are satisfied by $\tau$. Because ${\mathsf{\Psi }}_1={\wedge }_{C_i\in \mathsf{\Psi }}(C_i\vee x_i)$, there must be no less than two literals satisfied by $\tau$ for any clause of $C_i\vee x_i$. It is obvious that at least one literal of $C_i\in \mathsf{\Psi }$ is satisfied by $\tau$. We get that $\tau$ satisfies $\mathsf{\Psi }$, and $\mathsf{\Psi }$ is satisfiable.

Based on the reduction method, we obtain that if the d-regular ($k,s$)-SAT problem is an NP-complete problem, then the (1,0)-d-regular $(k+1,s)$-SAT also is an NP-complete problem for $k>3$.

The proof is completed.    □

Corollary 1.

If there is a d-regular $(k,s)$-CNF formula without a solution, then the (1,0)-d-regular $(k+1,s)$-SAT problem is an NP-complete problem, for $k>3$ and $s>d\ge 0$.

Proof. 

The corollary can be directly derived from Lemma 2 and Theorem 1.    □

Lemma 5.

For $k>4$ and $s>d\ge 0$, if a d-regular ($k,s$)-CNF formula is satisfiable but is (1,0)-unsatisfiable, then we can construct a forced-d-regular ($k,s$)-CNF formula.

Proof. 

Given a d-regular ($k,s$)-CNF formula $\mathsf{\Phi }$ that meets the requirements. A (1,0)-unsatisfiable formula can change into a (1,0)-satisfiable formula just by removing some clauses. Because it has a solution but no (1,0)-super solution, we remove some clauses of $\mathsf{\Phi }$ to obtain a minimal (1,0)-unsatisfiable formula (marked as ${\mathsf{\Phi }}_1$). According to definition, for every variable in ${\mathsf{\Phi }}_1$, the number of positive occurrences is at most $(s+d)/2$, and so is the number of negative occurrences. A conjunction of the removed clauses form a formula ${\mathsf{\Phi }}_2$. Then we construct $\mathsf{\Phi }={\mathsf{\Phi }}_1\wedge {\mathsf{\Phi }}_2$. Assuming ${\mathsf{\Phi }}_2$ has $m\ge 0$ clauses, and this showed that it has $mk$ literals. The clause set of ${\mathsf{\Phi }}_1$ is denoted as $C_1$ and the clause set of ${\mathsf{\Phi }}_2$ is denoted as $C_2$.

We will put forward a construction method to generate some forced-d-regular ($k,s$)-CNF formulas. There are three steps to our method, as described below.

Step 1. A clause c of ${\mathsf{\Phi }}_1$ is randomly selected. It is supposed that a new formula obtained by removing the clause c from ${\mathsf{\Phi }}_1$, has a (1,0)-super solution $\tau$. Obviously, for the clause c, only one literal can be satisfied by $\tau$. Let $\neg y$ be a literal of c unsatisfied by $\tau$. Let x be a new extra variable that does not appear in $\mathsf{\Phi }$. We generate $C=(C_1\backslash \left\{c\right\})\cup \left\{\tilde{c}\right\}$, with $\tilde{c}=(c\backslash \{\neg y\})\cup \left\{x\right\}$. Define $\tilde{\mathsf{\Phi }}:={\wedge }_{c_i\in C}{c}_i$.

Step 2. Introduce a fresh set of variables $Z=\{z_1,z_2,\dots ,z_{tk}\}$. Here, let $t>2m/(ks-4s)$. Using $mk$ literals of ${\mathsf{\Phi }}_2$ and the variable set Z, we generate a k-CNF formula ${\mathsf{\Phi }}_3$ that satisfies the following requirements.

(i)

For each variable z of Z, z appears exactly s-times, and $Pos({\mathsf{\Phi }}_3,z)=\lceil s/2\rceil$;

(ii)

Every literal of ${\mathsf{\Phi }}_2$ occurs only once in ${\mathsf{\Phi }}_3$;

(iii)

Any one of the clauses of ${\mathsf{\Phi }}_3$ includes no less than two positive literals from Z.

Step 3. Construct a new CNF formula ${\mathsf{\Phi }}^{\prime }=\tilde{\mathsf{\Phi }}\wedge {\mathsf{\Phi }}_3$.

Define a new truth assignment ${\tau }^{\prime }\left(u\right)$ as

$${\tau }^{\prime }\left(u\right):=\left\{\begin{array}{cc}\tau \left(u\right),& u\in var\left(\mathsf{\Phi }\right)\\ true,& u\in Zoru=x\end{array}\right..$$

For the formula obtained by removing the clause c from ${\mathsf{\Phi }}_1$, $\tau$ is a (1,0)-super solution of it. Therefore, at least two literals are satisfied by ${\tau }^{\prime }$ for any clause of ${\mathsf{\Phi }}^{\prime }$. That is, ${\tau }^{\prime }$ is a (1,0)-super solution of ${\mathsf{\Phi }}^{\prime }$.

Given any (1,0)-super solution of ${\mathsf{\Phi }}^{\prime }$, if it forces x to be $false$ or y to be $false$, then it must be a (1,0)-super solution of ${\mathsf{\Phi }}_1$. This is in contradiction with the claim that ${\mathsf{\Phi }}_1$ is the minimal (1,0)-unsatisfiable formula. Therefore, (1,0)-super solutions of ${\mathsf{\Phi }}^{\prime }$ all force two variables x and y to be $true$.

Each variable in $var\left({\mathsf{\Phi }}^{\prime }\right)$, except for $x,y$, occurs in exactly s clauses. Moreover, for any one of variables, the absolute difference between positive and negative occurrences is at most d. Hence, the formula ${\mathsf{\Phi }}^{\prime }$ we constructed is a forced-d-regular ($k,s$)-CNF formula.

Next, we will show that the construction of ${\mathsf{\Phi }}_3$ is feasible. In the subformula ${\mathsf{\Phi }}_3$, the number of clauses is $m+ts$, and the number of non-negative literals from Z is $tk\lceil s/2\rceil$. For $k>4$ and $t>4m/(ks-4s)$, we obtain that

$$tks-4ts>4m,tks/2>2m+2ts,tk\lceil s/2\rceil >2(m+ts).$$

Obviously, there are more than twice as many non-negative literals from Z in ${\mathsf{\Phi }}_3$ as clauses. That is, the formula ${\mathsf{\Phi }}_3$ can be constructed in polynomial time. Hence, in polynomial time the construction of ${\mathsf{\Phi }}^{\prime }$ can be done.

The proof is completed.    □

Theorem 2.

For $k\ge 4$ and $s>d\ge 0$, if there is a (1,0)-d-regular ($k+1,s$)-SAT instance that is (1,0)-unsatisfiable, then the (1,0)-d-regular ($k+1,s$)-SAT problem is an NP-complete problem.

Proof. 

Given a (1,0)-unsatisfiable d-regular ($k+1,s$)-CNF formula F. There are two cases to consider.

Case 1: Any assignment cannot satisfy the formula F. That is, we obtain $f(k+1,d)<s$. By Lemma 3, we also get $f(k,d)\le f(k+1,d)<s$. Therefore, we can found an unsatisfiable d-regular ($k,s$)-SAT instance. By Corollary 1, it means that (1,0)-d-regular ($k+1,s$)-SAT problem is a NP-complete problem.

Case 2: There exists an assignment that can satisfy the formula F but any one of the assignments is not a (1,0)-super solution of it. We first generate a forced-d-regular $(k+1,s)$-CNF formula $\mathsf{\Phi }$ by using the method in Lemma 5. Given any k-CNF formula $\mathsf{\Psi }$ with m clauses and $mk$ literals. Next, we will put forward a reduction method that can transform k-SAT to (1,0)-d-regular ($k+1,s$)-SAT in polynomial time. Table 1 shows some variable sets that we will introduce in the method. There are five steps to our reduction method, as described below.

Table 1. The variable sets introduced in the method.

Variable Set	Size
$X_1$	$mk(k-4)$
$X_2$	$mk$
$X_3$	m
$X_4$	$mk-m$
Y	$mk(k-2)$
Z	$mk$
U	$m+3mk+t(k+1)$

Step 1. With reference to the formula $\mathsf{\Phi }$, we generate some disjoint copies of it, denoted as ${\mathsf{\Phi }}_{ij},1\le i\le mk,1\le j\le k-2$. The two variables x and y in $\mathsf{\Phi }$ are renamed as $x_{i,j}$ and $y_{i,j}$ in ${\mathsf{\Phi }}_{ij}$. In addition, sets of variables of these formulas are pairwise disjoint. Define

$$\begin{array}{cc}\hfill X_1& =\left\{x_{i,j}\right\},1\le i\le mk,3\le j\le k-2,\hfill \\ \hfill X_2& =\left\{x_{i,1}\right\},1\le i\le mk,\hfill \\ \hfill X_3& =\left\{x_{i,2}\right\},1\le i\le m,\hfill \\ \hfill X_4& =\left\{x_{i,2}\right\},m+1\le i\le mk,\hfill \\ \hfill Y& =\left\{y_{i,j}\right\},1\le i\le mk,1\le j\le k-2.\hfill \end{array}$$

Construct a new formula ${\mathsf{\Psi }}_1={\wedge }_{1\le i\le mk}{\wedge }_{1\le j\le k-2}{\mathsf{\Phi }}_{ij}$.

Step 2. Introduce a new set of variables $Z=\left\{z_{i,j}\right\},1\le i\le m,1\le j\le k$. Replace $mk$ literals of $\mathsf{\Psi }$ with some variables of Z, and generate a new formula ${\mathsf{\Psi }}_2$.

$$\begin{array}{c}\hfill {\mathsf{\Psi }}_2={\wedge }_{1\le i\le m}(x_{i,2}\vee \left({\vee }_{1\le j\le k}{L}_{i,j}^{\prime }\right)),L_{i,j}^{\prime }=\left\{\begin{array}{cc}{z}_{i,j},& if{L}_{i,j}=v\hfill \\ \neg z_{i,j},& if{L}_{i,j}=\neg v\hfill \end{array}\right.,v\in var\left(\mathsf{\Psi }\right).\end{array}$$

Here, $L_{i,j}$ is denoted as the jth literal in the ith clause of $\mathsf{\Psi }$.

Step 3. The variables of Z are sorted by their subscripts. Let $d_i=z_i\vee \neg z_j\vee \neg x_{i,1}\vee \neg x_{i,2}\vee \dots \vee \neg x_{i,k-2}\vee x_{j,1}$, and generate ${\mathsf{\Psi }}_3={\bigwedge }_{1\le i\le mk}{d}_i$. Here $z_i,z_j\in Z$, and if $z_i$ replaces a variable v of $\mathsf{\Psi }$ then $z_j$ is set to be the next variable of Z which replaces v (if $z_i$ is the last variable in the variable set Z which replaces v, $z_j$ is set to be the first).

Step 4. Introduce a new variable set $U=\{u_1,u_2,\dots ,u_{m+3mk+t(k+1)}\}$. Here, $t>{\displaystyle \frac{mks+3ms-4mk-4m}{ks-3s}}$. Using these variable sets $X_1,X_2,X_3,X_4,Y,Z,U$, we construct a ($k+1$)-CNF formula ${\mathsf{\Psi }}_4$ satisfying the following conditions.

(i)

Every variable x of $X_1$ and $X_4$ occurs exactly in $s-2$ clauses and

$$0\le \mid Neg({\mathsf{\Psi }}_4,x)-Pos({\mathsf{\Psi }}_4,x)\mid \le d.$$

(ii)

Every variable x of $X_2$ and $X_3$ occurs exactly in $s-3$ clauses and

$$0\le \mid Neg({\mathsf{\Psi }}_4,x)+1-Pos({\mathsf{\Psi }}_4,x)\mid \le d.$$

(iii)

All variables of Y occur negatively exactly once.

(iv)

Each variable z of Z appears exactly ($s-3$)-times, and if z occurs positively in ${\mathsf{\Psi }}_2$,

$$0\le \mid Neg({\mathsf{\Psi }}_4,z)+1-Pos({\mathsf{\Psi }}_4,z)\mid \le d.$$

Otherwise

$$0\le \mid Neg({\mathsf{\Psi }}_4,z)-Pos({\mathsf{\Psi }}_4,z)-1\mid \le d.$$

(v)

Every variable u of U occurs exactly in s clauses and

$$Pos({\mathsf{\Psi }}_4,u)-Neg({\mathsf{\Psi }}_4,u)\le min(1,d).$$

(vi)

Any one of the clauses of ${\mathsf{\Psi }}_4$ includes no less than two positive literals from U.

Step 5. Construct a new formula ${\mathsf{\Psi }}^{\prime }=[{\mathsf{\Psi }}_1,{\mathsf{\Psi }}_2,{\mathsf{\Psi }}_3,{\mathsf{\Psi }}_4]$.

It is easy to see that the formula ${\mathsf{\Psi }}^{\prime }$ constructed by us is a d-regular ($k+1,s$)-CNF formula. Our biggest concern is the feasibility of constructing ${\mathsf{\Psi }}^{\prime }$. Constructing three formulas ${\mathsf{\Psi }}_1$, ${\mathsf{\Psi }}_2$ and ${\mathsf{\Psi }}_3$ apparently must be done in polynomial time. We will mainly analyze ${\mathsf{\Psi }}_4$.

In the subformula ${\mathsf{\Psi }}_4$, the number of clauses equals

$$\begin{array}{cc}\hfill \#cl\left({\mathsf{\Psi }}_4\right)& =\frac{(m+3mk+t(k+1\left)\right)s+(2mk+m)(s-3)}{k+1}\hfill \\ \hfill & +\frac{\left(mk\right(k-3)-m)(s-2)+mk(k-2)}{k+1}\hfill \\ \hfill & =\frac{m{k}^{2}s-m{k}^2+2mks-2mk+ms+tks+ts-m}{k+1}\hfill \\ \hfill & =mks-mk+ms+ts-m,\hfill \end{array}$$

and the number of non-negative occurrences of U equals

$$Pos({\mathsf{\Psi }}_4,U)=(m+3mk+t(k+1))\lceil s/2\rceil .$$

For $k\ge 4$ and $t>{\displaystyle \frac{mks+3ms-4mk-4m}{ks-3s}}$,

$$\begin{array}{cc}\hfill tks-3ts& >mks+3ms-4mk-4m,\hfill \\ \hfill ms+3mks+tks+ts& >4mks-4mk+4ms+4ts-4m,\hfill \\ \hfill (m+3mk+tk+t)\lceil s/2\rceil & >2(mks-mk+ms+ts-m),\hfill \\ \hfill Pos({\mathsf{\Psi }}_4,U)& >2\#cl({\mathsf{\Psi }}_4,U).\hfill \end{array}$$

Obviously, there are more than twice as many non-negative literals from U in ${\mathsf{\Psi }}_4$ as clauses. First arrange any two positive literals of U to each clause of ${\mathsf{\Psi }}_4$, and then randomly arrange others. The simple placement method can construct ${\mathsf{\Psi }}_4$. It can be seen that ${\mathsf{\Psi }}_4$ can be constructed in polynomial time.

Finally, we will show that iff $\mathsf{\Psi }$ is satisfiable, ${\mathsf{\Psi }}^{\prime }$ is (1,0)-satisfiable.

Let’s suppose that a (1,0)-super solution of ${\mathsf{\Psi }}^{\prime }$ is just an assignment $\tau$. That is, for any clause of ${\mathsf{\Psi }}^{\prime }$, no less than two literals are satisfied by $\tau$. Because all ${\mathsf{\Phi }}_{ij}$ are forced-d-regular $(k+1,s)$-CNF formulas, it is significant that $\tau \left(x_{i,j}\right)=true,\tau \left(y_{i,j}\right)=true$, for $1\le i\le mk,1\le j\le k-2$.

Substitute $\tau \left(x_{i,j}\right)$ into ${\mathsf{\Psi }}_3$, and simplify ${\mathsf{\Psi }}_3$. We obtain by Lemma 4 that in any one (1,0)-super solution the simplified ${\mathsf{\Psi }}_3$ can express n cyclic of implication. This suggests, if the same variable of $\mathsf{\Psi }$ is replaced by $z_i$ and $z_j$, we get $\tau \left(z_i\right)=\tau \left(z_j\right)$. Because of this, a new truth assignment ${\tau }^{\prime }$ is defined as

$${\tau }^{\prime }\left(v\right):=\tau \left(z\right),\begin{array}{c}ifavariablevof\mathsf{\Psi }isreplacedwithavariablezinZ.\hfill \end{array}$$

Because no less than two literals of every clause of ${\mathsf{\Psi }}_2$ are satisfied by the (1,0)-super solution $\tau$, for any clause of $\mathsf{\Psi }$, ${\tau }^{\prime }$ is guaranteed to satisfy at least one literal. Therefore, $\mathsf{\Psi }$ is satisfiable.

Let’s suppose that a truth assignment $\tau$ satisfies $\mathsf{\Psi }$ and an assignment ${\tau }_{i,j}$ is precisely a (1,0)-super solution of ${\mathsf{\Phi }}_{i,j}$, $1\le i\le mk,1\le j\le k-2$. We define a new truth assignment ${\tau }^{\prime }$ as

$${\tau }^{\prime }\left(v\right):=\left\{\begin{array}{cc}\tau \left(x\right),\hfill & ifv\in Zandavariablexofvar\left(\mathsf{\Psi }\right)isreplacedwithv\hfill \\ {\tau }_{i,j}\left(v\right),\hfill & ifv\in var\left({\mathsf{\Phi }}_{ij}\right)\hfill \\ true,\hfill & ifv\in U\hfill \end{array}\right..$$

As a (1,0)-super solution of ${\mathsf{\Phi }}_{i,j}$, ${\tau }_{i,j}$ is certain to satisfy two literals of any clause in ${\mathsf{\Phi }}_{i,j}$, it means that, for any clause of ${\mathsf{\Psi }}_1$, there are two literals is satisfied by ${\tau }^{\prime }$. Because ${\mathsf{\Phi }}_{i,j}$ is a forced-d-regular $(k+1,s)$-CNF formula, we infer that ${\tau }^{\prime }\left(x_{i,j}\right)=true$, ${\tau }^{\prime }\left(y_{i,j}\right)=true$, $1\le i\le mk$, $1\le j\le k-2$. In addition, $\tau$ satisfies at least one literal of every clause of $\mathsf{\Psi }$, so at least two literals of every clause of ${\mathsf{\Psi }}_2$ and ${\mathsf{\Psi }}_3$ are satisfied by ${\tau }^{\prime }$. Thus, ${\tau }^{\prime }$ is a (1,0)-super solution of ${\mathsf{\Psi }}^{\prime }$.

For $k\ge 4$, k-SAT problem is a NP-complete problem. Therefore, (1,0)-d-regular ($k+1,s$)-SAT problem is also a NP-complete problem.

The proof is completed.    □

Theorem 4 shows that for $k\ge 5$, if a d-regular $(k,s)$-CNF formula is (1,0)-unsatisfiable, then (1,0)-d-regular ($k,s$)-SAT problem is a NP-complete problem. But it is not known whether the conclusion is valid for $k=4$. When s is an odd number, $2\lceil s/2\rceil \ge s$. By modifying the reduction method used to proof Theorem 2, we can get that (1,0)-1-regular (4,5)-SAT, (1,0)-2-regular (4,4)-SAT, (1,0)-2-regular (4,6)-SAT are NP-complete.

Given a (4,4)-CNF formula F, its representation matrix is

$$\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\left(\begin{array}{cccc}+& +& -& -\\ +& -& +& -\\ -& +& +& -\\ +& -& -& +\end{array}\right).$$

Obviously, F has no (1,0)-super solution. However, we have no idea whether (1,0)-0-regular (4,4)-SAT and (1,0)-1-regular (4,6)-SAT are NP-complete.

5. The Transition Phenomenon of (1,0)-$\mathit{d}$-Regular $(\mathit{k},\mathit{s})$-SAT

We have proved (1,0)-$(k,s)$-SAT problem has a Transition Phenomenon for $k\ge 3$. In this section, we will focus on the transition phenomenon of (1,0)-d-regular $(k,s)$-SAT.

Theorem 3.

For $k\ge 5$ and $d\ge 0$, a critical function $\phi (k,d)$ can be found such that

(i)

for $s\le \phi (k,d)$ any one of d-regular ($k,s$)-CNF formulas is (1,0)-satisfiable and

(ii)

for $s>\phi (k,d)$ (1,0)-d-regular ($k,s$)-SAT problem is a NP-complete problem.

Proof. 

The corollary can be directly derived from Theorem 2.    □

It is clear that $\phi (k,d)$ is the maximum s can be set to ensure that all d-regular ($k,s$)-CNF formulas must be (1,0)-satisfiable. Then, we will give some properties of the critical function $\phi (k,d)$.

If all ($k,s$)-CNF formulas can find a (1,0)-super solution, all d-regular ($k,s$)-CNF formulas have a (1,0)-super solution. Therefore, we get $\phi (k,d)\ge \phi \left(k\right)$. Because the critical function $\phi \left(k\right)$ is an increasing function, proved in [27], we obtain $\phi (k,d)\ge \phi (k-1)$. Any d-regular ($k,s$)-CNF formula obviously should be a $(d+1)$-regular ($k,s$)-CNF formula, so we get $\phi (k,d)\ge \phi (k,d+1)$. For each variable of any one of regular ($k,s$)-CNF formulas, the absolute difference between positive and negative occurrences is at most $s-2$. Therefore, if $\phi \left(k\right)<s$, then $\phi (k,s-2)<s$. For $d=\phi \left(k\right)-1$, we get $\phi (k,d)=\phi \left(k\right)$. According to some properties of the critical function $f(k,d)$ and $\phi \left(k\right)$ presented in [12,27], we can obtain the following corollaries.

Corollary 2.

For $k\ge 5$ and $d\ge 0$, $\phi (k,d)\ge 2$.

Corollary 3.

For $k\ge 5$ and $d\ge 0$, $\phi (k+1,d)\ge \phi (k,d)$.

Corollary 4.

For $k\ge 5$ and $d\ge 0$, $\phi (k+1,2d)\ge 2\phi (k,d)+1$.

By Corollary 3, it can be known that $\phi (k,d)$ is an increasing function of k and a decreasing function of d. By Corollary 4, we can obtain a peculiar result that $\phi (k+1,0)\ge 2\phi (k,0)+1$.

Theorem 4.

For $k\ge 5$ and $d\ge 0$, we get $\phi (k,d)\le f(k-1,d)$.

Proof. 

We can find an unsatisfiable d-regular ($k-1,f(k-1,d)+1$)-CNF formula, because $f(k-1,d)$ is the critical function of d-regular ($k-1,s$)-SAT. By Corollary 1, we get (1,0)-d-regular ($k,f(k-1,d)+1$)-SAT is NP-complete. That is, $\phi (k,d)\le f(k-1,d)$.    □

Next, we will put forward a property of the critical function of $\phi \left(k\right)$ and then extend it to $\phi (k,d)$.

Theorem 5.

$\phi \left(2k\right)\ge f\left(k\right)$.

Proof. 

Given a $(2k,f(k)$)-CNF formula $\mathsf{\Phi }$ with m clauses, we break up every clause $C_i$ of $\mathsf{\Phi }$ into two parts with the same size, namely $C_{i1}$ and $C_{i2}$. Then, a new formula $\mathsf{\Psi }$ is formed by these divided clauses. Obviously, $\mathsf{\Psi }$ is a $(k,f(k)$)-CNF formula. Because $f\left(k\right)$ is the critical function of ($k-1,s$)-SAT, $\mathsf{\Psi }$ must be satisfiable. Let an assignment $\tau$ be a satisfying assignment of $\mathsf{\Psi }$. That is, $\tau$ satisfies every pair of $C_{i1}$ and $C_{i2}$. Every clause of $\mathsf{\Phi }$ is formed a pair of $C_{i1}$ and $C_{i2}$. Therefore, $\tau$ is (1,0)-super solution of $\mathsf{\Phi }$.

Every $(2k,f(k)$)-CNF formula must have (1,0)-super solution, so $\phi \left(2k\right)\ge f\left(k\right)$.    □

The clauses split method used to prove Theorem 5 keeps the number of positive occurrences or negative occurrences of any variable unchanged, so we can derive the following corollary by the method.

Corollary 5.

For $k\ge 5$ and $d\ge 0$, $\phi (2k,d)\ge f(k,d)$.

By this corollary mentioned above, we derive some bounds of the critical function $\phi (k,d)$.

$$\begin{array}{cc}\hfill & 2\le \phi (5,0)\le 8,2\le \phi (5,1)\le 7,2\le \phi (5,2)\le 6,2\le \phi (5,3)\le 4,\hfill \\ \hfill & 3\le \phi (6,0)\le 10,3\le \phi (6,1)\le 9,3\le \phi (6,4)\le 8,\hfill \\ \hfill & 3\le \phi (7,0)\le 16,3\le \phi (7,1)\le 15,3\le \phi (7,2)\le 14,3\le \phi (7,3)\le 13,3\le \phi (7,4)\le 12,\hfill \\ \hfill & 4\le \phi (8,d)\le \phi (9,d),5\le \phi (10,d)\le \phi (11,d),\hfill \\ \hfill & 7\le \phi (12,d)\le \phi (13,d),13\le \phi (14,d)\le \phi (15,d),\hfill \\ \hfill & 24\le \phi (16,d)\le \phi (17,d),41\le \phi (18,d)\le \phi (19,d).\hfill \end{array}$$

Finally, we will give some better results about the lower bound of $\phi (k,d)$ by The Lopsided Local Lemma.

Theorem 6.

For three positive integers $k\ge 4$, s and $(s+1)/2\ge t\ge 1$, if there is a real number $0<p<1$ such that

$$\frac{{p\left(1-p\right)}^{kt}{2}^k}{k+1}\ge 1,$$

(1)

then every ($k,s$)-CNF formula in which each literal occurs in at most t clauses must be (1,0)-satisfiable.

Proof. 

Given a ($k,s$)-CNF formula $\mathsf{\Psi }$ that each literal occurs at most t times. Let C be the set of clauses in $\mathsf{\Psi }$ and X be the set of variables. We define an undirected graph G with vertex set C. For any two clauses $c_1,c_2\in C$, if there is an edge between $c_1$ and $c_2$ if and only if there exists a variable x that occurs negated in one clause and without negation in the other. We pick a clause $c\in C$ at random and denote a clause set $S=C\backslash N^{+}\left(c\right)$. We generate a random assignment $\tau$ by setting each variable independently to be true with a probability of $1/2$. Let $A_c$ be the event that at most one literal of c is satisfied by the assignment $\tau$, $B_c$ be the event that at least two literals of each clause of S are satisfied by the assignment $\tau$.

We first show that the graph G is the lopsidependency graph for the events $A={\left\{A_c\right\}}_{c\in C}$. Let $X_1$ be the set of variables that occur both in the clause c and in some clauses of S. By the definition of G, we obtain that for each $x\in X_1$, x occurs with the same sign in c and S. That is, if x occurs positively in c, then x must not occur negatively in any one clause of S, and vice versa. Obviously, $\overline{A_c}$ and $B_c$ are both increasing because of these variables of $X_1$. By the FKG inequality on [32], we get that $\overline{A_c}$ and $B_c$ are positively correlated, and $A_c$ and $B_c$ are negatively correlated. That is to say,

$$Pr\left[\left.A_c\right|B_c\right]=Pr\left[A_c\left|\bigcap _{i\in S}\stackrel{-}{A_i}\right.\right]\le Pr\left[A_c\right].$$

Thus, the graph G is the lopsidependency graph for the events $A={\left\{A_c\right\}}_{c\in C}$.

Because every variable is assigned to true with probability $1/2$ and every clause has exactly t literals, the probability that the clause c has at most one literal satisfied is

$$Pr\left[A_c\right]={(1/2)}^k+k{(1/2)}^k=(k+1)/2^k.$$

In the formula $\mathsf{\Psi }$, each literal occurs at most t times. That is, for any variable in $\mathsf{\Psi }$, the number of positive occurrences and negative occurrences are all at most t. Let $deg\left(c\right)$ be the degree of c in G. By the definition of G, we obtain that for each $c\in C$, $deg\left(c\right)\le kt$. For $0<p<1$, we get

$$p\prod _{i\in N\left(c\right)}\left(1-p\right)=p{\left(1-p\right)}^{deg\left(c\right)}\ge p{\left(1-p\right)}^{kt}.$$

For $\frac{{p\left(1-p\right)}^{kt}{2}^k}{k+1}\ge 1$, we get ${p\left(1-p\right)}^{kt}\ge \frac{k+1}{2^k}$. So

$$Pr\left[A_c\right]\le p\prod _{i\in N\left(c\right)}\left(1-p\right).$$

By the Lopsided Local Lemma, we get $Pr\left[{\bigcap }_{c\in C}\stackrel{-}{A_c}\right]>0$. That is, for any clause of C, an assignment can satisfy at least two literals. Thus, the formula $\mathsf{\Psi }$ must be (1,0)-satisfiable.

The proof is completed.    □

For given k and t, if we can find a real number $0<p<1$ such that ${\displaystyle \frac{{p\left(1-p\right)}^{kt}{2}^k}{k+1}}\ge 1$, then every ($k,s$)-CNF formula, in which the number of positive and negative occurrences of all variables are at most t, must have a (1,0)-super solution. So we deduce that all 0-regular ($k,2t$)-CNF formulas, 1-regular ($k,2t-1$)-CNF formulas and 3-regular ($k,2t-3$)-CNF formulas must be (1,0)-satisfiable.

For a given k, the maximum value of t satisfying Equation (1) is useful in searching the lower bound of $\phi (k,d)$. We design an algorithm that can find rapidly the maximum value of t such that ${\displaystyle \frac{{p\left(1-p\right)}^{kt}{2}^k}{k+1}}\ge 1$, for $0<p<1$. Let $f(k,p,t)={\displaystyle \frac{{p\left(1-p\right)}^{kt}{2}^k}{k+1}}$. Figure 1 is the flowchart of the algorithm. When fixing t, the maximum value of the function f can be obtained for $p={\displaystyle \frac{1}{tk+1}}$.

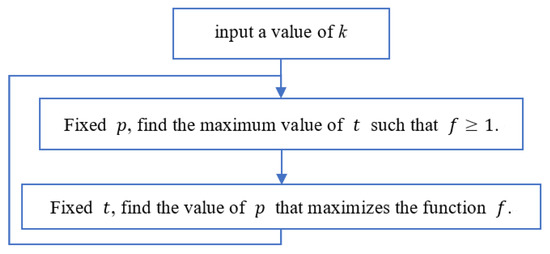
Figure 1. The flowchart of Algorithm 1, here $f(k,p,t)=\frac{{p\left(1-p\right)}^{kt}{2}^k}{k+1}$.

Utilizing Algorithm 1, we obtain some values of $k,p,t$ that satisfy Equation (1) and show it in Table 2.

Algorithm 1: An algorithm for finding the maximum value of t satisfying Equation (1)

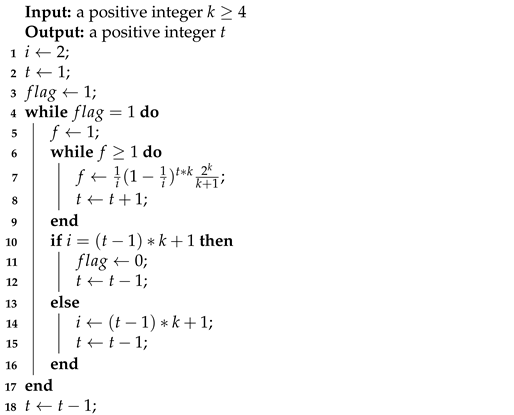Table 2. The values of $k,p,t$ that satisfy Equation (1).

k	p	t
8	1/10	1
9	1/19	2
10	1/34	3
11	1/64	5
12	1/116	9
13	1/215	16
14	1/402	28

Based on these results, we obtain the better lower bound of $\phi (k,d)$.

$$\begin{array}{cc}\hfill & \phi (9,0)\ge 4,\hfill \\ \hfill & \phi (10,0)\ge 6,\phi (10,1)\ge 5,\hfill \\ \hfill & \phi (11,0)\ge 10,\phi (11,1)\ge 9,\phi (11,2)\ge 8,\phi (11,3)\ge 7,\phi (11,4)\ge 6,\hfill \\ \hfill & \phi (12,0)\ge 18,\phi (12,1)\ge 17,\phi (12,2)\ge 16,\phi (12,3)\ge 15,\phi (12,4)\ge 14,\phi (12,5)\ge 13,\hfill \\ \hfill & \phi (13,0)\ge 32,\phi (13,1)\ge 31,\phi (13,2)\ge 30,\phi (13,3)\ge 29,\phi (13,4)\ge 28,\phi (13,5)\ge 27,\hfill \\ \hfill & \phi (14,0)\ge 56,\phi (14,1)\ge 55,\phi (14,2)\ge 54,\phi (14,3)\ge 53,\phi (14,4)\ge 52,\phi (14,5)\ge 51.\hfill \end{array}$$

6. Conclusions and the Future Work

Results of previous research indicate that the (1,0)-k-SAT problem is a P problem for $k=3$, and the k-SAT problem with a promise of g-satisfying assignment is also a P problem for $g\ge k/2$. We investigate the NP-completeness of (1,0)-d-regular $(k,s)$-SAT problem, and prove that it has a sudden jump from triviality to NP-completeness for $k\ge 5$. But for $k=4$, we are not clear about this problem. Similarly, the (3,4)-SAT problem, (4,5)-SAT problem and 0-regular (3,4)-SAT problem all have some unsatisfiable instances, the (7,6)-SAT problem and (8,7)-SAT problem all have an unsatisfiable instance, but we do not know if (5,6)-SAT has an unsatisfiable instance. Obviously, there are some unsolved problems for smaller k.

We obtain the better lower bound of $\phi (k,d)$ by the Lopsided Local Lemma. Moser and Tardos in [33] showed that, under the same conditions as the Local Lemma, there is an efficient algorithm to find a solution of k-SAT problem, but it is not clear whether this is also the case in (1,0)-k-SAT problem. That is, we expect to find an efficient algorithm for (1,0)-SAT. In addition, there is no good way to construct some unsatisfiable (1,0)-SAT instances. These unsatisfiable (1,0)-SAT instances are conducive to finding a better upper bound of $\phi (k,d)$. These questions are all worth probing into.