New Development in Quadratic ${\mathcal{L}}_2$ Performance of Switched Uncertain Stochastic Systems

Abstract

Global quadratic stability and ${\mathcal{L}}_2$ performance in probability (quadratic stability and ${\mathcal{L}}_2$ gain $\gamma$ in probability: abbreviated as GQ${\mathcal{L}}_2\left(\gamma \right)$-P) is studied for switched systems consisting of linear stochastic subsystems with norm-bounded uncertainties. Under the assumption that there is no single subsystem achieving GQ${\mathcal{L}}_2\left(\gamma \right)$-P, it is shown that if there exists a convex combination of subsystems achieving GQ${\mathcal{L}}_2\left(\gamma \right)$-P, then a state-dependent switching law, based on the convex combination of subsystems, is proposed under which the switched system achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P. Then, the discussion is extended to the case involving state feedback controller gain. A numerical example and the application to DC–DC boost converters are provided to demonstrate the proposed design condition and the algorithm.

1. Introduction

In the last three decades, there has been extensive interest and quantities of papers in switched systems, which are regarded to be good models representing practical systems; refer to [1,2,3,4,5,6,7] and the references therein. It is well-known that there are three basic problems in the area of switched systems and control, and the third one (most challenging problem) is to design a stabilizing switching law (strategy) for the case where each single subsystem is not stable as desired. When the switched linear systems are composed of unstable LTI deterministic subsystems, there are a few existing results. In [8,9], it is shown that if there exists a stable convex combination of subsystem matrices, then there exists a state-dependent switching rule quadratically stabilizing the switched system. For switched continuous-time and discrete-time linear systems with polytopic uncertainties, quadratic stabilizability via state-dependent switching has been discussed [10]. Ref. [11] investigates quadratic stability/stabilization of a class of switched nonlinear systems by using a nonlinear programming (Karush–Kuhn–Tucker condition) approach. Ref. [12] extends the discussion and results in [8,9] to achieve quadratic stability for switched linear systems with norm-bounded uncertainties, and a state-dependent switching law has been proposed for quadratic stabilization.

Recently, the results in [8,9] were extended in Ref. [13] to quadratic stabilization of switched linear systems where norm-bounded uncertainties exist in the subsystems. In that context, a convex combination of subsystems is defined including the subsystem matrices and the matrices denoting uncertainties, and is represented by a condition of ${\mathcal{H}}_{\infty }$ norm. It was shown in [13] that if we manage to obtain such a convex combination of subsystems, which is Hurwitz, and the ${\mathcal{H}}_{\infty }$ norm is smaller than the specified value, we can design a state-dependent switching law such that the switched system is quadratically stable, even though each subsystem is not. The convex combination approach was further discussed for switched affine systems in [14], and later extended to quadratic stabilization of switched uncertain stochastic systems (SUSS) by state- and output-dependent switching laws in [15,16].

Encouraged by these existing contribution, we here aim to study the convex combination approach developed in [8,9,13,15,16] for global quadratic ${\mathcal{L}}_2$ performance in probability (quadratic stability and ${\mathcal{L}}_2$ gain $\gamma$ in probability: abbreviated as GQ${\mathcal{L}}_2\left(\gamma \right)$-P) for SUSSs, which consist of a finite number of linear stochastic subsystems where there are norm-bounded uncertainties. As in the above literature, we challenge the third basic problem, i.e., we consider the situation that for a specified positive scalar $\gamma$, there is no subsystem that achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P. For our control problem, we define a new convex combination of subsystems that incorporates the norm-bounded uncertainties, ${\mathcal{L}}_2$ gain, and stochastic disturbance attenuation in an integrated manner. This is a major extension to the existing convex combination approach. If we can obtain such a convex combination of subsystems that achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P, then we propose a switching law using the Lyapunov matrix obtained by the convex combination system matrices, and prove the SUSS achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P under the switching law. When it is difficult to find such an appropriate convex combination, we proceed to consider designing the state feedback controller for each subsystem so that the convex combination approach may be applied for the closed-loop subsystems.

The outline of this manuscript is as follows. Some preliminaries are first recalled in Section 2 for general and linear stochastic control systems, quadratic stability, and quadratic ${\mathcal{L}}_2$ performance in probability; then, the control problem in this paper is formulated. Next, Section 3 introduces the new convex combination of subsystems and proposes a state-dependent switching law for the SUSS under consideration. It is shown that if we can obtain a convex combination of subsystems that achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P, then a state-dependent switching law can be designed such that the SUSS achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P. A numerical example is provided to show effectiveness of the proposed method. In Section 4, the simultaneous design of state feedback controllers and state-dependent switching laws is studied so that more flexibility is earned for the control system, and the application to a type of DC–DC boost converters is dealt with. Finally, Section 5 concludes the paper.

Notations	Descriptions
${\Re }^n$	n-dimensional Euclidean space
$I_n$	Identity matrix of size $n\times n$
$A^{\top }$	transpose of A
$\mathit{Tr}\left(A\right)$	trace of square matrix A
$\mathit{He}\left\{A\right\}$	$A+A^{\top }$
$W\succ 0(W\prec 0)$	W is symmetric and positive (negative) definite
$W⪰0(W⪯0)$	W is symmetric and non-negative (non-positive) definite
$\mathrm{E}[·]$	expectation value of a random variable
A is Hurwitz	all eigenvalues of A have negative real parts
SUSS	Switched uncertain stochastic systems
GQS-P (GAS-P)	globally quadratically (asymptotically) stable in probability
GQ${\mathcal{L}}_2\left(\gamma \right)$-P	global quadratic ${\mathcal{L}}_2$ performance $\gamma$ in probability

2. Preliminary Results and Problem Formulation

We first recall some stability results concerning stochastic control systems. For a more detailed description, refer to, for example, Ref. [17]. At the end of this section, we explain the control problem considered in this paper.

Let us start with the general stochastic system

$$\mathrm{d}x\left(t\right)=f\left(x\right(t\left)\right)\mathrm{d}t+g\left(x\right(t\left)\right)\mathrm{d}w\left(t\right)$$

(1)

where $x\left(t\right)\in {\Re }^n$ is the state, $w\left(t\right)$ is an r-dimensional normalized Wiener process defined on an appropriate probability space, and $\mathrm{d}x\left(t\right)$ is a stochastic differential of $x\left(t\right)$. $f:{\Re }^n\to {\Re }^n$ is the vector field, $g:{\Re }^n\to {\Re }^{n\times r}$ is the diffusion rate matrix function, and both functions are locally Lipschitz satisfying $f\left(0\right)=0$, $g\left(0\right)=0$. Similar to the Lyapunov stability theory [18] for deterministic systems, the following theorem provides the Lyapunov stability condition for the stochastic system (1).

Lemma 1

([19]). If there exist a ${\mathcal{C}}^2$ function $V\left(x\right)$, two class ${\mathcal{K}}_{\infty }$ functions ${\alpha }_1$ and ${\alpha }_2$, and a class $\mathcal{K}$ function ${\alpha }_3$, satisfying

$$\begin{array}{ccc}& & {\alpha }_1\left(\right|x\left|\right)\le V\left(x\right)\le {\alpha }_2\left(\right|x\left|\right)\hfill \\ & & \mathcal{L}V\left(x\right)=\frac{\partial V}{\partial x}f\left(x\right)+\frac{1}{2}Tr\left(g^{\top }\frac{{\partial }^{2}V}{\partial x^2}g\right)\le -{\alpha }_3\left(\right|x\left|\right),\hfill \end{array}$$

then, the equilibrium $x=0$ of (1) is globally asymptotically stable in probability (GAS-P).

If the function $V\left(x\right)$ in Lemma 1 is obtained having the form $V\left(x\right)=x^{\top }Px$, where $P\succ 0$, we say the equilibrium of the system (or simply the system) is globally quadratically stable in probability (GQS-P). Actually, when f and g in (1) are linear with respect to x, i.e., taking the form of

$$\mathrm{d}x\left(t\right)=Ax\left(t\right)\mathrm{d}t+Hx\left(t\right)\mathrm{d}w\left(t\right)$$

(2)

where $A,H\in {\Re }^{n\times n}$ are constant matrices, we can consider a candidate quadratic Lyapunov function $V\left(x\right)=x^{\top }Px$ with $P\succ 0$ for it. Translating Lemma 1 with this $V\left(x\right)$ and $f\left(x\right)=Ax,g\left(x\right)=Hx$, we obtain the following result.

Lemma 2.

If there exists a matrix $P\succ 0$ satisfying the linear matrix inequality (LMI) [20]

$$He\left\{PA\right\}+H^{\top }PH\prec 0,$$

(3)

then, the equilibrium $x=0$ of (2) is GQS-P.

Now, we deal with the case of involving uncertainties in the stochastic system (2) as

$$\mathrm{d}x\left(t\right)=(A+DF(t\left)E\right)x\left(t\right)\mathrm{d}t+Hx\left(t\right)\mathrm{d}w\left(t\right)$$

(4)

where $D\in {\Re }^{n\times m},E\in {\Re }^{p\times n}$ are constant matrices, $F\left(t\right)\in {\Re }^{m\times p}$ denotes the norm-bounded uncertainty and assumes $\parallel F\left(t\right)\parallel \le 1$ without losing generality. According to Lemma 2, the equilibrium $x=0$ of (4) is GQS-P if there exists a matrix $P\succ 0$ satisfying

$$He\left\{P(A+DF\left(t\right)E)\right\}+H^{\top }PH\prec 0$$

(5)

for any $F\left(t\right)$ within the norm bound.

The next well-known lemma is used to analyze the matrix inequality (5).

Lemma 3

([21]). Assume that $U\in {\mathcal{R}}^{n\times m}$ and $W\in {\mathcal{R}}^{p\times n}$ are constant matrices. Then,

$$He\left\{UFW\right\}⪯U{U}^{\top }+W^{\top }W$$

(6)

holds for any $F\in {\mathcal{R}}^{m\times p}$ satisfying $\parallel F\parallel \le 1$.

Using the above lemma and the Schur complement lemma for the matrix inequality (5), we obtain the following result.

Lemma 4.

If there exists a matrix $P\succ 0$ satisfying the LMI

$$\left[\begin{array}{cc}He\left\{PA\right\}+H^{\top }PH+E^{\top }E& PD\\ D^{\top }P& -I_m\end{array}\right]\prec 0,$$

(7)

then, the equilibrium $x=0$ of (4) is GQS-P.

Next, we consider the following uncertain stochastic system, which corresponds to the system (4) with disturbance input and controlled output.

$$\left\{\begin{array}{ccc}\hfill \mathrm{d}x\left(t\right)& =& \left[(A+DF(t\left)E\right)x\left(t\right)+Bv\left(t\right)\right]\mathrm{d}t+Hx\left(t\right)\mathrm{d}w\left(t\right)\hfill \\ \hfill z\left(t\right)& =& Cx\left(t\right)\hfill \end{array}\right.$$

(8)

Here, $v\left(t\right)\in {\Re }^q$ is the disturbance input; $z\left(t\right)\in {\Re }^r$ is the controlled output; and $B,C$ are constant matrices with proper dimension.

Definition 1.

The system (8) is said to achieve global quadratic ${\mathcal{L}}_2$ performance $\gamma$ in probability (GQ${\mathcal{L}}_2\left(\gamma \right)$-P) if it is GQS-P, and moreover, when $x\left(0\right)=0$,

$$E\left\{{\int }_0^t{z}^{\top }\left(\tau \right)z\left(\tau \right)d\tau \right\}<{\gamma }^2{\int }_0^t{v}^{\top }\left(\tau \right)v\left(\tau \right)d\tau$$

(9)

holds for any time $t>0$ and any disturbance input $v\left(t\right)$ satisfying ${\int }_0^{\infty }{v}^{\top }\left(\tau \right)v\left(\tau \right)d\tau <\infty$.

Lemma 5.

([19]). If there exists a matrix $P\succ 0$ satisfying the LMI

$$\left[\begin{array}{cc}He\left\{PA\right\}+H^{\top }PH+E^{\top }E+C^{\top }C& P\left(\begin{array}{cc}D& \frac{1}{\gamma }B\end{array}\right)\\ \left(\begin{array}{c}{D}^{\top }\\ \frac{1}{\gamma }{B}^{\top }\end{array}\right)P& -I_{m+q}\end{array}\right]\prec 0,$$

(10)

or equivalently,

$$\begin{array}{ccc}& & He\left\{PA\right\}+H^{\top }PH+E^{\top }E+C^{\top }{C}_1+P\left(D{D}^{\top }+\frac{1}{{\gamma }^2}B{B}^{\top }\right)P\prec 0,\hfill \end{array}$$

(11)

then, the system (8) achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P.

With the above preparation, we now proceed to describe our control problem in detail. Consider the switched uncertain stochastic system (SUSS)

$$\left\{\begin{array}{ccc}\hfill \mathrm{d}x\left(t\right)& =& \left[(A_{\sigma }+D_{\sigma }F\left(t\right)E_{\sigma })x\left(t\right)+B_{\sigma }v\left(t\right)\right]\mathrm{d}t+Hx\left(t\right)\mathrm{d}w\left(t\right)\hfill \\ \hfill z\left(t\right)& =& C_{\sigma }x\left(t\right)\hfill \end{array}\right.$$

(12)

where $x\left(t\right)\in {\Re }^n$ is the state, $v\left(t\right)\in {\Re }^q$ is the disturbance input, $z\left(t\right)\in {\Re }^r$ is the controlled output, and $w\left(t\right)$ and $\mathrm{d}x\left(t\right)$ are the same as in (1). The switching law (signal) $\sigma \left(t\right):[0,\infty )\to {\mathcal{I}}_{\mathcal{N}}$ determines the index number of the active subsystem at every time instant, where ${\mathcal{I}}_{\mathcal{N}}=\{1,2,\dots ,N\}$ is the index set. Thus, there are $\mathcal{N}$ subsystems that may be activated, and the dynamics of the i-th subsystem is represented by

$$\left\{\begin{array}{ccc}\hfill \mathrm{d}x\left(t\right)& =& \left[(A_i+D_{i}F\left(t\right)E_i)x\left(t\right)+B_{i}v\left(t\right)\right]\mathrm{d}t+Hx\left(t\right)\mathrm{d}w\left(t\right),\hfill \\ \hfill z\left(t\right)& =& C_{i}x\left(t\right),i=1,2,\dots ,\mathcal{N}\hfill \end{array}\right.$$

(13)

where $A_i,H\in {\Re }^{n\times n}$, $B_i\in {\Re }^{n\times q}$, $C_i\in {\Re }^{r\times n}$, $D_i\in {\Re }^{n\times m}$, $E_i\in {\Re }^{p\times n}$ are constant matrices and $F\left(t\right)\in {\Re }^{m\times p}$ denotes the norm-bounded uncertainty as in (4). It is assumed, as in the literature, that there is no jump in state x at the switching instants.

The control problem is formulated as follows: For given $\gamma >0$, design a state-dependent switching law $\sigma \left(x\right(t\left)\right)$ such that the SUSS (12) achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P.

If there is one subsystem in (13) achieving GQ${\mathcal{L}}_2\left(\gamma \right)$-P, we can choose to activate that subsystem for all time (without any switching) and, certainly, the switched system has the same performance. If there are more than two subsystems in (13) achieving GQ${\mathcal{L}}_2\left(\gamma \right)$-P, we may discuss the average dwell time approach [22,23,24] and multiple/piecewise Lyapunov functions approach [25,26,27]. Since we are here challenging the third basic problem in switched systems and control, we assume the following throughout this paper.

Assumption 1.

There is NO single subsystem in (13) achieving GQ${\mathcal{L}}_2\left(\gamma \right)$-P in the sense of Lemma 5. Alternatively, there is NOT any subsystem such that there exists $P\succ 0$ satisfying the LMI

$$\left[\begin{array}{cc}He\left\{P{A}_i\right\}+H^{\top }PH+E_i^{\top }{E}_i+C_i^{\top }{C}_i& P\left(\begin{array}{cc}{D}_i& \frac{1}{\gamma }{B}_i\end{array}\right)\\ \left(\begin{array}{c}{D}_i^{\top }\\ \frac{1}{\gamma }{B}_i^{\top }\end{array}\right)P& -I_{m+q}\end{array}\right]\prec 0,$$

(14)

or equivalently,

$$\begin{array}{ccc}& & He\left\{P{A}_i\right\}+H^{\top }PH+E_i^{\top }{E}_i+C_i^{\top }{C}_i+P\left(D_i{D}_i^{\top }+\frac{1}{{\gamma }^2}{B}_i{B}_i^{\top }\right)P\prec 0.\hfill \end{array}$$

(15)

3. Convex Combination Based State-Dependent Switching Law

In this section, we define our new convex combination of subsystems and then design the state-dependent switching law, based on the convex combination, such that the SUSS (12) achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P. A numerical example is then provided to illustrate the approach.

3.1. Design Condition and Switching Law

To describe our design condition, we first define the convex combination system of the subsystems in (13) as

$$\left\{\begin{array}{ccc}\hfill \mathrm{d}x\left(t\right)& =& \left[(A_{\lambda }+D_{\lambda }F\left(t\right)E_{\lambda })x\left(t\right)+B_{\lambda }v\left(t\right)\right]\mathrm{d}t+Hx\left(t\right)\mathrm{d}w\left(t\right),\hfill \\ \hfill z\left(t\right)& =& C_{\lambda }x\left(t\right)\hfill \end{array}\right.$$

(16)

where

$${\displaystyle A_{\lambda }=\sum _{i=1}^{\mathcal{N}}{\lambda }_i{A}_i,}$$

(17)

$B_{\lambda }$, $C_{\lambda }$, $D_{\lambda }$, $E_{\lambda }$ are constant matrices satisfying

$$\begin{array}{c}{\displaystyle B_{\lambda }{B}_{\lambda }^{\top }=\sum _{i=1}^{\mathcal{N}}{\lambda }_i{B}_i{B}_i^{\top },C_{\lambda }^{\top }{C}_{\lambda }=\sum _{i=1}^{\mathcal{N}}{\lambda }_i{C}_i^{\top }{C}_i,}\\ {\displaystyle D_{\lambda }{D}_{\lambda }^{\top }=\sum _{i=1}^{\mathcal{N}}{\lambda }_i{D}_i{D}_i^{\top },E_{\lambda }^{\top }{E}_{\lambda }=\sum _{i=1}^{\mathcal{N}}{\lambda }_i{E}_i^{\top }{E}_i,}\end{array}$$

(18)

and ${\lambda }_i$ ($i=1,\dots ,\mathcal{N}$) are non-negative scalars satisfying ${\sum }_{i=1}^{\mathcal{N}}{\lambda }_i=1$.

Remark 1.

For given $B_i$’s, $C_i$’s, $D_i$’s, $E_i$’s in the subsystems and ${\lambda }_i$’s, the matrices $B_{\lambda }$, $C_{\lambda }$, $D_{\lambda }$, and $E_{\lambda }$ satisfying (18) can be computed efficiently by using Cholesky decomposition method, which was numerically implemented in MATLAB.

Next, in addition to Assumption 1, we make the following assumption throughout this paper, which is actually the design condition of the switching law for the SUSS.

Assumption 2.

There exists a convex combination system (16) achieving GQ${\mathcal{L}}_2\left(\gamma \right)$-P in the sense of Lemma 5.

Recalling Lemma 5 and the Schur complement lemma, we observe that Assumption 2 is equivalent to the design condition of finding $P\succ 0$ and ${\lambda }_i$’s such that

$$\left[\begin{array}{cccc}He\left\{P{A}_{\lambda }\right\}+H^{\top }PH& P\left(\begin{array}{cc}{D}_{\lambda }& \frac{1}{\gamma }{B}_{\lambda }\end{array}\right)& C_{\lambda }^{\top }& E_{\lambda }^{\top }\\ \left(\begin{array}{c}{D}_{\lambda }^{\top }\\ \frac{1}{\gamma }{B}_{\lambda }^{\top }\end{array}\right)P& -I_{m+q}& 0& 0\\ C_{\lambda }& 0& -I_r& 0\\ E_{\lambda }& 0& 0& -I_p\end{array}\right]\prec 0.$$

(19)

Thus, how to solve the above matrix inequality is crucial. Due to the terms $He\left\{P{A}_{\lambda }\right\}$, $P{D}_{\lambda }$, and $P{B}_{\lambda }$, (19) is a bilinear matrix inequality (BMI) with respect to P and ${\lambda }_i$’s, and it is commonly known to be difficult to solve a general BMI globally. It is noted that one necessary condition for (19) is

$$\sum _{i=1}^{\mathcal{N}}{\lambda }_{i}He\left\{P{A}_i\right\}\prec 0⟺He\left\{P{A}_{\lambda }\right\}\prec 0,$$

(20)

which is equivalent to $A_{\lambda }$ being Hurwitz. This motivates that if we can manage to find the scalars ${\lambda }_i$ such that $A_{\lambda }$ is Hurwitz, we can use those scalars to solve the inequality (19) with respect to $P\succ 0$. However, it is commonly known that to find the set of stabilizing scalars, ${\lambda }_i$ is generally difficult. One comparatively efficient strategy to achieve such task (to solve (20) with ${\lambda }_i$’s and $P\succ 0$) is the so-called gridding method (or traversal search), which is based on the observation of ${\lambda }_i\ge 0$ and ${\sum }_{i=1}^n{\lambda }_i=1$. Here, we extend the gridding method in the following algorithm to solve (19) with respect to ${\lambda }_i$’s and $P\succ 0$. Due to continuity with respect to the scalars ${\lambda }_i$, if the matrix inequality (19) is feasible, the algorithm will succeed when the division integer m is large enough.

Algorithm for solving (19)

Step 1

Set the division number m of the interval $[0,1]$ as a moderate integer—for example, $m=10$—and define $\mathcal{M}=\{0,\frac{1}{m},\cdots ,\frac{m-1}{m}\}$.

Step 2

(1) choose ${\lambda }_1$ from $\mathcal{M}$ in ascending order; (2) fix ${\lambda }_1$ and choose ${\lambda }_2$ from $\mathcal{M}$ in ascending order under the constraint ${\lambda }_1+{\lambda }_2\le 1$; (3) fix ${\lambda }_1,{\lambda }_2$ and choose ${\lambda }_3$ from $\mathcal{M}$ in ascending order under the constraint ${\lambda }_1+{\lambda }_2+{\lambda }_3\le 1$; … (i) fix ${\lambda }_1,\dots ,{\lambda }_{i-1}$ and choose ${\lambda }_i$ from $\mathcal{M}$ in ascending order under the constraint ${\sum }_{j=1}^i{\lambda }_j\le 1$, and so on, until ${\lambda }_{\mathcal{N}}$ is chosen.

Step 3

Solve (19) with the ${\lambda }_i$’s chosen in Step 2. If (19) is feasible, record the solution and end the algorithm. If (19) is not feasible, go back to Step 2 for another set of ${\lambda }_i$’s. Or, go back to Step 1 to increase the division integer m.

Here is an example for searching parameters in Step 2. When $\mathcal{N}=3,m=3$, we are actually checking the linear matrix inequality (19) in P by fixing the parameters ${\lambda }_i$ in sequence as

$$\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\left(0,\frac{1}{3},\frac{2}{3}\right),\left(0,\frac{2}{3},\frac{1}{3}\right),\left(\frac{1}{3},0,\frac{2}{3}\right),\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right),$$

$$\left(\frac{1}{3},\frac{2}{3},0\right),\left(\frac{2}{3},0,\frac{1}{3}\right),\left(\frac{2}{3},\frac{1}{3},0\right).$$

The bigger m is, the more searching parameters there are in Step 2. Again, since the left side of the matrix inequality (19) is continuous in the parameters ${\lambda }_i$, we can expect to find a feasible solution for (19) when the division integer m is large enough.

Remark 2.

It is noted that the design condition (19) is reduced to

$$He\left\{P{A}_{\lambda }\right\}+H^{\top }PH+E_{\lambda }^{\top }{E}_{\lambda }+C_{\lambda }^{\top }{C}_{\lambda }+P\left({\displaystyle D_{\lambda }{D}_{\lambda }^{\top }+\frac{1}{{\gamma }^2}{B}_{\lambda }{B}_{\lambda }^{\top }}\right)P\prec 0,$$

(21)

or equivalently,

$$\begin{array}{c}\hfill \sum _{i=1}^{\mathcal{N}}{\lambda }_i\left(He\left\{P{A}_i\right\}+H^{\top }PH+E_i^{\top }{E}_i+C_i^{\top }{C}_i\right)+\sum _{i=1}^{\mathcal{N}}{\lambda }_{i}P\left({\displaystyle D_i{D}_i^{\top }+\frac{1}{{\gamma }^2}{B}_i{B}_i^{\top }}\right)P\prec 0,\end{array}$$

(22)

which turns out to be a convex combination of (15). This implies that, although we are in the situation that each single subsystem in (13) does not achieve GQ${\mathcal{L}}_2\left(\gamma \right)$-P, Assumption 2 requires the existence of a convex combination system (16) that should achieve GQ${\mathcal{L}}_2\left(\gamma \right)$-P, guaranteed by a convex combination of the matrix inequalities in (15).

Now, we use the obtained positive definite matrix P to define the state-dependent switching law as

$$\begin{array}{ccc}\hfill \mathcal{SW}1:\sigma \left(x\right)& =& {\displaystyle arg\underset{i\in {\mathcal{I}}_{\mathcal{N}}}{min}{f}_i\left(x\right)}\hfill \end{array}$$

(23)

$$\begin{array}{ccc}& & f_i\left(x\right)=x^{\top }(He\left\{P{A}_i\right\}+E_i^{\top }{E}_i+C_i^{\top }{C}_i)x+x^{\top }P\left(D_i{D}_i^{\top }+\frac{1}{{\gamma }^2}{B}_i{B}_i^{\top }\right)Px.\hfill \end{array}$$

(24)

Theorem 1.

Under Assumptions 1 and 2 and the switching law $\mathcal{SW}1$, the SUSS (12) achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P.

Proof. 

Since the matrix inequality (21) is satisfied, there always exists a positive scalar $\eta$ such that

$$\begin{array}{c}He\left\{P{A}_{\lambda }\right\}+H^{\top }PH+E_{\lambda }^{\top }{E}_{\lambda }+C_{\lambda }^{\top }{C}_{\lambda }+P\left({\displaystyle D_{\lambda }{D}_{\lambda }^{\top }+\frac{1}{{\gamma }^2}{B}_{\lambda }{B}_{\lambda }^{\top }}\right)P+\eta P\prec 0,\end{array}$$

(25)

and thus, for any $x\in {\Re }^n$,

$$\begin{array}{c}{x}^{\top }\left(He\left\{P{A}_{\lambda }\right\}+H^{\top }PH+E_{\lambda }^{\top }{E}_{\lambda }+C_{\lambda }^{\top }{C}_{\lambda }\right)x\\ +x^{\top }P\left({\displaystyle D_{\lambda }{D}_{\lambda }^{\top }P+\frac{1}{{\gamma }^2}{B}_{\lambda }{B}_{\lambda }^{\top }}\right)Px\le -\eta x^{\top }Px.\end{array}$$

(26)

With the definitions in (17) and (18), we obtain

$$\begin{array}{c}\sum _{i=1}^{\mathcal{N}}{\lambda }_i{x}^{\top }\left(He\left\{P{A}_i\right\}+H^{\top }PH+E_i^{\top }{E}_i+C_i^{\top }{C}_i\right)x\\ +\sum _{i=1}^{\mathcal{N}}{\lambda }_i{x}^{\top }P\left({\displaystyle D_i{D}_i^{\top }P+\frac{1}{{\gamma }^2}{B}_i{B}_i^{\top }}\right)Px\le -\eta x^{\top }Px.\end{array}$$

(27)

Notice that the left side of the above inequality is

$$\sum _{i=1}^{\mathcal{N}}{\lambda }_i{f}_i\left(x\right)+x^{\top }{H}^{\top }PHx.$$

Then, under the switching law $\mathcal{SW}1$, since $f_{\sigma }\left(x\right)\le f_i\left(x\right)$ holds for all i, we have

$$\begin{array}{c}{x}^{\top }\left(He\left\{P{A}_{\sigma }\right\}+H^{\top }PH+E_{\sigma }^{\top }{E}_{\sigma }+C_{\sigma }^{\top }{C}_{\sigma }\right)x\\ +x^{\top }P\left({\displaystyle D_{\sigma }{D}_{\sigma }^{\top }P+\frac{1}{{\gamma }^2}{B}_{\sigma }{B}_{\sigma }^{\top }}\right)Px\le -\eta x^{\top }Px.\end{array}$$

(28)

To show the SUSS (12) is GQS-P, we compute the Ito differential of $V\left(x\right)=x^{\top }Px$ along solutions of (12) as

$$\begin{array}{ccc}\hfill \mathrm{d}V& =& \mathcal{L}V\left(x\right)\mathrm{d}t+\frac{\partial V}{\partial x}Hx\mathrm{d}W=\mathcal{L}V\left(x\right)\mathrm{d}t+x^{\top }(H^{\top }P+PH)x\mathrm{d}W\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill \mathcal{L}V\left(x\right)& =& x^{\top }\left(He\left\{P(A_{\sigma }+D_{\sigma }F{E}_{\sigma })\right\}+H^{\top }PH\right)x+x^{\top }P{B}_{\sigma }v.\hfill \end{array}$$

(30)

When $v=0$, it is obtained from (30) and (28) that

$$\begin{array}{ccc}\hfill \mathcal{L}V\left(x\right)& \le & x^{\top }\left(He\left\{P{A}_{\sigma }\right\}+H^{\top }PH\right)x+x^{\top }\left(P{D}_{\sigma }{D}_{\sigma }^{\top }P+E_{\sigma }^{\top }{E}_{\sigma }\right)x\le -\eta V\left(x\right).\hfill \end{array}$$

(31)

According to Lemma 1, the SUSS (12) is GQS-P.

Next, we proceed to prove the GQ${\mathcal{L}}_2\left(\gamma \right)$-P property. First, using Lemma 3 for (30), we obtain

$$\begin{array}{ccc}\mathcal{L}V\left(x\right)\hfill & =\hfill & x^{\top }\left(He\left\{P(A_{\sigma }+D_{\sigma }F{E}_{\sigma })\right\}+H^{\top }PH\right)x+\left(\frac{{\displaystyle 1}}{{\displaystyle \gamma }}{x}^{\top }P{B}_{\sigma }\right)\left(\gamma v\right)\hfill \\ \hfill & \le \hfill & x^{\top }\left(He\left\{P{A}_{\sigma }\right\}+H^{\top }PH\right)x+x^{\top }\left(P{D}_{\sigma }{D}_{\sigma }^{\top }P+E_{\sigma }^{\top }{E}_{\sigma }\right)x\hfill \\ & \hfill & {\displaystyle +\frac{1}{{\gamma }^2}{x}^{\top }P{B}_{\sigma }{B}_{\sigma }^{\top }Px+{\gamma }^2{v}^{\top }v.}\hfill \end{array}$$

(32)

Letting $\Gamma \left(t\right)=z^{\top }\left(t\right)z\left(t\right)-{\gamma }^2{v}^{\top }\left(t\right)v\left(t\right)$, we obtain from (32) and (28) that

$$\mathcal{L}V\left(x\right)+\Gamma \left(t\right)\le -\eta V\left(x\right).$$

(33)

Combining the above discussion into (29), we have

$$\begin{array}{ccc}\hfill \mathrm{d}\left(e^{\eta t}V\right)& =& \eta e^{\eta t}V\mathrm{d}t+e^{\eta t}\mathrm{d}V=e^{\eta t}\left(\eta V\mathrm{d}t+\mathrm{d}V\right)\hfill \\ & \le & -e^{\eta t}\Gamma \left(t\right)dt+e^{\eta t}{x}^{\top }(H^{\top }P+PH)x\mathrm{d}W\hfill \\ & \le & -\Gamma \left(t\right)dt+e^{\eta t}{x}^{\top }(H^{\top }P+PH)x\mathrm{d}W.\hfill \end{array}$$

(34)

Taking expectation and integrating both sides of the above inequality from 0 to t, with the fact that $E\left[\mathrm{d}W\right]=0$, we reach

$$\mathrm{E}\left[e^{\eta t}V\left(x\left(t\right)\right)\right]-V\left(x\left(0\right)\right)\le -\mathrm{E}\left[{\int }_0^t\Gamma \left(\tau \right)d\tau \right].$$

(35)

Since $V\left(x\right(t\left)\right)\ge 0$, this leads to (9) obviously when $x\left(0\right)=0$. Thus, the SUSS achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P. □

Remark 3.

It is observed from the proof of the theorem that if we desire the convergence rate of $\alpha >0$ for the resultant switched system, we should replace $A_{\lambda }$ with $A_{\lambda }+\alpha I$ in the convex combination system (16) or the matrix inequality (19), and all the discussion remains valid.

3.2. Numerical Example

Example 1.

Let us consider the SUSS (12) whose contant coefficient matrices are

$$\begin{array}{c}\begin{array}{c}{A}_1=\left[\begin{array}{cc}-15.2& 9.6\\ 9.6& -0.8\end{array}\right],A_2=\left[\begin{array}{cc}-2.8& -13.6\\ -13.6& -23.2\end{array}\right],\\ B_1=\left[\begin{array}{c}1\\ 0\end{array}\right],B_2=\left[\begin{array}{c}-1\\ 1\end{array}\right]\\ C_1=\left[\begin{array}{cc}0.5& 1.5\end{array}\right],C_2=\left[\begin{array}{cc}-1.0& 0.5\end{array}\right],\\ D_1=\left[\begin{array}{cc}1& 0.6\\ 1& 0.2\end{array}\right],D_2=\left[\begin{array}{cc}0.6& 2.0\\ 0.2& 0\end{array}\right]\\ E_1=\left[\begin{array}{cc}2& 0\\ 2& 2\end{array}\right],E_2=\left[\begin{array}{cc}1.5& -1.5\\ 1.5& 3.0\end{array}\right],H=\left[\begin{array}{cc}0.5& -1.0\\ 1.0& 1.5\end{array}\right]\end{array}\end{array}$$

(36)

and the uncertainty term

$$\begin{array}{c}\hfill F\left(t\right)=\left[\begin{array}{cc}0.5sint-0.1cost& -0.2sint-0.3cost\\ -0.3sint-0.2cost& 0.1sint-0.4cost\end{array}\right]\end{array}$$

satisfies $\parallel F\left(t\right)\parallel \le 1$. It is easy to confirm that $A_1$ and $A_2$ are not Hurwitz. Therefore, Assumption 1 is true, and actually there is no $P\succ 0$ satisfying (14) for both subsystems.

When setting ${\lambda }_1=\frac{2}{3},{\lambda }_2=\frac{1}{3}$, we find that

$$A_{\lambda }=\frac{2}{3}{A}_1+\frac{1}{3}{A}_2=\left[\begin{array}{cc}\hfill -11.0667& \hfill 1.8667\\ \hfill 1.8667& \hfill -8.2667\end{array}\right]$$

is Hurwitz, whose eigenvalues are $\{-12.0000,-7.3333\}$. Furthermore, for given $\gamma =0.5$ and the same ${\lambda }_1,{\lambda }_2$, the matrix inequality (19) is feasible with

$$P=\left[\begin{array}{cc}\hfill 1.5108& \hfill 0.3939\\ \hfill 0.3939& \hfill 1.8546\end{array}\right],$$

which implies that Assumption 2 holds. In the present case, the coefficient matrices in the convex combination system (16) are

$$\begin{array}{c}{B}_{\lambda }=\left[\begin{array}{cc}\hfill 1.0000& \hfill 0\\ \hfill -0.3333& \hfill 0.4714\end{array}\right],C_{\lambda }=\left[\begin{array}{cc}\hfill 0.7071& \hfill 0.4714\\ \hfill 0& \hfill 1.1667\end{array}\right]\\ D_{\lambda }=\left[\begin{array}{cc}\hfill 1.5362& \hfill 0\\ \hfill 0.5121& \hfill 0.6667\end{array}\right],E_{\lambda }=\left[\begin{array}{cc}\hfill 2.6141& \hfill 1.3070\\ \hfill 0& \hfill 2.1699\end{array}\right].\end{array}$$

We set the initial state to $x\left(0\right)={\left[\begin{array}{cc}\hfill -5& \hfill 4\end{array}\right]}^{\top }$, and the disturbance input as $w\left(t\right)=2e^{-3t}cos2t$. Then, we use the switching law (23) for the present SUSS, and utilize the well-known Euler–Maruyama scheme for numerical simulation of the stochastic differential equation. With several patterns of white noise, we obtain the state trajectories of the SUSS plotted in Figure 1, which converge to zero quickly as desired. Further, the inequality (9) holds for the sampled patterns of random noise, which implies the desired quadratic stability and ${\mathcal{L}}_2$ performance in probability has been achieved.

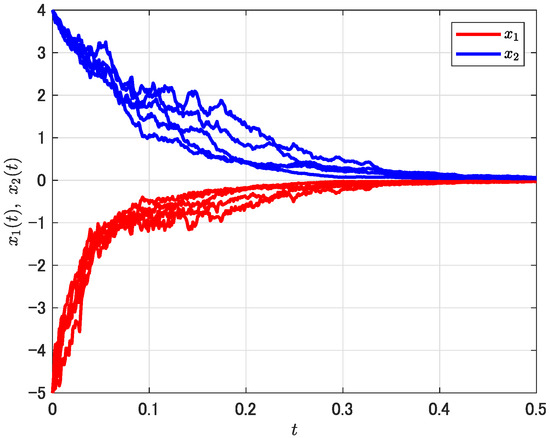
Figure 1. State trajectories of the SUSS under $\mathcal{SW}$1 in Example 1.

4. State Feedback Controller Design

We focused our attention on design condition and the switching law in the previous section. When Assumption 2 does not hold and feedback control is available, we shall incorporate state feedback controller design together with the switching law in this section.

4.1. Controller Design

Introducing control inputs into the switched system (12), we have

$$\begin{array}{ccc}\hfill \mathrm{d}x\left(t\right)& =& \left[(A_{\sigma }+D_{\sigma }F\left(t\right)E_{\sigma })x\left(t\right)+B_{\sigma }v\left(t\right)+G_{\sigma }u\left(t\right)\right]\mathrm{d}t+Hx\left(t\right)\mathrm{d}w\left(t\right)\hfill \end{array}$$

(37)

where $u\left(t\right)\in {\Re }^l$ is the control input and $G_i\in {\Re }^{n\times l}$ is the constant input matrix.

In the case of state feedback, the design issue is to propose $u=Kx$ with a constant feedback gain K, such that Assumption 2 holds for the closed-loop system

$$\begin{array}{ccc}\hfill \mathrm{d}x\left(t\right)& =& \left[(A_{\sigma }+G_{\sigma }K+D_{\sigma }F\left(t\right)E_{\sigma })x\left(t\right)+B_{\sigma }v\left(t\right)\right]\mathrm{d}t+Hx\left(t\right)\mathrm{d}w\left(t\right).\hfill \end{array}$$

(38)

Then, the discussion in the previous section is valid if we replace ${\displaystyle A_{\lambda }=\sum _{i=1}^{\mathcal{N}}{\lambda }_i{A}_i}$ with ${\displaystyle A_{K\lambda }=\sum _{i=1}^{\mathcal{N}}{\lambda }_i(A_i+G_{i}K)=A_{\lambda }+G_{\lambda }K}$, where ${\displaystyle G_{\lambda }=\sum _{i=1}^{\mathcal{N}}{\lambda }_i{G}_i}$. In other words, we are considering the following convex combination system of the subsystems in (37)

$$\begin{array}{ccc}\hfill \mathrm{d}x\left(t\right)& =& \left[(A_{\lambda }+D_{\lambda }F\left(t\right)E_{\lambda })x\left(t\right)+B_{\lambda }v\left(t\right)+G_{\lambda }u\left(t\right)\right]\mathrm{d}t+Hx\left(t\right)\mathrm{d}w\left(t\right).\hfill \end{array}$$

(39)

Using the matrix inequality (19) with $A_{\lambda }$ replaced by $A_{K\lambda }$, we obtain the design condition

$$\left[\begin{array}{cccc}He\left\{P{A}_{K\lambda }\right\}+H^{\top }PH& P\left(\begin{array}{cc}{D}_{\lambda }& \frac{1}{\gamma }{B}_{\lambda }\end{array}\right)& C_{\lambda }^{\top }& E_{\lambda }^{\top }\\ \left(\begin{array}{c}{D}_{\lambda }^{\top }\\ \frac{1}{\gamma }{B}_{\lambda }^{\top }\end{array}\right)P& -I_{m+q}& 0& 0\\ C_{\lambda }& 0& -I_r& 0\\ E_{\lambda }& 0& 0& -I_p\end{array}\right]\prec 0.$$

(40)

It is noted that in addition to the coupling between ${\lambda }_i$’s and P, the term $P{A}_{K\lambda }$ includes the matrix product $P{G}_{i}K$ in the above matrix inequality. To make (40) more trackable, we use the Schur complement lemma for (40) to reach

$$\left[\begin{array}{cccccc}He\left\{P{A}_{K\lambda }\right\}& P{D}_{\lambda }& \frac{1}{\gamma }P{B}_{\lambda }& C_{\lambda }^{\top }& E_{\lambda }^{\top }& H^{\top }\\ D_{\lambda }^{\top }P& -I_m& 0& 0& 0& 0\\ \frac{1}{\gamma }{B}_{\lambda }^{\top }P& 0& -I_q& 0& 0& 0\\ C_{\lambda }& 0& 0& -I_r& 0& 0\\ E_{\lambda }& 0& 0& 0& -I_p& 0\\ H& 0& 0& 0& 0& -P^{-1}\end{array}\right]\prec 0.$$

(41)

Multiplying the first row and column of (41) by $Q=P^{-1}$, we obtain

$$\left[\begin{array}{cccccc}He\{A_{\lambda }Q+G_{\lambda }M\}& D_{\lambda }& \frac{1}{\gamma }{B}_{\lambda }& Q{C}_{\lambda }^{\top }& Q{E}_{\lambda }^{\top }& Q{H}^{\top }\\ D_{\lambda }^{\top }& -I_m& 0& 0& 0& 0\\ \frac{1}{\gamma }{B}_{\lambda }^{\top }& 0& -I_q& 0& 0& 0\\ C_{\lambda }Q& 0& 0& -I_r& 0& 0\\ E_{\lambda }Q& 0& 0& 0& -I_p& 0\\ HQ& 0& 0& 0& 0& -Q\end{array}\right]\prec 0$$

(42)

where $M=KQ$. Therefore, if the matrix inequality (42) is feasible with the variables $Q\succ 0$, M, and ${\lambda }_i$’s, the state feedback gain is computed by $K=M{Q}^{-1}$, and the matrix $P=Q^{-1}$ will be used in the switching law defined later.

To summarize the above discussion up to now, we obtain the following theorem.

Theorem 2.

If there exist matrices $Q\succ 0$, M and non-negative scalars ${\lambda }_i$ satisfying ${\sum }_{i=1}^{\mathcal{N}}{\lambda }_i=1$ such that the matrix inequality (42) holds, then the SUSS (37) together with the state feedback $u=M{Q}^{-1}x$ achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P under the switching law

$$\begin{array}{ccc}\hfill \mathcal{SW}2:\sigma \left(x\right)& =& {\displaystyle arg\underset{i\in {\mathcal{I}}_{\mathcal{N}}}{min}{g}_i\left(x\right)}\hfill \\ & & g_i\left(x\right)=x^{\top }\left(He\left\{Q^{-1}(A_i+G_{i}K)\right\}+E_i^{\top }{E}_i+C_i^{\top }{C}_i+\right.\hfill \end{array}$$

(43)

$$\begin{array}{ccc}& & \left.Q^{-1}(D_i{D}_i^{\top }+\frac{1}{{\gamma }^2}{B}_i{B}_i^{\top })Q^{-1}\right)x.\hfill \end{array}$$

(44)

Proof. 

If the matrix inequality (42) holds, we obtain (40). Since $He\left\{P{A}_{K\lambda }\right\}=He\left\{P(A_{\lambda }+G_{\lambda }K)\right\}={\sum }_{i=1}^{\mathcal{N}}He\left\{P(A_i+G_{i}K)\right\}$, by using the proof of Theorem 1, the switched system (38) achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P under the switching law (44). □

Remark 4.

The matrix inequality (41) is equivalent to

$$\begin{array}{c}\hfill \sum _{i=1}^{\mathcal{N}}{\lambda }_i\left({\displaystyle He\left\{P(A_i+G_{i}K)\right\}+H^{\top }PH+E_i^{\top }{E}_i+C_i^{\top }{C}_i+P(D_i{D}_i^{\top }P+\frac{1}{{\gamma }^2}{B}_i{B}_i^{\top })P}\right)\prec 0,\end{array}$$

(45)

which is a convex combination of the matrix inequalities for each subsystem to achieve GQ${\mathcal{L}}_2\left(\gamma \right)$-P through a state feedback. Therefore, the condition of Theorem 2 requires that a convex combination of subsystems should achieve GQ${\mathcal{L}}_2\left(\gamma \right)$-P by a switching state feedback, although every single subsystem cannot make it. In this sense, this condition can be regarded as the state feedback version of the design condition in the previous section.

4.2. Application to Boost Converters

We consider the DC–DC boost converter model dealt with in [28], which is depicted in Figure 2. For simplicity and easiness to follow, suppose that there is only one transistor–diode switch S; thus, the system is composed of two subsystems. In the case of more than two switches in the circuit, the number of subsystems will be more than three, but the discussion and the results can be applied in the same manner.

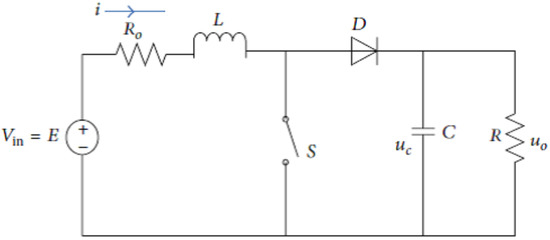
Figure 2. A boost converter with inductor ESR.

Let the inductor current $i\left(t\right)$ and the capacitance voltage $u_c\left(t\right)$ be the state variables, and combine them into the state vector $x\left(t\right)={\left[\begin{array}{cc}i\left(t\right)& u_c\left(t\right)\end{array}\right]}^{\top }.$ Suppose that $E\left(t\right)$ is the control input $u\left(t\right)$, $v\left(t\right)$ is the disturbance input of the input voltage, and the capacitance voltage $u_c\left(t\right)$ is the controlled output $z\left(t\right)$. Moreover, suppose that there are independent stochastic disturbance with the states $i\left(t\right)$ and $u_c\left(t\right)$.

Then, when the switch S is closed, the state space model is

$$\left\{\begin{array}{ccc}\hfill \mathrm{d}x\left(t\right)& =& \left(\left[\begin{array}{cc}-\frac{R_0+\Delta R_0}{L}& 0\\ 0& -\frac{1}{(R+\Delta R)C}\end{array}\right]x\left(t\right)+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right](u\left(t\right)+v\left(t\right))\right)\mathrm{d}t\hfill \\ & & +\left[\begin{array}{cc}{\kappa }_1& 0\\ 0& {\kappa }_2\end{array}\right]x\left(t\right)\mathrm{d}w\hfill \\ \hfill z\left(t\right)& =& \left[\begin{array}{cc}0& 1\end{array}\right]x\left(t\right),\hfill \end{array}\right.$$

(46)

and when the switch S is open, the state space model is

$$\left\{\begin{array}{ccc}\hfill \mathrm{d}x\left(t\right)& =& \left(\left[\begin{array}{cc}-\frac{R_0+\Delta R_0}{L}& -\frac{1}{L}\\ \frac{1}{C}& -\frac{1}{(R+\Delta R)C}\end{array}\right]x\left(t\right)+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right](u\left(t\right)+v\left(t\right))\right)\mathrm{d}t\hfill \\ & & +\left[\begin{array}{cc}{\kappa }_1& 0\\ 0& {\kappa }_2\end{array}\right]x\left(t\right)\mathrm{d}w\hfill \\ \hfill z\left(t\right)& =& \left[\begin{array}{cc}0& 1\end{array}\right]x\left(t\right).\hfill \end{array}\right.$$

(47)

In the above, $\Delta R_0$ and $\Delta R$ denote the variations of the load resistance $R_0$ and R, which are supposed to be bounded by $|\Delta R_0|\le \Delta R_{0MAX}$ and $|\Delta R|\le \Delta R_{MAX}$, respectively.

Observing the nominal part and the uncertain part in the system matrices of (46) and (47), we see that the above switched system takes the form of (13), where

$$\begin{array}{ccc}& & A_1=\left[\begin{array}{cc}-\frac{R_0}{L}& 0\\ 0& -\frac{1}{RC}\end{array}\right],A_2=\left[\begin{array}{cc}-\frac{R_0}{L}& -\frac{1}{L}\\ \frac{1}{C}& -\frac{1}{RC}\end{array}\right],B_1=B_2=G_1=G_2=\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]\hfill \\ & & C_1=C_2=\left[\begin{array}{cc}0& 1\end{array}\right],D_1=D_2=I_2,E_1=E_2=\left[\begin{array}{cc}\frac{\Delta R_{0MAX}}{L}& 0\\ 0& \frac{\Delta R_{MAX}}{R^{2}C}\end{array}\right]\hfill \end{array}$$

(48)

and $F_i{\left(t\right)}^{\top }{F}_i\left(t\right)⪯{\zeta }^2{I}_2$ with $\zeta =1$. It is noted that the first-order Taylor expansion is used in the above to separate the uncertainty from the term $\frac{1}{(R+\Delta R)C}$. Moreover, although we have only assumed the uncertainties in the load resistance $R_0$ and R, we can use the same formulation to deal with bounded uncertainties in L and C.

To perform the numerical simulation, we need to set up the physical parameters in the above state space models. Here, we assume $L={10}^2\mathrm{mH}$, $C={10}^5\mu F$, $R=100\Omega$, $R_0=0.1\Omega$, and the uncertainties are $\Delta R_0=0.05sin\left(100t\right)R_0$, $\Delta R=0.1cos\left(100t\right)R$. Substituting the above parameter values together with $\Delta R_{0MAX}=0.05$, $\Delta R_{MAX}=0.1$ into (48), we obtain the coefficient matrices

$$\begin{array}{c}\hfill \begin{array}{c}{A}_1=\left[\begin{array}{cc}-1.0& 0\\ 0& -0.1\end{array}\right],A_2=\left[\begin{array}{cc}-1.0& -10.0\\ 10.0& -0.1\end{array}\right]\\ B_1=B_2=G_1=G_2=\left[\begin{array}{c}10\\ 0\end{array}\right]\\ C_1=C_2=\left[\begin{array}{cc}0& 1\end{array}\right],D_1=D_2=I_2,\\ E_1=E_2=\left[\begin{array}{cc}0.5& 0\\ 0& 0.0001\end{array}\right],H=\left[\begin{array}{cc}0.2& 0\\ 0& 0.3\end{array}\right].\end{array}\end{array}$$

Since both $A_1$ and $A_2$ are Hurwitz, the achievable ${\mathcal{L}}_2$ gain $\gamma$ is essential. First, we try to solve the design condition (19) with $\gamma =0.2$ by adjusting the combination parameters ${\lambda }_1$ and ${\lambda }_2$, but there is no feasible solution, which means the desired quadratic stability with ${\mathcal{L}}_2$ gain $\gamma =0.2$ cannot be achieved through switching if there is NO state feedback.

Next, we set ${\lambda }_1=0.8$ (and thus, ${\lambda }_2=0.2$) to solve the design condition (42) with

$$A_{\lambda }=\left[\begin{array}{cc}\hfill -1.0& \hfill -2.0\\ \hfill 2.0& \hfill -0.1\end{array}\right].$$

It turns out that the condition (42) is feasible when $\gamma =0.2$, and the solutions are

$$\begin{array}{c}\hfill \begin{array}{c}Q=\left[\begin{array}{cc}\hfill 4.0310& \hfill -1.2201\\ \hfill -1.2201& \hfill 1.8291\end{array}\right],M=\left[\begin{array}{cc}\hfill -125.4222& \hfill -0.3109\end{array}\right].\end{array}\end{array}$$

Then, the feedback gain matrices K is computed by

$$\begin{array}{c}\hfill K=M{Q}^{-1}=\left[\begin{array}{cc}\hfill -39.0499& \hfill -26.2189\end{array}\right].\end{array}$$

To activate the switching laws (43) and (44), as stated in Theorem 2, we use

$$\begin{array}{c}\hfill P=Q^{-1}=\left[\begin{array}{cc}\hfill 0.3108& \hfill 0.2073\\ \hfill 0.2073& \hfill 0.6850\end{array}\right].\end{array}$$

With the initial value $x\left(0\right)={\left[\begin{array}{cc}\hfill 2& \hfill -1\end{array}\right]}^{\top }$ and the disturbance input $w\left(t\right)=e^{-2t}sint$, the state trajectories of $x_1,x_2$ in the switched system are depicted in Figure 3, which present good convergence. Moreover, it is confirmed that the inequality (9) holds for any $t>0$ on average when several trials are performed, which implies that the desired quadratic stability and ${\mathcal{L}}_2$ performance in probability has been achieved.

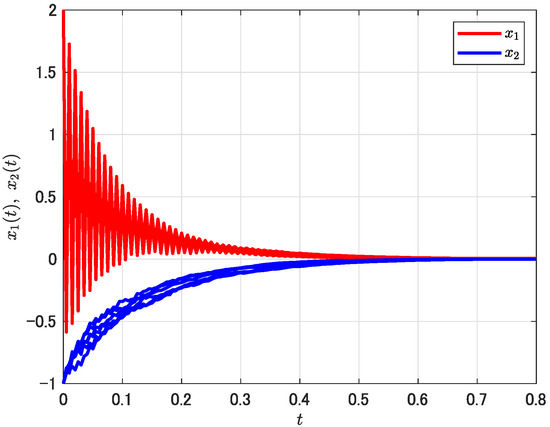
Figure 3. State trajectories of the boost converter under $\mathcal{SW}2$.

5. Conclusions

We have dealt with the global quadratic ${\mathcal{L}}_2$ performance analysis problem for a class of switched uncertain linear stochastic systems. Under the assumption that no single subsystem achieves GQ${\mathcal{L}}_2\left(\gamma \right)$-P but a convex combination of the subsystems can make it, we proposed a state-dependent switching law such that the SUSS achieves the desired GQ${\mathcal{L}}_2\left(\gamma \right)$-P. We also extended the discussion to the design of switching state feedback controller, together with its application to quadratic stabilization of a boost converter.

It is noted that the convex combination approach proposed in this paper incorporates norm-bounded uncertainties, ${\mathcal{L}}_2$ gain analysis (attenuation of ${\mathcal{H}}_{\infty }$ disturbance attenuation), and stochastic noise reduction in an integrated manner; thus, it is a major extension to the existing results in the literature. Our future work will consider the applicability and extension of such a convex combination approach to switched positive systems [29], switched affine systems [30,31], switched dynamical output feedback [32], fault detection observer design [33], and event-triggered control [34] for switched and hybrid systems. Furthermore, it is important to apply the proposed design condition and the algorithm for more practical electronic circuits and other real systems.