Abstract
This paper presents a novel low-power low-voltage analog implementation of the softmax function, with electrically adjustable amplitude and slope parameters. We propose a modular design, which can be scaled by the number of inputs (and of corresponding outputs). It is composed of input current–voltage linear converter stages (1st stages), MOSFETs operating in a subthreshold regime implementing the exponential functions (2nd stages), and analog divider stages (3rd stages). Each stage is only composed of p-type MOSFET transistors. Designed in a 0.18 µm CMOS technology (TSMC), the proposed softmax circuit can be operated at a supply voltage of 500 mV. A ten-input/ten-output realization occupies a chip area of 2570 µm2 and consumes only 3 µW of power, representing a very compact and energy-efficient option compared to the corresponding digital implementations.
1. Introduction
Deep neural networks (DNNs) are widely used in several application areas today, allowing us to implement data-driven modeling methods for pattern recognition, classification, clustering, medical applications, object detection, and so on [1,2]. DNNs are large networks realized by a huge number of interconnected computation units. Their highly parallelized and interconnected architecture is not naturally implementable by conventional arithmetic logic units (ALUs) of modern microprocessors. In this context, the possible implementation of DNNs fully or partially realized in the analog domain is attracting a lot of attention [1,2,3,4]. A DNN architecture is generally composed of one input layer, two or more hidden layers, and one output layer. For each layer, input data are first processed by a linear Vector-Matrix Multiplier (VMM), then they pass through nonlinear activation function (AF), which emulates the behavior of a biological neuron. Among the possible AF implementations, the s-shaped ones such as sigmoid and hyperbolic tangent functions are widely used [5,6,7].
Analog, digital or hybrid approaches have been proposed for the implementation of AFs in CMOS [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. When compared to digital implementations, analog designs are faster and more power-efficient [2,11]. Although this is normally achieved at the cost of higher sensitivity to process–voltage–temperature (PVT) variations, it is well known that this issue can be tolerated to some extent due to the inherent resilience of DNNs to variability [3].
Among the AF implementations, the softmax function is commonly used to mimic the output of neurons in a multi-class problem [17], where it assigns probabilities to each class. Softmax is brought to a sigmoid function normalized with respect to all the input signals of the output layer. Each output is driven not only by its corresponding input but also by the input signals of the other neurons belonging to the same level. Among the softmax proposed in the literature, only two references have implemented it with an analog circuit [15,16], while most of them have used digital implementations [17,18,19,20,21,22]. Digital blocks typically require an area of a few hundreds of thousands µm2, consuming a power in the range of 0.5 to 5 mW [17,18,19,20,21,22]. On the other hand, and as reported in [15], analog softmax can be realized with only N transistors, where N is the number of inputs and outputs. Indeed, it uses only one transistor for each input and output of the function. It is worth noting that the input and the output share the same node since input data are provided as a drain voltage, while the drain current is the output. The method in [15] claims a good precision in a very compact-area solution with very low power consumption. However, this straightforward implementation is not adequate for practical applications requiring current-mode inputs and distinct input/output nodes. In addition, transistors operated in subthreshold regime are very sensitive to process and temperature variations. A different analog softmax circuit proposed in [16] features a relatively high computation cost in terms of power consuming 690 µW at a supply voltage of 5 V and for N = 5 input. This is not a fixed limit since the operating power can be likely scaled by using more advanced CMOS technology nodes. However, the proposed topology achieves an approximate equation of the softmax model, where the exponential terms are approximated by their quadratic Taylor’s series.
In this work, we propose a low-power analog current-mode softmax topology, where both transfer-function slope and amplitude can be dynamically adjusted. This circuit is composed of three stages: the first implements a linear current–voltage conversion of the input signal, the second performs the exponential function of the signal coming from the first stage, and the third one acts as an analog divider. The topology can also operate with voltage-mode inputs by using only the second and the third stages. It is more reasonable to consider the whole system with current-mode inputs since most analog VMMs provide a current-mode output. For this reason, most of the results discussed in the following are shown for softmax with current-mode input. Our circuit was designed and simulated in a 180 nm CMOS technology. Simulation results demonstrated that our proposed topology features a good match to the theoretical softmax, a low voltage operation and a low power dissipation, and a strong robustness against PVT variations, exploiting the adjustability of the slope and of the amplitude of the transfer function.
The remainder of this paper is organized as follows. Section 2 deals with the use of softmax in neural networks, and it describes its mathematical equation and the technical details of the proposed circuit operation. Section 3 presents the obtained simulation results as well as the comparison against the state of the art. Finally, the main conclusions of this work are summarized in Section 4.
2. Analytical Model of the Proposed Softmax Analog Implementation
In this section, we first recall the theoretical equation of the softmax AF. Then, a CMOS circuit implementing the analog softmax and its analytical model are presented.
In a DNN, each neuron sums N weighted inputs—weighted by synapses—and passes the result to other neurons through a nonlinear AF. Each neuron is characterized by a threshold and by the specific nonlinearity, such as the hyperbolic tangent tanh or sigmoid AFs. The weight values represent the knowledge of the network and are established during a data-driven programming phase known as “training” [1]. Figure 1 shows the block diagram of a neuron: it receives an input vector related to the specific input of the network, with components , which are then multiplied by the appropriate weights and accumulated, before passing the result through a nonlinear AF (), as shown in Equation (1):
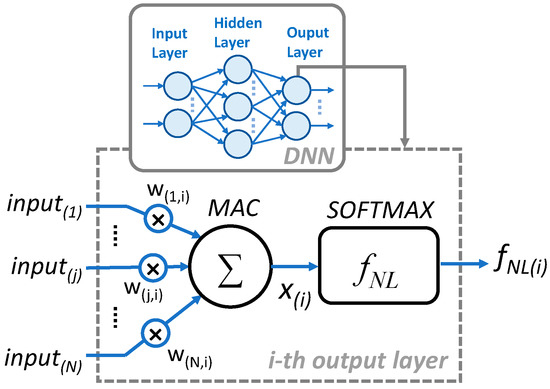
Figure 1.
Block diagram of an artificial neuron: it takes the weighted sum of N inputs and passes the result x(i) through a nonlinear activation function fNL to produce the elaborated output.
An M-sized softmax function, also known as normalized exponential function, consists of an array of M elements performing the normalization to the (0:1) interval of an array of M real-number input signals (i.e., the outputs of the multiply-and-accumulate operations). It is assumed that each input signal of the activation function, with , provides information linked to the probability of being part of the i-th class, among M classes. The value of can be negative, and the summation over the M s integers can be larger than one. The softmax elements then translate each into an output , so that each is expressed in a probability-distribution form: each output can be a real number in the (0:1) interval, and the output sum over the M is exactly 1. The analytical expression of the softmax is given in Equation (2), which shows that the probability associated with each i-th class is proportional to the exponential of the corresponding , and normalized by the sum of the exponentials performed on each input:
We propose to implement the softmax AF with an analog circuit by exploiting exponential function, sum, and division enabled by the device physics of the MOSFET and circuit laws. The block-level representation of the softmax circuit is shown in Figure 2, while the transistor-level schematic of the current–voltage conversion and exponential blocks (a) and analog divider (b) are shown in Figure 3a,b.
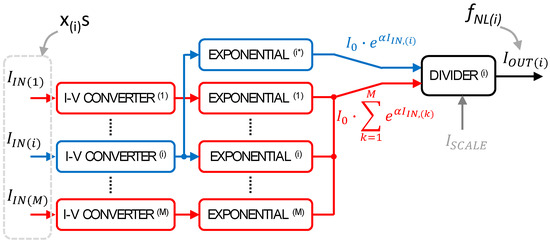
Figure 2.
Softmax diagram, composed of M conversion blocks, M + 1 exponentials, and one analog divider. Exponential blocks and the analog divider must be replicated to produce the other outputs.
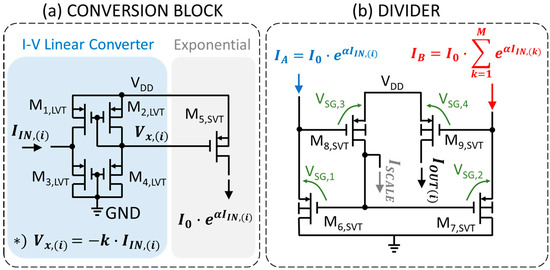
Figure 3.
Transistor-level schematics of the (a) input conversion block (current-to-voltage linear conversion and exponential conversion) and (b) the analog divider block.
The conversion block, depicted in Figure 3a, performs a linear conversion of the input current to a voltage signal, while the transistor M5 changes this voltage into a current, which is the exponential of the input since M5 is operated below the threshold voltage.
Current–voltage converter transistors (M1–M4) operate in strong inversion and saturation mode, with a nominal overdrive voltage of ; low threshold voltage (LVT) devices are used to increase the input range. Note that the converted voltage deviates linearly from as a function of the input current. This linear dependence is guaranteed if the transistor operates in saturation as expressed in Equation (3):
where Kp and VTH represent the pMOS transconductance coefficient and threshold voltage, respectively. The channel-length modulation is neglected by appropriately sizing the transistor length. The following relations for the input (Equation (4)) and output (Vx in Equation (5)) voltages can be derived as:
The output voltage range ensuring an appropriate transistor operating condition is:
This output voltage signal is applied to the gate of a pMOS in order to get the desired exponential behavior, as shown in Equation (7):
where Is is the reverse saturation current of source and drain p-diffusions/nwell junctions, n is the subthreshold slope factor, and Vt is the thermal voltage. Equation (7) implements the I–V converter and exponential blocks in Figure 2. For an M-sized softmax function, an M + 1 replica of these functional blocks is required.
The softmax model is finally obtained through the analog division of the current coming from the exponential stage of the considered input (i.e., the i-th input in the example provided in Figure 2), to the sum of all the currents coming from the exponential stages of every input, performed by the circuit shown in Figure 3b. The divider circuit is based on a subthreshold translinear loop [23], which uses devices operating in subthreshold to exploit their exponential current–voltage relationship. By Kirchhoff’s Voltage Law (KVL), the voltage around the loop that includes the four VSGs highlighted in Figure 3b must equal 0. This basically means that the sum of the VSGs oriented in the clockwise (CW) direction must equal the sum of the VSGs oriented in the counterclockwise (CCW) direction. Due to the current–voltage exponential relation, this implies that the product of CW device currents equals the product of CCW devices. By arbitrarily selecting three currents as inputs and one as output, both multiplication and division operations can be realized [24]. This circuit uses dynamic-threshold-voltage (DVT) transistors with shorted body and gate terminals in order to improve the transient response for a given supply voltage.
The analytical equations of the analog divider can be derived as follows. For each device of the divider, the current–voltage exponential relation is shown in Equation (8):
If the drain-to-source voltage VDS of the transistor is higher than 4·Vt, the term in Equation (8) can be neglected.
Applying KVL to the circuit shown in Figure 3b, we obtain:
By inverting Equation (8) and inserting the extracted VSGs in Equation (9), we finally obtain the following relation:
Finally, if ISCALE is set to a fixed value, it is possible to obtain the analog division between the other two inputs, i.e., IA/IB. The relation obtained by joining Equations (7) and (10) is:
Comparing Equation (11) with Equation (2), we conclude that the obtained transfer characteristic is equivalent to the mathematical equation of the ideal softmax model, where the term and ISCALE represent the softmax slope and amplitude, respectively.
To realize a full N-sized softmax array, the implementation of N analytical models such as the one shown in Equation (11) and then of N schematics such as the one sketched in Figure 2 is required, one for each input. However, from a circuital point of view, although the exponential stage and the analog divider must be replicated to produce each independent output, the input current–voltage stages can be shared among different outputs.
3. Analog Softmax Circuit Design and Performance
The proposed softmax circuit was designed and simulated with the 180 nm TSMC technology node using a supply voltage (VDD) of 500 mV. We selected a current of 10 nA as the nominal full-scale output current, corresponding to the ‘1’ output level of the softmax operation (i.e., 100% probability). As for the number of inputs—which corresponds to the number of outputs—N = 2 was used as a nominal case. The behavior as a function of the full-scale output current and of increasing N was also explored. Softmax transfer characteristics were simulated by sweeping only one normalized input from −5 to 5 in the normalized input range by keeping the other one (or the other ones, when N > 2) at 0. The input scale was normalized to get a nominal slope α equal to 1 for an easy comparison with the theoretical equation.
3.1. Softmax Nominal Operation and Impact of the Full-Scale Output Current and Number of Inputs
As we can see in Figure 4a, the proposed circuit implementation exhibits good agreement with the theoretical softmax model. We divided the transfer characteristics’ input range into three regions: in regions I and III, the function is well approximated by exponentials, while in region II, it shows an almost linear behavior.
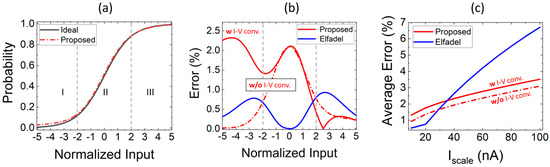
Figure 4.
(a) Proposed softmax design simulated transfer function and theoretical analytical model (M = 2). The simulated input signals have been arbitrarily normalized to get a softmax slope α = 1, while the output has been normalized to the output full scale (10 nA, in this plot). (b) Relative error of the proposed softmax design and of the one proposed in [15]. The error of our proposal is shown with/without considering the impact of the input voltage–current liner converter. (c) Impact of ISCALE on the error averaged over the (−5, 5) input range.
The vertical difference between the circuit transfer characteristics and the theoretical function, normalized to the theoretical value (i.e., the relative error), is shown in Figure 4b. Here, we report the transfer-function error of the full softmax circuit, as well as the one extracted without considering the current-to-voltage converter, i.e., isolating the “intrinsic” softmax with only exponential and divider blocks. The circuit proposed in [15] was also simulated with the same 180 nm TSMC technology models, enabling a fair comparison. Transistor sizing and input scale were independently optimized for each proposal, while the nominal ISCALE = 10 nA is the same. Our intrinsic softmax proposal features a bell-shaped error, with a peak error in the central part of 2.2%, which can be ascribed to an input offset. On the other hand, the error in topology proposed in [15] shows two peaks for an input close to −2.5 and 2.5 (of 0.8% and 1%, respectively). In addition, if we consider the impact of the current-to-voltage converter, there is an additional error contribution in regions I and III. This is ascribed to the upper and lower bounds of the conversion circuit given in Equation (6): only the one in III can be compensated by appropriate trimming of the ISCALE (already done in the figure). However, an error lower than 2.2% in the whole range is observed with an average value of ~1.4% in the investigated operating range (the corresponding value when the input current–voltage converter is not considered is <1%).
For the three options considered in Figure 4b, in Figure 4c, the average error is reported for ISCALE varied from 10 nA to 100 nA. This plot is relevant because it highlights that in our proposed softmax, the error increases only marginally with increasing ISCALE, and this is achieved because the slope parameter is practically independent of ISCALE. This is not the case with the counterpart, where slope and the output current scale are both varied when ISCALE is changed so that they cannot be optimized independently. This is the reason our proposal shows a lower relative error for a variable output-scale (e.g., ~3.4% versus ~6.8% at ISCALE = 100 nA).
In Figure 5a, the softmax transfer function simulated for an ISCALE of 10, 25 and 50 nA (with M = 2) is shown. Given that we are considering only two inputs, the softmax probability for each of them corresponds to 50% when their value is the same (i.e., zero in this example). In Figure 5b, a similar plot as in (a) is shown but for a fixed ISCALE of 10 nA and for M = 2, 5 and 10. Even in this case, only one input is swept, while all the other inputs are kept constant to 0. The softmax probability corresponds to 1/M when the values of all inputs are the same.
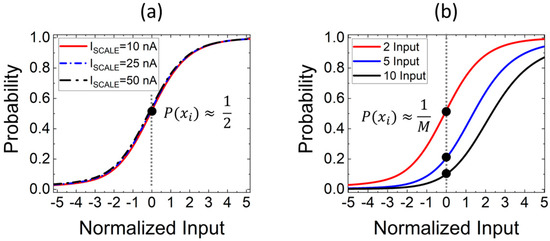
Figure 5.
Softmax transfer characteristics (a) at ISCALE = 10, 25 and 50 nA with M=2 and (b) at different number of inputs M for ISCALE = 10 nA.
We also performed transient simulations to estimate the latency, defined as the time needed by the output to reach the 99% of the final value when the input is instantaneously switched from −5 to +5. The latency was extracted at different ISCALE and for a different M, resulting in 3.41 µs, 1.66 µs, and 1.39 µs for ISCALE of 10, 25, and 50 nA, respectively, while no significant dependence on the number of inputs was observed.
3.2. Impact of Voltage and Temperature on the Softmax Slope
Beyond the possibility to change the output amplitude by varying the ISCALE current, the original property of our softmax circuit is the electrical adjustability of the slope α by varying VDD (see Equation (11)). This property can be exploited when temperature variations are considered, given that the effect of the temperature and voltage on the softmax characteristics is similar. This can be observed in Equation (11), where a similar dependence of the term on voltage and temperature parameters is described.
The proposed softmax circuit transfer characteristics were simulated in the [−50 °C, 50 °C] temperature range, as shown in Figure 6a. The circuit shows a different temperature sensitivity at different temperatures. For example, moving from −50 °C to −25 °C, the characteristic slope exhibits a variation of 38.31%, while moving from 25 °C to 50 °C, the slope variation is of 21.45%.
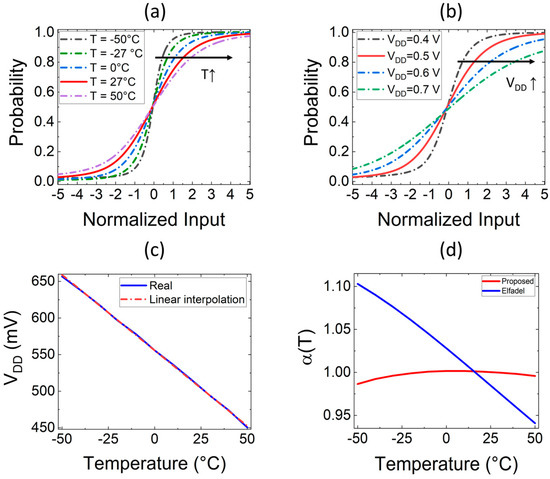
Figure 6.
Softmax circuit transfer characteristics (a) at different temperatures and (b) at different VDD. (c) VDD required to keep constant the softmax slope at a different temperature and linear interpolation. (d) Softmax slope as a function of temperature reported for the proposed softmax circuit (with linear correction given in (c)) and for the one proposed by Elfadel et al. in [15].
Similar behavior can be observed in simulation results with respect to the VDD variations, as shown in Figure 6b, where VDD is varied from 700 mV down to 400 mV. The similarity between the impact of VDD and thermal voltage (and temperature) variations is consistent with the analytical model in Equation (11). The proposed softmax circuit exhibits different voltage sensitivity at different voltage ranges. More precisely, the voltage sensitivity is higher for lower VDD values: the slope exhibits a variation of 45.19% from 400 mV to 500 mV, while a variation of 28.14% occurs for a VDD variation from 700 mV to 800 mV.
Due to the similar behavior of the slope with respect to temperature and VDD variations, it is possible to easily implement a correction at circuit level to get an almost constant softmax slope, for example, through an external circuit implementing a negative regulation of the VDD with respect to temperature. This concept is also shown in Figure 6c, where we calculated the VDD needed to keep the same softmax slope as the temperature changes. This flexibility allows our circuit to feature better temperature sensitivity with respect to the one proposed in [15], as highlighted in Figure 6d, where a linear VDD–temperature correction is implemented, i.e., VDD = 500 mV + (27 − T) × 2.064 mV/°C (where T is expressed in °C).
3.3. Mismatch and Process Variations
With regard to mismatch and process variations, the circuit behavior is shown in Figure 7, where transfer characteristics were computed for 100 statistical Monte Carlo runs. In this case, only the input scale is normalized, while on the y-axis, output currents are represented (with no normalization) to highlight the effects of variability on the amplitude. The impact of mismatch variations in Figure 7a is mainly related to the deviation of the characteristic amplitude, considering that the transfer characteristics exhibit a standard deviation of the maximum output current variation of 2.97% with respect to the mean value. On the other hand, process variations in Figure 7b behavior mainly result in a variation of the slope. In particular, the curves feature a ratio of the slope standard deviation to the slope average value of 16.83%, with a negligible variation of the amplitude. It is important to remark that amplitude and slope parameters are both adjustable in our proposal, meaning that any variation can be properly compensated through calibration, while this is not an option for other analog proposals.
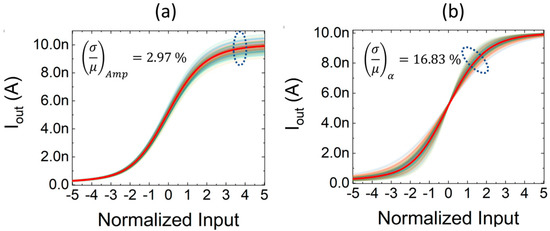
Figure 7.
Impact of (a) mismatch and of (b) process variations on the softmax transfer characteristics (two inputs, ISCALE = 10 nA) for 100 MC runs.
To provide additional details, in Figure 8, softmax transfer-characteristic parameters such as the slope (a), the amplitude (b), and the offset (c) are extracted for 1000 Monte Carlo runs, for both mismatch and process variability simulations. A small variation of offset (normalized to the input scale) is observed, although it is a second-order effect with respect to variations in slope and amplitude.
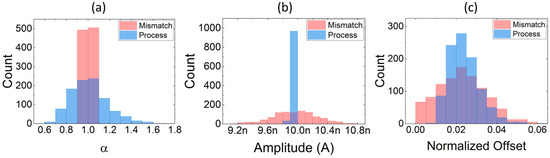
Figure 8.
Softmax transfer-characteristic parameters extracted for 1000 MC runs (two inputs, ISCALE = 10 nA). Histograms of (a) slope, (b) amplitude, and (c) offset error extracted for mismatch and process variability simulations.
3.4. Area and Power Consumption
Area and power consumption were both estimated by considering a design realized in a 0.18 µm CMOS technology.
Figure 9a shows the area overhead (estimated by considering the transistor gate area) for a variable number of input variables M. The proposed solution shows an area footprint of 466, 2.57 × 103 or 53 × 103 µm2 (requiring 22, 190 or 10,900 transistors) for M = 2, 10 or 100, respectively. Figure 9b shows the power consumption as a function of the output scale (for a variable number of M). It can be observed that our proposal shows a power consumption strongly dependent on the number of inputs, because the conversion blocks are the most power-hungry circuits, while ISCALE has a lower impact. A two-inputs design operated with VDD = 500 mV, and ISCALE = 10 nA shows an average power consumption of only 431 nW, among which almost 65% of power is dissipated by the input current-to-voltage conversion (280 nW). For a ten-inputs/ten-outputs case, the power increases to 3 µW for ISCALE = 10 nA, or to 3.55 µW for ISCALE = 100 nA.
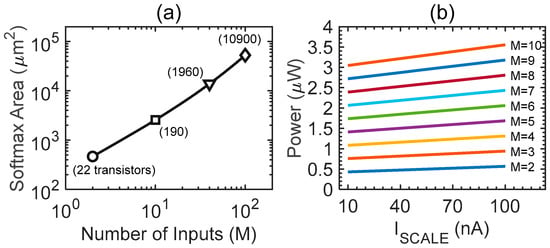
Figure 9.
(a) Area overhead as a function of the number of inputs and outputs (M) of the softmax assuming an implementation in a 180 nm CMOS technology node. The needed number of transistors is also reported for some conditions. (b) Power consumption as a function of ISCALE for different number of inputs. VDD = 500 mV.
3.5. Impact of the Technology Node Scaling
Finally, Figure 10 shows the transfer characteristics (a) and related errors (b) of a softmax function simulated with three different technology nodes, namely TSMC 180 nm, 65 nm, and 40 nm, in order to investigate the impact of technology scaling. The basic shape of the softmax function is preserved also for the smallest technology option, especially in the linear region. However, due to an increased offset as a result of ISCALE being adjusted to match the upper part, a worsened matching in the linear region can be observed, resulting in a higher relative error, with a peak value close to 6.5%, which can be still reasonable since there are simple DNNs which can operate with a reduced equivalent number of bits [3].
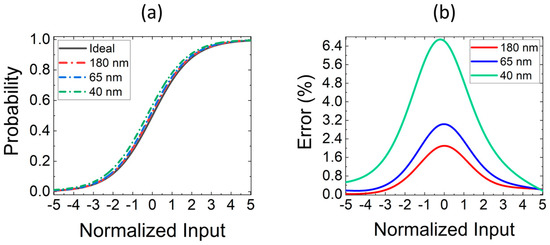
Figure 10.
(a) Transfer characteristic and corresponding relative error (b) for three technology node (180 nm, 65 nm, 40 nm) softmax circuits.
4. Conclusions
A novel analog implementation of the softmax function—an activation function largely used in deep neural networks—is presented in this paper. The proposed circuit is implemented in a modular fashion, being composed of three building blocks, which can be replicated and shared, to achieve a softmax function with an arbitrary number of inputs and outputs. The first stages linearly convert the input current signals to voltage signals, the second stages implement a voltage-to-current exponential conversion, and the last stage realizes the analog division. The main features of the circuit are the good match to the theoretical function and the possibility to dynamically adjust the transfer-characteristic amplitude and slope, leading to good stability performance against process and temperature variations. A ten-input/ten-output implementation of the proposed softmax circuit, designed in a 180 nm CMOS technology, occupies a small area of less than 3000 µm2 and consumes 3 µW when operated at VDD = 500 mV for an output scaling current of 10 nA, rendering it a very interesting option compared to the digital counterparts. These improvements are achieved with limited precision degradation, considering that the maximum and average relative errors, with respect to the theoretical softmax equation, are of 2.2% and 0.9% only, respectively.
Author Contributions
Conceptualization, M.V., T.M., S.S., L.T., A.V., M.L. and F.C.; Formal analysis, M.V., T.M., S.S., L.T., A.V., M.L. and F.C.; Investigation, M.V., T.M., S.S., L.T., A.V., M.L. and F.C.; Writing—review and editing, M.V., T.M., S.S., L.T., A.V., M.L. and F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sarpeshkar, R. Analog Versus Digital: Extrapolating from Electronics to Neurobiology. Neural Comput. 1998, 10, 1601–1638. [Google Scholar] [CrossRef] [PubMed]
- Haensch, W.; Gokmen, T.; Puri, R. The Next Generation of Deep Learning Hardware: Analog Computing. Proc. IEEE 2018, 107, 108–122. [Google Scholar] [CrossRef]
- Paliy, M.; Strangio, S.; Ruiu, P.; Rizzo, T.; Iannaccone, G. Analog Vector-Matrix Multiplier Based on Programmable Current Mirrors for Neural Network Integrated Circuits. IEEE Access 2020, 8, 203525–203537. [Google Scholar] [CrossRef]
- Danial, L.; Pikhay, E.; Herbelin, E.; Wainstein, N.; Gupta, V.; Wald, N.; Roizin, Y.; Daniel, R.; Kvatinsky, S. Two-terminal floating-gate transistors with a low-power memristive operation mode for analogue neuromorphic computing. Nat. Electron. 2019, 2, 596–605. [Google Scholar] [CrossRef]
- Veire, L.V.; De Boom, C.; De Bie, T. Sigmoidal NMFD: Convolutional NMF with Saturating Activations for Drum Mixture Decomposition. Electronics 2021, 10, 284. [Google Scholar] [CrossRef]
- Xing, S.; Wu, C. Implementation of A Neuron Using Sigmoid Activation Function with CMOS. In Proceedings of the 2020 IEEE 5th International Conference on Integrated Circuits and Microsystems (ICICM), Nanjing, China, 23–25 October 2020; pp. 201–204. [Google Scholar]
- Shamsi, J.; Amirsoleimani, A.; Mirzakuchaki, S.; Ahmade, A.; Alirezaee, S.; Ahmadi, M. Hyperbolic tangent passive resistive-type neuron. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 581–584. [Google Scholar]
- Fan, D.; Shim, Y.; Raghunathan, A.; Roy, K. STT-SNN: A Spin-Transfer-Torque Based Soft-Limiting Non-Linear Neuron for Low-Power Artificial Neural Networks. IEEE Trans. Nanotechnol. 2015, 14, 1013–1023. [Google Scholar] [CrossRef]
- Valle, M. Analog VLSI Implementation of Artificial Neural Networks with Supervised On-Chip Learning. Analog. Integr. Circuits Signal Process. 2002, 33, 263–287. [Google Scholar] [CrossRef]
- Ghomi, A.; Dolatshahi, M. Design of a new CMOS Low-Power Analogue Neuron. IETE J. Res. 2017, 64, 67–75. [Google Scholar] [CrossRef]
- Joubert, A.; Belhadj, B.; Temam, O.; Héliot, R. Hardware spiking neurons design: Analog or digital? In Proceedings of the the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–5. [Google Scholar]
- Khodabandehloo, G.; MirHassani, M.; Ahmadi, M. Analog Implementation of a Novel Resistive-Type Sigmoidal Neuron. IEEE Trans. Very Large Scale Integr. Syst. 2011, 20, 750–754. [Google Scholar] [CrossRef]
- Koosh, V.F.; Goodman, R. VLSI neural network with digital weights and analog multipliers. In Proceedings of the ISCAS 2001. The 2001 IEEE International Symposium on Circuits and Systems (Cat. No.01CH37196), Sydney, NSW, Australia, 6–9 May 2001; Volume 2, pp. 233–236. [Google Scholar]
- Koosh, V.; Goodman, R. Analog VLSI neural network with digital perturbative learning. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 2002, 49, 359–368. [Google Scholar] [CrossRef]
- Elfadel, I.M.; Wyatt, J.L. The “Softmax” nonlinearity: Derivation using statistical mechanics and useful properties as a multiterminal analog circuit element. In Proceedings of the 6th International Conference on Neural Information Processing Systems (NIPS’93), Denver, CO, USA, 1 January 1993; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993; pp. 882–887. [Google Scholar]
- Zunino, R.; Gastaldo, P. Analog implementation of the SoftMax function. In Proceedings of the 2002 IEEE International Symposium on Circuits and Systems. Proceedings (Cat. No.02CH37353), Phoenix-Scottsdale, AZ, USA, 26–29 May 2002; pp. II.117–II.120. [Google Scholar]
- Mohammed, A.A.; Umaashankar, V. Effectiveness of Hierarchical Softmax in Large Scale Classification Tasks. In Proceedings of the 2018 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Bangalore, India, 19–22 September 2018; pp. 1090–1094. [Google Scholar]
- Kouretas, I.; Paliouras, V. Hardware Implementation of a Softmax-Like Function for Deep Learning. Technologies 2020, 8, 46. [Google Scholar] [CrossRef]
- Li, Z.; Li, H.; Jiang, X.; Chen, B.; Zhang, Y.; Du, G. Efficient FPGA Implementation of Softmax Function for DNN Applications. In Proceedings of the 2018 12th IEEE International Conference on Anti-Counterfeiting, Security, and Identification (ASID), Xiamen, China, 9–11 November 2018; pp. 212–216. [Google Scholar]
- Dong, X.; Zhu, X.; Ma, D. Hardware Implementation of Softmax Function Based on Piecewise LUT. In Proceedings of the 2019 IEEE International Workshop on Future Computing (IWOFC), Hangzhou, China, 14–15 December 2019; pp. 1–3. [Google Scholar]
- Kagalkar, A.; Raghuram, S. CORDIC Based Implementation of the Softmax Activation Function. In Proceedings of the 2020 24th International Symposium on VLSI Design and Test (VDAT), Bhubaneswar, India, 23–25 July 2020; pp. 1–4. [Google Scholar]
- Alabassy, B.; Safar, M.; El-Kharashi, M.W. A High-Accuracy Implementation for Softmax Layer in Deep Neural Networks. In Proceedings of the 2020 15th Design & Technology of Integrated Systems in Nanoscale Era (DTIS), Marrakech, Morocco, 1–3 April 2020; pp. 1–6. [Google Scholar]
- Serrano-Gotarredona, T.; Linares-Barranco, B.; Andreou, A.G. A general translinear principle for subthreshold MOS transistors. IEEE Trans. Circuits Syst. I Regul. Pap. 1999, 46, 607–616. [Google Scholar] [CrossRef]
- Al-Absi, M.A.; Hussein, A.; Abuelma’Atti, M.T. A Novel Current-Mode Ultra Low Power Analog CMOS Four Quadrant Multiplier. In Proceedings of the 2012 International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 3–5 July 2012; pp. 13–17. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).