Abstract
Infrared positioning is a critical module in an indoor autonomous vehicle platform. In an infrared positioning system, the ego vehicle is equipped with an infrared emitter while the infrared receivers are fixed onto the ceiling. The infrared positioning result is accurate only when the number of valid infrared receivers is more than three. An infrared receiver easily becomes invalid if it does not receive light from the infrared emitter due to indoor occlusions. This study proposes an occlusion-aware path planner that enables an autonomous vehicle to navigate toward the occlusion-free part of the drivable area. The planner consists of four layers. In layer one, a homotopic A* path is searched for in the 2D grid map to roughly connect the initial and goal points. In layer two, a curvature-continuous reference line is planned close to the A* path using numerical optimal control. In layer three, a Frenet frame is constructed along the reference line, followed by a search for an occlusion-aware path within that frame via dynamic programming. In layer four, a curvature-continuous path is optimized via quadratic programming within the Frenet frame. A path planned within the Frenet frame may violate the curvature bounds in a real-world Cartesian frame; thus, layer four is implemented through trial and error. Simulation results in CarSim software show that the derived paths reduce the poor positioning risk and are easily tracked by a controller.
1. Introduction
Indoor positioning is an important area of development with wide applications in surveillance, human motion analysis, logistics, and entertainment [1,2,3,4,5]. As one of the most well-known indoor positioning approaches, infrared positioning is characterized by low energy consumption and high precision [6,7,8]. In an infrared positioning system, an infrared emitter is installed on a movable target that is required to be localized, and infrared receivers are fixed onto the ceiling. The infrared positioning result is accurate only when the number of valid infrared receivers is more than three. An infrared receiver becomes invalid if it does not receive the light originating from the infrared emitter due to indoor occlusions.
Automated guided vehicles (AGVs) are commonly used in warehouses for cargo delivery [9,10]. However, AGV positioning results easily become inaccurate when cargoes in a warehouse occlude the light beams originating from the emitter installed on an AGV. Instead of improving the positioning of the sensors, the current work considers the planning of occlusion-aware paths that would enable an AGV to drive in the occlusion-free part of the drivable area in a warehouse.
If the cargoes in a warehouse are permanently fixed, then the poor positioning regions may be estimated a priori and regarded as static obstacles in an AGV path planning scheme. In most cases, however, cargo placement is always changing, resulting in unfixed poor positioning regions. Thus, the concerned occlusion-aware path planner must work fast while guaranteeing its outputs are collision-free and kinematically feasible [11].
1.1. Related Work
The most prevalent path planners in robotics may be classified into sampling-, search-, optimization-, and learning-based methods.
Sampling-based planners generate candidate path/trajectory primitives and then connect selected ones to form a complete solution. Such primitives are typically formed using polynomials [12,13,14], state lattices [15,16,17], and closed-loop tracking [18].
Search-based methods divide a continuous solution space into nodes in a graph and then search for a link between the nodes in the graph. Typical searchers include dynamic programming (DP) [19,20], A* [16,21], and rapidly exploring random tree (RRT) [18,22].
An optimization-based planner formulates the concerned planning task as an optimal control problem (OCP) before solving the OCP numerically. Herein, solving an OCP numerically refers to discretizing it into a mathematical programming problem and solving it using a gradient-based optimizer. Typical mathematical programming problems include quadratic programming (QP) [20,23,24], quadratically constrained QP (QCQP) [25], nonlinear programming (NLP) [26,27,28], and unconstrained optimization problems [12,29]. Most gradient-based optimizers suitable for path planning only exhibit local optimization capabilities because global convergence requires a much longer runtime than one can afford. Given this property, the finally derived optimal path is close to the initial guess [30,31]. Therefore, identifying a good initial guess with global optimality contributes considerably toward finding a high-quality optimum. A sampling-/search-based planner is commonly used to provide a good initial guess [32,33].
A learning-based method generates vehicle motions based on trained data. Artificial neural networks [34], spline-constrained policy networks [35], and double deep Q-networks [36] are used in offline training. Reinforcement learning-based methods [37,38] are applied to online training.
The aforementioned four types of planners have their respective strengths and limitations. Sampling- and search-based methods do not handle the configuration space in its continuous form. Thus, they find suboptimal rather than optimal solutions. They even fail to find any feasible solution if the complexity of the planning scheme is beyond the sampling/search resolution level [23]. Increasing the resolution level is inapplicable when using a sampling-/search-based planner due to the curse of dimensionality. Despite their drawbacks, sampling-/search-based methods can efficiently describe the non-differentiable occlusion-related cost [39,40]. An optimization-based planner finds optimal paths in the continuous solution space; however, it has two typical limitations: (1) occlusion-related constraints/costs cannot be handled due to non-differentiability, and (2) the runtime is considerably longer than that of a sampling-/search-based method. Learning-based methods work fast online after a long offline training process, but they lack interpretability, and thus are rarely tested on real-world vehicles [41,42]. According to the above analysis, concluding that one type of planner fully outperforms another is difficult; instead, maximizing the advantages of each planner type while combining multiple types has been a common practice in this community.
Combining a sampling-/search-based planner with an optimization-based one renders a hierarchical planning framework; however, the optimization layer is time-consuming if the planning scheme is described in the Cartesian frame. At this point, the majority of path planners for on-road cruising scenarios describe the movements of an autonomous vehicle in the Frenet frame to enhance real-time performance. The Frenet frame, also known as the curvilinear frame, has been widely used to standardize the irregular trend of a road [43]. When using the Frenet frame, the ego vehicle is regarded as driving in a straight tunnel with left and right bounds. The Frenet frame helps convert an NLP problem into an easier form, making an optimization-based planner faster. However, the paths optimized in the Frenet frame may violate vehicle kinematic constraints because the conversions between the Cartesian and Frenet frames are neither unique nor uniform [44]. The situation worsens when the road is curvy, as it might be in our warehouse scenario. Therefore, a perfect solution that simultaneously considers kinematic feasibility, optimality, runtime efficiency, and occlusion-avoidance performance is not yet available.
1.2. Contributions
The current study aims to develop an occlusion-aware path planner for enhancing the indoor infrared positioning accuracy of an autonomous vehicle system. The planner is expected to be optimal and fast without violating fundamental restrictions, such as collision-avoidance and kinematic constraints. In particular, we adopt the first-search-then-optimize framework to combine search-based and optimization-based planners to find the global optimum. Both planners work within the Frenet frame, and thus time efficiency is enhanced. The optimizer is designed through trial and error; hence, the finally derived path is kinematically feasible within a real-world Cartesian frame.
1.3. Organization
2. Problem Statement
The purpose of this work is to generate a kinematically feasible and collision-free path for a car-like robot in a warehouse, such that the impact of infrared positioning inaccuracy can be reduced. The path planning task is described as the following OCP:
Herein, variable s stands for the distance that the ego vehicle has to travel; variable denotes the traveled distance when the ego vehicle reaches the destination, thus may not be known a priori; denotes the cost function w.r.t. travel efficiency, path smoothness, and positioning quality; denotes the state profiles; represents the control profiles; denotes the kinematic constraints written in the form of ordinary differential equations; and denote the kinematic constraints written as algebraic box constraints; and denote the two-point boundary constraints; denotes the partial workspace occupied by obstacles; suppose that denotes the entire workspace, then denotes the free space drivable for the ego vehicle; is a mapping from the vehicle state z to its footprint, thus represents the collision-avoidance constraints [45].
In addition, one may define the poor positioning regions in the workspace as , wherein the ego vehicle cannot touch enough infrared receivers. Ideally, one would expect the ego vehicle to always keep free from poor positioning and collisions, i.e., for any . However, this condition is too harsh when the infrared beams are seriously blocked by the cargoes. As depicted in Figure 1, no kinematically feasible paths exist in . Empirically, the temporary loss of positioning accuracy is not a serious problem because the inertial measurement units (IMUs) equipped onboard can accurately estimate the vehicle’s configuration within a short period. Therefore, (1) allows the ego vehicle to travel in , but penalizes traveling in for a long distance using the cost function J.
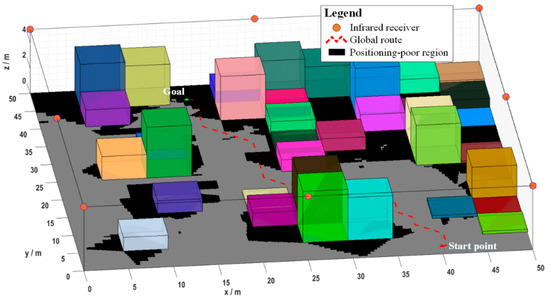
Figure 1.
A warehouse workspace with poor positioning regions. Note that there are no kinematically feasible paths if the ego vehicle follows the global route because the goal lies in the poor positioning region.
3. A Four-Layer Path Planning Method
Our proposed path planner consists of four layers. In layer one, an A* path is searched for in the 2D grid map to coarsely connect the initial and goal points. The A* path is deployed to determine the homotopy class. In layer two, a curvature-continuous reference line is planned close to the A* path via numerical optima control. The reference line is deployed to construct a Frenet frame. In layer three, a coarse occlusion-aware path is searched for within the Frenet frame using DP. In layer four, a curvature-continuous path is optimized using QP. The overall architecture is shown in Figure 2.
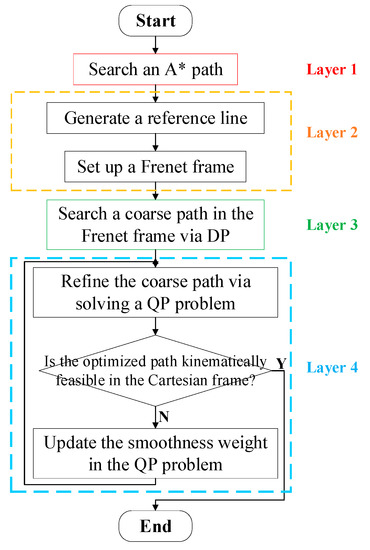
Figure 2.
Overall framework of occlusion-aware path planning method.
3.1. Layer One: Search an A* Path
As a preliminary step, the homotopy class needs to be identified, which decides how the ego vehicle bypasses each of the obstacles (i.e., cargoes) from the start point to the goal. This work uses the A* algorithm to find a coarse path, given that it explicitly reflects the determined homotopy class. Concretely, an occupancy grid map is formed based on the warehouse layout and cargo locations. Dilating the occupancy grid map by L renders a dilated map. In this work, L is set to the half-width of the ego vehicle. A 2D path is searched for in the dilated map via the A* algorithm [46], which coarsely connects the assigned starting and goal points. The output of layer one is a path presented in the form of N waypoints stored in a set, i.e., .
3.2. Layer Two: Generate a Reference Line
The preceding layer identifies a global route from the start point to the goal. This layer is focused on generating a curvature-continuous path that is close to the global route. The curvature-continuous path is denoted as a reference line, which is used to construct a Frenet frame for future usage. The principle for generating a reference line is as follows.
The global route derived in layer one is resampled as NFE equidistant waypoints . A reference line is generated by driving a virtual vehicle to track the waypoints. This process can be described as a trajectory planning-oriented OCP:
In (2), t is the time index, denotes the ego vehicle’s state profiles in the Cartesian frame, i.e., . Furthermore, refers to the location of the rear-axle midpoint of the ego vehicle, is the orientation angle, is the longitudinal velocity, is the corresponding acceleration, and is the steering angle. denotes the control profiles , wherein is the derivative of , and is the angular velocity of All of the constraints in (2) are kinematic constraints, which are presented by the well-known bicycle model [47]:
Herein, LW denotes the vehicle wheelbase (Figure 3). The boundary constraints and are defined as
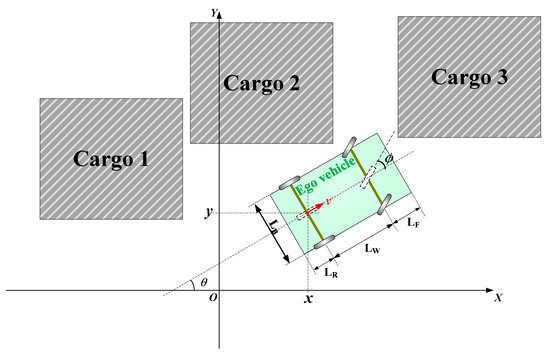
Figure 3.
Schematics for vehicle kinematics and geometrics.
The cost function is defined as:
wherein is a weighting parameter, and is a parametric trajectory formed by linearly connecting the NFE waypoints in a sequence.
Compared with (1), OCP (2) does not contain two-point constraints or collision-avoidance constraints. Thus, the resultant trajectory may not connect the start point to the goal and may not guarantee collision avoidance despite being kinematically feasible. At this point, it should be clarified that the resultant reference line is only used to construct a Frenet frame; the concerns about collision avoidance, occlusion avoidance, etc., will be handled in a subsequent layer based on the constructed Frenet frame.
OCP (2) is solved numerically, which involves discretizing the OCP into an NLP problem and then solving it via a gradient-based NLP solver, such as the interior-point method (IPM) [48,49]. The solution to the NLP problem is a vector of waypoints together with the corresponding state/control profiles in their discretized forms. A reference line is formed by connecting the resultant waypoints smoothly via spline interpolation.
3.3. Layer Three: Search for a DP Path in the Frenet Frame
This layer is focused on generating a coarse path within the Frenet frame with collision avoidance, occlusion awareness, travel efficiency, and path smoothness considered.
The first step is to map the start point and goal to the reference line so that their Frenet coordinate values are identified as (sstart, lstart) and (send, lend), respectively (Figure 4). The second step is to generate (NS + 1) equidistant skeleton points along the reference line ranging from (sstart, 0) to (send, 0). A normal line is drawn along each skeleton point, which is orthogonal to the reference line. Along each normal line, NL candidate grids are sampled (Figure 4), which range in an interval around the skeleton point. For the nominal line passing through the last skeleton point located at (send, 0), NL is set to 1 and the only candidate grid left is specified as the goal (send, lend).
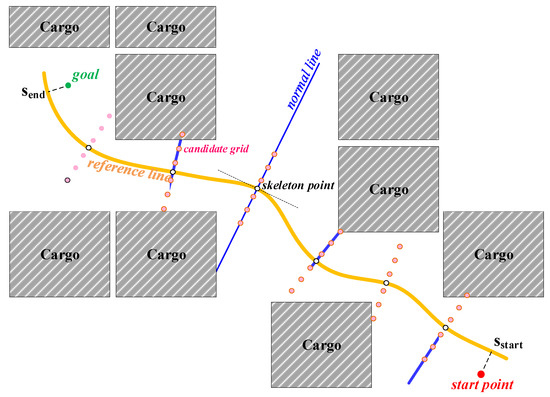
Figure 4.
Schematics for a graph of sampled grids in DP search.
The planning task in layer three is to select one and only one candidate grid along each of the normal lines such that the sequentially connected candidate grids are collision free, occlusion minimized, short, and smooth. DP is adopted to find the optimal choice for the candidate grid along each normal line [50]. Compared to enumeration, DP reduces the search complexity from to , and thus promises to find the optimum in a graph consisting of candidate grids. The brief principle of the DP search-based path planning method in layer three is presented as follows.
In Algorithm 1, each candidate grid is regarded as a node. InitializeNodes() is used to initialize the cost of each node as . TraceBack(opti_id) is used to identify a sequence of nodes from , , to its ancestors until . The node sequence, if output in inverse order, forms a coarse path within the Frenet frame. measures the cost of the path segment from Node1 to Node2. We define the cost function as a weighted sum of collision cost Jcollision, travel efficiency cost Jefficiency, smoothness cost Jsmoothness, and positioning-related cost Jpositioning. The collision cost penalizes the case that the ego vehicle collides with the surrounding cargoes when driving along the concerned path segment. Jcollision is set to a large value (e.g., ) if a collision occurs, otherwise, Jcollision is set to 0. The efficiency cost Jefficiency is written as the length of the concerned path segment because this term encourages the ego vehicle to travel across a short distance. Suppose the parent of Node1 is Node0, Jsmoothness is defined as Intuitively speaking, the smoothness cost Jsmoothness penalizes the case that the heading direction changes from Node0, Node1, to Node2. Jpositioning penalizes the case that the ego vehicle stays in the positioning-poor regions for a long distance. Furthermore, Nsample waypoints are evenly sampled along the concerned line segment from Node1 to Node2. Regarding the ith sampled waypoint , the corresponding coordinate value in the Cartesian frame is identified as via frame conversion. Suppose the infrared emitter is installed at the height of h onto the ego vehicle, one may draw a line from the 3D point to each infrared receiver and then check if the line is occluded by cargoes in the warehouse. If there is no occlusion, then the receiver is regarded as valid (Figure 5). If the total number of valid infrared receivers is larger than three, then the concerned waypoint is regarded as valid. Jpositioning measures the rate of valid waypoints along the concerned line segment from Node1 to Node2.
| Algorithm 1. Path planning via DP search. |
| Input: Reference line, scenario layout, location of cargoes; Output: A path ; 1. InitializeNodes(); 2. ; 3. For each , do 4. ; 5. ; 6. ; 7. End for 8. For each , do 9. For each , do 10. For each , do 11. ; 12. ; 13. If , then 14. ; 15. ; 16. End if 17. End for 18. End for 19. End for 20. ; 21. ; 22. Return. |
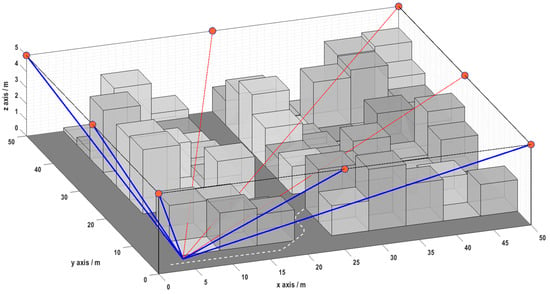
Figure 5.
Schematics for the infrared receiver validation check. Five blue infrared beams together with corresponding receivers are valid because they are not occluded by the cargoes.
3.4. Layer Four: Optimize a Curvature-Continuous Path
The preceding layer helps to identify a collision-free and occlusion-aware path, which consists of (NS + 1) waypoints. Since NS is not large, the derived path is quite coarse. This section is focused on how to refine the coarse path via numerical optimization within the Frenet frame. In this work, path refinement is performed via Baidu Apollo EM planner [20], which involves implementing path-velocity decomposition in an iterative loop before an optimum (rather than sub-optimum) is finally derived. Since there are only static obstacles, the EM planner is degraded as a run-once path planning method, the details of which are given as follows.
The first step is to identify the left and right bounds that surround the coarse path derived in layer three. As depicted in Figure 6, the left and right bounds are determined using an incremental check. The identified left and right bounds are denoted as functions of s, namely, ub(s) and lb(s). The optimization-based path planning task involves identifying a function l(s) between the left and right bounds subject to kinematic constraints and collision-avoidance constraints. In our concerned task, the decision variables include l(s), dl(s), ddl(s), and dddl(s), which obey the following kinematic constraints:
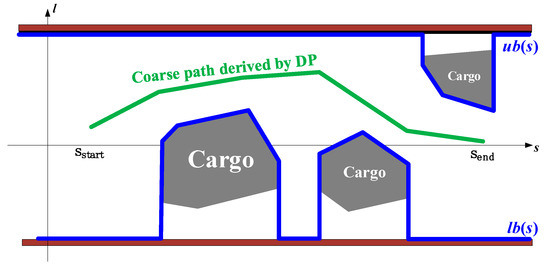
Figure 6.
Schematics for the construction of left/right bounds in EM planner.
Herein, , , and are parameters that determine how fast l changes with s, and thus are related to path smoothness. Empirically, the bounding parameters in (6) should not be set strictly, otherwise the vehicle kinematics easily become in conflict with the collision-avoidance constraints that will be introduced later. At this point, we believe that the path smoothness can be enhanced via the cost function without suffering from the infeasibility risk [23].
The two-point boundary constraints are written as
Herein, the parameters , , , and reflect the assigned initial and goal configurations. Particularly, and are related to the vehicle orientation angles at and , respectively.
Regarding the collision-avoidance constraints, the vehicle body should not collide with ub(s) or lb(s). Setting the vehicle body as rectangular is too complex, and thus we use a series of same-radius circles centered along the longitudinal axle of the ego vehicle to cover the rectangular vehicle body (Figure 7), and then require that each circle lies between lb(s) and ub(s). For a circle biased from the vehicle’s rear axle by , the collision-avoidance constraints are defined as
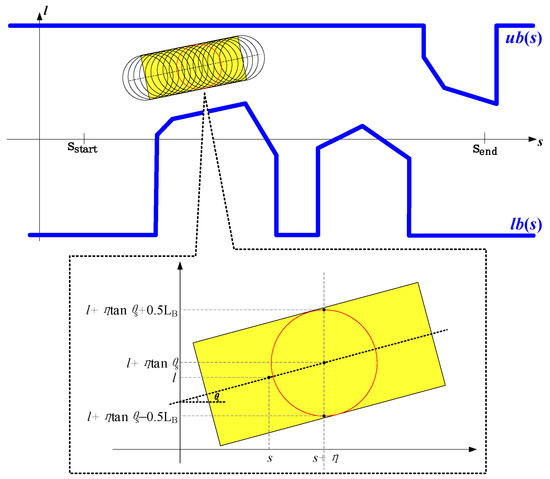
Figure 7.
Schematics for the formulation of collision-avoidance constraints in EM planner (zoom in to see more clearly).
The complete collision-avoidance constraints are formed by imposing (8) for any . Herein, denotes the vehicle’s orientation angle within the Frenet frame. Inherently, stands for the difference between the ego vehicle’s heading direction and the tangent direction along the reference line at s. is small because the ego vehicle’s heading direction, in most cases, is not much biased from the reference line. Thus, we have
This yields the following constraints:
The cost function is defined as
wherein w1, w2, w3, and w4 are weighting parameters, and denotes the coarse path derived by DP in layer three. An OCP is formed by combining (6), (7), (10), and (11). The discretized version of this OCP is a QP, which is easily solved using a QP solver, such as osqp [51] and qpOASES [52]. The resultant path, after being converted back to the Cartesian frame, may be infeasible if its curvature exceeds the allowable bounds. The infeasibility is inevitable because the vehicle kinematics cannot be accurately modeled within the Frenet frame [44]. As a remedy for this, we check the resultant path for violations of curvature limits in the Cartesian frame; if an infeasible solution is derived, w1 is set smaller before the QP problem is solved again. This process continues until a curvature-feasible path is derived.
4. Simulation Results and Discussion
This section discusses the efficacy, occlusion awareness, and closed-loop tractability of our proposed path planner.
4.1. Simulation Setup
Simulations were implemented in a MATLAB + CarSim platform and executed on an Intel Core i9-9900 CPU with 32 GB RAM that runs at 3.10 2 GHz. We define a warehouse with eight infrared receivers that are evenly distributed along the four edges of the rectangular ceiling, the height of which is 5 m. The geometric size of each cargo is , wherein h is a random value ranging from 0 to 5 m. Other parametric settings are presented in our source codes, which are available at https://github.com/libai1943/OcclusionAwarePathPlanningForAGV (accessed on 8 December 2021).
4.2. On the Efficacy of the Proposed Planner
The planning results of two typical simulation cases are depicted in Figure 8, which shows the efficiency of each layer. In each of the two cases, the finally derived path is collision free and kinematically feasible. Both properties can be reflected by the footprints and curvature profiles plotted in Figure 9.
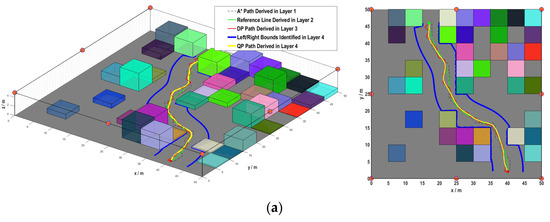
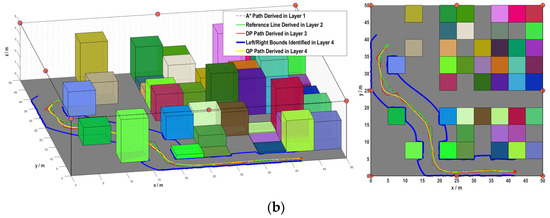
Figure 8.
Path planning results of typical simulation cases in side view and bird-eye view: (a) Case 1; (b) Case 2 (zoom in to see more clearly).
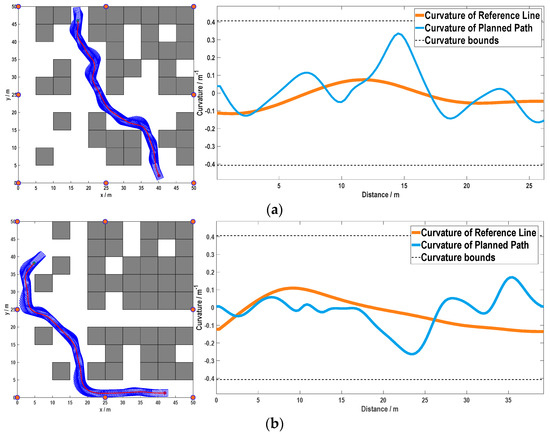
Figure 9.
Path planning performance, w.r.t. collision avoidance, and kinematic feasibility: (a) Case 1; (b) Case 2.
4.3. On the Occlusion Awareness of the Proposed Planner
This subsection investigates the occlusion awareness of the paths planned by the proposed method. Figure 10 shows the results with/without the positioning-related cost Jpositioning in layer three. When the cost term Jpositioning is discarded, the rate of good positioning distance along the entire path is 86.5% and 92.5% in the aforementioned two typical simulation cases, respectively. By contrast, with the cost term included, the rate grows to 97.0% and 96.5%. This comparative result clearly shows that our proposed planner can efficiently reduce the positioning inaccuracy caused by occlusions.
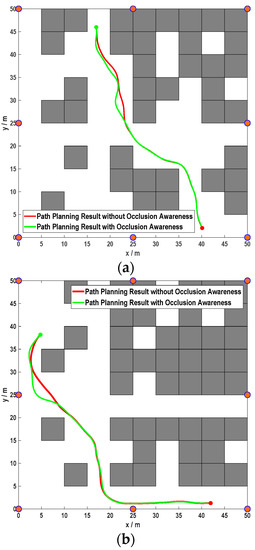
Figure 10.
Comparative path planning results, w.r.t. occlusion awareness: (a) Case 1; (b) Case 2.
4.4. On the Closed-Loop Tractability of the Proposed Planner
This subsection reports the closed-loop tracking performance in CarSim when following the open-loop paths planned by the proposed planner (Figure 11). A linear quadratic regulator (LQR) is adopted as the controller. As illustrated in Figure 12, the open-loop and closed-loop paths do not differ much, which indicates that the planned paths are sufficiently smooth and thus easy to track. The concrete closed-loop tracking simulation results are presented in the following video link: https://www.bilibili.com/video/av677126688 (accessed on 8 December 2021).
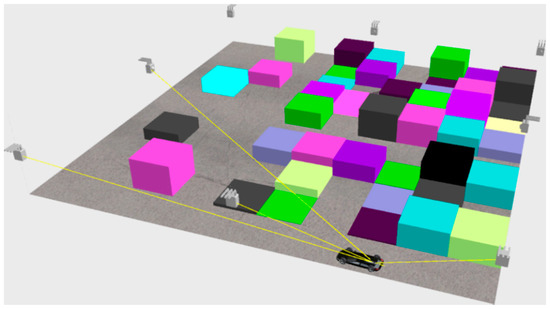
Figure 11.
CarSim simulation scenario layout and screenshot of simulation process.
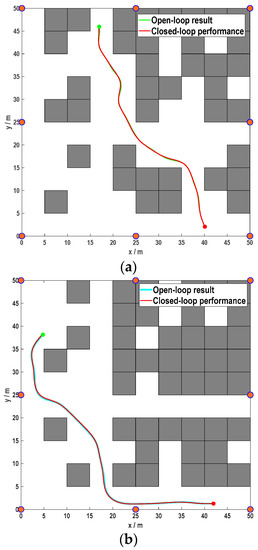
Figure 12.
Path planning results, w.r.t. tractability: (a) Case 1; (b) Case 2.
5. Conclusions
This paper has introduced a path planning method for an autonomous vehicle in a warehouse, wherein the cargoes may occlude the inflated signals emitted by the ego vehicle for inflated positioning. According to our conducted simulations, the proposed planner is efficient according to its w.r.t. collision avoidance, kinematic feasibility, occlusion awareness, and tractability.
Author Contributions
Conceptualization, B.L. and Y.Z.; methodology, B.L.; validation, S.T. and X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Fundamental Research Funds for the Central Universities of China, grant number 531118010509, National Natural Science Foundation of China, grant number 62103139, and Natural Science Foundation of Hunan Province, China, grant number 2021JJ40114.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jia, S.; Ma, L.; Yang, S.; Qin, D. Semantic and context-based image retrieval method using a single image sensor for visual indoor positioning. IEEE Sens. J. 2021, 21, 18020–18032. [Google Scholar] [CrossRef]
- Cengiz, K. Comprehensive analysis on least-squares lateration for indoor positioning systems. IEEE Internet Things J. 2021, 8, 2842–2856. [Google Scholar] [CrossRef]
- Lin, P.T.; Liao, C.; Liang, S. Probabilistic indoor positioning and navigation (PIPN) of autonomous ground vehicle (AGV) based on wireless measurements. IEEE Access 2021, 9, 25200–25207. [Google Scholar] [CrossRef]
- Seo, H.; Kim, H.; Kim, H.; Hong, D. Accurate positioning using beamforming. In Proceedings of the 2021 IEEE 18th Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2021; pp. 1–4. [Google Scholar]
- Chavez-Burbano, P.; Guerra, V.; Rabadan, J.; Perez-Jimenez, R. Optical camera communication system for three-dimensional indoor localization. Optik 2019, 192, 162870. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, B.; Huang, F.; Chen, Y.; Zhang, S.; Cheng, Y. Corners positioning for binocular ultra-wide angle long-wave infrared camera calibration. Optik 2020, 206, 163441. [Google Scholar] [CrossRef]
- Aparicio-Esteve, E.; Hernández, Á.; Ureña, J. Design, calibration and evaluation of a long-range 3D infrared positioning system based on encoding techniques. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Yao, W.; Ma, L. Research and application of indoor positioning method based on fixed infrared beacon. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 5375–5379. [Google Scholar]
- Martínez-Barberá, H.; Herrero-Pérez, D. Autonomous navigation of an automated guided vehicle in industrial environments. Robot. Comput.-Integr. Manuf. 2010, 26, 296–311. [Google Scholar] [CrossRef]
- Khedkar, A.; Kajani, K.; Ipkal, P.; Banthia, S.; Jagdale, B.N.; Kulkarni, M. Automated Guided Vehicle System with Collision Avoidance and Navigation in Warehouse Environments. Sensors 2020, 7, 5442–5448. [Google Scholar]
- Li, B.; Li, L.; Acarman, T.; Shao, Z.; Yue, M. Optimization-based maneuver planning for a tractor-trailer vehicle in a curvy tunnel: A weak reliance on sampling and search. IEEE Robot. Autom. Lett. 2021. accepted. [Google Scholar] [CrossRef]
- Cao, H.; Zhao, S.; Song, X.; Li, M. Toward high automatic driving by a dynamic optimal trajectory planning method based on high-order polynomials. SAE Tech. Pap. 2020, 1, 1–10. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Cao, D.; He, Z.; Zhu, Q. Real-time trajectory planning for autonomous urban driving: Framework, algorithms, and verifications. IEEE/ASME Trans. Mechatron. 2016, 21, 740–753. [Google Scholar] [CrossRef]
- Cao, H.; Zhao, S.; Song, X.; Bao, S.; Li, M.; Huang, Z.; Hu, C. An optimal hierarchical framework of the trajectory following by convex optimisation for highly automated driving vehicles. Veh. Syst. Dyn. 2019, 57, 1287–1317. [Google Scholar] [CrossRef]
- Jian, Z.; Chen, S.; Zhang, S.; Chen, Y.; Zheng, N. Multi-model-based local path planning methodology for autonomous driving: An integrated framework. IEEE Trans. Intell. Transp. Syst. 2020. accepted. [Google Scholar] [CrossRef]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Path planning for autonomous vehicles in unknown semi-structured environments. Int. J. Robot. Res. 2010, 29, 485–501. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Cao, D.; Liu, D.; He, H. Development of a new integrated local trajectory planning and tracking control framework for autonomous ground vehicles. Mech. Syst. Signal Process. 2017, 87, 118–137. [Google Scholar] [CrossRef]
- Kuwata, Y.; Teo, J.; Fiore, G.; Karaman, S.; Frazzoli, E.; How, J.P. Real-time motion planning with applications to autonomous urban driving. IEEE Trans. Control Syst. Technol. 2009, 17, 1105–1118. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Cheng, W.; Cui, X.; Su, B. Toward efficient trajectory planning based on deterministic sampling and optimization. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 1318–1323. [Google Scholar]
- Fan, H.; Zhu, F.; Liu, C.; Zhang, L.; Zhuang, L.; Li, D.; Zhu, W.; Hu, J.; Li, H.; Kong, Q. Baidu Apollo EM motion planner. arXiv 2018, arXiv:1807.08048. [Google Scholar]
- Ajanovic, Z.; Lacevic, B.; Shyrokau, B.; Stolz, M.; Horn, M. Search-based optimal motion planning for automated driving. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4523–4530. [Google Scholar]
- Ma, L.; Xue, J.; Kawabata, K.; Zhu, J.; Ma, C.; Zheng, N. Efficient sampling-based motion planning for on-road autonomous driving. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1961–1976. [Google Scholar] [CrossRef]
- Li, B.; Kong, Q.; Zhang, Y.; Shao, Z.; Wang, Y.; Peng, X.; Yan, D. On-road trajectory planning with spatio-temporal RRT* and always-feasible quadratic program. In Proceedings of the 2020 16th IEEE International Conference on Automation Science and Engineering (CASE), Hongkong, China, 20–21 August 2020; pp. 943–948. [Google Scholar]
- Tian, F.; Zhou, R.; Li, Z.; Li, L.; Gao, Y.; Cao, D.; Chen, L. Trajectory planning for autonomous mining trucks considering terrain constraints. IEEE Trans. Intell. Veh. 2021, 6, 772–786. [Google Scholar] [CrossRef]
- Lim, W.; Lee, S.; Sunwoo, M.; Jo, K. Hierarchical trajectory planning of an autonomous car based on the integration of a sampling and an optimization method. IEEE Trans. Intell. Transp. Syst. 2018, 19, 613–626. [Google Scholar] [CrossRef]
- Chen, J.; Liu, C.; Tomizuka, M. FOAD: Fast optimization-based autonomous driving motion planner. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 4725–4732. [Google Scholar]
- Li, B.; Zhang, Y. Fast trajectory planning in Cartesian rather than Frenet frame: A precise solution for autonomous driving in complex urban scenarios. IFAC-PapersOnLine 2020, 53, 17065–17070. [Google Scholar] [CrossRef]
- Chen, J.; Zhan, W.; Tomizuka, M. Autonomous driving motion planning with constrained iterative LQR. IEEE Trans. Intell. Veh. 2019, 4, 244–254. [Google Scholar] [CrossRef]
- Luo, S.; Li, X.; Sun, Z. An optimization-based motion planning method for autonomous driving vehicle. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 739–744. [Google Scholar]
- Ziegler, J.; Bender, P.; Dang, T.; Stiller, C. Trajectory planning for Bertha—A local, continuous method. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium (IV), Dearborn, MI, USA, 8–11 June 2014; pp. 450–457. [Google Scholar]
- Eiras, F.; Hawasly, M.; Albrecht, S.; Ramamoorthy, S. A two-stage optimization-based motion planner for safe urban driving. IEEE Trans. Robot. 2021. accepted. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Waslander, S.; Gong, J.; Xiong, G.; Yang, T.; Liu, K. Hybrid trajectory planning for autonomous driving in highly constrained environments. IEEE Access 2018, 6, 32800–32819. [Google Scholar] [CrossRef]
- Lim, W.; Lee, S.; Sunwoo, M.; Jo, K. Hybrid trajectory planning for autonomous driving in on-road dynamic scenarios. IEEE Trans. Intell. Transp. Syst. 2021, 22, 341–355. [Google Scholar] [CrossRef]
- Hegedüs, F.; Bécsi, T.; Aradi, S.; Gáldi, G. Hybrid trajectory planning for autonomous vehicles using neural networks. In Proceedings of the 2018 IEEE 18th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 21–22 November 2018; pp. 25–30. [Google Scholar]
- Acerbo, F.; Auweraer, H.; Son, T. Safe and computational efficient imitation learning for autonomous vehicle driving. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 647–652. [Google Scholar]
- Marchesini, E.; Farinelli, A. Discrete deep reinforcement learning for mapless navigation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 10688–10694. [Google Scholar]
- Chen, L.; Hu, X.; Tang, B.; Cheng, Y. Conditional DQN-based motion planning with fuzzy logic for autonomous driving. IEEE Trans. Intell. Transp. Syst. 2020. accepted. [Google Scholar] [CrossRef]
- Jaritz, M.; Charette, R.; Toromanoff, M.; Perot, E.; Nashashibi, R. End-to-end race driving with deep reinforcement learning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 2070–2075. [Google Scholar]
- Li, B. Occlusion-aware on-road autonomous driving: A trajectory planning method considering occlusions of Lidars. Optik 2021, 243, 167347. [Google Scholar] [CrossRef]
- Li, B.; Acarman, T.; Zhang, Y.; Kong, Q. Occlusion-aware on-road autonomous driving: A path planning method in combination with honking decision making. In Proceedings of the 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 7403–7408. [Google Scholar]
- Manzinger, S.; Pek, C.; Althoff, M. Using reachable sets for trajectory planning of automated vehicles. IEEE Trans. Intell. Veh. 2021, 6, 232–248. [Google Scholar] [CrossRef]
- Chen, J.; Li, S.; Tomizuka, M. Interpretable end-to-end urban autonomous driving with latent deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2020. accepted. [Google Scholar] [CrossRef]
- Werling, M.; Ziegler, J.; Kammel, S.; Thrun, S. Optimal trajectory generation for dynamic street scenarios in a Frenet frame. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 987–993. [Google Scholar]
- Li, B.; Ouyang, Y.; Li, L.; Zhang, Y. Autonomous driving on curvy roads without reliance on Frenet frame: A cartesian-based trajectory planning method. IEEE Trans. Intell. Transp. Syst. 2021. under review. [Google Scholar]
- Li, B.; Acarman, T.; Zhang, Y.; Ouyang, Y.; Yaman, C.; Kong, Q.; Zhong, X.; Peng, X. Optimization-based trajectory planning for autonomous parking with irregularly placed obstacles: A lightweight iterative framework. IEEE Trans. Intell. Transp. Syst. 2021. accepted. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Li, B.; Shao, Z. A unified motion planning method for parking an autonomous vehicle in the presence of irregularly placed obstacles. Knowl.-Based Syst. 2015, 86, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Shao, Z. Simultaneous dynamic optimization: A trajectory planning method for nonholonomic car-like robots. Adv. Eng. Softw. 2015, 87, 30–42. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Xu, W.; Pan, J.; Wei, J.; Dolan, J.M. Motion planning under uncertainty for on-road autonomous driving. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2507–2512. [Google Scholar]
- Stellato, B.; Banjac, G.; Goulart, P.; Bemporad, A.; Boyd, S. OSQP: An operator splitting solver for quadratic programs. Math. Program. Comput. 2020, 12, 637–672. [Google Scholar] [CrossRef] [Green Version]
- Ferreau, H.J.; Kirches, C.; Potschka, A.; Bock, H.G.; Diehl, M. qpOASES: A parametric active-set algorithm for quadratic programming. Math. Program. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).